Algorithm unfolding for block-sparse and MMV problems with reduced training overhead

In this study, we consider algorithm unfolding for the multiple measurement vector (MMV) problem in the case where only few training samples are available. Algorithm unfolding has been shown to empirically speed-up in a data-driven way the convergence of various classical iterative algorithms, but for supervised learning, it is important to achieve this with minimal training data. For this, we consider learned block iterative shrinkage thresholding algorithm (LBISTA) under different training strategies. To approach almost data-free optimization at minimal training overhead, the number of trainable parameters for algorithm unfolding has to be substantially reduced. We therefore explicitly propose a reduced-size network architecture based on the Kronecker structure imposed by the MMV observation model and present the corresponding theory in this context. To ensure proper generalization, we then extend the analytic weight approach by Liu and Chen to LBISTA and the MMV setting. Rigorous theoretical guarantees and convergence results are stated for this case. We show that the network weights can be computed by solving an explicit equation at the reduced MMV dimensions which also admits a closed-form solution. Toward more practical problems, we then considered convolutional observation models and show that the proposed architecture and the analytical weight computation can be further simplified and thus open new directions for convolutional neural networks. Finally, we evaluate the unfolded algorithms in numerical experiments and discuss connections to other sparse recovering algorithms.

1 Introduction

This study connects the multiple measurement vector (MMV) problem, block- or joint-sparsity and recent results of deep unfolding of the iterative shrinkage thresholding algorithm (ISTA) to reconstruct unknown joint-sparse vectors from given linear observations. Such vectors could be, for example, signals received at the different antennas in a wireless communication problem or, in a computational imaging setup, discrete images observed at different detectors or aggregation stages. Compressed sensing is a way to reconstruct compressive measurements from their underdetermined systems and first theoretical breakthroughs were achieved by Candés et al. [1] and Donoho [2], leading to an approach where fewer samples can be used, than stated within the Nyquist–Shannon sampling theorem [3]. They were able to show that unknown vectors can be reconstructed using convex optimization if the linear mapping fulfilled certain assumptions [1, 4]. These idea rely on minimizing ℓ₁-norm to promote sparsity and the approach of basis pursuit [5]. These convex optimization problems could then be solved with iterative algorithms, in Figueiredo et al. [6] gradient projection approaches are presented and in Fornasier and Rauhut [7] the idea of thresholding algorithms, which will be also discussed in this study. Although this is already a well researched field, in practice leading to high computational effort because of many iterations and large underlying systems and is thus not suitable for real-world applications. Thus, Karol Gregor and Yann LeCun proposed to use the iterative structure of these algorithms for a neural network and to train each iteration step [8], which is also referred to as deep unfolding and will be discussed in Section 2. Convergence for deep unfolding of the iterative thresholding algorithm has also been studied by Chen et al. [9]. Liu and Chen [10] proposed in to exclude the weight matrix from the data-driven optimization approach and pre-compute this by data-free optimization and thus presented Analytical LISTA (ALISTA). In recent results, Chen et al. could reduce the training procedure even more, by showing that only tuning three hyperparameters is sufficient, proposing HyperLISTA [11]. Creating large sets of training data is often difficult in practice, and thus, it is important to reduce the trainable parameters. Therefore, we will extend the already stated concepts for the block-sparse setting and especially for the multiple measurement vector problem, developing suitable learned algorithms, with only a few trainable parameters and similar theoretical guarantees as ALISTA.

1.1 Multiple measurement vector problems

Multiple measurement vector (MMV) problems occur in many applications, for example, in tomography [12], communication [13], blurred image reconstruction, or superresolution [14]. In the following, we derive the connection to block-sparsity. In an MMV problem, we assume that we derived d ∈ ℕ measurements y^l ∈ ℝ^m, l = 1, …, d from d sparse signal vectors x^l ∈ ℝⁿ sharing the same support $supp\left(x^l\right)=\left\{i:\left|x_i^l\right|\ne 0\right\}$, which is referred to as joint-sparsity [15, 16]. The MMV problem can then be presented as solving the following d equations

$\begin{array}{ll}{y}^l=K{x}^l+\widetilde{ϵ}& (1)\end{array}$

for l = 1, …, d and with K ∈ ℝ^m×n. This can be rewritten in the following matrix equation form

$\begin{array}{ll}Y=KX+Ẽ,& (2)\end{array}$

where X = (x¹, …, x^d) ∈ ℝ^n×d, Y = (y¹, …, y^d) ∈ ℝ^m×d. With the vectorizing operator vec(·), stacking each column of a matrix on each other, we can cast Equation (2) into a block-sparse problem. We have

$\begin{array}{c}Y=KX\\ \iff Y^T=X^T{K}^T\\ \iff \text{vec}\left(Y^T\right)=\left(K\otimes I_d\right)\text{vec}\left(X^T\right),\end{array}$

where we used the well-known vectorization property of matrix equations, see for example Schacke [17]. Here, ⊗ is the Kronecker product. The vector x = vec(X^T) is block-sparse with n blocks of length d, if the signals x^l are jointly sparse. With $D=\left(K\otimes I_d\right)\in {ℝ}^{n_y\times n_x}$, where n_y = m · d and n_x = n · d, we obtain the block-sparse setting considered in this work.

1.2 Block sparsity

In the more general setting, we want to reconstruct an unknown vector $x\in {ℝ}^{n_x}$ from a given matrix $D\in {ℝ}^{n_y\times n_x}$ and given $y\in {ℝ}^{n_y}$

$\begin{array}{ll}y=Dx+ϵ,& (3)\end{array}$

with n_x = nd, n_y = md for some n, m, d ∈ ℕ. We assume that noise $ϵ\in {ℝ}^{n_y}$ is added to Dx. In applications, we often have this problem is ill-posed, i.e., n_y < n_x or D is not invertible. We assume that x is the concatenation of n “smaller” vectors of length d, called blocks, i.e., x[i] ∈ ℝ^d,

$\begin{array}{ll}{x}^T={[{\displaystyle \underset{=x[1]}{{\displaystyle \underbrace{x_1\dots x_d}}}}{\displaystyle \underset{=x\left[2\right]}{{\displaystyle \underbrace{x_{d+1}\dots x_{2d}}}}}\dots {\displaystyle \underset{=x\left[n\right]}{{\displaystyle \underbrace{x_{n_x-d+1}\dots x_{n_x}}}}}]}^T.& (4)\end{array}$

Following the notation in Yonina and Eldar [18], we define

$\begin{array}{l}\Vert x{\Vert }_{2,0}={\displaystyle \sum _{i=1}^n}I\left(\Vert x\left[i\right]{\Vert }_2>0\right),\end{array}$

where I(‖x[i]‖₂ > 0) = 1 if ‖x[i]‖₂ > 0 and equal to zero otherwise and the ℓ₂-norm is defined as $\Vert x{\Vert }_2^2=\sum _{i=1}^n|x_i{|}^2$. We call $x\in {ℝ}^{n_x}$ s-block-sparse if ‖x‖_2,0 ≤ s. Similar to Equation (4), we can construct the matrix D in Equation (3) from n “smaller” matrices $D\left[i\right]\in {ℝ}^{n_y\times d}$, i = 1, …, n

$\begin{array}{l}D=\left(D\left[1\right]D\left[2\right]\dots D\left[n\right]\right).\end{array}$

Without loss of generality, we can assume that these blocks are orthonormal, see Yonina and Eldar [18], i.e., $D{\left[i\right]}^{T}D\left[i\right]=I_d$, where I_d is the d × d identity matrix. This assumption simplifies the presentation of several statements below.

Definition 1. The block-coherence of a matrix $D\in {ℝ}^{n_y\times n_x}$ is defined as

$\begin{array}{ll}{\mu }_b\left(D\right)={\displaystyle \underset{i\ne j}{max}}\frac{1}{d}\Vert D{\left[i\right]}^{T}D\left[j\right]{\Vert }_2.& (5)\end{array}$

Here, we use $\Vert A{\Vert }_2=\sqrt{{\lambda }_{max}\left(A^{T}A\right)}$, where λ_max denotes the largest eigenvalue of matrix A^TA. Note that the block coherence can also be introduced with a normalization factor 1/(‖D[i]‖₂‖D[j]‖₂), but since we assume orthonormal blocks, we can neglect this. This reduces to the already known coherence μ for d = 1

$\begin{array}{l}\mu \left(D\right)={\displaystyle \underset{i\ne j}{max}}\left|D_{:,i}^T{D}_{:,j}\right|,\end{array}$

where D_{:, i} denotes the ith column of D, see Donoho et al. [19]. In Yonina and Eldar [18], it is shown that 0 ≤ μ_b(D) ≤ μ(D) ≤ 1, and it is possible to derive recovery statements for small μ_b similar to μ, for details see Yonina and Eldar [18]. We can consider also the cross block coherence, which compares two matrices and will be important in the following.

Definition 2. For $B,D\in {ℝ}^{n_y\times n_x}$ with $B{\left[i\right]}^{T}D\left[i\right]=I_d$ the cross block coherence is defined as

$\begin{array}{ll}{\mu }_b\left(B,D\right)={\displaystyle \underset{i\ne j}{max}}\frac{1}{d}\Vert B{\left[i\right]}^{T}D\left[j\right]{\Vert }_2.& (6)\end{array}$

Similar to ordinary basis pursuit and LASSO [5, 20–22], we use the following ℓ_2,1-LASSO to solve Equation (3)

$\begin{array}{ll}{\displaystyle \underset{x\in {ℝ}^{n_x}}{min}}\frac{1}{2}\Vert Dx-y{\Vert }_2^2+\alpha \Vert x{\Vert }_{2,1}& (7)\end{array}$

where $\Vert x{\Vert }_{2,1}=\sum _{i=1}^n\Vert x\left[i\right]{\Vert }_2$ is the ℓ_2,1-norm of x, which will promote block-sparsity for the solution of Equation (7). This convex programm can be solved by the fixed point iteration known as the block iterative shrinkage thresholding algroithm (Block-ISTA/BISTA):

$\begin{array}{ll}{x}^{\left(k\right)}={\eta }_{\alpha \gamma }\left(x^{\left(k-1\right)}-\gamma \left[D^T\left(D{x}^{\left(k-1\right)}-y\right)\right]\right),& (8)\end{array}$

where η_α is the block-soft-thresholding operator, given as

$\begin{array}{ll}{\eta }_{\alpha }\left(x\right)\left[i\right]=max\left\{0,1-\frac{\alpha }{\Vert x\left[i\right]{\Vert }_2}\right\}x\left[i\right].& (9)\end{array}$

BISTA is an already well-studied proximal gradient algorithm based on the functional in Equation (7). It is known that the fixed point iteration in Equation (8) converges for $\gamma \in \left(0,\frac{1}{L}\right)$, where $L=\Vert D{\Vert }_2^2$ is the Lipschitz constant of the least squares term in Equation (7) w.r.t to x, to a solution of Equation (7), if at least one solution exists, see for example Byrne [23], Bauschke et al. [24], and Beck [25]. On the other hand, the choice of the regularization parameter α has to be done empirically and is very crucial for a “good” recovery. If α is set too large, this can lead to too much damping, possibly setting blocks to 0 that actually have a non-zero norm. If α is too small, we get reverse effects. In practice, this leads to problems since computing the iterations require high computational effort. Deep unfolding is a way to tackle these problems, i.e., reduce the number of iterations by learning optimal regularization parameters and step-sizes. There are already classical concepts in increasing the convergence speed by using an additional step in updating the current iterate x^(k), by using the previous x^(k−1), resulting in Block Fast ISTA [25, 26]. On the other hand, the choice of optimal parameters is still solved empirically.

2 Deep unfolding and learned BISTA

Recently, the idea of deep unfolding has been developed, where the goal is to optimize these parameters of such an iterative algorithm [8, 10, 27]. This in turn gives us an iterative algorithm with optimal chosen step-size γ and regularization parameters, but we will see that we do not have to restrict our self only to those parameters. Recently, Fu et al. proposed Ada-BlockLISTA by applying deep unfolding to block-sparse recovery [28]. They show an increase in the convergence speed with numerical examples but do not cover theoretical studies.

In the following, we are going to present the idea of deep unfolding, then we are going to derive Learned BISTA (LBISTA).

2.1 Deep unfolding

We will now formalize the concept of deep unfolding for an arbitrary operator that depends on a certain set of parameters, before we apply this to the previously presented fixed point iteration. To this end, we define an operator

$\begin{array}{ll}T\left(·;\theta ,y\right):X\to X& (10)\end{array}$

which depends on a set of parameters θ ∈ Θ, such as the stepsize of a gradient descent operator and an input y. For example, for BISTA, this would be θ = (α, γ) with

$\begin{array}{l}T\left(x;\theta ,y\right)={\eta }_{\alpha \gamma }\left(x-\gamma \left[D^T\left(Dx-y\right)\right]\right).\end{array}$

We assume that Fix(T(·;θ, y)) ≠ ∅ and that we have convergence for the fixed point iteration

$\begin{array}{ll}{T}^k\left(x^{\left(0\right)};\theta ,y\right)=x^{\left(k\right)}& (11)\end{array}$

for an arbitrary x⁽⁰⁾ ∈ X. Deep unfolding now interprets each iteration step as the layer of a neural network and uses the parameters θ ∈ Θ as trainable variables. In more detail, this means we look at the Kth iteration of Equation (11), i.e., the composition

$\begin{array}{l}{\displaystyle \underset{K\text{times}}{{\displaystyle \underbrace{\left(T\circ \cdots \circ T\right)}}}}\left(x^{\left(0\right)};\theta ,y\right)=x^{\left(K\right)}\end{array}$

for some K ∈ ℕ. By unfolding this iterative scheme, we define

$\begin{array}{l}{T}_{{\theta }^{\left(k-1\right)}}\left(·;y\right):=T\left(·;{\theta }^{\left(k\right)},y\right)\end{array}$

for k = 1, …, K and set θ^(k) as the set of trainable variables in this operator, so they can vary in each iteration step. For example, in LBISTA, we will get θ^(k) = (α^(k), γ^(k)) in the later called tied case. With this we get the following composition

$\begin{array}{ll}\left(T_{{\theta }^{\left(K-1\right)}}\circ \cdots \circ T_{{\theta }^{\left(0\right)}}\right)\left(x^{\left(0\right)};y\right)=x^{\left(K\right)}.& (12)\end{array}$

and define the operator

$\begin{array}{ll}{\mathcal{T}}_{\tilde{\theta }}:=T_{{\theta }^{\left(K-1\right)}}\circ \cdots \circ T_{{\theta }^{\left(0\right)}},& (13)\end{array}$

where we get the full parameter space $\tilde{\Theta }=\Theta \times \cdots \times \Theta$, with trainable variables $\tilde{\theta }={\bigcup }_{i=1}^K{\theta }^{\left(i\right)}$. ${\mathcal{T}}_{\tilde{\Theta }}$ will then be the neural network which will be trained with respect to $\tilde{\theta }$. So in the end, after training, we have an iterative algorithm with fixed but optimized parameters. It seems thus that deep unfolding can be applied to any iterative algorithm and help us to estimate the best choice of parameters, but we will only present deep unfolding for BISTA and consider deep unfolding for arbitrary operators in future studies.

2.2 Learning

In this section, we give an overview for the training procedure used in this study. The general idea of supervised learning is to choose model parameters such that the predictions are close, in some sense, to the unknown target, i.e., in our case, the unknown vector x in Equation (3) generating the measurement y. Hence, we aim to minimize an expected loss over an unknown distribution $\mathcal{D}$:

$\begin{array}{ll}{\displaystyle \underset{\theta }{min}}\left[R\left(\theta \right):={𝔼}_{x^{*}\text{˜}\mathcal{D}}\left[\ell \left(\widehat{x}-x^{*}\right)\right]\right]& (14)\end{array}$

where ℓ(·) is a given loss function, $\widehat{x}={\mathcal{T}}_{\tilde{\theta }}\left(x^{\left(0\right)};y\right)$ is the output of the model, and x^* is the ground-truth. Here, we will use the squared ℓ₂-loss $\ell \left(x\right)=\frac{1}{2}\Vert x{\Vert }_2^2$. The objective functional $R\left(\theta \right)={𝔼}_{x^{*}\mathrm{\text{˜}}\mathcal{D}}\left[\ell \left(\widehat{x}-x^{*}\right)\right]$ is also called risk of the model. Since the underlying distribution $\mathcal{D}$ is unknown, we take a batch of S independently drawn samples of input and output data $\left(x_j^{*},y_j\right)$ for j = 1, …, n_train according to Equation (3) and minimize instead data-driven the empirical risk

$\begin{array}{ll}{R}_S\left(\theta \right)=\frac{1}{n_{train}}{\displaystyle \sum _{j=1}^{n_{train}}}\ell \left({\widehat{x}}_j-x_j^{*}\right).& (15)\end{array}$

Proceeding in this way for all layer at once is sometimes referred as end-to-end learning. Because of the special structure of our deep unfolding models, and inspired by Musa et al. [29], we instead train the network layer-wise, by optimizing only ${\theta }_{case}^{\left(k-1\right)}$ for layer k yielding the following training procedure: Let k ∈ {1, …, K},

$\begin{array}{l}{\displaystyle \underset{{\theta }_{case}^{\left(k-1\right)}}{min}}{𝔼}_{x^{*}~\mathcal{D}}\left[\ell \left({\widehat{x}}^{\left(k\right)}-x^{*}\right)\right],\end{array}$

where ${\widehat{x}}^{\left(k\right)}$ is the output of the kth layer. We realized this training as follows, we generate a validation set $\left(x_{i,\mathrm{\text{validation}}}^{*},y_{i,\mathrm{\text{validation}}}\right)$, used to evaluate the model while training and a training set $\left(x_{i,\mathrm{\text{train}}}^{*},y_{i,\mathrm{\text{train}}}\right)$, i = 1, …, n_train, used to calculate (15). This objective is locally minimized by gradient descent methods. As a stopping criteria, we evaluate the normalized mean square error, defined as

$\begin{array}{l}NMSE\left(x,{\widehat{x}}^{\left(k\right)}\right)=\frac{\Vert {\widehat{x}}^{\left(k\right)}-x^{*}{\Vert }_2^2}{\Vert x^{*}{\Vert }_2^2},\end{array}$

depending on the validation set, and stop if the maximum of all evaluated NMSE stays the same for a given number of iterations. See Algorithm 1, where Adam is the ADAM Optimizer [30] depending on an training rate t_r and the functional which should be minimized with respect to given variables, here the loss function ℓ(·) with respect to θ^k−1.

ALGORITHM 1

Algorithm 1. Training.

2.3 Learned BISTA

In the following, we present four different unfolding techniques for BISTA. We present a tied (weights are shared between different layers) and untied (individual weights per layer) case, which refers to different training approaches

$\begin{array}{l}S=I-B^{T}D\\ B=\gamma D.\end{array}$

Tied LBISTA: The idea of LBISTA is now to fix the matrices S and B for all layers but also include them in our set of trainable variables:

$\begin{array}{ll}{x}^{\left(k\right)}={\eta }_{{\alpha }^{\left(k-1\right)}}\left(S{x}^{\left(k-1\right)}+B^{T}y\right).& (16)\end{array}$

For LBISTA (Equation 16), we get trainable variables

$\begin{array}{l}\theta =\left({\left({\alpha }^{\left(k\right)}\right)}_{k=0}^{K-1},S,B\right),\end{array}$

where we initialize S = I − B^TD and B = γD. Algorithm (16) is also referred to as vanilla LISTA in the sparse case. Inspired by the LISTA-CP model, i.e., LISTA with coupled parameters, proposed in Liu and Chen [10], we will also consider LBISTA-CP

$\begin{array}{ll}{x}^{\left(k\right)}={\eta }_{{\alpha }^{\left(k-1\right)}}\left(x^{\left(k-1\right)}-{\gamma }^{\left(k-1\right)}{B}^T\left(D{x}^{\left(k-1\right)}-y\right)\right).& (17)\end{array}$

For LBISTA-CP (Equation 17), we get

$\begin{array}{l}\theta =\left({\left({\alpha }^{\left(k\right)}\right)}_{k=0}^{K-1},{\left({\gamma }^{\left(k\right)}\right)}_{k=0}^{K-1},B\right),\end{array}$

where we initialize B = D.

Untied LBISTA: The idea of untied LBISTA is then to use in each layer different matrices S and B to train, i.e.,

$\begin{array}{ll}{x}^{\left(k\right)}={\eta }_{{\alpha }^{\left(k-1\right)}}\left(S^{\left(k-1\right)}{x}^{\left(k-1\right)}+{\left(B^{\left(k-1\right)}\right)}^{T}y\right).& (18)\end{array}$

For LBISTA (untied) Equation (18), we get trainable variables

$\begin{array}{l}\theta =\left({\left({\alpha }^{\left(k\right)}\right)}_{k=0}^{K-1},{\left(S^{\left(k\right)}\right)}_{k=0}^{K-1},{\left(B^{\left(k\right)}\right)}_{k=0}^{K-1}\right),\end{array}$

where we initialize S^(k) = I − B^TD and B^(k) = γD for every k = 0, …, K − 1. Inspired by Algorithm (17), we will also consider Algorithm (19), which will be referred to as LBISTA-CP (untied), [9, 10]:

$\begin{array}{ll}{x}^{\left(k\right)}={\eta }_{{\alpha }^{\left(k-1\right)}}\left(x^{\left(k-1\right)}-{\gamma }^{\left(k-1\right)}{\left(B^{\left(k-1\right)}\right)}^T\left(D{x}^{\left(k-1\right)}-y\right)\right).& (19)\end{array}$

For LBISTA-CP (untied) (Equation 19), we get

$\begin{array}{l}\theta =\left({\left({\alpha }^{\left(k\right)}\right)}_{k=0}^{K-1},{\left(B^{\left(k\right)}\right)}_{k=0}^{K-1}\right),\end{array}$

where we initialize B^(k) = D for every k = 0, …, K − 1. Hence, compared to $\mathcal{O}\left(n_y{n}_x+K\right)$ parameters in the tied case, now more training data and longer training time is required to train now $\mathcal{O}\left(K{n}_y{n}_x+K\right)$ parameters.

We initialize the trainable variables with values from original BISTA. In Chen et al. [9], it has been shown that convergence of LISTA-CP (untied) can be guaranteed if the matrices B^(k) belong to a certain set and their proof can be extended to block-sparsity. The steps are very similar to the convergence proof for learned block analytical ISTA given in the next section.

3 Analytical LBISTA

In the previous section, we presented several approaches for learned BISTA where optimal weights are optimized in a data-driven fashion. In Liu and Chen [10] instead proposed to analytically pre-compute the weights and only train step-size and threshold parameters. It turns out that this Analytic LISTA (ALISTA) with the so called analytical weight matrix is as good as the learned weights. In the following, we are going to extend and improving the theoretical statements for ALISTA to the block-sparse case and propose analytical LBISTA. In contrast to Liu and Chen [10], we will provide a direct solution and also show different ways to calculate the analytical weight matrix in different settings.

3.1 Upper and lower bound

This part of the study will focus on combining and extending several theoretical statements from Chen et al. [9] and Liu and Chen [10] and applying these for the block-sparse case. With the following two theorems, we are then going to present analytical LBISTA, by showing that this is as good as LBISTA-CP (untied) with a pre-computed B.

3.1.1 Upper bound

In this section, we start with an upper bound for the error of the approximation generated by Equation (19), i.e., LBISTA-CP (untied), and the exact solution x^* for given parameters. For this, we modify Assumption 1 from Liu and Chen [10] to be consistent with the block-sparse setting.

Assumption 1. We assume $\left(x,ϵ\right)\in {\mathcal{X}}_b\left(M,s,\sigma \right)$ with

$\begin{array}{l}\left(x,ϵ\right)\in {\mathcal{X}}_b\left(M,s,\sigma \right)\hfill \\ =\{x:\Vert x\left[i\right]{\Vert }_2\le M\forall i=1,\dots ,n,\Vert x{\Vert }_{2,0}\le s,\Vert ϵ{\Vert }_2\le \sigma \}.& (20)\end{array}$

As already mentioned, a matrix with small block-coherence has good recovery conditions. In Liu and Chen [10] proposed analytical LISTA, where the pre-computed matrix B is minimizing the mutual cross-coherence. This motivates the following definition.

Definition 3. With $D\in {ℝ}^{n_y\times n_x}$, we define the generalized mutual block-coherence

$\begin{array}{l}{\tilde{\mu }}_b\left(D\right)={\displaystyle \underset{{\displaystyle \underset{{\displaystyle \underset{\forall 1\le l\le n}{B^T\left[l\right]D\left[l\right]=I_d}}}{B\in {ℝ}^{n_y\times n_x}}}}{inf}}\left\{{\displaystyle \underset{{\displaystyle \underset{1\le i,j\le n}{i\ne j}}}{max}}\frac{1}{d}\Vert B^T\left[i\right]D\left[j\right]{\Vert }_2\right\}\\ ={\displaystyle \underset{{\displaystyle \underset{{\displaystyle \underset{\forall 1\le l\le n}{B^T\left[l\right]D\left[l\right]=I_d}}}{B\in {ℝ}^{n_y\times n_x}}}}{inf}}\{{\mu }_b\left(B,D\right)\}.& (21)\end{array}$

We define, analogously to Liu and Chen [10] with ${\mathcal{W}}_b\left(D\right)$ the set of all $B\in {ℝ}^{n_y\times n_x}$ which attain the infimum in Equation (21), i.e., ${\mathcal{W}}_b\left(D\right)=\left\{B\in {ℝ}^{n_y\times n_x}:{\mu }_b\left(B,D\right)={\tilde{\mu }}_b\left(D\right)\right\}$.

Note that the set ${\mathcal{W}}_b\left(D\right)$ is non-empty because the set of feasible matrices $\left\{B\in {ℝ}^{n_y\times n_x}:B^T\left[i\right]D\left[i\right]=I_d,1\le i\le n\right\}$ contains at least D because we assume $D^T\left[i\right]D\left[i\right]=I_d$, also $0\le {\tilde{\mu }}_b\left(D\right)\le {\mu }_b\left(D\right)$ and therefore, Equation (21) is a feasible and bounded program, see Supplementary material to [9]. We will call matrices from ${\mathcal{W}}_b\left(D\right)$ analytical weight matrices.

Definition 4. The block-support of a block-sparse-vector $x\in {\mathcal{X}}_B\left(b,s\right)$ is defined as

$\begin{array}{ll}{\text{supp}}_b\left(x\right)=\{i:\Vert x\left[i\right]{\Vert }_2\ne 0\forall i=1,\dots n\}.& (22)\end{array}$

We will now derive an upper bound for the ℓ₂-error and thus showing convergence of LBISTA-CP for a special matrix B and given parameters α^(k) and γ^(k). In [9], Liu et al. showed linear convergence for unfolded ISTA with additional noise, more precivesly for LISTA-CP (untied), if the matrices B^(k) belonged to a certain set. In Liu and Chen [10], it was shown that we can pre-compute such a matrix B, chose B^(k) = B, chosen by a data-free optimization problem and still have the same performance. For this, new proposed unfolded algorithm linear convergence was also shown, without additional noise. In Liu and Chen [10], convergence only in the noiseless case was shown, but the results derived in Chen et al. [9] were derived with bounded noise. Thus, we are going to combine these two proofs and extend it to block-sparsity:

For given (x, ϵ), y = Dx + ϵ and parameters ${\{{\theta }^{\left(k\right)}\}}_{k=1}^K$, we abbreviate with ${\{x^{\left(k\right)}\left(x,ϵ\right)\}}_{k=1}^K$ the sequence generated by (19) with x⁽⁰⁾ = 0. Further, we define

$\begin{array}{ll}\begin{array}{l}{C}_{\mathcal{X}}^{\left(k\right)}={\displaystyle \underset{\left(x,ϵ\right)\in {\mathcal{X}}_b\left(M,s,\sigma \right)}{sup}}\{\Vert x^{\left(k\right)}\left(x,ϵ\right)-x{\Vert }_{2,1}\}\\ C={\displaystyle \underset{k}{sup}}{\displaystyle \underset{j=1,...,n}{max}}|{\gamma }^{\left(k\right)}\Vert |B\left[j\right]{\Vert }_2\end{array}& (23)\end{array}$

Theorem 1. For any $B\in {\mathcal{W}}_b\left(D\right)$ and any sequence ${\gamma }^{\left(k\right)}\in \left(0,\frac{2}{\mu \left(2s-1\right)+1}\right)$ and parameters (B^(k): = B, α^(k), γ^(k)), for k ≤ K, with

$\begin{array}{ll}\frac{{\alpha }^{\left(k\right)}-C\sigma }{{\gamma }^{\left(k\right)}\mu \left(D\right)C_{\mathcal{X}}^{\left(k\right)}}\in \left[1,\kappa \right]& (24)\end{array}$

for some κ ≥ 1, with $\mu =d{\tilde{\mu }}_b\left(D\right)$. With M > 0 and s < (μ⁻¹ + 1)/2, we have

$\begin{array}{lll}{\text{supp}}_b& \left(x^{\left(k\right)}\left(x^{*}\right)\right)\subset {\text{supp}}_b\left(x^{*}\right)=:𝕊,& (25)\end{array}$

$\begin{array}{ll}\Vert x^{\left(k\right)}-x^{*}{\Vert }_2\le exp\left(-{\displaystyle \sum _{\tau =0}^{k-1}}ã\left(\tau \right)\right)sM& (26)\end{array}$

$\begin{array}{l}+C\sigma \left(1+{\displaystyle \sum _{\tau =0}^{k-1}}exp\left(-{\displaystyle \sum _{s=\tau }^{k-\tau }}ã\left(s\right)\right)\right).\end{array}$

where

$\begin{array}{l}ã\left(\tau \right)=-log\left({\gamma }^{\left(\tau \right)}\mu \left(\left(\kappa +1\right)s-1\right)+|1-{\gamma }^{\left(\tau \right)}|\right)\\ >0.\hfill \end{array}$

Note that in the noiseless case and with κ = 1, we obtain the results in Liu and Chen [10]. However, from the latter theorem, it follows that one can relax this condition to κ > 1. We also see from the proof of Theorem 1 that one needs at least ${\alpha }^{\left(k\right)}\ge d{\gamma }^{\left(k\right)}{\tilde{\mu }}_b\left(D\right)C_{\mathcal{X}}^{k\left(\right)}+C\sigma$ to have Equation (25). On the other hand, one can always find such a κ from the trained (and then fixed) parameters and thus use therefore the theorem afterward. Obviously, a worse α effects the upper bound of the ℓ₂-error and thus appears in ã(τ). Summarizing, above theorem shows now convergence on the training set even if κ ≠ 1.

3.1.2 Lower bound

This section states the lower bound for the ℓ_2,1-error, showing that for convergence in the ℓ_2,1-norm the defined parameters in Theorem 1 are optimally chosen. We now modify Assumption 2 from Liu and Chen [10] to be consistent with the block-sparse setting.

Assumption 2. x^* is sampled from P_X. P_X satisfies: 2 ≤ 𝕊 ≤ s and 𝕊 is uniformly distributed over the whole index set. The non-zero blocks of x^* satisfy the uniform distribution and ‖x[i]‖₂ ≤ M for all i ∈ 𝕊. And we assume, ϵ = 0.

The latter theorem states that the analytical weight matrix should minimize the generalized mutual block coherence. Therefore, for a lower bound, we will only consider matrices that are bounded away from the identity.

Definition 5. With $D\in {ℝ}^{n_y\times n_x}$, s ≤ 2, ${\bar{\sigma }}_{min}>0$ we set

$\begin{array}{lll}\bar{\mathcal{W}}& \left(D,s,{\bar{\sigma }}_{\text{min}}\right):=\{B\in {ℝ}^{n_y\times n_x}& (27)\end{array}$

$\begin{array}{l}:{\sigma }_{\text{min}}\left(I-{\left(B[(j\in S)]\right)}^{T}D[(j\in S)]\right)\ge {\overline{\sigma }}_{\min }\}.\end{array}$

The parameters are chosen from the following set.

Definition 6. Let ${\{x^{\left(k\right)}\}}_{k=1}^{\infty }$ be generated by $x^{\left(k+1\right)}={\eta }_{{\alpha }^{\left(k\right)}}\left(x^{\left(k\right)}-{\left(B^{\left(k\right)}\right)}^T\left(D{x}^{\left(k\right)}-y\right)\right)$ with parameters ${\{B^{\left(k\right)},{\alpha }^{\left(k\right)}\}}_{k=0}^{\infty }$ and x⁽⁰⁾ = 0. We define the set of all parameters guaranteeing no false positive blocks in x^(k) by

$\begin{array}{ll}\mathcal{T}=\{{\{B^{\left(k\right)}\in \bar{\mathcal{W}}\left(D,s,{\bar{\sigma }}_{\text{min}}\right),{\theta }^{\left(k\right)}\}}_{k=0}^{\infty }:& (28)\end{array}$

$\begin{array}{l}{\text{supp}}_B\left(x\right)\subset S,\forall x^{*}\in {\mathcal{X}}_b(M,s,0),\forall k\}.\end{array}$

This set is non-empty since Equation (25) holds true if α^(k) are chosen large enough. Following mainly the proof in Liu and Chen [10] by extending the setting from sparsity to block-sparsity, the lower bound for the ℓ_2,1-norm can be stated as follows.

Theorem 2. Let ${\{x^{\left(k\right)}\}}_{k=1}^{\infty }$ be generated by $x^{\left(k+1\right)}={\eta }_{{\alpha }^{\left(k\right)}}\left(x^{\left(k\right)}-{\left(B^{\left(k\right)}\right)}^T\left(D{x}^{\left(k\right)}-y\right)\right)$. Under Assumptions 2, ${\{W^{\left(k\right)}\in \bar{\mathcal{W}}\left(D,s,{\bar{\sigma }}_{\mathrm{\text{min}}}\right),{\theta }^{\left(k\right)}\}}_{k=0}^{\infty }\in \mathcal{T}$ and ϵ > 0, we have

$\begin{array}{ll}\Vert x^{\left(k\right)}-x^{*}{\Vert }_{2,1}\ge ϵ\Vert x^{*}{\Vert }_{2}exp\left(-ck\right),& (29)\end{array}$

with probability $1-ϵs^{\frac{3}{2}}-{ϵ}^2$ and $c=log3-log{\bar{\sigma }}_{min}$.

3.2 Analytical LBISTA

Analogously to Liu and Chen [10] and following the previous two theorems, decompose LBISTA-CP (untied), Algorithm 17, into two steps:

$\begin{array}{ll}{x}^{\left(k\right)}={\eta }_{{\alpha }^{\left(k-1\right)}}\left(x^{\left(k-1\right)}-{\gamma }^{\left(k-1\right)}{\tilde{B}}^T\left(D{x}^{\left(k-1\right)}-y\right)\right),& (30)\end{array}$

where, in the first step, $\tilde{B}$ is pre-computed, such that

$\begin{array}{l}{\mu }_b\left(\tilde{B},D\right)={\tilde{\mu }}_b\left(D\right).\end{array}$

In the second step, the parameters $\theta =\left({\left({\alpha }^{\left(k\right)}\right)}_{k=0}^{K-1},{\left({\gamma }^{\left(k\right)}\right)}_{k=0}^{K-1}\right)$ are trained layer wise, as discussed in the previous section. This results in a comparable method, with only $\mathcal{O}\left(K\right)$ trainable parameters, instead of $\mathcal{O}\left(n_y{n}_x+K\right)$ for LBISTA-CP (Equation 17) or even $\mathcal{O}\left(K{n}_y{n}_x+K\right)$ for LBISTA (untied) Equation 18.

4 Computing the analytical weight matrix

ALBISTA relies on the analytical weight matrix, deriving this matrix can be challenging in practice, thus this section focuses on computing this matrix. We follow the procedure in Liu and Chen [10] by estimating Equation (21) with an upper bound. But in addition to Liu and Chen [10], we state a closed form for the upper bound, and currently, this is done by a projected gradient descent approach.

4.1 Solving an upper bound

Since the objective in Equation (21) is not differentiable, one solves the following upper bound problem

$\begin{array}{ll}{\displaystyle \underset{B\in {ℝ}^{n_y\times n_x}}{min}}\frac{1}{d}\Vert B^{T}D{\Vert }_F^2& (31)\end{array}$

$\begin{array}{l}\text{s.t.}{B}^T\left[i\right]D\left[i\right]=I_d\text{for}i=1,\dots ,n.\end{array}$

This is derived from the following inequality

$\begin{array}{l}{\displaystyle \underset{i\ne j}{max}}\frac{1}{d}\Vert B^T\left[i\right]D\left[j\right]{\Vert }_2^2\le {\displaystyle \underset{i\ne j}{max}}\frac{1}{d}\Vert B^T\left[i\right]D\left[j\right]{\Vert }_F^2\\ \le \frac{1}{d}{\displaystyle \sum _{i,j}}\Vert B^T\left[i\right]D\left[j\right]{\Vert }_F^2\\ =\frac{1}{d}\Vert B^{T}D{\Vert }_F^2.\end{array}$

In Liu and Chen [10], this is solved by a projected gradient method, but since this is a constrained linear least squares problem in the vector space of matrices with Frobenius inner product the following Theorem states a closed form of the solution of Equation (31).

Theorem 3. The minimizer $B\in {ℝ}^{n_y\times n_x}$ of Equation (31) is given as the concatenation

$\begin{array}{l}B=\left(B\left[1\right],B\left[2\right],\dots ,B\left[n\right]\right),\end{array}$

where the n blocks are given as

$\begin{array}{l}B\left[i\right]=K_i^{+}\left(D\left[i\right]-E_i{H}_i\right)\end{array}$

with

$\begin{array}{l}{K}_i={\left(2D{D}^T\right)}^2+D\left[i\right]D{\left[i\right]}^T,\\ E_i=2D{D}^{T}D\left[i\right],\\ R_i=D\left[i\right]-2D{D}^T{K}_i^{+}{E}_i,\\ S_i=-D{\left[i\right]}^T{K}_i^{+}{E}_i,\\ L_i=R_i^T{R}_i+S_i^T{S}_i,\\ M_i=K_i^{+}{E}_i\left(I-L_i^{+}{L}_i\right),\\ H_i=L_i^{+}{S}_i^T+\left(I-L_i^{+}{L}_i\right){\left(I+M_i^T{M}_i\right)}^{-1}\\ {\left(K_i^{+}{E}_i\right)}^T{K}_i^{+}\left(D\left[i\right]-E_i{L}_i^{+}{S}_i^T\right),\end{array}$

for i = 1, …, n.

The proof can be found in Appendix C.

Let d = 1 and the singular value decomposition of D given as D = VΣU^T and assume $B=V\tilde{\Sigma }{U}^T$. Then, the solution of Equation (31) is given in an even simpler form since

$\begin{array}{l}\Vert B^{T}D{\Vert }_F^2=\Vert U\tilde{\Sigma }{V}^{T}V\Sigma U^T{\Vert }_F^2\\ =\Vert U\tilde{\Sigma }\Sigma U^T{\Vert }_F^2\\ =\Vert {\Sigma }^{+}\Sigma {\Vert }_F^2.\end{array}$

Choosing $B=D^{+,T}diag{\left(\tilde{d}\right)}^{-1}$, where $\tilde{d}=diag\left(D^{+}D\right)$, i.e., a normalized pseudo-inverse, yields also a solution for Equation (31). Here, diag follows the matlab/python notation, where diag of a matrix gives the vector of the main diagonal and gives a diagonal matrix with a given vector on its main diagonal. For d ≥ 2, the orthonormal block constraints in Equation (31) would not be met since with this construction we can only guarantee that the diagonal elements of B^TD are equal to one but cannot control what happens on the off-diagonal, thus not yielding a feasible solution.

4.2 Computing the analytical weight matrix in a MMV problem

In practice, often large data sets are obtained, i.e., by a large amount of measurements or measurements y^l, x^l representing pictures. For instance, 1, 000 pixels and 200 measurements lead to a matrix D with (1, 000·200)² elements. Applying the theory for analytical LBISTA could thus be difficult in practice. Although D is sparse, it can take a long time to calculate the analytical weight matrix. The following Theorem states the connection between the MMV setting and the block sparse setting for ALBISTA, showing that it is sufficient to minimize the generalized mutual coherence Equation (32), see Liu and Chen [10], for K instead of minimizing the generalized mutual block-coherence (Equation 21) for D = K ⊗ I_d. Moreover, in many applications the measurement model involves convolutions, see for example Ahmadi et al. [14], so we conclude this section by considering the cases where K is a circular or Toeplitz matrix.

Theorem 4. Let $\tilde{B}$ attain the minimum in

$\begin{array}{ll}{\displaystyle \underset{{\displaystyle \underset{{\displaystyle \underset{\forall 1\le i\le n}{{\tilde{B}}_{:,i}^T{K}_{:,i}=1}}}{\tilde{B}\in {ℝ}^{n\times n}}}}{inf}}{\displaystyle \underset{i\ne j}{\text{max}}}|{\tilde{B}}_{:,i}^T{K}_{:,j}|,& (32)\end{array}$

where ${\tilde{B}}_{:,i}$ refers to the ith column. Then the minimum of

$\begin{array}{l}{\displaystyle \underset{{\displaystyle \underset{{\displaystyle \underset{\forall 1\le l\le n}{B^T\left[l\right]D\left[l\right]=1}}}{B\in {ℝ}^{n_y\times n_x}}}}{inf}}\left\{{\displaystyle \underset{{\displaystyle \underset{1\le i,j\le n}{i\ne j}}}{max}}\frac{1}{d}\Vert B^T\left[i\right]D\left[j\right]{\Vert }_2\right\},\end{array}$

is given as $B=\tilde{B}\otimes I_d$, if D = K ⊗ I_d.

The proof can be found in Appendix D. Moreover, the following relation holds, if D = K ⊗ I_d,

$\begin{array}{l}{\mu }_b\left(D\right)=\frac{1}{d}\mu \left(K\right),\end{array}$

thus, the block-coherence of D can be enhanced by increasing the number of measurements d. It is feasible to solve Equation (31) by the pseudo inverse in the MMV setting, since this is solved for K, i.e., d = 1

4.3 Circular matrix case

Consider now the following setting, where the measurements y^l ∈ ℝⁿ are obtained by a circular convolution of x^l with vector k, i.e.,

$\begin{array}{ll}{y}^l=k⊛x^l& (33)\end{array}$

$\begin{array}{l}=K{x}^l,l=1,\dots ,d,\end{array}$

where K is a circular matrix generated by a vector k ∈ ℝⁿ, i.e., K = circ(k) ∈ ℝ^n×n. Applying Theorem 3 to the circular case yields the following lemma.

Lemma 1. Let k ∈ ℝⁿ and let B = circ(b) ∈ ℝ^n×n where b ∈ ℝⁿ is given by

$\begin{array}{ll}\left(\begin{array}{cc}2K{K}^T& k\\ k^T& 0\end{array}\right)\left(\begin{array}{c}b\\ \lambda \end{array}\right)=\left(\begin{array}{c}0\\ 1\end{array}\right),& (34)\end{array}$

λ ∈ ℝ. Then, B attains the minimum in Equation (31).

The latter statement implies a simpler way to compute b ∈ ℝⁿ by using singular value decomposition

$\begin{array}{l}{B}^{*}K=U^{*}diag\left(\sigma \left(B\right)\right)U{U}^{*}diag\left(\sigma \left(K\right)\right)U\\ =U^{*}diag\left(\sigma \left(B\right)\odot \sigma \left(K\right)\right)U,\end{array}$

where σ(B) ∈ ℝⁿ is the vector of singular values of B, respectively K, filled with zeros and U an unitary matrix. With $U=1/\sqrt{n}F$, where F is the Discrete Fourier Transform (DFT) matrix, this leads to the conclusion $\sigma \left(B\right)=Fb=\widehat{b}$, and thus

$\begin{array}{ll}b=F^{-1}\left(\overline{1/\widehat{k}}\right),& (35)\end{array}$

where $\widehat{k}=Fk$. The expression $1/\widehat{k}$ should be interpreted point wise and to be zero if ${\widehat{k}}_i=0$. This also concludes that the computation of B tends to be difficult in practice if K has not full rank, since this means that $\widehat{k}$ has at least one zero entry. In this case, b has to be scaled with $\frac{n}{rank\left(K\right)}$ since

$\begin{array}{l}{b}^{T}k=\frac{1}{n}{\widehat{b}}^T\widehat{k}=\frac{1}{n}\Vert \widehat{k}{\Vert }_0\\ =\frac{rank\left(K\right)}{n}\stackrel{!}{=}1.\end{array}$

4.4 Toeplitz matrix case

Considering the more general convolutional setting,

$\begin{array}{ll}y=k*x,& (36)\end{array}$

where $k\in {ℝ}^{\tilde{m}}$ and x ∈ ℝⁿ with $\tilde{m}<n$. This results in a Toeplitz matrix K

$\begin{array}{l}K=\left(\begin{array}{cccc}{k}_1& 0& \dots & 0\\ k_2& k_1& & 0\\ ⋮& ⋮& \ddots & ⋮\\ k_{\tilde{m}}& k_{\tilde{m}}& & ⋮\\ 0& k_{\tilde{m}}& & ⋮\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & k_{\tilde{m}}\end{array}\right)\in {ℝ}^{m\times n}.\end{array}$

The reasoning of the previous section cannot be applied to show that the solution of Equation (31) must be a Toeplitz matrix. But the following can be observed: Let b be constructed as discussed for $\tilde{K}=circ$(k), where k is the concatenation of k and a zero vector of suitable dimensions, i.e., the first column of K. The analytical weight matrix B w.r.t. K can be constructed as

$\begin{array}{l}{B}_{:,i}=T^{i-1}b,i=1,\dots ,n,\end{array}$

where T is the m × m cyclic shift matrix, i.e., only the m × n submatrix of $\tilde{B}=circ\left(b\right)\in {ℝ}^{m\times m}$ is used. The columns of K can also be expressed through the cyclic shift of k. Hence,

$\begin{array}{l}{B}_{:,i}^T{K}_{:,i}=b^T{T}^{-\left(i-1\right)}{T}^{i-1}k=b^{T}k=1,\end{array}$

i.e., B is a feasible solution of Equation (31) for K. On the other hand, the cross coherence is bounded since

$\begin{array}{l}{\displaystyle \underset{i,j\le n.i\ne j}{max}}\left|B_{:,i}^T{K}_{:,j}\right|={\displaystyle \underset{i,j\le n,i\ne j}{max}}\left|b^T{T}^{-\left(i-1\right)}{T}^{j-1}k\right|\\ ={\displaystyle \underset{i,j\le n,i\ne j}{max}}\left|b^T{T}^{j-i}k\right|\\ \le {\displaystyle \underset{i,j\le m,i\ne j}{max}}\left|b^T{T}^{j-i}k\right|\\ ={\displaystyle \underset{i,j\le m,i\ne j}{max}}\left|{\tilde{B}}_{:,i}^T{\tilde{K}}_{:,j}\right|\\ =\Vert {\tilde{B}}^T\tilde{K}-I_m{\Vert }_{\text{max}}\\ =\Vert \sqrt{n}{F}^{-1}diag\left(\sigma \left(B\right)\odot \sigma \left(K\right)\right)\frac{1}{\sqrt{n}}F-I_m{\Vert }_{\text{max}}\\ =\Vert F^{-1}{I}_{m}F-I_m{\Vert }_{\text{max}}=0,\end{array}$

where ‖D‖_max = max_i,j|d_ij| is the maximum norm and diag(σ(B)⊙σ(K)) = I_m derives from Equation (35). Note: To have this upper bound $\tilde{K}$ needs to have full rank, which is the case if the full time continuous FT of k has no zero points. Or one has to adjust the discrete grid. Thus, constructing B by extending K to a circular matrix is a feasible approach.

4.5 Connection to CNNs

It is known that using the Fast Fourier Transform (FFT) in CNNs can decrease the computation time if the convolutional filter is big [31, 32]. In Pratt et al. [31] showed that training weights in the Fourier domain can reduce training time while maintaining efficiency. By using this, the costs of $\mathcal{O}\left(n^2\right)$ operations could be reduced to $\mathcal{O}\left(nlog\left(n\right)\right)$ operations. To connect the theory of FFT-CNNs and of unrolling ISTA in the context of deconvolution (Equations 33 or 36), the gradient step can be viewed as follows:

$\begin{array}{l}x-\gamma b*\left(k*x-y\right)\\ =x-\gamma b*k*x+\gamma b*y\\ =\left(e-\gamma b*k\right)*x+\gamma b*y\\ =f\left(\gamma \right)*x+\gamma \tilde{b}.& (37)\end{array}$

This can be interpreted as a convolutional layer with kernel f(γ) = (e − γb * k) and bias $\tilde{b}=b*y$, where e = [1, 0, …, 0]. This means that ALISTA, with a Toeplitz matrix, can be interpreted as a CNN only two trainable parameters per layer, γ, λ. In the setting of FFT-CNN, the update rule can be formulated as

$\begin{array}{l}x-\gamma b*\left(k*x-y\right)\\ =F^{-1}\left(\left(ê-\gamma \widehat{b}\odot \widehat{k}\right)\odot \widehat{x}\right)+\gamma \tilde{b}.\end{array}$

On the other hand, using FFT CNNs shows only a speed up if we deal with large data sets, i.e. by evaluating high-resolution images, or large filters, i.e., if $\tilde{m}$ is greater than log(n).

5 Numerical examples

In the following, we are going to present numerical results achieved by the presented algorithms.¹ We will investigate two MMV scenarios. First, the measurements y^l are obtained with a random Gaussian matrix, and second obtained by a redcued-rank random circular convolution. In each scenario, we will enforce the Kronecker structure and thus reducing the training cost by training only low dimensional m × n matrices. Furthermore, in the convolutional setting, the circular structure will be also enforced, thus reducing the training costs even more. To have a fair comparison, all algorithms are initialized with the analytical weight matrix.

5.1 MMV setting

The training data are sampled from an unknown distribution $\mathcal{X}$ and generated as follows. The signals x are generated for a given number of blocks n, given block length d and a possibility if a block x[i] is active or not, i.e., if ‖x[i]‖₂ ≠ 0 or ‖x[i]‖₂ = 0, called pnz (probability of non-zeros). If a block is active, the elements of this blocks are given by a normal Gaussian distribution with variance σ² = 1. The measurements y are obtained by Equation (3), where the elements of ϵ are given from a normal Gaussian distribution with variance ${\sigma }^2=pnz·n_x/n_y·10^{-SN{R}_{dB}/10}$. SNR_dB is the signal-to-noise ratio given in decibel. We consider the following cases. In each case, we generate x with d = 15, n = 128, m = 32, and pnz = 10%.

Gaussian measurement matrix: In the Gaussian setting, we sample a m × n matrix K iid from a Gaussian distribution with variance σ² = 1. We normalize the columns, s.t. D has orthonormal blocks, as assumed in the beginning.

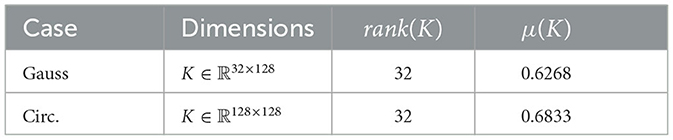
Circular convolution matrix: We construct the circular matrix as follows. At first, we generate a random iid sampled vector ã but set a certain amount of elements to zero. We define k = ℜ(F⁻¹ã), and thus we can generate a rank deficient Matrix D = K ⊗ I_d, where K = circ(k). Thus, y^l is obtained through a circular convolution with symmetric $\widehat{k}=Fk$. It is important for this section to generate a rank deficient matrix to have compressive observations. Otherwise, we would get a trivial problem if K, respectively D, has full rank. Computing D = K ⊗ I_d yields the desired matrix. The properties of these two matrices can be found in Table 1.

TABLE 1

Table 1. Properties of matrix K in both scenarios.

5.2 Discussion

The results of the proposed methods can be found in Figure 1A for the Gaussian Problem case in Figure 1B for the circular case. We also consider the performance of a version of AMP [33]. AMP can be viewed as an Bayesian extension of ISTA with an additional Onsager correction term, before applying the thresholding operator, i.e.,

$\begin{array}{l}{v}^{\left(k\right)}=y-D{x}^{\left(k\right)}+b^{\left(k\right)}{v}^{\left(k-1\right)}\\ x^{\left(k+1\right)}={\eta }_{\alpha }\left(x^{\left(k\right)}+\gamma D^T{v}^{\left(k\right)}\right)\end{array}$

where b^(k) = 𝔼[η′(x^(k))]. Here, we will train only γ, α, with the same procedure as already discussed and choose D^T = B^T. By using B^T instead of D^T we are resembling Orthogonal AMP (OAMP) [34], which follows a similar idea as ALISTA. In Ma and Ping [34], B is chosen to be de-correlated with respect to K, i.e.,

$\begin{array}{l}\text{tr}\left(I_{n_y}-B^{T}D\right)=0.\end{array}$

The analytical weight matrix B satisfies also this condition. Moreover, in Ma and Ping [34], the choice of different matrices is also discussed. Thus, untrained ALISTA with correction term can be viewed as a special case of OAMP. Note also, that the structure of Trainable ISTA, proposed in Ito et al. [35], is also based on OAMP and thus there are interrelations between AMP, unfolding ISTA, and analytical ISTA. We refer to learned AMP with analytical matrix as ALAMP. Different from Ma and Ping [34], we use the ℓ_2,1-regularizer, instead of only ℓ₁-regularization, since we consider the MMV setting. This is also discussed in [36, 37]. Every proposed algorithm performs better, in terms of NMSE, as their untrained original. Interestingly learned AMP, with analytical weight matrix B, has a performance almost as good as LBISTA (untied) with only a fraction of trainable parameters. This may come from the fact, that block-soft thresholding is not the correct MMSE estimator for the generated signals x and thus the correction of b^(k) yields the better estimation for x. As expected, we get almost the same performance of ALBISTA and LBISTA CP (untied). In Figure 2A, we show similar plots for the justification of Theorem 1, as also seen in Liu and Chen [10]. In particular, Figure 2A shows that $\frac{{\alpha }^{\left(k\right)}}{{\gamma }^{\left(k\right)}}$ is proportional to the maximal ℓ_2,1-error over all training signals. An interesting behavior, which carries over from the sparse case, is that the learned ℓ_2,1-regularization parameters approach zero, as k increases. If α is close to zero, we approach a least-squares problem. This means that after LBISTA found the support of the unknown signal x^* the algorithm consist only of the least squares fitting. Figure 2B shows that the trained γ^(k) are bound in an interval. Note that, in contrast to Liu and Chen [10], Theorem 1 is based on a more general assumption, onto the thresholding parameters. One can take a suitable κ and obtains the upper bound for the ℓ₂-error and thus have convergence on the training set if the sparsity assumptions are met. Figure 3 shows the training loss over the training iterations for the results presented in Figure 1. One can see that ALBISTA needs less training iterations as LBISTA CP (untied) or LBISTA (untied) and thus less training data. The observed jumps occur when moving from one layer to the next due to the layer-wise training, Algorithm 1. A layer is defined to be optimized if NMSE converged within 1e − 5.

FIGURE 1

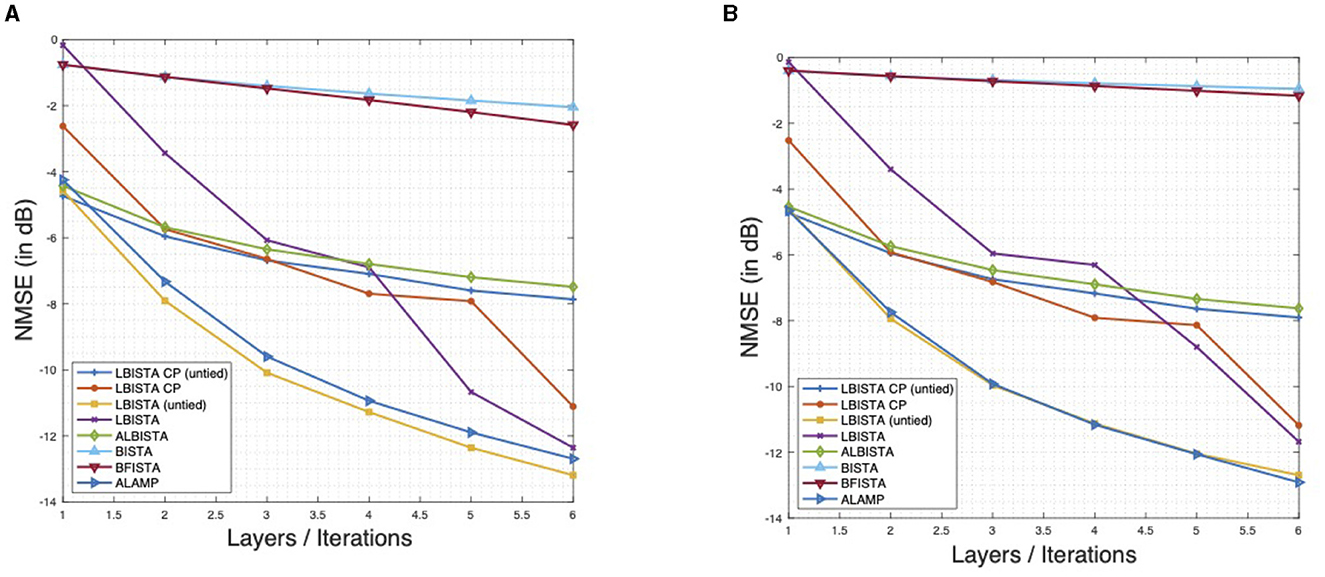
Figure 1. NMSE in dB over layers/iterations, pnz = 10%, without noise. BISTA, and FastBISTA are evaluated with α = 1 and γ = 1/(1.01‖D‖²). (A) Gaussian measurement problem. (B) Circular convolution problem.

FIGURE 2

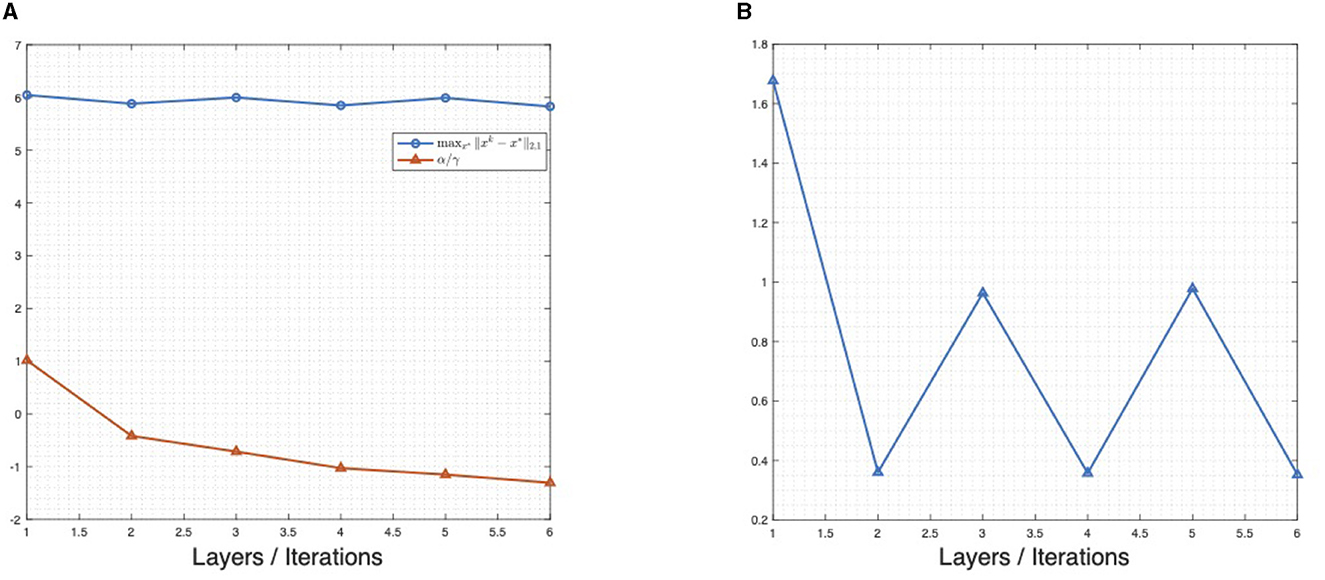
Figure 2. Plots justifying results in Theorem 1. (A) Parameters and maximal ℓ_2,1-error in the noiseless case on the problem with circular convolution matrix. (B) Trained γ over layers/iterations on the problem with Gaussian measurement matrix.

FIGURE 3

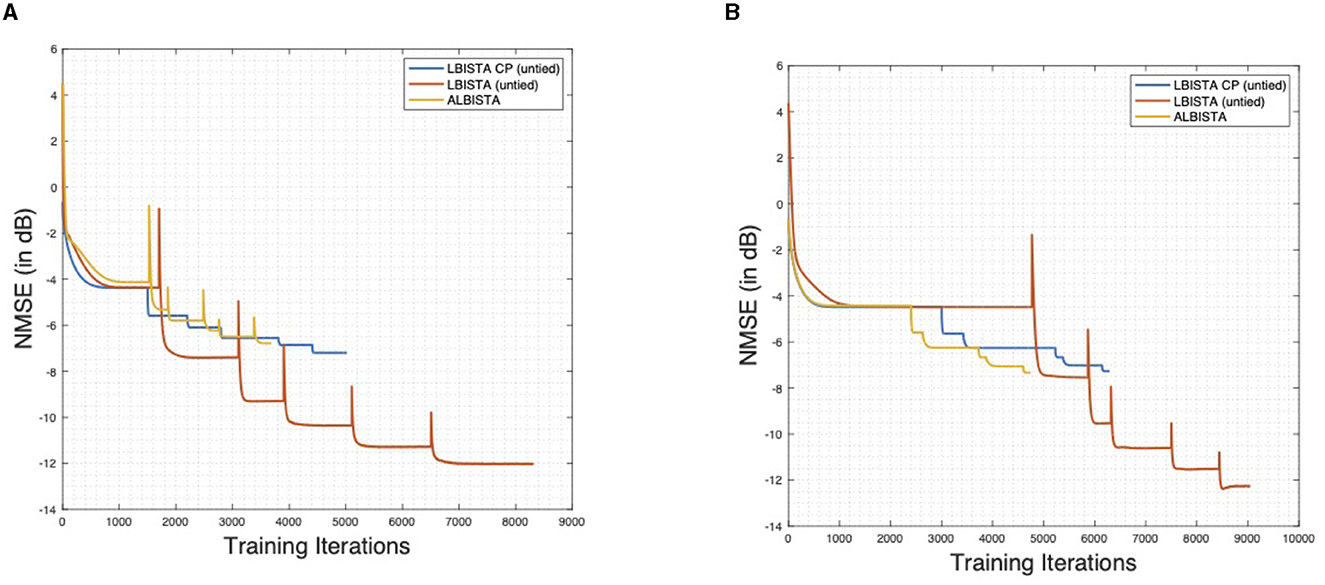
Figure 3. Training history for results shown in Figure 1A respectively Figure 1B. One can see that ALBISTA needs less training iterations than LBISTA CP (untied) or LBISTA (untied). (A) Gaussian measurement problem. (B) Circular convolution problem.

6 Conclusion

We proposed ALISTA for the block-sparse and MMV case, important for many real-world applications, and derived corresponding theoretical convergence and recovery results. We relaxed the conditions for the regularization parameter and thus obtained a more precise upper-bound after ALISTA is trained. Nevertheless, this is still dependent on a sharp sparsity assumption on the unknown signals. We investigated and derived a direct solution for the analytical weight matrix in the general block sparse setting as well for one convolutional scenarios. The last section provides numerical results and includes interrelations to AMP.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://github.com/janhauffen/Block-ALISTA.

Author contributions

JH, NM, and PJ contributed to the concept of the work. JH wrote the first draft of the article. NM and PJ supervised the work. All authors contributed to manuscript revision, read, and approved the submitted version.

Acknowledgments

We acknowledge support by the German Research Foundation and the Open Access Publication Fund of TU Berlin.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2023.1205959/full#supplementary-material

Footnotes

1. ^Code: https://github.com/janhauffen/Block-ALISTA.

References

1. Candès EJ, Romberg J, Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Trans Inf Theory. (2006) 52:489–509. doi: 10.1109/TIT.2005.862083

CrossRef Full Text | Google Scholar

2. Donoho DL. Compressed sensing. IEEE Trans Inf Theory. (2006) 52:1289–306. doi: 10.1109/TIT.2006.871582

CrossRef Full Text | Google Scholar

3. Shannon CE. Communication in the presence of noise. Proc IRE. (1949) 37:10–21. doi: 10.1109/JRPROC.1949.232969

CrossRef Full Text | Google Scholar

4. Candes EJ, Tao T. Decoding by linear programming. IEEE Trans Inf Theory. (2005) 51:4203–15. doi: 10.1109/TIT.2005.858979

CrossRef Full Text | Google Scholar

5. Rudelson M, Vershynin R. Geometric approach to error-correcting codes and reconstruction of signals. Int Mathem Res Notices. (2005) 2005:4019–41. doi: 10.1155/IMRN.2005.4019

CrossRef Full Text | Google Scholar

6. Figueiredo MA, Nowak RD, Wright SJ. Gradient projection for sparse reconstruction: application to compressed sensing and other inverse problems. IEEE J Sel Top Signal Process. (2007) 1:586–97. doi: 10.1109/JSTSP.2007.910281

CrossRef Full Text | Google Scholar

7. Fornasier M, Rauhut H. Iterative thresholding algorithms. Appl Comput Harmon Anal. (2008) 25:187–208. doi: 10.1016/j.acha.2007.10.005

CrossRef Full Text | Google Scholar

8. Gregor K, LeCun Y. Learning fast approximations of sparse coding. In: Proceedings of the 27th International Conference on International Conference on Machine Learning (2010). p. 399–406.

Google Scholar

9. Chen X, Liu J, Wang Z, Yin W. Theoretical linear convergence of unfolded ISTA and its practical weights and thresholds. In: Conference on Neural Information Processing Systems (NeurIPS 2018) (2018).

Google Scholar

10. Liu J, Chen X. ALISTA: Analytic weights are as good as learned weights in LISTA. In: International Conference on Learning Representations (ICLR) (2019).

Google Scholar

11. Chen X, Liu J, Wang Z, Yin W. Hyperparameter tuning is all you need for LISTA. In: Advances in Neural Information Processing Systems (2021). p. 34.

Google Scholar

12. Gorodnitsky IF, George JS, Rao BD. Neuromagnetic source imaging with FOCUSS: a recursive weighted minimum norm algorithm. Electroencephalogr Clin Neurophysiol. (1995) 95:231–51. doi: 10.1016/0013-4694(95)00107-A

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Fengler A, Musa O, Jung P, Caire G. Pilot-based unsourced random access with a massive MIMO receiver, interference cancellation, and power control. IEEE J Select Areas Commun. (2022) 40:1522–34. doi: 10.1109/JSAC.2022.3144748

CrossRef Full Text | Google Scholar

14. Ahmadi S, Burgholzer P, Mayr G, Jung P, Caire G, Ziegler M. Photothermal super resolution imaging: a comparison of different thermographic reconstruction techniques. NDT E Int. (2020) 111:102228. doi: 10.1016/j.ndteint.2020.102228

CrossRef Full Text | Google Scholar

15. Ziniel J, Schniter P. Efficient high-dimensional inference in the multiple measurement vector problem. IEEE Trans Signal Proc. (2012) 61:340–54. doi: 10.1109/TSP.2012.2222382

CrossRef Full Text | Google Scholar

16. Chen J, Huo X. Theoretical results on sparse representations of multiple-measurement vectors. IEEE Trans Signal Proc. (2006) 54:4634–43. doi: 10.1109/TSP.2006.881263

CrossRef Full Text | Google Scholar

17. Schacke K. On the kronecker product. Master's thesis, University of Waterloo. (2004).

Google Scholar

18. Yonina C, Eldar HB. Block-sparsity: coherence and efficient recovery. arXiv preprint arXiv:08120329. (2008). doi: 10.48550/arXiv.0812.0329

CrossRef Full Text | Google Scholar

19. Donoho DL, Elad M, Temlyakov VN. Stable recovery of sparse overcomplete representations in the presence of noise. IEEE Trans Inf Theory. (2005) 52:6–18. doi: 10.1109/TIT.2005.860430

CrossRef Full Text | Google Scholar

20. Chen SS, Donoho DL, Saunders MA. Atomic decomposition by basis pursuit. SIAM Rev. (2001) 43:129–59. doi: 10.1137/S003614450037906X

CrossRef Full Text | Google Scholar

21. Kutyniok G. Compressed sensing. Mitteilungen der Deutschen Mathematiker-Vereinigung. (2014) 1:24–9. doi: 10.1515/dmvm-2014-0014

CrossRef Full Text | Google Scholar

22. Foucart S, Rauhut H. A mathematical introduction to compressive sensing. Bull Am Math. (2017) 54:151–65. doi: 10.1090/bull/1546

CrossRef Full Text | Google Scholar

23. Byrne CL. Applied Iterative Methods. Wellesley, MA: AK Peters. (2008). doi: 10.1201/9780429295492

CrossRef Full Text | Google Scholar

24. Bauschke HH, Combettes PL, Bauschke HH, Combettes PL. Convex Analysis and Monotone Operator Theory in Hilbert Spaces. New York, NY: Springer. (2011). doi: 10.1007/978-1-4419-9467-7

CrossRef Full Text | Google Scholar

25. Beck A. A fast iterative shrinkage-thresholding algorithm for linear inverse problem. Soc Ind Appl Mathem. (2009) 2:183–202. doi: 10.1137/080716542

CrossRef Full Text | Google Scholar

26. Combettes PL, Pesquet JC. Proximal splitting methods in signal processing. In: Fixed-Point Algorithms for Inverse Problems in Science and Engineering. Springer (2011). p. 185–212. doi: 10.1007/978-1-4419-9569-8_10

CrossRef Full Text | Google Scholar

27. Kim D, Park D. Element-wise adaptive thresholds for learned iterative shrinkage thresholding algorithms. IEEE Access. (2020) 8:45874–86. doi: 10.1109/ACCESS.2020.2978237

CrossRef Full Text | Google Scholar

28. Fu R, Monardo V, Huang T, Liu Y. Deep unfolding network for block-sparse signal recovery. In: ICASSP 2021–2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE (2021). p. 2880–2884. doi: 10.1109/ICASSP39728.2021.9414163

CrossRef Full Text | Google Scholar

29. Musa O, Jung P, Caire G. Plug-and-play learned gaussian-mixture approximate message passing. In: ICASSP 2021–2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE (2021). p. 4855–4859. doi: 10.1109/ICASSP39728.2021.9414910

CrossRef Full Text | Google Scholar

30. Kingma DP, Ba J. Adam: a method for stochastic optimization. arXiv preprint arXiv:1412.6980 (2015). doi: 10.48550/arXiv.1412.6980

CrossRef Full Text | Google Scholar

31. Pratt H, Williams B, Coenen F, Zheng Y. FCNN: Fourier convolutional neural networks. In: Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Springer (2017). p. 786–798. doi: 10.1007/978-3-319-71249-9_47

CrossRef Full Text | Google Scholar

32. Chitsaz K, Hajabdollahi M, Karimi N, Samavi S, Shirani S. Acceleration of convolutional neural network using FFT-based split convolutions. arXiv preprint arXiv:200312621. (2020). doi: 10.48550/arXiv.2003.12621

CrossRef Full Text | Google Scholar

33. Donoho DL, Maleki A, Montanari A. Message-passing algorithms for compressed sensing. Proc Nat Acad Sci. (2009) 106:18914–9. doi: 10.1073/pnas.0909892106

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Ma J, Ping L. Orthogonal amp. IEEE Access. (2017) 5:2020–33. doi: 10.1109/ACCESS.2017.2653119

CrossRef Full Text | Google Scholar

35. Ito D, Takabe S, Wadayama T. Trainable ISTA for sparse signal recovery. IEEE Trans Signal Proc. (2019) 67:3113–25. doi: 10.1109/TSP.2019.2912879

CrossRef Full Text | Google Scholar

36. Kim J, Chang W, Jung B, Baron D, Ye JC. Belief propagation for joint sparse recovery. arXiv preprint arXiv:1102.3289. (2011). doi: 10.48550/arXiv.1102.3289

CrossRef Full Text | Google Scholar

37. Chen Z, Sohrabi F, Yu W. Sparse activity detection for massive connectivity. IEEE Trans Signal Proc. (2018) 66:1890–904. doi: 10.1109/TSP.2018.2795540

CrossRef Full Text | Google Scholar