
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Appl. Math. Stat., 13 March 2023
Sec. Dynamical Systems
Volume 9 - 2023 | https://doi.org/10.3389/fams.2023.1115227
This article is part of the Research TopicInsights in Dynamical Systems 2022View all 7 articles
The dynamic buckling of circular rings is a pervasive instability problem with a major impact in various fields, such as structural, nuclear and offshore engineering, robotics, electromechanics, and biomechanics. This phenomenon may be simply seen as the complex motion that occurs deviating from the original circular shape under, for instance, any kind of time-dependent forcing load. Despite the fact that this topic has progressively gained importance since the mid-20th century, it seems that the same points have not been made completely clear. In fact, even some subtleties in the derivation of classical static buckling load may still give rise to misinterpretations and lead to misleading results. A fortiori, research concerning the nonlinear dynamics of rings still suffers the inherent difficulties associated with different possible analytical formulations of post-buckling dynamics. Advancement in this respect would be relevant, both from a theoretical and a practical point of view, since the applications are endless, with countless possibilities, especially in the biomedical and biotechnological fields: buckling-driven transformations of thin-film materials for applications in electronic microsystems, self-excited oscillations in collapsible tubes and pliable fluid-carrying shells, vocal-fold oscillations during phonation and snoring, pulse wave propagation in arteries, closure and reopening of pulmonary airways, stability of cardiac and venous valves during vascular surgery, stability of annuloplasty devices, flow-induced deformation and ultimate rupture of a cerebral aneurysm, and much more. The present article, in the framework of a critical review of the classic formulation of elastic ring buckling, proposes a straightforward approach for the nonlinear dynamics of an elastic ring that leads to a Mathieu–Duffing equation. In such a manner, some possible evolutions of the system under pulsing loads are analyzed and discussed, showing the inherent complexity of its dynamic behavior.
The stability of circular rings is a classic and important topic that has attracted considerable interest among scholars and researchers. The problem may affect many fields with endless practical applications: structural, nuclear and offshore engineering, robotics, electromechanics, biomechanics, biomedical and biotechnological sciences, just to mention a few. The ways of approaching the stability of a ring can be very different depending on the perspective from which one decides to face the problem: Buckliphobia or Buckliphilia [1, 2].
From a Buckliphobia standpoint, the buckling of a ring is a failure mechanism to be avoided. Consider, for example, the loss of stability of collapsible tubes or pliable shells conveying pressurized and high-velocity fluid, such as gas, fuel, and blood [3–5]. The interaction between the internal flow and the tube, under certain critical conditions (e.g., negative transmural pressure of critical magnitude), can induce self-excited oscillations with finite amplitudes and, consequently, catastrophic collapse of the tube/shell [6]. There are a number of examples of such instability phenomena in everyday life: the aeroelastic stability (i.e., fluttering) of curved aircraft wings, for instance, is a topic of great interest in engineering since it induces painful limitations in the operational condition of the aircraft [7]; in the same area, one can mention the buckling and the postbuckling of chemical plant piping, offshore pipelines, or undersea vessels induced by hydroelastic interaction [8, 9] as they can affect the normal operation of plants or vessels.
More complex dynamical phenomena can be encountered in the physiological and medical fields due to the high flexibility of the biological tubes and the low Reynolds numbers of the biological flows: the high-frequency Korotokoff sound, i.e., a puzzling phenomenon induced by the resonant motion of arterial blood vessels, which trigger a dynamic transition from a buckled state to an expanding state (see Figure 1 and [10]); crackling sounds generated when a collapsed airway opens, e.g., the snoring produced by the oscillations of the soft palate, pharyngeal walls, epiglottis, and tongue during sleep when the pharyngeal muscles relax and block the airway [11]; the flow limitation during forced expiration induced by the interaction between airways and air [12]; the micturition induced by the interaction between urethras and urine [13]; and the pulse wave propagation in the cardiovascular system that can induce several cardiovascular pathologies, such as heart failure, stenosis [14], flow-induced deformation, and ultimate rupture of aneurysms; all come to mind as just a few of the more outstanding examples. A comparatively large share of the scientific and technological interest focuses on the instability of elastic rings subjected to external confinement [15, 16]. Curved film-substrate structures, in particular, have drawn special attention in the biomedical field because of the wide variety of folding phenomena that are observable in the human body: the formation of creases in the colon due to the growth of mucous membrane or the wrinkling patterns that can be observed on the surface of the bronchus lumen (Figure 2A), crumpled gut surfaces, the sulci and gyri of the brain, or the morphological evolution of tumor growth (Figure 2B), which is guided by the buckling mechanism of layered structures [17, 18].
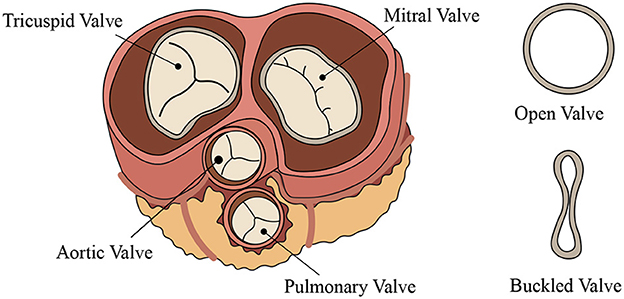
Figure 1. Schematic representation of heart valves (left) and their possible buckled configuration (right).
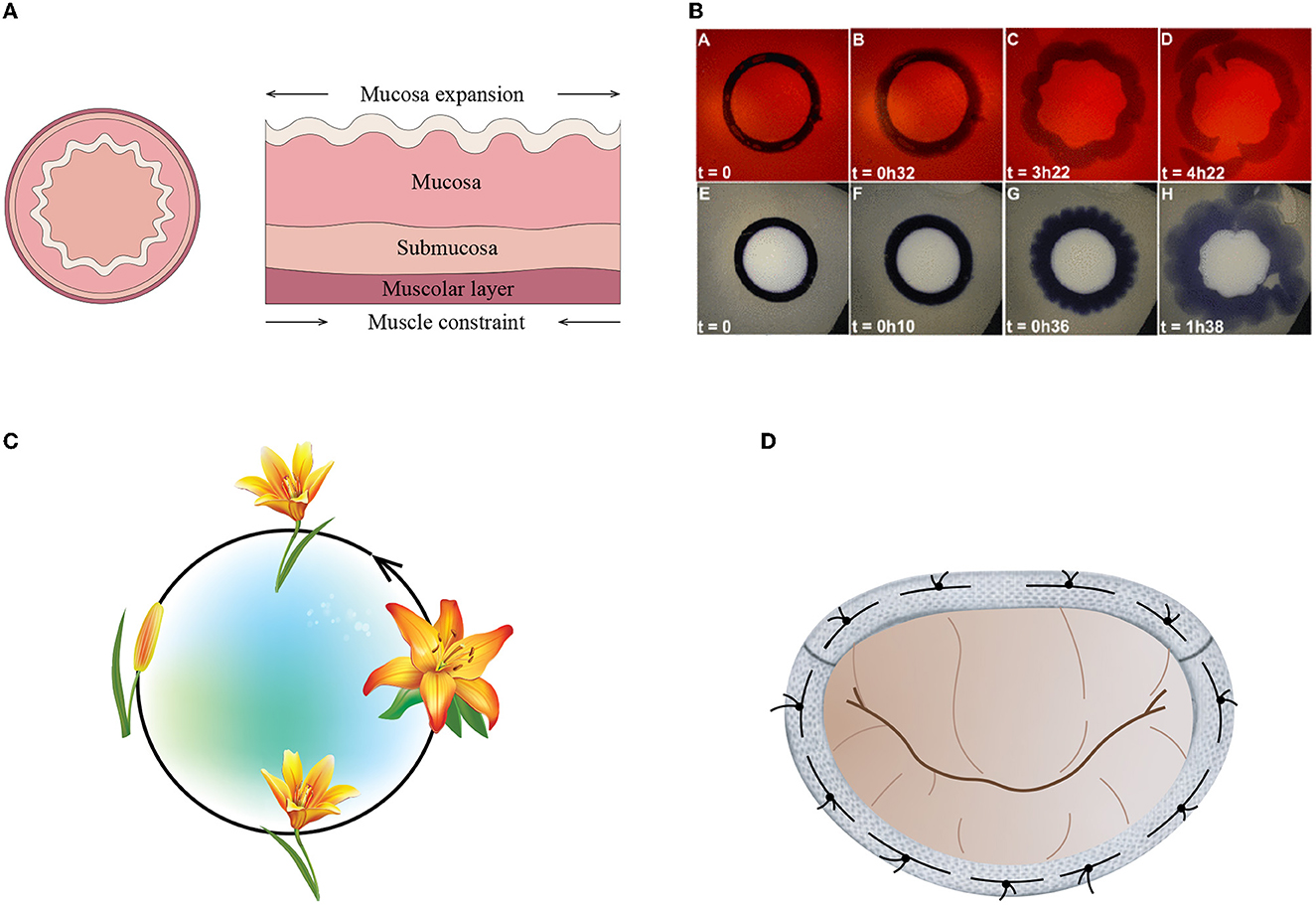
Figure 2. (A) Schematic representation of the uniaxial patterns that develop in the lumen of human tubular structures (left); the organ wall structure in the digestive, respiratory, or reproductive tracts with the mechanism for the formation of the wavy morphology (right). Redrafting of an original drawing of [17]. (B) Typical sequences of evolution for two thin circular artificial tumors confined at the periphery [18]. (C) Lily morphological transitions. (D) Mitral valve repair with an annuloplasty ring.
On the contrary, from a Buckliphilia standpoint, the nonlinear ring dynamics can be regarded as a potential resource to be exploited. Biological phenomena are often based on the control ad tuning of buckling. Take, for instance, the wavy or wrinkled morphology of petals (Figure 2C), leaves, stems, or fungi that confers them unique physical, mechanical, and optical properties, such as the capability to actively control morphological transitions [19].
Mimicking such an aptitude, a new generation of tunable/adaptive micro-/macro-electronic devices, actuators, and controlled fabric folding can take advantage of the control of ring dynamics to attain a desirable feature. The issue is scientifically fascinating and technically important, especially in the field of soft matter mechanics and structures [20]. Soft materials undergo large and reversible deformations with a variety of instability modes, such as wrinkling and creasing modes. Such a behavior can be usefully exploited in a variety of functional smart applications by controlling, switching, and tuning the formation and disappearance of wrinkles and creases in such a way as to create custom-made topography, control chemical patterning, adhesion properties, shape morphing, and configuration, and so on [21, 22]. The range of innovative applications in the biomedical engineering field is equally wide. Venous valves used in vascular surgery and annuloplasty devices (Figure 2D), for instance, may benefit from the control of ring dynamic behavior providing a major socio-economic impact and/or potential for investment in addition to an improvement of their performances, efficiency, and reliability. In the optic field, intensive investigations are going on tunable resonators, photonic modulators, wavelength division multiplexing filters, and switches [23–26]. Taking advantage of the resonance characteristics of micro-rings, such devices offer many desirable characteristics and unique performance metrics such as ultra-compact physical size, ultra-high modulation speed, low power consumption, ultra-low modulation power, high energy efficiency, and so on. However, to date, the high susceptibility of micro-ring resonators/modulators to thermal fluctuations and manufacturing tolerances and their resonant nature make their practical applications still challenging. Another interesting field of application is voice control. During phonation, in fact, the position, the shape, and the internal surface tension of the glottis actively control the frequency and amplitude of the vocal cords oscillations [27].
From a purely theoretical point of view, there is extremely rich and interesting literature dealing with elastic ring instability problems (buckling in the plastic range poses much more complex and still debated problems [3–5, 28]). Most of these studies are devoted to the buckling and the initial postbuckling of rings under external pressure, while only a few articles are devoted to the complex nonlinear dynamics of elastic rings. In the present study, a unified approach will be pursued; that is, a set of the possible equations of motion will be derived from the static formulation of ring buckling.
The first contributions in this respect to the topic were given in the second half of the 19th century by Bresse [29], Boussinesq [30], and Levy [31] and were concerned with the static in-plane buckling of inextensible rings subjected to uniform external pressure. Significant advancements were successively provided by several authors in the 20th century [32–40]. The general agreement is that the critical value of the pressure magnitude, by neglecting the effect of the axial and the shear deformations, is
where EI is the bending stiffness of the ring wall (E is the Young's modulus of the material and I is the inertia of the cross section, respectively), R is the mean ring radius, and k is the buckling coefficient, which is dependent on the boundary and pressure-type loading conditions. In particular, for the hydrostatic pressure it is [37, 41–46]
so that for a two-wave deformation, n = 2,
holds true (note that n = 1 corresponds to a rigid-body motion). However, despite the long history of studies on the subject, the accuracy of the results, especially numerically, may still be an issue sometimes. Indeed, considering different constitutive assumptions, such as linear elastic material and Neo-Hookean materials, either compressible or incompressible, the case of the static, axially symmetric, deflection of a ring under internal and external pressure is analyzed in [47], and the obtained results show that also widely used commercial finite element programs may give inaccurate results in the case of linearly elastic rings undergoing large strains. Similar findings have been found and discussed in [48].
One of the first contributions to the study of the dynamic stability of the circular ring dates back to 1871 by Hoppe [49], who derived the frequency equation for the in-plane vibrations of a thin circular ring. Later, Love [50] and other authors proposed different linear and nonlinear approaches (e.g., [51–58]). In the midst of the 20th century, several authors analyzed the ring under uniform radial pressure periodically varying with time (e.g., [59–63]). More specifically, they generally analyzed the nonlinear parametric stability problem in the hypothesis of small perturbations from the initial motion, ring midline inextensibility, and negligible shear deformation by linearizing the problem in some way. For thick rings, some authors took into account a sort of shear deformability in the vibration analysis (e.g., [64–69]). With respect to the inextensibility, Cooley and Parkey made interesting considerations regarding the vibration of high-speed rotating elastic rings [70]. Other authors dealt with the stability of rings subjected to impulsive or step loads (e.g., [56, 71–77]). They essentially showed that the dynamic buckling of elastic rings is triggered by flexural modes governed by a Mathieu equation. The solution of this type of equation is expressed in terms of Mathieu functions, which are periodic in their argument only for certain so-called characteristic values of the ratio between the system and the loading frequencies. The solution may be stable, i.e., bounded, or unstable, i.e., diverging. The transition curves between stable and unstable domains in the plane of parameters are related to the characteristic values [78]. The dynamical post-buckling behavior of circular rings under external pressure shows an imperfection sensitivity for some types of loading different from the hydrostatic one [9, 39, 79–84]. In this regard, it is noteworthy that the omission of some nonlinear terms led Rehfield [79, 85] to the misleading prediction of imperfection sensitivity also for rings under hydrostatic pressure. Inconsistent results can also be found in [86] again because of erroneously neglected cubic and quartic terms in the energy of the loads [79].
As stated earlier, in the next sections, the present study will move from the basic formulation of the static buckling problem (Section 2), highlighting some underlying subtleties in mathematical modeling and will provide in this framework a set of very simple equations that nevertheless allow sketching the very complex and fascinating nonlinear behavior of the ring dynamics (Sections 3 and 4).
For the classical static buckling analysis, it is assumed that the ring wall is undeformable from the axial and the shear standpoint, and it can only experience flexural deformation. Here, it will be shown that the way in which axial inextensibility is imposed may have significant implications for the nonlinear dynamics of the problem.
With reference to the geometry of a buckled circular ring (see Figure 3), the axial strain εθθ = εθθ(θ, t) at the ring centerline, the cross-sectional rotation ϕ = ϕ(θ, t), and the change of curvature κ = κ(θ, t) of the ring, respectively, are [37, 38]
where R is the mean ring radius, v = v(θ, t) and w = w(θ, t) are the tangential and normal displacement to the ring wall midline (see Figure 4), and κℓ = κℓ(θ, t) is the linear change of curvature,
In all formulae, the subscript comma indicates differentiation with respect to the subsequent variables (in the case of the previous equations, the polar coordinate θ). No shear deformation is allowed for the ring wall.
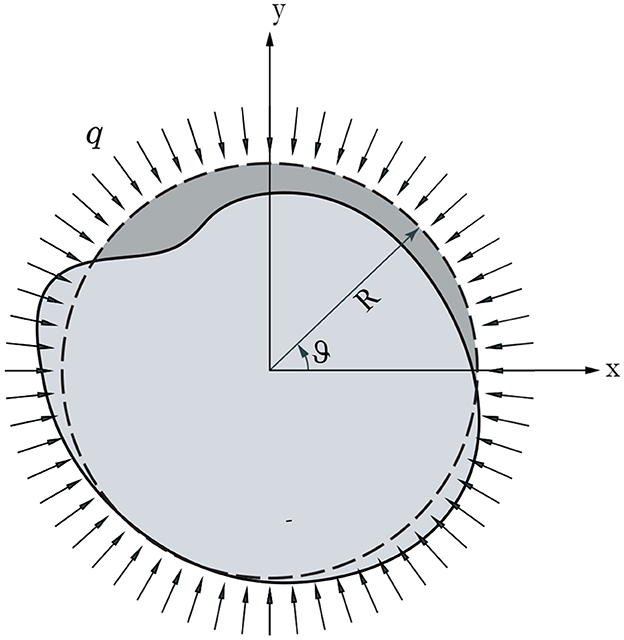
Figure 3. Circular ring under external hydrostatic pressure. Dashed and continuous lines mark the initial undeformed configuration and the buckled configuration of the ring, respectively.
The total potential energy of the ring is
where the strain energy V is the sum of the stretching and bending energies as follows
It is worth noticing that, to obtain the buckling pressure given by Equation (1), it is sufficient to assume κ ≈ κℓ.
The load potential due to a uniform external load per unit length q = q(t) is
where describes the difference between the area enclosed in the ring centerline before and after the deformation (Figure 3), which can be expressed as follows [38]
The kinetic energy is
where μ stands for the mass per unit length of the ring wall.
The Lagrangian function is
and, by virtue of the Euler–Lagrange equation, the partial differential equations (PDEs) of motion can be written as follows
and
where F = F(θ, t) and G = G(θ, t) are dimensionless functions defined as follows
Substituting Equation (16) in Equation (4) and imposing the inextensibility of the ring (i.e., εθθ = 0) gives
which leads to four solutions in the form
In the following, we will make reference to Equations (18) that are independent of the radius R. It is interesting to recall that to evaluate the instability pressure given by Equation (1), classical static solutions (see, e.g., [37, 38]) assume that the inextensibility of the centerline is obtained by simply requiring that
which makes the linear part of Equation (4) null in virtue of the first of Equations (18). Indeed, the displacements corresponding to the first classic buckling pressure are given in Equation (1), i.e.,
which do not satisfy the equality, εθθ = 0 in toto.
Interestingly, should one use Equation (11) in the case of a hydrostatic load, the coefficient k of the buckling pressure would result 36/13, instead of the classic value given in Equation (3) [48]. To overcome this drawback, Equations (18) are both taken into consideration only to reduce Equation (11) [48] to
Continuing to build on the Equations (18), in the present section, a set of equations governing the nonlinear elastic ring dynamics in the form of a Mathieu–Duffing equation will be developed.
First of all, to capture the post-buckling behavior, Equation (5) needs to be expanded to the third-order powers as follows
and it is further assumed that v3 → 0 and so that Equation (6) can be written as shown in Equation (26),
Inserting Equations (18) into Equation (26), the change of curvature is expressed in terms of w and its derivatives only, and the internal energy given by Equation (9) becomes
Similarly, inserting Equation (24) in Equation (10), the work of external loads takes the form
and the kinetic energy given by Equation (12) becomes
Thus, the Euler–Lagrange equation associated with the functional (13) is
and by introducing the dimensionless variables
Equation (30) can be written as
Making resort to the Galerkin method, the partial differential Equation (32) can be written as a set of ordinary differential equations (ODEs) by setting
where n ∈ ℕ indicates the nth mode shape, and N ∈ ℕ is the relevant number of mode shapes. By inserting Equation (33) in Equation (32), multiplying both sides by the weighting functions sin mθ, m ∈ {1, 2, …, N}, and integrating over the angle interval from 0 to 2π, one obtains the motion ODEs, which can be conveniently written as a first-order system, i.e.,
where a dot stands for differentiation with respect to the time τ, the coefficients i = 1, 2, 3 are
and the coefficients and i, j, k = 1, …, N, that produce the coupling between modal forms are omitted for the sake of compactness.
It is worth pointing out that the shape functions in Equation (33) do not make the change of curvature (26) null, exactly as it happens in the case of the classic first buckling shape (23). In this respect, the inextensibility represented by both Equations (18) plays only the role of an internal constraint that simplifies the formulation from a mathematical point of view, even if it reflects the physical aptitude of a thin ring to prefer bending over extensional deformation, as indeed it is also the case of thin hollow tubes also do [87].
Suppose that φ = φ(τ) is the stationary (i.e., non-transient) solution vector of Equations (34) and (35), and the motion is bounded. Then, the trajectories of the system cannot pass through all points of the phase space but are confined to moving in a compact (closed and bounded) manifold embedded in it. The phase space of a system is the space whose points uniquely represent all and only the possible states of the system itself. In general, the phase space has a dimension that is two times the number of degrees of freedom of the system, and the choice of coordinates needed to generate it, such as positions and velocities, is crucial in characterizing the system and its equations of motion. In the phase space, the evolution appears as a sequence of points or as a curve, depending on whether the system is discrete or continuous. To infer in a qualitative way the topology of the manifold on which the trajectories move, let one consider the motion φn, which is the nth component of φ, to be periodic and somehow modulated by another periodic motion, for instance, the forcing term Q (provided that it is assigned as a periodic function with non-vanishing frequency). The two motions can be represented by a trajectory on the surface of a two-dimensional torus, an invariant subspace of a three-dimensional phase space. Such a trajectory is indeed given by the combination of the two motions in the toroidal and poloidal directions through the remapping rules,
where is the toroidal angle (see Figure 5A).
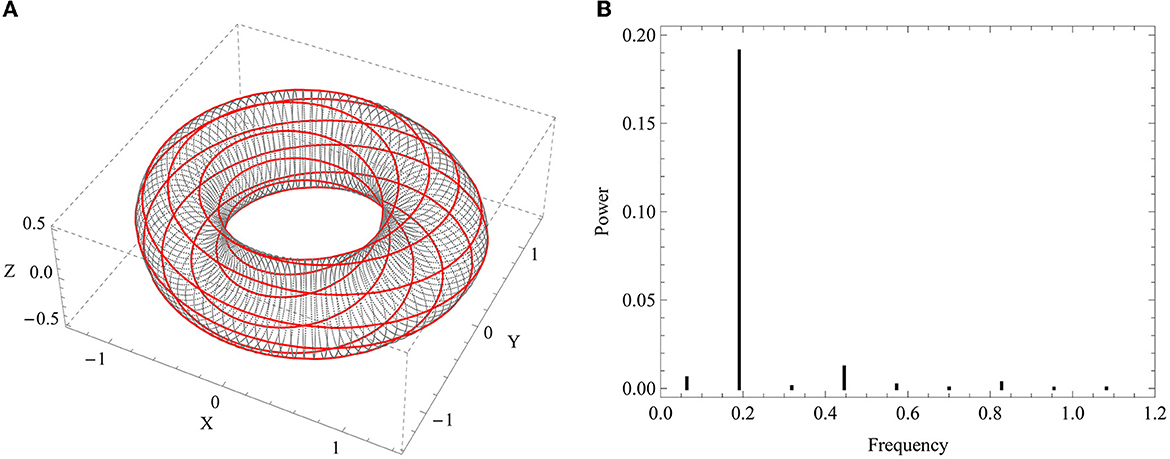
Figure 5. (A) Periodic solution (red curve) on the resonant torus. The hidden geometry of the torus in the space XYZ, i.e., the Cartesian coordinates of the flow computed via toroidal remapping, is made visible using poloidal sections drawn as dotted and gray lines. (B) Power spectrum of the periodic trajectory, which contains equally spaced spikes.
The ratio ρ between the modulated and modulating frequencies is called the rotation number. If ρ is a rational number (ρ ∈ ℚ), the motion is periodic with period ρT, where T is the period of modulating motion, taken as fundamental. In such a case, the frequencies are commensurate, and the trajectory is a closed curve on the torus (the red curve in Figure 5A), which is said to be a resonant torus. For this type of solution, it is possible to write explicitly, through a Fourier expansion, the power spectrum, which consists of equally spaced pulses or spikes (see Figure 5B). Typically, one calls harmonic responses (with respect to Q, for instance) the solutions with ρ = 1 and subharmonic responses those with ρ > 1.
If ρ is an irrational number, the frequencies are incommensurate, and the trajectory cannot close itself since the solution will not repeat periodically anymore. As the time increases, the trajectory becomes arbitrarily close to each point on the toroidal surface, densely filling it (for τ → ∞) in a neat way. In such a case, the response is a quasiperiodic motion, and the corresponding torus is non-resonant.
The third class of possible solutions is that of chaotic responses. A chaotic motion is indeed an aperiodic long-term behavior arising in a deterministic system, without any random or noisy input, as a consequence of the nonlinearity. Differently from periodic and quasiperiodic behaviors, the chaotic responses exhibit a strongly sensitive dependence on initial conditions, making nearby trajectories diverge exponentially fast.
In addition, the very basic information about the main types of stationary motions reported in Section 3.2, the qualitative description of the solution of Equations (34) and (35) can be rather complicated. It is possible to reduce the dynamics by constructing a discrete dynamical system of co-dimension 1 with respect to the original continuous system, in which the relevant properties of the orbits are preserved. Such a discrete description is named stroboscopic map, return map, first recurrence map, or Poincaré map, after Henri Poincaré (1854–1912), and it can be intuitively constructed as follows.
Without loss of generality, let one consider the flow shown in Figure 5A, which lies on a two-dimensional torus, and set a specified plane, which is called a phase plane, transversely to the torus. As time increases, the trajectory on the torus intersects the phase plane at the coordinates k = 1, 2, …, and it will do so infinitely as τ → ∞. Therefore, the Poincaré map associates the first point to the second and so on, from which the name first recurrence map. The Poincaré section is normal to the flow in the sense that periodic orbits starting on that subspace flow through it and not parallel to it. The graph of the map is, therefore, built by collecting the intersection coordinates on the phase plane. It must be observed that, in the general case, the Poincaré section is a hyper-surface of co-dimension 1, like the corresponding map. The resulting set of points from the Poincaré map forms a pattern that can be either regular or irregular.
If φn is a ρ-periodic function (with reference to Q, provided that it is assumed to be the fundamental modulating motion), a set of ρ points will be mapped on the Poincaré section. In the case of quasiperiodic motion, the Poincaré maps produce a closed curve in the phase plane, which can be interpreted, from a geometric point of view, as the cross section of the torus. Finally, Poincaré maps exhibit a folded and stretched fractal structure in case of a chaotic response. The transition from a quasiperiodic motion to a chaotic one implies the breaking of the torus, which is indeed one of the strongest indicators of chaotic behavior.
On the basis of the formulation introduced in Section 3.1 for the nonlinear dynamics of an elastic ring, results from several numerical simulations are collected in Figures 7, 8 in terms of Poincaré maps. To understand the dynamic behavior, several sets of initial conditions are considered. In particular, Equations (34) and (35) are integrated assuming that all the initial conditions, but φk(0) and , vanish, and we call the mode k the dominant degree of freedom. Therefore, it is set as follows:
It can be observed, and numerically verified, that such a choice implies that all the coupling terms in Equation (35) vanish. The results reported below are obtained by choosing the second mode (k = 2) as the dominant one. With reference to Figure 6, the motion is assumed to start at a configuration that is perturbed from the initial perfect round one (Figure 6A), and this allows the circular ring to deform dynamically (Figure 6B) also for maximum values of the forcing load, which would result below the statical critical pressure.
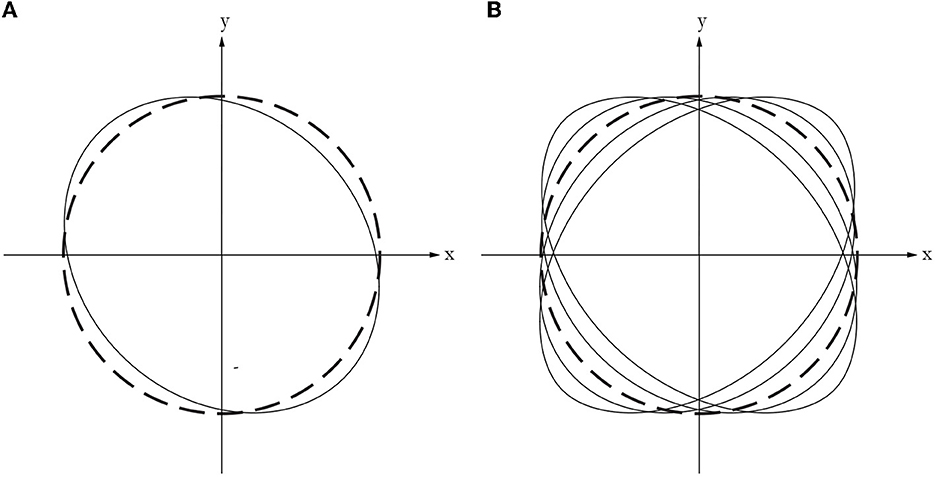
Figure 6. (A) Sketch of sample initial configuration, φk(0) = Φ, (continuous line), and (B) sketch of possible modes of vibrations (continuous lines) vs. undeformed configuration (dashed lines).
Provided that the forcing load is set as
the equation of motion of the parametrically excited dominant shape results from the Mathieu–Duffing type [78]. In the performed calculations, it is set Ω = 4.0, and the intensity δ ranges from 0.5 to 5.0 (δ = 1.0 being the static buckling load).
To depict the Poincaré sections with a sufficiently defined pattern, a sufficient number of points must be collected. Therefore, the simulation time spans over the interval 0 ≤ τ ≤ 2cπ/Ω, with c being a sufficiently large number of cycles of Q. In the following, c = 5 × 103 is set if not otherwise stated.
Figures 7, 8 appear as layered tori, each torus being an invariant manifold fixed by the initial conditions. These stable tori occupy a precise, simply or multiply connected, region of the phase space. The outside regions are unstable with rapidly divergent solutions. For instance, in the case of a simply connected stable region, the unstable one can be found by choosing initial conditions such that Φ ≈ ±5/9, and This is interesting since, according to the definitions given in Equation (3.1), it is Focusing on the stable solution of which the vast majority is quasiperiodic, it can be noticed that some periodic solutions can be found, too.
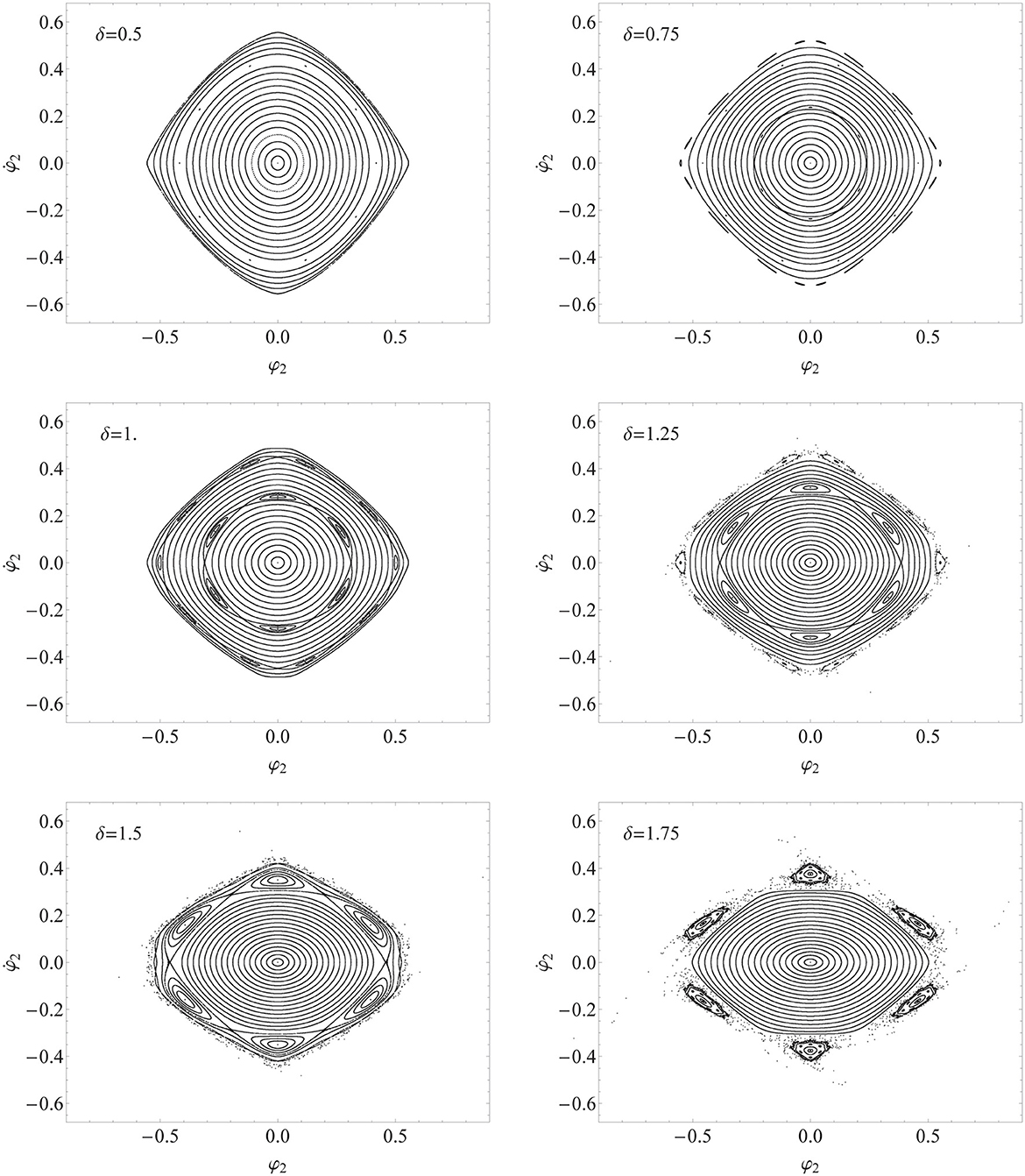
Figure 7. Poincaré maps in the displacement-velocity phase plane for several sets of initial conditions, see Equation (40), and load amplitude δ from half of the value of the first static critical load, (δ = 0.5), to δ = 1.75, at fixed load frequency (Ω = 4.0).
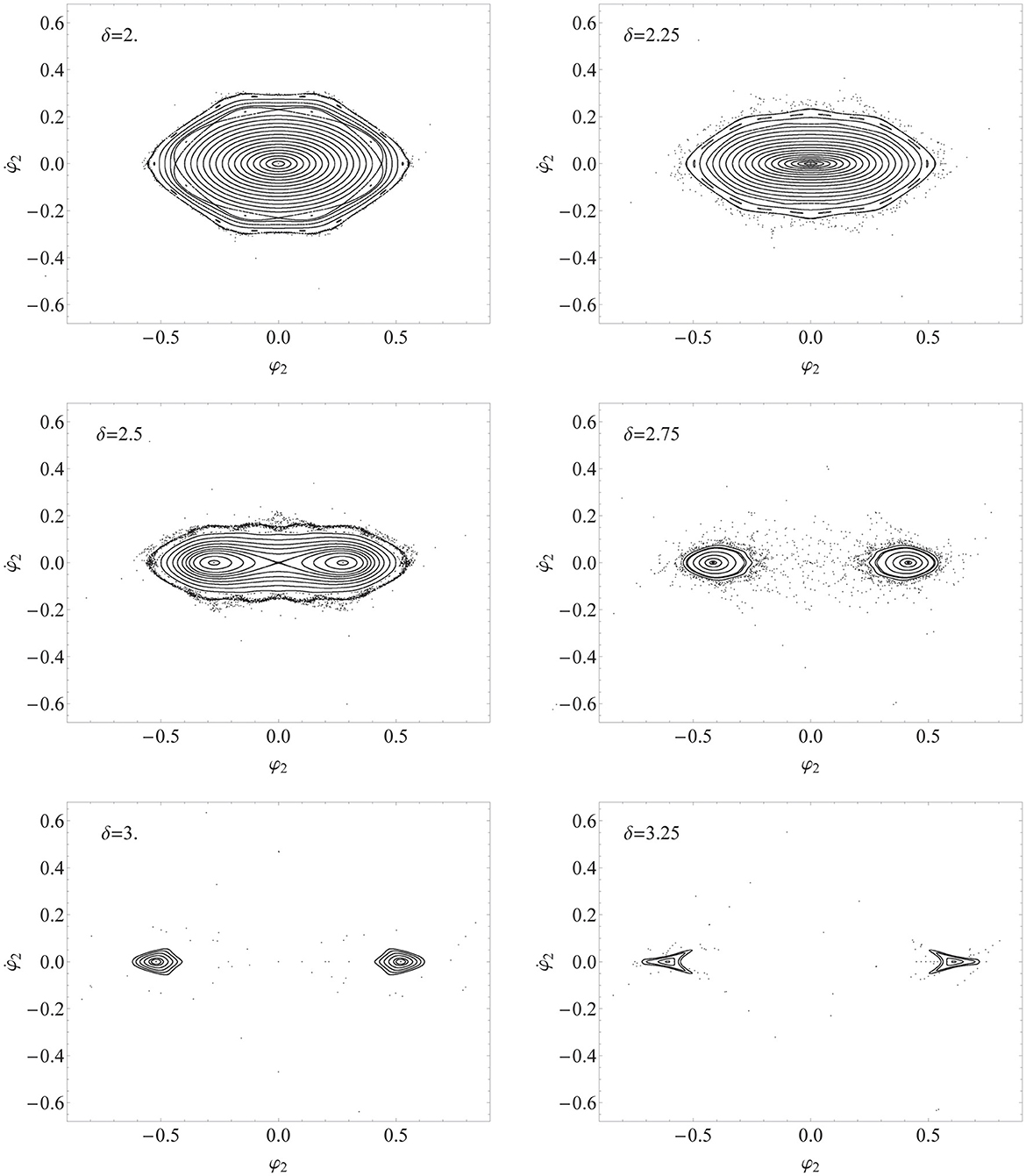
Figure 8. Poincaré maps in the displacement-velocity phase plane for several sets of initial conditions, see Equation (40), and load amplitude δ from two times the value of the first critical load (δ = 2.) up to δ = 3.25, at fixed load frequency (Ω = 4.0).
At δ = 0.5, a resonant solution is found for Φ = 0.4185636 and Since the trajectory in the phase space goes through the Poincaré plane 10 times per cycle of the forcing load, this is a subharmonic of order 10, i.e., a solution of period 10 with respect to Q. Such a periodic solution is shown in Figure 5A and can contribute to explaining the behavior of a resonant torus. In the corresponding power spectrum, (Figure 5B), the first pulse appears at a frequency of exactly Ω/(10 × 2π). The 10 points are located inside islands, which can be detected with the proper refinement of the grid of the initial conditions, as can be seen in Figure 9A. The islands correspond to tori showing multiply connected sections (i.e., multiperiodic tori). In the case under consideration, since the cross sections of the tori are made of 10 islands, we have 10-periodic tori. The points corresponding to the periodic solutions are called elliptic points and are alternated with hyperbolic ones. These latter are actually saddle points (see Figure 9B). The lines connecting the hyperbolic points represent the boundaries of the islands and separate regions of tori with different periodicities.
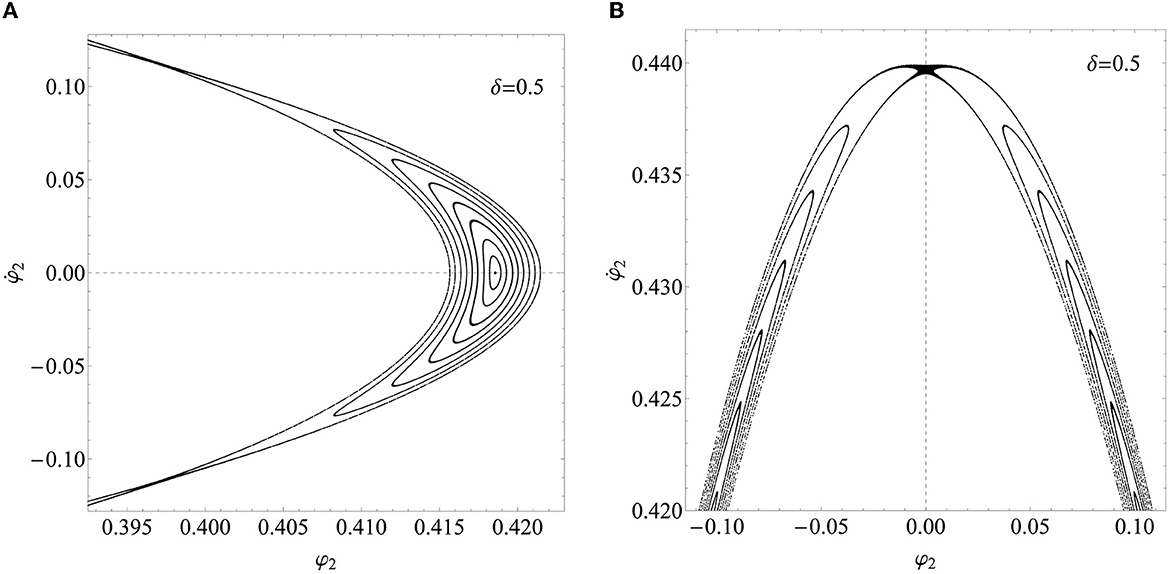
Figure 9. View enlargement of the Poincaré map for the solutions at δ = 0.5. In (A), one of the 10 islands, namely, that symmetric to the axis for positive φ2, is shown. The elliptic point, two hyperbolic points formed by the stable and unstable manifold bounding the island, and a number of 10-periodic tori are visible. In (B), the hyperbolic point on the axis φ2 = 0 for positive is shown (there is a symmetric one for negative ).
At δ = 0.75, the resonant solution of period 10 can still be found closer to the unstable region, but the small islands are still not visible at the resolution of the graphics in Figure 7. More interestingly, a new stratum of islands appears. Differently from the case of the 10-periodic tori, here two families of 3-periodic tori (i.e., their cross sections are made of three islands), develop approximately two 3-periodic solutions. In the case of the 10-periodic tori, initial conditions that are symmetric with respect to the origin of the axes lead to the same trajectory. By contrast, in the case of the two families of 3-periodic tori, two sets of symmetric conditions lead to two different trajectories, one on a torus of the first family and the other on a torus of the second. The islands belonging to a family of tori are alternated with those belonging to the other.
At δ = 1.00, the islands of the external 10-periodic tori and the two internal 3-periodic tori are larger. At both strata, elliptic and hyperbolic points are found.
The section at δ = 1.25 shows that the islands of the 3-periodic tori are still increasing and, at the same time, radially pushed toward the unstable region by that of the internal (simply connected or single) tori. These islands progressively enlarge as the load intensity δ increases. As a consequence, the 10-periodic tori enter the unstable region, and their islands progressively lose their stability.
Such a phenomenon is confirmed at δ = 1.50 and it is even more evident at δ = 1.75 where 3-periodic tori are detached from the stable region and show distorted shapes. More interestingly, other small islands, apparently corresponding to 18-periodic tori, develop inside the 3-periodic tori islands.
As δ increases, the onset of new periodic solutions can be observed (see δ = 2 and δ = 2.25).
About δ = 2.25, the cross section of internal tori starts to shrink along the −axis. At δ = 2.5, a saddle at the origin of axes separates an external stratum of single tori from an internal family of 2-periodic tori. These latter tori will survive for a while (δ = 2.75 and more), even after the destruction of the external single tori that vanish in the unstable region.
However, for some values of δ above 3.25, where the islands are already distorted, no stable solutions can be found, at least in the region of parameters that have been considered (0.5 ≤ δ ≤ 5).
Overall, the variety of dynamic behaviors of the elastic rings yielded by the solution of Equations (34) and (35) summarizes some results of the Kolmogorov–Arnold–Moser (KAM) theorem and of the related theory. The KAM theorem proved for the first time that, in Hamiltonian systems, quasiperiodic motions are generic and, thus, it radically changed the previously accepted idea that their dynamics were close to being integrable [88]. Without entering details, if a Hamiltonian (as in the present case, where no source of dissipation is considered) dynamical system is subject to a weakly nonlinear perturbation, some of the invariant tori are deformed while others are destroyed. In the present study, the process has been driven by changing initial conditions since neighboring initial conditions can be thought of as mutual perturbations. The criterion by which this occurs is a condition of “quasiresonance” on the frequencies of the motions (commensurability), and the KAM theorem quantifies the conditions on the perturbations for this to happen. Indeed, the deformed tori have an even number of points, appearing in pairs of elliptic and hyperbolic fixed points, in common with the undeformed tori. At the elliptic fixed points, the dynamics is the same as the main system, giving rise to a self-similar structure. Hyperbolic points, being fixed saddle points, present trajectories entering or moving away from the fixed point, and they are both invariant sets, i.e., stable and unstable manifolds, respectively. Noteworthy, the considered system may exhibit chaotic behavior originating from hyperbolic points. The region of phase space where the chaos develops must be confined and that happens in the case an erratic motion arises between invariant tori, which play the role of barriers. Since often the erratic motions that have been found in the present study develop in places very close to the unstable region, additional investigations would be necessary to determine if any of the motions shown in Figures 7, 8 may be classified as chaotic, or they are just unstable solutions that will diverge after a sufficiently long time.
In the present study, starting from a brief resumè of the possible implications in various fields of physics, engineering, and biology of the buckling instability and nonlinear dynamics of circular elastic rings, attention has been focused on the fundamental hypotheses at the basis of most classic treatments of the problem.
In this respect, a simple model for analyzing the nonlinear dynamic behavior of elastic rings under external pulsating loads has been proposed, and a depiction of the possible evolution of the dynamical system has been discussed in detail.
In the literature, the behavior of rings under external pressure load has been recognized to be governed by the Mathieu equation, which can actually be used as a mathematical model in a number of problems in engineering and physics. To cite but a few, these are the vibrations in elliptic membranes, the motion of an inverted pendulum with the suspension point undergoing vertical vibration, the stability of floating bodies, the ion trap, and the elastic oscillations of a ferromagnetic material. The solution of the Mathieu equation is expressed in terms of Mathieu functions, which are periodic in their argument only for certain so-called characteristic values of the ratio between the system and the loading frequencies. The solution may be stable, i.e., bounded, or unstable, i.e., diverging, and the transition curves between stable and unstable domains in the plane of parameters are related to the characteristic values.
The simple modeling proposed in this study leads to a nonlinear version of the Mathieu equation called the Mathieu–Duffing equation due to the presence of cubic nonlinearity. Indeed, the Mathieu–Duffing equation is a relevant combination of the Mathieu and Duffing equations, the latter being perhaps the most well-known and celebrated oscillator with cubic nonlinearity.
The analysis of the obtained results has shown that even the simple problem under consideration can give origin to very complex dynamics in the phase space. Since the considered equation of motion does not contain any dissipative term, the resulting dynamics is Hamiltonian, with a wide prevalence of quasiperiodic responses. This means that invariant tori are characterized by two not commensurate frequencies and curves over these tori are not closed and fill the tori, which are non-resonant. In the case of commensurate frequencies, the responses are periodic and close to themselves.
The implications for many of the practical problems of elasticity described in Section 1 can be countless, depending on the specific application. It goes without saying that adaptations of the governing equations may be needed with respect to the type of loading, the material model, and so on.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
IM and FG conceived the study. EB, IM, and FG contributed to the design of the study. IM developed the literature review related to the state of the art. EB developed the code and performed the numerical computations. EB and IM prepared the figures, edited the visualization, and drafted the manuscript. All authors contributed to the revision of the manuscript and read and approved the submitted version.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be interpreted as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Reis PM. A perspective on the revival of structural (in)stability with novel opportunities for function: from Buckliphobia to Buckliphilia. J Appl Mech. (2015) 82:111001. doi: 10.1115/1.4031456
2. Champneys AR, Dodwell TJ, Groh RM, Hunt GW, Neville RM, Pirrera A, et al. Happy catastrophe: recent progress in analysis and exploitation of elastic instability. Front Appl Math Stat. (2019) 5:34. doi: 10.3389/fams.2019.00034
3. Shamass R, Alfano G, Guarracino F. An investigation into the plastic buckling paradox for circular cylindrical shells under non-proportional loading. Thin Walled Struct. (2015) 95:347–62. doi: 10.1016/j.tws.2015.07.020
4. Shamass R, Alfano G, Guarracino F. An analytical insight into the buckling paradox for circular cylindrical shells under axial and lateral loading. Math Probl Eng. (2015) 2015:514267. doi: 10.1155/2015/514267
5. Shamass R, Alfano G, Guarracino F. On elastoplastic buckling analysis of cylinders under nonproportional loading by differential quadrature method. Int J Struct Stabil Dyn. (2017) 17:1750072. doi: 10.1142/S0219455417500729
6. Matsuzaki Y. Self-excited oscillation of a collapsible tube conveying fluid. In: Schmid-Schönbein GW, Woo SLY, Zweifach BW, editors, Frontiers in Biomechanics, New York, NY: Springer (1986). p. 342–50. doi: 10.1007/978-1-4612-4866-8_24
7. Amoozgar M, Fazelzadeh S, Khodaparast HH, Friswell M, Cooper J. Aeroelastic stability analysis of aircraft wings with initial curvature. Aerospace Sci Technol. (2020) 107:106241. doi: 10.1016/j.ast.2020.106241
8. Fraldi M, Guarracino F. Towards an accurate assessment of UOE pipes under external pressure: effects of geometric imperfection and material inhomogeneity. Thin Walled Struct. (2013) 63:147–62. doi: 10.1016/j.tws.2012.10.007
9. Kerdegarbakhsh M, Kiani Y, Esfahani S, Eslami M. Postbuckling of FGM rings. Int J Mech Sci. (2014) 85:187–95. doi: 10.1016/j.ijmecsci.2014.05.021
10. Babbs CF. The origin of Korotkoff sounds and the accuracy of auscultatory blood pressure measurements. J Am Soc Hypertens. (2015) 9:935–50. doi: 10.1016/j.jash.2015.09.011
11. Pevernagie D, Aarts RM, De Meyer M. The acoustics of snoring. Sleep Med Rev. (2010) 14:131–44. doi: 10.1016/j.smrv.2009.06.002
12. Hazel AL, Heil M. Surface-tension-induced buckling of liquid-lined elastic tubes: a model for pulmonary airway closure. Pro. of the Royal Soc. A: Math., Phy. and Engg Sci. (2005) 461:1847–68. doi: 10.1098/rspa.2005.1453
13. Schäfer W. Some biomechanical aspects of continence function. Scand J Urol Nephrol. (2001) 35:44–60. doi: 10.1080/003655901750174890
14. Van de Vosse FN, Stergiopulos N. Pulse wave propagation in the arterial tree. Annu Rev Fluid Mech. (2011) 43:467–99. doi: 10.1146/annurev-fluid-122109-160730
15. Hazel AL, Mullin T. On the buckling of elastic rings by external confinement. Philos Trans R Soc A Math Phys Eng Sci. (2017) 375:20160227. doi: 10.1098/rsta.2016.0227
16. Box F, Kodio O, O'Kiely D, Cantelli V, Goriely A, Vella D. Dynamic buckling of an elastic ring in a soap film. Phys Rev Lett. (2020) 124:198003. doi: 10.1103/PhysRevLett.124.198003
17. Chan HF, Zhao R, Parada GA, Meng H, Leong KW, Griffith LG, et al. Folding artificial mucosa with cell-laden hydrogels guided by mechanics models. Proc Natl Acad Sci USA. (2018) 115:7503–8. doi: 10.1073/pnas.1802361115
18. Dervaux J, Couder Y, Guedeau-Boudeville MA, Amar MB. Shape transition in artificial tumors: from smooth buckles to singular creases. Phys Rev Lett. (2011) 107:018103. doi: 10.1103/PhysRevLett.107.018103
19. Antoniou Kourounioti RL, Band LR, Fozard JA, Hampstead A, Lovrics A, Moyroud E, et al. Buckling as an origin of ordered cuticular patterns in flower petals. J R Soc Interface. (2013) 10:20120847. doi: 10.1098/rsif.2012.0847
20. Li B, Cao YP, Feng XQ, Gao H. Mechanics of morphological instabilities and surface wrinkling in soft materials: a review. Soft Matter. (2012) 8:5728–45. doi: 10.1039/c2sm00011c
21. Chen D, Jin L, Suo Z, Hayward RC. Controlled formation and disappearance of creases. Mater Horizons. (2014) 1:207–13. doi: 10.1039/C3MH00107E
22. Terwagne D, Brojan M, Reis PM. Smart morphable surfaces for aerodynamic drag control. Adv Mater. (2014) 26:6608–11. doi: 10.1002/adma.201401403
23. Guarino A, Poberaj G, Rezzonico D, Degl'Innocenti R, Günter P. Electro–optically tunable microring resonators in lithium niobate. Nat Photon. (2007) 1:407–10. doi: 10.1038/nphoton.2007.93
24. Wolf R, Breunig I, Zappe H, Buse K. Cascaded second-order optical nonlinearities in on-chip micro rings. Opt Exp. (2017) 25:29927–33. doi: 10.1364/OE.25.029927
25. Liang G, Huang H, Mohanty A, Shin MC, Ji X, Carter MJ, et al. Robust, efficient, micrometre-scale phase modulators at visible wavelengths. Nat Photon. (2021) 15:908–13. doi: 10.1038/s41566-021-00891-y
26. Wang Z, Ming D, Wang Y, Qiu C, Tan M. Resolving the scalability challenge of wavelength locking for multiple micro-rings via pipelined time-division-multiplexing control. Opt Exp. (2022) 30:24984–94. doi: 10.1364/OE.459927
27. Zhang Z, Neubauer J, Berry DA. Physical mechanisms of phonation onset: a linear stability analysis of an aeroelastic continuum model of phonation. J Acoust Soc Am. (2007) 122:2279–95. doi: 10.1121/1.2773949
28. Guarracino F, Simonelli M. The torsional instability of a cruciform column in the plastic range: analysis of an old conundrum. Thin Walled Struct. (2017) 113:273–86. doi: 10.1016/j.tws.2016.11.007
29. Bresse JAC. Cours de mécanique appliquée, professé à l'École impériale des ponts et chausées. Gauthier-Villars (1865).
30. Boussinesq J. Resistance d'un anneau à la flexion, quand sa surface extérieure supporte une pression normale, constante par unité de longueur sa fibre moyenne. Comptes Rendus. (1883) 97:843–48.
31. Lévy M. Memoire sur un nouveau cas intégrable du problème de l'élastique et l'une de ses applications. J Math Pures Appl. (1884) 10:5–42.
32. Chwalla E, Kollbrunner CF. Beiträge zum Knickproblem des Bogenträgers und des Rahmens. Stahlbau. (1938) 11:73–8.
33. Biezeno CB, Koch JJ. The generalized buckling problem of the circular ring. Koninklijke Nedetiansche Akademie van Wetenschappen, (1945) 49:477–86.
34. Boresi AP. A refinement of the theory of buckling of rings under uniform pressure. J Appl Mech. (1955) 22:95–102. doi: 10.1115/1.4010976
35. Timoshenko SP, Gere JM. Theory of Elastic Stability. New York, NY: McGraw-Hill Book Co. Inc. (1961).
36. Singer J, Babcock CD. On the buckling of rings under constant directional and centrally directed pressure. J Appl Mech. (1970) 37:215–8.
37. Budiansky B. Theory of buckling and post-buckling behavior of elastic structures. Adv Appl Mech. (1974) 14:1–65.
39. El Naschie MS. The initial post-buckling of an extensional ring under external pressure. Int J Mech Sci. (1975) 17:387–8.
40. Simitses GJ. An Introduction to the Elastic Stability of Structures. Englewood Cliffs, NJ: Prentice-Hall (1976).
42. Armenakas A, Herrmann G. Vibrations of infinitely long cylindrical shells under initial stress. AIAA J. (1963) 1:100–6.
43. Armenakas AE, Herrmann G. Buckling of thin shells under external pressure. J Eng Mech Div. (1963) 89:131–46.
45. El Naschie MS. A note on the conservativeness of a certain type of external pressure. J Appl Math Mech (1976) 56:557.
46. Hasegawa A, Matsuno T, Nishino F. Planar buckling and post-buckling behaviors of rings and arches subject to displacement dependent loads. Doboku Gakkai Ronbunshu. (1989) 1989:71–9.
47. Breslavsky ID, Amabili M, Legrand M, Alijani F. Axisymmetric deformations of circular rings made of linear and Neo-Hookean materials under internal and external pressure: a benchmark for finite element codes. Int J Nonlinear Mech. (2016) 84:39–45. doi: 10.1016/j.ijnonlinmec.2016.04.011
48. Mascolo I, Guarracino F. Revisitation of elastic buckling of circular rings: some analytic and numerical issues. Thin Walled Struct. (2022) 182:110287. doi: 10.1016/j.tws.2022.110287
50. Love AEH. A Treatise on the Mathematical Theory of Elasticity. New York, NY: Dover Publications (1944).
51. Rao S. Effects of transverse shear and rotatory inertia on the coupled twist-bending vibrations of circular rings. J Sound Vibrat. (1971) 16:551–66.
53. Goodier J, McIvor I. The elastic cylindrical shell under nearly uniform radial impulse. J Appl Mech. (1964) 31:259–66.
55. Hawkings D. A generalized analysis of the vibrations of circular rings. J Sound Vibrat. (1977) 54:67–74.
56. Simmonds J. Accurate nonlinear equations and a perturbation solution for the free vibrations of a circular elastic ring. J Appl Mech. (1979) 46:156–60.
57. Chidamparam P, Leissa AW. Vibrations of planar curved beams, rings, and arches. Appl Mech Rev. (1993) 46:467–83.
58. Dempsey K. Dynamic non linear forcing of elastic rings. Proc R Soc Lond Ser A Math Phys Eng Sci. (1996) 452:1927–43.
59. Dzhanelidze G, Radtsig M. On the dynamic stability of an elastic ring subjected to periodic uniform distributed loading (in Russian). Priklad Matam i Mekh 4. (1940) 55.
61. Langhaar H, Boresi AP, Carver D. Energy theory of buckling of circular elastic rings and arches. In: Proceedings of Second U.S. National Congress of Applied Mechanics. Ann Arbor, MI: University of Michigan (1954) 437–43
62. Boresi AP, Reichenbach HC. Energy methods in parametric excitation of rings. Nuclear Eng Design. (1967) 6:196–202.
64. Seidel B, Erdelyi E. On the vibration of a thick ring in its own plane. J Manufact Sci Eng. (1964) 86:240–44.
66. Matsunaga H. Effects of higher-order deformations on in-plane vibration and stability of thick circular rings. Acta Mech. (1997) 124:47–61.
67. Friedman Z, Kosmatka J. An accurate two-node finite element for shear deformable curved beams. Int J Num Methods Eng. (1998) 41:473–98.
68. Eisenberger M, Efraim E. In-plane vibrations of shear deformable curved beams. Int J Num Methods Eng. (2001) 52:1221–34. doi: 10.1002/nme.246
69. Forgit C, Lemoine B, Le Marrec L, Rakotomanana L. A Timoshenko-like model for the study of three-dimensional vibrations of an elastic ring of general cross-section. Acta Mech. (2016) 227:2543–75. doi: 10.1007/s00707-016-1618-1
70. Cooley CG, Parker RG. Limitations of an inextensible model for the vibration of high-speed rotating elastic rings with attached space-fixed discrete stiffnesses. Eur J Mech A Solids. (2015) 54:187–97. doi: 10.1016/j.euromechsol.2015.06.012
71. Lindberg HE. Buckling of a very thin cylindrical shell due to an impulsive pressure. J Appl Mech. (1964) 31:267–72.
72. Florence A. Buckling of viscoplastic cylindrical shells due to impulsive loading. AIAA J. (1968) 6:532–7.
73. Anderson D, Lindberg H. Dynamic pulse buckling of cylindrical shells under transient lateral pressures. AIAA J. (1968) 6:589–98.
74. Lindberg HE. Stress amplification in a ring caused by dynamic instability. J Appl Mech. (1974) 41:392–400.
75. Lindberg HE, Florence AL. Dynamic Pulse Buckling: Theory and Experiment. Dordrecht: Martinus Nijhoff Publishers (1987).
76. Amabili M, Païdoussis MP. Review of studies on geometrically nonlinear vibrations and dynamics of circular cylindrical shells and panels, with and without fluid-structure interaction. Appl Mech Rev. (2003) 56:349–81. doi: 10.1115/1.1565084
77. Putelat T, Triantafyllidis N. Dynamic stability of externally pressurized elastic rings subjected to high rates of loading. Int J Solids Struct. (2014) 51:1–12. doi: 10.1016/j.ijsolstr.2013.08.002
78. Babilio E. The Duffing–Mathieu equation arising from dynamics of post–buckled beams. In: Lacarbonara W, Balachandran B, Ma J, Tenreiro Machado JA, Stepan G, editors. Nonlinear Dynamics of Structures, Systems and Devices. Cham: Springer International Publishing (2020). p. 267–75.
80. Kyriakides S, Babcock CD. Large deflection collapse analysis of an inelastic inextensional ring under external pressure. Int J Solids Struct. (1981) 17:981–93.
81. Thurston GA. Application of Newton's Method to Postbuckling of Rings Under Pressure Loadings. NASA techical report, NASA Langley Research Center, Hampton. (1989).
82. Fu L, Waas A. Initial post-buckling behavior of thick rings under uniform external hydrostatic pressure. J Appl Mech. (1995) 62:338–45.
83. Kim D, Chaudhuri RA. Postbuckling of moderately thick imperfect rings under external pressure. J Eng Mech. (2006) 132:1273–6. doi: 10.1061/(ASCE)0733-9399(2006)132:11(1273)
84. Wu B, Yu Y, Li Z. Analytical approximations to large post-buckling deformation of elastic rings under uniform hydrostatic pressure. Int J Mech Sci. (2007) 49:661–8. doi: 10.1016/j.ijmecsci.2006.11.003
85. Rehfield L. Initial postbuckling of circular rings under pressure loads. AIAA J. (1972) 10:1358–9.
86. El Naschie MS, El Nashai A. Influence of loading behavior on the post buckling of circular rings. AIAA J. (1976) 14:266–7.
87. Angelillo M, Babilio E, Fortunato A. Folding of thin walled tubes as a free gradient discontinuity Problem. J Elast. (2006) 82:243–71. doi: 10.1007/s10659-005-9033-1
Keywords: circular rings, buckling, nonlinear dynamics, Hamiltonian system, Mathieu-Duffing equation
Citation: Babilio E, Mascolo I and Guarracino F (2023) From static buckling to nonlinear dynamics of circular rings. Front. Appl. Math. Stat. 9:1115227. doi: 10.3389/fams.2023.1115227
Received: 03 December 2022; Accepted: 13 February 2023;
Published: 13 March 2023.
Edited by:
Axel Hutt, Inria Nancy - Grand-Est Research Centre, FranceReviewed by:
Paolo S. Valvo, University of Pisa, ItalyCopyright © 2023 Babilio, Mascolo and Guarracino. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ida Mascolo, aWRhLm1hc2NvbG9AdW5pbmEuaXQ=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.