Salt and Pepper Noise Removal Method Based on the Edge-Adaptive Total Variation Model

Introduction

Image denoising is an important pre-processing step in the field of digital image processing. In real world, due to the working environment, electronic devices, and image transmission channels in the image acquisition process, the image could be polluted by noise, which will eventually lead to the degradation of image quality. With the application fields of biomedicine, aerospace, military, and public security, the requirements for image quality are getting higher and higher, and the quality of noise pre-processing greatly affects the subsequent steps of image processing such as segmentation, restoration, and feature extraction. Image denoising technology is particularly important and has attracted extensive attention from the academic community. It is generally believed that image denoising methods are divided into two categories: spatial domain and transform domain denoising methods [1]. The spatial domain denoising method is relatively straightforward. It directly denoises by processing the mutant pixels. Its representative methods include median filtering, neighborhood averaging, mean filtering, etc. The transform domain denoising method first needs to transform the image from the two-dimensional image domain to a more tractable target domain, and then perform subsequent processing. Common transformation methods include Fourier Transform, Haar Transform, Discrete Cosine Transform, wavelet transform, and so on.

Traditional denoising algorithms generally have a trade-off between the denoising effect and the preservation of edges. For example, for salt and pepper noise, median filtering is widely regarded as an effective processing method. In 1971, researcher Turkey first proposed the concept of median filtering [2], however, this method adopts the same filtering method for all pixels, which removes noise and also causes over-smoothing of edge and texture areas, which weakens image features. Similarly, neighborhood filtering, Gaussian filtering, etc., also have such drawbacks. At present, the denoising method based on a partial differential equation is widely considered to have a better preservation effect for edge and texture area while denoising. In 1992, Rudin et al. [3] creatively proposed the ROF model based on the second-order partial differential equations for the first time in image denoising. It minimizes the total variation norm of the image under the constraint of Lagrangian multipliers so that the image details polluted by the Gaussian noise can be better processed. However, because of its large amount of computation, it has the disadvantage of taking a long time to run. Moreover, it has a large dependence on the regularization parameter. When the value of the regularization parameter is too small, it will lead to the appearance of the staircase effect. Based on the model of Rudin et al., Chen et al. [4] introduced an adaptive regularization parameter to propose an adaptive total variation model. The model deals with gamma noise, which improves the model's ability to remove noise in uniform areas. In 2003, Bing et al. [5] proposed a new adaptive model to remove the staircase effect of the ROF model. However, the effect of the model to remove noise has a strong dependence on the model parameters. In 2006, Zhang et al. [6] proposed an adaptive total variation model, which overcomes the defect of over-reliance on model parameters. In 2011, Liu et al. [7] proposed an adaptive total variation model for fast denoising to better preserve the edge details of the image, which has great advantages in the processing of Gaussian noise. In 2017, Pan [8] proposed an image block denoising method based on adaptive total variation to solve the problem of insufficient boundary processing of the traditional total variation algorithm, but this model cannot handle salt and pepper noise well. In 2019, Fu et al. [9] proposed an image denoising algorithm based on generative classification. The algorithm takes the noisy block as the basic unit and adopts the patch clustering method to optimize the repaired dataset to obtain a better denoising effect. It is an effective method to remove salt and pepper noise of different intensities. In 2019, Zhou et al. [10] proposed an improved adaptive inverse distance weighting algorithm, which not only has a better filtering effect on salt and pepper noise but also preserves the edge information of the image. In 2019, Fu et al. [11] combined the NLSF processing step and the CNN training step. They propose a non-local switching filter convolutional neural network denoising algorithm (NLSF-CNN) for salt and pepper noise removal. In 2019, Zhang et al. [12] proposed a Mixed Variational with L¹ Fidelity Model for Removal of Salt and Pepper Noise. The model has good denoising performance and edge preservation ability, and the algorithm also has high execution efficiency. In 2019, Fu et al. [13] proposed a Patch-based contour prior image denoising for salt and pepper noise, which can effectively retain image details while denoising. In 2020, Xu et al. [14] proposed a method for Iterative Inverse Distance Weighting (IIDW) filtering to remove salt and pepper noise. The algorithm can run faster while having a higher denoising ability. In 2020, the adaptive weighted mean filtering algorithm proposed by Zha et al. [15] has a good denoising effect on high-density salt and pepper noise images. In 2020, Guo et al. [16] proposed an adaptive iterative mean filtering algorithm to remove salt and pepper noise. The algorithm only filters the noise points and does not process the non-noise points, so the method has a good denoising effect. In 2020, Yan [17] improved Zhang Hongying's adaptive total variation model, so that the model cannot only effectively suppress the staircase effect, but also adaptively control the diffusion of different areas of the image to different degrees and retain more edge texture information. But its time complexity is very high and how to choose more reasonable parameters needs further research. In 2021, Fu et al. [18] proposed a Texture-Aware Neural Network called TANet. The method successfully uses deep neural networks for image denoising. And it can protect the details of the image while denoising. In 2021, Thanh et al. [19] proposed a robust impulse denoising method based on noise accumulation and harmonic analysis technique (NAHAT filter). This method can effectively remove high-density impulse noise while preserving image structures such as edges and textures. In 2021, Li et al. [20] proposed a median filter algorithm (SSMF) to remove high-density salt and pepper noise. The algorithm performs noise detection on the salt and pepper noise image, and then only uses the signal points around the noise pixels to perform median filtering on the noise points. So it has better denoising ability and detail protection ability. In 2021, Ma et al. [21] proposed a high-speed adaptive median filtering algorithm for salt and pepper noise. The algorithm can save a lot of computing time while effectively removing salt and pepper noise. In 2021, He [22] proposed a salt and pepper noise image denoising method based on L1 norm and adaptive total variation. This method can effectively remove high-density salt and pepper noise and has a good edge preservation effect.

Combined with the adaptive total variation model, the characteristics of the main edges of the image can be effectively preserved during denoising, and the median filter has the characteristics of good removal of salt and pepper noise without considering the preserved edges. This paper proposes an edge-adaptive total variational model. The model first obtains the binary image of the edge area and non-edge area of the image polluted by salt and pepper noise through basic operations such as edge extraction, expansion, and image inversion, and compares them with the ATV model and the image after the median filtering. Multiply and finally get the denoised image through image addition. Compared with the processing results of other denoising methods, the model proposed in this paper has a significant improvement in the preservation of edge regions and details while denoising. The components of the paper are as follows: the first part introduces the importance, existing problems, and research status of image denoising; the second part discusses the salt and pepper noise, median filter, adaptive total variational model, and the edge-adaptive variational model proposed in this paper; the third part shows the processing results of the edge-adaptive total variation model on the test image, and compares the values of PSNR (Peak Signal to Noise Ratio) and SSIM (Structural Similarity) of the processing results of this method and other denoising methods; the fourth part summarizes the experiment. Finally, the references of this article are listed.

Edge-Adaptive Total Variation Model for Image Denoising

Salt and Pepper Noise

Salt and pepper noise is composed of pepper noise and salt noise, and is generally generated due to factors such as external environment and device performance during image transmission and acquisition. The black pixels corresponding to pepper noise usually appear in the brighter areas of the image, and the white pixels corresponding to salt noise usually appear in the darker areas of the image [23]. The two kinds of noise appear at the same time and are randomly distributed, and the image will show a noisy effect of black and white noise. Salt and pepper noise is usually not conducive to image edge extraction, restoration, and other operations. Since the pixel value of the noise point is quite different from the pixel value of its neighbors [24], it can usually be removed by a median filter. Images contaminated by salt and pepper noise of different intensities are shown in Figure 1.

FIGURE 1

Figure 1. (A) is the original image; (B) is the image contaminated by salt and pepper noise with an intensity of 5; (C) is an image contaminated by salt and pepper noise with an intensity of 40.

Median Filter Denoising

The standard median filter is a typical nonlinear filtering method with a simple idea and fast processing, which is most suitable for processing impulse noise such as salt and pepper noise. The image consists of thousands of pixels, and the pixels polluted by noise are often isolated from each other. To remove these isolated pixels, a simple idea is to replace the pixel value with its surrounding pixel value. The median filter is based on this idea, which establishes a window of size n^*n. It scans each pixel from left to right and from top to bottom, sorts the n² pixels contained by the pixel value, and selects the intermediate value to replace the pixel value of the processing pixel, thereby removing impulse noise. This simple processing works well for images with low noise contamination density, but as the noise density increases, the noises are no longer isolated. To ensure the removal effect, the window size needs to be enlarged, which also leads to blurred edges and details.

As shown in Figure 2, when image A is polluted by salt and pepper noise with a density of 0.1, A 3^*3 window is used. The result image C shows that the noise is completely removed. Compared with the original image A, the edge of the coin is better preserved. When the noise density is increased to 0.3, the 3^*3 window size cannot completely remove the noise. Using 5^*5 window size processing, although the noise in the result image F is removed, serious blurring occurs at the edges and details of coins. By comparing Figures 2A,C–F, it is seen that the smoothed area after median filtering is basically the same as the corresponding area of the original image, and the smoothed area does not depend strongly on the size of the filtering window. Therefore, median filtering is more suitable for processing smooth regions.

FIGURE 2

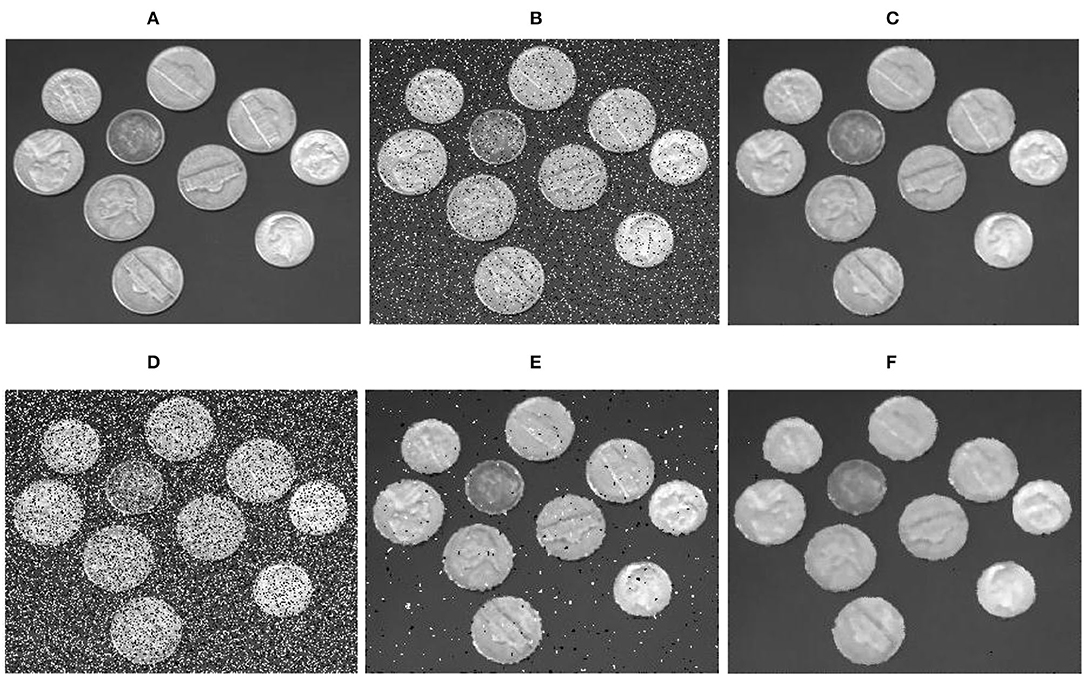
Figure 2. (A) is the original image, (B) is the image polluted by salt and pepper noise with a density of 0.1, (C) is an image after median filtering with a window size of 3*3, (D) is an image polluted by salt and pepper noise with a density of 0.3, (E) is the image after median filtering with a window size of 3*3, and (F) is the image after median filtering with a window size of 5*5.

Adaptive Total Variation Model

The difference between adjacent pixels in an image is called the image gradient. The larger the image gradient, the larger the difference between adjacent pixels, and the more noise points the image may contain. Conversely, there are relatively few noise points in the image. The Total variation model can be used to represent the sum of squares of image gradients. Since the pixels of the image have discrete characteristics, we assume that u_{i, j} represents the pixels in the i-th row and the j-th column of the image polluted by salt and pepper noise. So TV(u) can be expressed as:

$\begin{array}{ll}TV(u)={\displaystyle \sum _{i,j}}|u_{i+1,j}-u_{i,j}|+|u_{i,j+1}-u_{i,j}|& (1)\end{array}$

Image denoising needs to make the gradient of the denoised image smaller on the premise that the basic information of the original noise image is preserved. We assume that f_{i, j} is the pixel of the original noise image, and u_{i, j} is the denoised image pixel. The total variation image denoising model proposed by Rudin et al. in [3] can be expressed as:

$\begin{array}{ll}TV{F}_{\mu }(u)={\displaystyle \underset{u}{\text{arg }minTV(u)}}+\frac{\mu }{2}{{\displaystyle \sum _{i,j}}(f_{i,j}-u_{i,j})}^2& (2)\end{array}$

In Equation (2), $\frac{\mu }{2}{\sum _{i,j}(f_{i,j}-u_{i,j})}^2$ is the fidelity term used to preserve the characteristics of the image, and TV(u) is the regular term used to ensure the smoothness of the image. We use μ as the regularization parameter. The smaller the μ, the stronger the denoising ability. However, when the value of μ is too small, the edge texture information in the denoised image will be over-smoothed, and a staircase effect will also occur. In 2001, Liu et al. proposed an Adaptive Total Variational image denoising model [7]:

$\begin{array}{ll}ATV{F}_{\mu }(u)=\text{arg}{\displaystyle \underset{u}{\text{min}}}\lambda TV(u)+\frac{\mu }{2}{{\displaystyle \sum _{i,j}}(f_{i,j}-u_{i,j})}^2& (3)\end{array}$

The model firstly pre-processes the original noise image to obtain the image a after image edge enhancement. To eliminate the noise and better protect, the information such as the details and texture of the image, the model introduces an adaptive parameter λ , which has different response values in the edge area and non-edge area of the image. The value of λ is calculated using the image edge detection operator [25] on the preprocessed image a. When α = 0°, d${}_{0^{\bullet }}$ = $d_{0^{°}}=\frac{1}{12}\left[\begin{array}{ccc}& A_1& \\ A_2& M& A_2\\ & A_1& \end{array}\right]$, M = $\left[\begin{array}{c}1\\ \mathrm{\text{-}}1\\ \end{array}\begin{array}{c}2\\ \mathrm{\text{-}}2\\ \end{array}\begin{array}{c}2\\ \mathrm{\text{-}}2\\ \end{array}\begin{array}{c}1\\ \mathrm{\text{-}}1\\ \end{array}\right]$, A₁ = $\left[\begin{array}{c}0\\ 0\\ \end{array}\begin{array}{c}0\\ 0\\ \end{array}\begin{array}{c}0\\ 0\\ \end{array}\begin{array}{c}0\\ 0\\ \end{array}\begin{array}{c}0\\ 0\\ \end{array}\begin{array}{c}0\\ 0\\ \end{array}\right]$, A₂ = $\left[\begin{array}{c}0\\ 0\\ \end{array}\right]$, define the edge detection operator d_α to be obtained by rotating d${}_{0^{\bullet }}$ by an angle α∈{0°, 45°, 90°, 135°} [7]. According to the definition of edge detection operator d_α, we assume that ⊗ represents the convolution operation, then the adaptive parameter in the Adaptive Total Variational model formula (3) is

$\begin{array}{ll}\lambda =\frac{1}{1+\sqrt{{\displaystyle \sum _{\alpha \in \Phi }}{(d_{\alpha }\otimes a)}^2}}\in (0,1]& (4)\end{array}$

The purpose of our definition of convolution is that by performing convolution operations on the image in four directions of 0°, 45°, 90°, and 135°, we can get response values of different sizes. The convolution operation of the image edge area will get a larger response value, and the convolution operation of the non-edge area will get a smaller response value, and the value of λ will change with the change of the response value.

Then we analyze the formula (4) in detail, in non-edge areas of the image, $\sum _{\alpha \in \Phi }{(d_{\alpha }\otimes a)}^2$ tends 0 and λ tends 1. At this time, the Adaptive Total Variation Model (3) has a similar denoising effect as the Total Variation Model (2). However, in the edge region of the image, $\sum _{\alpha \in \Phi }{(d_{\alpha }\otimes a)}^2$ tends to infinity, and λ tends to 0. When the regularization parameter μ takes the same value, the fidelity term in the Adaptive Total Variation Model (3) has a larger proportion than the fidelity term in the Total Variation Model (2), while the proportion of the sum of image gradients is small. This operation can ensure the image owns a certain edge-preserving effect in the edge area denoising.

As shown in Figure 3, when μ = 0.01, it can be seen that the ATV model retains the main edge well, but there is a staircase effect in the non-edge region. When μ = 0.015, the salt and pepper noise in non-edge regions cannot be removed well, but the main edge preservation effect is still good.

FIGURE 3

Figure 3. Example of denoising results (A) is the ATV denoising image with μ = 0.01; (B) is the ATV denoising image with μ = 0.015.

Edge-Adaptive Total Variational Model

Combining the characteristics of the above two denoising methods, we propose an edge-adaptive total variation method. The specific steps are as follows:

Here, we assume that the time complexity of matlab's system function is O(1), then the analysis of the time complexity of the edge adaptive total variation model is as follows:

According to the algorithm pseudocode of the image preprocessing stage (Algorithm 1), we can easily conclude that the time complexity of this part of the algorithm is O(1).

ALGORITHM 1

Algorithm 1. Image preprocessing.

According to the pseudocode of Algorithm 2, it can be concluded that the edge-preserving ATV model uses at most triple loops in image denoising processing. The time complexity of the algorithm statement in the loop structure is O(1). Therefore, according to the calculation of the time complexity, it is easy to get the time complexity of this part to be O(n³).

ALGORITHM 2

Algorithm 2. Adaptive total variation model denoising.

According to the pseudo code of Algorithm 3, we can see that this part of the algorithm calls the edge-preserving ATV model shown in Algorithm 2 in the second line, and the rest of the lines call the processing function provided by the system, so according to the calculation of time complexity properties, we can obtain that the time complexity of the edge-adaptive total variational model is O(n³).

ALGORITHM 3

Algorithm 3. Image sub-regional denoising and stitching.

Experiment

The experimental environment of this paper is Windows 10 operating system, and the experimental platform is Matlab R2016a. To verify the denoising ability of the salt and pepper noise based on the edge-adaptive total variation model, the parameter μ of the model is set to 0.01, and the experimental images under different noise intensities are denoised. The denoised image is shown in Figure 4. The values of PSNR and SSIM of this method are calculated, and the values of this method are compared with those of median filter, Detail-preserving median based filters in image processing (SWM), A Dynamic Median Filter Algorithm for Adaptive Adjusting Window Dimension (DMFA), two-dimensional Adaptive Denoising Filtering, Noise Adaptive Switching Edge Preserving Filtering (NASEPF), Total Variation Model (TV), and Adaptive Total Variation Model (ATV), as shown in Table 1. Among these methods, the median filter, Total Variation Model (TV) and Adaptive Total Variation Model (ATV) have been introduced above, and the introduction of two-dimensional Adaptive Denoising Filtering, DMFA and Noise Adaptive Switching Edge Preserving Filtering (NASEPF) is as follows:

FIGURE 4

Figure 4. The result of the edge-adaptive total variation for different intensities of salt and pepper noise (A) 10% salt and pepper noise map; (B) 20% salt and pepper noise map; (C) 30% salt and pepper noise map; (D) 10% salt and pepper noise map noise result graph; (E) 20% salt and pepper noise result graph; (F) 30% salt and pepper noise result graph; (G) 40% salt and pepper noise graph; (H) 50% salt and pepper noise graph; (I) 60% salt and pepper noise graph; (J) 40% salt and pepper noise result graph; (K) 50% salt and pepper noise result graph; and (L) 60% salt and pepper noise result graph.

TABLE 1

Table 1. PSNR and SSIM scoring results for different salt and pepper noise levels.

The DMFA method first estimates the image noise density, and then determines the optimal window dimension corresponding to the traditional median filter under different noise densities, and establishes a functional relationship, and uses the functional relationship to adaptively adjust the window dimension. Pixel values are replaced with filtered-fixed pixel values to prevent details from being blurred. Two-dimensional adaptive denoising filtering works by adaptively applying a Wiener filter (a type of linear filter) to an image. The Wiener filter adapts itself to the local variance of the image. Noise Adaptive Switching Edge Preserving Filtering refers to a special kind of filter that adaptively denoises in the filtering process and can effectively preserve the edge information in the image.

When adding salt and pepper noise with an intensity of 20 to different experimental images, set μ to 0.016. The obtained experimental results are shown in Figure 5. The experimental data corresponding to the experiment are shown in Table 2.

FIGURE 5

Figure 5. The result of edge-adaptive total variation on different images with 20% salt and pepper noise (A) 20% noise map of house image; (B) 20% noise map of feather image; (C) 20% noise map of toysflash image; (D) house denoising map; (E) feather denoising map; (F) toysflash denoising map.

TABLE 2

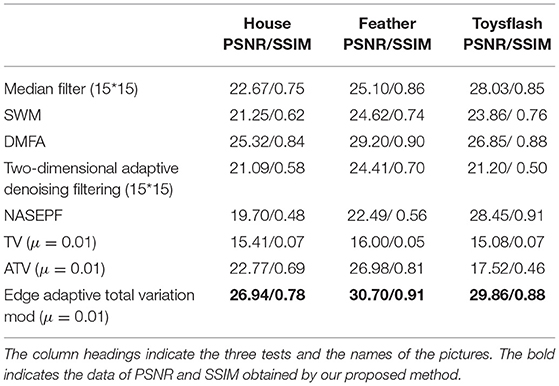
Table 2. PSNR and SSIM scoring results of different images with 20% salt and pepper noise intensity.

The experimental results show that when the salt and pepper noise intensity is small, the edge-adaptive total variation model has good denoising and edge retention effects. At the same time, the intensity of salt and pepper noise is high, the processing effect of the edge-adaptive total variation model needs to be improved.

Conclusion

Summary of Research Work

Denoising of images with salt and pepper noise has always been a research hotspot in the field of image processing. How to make a reasonable trade-off between denoising effect and edge preservation has triggered successive studies by a large number of scholars. The characteristic of the median filter makes it perfectly suitable for noise processing in the smooth area of the image, but when the filter window is too large, the edge information of the denoised image cannot be well preserved. However, the adaptive total variation model has stricter requirements on the regularization parameters when denoising salt and pepper noise. When the value of the regularization parameter is too small, the denoised image will have a staircase effect, and when the regularization parameter is too large, although the step effect can be better overcome, the salt and pepper noise cannot be removed well. But in both cases, the denoised images have good edge preservation. By analyzing their advantages and combining edge detection, image stitching and other technologies, this paper proposes an edge-adaptive variational model. The experimental results show that the model can effectively protect the main edge information of the image while removing the salt and pepper noise.

Future Expectations

The edge-adaptive total variation model not only has a good denoising effect but also can preserve the main edge information of the noisy image. However, the experimental results show that when the edge-adaptive total variation model processes images with high-intensity salt and pepper noise, the processing effect of the model needs to be improved. Second, the model has ordinary processing effects on the more detailed edges of the image. So the model can be optimized for this problem in the future. Finally, since the model involves a large number of operations such as image gradients and partial differential equations during image denoising, the algorithm runs for a long time when the scale of the processed images is large. Therefore, how to optimize the algorithm to make it have a shorter running time will also be the focus of the next research work.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

BF provided professional guidance for the presentation and writing of this article. YJ analyzed the characteristics of the TV model and the ATV model, combined the ATV model with image segmentation and splicing, conducted experiments on the edge-adaptive total variation model proposed in this paper, provided the experimental results, and participated in the writing of the manuscript. HW is mainly responsible for the processing and writing of image segmentation, negation, and dilation in the experiment. YC has conducted extensive information gathering and manuscript writing on other approaches to dealing with salt and pepper noise. All authors revised, read, and approved the submitted version.

Funding

This work was supported by Natural Science Basic Research Project (for Universities of Liaoning) of Liaoning Provincial Department of Education, China (No. LJKZ0986), and Science and Technology Innovation Found (Youth Science and Technology Star) of Dalian, China (No. 2018RQ65).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Fu B. Research on image denoising method based on multi-scale transformation. [master's thesis]. Liaoning Normal University, Dalian (2009).

Google Scholar

2. Tuckey JW. Exploratory Data Analysis. Boston, MA: Ad-dison-Wesley Pub. Co (1997).

Google Scholar

3. Rudin LI, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms. Physica D: Nonlinear Phenomena. (1992) 60:259–68. doi: 10.1016/0167-2789(92)90242-F

CrossRef Full Text | Google Scholar

4. Chen DQ, Cheng LZ. Spatially adapted total variation model to remove multiplicative noise. IEEE Trans Image Process. (2012) 21:1650–62. doi: 10.1109/TIP.2011.2172801

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Bing S. Topics in variational PDE image segmentation, inpainting and denoising. [master's thesis]. University of California Los Angeles, California (2003).

Google Scholar

6. Zhang HY, Peng QC. Total variation adaptive image denoising model. Optoelectronic Eng. (2006) 33:50–3. doi: 10.3969/j.issn.1003-501X.2006.03.012

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Liu W, Wu CS, Xu T. Adaptive total variation image denoising model and its fast solution. Appl Res Comput. (2011) 28:4797–800.

PubMed Abstract | Google Scholar

8. Pan JQ. Image block denoising method based on adaptive total variation. [master's thesis]. Jinan University, Jinan (2017).

PubMed Abstract | Google Scholar

9. Fu B, Zhao X, Song C, Li X, Wang X. A salt and pepper noise image denoising method based on the generative classification. Multimed Tools Appl. (2019) 78:12043–53. doi: 10.1007/s11042-018-6732-8

CrossRef Full Text | Google Scholar

10. Zhou C, Zhang PC, Liu H, Gui ZG. Adaptive inverse distance weighted interpolation (idwi) method to filter salt and pepper noise. J North Central Univ. (2019) 40:372–377+384. doi: 10.3969/j.issn.1673-3193.2019.04.013

CrossRef Full Text | Google Scholar

11. Fu B, Zhao X, Li Y, Wang X, Ren Y. A convolutional neural networks denoising approach for salt and pepper noise. Multimed Tools Appl. (2019) 78:30707–21. doi: 10.1007/s11042-018-6521-4

CrossRef Full Text | Google Scholar

12. Zhang L, Liu ZX, Liu HC. Mixed variational with l1 fidelity model for removal of salt and pepper noise. Comput Appl Eng. (2019) 55:210–6. doi: 10.3778/j.issn.1002-8331.1709-0295

CrossRef Full Text | Google Scholar

13. Fu B, Zhao X, Li Y, Wang X. Patch-based contour prior image denoising for salt and pepper noise. Multimed Tools Appl. (2019) 78:30865–75. doi: 10.1007/s11042-018-6811-x

CrossRef Full Text | Google Scholar

14. Xu SJ, Ding MY. Iterative inverse distance weighted filtering to remove salt and pepper noise. Life Sci Instrum. (2020) 18:39–44. doi: 10.11967/2020181205

CrossRef Full Text | Google Scholar

15. Zha B, Jiang JL, Liu GM, Han SG, Huang Z. Adaptive weighted mean filtering algorithm for removing high density salt and pepper noise. J Chizhou University. (2020) 34:43–5. doi: 10.13420/j.cnki.jczu.2020.06.008

CrossRef Full Text | Google Scholar

16. Guo HJ, Bai WJ, Yue YX, Lin F, Bai XF. Adaptive iterative mean filtering algorithm for removing salt and pepper noise in images. J Taiyuan Univ. (2020) 38:23–8. doi: 10.14152/j.cnki.2096-191X.2020.03.006

CrossRef Full Text | Google Scholar

17. Yan Gy. (Research on image denoising based on partial differential equation and nonlocal mean. [master's thesis]. Kunming University of Science and Technology, Kunming (2020).

Google Scholar

18. Fu B, Wang L, Luo Z. Robust Image Denoising with Texture-Aware Neural Network. In: 2021 IEEE International Conference on Multimedia and Expo. New York, NY: IEEE Computer Society (2021). doi: 10.1109/ICME51207.2021.9428158

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Thanh DN, Prasath VS, Phung TK, Hung NQ. Impulse denoising based on noise accumulation and harmonic analysis techniques. Optik. (2021) 241:166163. doi: 10.1016/j.ijleo.2020.166163

CrossRef Full Text | Google Scholar

20. Li Q, Chen CX, Huang T, Huang Z, Hua JX, Li LL. A median filtering algorithm for removing high density salt and pepper noise. Comput Knowl Technol. (2021) 17:137–9. doi: 10.14004/j.cnki.ckt.2021.3470

CrossRef Full Text | Google Scholar

21. Ma L, Li L. A high speed adaptive median filtering algorithm for salt and pepper noise removing. Comput Times. (2021) 40:68–71. doi: 10.16644/j.cnki.cn33-1094/tp.2021.10.017

CrossRef Full Text | Google Scholar

22. He M. Salt and pepper noise image based on l1 norm and adaptive total variation. J. Southwest China Normal Univ. (2021) 46:115–20. doi: 10.13718/j.cnki.xsxb.2021.05.017

CrossRef Full Text | Google Scholar

23. Deng ZD. Research and application of image salt and pepper noise denoising algorithm. [master's thesis]. Hunan University, Changsha (2018).

PubMed Abstract | Google Scholar

24. Bing Z. Research on edge-preserving filtering algorithm of image salt and pepper noise. [master's thesis]. Anqing Normal University, Anqing (2021).

PubMed Abstract | Google Scholar

25. Almeida MS, Almeida LB. Blind and semi-blind deblurring of natural images. IEEE Trans Image Process. (2009) 19:36–52. doi: 10.1109/TIP.2009.2031231

PubMed Abstract | CrossRef Full Text | Google Scholar