
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Appl. Math. Stat., 27 June 2022
Sec. Statistics and Probability
Volume 8 - 2022 | https://doi.org/10.3389/fams.2022.914932
In the typology of coefficients of correlation, we seem to miss such estimators of correlation as rank–polyserial (RRPS) and rank–polychoric (RRPC) coefficients of correlation. This article discusses a set of options as RRP, including both RRPS and RRPC. A new coefficient JTgX based on Jonckheere–Terpstra test statistic is derived, and it is shown to carry the essence of RRP. Such traditional estimators of correlation as Goodman–Kruskal gamma (G) and Somers delta (D) and dimension-corrected gamma (G2) and delta (D2) are shown to have a strict connection to JTgX, and, hence, they also fulfil the criteria for being relevant options to be taken as RRP. These estimators with a directional nature suit ordinal-scaled variables as well as an ordinal- vs. interval-scaled variable. The behaviour of the estimators of RRP is studied within the measurement modelling settings by using the point-polyserial, coefficient eta, polyserial correlation, and polychoric correlation coefficients as benchmarks. The statistical properties, differences, and limitations of the coefficients are discussed.
Over the years, scholars have developed many estimators of the association of two variables X and Y, depending on their scale properties. Usually, these are based either on the covariance between X and Y (e.g., Pearson's tetrachoric, biserial, polyserial, point-biserial, point-polyserial, or polychoric correlation) or the ratio of the favourable combinations and all combinations (e.g., Cureton's rank-biserial correlation, Goodman–Kruskal tau, lambda, gamma, Kendall's tau family, Pearson's eta and phi, or Somers' delta). These coefficients are divided into coefficients of observed and inferred association (see [1]). The observed association is estimated for the manifested variables and the inferred association for the latent variables or for the combination of an observed and a latent variable (see Figure 1). This difference between the latent and observed variables is discussed first, after which the factual estimators are discussed.
Assume two continuous variables ξ and η with the unknown joint distribution. For the later use of variables with different scales related to the proposed rank–polyserial coefficients of correlation, let these latent variables be manifested as two observed variables g with a narrower scale and X with a wider scale with xi = 1, …, r with distinctive ordinal categories and X with yi = 1, …, c distinctive categories with metric properties (ordinal, interval, pseudo-continuous1 or continuous scales), respectively, and r < < c. The variable g is related to ξ and X to η with the class limits or thresholds γi and τj so that
and
For the observed values, x1 < x2 < ... < xr−1 and y1 < y2 < ... < yr−1, and for convenience, γ0 = τ0 = −∞ and γr = τc = +∞. The relation of the variables with related symbols is illustrated in Figure 1 where ngX denotes the number of times the observation (g, X) is obtained in the sample, and the latent variables are assumed to be normally distributed.
In the measurement modelling settings used in the numerical examples, an item g and a score variable X compiled by a set of test items share the common latent variable θ, such as achievement in mathematics, which is manifested in two variables, item g and the test score X. As above, the threshold values of θ for each category in g and X are denoted by γi and, respectively. Hence, g with r = 1, …, r distinctive ordinal categories and score variable X with c = 1, …, c distinctive categories with a metric scale are related to θ so that g = xi, if γi−1 ≤ θ < γi, i = 1, 2, …, r and X = yj, if τj−1 ≤ θ < τj, j = 1, 2, …, c, and γ0 = τ0 = −∞ and γR = τC = +∞. Often, the scoring starts from zero, which is illustrated in Figure 2. Then, the degrees of freedom are df (g) = r – 1 and df (X) = c – 1.
The estimators of the association are really many. Olsson et al. [1] collected some estimators as a typology, and their work is elaborated and rethought in what follows (see Table 1).
At the beginning of the twentieth Century, Karl Pearson initiated and developed many coefficients for the observed association that still are in our use. The mechanics of the product-moment correlation coefficient between two observed variables with a metric scale (PMC; Pearson [4] onwards based on Bravais [5]) is used in the point–biserial correlation (RPB = ρgX) between an observed dichotomized or binary g and a metric-scaled X and in point–polyserial correlation (RPP = ρgX) between a polytomous ordinal g and a metric-scaled X. These are classic estimators of the item–score association in the measurement modelling settings.
Pearson also presented coefficient phi [6] suitable for two observed nominal-scaled variables, and coefficient eta [7, 8] suitable for an observed nominal- or ordinal-scaled variable and a metric variable. Later, such robust, non-parametric coefficients were developed for the observed association for ordinal-scaled variables as Goodman's and Kruskal's lambda, tau, and gamma (G) [9, 10], the family of Kendall's Tau ([11] onwards) and the family of Somers' D [12], including Cureton's rank-biserial correlation (RRB) [3, 13, 14]; RRB is a special case of D in the case of a binary variable g and ordinal-scaled X (see Newson [15]). This relationship is deepened later.
For the coefficients for inferred association between the latent variables ξ and η, the most known is the polychoric correlation (RPC = ρξη) and its special case, tetrachoric correlation suitable for two latent, dichotomized variables (RTC = ρξη) [16, 17]. Pearson also initiated polyserial correlation (RPS = ρξX) between a latent variable related to the variable with a shorter scale (ξ) and observed X, and its special case, the biserial correlation for the dichotomized ξ and observed X (RBS) [17, 18]. Common to all these is that we intend to infer what could the correlation between the variables be if measured in their latent, unobservable form.
When it comes to the factual estimation of the inferred association of two observed ordinal or interval-scaled variables with (theoretical, unobservable) latent variables, we have established routines for estimating RPC (e.g., [19–21]; see also [22]), as well as RBS and RPS (see [23]). The traditional routines of calculating the estimates by RBS and RPS led, however, to practicalities that the estimates reached out of range values (RBS, RPS>> +1) if the embedded PMC and the item variance are high to start with (e.g., [24]; see the discussion in, e.g., [25, 26]; see the computational form in Eq. 34). One of the best alternatives for RBS and RPS, if not the best, is a coefficient called r-bireg and r-polyreg correlation (RREG; see [27, 28]; see Eq. 37), which have behaved quite optimally in simulations (see, e.g., [29]).
As highlighted in Table 1, we seem to miss a set of coefficients for the ordinal variables: rank–polyserial and rank–polychoric correlation coefficients (RRP) for the observed association between the ordinal-scaled or metric variables. In the ERIC database with more than 1.2 million articles and research papers, we found no hits with the fixed keywords “rank polyserial” or “rank polychoric” at the time of finalising the article (April 2022). Nevertheless, some possible options such as RRP are available. These are discussed in this article.
This article discusses and studies the characteristics of a set of coefficients of correlation that could be called either rank polyserial or rank polychoric correlation coefficient. In what follows, the name rank–polyserial is preferred because of its connection to rank–biserial (RRB) correlation by Cureton. Although the options for RRP discussed here are not restricted to item analysis settings, their characteristics are studied in the framework of measurement modelling. After all, estimators of the association have a central role to play, for example, as the estimators of the item–score association and embedded to estimators of reliability (see discussion in, e.g., [26, 29, 30]). This perspective leads us to compare the options of RRP with its traditional alternatives: RPP = ρgX, often called item–total correlation (Rit), Henrysson's corrected item–total correlation (RPPH) [31], also known as item–rest correlation (Rir), coefficient eta directed so that X explains the order in g or “g given X”2, that is, η(g|X), as well as polyserial and polychoric coefficients of correlation (RPS, RPC).
After introducing a set of possible coefficients relevant to be taken as RRP, the following questions are asked:
1) What are the statistical properties of the new coefficients?
2) What are the general characteristics of the new coefficient in comparison with other classical estimators of association?
Empirical notes of the comparison are given based, first, on a simple numeric example, to introduce the manual computation; second, on a larger dataset with 6,932 items from 1,440 tests from real-world testing settings to study the performance of the estimators in real-life settings; and third, a simulation dataset of 22,842 estimates related to a hypothetic design there two identical items are truncated into two different forms to study their tendency to give deflated estimates. Characteristics of the dataset are discussed later with numerical examples.
In what follows, first, rank–biserial correlation is discussed. In Rank–Biserial Correlation and U-Test Statistic Section, Cureton's ρRB is shown to be strictly related to the directed Mann–Whitney U-test statistic ([40]; see [14, 41]), and, hence, second, this connection is utilised when deriving a new coefficient of correlation, rank–polyserial correlation in Rank–Polyserial Correlation and JT-Test Statistic section. Third, another possible coefficient of rank–polyserial coefficients is introduced in Identity of JTgX and Somers D, Relation of JTgX and Goodman–Kruskal G, and Dimension-Corrected G and D as Options for the Coefficient of Rank–Polyserial Correlation sections where their connexion to Jonckheere–Terpstra test statistic is shown. Numerical examples of computing the estimators are given later.
Assume two sub-samples i = 0 and j = 1 where i and j could be males and females or incorrect and correct answers in a test item. The standard procedure of the U-test produces two statistics, where U1 refers to the higher values and U2 refers to the lower values (see the estimation of U-test in, e.g., [33, 37]). Wendt's [14] modification of ρRB is
related to the lower of the groups i, j regardless of the statistics U1 and U2; this is discussed later.
The original idea by Cureton was based on the proportion of favourable cases (f) and unfavourable cases (u)
and this idea is used later in deriving the corresponding rank–polyserial correlation. To compute the proportion of favourable cases, the mechanics and heuristics of U-test statistics could be used. The heuristic of the observed U statistic is to compute the number of “favourable” incidents of how many observations from the subsample i = 0 fall below each observation from the subsample j = 1 after the variable of interest g is ordered by a metric variable X. If no tied pairs are obtained, the observed U statistic related to the sub-population j = 1 () is the sum of those sums (see, e.g., [33, 37]). With tied cases, Wilcoxon's method [42] produces the correct value; this is discussed later. The maximal value of the U statistic is reached when all cases in the subsample i = 0 (altogether, n0 cases) are ranked lower than all cases in subsample j = 1 (altogether, n1 cases):
In the binary (ordinal) case, the proportion of “favourable” cases is the ratio of the observed and maximal U statistic that varies between 0 and 1. This ratio is rescaled by multiplying it with 2 and relocated by −1, and we get the values ranging from −1 to +1 as is standard in coefficients of correlation:
Notably, Eq. (5) is identical to Eq. (1), while Wendt's formula (Eq. 2) is based on the subsample i = 0, and Eq. (5) is based on the subsample j = 1. All in all, RRB is the rescaled and relocated proportion of logically (ascending) located cases within the categorical (ordinal) variable g after they are ordered by the metric variable X. Notably, Eq. (5) strictly corresponds with Cureton's idea (RRB = 2×f – 1; see Eq. 3). The further the erroneous locations from the deterministic position are and the more these erroneous locations are, the lower the value in the estimate. This is illustrated later with a numerical example.
Jonckheere–Terpstra test statistic (JT) [43, 44], also known as Jonckheere trend test [43], with a directional nature generalises U-test statistic and its heuristic to polytomous ordinal cases (see [33, 37]). This connection is used in proposing a new estimator of correlation, carrying characteristics relevant to RRP.
Assume an ordinal variable g with observed categories r = i, j, and i < j and the metric variable X. Then, ni and nj are the numbers of cases in the subsamples i and j in variable g. In the 5-point Likert scale, as an example, one pair of subsamples is i = 1 and j = 4. In general, we have r(r − 1)/2 possible values for the statistics. In the case of the 5-point Likert scale, as an example, we obtain 5 × 4/2 = 10 values: U12, U13, U14, U15, U23, U24, U25, U34, U35, and U45. In the computational procedure in what follows, the sum of the ranks in the higher of the subsamples i, j, is of interest.
In the same manner, as with RRB, the essence of the new coefficient is the ratio of the observed and maximal JT statistics ( and , respectively). can be expressed by using the U statistic:
(see [33, 37]) where refers to the observed U statistics related to all the pairs of subsamples i and j. This statistic indicates the number of “favourable” incidents where, after ordering by X, the cases with a higher value in X have a higher value also in g. The observed U statistic for the observed JT statistic can be computed by using Wilcoxon's W statistic [42]:
where Wj is the sum of the ranks of the higher of the subsamples i and j. The maximal value for each U statistic is reached when all the test-takers in subsample j (altogether, nj cases) are ranked higher than all test-takers in the subsample i (altogether, ni cases). Hence, with each pair of subsamples,
and the maximal value of the observed JT statistic is the sum of these values
Because Eqs. (6), (7), (8), and (9), paralleled with the rank–polyserial correlation, a new coefficient rank–polyserial correlation is defined as:
where r refers to the number of categories in the variable with a narrower scale (g), j refers to the higher number of the subsamples i and j in g, and Wj is the sum of the ranks in the higher number of the subsamples i and j.
The core of the coefficient JTgX is the probability statistics of the ratio of observed and maximal JT statistic , that is, the proportion of “favourable” cases in the spirit of Cureton that varies between 0 and 1. This ratio is rescaled by multiplying it by 2 and relocated by −1 to the same scale as the Pearson correlation. This coefficient could be called either rank–polyserial correlation as a legacy to Cureton's rank–biserial correlation or rank–polychoric coefficient as a robust counterpart to the classic polychoric correlation; here, the former is used, but an abbreviation RRP is used to keep both interpretations open.
The value JTgX = +1 indicates the positive deterministic pattern in g; after being ordered by X, all the observations in the higher subsample(s) j are ordered higher than those in the lower subsample(s) i. By using the concept of “concordant pairs” familiar from many robust coefficients of association such as Somers D and Goodman–Kruskal G, JTgX = +1 refers to the situation where all the pairs of observations are concordant. The further the erroneous locations from the deterministic position are and the more these erroneous locations are, the closer is the magnitude in JTgX to zero. The value JTgX = 0 refers to a situation where the observations are randomly spread in variable g after being ordered by X. The value JTgX = −1 indicates the ultimate situation that all the cases in the lower subsample(s) i would be ranked higher than those in the higher subsample(s) j. By using the concept “discordant pairs,” the last refers to the situation in which all the pairs of observations are discordant. The interpretation of the magnitude of the estimates by JTgX is the same as that in RPP (ρgX), with the note that, in real-life datasets, RPP cannot reach perfect +1 or −1 (see e.g., [29, 45]) while JTgX can.
In the specific case that there are only two categories in g, for example, when only two categories are obtained in a Likert type of scale (see later the numerical example) or in a binary case, includes only one U statistic, Uij, and is reduced to ordinary U-test statistic related to the higher number of the subsamples i, j. Hence, because of Eqs. (10), (2), (4), (5), in the binary or dichotomous case, RRB is a special case of JTgX:
JTgX has the identity of Somers' D directed, so that “g given X,” that is, D(g|X), henceforth, plainly D. Assume two variables, ordinal g with the subsamples i < r with observed values xi and ordinal X with subsamples with observed values yj sampled from the same bivariate distribution forming an r × c cross-tabulation. The number of cases in the subsamples related to g is ni and
The computational form of D directed so that “g given X” can be expressed as
(e.g., [32, 33, 37]) where P is the sum of the concordant pairs of two observations xi and xj, and, correspondingly, yi and yj, and Q is the sum of the discordant pairs. Because of Eq. (12),
(see [32]). Hence, because of Eqs. (13) and (14), D can be rewritten as
When all the pairs are concordant, Q equals 0, and
and, consequently,
The statistic Q is strictly related to PMax:
Hence, because of Eqs. (17) and (18),
and D(g|X) can be rewritten as
Notably, from the JT statistic viewpoint, the observed JT statistic is the number of concordant pairs in the positive direction:
Because of Eqs. (10), (21), and (20), JTgX can be expressed as
Hence, because both JTgX(= RRP) and Cureton's (and Glass' and Wendt's) RRB is a special case of Somers' D (of the derivation for RRB, see [15]), these coefficients form a family related to Somers' D(X|Y); see other coefficients and test statistics related to the same family in, e.g., Metsämuuronen [32]. Although JTgX is a specific case of Somers' D(g|X), the advantage over D in measurement modelling settings is that it leads us strictly to the correct form of the three alternatives produced by the standard procedures of calculating Somers' D.
Because JTgX has the identity of D, it carries the same advantages and weaknesses as D does. One of the advances is that the sampling variance and asymptotic standard errors of JTgX are known (see, e.g., [32, 46, 47]; see Supplementary Appendix 1). One of the weaknesses of D is that it tends to underestimate item–score association in an obvious manner when the number of categories exceeds 3 (see [25, 48, 49]). This characteristic is discussed later.
Although it is not a generally known fact, Goodman–Kruskal gamma (G) is a directional measure in the same direction as D(g|X) (see the proof in [32]), although, usually, G is taken as a symmetric measure (see, e.g., [50]) because it produces only one estimate of correlation. However, if there are no tied pairs in the dataset, as is the case when the metric variable has no tied cases (see other cases in [32]), G equals D(g|X) and not D(X|g) nor D (Symmetric).
Except for the special case of no tied cases, the estimates by G are more liberal than those by D. The main difference between G and D is how they treat the tied pairs. By using the concepts of concordant and discordant pairs (P and Q) as with D, G is computed by
The number of all possible pairs can be expressed as
(see, e.g., [32]) where 4Tg refers to the number of tied pairs, that is, the pairs where the direction is not known, and the magnitude of P, Q, and Tg is thought double-sized than the simplified formulae indicate3. In computing the probability by G, the tied pairs are omitted and, hence, the number of pairs used in the estimation is
Then, because of Eq. (14) and because Eq. (25), , and
and, because of Eq. (21),
(see footnote 3 discussion of the double content of P and, consequently, of Tg). Then,
[32]. Hence, in G, the core is the probability measure referring to the proportion of the “favourable” cases of logically (ascending) ordered observations in g after they are ordered by X while considering only those cases for which we know the order where the pairs are omitted, of which the direction is not known. Notably, the same logic of computing probability is used in such famous procedures as the sign test (traced to [52]; see [33]) and Wilcoxon signed-rank test [42]. In the specific case that there are no tied pairs, Tg = 0 and G = D = JTgX.
Simulations within the measurement modelling settings have shown that coefficients G and D have a major deficiency to underestimate the association between an item and a score in an obvious manner, with polytomous items having more than three categories (in D) or four categories (in G) (see Metsämuuronen [25, 45, 49]; see also [48])4. To overcome this obvious deficiency, two related estimators have been suggested: dimension-corrected G and dimension-corrected D.
Because of the obvious conservative nature of G and D with polytomous items in the measurement settings with wide-ish scales, Metsämuuronen [45, 49] proposed two new estimators, dimension-corrected G and D (G2 and D2) specific for the measurement modelling settings5. The computational form of G2 is [45],
where G is the observed value of G, abs(G) is the absolute value of G, and
where df (g) = (number of categories in variable g−1). Correspondingly, the computational form of D2 is
(originally, in [49], corrected [45]) where D is the observed value of D(g|X), and A is as in Eq. (30). Sampling variances and asymptotic standard errors of these estimators are discussed in Metsämuuronen [45] (see also Supplementary Appendix 1).
Inherited from G and D, G2 and D2 are based on probability, but, because of the third-order element A, they are described as semi-trigonometric in nature (see [29]). Coefficients G2 and D2 can be used both with binary and polytomous items, and, when D = G = 1 and with binary items, G2 = G and D2= D. In simulations [29, 45], G2 tends to give estimates with a magnitude of close to those by RPC. Of G2 and D2, D2 gives more conservative estimates. This is inherited from the behaviour of D towards G.
To condense the discussion by far, on the one hand, the new coefficient of correlation JTgX can be taken as a coefficient of rank–polyserial correlation with a directional nature of the same manner and same direction as D, G, eta, and RPP are directed6. JTgX is the general case for the classic rank–biserial coefficient of correlation RRB. On the other hand, JTgX has the identity of Somers' D directed so that “g given X” (or “X dependent” in the GLM settings), and, in the case that there are no tied pairs in the dataset, JTgX also has the identity of Goodman–Kruskal G. The statistical properties of JTgX are identical to those by D. Because the underlying coefficients G and D can be taken as rank–polyserial coefficients of correlations, G2 and D2 could be taken dimension-corrected rank–polyserial coefficients of correlations.
In what follows, the behaviour of JTgX = D, G, G2, and D2 is studied in comparison with relevant benchmarking estimators in the context of measurement modelling: item–total correlation (Rit = RPP), Henrysson's item–rest correlation (Rir = RPPH), coefficient eta, polyserial correlation (RPS), and polychoric correlation (RPC). The computational forms of these estimators are discussed with numerical examples. First, a simple example is given with which the computation of the estimates is discussed in Section Simple Comparison of the Options for RRP. Second, a published dataset of 6,932 polytomous items from a real-world test is used to study the differences between the estimators in Section Comparison of the Estimates With a Larger Dataset. Third, their tendency to resist deflation in the estimates is discussed in Section Deflation in the Estimates.
Assume a simple dataset with four items with a Likert type of scale and the score X as in Table 2. Two of the items (g1 and g2) represent a deterministically discriminating response pattern, while two others (g3 and g4) include stochastic error either in minor extent (g3) or wider extent (g4).
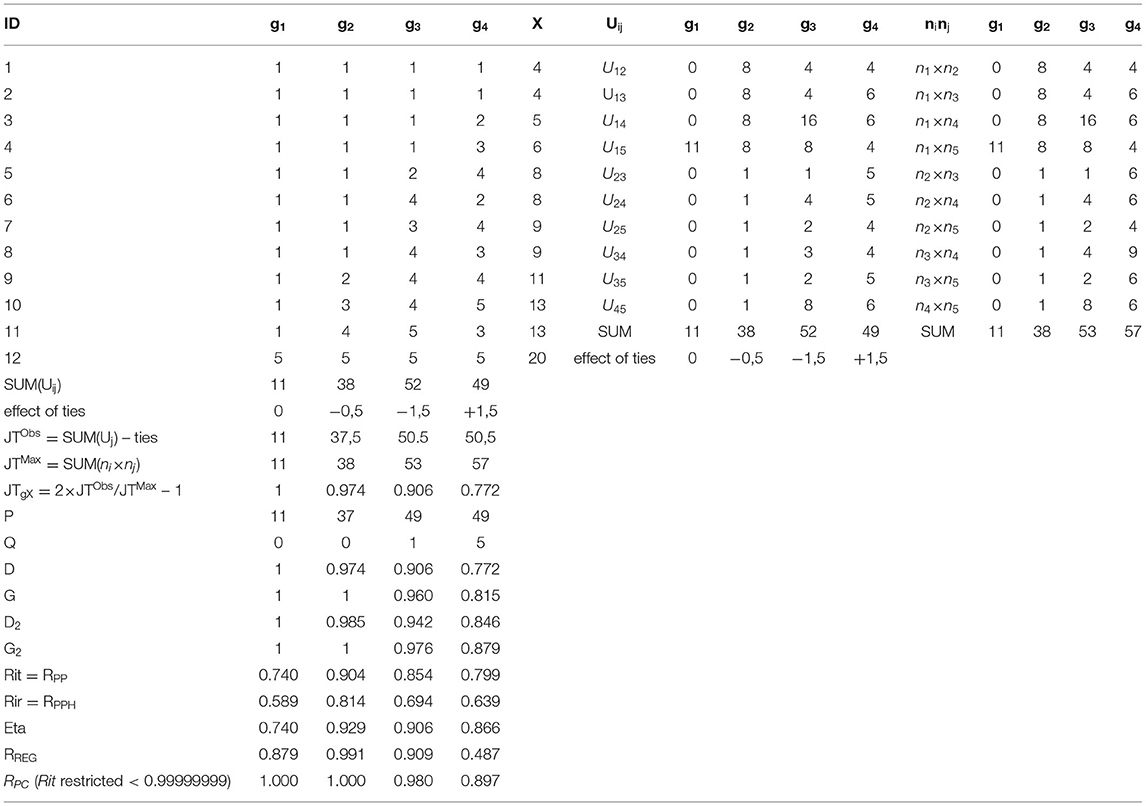
Table 2. A hypothetic dataset to illustrate the computing of coefficients of rank–polyserial correlation.
Item g1 represents items with an extreme “difficulty” level where we expect to see obvious underestimation by Rit, Rir, and coefficient eta (see [2]). With these kinds of items, G and D, and consequently, JTgX detect the deterministic pattern as G = D = JTgX = 1. Item g2 is a deterministic one, but it includes a minor tie in X, and, hence, the estimate by D = JTgX is expected to give a slightly more conservative estimate of the association in comparison with that by G. Items g3 and g4 have both tied cases and error in the order, and, hence, both G and D are expected to give estimates with the magnitude of . In all cases, the estimates by G2 and D2 are expected to be higher than those by G and D.
The manual calculation of the estimates of the coefficients is discussed by using item g4 as an example. The statistics related to Wilcoxon's statistics are seen in Table 3 and the contingency table of g4 × X in Table 4.
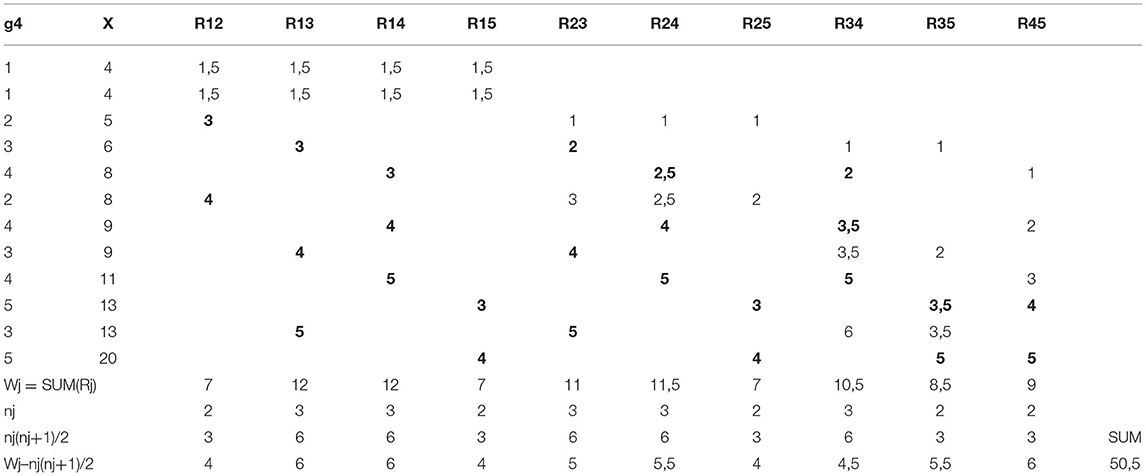
Table 3. Rank-orders (R) in different pairs of i, j between variables g4 and X; the ranks of the higher sub-population j are highlighted.
By using the heuristics of U-test statistic, assuming no ties, the sum of the statistics Ug4Xij equals 49 and the ties add 1.5, totaling to = 50.5 (Table 2). The same is obtained strictly by using the routine of Wilcoxon (Eq. 7; see Table 3). The maximal value is (Eq. 9; Table 2). This can be obtained also by using Eq. (14) and Table 4: the maximum value is . Then, JTg4X = = 2 × (50.5/57)−1 = 0.772. The core in the estimator, = 50.5/57 = 0.886 indicates that 88.6% of the observations in item g4 are logically (ascending) located after they are ordered by the score X.
For Table 2, the estimates by JTgX were computed manually by using the information from Table 2. However, in real-life settings, JTgX has the identity of D(g|X). Then, it is easy to use traditional software packages, such as IBM SPSS, Stata, SAS, or R-packages for calculation. For instance, with IBM SPSS, the syntax for D is CROSSTABS /TABLES = item BY Score/STATISTICS = D. In Stata, a module by Newson [54] is available. In SAS, the command PROC FREQ provides D by specifying the TEST statement by D, SMDC and R options. Correspondingly, in R, D can be computed by Somers Delta (x, y = NULL, direction = c(“row,” “column”), conf.level = NA, ...) (see https://rdrr.io/cran/DescTools/man/). From the output, the option “X dependent” is selected.
When it comes to coefficients D and G, statistics P and Q are needed for the manual calculation. These can be computed by using a contingency table (Table 4). By using the strategy of “count all entries that lie to the ‘Southeast’ of the particular entry” (see the manual calculation, e.g., [33, 37]), the number of pairs in the same direction is P = (2×) 49. Parallel, the number of pairs in the opposite directions is counted by using the strategy of “count all entries that lie to the ‘Southwest’ of the particular entry”: Q = (2 ×) 5. Consequently, 2 × (P – Q) = 2 × 44 and 2 × (P + Q) = 2 × 54. The number of all pairs in the direction of “g given X” is . Then, G = 44/54 = 0.815 and D(g4|X) = (2 × 44)/114 = 0.772. Notably, the latter equals the estimate by JTg4X because of Eq. (22).
For Table 2, the estimates by D and G were calculated manually based on contingency tables. In traditional software packages, such as IBM SPSS, for instance, the syntax for G is CROSSTABS/TABLES = item BY Score/STATISTICS = GAMMA and the syntax for D is CROSSTABS/TABLES = item BY Score/STATISTICS = D. In Stata, the command tabulate g X [if] [in] [weight] [,gamma] produces G (see [55]), and Newson's module [54] produces D. In SAS, the command PROC FREQ provides G and D by specifying the TEST statement by GAMMA, D, SMDCR options. Correspondingly, by using R, G can be computed by GoodmanKruskalGamma (x, y = NULL, conf.level = NA, ...) and D by Somers Delta (x, y = NULL, direction = c (“row,” “column”), conf.level = NA, ...) (see https://rdrr.io/cran/DescTools/man/). From the output related to D, the option “X dependent” is selected.
The dimension-corrected rank–polyserial coefficients D2 and G2 are based on the observed values of D and G and knowledge of the number of categories in the item. In the case of g4, df (g) = 5–1 = 4. For the calculation, A = (3/4)3 = 0.421. Then, by using Eq. (31), an estimate of item–score association is D2(g4|X) = D2 = 0.772 × [1 + (1–0.772) × 0.421] = 0.846 and, by using Eq. (29), G2(g4|X)= G2 = 0.815 × [1+ (1–0.815) × 0.421] = 0.879. For Table 2, these were computed manually by using traditional spreadsheet software.
When it comes to the benchmarking estimators, the mechanics of PMC are used in the point–polyserial correlation, that is, in item-total correlation for observed association of the item and the score:
and in Henrysson's item–the rest correlation
where σgX, σg, and σX are covariation and standard deviations of the item (g) and the score (X), and σgP are the covariation and standard deviation of the item g and modified score P where the item in interest has been omitted from the compilation.
For item g4, the estimates are Rit = 0.799 and Rir = 0.639. In the real-life testing settings, the magnitude of the estimates by Rir is always lower than those by Rit (see algebraic reasons in, e.g., [56]), and both estimators underestimate item–score association when the scales are not equal (e.g., [29]) as is the case with g4 and X. From this viewpoint, it is known that in the hypothetical example in Table 2, D needs to underestimate the association in an obvious manner as 0.772 < 0.799; this type of obvious underestimation was the reason why the dimension-corrected estimators D2 and G2 were developed (see the discussion in [25, 45, 49]). In the case of g4, the estimate by G (0.815) exceeds the one by Rit. However, this is not true in general; when the number of categories in an item exceeds 4 as here, in real-life testing settings, G tends to give estimates that are lower in magnitude than those by Rit (see [29]; see also later Figure 3).
For Table 2, the estimates by Rit and Rit were computed manually by using standard spreadsheet software. Both indices are defaults for the classical item analysis in the widely used general software packages, such as IBM SPSS [50], SAS (e.g., [57]), STATA [55], and in some libraries of R (e.g., [58, 59]).
Coefficient eta is a close sibling to Rit; with binary and dichotomous items, eta = Rit (see [60, 61]), and with polytomous items Rit follows closely the direction of η(g|X), henceforth, just eta, usually denoted as “X dependent”—which is the same direction as in D(g|X)—and not the opposite direction η(X|g) (see [2]). This is its traditional direction in settings related to GLM (“X dependent”). One of the advances of eta over Rit is that, unlike Rit, eta can detect the possible non-linear pattern in the item, and, hence, in the polytomous settings, the magnitudes of the estimates by eta are always somewhat higher than those by Rit (see the algebraic reasons in, for example [2]).
The traditional form for is
(e.g., [62]) where refers to the means of X in different categories in g, and is the grand mean of X. However, Metsämuuronen [2] suggests that a better form—also considering the possible negative values of eta—would be
This is a relevant modification because using variances in the estimation of eta automatically leads to a positive outcome even if the true association would be negative.
In Table 2, the identity of eta and Rit is seen in g1(0.740), which is, factually, a dichotomous item because only two categories are obtained. In the case of g4, the magnitude of the estimate by eta is notably higher [η(g|X) = 0.866] than that by Rit (ρgX= 0.799).
For Table 2, the estimates by eta were computed by using IBM SPSS software by using the syntax Crosstabs/Tables = g by X/Statistics = ETA. In Stata, the positive values of eta can be obtained by taking the square root of eta squared obtained by the command estatesize after the ANOVA command. In SAS, the positive values of eta can be found by taking the square root of etasquared after PROC GLM with the option EFFECTSIZE. Correspondingly, by using R, eta is computed by eta (x, y, breaks = NULL, na.rm = FALSE) (see https://rdrr.io/cran/ryouready/man/eta.html).
The parametric polyserial coefficients of correlations are the natural counterparts for the robust rank–polyserial coefficients of correlation. While the previous estimators are intended to estimate observed correlation, RPS is intended to estimate the inferred correlation between a latent g and observed X. In the early years of item analysis, the traditional RPS was the most used estimator of the item–score association (see [24]). However, from early on, it was known that the traditional way of estimating RPS leads to obvious overestimation with out-of-range values if the embedded ρgX and σg are high to start with (RPS>>1.000). During the years, Clemans [24], Turnbull [63], Brogden [64], and Henrysson [65], as examples, offered solutions to the challenge of overestimation (see the history in [28]). By far, the most promising option in this family is a coefficient called r-polyreg correlation (RREG; see [27, 28]), which produces estimates that do not exceed 1, nor does it rely on bivariate normality assumptions. It has shown to be very resistant to deflation, although, with short scales in X, it seems to give underestimations (see [29]; see also later Section Comparison of the Estimates With a Larger Dataset).
For the general interest, the traditional estimates by RPS were computed for the items in Table 2, although they are not seen in the table. The estimates are ρPS_g1 = 1.334, ρPS_g2 = 1.120, ρPS_g3 = 0.945, and ρPS_g4 = 0.841. The two first ones are, obviously, out of range in magnitude, and there is a reasonable doubt also with the other estimates. In Table 2, the estimates by RREG are seen. By using RREG in estimating the inferred association related to the item g1, the estimates are notably higher in magnitude (0.879) than those by Rit, Rir, and eta (≤0.740), although the magnitude is far lower than those by G, G2, and RPC (1.000), which are known to detect the deterministic pattern accurately (see [29, 45]). With g2, also with a deterministic pattern, the estimate by RREG (0.991) is very close to those by G, G2, and RPC (1.000). With g3, the estimate by RREG (0.909) is close to that by D (0.906) but lower than those by G (0.960) and RPC (0.980). Notably, with item g4, RREG seems to underestimate association in an obvious manner (0.487).
The traditional RPS can be obtained by the two-step procedure introduced by Olsson et al. ([1], see also [23]) where, in the first phase, the marginal proportions of the categorical ordinal variable (pj) are used to obtain the threshold estimates (γj), and these are used, in the second phase, to give estimates by RPS. The estimate by RPS can be obtained by
(e.g., [23]) where ρgX is the point–polyserial correlation between g and X, σg is the standard deviation of the categorical ordinal variable, is the inverse of the standard normal density, is the standard normal density, and gj is the category in the ordinal variable g. The last is not needed when all the categories are met as they are in items g2 – g4; in these cases, gj+1-gj = 1. However, in item g1, gj+1 – gj = 5 – 1 = 4.
For computing RREG, a statistic βi is needed. This is the slope parameter of the probit regression model P(xi ≤ 1|y) = Φ(ai − βiy) where Φ is the standard normal cumulative distribution function and ai and βi are intercept and slope parameters. The β-value can be computed, for example, in IBM SPSS software using the syntax
After the estimates of β and the population variance of the score variable X ( and , respectively) are computed, RREG is estimated as
For Table 2, the β values were computed by using SPSS software, and the estimates of and RREG were computed manually by using a spreadsheet software package. Note that the standard outputs of generally known software packages produce, usually, the sample variance. This is transformed into the “population” variance by multiplying the outcome with (N − 1)/N. If using MS-Excel, as an example, we can select whether the sample variance (= VAR.S) or population variance (= VAR.P) is used. The latter is used in Table 2.
As RBS above, also the parametric coefficient of correlation is a natural counterpart for the nonparametric or robust rank–polyserial (or polychoric) coefficients of correlation. RPC differs from the previous ones in that no closed-form expression for the relation between RPP and RPC is available. Instead, several alternatives for the process to obtain the estimates are suggested, which produce slightly different estimates (see [23]). As an estimator of correlation, RPC is advantageous over RPP, specifically, with ordinal datasets (e.g., [66–69]), and it is very resistant against several sources of deflation (see [29, 45]). Also, it is robust in accurate reproduction of the measurement models with unbiased standard errors even in small sample sizes (e.g., [66–68]).
One practical challenge in from the item analysis viewpoint is that we do not know what kind of composite the item discrimination refers to; the estimates refer to hypothetical composites to the research is not privy to (see [25, 70]). Also, the computational challenges are well-known; the estimation needs complicated procedures (e.g., [71]). Additionally, the established routines for estimating ρPC (e.g., [19–22]) cannot reach the extreme values +1 and −1 because the deterministic patterns lead to computational problems. The last challenge is easy to solve though (see below the restrictions used in estimation).
In reference to Table 2, RPC accurately detects the deterministic patterns in items g1 and g2. This is expected by its behaviour in simulations (e.g., [29, 45]). Also, the magnitudes of the estimates in g3 and g4 (0.980 and 0.897, respectively) seem to be quite close to those by G2 (0.976 and 0.879, respectively). Hence, if the estimates by RPC are taken as the closest approximation of the latent variables manifested in ordinal or interval-scaled form, it seems that, of the options for rank–polyserial coefficients of correlation, G2 could be taken a quite close match to RPC. In-depth studies are needed to confirm this. Some light on this matter is given in the next section, with a comparison with a larger dataset.
In IBM SPSS [50], the syntax for RPC is not available, although some macros have been published (e.g., [72]). In SAS, the command PROC CORR provides RPC. Correspondingly, in R, RPC can be computed by CorPolychor (x, y, ML = FALSE, control = list(), std.err = FALSE, maxcor = 0.9999)## S3 method for class “CorPolychor” print (x, digits = max (3, getOption (“digits”)-3),...) (see https://rdrr.io/cran/DescTools/man/CorPolychor.html). In computing the estimates in Table 2, the two-step estimator by Martinson and Hamdan [20] was used. Simplified by Zaionts [73], the task is to find an estimate of RPP = ρgX, which maximises the log-likelihood function LL, where
In the first step, the threshold coefficients γi and τj are estimated for both g and X, and in the second step by iteration, we find RPP that maximises LL. The estimates were computed manually by modifying Zaionts' [73] procedure for MS-Excel: Rit was restricted to be Rit < 0.99999999, and, in each operation with logarithm, an additional 0.000000001 was added. The latter is for the cases of deterministic patterns, causing value 0 in the cell; the logarithm of zero is not defined. Hence, technically, RPC cannot reach the ultimate correlation. In Table 2, this is denoted by value 1.000 instead of 1 as with G and G2.
The coefficients of RRP are compared with relevant estimators by using 6,932 real-world items from 1,440 datasets. The estimators are studied from three viewpoints. First, how the factual estimates differ from each other in different situations by varying the number of categories in the item and the score, varying the item difficulty, and varying the number of observations in the sample. Second, the estimators are compared from the viewpoint of how efficiently they reflect the population value. Third, the estimators are briefly compared related to their tendency to resist deflation as estimators of the item–score association.
The dataset used in the comparison is a public one. The dataset of 14,888 estimates of item–score association is published at doi: 10.13140/RG.2.2.10530.76482 in CSV format and at doi: 10.13140/RG.2.2.17594.72641 in SPSS format. Of these items, 6,932 are polytomous, and these are used in the comparison.
The datasets are formed by different compilations of 20–30 binary items and their sums forming items with 2 to 15 categories (to form polytomous items). Randomly selected test-takers of n = 25, 50, 100, and 200 were picked from a nationally representative dataset of a mathematics test for Grade 9 [74] with N = 4,023. The items and scores formed 1,440 tests with different numbers of test-takers (n), test lengths (k), difficulty levels (), reliabilities (α), and a number of categories in the items and scores [df (g) and df (X), respectively].
First, an obvious lift of the comparison of the estimators is that the estimates by JTgX = D and G underestimate item–score association in an obvious manner when the number of categories exceeds 3 (in D) and 4 (in G) (see Figure 3 also including the binary items; see Table 1 in Supplementary Appendix 2). This is also known by previous simulations (e.g., [29, 45]). The phenomenon is known from the fact that the estimates by RPP are always deflated whenever the scales are not identical in two variables (see the algebraic reasons in [75, 76]) as is always the case with an item and a score. Notably, the magnitude of the estimates by RPP tends to exceed those by D and G with items with a wide scale.
Second, the estimates by D2 tend to be close to those by RREG and RPC, and the estimates by G2 tend to be slightly higher than those by RPC regardless of the number of categories in the items. These are not general characteristics though. It is to be seen that, more frequently, the magnitude of the estimates by D2 tends to be close to those by RREG and the magnitude of the estimates by G2 tends to be close to those by RPC.
Third, the binary case is given as a benchmark here; the estimates by RPP and eta are notably deflated with the binary dataset. With the special case suitable for a point–biserial correlation, all other estimators than RPP and eta would produce closely the same estimate. The differences between the estimators come with items with a wide scale [df (g) > 3]. In what follows, the binary cases are omitted, and just k = 6,932 items with polytomous nature are used in the study.
Regarding the number of categories in the score, it seems that the estimates are stable if the score has more than 15 categories (Figure 4; see Table 2 in Supplementary Appendix 2). If the number of categories is less than 16, all the estimators tend to produce unstable estimates. The instability in the estimates with tests with a narrow scale in a score is discussed later with the efficiency of the estimators to reflect the population value. When it comes to the magnitude of the estimate, the estimators seem to form three groups. With scores wider than 15 categories, RRP based on D tends to give estimates with notably lower magnitude than the other estimators. RRP based on G tends to give estimates that are at the same level as those by RPP and eta. RRP based on G2 and D2 tends to give estimates that are at the same level as those by RREG and RPC. Of these estimators, the magnitude of the estimates by D2 tends to follow closely those by RREG, and the magnitude of the estimates by G2 tends to follow those by RPC.
When it comes to the difficulty levels of the items, the traditional RPP and eta include obvious deflation in estimates with extremely easy and difficult items—and in the binary case, as discussed in Figure 3 (Figure 5, see Table 3 in Supplementary Appendix 2). The phenomenon is known from the previous simulations (e.g., [25, 29, 45, 49]). In the given dataset, this phenomenon is indicated by the notably lower magnitude of the very easy items—extremely difficult polytomous items were not obtained in the polytomous dataset. The magnitude of estimates by JTgX = D and G tends to be lower than by the other estimators with items of medium difficulty levels, but, with items with extreme difficulty levels, they tend to not differ from those by the other estimators. This is caused by the fact that the probability to obtain deterministic patterns is high with items with extreme difficulty levels. Then, the magnitude of the estimates by D and G tends to get closer to D2 and G2. Correspondingly, the magnitude of the estimates by D2 and G2 does not differ notably from the benchmarking estimators RREG and RPC.
When it comes to sample size, all estimators tend to give stable estimates when the sample size n = 50 is reached (Figure 6; see also Table 3 in Supplementary Appendix 2). When the sample size is very small (n = 25 in the dataset), the magnitudes of the estimates are deflated. As above, the magnitude of the estimates by D2 tends to follow closely those by RREG, and the magnitude of the estimates by G2 tends to follow those by RPC. The estimates by D, G, RPP, and eta tend to be deflated in comparison with RPC and G2. The estimators of RRP form four distinguished estimators when it comes to magnitude of the estimates. Coefficient D is known to be the most conservative of the options for RRP, and, hence, the magnitude of the estimates by JTgX and D is the lowest in comparison. Coefficient G is more liberal than D, and the magnitudes of the estimates tend to follow the tendency of RPP and eta when the number of sample size exceeds n = 50. Coefficient D2 is somewhat more conservative in comparison with G2, but the magnitudes of the estimates are notably higher than those by D and G. Notably, with very small sample size (n = 25 in the dataset), the magnitude of the estimates by D2 seems to be very close to those by eta, and, when the sample sizes reach n = 50, the magnitude starts to follow the tendency of RREG. The highest magnitudes of the estimates are given by G2, and its trend follows closely the tendency by RPC.
To condense the results by far, it seems that, with items with wide or wide-ishscale (more than 3–4 categories), the estimators JTgX = D and G tend to underestimate item–score association in an obvious manner, while the magnitude of the estimates by D2 tends to be close to those by RREG, and magnitude of the estimates by G2 tends to be close to those by RPC. The magnitudes of the estimates tend to be as follows:
This order is expected because of the known characteristics of the estimators; the estimates by D are more conservative than those by G (see, e.g., [45]), and the estimates by D2 are more conservative than those by G2 (e.g., [29]).
The efficiency of the estimators of RRP and related benchmarking estimators to reflect the population value is studied by comparing the sample and “population” estimates computed from the original real-world dataset of 4,023 test-takers. As a combination of different sets of items, the procedure for producing the simulation dataset came up with 137 different score variables related to polytomous items. These all produce slightly different population values. The average estimates are collected in Table 5.
Because we do not know the real population value of item–score association in the real-life datasets, each estimator races its own race against itself: D from the sample is compared with the corresponding D from the population, as an example. A simple and straightforward statistic is computed: the difference (d) between the sample estimate and the population estimate. If d > 0, the population value was overestimated, if d = 0, the estimate was equal in the sample and the population, and if d < 0, the population value was underestimated. This statistic is denoted as d in the name of the coefficient: dD refers to a difference between the sample D and population D.
When it comes to the number of categories in the item, the first point to make is that the estimates by D2 and G2 are the least effective in reaching the population value—they tend to underestimate the population value the greatest (Figure 7; see Table 5 in Supplementary Appendix 2). In contrast, second, the estimates by eta tend to be overestimated with items with wide scales. This is an interesting phenomenon, knowing that eta tends to give obvious underestimates in the same manner as RPP does. It means that the wider the number of categories gets, the more probable it is to find association by eta from the population (or in large sample size), with a lower magnitude in comparison with the sample estimates. This seems to be the opposite with D2 and G2. Third, except RREG, all estimators in comparison share the common characteristic that the narrower the scale in item (up to 8 categories) is, the more the estimator tends to underestimate the population parameter up to 0.02 units of correlation. RREG seems to be surprisingly robust against the effect of the scale in item; regardless of the length of the scale, the estimates tend to be very close to the population value.
When it comes to the number of categories in the score, above, it was noted that, when the number of categories in the score exceeds 15, the estimates tend to be stable. From the perspective of reflecting the population estimate, except RREG, all estimators tend to notably underestimate item–score association with tests with a narrow scale in the score, that is, when df (X) < 15 (Figure 8, see Table 6 in Supplementary Appendix 2). In this respect, there seem to be no differences between the estimators except that RREG produces robust estimates and eta does not underestimate the association as much as the other estimators.
When it comes to the difficulty of the items, all estimators tend to underestimate the population correlation with difficult items (Figure 9, see Table 7 in Supplementary Appendix 2), and the underestimation may be notable up to 0.09 units of correlation. Notably, the dataset used in the comparison does not include polytomous items, with an extreme difficulty level; it is possible that, with more extreme (difficult) items, the underestimation may be more drastic. Notably, with extremely easy items, the underestimation is not as radical as with extremely difficult items (<0.02 units of correlation). Systematic studies in this respect would be beneficial. In this respect, there are no notable differences between the estimators of RRP —all are conservative. Again, it seems that RREG is more robust than the other estimators.
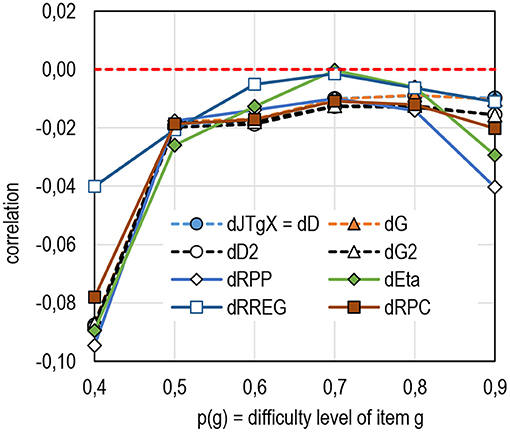
Figure 9. The average difference between the sample and population by the item difficulty (k = 6,932).
Finally, when it comes to the sample size, except eta, all estimators tend to be conservative; they underestimate the population estimate (Figure 10; see also Table 8 in Supplementary Appendix 2). With a very small sample size (n = 25), the underestimation is notable (0.04–0.05 units of correlation), and, when the sample size is n = 50 or higher, all estimators tend to give estimates that are close to the population estimate. The pattern is notably identical with all estimators except RREG and eta; the sample eta overestimates mildly the population eta (<0.005 units of correlation) and the population RREG gives roughly the same estimate as is the population RREG regardless of the sample size.
It is a well-known fact that PMC is prone both to attenuation caused by errors in measurement modelling and to radical deflation caused by a technical or mechanical errors in the calculation process. These concepts are discussed, amongst others, by Chan [77], Gadermann et al. [78], Lavrakas [79], and Metsämuuronen [26, 30, 80].
Both attenuation and deflation in PMC are artificial and systematic. Sometimes, attenuation has been connected to the phenomenon called restriction of a range or range restriction (see literature, e.g., in [81–84]). Pearson (5) himself was the first to offer a solution to the attenuation problem, and many solutions have been offered to correct the attenuation in the X variable (see the typology in [82]). However, even if there is no manifestation of range restriction in X in the sense discussed by Sacket et al. [82], PMC is very vulnerable to several sources of mechanical error in the estimates of correlation causing deflation. Metsämuuronen [29, 45] found seven such sources: (1) the division of subpopulations in g (or item difficulty in the measurement modelling settings), (2) the discrepancy in scales of the variables, (3) the distribution of the latent variable, (4) the number of categories in g, (5) the number of categories in X, (6) the number of items forming the score, and (7) the number of tied cases in the score. In practical terms, the deflation is obvious when assuming two identical normally distributed variables with obvious perfect correlation. If we dichotomized one variable (g) and polytomize the other (X), PMC and many other estimators based on covariation cannot reach the (obvious) perfect (latent) correlation (see the algebraic reasons for PMC in [75, 76], and for coefficient eta in [2]). The deflation, that is, the underestimation of the true latent association because of technical or mechanical reasons is the greater the more extreme is the division (or the difficulty level) in g.
While the effect of attenuation may be nominal in the dataset, deflation in PMC = RPP may be radical; it approximates 100% if the variance in the item is small, that is, with an item with an extreme difficulty level, causing a small item–total covariation; this is strictly inherited by the formula of PMC (see Eq. 32). To make this radical deflation visible in the measurement model, Metsämuuronen [26, 29, 30] has proposed a general measurement model, combining a latent variable (θ), observed values of an item (xi), and a weight factor wiθ that links θ with item i, and the measurement error eiθ:
generalised from the traditional measurement model (see, e.g., [85, 86]).
In the general model, the unobservable θ may be manifested as a varying type of relevantly formed compilation of items, including a theta score formed by the raw score (θX), a principal component score (θPC), a factor score (θFA), item response theory (IRT) or Rasch modelling (θIRT), or various non-linear combination of the items (θNon−Linear). The weight factor wiθ is a coefficient of correlation in some form, also including a principal component and factor loadings (λi). In a normal case, wiθ varies −1 ≤ wiθ ≤ +1; values higher than +1 or smaller than −1, sometimes obtained by bi- and polyserial correlation or by factor loadings, are taken out-of-range values.
The mechanical error in the estimation of correlation leading to deflation in the estimates has been re-conceptualised in the measurement model as
(e.g., [29]), where the notation in the element ewi θ _MEC refers to the fact that the magnitude of deflation caused by the mechanical error in the estimation (MEC) depends on the weighting factor w, item i, and score variable θ. This characteristic of the rank–polyserial coefficients of correlation is discussed in what follows.
Based on a simulation of 11 sources of mechanical error, causing deflation in estimates of the item–score association [29], of the options for RRP, the estimators D and D2 were noticed to be the most prone to deflation, while the estimators G and G2 tended to be close to be deflation free. Of the benchmarking estimators, RPC appeared to be close to deflation free, while RREG is mildly defected by the number of categories in the item and the score, the distribution of the latent variable, and RPP is severely affected by several sources of deflation. That D and D2 were ranked lower in comparison is caused by the fact that, in a theoretical dataset with identical latent variables, D and D2 tend to be sensitive to the number of categories in the item and the score as well as for the distribution of the latent variable (see Table 6). However, in real-life datasets, as seen in the previous sections, the factual magnitude of the estimates by D2 tends to follow the magnitude of those by RREG (see Section Comparison of the Estimates With a Larger Dataset).
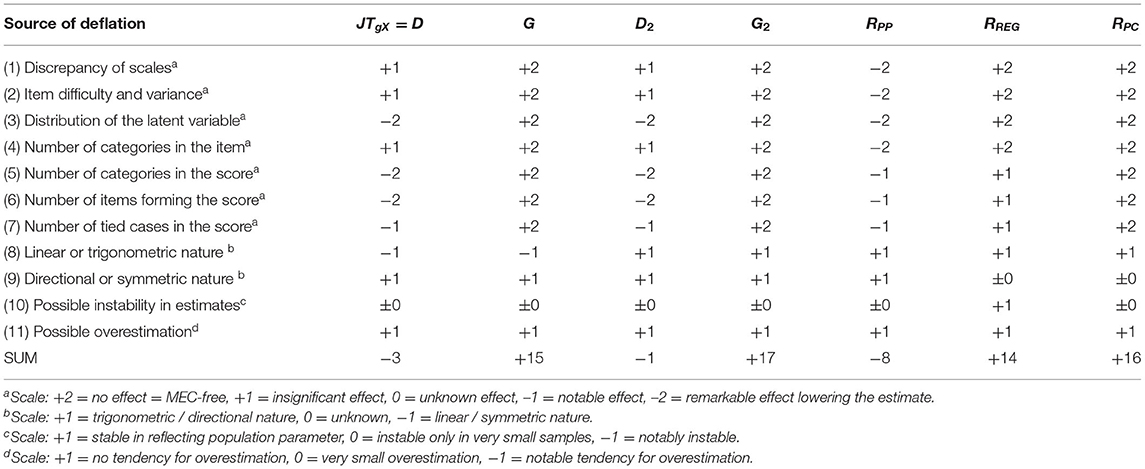
Table 6. Sensitivity of the estimators of RRP to deflation (based on Metsämuuronen [29]).
Simulations have shown that such coefficients of correlation in Table 1 related to PMC as RPP and coefficient eta include a notable magnitude of deflation in the estimates (see [2, 29, 45]). This can be easily verified by using a simple example related to Figure 2 and the related discussion. Take two identical variables with a continuous scale, and they (obviously) have a perfect correlation (ρθθ = 1). In the case we truncate one into 5 categories as in Section Simple Comparison of the Options for RRP (categories 1–5; Item g) and the other into more than two categories (Score X); these estimators of association cannot reach the factual latent correlation. Depending on the cut-offs of the values in g, that is, the “difficulty level” of the items and the number of categories in X, the deflation in the estimates may be notable, approximating 100% with extremely difficult items. In contrast, such estimators as RPC, RREG, G, and D include notably less mechanical error (MEC) than Rit if not being MEC free (see [29, 45]). This phenomenon of deflation is illustrated in Figure 11.
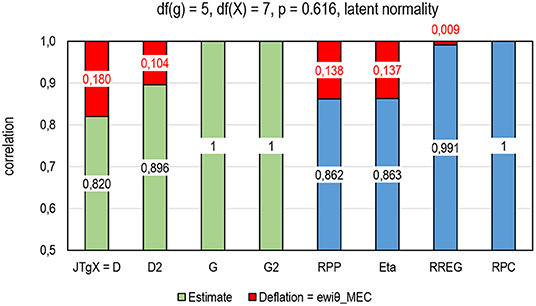
Figure 11. Deflation in the estimates in an item with p = 0.616, df(g) = 4, and df(X) = 7, latent normality, n = 1,000.
Let us assume an item close to g4 in Table 2. Two identical variables with 1,000 cases with a normal distribution are truncated so that the other includes 5 categories [df (g) = 4] and the other 8 categories [df (X) = 7], and the cut-offs in the item are selected so that p = 0.6167. Figure 10 presents the estimates. The outcome is that, if we would have two perfectly correlated variables and their technical manifestations would have been like in g4, we would expect that an estimate by D would have deflation of 0.180 units of correlation and D2 would have deflation of a magnitude of 0.104 units of correlation. Correspondingly, G and G2 can detect the perfect latent correlation in the same manner as RPC does—no deflation is detected. Of the benchmarking estimators, RREG includes a minor amount of deflation (0.009), while RPP and eta include a notable magnitude of deflation (0.138 and 0.137 units of correlation, respectively. This phenomenon explains—at least partly—why the magnitude of the estimates by D is lower than those by G, for example.
All in all, referring to the measurement model in Eq. (40) and the element ewiθ_MEC related to the deflation caused by the mechanical error in the estimating process (MEC), we end up with the following relation of the deflation in the estimators of RRP: eJTgXi_MEC = eDi_MEC > eD2i_MEC > eGi_MEC = eG2i_MEC ≈ 0.
This article started with the note that we seem to miss a coefficient of correlation that could be used as the rank–polyserial coefficient of the observed correlation between a categorical ordinal variable and an interval- or ordinal-scaled variable. The quest for finding the “missing” coefficient led us, first, to a new coefficient of correlation, rank–biserial correlation between an ordinal variable g and a metric variable X(JTgX) that was derived by generalising rank–biserial correlation into polytomous ordinal cases by using Jonckheere–Terpstra test statistics—hence, the name JTgX. It was shown that two traditional coefficients of correlation, Somers D and Goodman–Kruskal G, are strictly related to JTgX, and, hence, these also could be considered as rank–polyserial coefficients. Furthermore, two related estimators of correlation, dimension-corrected D and G (D2 and G2), are strictly related to D and G, and, hence, those could be considered dimension-corrected coefficients rank–polyserial correlation.
To conclude the outcomes from the empirical section, by using different estimators carrying characteristics of rank–polyserial coefficient, the estimates by JTgX = D, G, D2, and G2 tend to follow the following pattern: The magnitude of the estimates by JTgX and D is the lowest; D is the most affected by several sources of deflation. The magnitude of the estimates by G tends to be higher than those by D, and the estimates tend to follow the tendency of RPP and eta when the sample size exceeds n = 50. The magnitude of the estimates by D2 is higher than those by D and G, and the estimates seem to follow the tendency of RREG when the sample size exceeds n = 50. The highest magnitudes of the estimates are given by G2, and its trend follows closely the tendency of the estimates by RPC.
Hence, on the one hand, if the estimates by RREG and RPC are taken as accurate reflections of the latent item–score correlations, rank–polyserial coefficients based on D2 and G2 seem to be relevant options to use as RRP and to study more. These are based on observed variables because the underlying estimators D and G are based on observed variables. On the other hand, rank–polyserial coefficients based on D and G given the possibility of an interesting practical interpretation because of Eqs. (20) and (28): 0.5 × D + 0.5 and 0.5 × G + 0.5 strictly indicate the proportion of logically (ascending) ordered observations in Item g after they are ordered by the score. Hence, if D = 0.90, 95% of the observations (0.5 × 0.90 + 0.5 = 0.95) are logically ordered in the item.
Characteristic of all these estimators proposed as estimators of RRPis that they all are directional—the same also holds with the rank–biserial correlation. They all indicate to what extent the variable with a wider scale (X)—ordinal, interval, pseudo-continuous, or continuous scale—explains the ordinal pattern in the variable with a narrower ordinal scale (g). In the measurement modelling settings, this can be taken as an advance. After all, the whole apparatus in testing settings is based on the idea that the latent variable manifested as the score variable explains the behaviour in a test item, and the other direction does not make sense. All the options of RRP discussed in this article are directed to favour this direction. A possible advantage of the new coefficient JTgX is that it leads us strictly to the correct form of the three alternatives produced by the standard procedures of calculating Somers' D.
An obvious limitation in the study is that the characteristics of the behaviour of the coefficients were illustrated only by using a limited real-world dataset with very limited sample sizes. Although the sample sizes may be taken relevant from the practical testing setting viewpoint—after all, arguably, most tests in the world are administered in the classroom situation or lectures with a very limited number of test takers. However, controlled simulations with the known true association and with large sample sizes would be beneficial. In this, using the character in D and G to strictly indicate the proportion of logically ordered observations after ordered by the score could be utilised.
The simulation is Section Comparison of the Estimates With a Larger Dataset did not include very difficult items—this is clearly a deficiency in the original dataset. Hence, systematic studies of the behaviour of the options for RRP with items with extreme difficulty levels would be beneficial.
Publicly available datasets were analysed in this study. This data can be found here: http://dx.doi.org/10.13140/RG.2.2.10530.76482; http://dx.doi.org/10.13140/RG.2.2.17594.72641; http://dx.doi.org/10.13140/RG.2.2.17241.65127; and http://dx.doi.org/10.13140/RG.2.2.20111.30882.
Ethical approval was not provided for this study on human participants because the dataset is collected as part of national assessment and evaluation by the National Authority. Dataset is anonymized and used by permission. Written informed consent from the participants' legal guardian/next of kin was not required to participate in this study in accordance with the national legislation and the institutional requirements.
The author confirms being the sole contributor of this work and has approved it for publication.
Open access support was provided by Centre for Learning Analytics, University of Turku.
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2022.914932/full#supplementary-material
1. ^The contemporary measurement modelling settings result in score variables that are, factually, categorical ones, either ordinal, interval-scaled, or pseudo-continuous type, with the limited number of categories (see the discussion in, e.g., [2]). To obtain a truly continuous scale necessitates a truly continuous scale in at least one test item and a very large number of test takers. This kind of scale always leads to an even distribution because all test takers will get a unique score. Truly continuous scales are very rare in the testing settings. A raw score forms usually a categorical (ordinal or interval-scaled) score and the one-parameter item response theory (IRT) modelling or Rasch modelling forms a pseudo-continuous score where the number of categories in the score variable equals the number of the raw score, but the “names” of the categories come from a continuous scale. The scores by factor analysis and two- or three-parameter IRT models produce scales with more categories, although these, too, are pseudo-continuous scales where the number of categories is strictly bound to the number of test takers, the number of items, and the number of categories in the items.
2. ^A specific peculiarity in naming of the directions may be necessary to discuss here (see also [2, 29, 32]) because the directional estimators are used in what follows. With the truly directional estimators D and eta, in widely used software packages as IBM SPSS, SAS, and R-libraries, this specific direction is traditionally named as “X dependent” (see, e.g., [15, 33–37]). This naming is relevant in the general linear modelling (GLM) settings related to eta squared where the score cannot explain, for example, the sex of the test takers (g), and, hence, the score X must be a dependent variable. However, opposite thinking for the same direction is used in the measurement modelling settings, where the score variable explains the behaviour in the test item and the other direction does not make sense (see, e.g., [38, 39]). This is the case also in the nonparametric testing with U-test or Jonckheere–Terpstra test, as examples, where the idea is to first order the cases by X, after which the order of the cases in the item is analyzed. Hence, the score explains the order of the observations in g, and then, this direction should be named as “g dependent” or “g given X”. In this article, the notations D(g|X) and η(g|X) refer to the direction of “g given X,” which, in the widely used statistical packages, would be named as “X dependent”.
3. ^In the simplified notation of P and Q, they are usually seen without doubling. Technically though, P and Q are always calculated two times (see, e.g., [32, 51]). Hence, in the form of D, the doubling is seen strictly in the form (Eq. 13), but, in the form on G, both P and Q need to be thought doubled. Hence, 2 × in Eqs. (23) and (24).
4. ^This character is typical for the measurement modelling setting, but it is not relevant in general. Both G and D estimate probability, and this they make without underestimation. However, probability with a linear nature tends to give lower values of association than covariance with a trigonometric nature when two variables are continuous (see discussion in, e.g., [29, 34, 53]). This phenomenon is reflected in the item–score association with polytomous items.
5. ^These are specific coefficients for the measurement modelling settings because they are developed in the settings related to measurement modelling settings, and they are not studied in other contexts. They may be applicable in general settings, too, but more studies are needed to confirm or reject this.
6. ^The directionality of the point–biserial and point–polyserial correlation is generally not known. However, this is obvious because of the relation between PMC and coefficient eta. In the binary settings, RPB equals η(g|X) and not η(X|g). In polytomous settings, RPP follows closely the direction of η(g|X) and not that of η(X|g) (see [2]).
7. ^A dataset in CSV format at doi: 10.13140/RG.2.2.17241.65127 and in SPSS format at doi: 10.13140/RG.2.2.20111.30882 is available for the comparison of two identical variables truncated into two different forms. The dataset consists of 22,824 estimates related to three types of a latent variable (normal, even, gamma), different difficulty levels (p = 0.002–0.998), several score variables [df (X) = 5, 7, 13, 21, 26, 31, 41, and 61] and items with df (g) = 1–4, that is, the usual scales from binary to Likert type of scale are covered.
1. Olsson U, Drasgow F, Dorans NJ. The polyserial correlation coefficient. Psychometrika. (1982) 47:337–47. doi: 10.1007/BF02294164
2. Metsämuuronen J. Artificial systematic attenuation in eta squared and some related consequences. Attenuation-corrected eta and eta squared, negative values of eta, and their relation to Pearson correlation. Behaviormetrika. (2022) 2022:1–35. doi: 10.1007/s41237-022-00162-2
4. Pearson K. Mathematical contributions to the theory of evolution III. Regression, heredity, and panmixia. Philos Trans R Soc Lond Ser A. (1896) 187:253–318. doi: 10.1098/rsta.1896.0007
5. Bravais A. AnalyseMathematique. Sur les probabilités des erreurs de situation d'un point. (Mathematical analysis. Of the probabilities of the point errors). Mémoiresprésentés par divers savants à l'Académie Royale des Siences de l'Institut de France (Memoirs presented by various scholars to the Royal Academy of Sciences of the Institute of France) 9:255–332. Available online at: https://books.google.fi/books?id=7g_hAQAACAAJandredir_esc=y (accessed November 6, 2022).
6. Pearson K. On the Theory of Contingency and Its Relation to Association and Normal Correlation. Drapers' Company Research Memoirs. Biometric Series I, XIII. London: Dulau and Co (1904).
7. Pearson K. I Mathematical contributions to the theory of evolution. XI. On the influence of natural selection on the variability and correlation of organs. Philos Trans R Soc A. Math Phys Eng Sci. (1903) 200:1–66. doi: 10.1098/rsta.1903.0001
8. Pearson K. On the General Theory of Skew Correlation Non-Linear Regression. London: Dulau Co (1905). Available online at: https://onlinebooks.library.upenn.edu/webbin/book/lookupid?key=ha100479269 (accessed November 6, 2022).
9. Goodman LA, Kruskal WH. Measures of association for cross classifications. J Am Stat Assoc. (1954) 49:732–64. doi: 10.1080/01621459.1954.10501231
10. Goodman LA, Kruskal WH. Measures of association for cross classifications: II. Further discussion and references. J Am Stat Assoc. (1959) 54:123–63. doi: 10.1080/01621459.1959.10501503
11. Kendall MG. A new measure of rank correlation. Biometrika. (1938) 30:81–93. doi: 10.2307/2332226
12. Somers RH. A new asymmetric measure of association for ordinal variables. Am Sociol Rev. (1962) 27:799–811. doi: 10.2307/2090408
13. Glass GV. Note on rank biserial correlation. Educ Psychol Measur. (1966) 26:623–31. doi: 10.1177/001316446602600307
14. Wendt HW. Dealing with a common problem in social science: a simplified rank biserial coefficient of correlation based on the U statistic. Eur J Soc Psychol. (1972) 2:463–5. doi: 10.1002/ejsp.2420020412
15. Newson R. Identity of Somers' D the Rank Biserial Correlation Coefficient. (2008). Available online at: http://www.rogernewsonresources.org.uk/miscdocs/ranksum1.pdf
16. Pearson K. Mathematical contributions to the theory of evolution. VII. On the correlation of characters not quantitatively measurable. Philos Trans R Soc A. Math Phys Eng Sci. (1900) 195:1–47. doi: 10.1098/rsta.1900.0022
17. Pearson K. On the measurement of the influence of “broad categories” on correlation. Biometrika. (1913) 9:116–39. doi: 10.1093/biomet/9.1-2.116
18. Pearson K. On a new method of determining correlation between a measured character A, and a character B, of which only the percentage of cases wherein B exceeds (or falls short of) a given intensity is recorded for each grade of A. Biometrika. (1909) 7:96–105. doi: 10.1093/biomet/7.1-2.96
19. Lancaster HO, Hamdan MA. Estimation of the correlation coefficient in contingency tables with possibly nonmetrical characters. Psychometrika. (1964) 29:383–91. doi: 10.1007/BF02289604
20. Martinson EO, Hamdan MA. Maximum likelihood and some other asymptotical efficient estimators of correlation in two-way contingency tables. J Stat Comput Simul. (1972) 1:45–54. doi: 10.1080/00949657208810003
21. Tallis G. The maximum likelihood estimation of correlation from contingency tables. Biometrics. (1962) 18:342–53. doi: 10.2307/2527476
22. Olsson U. Maximum likelihood estimation of the polychoric correlation coefficient. Psychometrika. (1979) 44:443–60. doi: 10.1007/BF02296207
23. Drasgow F. Polychoric and polyserial correlations. In: Kotz S, Johnson NL, editor. Encyclopedia of Statistical Sciences, Vol 7. London: John Wiley (1986). p. 68–74
24. Clemans WV. An index of item-criterion relationship. Educ Psychol Meas. (1958) 18:167–72. doi: 10.1177/001316445801800118
25. Metsämuuronen J. Somers' D as an alternative for the item–test and item–rest correlation coefficients in the educational measurement settings. Int J Educ Methodol. (2020) 6:207–21. doi: 10.12973/ijem.6.1.207
26. Metsämuuronen J. Deflation-corrected estimators of reliability. Front Psychol. (2022) 12:748672. doi: 10.3389/fpsyg.2021.748672
27. Livingston SA, Dorans NJ. A Graphical Approach to Item Analysis. Research Report No. RR-04-10. Educational Testing Service (2004). doi: 10.1002/j.2333-8504.2004.tb01937.x
28. Moses T. A review of developments and applications in item analysis. In Bennett R and von Davier M, editor. Advancing Human Assessment. The Methodological, Psychological and Policy Contributions of ETS (pp. 19–46). Educational Testing Service. Heidelberg: Springer Open (2017).
29. Metsämuuronen J. Effect of various simultaneous sources of mechanical error in the estimators of correlation causing deflation in reliability. Seeking the best options of correlation for deflation-corrected reliability. Behaviormetrika. (2022) 41:91–130 doi: 10.1007/s41237-022-00158-y
30. Metsämuuronen J. Attenuation-corrected estimators of reliability. Appl Psychol Measure (2022). doi: 10.1177/01466216221108131
31. Henrysson S. Correction of item–total correlations in item analysis. Psychometrika. (1963) 28:211–8. doi: 10.1007/BF02289618
32. Metsämuuronen J. Directional nature of Goodman-Kruskal gamma and some consequences. Identity of Goodman-Kruskal gamma and Somers delta, and their connection to Jonckheere-Terpstra test statistic. Behaviormetrika. (2021) 48:2. doi: 10.1007/s41237-021-00138-8
33. Metsämuuronen J. Basics of nonparametric statistics. In: Metsämuuronen J, editor. Essentials of Research Methods in Human Sciences. Vol 3: Advanced Analysis. London: SAGE Publications (2017). p. 1–282.
34. Newson R. Parameters behind “nonparametric” statistics: Kendall's tau, Somers' D and median differences. Stata J. (2002) 2:45–64.
35. Newson R. Confidence intervals for rank statistics: Somers' D and extensions. Stata J. (2006) 6:309–34.
36. Newson R. Interpretation of Somers' D Under Four Simple Models. (2014). Available online at: https://pdfs.semanticscholar.org/f2b5/e97c4c28a917016471c38ea908713d8a6436.pdf (accessed November 6, 2022).
37. Siegel S, Castellan NJ Jr. Nonparametric Statistics for the Behavioral Sciences. 2nd edition. London: McGraw-Hill (1988).
38. Byrne BM. Structural Equation Modelling With AMOS Basic Concepts, Applications, and Programming. 3rd Edition. New York: Routledge (2016).
39. Metsämuuronen J. Basics of SEM and Path modelling in AMOS Environment. In: Metsämuuronen J, editor. Essentials of Research Methods in Human Sciences. Vol 3: Advanced Analysis. London: SAGE Publications (2013). p. 533–96.
40. Mann HB, Whitney DR. On a test of whether one of two random variables is stochastically larger than the other. Ann Math Stat. (1947) 18:50–60. doi: 10.1214/aoms/1177730491
41. Berry KJ, Johnston JE, Mielke PW Jr. The Measurement of Association. A Permutation Statistical Approach. Berlin: Springer (2018). doi: 10.1007/978-3-319-98926-6
42. Wilcoxon F. Individual comparisons by ranking methods. Biometrics. (1945) 1:80–3. doi: 10.2307/3001968
43. Jonckheere AR. A distribution-free k–sample test against ordered alternatives. Biometrika. (1954) 41:133–45. doi: 10.1093/biomet/41.1-2.133
44. Terpstra TJ. The asymptotic normality and consistency of Kendall's test against trend, when ties are present in one ranking. IndagationesMathematicae. (1952) 14:327–33. doi: 10.1016/S1385-7258(52)50043-X
45. Metsämuuronen J. Goodman–Kruskal gamma and dimension-corrected gamma in educational measurement settings. Int J Educ Methodol. (2021) 7:95–118. doi: 10.12973/ijem.7.1.95
47. Goodman LA, Kruskal WH. Measures of Association for Cross Classification. Berlin: Springer (1979).
48. Göktaş A, Işçi OA. Comparison of the most commonly used measures of association for doubly ordered square contingency tables via simulation. Metodološkizvezki. (2011) 8:17–37.
49. Metsämuuronen J. Dimension-corrected Somers' D for the item analysis settings. Int J Educ Methodol. (2020) 6:297–317. doi: 10.12973/ijem.6.2.297
51. Van der Ark LA, Van Aert RCM. Comparing confidence intervals for Goodman and Kruskal's gamma coefficient. J Stat Comput Simul. (2015) 85:2491–505. doi: 10.1080/00949655.2014.932791
52. Arbuthnot J. An argument for divine providence, taken from the constant regularity observed in the births of both sexes. Philos Trans R Soc Lond. 27:186–90. doi: 10.1098/rstl.1710.0011
53. Kendall M. Rank and product–moment correlation. Biometrika. (1949) 36:177–93. doi: 10.2307/2332540
54. Newson R. SOMERSD: Stata module to calculate Kendall's tau-a, Somers' D and median differences. Statistical Software Components, S336401, Boston College Department of Economics (2020). Available online at: https://ideas.repec.org/c/boc/bocode/s336401.html (accessed April 16, 2020).
55. Stata Corp. Stata Manual. (2018). Available onine at: https://www.stata.com~/manuals13/mvalpha.pdf (accessed November 6, 2022).
56. Metsämuuronen J. Item–rest correlations revisited. Algebraic reasons why the estimates by item–rest correlation are more deflated than those by item–test correlation, and some coefficients to consider as alternatives. Preprint. (2022). doi: 10.13140/RG.2.2.24704.71687
57. Chen Y-H., Li I. IA_CTT: A SAS® Macro for Conducting Item Analysis Based on Classical Test Theory. Paper CC184. (2015). Available onine at: https://analytics.ncsu.edu/sesug/2015/CC-184.pdf (accessed November 6, 2022).
58. Lüdecke D. Item Analysis of a Scale or An Index. (2021). Available online at: https://cran.r-project.org/web/packages/sjPlot/vignettes/sjtitemanalysis.html (accessed November 26, 2021)
59. Martinkova P, Drabinova A. ShinyItemAnalysis for teaching psychometrics and to enforce routine analysis of educational tests. R J. (2018) 10:503–515. doi: 10.32614/RJ-2018074
60. Eikeland HM. On the generality of univariate eta. Scand J Educ Res. (1971) 15:149–67. doi: 10.1080/0031383710150109
61. Wherry RJ, Taylor EK. The relation of multiserial eta to other measures of correlation. Psychometrika. (1946) 11:155–61. doi: 10.1007/BF02289296
62. Kerlinger FN. Foundations of Behavioral Research. New York, NY: Holt, Rinehart and Winston (1964).
63. Turnbull WW. A normalized graphic method of item analysis. J Educ Psychol. (1946) 37:129–41. doi: 10.1037/h0053589
64. Brogden HE. A new coefficient: application to biserial correlation and to estimation of selective efficiency. Psychometrika. (1949) 14:169–82. doi: 10.1007/BF02289151
65. Henrysson S. Gathering, analyzing and using data on test items. In: Thorndike RL, editor. Educational Measurement (2nd ed.). American Council on Education (1971). p. 130–159
66. Flora DB, Curran PJ. An empirical evaluation of alternative methods of estimation for confirmatory factor analysis with ordinal data. Psychol Methods. (2004) 9:466–91. doi: 10.1037/1082-989X.9.4.466
67. Holgado-Tello FP, Chacón-Moscoso S, Barbero-García I, Vila–Abad E. Polychoric versus Pearson correlations in exploratory and confirmatory factor analysis of ordinal variables. Quad Quan. (2010) 44:153–66. doi: 10.1007/s11135-008-9190-y
68. Rigdon EE, Ferguson CEJr. The performance of the polychoric correlation coefficient and selected fitting functions in confirmatory factor analysis with ordinal data. J Market Res. (1991) 28:491–7. doi: 10.1177/002224379102800412
69. Jöreskog KG. On the estimation of polychoric correlations and their asymptotic covariance matrix. Psychometrika. (1994) 59:381-9. doi: 10.1007/BF02296131
70. Chalmers RP. On misconceptions and the limited usefulness of ordinal alpha. Educ Psychol Meas. (2017) 78:1056–71. doi: 10.1177/0013164417727036
71. Olson U. Measuring correlation in ordered two-way contingency tables. J Market Res. (1980) 17:391–4. doi: 10.1177/002224378001700315
72. Lorenzo-Seva U, Ferrando PJ. POLYMAT-C: a comprehensive SPSS program for computing the polychoric correlation matrix. Behav Res Methods. (2015) 47:884–9. doi: 10.3758/s13428-014-0511-x
73. Zaionts C. Real Statics Using Excel. Polychoric Correlation using Solver (2022). Available online at: http://www.real-statistics.com/correlation/polychoric-correlation/polychoric-correlation-using-solver/ (accessed November 6, 2022).
74. FINEEC. National Assessment of Learning Outcomes in Mathematics at Grade 9 in 2004. Unpublished dataset opened for the re-analysis 18.2.2018. Finnish: Finnish National Education Evaluation Centre (2018).
75. Metsämuuronen J. Item–total correlation as the cause for the underestimation of the alpha estimate for the reliability of the scale. GJRA. (2016) 5:471–7.
76. Metsämuuronen J. Basics of test theory. In: Metsämuuronen J, editor. Essentials of Research Methods in Human Sciences. Vol 1: Elementary Basics. London: SAGE Publications (2017). p. 66–183
77. Chan D. So why ask me? Are self-report data really that bad? In: Lance CE, Vanderberg RJ, editor. Statistical and Methodological Myths and Urban Legends. Boca Raton: Routledge (2008). p. 309–326.
78. Gadermann AM, Guhn M, Zumbo BD. Estimating ordinal reliability for Likert-type and ordinal item response data: a conceptual, empirical, and practical guide. Pract Assess Res Eval. (2012) 17:1–13. doi: 10.7275/n560-j767
79. Lavrakas PJ. Attenuation. In: Lavrakas PJ, editor. Encyclopedia of Survey Methods. London: Sage Publications, Inc. (2008).
80. Metsämuuronen J. How to obtain the most error-free estimate of reliability? Eight sources of underestimation of reliability. PARE (2022) 27:10. Available online at: https://scholarworks.umass.edu/pare/vol27/iss1/10
81. Meade AW. Restriction of range. In: Salkind NJ, editor. Encyclopedia of Research Design. London: SAGE Publications (2010). p. 1278–80.
82. Sackett PR, Lievens F, Berry CM, Landers RN. A cautionary note on the effect of range restriction on predictor intercorrelations. J Appl Psychol. (2007) 92:538–44. doi: 10.1037/0021-9010.92.2.538
83. Schmidt FL, Hunter JE. Methods of Meta-Analysis: Correcting Error and Bias in Research Findings (3rd ed.). London: SAGE Publications (2015).
84. Walk MJ, Rupp AA. Pearson product-moment correlation coefficient. In: Salkind NJ, editor. Encyclopedia of Research Design. London: SAGE Publications (2010). p. 1022–6.
85. Cheng Y, Yuan K-H, Liu C. Comparison of reliability measures under factor analysis and item response theory. Educ Psychol Meas. (2012) 72:52–67. doi: 10.1177/0013164411407315
Keywords: rank–biserial correlation, rank–polyserial correlation, point-polyserial correlation, polyserial correlation, Goodman–Kruskal G, Somers D, dimension-corrected G, dimension-corrected D
Citation: Metsämuuronen J (2022) Rank–Polyserial Correlation: A Quest for a “Missing” Coefficient of Correlation. Front. Appl. Math. Stat. 8:914932. doi: 10.3389/fams.2022.914932
Received: 07 April 2022; Accepted: 30 May 2022;
Published: 27 June 2022.
Edited by:
Min Wang, University of Texas at San Antonio, United StatesReviewed by:
Zifei Han, Beijing University of International Business and Economics, ChinaCopyright © 2022 Metsämuuronen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jari Metsämuuronen, amFyaS5tZXRzYW11dXJvbmVuQGdtYWlsLmNvbQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.