
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Appl. Math. Stat., 13 May 2022
Sec. Dynamical Systems
Volume 8 - 2022 | https://doi.org/10.3389/fams.2022.903563
This article is part of the Research TopicDynamical Systems, PDEs and Networks for Biomedical Applications: Mathematical Modeling, Analysis and SimulationsView all 18 articles
 Vladimir Zykov1*
Vladimir Zykov1* Eberhard Bodenschatz1,2,3,4
Eberhard Bodenschatz1,2,3,4The stability of rigidly rotating spiral waves is a very important topic in the study of nonlinear reaction-diffusion media. Computer experiments carried out with a slightly modified Barkley model showed that, in addition to one region of instability observed earlier in the original Barkley model, there is another one exhibiting completely different properties. The wave instability in the second region is not related to the Hopf bifurcation. Moreover, hysteresis effects are observed at the boundary of the region. This means that in the vicinity of this region of instability, direct integration of the model equations leads either to a rigidly rotating or meandering spiral, depending on the initial conditions.
Excitable media represent a broad class of non-equilibrium reaction-diffusion systems that play an important role in physical, chemical, and biological applications [1–4]. For example, wave processes in excitable media are intensively studied in various distributed systems, including the colonies of Dictyostelium discoideum [5], the Belousov-Zhabotinsky chemical reaction [6], the heart muscle [7], the eye retina [8], the neocortex [9], CO oxidation on the platinum single crystal surface [10], and many others.
An excitable medium can be viewed as an ensemble of active elements coupled locally by diffusion-like transport processes. Each individual active element has a resting state, resistant to small external perturbations. However, it can be excited by the application of a suprathreshold stimulus or by interacting with their neighbors. Therefore, locally induced excitation can propagate through the medium as a self-sustaining wave. Such a wave represents a rapid transition from a stable resting state to an excited one followed by a slow recovery transition (refractory) back to the resting state. Under normal conditions, the wave back follows the wavefront, and they never touch each other.
However, under some special conditions, the propagating wavefront can be broken [1, 11]. Then the front and the back of the wave propagating in a two-dimensional medium coincide at one point called a phase change point [2]. Near this point, the front and the back are moving in opposite directions and the boundary of the excited region curls around this singularity point. As a result, the broken wave is winding up into a spiral permanently rotating within the medium.
Such self-sustained activity unexpectedly appearing in cardiac or neuronal tissues strongly destroys their dynamics that results in life-threating diseases. In this context, an understanding of possible scenarios of spiral wave dynamics is of great theoretical importance and has many practical applications.
One important aspect of this study is investigation of spiral wave stability. In a homogeneous low excitable two-dimensional medium spiral wave rigidly rotates around a round core. However, under a variation of the medium's parameters this well-ordered dynamics can be destroyed that leads to a transformation of a circular trajectory of the spiral wave tip into the so-called meandering one, e.g., hypotrochoid or epitrochoid [12, 13].
Spiral wave meander has been observed in experiments with chemical solutions [14] and in computations performed with different reaction-diffusion models [15–17]. The investigation of spiral wave instability attracts a great attention from a theoretical point of view [18–21].
In this study we would like to find out domains of the spiral wave meandering within the parameter space of a slightly modified Barkley model of an excitable medium.
In many studies it was demonstrated that the basic features of the wave dynamics can be reproduced by the two-component reaction-diffusion system
where the variables u and v represent the activator and inhibiter species, respectively. Typically the nullcline F(u, v) = 0 is a non-monotonic function creating possibility for undamped wave propagation. The second nullcline G(u, v) = 0 is monotone and intersects the first one at only one point (u0, v0). Below the functions F(u, v) and G(u, v) are taken in the form proposed by Barkley [22]:
Note, that in the original Barkley model the value of the parameter kϵ is fixed as kϵ = 1. Three other constants a, b, and ϵ have been used as important control parameters. A variation of each of these three parameters results in a simultaneous influence on such important medium's characteristics as the propagation velocity, pulse duration and refractoriness. In the modified model under consideration the constant kϵ is introduced, which has no influence on the duration of a single pulse and its propagation velocity. However, this parameter allow us to control the recovery process because its characteristic time is determined as the product kϵϵ. Thus the activation and the recovery processes have different time constants, if kϵ≠1. Such a jump in the characteristic time constant is a fairly common and useful tool in simulations of excitable media [12, 23, 24].
In all computations below the parameter D is fixed as D = 1. The Laplacian in Equation (1) was approximated using the five-point finite-difference method on the rectangular 500 × 500 grid with spatial step Δx = Δy = 0.3. After this spatial discretization the model equations are integrated in time with the explicit forward Euler method with time step Δt = 0.01 and no-flux boundary conditions. The spiral wave tip is determined as a point where u = 0.5 and du/dt = 0. A part of an isoconcentration line u(x, y, t) = 0.5 corresponds to the wave front where du/dt>0, and another part, where du/dt < 0, represents the wave back.
As the first step of our study the parameters are fixed as ϵ = 0.01 and kϵ = 2, while the constants a and b are used as important control parameters. The obtained computational results are illustrated in Figures 1, 2.
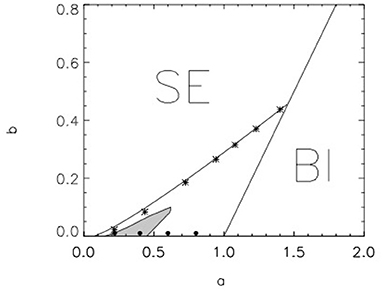
Figure 1. Parameter space of the modified Barkley model with ϵ = 0.01 and kϵ = 2. Within the SE region wave segments created in two dimensional medium are shrinking. Within the BI region the system (1)–(3) exhibits the bistability. Rotating spiral waves are analyzed between these two regions. Within the white domain spiral waves rotates around a circular core, while they are meandering within the light gray domain. Black spots correspond to parameter values used in Figure 2.
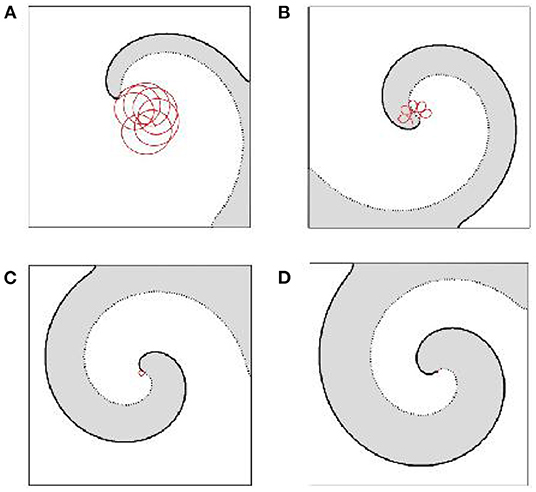
Figure 2. Spiral waves dynamics obtained for the system (1)–(3) with ϵ = 0.01, kϵ = 2 and b = 0.01 for different values of the parameter a. In (A) a = 0.22, in (B) a = 0.4, in (C) a = 0.6, and in (D) a = 0.8. Thick and dotted solids represent the wave front and back, correspondingly. The trajectory of the spiral wave tip is shown in red.
Within the parameter space shown in Figure 1 there is a line
which determines the boundary of the bistability (BI) domain, where b< a−1. Here the nullclines of the system (1)–(3) have two intersections points.
We analyse another part of the parameter space, where b>a−1 and the system has only one rest point. Here he existence of spiral waves is limited by another line, where the radius of the core of the spiral wave becomes infinitely large. In the subexcitable (SE) region above this line, the wave segments formed after a wave break are not able to curl around the created singularity point, but simply shrink and disappear. An analytical expression for this line was obtained earlier [25] and has the form
where Bc = 0.535 is a critical value of the parameter , as it was shown in [26]. Here du and cp are the duration and the propagation velocity of a single pulse through a one dimensional medium, correspondingly. It can be seen, that the analytical approximation expressed by Equation (4) is in good agreement with the direct reaction-diffusion calculations illustrated by asterisk in Figure 1.
In order to analyse the dynamics of the spiral wave, numerous calculations were performed at various points in the parameter space. A broken plane excitation wave [2] was used as initial conditions. Initially, we fixed a relatively small value of the parameter b. A rigidly rotating spiral wave with a large core was generated near the boundary of the SE region. Then the parameter a increases step by step from one calculation to the next. The size of the core decreases as a increases, and the rotation period decreases. At some computational step, rigid rotation becomes impossible, and a meandering trajectory of the spiral wave tip is observed. This occurs on the left boundary of the light gray region in the Figure 1.
Meandering spirals were observed in the entire light gray region. It is found that in this meandering region the trajectory of the spiral wave tip may look like an epitrochoid (Figure 2A) or a hypotrochoid (Figure 2B). In the white region, to the right of the light gray region and until the BI domain, the tip of the spiral wave moves along a circular trajectory. The radius of this trajectory strongly decreases as a increases.
The computational data shown in Figures 1, 2 look qualitatively similar to ones obtained earlier for the original Barkley model with kϵ = 1 and ϵ = 0.02 [22, 27]. However, the size of the instability domain is considerably smaller in the case under consideration. Note, that while the used value of the parameter ϵ is smaller, the characteristic recovery time determined by the product kϵϵ remains the same.
In the second part of our study the value of the parameter ϵ is further decreased to ϵ = 0.005 and kϵ is increased to kϵ = 4 in order to conserve the characteristic recovery time. The data obtained in the corresponding computations are shown in Figures 3, 4.
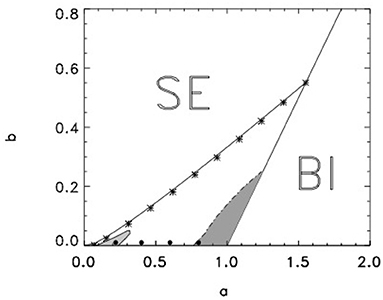
Figure 3. Parameter space of the modified Barkley model with kϵ = 4 and ϵ = 0.005. Within the light gray domain tip trajectories look like epi- or hypo-trohoids, like in Figure 1. Within the dark gray domain the tip trajectories are more complicated and disordered. Within the white domain spiral waves rotates around a circular core. Black spots correspond to parameter values used in Figure 4.
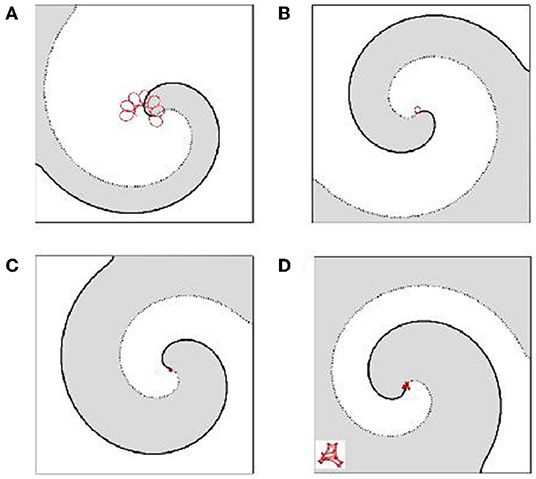
Figure 4. Spiral waves dynamics obtained for the system (1)–(3) with ϵ = 0.005, kϵ = 4, and b = 0.01 for different values of the parameter a. In (A) a = 0.22, in (B) a = 0.4, in (C) a = 0.6, and in (D) a = 0.8. Thick and dotted solids represent the wave front and back, correspondingly. The trajectory of the spiral wave tip is shown in red. In the left lower corner of (D) the trajectory is magnified.
As well as in the previous case, the existence of spiral waves here is limited by the lines defined by Equations (4) and (5). Note that the accuracy of the analytical estimate represented by Equation (5) becomes better as ϵ decreases.
Figure 3 clearly shows that there are two regions of instability in the parameter space. The spiral waves in the light gray region show dynamics very similar to those observed in the light gray region in Figure 1. Here, the trajectories of the spiral wave tips resemble epitrochoids or hypotrochoids, for example (see Figure 4A).
In the dark gray region, the tip trajectories become much more complex and are not as well ordered as shown in Figure 4D. In the parameter region surrounding these two regions, the trajectory of the spiral tip is circular.
Note that the light gray domain in Figure 3 is much smaller than in Figure 1. You can also see that the radius of the circular trajectory of the spiral tip is much smaller for these ϵ and kϵ values, while the values of a and b are the same. This follows from a comparison of Figures 1B,C with Figures 3B,C.
As the next step of our study the value of the parameter ϵ is considerably decreased to ϵ = 0.001 in the numerical computations. Simultaneously the parameter kϵ is increased to kϵ = 20 in order to conserve the characteristic recovery time.
Under these modified values a part of the parameter space shown in Figure 5 looks qualitatively similar to the picture obtained for the original Barkley model as well as for one shown in Figure 1. Within the subexcitable region SE there are no self-sustained spiral waves. Wave segments initiated in this parameter region are shrinking and disappear. Within the rest of the parameter space presented in Figure 5 self-sustained spiral waves have been observed. They are rotating rigidly within the white region, while inside the light gray region they are meandering. Some examples of spiral wave dynamics are shown in Figure 6.
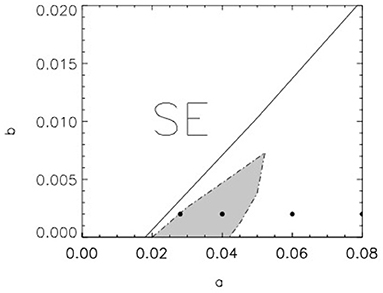
Figure 5. A small part of the parameter space of the modified Barkley model with kϵ = 20 and ϵ = 0.001. The 2D medium does not support self-sustained spiral waves within the SE domain. Within the gray region spiral waves are unstable. Black spots correspond to parameter values used in Figure 6.
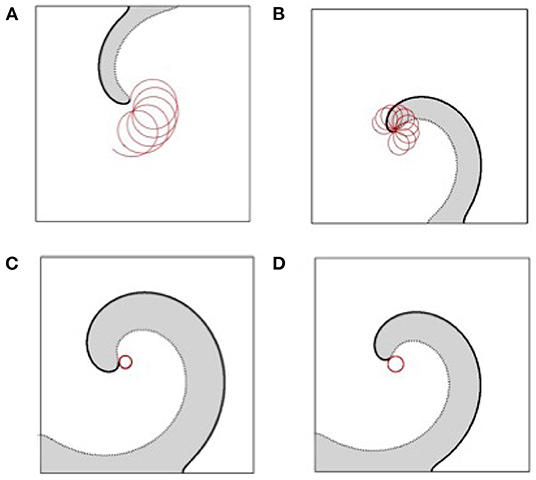
Figure 6. Four examples of the trajectories of the spiral wave tip observed within the gray parameter region shown in Figure 5 with b = 0.002 and (A) a = 0.028, (B) a = 0.04, (C) a = 0.06, (D) a = 0.08.
However, this is only a very small part of the entire parameter space investigated at these parameter values. The results obtained in a wider parameter space are shown in Figure 7. The regions of subexcitability (SE) and bistability (BI) are indicated here. Self-sustaining spiral waves are observed between these two regions. Within the narrow white region, the rigid rotation of spiral waves is stable. The transition to meandering spiral motion occurs in a very small light gray region with a≪1 and b≪1, which is almost invisible in Figure 7 but is shown in Figure 5.
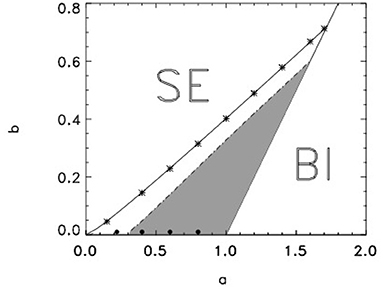
Figure 7. Parameter space of the modified Barkley model with kϵ = 20 and ϵ = 0.001. The 2D medium does not support self-sustained spiral waves within the SE domain. Within the dark gray region spiral waves are unstable. Within the white region between these two domains rigidly rotating spirals with a circular core have been observed. Black spots correspond to parameter values used in Figure 8.
In the dark gray region, the trajectories of the spiral tips are very different from those of the hypotrachoids and epitrachoids shown in Figure 6. A step by step increase of the parameter a within the dark gray domain results in a strong transformation of the spiral tip trajectory. Indeed, rigidly rotating spiral describing a perfect circular shown in Figure 8A transforms into a jagged trajectory in Figure 8B. Further increase of a results in increasing of angular loops of the trajectory in Figure 8C and their dynamics becomes more irregular in Figure 8D.
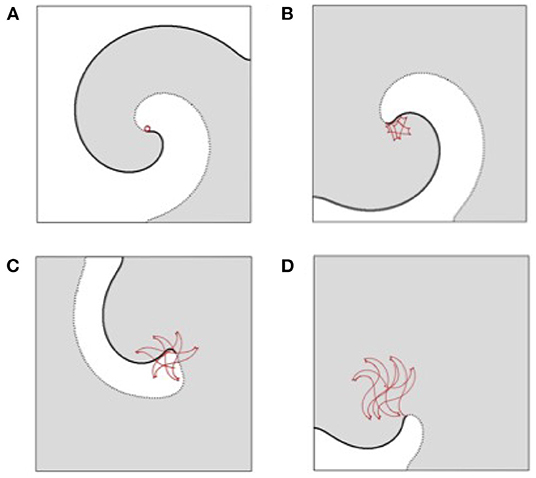
Figure 8. Four examples of the trajectories of the spiral wave tip observed within the gray parameter region shown in Figure 5 with b = 0.01 and (A) a = 0.22, (B) a = 0.4, (C) a = 0.6, (D) a = 0.8.
Moreover, at the boundary of this region a hysteresis effect in the spiral wave dynamics has been observed. This phenomenon is illustrated in Figure 9. Here the trajectories of the spiral wave tip are shown obtained for different values of the parameter a and b = 0.015. The computations have been started at a = 0.31 and result in rigidly rotating spiral shown in Figure 9A. This stationary rotating wave is used as the initial conditions for the next computations performed with a = 0.32 and illustrated in Figure 9B. After a short transient process the spiral wave trajectory approaches the circular shape. However, a jump to a = 0.325 leads to a destabilization of the rigid rotation and appearance of a rather complicated trajectory, shown in Figure 9C. This wave pattern has been used as the initial conditions for the computations in which the parameter a has been returned back to a = 0.32. However, the spiral tip trajectory does not return back to a circular one, as can be seen in Figure 9D. A rigid rotation restores only for a = 0.31. The further decrease of a also results in a circular trajectory. Thus, it is demonstrated that for a = 0.32 the shape of the spiral tip trajectory depends on the initial conditions.
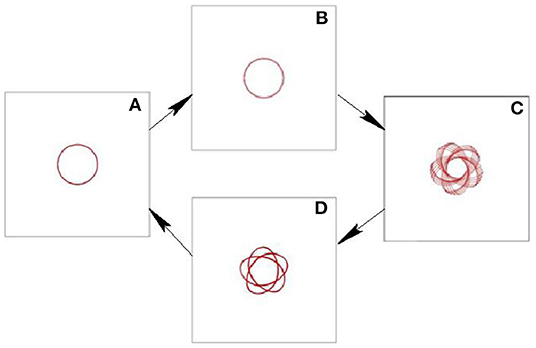
Figure 9. The trajectories of the spiral wave tips obtained numerically for the modified Barkley model with the parameter b fixed as b = 0.015 and varied parameter a. (A) a = 0.31, (B) a = 0.32, (C) a = 0.325, (D) a = 0.32.
The observed hysteresis effect exists not only for b = 0.015, but for all other values of b corresponding to the boundary of the instability domain represented by a dashed-dotted line in Figure 9. In particular for a = 1.0 and b = 0.328, as well as for a = 1.4 and b = 0.51. It has been observed not only by a variation of the parameter a and fixed parameter b, but also by a variation of the parameter b and fixed a.
Thus, the numerical computations performed with a slightly modified Barkley model demonstrate the existence of two quite different parameter regions of spiral wave instability. Within a region located near the SE domain a transition from rigid rotation to spiral meandering follows a well known scenario. Here the instability is induced by the Hopf bifurcation that results in a hypotrachoidal or epitrachoidal trajectory of the spiral wave tip.
The spiral tip trajectories look more complex in the new found region (see Figure 4). The smooth circular trajectory transforms here into a jagged one and even becomes randomized (see Figure 8). This resembles a transition to hypermeandering spiral dynamics reported for the FitzHugh-Nagumo model [13], but is very unusual for the well studied Barkley model. The observed instability cannot be explained by the Hopf bifurcation as was done for the original Barkley model.
At the boundary of this new found instability region the hysteresis phenomenon was detected (see Figure 9). Note, that the similar hysteresis phenomenon was recently observed in the context of the Barkley model within the bistability region [25]. Moreover, a hysteresis phenomenon has been described in context of the FitzHugh-Nagumo model [28, 29].
Thus, the results obtained are quite general and applicable to quite different reaction-diffusion models, which should stimulate further research in this area.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
VZ performed the computations. Both authors conceived of the presented idea, discussed the results, and contributed to the final manuscript.
This work was supported by the Max Planck Society and the German Center for Cardiovascular Research (DZHK).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
2. Zykov VS. Simulation of Wave Processes in Excitable Media. New York, NY: Manchester University Press (1987).
3. Mikhailov AS. Foundations of Synergetics. Berlin; Heidelberg: Springer (1990). doi: 10.1007/978-3-642-97269-0
5. Gerisch G. Periodische Signale steuern die Musterbildung in Zellverbaenden. Naturwissenschaften (1971) 58:430–8. doi: 10.1007/BF00624616
6. Zaikin AN, Zhabotinsky AM. Concentration wave propagation in two-dimensional liquid-phase self-oscillating systems. Nature. (1970) 225:535–7. doi: 10.1038/225535b0
7. Allesie MA, Bonke FIM, Schopman FJG. Circus movement in rabbit atrial muscle as a mechanism of tachycardia. Circ Res. (1973) 41:9–18. doi: 10.1161/01.RES.41.1.9
8. Gorelova NA, Bures J. Spiral waves of spreading depression in the isolated chicken retina. J Neurobiol. (1983) 14:353–63. doi: 10.1002/neu.480140503
9. Huang X, Xu W, Liang J, Takagaki K, Gao X, Wu J-Y. Spiral wave dynamics in neocortex. J Neurobiol. (2010) 68:978–90. doi: 10.1016/j.neuron.2010.11.007
10. Jakubith S, Rotermund HH, Engel W, von Oertzen A, Ertl G. Spatiotemporal concentration patterns in a surface-reaction - propagating and standing waves, rotating spirals, and turbulence. Phys Rev Lett. (1990) 65:3013–6. doi: 10.1103/PhysRevLett.65.3013
11. Zykov VS. Spiral wave initiation in excitable media. Philos Trans R Soc A. (2018) 376:2017. doi: 10.1098/rsta.2017.0379
13. Winfree AT. Varieties of spiral wave behavior: an experimentalists approach to the theory of excitable media. Chaos. (1971) 1:303–34. doi: 10.1063/1.165844
14. Winfree AT. Spatial and temporal organization in the zhabotinsky reaction. Adv Biol Med Phys. (1977) 16:115–36. doi: 10.1016/B978-0-12-005216-5.50011-6
15. Rossler OE, Kahlert C. Winfree meandering in a 2-dimensional 2-variable excitable medium. Z Naturforsch. (1979) 34:565–70. doi: 10.1515/zna-1979-0507
16. van Capelle FJ, Durrer D. Computer simulation of arrhythmias in a network of coupled excitable elements. Circ Res. (1979) 47:454–66. doi: 10.1161/01.RES.47.3.454
17. Pertsov AM, Panfilov A, Medvedeva FU. Instabilities of autowaves in excitable media associated with critical curvature phenomenon. Biofizika. (1983) 28:100–2.
18. Lugosi E. Analysis of meandering in Zykov kinetics. Phys D. (1989) 40:331–7. doi: 10.1016/0167-2789(89)90047-X
19. Barkley D. Linear stability analysis of rotating spiral waves in excitable media. Phys Rev Lett. (1992) 68:2090–3. doi: 10.1103/PhysRevLett.68.2090
20. Ouyang Q, Swinney HL, Li G. Transition from spirals to defect-mediated turbulence driven by a Doppler instability. Phys Rev Lett. (2000) 84:1047–50. doi: 10.1103/PhysRevLett.84.1047
21. Qu Z, Xie F, Garfinkel A, Weiss JN. Origins of spiral wave meander and breakup in a two-dimensional cardiac tissue model. Ann Biomed Eng. (2000) 40:755–71. doi: 10.1114/1.1289474
22. Barkley D. A model for fast computer-simulation of waves in excitable media. Phys D. (1991) 49:61–70. doi: 10.1016/0167-2789(91)90194-E
23. Fenton F, Karma A. Vortex dynamics in three-dimensional continuous myocardium with fiber rotation: filament instability and fibrillation. Chaos. (1998) 8:20–47. doi: 10.1063/1.166311
24. Zykov VS, Bodenschatz E. Periodic sequence of stabilized wave segments in an excitable medium. Phys Rev E. (2018) 97:030201. doi: 10.1103/physreve.97.03.030201
25. Zykov VS, Bodenschatz E. Spiral waves within a bistability parameter region of an excitable medium. New J Phys. (2022) 24: 3036. doi: 10.1088/1367-2630/ac47ca
26. Karma A. Universal limit of spiral wave propagation in excitable media. Phys Rev Lett. (1991) 66:2274–7. doi: 10.1103/PhysRevLett.66.2274
27. Alonso S., Sagues F., Mikhailov A S Taming Winfree turbulence of scroll waves in 223 excitable media, Science. (2003) 299: 1722. doi: 10.1126/science.1080207
28. Winfree AT. Alternative stable rotors in an excitable medium. Phys D. (1991) 102:125–40. doi: 10.1016/0167-2789(91)90202-K
Keywords: excitable media, spiral wave, instability, hysteresis, modified Barkley model
Citation: Zykov V and Bodenschatz E (2022) Two Domains of Meandering Spiral Waves in a Modified Barkley Model. Front. Appl. Math. Stat. 8:903563. doi: 10.3389/fams.2022.903563
Received: 24 March 2022; Accepted: 25 April 2022;
Published: 13 May 2022.
Edited by:
Erik Andreas Martens, Lund University, SwedenReviewed by:
Vadim N. Biktashev, University of Exeter, United KingdomCopyright © 2022 Zykov and Bodenschatz. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Vladimir Zykov, dmxhZGltaXIuenlrb3ZAZHMubXBnLmRl
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.