- 1Department of Mathematics and Statistics, University of Missouri–St. Louis, St. Louis, MO, United States
- 2The Air Force Research Laboratory, AFRL/RISB, Rome, NY, United States
- 3The Air Force Research Laboratory, AFRL, Rome, NY, United States
- 4Department of Mathematics, Wichita State University, Wichita, KS, United States
The synchrosqueezing transform (SST) and its variants have been developed recently as an alternative to the empirical mode decomposition scheme to model a non-stationary signal as a superposition of amplitude- and frequency-modulated Fourier-like oscillatory modes. In particular, SST performs very well in estimating instantaneous frequencies (IFs) and separating the components of non-stationary multicomponent signals with slowly changing frequencies. However its performance is not desirable for signals having fast-changing frequencies. Two approaches have been proposed for this issue. One is to use the 2nd-order or high-order SST, and the other is to apply the instantaneous frequency-embedded SST (IFE-SST). For the SST or high order SST approach, one single phase transformation is applied to estimate the IFs of all components of a signal, which may yield not very accurate results in IF estimation and component recovery. IFE-SST uses an estimation of the IF of a targeted component to produce accurate IF estimation. The phase transformation of IFE-SST is associated with the targeted component. Hence the IFE-SST has certain advantages over SST in IF estimation and signal separation. In this article, we provide theoretical study on the instantaneous frequency-embedded short-time Fourier transform (IFE-STFT) and the associated SST, called IFE-FSST. We establish reconstructing properties of IFE-STFT with integrals involving the frequency variable only and provide reconstruction formula for individual components. We also consider the 2nd-order IFE-FSST.
1. Introduction
Recently the continuous wavelet transform-based synchrosqueezed transform (WSST) was developed in [1] as an empirical mode decomposition (EMD)-like tool to model a non-stationary signal x(t) as
with , where Ak(t) is called the instantaneous amplitudes and the instantaneous frequencies (IFs). The representation (1) of non-stationary signals is important to extract information hidden in x(t). WSST not only sharpens the time-frequency representation of a signal, but also recovers the components of a multicomponent signal. The synchrosqueezing transform (SST) provides an alternative to the EMD method introduced in [2] and its variants considered in many articles such as [3–12], and it overcomes some limitations of the EMD and ensemble EMD schemes such as mode-mixing. Many works on SST have been carried out since the publication of the seminal article [1]. For example, the short-time Fourier transform (STFT)-based SST (FSST) [13–15], the 2nd-order SST [16–18], the higher-order FSST [19, 20], a hybrid EMD-WSST [21], the WSST with vanishing moment wavelets [22], the multitapered SST [23], the synchrosqueezed wave packet transform [24] and the synchrosqueezed curvelet transform [25] were proposed. Furthermore, the adaptive SST with a window function having a changing parameter was proposed in [26–31]. SST has been successfully used in machine fault diagnosis [32, 33], and medical data analysis applications [see [34] and references therein]. [35] proposed a direct time-frequency method (called SSO) based on the ridges of spectrogram for signal separation. This method has been extended recently to the linear chirp-based models [36, 37] and the models based on the CWT scaleogram [38, 39]. A hybrid EMD-SSO computational scheme was developed in [40].
If the IFs of the components xk(t) of a non-stationary multicomponent signal change slowly or change slowly compared with ϕk(t), then SST performs very well in estimating and separating the components xk(t) from x(t). However its performance is not desirable for signals having fast-changing frequencies. The 2nd-order and high-order SSTs were proposed for this issue and they do improve the accuracy of IF estimation and component recovery. The problem with the 2nd-order and high-order SSTs is that, like the convectional SST, one single phase transformation is applied to estimate the IFs of all components of a signal, which may not yield desirable results in IF estimation or component recovery.
Another approach is to demodulate the original signal to change a wide-band component into a narrow-band component. Li and Liang [41] and Meignen et al. [42] demodulate the original signal into a pure carrier signal and apply WSST and the 2nd-order FSST to the demodulated signal, respectively. FSST based on another demodulation was proposed in [43]. The demodulation introduced in [43] transforms a one-dimensional signal, as a function of time only, into a two-dimensional bivariate function of time and time-shift. The STFT of the demodulated signal has more concentrated time-frequency representation than the conventional STFT, and in the meantime it well characterizes time-frequency properties of the signal [43]. The demodulation approach of [43] is considered in [44] in the setting of CWT. The associated CWT and SST are called in [44] the instantaneous frequency-embedded CWT (IFE-CWT) and IFE-SST, respectively. For consistency, we call the STFT of the demodulated signal and the associated FSST in [43]: the IFE-STFT and IFE-FSST respectively. [43] shows that IFE-FSST results in sharp time-frequency representations of signals. However component recovery of a multicomponent signal was not discussed in [43]. In this article, we consider theoretical analysis of IFE-STFT for establishing the component recovery with IFE-FSST. Compared with the study of IFE-SST in [44], we derive in this article mathematically rigorous phase transformation for IFE-FSST. In addition, in this article we also consider the 2nd-order IFE-FSST and derive the associate phase transformation.
The rest of this article is organized as follows. In Section 2, we briefly review FSST and the 2nd-order FSST. After that, we consider in Section 3 the IFE-STFT and establish reconstructing properties of IFE-STFT with integrals involving the frequency variable only. In Section 4, we derive mathematically rigorous phase transformations for IFE-FSST and the 2nd-order IFE-FSST. In addition, we provide reconstruction formula for individual components. Implementations and IFE-FSST-based component recovery algorithms are discussed in Section 5. Some experimental results are also provided in Section 5.
2. Short-Time Fourier Transform-Based SST
The (modified) short-time Fourier transform (STFT) of x(t) is defined by
where g(t) is a window function with g(0) ≠ 0. x(t) can be reconstructed from its STFT:
x(t) can also be recovered back from its STFT with an integral involving only the frequency variable η:
In addition, one can show that if g(t) and x(t) are real-valued, then
Furthermore, one can verify that STFT can be written as
The STFT Vx(t, η) of a slowly growing x(t) is well-defined and the above formulas still hold if the window function g(t) has certain smoothness and certain decaying order as t → ∞, for example g(t) is in the Schwarz class . In this article, unless otherwise stated, we always assume that a window function g(t) has certain smoothness and decaying properties and g(0) ≠ 0, and assume that a signal x(t) is a slowly growing function.
2.1. FSST
The idea of FSST is to re-assign the frequency variable η of Vx(t, η). First we look at the STFT of , where ξ0 is a positive constant. With
we can obtain the IF ξ0 of x(t) by
where throughout this article, ∂t denotes the partial derivative with respect to variable t. For a general x(t), at (t, η) for which Vx(t, η) ≠ 0, a good candidate for the IF of x(t) is
In the following, denote
which is called the “phase transformation” [1], “instantaneous frequency information” [13], or the “reference IF function” in [21]. FSST is to re-assign the frequency variable η by transforming the STFT Vx(t, η) of x(t) to a quantity, denoted by , on the time-frequency plane defined by
where ξ is the frequency variable, h(t) a compactly supported function with certain smoothness and , γ > 0 is the threshold for zero and λ > 0 is a dilation. As λ, γ → 0, FSST is rewritten as
For simplicity of presentation, throughout this article SSTs will be expressed as (7).
Due to (4), we have that the input signal x(t) can be recovered from its FSST by
If in addition, g(t) and x(t) are real-valued, then by (5),
For a multicomponent signal x(t) given by (1), when Ak(t), ϕk(t) satisfy certain conditions, each component xk(t) can be recovered from its FSST:
for certain Γ > 0, where IFk(t) is an estimate to . See [13–15] for the details.
In practice, t, η, ξ are discretized. Suppose tn, ηj, ξm are the sampling points of t, η, ξ respectively. Then the FSST of x(t) is given by
where △ηj = ηj − ηj−1, and γ > 0 is a threshold for the condition |Vx(t, η)| > 0. The recovering formulas (8) and (9) result in
and for real-valued g(t) and x(t),
where △ξm = ξm − ξm−1.
2.2. Second-Order FSST
The 2nd-order FSST was introduced in [16]. The main idea is to define a new phase transformation such that when x(t) is a linear frequency modulation (LFM) signal (also called a linear chirp), then is exactly the IF of x(t). We say x(t) is a LFM signal or a linear chirp if
with phase function , IF ϕ′(t) = c + rt and chirp rate ϕ″(t) = r. In [16], the reassignment operators are used to derive . Different phase transformation for the 2nd-order SST can be derived without using the reassignment operators see [28, 29].
Let g be a given window function. Denote
Recall that Vx(t, η) denotes the STFT of x(t) with g defined by (2). In this article, we let denote the STFT of x(t) with g1(t), namely, the integral on the right-hand side of (2) with g(t) replaced by g1(t). Define
where
Then one can show that is exactly the IF ϕ′(t) of x(t) if x(t) is an LFM signal given by (11), see [19, 28]. Thus, we may define in (13) as the phase transformation for the 2nd-order FSST. Very recently a simple phase transformation for the 2nd-order FSST was proposed in [18].
3. Instantaneous Frequency-Embedded STFT
IFE-FSST is based on the IFE-STFT, which is defined below.
Definition 1. Suppose φ(t) is a differentiable function with φ′(t) > 0. Let η0 > 0. The IFE-STFT of x(t) ∈ L2(ℝ) with φ(t), η0 and a window function g(t) is defined by
In the above definition, we assume x(t) ∈ L2(ℝ). The definition of IFE-STFT can be extended to slowly growing functions x(t) if g(t) has certain smoothness and certain decaying order as t → ∞.
Li and Liang [41] proposed the modulation and applied WSST to the modulated signal , while [42] applied the 2nd-order FSST to . The modulation:
introduced in [43] for IFE-FSST and also used in [44] for IFE-WSST is different from that used in [41, 42]. IFE-STFT and IFE-CWT with such a modulation not only have more concentrated time-frequency representation than the conventional STFT and CWT respectively, but also well keep the IF of the signal. The reader is referred to [43] and [44] for detailed discussions.
[43] provides a reconstruction formula with IFE-STFT for the whole signal x(t), which is similar to (3) and involves an integral with both the time and frequency variables. [43] does not consider individual component recovery formula with IFE-FSST. In this article, we provide such a component recovery formula. To this regard, in this section we establish a reconstruction formula with IFE-STFT like (4), which involves an integral with the frequency variable only. First we have the following property about the IFE-STFT.
Proposition 1. Let be the IFE-STFT of x(t) defined by (14). Then
where
Proof. We have
where the last equality follows from (6).□
The next theorem shows that x(t) can be recovered from its IFE-STFT with an integral involving η only.
Theorem 1. Let x(t) be a function in L2(ℝ). Then
Proof. Let be the function defined by (16). From (15), we have
Thus, Equation (17) holds.□
If one is interested in with the positive frequency η > 0 only, then we have the following result on how to recover x(t) from .
Theorem 2. Suppose supp for some Δ, and φ′(t) ≥ Δ. Let y(t) = x(t)e−i2πφ(t). If , η ≤ B for some constant B, then for any η0 ≥ −B,
Proof. Let be the function defined by (16). Then . Thus, . Therefore, from (15), we have
When ξ ≥ B and η0 ≥ −B, we have . This and the assumption supp lead to
Hence,
Thus, Equation (18) holds.□
Next theorem shows that when the condition , η ≤ B in Theorem 2 does not hold, the integral in the right-hand side of (18) can still approximate x(t) well if η0 is large.
Theorem 3. Let y(t) = x(t)e−i2πφ(t). Then
with
Proof. By Theorem 1,
Thus,
With
we conclude that (19) holds.□
4. IFE-STFT Based Synchrosqueezing Transform
In this section, we consider IFE-FSST, the synchrosqueezing transform based on IFE-STFT. First we show how to derive the phase transformation associated with (the 1st-order) IFE-FSST. After that we introduce the 2nd-order IFE-FSST.
4.1. IFE-FSST
To define IFE-FSST, first we need to define the corresponding phase transformation . Let us consider the case for some ξ0 > 0. With , we have
On the other hand,
where denotes the IFE-STFT of x(t) defined by (14) with φ(t) and the window function g′ given by (12). Thus, if , then
Based on the above discussion, for a general signal x(t), we define the phase transformation of the IFE-FSST of x(t) to be
Definition 2. Suppose φ(t) is a differentiable function with φ′(t) > 0. The IFE-FSST of a signal x(t) with φ and ξ0 is defined by
where is the phase transformation defined by (21).
The IFE-FSST is called the demodulation transform-based SST in [43]. The corresponding phase transformation in [43] is different from our defined in (21).
By (18) in Theorem 1, we know the input signal x(t) can be recovered from its IFE-FSST as shown in the following:
For x(t) ∈ L2(ℝ),
and if, in addition, the conditions in Theorem 2 hold, then
For a multicomponent signal x(t) in the form (1), if lie in different time-frequency zones, then following (18), we know xk(t) can be recovered from its IFE-FSST:
for certain Γ1 > 0, where IFk(t) is an estimate of . If xk(t) and g(t) are real-valued, then
4.2. 2nd-Order IFE-FSST
In this subsection, we propose the 2nd-order IFE-FSST. The key point is, based on IFE-STFT, to define a phase transformation which is the IF ϕ′(t) of x(t) when x(t) is a linear chirp given by (11). As above, for g1(t) = tg(t), we use to denote the IFE-STFT of x(t) with the window function g1(t), namely, the integral on the right-hand side of (14) with g(t) replaced by g1(t). Next we define the phase transformation for the 2nd-order IFE-FSST to be:
where is defined by (21), and
Theorem 4. If x(t) is a linear chirp signal given by (11), then at (t, η) where , , defined by (26) is the IF of x(t), namely .
Proof. Here, we provide the proof of for more general linear chirp signals given by
where p, q are real numbers.
For the simplicity of presentation, we denote
and thus, can simply be written as
Observe that for x(t) given by (28), we have
Thus,
On the other hand, as shown above, is equal to the quantity in (20). Therefore,
Hence, at (t, η) on which , we have
Taking partial derivative ∂η to the both sides of (29), we have
which leads to
for (t, η) with , where Q0(t, η) is defined by (27).
Returning back to (29) with replaced by Q0(t, η), we have
Since c + rt is real, taking the real parts of the quantities in the above equation, we have
which is . This completes the proof of Theorem 4.□
With the phase transformation in (26), we have the corresponding 2nd-order IFE-FSST of a signal x(t) with φ, ξ0 and window function g defined by
One has reconstruction formulas with similar to (22)–(25).
5. Implementation and Experimental Results
5.1. Calculating and
First we consider the IFE-FSST. We need to calculate . We will use (15) so that FFT can be applied to (discrete signals) x and xφ′ to calculate VI(t, η), and . can be obtained by (15) with x replaced by xφ′. As long as is concerned, observe that the Fourier transform of g′ is . Hence
After obtaining VI(t, η), and , we get and then the IFE-FSST.
For the 2nd-order IFE-FSST, we need to calculate
Note that the Fourier transform of τg(τ) is
Thus, we conclude
By the fact , we can obtain and as well via (31).
To calculate , with , where , we need to calculate the Fourier transform of g2(τ), which is
Therefore,
For , we need to calculate the Fourier transform of τg′(τ), denoted by (τ g′(τ))∧(ξ). Indeed,
Thus,
With the formulas (31), (32), and (33), we can obtain Q0(t, η) and then, .
5.2. IFE-FSST Algorithms for IF Estimation and Component Recovery and Experiments
To apply IFE-STFT or IFE-FSST, first of all we need to choose φ(t) and φ′(t). For the purpose of estimating the IF of the kth component xk(t) and/or recover xk(t) of a multicomponent signal x(t), we should choose φ(t) and φ′(t) close to ϕk(t) (up to a constant) and respectively. One way is to use the ridges of the STFT. More precisely, suppose {tn}0≤n<N, {ηj}0≤j<J, {ξm}0≤m<M are the sampling points of t, η, ξ respectively for STFT Vx(t, η), FSST Rx(t, ξ), and IFE-FSST . Let be the STFT ridge corresponding to xk(t) given by
for each n, 0 ≤ n < N, where for each n, is an interval containing (with convention: ϕ0(t) ≡ 0) at the time instant tn, and form a disjoint union of {η : |Vx(tn, η)| > γ}, namely for each tn,
See more details on in [37].
is called a ridge of the STFT plane or a ridge of the spectrogram |Vx(t, η)|. It provides an approximation to [see [36, 37, 45]]. Thus, we can use
as discrete φ′(t) and φ(t) to define IFE-STFT and IFE-FSST, where △tℓ = tℓ − tℓ−1.
To recover a component by either FSST or IFE-FSST, we need an estimate IFk(t) for so that (10) or (24)/(25) can be applied. One way is to use the ridges of FSST and IFE-FSST to approximate . More precisely, let be the FSST ridge defined similarly to the STFT ridge in (34):
Then Equation (10) becomes
for some M0 ∈ ℕ, where △ξm = ξm − ξm−1.
Similarly, Equation (24) implies that xk(t) can be recovery from (discrete) IFE-FSST:
where are the indices for IFE-FSST ridge defined as (36) with Rx(tn, ξm) replaced by :
For real-valued xk(t) and g(t), the recovery formulas (37) and (38) are respectively
and
To summarize, we have the following algorithm to estimate IF and recover xk(t) by IFE-FSST.
Algorithm 1. (IFE-FSST algorithm for IF estimation and component recovery) Let x(t) be a signal of the form (1). To estimate and recover xk(t) by IFE-FSST, do the following.
Step 1. Obtain the STFT ridge by (34) and by (35).
Step 2. Calculate IFE-FSST with φ′, φ obtained in Step 1. The ridge defined by (39) is an estimate of and in (38) is an approximation to xk(t).
We can use Algorithm 1 to recover each component xk(t) one by one. We can also apply Algorithm 1 to the remainder to recover another component after xk(t) is recovered; and we can repeat this procedure. The procedure of this iterative method is described as follows.
Algorithm 2. (Iterative IFE-FSST algorithm for IF estimation and component recovery) Let x(t) be a signal of the form (1).
Step 1. Apply Algorithm 1 to obtain .
Step 2. Let . Apply Algorithm 1 to y1 to obtain .
Step 3. Let . Apply Algorithm 1 to y2 to obtain . Repeat this process to obtain , and finally .
Step 4. Apply Algorithm 1 to to recover x1(t). Let be the recovered x1(t). Then Apply Algorithm 1 to to recover x2(t). Let be the recovered x2(t). Obtain by applying Algorithm 1 to . Repeat this process to obtain , and finally .
We can repeat the procedure in Step 4 of Algorithm 2. That is why we call Algorithm 2 an iterative algorithm.
Next we consider two examples. We let
be the window function, where σ > 0. First we consider a mono-component signal
where x(t) is uniformly sampled with sample points . The IF of x(t) is ϕ′(t) = 16+32t and it is shown in the 1st row of Figure 1. The FSST and IFE-FSST of x(t) are provided in the 2nd row; and the 2nd-order FSST and IFE-FSST are shown in the 3rd row. In this example we let . As mentioned above, discrete φ′(t) and φ(t) defined by (35) are used to define IFE-STFT and the 2nd-order IFE-STFT. Obviously IFE-FSST provides a much sharper time-frequency representation of x(t) than FSST. Both the 2nd-order FSST and the 2nd-order IFE-FSST as well give sharp time-frequency representations of x(t).
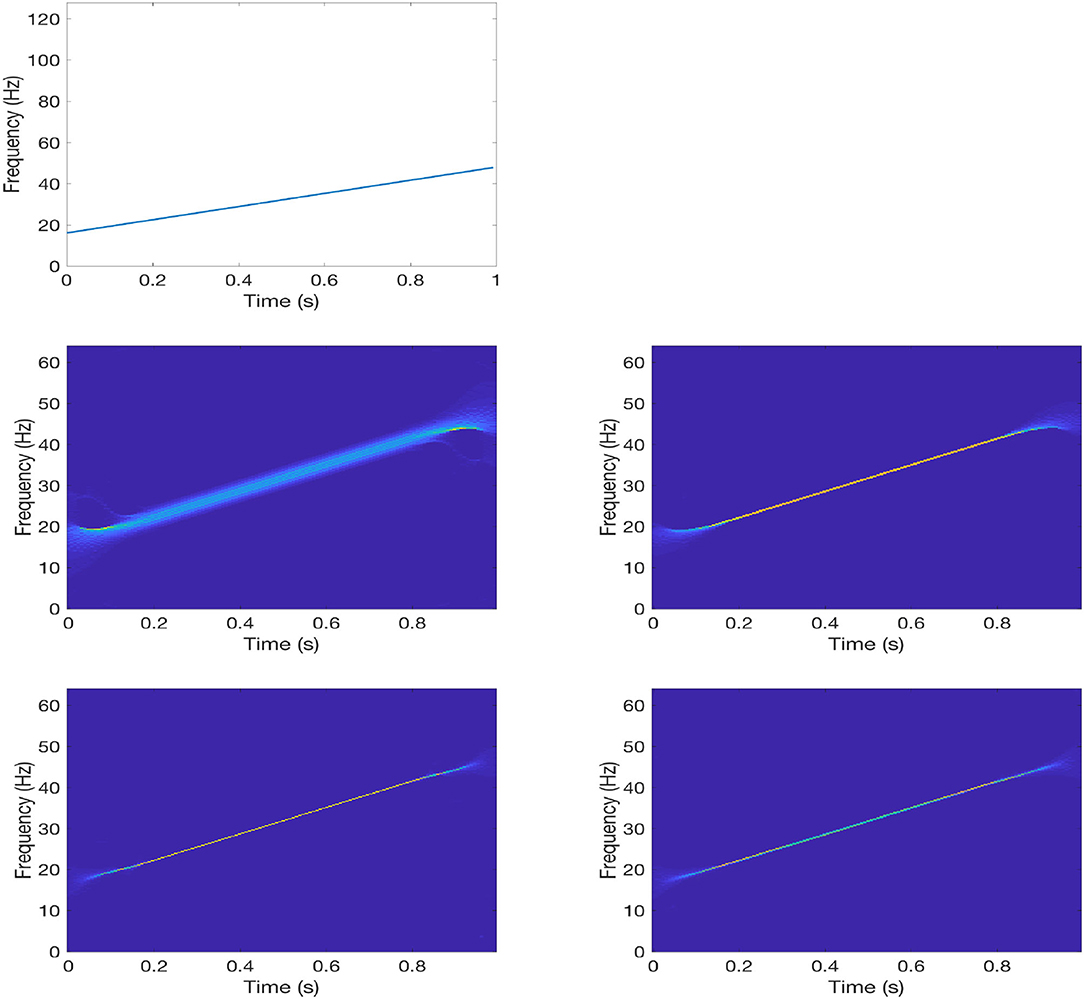
Figure 1. Experiment with x(t) in (43). 1st row: IF ϕ′(t); 2nd row: FSST |Rx(t, η)| (left) and IFE-FSST (right); 3rd row: 2nd-order FSST (left) and 2nd-order IFE-FSST (right).
For a mono-component signal x(t) as given by (43), since x(t) can be recovered from FSST or IFE-FSST as shown in (8) and (22) respectively, theoretically, either (40) or (41) gives high accurate approximation to x(t) as long as M0 is large enough. We choose a small M0 so that the recovery errors with it show how sharp the time-frequency representations with FSST and IFE-FSST are. Here and below we set M0 = 8.
In Figure 2, we provide the recovery errors , for x(t) by FSST and IFE-FSST, where and are given by (40) and (41) respectively with M0 = 8. Here, we show the error on [0.125, 0.875) only to ignore the boundary effect. Obviously, IFE-FSST provides a much sharper time-frequency representation than FSST.
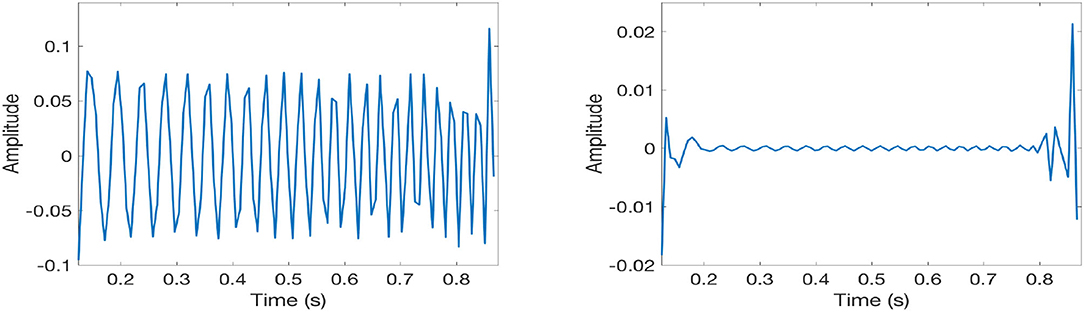
Figure 2. Recovery errors for x(t) given in (43) on [0.125, 0.875) by FSST (left) and IFE-FSST (right).
Next we consider a two-component signal given by
where t ∈ [0, 2), and x(t) is uniformly sampled with sample points tn = n△t, 0 ≤ n < N = 512, . Thus, IFs of x1(t), x2(t) are , , which are shown on the top-left panel of Figure 3. In this example we let for the window function.
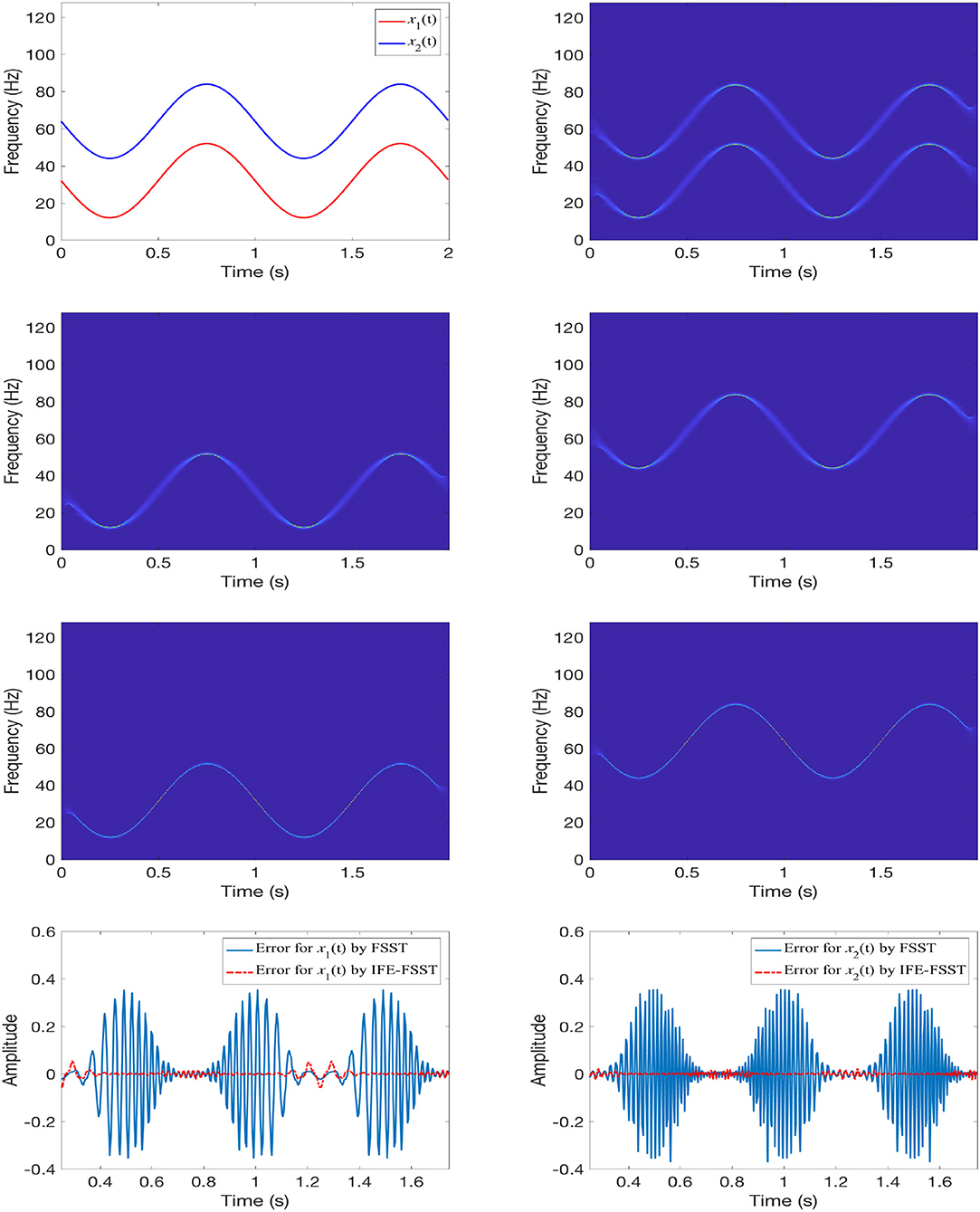
Figure 3. Experiment with x(t) in (44). 1st row: IFs (left) and FSST |Rx(t, η)| (right); 2nd row: FSST for x1(t) (left) and FSST for x2(t) (right); 3rd row: IFE-FSST for x1(t) (left) and IFE-FSST for x2(t) (right). 4th row: recovery errors on [0.125, 1.875) by FSST and IFE-FSST for x1(t) (left) and x2(t) (right).
To this two-component signal, we apply Algorithm 2 to obtain and . In the 3rd row of Figure 3 we show the IFE-FSSTs of and . The FSST of x(t) is provided in the top-right panel of Figure 3. Of course, we can also apply iterative method to FSST to recover components one by one. Namely, we apply FSST to obtain , then apply FSST to to obtain . After that we apply FSST to to obtain , and finally to obtain by applying FSST to . The 2nd row of Figure 3 shows the FSSTs of and . Comparing the FSST of x in the top-right panel with the individual FSSTs in the 2nd row, we see there is not much improvement of the time-frequency representation of FSST of x after we apply the iterative component recovery procedure.
In the 4th row of Figure 3, we provide the recovery errors for x1(t), x2(t) by FSST and IFE-FSST. Here, we show the error on [0.125, 1.875). From Figure 3, we see IFE-FSST provides a much sharper time-frequency representation for x(t). We also consider FSST and IFE-FSST of two-component x(t) in the noisy environment and our experiments show that IFE-FSST provides a sharp time-frequency representation in the noisy environment. In addition, we consider the 2nd-order IFE-FSST for component recovery. It does not provide much improvement than IFE-FSST. This may be due to that the results from IFE-FSST are hard to improve. Due to that only 15 pictures are allowed to be included in a article in this journal, we do not present these results here.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Ethics Statement
This article was approved by AFRL for public release on 03 Dec. 2021, Case Number: AFRL-2021-4285, Distribution unlimited.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work was supported in part by Simons Foundation (Grant No. 353185) and the 2020 Air Force Summer Faculty Fellowship Program (SFFP).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Daubechies I, Lu J, Wu H-T. Synchrosqueezed wavelet transforms: an empirical mode decomposition-like tool. Appl Comput Harmon Anal. (2011) 30:243–61. doi: 10.1016/j.acha.2010.08.002
2. Huang NE, Shen Z, Long SR, Wu ML, Shih HH, Zheng Q, et al. The empirical mode decomposition and Hilbert spectrum for nonlinear and nonstationary time series analysis. Proc R Soc Lond A. (1998) 454:903–95. doi: 10.1098/rspa.1998.0193
3. Wu Z, Huang NE. Ensemble empirical mode decomposition: a noise-assisted data analysis method. Adv Adapt Data Anal. (2009) 1:1–41. doi: 10.1142/S1793536909000047
4. Flandrin P, Rilling G, Goncalves P. Empirical mode decomposition as a filter bank. IEEE Signal Proc Lett. (2004) 11:112–4. doi: 10.1109/LSP.2003.821662
5. Li L, Ji H. Signal feature extraction based on improved EMD method. Measurement. (2009) 42:796–803. doi: 10.1016/j.measurement.2009.01.001
6. Rilling G, Flandrin P. One or two frequencies? The empirical mode decomposition answers. IEEE Trans Signal Proc. (2008) 56:85–95. doi: 10.1109/TSP.2007.906771
7. Lin L, Wang Y, Zhou HM. Iterative filtering as an alternative algorithm for empirical mode decomposition. Adv Adapt Data Anal. (2009) 1:543–60. doi: 10.1142/S179353690900028X
8. Xu Y, Liu B, Liu J, Riemenschneider S. Two-dimensional empirical mode decomposition by finite elements. Proc R Soc Lond A. (2006) 462:3081–96. doi: 10.1098/rspa.2006.1700
9. van der Walt MD. Empirical mode decomposition with shape-preserving spline interpolation. Results Appl Math. (2020) 5:100086. doi: 10.1016/j.rinam.2019.100086
10. Wang Y, Wei G-W, Yang SY. Iterative filtering decomposition based on local spectral evolution kernel. J Sci Comput. (2012) 50:629–64. doi: 10.1007/s10915-011-9496-0
11. Zheng JD, Pan HY, Liu T, Liu QY. Extreme-point weighted mode decomposition. Signal Proc. (2018) 42:366–74. doi: 10.1016/j.sigpro.2017.08.00
12. Cicone A, Liu JF, Zhou HM. Adaptive local iterative filtering for signal decomposition and instantaneous frequency analysis. Appl Comput Harmon Anal. (2016) 41:384–411. doi: 10.1016/j.acha.2016.03.001
13. Thakur G, Wu H-T. Synchrosqueezing based recovery of instantaneous frequency from nonuniform samples. SIAM J Math Anal. (2011) 43:2078–95. doi: 10.1137/100798818
14. Wu H-T. Adaptive analysis of complex data sets. Ph.D. dissertation. Princeton University Press, Princeton, NJ, United States (2012).
15. Oberlin T, Meignen S, Perrier V. The Fourier-based synchrosqueezing transform. In: Proc. 39th Int. Conf. Acoust., Speech, Signal Proc. (ICASSP). Beijing (2014). p. 315–9. doi: 10.1109/ICASSP.2014.6853609
16. Oberlin T, Meignen S, Perrier V. Second-order synchrosqueezing transform or invertible reassignment? Towards ideal time-frequency representations. IEEE Trans Signal Proc. (2015) 63:1335–44. doi: 10.1109/TSP.2015.2391077
17. Oberlin T, Meignen S. The 2nd-order wavelet synchrosqueezing transform. In: 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). New Orleans, LA (2017). doi: 10.1109/ICASSP.2017.7952906
18. Lu J, Alzahrani JH, Jiang QT. A second-order synchrosqueezing transform with a simple phase transformation. Num Math Theory Methods Appl. (2021) 14: 624–49. doi: 10.4208/nmtma.OA-2020-0077
19. Pham D-H, Meignen S. High-order synchrosqueezing transform for multicomponent signals analysis - With an application to gravitational-wave signal. IEEE Trans Signal Proc. (2017) 65:3168–78. doi: 10.1109/TSP.2017.2686355
20. Li L, Wang ZH, Cai HY, Jiang QT, Ji HB. Time-varying parameter-based synchrosqueezing wavelet transform with the approximation of cubic phase functions. In: 2018 14th IEEE Int'l Conference on Signal Proc. ICSP. New Orleans, LA (2018). p. 844–8. doi: 10.1109/ICSP.2018.8652362
21. Chui CK, van der Walt MD. Signal analysis via instantaneous frequency estimation of signal components. Int J Geomath. (2015) 6:1–42. doi: 10.1007/s13137-015-0070-z
22. Chui CK, Lin Y-T, Wu H-T. Real-time dynamics acquisition from irregular samples - with application to anesthesia evaluation. Anal Appl. (2016) 14:537–90. doi: 10.1142/S0219530515500165
23. Daubechies I, Wang Y, Wu H-T. ConceFT: concentration of frequency and time via a multitapered synchrosqueezed transform. Philos Trans R Soc A. (2016) 374:20150193. doi: 10.1098/rsta.2015.0193
24. Yang HZ. Synchrosqueezed wave packet transforms and diffeomorphism based spectral analysis for 1D general mode decompositions. Appl Comput Harmon Anal. (2015) 39:33–66. doi: 10.1016/j.acha.2014.08.004
25. Yang HZ, Ying LX. Synchrosqueezed curvelet transform for two-dimensional mode decomposition. SIAM J. Math Anal. (2014) 3:2052–83. doi: 10.1137/130939912
26. Sheu Y-L, Hsu L-Y, Chou P-T, Wu H-T. Entropy-based time-varying window width selection for nonlinear-type time-frequency analysis. Int J Data Sci Anal. (2017) 3:231–45. doi: 10.1007/s41060-017-0053-2
27. Berrian AJ, Saito N. Adaptive synchrosqueezing based on a quilted short-time Fourier transform. arXiv [Preprint] arXiv:1707.03138v5. (2017). doi: 10.1117/12.2271186
28. Li L, Cai HY, Han HX, Jiang QT, Ji HB. Adaptive short-time Fourier transform and synchrosqueezing transform for non-stationary signal separation. Signal Proc. (2020) 166:107231. doi: 10.1016/j.sigpro.2019.07.024
29. Li L, Cai HY, Jiang QT. Adaptive synchrosqueezing transform with a time-varying parameter for non-stationary signal separation. Appl Comput Harmon Anal. (2020) 49:1075–106. doi: 10.1016/j.acha.2019.06.002
30. Cai HY, Jiang QT, Li L, Suter BW. Analysis of adaptive short-time Fourier transform-based synchrosqueezing transform. Anal Appl. (2021) 19:71–105. doi: 10.1142/S0219530520400047
31. Lu J, Jiang QT, Li L. Analysis of adaptive synchrosqueezing transform with a time-varying parameter. Adv Comput Math. (2020) 46:72. doi: 10.1007/s10444-020-09814-x
32. Li C, Liang M. Time frequency signal analysis for gearbox fault diagnosis using a generalized synchrosqueezing transform. Mech Syst Signal Proc. (2012) 26:205–17. doi: 10.1016/j.ymssp.2011.07.001
33. Wang SB, Chen XF, Selesnick IW, Guo YJ, Tong CW, Zhang XW. Matching synchrosqueezing transform: a useful tool for characterizing signals with fast varying instantaneous frequency and application to machine fault diagnosis. Mech Syst Signal Proc. (2018) 100:242–88. doi: 10.1016/j.ymssp.2017.07.009
34. Wu H-T. Current state of nonlinear-type time-frequency analysis and applications to high-frequency biomedical signals. Curr Opin Syst Biol. (2020) 23:8–21. doi: 10.1016/j.coisb.2020.07.013
35. Chui CK, Mhaskar HN. Signal decomposition and analysis via extraction of frequencies. Appl Comput Harmon Anal. (2016) 40:97–136. doi: 10.1016/j.acha.2015.01.003
36. Li L, Chui CK, Jiang QT. Direct signal separation via extraction of local frequencies with adaptive time-varying parameter. arXiv [Preprint] arXiv:2010.01866. (2020).
37. Chui CK, Jiang QT, Li L, Lu J. Analysis of an adaptive short-time Fourier transform-based multicomponent signal separation method derived from linear chirp local approximation. J Comput Appl Math. (2021) 396:113607. doi: 10.1016/j.cam.2021.113607
38. Chui CK, Han NN. Wavelet thresholding for recovery of active sub-signals of a composite signal from its discrete samples. Appl Comput Harmon Anal. (2021) 52:1–24. doi: 10.1016/j.acha.2020.11.003
39. Chui CK, Jiang QT, Li L, Lu J. Signal separation based on adaptive continuous wavelet-like transform and analysis. Appl Comput Harmon Anal. (2021) 53:151–79. doi: 10.1016/j.acha.2020.12.003
40. Chui CK, Mhaskar HN, van der Walt MD. Data-driven atomic decomposition via frequency extraction of intrinsic mode functions. Int J Geomath. (2016) 7:117–46. doi: 10.1007/s13137-015-0079-3
41. Li C, Liang M. A generalized synchrosqueezing transform for enhancing signal time-frequency representation. Signal Proc. (2012) 92:2264–74. doi: 10.1016/j.sigpro.2012.02.019
42. Meignen S, Pham D-H, McLaughlin S. On demodulation, ridge detection, and synchrosqueezing for multicomponent signals. IEEE Trans Signal Proc. (2017) 65:2093–103. doi: 10.1109/TSP.2017.2656838
43. Wang SB, Chen XF, Cai GG, Chen BQ, Li X, He ZJ. Matching demodulation transform and synchrosqueezing in time-frequency analysis. IEEE Trans Signal Proc. (2014) 62:69–84. doi: 10.1109/TSP.2013.2276393
44. Jiang QT, Suter BW. Instantaneous frequency estimation based on synchrosqueezing wavelet transform. Signal Proc. (2017) 138:167–81. doi: 10.1016/j.sigpro.2017.03.007
Keywords: short-time Fourier transform, synchrosqueezing transform, instantaneous frequency-embedded STFT, instantaneous frequency-embedded SST, instantaneous frequency estimation
AMS Mathematics Subject Classification: 42C15, 42A38
Citation: Jiang Q, Prater-Bennette A, Suter BW and Zeyani A (2022) Instantaneous Frequency-Embedded Synchrosqueezing Transform for Signal Separation. Front. Appl. Math. Stat. 8:830530. doi: 10.3389/fams.2022.830530
Received: 07 December 2021; Accepted: 17 February 2022;
Published: 17 March 2022.
Edited by:
Hau-Tieng Wu, Duke University, United StatesReviewed by:
Duong Hung Pham, UMR5505 Institut de Recherche en Informatique de Toulouse (IRIT), FranceAnouar Ben Mabrouk, University of Kairouan, Tunisia
Copyright © 2022 Jiang, Prater-Bennette, Suter and Zeyani. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qingtang Jiang, amlhbmdxQHVtc2wuZWR1
 Qingtang Jiang
Qingtang Jiang Ashley Prater-Bennette2
Ashley Prater-Bennette2 Abdelbaset Zeyani
Abdelbaset Zeyani