- Department of Mathematics, College of Science, National University of Defense Technology, Changsha, China
In this paper, we propose a new algorithm called ModelBI by blending the Bregman iterative regularization method and the model function technique for solving a class of nonconvex nonsmooth optimization problems. On one hand, we use the model function technique, which is essentially a first-order approximation to the objective function, to go beyond the traditional Lipschitz gradient continuity. On the other hand, we use the Bregman iterative regularization to generate solutions fitting certain structures. Theoretically, we show the global convergence of the proposed algorithm with the help of the Kurdyka-Łojasiewicz property. Finally, we consider two kinds of nonsmooth phase retrieval problems and propose an explicit iteration scheme. Numerical results verify the global convergence and illustrate the potential of our proposed algorithm.
1. Introduction
In this paper, we consider the following optimization problem
where f, R : ℝd → (−∞, +∞] are given extended real-valued functions, and μ > 0 is some fixed parameter.
Bregman iterative regularization, originally proposed in Osher et al. [1] for total-variation-based image restoration, has become a popular technique for solving optimization problems with the form (). To simplify its computation, the linearized Bregman iterations (LBI) [2] and their variants [3–5] were proposed with lots of applications in signal/image processing and compressed sensing. Previous studies mainly focused on convex smooth optimization in the sense that both functions f and R in () are convex and f is also smooth. Very recently, nonconvex smooth extensions of LBI were considered in Benning et al. [6] and later in Zhang et al. [7]. However, it seems unclear whether the LBI can be extended to nonconvex and nonsmooth cases. In other words, can we develop the LBI to solve () with a nonconvex nonsmooth function f? This question is the main motivation of this study.
A basic algorithmic strategy for optimization problem () is to successively minimize simple objective functions, usually called model functions, which approximate the original objective ψ near the current iterate. The LBI method is in the same spirit as this strategy; it uses a second-order Taylor expansion of f to approximate the smooth function f and uses a Bregman distance to replace the regularization function R. To deal with nonsmooth function f, however, it is impossible to use Taylor approximations. Fortunately, there recently developed several “Taylor-like” model functions techniques [8–10] to approximate and minimize a nonsmooth objective function f. In particular, the authors of Mukkamala et al. [10] introduced the concept of model approximation property (MAP) for extending the Bregman proximal gradient method to minimize a nonsmooth f.
In this paper, we will blend the techniques involved in LBI and MAP to propose a new iterative scheme for solving nonconvex and nonsmooth optimization problems (), along with completed convergence analysis. Moreover, we apply our proposed method to nonsmooth phase retrieval problems to demonstrate our findings, both theoretically and numerically.
The remainder of the paper is organized as follows. In Section 2, we introduce the Bregman distance, the concept of MAP, and also the Kurdyka-Łojasiewicz (KL) property. In Section 3, we propose our algorithmic scheme and a group of assumptions. In Section 4, we present a convergence analysis. The application demonstrations are given in Section 5 and Section 6. Finally, concluding remarks are discussed in Section 7.
2. Preliminaries
Throughout the paper, we work in a d-dimensional Euclidean vector space ℝd equipped with inner product 〈·, ·〉 and induced norm ||·||, where d ∈ ℕ\{0} (ℕ is the set of non-negative integers). The notation and almost all the facts about the convex analysis we employ are primarily taken from Rockafellar [11]. For a set B ⊂ ℝd, defined . Let h be a convex function, dom h (h*, ∇h, ∂h) denotes the domain of h (conjugate function of h, gradient of h, and subgradient of h, respectively), and int dom h denote the interior domain of h. In addition, let ∂xf(x; y) denote the subgradient of the function f(x; y) with respect to the first variable, ∂yf(x; y) denote the subgradient of the function f(x; y) with respect to the second variable, and ∂f(x; y) denote the subgradient of f(x; y) with respect to (x, y).
2.1. Bregman distance
The concept of Bregman distance [12] is the most important technique in Bregman iterative regularization. Given a smooth convex function h, its Bregman distance between two points x and y is defined as
Due to the convexity of h, it is essential that Dh is nonnegative but fails to hold the symmetry and the triangle inequality in general. The class of Legendre functions [13] provides a choice to generate Bregman distance.
Definition 2.1. (Legendre functions, Rockafellar [11]) Let h : ℝd → (−∞, +∞] be a proper lower semi-continuous (lsc) convex function. It is called:
• essentially smooth, if int dom h ≠ ∅, h is differentiable on int dom h, and ||∇h(xk)|| → ∞ for every sequence converging to a boundary point of dom h as k → ∞;
• of Legendre type, if h is essentially smooth and strictly convex on int dom h.
As a special case of Legendre functions, the energy kernel yields the classical squared Euclidean distance.
Note that the common sparsity constraint R(·) = ||·||1 is not of Legendre type since it is nonsmooth. It leads to the concept of generalized Bregman distance introduced by Kiwiel [14]. Given a proper lsc convex function R, the generalized Bregman distance associated with R between x, y with respect to a subgradient y* is defined by
Properties of Bregman distances and examples of kernels can be referred to Kiwiel [14, 15], Chen and Teboulle [16], and Bauschke et al. [17].
2.2. Model function and model approximation property
Section 1 has briefly mentioned the model function and the MAP. Now we state its formal definition in Mukkamala et al. [10].
Definition 2.2. (Model function [10]) Let f be a proper lsc function. A function with is called a model function for f around the model center , if there exists a growth function such that the following is satisfied:
The model function is essentially an approximation to f, and the growth function can be considered as a bound on the model error. Based on Definition 2.2, a modification of the model approximation property (MAP) (Definition 7, [10]) can be stated as below:
Definition 2.3 (Model approximation property). Let h be a Legendre function that is continuously differentiable over int dom h. A proper lsc function f with dom f ⊃ dom h and model function for f around satisfy the model approximation property at , with the constant L > 0, if for any the following holds:
2.3. Kurdyka-Łojasiewicz property
The Kurdyka-Łojasiewicz property is a significant tool for our global convergence analysis, which is defined as follows:
Definition 2.4. (Kurdyka-Łojasiewicz property and function [18]) The function F : ℝd → (−∞, +∞] is said to have the Kurdyka-Łojasiewicz property at x* ∈ dom(∂F) if there exists η ∈ (0, +∞], a neighborhood U of x* and a continuous concave function φ:[0, η) → ℝ+ such that
(i) φ(0) = 0.
(ii) φ is C1 on (0, η).
(iii) for all s ∈ (0, η), φ′(s) > 0.
(iv) for all x in U ∩ [F(x*) < F(x) < F(x*) + η], the Kurdyka-Łojasiewicz inequality holds
Additionally, a proper lsc function F that satisfies the Kurdyka-Łojasiewicz inequality at each point of dom(∂F) is called a KL function.
Usually, it may be difficult to verify the KL property of a function. Bolte et al. [19, 20] established a nonsmooth version of Kurdyka-Łojasiewicz inequality:
Lemma 2.5. Let F : ℝd → (−∞, +∞] be a proper lsc function. If F is semi-algebraic then it satisfies the KL property at any point of dom F.
Lemma 2.5 provides a result that KL property holds for the class of semi-algebraic functions. Semi-algebraic examples are common such as derivatives and ||·||p. In addition, the class of semi-algebraic sets is stable under finite sums, compositions, or products [18].
3. Problem setting and ModelBI algorithm
Throughout this paper, we consider the optimization problem () and make the following assumptions about the relative function h, the regularized function R, and the loss function f.
Assumption 3.1. (i) h : ℝd → (−∞, +∞] is of Legendre type and of over int dom h.
(ii) is proper lsc convex with dom ∂R ⊃ int dom h and dom R ∩ int dom h ≠ ∅.
(iii) f:ℝd → (−∞, +∞] is proper lsc nonconvex nonsmooth with dom f ⊃ dom h and continuous on dom h. Moreover, the MAP holds for the pair of functions (f, h).
(iv) .
Assumption 3.2. Let pk ∈ ∂R(xk). If {xk} ⊂ int dom h converges to some x ∈ dom h, then and .
Assumption 3.3. For any bounded subset U ⊂ int dom h, there exists a constant Lh > 0 such that for any x ∈ U, h has bounded second derivative .
Assumption 3.4. For any bounded set B ⊂ dom f, there exists c > 0 such that for any x, y ∈ B we have
Assumption 3.5. The regularized function R has locally bounded subgradients in the sense that if for any bounded set U ⊂ dom R there exists a constant C > 0 such that for any x ∈ U and all p ∈ ∂R(x) we have ||p|| ≤ C.
A few remarks about the assumptions are as follows:
• Assumptions 3.1(i) and (iii) are required by the MAP, among which is needed for the surrogate function in Section 4. The assumptions of domains in (ii) ensure that the objective in Algorithm 1 is well-defined for xk ∈ int dom h. (ii) can be satisfied if R is real-valued, for example, R(x) = ||x||1. With respect to (iv), an lsc coercive function can ensure the compactness of its lower level set.
• A real-valued convex function R always holds that as xk → x due to the continuity of R [21, Theorem 3.16] and has locally bounded subgradients, which verifies Assumption 3.2 and Assumption 3.5.
• Assumption 3.4 governs the variation of the model function around the model center [10]. We can take the composite function f(G(x)) = |x2 − 1| as a simple example. Its model function is . Then the subdifferential of the model function is given by , where sgn(x) = x/|x| if x ≠ 0 while sgn(0) ∈ [−1, 1]. Since |sgn(x)| ≤ 1, we have .
Equipped with the above assumptions, the ModelBI algorithm for solving the nonconvex nonsmooth composite problem () is described in Algorithm 1.
There are some remarks to understand ModelBI:
• First, note that ModelBI is a generalization of LBI. It replaces the linearized term of LBI with a model function that keeps the first-order information of f. For smooth f and model function f(x; xk) = f(xk) + 〈∇f(xk), x − xk〉, Algorithm 1 is actually the LBI algorithm in Zhang et al. [7].
• Denote , then is a set of minimizers. When is a singleton, the update step becomes .
• A potential problem is the choice of ξk+1 if the model function is also nonsmooth. We need to pick a specific element from the set for this case. Corollary 4.7 shows that a random element from is acceptable as ξk → 0 (k → ∞) under some standard assumptions. Section 6 further verifies this strategy via numerical experiments.
4. Global convergence analysis
In this section, we analyze the convergence of the ModelBI algorithm. We first present that our algorithm results in monotonically nonincreasing function values.
Lemma 4.1 (Sufficient descent property of {f(xk)}). Let Assumption 3.1 hold and {xk} be a sequence generated by the ModelBI algorithm; then for k ≥ 0, we have that
where . In particular,
Proof. Due to Equation (1), we have
From the MAP,
where the last equality follows from the definition of the model function. As , we obtain the sufficient descent property in function values.
Summing Equation (2) from k = 0 to n we get
Taking the limit as n → ∞, we obtain and , from which we deduce that
This completes the proof.
To further show the convergence of the sufficient desent sequence {f(xk)}, we now define the set of all limit points of {xk} as follows
Lemma 4.2 (Function value convergence). Let the same assumptions hold true as in Lemma 4.1. Suppose further that Assumption 3.2 holds, that h is strongly convex on dom h with dom h = dom h and that the level set {x : f(x) ≤ f(x0)} is bounded. Then, Ω ≠ ∅ and for any limit point x* ∈ Ω,
Proof. The boundness of {x:f(x) ≤ f(x0)} and the sufficient descent property of {f(xk)} ensure the boundedness of {xk}, hence Ω ≠ ∅.
Take x* ∈ Ω. There exists a subsequence such that . Together with (3) in Lemma 4.1 and the strong convexity of h, we can conclude that and as i → ∞.
In light of (1), we have
The MAP yields . As ,
Thus, we have
Using the lsc property of f, we obtain
Therefore, we get
Note that {f(xk)} is also lower bounded by and hence it is convergent. Then we have , which completes the proof.
In order to derive the global convergence of {xk}, we should introduce a modified surrogate function F : ℝd × ℝd × ℝd → (−∞, +∞]:
where R* is the convex conjugate of R.
Remark 1. The modified surrogate function is inspired by Benning et al. [6] and Zhang et al. [7]. However, their surrogate functions are invalid for our global convergence analysis, because the standard assumptions do not contain the subgradient relationship between the nonsmooth f and the model function. Thus, we replace the loss function with a Lyapunov function f(x; y) + LDh(x, y) that appeared in Mukkamala et al. [10] to construct a new one. The new surrogate function imposes an additional variable, where we should make a mild assumption about the lower bound of the subgradient with respect to this variable (refer to Assumption 3.4). In addition, we have known that the Lyapunov function is a KL function [10]. As is mentioned in Section 2, the KL property holds under finite sums, which verifies that the proposed surrogate function (6) is also a KL function.
In the following, we present the sufficient descent property of F and its subgradient bounds, which are the basis of the convergence analysis. To this end, we introduce the notation sk: = (xk, xk−1, pk−1) for all k ∈ ℕ, and thus F(sk) = F(xk, xk−1, pk−1).
Lemma 4.3 (Sufficient descent property of {F(sk)}). Let the same assumptions hold true as in Lemma 4.1 and μk ≥ μ ≥ 0. Then we have the following decent estimate:
Proof. Similar to the proof of Lemma 4.1, we have due to Equation (1), and from the MAP. Note that for xk ∈ ∂R*(pk). Hence, combining the above formulas, we derive that
which completes the proof.
Remark 2. From the definition of the surrogate function, we know that . Together with the sufficient decent property, the sequence {F(sk)} is also bounded.
Note that the subdifferential of the surrogate function reads as
Then, a lower bound for its subgradients at the iterates computed with ModelBI can be deduced.
Lemma 4.4 (Subgradient lower bound of F(sk)). Let the same assumptions hold true as in Lemma 4.3. Suppose further that Assumption 3.3 holds for h and Assumption 3.4 holds for f. Then the subgradient is lower bounded by the iterates gap:
Proof. Using the fact that pk+1 ∈ ∂R(xk+1) and xk ∈ ∂R*(pk), we know
The optimality of xk+1 in Equation (1) implies the existence of such that the following condition holds: . Then the first term of the right hand side in Equation (9) is bounded by
where in the last inequality we applied the Lagrange mean value theorem along with the fact that the entity ∇2h(xk+1 + s(xk+1 − xk)) (s ∈ [0, 1]) is bounded by a constant Lh. Considering the second term in Equation (9), we have
where in the last inequality we used Assumption 3.4 and the fact that ||∇2h(xk)|| is bounded by Lh. Note that there is no loss of generality to take the same Lh as the upper bound. We therefore estimate
This completes the proof.
Recall that {sk} = {(xk, xk−1, pk−1)} is a sequence generated by ModelBI from starting points x0 and p0. Denote the set of limit points of {sk} as
Before we show the global convergence of the ModelBI sequence to a critical point of f, we need to verify that (i) Ω0 is a nonempty, compact, and connected set, and (ii) the surrogate function F converges to f on Ω0. Both of them are guaranteed by the following lemma.
Lemma 4.5 (Function value convergence of {F(sk)}). Under the conditions of Lemma 4.4, let Assumption 3.2 hold and Assumption 3.5 hold for R. Suppose that , that h is strongly convex on dom h with dom h = dom h, and that the level set {x:f(x) ≤ f(x0)} is bounded. Then Ω0 is a nonempty, compact, and connected set, and for any , we have and
Proof. By the boundedness of {xk}, there exists an increase of integers {ij}j∈ℕ such that . With and the subgradient local boundedness of R(x), we know that must be bounded, and thus, there exists a subsequence {ki} ⊂ {ij} such that . Due to Equation (1), it holds that
Due to Equation (3) in Lemma 4.1 and the strong convexity of h, we know that and . Together with and the boundedness of , we conclude that there exists a point p* such that (p* may be different to ). Therefore, s* = (x*, x*, p*) indeed belongs to Ω0 which shows the nonemptiness of Ω0. Furthermore, x* ∈ Ω for each .
From Theorem 3.7 in Rubin [22], the set Ω0 must be closed since it is the set of cluster points of {sk}. The boundedness of Ω0 comes from the boundedness of {xk} and {pk}. Therefore, the set Ω0 is compact and hence by the definition of limit points.
Note that by definition of F we have
The MAP gives . As in Lemma 4.1 and in Lemma 4.2, we deduce that
which completes the proof.
Now we are ready to present the following global convergence result for ModelBI.
Theorem 4.6 (Finite length property). Let {sk} = {(xk, xk−1, pk−1)} be the sequence generated by the ModelBI algorithm. Suppose that F is a KL function in the sense of Definition 2.4. Let Assumptions 3.1–3.2 hold, Assumption 3.3 hold for h, Assumption 3.4 hold for f, and Assumption 3.5 hold for R. In addition, let h be σh-strongly convex with dom h = dom h, the level set {x : f(x) ≤ f(x0)} is bounded, the parameters δk satisfy , and μk satisfy μk ≥ μ and . Then, the sequence {xk} has a finite length in the sense that
Proof. We show Equation (10) by modifying the methodology in Zhang et al. [7]. Let us begin with any point . Then, there exists an increasing integer sequence {ki}i∈ℕ such that as i → ∞. From Lemma 4.5 and recalling that sk = (xk, xk−1, pk−1), we know .
Note that the convergent sequence {F(sk)} is nonincreasing from Lemma 4.3. If there exists an integer such that , then F(sk) ≡ f(x*) for and hence for from Equation (7), which implies that for due to the strong convexity of h. Hence, the result (Equation 10) follows trivially. If there does not exist such an index, then F(sk) > f(x*) holds for all k > 0. Since , for any η > 0 there must exist an integer such that F(sk) < f(x*) + η for all . Similarly, from Lemma 4.5 implies for any ζ > 0 there must exist an integer such that for all . Therefore, for all we have
Thus, we apply Definition 2.4 to get,
Using Equation 4.4 in Lemma 4.4 and , we get that
where . On the other hand, from the concavity of φ, we know that
holds for all x, y ∈ [0, η), x > y. Hence, by taking x = F(sk) − f(x*) and y = F(sk+1) − f(x*) in the inequality above, we get
where φk: = φ(F(sk) − f(x*)) and . The last inequality follows from Equation (7) and the strong convexity property . Therefore, from Equations (11)–(13), we get
Based on Young's inequality of form , we further get
Subtracting ||xk+1 − xk|| and summing the inequality above from k = l, ⋯ , N yields
With the boundedness of {pk} and , we obtain the finite length property by letting N → ∞.
Corollary 4.7. Under the same assumptions as Theorem 4.6, the sequence {xk} converges to a critical point of f in the sense that 0 ∈ ∂f(x*). In addition, we have the following rate of convergence result:
Proof. The finite length property Theorem 4.6 implies that as l → ∞. Thus, for any m > n ≥ l we have
which implies that {xk} is a Cauchy sequence. ModelBI gives
Summing from k = 0, ⋯ , n leads to
Assume that the limit point ξ* ≠ 0. Noting that and , we apply Lemma 4.8 in Zhang et al. [7] to conclude that ||p0 − pn+1|| → ∞ as n → ∞, which contradicts the boundedness of {pk}. Therefore, we have ξ* = 0 ∈ ∂f(x*).
Recalling (4) in Lemma 4.1, we have
which immediately leads to the result of a convergence rate due to the strong convexity of h.
5. Application to phase retrieval problems
This section illustrates the potential of the proposed algorithm. To this end, we consider two kinds of nonsmooth phase retrieval problems and construct the corresponding model functions that the MAP holds. Then, we show how ModelBI can be applied to these problems.
The standard phase retrieval problem can be described as follows. Given a finite number of measurement vectors , describing the model, and a vector b ∈ ℝm describing the possibly corrupted measurement data, our goal is to find x ∈ ℝd that solves the system
It is a natural extension of the standard linear inverse problem, as the linear measurements are replaced by their modules. This type of problem has been and is still being intensively studied in the literature; readers can refer to Dong et al. [23] for a brief review.
The considered system (Equation 15) is commonly underdetermined, and thus some prior information of the target vector is brought into the model by means of some regularizer R. Adopting the usual mean-value or least-square loss function f to measure the error, the problem can be reformulated in the form of (). What we are concerned about are the following two nonsmooth models:
(A) Mean-value loss function with intensity-only measurements [24], i.e.,
(B) Least-square loss function with amplitude-only measurements [25], i.e.,
For simplicity and generalization, in both cases (A) and (B), we use the Legendre function and the convex ℓ1-norm regularization R(x) = ||x||1.
5.1. Model A
With the usual mean-value loss function, we can reformulate (Equation 15) as the following nonconvex nonsmooth optimization problem
where , i = 1, …, m are symmetric matrices.
To apply ModelBI to this model, we first need to identify an appropriate model function such that the MAP holds for the pair (f, h). Consider the composite function , where and for all i = 1, …, m. The structure of f(G(x)) enables us to construct the model function as follows:
where . With , we now show that there exists L > 0 such that .
Proposition 5.1. Let f, G, h, and the model function be as defined above. Then, for any L satisfying
the MAP holds for the function pair (f, h).
Proof. Let x ∈ ℝd and xk be the current iterate. Since G is on ℝd, we obtain the following model function by straightly computing:
Then, the error between the loss function and the model function is quantified by
Note that h is strongly convex and . Therefore, taking yields , which proves the desired result.
It is straightforward to verify that the setting implies Assumptions 3.1–3.5. Thus, the sequence {xk} generated by ModelBI globally converges to a critical point of f due to Corollary 4.7. With the notation , we can rewrite the main computational gradient map in Equation (1) as follows
Observing that there are two nonsmooth terms in this subproblem, it is difficult to deduce the closed form solutions. Here, we propose the alternating direction method of multipliers (ADMM) as a choice.
Let and ; then the subproblem (Equation 17) can be reformulated as the 2-block optimization problem
With a regular parameter ρ and a vector z ∈ ℝm, the Augmented Lagrangian function for the reformulated problem is
Based on the dual ascent method, ADMM separates the variants of Lρ(x, y, z) and iterates alternately by the following scheme:
With the well-known soft-thresholding operator Sτ(·) = max{| · | − τ, 0}sgn(·), the ADMM scheme admits explicit iteration steps. Here, we present the derived results below for computation:
where the solution of the first variant xk+1 is derived by linearized ADMM (L-ADMM) [26] for the quadratic regularization term in Equation (18), and ηk is the stepsize.
Remark 3. We utilized ADMM with single-step iteration to solve the first subproblems of both nonsmooth models. As the finite length property ensures the global convergence of our proposed algorithm, we do not need a high-accuracy solution from ADMM in each iteration.
5.2. Model B
Another nonconvex nonsmooth optimization problem in phase retrieval is recovering a solution from the amplitude-based objective [25]. With the least-squared criterion and amplitude-only measurements, we can reformulate (Equation 15) as follows:
To apply ModelBI as Model A, we first need to handle the loss function . The structure is totally different from that of Model A as the inner functions |〈ai, x〉| are nonsmooth. Thus, the linearized technique is not feasible for its model function. Fortunately, by considering the equivalent form of amplitude and adding an error term at the current iterate, we construct its model function that satisfies the MAP with the Legendre function :
Proposition 5.2. Let f, h, and the model function be as defined above. Assume that the error around the current iterate satisfies ||x − xk|| ≤ 1. Then, for any L satisfying
the MAP holds for the function pair (f, h).
Proof. Let x ∈ ℝd and xk be the current iterate. We obtain the error between the loss function and the model function by straightly computing:
where the third inequality comes from , and the last inequality comes from ||x − xk|| ≤ 1. Note that h is strongly convex and . Therefore, taking yields , which proves the desired result.
Remark 4. Our proposed model function (Equation 19) is inspired by the smoothing phase retrieval algorithm [25], in which each amplitude term |〈ai, x〉| is smoothed by with μ ∈ ℝ++. However, the smoothing term cannot be used as the model function, as it approximates |〈ai, x〉| independent of xk.
Remark 5. Note that the assumption that ||x − xk|| ≤ 1 is not nontrivial. It can be satisfied by preconditioning the model data. For a certain random model, an initial vector x0 via the spectral method can reach sufficient accuracy with high probability [27].
It is straightforward to verify that Assumptions 3.1–3.5 holds. Thus, Corollary 4.7 imply that the sequence {xk} generated by ModelBI globally converges to a critical point of f. With the notation , we can also rewrite the main computational gradient map as Equation (17).
Though the model function (Equation 19) is smooth, its structure still hinders us from obtaining the closed form solutions in the subproblem, which again needs the help of ADMM in the following.
Let and ; then the subproblem (17) can be reformulated as the 2-block optimization problem
With a regular parameter ρ and a vector z ∈ ℝm, the Augmented Lagrangian function for the reformulated problem is
Based on the dual ascent method, ADMM separates the variants of Lρ(x, y, z) and iterates alternately by the following scheme:
With the soft-thresholding operator Sτ, the ADMM scheme admits explicit iteration steps, which are presented below:
where the solution of the first variant xk+1 is derived by L-ADMM for the last two terms of the Augmented Lagrangian function (Equation 18), and ηk is the stepsize.
Remark 6. It is mentioned that the Legendre function used above is aimed at simplifying analysis and deriving the iteration steps. Other Legendre functions might have better propositions in applications, while they bring more complicated solutions. For example, equipped with , Models A and B need to find the roots of cubic equations additionally in each iteration step.
6. Experiments
In this section, we provide numerical experiments of the phase retrieval models in Section 5 to demonstrate the global convergence of ModelBI.
In all reported experiments, (i) the target vector x ∈ ℝ is a k-sparse signal, which is generated first using and then followed by setting (n − k) entries to zero uniformly at random; (ii) the measurement vectors ai are i.i.d. , i = 1, …, m; (iii) the Gaussian noise ωi are i.i.d. , i = 1, …, m. Then, we postulate the noisy Gaussian data model for Model A, and bi = |〈ai, x〉| + ωi for Model B, and take the mean-squared error (MSE) [27] to quantify the error between the k-th iterate and the target vector.
For simplicity, we set the regular parameters μ = 1/2 and ρ = 1 for both models, and then choose constant stepsizes μk ≡ μ, ηk ≡ 1 and δk ≡ 1/2L in all the iterations. We fixed the dimension d = 128 and the sparsity level k = 5. The number of measurements is fixed to m = 4.5d, as gradient decent algorithms such as Wirtinger flow can exactly recover the target vectors with high probability from more than 4.5d Gaussian phaseless measurements [27].
With these settings, we conduct 100 trials for each model. The noise level σ2 ranges from 0.002 to 0.008 with a 0.002 interval. Then we report the convergence results by average curves.
The first experiment examines the convergence behavior of our algorithm for Model A in the case of noisy data. We set due to Proposition 5.1. We stop after 200 iterations in each trial and report the convergence results in Figure 1. Figure 1A demonstrates the sufficient desent and convergent property of the function value when ModelBI applies to Model A with the model function (Equation 16). Figure 1B further demonstrates that our algorithm results in a convergent sequence {xk} with 0 ∈ ∂f(x*). In addition, Figure 1C verifies the bound of the convergent rate in Equation (14).
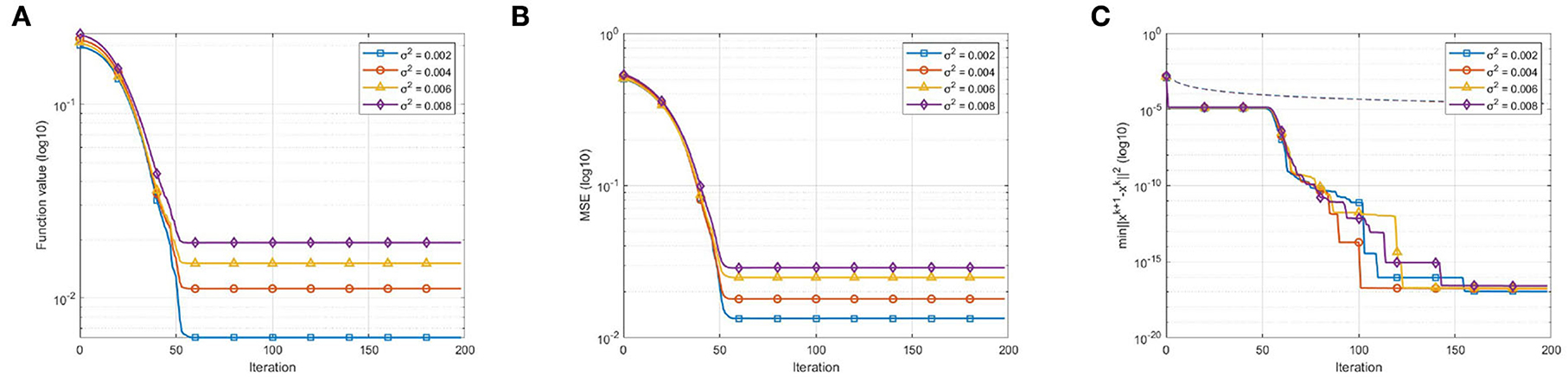
Figure 1. Convergence behavior in the case of noisy data: (A) Function value vs. number of iterations, demonstrates the sufficient desent and convergent property of the function value sequence {f(xk)}; (B) MSE vs. number of iterations, demonstrates the convergent property of the point sequence {xk}; (C) vs. number of iterations, where the dotted lines indicate the right side of Equation (14), verifies the bound of convergent rate.
The second experiment examines the convergence behavior of the ModelBI algorithm for Model B. The initialization step is obtained by applying 50 iterations of the power method in Candès et al. [27, Algorithm 3] to ensure the assumption ||x0 − x|| ≤ 1 in Proposition 5.2 with high probability. The constant for the MAP is set to due to Proposition 5.2. We stop after 2000 iterations in each trial and report the convergence results in Figure 2. As is shown in Figure 2, the sequence {xk} generated by ModelBI results in a sufficient desent sequence {f(xk)} and a critical point x* with the convergent rate bound in Equation (14).

Figure 2. Convergence behavior in the case of noisy data: (A) Function value vs. number of iterations, demonstrates the sufficient descent and convergent property of the function value sequence {f(xk)}; (B) MSE vs. number of iterations, demonstrates the convergent property of the point sequence {xk}; (C) vs. number of iterations, where the dotted lines indicate the right side of Equation (14), verifies the bound of convergent rate.
Remark 7. In Figure 1C, we observe that the curves are piecewise descending. This convergence behavior is due to the structure of the model function. The model function (16) constructed for Model A is still nonsmooth. As mentioned in Section 3, we picked a specific element ξk+1 from the set at random in the first experiment. This strategy manifests itself as the piecewise decending curves in Figure 1C.
Remark 8. In Figure 2B, the MSE curves descend at first and slightly rise later. We observe that the ModelBI using a smooth model function makes the sequence {xk} rapidly converge to the true solution in early iterates. Afterward, the sequence gradually converges into a noisy solution. The rising range is determined by the noise level σ. As Figure 2B shows, after about 400 iterates, the MSE curve with σ2 = 0.002 rises less than that with σ2 = 0.008. A proper stopping criterion can output a better result, but that is not what the manuscript mainly concerned about.
The third experiment presents the special behavior of iterative regularization by comparing our algorithm with the recently reported Model BPG algorithm [10]. The settings are respectively the same as that used in the experiments above. We do not have explicit solutions for Model BPG with these settings. For comparative purposes, we also apply ADMM with single-step iteration to the main computational step of Model BPG. For Model A, we stop after 200 iterations in each trial and report the convergence behaviors with σ2 = 0.004 in Figure 3A. For Model B, we stop after 2,000 iterations in each trial and report the convergence behaviors with σ2 = 0.004 in Figure 3B.
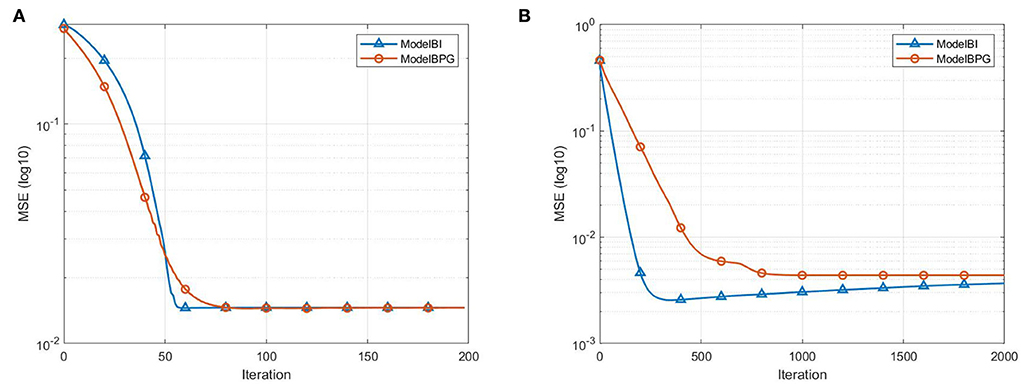
Figure 3. Convergence behavior in the case of noisy data with σ2 = 0.004: (A) MSE vs. number of iterations, presents the convergence behavior of ModelBI and Model BPG for Model A; (B) MSE vs. number of iterations, presents the convergence behavior of ModelBI and Model BPG for Model B.
7. Conclusion
Bregman iterative regularization and its variants have attracted widespread attention in solving nonconvex problems, while it is still difficult in extending to generic nonsmooth composite optimization. In this regard, we proposed the ModelBI algorithm that is applicable to nonconvex nonsmooth problems based on the recent developments of the LBI and the model function. By taking advantage of the MAP, we drive the global convergence analysis of the ModelBI sequence. Moreover, we present the application of two kinds of nonsmooth phase retrieval problems by designing their model functions and iterative schemes. The application demonstrates the power of ModelBI, which appears to be the first Bregman iterative regularization method for solving these two kinds of problems.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
HZ and HY conceived of the presented idea. HY developed the theory and performed the computations. HW and LC verified the analytical methods. HW encouraged HY to investigate nonconvex phase retrieval model and supervised the findings of this work. All authors discussed the results and contributed to the final manuscript.
Funding
This study was supported in part by the National Natural Science Foundation of China (Nos. 11971480 and 61977065) and the 173 Program of China (No. 2020-JCJQ-ZD-029).
Acknowledgments
The authors would like to thank the referees and the associate editor for valuable suggestions and comments, which allowed us to improve the original presentation.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Osher S, Burger M, Goldfarb D, Xu J, Yin W. An iterative regularization method for total variation-based image restoration. SIAM J Multiscale Model Simulat. (2005) 4:460–89. doi: 10.1137/040605412
2. Yin W, Osher S, Goldfarb D, Darbon J. Bregman iterative algorithms for ℓ1-minimization with applications to compressed sensing. SIAM J Imaging Sci. (2008) 1:143–68. doi: 10.1137/070703983
3. Lorenz DA, Schöpfer F, Wenger S. The linearized bregman method via split feasibility problems: analysis and generalizations. SIAM J Imaging Sci. (2014) 7:1237–62. doi: 10.1137/130936269
4. Lai MJ, Yin W. Augmented ℓ1 and nuclear-norm models with a globally linearly convergent algorithm. SIAM J Imaging Sci. (2013) 6:1059–91. doi: 10.1137/120863290
5. Zhang H, Yin W. Gradient methods for convex minimization: better rates under weaker conditions. CAM Report 13-17, UCLA (2013).
6. Benning M, Betcke MM, Ehrhardt MJ, Schönlieb CB. Choose your path wisely: gradient descent in a Bregman distance framework. SIAM J Imaging Sci. (2021) 14:814–43. doi: 10.1137/20M1357500
7. Zhang H, Zhang L, Yang HX. Revisiting linearized bregman iterations under lipschitz-like convexity condition. arXiv:2203.02109. (2022) doi: 10.1090/mcom/3792
8. Drusvyatskiy D, Ioffe AD, Lewis AS. Nonsmooth optimization using Taylor-like models: error bounds, convergence, and termination criteria. Math Program. (2021) 185:357–83. doi: 10.1007/s10107-019-01432-w
9. Ochs P, Fadili J, Brox T. Non-smooth non-convex bregman minimization: unification and new algorithms. J Optim Theory Appl. (2019) 181:244–78. doi: 10.1007/s10957-018-01452-0
10. Mukkamala MC, Fadili J, Ochs P. Global convergence of model function based Bregman proximal minimization algorithms. J Glob Optim. (2021) 83:753–81. doi: 10.1007/s10898-021-01114-y
12. Bregman LM. The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming. Ussr Comput Math Math Phys. (1967) 7:200–17. doi: 10.1016/0041-5553(67)90040-7
13. Bauschke HH, Borwein JM. Legendre functions and the method of random bregman projections. J Convex Anal. (1997) 4:27–67.
14. Kiwiel KC. Proximal minimization methods with generalized Bregman functions. SIAM J Control Optim. (1997) 35:1142–68. doi: 10.1137/S0363012995281742
15. Kiwiel KC. Free-Steering relaxation methods for problems with strictly convex costs and linear constraints. Math Oper Res. (1997) 22:326–49. doi: 10.1287/moor.22.2.326
16. Chen G, Teboulle M. Convergence analysis of a proximal-like minimization algorithm using Bregman functions. SIAM J Optim. (1993) 3:538–43. doi: 10.1137/0803026
17. Bauschke HH, Bolte J, Teboulle M. A descent lemma beyond Lipschitz gradient continuity: first-order methods revisited and applications. Math Operat Res. (2017) 42:330–48. doi: 10.1287/moor.2016.0817
18. Bolte J, Sabach S, Teboulle M. Proximal alternating linearized minimization for nonconvex and nonsmooth problems. Math Program. (2014) 146:459–94. doi: 10.1007/s10107-013-0701-9
19. Bolte J, Daniilidis A, Lewis A. The Łojasiewicz inequality for nonsmooth subanalytic functions with applications to subgradient dynamical systems. SIAM J Optim. (2007) 17:1205–23. doi: 10.1137/050644641
20. Bolte J, Daniilidis A, Lewis A, Shiota M. Clarke subgradients of stratifiable functions. SIAM J Optim. (2007) 18:556–72. doi: 10.1137/060670080
21. Beck A. First-Order Methods in Optimization. SIAM-Soc Ind Appl Math. (2017) doi: 10.1137/1.9781611974997
23. Dong J, Valzania L, Maillard A, an Pham T, Gigan S, Unser M. Phase retrieval: from computational imaging to machine learning. arXiv:2204.03554. (2022). doi: 10.48550/arXiv.2204.03554
24. Hilal A, Duchi JC. The importance of better models in stochastic optimization. Proc Natl Acad Sci USA. (2019) 116:22924–30. doi: 10.1073/pnas.1908018116
25. Pinilla S, Bacca J, Arguello H. Phase retrieval algorithm via nonconvex minimization using a smoothing function. IEEE Trans Signal Process. (2018) 66:4574–84. doi: 10.1109/TSP.2018.2855667
26. Ouyang Y, Chen Y, Lan G, Pasiliao E. An accelerated linearized alternating direction method of multipliers. SIAM J Imaging Sci. (2015) 8:644–81. doi: 10.1137/14095697X
Keywords: Bregman iterations, model approximation property, phase retrieval problem, regularization, nonconvex nonsmooth minimization
Citation: Yang H, Zhang H, Wang H and Cheng L (2022) Bregman iterative regularization using model functions for nonconvex nonsmooth optimization. Front. Appl. Math. Stat. 8:1031039. doi: 10.3389/fams.2022.1031039
Received: 29 August 2022; Accepted: 28 October 2022;
Published: 22 November 2022.
Edited by:
Jianfeng Cai, Hong Kong University of Science and Technology, Hong Kong SAR, ChinaReviewed by:
Ming Yan, Michigan State University, United StatesYuping Duan, Tianjin University, China
Copyright © 2022 Yang, Zhang, Wang and Cheng. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hui Zhang, aC56aGFuZzE5ODQmI3gwMDA0MDsxNjMuY29t
†ORCID: Hui Zhang orcid.org/0000-0002-8728-7168
 Haoxing Yang
Haoxing Yang Hui Zhang*†
Hui Zhang*†