- Laboratoire de Mathématiques de Besançon, UMR - CNRS 6623, Université de Bourgogne Franche-Comté, Besançon, France
1. Introduction
Despite the fact that mathematical applications to biology and medicine have been mentioned since the eighteenth century [1] [or even earlier, if we think of Fibonacci's example of a rabbit population growth [2]], the evolution of this research field was slow until the twentieth century. Unlike mathematical applications to physical problems (where equations can describe accurately the physical reality), applications to biological problems are much more complex due to the evolutionary nature of the living matter [3, 4]. Moreover, this evolution of biological systems occurs on different spatial and temporal scales (see Figure 1), which renders the modeling much more challenging. Also, the mathematical and statistical investigation of these multi-scale models is more challenging, due to the complexities of the interactions between the scales.
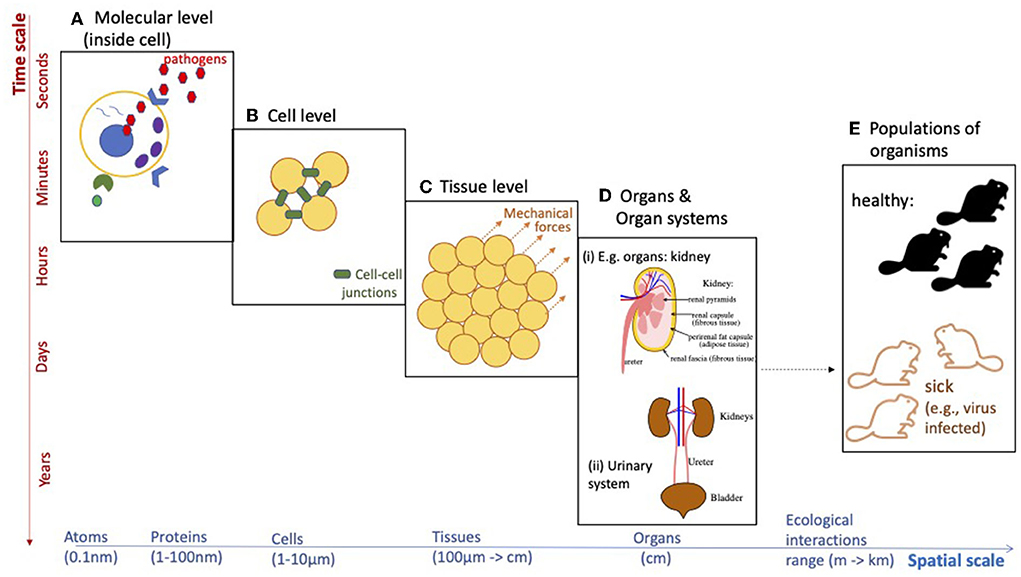
Figure 1. Diagram emphasizing the multi-scale aspects of various biological phenomena. Such biological processes can take place across different spatial and/or temporal scales. (A) Molecular level (inside cell), (B) cell level, (C) tissue level, (D) organs and organ systems, and (E) populations of organisms.
The multi-scale mathematical models developed to describe biological phenomena can be qualitative or quantitative [5, 6]. While the qualitative models are used to make general predictions about the biological system, the quantitative models are more precise and specific about the system, being parameterized with specific data. The advances over the last two decades in terms of collecting various types of single-scale and multi-scale data in ecology, epidemiology, cell biology, immunology, neurobiology, plant biology, social sciences, etc., led to the development of more and more models parameterized with data and used to obtain new quantitative results [7, 8]. In the following we discuss briefly some current research aspects related to multi-scale modeling in mathematical biology, as well as model parametrization using multi-scale historical data, and conclude by mentioning the digital twin concept—an emerging technology that uses real-time data and will impact most biology/mathematical biology areas.
2. Multi-scale aspects in mathematical biology
The last decade has seen an emphasis on the multi-scale aspects of different biological phenomena: from the multi-scale aspects of collective migration in bacteria/cells/animals [9], to the multi-scale landscape studies investigating the impact of environmental or habitat factors on the abundance or occurrence of species [10, 11], the multi-scale structure of cellular biological systems [12–14], or the multi-scale aspects of viral infections in the context of immuno-epidemiology [15]. However, our mechanistic understanding of these multi-scale aspects of various biological phenomena is still in its infancy, and more quantitative and qualitative modeling studies are necessary to advance the field. As an example, the current SARS-CoV-2 pandemic has highlighted the need to understand the impact of anti-viral immunity (at meso-scale) on virus evolution (at micro-scale) and virus transmission among individuals (at macro-scale), and the epidemiological and evolutionary implications of immune escape [15]. Despite the large number of mathematical studies investigating single-scale and multi-scale dynamics of different viruses [e.g., influenza [16], HIV [17]], the SARS-CoV-2 offered unexpected surprises that could not have been predicted by past modeling approaches, and which are still open questions. Such questions range from the mechanisms underlying the development of long COVID-19, to the number of viral particles a patient is exposed to (and how to quantify it) and the impact of this viral load on immune responses. Moreover, since current climate change will result in the emergence of new pathogens with new characteristics and increased cross-species transmission risks [18], one of the challenges of the future will be the development of new multi-scale models that combine evolutionary aspects of the new pathogens, with immunological aspects of pathogen infections, as well as epidemiological and ecological aspects of disease transmission at the level of populations (see Figure 1).
The development of these different multi-scale models is accompanied by challenges related to the development of new mathematical theories required to understand the behavior of these models. For example, new numerical approaches are required to be developed to better deal with the numerical blow-up of solution densities in a class of (advection dominated) non-local multi-scale moving-boundary models developed in the context of multi-scale cancer spread [19, 20]. As another example, the current bifurcation theory will have to be extended to consider also the bifurcation of patterns at multiple scales, especially when the bifurcation parameter connects the different scales; see Figure 1.
3. Data, model parametrization, uncertainty
The last few decades, and especially the last few years, have seen an explosion in data collection throughout all biological fields and across multiple spatial and temporal scales [21–24]. As an example we mention the molecular-level data collected via super-resolution microscopy (SRM)—whose development was acknowledged with a Nobel prize in 2014 [25, 26]. Such SRM methods can be used to generate live imaging molecular maps of protein complexes, and to extract quantitative information on the number, size, distribution, and spatial organization of various molecules inside cells [26–28], including viruses such as SARS-CoV-2 [29]. While live imaging approaches will play more and more important roles across all biological fields [26, 30], their use opens up new challenges in understanding the huge amount of generated data: from new approaches to deal with high data volumes generated at higher and higher speeds and that could be presented in a variety of forms (structured, semi-structured, and/or unstructured data) [24], to new approaches to deal with data heterogeneity [22, 24], or deal with incomplete data [21, 24] or even irreproducible data—which is a major issue at least in immunology and cell biology [31, 32], and even challenges in understanding the biological mechanisms behind the data [33]. While artificial intelligence techniques (e.g., machine learning, natural language processing, computational intelligence) can provide faster and more accurate results in data analytics compared to classical statistical methods [24] (especially if the training data is not biased in any way) they don't provide us with a mechanistic understanding of the data. This can be done by using collected data to parameterize mathematical models. However, model parametrization using poor data can lead to uncertainty in the predictions, which adds to the uncertainty arising from model formulation (e.g., deterministic vs. stochastic models, spatial vs. non-spatial models, simple vs. complex models) and to the uncertainty arising from the numerical approximation of the solution [As a note, uncertainty can arise also from the whole data analytics process: collecting, organizing, and analyzing the data [24]].
Uncertainty in the model results can be investigated using sensitivity analysis [34]. Sensitivity analysis for single-scale models is a well-accepted approach across various sub-disciplines of mathematical biology: from ecology [35], to cancer research [36, 37], immunology [36], pharmacology [38], epidemiology [39], etc. In the large majority of cases such an analysis (either local—where one parameter is varied at a time, or global—where multiple/all parameters are varied at a time) has been applied mainly to deterministic and stochastic ordinary differential equations models [34, 40]. For models described by partial differential equations, the sensitivity and uncertainty analysis approaches are not always standard, due to challenges caused by the multi-dimensionality of such models. In fact, very few studies perform spatially-explicit sensitivity and uncertainty analysis, and many of these studies focus on various environmental modeling aspects [41, 42].
In regard to the application of sensitivity analysis to multi-scale models, there are various ways to approach this, as summarized in Renardy et al. [34]: (a) all-in-one sensitivity, which treats the whole model as a black box and model outputs are evaluated after all or a subset of model parameters are varied; (b) intra/inter-compartmental sensitivity analysis, which varies parameters for a given scale and compares the results with the outputs at the same scale or at a different scale; (c) hierarchical sensitivity analysis, which focuses first on the analysis of the top/highest-level model, then on the next lower level sub-model where the outputs of this sub-model are replaced with constant parameters that become inputs for the higher-level model. It should be noted that very large numbers of model parameters, which might even depend on time and/or space, can lead to a computational burden when sensitivity analysis is performed (due to the sampling of the parameter values within specified ranges) [34]. Finding systematic approaches to reduce the computational time by reducing model complexity and/or reducing the number parameters investigated through this analysis, while preserving the biological realism of the model, is still an open problem for many multi-scale mathematical models.
Overall, data-driven multi-scale mathematical models are more challenging to be parameterized, and it is thus expected that in the future new multi-scale methods for data assimilation will be developed in the context of various biological problems. Some of these data assimilation approaches will likely be imported and adapted from other fields [e.g., from engineering [43]]. Moreover, it is expected that such new data assimilation approaches will focus on the automatic parameter estimation [e.g., via Bayesian approaches [8, 44]] using collected as well as real-time data, with the goal of making real-time forecasting.
4. The emergence of digital twins
One of the main issues associated with big data in biology is related to the speed at which data is produced (e.g., continuously-produced medical sensor data), which should meet the speed with which the data is processed so that fast decisions are being made [24]. In this context, the COVID-19 pandemics has led to an explosion of references to the “digital twins” concept across various areas of the mathematical biology field. A digital twin is a computer replica of a real-life system [e.g., cells [45], tissues [46], or even natural environment [47]], which allows us to integrate real-time and historical data and information about their functionality with the goal of making predictions about their future. This concept, which initially emerged in 1960's in the engineering field [48, 49], is not always very clear, mainly due to the interpretation of the connection between the data and the mathematical model. In Figure 2 we summarize the three sub-categories proposed by Kritzinger et al. [50] based on the level of data integration, while adapting them to biological systems [51]: (a) in a digital model, the data between the biological object and the digital object is exchanged manually; (b) in a digital shadow the data flow from the biological object to the digital object is automatic, while the reversed flow is manual; (c) in a digital twin there is a bi-directional automatic data flow between the biological object and the digital object.
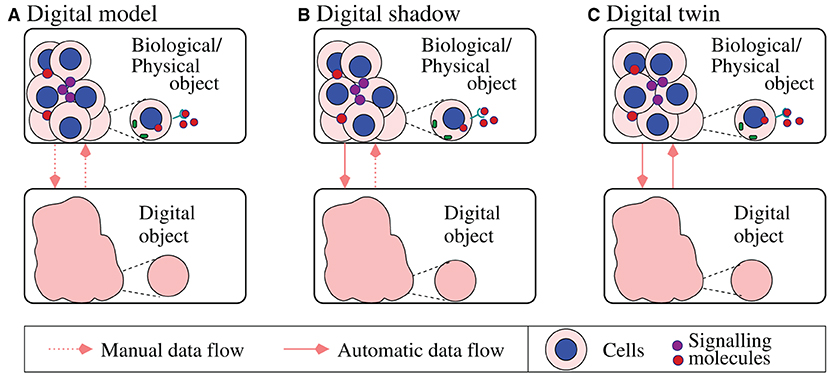
Figure 2. Summary of three sub-categories of digital objects proposed in Kritzinger et al. [50] and adapted here to biological systems: (A) digital model; (B) digital shadow; (C) digital twin. The diagram shows a caricature description of various cell–cell interactions (at cell/tissue levels) and a zoom-in on a single cell and protein dynamics inside this cell (at molecular-level), to emphasize the multi-scale aspect of some of these biological digital objects.
The large majority of the published quantitative studies in mathematical biology focus on the manual flow between the biological object (i.e., molecules, cells, tissues, organs, whole patients) and the corresponding digital object; i.e., these are digital-model/digital-shadow types of models (see Figure 2). Among the very few true digital twins developed in the context of mathematical biology we mention here the artificial pancreas [52], where mathematical models developed since 1970's [53] have been combined with real-time data to better control the blood glucose levels. The slow application of digital twins in biology and medicine is the result of a lack of understanding of the many biological laws that govern the complex single-scale and multi-scale processes in various living systems [51, 54, 55]. Very recently, the concept of digital twins has started to be discussed also in the context of the human immune system [56], as well as different environmental systems [47, 57, 58], and more biological applications will be identified over the next few years.
To return to the discussion in section 3, we emphasize that the lack of understanding of biological laws it is expected to diminish in the future due to the continuous development of new live imaging methods [26, 59, 60]. The generation of huge amounts of live imaging data will have a major impact on the future of digital twins. It will lead not only to the development of new (multi-scale) mathematical models to be parameterized in real time by such live data, but it will also lead to the development of various other mathematical areas: from the development of new statistical and artificial intelligence methods to analyse the collected data [61, 62], to the development of mathematical methods and computer algorithms for accurate reconstruction of super-resolution images [59, 63].
5. Conclusion
The field of mathematical biology will continue to develop over the next decades, being supported by the development of new methods for real-time multi-scale data acquisition and analysis at different space/time scales and across various biological disciplines, which will then lead to the development of new mathematical models that will be digital twins of real-life biological processes. In turn, this will lead to the development of new analytical and numerical approaches to investigate these models and take our understanding of the real-life biological phenomena even further.
The Mathematical Biology section of Frontiers in Applied Mathematics and Statistics aims to promote the development of a variety of mathematical/statistical/computational models that describe various single-scale and multi-scale phenomena in biology, as well as the investigation of the dynamics exhibited by these models, with the overall aim of advancing the field. Also, by supporting the development of joint research topics between mathematics and various other biological disciplines, the Mathematical Biology section aims to emphasize the role of mathematical/statistical/computational approaches to understand life in general.
Author contributions
RE designed and wrote the manuscript.
Funding
RE work was supported by ANR (France) funding through the grant number ANR-21-CE45-0025-01 and a “Chrysalides: Soutien aux Nouveaux Arrivants” grant (Université de Bourgogne-Franche-Comté, France).
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Bernoulli D. Essai d'une nouvelle analyse de la mortalité causée par la petite vérole et des avantages de l'inoculation pour la prévenir. Hist L'acad R Sci Avec Mémo. (1760) 1760:1–45.
2. Sigler JM. Fibonacci's Liber Abaci. A Translation into Modern English of Leonardo Pisano's Book of Calculation. New York, NY: Springer (2002).
3. Hartwell HL, Hopfield JJ, Leibler S, Murray AW. From molecular to modular cell biology. Nature. (1999) 402:c47–52. doi: 10.1038/35011540
5. Bondavalli C, Favilla S, Bodini A. Quantitative versus qualitative modeling: a complementary approach in ecosystem study. Comput Biol Chem. (2008) 33:22–8. doi: 10.1016/j.compbiolchem.2008.07.012
6. Saadatpour A, Albert R. A comparative study of qualitative and quantitative dynamic models of biological regulatory networks. EPJ Nonlin Biomed Phys. (2016) 4:5. doi: 10.1140/epjnbp/s40366-016-0031-y
7. Hasenauer J, Jagiella N, Hross S, Theis FJ. Data-driven modelling of biological multi-scale processes. J Coupl Syst Multis Dyn. (2015) 3:101–21. doi: 10.1166/jcsmd.2015.1069
8. Tran JS, Schiavazzi DE, Ramachandra AB, Kahn AM, Marsden AL. Automated tuning for parameter identification and uncertainty quantification in multi-scale coronary simulations. Comput Fluids. (2017) 142:128–38. doi: 10.1016/j.compfluid.2016.05.015
9. Deutsch A, Friedl P, Preziosi L, Theraulaz G. Multi-scale analysis and modelling of collective migration in biological systems. Philos Trans R Soc B. (2020) 1807:20190377. doi: 10.1098/rstb.2019.0377
10. Holland JD, Yang S. Multi-scale studies and the ecological neighbourhood. Curr Landscape Ecol Rep. (2016) 1:135–45. doi: 10.1007/s40823-016-0015-8
11. McGarigal K, Wan HY, Zeller KA, Timm BC, Cushman SA. Multi-scale habitat selection modelling: a review and outlook. Landscape Ecol. (2016) 31:1161–75. doi: 10.1007/s10980-016-0374-x
12. Petridou NI, Spiró Z, Heisenberg CP. Multiscale force sensing in development. Nat Cell Biol. (2017) 19:581–8. doi: 10.1038/ncb3524
13. Schaffer LV, Ideker T. Mapping the multiscale structure of biological systems. Cell Syst. (2021) 12:622–35. doi: 10.1016/j.cels.2021.05.012
14. Montagud A, de Leon MP, Valencia A. Systems biology at the giga-scale: large multi-scale models of complex, heterogeneous multicellular systems. Curr Opin Syst Biol. (2021) 28:100385. doi: 10.1016/j.coisb.2021.100385
15. Saad-Roy CM, Metcalf CJE, Grenfell BT. Immuno-epidemiology and the predictability of viral evolution. Understanding viral evolution depends on a synthesis of evolutionary biology and immune-epidemiology. Science. (2022) 376:1161–2. doi: 10.1126/science.abn9410
16. Rüdiger D, Kupke SY, Laske T, Zmora P, Reichl U. Multiscale modelling of influenza A virus replication in cell cultures predicts infection dynamics for highly different infection conditions. PLoS Comput Biol. (2019) 15:e1006819. doi: 10.1371/journal.pcbi.1006819
17. Hosseini I, Gabhann FM. Multi-scale modeling of HIV infection in vitro and APOBEC3G-based anti-retroviral therapy. PLoS Comput Biol. (2012) 8:e1002371. doi: 10.1371/journal.pcbi.1002371
18. Carlson CJ, Albery GF, Merow C, Trisos CH, Zipfel CM, Eskew EA, et al. Climate change increases cross-species viral transmission risk. Nature. (2022) 607:555–62. doi: 10.1038/s41586-022-04788-w
19. Suveges S, Eftimie R, Trucu D. Directionality of macrophages movement in tumour invasion: a multiscale moving-boundary approach. Bull Math Biol. (2020) 82:148. doi: 10.1007/s11538-020-00819-7
20. Suveges S, Chamseddine I, Rejniak KA, Eftimie R, Trucu D. Collective cell migration in a fibrous environment: a hybrid multi-scale modelling approach. Front Appl Math Stat. (2021) 7:680029. doi: 10.3389/fams.2021.680029
21. Conde DA, Staerk J, Colchero F, da Silva R, Schöley J, Baden HM, et al. Data gaps and opportunities for comparative and conservation biology. Proc Natl Acad Sci USA. (2019) 116:9658–64. doi: 10.1073/pnas.1816367116
22. Farley SS, Dawson A, Goring SJ, Williams JW. Situating ecology as a big-data science: current advances, challenges, and solutions. BioScience. (2018) 68:563–76. doi: 10.1093/biosci/biy068
23. Dolinski K, Troyanskaya OG. Implications of Big Data for cell biology. Mol Biol Cell. (2015) 26:2575–8. doi: 10.1091/mbc.E13-12-0756
24. Hariri RH, Fredericks EM, Bowers KM. Uncertainty in big data analytics: survey, opportunities, and challenges. J Big Data. (2019) 6:44. doi: 10.1186/s40537-019-0206-3
25. Prakash K, Diederich B, Heintzmann R, Schermelleh L. Super-resolution microscopy: a brief history and new avenues. Philos Trans R Soc A. 2(2022) 380:20210110. doi: 10.1098/rsta.2021.0110
26. Sydor AM, Czymmek KJ, Puchner EM, Mennella V. Super-resolution microscopy: from single molecules to supramolecular assemblies. Trends Cell Biol. (2015) 25:730–48. doi: 10.1016/j.tcb.2015.10.004
27. Ruan Q, MacDonald PJ, Swift KM, Tetin SY. Direct single-molecule imaging for diagnostic and blood screening assays. Proc Natl Acad Sci USA. (2021) 118:e2025033118. doi: 10.1073/pnas.2025033118
28. Turkowyd B, Schreiber S, Wörtz J, Segal ES, Mevarech M, Duggin IG, et al. Establishing live-cell single-molecule localization microscopy imaging and single-particle tracking in the archaeon Haloferax volcanii. Front Microbiol. (2020) 11:583010. doi: 10.3389/fmicb.2020.583010
29. Putlyaeva LV, Lukyanov KA. Studying SARS-CoV-2 with fluorescence microscopy. Int J Mol Sci. (2021) 22:6558. doi: 10.3390/ijms22126558
30. Qin H, Li X, Liang J, Peng Y, Zhang C. DeepFish: accurate underwater live fish recognition with a deep architecture. Neurocomputing. (2016) 187:49–58. doi: 10.1016/j.neucom.2015.10.122
31. Errington TM, Denis A, Iorns E, Nosek BA. Challenges for assessing replicability in preclinical cancer biology. eLife. (2021) 10:e67995. doi: 10.7554/eLife.67995
32. Hirsch C, Schildknecht S. In Vitro research reproducibility: keeping up high standards. Front Pharmacol. (2019) 10:1484. doi: 10.3389/fphar.2019.01484
33. Lele SR. How should we quantify uncertainty in statistical inference? Front Ecol Evol. (2020) 8:35. doi: 10.3389/fevo.2020.00035
34. Renardy M, Hult C, Evans S, Linderman JJ, Kirschner DE. Global sensitivity analysis of bioogical multiscale models. Curr Opin Biomed Eng. (2019) 11:109–16. doi: 10.1016/j.cobme.2019.09.012
35. Barabás G, Pásztor L, Meszéna G, Ostling A. Sensitivity analysis of coexistence in ecological communities: theory and application. Ecol Lett. (2014) 17:1479–94. doi: 10.1111/ele.12350
36. Dela A, Shtylla B, de Pillis L. Multi-method global sensitivity analysis of mathematical models. J Theor Biol. (2022) 546:111159. doi: 10.1016/j.jtbi.2022.111159
37. Eftimie R, Barelle C. Mathematical investigation of innate immune responses to lung cancer: the role of macrophages with mixed phenotypes. J Theor Biol. (2021) 524:110739. doi: 10.1016/j.jtbi.2021.110739
38. Zhang XY, Trame M, Lesko L, Schmidt S. Sobol sensitivity analysis: a tool to guide the development and evaluation of systems pharmacology models. CTP Pharmacomet Syst Pharmacol. (2015) 4:e6. doi: 10.1002/psp4.6
39. Massard M, Eftimie R, Perasso A, Saussereau B. A multi-strain epidemic model for COVID-19 with infected and asymptomatic cases: application to French data. J Theor Biol. (2022) 545:111117. doi: 10.1016/j.jtbi.2022.111117
40. Marino S, Hogue IB, Ray CJ, Kirschner DE. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J Theor Biol. (2008) 254:178–96. doi: 10.1016/j.jtbi.2008.04.011
41. Lilburne L, Tarantola S. Sensitivity analysis of spatial models. Int J Geograph Inform Sci. (2009) 23:151–68. doi: 10.1080/13658810802094995
42. Razavi S, Jakeman A, Saltelli A, Prieur C, Iooss B, Borgonovo E, et al. The future of sensitivity analysis: an essential discipline for systems modelling and policy support. Environ Modell Softw. (2021) 137:104954. doi: 10.1016/j.envsoft.2020.104954
43. de Moraes RJ, Hajibeygi H, Jansen JD. A multiscale method for data assimilation. Comput Geosci. (2020) 24:425–42. doi: 10.1007/s10596-019-09839-2
44. Deshpande S, Lengiewicz J, Bordas SPA. Probabilistic deep learning for real-time large deformation simulations. ArXiv. ArXiv:2111.01867. (2022). doi: 10.1016/j.cma.2022.115307
45. Filippo MD, Damiani C, Vanoni M, Maspero D, Mauri G, Alberghina L, et al. Single-cell digital twins for cancer preclinical investigation. Methods Mol Biol. (2020) 2088:331–43. doi: 10.1007/978-1-0716-0159-4_15
46. Möller J, Pörtner R. Digital twins for tissue culture techniques – concepts, expectations, and state of the art. Processes. (2021) 9:447. doi: 10.3390/pr9030447
47. Blair GS. Digital twins of the natural environment. Patterns. (2021) 2:100359. doi: 10.1016/j.patter.2021.100359
48. Bonney MS, Wagg D. Historical perspective of the development of digital twins. In: Special Topics in Structural Dynamics and Experimental Techniques. Vol. 5. Cham: Springer (2022) p. 15–20.
49. Guo J, Lv Z. Application of Digital Twins in multiple fields. Multimed Tools Appl. (2022) 81:26941–67. doi: 10.1007/s11042-022-12536-5
50. Kritzinger W, Karner M, Traar G, Henjes J, Sihn W. Digital twin in manufacturing: a categorical literature review and classification. IFAC PapersOnLine. (2018) 51:1016–22. doi: 10.1016/j.ifacol.2018.08.474
51. Eftimie R, Mavrodin A, Bordas SPA. From digital control to digital twins in medicine: a brief review and future perspectives. Adv Appl Mech. (2022) 56.
52. Brown SA, Kovatchev BP, Raghinaru D, Lum JW, Buckingham BA, Kudva YC, et al. Six-month randomized, multicenter trial of closed-loop control in type 1 diabetes. N Engl J Med. (2019) 381:1701–17. doi: 10.1056/NEJMoa1907863
53. Bergman RN. Origins and history of the minimal model of glucose regulation. Front Endocrinol. (2021) 11:583016. doi: 10.3389/fendo.2020.583016
54. Dhar P, Giuliani A. Laws of biology: why so few? Syst Synth Biol. (2010) 4:7–13. doi: 10.1007/s11693-009-9049-0
55. Dorato M. Mathematical biology and the existence of biological laws. In: Dieks D, Gonzales W, Hartmann S, Uebel T, Weber M, editors. Probabilities, Laws and Structure. Dordrecht: Springer (2011). p. 109–21. doi: 10.1007/978-94-007-3030-4_8
56. Laubenbacher R, Niarakis A, Helikar T, An G, Shapiro B, Malik-Sheriff RS, et al. Building digital twins of the human immune system: toward a roadmap. NPJ Digit Med. (2022) 5:64. doi: 10.1038/s41746-022-00610-z
57. Nativi S, Mazzetti P, Craglia M. Digital ecosystems for developing digital twins of the Earth: the destination Earth case. Remote Sens. (2021) 13:2119. doi: 10.3390/rs13112119
58. Zhao D, Li X, Wang X, Shen X, Gao W. Applying digital twins to research the relationship between urban expansion and vegetation coverage: a case study of natural preserve. Front Plant Sci. (2022) 13:840471. doi: 10.3389/fpls.2022.840471
59. Lelek M, Gyparaki MT, Beliu G, Scueder F, Griffié J, Manley S, et al. Single-molecule localization microscopy. Nat Rev. (2021) 1:39. doi: 10.1038/s43586-021-00038-x
60. Moerner WE. Viewpoint: Single molecules at 31: What's next? Nano Lett. (2020) 20:8427–9. doi: 10.1021/acs.nanolett.0c04042
61. Khater IM, Nabi IR, Hamameh G. A review of super-resolution single-molecule localization microscopy cluster analysis and quantification methods. Patterns. (2020) 1:100038. doi: 10.1016/j.patter.2020.100038
62. Lee A, Tsekouras K, Calderon C, Bustamante C, Pressé S. Unraveling the thousand word picture: an introduction to super-resolution data analysis. Chem Rev. (2017) 117:7276–330. doi: 10.1021/acs.chemrev.6b00729
Keywords: mathematical biology, multi-scale biological interactions, digital twins, data, uncertainty, mathematical models
Citation: Eftimie R (2022) Grand challenges in mathematical biology: Integrating multi-scale modeling and data. Front. Appl. Math. Stat. 8:1010622. doi: 10.3389/fams.2022.1010622
Received: 03 August 2022; Accepted: 30 August 2022;
Published: 26 September 2022.
Edited and reviewed by: Charles K. Chui, Stanford University, United States
Copyright © 2022 Eftimie. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Raluca Eftimie, cmFsdWNhLmVmdGltaWVAdW5pdi1mY29tdGUuZnI=
 Raluca Eftimie
Raluca Eftimie