- 1Institut für Mathematik, Technische Universität Berlin, Berlin, Germany
- 2Institut für Theoretische Physik, Technische Universität Berlin, Berlin, Germany
This work introduces a methodology for studying synchronization in adaptive networks with heterogeneous plasticity (adaptation) rules. As a paradigmatic model, we consider a network of adaptively coupled phase oscillators with distance-dependent adaptations. For this system, we extend the master stability function approach to adaptive networks with heterogeneous adaptation. Our method allows for separating the contributions of network structure, local node dynamics, and heterogeneous adaptation in determining synchronization. Utilizing our proposed methodology, we explain mechanisms leading to synchronization or desynchronization by enhanced long-range connections in nonlocally coupled ring networks and networks with Gaussian distance-dependent coupling weights equipped with a biologically motivated plasticity rule.
1 Introduction
In nature and technology, complex networks serve as a ubiquitous paradigm with a broad range of applications from physics, chemistry, biology, neuroscience, socioeconomic, and other systems [1]. Dynamical networks consist of interacting dynamical units, such as neurons or lasers. Collective behavior in dynamical networks has attracted much attention in recent decades. Depending on the network and the specific dynamical system, various synchronization patterns with increasing complexity were explored [2–5]. Even in simple models of coupled oscillators, patterns such as complete synchronization [6, 7], cluster synchronization [8–11], and various forms of partial synchronization have been found, such as frequency clusters [12], solitary [13–15], or chimera states [16–20]. In particular, synchronization is believed to play a crucial role in brain networks, for example, under normal conditions in the context of cognition and learning [21, 22], and under pathological conditions, such as Parkinson’s disease [23–25], epilepsy [26–29], tinnitus [30, 31], schizophrenia, to name a few [32].
The powerful methodology of master stability function [33] has been a milestone for the analysis of synchronization phenomena. This method allows for the separation of dynamic and structural features in dynamical networks. It greatly simplifies the problem by reducing the dimension and unifying the synchronization study for different networks. Since its introduction, the master stability approach has been extended and refined for various complex systems [34–42], and methods beyond the local stability analysis have been developed [43–47]. More recently, the master stability approach has been extended to another class of oscillator networks with high application potential, namely adaptive networks [48].
Adaptive networks are commonly used models for various systems from nature and technology [49–57]. A prominent example are neuronal networks with spike-timing dependent plasticity, in which the synaptic coupling between neurons changes depending on their relative spiking times [58–61]. There are a large number of studies investigating the dynamic properties induced by this form of synaptic plasticity [62]. However, analysis is usually limited to only one or two forms of spike timing-dependent plasticity within a neuronal population. On the other hand, experimental studies indicate that different forms of spike timing-dependent plasticity may be present within a neuronal population, where the form depends on the connection structure between the axons and dendrites [63]. Among all structural aspects, an important factor for the specific form of the plasticity rule is the distance between neurons [64–66]. More specifically, it has been found that the plasticity rule between proximal or distal neurons, respectively, can change from Hebbian-like to anti-Hebbian-like [67, 68].
This work introduces a methodology to study synchronization in adaptive networks with heterogeneous plasticity (adaptation) rules. As a paradigmatic system, we consider an adaptively coupled phase oscillator network [69–75], which is proven to be useful for predicting and describing phenomena occurring in more realistic and detailed models [76–79]. More specifically, in the spirit of the master stability function approach, we consider the synchronization problem as the interplay between network structure and a heterogeneous adaptation rule arising from distance- (or location-)dependent synaptic plasticity. For a given heterogeneous adaptation rule, our master stability function provides synchronization criteria for any coupling configuration. As illustrative examples, we consider a nonlocally coupled ring with biologically motivated plasticity rule, and a network with a Gaussian distance-dependent coupling weights. We explained such intriguing effects as synchronization or desynchronization by enhancement of long-distance links.
We introduce the model in Section 2. Building on findings from [48], we develop a master stability approach in Section 3 that takes a heterogeneous adaptation rule in account. In Section 4.1, we provide an approximation of the structural eigenvalues that determine the stability of the synchronous state. We then consider two different setups: a nonlocally coupled ring in Section 4.2 and a weighted network with Gaussian distance distribution of coupling weights in Section 4.3. Both systems are equipped with a biologically motivated plasticity rule. In Section 5, we summarize the results.
2 Model
In this work, we study the synchronization on networks with adaptive coupling weights, where the adaptation (plasticity) rule depends on the distance between oscillators (neurons). We consider the model of adaptively coupled phase oscillators, which has proven to be useful for understanding dynamics in neuronal systems with spike timing-dependent plasticity [77, 79, 48]. The model reads as follows:
where
The main difference of system Eqs. 1, 2 from the models considered previously in the literature [40, 70, 71, 74, 82], is that the plasticity functions
A solution to Eqs. 1, 2 is called phase-locked if, for all
In the case of in-phase synchronous state, we can set
where we assume that the weighted row sum
In the following section, we show how the stability of the synchronous state is determined in a master-stability-like approach.
3 Master Stability Approach
In Section 2, we have introduced a general class of models and the synchronous state, that are considered throughout this paper. In this section, we derive a framework for the local stability analysis of the synchronous states. We note that the master stability approach for homogeneous adaptations
To describe the local stability, we introduce the variations
where
The time-independent matrices B and C are
where
Note that due to the shift symmetry of Eqs. 1, 2, the Jacobian J in Eq. 5 is time independent. Therefore, the real parts of the
Proposition 1. Suppose
where
Proof. We remind that system Eq. 5 determines the spectrum (Lyapunov exponents) of the synchronous state. The Jacobian matrix in Eq. 5 is sparse with a large
This system has at least
with
where
Proposition 2. Assume that
where
where we have used the transformation Q that brings
The latter equation is almost diagonal. The only off-diagonal components remain from
where
These conditions agree with the black dashed lines in Figure 1 and are used subsequently to describe stability for certain network models.
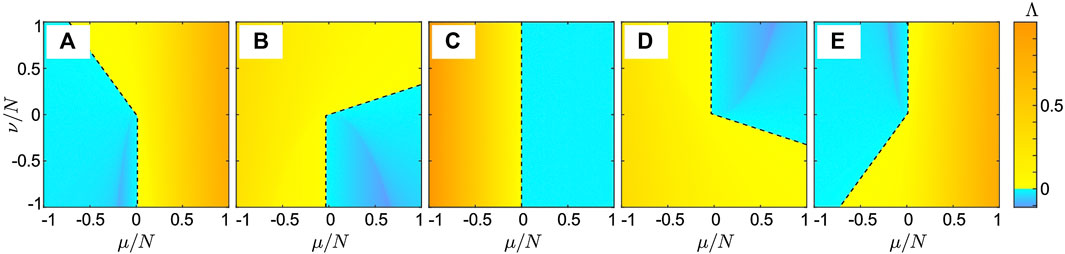
FIGURE 1. The master stability function
4 Synchronization on Networks With Distance-Dependent Plasticity
In the previous section, we established a generic analytic tool for studying stability of synchronous states. In this section, we focus on the application of the tool to certain network models. For the rest of the work, we restrict our attention to the following generalization of the Kuramoto-Sakaguchi system with distance-dependent synaptic plasticity
The plasticity function h depends on the phase difference
With this form of the adaptation function, we have a symmetric
where the distance dependence is encoded in the phase shift function
In Figure 2A, we illustrate the distance-dependent plasticity function Eqs. 18–20 for a network of
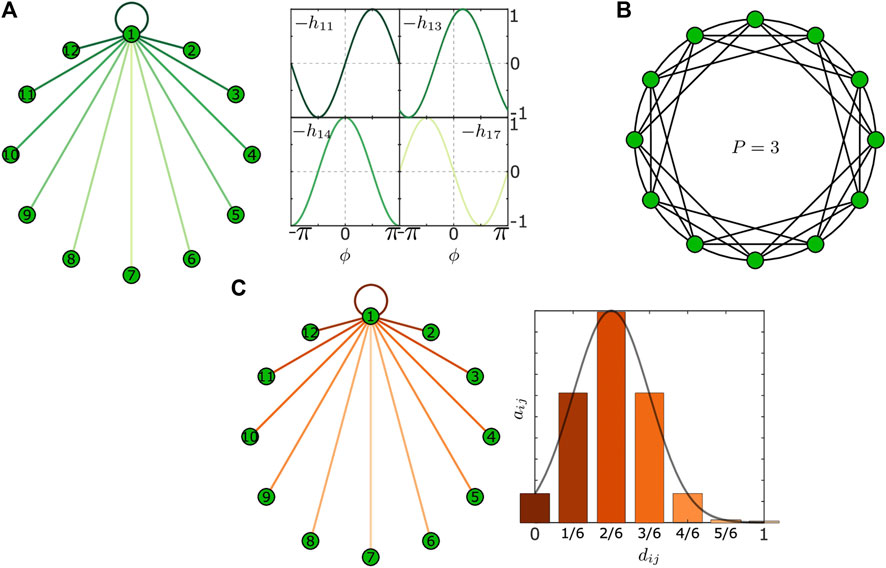
FIGURE 2. Panel (A) shows the plasticity function
If not indicated differently, we consider the coupling structure given by
where
In the following section, we provide an approximation for the eigenvalues of
4.1 Approximation of the Eigenvalues for Large Systems With Circulant Structure
In the previous part, we have defined the plasticity functions
In this section, we briefly recall how one can derive the eigenvalues
For the case of
with
Due to the definition of h and the symmetry of
for any k. This explicit expression allows studying the distribution of the eigenvalues
We note that
The results from Eqs. 23 and 24 are applied in the next sections to analyze different networks.
4.2 Synchronization on Nonlocally Coupled Ring Networks
In this section, we analyze the effect of long distance connections on the stability of synchronous states in nonlocally coupled ring networks. We consider the coupling structure given by
This means that any two oscillators are coupled if they are separated at most by the coupling range P. The coupling Eq. 25 defines a nonlocal ring structure with coupling range p to each side and two special limiting cases: local ring for
In order to study the influence of the coupling range, we use the approximations for the eigenvalues
for the eigenvalues
for
In Figure 3A, we provide an error analysis of the approximations Eqs. 26 and 27 compared to the exact eigenvalues given by Eq. 22. As expected, the errors tend to zero as the number of oscillators increases. Additionally in Figures 3B,C, we display
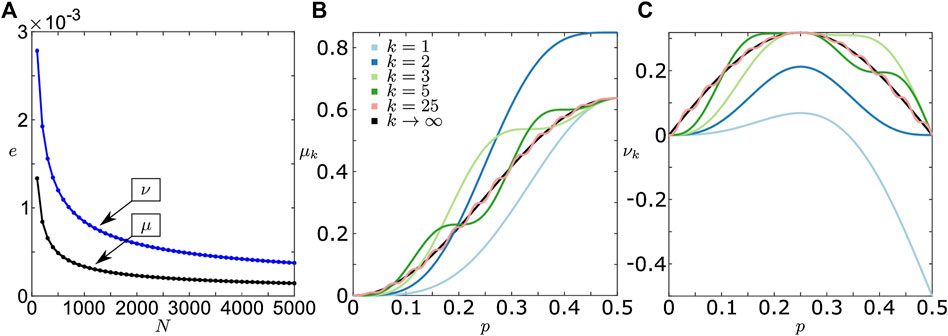
FIGURE 3. Panel (A) shows the errors
It is important to note, that our choice of the circulant adaptation functions imply that the matrices
Combining the fact
In Figure 4, we show different scenarios for the stability of the synchronous state depending on the phase lag parameter α and the coupling range p. Due to the necessary condition
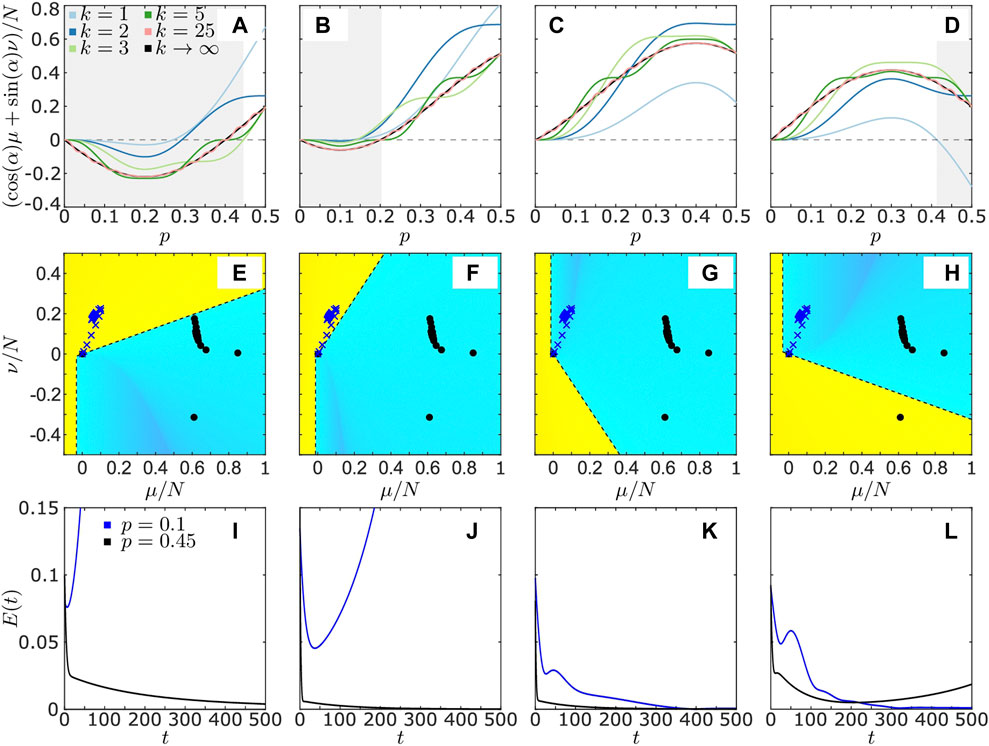
FIGURE 4. Stability analysis of the synchronous state of system Eqs. 16, 17 with plasticity rule Eqs. 18–20 and coupling structure Eq. 25. Panels (A–D) show the function
The situation changes for
We have shown that long distance interactions may stabilize or destabilize the synchronous state depending on the phase lag parameter α. In this section, all links have the same weight independent of the corresponding distance. In the next section, we analyze a network with a more realistic structure with a distance-dependent distribution of weights.
4.3 Synchronization on Isotropic and Homogeneous Network With Gaussian Distance Distribution
In the previous section, we used the prototypical example of a nonlocally coupled rings to study the effects of long-range interaction on synchronization. In this setup, however, all links are equally weighted. In realistic systems, in contrast, the number of links with a certain distance are distributed, see [67] for details. To incorporate this into our network model, we weight the links with respect to a distance distribution. Measurements suggest that the distance distribution can be estimated by a mean and a distribution width [67]. The Gaussian distributions is a paradigmatic distribution that allows for studying effects emanating from the mean and the distribution width. For the remainder of the section, we consider the link distance distribution given by a Gaussian distribution, and weight the links of the network connectivity structure A accordingly, i.e.
where ξ and σ are the mean value and the standard deviation, respectively. Note that the standard deviation characterizes the width of the distribution. For the numerical simulations, we normalize each row of A by
As we know from Eqs. 14 and 15, for
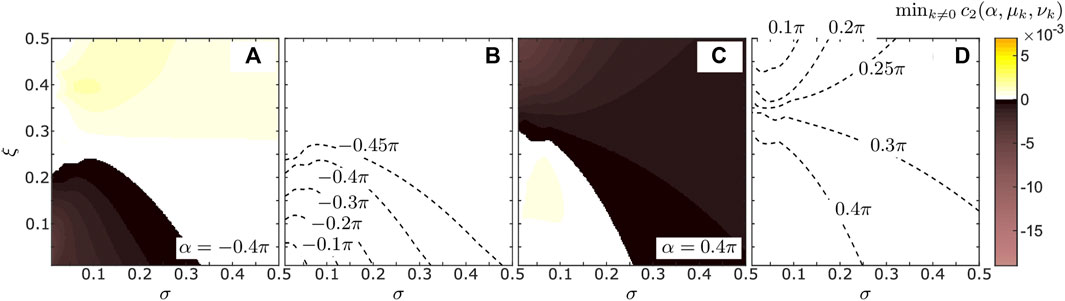
FIGURE 5. Stability analysis of the synchronous state of system Eqs. 16, 17 with plasticity rule Eqs. 18–20 and coupling structure Eq. 28. Panels (A, C) show the minimum over all
An opposite scenario is shown in Figure 5C for
5 Conclusion
In summary, we have investigated the phenomenon of synchronization on adaptive networks with heterogeneous plasticity rules. In particular, we have modeled systems with distance-dependent plasticity as they have been found in neuronal networks experimentally [64–67] as well as computational models [68]. For the realization, we have used a ring-like network architecture and associated the distance of two nodes with the distance of their placement on the ring.
In Section 3, we have developed a generalized master stability approach for phase oscillator models that are adaptively coupled and where each link has its own adaptation rule (plasticity). By using an explicit splitting of the time scales between fast dynamics of the phase oscillators and slow dynamics of the link weights, we have established an explicit stability condition for the synchronous state. More precisely, we found that the stability is governed by the coupling function and the eigenvalues of two structure matrices. These structure matrices
In Section 4, we applied the novel technique to a system of adaptively coupled oscillators with distance-dependent plasticity. Here, we have used a ring-like network structure to study the impact of long- and short-distance connections on the stability of synchronization. For this purpose we introduced an approximation of the eigenvalues for the structure matrices in Section 4.1. This approximation allows for a comprehensive analysis of the stability as a function of various system parameters. Moreover, it enables us to identify critical eigenvalues that govern the stability of the synchronous state. In Sections 4.2 and 4.3, we have brought together all methodological findings and applied them to systems with a nonlocally coupled ring structure and with a Gaussian distribution of link weights. The latter structure accounts for the fact that in realistic neuronal populations the number of links with different distances are not uniformly distributed [67]. We found that long-distance connections can stabilize or destabilize the synchronous state, depending on the coupling function between the oscillators. A remarkable fact with respect to neuronal applications relates to the destabilization scenario. Here we observed that the destabilization can be attributed to the pronounced change of the plasticity rule from Hebbian to anti-Hebbian. For more realistic connectivity structures, we found that weight distributions of the connectivity structure with sharp peaks at long distances lead to destabilization for a wide range of the coupling function.
All in all, in this article, we have provided a general framework to study the emergence of synchronization in neuronal system with a heterogeneous plasticity rule. The developed methodology is not limited to distance-dependent types of plasticity and can also be used for non-symmetric setups. For the latter case, we have provided the necessary analytical result. In this work, we have restricted our attention to the case of phase oscillators, but the methods can be extended to more realistic neuron models by using techniques established, for example, in [48]. Moreover, techniques are available that allow for further generalization toward systems with slightly different local dynamics at each node [87]. On the one hand, the master stability approach offers a great tool to study the stability of the synchronous state depending on the networks structure. On the other hand, this approach allows for characterizing the network structures that are, in some sense, optimal for synchronization [88, 89]. In this regard, it remains an open question as to how plasticity optimizes the synchronizability of the network in a self-organized way. In addition, recent studies have shown that there is a great interest in synchronization phenomena to understand diseases such as Parkinson’s disease [90–92] or epilepsy [29, 93] for the development of proper therapeutic treatments. We believe that our work provides an important step toward understanding synchronization under realistic conditions.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
RB designed the study and did the numerical simulations. RB and SY developed the analytical results. Both authors contributed to the preparation of the manuscript. Both authors read and approved the final manuscript.
Funding
This work was supported by the German Research Foundation DFG, Project Nos. 411803875 and 440145547, and the Open Access Publication Fund of TU Berlin.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Newman, MEJ. The Structure and Function of Complex Networks. SIAM Rev (2003) 45:167–256. doi:10.1137/s003614450342480
2. Pikovsky, A, Rosenblum, M, and Kurths, J. Synchronization: A Universal Concept in Nonlinear Sciences. 1st ed. Cambridge: Cambridge University Press (2001).
4. Arenas, A, Díaz-Guilera, A, Kurths, J, Moreno, Y, and Zhou, C. Synchronization in Complex Networks. Phys Rep (2008) 469:93–153. doi:10.1016/j.physrep.2008.09.002
5. Boccaletti, S, Pisarchik, AN, del Genio, CI, and Amann, A. Synchronization: From Coupled Systems to Complex Networks. Cambridge: Cambridge University Press (2018).
7. Pecora, LM, Carroll, TL, Johnson, GA, Mar, DJ, and Heagy, JF. Fundamentals of Synchronization in Chaotic Systems, Concepts, and Applications. Chaos (1997) 7:520–43. doi:10.1063/1.166278 https://doi.org/10.1063/1.166278
8. Yanchuk, S, Maistrenko, Y, and Mosekilde, E. Partial Synchronization and Clustering in a System of Diffusively Coupled Chaotic Oscillators. Mathematics Comput Simulation (2001) 54:491–508. doi:10.1016/S0378-4754(00)00276-7
9. Choe, C-U, Dahms, T, Hövel, P, and Schöll, E. Controlling Synchrony by Delay Coupling in Networks: from In-phase to Splay and Cluster States. Phys Rev E (2010) 81:025205. doi:10.1103/physreve.81.025205
10. Belykh, I, and Hasler, M. Mesoscale and Clusters of Synchrony in Networks of Bursting Neurons. Chaos (2011) 21:016106. doi:10.1063/1.3563581
11. Zhang, Y, and Motter, AE. Symmetry-independent Stability Analysis of Synchronization Patterns. SIAM Rev (2020) 62:817–36. doi:10.1137/19m127358x
12. Berner, R, Schöll, E, and Yanchuk, S. Multiclusters in Networks of Adaptively Coupled Phase Oscillators. SIAM J Appl Dyn Syst (2019) 18:2227–66. doi:10.1137/18m1210150
13. Jaros, P, Brezetsky, S, Levchenko, R, Dudkowski, D, Kapitaniak, T, and Maistrenko, Y. Solitary States for Coupled Oscillators with Inertia. Chaos (2018) 28:011103. doi:10.1063/1.5019792
14. Teichmann, E, and Rosenblum, M. Solitary States and Partial Synchrony in Oscillatory Ensembles with Attractive and Repulsive Interactions. Chaos (2019) 29:093124. doi:10.1063/1.5118843
15. Berner, R, Polanska, A, Schöll, E, and Yanchuk, S. Solitary States in Adaptive Nonlocal Oscillator Networks. Eur Phys J Spec Top (2020) 229:2183–203. doi:10.1140/epjst/e2020-900253-0
16. Kuramoto, Y, and Battogtokh, D. Coexistence of Coherence and Incoherence in Nonlocally Coupled Phase Oscillators. Nonlin Phen Complex Sys (2002) 5(4):380–5.
17. Abrams, DM, and Strogatz, SH. Chimera States for Coupled Oscillators. Phys Rev Lett (2004) 93:174102. doi:10.1103/physrevlett.93.174102
18. Schöll, E. Synchronization Patterns and Chimera States in Complex Networks: Interplay of Topology and Dynamics. Eur Phys J Spec Top (2016) 225:891–919. doi:10.1140/epjst/e2016-02646-3
19. Omel’chenko, OE. The Mathematics behind Chimera States. Nonlinearity (2018) 31:R121. doi:10.1088/1261-6544/aaaa07
20. Omel’chenko, OE, and Knobloch, E. Chimerapedia: Coherence-Incoherence Patterns in One, Two and Three Dimensions. New J Phys (2019) 21:093034. doi:10.1088/1367-2630/ab3f6b
21. Singer, W. Neuronal Synchrony: A Versatile Code for the Definition of Relations? Neuron (1999) 24:49–65. doi:10.1016/s0896-6273(00)80821-1
22. Fell, J, and Axmacher, N. The Role of Phase Synchronization in Memory Processes. Nat Rev Neurosci (2011) 12:105–18. doi:10.1038/nrn2979
23. Hammond, C, Bergman, H, and Brown, P. Pathological Synchronization in Parkinson's Disease: Networks, Models and Treatments. Trends Neurosciences (2007) 30:357–64. doi:10.1016/j.tins.2007.05.004
24. Goriely, A, Kuhl, E, and Bick, C. Neuronal Oscillations on Evolving Networks: Dynamics, Damage, Degradation, Decline, Dementia, and Death. Phys Rev Lett (2020) 125:128102. doi:10.1103/physrevlett.125.128102
25. Pfeifer, KJ, Kromer, JA, Cook, AJ, Hornbeck, T, Lim, EA, Mortimer, BJP, et al. Coordinated Reset Vibrotactile Stimulation Induces Sustained Cumulative Benefits in Parkinson's Disease. Front Physiol (2021) 12:624317. doi:10.3389/fphys.2021.624317
26. Jiruska, P, de Curtis, M, Jefferys, JGR, Schevon, CA, Schiff, SJ, and Schindler, K. Synchronization and Desynchronization in Epilepsy: Controversies and Hypotheses. J Physiol (2013) 591(4):787–97. doi:10.1113/jphysiol.2012.239590
27. Jirsa, VK, Stacey, WC, Quilichini, PP, Ivanov, AI, and Bernard, C. On the Nature of Seizure Dynamics. Brain (2014) 137:2210–30. doi:10.1093/brain/awu133
28. Andrzejak, RG, Rummel, C, Mormann, F, and Schindler, K. All Together Now: Analogies between Chimera State Collapses and Epileptic Seizures. Sci Rep (2016) 6:23000. doi:10.1038/srep23000
29. Gerster, M, Berner, R, Sawicki, J, Zakharova, A, Škoch, A, Hlinka, J, et al. FitzHugh-Nagumo Oscillators on Complex Networks Mimic Epileptic-Seizure-Related Synchronization Phenomena. Chaos (2020) 30:123130. doi:10.1063/5.0021420
30. Tass, PA, Adamchic, I, Freund, H-J, von Stackelberg, T, and Hauptmann, C. Counteracting Tinnitus by Acoustic Coordinated Reset Neuromodulation. Restor Neurol Neurosci (2012) 30:137–59. doi:10.3233/rnn-2012-110218
31. Tass, PA, and Popovych, OV. Unlearning Tinnitus-Related Cerebral Synchrony with Acoustic Coordinated Reset Stimulation: Theoretical Concept and Modelling. Biol Cybern (2012) 106:27–36. doi:10.1007/s00422-012-0479-5
32. Uhlhaas, P, Pipa, G, Lima, B, Melloni, L, Neuenschwander, S, Nikolic, D, et al. Neural Synchrony in Cortical Networks: History, Concept and Current Status. Front Integr Neurosci (2009) 3:17. doi:10.3389/neuro.07.017.2009
33. Pecora, LM, and Carroll, TL. Master Stability Functions for Synchronized Coupled Systems. Phys Rev Lett (1998) 80:2109–12. doi:10.1103/physrevlett.80.2109
34. Flunkert, V, Yanchuk, S, Dahms, T, and Schöll, E. Synchronizing Distant Nodes: a Universal Classification of Networks. Phys Rev Lett (2010) 105:254101. doi:10.1103/physrevlett.105.254101
35. Dahms, T, Lehnert, J, and Schöll, E. Cluster and Group Synchronization in Delay-Coupled Networks. Phys Rev E (2012) 86:016202. doi:10.1103/physreve.86.016202
36. Keane, A, Dahms, T, Lehnert, J, Suryanarayana, SA, Hövel, P, and Schöll, E. Synchronisation in Networks of Delay-Coupled Type-I Excitable Systems. Eur Phys J B (2012) 85:407. doi:10.1140/epjb/e2012-30810-x
37. Kyrychko, YN, Blyuss, KB, and Schöll, E. Synchronization of Networks of Oscillators with Distributed Delay Coupling. Chaos (2014) 24:043117. doi:10.1063/1.4898771
38. Lehnert, J. Controlling Synchronization Patterns in Complex Networks. Springer Theses. Heidelberg: Springer (2016).
39. Tang, L, Wu, X, Lü, J, Lu, JA, and D'Souza, RM. Master Stability Functions for Complete, Intralayer, and Interlayer Synchronization in Multiplex Networks of Coupled Rössler Oscillators. Phys Rev E (2019) 99:012304. doi:10.1103/PhysRevE.99.012304
40. Berner, R, Sawicki, J, and Schöll, E. Birth and Stabilization of Phase Clusters by Multiplexing of Adaptive Networks. Phys Rev Lett (2020) 124:088301. doi:10.1103/physrevlett.124.088301
41. Börner, R, Schultz, P, Ünzelmann, B, Wang, D, Hellmann, F, and Kurths, J. Delay Master Stability of Inertial Oscillator Networks. Phys Rev Res (2020) 2:023409. doi:10.1103/physrevresearch.2.023409
42. Mulas, R, Kuehn, C, and Jost, J. Coupled Dynamics on Hypergraphs: Master Stability of Steady States and Synchronization. Phys Rev E (2020) 101:062313. doi:10.1103/physreve.101.062313
43. Belykh, VN, Belykh, IV, and Hasler, M. Connection Graph Stability Method for Synchronized Coupled Chaotic Systems. Physica D: Nonlinear Phenomena (2004) 195:159–87. doi:10.1016/j.physd.2004.03.012
44. Belykh, I, de Lange, E, and Hasler, M. Synchronization of Bursting Neurons: What Matters in the Network Topology. Phys Rev Lett (2005) 94:188101. doi:10.1103/physrevlett.94.188101
45. Belykh, I, Belykh, V, and Hasler, M. Generalized Connection Graph Method for Synchronization in Asymmetrical Networks. Physica D: Nonlinear Phenomena (2006) 224:42–51. doi:10.1016/j.physd.2006.09.014
46. Belykh, I, Belykh, V, and Hasler, M. Synchronization in Asymmetrically Coupled Networks with Node Balance. Chaos (2006) 16:015102. doi:10.1063/1.2146180 https://doi.org/10.1063/1.2146180
47. Daley, K, Zhao, K, and Belykh, IV. Synchronizability of Directed Networks: The Power of Non-existent Ties. Chaos (2020) 30:043102. doi:10.1063/1.5134920
48. Berner, R, Vock, S, Schöll, E, and Yanchuk, S. Desynchronization Transitions in Adaptive Networks. Phys Rev Lett (2021) 126:028301. doi:10.1103/physrevlett.126.028301
49. Jain, S, and Krishna, S. A Model for the Emergence of Cooperation, Interdependence, and Structure in Evolving Networks. Proc Natl Acad Sci (2001) 98:543–7. doi:10.1073/pnas.98.2.543
50. Proulx, S, Promislow, D, and Phillips, P. Network Thinking in Ecology and Evolution. Trends Ecol Evol (2005) 20:345–53. doi:10.1016/j.tree.2005.04.004
51. Gross, T, D’Lima, CJD, and Blasius, B. Epidemic Dynamics on an Adaptive Network. Phys Rev Lett (2006) 96:208701. doi:10.1103/physrevlett.96.208701
52. Martens, EA, and Klemm, K. Transitions from Trees to Cycles in Adaptive Flow Networks. Front Phys (2017) 5:62. doi:10.3389/fphy.2017.00062
53. Kuehn, C. Multiscale Dynamics of an Adaptive Catalytic Network. Math Model Nat Phenom (2019) 14:402. doi:10.1051/mmnp/2019015
54. Horstmeyer, L, and Kuehn, C. Adaptive Voter Model on Simplicial Complexes. Phys Rev E (2020) 101:022305. doi:10.1103/physreve.101.022305
55. Meisel, C, and Gross, T. Adaptive Self-Organization in a Realistic Neural Network Model. Phys Rev E (2009) 80:061917. doi:10.1103/physreve.80.061917
56. Mikkelsen, K, Imparato, A, and Torcini, A. Emergence of Slow Collective Oscillations in Neural Networks with Spike-Timing Dependent Plasticity. Phys Rev Lett (2013) 110:208101. doi:10.1103/physrevlett.110.208101
57. Mikkelsen, K, Imparato, A, and Torcini, A. Sisyphus Effect in Pulse-Coupled Excitatory Neural Networks with Spike-timing-dependent Plasticity. Phys Rev E (2014) 89:062701. doi:10.1103/physreve.89.062701
58. Markram, H, Lübke, J, Frotscher, M, and Sakmann, B. Regulation of Synaptic Efficacy by Coincidence of Postsynaptic APs and EPSPs. Science (1997) 275:213–5. doi:10.1126/science.275.5297.213
59. Abbott, LF, and Nelson, SB. Synaptic Plasticity: Taming the Beast. Nat Neurosci (2000) 3:1178–83. doi:10.1038/81453
60. Caporale, N, and Dan, Y. Spike Timing-dependent Plasticity: A Hebbian Learning Rule. Annu Rev Neurosci (2008) 31:25–46. doi:10.1146/annurev.neuro.31.060407.125639
61. Popovych, OV, Yanchuk, S, and Tass, PA. Self-organized Noise Resistance of Oscillatory Neural Networks with Spike Timing-dependent Plasticity. Sci Rep (2013) 3:2926. doi:10.1038/srep02926
62. Zenke, F, Agnes, EJ, and Gerstner, W. Diverse Synaptic Plasticity Mechanisms Orchestrated to Form and Retrieve Memories in Spiking Neural Networks. Nat Commun (2015) 6:6922. doi:10.1038/ncomms7922
63. Tazerart, S, Mitchell, DE, Miranda-Rottmann, S, and Araya, R. A Spike-timing-dependent Plasticity Rule for Dendritic Spines. Nat Commun (2020) 11:4276. doi:10.1038/s41467-020-17861-7
64. Froemke, RC, Poo, M-m., and Dan, Y. Spike-timing-dependent Synaptic Plasticity Depends on Dendritic Location. Nature (2005) 434:221–5. doi:10.1038/nature03366
65. Sjöström, PJ, and Häusser, M. A Cooperative Switch Determines the Sign of Synaptic Plasticity in Distal Dendrites of Neocortical Pyramidal Neurons. Neuron (2006) 51:227–38. doi:10.1016/j.neuron.2006.06.017
66. Froemke, RC, Letzkus, JJ, Kampa, BM, Hang, GB, and Stuart, GJ. Dendritic Synapse Location and Neocortical Spike-timing-dependent Plasticity. Front.Syna.Neurosci. (2010) 2:29. doi:10.3389/fnsyn.2010.00029
67. Letzkus, JJ, Kampa, BM, and Stuart, GJ. Learning Rules for Spike Timing-dependent Plasticity Depend on Dendritic Synapse Location. J Neurosci (2006) 26:10420–9. doi:10.1523/jneurosci.2650-06.2006
68. Meissner-Bernard, C, Tsai, MC, Logiaco, L, and Gerstner, W. Dendritic Voltage Recordings Explain Paradoxical Synaptic Plasticity: A Modeling Study. Front Synaptic Neurosci (2020) 12:585539. doi:10.3389/fnsyn.2020.585539
69. Aoki, T, and Aoyagi, T. Co-evolution of Phases and Connection Strengths in a Network of Phase Oscillators. Phys Rev Lett (2009) 102:034101. doi:10.1103/physrevlett.102.034101
70. Kasatkin, DV, Yanchuk, S, Schöll, E, and Nekorkin, VI. Self-organized Emergence of Multilayer Structure and Chimera States in Dynamical Networks with Adaptive Couplings. Phys Rev E (2017) 96:062211. doi:10.1103/physreve.96.062211
71. Kasatkin, DV, and Nekorkin, VI. The Effect of Topology on Organization of Synchronous Behavior in Dynamical Networks with Adaptive Couplings. Eur Phys J Spec Top (2018) 227:1051–61. doi:10.1140/epjst/e2018-800077-7
72. Berner, R, Fialkowski, J, Kasatkin, D, Nekorkin, V, Yanchuk, S, and Schöll, E. Hierarchical Frequency Clusters in Adaptive Networks of Phase Oscillators. Chaos (2019) 29:103134. doi:10.1063/1.5097835
73. Berner, R, Yanchuk, S, and Schöll, E. What Adaptive Neuronal Networks Teach Us about Power Grids. Phys Rev E (2021) 103:042315. doi:10.1103/physreve.103.042315
74. Feketa, P, Schaum, A, and Meurer, T. Synchronization and Multi-Cluster Capabilities of Oscillatory Networks with Adaptive Coupling. IEEE Trans Automat Control (2020) 66(7):3084. doi:10.1109/tac.2020.3012528
75. Franović, I, Yanchuk, S, Eydam, S, Bačić, I, and Wolfrum, M. Dynamics of a Stochastic Excitable System with Slowly Adapting Feedback. Chaos (2020) 30:083109. doi:10.1063/1.5145176
76. Popovych, OV, Xenakis, MN, and Tass, PA. The Spacing Principle for Unlearning Abnormal Neuronal Synchrony. PLoS ONE (2015) 10:e0117205. doi:10.1371/journal.pone.0117205
77. Lücken, L, Popovych, OV, Tass, PA, and Yanchuk, S. Noise-enhanced Coupling between Two Oscillators with Long-Term Plasticity. Phys Rev E (2016) 93:032210. doi:10.1103/physreve.93.032210
78. Chakravartula, S, Indic, P, Sundaram, B, and Killingback, T. Emergence of Local Synchronization in Neuronal Networks with Adaptive Couplings. PLoS ONE (2017) 12:e0178975. doi:10.1371/journal.pone.0178975
79. Röhr, V, Berner, R, Lameu, EL, Popovych, OV, and Yanchuk, S. Frequency Cluster Formation and Slow Oscillations in Neural Populations with Plasticity. PLoS ONE (2019) 14:e0225094. doi:10.1371/journal.pone.0225094
80. Sakaguchi, H, and Kuramoto, Y. A Soluble Active Rotater Model Showing Phase Transitions via Mutual Entertainment. Prog Theor Phys (1986) 76:576–81. doi:10.1143/ptp.76.576
81. Madadi Asl, M, Valizadeh, A, and Tass, PA. Dendritic and Axonal Propagation Delays Determine Emergent Structures of Neuronal Networks with Plastic Synapses. Sci Rep (2017) 7:39682. doi:10.1038/srep39682
82. Madadi Asl, M, Valizadeh, A, and Tass, PA. Dendritic and Axonal Propagation Delays May Shape Neuronal Networks with Plastic Synapses. Front Physiol (2018) 9:1849. doi:10.3389/fphys.2018.01849
83. Vock, S, Berner, R, Yanchuk, S, and Schöll, E. Effect of Diluted Connectivities on Cluster Synchronization of Adaptively Coupled Oscillator Networks. Scientia Iranica D (2021) 28(3):1669.
84. Liesen, J, and Mehrmann, V. Linear Algebra. Cham: Springer (2015). doi:10.1007/978-3-319-24346-7
85. Gray, RM Toeplitz and Circulant Matrices: A Review. Found. Trends Commun. Inf. Theory, Hanover, MA, USA: Now Publishers Inc. (2006). p. 155–239.
86. Aoki, T, and Aoyagi, T. Self-organized Network of Phase Oscillators Coupled by Activity-dependent Interactions. Phys Rev E (2011) 84:066109. doi:10.1103/physreve.84.066109
87. Sun, J, Bollt, EM, and Nishikawa, T. Master Stability Functions for Coupled Nearly Identical Dynamical Systems. Europhys Lett (2009) 85:60011. doi:10.1209/0295-5075/85/60011
88. Skardal, PS, Taylor, D, and Sun, J. Optimal Synchronization of Complex Networks. Phys Rev Lett (2014) 113:144101. doi:10.1103/physrevlett.113.144101
89. Acharyya, S, and Amritkar, RE. Synchronization of Nearly Identical Dynamical Systems: Size Instability. Phys Rev E (2015) 92:052902. doi:10.1103/physreve.92.052902
90. Kromer, JA, and Tass, PA. Long-lasting Desynchronization by Decoupling Stimulation. Phys Rev Res (2020) 2:033101. doi:10.1103/physrevresearch.2.033101
91. Kromer, JA, Khaledi-Nasab, A, and Tass, PA. Impact of Number of Stimulation Sites on Long-Lasting Desynchronization Effects of Coordinated Reset Stimulation. Chaos (2020) 30:083134. doi:10.1063/5.0015196
92. Khaledi-Nasab, A, Kromer, JA, and Tass, PA. Long-Lasting Desynchronization of Plastic Neural Networks by Random Reset Stimulation. Front Physiol (2021) 11:622620. doi:10.3389/fphys.2020.622620
Keywords: synaptic plasticity, adaptive networks, phase oscillator, synchronization, distance-dependent synaptic plasticity, nonlocally coupled rings, master stability approach
Citation: Berner R and Yanchuk S (2021) Synchronization in Networks With Heterogeneous Adaptation Rules and Applications to Distance-Dependent Synaptic Plasticity. Front. Appl. Math. Stat. 7:714978. doi: 10.3389/fams.2021.714978
Received: 26 May 2021; Accepted: 21 June 2021;
Published: 15 July 2021.
Edited by:
Jun Ma, Lanzhou University of Technology, ChinaCopyright © 2021 Berner and Yanchuk. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rico Berner, cmljby5iZXJuZXJAcGh5c2lrLnR1LWJlcmxpbi5kZQ==
 Rico Berner
Rico Berner Serhiy Yanchuk
Serhiy Yanchuk