- 1Division of Mathematics, University of Dundee, Dundee, United Kingdom
- 2Department of Integrated Mathematical Oncology, H. Lee Moffitt Cancer Center and Research Institute, Tampa, FL, United States
- 3Department of Oncologic Sciences, Morsani College of Medicine, University of South Florida, Tampa, FL, United States
- 4Laboratoire Mathématiques de Besançon, Université de Bourgogne Franche-Comté, Besançon, France
The specific structure of the extracellular matrix (ECM), and in particular the density and orientation of collagen fibres, plays an important role in the evolution of solid cancers. While many experimental studies discussed the role of ECM in individual and collective cell migration, there are still unanswered questions about the impact of nonlocal cell sensing of other cells on the overall shape of tumour aggregation and its migration type. There are also unanswered questions about the migration and spread of tumour that arises at the boundary between different tissues with different collagen fibre orientations. To address these questions, in this study we develop a hybrid multi-scale model that considers the cells as individual entities and ECM as a continuous field. The numerical simulations obtained through this model match experimental observations, confirming that tumour aggregations are not moving if the ECM fibres are distributed randomly, and they only move when the ECM fibres are highly aligned. Moreover, the stationary tumour aggregations can have circular shapes or irregular shapes (with finger-like protrusions), while the moving tumour aggregations have elongate shapes (resembling to clusters, strands or files). We also show that the cell sensing radius impacts tumour shape only when there is a low ratio of fibre to non-fibre ECM components. Finally, we investigate the impact of different ECM fibre orientations corresponding to different tissues, on the overall tumour invasion of these neighbouring tissues.
Introduction
A large proportion of cancer research is currently focused on the role of tumour microenvironment on cancer progression, and in this context particular attention has been given to the interactions between the cancer cells and the extracellular matrix (ECM) and its components [1]. The ECM is composed of water, minerals, proteoglycans and fibrous proteins secreted by various cells, and these components appear in specific percentages in each organ in the body, according to the needs of the tissues [1]. Collagen is the most abundant fibrous protein in the ECM, and its importance is not only given by its role in the ECM architecture [1], but also by its role on tumour tissue stiffness, in promoting tumour metastasis and in the regulation of tumour immunity [2]. Different tissues have different levels of collagen [3]: from
Diseases can lead to a loss of orientation of collagen fibres as well, which adopt a more random distribution; this was observed, for example, in liver fibrosis [9], in heart diseases [8], or in denervated bones with reduced mechanical stress [6]. Cancer cells are also involved in the re-orientation of collagen fibres around tumours, by changing the typical tangled and disorganised collagen fibres that can be found within the stroma, towards thickened collagen fibres that are aligned perpendicularly to the boundary of the invading tumour [1, 10]. The density and orientation of collagen fibres inside the ECM plays an important role also in the evolution of cancer, as cancer cells not only move along collagen fibres [1, 10], but they also remodel the ECM through degradation [e.g., via matrix metalloproteases (MMPs)] and deposition of new matrix proteins [11], which interfere with cell-cell and cell-ECM adhesion, as well as cell polarity [1].
Despite all this wealth of information regarding the role of ECM in cancer progression, there is still a poor understanding of the roles of collagen fibre orientation on the individual and collective migration of cancer cells (and the non-local interactions between cells via these stiffened fibres), how the cells remodel the ECM, and how these complex cell-fibre interactions impact the overall tumour shape and invasion pattern. In a seminal paper, Friedl and Alexander [12] have reviewed the different mechanisms of individual and collective cancer cell migration: from single cells amoeboid and mesenchymal migration, to multicellular amoeboid and mesenchymal streaming, and various types of collective cell migration (clusters, strands, or files). Friedl and Alexander [12] also mentioned the spatially-expanding tumours that undergo growth and thus passively move by pushing the surrounding tissue. In contrast to the cancer cells that actively move in a collective manner along collagen fibres, the spatially-expanding tumours can be found within a capsule of ECM formed of aligned collagen fibres that are circularly disposed around this growing tumour. The different modes of migration are unstable and can change upon variations in cell-cell and cell-ECM adhesion [12].
While many studies [12] discuss the various types of invasion of tumour aggregations (as a result of single cell interactions with other cells or with the ECM), it is still not fully understood how cells perceive other cells further away (although it seems that they can mechanically sense and react to the presence of other cells up to 100 µm away [13]), and how this perception can impact the overall tumour shape. Moreover, it is still not fully understood how the various tissue types can impact the migration of tumour cells and tumour aggregations (as tumours can develop at the boundaries of different tissues with different characteristics).
The goal of this study is to investigate migration cell patterns in various tissues with different levels of ECM fibres and different alignment levels, as we vary: 1) cells sensing radius, 2) cell-cell and cell-ECM adhesion strengths, 3) the orientation of ECM fibres and the ratio of fibres to non-fibres ECM components, 4) the structure of the domain, with various tissue patches that have different fibre orientations. To this end, we consider a hybrid multi-scale modelling approach where cells are modeled as discrete entities while the ECM (with its two phases: fibrous and non-fibrous) is continuous. We show that this hybrid model can reproduce a variety of cell migration types (e.g., cluster, strand or files) as well as a variety of tumour shapes: circular, elongated or irregular (with finger-like protrusions). We also show that cell sensing radius has an impact on tumour shape and migration pattern only when the ratio of fibres to non-fibres ECM components is increased from lower to higher ratios. Finally, we show that the evolution of tumours that arise at the boundaries of different tissues with different fibre orientations is influenced by the directionality of these fibres.
The paper is structured as follows. In The Multi-Scale Hybrid Model section we describe the multi-scale hybrid model for cell-cell and cell-ECM interactions. In Results section we discuss variety of numerical simulations obtained with this model, as we vary the above mentioned parameters. We conclude in Summary and Discussion section with a summary and a discussion of the importance of these results.
The Multi-Scale Hybrid Model
There are two main types of models that are often used to capture the dynamics of tumour development, namely discrete and continuous models. Both have advantages and drawbacks over the other [14] and to minimise these disadvantages, recent extensive efforts have been made to combine these models into hybrid ones [15].
We employ here a hybrid modeling framework [15] that combines the off-lattice agent based model MultiCell-LF [16–18] to represent the cells, and a multi-scale continuous framework [19–23] to represent the microenvironment. To facilitate the description of this multi-scale hybrid model, let us first introduce some useful notations from both frameworks. The model is defined within a maximal tissue cube
To connect the discrete model to the continuous one, we first need to generate a cancer cell density by using the individual cell properties. For this, let us first observe that such density can be determined by using the fraction of unit space that is occupied by the cancer cells. Therefore, at any macro-scale spatio-temporal position
where
Besides the discrete cancer cell population, here, also we consider the dynamics of a continuous multi-scale two-phase ECM. Specifically, we consider a fibre ECM phase, accounting for all major fibres (for instance collagen and fibronectin) whose macro-scale density and spatial bias are denoted by
Finally, for compact notation we denote by
where u represents the global three-dimensional tumour vector
The MultiCell-LF Model
For each single cell in the MultiCell-LF (Multi-Cell Lattice-Free) model, several individually-regulated life processes are included, such as cell ageing, cell growth, cell division, cell-cell and cell-ECM interactions, and cell contact inhibition.
The Cell Cycle
The lifespan of each cell is traced with the current cell age
Cell Growth and Division
The radius
where ϕ is an angle randomly chosen from
where
Cell Contact Inhibition
Once the whole cell colony grows in size, individual cells may become overcrowded and growth-arrested due to the contact inhibition signals from the neighbouring cells. The overcrowding condition is modelled by counting the number of cells
where
When the number of neighbouring cells reaches a specified threshold
The Hybrid Cell Movement
To model cancer cell passive relocation (due to cell-cell interactions) and active migration (due to cell-ECM interactions), we combine both discrete and continuous approaches. While for cell-cell interactions (both repulsive and adhesive forces) we use the agent-based approach, the cell- ECM (both fibre-based and non-fibre adhesions) are modelled by using a continuous technique. Ultimately, these forces collectively influence the direction of motion of each individual cell, leading to complex tumour dynamics and to the emergence of various tumour morphologies.
Discrete Cell-Cell Repulsive Interactions
The repulsive forces between nearby cells are introduced to maintain cell volume and to avoid cell overlapping during its movement or division (see Cell Growth and Division). Following our previous work [17, 18], these forces are modelled as linear Hookean springs. Hence, considering two arbitrary but distinct cells
where
Discrete Cell-Cell Adhesive Interactions
The adhesive forces are activated between non-overlapping but nearby cells in order to keep the cell cluster compact. These forces are modelled using Hooke’s law with a constant spring stiffness
Similarly to the repulsive forces, each cell can be subjected to multiple adhesive forces, thus the cumulative adhesive force which acts on cell
Continuous Cell-ECM Adhesive Interactions
Besides the cell-cell interactions described above, of particular importance, are the cell-ECM adhesions [28–31] that we explore here through a cell-non-fibre ECM adhesion [32–35] as well as a cell-fibre ECM adhesion [36, 37]. In the existing literature [19–23, 38–42], this type of interaction is usually modelled by a non-local adhesion integral with a sensing region
where R represents the maximum range within which a cell
and similarly
where
where
Finally, in Eq. 5
For completeness, here we also briefly discuss the numerical approach for the cell-ECM adhesion integral
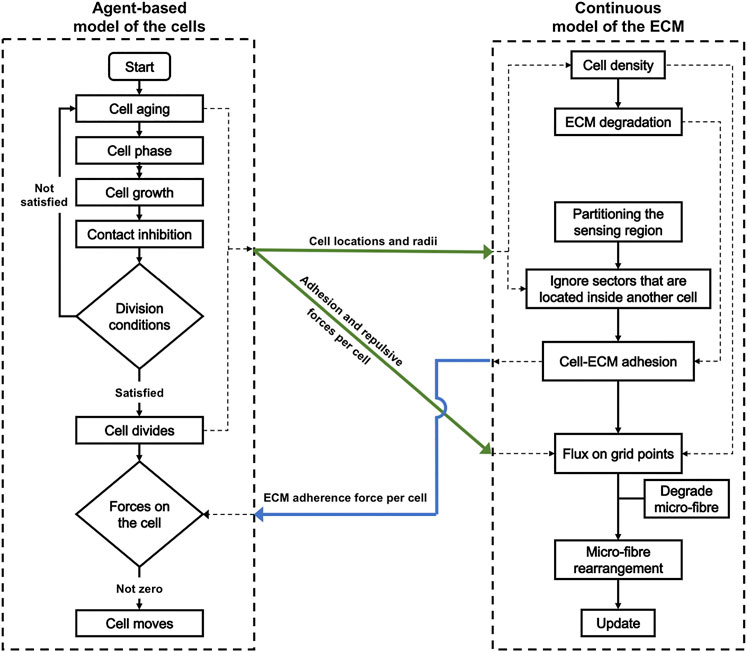
FIGURE 1. (A) Schematics of the multi-scale fibre dynamics, including the bottom-up and top-down links between the macro-scale and the fibre micro-scale (with: the green lines within
Thus, as shown in Figure 1C, the sensing region
Further, let us now denote these annulus sectors by
The Overall Direction of Cell Movement
Ultimately, the overall movement direction of a cell
where η is the damping coefficient and
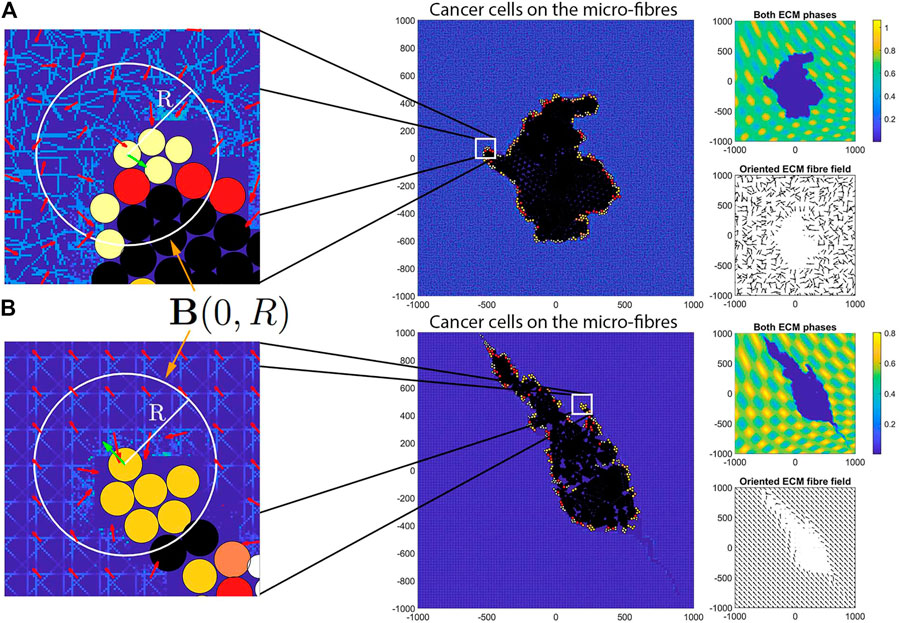
FIGURE 2. Illustration of the sensing region
The Continuous Multi-Scale ECM
Tumour development is a complex and multi-scale phenomena where the macro-scale events are accompanied by several related micro-scale processes. One of the most important of these processes is the re-distribution of the fibres ECM micro-constituents triggered by various cell-generated forces. Hence, here we first describe the macro-scale dynamics of the continuous two-phase ECM and then we detail its micro-scale dynamics.
Similarly to the cancer cell density, to achieve connection between the discrete and continuous parts of the model, we first need to appropriately approximate the generated cell forces (
where again
The Two-phase ECM
Besides the cancer cells, in this work we also take into account the dynamics of a two-phase ECM to capture not only the fibrous proteins in the fibres ECM, but also every other ECM constituents which are collected into the non-fibre ECM phase. It is well-known that MMPs are responsible for degrading the fibrous ECM proteins [43, 44], and since cancer cell do produce several types of MMPs [45, 46], here we consider the fibres ECM to be degraded by the cancer cell population at a constant rate
Here, we used the macro-scale density of the cancer cell population
Fibre Representation
Let us now focus our attention to the two macro-scale representations of the fibres ECM, namely its amount
where
In this context, the second characteristic of the fibres ECM, i.e., its amount
which in fact represents the mean-value of the micro-fibre distribution on the micro-domain
Fibre Rearrangement Process
As the individual cancer cells move and invade, they interact with the micro-fibre structure and thereby push them in the direction of travelling, ultimately resulting in the rearrangement of the micro-fibres. Following Shuttleworth and Trucu [19], here we consider this complex process to be initiated by the spatial flux of the cancer cell population
where the weight
Ultimately, the new position
where
and the amount of fibres that is reallocated from z to
which tracks the free space available at the new position
Finally, since this rearrangement process that redistributes the fibres ECM micro constituents is initiated by the macro-scale cancer cell flux
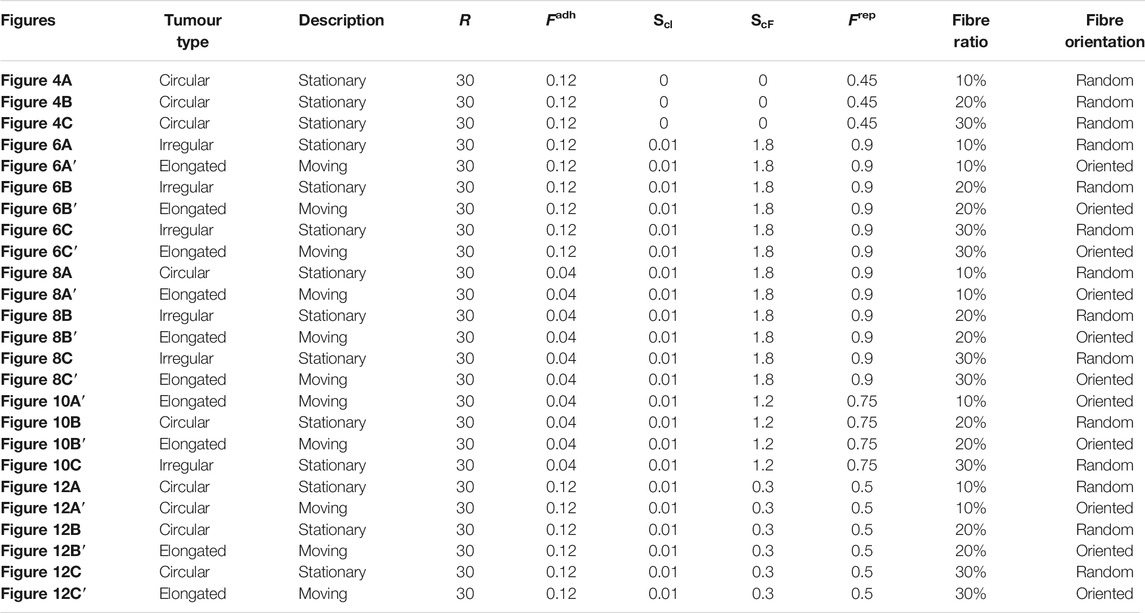
For a diagrammatic description of the full hybrid model, with the exact stages where the agent-based model of the cells connects with the continuous model of the ECM, please see Figure 15 in Appendix B.
Results
In the context of the above described multi-scale hybrid framework, here we present some numerical simulations of the model, which highlight different migration cell patterns in various tissues with different levels of ECM fibres and different alignment levels. To this end, we start each simulation with a single cancer cell with well defined properties located at a point
which can be seen in Figure 3A that is in-silico representation of the heterogeneous distribution of the non-fibre ECM. For illustrative purposes, in Figure 3 (as well as throughout the rest of this Section) we present the non-fibre ECM initial conditions only on the domain of
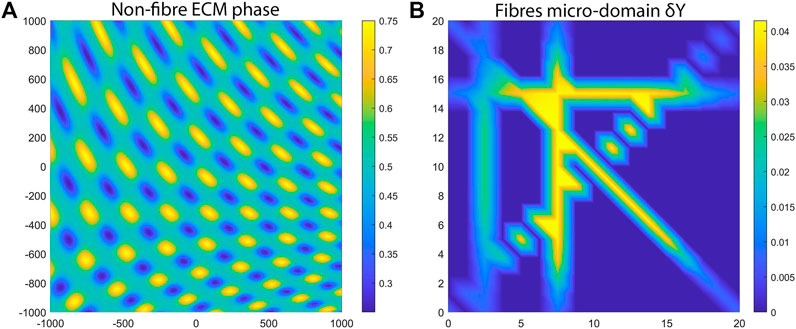
FIGURE 3. Initial ECM conditions used for the numerical simulations. (A) The macro-scale non-fibres ECM density. (B) One aligned micro-fibres domain
To shed some light on the importance of ECM characteristics on cancer invasion, throughout this section we investigate numerically the type of cancer migration and invasion patterns obtained when we consider different cell sensing radii. We note here that the sensing radius is determined not only by the length of cell membrane protrusions called pseudopodia (which have lengths greater than 2 µm [50, 51]), but also by the long-range cell sensing due to stress transmission via aligned ECM fibres (which allows cells to sense other cells up to 100 µm away [13]). Throughout this study we investigate the impact of two sensing radii,
Simulations Without Cell-ECM Adhesions in a Random Fibrous Environment
We start our numerical investigation of this hybrid multi-scale model by showing some baseline simulations for the case without cell-ECM adhesions, as we vary the fibre ECM density (i.e.,
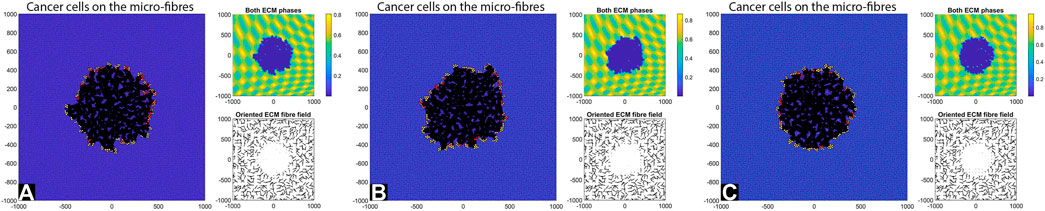
FIGURE 4. Simulation results at final time T = 28 days with random fibres, sensing radius
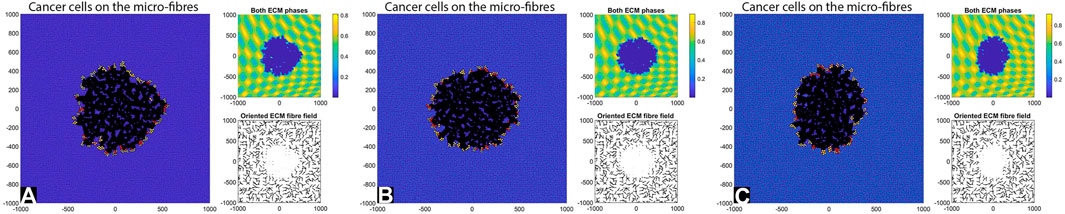
FIGURE 5. Simulation results at final time T = 28 days with random fibres, sensing radius
By comparing the numerical results in Figures 4, 5 we can conclude that in the absence of any cell-ECM adhesion, the tumour colonies have an almost circular shape, and they are stationary (i.e., they do not move through the domain). Moreover, the larger cell sensing radius does not seem to have a significant impact on tumour structure.
Simulations With Cell-ECM Adhesions in a Random Fibrous Environment
Next, we consider cell-ECM adhesion forces (
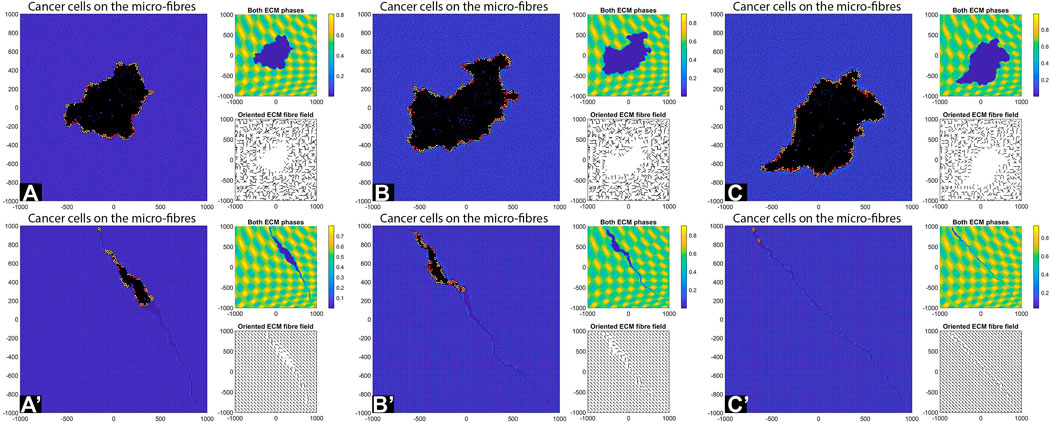
FIGURE 6. Simulation results with random and aligned fibres, sensing radius
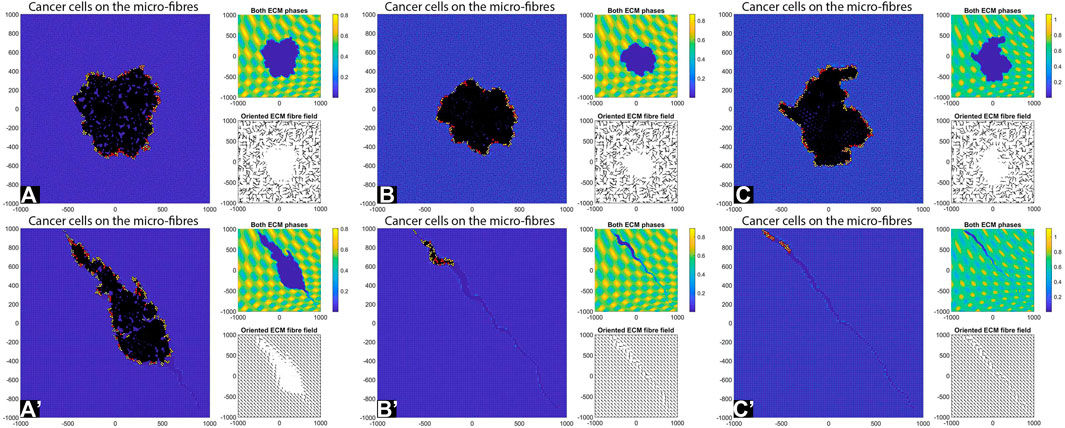
FIGURE 7. Simulation results with random and aligned fibres, sensing radius
First, we see that cell-ECM interactions can lead to irregular-shaped tumour aggregations as well as elongated tumour aggregations. The random fibres are associated with stationary cell aggregations [sub-panels (A)-(C)], while the aligned fibres are associated with moving cell aggregations [sub-panels (A’)–(C’)].
The increase in sensing region (from
Finally, the increase in cell sensing radius to
Decreasing the Cell-Cell Adhesion Strength
Previous simulations were performed with a relatively high cell-cell adhesion strength (
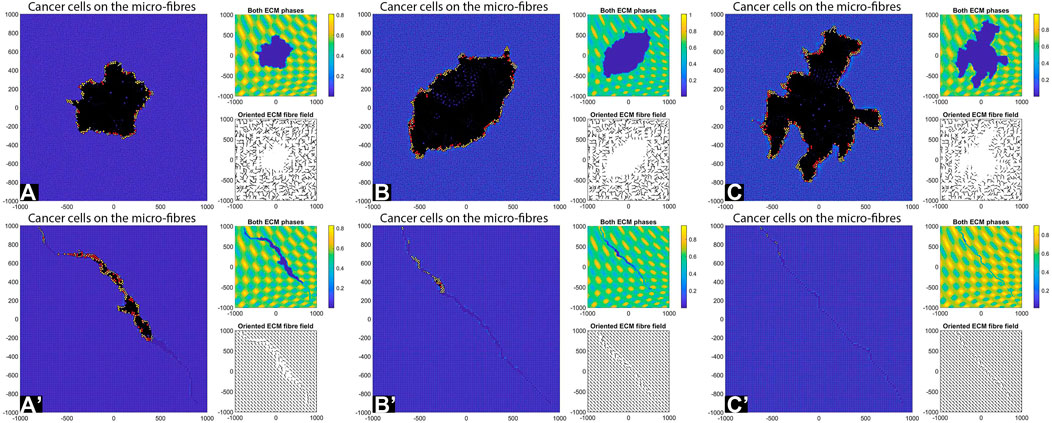
FIGURE 8. Simulation results with random and aligned fibres, sensing radius
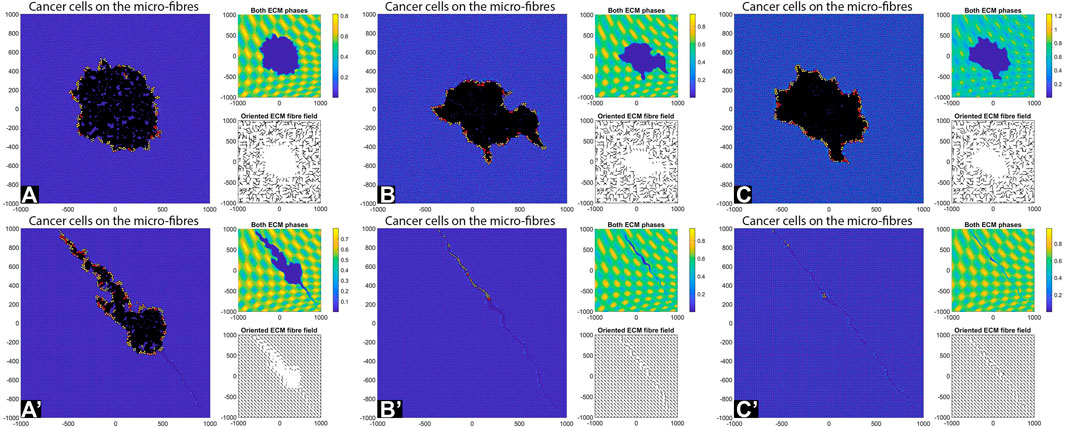
FIGURE 9. Simulation results with random and aligned fibres, sensing radius
Decreasing the Cell-Fibre ECM Adhesion Strength
Since the previous simulations had low cell-cell adhesion but high cell-fibre ECM adhesion, next we investigate tumour invasion patterns when we lower the cell-fibre adhesion strength to
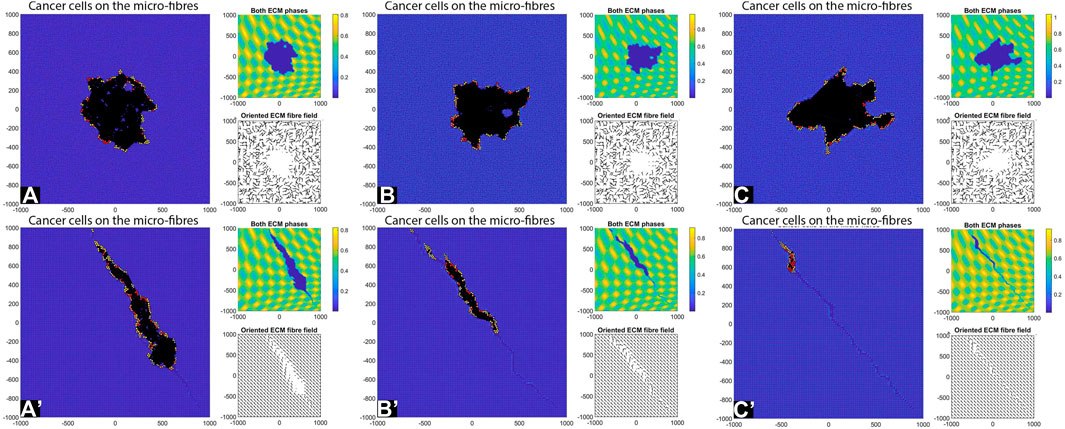
FIGURE 10. Simulation results with random and aligned fibres, sensing radius
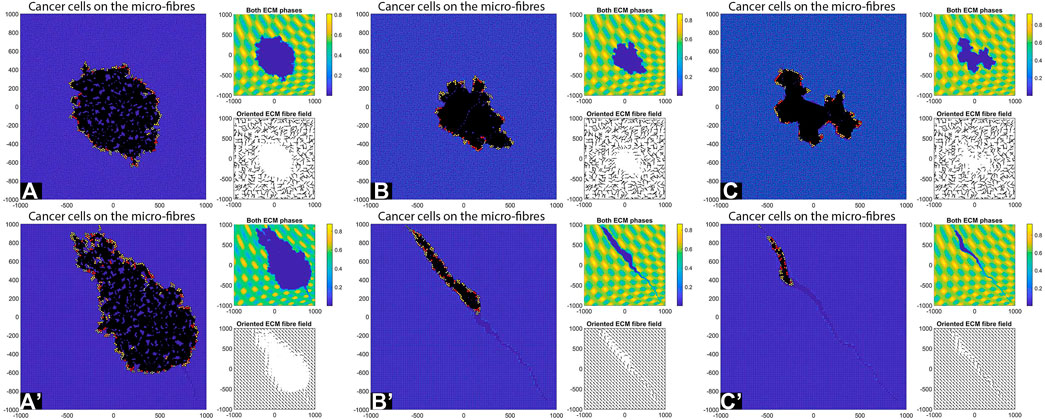
FIGURE 11. Simulation results with random and aligned fibres, sensing radius
Consider now an even lower cell-ECM adhesion strength,
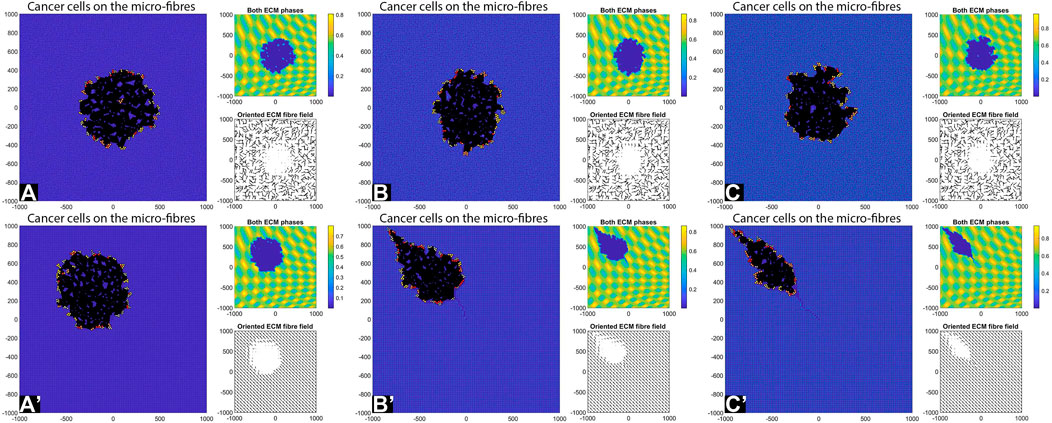
FIGURE 12. Simulation results with random and aligned fibres, sensing radius
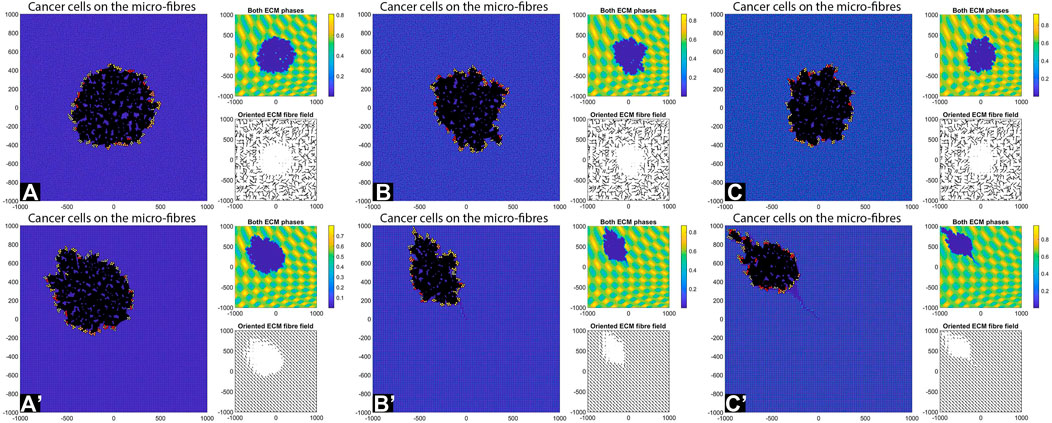
FIGURE 13. Simulation results with random and aligned fibres, sensing radius
We emphasise that the simulations in sub-panels (B’)–(C’) in the above figures were ran for shorter times, since for longer times the cells leave the domain.
Different Tissues With Different Fibre Orientations
Finally, we investigate numerically what happens with tumour shape and its invasion pattern when the ECM domain is formed of patches of random and aligned fibres, corresponding to different types of tissues (see the discussion in the Introduction). For this we start with a cluster of cells (e.g., 19 cells, for illustration purposes) instead of just one cell. Moreover, we consider here again the parameter values used for the results in Figures 6C–C′, namely:

FIGURE 14. Simulation results with different aligned fibre structures, sensing radius
The simulations in Figure 14 show that the initial position of the cluster of tumour cells, together with the ECM alignment in that region, influences the direction of migration of these cells. In sub-panels (A)–(B) the cells migrate in the direction of fibre alignment, while in sub-panel (C) the cells migrate along the boundary between two regions with opposite alignment. A similar migration pattern is observed in sub-panel (D). Finally, in sub-panels (E) and (F) we observe that when the original tumour cell cluster is positioned in an area surrounded by different ECM alignment, the tumour tends to stay in that area and to very slowly invade the neighbouring tissues (with different ECM orientations). All these different tumour invasive patterns are consistent with the experimental results in [10, 52], which showed that aligned collagen fibres perpendicular to tumour boundary are associated with tumour invasion along those fibres, and the experiments in [52] which showed that aligned collagen fibres parallel to tumour boundary impede invasion.
Summary and Discussion
The composition and structural characteristics of the extracellular matrix (ECM) are known to vary widely among different tissues [11], and this has a significant impact on the evolution of cancer. Since there is an increasing need for understanding the spatio-temporal changes in ECM and their roles in cancer progression, in this study we introduced a new multi-scale hybrid mathematical model for cell-cell and cell-ECM interactions, and used it to investigate numerically the impact of ECM fibre orientation and fibre density on cancer cell invasion patterns. To this end, we varied a number of parameters associated with the cell-cell interactions (e.g., cell sensing radius R, cell-cell adhesion stiffness
Through numerical simulations, we tested a variety of scenarios: from the impact of smaller/larger cell sensing radius on tumour aggregations, to the impact of random vs. aligned fibres on the migration and invasion of cancer cells into nearby tissues, the role of different fibre orientation in the neighbourhood of initial tumour, and the roles of cell-cell and cell-ECM strengths on the shape of solid tumours. We summarise all these numerical results in Table 1 (for the case
The results in Figure 14 suggest that if we could know the orientation of collagen fibres surrounding the tumour (which may be spanning different tissues with different ECM structures) we could predict the fast or slow evolution of the solid tumour, as well as potential cell migration directions. Since collagen can be easily visualised in standard histopathology slides through second harmonic generation microscopy [10] or via multiphoton tomography [55], such predictions on the evolution of tumours might help treatment decisions, e.g., by deciding to resect more surrounding tissue if the imaging shows collagen fibres aligned perpendicular to tumour boundary in a certain area, or by deciding to preserve more surrounding tissue if the imaging shows collagen fibres parallel to tumour boundary. Intraoperative visualisation of tumour microenvironment, including collagen alignment in resected tissues [56], could be further combined with mathematical simulations in 2D (and even in 3D, although this is expected to carry a considerably higher computational cost) to improve such treatment decisions.
Finally, our numerical simulations suggest that the sensing radius R (determined by the length of membrane protrusions called pseudopodia [50, 51], as well as by the long-range sensing due to stress transmission via aligned ECM fibres [13]) impacts the shape of tumour colonies in an aligned fibrous ECM environment with relatively low ratios of fibres to non-fibres. More precisely, when the ECM ratio of fibres to non-fibres is 10%: 90%, larger R leads to more compact tumor cell colonies (compare with the cluster invasion pattern in [12]). For higher fibres: non-fibres ratios this sensing radius has almost no impact, the tumour being extremely elongated as the cells move quickly along the collagen fibres (compare with the strands and files patterns in [12]).
Overall, this study not only confirmed some of the previous experimental results on the importance of alignement of ECM collagen fibres on tumour invasion [10, 52], but also proposed new hypotheses on the biological mechanisms involved in the shape of the tumour colonies (e.g., the roles of sensing radius vs. fibres to non-fibres ratios; the roles of sensing radius vs. cell-cell and cell-ECM mechanical forces). Moreover, this multi-scale hybrid modelling, which incorporates ECM remodelling and fibre rearrangement in the direction of cell travelling (via cell flux
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work was supported by an EPSRC UK award, EPSRC DTA EP/R513192/1, and by the National Institutes of Health, National Cancer Institute Grant NIH/NCI U01-CA202229 (to KR).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Walker, C, Mojares, E, and del Río Hernández, A. Role of Extracellular Matrix in Development and Cancer Progression. Int J Mol Sci (2018). 19:3028. doi:10.3390/ijms19103028
2. Xu, S, Xu, H, Wang, W, Li, S, Li, H, Li, T, et al. The Role of Collagen in Cancer: from Bench to Bedside. J Transl Med (2019). 17:309. doi:10.1186/s12967-019-2058-1
3. Padhi, A, and Nain, AS. ECM in Differentiation: A Review of Matrix Structure, Composition and Mechanical Properties. Ann Biomed Eng (2019). 48:1071–89. doi:10.1007/s10439-019-02337-7
4. Lin, J, Shi, Y, Men, Y, Wang, X, Ye, J, and Zhang, C. Mechanical Roles in Formation of Oriented Collagen Fibers. Tissue Eng B: Rev (2020). 26:116–28. doi:10.1089/ten.teb.2019.0243
5. Yasui, T, Tohno, Y, and Araki, T. Determination of Collagen Fiber Orientation in Human Tissue by Use of Polarisation Measurement of Molecular Second-Harmonic-Generation Light. Appl Opt (2004). 43:2861–7. doi:10.1364/ao.43.002861
6. Suda, K, Abe, K, and Kaneda, K. Changes in the Orientation of Collagen Fibers on the Superficial Layer of the Mouse Tibial Bone after Denervation. Scanning Electron Microscopic Observations. Arch Histology Cytol (1999). 62:231–5. doi:10.1679/aohc.62.231
7. Holmes, DF, Gilpin, CJ, Baldock, C, Ziese, U, Koster, AJ, and Kadler, KE. Corneal Collagen Fibril Structure in Three Dimensions: Structural Insights into Fibril Assembly, Mechanical Properties, and Tissue Organization. Proc Natl Acad Sci (2001). 98:7307–12. doi:10.1073/pnas.111150598
8. Weber, KT. Cardiac Interstitium in Health and Disease: the Fibrillar Collagen Network. J Am Coll Cardiol (1989). 13:1637–52. doi:10.1016/0735-1097(89)90360-4
9. Lin, J, Pan, S, Zheng, W, and Huang, Z. Polarization-resolved Second-Harmonic Generation Imaging for Liver Fibrosis Assessment without Labeling. Appl Phys Lett (2013). 103:173701. doi:10.1063/1.4826516
10. Conklin, MW, Eickhoff, JC, Riching, KM, Pehlke, CA, Eliceiri, KW, Provenzano, PP, et al. Aligned Collagen Is a Prognostic Signature for Survival in Human Breast Carcinoma. Am J Pathol (2011). 178:1221–32. doi:10.1016/j.ajpath.2010.11.076
11. Malandrino, A, Mak, M, Kamm, RD, and Moeendarbary, E. Complex Mechanics of the Heterogeneous Extracellular Matrix in Cancer. Extreme Mech Lett (2018). 21:25–34. doi:10.1016/j.eml.2018.02.003
12. Friedl, P, and Alexander, S. Cancer Invasion and the Microenvironment: Plasticity and Reciprocity. Cell (2011). 147:992–1009. doi:10.1016/j.cell.2011.11.016
13. Ma, X, Schickel, ME, Stevenson, MD, Sarang-Sieminski, AL, Gooch, KJ, Ghadiali, SN, et al. Fibers in the Extracellular Matrix Enable Long-Range Stress Transmission between Cells. Biophysical J (2013). 104:1410–8. doi:10.1016/j.bpj.2013.02.017
14. Schaller, G, and Meyer-Hermann, M. Continuum versus Discrete Model: a Comparison for Multicellular Tumour Spheroids. Phil Trans R Soc A (2006). 364:1443–64. doi:10.1098/rsta.2006.1780
15. Chamseddine, IM, and Rejniak, KA. Hybrid Modeling Frameworks of Tumor Development and Treatment. Wires Syst Biol Med (2020). 12:e1461. doi:10.1002/wsbm.1461
16. Kim, M, Reed, D, and Rejniak, KA. The Formation of Tight Tumor Clusters Affects the Efficacy of Cell Cycle Inhibitors: A Hybrid Model Study. J Theor Biol (2014). 352:31–50. doi:10.1016/j.jtbi.2014.02.027
17. Karolak, A, Poonja, S, and Rejniak, KA. Morphophenotypic Classification of Tumor Organoids as an Indicator of Drug Exposure and Penetration Potential. Plos Comput Biol (2019). 15:e1007214. doi:10.1371/journal.pcbi.1007214
18. Berrouet, C, Dorilas, N, Rejniak, KA, and Tuncer, N. Comparison of Drug Inhibitory Effects (IC50) in Monolayer and Spheroid Cultures. Bull Math Biol (2020). 82:68. doi:10.1007/s11538-020-00746-7
19. Shuttleworth, R, and Trucu, D. Multiscale Modelling of Fibres Dynamics and Cell Adhesion within Moving Boundary Cancer Invasion. Bull Math Biol (2019). 81:2176–219. doi:10.1007/s11538-019-00598-w
20. Shuttleworth, R, and Trucu, D. Cell-scale Degradation of Peritumoural Extracellular Matrix Fibre Network and its Role within Tissue-Scale Cancer Invasion. Bull Math Biol (2020). 82:65. doi:10.1007/s11538-020-00732-z
21. Shuttleworth, R, and Trucu, D. Multiscale Dynamics of a Heterotypic Cancer Cell Population within a Fibrous Extracellular Matrix. J Theor Biol (2020). 486:110040. doi:10.1016/j.jtbi.2019.110040
22. Suveges, S, Eftimie, R, and Trucu, D. Directionality of Macrophages Movement in Tumour Invasion: A Multiscale Moving-Boundary Approach. Bull Math Biol (2020). 82. doi:10.1007/s11538-020-00819-7
23. Suveges, S, Eftimie, R, and Trucu, D. Re-polarisation of Macrophages within a Multi-Scale Moving Boundary Tumour Invasion Model. arXiv:2103.03384 (2021). 1–50.
24. Alberts, B, Johnson, A, Lewis, J, Raff, M, Roberts, K, and Walter, P. Molecular Biology of the Cell. New York: Garland Science (2002).
25. Tyson, JJ, and Novak, B. Temporal Organization of the Cell Cycle. Curr Biol (2008). 18:R759–R768. doi:10.1016/j.cub.2008.07.001
26. Pérez-Velázquez, J, and Rejniak, KA. Drug-Induced Resistance in Micrometastases: Analysis of Spatio-Temporal Cell Lineages. Front Physiol (2020). 11:319. doi:10.3389/fphys.2020.00319
27. Cooper, G. The Cell : A Molecular Approach. Washington, D.C. Sunderland, Mass: ASM Press Sinauer Associates (2000).
28. Huda, S, Weigelin, B, Wolf, K, Tretiakov, KV, Polev, K, Wilk, G, et al. Lévy-like Movement Patterns of Metastatic Cancer Cells Revealed in Microfabricated Systems and Implicated In Vivo. Nat Commun (2018). 9:4539. doi:10.1038/s41467-018-06563-w
29. Petrie, RJ, Doyle, AD, and Yamada, KM. Random versus Directionally Persistent Cell Migration. Nat Rev Mol Cel Biol (2009). 10:538–49. doi:10.1038/nrm2729
30. Weiger, MC, Vedham, V, Stuelten, CH, Shou, K, Herrera, M, Sato, M, et al. Real-time Motion Analysis Reveals Cell Directionality as an Indicator of Breast Cancer Progression. PLOS ONE (2013). 8:e58859–12. doi:10.1371/journal.pone.0058859
31. Wu, P-H, Giri, A, Sun, SX, and Wirtz, D. Three-dimensional Cell Migration Does Not Follow a Random Walk. Proc Natl Acad Sci (2014). 111:3949–54. doi:10.1073/pnas.1318967111
32. Ghosh, S, Salot, S, Sengupta, S, Navalkar, A, Ghosh, D, Jacob, R, et al. p53 Amyloid Formation Leading to its Loss of Function: Implications in Cancer Pathogenesis. Cell Death Differ (2017). 24:1784–98. doi:10.1038/cdd.2017.105
33. Gras, SL. Surface- and Solution-Based Assembly of Amyloid Fibrils for Biomedical and Nanotechnology Applications. In: RJ Koopmans, editor. Engineering Aspects of Self-Organizing Materials. Advances in Chemical Engineering, 35. Academic Press (2009). p. 161–209. doi:10.1016/S0065-2377(08)00206-8
34. Gras, SL, Tickler, AK, Squires, AM, Devlin, GL, Horton, MA, Dobson, CM, et al. Functionalised Amyloid Fibrils for Roles in Cell Adhesion. Biomaterials (2008). 29:1553–62. doi:10.1016/j.biomaterials.2007.11.028
35. Jacob, RS, George, E, Singh, PK, Salot, S, Anoop, A, Jha, NN, et al. Cell Adhesion on Amyloid Fibrils Lacking Integrin Recognition Motif. J Biol Chem (2016). 291:5278–98. doi:10.1074/jbc.m115.678177
36. Wolf, K, Alexander, S, Schacht, V, Coussens, LM, von Andrian, UH, van Rheenen, J, et al. Collagen-based Cell Migration Models In Vitro and In Vivo. Semin Cel Develop Biol (2009). 20:931–41. doi:10.1016/j.semcdb.2009.08.005
37. Wolf, K, and Friedl, P. Extracellular Matrix Determinants of Proteolytic and Non-proteolytic Cell Migration. Trends Cel Biol (2011). 21:736–44. doi:10.1016/j.tcb.2011.09.006
38. Armstrong, NJ, Painter, KJ, and Sherratt, JA. A Continuum Approach to Modelling Cell-Cell Adhesion. J Theor Biol (2006). 243:98–113. doi:10.1016/j.jtbi.2006.05.030
39. Gerisch, A, and Chaplain, MAJ. Mathematical Modelling of Cancer Cell Invasion of Tissue: Local and Non-local Models and the Effect of Adhesion. J Theor Biol (2008). 250:684–704. doi:10.1016/j.jtbi.2007.10.026
40. Domschke, P, Trucu, D, Gerisch, A, and A. J. Chaplain, M. Mathematical Modelling of Cancer Invasion: Implications of Cell Adhesion Variability for Tumour Infiltrative Growth Patterns. J Theor Biol (2014). 361:41–60. doi:10.1016/j.jtbi.2014.07.010
41. Domschke, P, Trucu, D, Gerisch, A, and Chaplain, MAJ (2017). Structured Models of Cell Migration Incorporating Molecular Binding Processes. J. Math. Biol. 75, 1517–1561. doi:10.1007/s00285-017-1120-y
42. Peng, L, Trucu, D, Lin, P, Thompson, A, and Chaplain, MAJ. A Multiscale Mathematical Model of Tumour Invasive Growth. Bull Math Biol (2017). 79:389–429. doi:10.1007/s11538-016-0237-2
43. Nagase, H, Visse, R, and Murphy, G. Structure and Function of Matrix Metalloproteinases and TIMPs. Cardiovasc Res (2006). 69:562–73. doi:10.1016/j.cardiores.2005.12.002
44. Visse, R, and Nagase, H. Matrix Metalloproteinases and Tissue Inhibitors of Metalloproteinases. Circ Res (2003). 92:827–39. doi:10.1161/01.RES.0000070112.80711.3D
45. Hanahan, D, and Weinberg, RA. Hallmarks of Cancer: The Next Generation. Cell (2011). 144:646–74. doi:10.1016/j.cell.2011.02.013
47. Stix, B, Kähne, T, Sletten, K, Raynes, J, Roessner, A, and Röcken, C. Proteolysis of AA Amyloid Fibril Proteins by Matrix Metalloproteinases-1, -2, and -3. Am J Pathol (2001). 159:561–70. doi:10.1016/s0002-9440(10)61727-0
48. Liao, M-C, and Van Nostrand, WE. Degradation of Soluble and Fibrillar Amyloid β-Protein by Matrix Metalloproteinase (MT1-MMP) In Vitro. Biochemistry (2010). 49:1127–36. doi:10.1021/bi901994d
50. Murphy, DA, and Courtneidge, SA. The 'ins' and 'outs' of Podosomes and Invadopodia: Characteristics, Formation and Function. Nat Rev Mol Cel Biol. (2012). 12:413–26. doi:10.1038/nrm3141
51. Klemke, RL. Trespassing Cancer Cells: 'fingerprinting' Invasive Protrusions Reveals Metastatic Culprits. Curr Opin Cel Biol (2012). 24:662–9. doi:10.1016/j.ceb.2012.08.005
52. Provenzano, PP, Inman, DR, Eliceiri, KW, Trier, SM, and Keely, PJ. Contact Guidance Mediated Three-Dimensional Cell Migration Is Regulated by Rho/ROCK-dependent Matrix Reorganization. Biophysical J (2008). 95:5374–84. doi:10.1529/biophysj.108.133116
53. Han, W, Chen, S, Yuan, W, Fan, Q, Tian, J, Wang, X, et al. Oriented Collagen Fibers Direct Tumor Cell Intravasation. Proc Natl Acad Sci USA (2016). 113:11208–13. doi:10.1073/pnas.1610347113
55. Uchugonova, A, Zhao, M, Weinigel, M, Zhang, Y, Bouvet, M, Hoffman, RM, et al. Multiphoton Tomography Visualizes Collagen Fibers in the Tumor Microenvironment that Maintain Cancer-Cell anchorage and Shape. J Cel Biochem. (2013). 114:99–102. doi:10.1002/jcb.24305
56. Sun, Y, You, S, Tu, H, Spillman, DR, Chaney, EJ, Marjanovic, M, et al. Intraoperative Visualization of the Tumor Microenvironment and Quantification of Extracellular Vesicles by Label-free Nonlinear Imaging. Sci Adv (2018). 4:eaau5603. doi:10.1126/sciadv.aau5603
57. Cox, TR, and Erler, JT. Remodeling and Homeostasis of the Extracellular Matrix: Implications for Fibrotic Diseases and Cancer. Dis Models Mech (2011). 4:165–78. doi:10.1242/dmm.004077
58. Shashni, B, Ariyasu, S, Takeda, R, Suzuki, T, Shiina, S, Akimoto, K, et al. Size-based Differentiation of Cancer and normal Cells by a Particle Size Analyzer Assisted by a Cell-Recognition Pc Software. Biol Pharm Bull (2018). 41:487–503. doi:10.1248/bpb.b17-00776
59.NCI. NCI-60 Human Tumor Cell Lines Screen [internet]. on line (2015). Available from: https://dtp.cancer.gov/discovery˙_development/̵nci- ̵60/.
60. Baumgartner, W, and Drenckhahn, D. Transmembrane Cooperative Linkage in Cellular Adhesion. Eur J Cel Biol (2002). 81:161–8. doi:10.1078/0171-9335-00233
61. Rejniak, KA, and Dillon, RH. A Single Cell-Based Model of the Ductal Tumour Microarchitecture. Comput Math Methods Med (2007). 8:51–69. doi:10.1080/17486700701303143
62. Shimolina, LE, Izquierdo, MA, López-Duarte, I, Bull, JA, Shirmanova, MV, Klapshina, LG, et al. Imaging Tumor Microscopic Viscosity In Vivo Using Molecular Rotors. Sci Rep (2017). 7:41097. doi:10.1038/srep41097
Appendix A: parameter set
In Table 3 we summarise the parameter values (and parameter ranges) used throughout the numerical simulations performed in this study.
Appendix B: description of the connection between the individual-cells dynamics and continuum ecm dynamics
Keywords: cell migration, multi-scale hybrid mathematical model, agent based discrete cell-cell interactions, continuous cell-extracellular matrix interactions, orientation of extracellular matrix fibres, numerical simulations
Citation: Suveges S, Chamseddine I, Rejniak KA, Eftimie R and Trucu D (2021) Collective Cell Migration in a Fibrous Environment: A Hybrid Multiscale Modelling Approach. Front. Appl. Math. Stat. 7:680029. doi: 10.3389/fams.2021.680029
Received: 12 March 2021; Accepted: 25 May 2021;
Published: 25 June 2021.
Edited by:
Jun Ma, Lanzhou University of Technology, ChinaReviewed by:
Paul Van Liedekerke, Institut National de Recherche en Informatique et en Automatique (INRIA), FranceYang Jiao, Arizona State University, United States
Wanda Strychalski, Case Western Reserve University, United States
Copyright © 2021 Suveges, Chamseddine, Rejniak, Eftimie and Trucu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dumitru Trucu, dHJ1Y3VAbWF0aHMuZHVuZGVlLmFjLnVr
 Szabolcs Suveges1
Szabolcs Suveges1 Ibrahim Chamseddine
Ibrahim Chamseddine Katarzyna A. Rejniak
Katarzyna A. Rejniak Raluca Eftimie
Raluca Eftimie Dumitru Trucu
Dumitru Trucu