Joint Interpolation and Representation Learning for Irregularly Sampled Satellite-Derived Geophysical Fields

Earth observation satellite missions provide invaluable global observations of geophysical processes in play in the atmosphere and the oceans. Due to sensor technologies (e.g., infrared satellite sensors), atmospheric conditions (e.g., clouds and heavy rains), and satellite orbits (e.g., polar-orbiting satellites), satellite-derived observations often involve irregular space–time sampling patterns and large missing data rates. Given the current development of learning-based schemes for earth observation, the question naturally arises whether one might learn some representation of the underlying processes as well as solve interpolation issues directly from these observation datasets. In this article, we address these issues and introduce an end-to-end neural network learning scheme, which relies on an energy-based formulation of the interpolation problem. This scheme investigates different learning-based priors for the underlying geophysical field of interest. The end-to-end learning procedure jointly solves the reconstruction of gap-free fields and the training of the considered priors. Through different case studies, including observing system simulation experiments for sea surface geophysical fields, we demonstrate the relevance of the proposed framework compared with optimal interpolation and other state-of-the-art data-driven schemes. These experiments also support the relevance of energy-based representations learned to characterize the underlying processes.

1 Introduction

When dealing with spaceborne earth observation, available observation datasets do not involve gap-free and regularly gridded signals or images. The irregular sampling may result both from the characteristics of the sensors and sampling strategy, for example, considered orbits and swaths, as well as environmental conditions which may affect the sensor, for example, atmospheric conditions and clouds for earth observation. This is a critical feature to be dealt with to fully exploit the potential of available satellite-derived earth observation dataset.

A rich literature exists on interpolation for irregularly sampled signals and images (also referred to as inpainting in image processing (Bertalmio et al., 2000)). A classic framework states the interpolation issue as the minimization of an energy, which may be interpreted in a Bayesian framework. A variety of energy forms have been considered, including Markovian priors (Freeman and Liu, 2011), patch-based priors (Peyr et al., 2011), gradient norms in variational and/or PDE-based formulations (Bertalmio et al., 2000), and Gaussian priors (Galerne et al., 2011), as well as dynamical priors in fluid dynamics (Bertalmio et al., 2001). It also relates to optimal interpolation and kriging (Cressie and Wikle, 2015), which are among the state-of-the-art operational schemes in geoscience (Evensen, 2009). Optimal interpolation schemes classically involve the inference of the considered covariance-based priors from irregularly sampled data. This may however be at the expense of Gaussianity and linearity assumptions, which do not often apply for real signals and images. For the other types of energy forms, their parameterizations are generally set a priori and not learned from the data. Regarding more particularly data-driven and learning-based approaches, most previous works (Peyr et al., 2011; Alvera-Azcarate et al., 2016; Fablet et al., 2017) have addressed the learning of interpolation schemes under the assumption that a representative gap-free dataset is available. This gap-free dataset may be the image itself (Criminisi et al., 2004; Lorenzi et al., 2011; Peyr et al., 2011). For numerous application domains, as mentioned above, this assumption cannot be fulfilled. Regarding recent advances in learning-based schemes, a variety of deep learning models (e.g., Chen et al., 2015; Liu et al., 2018; Xie et al., 2012) have been proposed. Most of these works focus on learning an interpolator. One may however expect to learn not only an interpolator but also some representation of the considered data, which may be of interest for other applications. In this respect, RBM models (restricted Boltzmann machines) (Salakhutdinov and Hinton, 2009; Chen et al., 2015) are particularly appealing at the expense, however, of computationally expensive MCMC (Markov chain Monte Carlo) schemes.

In this article, we aimed to jointly learn representations of 2 days or 2 days + t processes from irregularly sampled observation datasets and solve the associated interpolation issue. Our contribution is three-fold:

• An end-to-end learning of energy-based representations from irregularly sampled training data. Based on a neural network architecture backed by a variational formulation, it jointly embeds the considered energy form and an associated interpolation scheme.

• Besides classic auto-encoder representations, we introduce neural network–based Gibbs energy representations, which relate to Gibbs priors embedded in convolutional neural networks (CNNs).

• The demonstration of the relevance of the proposed end-to-end learning framework, especially for very high missing data rates in spatiotemporal satellite-derived sea surface fields.

The remainder is organized as follows. Section 2 formally states the considered issue. We introduce the proposed end-to-end learning scheme in Section 3. We report numerical experiments in Section 4 and discuss our contribution with respect to related work in Section 5.

2 Problem Statement

In this section, we formally introduce the considered issue, namely, the end-to-end learning of representations and interpolators from irregularly sampled data. Within a classic Bayesian or an energy-based framework, interpolation issues may be stated as a minimization issue.

$\widehat{X}=\arg \underset{X}{\min }{U}_{\theta }\left(X\right)\hspace{0.17em}\text{subject to}\hspace{0.17em}{X}_{\Omega }=Y_{\Omega },(1)$

where X is the considered signal, image, or image series (referred to hereafter as the hidden state); Y the observation data, only available on a subdomain $\Omega$ of the entire domain $\mathcal{D}$; and $U_{\theta }\left(\right)$ the considered energy prior parameterized by θ. As further discussed in Section 5, a variety of energy priors have been proposed in the literature. We let the reader refer to Section 5 for a discussion of the relationships between the proposed scheme detailed below and this literature.

We assume we are provided with a series of irregularly sampled observations, that is, to say a set ${\left\{Y^{\left(i\right)},{\Omega }^{\left(i\right)}\right\}}_{i\in \left\{1,\dots ,N\right\}}$, such that ${\Omega }^{\left(i\right)}\subset \mathcal{D}$ and $Y^{\left(i\right)}$ is only defined on the subdomain ${\Omega }^{\left(i\right)}$. Assuming that all $X^{\left(i\right)}$ share some underlying energy representation $U_{\theta }\left(\right)$, we may define the following interpolation operator ${\mathrm{ℐ}}_{}$ as:

$\mathrm{ℐ}\left(U_{\theta },Y^{\left(i\right)},{\Omega }^{\left(i\right)}\right)=\arg \underset{X}{\min }{U}_{\theta }\left(X\right)\hspace{0.17em}\mathrm{s}.\text{t}.\hspace{0.17em}{X}_{{\Omega }^{\left(i\right)}}=Y_{{\Omega }^{\left(i\right)}}^{\left(i\right)}.(2)$

We expect interpolation $\mathrm{ℐ}\left(Y^{\left(i\right)},{\Omega }^{\left(i\right)}\right)$ to be close to true state $X^{\left(i\right)}$. We may consider different strategies to design interpolation operator $\mathrm{ℐ}$. For instance, with a linear–quadratic prior as used in optimal interpolation (OI) schemes, we may derive a least-square estimate. Optimal interpolation (OI) (Cressie and Wikle, 2015) amounts to minimizing an energy formulation of the form

$\widehat{X}=\text{arg}\underset{X}{\text{min}}{X}^t{\text{Σ}}_X^{-1}X+\mathrm{\lambda }{\Vert X-Y\Vert }_{\Omega }^2.(3)$

Assuming state X is a zero-mean multivariate random variable, ${\text{Σ}}_X$ is the covariance prior on state X and λ relates to the variance of the observation model. ${\Vert \cdot \Vert }_{\Omega }^2$ refers to the squared norm computed on some observed domain $\Omega$. We may point out that minimization (Eq. 1) may be restated as a similar unconstrained variational minimization using Lagrangian multipliers.

Here, we do not restrict to linear quadratic priors, and we aim to learn the parameters θ of energy $U_{\theta }\left(\right)$ from the available observation dataset ${\left\{Y^{\left(i\right)},{\Omega }^{\left(i\right)}\right\}}_i$. Assuming operator $\mathrm{ℐ}$ is known, this learning issue can be stated as the minimization of the reconstruction error for the observed data:

$\widehat{\theta }=\arg \underset{\theta }{\min }{\displaystyle \sum _i{\left|\left|Y^{\left(i\right)}-\mathrm{ℐ}\left(U_{\theta },Y^{\left(i\right)},{\Omega }^{\left(i\right)}\right)\right|\right|}_{{\Omega }^{\left(i\right)}}^2},(4)$

where ${\Vert \cdot \Vert }_{\Omega }^2$ refers to the L2 norm evaluated on the subdomain $\Omega$.

Given this general formulation, the end-to-end learning issue comes to solve minimization (Eq. 4) according to some given parameterization of energy $U_{\theta }\left(\right)$. In Eq. 4, interpolation operator $\mathrm{ℐ}$ is clearly critical. In Section 3, we investigate a neural network implementation of this general framework, which embeds neural network formulations both for energy $U_{\theta }\left(\right)$ and interpolation operator $\mathrm{ℐ}$.

3 Proposed End-To-End Learning Framework

In this section, we detail the proposed neural network–based implementation of the end-to-end formulation introduced in the previous section. We first present the considered paramaterizations for energy $U_{\theta }\left(\right)$ in Eq. 4 (Section 3.1). We derive the associated NN-based interpolation operator $\mathrm{ℐ}$ (Section 3.2) and describe the resulting NN architecture for the end-to-end learning of representations and interpolators from irregularly sampled datasets (Section 3.3).

3.1 NN-Based Energy Formulation

We first investigate NN-based energy representations based on auto-encoders (LeCun et al., 2015). Let us denote the encoding and decoding operators of an auto-encoder (AE) by ${\varphi }_E$ and ${\varphi }_D$, respectively, which may comprise both dense auto-encoders and convolutional AEs, as well as recurrent AEs, when dealing with time-related processes. The key feature of AEs is that the encoding operator ${\varphi }_E$ maps state X into a lower-dimensional space. Auto-encoders are naturally associated with the following energy:

$U_{\theta }\left(X\right)={\Vert X-{\varphi }_D\left({\varphi }_E\left(X\right)\right)\Vert }^2.(5)$

Minimizing (Eq. 1) according to this energy amounts to retrieving state X whose low-dimensional representation in the encoding space matches the observed data in the original decoded space. Here, parameters θ comprise the parameters of the encoder ${\varphi }_E$ and of the decoder ${\varphi }_D$, respectively, ${\theta }_E$ and ${\theta }_D$.

The mapping to a lower-dimensional space may be regarded as a likely loss in the representation potential. Gibbs models provide an appealing framework for an alternative energy-based representation, with no such dimensionality reduction constraint. Gibbs models introduced in statistical physics have also been widely explored in computer vision and pattern recognition (Geman, 1990) from the 80s. Gibbs models relate to the decomposition of $U_{\theta }$ as a sum of potential $U_{\theta }\left(X\right)={\displaystyle {\sum }_{c\in \mathcal{C}}{V}_c\left(X_c\right)}$, where $\mathcal{C}$ is a set of cliques, that is, a set of interacting sites (typically, local neighbors), and $V_c$ the potential on clique c. In statistical physics, this formulation states the global energy of the system as the sum of local energies (the potential over locally interacting sites). Here, we focus on the following parameterization of the potential function:

$U_{\theta }\left(X\right)={\displaystyle \sum _{s\in \mathcal{D}}{\Vert X_s-\psi \left(X_{{\mathcal{N}}_s}\right)\Vert }^2},(6)$

where ${\mathcal{N}}_s$ is the set of neighbors of site s for the entire domain $\mathcal{D}$ and ψ is a potential function. Low-energy states for this energy refer to state X for which operator ψ provides a good prediction at any site s given the neighborhood ${\mathcal{N}}_s$ of s. This type of Gibbs energy relates to Gaussian Markov random fields, where the conditional likelihood at one site given its neighborhood follows a Gaussian distribution. They also relate to fields of experts considered in Roth and Black (2009).

We implement this type of Gibbs energy using the following NN-based parameterization of operator ψ:

$\psi \left(X\right)={\psi }_2\left({\psi }_1\left(X\right)\right).(7)$

It involves the composition of a space and/or time convolutional operator ${\psi }_1$ and a coordinate-wise operator ${\psi }_2$. The convolutional kernel for operator ${\psi }_1$ is such that the coefficients for the center of the convolutional window are set to zero. This property fulfills the constraint that $X_s$, that is, X at site s, is not involved in the computation of $\psi \left(X_{{\mathcal{N}}_s}\right)$, with $X_{{\mathcal{N}}_s}$ being the restriction of the field X to the neighborhood ${\mathcal{N}}_s$ of site s. As an example, for a univariate 2 day field, ${\psi }_1$ can be set as a convolutional layer with $N_F$ filters with kernels of size $\left(2K+1\right)\times \left(2K+1\right)\times 1$ such that for each kernel $K_f$, we impose $K_f\left(K,K,0\right)=0$. In such a case, operator ${\psi }_2$ would be a convolution layer with one filter with a kernel of size 1x1x$N_F$. Both ${\psi }_1$ and ${\psi }_2$ can also involve nonlinear activations. Without loss of generality, given this parameterization for operator ψ, we may rewrite energy $U_{\theta }$ as $U_{\theta }\left(X\right)={\left|\left|X-\psi \left(X\right)\right|\right|}^2$, where $\psi \left(X\right)$ at site s is given by $\psi \left(X_{{\mathcal{N}}_s}\right)$.

Overall, we may use the following common formulation for the two types of energy-based representations:

$U_{\theta }\left(X\right)={\left|\left|X-\psi \left(X\right)\right|\right|}^2.(8)$

They differ in the parameterization chosen for operator ψ and in the associated assumption on some underlying lower-dimensional space or manifold which describes the considered state X.

3.2 NN-Based Interpolator

Besides the NN-based energy formulation, the general formulation stated in Eq. 4 involves the definition of interpolation operator $\mathrm{ℐ}$, which refers to minimization (Eq. 1). We here derive NN-based interpolation architectures from the considered NN-based energy parameterization.

Given parameterization (Eq. 8), a simple fixed-point algorithm may be considered to solve for (Eq. 4). This algorithm is at the basis of DINEOF algorithm and matrix completion under subspace constraints (Alvera-Azcarate et al., 2016; Jain et al., 2013). Given some dictionary-based representation, including, for instance, principal component analysis (PCA), also referred to as empirical orthogonal function (EOF) in geoscience, and low-rank decomposition, these approaches iteratively apply projections onto the considered dictionary-based representation. Here, the projection of a given state X is given by $\psi \left(X^{\left(k\right)}\right)$. For instance, for a PCA decomposition, it comes to $\psi \left(X^{\left(k\right)}\right)=A^t\cdot A\cdot X$ with A the projection matrix formed by the eigenvectors of the PCA as used in DINEOF algorithms (Alvera-Azcarate et al., 2016). Overall, the resulting projection-based iterative update comes to

$\begin{array}{l}{X}_p^{\left(k+1\right)}=\psi \left(X^{\left(k\right)}\right),\\ X^{\left(k+1\right)}\left(\Omega \right)=Y\left(\Omega \right),\\ X^{\left(k+1\right)}\left(\overline{\Omega }\right)=X_p^{\left(k+1\right)}\left(\overline{\Omega }\right).\end{array}(9)$

Interestingly, this algorithm is parameter free and can be readily implemented in an NN architecture, given the number of iterations to be considered. We may point out that a similar end-to-end architecture has also been proposed in Barth et al. (2020).

Given some initialization, one may also consider an iterative gradient-based descent which applies at each iteration k

$\begin{array}{ccc}{X}_p^{\left(k+1\right)}& =& X^{\left(k\right)}-\lambda J_{U_{\theta }}\left(X^{\left(k\right)}\right)\\ X^{\left(k+1\right)}(\Omega )& =& Y(\Omega )\\ X^{\left(k+1\right)}\left(\overline{\Omega }\right)& =& X_p^{\left(k+1\right)}\left(\overline{\Omega }\right)\end{array}.(10)$

where $J_{U_{\theta }}$ is the gradient of energy $U_{\theta }$ with respect to state X, λ the gradient step, and $\overline{\Omega }$ the missing data area. Automatic differentiation tools embedded in neural network frameworks may provide the numerical computation for gradient $J_{U_{\theta }}$, given the NN-based parameterization for energy $U_{\theta }$. This may prove numerically expensive and was not further investigated in this work. Given the considered form for energy $U_{\theta }$, its gradient with respect to X decomposes as a product

$J_{U_{\theta }}\left(X\right)=J_{\psi }\left(X\right)\left(X-\psi \left(X\right)\right),(11)$

and $X-\psi \left(X\right)$ may be regarded as a suboptimal gradient descent. Hence, rather than considering the true Jacobian $J_{\psi }$ for operator ψ, we may consider an approximation through a trainable network $G\left(\right)$ such that the gradient descent becomes

$\begin{array}{l}{X}_p^{\left(k+1\right)}=X^{\left(k\right)}-G\left(X^{\left(k\right)},\psi \left(X^{\left(k\right)}\right)\right),\\ X^{\left(k+1\right)}\left(\Omega \right)=Y\left(\Omega \right),\\ X^{\left(k+1\right)}\left(\overline{\Omega }\right)=X_p^{\left(k+1\right)}\left(\overline{\Omega }\right).\end{array}(12)$

Here, $G\left(X^{\left(k\right)},\psi \left(X^{\left(k\right)}\right)\right)=\tilde{G}\left(X^{\left(k\right)}-\psi \left(X^{\left(k\right)}\right)\right)$, and $\tilde{G}$ is a neural network to be learned jointly to ψ during the learning stage. Interestingly, this gradient descent embeds the fixed-point algorithm when $\tilde{G}$ is the identity.

Let us denote, respectively, by ${\mathrm{ℐ}}_{FP}$ and ${\mathrm{ℐ}}_G$ the fixed-point and gradient-based NN-based interpolators, which implement $N_I$ iterations of the proposed interpolation updates. Below, ${\mathrm{ℐ}}_{NN}$ will denote both ${\mathrm{ℐ}}_{FP}$ and ${\mathrm{ℐ}}_G$. Whereas ${\mathrm{ℐ}}_{FP}$ is parameter free, ${\mathrm{ℐ}}_G$ involves the parameterization of operator G. We typically consider a CNN with ReLu activations with increasing numbers of filters through layers up to the final layer, which applies to a linear convolution with a number of filters given by the dimension of state X.

3.3 End-To-End Architecture and Implementation Details

Given the parameterizations for energy $U_{\theta }$ and the associated NN-based interpolators presented previously, we design an end-to-end learning for energy representation $U_{\theta }$ and associated interpolator ${\mathrm{ℐ}}_{NN}$. It uses as inputs an observed sample $Y^{\left(i\right)}$ and the associated missing data-free domain ${\Omega }^{\left(i\right)}$. Using a normalization preprocessing step, we initially fill missing data with zeros to provide an initial interpolated state to the architecture. We provide a sketch of the architecture in Figure 1. As illustrated, this architecture applies a number of elementary blocks $B_{\psi ,G}$, with each block corresponding to one iterative update using either fixed-point update (Eq. 9) or gradient-based update (Eq. 12). Each block uses as input the output of the previous block along with the missing data mask $\Omega$. The number of blocks $N_I$ refers to the number of iterations of the considered iterative solver.

FIGURE 1

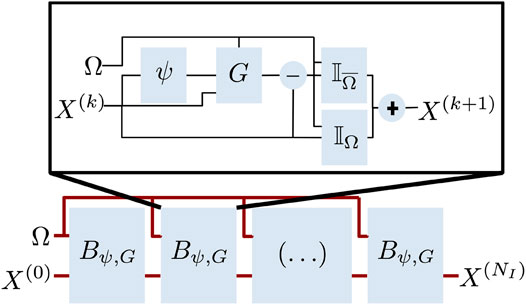
FIGURE 1. Sketch of the considered end-to-end architecture: We depict the considered $N_I$-block architecture which implements a $N_I$-step interpolation algorithm described in Section 3.2. Each block $B_{\psi ,G}$ refers to iterative fixed-point update (Eq. 9) or gradient-based update (Eq. 12). Operator ψ is defined through energy representation (Eq. 8), and G refers to the NN-based approximation of the gradient-based update for considered iterative update. This architecture uses as input a mask $\Omega$ corresponding to the missing data-free domain and an initial gap-filling $X^{\left(0\right)}$ for state X. We typically initially fill missing data with zeros for centered and normalized states.

Regarding implementation details, beyond the design of the architectures, which may be application dependent for operators ψ and G (see Section 4), we consider an implementation under tensor flow/Keras. Regarding the training strategy, we use Adam optimizer. We iteratively increase the number of blocks $N_I$ to avoid the training to diverge. Similarly, we decrease the learning rate across iterations, typically from 1e-3 to 1e-6 every 50 epochs. In our experiments, we typically consider from 5 to 15 blocks. The batch size is typically set according to the available RAM on the considered GPU. We refer the reader to our Keras implementation available online, which provides the details of the considered experimental setting. Regarding computational complexity issues, the complexity of the end-to-end architecture mainly depends on the neural network parameterization of operator ψ. A typical training phase with several hundreds of epochs typically lasts a few hours using an NVIDIA V100 GPU for the considered space–time case studies.

4 Experiments

In this section, we report numerical experiments on different datasets to evaluate and demonstrate the relevance of the proposed scheme. We first report numerical experiments on a simple synthetic 2D case study using MNIST data to gain insights on the different key components of the proposed framework. We then consider two observing system simulation experiments (OSSEs) corresponding to realistic sampling patterns for satellite-derived sea surface geophysical fields, namely, sea surface temperature (SST) derived from infrared satellite sensors and sea surface height (SSH) derived from narrow-swath and wide-swath satellite altimeters. In all experiments, we refer to the AE-based frameworks, respectively, as FP(d)-ConvAE and G(d)-ConvAE using the fixed-point or gradient-based interpolator, where d refers to the number of blocks ${\mathrm{ℬ}}_{\Psi ,G}$ in Figure 1, that is, the number of iterative updates of the considered interpolation procedures (see Section 3.2 for more details). Similarly, we refer to the Gibbs-based frameworks, respectively, as FP(d)-GENN and G(d)-GENN.

As evaluation metrics, we consider the reconstruction score computed over the observation domain, referred to as the R-score.

$R-\text{score}=1-\frac{1}{N{\sigma }^2}{\displaystyle \sum _i\frac{1}{\left|{\Omega }_i\right|}{\displaystyle \sum _{s\in {\Omega }_i}{\left(X_{i,s}^{true}-X_{i,s}\right)}^2}},$

where $X_{i,s}$ is the interpolated state for the $i^{th}$ sample at site s, $X_{i,s}^{true}$ is the associated groundtruthed state at site s, N is the total number of samples, ${\Omega }_i$ is the subset of observed sites in domain $\mathcal{D}$ for the $i^{th}$ sample, and σ is the pixel-level variance of the considered dataset. Similarly, we define an interpolation score, referred to as I-score, which evaluate the reconstruction performance for gaps

$\text{I}-\text{score}=1-\frac{1}{N{\sigma }^2}{\displaystyle \sum _i\frac{1}{\left|{\overline{\Omega }}_i\right|}{\displaystyle \sum _{s\in {\overline{\Omega }}_i}{\left(X_{i,s}^{true}-X_{i,s}\right)}^2}.}$

We also evaluate the quality of the trained representation ψ through the AE-score defined as

$\text{AE}-\text{score}=1-\frac{1}{N{\sigma }^2}N{\displaystyle \sum _i\frac{1}{\left|\mathcal{D}\right|}{\displaystyle \sum _{s\in \mathcal{D}}{\left(X_{i,s}^{true}-\psi \left(X_i^{true}\left(s\right)\right)\right)}^2}}.$

When considering the training scheme which only relies on observation data, that is, we never exploit the gap-free dataset during the training stage, we may compute these metrics both for the training and test datasets.

4.1 MNIST Case Study

We evaluate the proposed framework on MNIST dataset for which we simulate missing data patterns. MNIST dataset provides a dataset of 28 × 28 grayscale images of digits, which make it well suited for evaluation purposes. For this dataset, we only evaluate the AE-based setting. We consider the following convolutional AE architecture with a 20-dimensional encoding space:

• Encoder operator ${\varphi }_E$: Conv2D (20)+ ReLU + AvPooling + Conv2D (40) + ReLU + AveragePooling + Dense (80) + ReLU + Dense (20);

• Decoder operator ${\varphi }_E$: Conv2DTranspose (40) + ResNet + ResNet; where, ResNet is a simple residual network (He et al., 2016) with the following residual unit Conv2D (40) + ReLU + Conv2D (20).

This parameterization was selected from experiments on gap-free data to check that the resulting 20-dimensional representation accounts for more than 90% of the total variance of the MNIST test dataset. We noted experimentally that the training and interpolation performance did not vary a lot when modifying the parameteriration of the hidden layers of the encoder and decoder. In these experiments, we consider a batch size of 256. We used the reference training and test MNIST datasets. The training phase involved 100 epochs.

We generate random missing data patterns composed of $N_S$ squares of size $W_S\times W_S$, where the center of the square is randomly sampled uniformly over the image grid. As illustrated in Figure 2, we consider four missing data patterns: $N_S=20$ and $W_S=5$, $N_S=30$ and $W_S=5$, $N_S=3$ and $W_S=9$, and$N_S=6$ and $W_S=9$. To illustrate the considered training procedure, we report in Supplementary Appendix an example of plot of the training loss computed for the training and test datasets as a function of the number of epochs for FP(15)-ConvAE architecture and the missing data pattern $N_S=3$ and $W_S=9$.

FIGURE 2

FIGURE 2. Illustration of the considered MNIST dataset with the selected missing data patterns: We randomly remove data from N$W\times W$ square areas.

As mentioned above, we evaluate as performance measures an interpolation score (I-score), a global reconstruction score (R-score) for the interpolated images, and an auto-encoding (AE-score) score of the trained auto-encoder applied to gap-free data, in terms of explained variance. We also evaluate a classification score (C-score), in terms of mean accuracy, using the 20-dimensional encoding space as feature space for classification with a 3-layer multilayer perceptron (MLP). The results are consistent across the different missing data configurations. We report the performance measures for the test dataset in Table 1 for $N_S=3$ and $W_S=9$, and in Supplementary Appendix: detailed results for the MNIST dataset for the three other ones.

TABLE 1

TABLE 1. Performance of AE schemes in the presence of missing data for the MNIST dataset: for a given convolutional AE architecture (see main text for details), the EOF and ConvAE models trained on gap-free data with a 15-iteration projection-based interpolation (resp., DINEOF and DINConvAE); a zero-filling strategy with the same ConvAE architecture, which can be regarded as an instance of the proposed scheme with a fixed-point solver using only one iteration (FP(1)-ConvAE); and the fixed-point and gradient-based versions of the proposed scheme. For each experiment, we evaluate four measures: the mean of the reconstruction performance for the known image areas (R-score), the interpolation performance for the missing data areas (I-score), the reconstruction performance of the trained AE when applied to gap-free images (AE score), and the classification score of a multilayer perceptron (MLP) classifier trained in the trained latent space for training images involving missing data. The metrics are evaluated for both the training dataset (first row of each model) and the test dataset (second row; numbers in parentheses). We report here the results for missing patterns with 3 9 × 9 missing data areas ($N_S=3$ and $W=9$). R-score, I-score, and AE-score values are given as percentage of explained variance. The results for the other missing data patterns are reported in Supplementary Table S1.

With a view to illustrating the training pattern of the considered end-to-end learning approach for the MNIST dataset, we display in Figure 3 the training loss and the I-score as a function of the number of epochs for a FP-ConvAE architecture and the missing data pattern given by $N_S=3$ and $W_S=9$. At epoch 12, we increase the number of fixed-point iterations from 1 to 5, which leads to an abrupt decrease of the I-score, which may also be observed in the training loss. By contrast, the increase from 5 to 10 fixed-point iterations at epoch 40 leads to a much smaller improvement: here only a few percent. The same occurs with the increase from 10 to 15 fixed-point iterations with an improvement below 1%. We noticed experimentally that increasing the number of fixed-point iterations may result in numerical instabilities, leading the training procedure to diverge if the learning rate is not appropriately set.

FIGURE 3

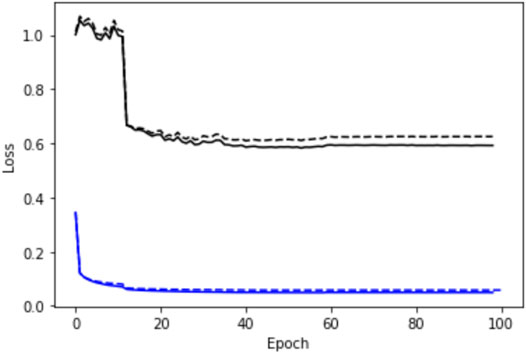
FIGURE 3. Illustration of the training pattern of the proposed end-to-end learning scheme: We plot the evolution of the training loss (blue) for the training (-) and the test (–) datasets as a function of the number of training epochs for a FP-ConvAE architecture and the MNIST dataset with three randomly sampled $9\times 9$ gaps. We also plot the evolution of the I-score (black). We increase the number of fixed-point iterations from one to five at epoch 12 and from five to 10 at iteration 40 and from 10 to 15 at iteration 80.

For benchmarking purposes, we also report the performance of the DINEOF framework (Alvera-Azcarate et al., 2016; Ping et al., 2016), which uses a 20-dimensional EOF trained on the gap-free dataset; the auto-encoder architecture (ConvAE) also trained on a gap-free dataset, and the considered convolutional auto-encoder trained using an initial zero filling for missing data areas and a training loss computed only of observed data areas. The latter can be regarded as a FP(1)-ConvAE architecture using a single fixed-point block in Figure 1. Overall, for $N_S=3$ and $W_S=9$, we retrieve the best interpolation and reconstruction performance (e.g., best I-score up to 44.1% for the test dataset) using the proposed end-to-end learning framework. By contrast, auto-encoder representations trained on gap-free data and used as a plug-and-play prior in fixed-point iterative interpolation scheme lead to significantly worse performance (resp. I-score of -44.8 and 1.2% using an EOF decomposition and the proposed ConvAE auto-encoder). We also report a gain of more than 40% in the interpolation score with respect to a straightforward zero-filling strategy combined with the considered auto-encoder architecture. Regarding the comparison between the fixed-point and gradient-based architectures, we report relatively similar performance, with slightly better I-scores for the fixed-point setting and R-scores for the gradient-based one. Interpolation examples reported in Figure 4 are in line with these quantitative results.

FIGURE 4

FIGURE 4. Illustration of reconstruction results for MNIST examples: For each panel, the first column refers to zero-ConvAE results and the second one to FP(15)-ConvAE. The first row depicts the reference image, the second row themissing datamask, and the third one the interpolated image. The first two panels illustrate interpolation results for training data and the last two for test data. We depict grayscale amid images using false colors to highlight differences.

In terms of representation power, the auto-encoder representations learned with missing data reach a representation score above 90%, which is only slightly below the score of the same architecture trained from gap-free data (AE scores of 91.0 vs. 92.3%). Similar conclusions can be drawn from the other missing data patterns as detailed in Supplementary Appendix: detailed results for the MNIST dataset. Overall, the proposed scheme guarantees a good representation in terms of AE score with an additional gain in terms of interpolation performance, typically between $\approx$ 15 and 30%, depending on the missing data patterns, with the gain being greater when considering larger missing data areas. Interestingly, the representation scores of the auto-encoders trained with missing data do not vary a lot.

4.2 Sea Surface Temperature (SST) Case Study

The second case study addresses satellite-derived sea surface temperature (SST) fields. Given their relatively high sampling in space and time, SST data play a key role in the analysis and reconstruction of upper ocean dynamics. Due to the sensitivity of high-resolution SST sensors to the cloud cover, SST datasets issued from infrared sensors may involve large missing data rates (typically, between 70 and 90%, see the second row of Figures 5, 6 for an illustration). For evaluation purposes, we consider an OSSE to build a groundtruthed dataset from high-resolution numerical simulations, namely, NATL60 data (Molines, 2018) and real cloud masks from the METOP AVHRR sensor (Ouala et al., 2018). We consider series of 128 × 512 images over eleven consecutive days from June to August at a 0.05 resolution in an open ocean region in the North East Atlantic from (40.58°N, 46.3°W) to (53.04°N, 16.18°W). Overall, we randomly sample 400 128 × 512 × 11 image series as training data and 150 as the test dataset.

FIGURE 5

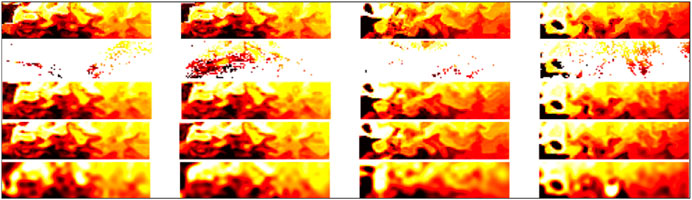
FIGURE 5. Interpolation examples for SST data used during training: the first row, reference SST images corresponding to the center of the considered 11-day time window; the second row, associated SST observations with missing data; the third row, interpolation issued from the FP(15)-GENN₂ model; and the last row, reconstruction of the gap-free image series issued from the FP(15)-GENN₂ model; interpolation issued from an OI scheme using a Gaussian covariance model with empirically tuned parameters.

FIGURE 6

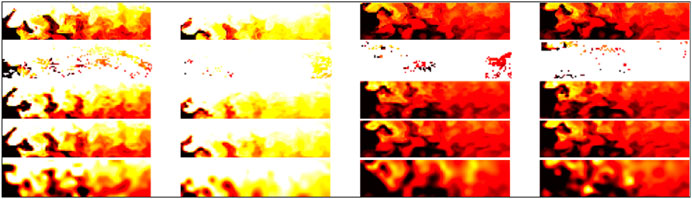
FIGURE 6. Interpolation examples for SST data never seen during training: the first row, reference SST images corresponding to the center of the considered 11 day time window; the second row, associated SST observations with missing data; the third row, interpolation issued from the FP(15)-GENN₂ model; and the last row, reconstruction of the gap-free image series issued from the FP(15)-GENN₂ model; interpolation issued from an OI scheme using a Gaussian covariance model with empirically tuned parameters.

For this case study, we consider the following four architectures for the AEs and the GENNs:

• ConvAE₁: The first convolutional auto-encoder involves the following encoder architecture: five consecutive blocks with a Conv2D layer, a ReLu layer, and a 2 × 2 average pooling layer: the first one with 20 filters, the following four ones with 40 filters, and a final linear convolutional layer with 20 filters. The output of the encoder is 4 × 16 × 20. The decoder involves a Conv2DTranspose layer with ReLu activation for an initial 16 × 16 upsampling stage, a Conv2DTranspose layer with ReLu activation for an additional 2 × 2 upsampling stage, a Conv2D layer with 16 filters, and a last Conv2D layer with 5 filters. All Conv2D layers use 3 × 3 kernels. Overall, this model involves $\approx$ 400,000 parameters.

• ConvAE₂: We consider a more complex auto-encoder with an architecture similar to ConvAE_1, where the number of filters is doubled (e.g., the output of the encoder is a 4 × 16 × 40 tensor). Overall, this model involves $\approx$ 900,000 parameters.

• GENN_1,2: We consider two GENN architectures. They share the same global architecture with an initial 4 × 4 average pooling, a Conv2D layer with ReLu activation with a zero-weight constraint on the center of the convolution window, a 1 × 1 Conv2D layer with N filters, a ResNet with a bilinear residual unit composed of an initial mapping to an initial 32 × 128x (5*N) space with a Conv2D + ReLu layer, a linear 1 × 1 Conv2D + ReLu layer with N filters, and a final 4 × 4 Conv2DTranspose layer with a linear activation for an upsampling to the input shape. GENN₁ and GENN₂ differ in the convolutional parameters of the first Conv2D layers and in the number of residual units. GENN₁ involves 5 × 5 kernels, $N=20$ and three residual units for a total of $\approx$ 30,000 parameters. For GENN₂, we consider 11 × 11 kernels, $N=100$ and 10 residual units for a total of $\approx$ 570,000 parameters.

These different parameterizations were selected so that ConvAE₁ and GENN₂ involve similar modeling complexities. Empirically, we noted that GENN architectures were more relevant when applied on a subsampled version of the SST fields. As such, the considered architecture for operator ψ involves an initial average pooling layer to subsample the spatial domain by a factor of four and a final upsampling block so that the output shape is the same size as the input shape. The application of GENNs to the finest resolution showed a lower performance. This is regarded as an illustration of the requirement for considering a scale-selection problem when applying a given prior. The upsampling block involves the combination of a Conv2DTranspose layer with 11 filters, a Conv2D layer with ReLu activation with 22 filters, and a linear Conv2D layer with 11 filters. Regarding the training procedure, we considered a batch size of 4, 400 epochs and an early stopping criterion to select the best performance on the training dataset. For benchmarking purposes, we proceed similar to the MNIST case study. As OI is the most widely applied interpolation method in geoscience, we include an OI with a Gaussian covariance model tuned using cross-validation.

Similar to the MNIST dataset, we report the performance of the different models in terms of interpolation score (I-score), reconstruction score (R-score), and the auto-encoding score (AE-score) both for the training and the test dataset. As for a given type of architecture for operator $\Phi$ (e.g., EOF vs. ConvAE vs. GENN), the different parameterizations lead to similar results, we only report in Table 2 the performance for the parameterization leading to the best interpolation scores. The detailed version of these results are included in Supplementary Appendix. Overall, the NN models clearly outperform the EOF-based scheme in terms of interpolation and reconstruction scores close to 80% when the EOF-based scheme reaches a score below 35%. GENN and ConvAE models retrieve relatively similar reconstruction scores (e.g., I-score of 89.2 vs. 88%). We might however notice that GENN schemes involve a much lower complexity (e.g., 30,000 parameters for GENN₁ vs. 900,000 parameters for ConvAE₂). The gradient-based interpolators slightly outperform the fixed-point architectures (e.g., I-scores of 89.2 vs. 87.5% for GENN₁ architectures). Compared with zero-filling schemes, we report a very significant improvement of all scores when considering ConvAE architectures (e.g., 80.8 vs. 54.8% for the AE-score). This improvement is not as significant for GENN schemes for the interpolation and reconstruction scores. However, in such settings, the representation learned with a zero-filling strategy is meaningless (a negative AE score to be compared to a 91.0% AE score for the gradient-based GENN interpolator). We may also point out the significant gain in terms of the reconstruction score with respect to an OI with a Gaussian covariance model (57.29% for the OI vs. 89.16% for G (12)-GENN₁ in terms of the interpolation score of the test dataset). For the detailed results reported in Supplementary Appendix: detailed results for SST case study, we may note that changes in the complexity of the considered auto-encoder architectures only weakly affect the performance. As such, the choice of the auto-encoder type and of the considered interpolation scheme seems to be a stronger driver of the reported performance.

TABLE 2

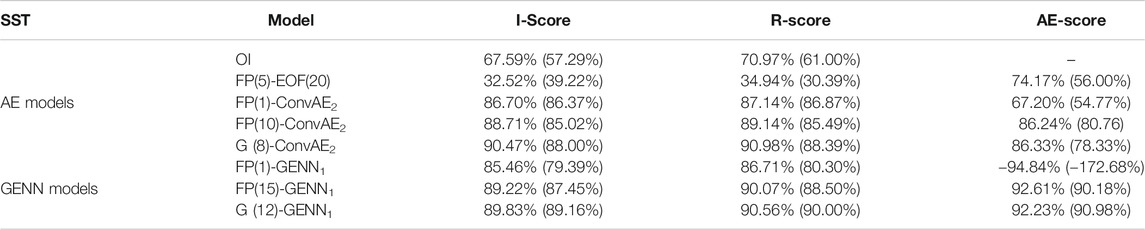
TABLE 2. Performance on the SST dataset: We evaluate for each model interpolation, reconstruction, and auto-encoding scores, respectively, I-score, R-score, and AE-score, in terms of percentage of explained variance, respectively, for the interpolation of missing data areas, the reconstruction of the whole fields with missing data, and the reconstruction of gap-free fields. For each model, we evaluate these scores for the training data (first row) and the test dataset (second row in brackets). In these experiments, we considered four different auto-encoder models: namely, 20- and 80-dimensional EOFs and ConvAE_1,2 models and two GENN models. GENN_1,2, combined with three interpolation strategies: the classic zero-filling strategy (zero), the proposed iterative fixed-point (FP) and gradient-based (G) schemes, the figure in brackets denoting the number of iterations. For instance, FP(10)-GENN₁ refers to GENN₁ with a 10-step fixed-point interpolation scheme. The EOFs are trained from gap-free data. We also consider an OI scheme with a space–time Gaussian covariance with empirically tuned parameters. We refer the reader to the main text for the detailed parameterization of the considered models. Here, we report, for each auto-encoder type, the best configuration in terms of the interpolation score. The detailed results are reported in Supplementary Appendix.

We illustrate these results in Figures 5, 6, which further stresses the gain with respect to OI for the reconstruction of finer-scale structures. The consistency between the interpolation results and the reconstruction of the gap-free image from the learned energy-based representation further stresses the ability of the proposed approach to extract a generic representation from irregularly sampled data. These results also emphasize a much greater ability of the proposed learning-based scheme to reconstruct finer structures, which can hardly be reconstructed by an OI scheme with a Gaussian space–time covariance model. We may recall that the latter is the state-of-the-art approach for the processing of satellite-derived earth observation data (Cressie and Wikle, 2015).

4.3 Sea Surface Height Case Study

This case study addresses satellite altimetry, which is the main source of observation data to retrieve sea surface currents on a global scale (Chelton and Wentz, 2005; Dufau et al., 2016). Current and upcoming satellite altimetry missions involve narrow-swath and wide-swath sensors on polar-orbiting satellites characterized by very high missing data rates with respect to a reference global grid, typically above 95% as illustrated in Figure 7. The space–time interpolation of satellite altimetry data is then a key challenge to produce sea surface current fields (Pascual et al., 2007; Ballarota et al., 2019). Here, we implement an OSSE for both nadir along-track altimeter data and of wide-swath altimeter data from the upcoming SWOT mission (Gaultier et al., 2015). For the former, we simulate the 2013 4-altimeter configuration for nadir along-track altimeter data. The OSSE relies on NATL60 high-resolution deterministic ocean simulation of the North Atlantic (Molines, 2018). As the case study region, we focus on a region along the Gulf Stream [33°N, 43°N; −65°W, −55°W] mainly driven by energetic mesoscale dynamics.

FIGURE 7

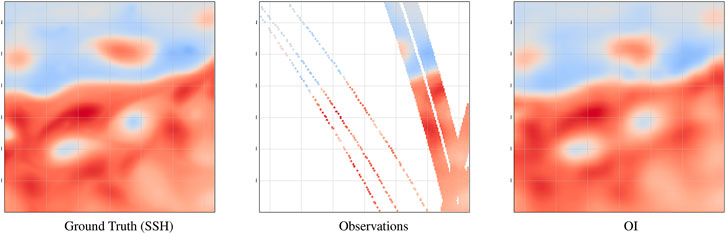
FIGURE 7. Illustration of the considered SSH dataset on April 8th, 2013: from left to right, reference SSH field (groundtruth), satellite-derived observation data (nadir along-track data and SWOT data), and optimally interpolated field (OI).

As baseline, we consider the operational processing chain for gridded altimeter fields, which relies on an OI scheme. All methods are applied to the anomaly with respect to this OI baseline. For benchmarking purposes, we run two state-of-the-art data-driven approaches, namely, the analog data assimilation (AnDA) (Lguensat et al., 2017) and the DINEOF algorithm (Ping et al., 2016). As for the SST case study, we train the EOF representation from the gap-free version of the training dataset. The AnDa scheme combines the exploitation of a gap-free reference dataset to design an analog dynamical model with a state-of-the-art ensemble Kalman filter to address the interpolation issue. Here, we implement the patch-based version of AnDA as presented in Fablet et al. (2017). As AnDA and DINEOF schemes rely on some training on a gap-free dataset, we use for evaluation purposes a 20-day test period in December, with the remaining data being used as training data except 10 days before and after the 20-day test period.

Regarding the proposed end-to-end learning framework, we consider architectures similar to the ones applied to the SST case study, namely, architectures ConvAE₁ and GENN₁ for operator ψ in (Eq. 5). To account for the knowledge of the OI baseline, states X and observations Y concatenate two components: a coarse-scale SSH component corresponding to the OI baseline and a fine-scale SSH component corresponding to the anomaly of the SSH field with respect to the OI baseline. Here, we consider 5-day time windows. This amounts to considering tensors X and Y of dimension 10 × 200 × 200. Similar to the SST case study, we gradually increased the number of iterations $N_I$ of the solver from 5 to 15 with a batch size of four and up to 300 epochs. We obtained the best performance over the test period using five or 10 iterations depending on the parameterization.

Similar to the SST case study, we first applied the proposed unsupervised end-to-end learning strategy as synthesized in Table 3. As SSH fields involve a rather low contrast, we compute all performance metrics for the norm of the gradient of the SSH fields, which relate to the norm of sea surface current. We may notice that ConvAE architectures lead to poor performance and even degrade the reconstruction with respect to the OI baseline. These results suggest that auto-encoder architectures applied globally cannot account for the space–time variability observed in the case study area for spatial scales below a few hundreds of kilometers. This is particularly emphasized by poor AE scores. By contrast, GENN architectures seem more adapted with the best performance issued from the fixed-point solver. However, in the unsupervised case, we only report a relatively marginal gain with respect to the OI baseline. We hypothesize that this relates to the very high missing data rates. In such cases, we also noted an early stopping criterion to be necessary after 10 to 20 epochs to avoid over-fitting issues.

TABLE 3

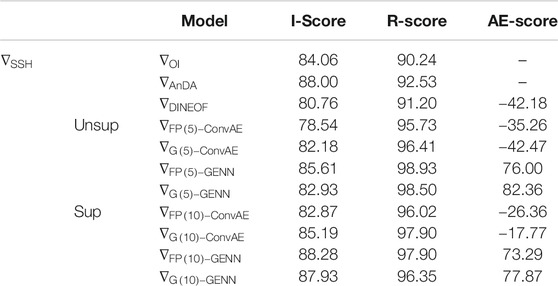
TABLE 3. Evalulation of the benchmarked methods for the SSH case study using an unsupervised and supervised training strategy: we evaluate for the gradient norm of the SSH fields $\left(\nabla SSH\right)$, the interpolation, and reconstruction scores, respectively, the I-score, as well as auto-encoding scores when relevant. For benchmarking purposes, we consider OI, AnDA, and DINEOF schemes. Regarding the proposed framework, we evaluate two settings using an iterative fixed-point procedure: namely, FP(5)-ConvAE architecture based on a convolutional auto-encoder architecture and FP(5)-GENN based on a Gibbs energy representation.

To further evaluate this point, we perform a supervised learning experiment, where all end-to-end learning architectures are trained to minimize the reconstruction of the true field, assuming we are provided with a fully groundtruthed gap-free training dataset. Interestingly, using such a supervised learning strategy, we report much greater improvement for the reconstruction of the SSH gradients, for example, I-scores of $\approx$ 88.3% for FP(5)-GENN architecture vs. 84.06% for the OI baseline. When comparing to DINEOF and AnDA schemes, we slightly outperform AnDA in the supervised case. We may notice that AnDA also requires the existence of a gap-free reference dataset. By contrast, DINEOF, similar to ConvAE architectures, reports worse performance for the reconstruction of the norm of the SSH gradient, which emphasizes the limitation of methods based on global dictionaries to decompose the space–time variability of SSH fields.

In Figure 8, we visualize interpolation examples for specific data of the test period. They further illustrate the low relevance of DINEOF and ConvAE approaches to improve the reconstruction of SSH gradients with respect to the OI baseline. They also make clear the much better reconstruction performance of GENN architectures trained in a supervised fashion rather than in a non-supervised one. In these experiments, gradient-based end-to-end architectures may generate local artifacts, whereas the fixed-point ones appear more stable. We refer the reader to the study by Beauchamp et al. (2020) for a detailed intercomparison of data-driven approaches for the interpolation of SSH fields for different satellite altimeter datasets.

FIGURE 8

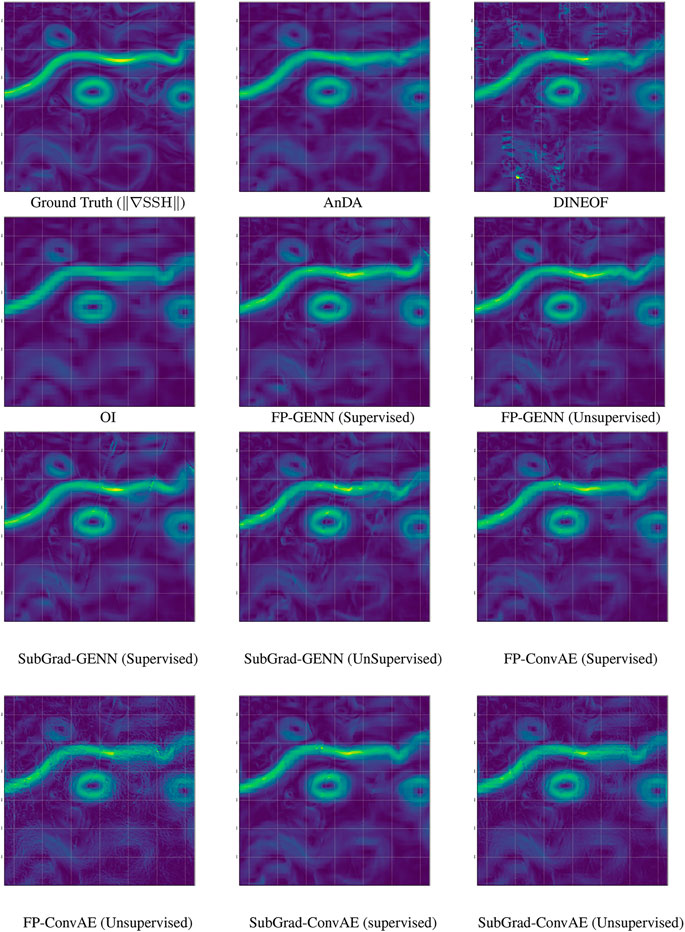
FIGURE 8. Comparison of data-driven interpolation methods for the norm of the gradient of the SSH field on April 8th, 2013: reference SSH field (groundtruth), optimally interpolated field (OI) (left panel), and data-driven interpolations of the SSH field using DINEOF, AnDA, FP(5)-ConvAE, and FP(5)-GENN methods. We refer the reader to the main text for details on these methods.

5 Related and Future Work

This section further discusses the proposed framework with respect to the related work, especially optimal interpolation, learning-based interpolator, and energy-based representation of signals and images.

Optimal interpolation: As stated in (Eq. 3), OI can be regarded as a relaxed version of (Eq. 1), where energy $U_{\theta }$ involves a quadratic form associated with the covariance model ${\text{Σ}}_X$. Such OI formulation can be solved analytically from the inversion of the covariance matrix ${\text{Σ}}_X$. We refer the reader to the study by Cressie and Wikle (2015) for a review on the main types of covariance models and on their application for time, space, and space–time interpolation issues. Similar to covariance models, the proposed representation amounts to defining a prior on state X through an energy formulation, but this is not restricted to linear–quadratic forms. From the considered NN-based architectures, we embed nonlinear transforms. Whereas in the present work, we consider fixed-point and gradient-based schemes corresponding to the limit case, $\lambda =\infty$; future work could investigate these minimization schemes coupled with observation noise models as in (Eq. 4). In this context, ADMM algorithms Boyd et al. (2010) may also be of great interest to address more complex observation models.

Learning interpolators: A significant amount of work has been dedicated to the development of learning-based schemes for interpolation issues. Regarding deep learning models, most of the proposed approaches focus on directly learning the interpolation algorithms using some initialization, typically a zero-filling initialization (Xie et al., 2012; Yan et al., 2018). Examples of such approaches include both auto-encoder–like CNN architectures (Xie et al., 2012; Yan et al., 2018) and CNN architectures inspired from reaction–diffusion PDEs (Chen et al., 2015) derived from variational formulations (Bertalmio et al., 2000). Rather than deriving the architecture from the gradient descent algorithm associated with some a priori energy formulation, we here aimed to jointly learn an energy-based representation of the class of signals or images of interest and the NN-based implementation of the associated minimization scheme. Regarding the latter, we have shown that the parameter-free fixed-point architecture may prove efficient. In Barth et al. (2020), a similar end-to-end architecture is proposed; however, it does not explicitly rely on an underlying variational formulation and only explores auto-encoder architecture. Recent studies have also investigated the learning of variational formulations associated with gradient-based solvers (Kobler et al., 2020). Gradient-based solvers appear more flexible than fixed-point ones to account for more complex observation models. In this context, future work could further explore and benchmark the derivation and learning of computationally efficient minimization architectures including using ideas from meta-learning approaches (Hospedales et al., 2020).

Representation learning and energy-based representations: Representation learning is among the key feature of deep learning methods to infer relevant computational representations of some underlying processes given observation data (Bengio et al., 2013). One may cite a variety of case studies showing neural networks trained on a given task embedded in some representation, which is of interest for many other tasks. Here, we consider the auto-encoder score to evaluate the representation capacity of a model trained from irregularly sampled data. Our results point out that given some appropriate design of the end-to-end architecture, the model learned from data with very high missing data rates can infer a relevant representation of the gap-free states. To this end, we rely on energy-based representations. Such representations have been widely explored as such representations are the core of physics-informed representations, for example, Gibbs models in statistical physics and Hamiltonian representations in mechanics (Geman, 1990). From the mid-70s, both continuous and discrete energy representations have been considered in signal and image processing to address inverse problems. Among others, we may cite denoising, interpolation, segmentation, and super-resolution issues (Geman, 1990; Roth and Black, 2009; Freeman and Liu, 2011). In Roth and Black (2009), higher-order Markovian fields were investigated with nonlinear functions of many filter responses. Similar to these energy priors, the proposed GENN architecture decomposes as a sum of terms which only involves local neighborhoods. The latter relates to the Markovian property embedded in Gibbs priors. Whereas the calibration of such Gibbs models generally involves a relatively low number of parameters, their NN-based implementation allows us to consider much more complex parameterizations as well as to learn such representations in unobserved (latent) spaces. In the reported application, we consider an energy-based representation in a downscaled version of the considered spatial domain and learn the associated upscaling operator. As shown here, it also provides new means to jointly learn such priors and solve the associated inverse problem when considering irregularly sampled training data. Regarding deep learning models, restricted Boltzman machines (RBMs) are active research topics (Salakhutdinov and Hinton, 2009; Zhang et al., 2018). They also involve an energy-based formulation which relates the observed data to latent variables. A number of applications support their relevance, including when dealing with missing data. Numerically speaking, they exploit MCMC techniques, which are computationally expensive and may make their combination with other DL architectures more difficult. Here, through the considered parameterization (Eq. 8), we can derive simple and efficient inversion schemes from a learned energy representation. This property may open new avenues for a plug-and-play exploitation of such trainable priors for addressing other tasks than those considered during training. Besides, future work may also extend the proposed framework to trainable observation models.

Dealing with missing data: As stated in the introduction, dealing with missing data is often critical to address real-world issues and datasets, especially in spaceborne earth observation. Missing data may be due to sensor characteristics (sensitivity to acquisition conditions, acquisition sampling patterns, …) as well as to intrinsic features of the considered systems and processes. As a typical example, ocean dynamics (e.g., currents and geophysical tracer dynamics) are only defined within the ocean. Hence, the application of deep learning schemes to gridded representations of the ocean has to deal with missing data areas, including land areas. Given the texture-like and relatively low-contrast patterns depicted by geophysical dynamics, zero-filling strategies are most likely to lead to artifacts. CNNs defined on irregular graphs (Defferrard et al., 2016; Vialatte et al., 2016) may be an alternative. Here, we consider another alternative where the trainable energy-based representation applies to the entire regularly gridded domain. Among others, the proposed approach makes, for instance, the learning of representations feasible, which apply both on the open ocean (in areas with no land regions) and in coastal areas. Overall, future work will further explore the potential of the proposed framework for the identification and exploitation of deep learning representations for the characterization, modeling, and reconstruction of geophysical dynamics from satellite remote sensing data.

Unsupervised vs. supervised learning: The reported experiments suggest that for missing rates up to 80% of the considered domain, as illustrated by MNIST and SST case studies, we may be able to learn directly the interpolation scheme and the underlying variational representation from observation datasets involving gaps. This is of key interest for a plug-and-play application to real datasets with no preprocessing steps. We also expect the proposed AE and GENN architectures to be flexible and generic to adapt to a variety of multivariate signals, images, and image time series. For larger missing data above 90%, the experiments reported for the SSH case study suggest that the training phase should be constrained by complementary data to lead to a relevant interpolation performance. Whereas we tested an idealized fully supervised setting, one may expect the same performance with a reference target dataset with gaps if the latter is sufficiently large. For a given observing system, such a reference dataset could be provided by another observing system, which could sense the considered process for specific time periods and/or regions, possibly according to an irregular space–time sampling. These results open research avenues to further investigate irregularly sampled multisensor datasets during the training phase of the proposed end-to-end architecture. The fast-sampling phase of the upcoming SWOT mission could be a typical example (Gaultier et al., 2015). During this fast-sampling phase, some ocean regions will involve a better space–time sampling. As such, one could explore the related SSH datasets as relevant groundtruthed reference datasets to train end-to-end architectures using as inputs other narrow-swath altimeters as well as other sea surface tracers. Here, we believe that multimodal extensions of the proposed framework could be of key interest.

Data Availability Statement

The data used in the reported experiments are available from the following link: https://github.com/CIA-Oceanix/DINAE_keras.

Author Contributions

RF, LD, and FR have designed the proposed methodology. RF and MB. have implemented the proposed framework and run numerical experiments. RF and MB have prepared the original draft.

Funding

This work was supported by LEFE program (LEFE MANU project IA-OAC), CNES (grant SWOT-DIEGO), and ANR Projects Melody and OceaniX. It benefited from HPC and GPU resources from Azure (Microsoft EU Ocean awards) and from GENCI-IDRIS (Grant 2020-101030).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2021.655224/full#supplementary-material

References

Alvera-Azcárate, A., Barth, A., Parard, G., and Beckers, J.-M. (2016). Analysis of SMOS sea surface salinity data using DINEOF. Remote Sensing Environ. 180, 137–145. doi:10.1016/j.rse.2016.02.044

CrossRef Full Text | Google Scholar

Ballarotta, M., Ubelmann, C., Pujol, M.-I., Taburet, G., Fournier, F., Legeais, J.-F, et al. (2019). On the resolutions of ocean altimetry maps. Ocean Sci. 15, 1091–1109. doi:10.5194/os-15-1091-2019

CrossRef Full Text | Google Scholar

Barth, A., Alvera-Azcárate, A., Licer, M., and Beckers, J.-M. (2020). DINCAE 1.0: a convolutional neural network with error estimates to reconstruct sea surface temperature satellite observations. Geosci Model Dev. 13, 1609–1622. doi:10.5194/gmd-13-1609-2020

CrossRef Full Text | Google Scholar

Beauchamp, M., Fablet, R., Ubelmann, C., Ballarotta, M., and Chapron, B. (2020). Intercomparison of Data-Driven and Learning-Based Interpolations of Along-Track Nadir and Wide-Swath SWOT Altimetry Observations. Remote Sensing. 12(22), 3806. doi:10.3390/rs12223806

CrossRef Full Text | Google Scholar

Bengio, Y., Courville, A., and Vincent, P. (2013). Representation Learning: A Review and New Perspectives. IEEE Trans Pattern Anal Mach Intell. 35, 1798–1828. doi:10.1109/tpami.2013.50

PubMed Abstract | CrossRef Full Text | Google Scholar

Bertalmio, M, Sapiro, G, Caselles, V, and Ballester, C (2000). Image inpainting. ACM SIGGRAPH, 417–424. doi:10.1145/344779.344972

Bertalmio, M, Bertozzi, AL, and Sapiro, G (2001). Navier-Stokes, fluid dynamics, and image and video inpainting. Proc IEEE CVPR. 355–362.

Google Scholar

Boyd, S., Parikh, N, Chu, E, Peleato, B, and Eckstein, J (2010). Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. FNT Machine Learn. 3, 1–122. doi:10.1561/2200000016

CrossRef Full Text | Google Scholar

Chelton, D. B., and Wentz, F. J. (2005). Global Microwave Satellite Observations of Sea Surface Temperature for Numerical Weather Prediction and Climate Research. Bull Amer Meteorol Soc. 86, 1097–1116. doi:10.1175/bams-86-8-1097

CrossRef Full Text | Google Scholar

Chen, Y, Yu, W, and Pock, T (2015). On Learning Optimized Reaction Diffusion Processes for Effective Image Restoration. Proc IEEE CVPR 5261–5269.

Google Scholar

Chen, C. L. P., Zhang, C.-Y., Chen, L., and Gan, M. (2015). Fuzzy Restricted Boltzmann Machine for the Enhancement of Deep Learning. IEEE Trans Fuzzy Syst 23, 2163–2173. doi:10.1109/tfuzz.2015.2406889

CrossRef Full Text | Google Scholar

Cressie, N, and Wikle, C (2015). Statistics for Spatio-Temporal Data. Hoboken, NJ: John Wiley and Sons.

Criminisi, A., Perez, P., and Toyama, K. (2004). Region filling and object removal by exemplar-based image inpainting. IEEE Trans Image Process. 13, 1200–1212. doi:10.1109/tip.2004.833105

PubMed Abstract | CrossRef Full Text | Google Scholar

Defferrard, M, Bresson, X, and Vandergheynst, P (2016). Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering. Proc NIPS 3844–3852.

Google Scholar

Dufau, C., Orsztynowicz, M., Dibarboure, G., Morrow, R., and Le Traon, P. Y. (2016). Mesoscale resolution capability of altimetry: Present and future. J Geophys Res Oceans. 121, 4910–4927. doi:10.1002/2015jc010904

CrossRef Full Text | Google Scholar

Evensen, G (2009). Data Assimilation. Berlin, Heidelberg: Springer Berlin Heidelberg.

Fablet, R., Viet, P. H., and Lguensat, R. (2017). Data-Driven Models for the Spatio-Temporal Interpolation of Satellite-Derived SST Fields. IEEE Trans Comput Imaging. 3:647–657. doi:10.1109/tci.2017.2749184

CrossRef Full Text | Google Scholar

Freeman, WT, and Liu, C. (2011). Markov Random Fields for Super-Resolution. Advances in Markov Random Fields for Vision and Image Processing. Cambridge, MA: MIT Press.

Google Scholar

Galerne, B., Gousseau, Y., and Morel, J.-M. (2011). Random Phase Textures: Theory and Synthesis. IEEE Trans Image Process 20(1), 257–267. doi:10.1109/tip.2010.2052822

PubMed Abstract | CrossRef Full Text | Google Scholar

Gaultier, L., Ubelmann, C., and Fu, L. L. (2015). The Challenge of Using Future SWOT Data for Oceanic Field Reconstruction. JAOT 33:119–126.

Google Scholar

Geman, D (1990). Random fields and inverse problems in imaging. LNM 1427:113–193.

Google Scholar

He, K, Zhang, X, Ren, S, and Sun, J (2016). Deep Residual Learning for Image Recognition IEEE CPVR, Las Vegas, USA (IEEE). doi:10.1109/cvpr.2016.90

CrossRef Full Text

Hospedales, T, Antoniou, A, Micaelli, P, and Storkey, A (2020). Meta-learning in Neural Networks: A Survey.arXiv:200405439.

Jain, P, Netrapalli, P, and Sanghavi, S (2013). Low-rank Matrix Completion Using Alternating Minimization. ACM STOC 665–674. doi:10.1145/2488608.2488693

Google Scholar

Kobler, E, Effland, A, Kunisch, K, and Pock, T (2020). Total Deep Variation for Linear Inverse Problems. arXiv:200105005. doi:10.1109/CVPR.2015.7299163

CrossRef Full Text

LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learning. Nature 521, 436–444. doi:10.1038/nature14539

PubMed Abstract | CrossRef Full Text | Google Scholar

Lguensat, R., Huynh Viet, P., Sun, M., Chen, G., Fenglin, T., Chapron, B., et al. (2017). Data-driven Interpolation of Sea Level Anomalies using Analog Data Assimilation. Remote Sens. 11(7), 858. doi:10.3390/rs11070858

CrossRef Full Text | Google Scholar

Liu, G., Reda, F., Shih, K., Wang, T., Tao, A., and Catanzaro, B. (2018). Image Inpainting for Irregular Holes Using Partial Convolutions. Proc ECCV 85–100.

Google Scholar

Lorenzi, L., Melgani, F., and Mercier, G. (2011). Inpainting Strategies for Reconstruction of Missing Data in VHR Images. IEEE Geosci Remote Sensing Lett 8, 914–918. doi:10.1109/lgrs.2011.2141112

CrossRef Full Text | Google Scholar

Molines, J. M. (2018). MEOM configurations NATL60-CJM165: NATL60 code used for CJM165 experiment. Zenodo. doi:10.5281/zenodo.1210116

CrossRef Full Text | Google Scholar

Ouala, S, Fablet, R., Herzet, C., Chapron, B., Pascual, A., Collard, F, et al. (2018). Neural-Network-based Kalman Filters for the Spatio-Temporal Interpolation of Satellite-derived Sea Surface Temperature. Rem Sens 20, 1791.

Google Scholar

Pascual, A., Pujol, M.-I., Larnicol, G., Le Traon, P.-Y., and Rio, M.-H. (2007). Mesoscale mapping capabilities of multisatellite altimeter missions: First results with real data in the Mediterranean Sea. J Mar Syst. 65, 190–211. doi:10.1016/j.jmarsys.2004.12.004

CrossRef Full Text | Google Scholar

Peyr, G, Bougleux, S, and Cohen, L (2011). Non-local Regularization of Inverse Problems. Inverse Probl Imaging 5, 511–530.

Google Scholar

Ping, B, Su, F, and Meng, Y (2016). An Improved DINEOF Algorithm for Filling Missing Values in Spatio-Temporal Sea Surface Temperature Data. PLoS One 11, e0155928. doi:10.1371/journal.pone.0155928

PubMed Abstract | CrossRef Full Text | Google Scholar

Roth, S., and Black, M. J. (2009). Fields of Experts. Int J Comput Vis 82, 205–229. doi:10.1007/s11263-008-0197-6

CrossRef Full Text | Google Scholar

Salakhutdinov, R, and Hinton, G (2009). Deep Boltzmann Machines. Artificial intelligence and statistics, Clearwater Beach, FL (PMLR). 448–455.

Vialatte, J, Gripon, V, and Mercier, G (2016). Generalizing the Convolution Operator to extend CNNs to Irregular Domains. arXiv: 1606.01166.

Google Scholar

Xie, J, Xu, L, and Chen, E (2012). Image Denoising and Inpainting with Deep Neural Networks. Proc NIPS 341–349.

Google Scholar

Yan, Z., Li, X., Li, M., Zuo, W., and Shan, S. (2018). Shift-Net: Image Inpainting via Deep Feature Rearrangement. Proc ECCV 11218, 3–19. doi:10.1007/978-3-030-01264-9_1

CrossRef Full Text | Google Scholar

Yu, W, Heber, S, and Pock, T (2015). On Learning Optimized Reaction Diffusion Processes for Effective Image Restoration. Proc IEEE CVPR 5261–5269.

Google Scholar

Zhang, N., Ding, S., Zhang, J., and Xue, Y. (2018). An overview on Restricted Boltzmann Machines. Neurocomputing 275, 1186–1199. doi:10.1016/j.neucom.2017.09.065

CrossRef Full Text | Google Scholar