- 1ICMM, Consejo Superior de Investigaciones Cientificas, Madrid, Spain
- 2Department of Biology, University of Fribourg, Fribourg, Switzerland
- 3Department of Mathematics, University of Copenhagen, Copenhagen, Denmark
The COVID-19 pandemic has had worldwide devastating effects on human lives, highlighting the need for tools to predict its development. The dynamics of such public-health threats can often be efficiently analyzed through simple models that help to make quantitative timely policy decisions. We benchmark a minimal version of a Susceptible-Infected-Removed model for infectious diseases (SIR) coupled with a simple least-squares Statistical Heuristic Regression (SHR) based on a lognormal distribution. We derive the three free parameters for both models in several cases and test them against the amount of data needed to bring accuracy in predictions. The SHR model is
1 Introduction
The consequences of a pandemic like COVID-19 caused by the virus SARS-CoV-2 cannot be overstated (Nature, 2021). Accurate mathematical tools allowing to monitor and forecast the evolution of the contagious disease are useful to guide social, economic and public health decisions made by governments. Nevertheless, despite the availability of powerful mathematical models (Anderson et al., 2020), initial forecasting by some organizations underestimated the evolution of the epidemics, hampering the immediate taking of necessary actions (Economist, 2020; Herzberge and Hecketsweller, 2020).
This study aims to take advantage of available worldwide data on COVID-19 (Roser et al., 2021; Dong et al., 2020) to benchmark and assign error bars to minimal models, like the susceptible-infected-recovered (SIR) with different sophistication levels (Kermack and McKendrick, 1927; Weiss, 2013; He et al., 2020a; Yang and Wang, 2020; Khan et al., 2020; Annas et al., 2020), a straightforward least-squares best-fit (LS) Statistical Heuristic Regression based on a lognormal distribution (Lam, 1988), or basic Monte-Carlo simulation (Girona, 2020; Gang, 2020). It is well-known that finding a global minimum of non-linear least-squares problems for p free parameters requires, at worst, a brute force search in p-dimensional parameter space. If each parameter can take m values inside a given interval, it is a non-polynomial task that scales like
Other efforts to modeling the pandemics include sensitivity and meta-analysis to estimate averaged values for the reproduction number, incubation time, infection rate and fatality rate (He et al., 2020b), wavelet-coupled random vector functional link networks (Hazarika and Gupta, 2020), machine learning (Dhaka and Singh, 2020), and Advanced Autoregressive Integrated Moving Average Model (Singh et al., 2020). Approaches via learning algorithms are usually compared via corresponding tests (Demsar, 2006), where we recall the significant differences to statistics (Breiman, 2001).
The paper is organized as follows. In Section 2 (results and discussion), we introduce the Statistical Heuristic Regression model (SHR, section 2.1), the Susceptible-Infected-Removed model (SIR, section 2.2), and the Spatial Stochastic Individual-Based model (MC, section 2.3). After each topic, we analyze the corresponding application to different countries or regions, most notably Spain and Germany. Finally, in the section of Conclusions, we summarize and review our approaches and further discuss the application of the cases analyzed and future venues.
2 Results and Discussion
2.1 Statistical Heuristic Regression (SHR)
Epidemics can efficiently be modeled as a geometric process related to independent random events (Lam, 1988). This method yields a regression curve that describes the temporal variation of a contagious disease for the number of deaths, infections or some other relevant observable variable. Such a statistical heuristic approach results in a lognormal function,
which is the probability distribution function of a random variable whose logarithm,
Starting from the model
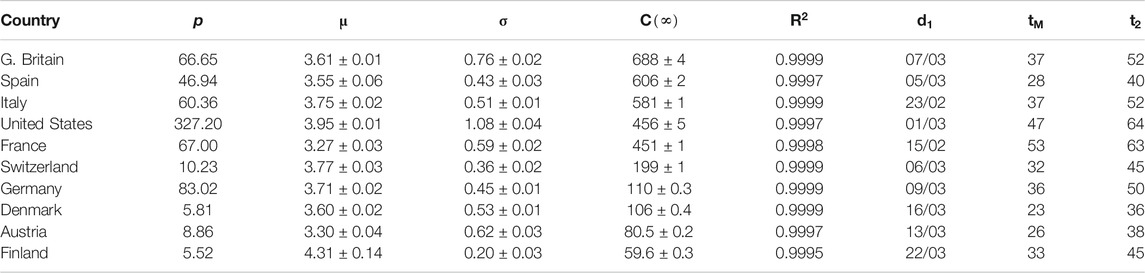
TABLE 1. Parameters for SHR model (confirmed deaths, first wave). p: country’s population (millions). μ and σ: parameters in the lognormal distribution.
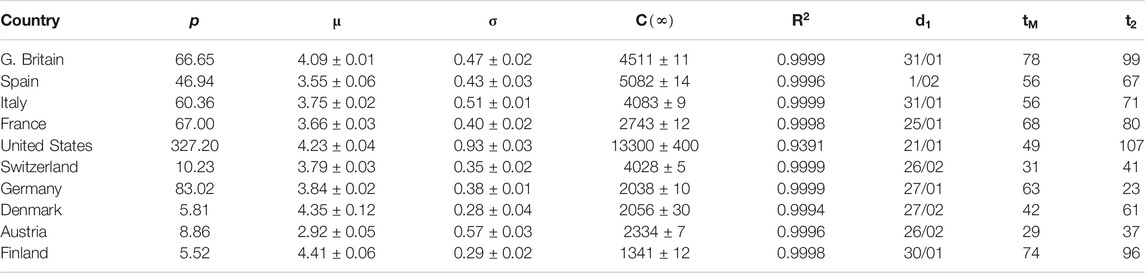
TABLE 2. Parameters for SHR model (confirmed infections, first wave). p: country’s population (millions). μ and σ: parameters in the lognormal distribution.
The corresponding accumulated cases are,
Given arbitrary precision,
Next, we aim to prove that the ansatz in Eqs 1, 2 reproduces the behavior of COVID-19 in ten different western countries using actual data up to the time of submission (revised version, March 2021). We observe a first wave that is relatively homogeneous among all countries (if properly normalized) and that could be considered strongly mitigated around May-June everywhere (Section Averaged profile). Other waves have later developed, which are more heterogeneous because they reflect each country’s different responses to the epidemics. A superposition of individual elementary peaks has been used to model these ulterior waves. Even if SHR merely amounts to a precise fit of the data, we observe that it carries significant advantages over the mere manipulation of the data series,
2.1.1 Spain
Spain is a country where the disease was particularly virulent in its first wave, spreading with remarkable strength. The SHR model agrees well with the data for both deaths and infections (Figure 1 and Tables 1 and 2; a common color code is applied to facilitate comparisons: red is used for daily cases (empty dots for actual data and dashed/dotted lines for models), black for 7 days moving averages of daily cases, and blue is used for accumulated cases (again, empty dots for actual data and dashed/dotted lines for models). We have used red vs magenta for daily cases and blue vs cyan for accumulated cases to allow easy comparison between models. Other details are given in the figure captions. Together, these two variables provide a better idea of the epidemic’s course by identifying two critical items: the impact on the population via infections and, the impact on the health system via deaths. Three simple features defining the epidemics that will be rationalized later in the context of the SIR model are: 1) the exponential behavior near the origin, 2) the position and value of the single maximum in the daily number of cases and, 3) an asymmetric decay toward the future w.r.t the past. The ratio between total infections and deaths has evolved from about 1% in March to a maximum of 12% in August, but it has significantly decayed for the second wave to about 4% at the end of September (inset in left-hand side in Figure 1).
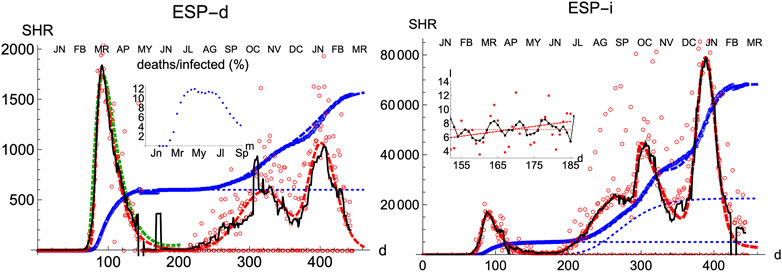
FIGURE 1. SHR/Spain. Left/Right panels: deaths/infections related to COVID-19. Data (circles) are taken from Roser et al. (2021); Dong et al. (2020). Dashed curves fit the data using Eqs 1, 2. Blue: total accumulated cases per million inhabitant. Red: daily cases per one hundred million inhabitants (the factor
Three regions are identified in the plots, both for deaths and infections. The first region (I, wave 1) finishes approximately on the first of May 2020
Neither the SHR nor the SIR models can account for a sustained period of constant infections, although they can accommodate this regime via the slowly decaying queue of the distribution where the derivative of the function is very low. In contrast, such behavior can be naturally described via Monte-Carlo simulation. Likewise, while MC can describe several waves by producing more than one local maxima due to spatial inhomogeneous dynamics, SHR and SIR can only describe such a scenario via a linear combination of individual waves, each one governed with its own parameters.
Finally, in a third region (III, wave 2) the collective transmission displays again a similar behavior to the region I, marking the evolution of an out-of-control disease. The superposition of these multiple regimes, plus other waves if needed, describes the overall function well. We notice that the accuracy in the fit for any wave is not expected to be reasonably stable until at least the corresponding maximum is well developed (Section Accuracy of SHR). However such incertitude, the model predicts that in Spain the number of infections due to the second wave should be reaching its maximum in December 2020, at most in January 2021. In addition, the model predicts that the strength of the second wave is approximately weaker than the first one by a factor two, as measured by the number of accumulated certified deaths from SARS-Cov-2. Although these predictions may be affected by large error bars since the maximum in the second wave is not yet well developped, those values offer sound guidance about the course of the disease. We have used this model to extrapolate the shape of the curve by a fortnight after the last day of the corresponding available data; the resemblance to the ulterior course of the disease will be seen in the next weeks.
The accompanying number of registered infections yields a picture of the likely evolution of deaths in the following days, even if the variation in the absolute numbers from the first to the second wave is dominated by the change in the number of tests performed. Given the large dispersion of raw data due to difficulties to collect them it is clear the necessity to perform moving averages and the advantages of working with least-square approximants that can be extrapolated a few days ahead, a statement that is true for the behavior of other countries. While deaths only show two waves so far, infections identify at least four local maxima that can be correlated with different events, like the end of the summer vacations or the occurrence of several bank holidays in Spain where the population has been moving and mixing in great numbers.
2.1.2 Germany
Compared with other countries with large populations, Germany has managed the pandemics quite well, as it is observed by comparing the number of cases per inhabitant. Moreover, its evolution has been recorded with consistency both for deaths and infections. Therefore, it is an appropriate benchmark for any model.
Similarly to Spain, the SHR model can be used to accurately represent the disease evolution using only three parameters per wave (Figure 2). Curiously enough, best-fit values for μ and σ are quite similar to Spain (Tables 1, 2), indicating that, independently of the absolute strength, there are common underlying features in both cases. Therefore, it is interesting to explore the ability of a single normalized averaged curve to represent such contrasting cases as Spain and Germany, using
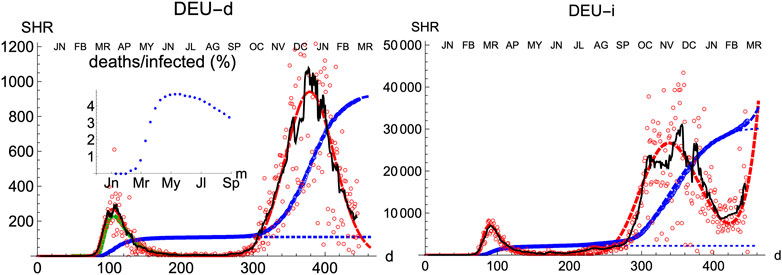
FIGURE 2. SHR/Germany. Symbols as in Figure 1.
2.1.3 Other Countries
We also prove the capabilities and versatility of the SHR ansatz to reproduce the observed data by applying the same methodology to a pool of western countries: Great Britain (GBR), Italy (ITA), United States (United States), France (FRA), Switzerland (CHE), Denmark (DNK), Austria (AUT) and Finland (FIN), cf. Figures 3, 4. In general, the agreement is quite good, both for deaths and infections. Among other advantages, this procedure allows a quick and simple monitoring of the evolution of the disease in the different countries. In particular, it is a useful tool to identify and forecast the appearance of a second wave. At the moment of writing, only the United States has fully developed the maximum associated with the second wave and, from the combined behavior of deaths and infections, it could be argued that the country is clearly heading toward a third wave. Since this is the only case so far, it is not possible to characterize well such a second wave by a proper average of different countries, although it seems fair to say that it is represented by a wider distribution of daily deaths, (e.g. the second component represented by the dotted red curve corresponds to having
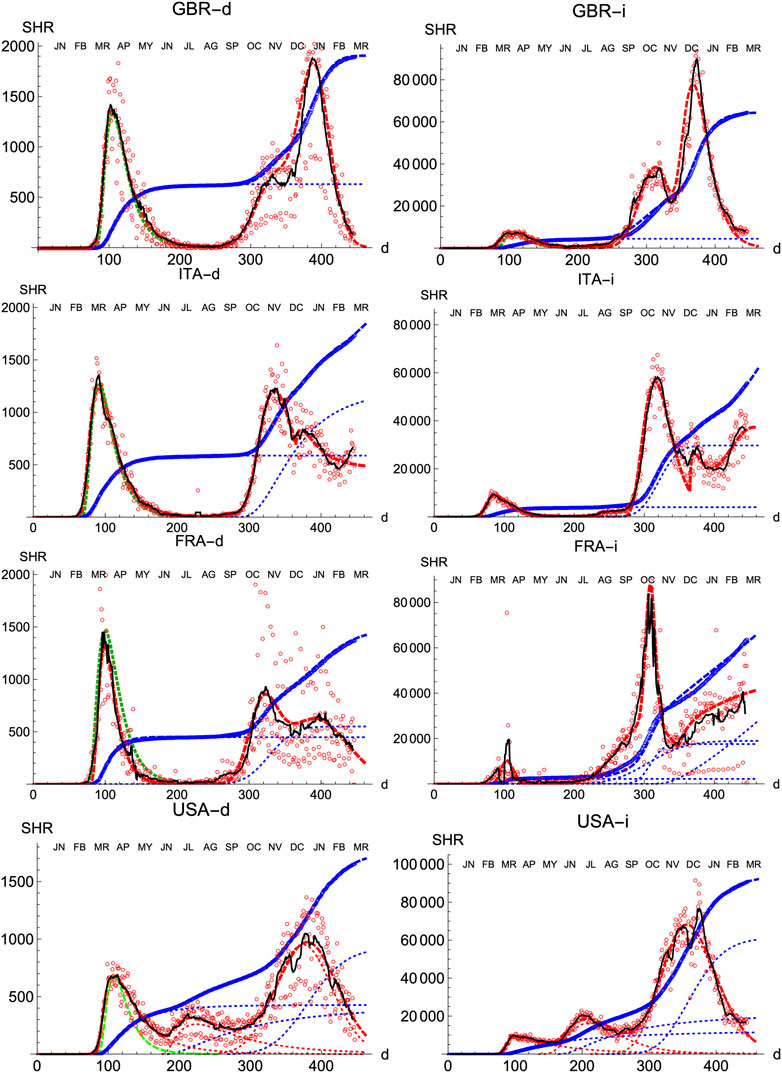
FIGURE 3. SHR/Other countries (I). Symbols as in Figure 1. Changes in methodology took place in United Kingdom (GRB) on May 20th and July 3rd, and in France (FRA) on May 28th.
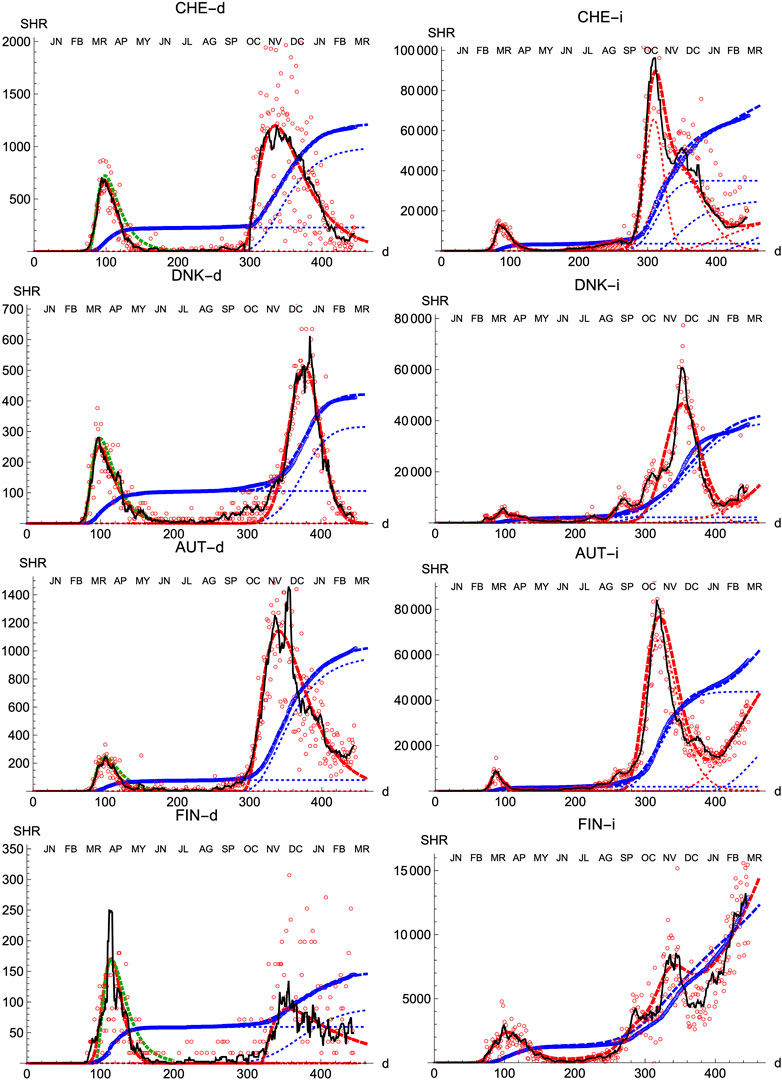
FIGURE 4. SHR/Other countries (II). Symbols as in Figure 1.
2.1.4 Regions: NYC vs Madrid
Prominent places where the infection spreads quickly are densely populated regions, which constitute the core of the propagation of the disease. Therefore, it is interesting to compare the distribution of cases in those regions. We have juxtaposed the performance of New York City (9.1 M-people, NYC) and the Community of Madrid (6.7 M-people, CAM) in the first wave (Figure 5). To highlight the similarities rather than the differences they are superimposed in such a way that the position (day) of the maximum coincides. Furthermore, CAM has been scaled by the ratio of respective populations, which makes the value at the maximum very similar for both regions. Despite all the differences between these regions, it is clear that a typical pattern emerges, which leads us to investigate the advantages of working with averages.
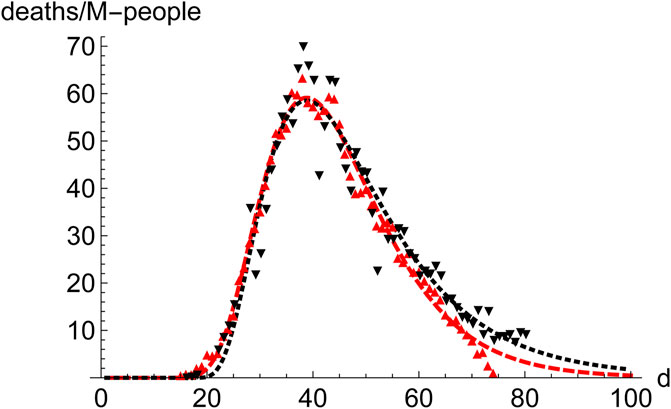
FIGURE 5. Comparison of the evolution of number of deaths in NYC and the region of Madrid (CAM) during the first wave. NYC (9.1 M people, red, down pointing triangles,
2.1.5 Averaged Profile
Normalizing and superimposing the curves for COVID-19 deceases on different countries such that the maximum in
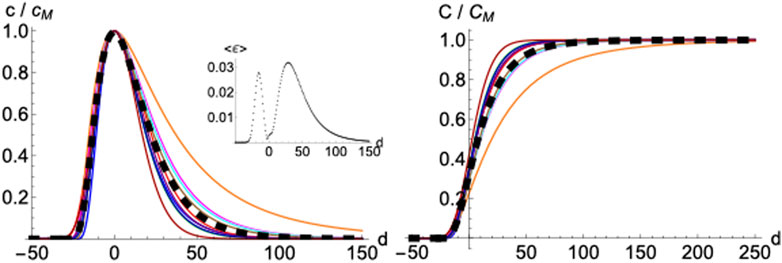
FIGURE 6. Averaged profile. Daily
2.1.6 Accuracy of SHR
To be able to confidently use a least-squares statistical regression to a given data set
A simple target to quantify the error is to study the behavior of the expected total number of cases,
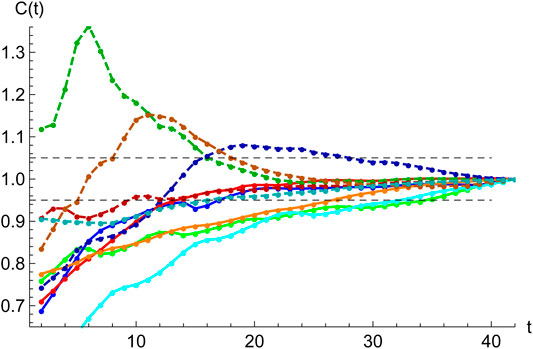
FIGURE 7. Accuracy of SHR best fits. Starting at the second inflection point,
2.2 Susceptible-Infected-Removed (SIR)
So far, we have shown that SHR qualifies as a quick and straightforward way to describe the evolution of an infectious disease. If adequately used, i.e., attached with appropriate error bars, it can be extrapolated to make predictions in the near future, since the functional forms associated with Eqs 1, 2 adapt so well to the observed data.
However, a better understanding of the dynamics of the epidemics can be obtained from a set of differential equations which describe its time evolution. The simplest model for the evolution of a contagious disease is to postulate that the rate of new infections is proportional to the number of infected people itself,
Such a simple model does not take into account how the rate of infections decreases as the number of infections approaches the total population. Therefore, a refined version is to divide a given population of size N into three classes
where we assume generalized mass-action kinetics (Müller and Regensburger, 2012) (with slightly different scaling with respect to N). First, it is assumed that the number of susceptible individuals decreases at a rate proportional to the density of infected,
where
Removed entities originate from infected; therefore, its variation is assumed to be proportional to the number of infected,
where
Lastly, the infected vary according to the inflow of susceptible individuals who become infected minus the outflow of infected that have been removed,
The derivative
The task at hand for a given population of N elements is to determine the parameters,
First, we focus on the task of simulating a population where
1) We use the daily number of deaths to identify the position and maximum value in the infections/deaths data:
2)
3) We get an approximate value for
4) The value
5) We minimize the root-mean square deviation,
2.2.1 Spain
Similarly to the SHR analysis we have presented above, we illustrate the performance of the SIR model by first looking at the distribution of deaths and infections in Spain (Figure 8). The lower left panel shows how numerical solutions to SIR equations match very well the temporal behavior of the epidemics under the condition
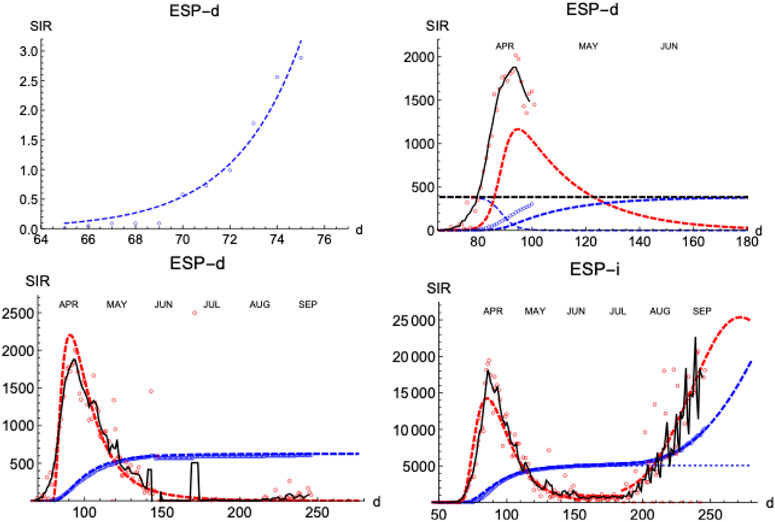
FIGURE 8. SIR/Spain. Left upper panel: exponential fit near the onset. Right upper panel: initial iteration for deaths (see text). Left lower panel: final iterations for deaths. Right lower panel: final iterations for infections. Blue: accumulated cases,
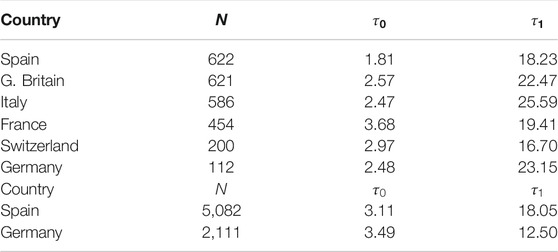
TABLE 3. Parameters for SIR model (first wave).N (number of individuals),
The proposed procedure works for the deaths subset as follows. First, the curve of daily cases is followed up to the appearance of its maximum, which to circumvent the noise is identified from a smoothed curve obtained by a five-day moving average,
Once the maximum is identified, the quasi-exponential behavior near the origin is used to estimate an initial value for
Next, we explore how the SIR model represents the evolution of the number of infections. The number of infections is a magnitude that carries larger error bars, but it can provide timely information on the evolution of the epidemics (Figure 8, right-lower panel shows the case for Spain). As expected, infections start earlier than the deaths (
A prominent feature is the existence of the second wave of infections separated from the first one by a region of sustained constant number of cases, as we have discussed in Figure 1. To fit the data, we superpose the two waves, each with its own defining parameters. However, the constant region between waves cannot be easily accommodated in these models and it is a clear indication of a different stage in the epidemics with low but sustained transmission of the disease at a pace similar to the one at which individuals are removed (while in the SIR model usually it is assumed that
2.2.2 Germany
We have applied the same procedure to Germany, a country which had in the first wave about four times less casualties per million inhabitant than Spain. The left panel of Figure 9 shows the final iteration for the daily and accumulated number of deaths, which again predicts the total number due to the first wave with accuracy
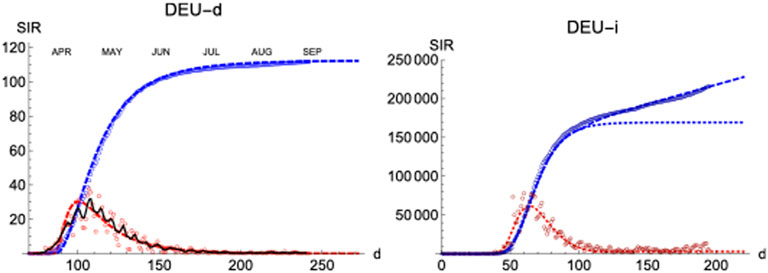
FIGURE 9. SIR/Germany. Left/Right panels: Deaths/Infections. Blue: total cases,
Regarding the infections, it is interesting that the region of sustained infection is also observed, although a second wave is only weakly apparent up to the present day (t = 200). Again, infections start earlier (
2.2.3 Other Countries
Finally, similar results have been observed in four more countries: France, Italy, Great Britain and Switzerland (Figure 10; Table 3).
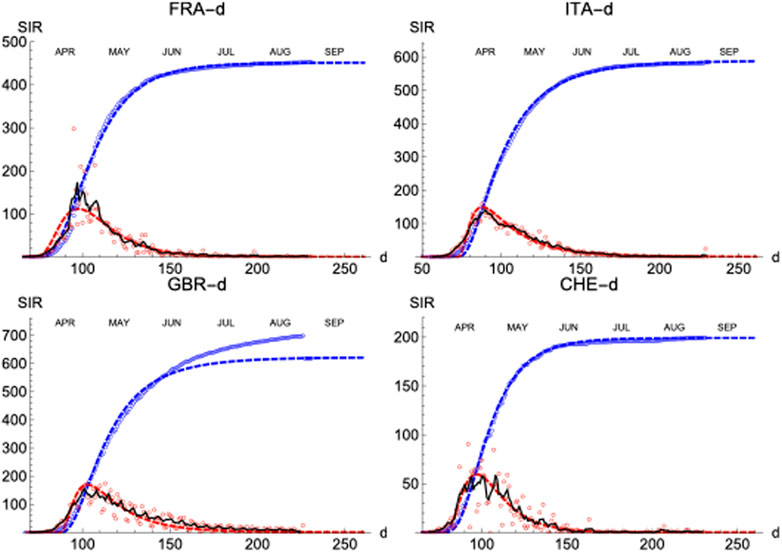
FIGURE 10. SIR (deaths)/FRA, ITA, GBR, and CHE. Respectively left to right and top to bottom. Symbols and lines as in Figure 8.
2.3 Spatial Individual-Based Model
To gain further insight into the spatio-temporal evolution of COVID-19, we consider next a stochastic discrete-time individual-based model in which the spread propagates on a two-dimensional
First, we start with a single isolated case of infection per
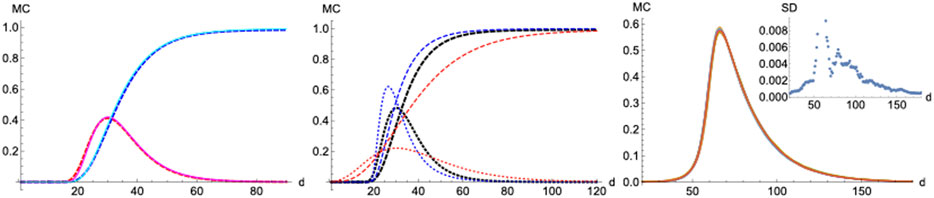
FIGURE 11. Monte-Carlo simulations. Left panel: MC (continous) vs SIR (dashed).
On the other hand, a scenario where the infection probability is kept constant (
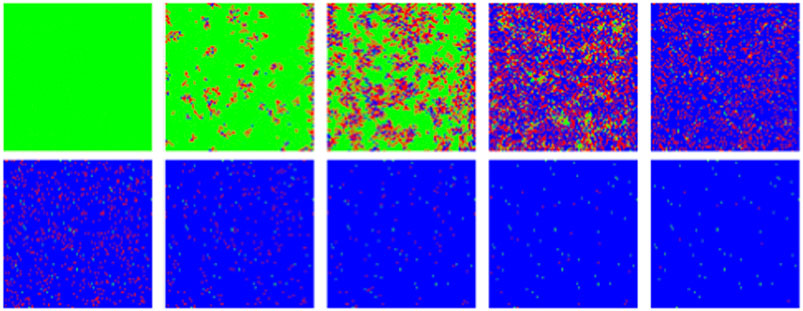
FIGURE 12. MC/Spatial. Typical evolution of individuals (pixels) with MC steps (10 steps between frames). Green, red and blue correspond to susceptible, infected and recovered. Other parameters are:
Unlike SIR, this model can sustain in a natural way a constant background of infections if at some point in the epidemics
Finally, we checked how statistical properties of the model perform and scale under different lattice sizes and parameters via simulation. The distributions over time for
Conclusion and Future Venues
We have analyzed and compared three mathematical approaches of increasing complexity to investigate the dynamics of COVID-19. A take-home message is that all three approaches have enough flexibility to embody the pandemics’ actual behavior for ten arbitrarily chosen countries. However, they display different error bars and have different abilities to be extrapolated into the future to produce valuable predictions.
We have proved that a least-squares SHR-model based on the lognormal distribution is well suited to describe the epidemic’s evolution using only two free parameters per infection wave. Confronted against real data up to the second inflexion point, the values determined for these parameters are well converged and stable, guaranteeing fractional error bars of
While such simple dynamics ignore individual, spatial or further inhomogeneities (e.g., genetic, socioeconomic, or other differences) we have proven that they can reproduce, predict and forecast relevant features of the actual COVID-19 dynamics. In particular, they provide reasonably robust ways to monitor and forecast the actual temporal evolution of contagious diseases in different environments, while only requiring basic mathematical tools.
The analysis of ten different countries makes us conclude that the SHR model can be extrapolated into the future with at most a 5% fractional error after a fortnight passed the second inflexion point. On the other hand, the SIR model, which includes two free parameters only too, seems more stable and can be used with a similar accuracy about one week passed the maximum. Finally, the MC model is helpful to study the interactions between separated regions developing the epidemics.
By comparing SHR and SIR we find an excellent correlation between functions
Our results strongly suggest that useful bounds can be found for
On the other hand, the excellent agreement between SIR and MC (provided the transition probabilities are chosen in accordance with the hypothesis behind the SIR model) opens new prospects to whrite spatially resolved SIR-like models that might be solved applying Markov chains techniques.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
All the authors contributed equally to the research and the manuscript.
Funding
LH is supported by the Swiss National Science Foundations Early Postdoc. Mobility grant (P2FRP2_188023). This work has been financed by the Spanish MINECO (MAT2017-85089-C2-1-R) and the European Research Council under contract (ERC-2013-SYG-610256 NANOCOSMOS). Computing resources have been provided by CTI-CSIC. Open access is partly funded by CSIC. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. The authors have declared that no competing interests exist.
Conflict of Interest
Since July 2020, the co-author LA-B has been employed by Frontiers Media SA. L-AB declared her affiliation with Frontiers, and the handling Editor states that the process nevertheless met the standards of a fair and objective review.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors are grateful to F. Flores and R. Ramirez for useful suggestions and comments on this manuscript.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2021.650716/full#supplementary-material
References
Anderson, R. The Kermack-McKendrick epidemic threshold theorem. Bull Math Biol (1991). 53, 3–32. doi:10.1016/s0092-8240(05)80039-4
Anderson, R. M., Heesterbeek, H., Klinkenberg, D., and Hollingsworth, T. D. How will country-based mitigation measures influence the course of the COVID-19 epidemic? The Lancet (2020). 395, 931–4. doi:10.1016/S0140-6736(20)30567-5
Annas, S., Isbar Pratama, M., Rifandi, M., Sanusi, W., and Side, S. Stability analysis and numerical simulation of seir model for pandemic covid-19 spread in indonesia. Chaos, Solitons and Fractals (2020). 139, 110072. doi:10.1016/j.chaos.2020.110072
Breiman, L. Statistical Modeling: The Two Cultures (with comments and a rejoinder by the author). Statist Sci (2001). 16, 199–231. doi:10.1214/ss/1009213726
Chan, J. S. K., Yu, P. L. H., Lam, Y., and Ho, A. P. K. Modelling sars data using threshold geometric process. Statist Med (2006). 25, 1826–39. doi:10.1002/sim.2376
Demsar, J. Statistical comparisons of classifiers over multiple data sets. J Machine Learn Res (2006). 7, 1–30.
Dhaka, A., and Singh, P. (2020). Comparative analysis of epidemic alert system using machine learning for dengue and chikungunya. In 10th International Conference on Cloud Computing, Data Science and Engineering, Dhaka, Bangladesh, 12 October, 2020. 798–804. doi:10.1109/Confluence47617.2020.9058048
Dong, E., Du, H., and Gardner, L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect Dis (2020). 20, 533–4. doi:10.1016/S1473-3099(20)30120-1
Economist. The Economist (2020). Forecasting covid-19–a terrible toll. https://www.economist.com/graphic-detail/2020/05/23/early-projections-of-covid-19-in-america-underestimated-its-severity. 23rd May. 77.
Gang, X. A novel monte carlo simulation procedure for modelling covid-19 spread over time. Scientific Rep (2020). 10, 13120. doi:10.1038/s41598-020-70091-1
Girona, T. (2020). Confinement time required to avoid a quick rebound of covid-19: Predictions from a monte carlo stochastic model. Front Phys 8, 7. doi:10.3389/fphy.2020.00186
He, J., Chen, G., Jiang, Y., Jin, R., Shortridge, A., Agusti, S, et al. (2020a). Comparative infection modeling and control of covid-19 transmission patterns in china, south korea, italy and iran. Sci Total Environ 747, 141447. doi:10.1016/j.scitotenv.2020.141447
He, W., Yi, G. Y., and Zhu, Y. (2020b). Estimation of the basic reproduction number, average incubation time, asymptomatic infection rate, and case fatality rate for COVID‐19: Meta‐analysis and sensitivity analysis. J Med Virol 92, 2543–50. doi:10.1002/jmv.26041
Herzberge, N., and Hecketsweller, C. (2020). Les modèles déboussoles pour prédire l’évolution de l’épidémie due au coronavirus. https://www.lemonde.fr/planete/article/2020/05/26/les-modeles-deboussoles-pour-predire-l-evolution-de-l-epidemie-de-covid-19–“6040726–“3244.html.
Hethcote, H. W. (2000). The mathematics of infectious diseases. SIAM Rev 42:599–653. doi:10.1137/s0036144500371907
Johnson, N. L., Kotz, S., and Balakrishnan, N. (1994). Continous Univariate Distributions. NY, United States: Wiley and Sons.
Kermack, W. O., and McKendrick, A. (1927). A contribution to the mathematical theory of epidemics. Proc R Soc. Lond. 115, 700–21.
Khan, Z. S., Van Bussel, F., and Hussain, F. (2020). A predictive model for Covid-19 spread - with application to eight US states and how to end the pandemic. Epidemiol Infect 148, e249. doi:10.1017/S0950268820002423
Lam, Y. (1988). Geometric process and replacement problem. Acta Mathematica Appl Sinica 4, 366–77. doi:10.1007/BF02007241
Müller, S., and Regensburger, G. (2012). Generalized mass action systems: Complex balancing equilibria and sign vectors of the stoichiometric and kinetic-order subspaces. SIAM J Appl Math 72, 1926, 47. doi:10.1137/110847056
Nature (2021). Nature wades through the literature on the new coronavirus – and summarizes key papers as they appear. Nature doi:10.1038/d41586-020-00502-w
Peliti, L. (2011). Statistical Mechanics in a Nutshell. Princeton, NJ: Princeton University Press. doi:10.1515/9781400839360
Press, W., Flannery, B., Teukolsky, S., and Vetterling, W. (2007). Numerical Recipes. 3 edn. Cambridge, United Kingdom: Cambridge University Press.
Roser, M., Ritchie, H., Ortiz-Ospina, E., and Hasell, J. (2021). Coronavirus pandemic (covid-19). Our World in Data Https://ourworldindata.org/coronavirus.
Singh, R. K., Rani, M., Bhagavathula, A. S., Sah, R., Rodriguez-Morales, A. J., Kalita, H, et al. (2020). Prediction of the covid-19 pandemic for the top 15 affected countries: Advanced autoregressive integrated moving average (arima) model. JMIR Public Health Surveill 6, e19115. doi:10.2196/19115
Wenbin, W., Ziniu, W., Chunfeng, W., and Hu, R. Modelling the spreading rate of controlled communicable epidemics through an entropy-based thermodynamic model. Sci China Ser G Phys Mech Astron (2013). 56, 2143–50. doi:10.1007/s11433-013-5321-0
Keywords: statistical heuristic regression, susceptible-infected-removed model, spatial stochastic, Monte-Carlo, COVID-19, SARS-CoV-2
Citation: de Andres P, de Andres-Bragado L and Hoessly L (2021) Monitoring and Forecasting COVID-19: Heuristic Regression, Susceptible-Infected-Removed Model and, Spatial Stochastic. Front. Appl. Math. Stat. 7:650716. doi: 10.3389/fams.2021.650716
Received: 07 January 2021; Accepted: 12 April 2021;
Published: 21 May 2021.
Edited by:
Waleed Isa Al Mannai, New York Institute of Technology Bahrain, BahrainReviewed by:
Deepak Gupta, National Institute of Technology, IndiaYunlong Feng, University at Albany, United States
Ning Zhang, St. Ambrose University, United States
Lu Xiong, Middle Tennessee State University, United States
Copyright © 2021 de Andres, de Andres-Bragado and Hoessly. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: P.L. de Andres, pedro.deandres@csic.es
 P.L. de Andres
P.L. de Andres L. de Andres-Bragado
L. de Andres-Bragado L. Hoessly
L. Hoessly