Cortex-Like Complex Systems: What Occurs Within?

We consider cortex-like complex systems in the form of strongly connected, directed networks-of-networks. In such a network, there are spiking dynamics at each of the nodes (modelling neurones), together with non-trivial time-lags associated with each of the directed edges (modelling synapses). The connections of the outer network are sparse, while the many inner networks, called modules, are dense. These systems may process various incoming stimulations by producing whole-system dynamical responses. We specifically discuss a generic class of systems with up to 10 billion nodes simulating the human cerebral cortex. It has recently been argued that such a system’s responses to a wide range of stimulations may be classified into a number of latent, internal dynamical modes. The modes might be interpreted as focussing and biasing the system’s short-term dynamical system responses to any further stimuli. In this work, we illustrate how latent modes may be shown to be both present and significant within very large-scale simulations for a wide and appropriate class of complex systems. We argue that they may explain the inner experience of the human brain.

1 Introduction

In [1] it was argued that the human brain’s response to incoming stimuli can be thought of as incorporating two distinct mechanisms: firstly, the brain must interpret what is going on (externally), and recognize the various possible stimuli as representing external elements that are at play, by utilizing a hierarchy of possible physical elements of increasing complexity and abstraction. Secondly, the brain can recognize, and so we experience, “internal elements” that are internal to itself, such as feelings, qualia, and sensations, that account for subjective, internal, and hierarchical [2] experiences and emotions. In [1] it was posited that both mechanisms are both achieved with the same apparatus: a special architecture of ten billion excitatory-inhibitory, delay connected, firing (excitable and refractory) neurones.

That apparatus is understood in the form of a network-of-networks [1, 3, 4]. The former, outer network is relatively sparse; the latter, localized networks are tightly (strongly) connected groups of individual neurones. For the reasons we set out in Section 2, each such tight sub-network is treated as being capable of localized multi-hypothesis decision making, acting to relay and amplify information. In networks science terms the inner networks can be thought of as densely connected modules within a highly modular global network [5].

It has recently been shown [7] that such a dynamical system’s responses to a wide range of distinct stimulations may be classified into a number of latent, internal, dynamical modes, displaying similar dynamical firing patterns—in time, and across the network. The modes are internal and are to be interpreted as subjective to the system. We will discuss that work in detail in Section 3.

The brain’s possession of many internal modes leads them to take the role of latent variables. We will show that latent variables provide long-range feedback and biases that constrain the processes of recognizing real elements (in perceiving the external world). This implies an important evolutionary role for such internal modes, not least in developing rapid decision making. Understanding such decision-making frameworks is important, as researchers [8] have sought to understand how rapid decision might result in systematic cognitive illusions and subconscious biases, and thus consistent and predictable irrational errors.

Furthermore, each of the internal modes can be naturally paired with (and triggered by) a collage of the external elements referred to by [1]. This can, for example, take on the form of feeling grief, embarrassment, or fear. Mathematically, they do not rely on random noise, stochastics, instabilities, or any other dynamical pattern formation mechanisms [1].

In this work, each complex system will exhibit a set of internal modes. Cross comparisons between two such sets might reveal some relatively common modes (that could be in one to one correspondence where the systems are subjected to identical or similar stimuli), while other modes might be individual modes.

Moreover, it might be possible to understand the modes in a hierarchical framework, with some modes emerging as the simultaneous combination of more fundamental modes [1]. These higher level modes might be interpreted as corresponding to global, abstract feelings: this idea is related to the discussion in [2], where it is argued that there are five levels of qualia. Specifically [2], argues that “the latter three levels constitute explicit mental representations of experience. These five levels put unconscious and conscious processes on a continuum characterized by progressively increasing degrees of differentiation and complexity of the schemata used to process emotional information.” Whether or not a de-lineation into five levels is correct, is no matter: a hierarchical framework concept allows to move from local internal modes, dominated by just a few local modules at the lowest level of the hierarchy, through to more global modes. This idea was discussed independently as a consequence of the “dual hierarchy model” proposed in [1], where it was analogous to the hierarchy of external perceptions (the recognition of objects, actions, narratives, scenarios, …).

Philosophical zombies are conceived of as being functionally and physically identical in all ways to a human, but without having internal experiences and feelings [9]. We must deny that such zombies are possible: if there is any brain that is physically and functionally identical to ours, then that brain would have the same internal modes and would thus have the same qualia: an identical functional system with no qualia (that is, a zombie) is not possible.

The oft mentioned hard problem of consciousness “is the problem of experience. Humans beings have subjective experience: there is something it is like to be them. We can say that a being is conscious in this sense—or is phenomenally conscious, as it is sometimes put—when there is something it is like to be that being. A mental state is conscious when there is something it is like to be in that state.” [10]. Here, we are stating unambiguously that the experience of being within a certain internal mental state is nothing more than the experience of these internal modes being activated (that is, they are responses to the present collage of external stimuli). The question about how and why we should experience feelings and qualia, in isolation or independently from the underlying architecture and processing, is thus a red herring.¹ We are enthusiastic physicalists: internal sensations are merely interpreted as the experience of these internal modes kicking in. These are sensations that we label appropriately—and they are a natural consequence of exploiting a multi-state interpreter. Some philosophers might argue strongly against this, saying that qualia are fundamental experiences. We must reject this, since latent variables controlling the mode, that is, the state of mind, would occur naturally as a consequence of the network-of-networks processing architecture, the time-lagged connections and the individual nodal dynamics. The internal states would gain consistency with the frequency of occurrence, and they would become associated (labelled) with some of the attributes of their own collage of catalysing physical elements.

In this work, no emergent phenomena (whether weak or strong [11]) are relied upon in supporting such hypotheses and deductions. Instead, we continue to proceed directly from a knowledge of the dynamical properties and delay-coupling over networks-of-networks [1]. In our view, emergence is a second, different, red herring.

The specific purpose of this paper is to further examine the possible functionality and consequences of the cortex-like network-of-networks model. We will interpret the class very large system simulations and analyses that were set out recently [7]. That work represents some of the largest numbers of simulations using massive cortex-like complex systems that have ever been made [12, 13]. This endeavour requires significant resources. IBM has been particularly active and has carried out TrueNorth simulations with 64 million neurones in 2019 [14], realizing the vision of the 2008 DARPA Systems of Neuromorphic Adaptive Plastic Scalable Electronics (SyNAPSE) program. The simulations and analytics carried out in [7] can be carried out on the SpiNNaker 1 million-core platform [15–17] which was designed specifically for these types of experiments, supported by the EU Human Brain Project [18].

While [7] gives a technical account of this type of mathematical modelling, simulation, and post-processing analytics, here we shall set out the implications of those results for the most basic element of human consciousness: how and why does the architecture and dynamics of the human cortex give rise to internal feelings? We shall show that such systems, which are simply large-scale models for a human brain, necessarily exhibit internal (latent) modes in their dynamical response.

The cortex-like complex systems were stimulated in many different ways in very large-scale computes, and thence the responses allowed the system to be reverse-engineered. The very large-scale of the highly modular systems’ architecture and dynamical specifications and the multiple simulation tasks required the development of observational (watching) and analytical (post-processing) methods. For those synthetic simulations one can look inside at any and all scales, right down to the individual nodes (neurones): which would be impossible for any human brain. We will build upon the technical results given in [7] to discuss what lies inside the workings of all such systems and how they must consequently possess latent dynamical modes. There need be nothing more.

2 The Physical Brain: A Network-Of-Networks

The cerebral cortex is the outer layer of neural tissue of the human brain, that is wrapped over the limbic, reptilian, brain (which itself controls more basic operational functions). It is usually assumed to play a role in memory, perception, thought, language, and consciousness. The cerebral cortex contains roughly 10 billion, i.e., ${10}^{10}$, neurones, that are networked together by 100 trillion, i.e., ${10}^{14}$, (directed) synaptic connections [19]. So, considered globally, the network is sparse.

The human cerebral cortex is 2–3 mm thick, and is composed of horizontal layers: in the neocortex about six layers can be recognized although in some regions far fewer layers are present.

Neurones within the different layers connect vertically to form-up relatively small, but tightly coupled subsets, called cortical hyper-columns, or cortical modules. The neurone-to-neurone connections, up and down through the layers, within a single cortical module are much denser than the connections that spread out laterally from module to neighbouring module [20–23].

There are approximately 10,000 neurones within a single cortical module. Assuming some duplication of neurone-to-neurone synaptic connections, the edge density of a single module may be approximately $70\text{\%}$. Considered locally, within modules, the sub-network is dense. There are about 1 million cortical modules in all, arranged in a two dimensional sheet, that is corrugated up, and wrapped across the top of the brain. Hence, the total of 10 billion cortical neurones [24].

As we have noted these 1 million cortical modules sitting within the entire network are completely analogous to the mathematical graph/network-theoretic concept of modules [5]. Mathematically, the modules can be viewed as densely connected sub-networks (that are also sometimes referred to as “clusters,” or “communities” within graphs) that are themselves loosely connected up, with each acting as some type of multimodal information processor [1].

Each neurone itself possesses an excitable and refractory depolarizing “spiking” dynamic. When it is sufficiently stimulated, by spiked waves of membrane (electrical) depolarization, incoming from a synapse, along a dendrite, into its soma, during a moment when it is ready to fire itself, then the neurone will do so. Once it has fired a neurone must undergo a refractory period, as the ions (for example, Na⁺ and K⁺) re-equilibrate across it cellular membrane, during which time it cannot be re-stimulated to fire. This is the so-called “refractory period.” Once this period is complete then the neurone is ready to fire again, when stimulated. The transmission of an excitatory signal between one neurone and another takes some non-trivial time, relative to the time of a single excitatory firing spike: physically, a wave of membrane depolarization leaves one soma, out along an axon, jumps a synapse, and then travels up a dendrite and into the soma of the neighbour. We refer to this feature as time-lagged excitatory coupling. We note that there are a number of alternative models that could be adopted as the basis for the nodal neurone firing dynamics: what is critical is that each encodes a non-trivial refractory period.

In summary, a physical model of the human cortex should comprise a directed graph with 1 million modules, with each module containing approximately 10,000 neurones. Dense directed connections within modules means that the average number of up and downstream neurone adjacencies within a module is approximately 75,000,000. Hence, models and computer simulations require 10 billion nodes (neurones) with 75 trillion directed connections.

3 Design of Large-Scale Simulations, Experiments, and Output Analysis

Here we give a short description of the large-scale simulations and analysis set out and performed in [7]. It is clear that such simulations must exploit a massive processing platform, such as that available in the 1 million-core platform [17], which was designed for these types of experiments [15, 16].

3.1 Architecture

We introduce two-dimensional arrays of modules considered in [7]. Consider an architecture with an M by M array of modules. Each module will consist of K nodes (neurones) coupled together as a dense strongly connected sub-network. Within each module we will arrange to have approximately Q neurone-to-neurone connections. Hence, the mean nodal in and out degree is $z=Q/K$.

The appendix of [6] sets out a method to randomly generate such modules, for given values of K and $z=Q/K$, even when K is very large (the requirement for strong connectivity being non-trivial). Finally we add a few connections between randomly selected neurones belonging to pairs of modules that are adjacent within the M by M grid.

Figure 1 shows a small example of such a network on $N\equiv K{M}^2=900$ nodes where $\left(K,M,z\right)=\left(\mathrm{100,3,3}\right)$ and we have added two connecting directed edges between neighbouring modules (one each way).

FIGURE 1

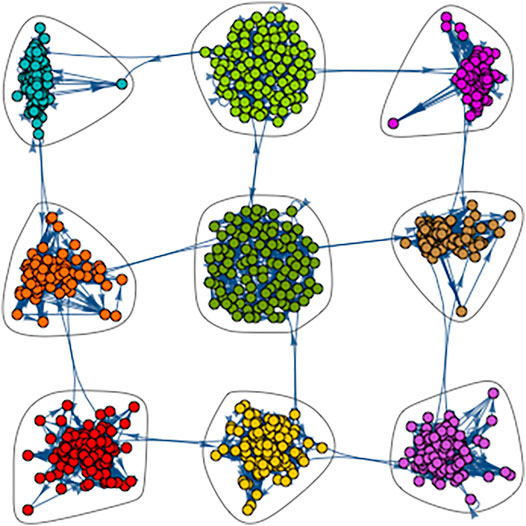
FIGURE 1. An $M\times M$ grid of K-vertex modules (strongly connected sub-networks inside each bubble) with $\left(K,M\right)=\left(\mathrm{100,3}\right)$ and an average in and out degree $z=Q/K\approx 3$: the whole is strongly connected.

In [7] a number $J\left(\ll K\right)$ of the nodes within each module were selected at random to act as watch-nodes. The firing patterns over time for the watch-nodes were all monitored within the various simulations, taking their dynamics as representative of the forced responsive behaviour of the whole module. Typically one might take $J=K/100$ or $K/1000$.

The aim of [7] was to make simulations on these cortex-like network architectures, increasing both K and M up towards 10,000 and 1,000, respectively (their natural values in vivo). Then $N=K{M}^2$ might reach 10B.

3.2 Dynamics and Time-Lagged Couplings

Next consider the active dynamics at each node and the node-to-node transmissions that were deployed in [7]. Each directed neurone-to-neurone connection, whether within a single module or between neighbouring modules, had a time-lag associated with it. The time-lag is drawn randomly from a given distribution of real numbers. The average time lags should be of the same order as the refractory period associated with post-firing of the neurones. In that way, a round trip between two nodes that are connected in both directions would be viable. For simplicity we might use the nodal dynamical model instantiated within platforms such as SpiNNaker [15, 16] with an identical refractory period at each node. Alternative firing models are common: typical examples include the discrete [6], integrate and fire, FitzHugh-Nagumo, and Hodgkin-Huxley models [25]. The aim is to avoid generating phenomena that are reliant on the particular form of the chosen firing model: the model simply needs to be both excitable (firing in response to incoming signals, if ready to do so) and refractory (unable to re-fire for a certain period post any firing). Our view is that our model of neural information processing and conscious phenomena should be robust: we specifically hypothesize that these phenomena are predominantly a product of the transmission delays and the neural architecture, rather than the finer details of the firing dynamics.

As pointed out in [1], if transmission delays are restricted to integer multiples of some basic time interval, or even that all delays are set to a common constant (an assumption oft made implicitly by allowing direct iterative updating) [26], then the sophistication of each individual module’s possible dynamical behaviour may collapse somewhat as all path-wize signals take integer-equivalent times to arrive.

3.3 Simulations

Having established this class of complex system, in [7] the authors performed a large number of separate experiments. In each experiment exactly one of the $J{M}^2$ watch-nodes was forced with a $p-$periodic super-threshold stimulus. All watch-nodes were monitored. Succinctly, a spike was offered periodically to the selected watch-node and was accepted (producing a real spike) provided the watch-node was not within its refractory period (which would follow an immediately earlier spike). Thus, given p, they obtained $N_{exp}=J{M}^2$ independent simulations, observed at the same $J{M}^2$ watch-nodes.

3.4 Post-Processing and Reverse-Engineering

In many ways running very large-scale simulations is only half the battle. The results of carrying out many, many (information processing) experiments with a very large-scale complex system generates its own big data problem.

Fixing $\left(M,K,Q,J\right)$, the results of these experiments were analysed as follows in [7]. Each of the $N_{exp}=J{M}^2$ experiments was represented by a real vector of length $J{M}^2$ containing the phases (mod p) of the firings of each watch-node (relative to their average firing time, which was set to zero mod p in each case) within that resulting global dynamical pattern. Whilst a range of choices for $\left(M,K,Q,J\right)$ could be made, it is most important that we capture the network-of-networks structure in our model. It is thus, for example, important to be pragmatic about the value of J we will use.

The phase vectors may be compared pairwise by finding the sum (over all of the watch-nodes) of the minimum distances (mod p) between the corresponding pair of nodal firing phases. Next, employing the full pairwise experimental distances matrix, the phase vectors were clustered, in order to become grouped-up and summarized by a smaller number of modal responses, with each cluster/mode representing an internal response class that is a functional consequence of the various relevant dynamical forcing experiments.

In [7] standard Ward clustering [27] was employed for this task, where the objective function is the in-cluster sum of squared errors. This method successively groups together smaller clusters, starting off with all elements as singletons, within their own clusters (no information), and ending with all elements within a single common cluster (no information). There are many ways to perform aggregative clustering and to decide a suitable point at which to halt the clustering steps (see the illustrative results below). This was not the moment to invent something new and untried.

In our application the clusters are the (hidden) latent internal modes summarizing the system’s alternative information processing behaviours.

Of course clustering always succeeds for any distance (dissimilarity) matrix: so one must ask how significant are the resultant latent modes (clusters)? This may be tested as follows. We have a distance matrix that is $N_{exp}\times N_{exp}$. At any point within the clustering process we can measure the SSE (sum of squared errors/distances) metric for each cluster, $C_i$ say, given by $SSE\left(C_i\right)={\displaystyle \sum }_{x,y\in C_i}d{\left(x,y\right)}^2;$ and then sum this over the set of all clusters.

As the number of clusters consolidates from $N_{exp}$ down to one, one obtains a convex curve running from 0 up to the total sum of all of the squared distances (this last is shown in black in Figure 2 for example). Next one can perturb the data by randomly and independently redrawing a fraction of the inter-experiment distances from the whole distribution of such distances. This maintains the overall distribution but, for each bootstrapped case, it replaces part of the actual structure with some randomly generated structure(s). For those intermediate cluster steps where the actual curve lies significantly below the envelope of curves achieved for the partially bootstrap-resampled data sets (distance matrices) we can be assured of some significance. A range of such tests were carried out in [7].

FIGURE 2

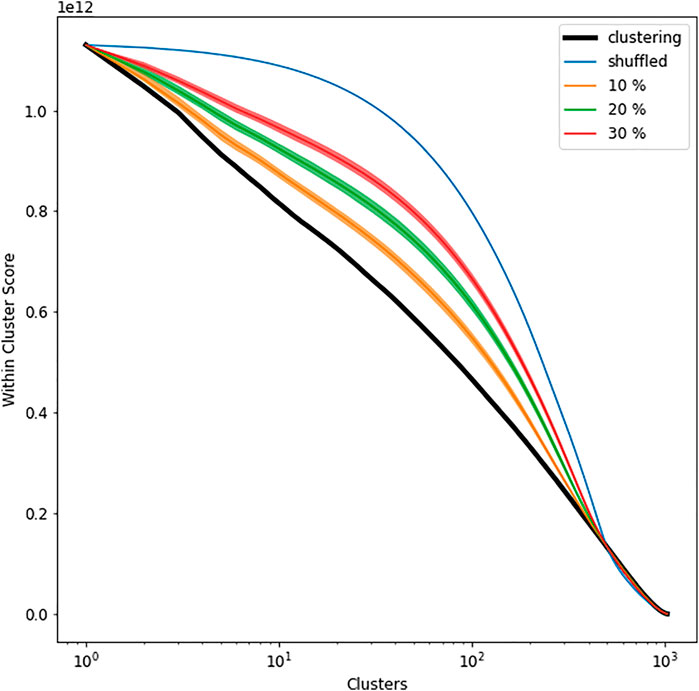
FIGURE 2. The cluster total of the in-cluster sum of square distances versus the number of clusters (log scale): the black curve shows the calculation for Ward clustering of the actual data; blue curves shows an envelope of the equivalent calculated curves where all of the pairwise experimental distances are randomly permuted; the yellow, green, and red curves show envelopes based on 1,000 samples for each line where a random 10% 20 and 30% of the pairwise experimental distances are redrawn from the distribution of all such values (with replacement): in each case a dark median is drawn together with the 1st to 99th percentiles.

3.5 Example Output

We present an illustrative example by taking $N=1.05{10}^6$ and $\left(M,K,z,J\right)=\left(\mathrm{32,1024,750,1}\right)$. We show the same type of simulation as those presented in [7]. Since there is one watch-node within each module, $M^2=1.024{10}^3$ separate simulation experiments were carried out for the same system. The results are shown in Figures 3, 4.

FIGURE 3

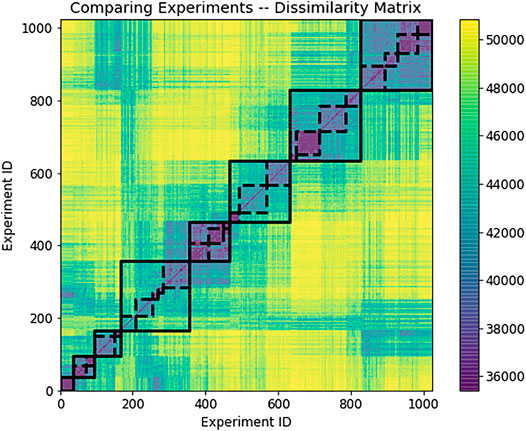
FIGURE 3. There are $M^2=1024$ forcing experiments in total, carried out on an $N\approx {10}^6$-node system, with $\left(K,M\right)=\left(\mathrm{1024,32}\right)$, and average in and out degree $z=Q/K\approx 750$, similar to the simulations discussed in [7]. This depicts the $M^2\times M^2$ pairwise dissimilarity matrix, with the experiments ordered appropriately, as well the discovered hierarchical partition into 8 and 24 modes that are shown in Figure 4. (Note that the colours indicate the dissimilarity score, but the colour-bar is truncated at the values for the 2.5 and 97.5% percentiles.)

FIGURE 4

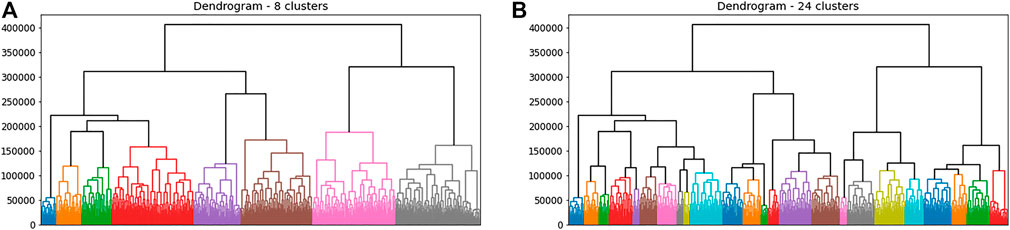
FIGURE 4. Hierarchical recognition of 8 large and 24 smaller modes discovered as subsets of relatively similar outputs from distinct dynamical experiments, using the dissimilarity matrix from Figure 3. There were 1,024 forcing experiments in total, carried out on an $N\approx {10}^6$ node system, with $\left(K,M\right)=\left(\mathrm{1024,32}\right)$, and average in and out degree $z=Q/K\approx 7500$.

As in the previous subsection we can measure the efficacy of a clustered partition as the total sum of the in-cluster sums of squared distances (pairwise experimental distances). As we move from $N_{exp}$ separate singleton clusters down to a single global cluster, this measure increases from zero up to the total sum of squares of all of the pairwise experimental distances. We can perturb the actual data (and clustering performance) by resampling a random fraction of the actual pairwise distances by drawing replacement vales independently from the distribution of all observed values. The result is shown in Figure 2.

Figure 2 can be interpreted as a hypothesis test. Reading off the graph for this illustrative example, the partitions for the actual data containing broadly more than 300 clusters (modes) are not significant at all, whereas those with between 50 and 100 clusters are the most significant when contrasted with the curves achieved under the statistical null hypothesis that the performance is no better than that achievable using exactly the same pairwise experimental distances distribution, but having them randomly permuted (which yields only random structures beyond the pairwise distances). Similarly, those clusterings are significant when compared against the cases where only 10–30% of the pairwise distances are resampled (from the observed distribution of such distances). Further discussion is given in [7].

For our purposes we note that the clusters obtained within the wide range of actual experimental responses are significantly stronger (with lower $SSE$ totals, and hence accounting for genuine differences between the modal responses) than those achievable for similar distance matrices with random (though realistic) elements. We may thus be assured that the discovered clusters, representing internal (latent) modes, are a consequence of genuine internal structure and not merely an artefact of a remorseless clustering process.

3.6 Very Large-Scale System Output

In [7] the authors deployed SpiNNaker [17] during 2019/20. The largest simulations made to date were parameterized by $N=1.024{10}^7$, where $\left(M,K,z,J\right)=\left(\mathrm{32,10000,7500,2}\right)$, solving delay equations with a range of time-delays for all connections (that is, roughly 75B synaptic directed connections). For SpiNNaker “the range of delays allowed depends upon the time-step of the simulation. The range is between 1 and 144 time-steps” [28, 29].

This should be contrasted with the desire for a full cortex simulation, with $N\approx 10B$, and the simulations in [14] during 2019, which reached $N={6.410}^7$ deploying TrueNorth chips to instantiate discrete iterative dynamics with all neurone-to-neurone interactions having the same unitary delays, so the whole can be updated in a each single iteration.

This research is continuing.

4 Interpretation and Consequences

The brain may sometimes be thought of as an information processor, with stimulating inputs producing neural signals which become passed along until they reach output nodes. In this work, we have carefully set out a modelling framework that studies a network-of-networks representing the neural signals and dynamics. So where are the internal feelings and sensations? Why must they be present? We argue that a network-of-networks modelling narrative demonstrates the existence of a rather wide set of latent, internal, common dynamical modes of operational behaviour, that can naturally be associated with such feelings and sensations.

Cortex-like complex systems, linking together excitable-refractory neurones with transmission time-delays, have, traditionally, been hard to analyse due to i) their sheer size and ii) the dynamical aspects of time-delays. Even the simplest delay-differential systems produce exotic stability (pattern forming) behaviour (that these days are unlocked by the Lambert-W function and other mathematical tools [30]). When such systems have a modular structure there has been no analytical work, other than the type of direct simulations discussed in this work.

Perhaps the closest analogue, without whole brain-scale simulations, was the development of Kuramoto models, with massive arrays (or continua) of adjacency-coupled simple clocks [32–33]. In fact, one may think of isolated modules (isolated columns) as $k\ge 1$ dimensional clocks [6] (winding maps over k-dimensional tori): so the whole complex system is analogous to an array of high dimensional clocks, all coupled together; with each clock having many (k, not uniform) resonant modes. Hence the comparison with generalized Kuramoto systems: yet, here we need both time-delays and higher dimensional clocks.

Even though all cortex-like systems have internal dynamical modes, their detection essentially requires the observation of firing patterns across the network and over an interval of time, though. One cannot take a simple, single time snapshot of the firing neurones. The modal responses are themselves dynamical objects defined over the network architecture and over time.

In particular, we have shown how such internal modes can be detected, being reverse-engineered out of performance experiments on cortex-like networks. Of course, we rely on mathematical and data scientific expertize, but the simulations allow us to address simultaneously vast numbers of single neurones within the whole for the first time. Hence, the new insights gained are completely dependent upon the provision of modern large-scale brain simulation programmes and platforms, such as [14, 29]. This demonstration of the wide array of latent modes should result in a step-change in our understanding of, and the way we talk about, internal brain function. We can see what lies within, that was previously hidden and inaccessible to scientists and philosophers alike.

In this paper we have explained how large cortex-like networks may be experimented upon by stimulating them in vastly many distinct ways. The result of each experiment is a very large amount of data (potentially the firing records over time for every neurone), and we also have to consider many such experiments. For that reason reverse-engineering, though plainly possible, requires a data-scientific approach. Here we have discussed the use of the simplest unsupervized clustering to recognize the internal classes of common firing patterns as internal dynamical modes. These are prime candidates for qualia, sensations and feelings. They are a direct consequence of the neuronal dynamics, the transmission delays, and the highly modular cortex architecture. We have shown how they can be reverse-engineered from the myriad of experiments.

Future students of the brain should begin dealing with the concept of internal dynamical modes of the systems’ response behaviour. This idea and vocabulary is grounded here within demonstrable network analysis and it offers a prism with which to interpret both common attributes of brain performance and anomalies. This approach would enable the recognition of the behavioural response of the brain as opposed to any detailed physiological response. We aver that the human brain cannot be interpreted without embracing the existence of latent modes that can be separately conjured by suitable stimuli, and even self-generated stimuli, which we call the generative collage.

Modes are necessarily present within a wide class of modular complex systems, and systematic investigation can lead to their discovery. The modes are a direct consequence of the architecture and dynamics, that is, the physical dynamical complex system. These are obvious candidates for the brain’s subjective internal feelings, that must lie within. There.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

PG conceptualized and designed the study, reviewed the data and analysed it, wrote and reviewed this article. CL ran the computer simulations that generated the data.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors thank their colleague Clive E. Bowman for challenging us and for commenting on successive ideas and drafts, and Aaron Sloman for his interest. They also thank members of the Oxford Mathematics of Consciousness and Applications Network (OMCAN) and attendees at the Models of Consciousness Conference (September 2019, Mathematical Institute, Oxford) for their comments following an early presentation of the main part of this research. The views expressed herein are personal to the authors and do not represent in any way those of the University of Oxford or any other body to which the authors are, or have been, affiliated. No competing claims are known.

Footnotes

¹A red herring is something that distracts from the question at hand. The term was employed by William Cobbett in 1807, who claimed to have used a kipper (a smelly smoked herring) to divert hounds from their pursuit of a hare.

References

1. Grindrod, P. On Human Consciousness: a Mathematical Perspective. Netw Neurosci (2018) 2(1):23–40. doi:10.1162/netn_a_00030

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Lane, RD. Hierarchical Organisation of Emotional Experience and its Natural Sub-straights, Emotions, Qualia, and Consciousness. In: A Kaszniak, editor. Series on Biophysics and Biocybernetics, 10 (2001).Singapore: World Scientific.

Google Scholar

3. Meunier, D, Lambiotte, R, and Bullmore, ET. Modular and Hierarchically Modular Organization of Brain Networks. Front Neurosci (2010) 4:200. Available at: https://www.frontiersin.org/article/10.3389/fnins.2010.00200. doi:10.3389/fnins.2010.00200

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Betzel, RF, Medaglia, JD, Papadopoulos, L, Baum, GL, Gur, R, Gur, R, et al. The Modular Organization of Human Anatomical Brain Networks: Accounting for the Cost of Wiring. Netw Neurosci (2017) 1(1):42–68. doi:10.1162/netn_a_00002

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Newman, MEJ. Networks: An Introduction. Oxford, New York: Oxford University Press (2010).

Google Scholar

6. Grindrod, P, and Lee, TE. On Strongly Connected Networks with Excitable-Refractory Dynamics and Delayed Coupling. R Soc Open Sci (2017) 4(4):160912. doi:10.1098/rsos.160912

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Lester, C, Bowman, CE, Grindrod, P, and Rowley, A. Large-scale Modelling and Computational Simulations of Cortex-like Complex Systems. preprint (2020).

Google Scholar

8 Ariely, D. Predictably Irrational: The Hidden Forces that Shape Our Decisions. New York: Harper Perennial (2010).

Google Scholar

9. Chalmers, DJ. The Conscious Mind: In Search of a Fundamental Theory. New York and Oxford: Oxford University Press (1996).

Google Scholar

10. Chalmers, DJ (2003), Consciousness and its Place in Nature, in Blackwell Guide to the Philosophy of Mind. Oxford: Blackwell, SP Stich, and TA Warfield (eds.), Oxford, pp. 102–42.

Google Scholar

11. Chalmers, DJ. Strong and Weak Emergence. In: P Davies, and P Clayton, editors. The Re-emergence of Emergence. Oxford University Press (2006). Available at: http://www.consc.net/papers/emergence.pdf.

Google Scholar

12. Eliasmith, C, and Trujillo, O. The Use and Abuse of Large-Scale Brain Models. Curr Opin Neurobiol (2014) 25:1–6. doi:10.1016/j.conb.2013.09.009

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Chen, S, He, Z, Han, X, He, X, Li, R, Zhu, H, et al. How Big Data and High-Performance Computing Drive Brain Science. Genomics, Proteomics & Bioinformatics (2019) 17:381–92. doi:10.1016/j.gpb.2019.09.003

PubMed Abstract | CrossRef Full Text | Google Scholar

14. DeBole, MV, Appuswamy, R, Carlson, PJ, Cassidy, AS, Datta, P, Esser, SK, et al. TrueNorth: Accelerating from Zero to 64 Million Neurons in 10 Years. Computer (2019) 52(5):20–9. Available at: https://www.dropbox.com/s/5pbadf5efcp6met/037.IEEE_Computer-May_2019_TrueNorth.pdf?dl=0. doi:10.1109/mc.2019.2903009

CrossRef Full Text | Google Scholar

15. Temple, S, and Furber, S. Neural Systems Engineering. J R Soc Interf (2007) 4(13):193–206. doi:10.1098/rsif.2006.0177

CrossRef Full Text | Google Scholar

16. Furber, SB, Galluppi, F, Temple, S, and Plana, LA. The SpiNNaker Project. Proc IEEE (2014) 102(5):652–65. doi:10.1109/JPROC.2014.2304638

CrossRef Full Text | Google Scholar

17. Moss, S. SpiNNaker Brain Simulation Project Hits One Million Cores on a Single Machine Modeling the Brain Just Got a Bit Easier. Data Center Dynamics (2018). Available at: https://www.datacenterdynamics.com/en/news/spinnaker-brain-simulation-project-hits-one-million-cores-single-machine/ (October 16, 2018).

Google Scholar

18.Wikipedia. The Human Brain Project (2020). Available at: https://en.wikipedia.org/wiki/Human_Brain_Project (extracted May, 2020).

Google Scholar

19. Azevedo, FAC, Carvalho, LRB, Grinberg, LT, Farfel, JM, Ferretti, REL, Leite, REP, et al. Equal Numbers of Neuronal and Nonneuronal Cells Make the Human Brain an Isometrically Scaled-Up Primate Brain. J Comp Neurol (2009) 513(5):532–41. doi:10.1002/cne.21974

CrossRef Full Text | Google Scholar

20. Mountcastle, V. The Columnar Organization of the Neocortex. Brain (1997) 120(4):701–22. doi:10.1093/brain/120.4.701

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Hubel, DH, and Wiesel, TN. Receptive fields of Single Neurones in the Cat's Striate Cortex. J Physiol (1959) 148(3):574–91. doi:10.1113/jphysiol.1959.sp006308

CrossRef Full Text | Google Scholar

22. Dombrowski, SM, Hilgetag, CC, and Barbas, H. Quantitative Architecture Distinguishes Prefrontal Cortical Systems in the Rhesus Monkey. Cereb Cortex (2001) 11(10):975–88. doi:10.1093/cercor/11.10.975

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Leise, EM. Modular Construction of Nervous Systems: a Basic Principle of Design for Invertebrates and Vertebrates. Brain Res Rev (1990) 15(1):1–23. doi:10.1016/0165-0173(90)90009-d

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Krueger, JM, Rector, DM, Roy, S, Van Dongen, HPA, Belenky, G, and Panksepp, J. Sleep as a Fundamental Property of Neuronal Assemblies. Nat Rev Neurosci (2008) 9(12):910–9. doi:10.1038/nrn2521

PubMed Abstract | CrossRef Full Text | Google Scholar

25.Wikipedia. (2019). Available at: https://en.wikipedia.org/wiki/Biological_neuron_model (extracted March, 2019). Biological Neurone Model.

Google Scholar

26. Cassidy, AS, Merolla, P, Arthur, JV, Esser, SK, Jackson, B, Alvarez-Icaza, R, et al. Cognitive Computing Building Block: A Versatile and Efficient Digital Neuron Model for Neurosynaptic Cores, The 2013 International Joint Conference on Neural Networks; Dallas, TX. Piscataway, NJ: IJCNN (2013). p. 1–10. doi:10.1109/IJCNN.2013.6707077

CrossRef Full Text | Google Scholar

27. Ward, JH. Hierarchical Grouping to Optimize an Objective Function. J Am Stat Assoc (1963) 58:236–44. doi:10.1080/01621459.1963.10500845

CrossRef Full Text | Google Scholar

28.SpiNNaker. Running PyNN Simulations on SpiNNaker. Github: University of Manchester (2018). Available at: http://spinnakermanchester.github.io/spynnaker/3.0.0/RunningPyNNSimulationsonSpiNNaker-LabManual.pdf.

Google Scholar

29. Rhodes, O, Bogdan, PA, Brenninkmeijer, C, Davidson, S, Fellows, D, Gait, A, et al. sPyNNaker: A Software Package for Running PyNN Simulations on SpiNNaker. Front Neurosci (2018) 12:816. Available at: https://www.frontiersin.org/article/10.3389/fnins.2018.00816, doi10.3389/fnins.2018.00816. doi:10.3389/fnins.2018.00816

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Grindrod, P, and Pinotsis, DA. On the Spectra of Certain Integro-Differential-Delay Problems with Applications in Neurodynamics. Physica D: Nonlinear Phenomena (2011) 240(1):13–20. doi:10.1016/j.physd.2010.08.002

CrossRef Full Text | Google Scholar

31. Kuramoto, Y. Self-entrainment of a Population of Coupled Non-linear Oscillators. In: H Arakii, editor. International Symposium on Mathematical Problems in Theoretical Physics: January 23-29, 1975, Kyoto University. Lecture Notes in Physics, 39. New York: Springer-Verlag (1975). p. p420.

Google Scholar

32. Rodrigues, FA, Peron, TKD, Ji, P, and Kurths, J. The Kuramoto Model in Complex Networks. Phys Rep (2016) 610(1):1–98. doi:10.1016/j.physrep.2015.10.008

CrossRef Full Text | Google Scholar

33. Heitmann, S, and Ermentrout, GB. Synchrony, Waves and Ripple in Spatially Coupled Kuramoto Oscillators with Mexican Hat Connectivity. Biol Cybern (2015) 109:333–47. doi:10.1007/s00422-015-0646-6

PubMed Abstract | CrossRef Full Text | Google Scholar