Data-Driven Supervised Learning for Life Science Data

Life science data are often encoded in a non-standard way by means of alpha-numeric sequences, graph representations, numerical vectors of variable length, or other formats. Domain-specific or data-driven similarity measures like alignment functions have been employed with great success. The vast majority of more complex data analysis algorithms require fixed-length vectorial input data, asking for substantial preprocessing of life science data. Data-driven measures are widely ignored in favor of simple encodings. These preprocessing steps are not always easy to perform nor particularly effective, with a potential loss of information and interpretability. We present some strategies and concepts of how to employ data-driven similarity measures in the life science context and other complex biological systems. In particular, we show how to use data-driven similarity measures effectively in standard learning algorithms.

Introduction

Life sciences comprise a broad research field with challenging questions in domains such as (bio-)chemistry, biology, environmental research, or medicine. Not only recent technological developments allow the generation of large, high dimensional and very complex data sets in these fields, but also, the structure of the measured data representing an object of interest is often challenging. The data may be compositional, such that classical vectorial functions are not easy to apply and could also be very heterogeneous by combining different measurement sources. Accordingly, new strategies and algorithms are needed to cope with the complexity of life science applications. In general, it is a promising way to reflect characteristic data properties in the employed data processing pipeline. This typically leads to increased performance in tasks such as clustering, classification, and non-linear regression, which are commonly addressed by machine learning methods. One possible way to achieve this is to adapt the used metric according to the underlying data properties and application, respectively [1]. Basically, all machine learning and data analysis algorithms employ the comparison of objects referred to as similarities or dissimilarities, or more general as proximities. Hence, the representation of these proximities is a crucial part. These measures enter the modeling algorithm either by means of distance measures, e.g., in the standard k-means algorithm or by inner products as employed in the famous support vector machine (SVM) [2]. The calculation of these proximities is typically based on a vectorial representation of the input data. If the used machine learning approach is solely based on proximities, a vectorial representation is in general not needed, but the pairwise proximity values are sufficient. This approach is referred to as similarity-based learning, where the data are represented by metric pairwise similarities only.

We can distinguish similarities, indicating how close or similar two items are to each other and dissimilarities in the opposite sense. In the following, we expect that these proximities are at least symmetric, but do not necessarily obey metric properties. See e.g., [3] for an extended discussion.

Non-metric measures are common in many disciplines and occasionally entail so-called non positive semi-definite (non-psd) kernels if a similarity measure is used. This is particularly interesting because many classical learning algorithms can be kernelized [4], but are still expecting a psd measure. As we will outline in this paper, we can be more flexible in the use of a proximity measure as long as some basic assumptions are fulfilled. In particular, it is not necessary, for many real-world life science data, to restrict the analysis pipeline to a vectorial Euclidean representation of the data.

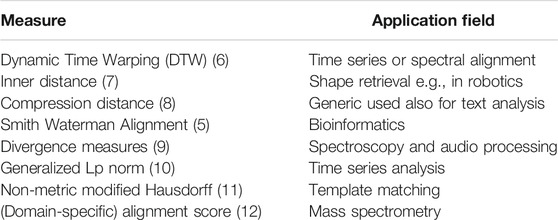
In the various domains like spectroscopy, high throughput sequencing, or medical image analysis, domain-specific measures have been designed and effectively used. Classical sequence alignment functions (e.g., Smith-Waterman [5]) produce non-metric proximity values. There are many more examples and use cases, as listed in Table 1 and detailed later on.

TABLE 1

TABLE 1. List of commonly used non-metric proximity measures in various domains.

Multiple authors argue that the non-metric part of the data contains valuable information and should not be removed [13, 14]. In this work, we highlight recent achievements in the field of similarity-based learning for non-metric measures and provide conceptual and experimental evidence on a variety of scenarios that non-metric measures are legal and effective tools in analyzing such data. We argue that a restriction to mathematically more convenient, but from the data perspective unreliable, measures are not needed anymore.

Along this line, we first provide an introduction to similarity-based learning in non-metric spaces. Then we provide an outline and discussion of preprocessing techniques, which can be used to implement a non-metric similarity measure within a classical analysis pipeline. In particular, we highlight a novel advanced shift correction approach. Here we extend prior work published by the authors in 15, which is substantially extended by novel theoretical findings (Section 2.4, in particular, the eigenvalue approximation via Gershgorin), experimental results (Section 3, with additional experiments and datasets), and an extended discussion. The highlights of this paper:

• We provide a broad study of life science data encoded by proximities only.

• We reveal the limitations of former encodings used to enable standard kernel methods.

• We derive a novel encoding concept widely preserving the data’s desired properties while showing considerable performance.

• We improve the efficiency of the encodings using an approximation concept not considered so far with almost no loss of performance in the classification process.

In the experiments, we show the effectiveness of appropriately preprocessed non-metric measures in a variety of real-life use cases. We conclude by a detailed discussion and provide practical advice in applying non-metric proximity measures in the analysis of life science data.

Materials and Methods

Notation and Basic Concepts

Given a set of N data items (like N spectral measurements or N sequences), their pairwise proximity (similarity or dissimilarity) measures can be conveniently summarized in a $N\times N$ proximity matrix. These proximities can be very generic in practical applications, but most often come either in the form of symmetric similarities or dissimilarities only. Focusing on one of the respective representation forms is not a substantial restriction. As outlined in 16, a conversion from dissimilarities to similarities is cheap regarding to computational costs. Also, an out of sample extension can be easily provided. In the following, we will refer to similarity and dissimilarity type proximity matrices as S and D, respectively. These notions enter into models by means of proximity or score functions $f\left(x,x^{\prime }\right)\in \mathrm{ℝ}$ where x and $x^{\prime }$ are the compared objects (both are data items). The objects $x,x^{\prime }$ may exist in a d-dimensional vector space, so that $x\in {\mathrm{ℝ}}^d$, but can also be given without an explicit vectorial representation, e.g., as biological sequences.

As outlined in 17, the majority of analysis algorithms are applicable only in a tight mathematical setting. In particular, it is expected that $f\left(x,x^{\prime }\right)$ obeys a variety of properties. If $f\left(x,x^{\prime }\right)$ is a dissimilarity measure, it is often assumed to be a metric measure. Many algorithms become invalid or do not converge if $f\left(x,x^{\prime }\right)$ does not fulfill metric properties.

For example, the support vector machine formulation [18] no longer leads to a convex optimization problem [19] when the given input data is non-metric. Prominent solvers, such as sequential minimization (SMO), will converge to only a local optimum [20, 21] and other kernel algorithms may not converge at all. Accordingly, dedicated strategies for non-metric data are very desirable.

The score function $f\left(x,x^{\prime }\right)$ could violate the metric properties to different degrees. In general it is at least expected that $f\left(x,x^{\prime }\right)$ obeys the symmetry property such that $f\left(x,x^{\prime }\right)=f\left(x^{\prime },x\right)$. In general, this property is a fundamental condition, because a large number of algorithms become meaningless for asymmetric data. We will also make this assumption. In the considered cases, the proximities are either already symmetric or can be symmetrized without expecting a negative impact. While symmetry is a reasonable assumption, the triangle inequality is frequently violated, proximities become negative, or self-dissimilarities are not zero. Such violations can be attributed to noise as addressed in 22 or are a natural property of the proximity function f.

If noise is the source, often a simple eigenvalue correction [23] can be used, although this can become costly for large datasets. As we will see later on, the noise may cause eigenvalue contributions close to zero. A simple way to eliminate these contributions is to calculate a low-rank approximation of the matrix, which can be realized with small computational cost [24, 25]. In particular, the small eigenvalues could become negative, also leading to problems in the use of classical learning algorithms. A recent analysis of the possible sources of negative eigenvalues is provided in 26. Such an analysis is particularly helpful in selecting the appropriate eigenvalue correction method applied to the proximity matrix. Non-metric proximity measures are part of the daily work in various domains [27]. An area, frequently applying such such non-metric proximity measures, is the field of bioinformatics, spectroscopy, or alike, where classical sequence alignment algorithms (e.g., Smith-Waterman - [5]) produce non-metric proximity values. For such data, some authors argue that the non-metric part of the data contains valuable information and should not be removed [13]. In particular, this is the motivation for our work. Evaluating such data with machine learning models typically asks for discriminative models. In particular, for classification tasks, a separating plane has to be determined in order to separate the given data according to their classes. However, in practice, a linear plane in the original feature space is rarely separating two classes of such complexity. A common generalization is to map the training vectors $x_i$ into a higher dimensional space by the function ϕ. In this space, it is expected that the machine learning model finds a linear separating hyperplane with a maximal margin. The principle behind such a so-called kernel function is explained in more detail in Section 2.1.1. In our setting, the mapping is provided by some data-driven similarity function, which, however, may not lead to a psd kernel and hence has to be preprocessed (for more details, see Section 2.1.4). As a primal representation, we will focus on similarities because the wide majority of algorithms is specified in the kernel space. A brief introduction is given in the following section.¹

Kernels and Kernel Functions

Let $\mathcal{X}$ be a collection of N objects $x_i$, $i=\mathrm{1,2},\dots ,N$, in some input space. Further, let $\varphi :\mathcal{X}\mapsto \mathrm{\mathscr{H}}$ be a mapping of patterns from $\mathcal{X}$ to a high-dimensional or infinite-dimensional Hilbert space $\mathrm{\mathscr{H}}$ equipped with the inner product ${\langle \cdot ,\cdot \rangle }_{\mathrm{\mathscr{H}}}$. The transformation ϕ is, in general, a non-linear mapping to a high-dimensional space $\mathrm{\mathscr{H}}$ and may commonly not be given in an explicit form. Instead of this, a kernel function $k:\mathcal{X}\times \mathcal{X}\mapsto \mathrm{ℝ}$ is given which encodes the inner product in $\mathrm{\mathscr{H}}$. The kernel k is a positive (semi) definite function such that $k\left(x,x^{\prime }\right)=\langle \varphi {\left(x\right)}^{\mathrm{\top }},\varphi \left(x^{\prime }\right)\rangle$ for any $x,x^{\prime }\in \mathcal{X}$. The matrix $K:={\text{Φ}}^{\mathrm{\top }}\text{Φ}$ is an $N\times N$ kernel matrix derived from the training data, where $\text{Φ}:\left[\varphi \left(x_1\right),\dots ,\varphi \left(x_N\right)\right]$ is a matrix of images (column vectors) of the training data in $\mathrm{\mathscr{H}}$. The motivation for such an embedding comes with the hope that the non-linear transformation of input data into higher dimensional $\mathrm{\mathscr{H}}$ allows for using linear techniques in $\mathrm{\mathscr{H}}$. Kernelized methods process the embedded data points in a feature space utilizing only the inner products ${\langle \cdot ,\cdot \rangle }_{\mathrm{\mathscr{H}}}$ (kernel trick) [28], without the need to calculate ϕ explicitly. The specific kernel function can be very generic, but in general, the kernel is expected to fulfill Mercer conditions [28]. Most prominent are the linear kernel with $k\left(x,x^{\prime }\right)=x^{\mathrm{\top }}{x}^{\prime }$ as the Euclidean inner product or the RBF kernel $k\left(x,x^{\prime }\right)=\text{exp}\left(-\left({\Vert x-x^{\prime }\Vert }^2/2{\sigma }^2\right)\right)$, with σ as a free parameter.

Support Vector Machine

In this paper, we address data-driven supervised learning; accordingly, our focus is primal on a domain-specific representation of the data by means of a generic similarity measure. There are many approaches for similarity-based learning and, in particular, kernel methods [28]. We will evaluate our data-driven encodings employing the support vector machine (SVM) as a state of the art supervised kernel method.

Let $x_i\in X,i\in \left\{1,\dots ,N\right\}$ be training points in the input space X , with labels $y_i\in \left\{-\mathrm{1,1}\right\}$, representing the class of each point.² The input space X is often considered to be ${\mathrm{ℝ}}^d$ but can be any suitable space due to the kernel trick. For a given positive penalization term C, the SVM is the minimum of the following regularized empirical risk functional.

$\underset{\omega ,\xi ,b}{\text{min}}\frac{1}{2}{\omega }^{\mathrm{\top }}\omega +C\stackrel{M}{{\displaystyle \sum }_{i=1}}{\xi }_i(1)$

subject to $y_i\left({\omega }^{\mathrm{\top }}\varphi \left(x_i\right)+b\right)\ge 1-{\xi }_i$ and ${\xi }_i\ge 0$. Here ω is the parameter vector of a separating hyperplane and b a bias term. The variables ξ are so-called slack variables. The goal is to find a hyperplane that correctly separates the data while maximizing the sum of distances to the closest positive and negative points (the margin). The parameter C controls the weight of the classification errors ($C=\infty$ in the separable case). Details can be found in 28.

In case of a positive semi-definite kernel function without metric violations, the underlying optimization problem is easily solved using, e.g., the Sequential Minimal Optimization Algorithm [20]. The objective of a SVM is to derive a model from the training set, which predicts class labels of unclassified feature sets in the test data. The decision function is given as:

$f\left(x\right)={\displaystyle \sum }_{i=1}^N{y}_i{\alpha }_{i}k\left(x_i,x\right)+b,$

where the ${\alpha }_i$ are the optimized Lagrange parameters of the dual formulation of Eq. 1. In case of a non-psd kernel function, the optimization problem of a SVM is no longer convex, but only a local optimum is obtained [19, 21]. As a result, the trained SVM model can become inaccurate and incorrect. However, as we will see in Section 2.1.4, there are several methods to handle non-psd kernel matrices within a classical SVM.

Representation in the Krein Space

A Krein space is an indefinite inner product space endowed with a Hilbertian topology. Let $\mathcal{K}$ be a real vector space. An inner product space with an indefinite inner product ${\langle \cdot ,\cdot \rangle }_{\mathcal{K}}$ on $\mathcal{K}$ is a bi-linear form where all $f,g,h\in \mathcal{K}$ and $\alpha \in \mathrm{ℝ}$ obey the following conditions:

$•\text{Symmetry}:{\langle f,g\rangle }_{\mathcal{K}}={\langle g,f\rangle }_{\mathcal{K}};$

$•\text{linearity}:{\langle \alpha f+g,h\rangle }_{\mathcal{K}}=\alpha {\langle f,h\rangle }_{\mathcal{K}}+{\langle g,h\rangle }_{\mathcal{K}};$

$•{\langle f,g\rangle }_{\mathcal{K}}=0\text{implies}f=0$

An inner product is positive semi definite if $\forall f\in \mathcal{K}$, ${\langle f,f\rangle }_{\mathcal{K}}\ge 0$, negative definite if $\forall f\in \mathcal{K}$, ${\langle f,f\rangle }_{\mathcal{K}}<0$, otherwise it is indefinite. A vector space $\mathcal{K}$ with inner product ${\langle \cdot ,\cdot \rangle }_{\mathcal{K}}$ is called an inner product space.

An inner product space $\left(\mathcal{K},{\langle \cdot ,\cdot \rangle }_{\mathcal{K}}\right)$ is a Krein space if we have two Hilbert spaces ${\mathrm{\mathscr{H}}}_{+}$ and ${\mathrm{\mathscr{H}}}_{-}$ spanning $\mathcal{K}$ such that $\forall f\in \mathcal{K}$ we have $f=f_{+}+f_{-}$ with $f_{+}\in {\mathrm{\mathscr{H}}}_{+}$ and $f_{-}\in {\mathrm{\mathscr{H}}}_{-}$ and $\forall f,g\in \mathcal{K}$, ${\langle f,g\rangle }_{\mathcal{K}}={\langle f_{+},g_{+}\rangle }_{{\mathrm{\mathscr{H}}}_{+}}-{\langle f_{-},g_{-}\rangle }_{{\mathrm{\mathscr{H}}}_{-}}$.

As outlined before, indefinite kernels are typically observed by means of domain-specific non-metric similarity functions (such as alignment functions used in biology [29]), by specific kernel functions - e.g., the Manhattan kernel $k\left(x,x^{\prime }\right)=-{\Vert x-x^{\prime }\Vert }_1$, tangent distance kernel [30] or divergence measures, plugged into standard kernel functions [9]. A finite-dimensional Krein-space is a so-called pseudo-Euclidean space.

Given a symmetric dissimilarity matrix with zero diagonal, an embedding of the data in a pseudo-Euclidean vector space determined by the eigenvector decomposition of the associated similarity matrix S is always possible [31] - as mentioned above, e.g., by a prior double centering. Given the eigendecomposition of S: $S=U\text{Λ}{U}^{\mathrm{\top }}$, we can compute the corresponding vectorial representation V in the pseudo-Euclidean space by

$V=U_{p+q+z}|{\text{Λ}}_{p+q+z}{|}^{1/2}(2)$

where ${\text{Λ}}_{p+q+z}$ consists of p positive, q negative non-zero eigenvalues and z zero eigenvalues. $U_{p+q+z}$ consists of the corresponding eigenvectors. The triplet $\left(p,q,z\right)$ is also referred to as the signature of the pseudo-Euclidean space. A detailed presentation of similarity and dissimilarity measures and mathematical aspects of metric and non-metric spaces is provided in 17, 32, 33.

Indefinite Proximity Functions

Proximity functions can be very generic but are often restricted to fulfill metric properties to simplify the mathematical modeling and especially the parameter optimization. In 32, a large variety of such measures was reviewed and basically most common methods nowadays make still use of metric properties. While this appears to be a reliable strategy, researchers in the field of e.g., psychology [34, 35], vision [14, 26, 36, 37] and machine learning [13, 38] have criticized this restriction as inappropriate in multiple cases. In fact, in 38 was shown that many real-life problems are better addressed by proximity measures, which are not restricted to be metric.

The triangle inequality is frequently violated, if we consider object comparisons in daily life problems, like the comparisons of text documents, biological sequence data, spectral data or graphs [23, 39, 40]. These data are inherently compositional and a representation as explicit (vectorial) features leads to information loss. As an alternative, tailored dissimilarity measures such as pairwise alignment functions, kernels for structures, or other domain-specific similarity and dissimilarity functions can be used as an interface to the data [41, 42]. Also for vectorial data, non-metric proximity measures are quite common in some disciplines. An example of this type is the use of divergence measures [9, 43, 44] which are very popular for spectral data analysis in chemistry, geo- and medical sciences [45–49], and are not metric in general. Also the popular Dynamic Time Warping (DTW) [6] algorithm provides a non-metric alignment score, which is often used as a proximity measure between two one-dimensional functions of different lengths. In image processing and shape retrieval, indefinite proximities are often obtained by means of the inner distance. This measure specifies the dissimilarity between two objects, which are represented by their shape only. Thereby, several seeding points are used and the shorted paths within the shape are calculated in contrast to the Euclidean distance between the landmarks. Further examples can be found in physics where problems of the special relativity theory or other research topics naturally lead to indefinite spaces [50].

A list of non-metric proximity measures is provided in Table 1 and some are exemplarily illustrated in Figures 1 and 2. Most of these measures are very popular but often violate the symmetry or triangle inequality condition or both. Hence many standard proximity-based machine learning methods like kernel methods are not easily accessible for these data.

FIGURE 1

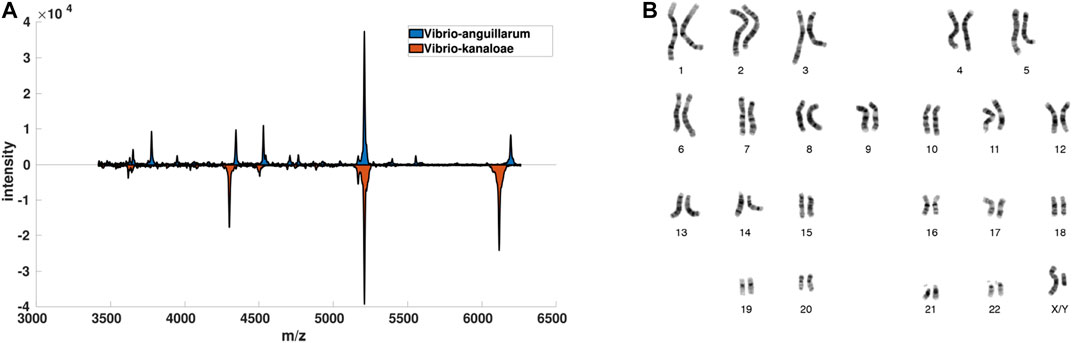
FIGURE 1. Visualization of data-driven data description scenarios. In (A) for some Vibrio bacteria and in (B) for Chromosome data. Both datasets are used in the experiments.

FIGURE 2

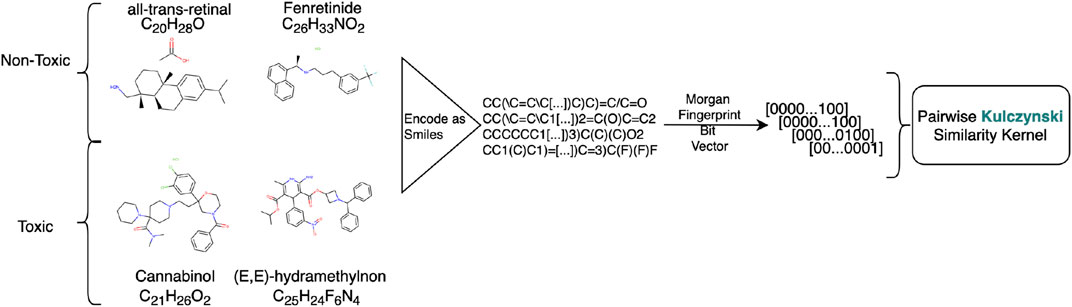
FIGURE 2. Preprocessing workflow for creating the Tox-21 datasets. Chemicals represented as SMILE codes are translated to Morgan Fingerprints. The kernel is created by using an application related pairwise similarity measure on the Morgan Fingerprints, in this case so-called Kulczynski.

Eigenspectrum Corrections

Although native models for indefinite learning are available (see e.g., [27, 51, 52]), they are not frequently used. This is mainly due to three reasons: 1) the proposed algorithms have in general, quadratic or cubic complexity [53], 2) the obtained models are non-sparse [54], and 3) the methods are complicated to implement [27, 55]. Considering the wide spread of machine learning frameworks, it would be very desirable to use the therein implemented algorithms - like an efficient support vector machine, instead of having the burden to implement another algorithm, and in general another numerical solver. Therefore, we focus on eigenspectrum corrections, which can be effectively done in a large number of frameworks without much effort.

A natural way to address the indefiniteness problem and to obtain a psd similarity matrix is to correct the eigenspectrum of the original similarity matrix S. Popular strategies include eigenvalue correction by flipping, clipping, squaring, and shifting. The non-psd similarity matrix S is decomposed by an eigendecomposition: $S=U\text{Λ}{U}^{\mathrm{\top }},$ where U contains the eigenvectors of S and $\text{Λ}$ contains the corresponding eigenvalues ${\lambda }_i$. Now, the eigenvalues in $\text{Λ}$ can be manipulated to eliminate all negative parts. After the correction, the matrix can be reconstructed, now being psd.

Clip Eigenvalue Correction

All negative eigenvalues in $\text{Λ}$ are set to 0 (see Figure 3B). The spectrum clip leads to the nearest psd matrix S in terms of the Frobenius norm [56]. Such a correction can be achieved by an eigendecomposition of the matrix S, a clipping operator on the eigenvalues, and the subsequent reconstruction. This operation has a complexity of $\mathcal{O}\left(N^3\right)$. The complexity might be reduced by either a low-rank approximation or the approach shown by 22 with roughly quadratic complexity.

FIGURE 3

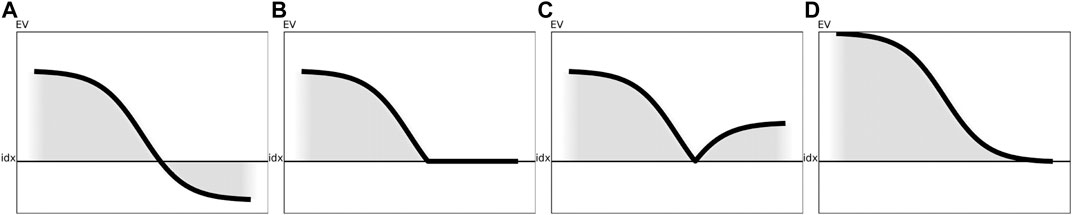
FIGURE 3. Visualization of the various preprocessing techniques for a generic eigenspectrum as obtained from a generic similarity matrix. The black line illustrates the impact of the respective correction method on the eigenspectrum without reordering of the eigenvalues. (A) Visualization of a sample eigenspectrum with pos./neg. eigenvalues. (B) Preprocessing of the eigenspectrum from Figure 3A using clip. (C) Preprocessing of the eigenspectrum from Figure 3A using flip. (D) Preprocessing of the eigenspectrum from Figure 3A using shift.

Flip Eigenvalue Correction

All negative eigenvalues in $\text{Λ}$ are set to ${\lambda }_i:=\left|{\lambda }_i\right|\forall i$, which at least keeps the absolute values of the negative eigenvalues and keeps potentially relevant information [17]. This operation can be calculated with $\mathcal{O}\left(N^3\right)$ or $\mathcal{O}\left(N^2\right)$ if low-rank approaches are used. Flip is illustrated in Figure 3C.

Square Eigenvalue Correction

All negative eigenvalues in $\text{Λ}$ are set to ${\lambda }_i:={\lambda }_i^2\forall i$ which amplifies large and very small eigenvalues. The square eigenvalue correction can be achieved by matrix multiplication [57] with $\approx \mathcal{O}\left(N^{2.8}\right)$.

Classical Shift Eigenvalue Correction

The shift operation was already discussed earlier by different researchers [58] and modifies $\text{Λ}$ such that ${\lambda }_i:={\lambda }_i-{\text{min}}_{ij}\text{Λ}\forall i$. The classical shift eigenvalue correction can be accomplished with linear costs if the smallest eigenvalue ${\lambda }_{\text{min}}$ is known. Otherwise, some estimator for ${\lambda }_{\text{min}}$ is needed. A few estimators for this purpose have been suggested: analyzing the eigenspectrum on a subsample, making a reasonable guess, or using some low-rank eigendecomposition. In our approach, we suggest employing a power iteration method, for example the von Mises approach, which is fast and accurate [59] or using the Gershgorin circle theorem [60, 61].

A spectrum shift enhances all the self-similarities and, therefore, the eigenvalues by the amount of ${\lambda }_{min}$ and does not change the similarity between any two different data points. However, it may also increase the intrinsic dimensionality of the data space and amplify noise contributions, as shown in Figure 3D. As already mentioned by 23, small eigenvalue contributions could be linked to noise in the original data. If now an eigencorrection step amplifies tiny eigenvalues, this can be considered as a noise amplification.

Limitations

Multiple approaches have been suggested to correct a similarity matrix’s eigenspectrum to obtain a psd matrix [17, 27]. Most approaches modify the eigenspectrum in a radical way and are also costly due to an involved cubic eigendecomposition. In particular, the flip, square and clip operator have an apparent strong impact. The flip operator affects all negative eigenvalues by changing the sign and this will additionally lead to a reorganization of the eigenvalues. The square operator is similar to flip but additionally emphasizes large eigencontributions while fading out eigenvalues below 1. The clip method is useful in case of noise; it may also remove valuable contributions. The clip operator only removes eigenvalues, but generally keeps the majority of the eigenvalues unaffected. The classical shift is another alternative operator changing only the diagonal of the similarity matrix leading to a shift of the whole eigenspectrum by the provided offset. This may also lead to reorganizations of the eigenspectrum due to new non-zero eigenvalue contributions. While this simple approach seems to be very reasonable, it has the significant drawback that all (!) eigenvalues are shifted, which also affects small or even 0 eigenvalue contributions. While 0 eigenvalues have no contribution in the original similarity matrix, they are artificially upraised by the classical shift operator. This may introduce a large amount of noise in the eigenspectrum, which could potentially lead to substantial numerical problems for employed learning algorithms, for example, kernel machines. If we consider the number of non-vanishing eigenvalues as a rough estimate of the intrinsic dimension of the data, a classical shift will increase this value. This may accelerate the curse of dimension problem on this modified data [62].

Advanced Shift Correction

To address the aforementioned challenges, we suggest an alternative formulation of the shift correction, subsequently referred to as advanced shift. In particular, we would like to keep the original eigenspectrum structure and aim for a sub-cubic eigencorrection. As mentioned in Section 2.3 the classical shift operator introduces noise artifacts for small eigenvalues. In the advanced shift procedure, we will remove these artificial contributions by a null space correction. This is particularly effective if non-zero, but small eigenvalues are also taken into account. Accordingly, we apply a low-rank approximation of the similarity matrix as an additional preprocessing step. The procedure is summarized in Algorithm 1.

The first part of the algorithm applies a low-rank approximation on the input similarities S using a restricted SVD or other technique [63]. If the number of samples $N\le 1000$, then the rank parameter $k=30$, otherwise $k=100$.³ The shift parameter λ is calculated on the low-rank approximated matrix, using a von Mises or power iteration [59] to determine the respective largest negative eigenvalue of the matrix. As shift parameter, we use the absolute value of λ for further steps. This procedure provides an accurate estimate of the largest negative eigenvalue, instead of making an educated guess as frequently suggested [51]. This is particularly relevant because the scaling of the eigenvalues can be very different between the various datasets, which may lead to an ineffective shift (still with negative eigenvalues left) if the guess is incorrect. The basis $\mathbf{B}$ of the nullspace is calculated, again by a restricted SVD. The nullspace matrix $\mathbf{N}$ is obtained by calculating a product of $\mathbf{B}$. Due to the low-rank approximation, we ensure that small eigenvalues, which are indeed close to 0 due to noise, are shrunk to 0 [64]. In the final step, the original S or the respective low-rank approximated matrix $\widehat{S}$ is shifted by the largest negative eigenvalue λ that is determined by von Mises iteration. By combining the shift with the nullspace matrix $\mathbf{N}$ and the identity matrix I, the whole matrix will be affected by the shift and not only the diagonal matrix. Finally, the doubled shift factor 2 ensures that the largest negative eigenvalue ${\widehat{\lambda }}^{\text{*}}$ of the new matrix ${\widehat{S}}^{\text{*}}$ will not become 0, but are kept as a contribution.

Complexity: The advanced shift approach shown in Algorithm 1 is comprised of various subtasks with different complexities. The low-rank approximation can be achieved with $\mathcal{O}\left(N^2\right)$ as well as the nullspace approximation. The shift parameter is calculated by von Mises iteration with $\mathcal{O}\left(N^2\right)$. Since $\mathbf{B}$ is a rectangular $N\times k$ matrix, the matrix $\mathbf{N}$ can be calculated with $\mathcal{O}\left(N^2\right)$. The final eigenvalue correction to obtain ${\widehat{S}}^{\text{*}}$ is also $\mathcal{O}\left(N^2\right)$. In summary, the low-rank advanced shift eigenvalue correction can be achieved with $\mathcal{O}\left(N^2\right)$ operations.

Efficient Approximation of the Smallest Eigenvalue

An alternative method to accelerate the estimation of the shift parameter λ is to approximate the region in which the smallest eigenvalue can be found. The identification of this region can be efficiently achieved by the Gershgorin circle theorem [60, 61]. Let $S=\left(s_{ij}\right)$ be a square matrix ($N\times N$) and $r_i={\displaystyle \sum }_{j\ne i}\left|s_{ij}\right|$ the row sums of this matrix. Then, within the Gershgorin circle theorem, one may define a disc $D_i$ in the complex plane with center $s_{ii}$ and radius $r_i$. In 61, it is shown why this can be employed to obtain a valid estimate of the eigenvalues of S. With $D_i=\left\{z\in \mathrm{ℂ}:\left|z-s_{ii}\right|\le r_i\right\}$, we obtain ranges that contain the eigenvalues of S: $\left[s_{ii}-r_i,s_{ii}+r_i\right]$. Hence one only has to calculate N row-sums and to evaluate the main diagonal of S. The obtained results can be used to find the minimum eigenvalue of S.

As an example, consider the following $3\times 3$ matrix for S:

$S=\left(\begin{array}{ccc}-6& 1& -1\\ 1& -2& 5\\ -1& 5& 10\end{array}\right)(3)$

The matrix is symmetric, so all eigenvalues are real. For each row in S, there is one Gershgorin circle defined by its center and its radius:

• $D_1$ with the center point $c_1=s_{11}=-6$ and $r_1=\left|1|+|-1\right|=2$

• $D_2$ with the center point $c_2=s_{22}=-2$ and $r_2=\left|1|+|5\right|=6$

• $D_3$ with the center point $c_3=s_{33}=10$ and $r_3=\left|-1|+|5\right|=6$

This implicates, all eigenvalues of S must lie in one of the ranges

$\left[s_{11}-r_1,s_{11}+r_1]=[-8,-4],[s_{22}-r_2,s_{22}+r_2]=[-\mathrm{8,4}],[s_{33}-r_3,s_{33}+r_3]=[\mathrm{4,16}\right].$

Performing the numerical computation shows that the eigenvalues are approximately $\left\{-6.6,-3.2,11.8\right\}$, all inside the determined ranges. Using the Gershgorin circle approach, we see that the minimum eigenvalue cannot be smaller than the minimum border value, in this example $-8$, while the right value is $\approx -6.6$. Figure 4 shows that all eigenvalues (green dots) of our matrix are within at least one of the circles.

FIGURE 4

FIGURE 4. Visualization of Gershgorin’s circle theorem on an exemplary matrix.

Since in a squared matrix, all centers of the circle are already given by their diagonals and the calculation of the radius only covers the summation of the elements in the respective row, this variant of the ShiftParameterDetermination in Algorithm 1 has a complexity of $\mathcal{O}\left(N\right)$. In the experiments, we apply the advanced shift correction on a low-rank approximation of S.

Structure preservation

In this context, the term structure preservation refers to the structure of the eigenspectrum with the requirement that those eigenvalues with a contribution in the original spectrum should keep their contribution in the new (but psd) spectrum. Those parts of the eigenspectrum that have no need for correction to construct a psd matrix should be kept unchanged. As illustrated by a synthetic example above in 3a - 3d, the various correction methods differently modify the eigenspectrum and some of them fundamentally change the structure of the eigenspectrum. Those modifications to the eigenvalues (and implicitly on the contribution to the matrix) are: changing the sign of an eigenvalue, changing its magnitude, removing the impact of an eigenvalue, adding artificial contribution to eigenvalues that had zero contribution in the original matrix, or changing the position of the eigenvalue with respect to the original ranking causing a profound reorganization of the eigenspectrum. Especially the last one is highly relevant in learning models that make use of only a few eigenvalues/eigenvectors such as kernel PCA or similar methods that reduce the dimensionality or make use of only the most meaningful eigenvalues and eigenvectors.

In order to illustrate the effects of the various correction methods, Figure 5 shows the impact of the most relevant correction methods on the properties of the eigenspectrum of a real-world dataset, here the protein dataset is used (see Section 2.5 for more details about this dataset).

FIGURE 5

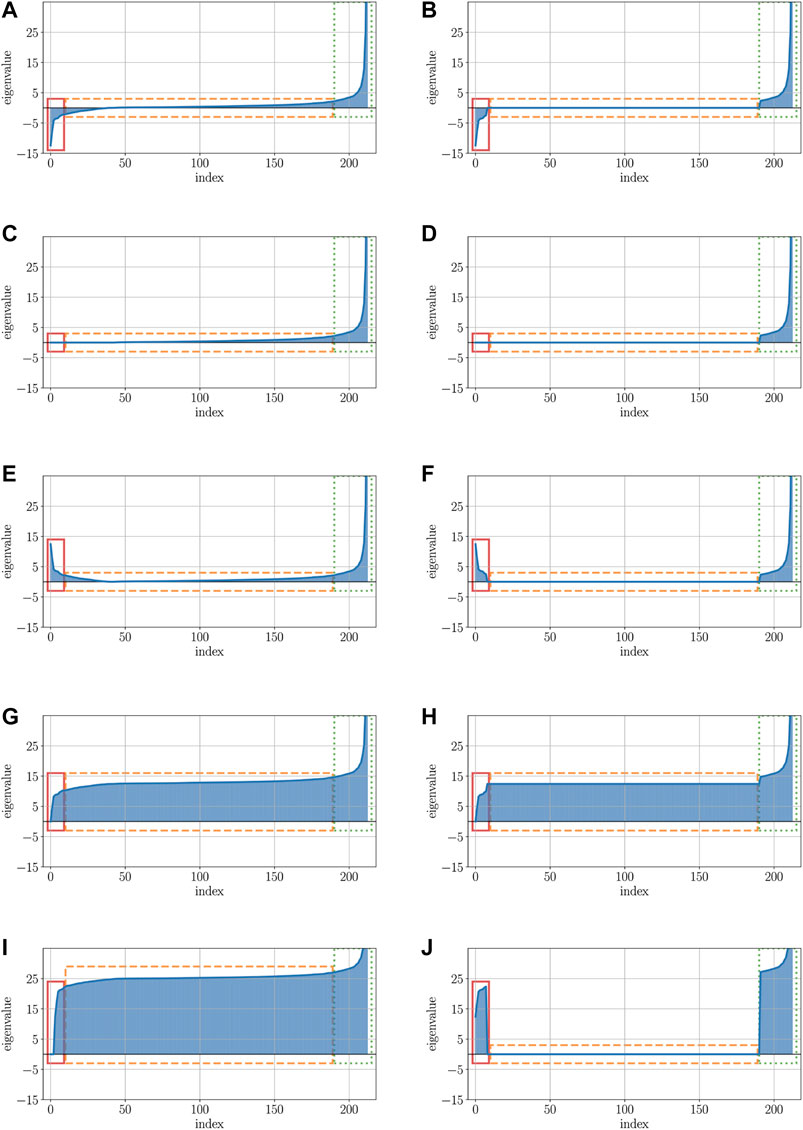
FIGURE 5. Visualizations of the protein data’s eigenspectra after applying various correction methods. (A) Visualization of the original eigenspectrum with pos. and neg. eigenvalues of the protein dataset. (B) Low-rank representation of the original eigenspectrum from Figure 5A. (C) Visualization of the original eigenspectrum of Figure 5A after clipping all neg. eigenvalues. (D) Visualization of the low-rank approximated eigenspectrum after clipping all neg. eigenvalues. (E) Visualization of the original eigenspectrum of Figure 5A after flipping all neg. eigenvalues. (F) Visualization of the low-rank approximated eigenspectrum after flipping all neg. eigenvalues. (G) Visualization of the original eigenspectrum of Figure 5A after shifting all neg. eigenvalues. (H) Visualization of the low-rank approximated eigenspectrum after shifting all neg. eigenvalues. (I) Visualization of the original eigenspectrum of Figure 5A after advanced shift. (J) Visualization of the low-rank approximated eigenspectrum of Figure 5B after advanced shift.

Here, the x-axis represents the index of the eigenvalue, while the y-axis illustrates the contribution value (or impact) of the eigenvalue. The left column of Figure 5 (Subfigures 5a, 5c, 5e, 5g, 5i) shows the eigenspectra without a low-rank representation, the right column (Subfigures 5b, 5d, 5f, 5h, 5j) comprises the low-rank version of the eigenspectrum: Figure 5A illustrates the eigenspectrum of the original dataset without any modification. The red rectangle (solid line) highlights the negative parts of the eigenvalues for which their contribution must be preserved in the data. The orange rectangle (dashed line) represents those eigenvalues that are close to zero or zero. The values of particularly these eigenvalues should be kept untouched such that their contribution is still irrelevant after the correction. The green rectangle (dotted line) highlights the positive parts of the eigenvalues which contribution should also be kept unchanged in order not to manipulate the eigenspectrum too aggressively. Figure 5B shows the low-rank representation of the original data of 5a. Here, the major negative and major positive eigenvalues (red/solid and green/dotted rectangle) are still present, but many eigenvalues that have been close to zero before, have now been set to exactly 0 (black/dashed rectangle).

Figures 5 C and D show the eigenvalues after applying the clip operator to the eigenvalues shown in Figures 5 A and B. In both cases, the major positive eigenvalues (green/dotted rectangle) remain unchanged, as well as the positive values close to 0 and exactly 0. However, the negative eigenvalues close to 0 (parts of the orange/dashed rectangle) and, in particular, the major negative eigenvalues (red/solid rectangle) are all set to exactly 0. By using the clip operator, the contribution to the eigenspectrum of both major negative and slightly negative eigenvalues is completely eliminated.

In contrast to clipping, the flip corrector preserves the contribution of the negative and slightly negative eigenvalues, shown in Figures 5 E and F. When using the flip corrector, only the negative sign of the eigenvalue is changed; thus, only the diagonal of the matrix is changed and not the rest. Since the square operator behaves almost analogously to the flip operator and only squares the negative eigenvalues in addition to flipping them, it was not listed separately here. Squaring the values of a matrix drastically increases the impact of the major eigenvalues compared to the minor eigenvalues. If an essential part of the data’s information is located in the small eigenvalues, this part gets a proportionally reduced contribution against the significantly increased major eigenvalues.

The modified eigenspectra after applications of the classical shift operator are presented in Figures 5 G and H: by increasing all eigenvalues of the spectrum, the part with the larger negative eigenvalues (red/solid rectangle) that had a higher impact now only remains with zero or close to zero contribution. Furthermore, a higher contribution was assigned to those eigenvalues that previously had no or nearly no effect on the eigenspectrum (orange/dashed rectangle). As a result, the classical shift increases the number of non-zero eigencontributions by introducing artificial noise into the data. The same is also evident for the advanced shift without low-rank approximation depicted in Figure 5I. Since there are many eigenvalues close to zero but not exactly zero in this data set, all these eigenvalues are also increased in the advanced shift, but can be cured in the low-rank approach.

Unlike the advanced shift approach without low-rank approximation, depicted in Figure 5I, a low-rank representation of the data leads to a shifting of only those eigenvalues that had relevant contributions before (red/solid rectangle). Eigenvalues with previously slightly zero contribution (orange/dashed rectangle), derive a contribution of exactly zero by the approximation and are therefore not shifted in the advanced shift method.

Considering the description of structure preservation outlined in 2.4, we observe that only the flip and the advanced shift correction (only with low-rank approximation) widely preserve the structure of the given eigenspectrum. For all other methods, the eigenspectrum is substantially modified in particular contributions are removed, amplified, or artificially introduced. In particular, this also holds for the clip or the classical shift corrector, which, however, are frequently recommended in the literature. Although this section contained results exclusively for the protein dataset, we observed similar findings for other indefinite datasets as well. Our findings show that a more sophisticated treatment of the similarity matrix is needed to obtain a suitable psd matrix. This makes our method more appropriate compared to simpler approaches such as the classic shift or clip.

Materials & Experimental Setup

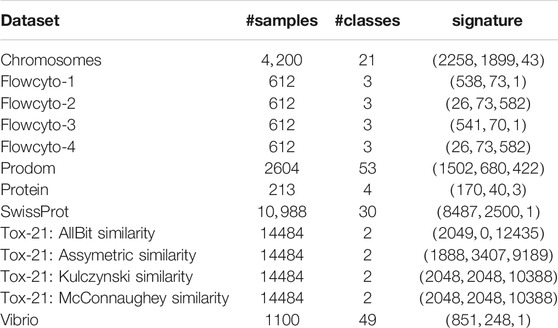
This section contains a series of experiments to highlight the effectiveness of our approach in combination with a low-rank approximation. We evaluate the algorithm for a set of benchmark data that are typically used in the context of proximity-based learning. The data are briefly described in the following and summarized in Table 2, with details given in the references. After a brief overview of the datasets used for the evaluation, the experimental setup, and the performance of the different eigenvalue correction methods on the benchmark datasets are presented and discussed in this section.

TABLE 2

TABLE 2. Overview of the different datasets. Details are given in the textual description.

Datasets:

In the experiments, all datasets exhibit indefinite spectral properties and are commonly characterized by pairwise distances or (dis-)similarities. As mentioned above, if the data are given as dissimilarities, a corresponding similarity matrix can be obtained by double centering [17]: $S=-JDJ/2$ with $J=\left(I-{11}^{\mathrm{\top }}/N\right)$, with identity matrix I and vector of ones 1. These datasets constitute typical examples of non-Euclidean data. In particular, the focus is on proximity-based data from the life science domain. We consider a broad spectrum of domain-specific data: from sequence analysis, mass spectrometry, chemical structure analysis to flow cytometry. In particular, the later one of flow cytometry [65] could also be important in the analysis of viral data like SARS-CoV-2 [66]. In all cases, dedicated preprocessing steps and (dis-)similarity measures for structures were used by the domain experts to create this data with respect to an appropriate proximity measure. The (dis-)similarity measures are inherently non-Euclidean and cannot be embedded isometrically in a Euclidean vector space. The datasets used for the experiments are described in the following and summarized in Table 2, with details given in the references.

1. Chromosomes: The Copenhagen chromosomes data set constitutes a benchmark from cytogenetics [67] with a signature (2258, 1899, 43). Karyotyping is a crucial process to classify chromosomes into standard classes and the results are routinely used by the clinicians to diagnose cancers and genetic diseases. A set of 4,200 human chromosomes from 21 classes (the autosomal chromosomes) are represented by grey-valued images. These are transferred to strings measuring the thickness of their silhouettes. These strings are compared using edit distance with insertion/deletion costs 4.5 [40].

2. Flowcyto This dissimilarity dataset is based on 612 FL3-A DNA flow cytometer histograms from breast cancer tissues in 256 resolution. The initial data were acquired by M. Nap and N. van Rodijnen of the Atrium Medical Center in Heerlen, The Netherlands, during 2000-2004, using tubes 3, 4,5, and 6 of a DACO Galaxy flowcytometer. Overall, this data set consists of four datasets, each representing the same data, but with different proximity measure settings. Histograms are labeled in 3 classes: aneuploid (335 patients), diploid (131), and tetraploid (146). Dissimilarities between normalized histograms are computed using the L1 norm, correcting for possible different calibration factors [68].

3. Prodom: the ProDom dataset with signature (1502,680,422) consists of 2604 protein sequences with 53 labels. It contains a comprehensive set of protein families and appeared first in the work of [69]. The pairwise structural alignments were computed by 69. Each sequence belongs to a group labeled by experts; here, we use the data as provided in 68.

4. Protein: the Protein data set has sequence-alignment similarities for 213 proteins and is used for comparing and classifying protein sequences according to its four classes of globins: heterogeneous globin (G), hemoglobin-A (HA), hemoglobin-B (HB) and myoglobin (M). The signature is (170,40,3), where class one through four contains 72, 72, 39, and 30 points, respectively [70].

5. SwissProt: the SwissProt data set (SWISS), with a signature (8487,2500,1), consists of 10,988 points of protein sequences in 30 classes taken as a subset from the popular SwissProt database of protein sequences [71]. The considered subset of the SwissProt database refers to the release 37. A typical protein sequence consists of a string of amino acids, and the length of the full sequences varies between 30 to more than 1000 amino acids depending on the sequence. The ten most common classes such as Globin, Cytochrome b, Protein kinase st, etc. provided by the Prosite labeling [72] were taken, leading to 5,791 sequences. Due to this choice, an associated classification problem maps the sequences to their corresponding Prosite labels. These sequences are compared using Smith-Waterman, which computes a local alignment of sequences [5]. This database is the standard source for identifying and analyzing protein sequences such that an automated classification and processing technique would be very desirable.

6. Tox-21: The initial intention of the Tox-21 challenges is to predict whether certain chemical compounds have the potential to disrupt processes in the human body that may lead to adverse health effects, i. e. are toxic to humans [73]. This version of the dataset contains 14484 molecules encoded as Simplified Molecular Input Line Entry Specification (SMILE) codes. SMILE codes are ASCII-strings to encode complex chemical structures. For example, Lauryldiethanolamine has the molecular formula of C$16$H$35$NO$2$ and is encoded as CCCCCCCCCCCCN(CCO)CCO. Each smile code is described as a morgan fingerprint [74, 75] and encoded as a bit-vector with a length of 2048 via the RDKit⁴ framework. The molecules are compared to each other using the non-psd binary similarity metrics AllBit, Kulczynski, McConnaughey, and Asymmetric provided by the RDKIT. The similarity matrix is constructed based on these pairwise similarities. According to the applied similarity metrics, the resulting matrices are varying in their signatures: AllBit (2049, 0, 12435), Asymmetric (1888, 3407, 9189), Kulczynski (2048, 2048, 10388), McConnaughey (2048, 2048,10388). The task of the dataset is binary classification, which is either toxic or non-toxic for every given molecule and should be predicted by a machine learning algorithm. Note that also graph-based representations for smile data are possible [76].

7. Vibrio: Bacteria of the genus Vibrio are Gram-negative, primarily facultative anaerobes, forming motile rods. Contact with contaminated water and consumption of raw seafood are the primary infection factors for Vibrio-associated diseases. Vibrio parahaemolyticus, for instance, is one of the leading causes of foodborne gastroenteritis worldwide. The Vibrio data set consists of 1,100 samples of Vibrio bacteria populations characterized by mass spectra. The spectra encounter approximately 42,000 mass positions. The full data set consists of 49 classes of vibrio-sub-species. The mass spectra are preprocessed with a standard workflow using the BioTyper software [12]. As usual, mass spectra display strong functional characteristics due to the dependency of subsequent masses, such that problem-adapted similarities such as described in 12, 77 are beneficial. In our case, similarities are calculated using a specific similarity measure as provided by the BioTyper software [12] with a signature (851,248,1).

Results

In this section, we evaluate our strategy of data-driven proximity-based analysis and highlight the performance of the proposed advanced shift correction on the previously mentioned datasets against other eigenvalue correction methods using a standard SVM classifier. For this purpose, the correction approaches ensure that the input similarity, herein used as a kernel matrix, is psd. This is particularly important for kernel methods to keep expected convergence properties. During the experiments, we measured the algorithm’s mean accuracy and its standard deviation in a ten-fold cross-validation. Additionally, we captured the complexity of the model based on the number of necessary support vectors for the SVM. Therefore, we track the percentage of training data points, the SVM model needs as support vectors to indicate the model’s complexity.

In each experiment, the parameter C has been selected for each correction method by a grid search on independent data not used during the tests. For better comparability of the considered methods, the results presented here refer exclusively to the use of the low-rank approximated matrices in the SVM. Only when employing the original data for the SVM, no low-rank approximation was implemented to ensure that small negative eigenvalues were not inadvertently removed if they were of low-rank. Please note, that a low-rank approximation only, does not lead to a psd matrix. Accordingly, convergence problems and uncontrolled information loss, by means of discrimination power, may still occur. Furthermore, both proposed methods for the determination of the shift parameter proposed in section 2.4 were tested on the low-rank approximated datasets against the other eigenvalue correction methods. The results for the classification performance for the advanced shift methods against the other correction methods are shown in Table 3. In column Adv. Shift, we show the classification performance for the advanced shift with the exact determination of the smallest eigenvalue, whereas column Adv.-GS contains the classification performance of the advanced shift, which applied the Gershgorin theorem to approximate the smallest eigenvalue. For the Prodom data, it is known from 27 that the SVM has convergence problems (not converged - subsequently n.c.) on the indefinite input matrix.

TABLE 3

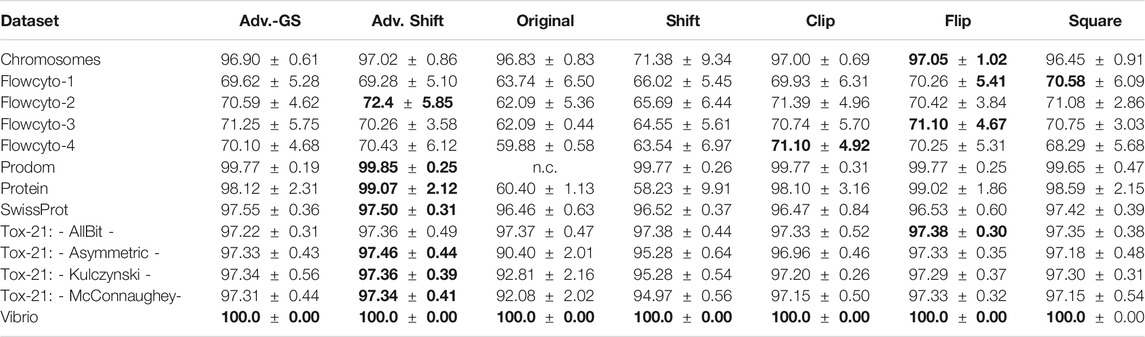
TABLE 3. Prediction accuracy (mean $\pm$ standard-deviation) for the various data sets and methods in comparison to the advanced shift method. Column Adv. Shift shows the performance of the advanced shift method and column Adv.-GS provides the performance of the advanced shift using the Gershgorin approach to estimate the minimum eigenvalue.

In general, the accuracies of the various correction methods are quite similar and rarely differ significantly. As expected, a correction step is needed and the plain use of uncorrected data is suboptimal, often with a clear drop in the performance or may fail. Also, the use of the classical shift operator can not be recommended due to suboptimal results in various cases. In summary, the presented Advanced Shift with the exact determination of the shift parameter performed best, followed by the flip corrector. The results in Table 3 also show that the accuracy of the Gershgorin shift variant is not substantially lower compared to the other methods.

In most cases, the Gershgorin advanced shift performs as well as the clip and the square correction method. Compared to the classic shift, our Gershgorin advanced shift consistently results in much better accuracies. The reason for this is the appropriate preservation of the structure of the eigenspectrum, as shown in Section 2.4. It becomes evident that not only the dominating eigenvalues have to be kept, but the preservation of the entire structure of the eigenspectrum is important to obtain reliable results in general. As the application of the low-rank approximation to similarity matrices leads to a large number of truly zero eigenvalues, both variants of the advanced shift corrections become more effective. Both proposed approaches benefit from eigenspectra with many close to zero eigenvalues, which occurs in many practical data, especially in complex domains like life sciences. Surprisingly, the classical shift operator is still occasionally preferred in the literature [51, 58, 78], despite its reoccurring limitations. The herein proposed advanced shift outperforms the classical shift in almost every experimental setup. In fact, many datasets have an intrinsic low-rank nature, which we employ in our approach but which is not considered in the classical eigenvalue shift. In any case, the classical shift increases the intrinsic dimensionality, also if many eigenvalues have already been of zero contribution in the original matrix. This leads to substantial performance loss in the classification models, as seen in the results. Considering the results of Table 3, the advanced shift correction is preferable in most scenarios.

Additionally to the accuracy of the different correction methods, the number of support vectors of each SVM model was gathered. Table 4 shows the complexity of the generated SVM models in terms of their required support vectors. Thus, the number of support vectors is set in relation to the number of all the available training data points required to build a solid decision boundary. The higher this percentage, the more data points were needed to create the separation plane, leading to a more complex model. As explained in 79 or 80, the run time complexity can become considerably higher with an increasing number of support vectors.

TABLE 4

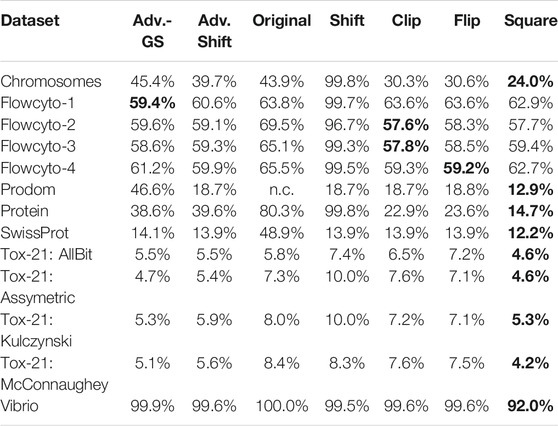
TABLE 4. Average percentage of data points that are needed by the SVM models for building a well-fitting decision hyperplane.

Compared to the original SVM without the low-rank approximation, it becomes evident that our approach generally requires fewer and occasionally significantly fewer support vectors and is therefore considerably less complex. Furthermore, in comparison to the classic shift corrector, the advanced shift is significantly superior in both accuracy and required support vectors. However, compared to clip, flip, and square, things are slightly different: Table 4 shows, the advanced shift can keep up with the clipping and flipping but has a higher percentage of support vectors compared to the square correction method. Considering the slightly better accuracy and the lower computational cost from Section 2.2 than clip and flip, the advanced shift is preferable to clip and flip eigenvalue correction and competitive to the square correction.

In summary, as pointed out also in previous work, there is no simple solution for handling non-psd matrices or the correction of eigenvalues. The results make evident that the proposed variants of the advanced shift correction are especially useful if the negative eigenvalues are meaningful and a low-rank approximation of the similarity matrix preserves the relevant eigenvalues. The analysis also shows that domain-specific measures by means of a data-driven analysis are effectively possible and keep relevant information. The presented strategies allow the use of standard machine learning approaches, like kernel methods without much hassle.

Discussion

In this paper, we addressed the topic of data-driven supervised learning by general proximity measures. In particular, we presented an alternative formulation of the classical eigenvalue shift, preserving the structure of the eigenspectrum of the data, such that the inherent data properties are kept. For this advanced shift method, we also presented a novel strategy that approximates the shift parameter based on the Gershgorin circles theorem.

Furthermore, we pointed to the limitations of the classical shift induced by the shift of all eigenvalues, including those with small or zero eigenvalue contributions. Surprisingly, the classical shift eigenvalue correction is nevertheless frequently recommended in the literature, pointing out that only a suitable offset needs to be applied to shift the matrix to psd. However, it is rarely mentioned that this shift affects the entire eigenspectrum and thus increases the contribution of eigenvalues that had no contribution in the original matrix.

As a result of our approach, the eigenvalues that had vanishing contribution before the shift remain irrelevant after the shift. Those eigenvalues with a high contribution keep their relevance, leading to the preservation of the eigenspectrum but with a positive (semi-)definite matrix. In combination with the low-rank approximation, our approach was, in general, better compared to the classical methods. Moreover, also the approximated version of the advanced shift via Gershgorin circles theorem performed as well as the classical methods.

We analyzed the effectiveness of data-driven learning on a broad spectrum of classification problems from the life science domain. The use of domain-specific proximity measures originally caused a number of challenges for practitioners, but with the recent work on indefinite learning, substantial improvements are available. In fact, our experiments with eigenvalue correction methods, especially the advanced shift approach, which keeps the eigenspectrum intact, have shown promising results on many real-life problems. In this way, domain-specific non-standard proximity measures allow the effective analysis of life science data in a data-driven way.

Future work on this subject will include the reduction of the computational costs using advanced matrix approximation and decomposition techniques in the different sub-steps. Another field of interest is a possible adoption of the advanced shift to unsupervised scenarios.

Finally, it remains to be said that the analysis of life science data offers tremendous potential for understanding complex processes in domains such as (bio)chemistry, biology, environmental research, or medicine. Many challenges have already been tackled and solved, but there are still many open issues in these areas where the analysis of complex data can be a key component in understanding these processes.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://bitbucket.fiw.fhws.de:8443/users/popp/repos/proximitydatasetbenchmark/browse.

Author Contributions

MM, CR and FMS contributed conception and design of the study; CR preprocessed and provided the Tox-21 database; MM performed the statistical analysis; MM and FMS wrote the first draft of the manuscript; MM, CR, FMS and MB wrote sections of the manuscript. All authors contributed to manuscript revision, read and approved the submitted version.

Funding

FMS, MM are supported by the ESF program WiT-HuB/2014-2020, project IDA4KMU, StMBW-W- IX.4-170792. FMS, CR are supported by the FuE program of the StMWi, project OBerA, grant number IUK-1709- 0011// IUK530/010.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Gaelle Bonnet-Loosli for providing support with indefinite learning and R. Duin, Delft University for various support with DisTools and PRTools. We would like to thank Dr. Markus Kostrzewa and Dr. Thomas Maier for providing the Vibrio data set and expertise regarding the biotyping approach and Dr. Katrin Sparbier for discussions about the SwissProt data (all Bruker Corp.). A related conference publication by the same authors was published at ICPRAM 2020 see [15] - copyright related material is not affected.

Footnotes

¹ For data given as dissimilarity matrix, the associated similarity matrix can be obtained, in a non-destructive way, by double centering (17) of the dissimilarity matrix. $S=-JDJ/2$ with $J=\left(I-{11}^{\mathrm{\top }}/N\right)$, identity matrix I and vector of ones ?.

² In case of more than two classes we use the one vs all approach.

³ The settings for k are taken as a rule of thumb without further fine-tuning.

⁴ https://www.rdkit.org/

References

1. Biehl, M, Hammer, B, Schneider, P, and Villmann, T. Metric learning for prototype-based classification. In: M Bianchini, M Maggini, F Scarselli, LC Jain, editors. Innovations in Neural Information Paradigms and Applications. Studies in Computational Intelligence, Vol. 247: Springer (2009). p. 183–99

Google Scholar

2. Hastie, T, Tibshirani, R, and Friedman, J. The Elements of Statistical Learning. New York: Springer (2001).

Google Scholar

3. Nebel, D, Kaden, M, Villmann, A, and Villmann, T. Types of (dis-)similarities and adaptive mixtures thereof for improved classification learning. Neurocomputing (2017). 268:42–54. doi:10.1016/j.neucom.2016.12.091CrossRef Full Text

CrossRef Full Text | Google Scholar

4. Schölkopf, B, and Smola, A. Learning with Kernels. MIT Press (2002).

Google Scholar

5. Gusfield, D. Algorithms on Strings, trees, and sequences: Computer science and computational biology. Cambridge University Press (1997).

Google Scholar

6. Sakoe, H, and Chiba, S. Dynamic programming algorithm optimization for spoken word recognition, IEEE Trans Acoust Speech Signal Process (1978). 26:43–49. doi:10.1109/tassp.1978.1163055CrossRef Full Text

Google Scholar

7. Ling, H, and Jacobs, DW. Using the inner-distance for classification of articulated shapes. In 2005 IEEE computer society conference on computer vision and pattern recognition (CVPR 2005), 20-26 June 2005. San Diego, CA, USA: IEEE Computer Society (2005). p 719–26.

Google Scholar

8. Cilibrasi, R, and Vitányi, PMB. Clustering by compression. IEEE Trans Inform Theory (2005). 51:1523–45. doi:10.1109/tit.2005.844059CrossRef Full Text

CrossRef Full Text | Google Scholar

9. Cichocki, A, and Amari, S-I. Families of alpha- beta- and gamma- divergences: Flexible and robust measures of similarities. Entropy (2010). 12:1532–68. doi:10.3390/e12061532CrossRef Full Text

CrossRef Full Text | Google Scholar

10. Lee, J, and Verleysen, M. Generalizations of the lp norm for time series and its application to self-organizing maps. In: M. Cottrell, editor. 5th Workshop on Self-Organizing Maps. Vol. 1 (2005). p 733–40.

Google Scholar

11. Dubuisson, MP, and Jain, A. A modified hausdorff distance for object matching. In Pattern recognition, 1994. Vol. 1–conference A: Computer vision amp; Image processing., proceedings of the 12th IAPR international conference. Vol. (1994). p. 566–568.

CrossRef Full Text | Google Scholar

12. Maier, T, Klebel, S, Renner, U, and Kostrzewa, M. Fast and reliable maldi-tof ms–based microorganism identification. Nature Methods (2006). 3:1–2. doi:10.1038/nmeth870.

CrossRef Full Text | Google Scholar

13. Pekalska, E, Duin, RPW, Günter, S, and Bunke, H. On not making dissimilarities euclidean. In SSPR&SPR 2004 (2004). p. 1145–1154.

Google Scholar

14. Scheirer, WJ, Wilber, MJ, Eckmann, M, and Boult, TE. Good recognition is non-metric. Patt Recog (2014). 47:2721–2731. doi:10.1016/j.patcog.2014.02.018CrossRef Full Text

Google Scholar

15. Münch, M., Raab, C., Biehl, M, and Schleif, F. Structure preserving encoding of non-euclidean similarity data. In Proceedings of the 9th international conference on pattern recognition applications and methods–Volume 1: ICPRAM,. INSTICC (SciTePress) (2020). p 43–51. doi:10.5220/0008955100430051

CrossRef Full Text | Google Scholar

16. Gisbrecht, A, and Schleif, FM. Metric and non-metric proximity transformations at linear costs. Neurocomputing (2015). 167:643–57. doi:10.1016/j.neucom.2015.04.017CrossRef Full Text

Google Scholar

17. Pekalska, E, and Duin, R. The dissimilarity representation for pattern recognition. World Scientific (2005).

Google Scholar

18. Vapnik, V. The nature of statistical learning theory. Statistics for engineering and information science. Springer (2000).

Google Scholar

19. Ying, Y, Campbell, C, and Girolami, M. Analysis of svm with indefinite kernels. In: Y Bengio, D Schuurmans, J D Lafferty, CKI Williams, A Culotta, editors Advances in neural information processing systems 22: Curran Associates, Inc. (2009). p 2205–13.

Google Scholar

20. Platt, JC. Fast training of support vector machines using sequential minimal optimization. In: Advances in kernel methods: Support vector learning. Cambridge, MA: MIT Press (1999). p 185–208.

Google Scholar

21. Lin, H, and Lin, C. A study on sigmoid kernels for SVM and the training of non-PSD kernels by SMO-type methods. Neural Comput (2003). 1–32. doi:10.1.1.14.6709

CrossRef Full Text | Google Scholar

22. Luss, R, and d’Aspremont, A. Support vector machine classification with indefinite kernels. Math Prog Comp (2009). 1:97–118. doi:10.1007/s12532-009-0005-5CrossRef Full Text

Google Scholar

23. Chen, Y, Garcia, E, Gupta, M, Rahimi, A, and Cazzanti, L. Similarity-based classification: concepts and algorithms. J Mac Learn Res (2009). 10:747–76.

Google Scholar

24. Indyk, P, Vakilian, A, and Yuan, Y. Learning-based low-rank approximations. In: HM Wallach, H Larochelle, A Beygelzimer, F d’Alché-Buc, EB Fox, R Garnett, editors. Advances in Neural Information Processing Systems 32: Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, 8-14 December 2019, Vancouver, BC, Canada (2019). p. 7400–10.

Google Scholar

25. Williams, CKI, and Seeger, MW. Using the nyström method to speed up kernel machines. In: TK Leen, TG Dietterich, and V Tresp editors Advances in neural information processing systems 13, Papers from neural information processing systems (NIPS) 2000 Denver, CO: MIT Press (2000). p 682–688.

Google Scholar

26. Xu, W, Wilson, R, and Hancock, E. Determining the cause of negative dissimilarity eigenvalues. LNCS 6854: LNCS (2011). p 589–597.

Google Scholar

27. Schleif, FM, and Tiño, P. Indefinite proximity learning: A review. Neural Computation (2015). 27:2039–96. doi:10.1162/neco_a_00770CrossRef Full Text | Pubmed

Google Scholar

28. Shawe-Taylor, J, and Cristianini, N. Kernel methods for pattern analysis and discovery. Cambridge University Press (2004).

Google Scholar

29. Smith, TF, and Waterman, MS. Identification of common molecular subsequences. J Mol Biol (1981). 147:195–197. doi:10.1016/0022-2836(81)90087-5

Pubmed | CrossRef Full Text | Google Scholar

30. Haasdonk, B, and Keysers, D. Tangent distance kernels for support vector machines. ICPR (2002). (2). 864–868. doi:10.1109/icpr.2002.1048439

CrossRef Full Text | Google Scholar

31. Goldfarb, L. A unified approach to pattern recognition. Patt Recog (1984). 17:575–582. doi:10.1016/0031-3203(84)90056-6CrossRef Full Text

Google Scholar

32. Deza, M, and Deza, E. Encyclopedia of Distances. Springer (2009).

Google Scholar

33. Ong, CS, Mary, X, Canu, S, and Smola, AJ. Learning with non-positive kernels. In: CE Brodley editor. Machine learning, proceedings of the twenty-first international conference (ICML 2004), Banff, Alberta, Canada, July 4-8, 2004. ACM international conference proceeding series: ACM, Vol. 69 (2004). p 81. doi:10.1145/1015330.1015443

Google Scholar

34. Hodgetts, CJ, and Hahn, U. Similarity-based asymmetries in perceptual matching. Acta Psychologica (2012). 139:291–299. doi:10.1016/j.actpsy.2011.12.003

PubMed | CrossRef Full Text | Google Scholar

35. Hodgetts, CJ, Hahn, U, and Chater, N. Transformation and alignment in similarity. Cognition (2009). 113:62–79. doi:10.1016/j.cognition.2009.07.010

CrossRef Full Text | Pubmed | Google Scholar

36. Kinsman, T, Fairchild, M, and Pelz, J. Color is not a metric space implications for pattern recognition, machine learning, and computer vision. In Proceedings of Western New York image processing workshop, WNYIPW 2012 (2012). p. 37–40.

Google Scholar

37. Van Der Maaten, L, and Hinton, G. Visualizing non-metric similarities in multiple maps. Mac Learn (2012). 87:33–55. doi:10.1007/s10994-011-5273-4

Google Scholar

38. Duin, RPW, and Pekalska, E. Non-euclidean dissimilarities: causes and informativeness. In SSPR&SPR 2010 (2010). p. 324–33.

Google Scholar

39. Kohonen, T, and Somervuo, P. How to make large self-organizing maps for nonvectorial data. Neural Networks (2002). 15:945–52. doi:10.1016/s0893-6080(02)00069-2

PubMed | CrossRef Full Text | Google Scholar

40. Neuhaus, M, and Bunke, H. Edit distance-based kernel functions for structural pattern classification. Patt Recog (2006). 39:1852–63. doi:10.1016/j.patcog.2006.04.012CrossRef Full Text

Google Scholar

41. Gärtner, T, Lloyd, JW, and Flach, PA. Kernels and distances for structured data. Mac Learn (2004). 57:205–32. doi:10.1023/B:MACH.0000039777.23772.30CrossRef Full Text

Google Scholar

42. Poleksic, A. Optimal pairwise alignment of fixed protein structures in subquadratic time. J Bioinform Comput Biol (2011). 9:367–82. doi:10.1142/s0219720011005562CrossRef Full Text

Google Scholar

43. Zhang, Z, Ooi, BC, Parthasarathy, S, and Tung, AKH. Similarity search on Bregman divergence. Proc VLDB Endow (2009). 2:13–24. doi:10.14778/1687627.1687630CrossRef Full Text

Google Scholar

44. Schnitzer, D, Flexer, A, and Widmer, G. A fast audio similarity retrieval method for millions of music tracks. Multimed Tools Appl (2012). 58:23–40. doi:10.1007/s11042-010-0679-8CrossRef Full Text

Google Scholar

45. Mwebaze, E, Schneider, P, and Schleif, FM. Divergence based classification in learning vector quantization. Neurocomputing (2010). 74:1429–35. doi:10.1016/j.neucom.2010.10.016

CrossRef Full Text | Google Scholar

46. Nguyen, NQ, Abbey, CK, and Insana, MF. Objective assessment of sonographic: Quality ii acquisition information spectrum. IEEE Trans Med Imag (2013). 32:691–98. doi:10.1109/tmi.2012.2231963

PubMed | CrossRef Full Text | Google Scholar

47. Tian, J, Cui, S, and Reinartz, P. Building change detection based on satellite stereo imagery and digital surface models. IEEE Trans Geosci Remote Sens (2013). 52(1):406–417. doi:10.1109/tgrs.2013.2240692

CrossRef Full Text | Google Scholar

48. van der Meer, F. The effectiveness of spectral similarity measures for the analysis of hyperspectral imagery. Int J Appl Earth Obser Geoinf (2006). 8:3–17. doi:10.1016/j.jag.2005.06.001CrossRef Full Text

Google Scholar

49. Bunte, K, Haase, S, Biehl, M, and Villmann, T. Stochastic neighbor embedding (SNE) for dimension reduction and visualization using arbitrary divergences. Neurocomputing (2012). 90:23–45. doi:10.1016/j.neucom.2012.02.034CrossRef Full Text

Google Scholar

50. Mohammadi, M, Petkov, N, Bunte, K, Peletier, RF, and Schleif, FM. Globular cluster detection in the GAIA survey. Neurocomputing (2019). 342:164–171. doi:10.1016/j.neucom.2018.10.081CrossRef Full Text

Google Scholar

51. Loosli, G. Trik-svm: an alternative decomposition for kernel methods in krein spaces. In: M Verleysen editor. Proceedings of the 27th european symposium on artificial neural networks (ESANN) 2019. Evere, Belgium: D-side Publications (2019). p. 79–94

Google Scholar

52. Mehrkanoon, S, Huang, X, and Suykens, JAK. Indefinite kernel spectral learning. Patt Recog (2018). 78:144–153. doi:10.1016/j.patcog.2018.01.014CrossRef Full Text

Google Scholar

53. Schleif, F, Tiño, P, and Liang, Y. Learning in indefinite proximity spaces - recent trends. In: 24th european symposium on artificial neural networks, ESANN 2016; 2016 April 27-29; Bruges, Belgium. (2016). p. 113–122.

Google Scholar

54. Loosli, G, Canu, S, and Ong, CS. Learning SVM in Kreĭn spaces. IEEE Trans Patt Anal Mach Intell (2016). 38:1204–16. doi:10.1109/tpami.2015.2477830

Pubmed | CrossRef Full Text | Google Scholar

55. Schleif, FM, and Tiño, P. Indefinite core vector machine. Patt Recog (2017). 71:187–195. doi:10.1016/j.patcog.2017.06.003. CrossRef Full Text

Google Scholar

56. Higham, NJ. Computing a nearest symmetric positive semidefinite matrix. Linear Algebra and Its Applications (1988). 103:103–118. doi:10.1016/0024-3795(88)90223-6CrossRef Full Text

Google Scholar

57. Strassen, V. Gaussian elimination is not optimal. Numer Math (1969). 13:354–356. doi:10.1007/bf02165411CrossRef Full Text

Google Scholar

58. Filippone, M. Dealing with non-metric dissimilarities in fuzzy central clustering algorithms. International Journal of Approximate Reasoning (2009). 50:363–384. doi:10.1016/j.ijar.2008.08.006CrossRef Full Text

Google Scholar

59. Mises, RV, and Pollaczek-Geiringer, H. Praktische Verfahren der Gleichungsauflösung. Z Angew Math Mech (1929). 9:152–164. doi:10.1002/zamm.19290090206CrossRef Full Text

Google Scholar

60. Gerschgorin, S. Ueber die abgrenzung der eigenwerte einer matrix. Izvestija Akademii Nauk SSSR, Serija Matematika (1931). 7:749–54.

Google Scholar

61. Varga, RS. Geršgorin and his circles. In: Springer series in computational mathematics. Springer Berlin Heidelberg (2004).

Google Scholar

62. Verleysen, M, and François, D. The curse of dimensionality in data mining and time series prediction. In: J Cabestany, A Prieto, and FS Hernández, editors. Computational intelligence and bioinspired systems, 8th international work-conference on artificial neural networks, IWANN 2005. Lecture Notes in Computer Science; 2005 June 8-10; Vilanova i la Geltrú, Barcelona, Spain, Proceedings: Vol. 3512: Springer (2005). p. 758–770.

Google Scholar

63. Sanyal, A, Kanade, V, and Torr, PHS. Low rank structure of learned representations. CoRR (2018). doi:CoRR abs/1804.07090

Google Scholar

64. Ilic, M, Turner, IW, and Saad, Y. Linear system solution by null-space approximation and projection (SNAP). Numer Linear Algebra Appl (2007). 14:61–82.

Google Scholar

65. Aghaeepour, N, Finak, G, Hoos, H, Mosmann, TR, Brinkman, R, Gottardo, R, et al. Critical assessment of automated flow cytometry data analysis techniques. Nat Methods (2013). 10:228–238. doi:10.1038/nmeth.2365

PubMed | CrossRef Full Text | Google Scholar

66. Ou, X, Liu, Y, Lei, X, Li, P, Mi, D, and Ren, L. Characterization of spike glycoprotein of sars-cov-2 on virus entry and its immune cross-reactivity with sars-cov. Nat Commun (2020). 11:1620. doi:10.1038/s41467-020-15562-9

PubMed | CrossRef Full Text | Google Scholar

67. Lundsteen, C, Phillip, J, and Granum, E. Quantitative analysis of 6985 digitized trypsin g-banded human metaphase chromosomes. Clin Genet (1980). 18:355–370 doi:10.1111/j.1399-0004.1980.tb02296.x

PubMed | CrossRef Full Text | Google Scholar

68. Duin, RP [Dataset]: PRTools (2012).

Google Scholar

69. Roth, V, Laub, J, Buhmann, JM, and Müller, KR. Going metric: denoising pairwise data. In: NIPS (2002). p. 817–824.

Google Scholar

70. Hofmann, T, and Buhmann, JM. Pairwise data clustering by deterministic annealing. IEEE Trans Patt Anal Machine Intell (1997). 19:1–14. doi:10.1109/34.566806CrossRef Full Text

Google Scholar

71. Boeckmann, B, Bairoch, A, Apweiler, R, Blatter, MC, Estreicher, A, and Gasteiger, E. The swiss-prot protein knowledgebase and its supplement trembl in 2003. Nucleic Acids Res (2003). 31:365–370. doi:10.1093/nar/gkg095

Pubmed | CrossRef Full Text | Google Scholar

72. Gasteiger, E, Gattiker, A, Hoogland, C, Ivanyi, I, Appel, R, and Bairoch, A. Expasy: the proteomics server for in-depth protein knowledge and analysis. Nucleic Acids Res (2003). 31. doi:10.1093/nar/gkg563

PubMed | CrossRef Full Text | Google Scholar

73. Huang, R, Xia, M, Nguyen, DT, Zhao, T, Sakamuru, S, and Zhao, J. Tox21challenge to build predictive models of nuclear receptor and stress response pathways as mediated by exposure to environmental chemicals and drugs. Front Environ Sci (2016). 3:85. doi:10.3389/fenvs.2015.00085CrossRef Full Text

Google Scholar

74. Figueras, J. Morgan revisited. J Chem Inf Model (1993). 33, 717–718. doi:10.1021/ci00015a009CrossRef Full Text

Google Scholar

75. Ralaivola, L, Swamidass, SJ, Saigo, H, and Baldi, P. Graph kernels for chemical informatics. Neural Networks (2005). 18:1093–1110. doi:10.1016/j.neunet.2005.07.009CrossRef Full Text

Google Scholar

76. Bacciu, D, Lisboa, P, Martín, JD, Stoean, R, and Vellido, A. Bioinformatics and medicine in the era of deep learning. In: 26th european symposium on artificial neural networks, ESANN 2018; 2018 April 25-27; Bruges, Belgium (2018). p. 345–354.

Google Scholar

77. Barbuddhe, SB, Maier, T, Schwarz, G, Kostrzewa, M, Hof, H, and Domann, E. Rapid identification and typing of listeria species by matrix-assisted laser desorption ionization-time of flight mass spectrometry. Appl Environ Microbiol (2008). 74:5402–5407. doi:10.1128/aem.02689-07

PubMed | CrossRef Full Text | Google Scholar

78. Chakraborty, J. Non-metric pairwise proximity data. [PhD thesis]: Berlin Institute of Technology (2004).

Google Scholar

79. Burges, CJC. Simplied support vector decision rules. Icml (1996).

Google Scholar

80. Osuna, E, and Girosi, F. Reducing the run-time complexity of support vector machines. International conference on pattern recognition (1998).

Google Scholar