Financial Forecasting With α-RNNs: A Time Series Modeling Approach

The era of modern financial data modeling seeks machine learning techniques which are suitable for noisy and non-stationary big data. We demonstrate how a general class of exponential smoothed recurrent neural networks (α-RNNs) are well suited to modeling dynamical systems arising in big data applications such as high frequency and algorithmic trading. Application of exponentially smoothed RNNs to minute level Bitcoin prices and CME futures tick data, highlight the efficacy of exponential smoothing for multi-step time series forecasting. Our α-RNNs are also compared with more complex, “black-box”, architectures such as GRUs and LSTMs and shown to provide comparable performance, but with far fewer model parameters and network complexity.

1. Introduction

Recurrent neural networks (RNNs) are the building blocks of modern sequential learning. RNNs use recurrent layers to capture non-linear temporal dependencies with a relatively small number of parameters (Graves, 2013). They learn temporal dynamics by mapping an input sequence to a hidden state sequence and outputs, via a recurrent layer and a feedforward layer.

There have been exhaustive empirical studies on the application of recurrent neural networks to prediction from financial time series data such as historical limit order book and price history (Borovykh et al., 2017; Dixon, 2018; Borovkova and Tsiamas, 2019; Chen and Ge, 2019; Mäkinen et al., 2019; Sirignano and Cont, 2019). Sirignano and Cont (2019) find evidence that stacking networks leads to superior performance on intra-day stock data combined with technical indicators, whereas (Bao et al., 2017) combine wavelet transforms and stacked autoencoders with LSTMs on OHLC bars and technical indicators. Borovykh et al. (2017) find evidence that dilated convolutional networks out-perform LSTMs on various indices. Dixon (2018) demonstrate that RNNs outperform feed-forward networks with lagged features on limit order book data.

There appears to be a chasm between the statistical modeling literature (see, e.g., Box and Jenkins 1976; Kirchgässner and Wolters 2007; Hamilton 1994) and the machine learning literature (see. e.g., Hochreiter and Schmidhuber 1997; Pascanu et al. 2012; Bayer 2015). One of the main contributions of this paper is to demonstrate how RNNs, and specifically a class of novel exponentially smoothed RNNs (α-RNNs), proposed in (Dixon, 2021), can be used in a financial time series modeling framework. In this framework, we rely on statistical diagnostics in combination with cross-validation to identify the best choice of architecture. These statistical tests characterize stationarity and memory cut-off length and provide insight into whether the data is suitable for longer-term forecasting and whether the model must be non-stationary.

In contrast to state-of-the-art RNNs such as LSTMs and Gated Recurrent Units (GRUs) (Chung et al., 2014), which were designed primarily for speech transcription, the proposed class of α-RNNs is designed for times series forecasting using numeric data. α-RNNs not only alleviate the gradient problem but are designed to i) require fewer parameters and numbers of recurrent units and considerably fewer samples to attain the same prediction accuracy¹; ii) support both stationary and non-stationary times series²; and iii) be mathematically accessible and characterized in terms of well known concepts in classical time series modeling, rather than appealing to logic and circuit diagrams.

As a result, through simple analysis of the time series properties of α-RNNs, we show how the value of the smoothing parameter, α, directly characterizes its dynamical behavior and provides a model which is both more intuitive for time series modeling than GRUs and LSTMs while performing comparably. We argue that for time series modeling problems in finance, some of the more complicated components, such as reset gates and cell memory present in GRUs and LSTMs but absent in α-RNNs, may be redundant for our data. We exploit these properties in two ways i) first, we using a statistical test for stationarity to determine whether to deploy a static or dynamic α-RNN model; and ii) we are able to reduce the training time, memory requirements for storing the model, and in general expect α-RNN to be more accurate for shorter time series as they require less training data and are less prone to over-fitting. The latter is a point of practicality as many applications in finance are not necessarily big data problems, and the restrictive amount of data favors an architecture with fewer parameters to avoid over-fitting.

The remainder of this paper is outlined as follows. Section 2 introduces the static α-RNN. Section 3 bridges the time series modeling approach with RNNs to provide insight on the network properties. Section 4 introduces a dynamic version of the model and illustrates the dynamical behavior of α. Details of the training, implementation and experiments using financial data together with the results are presented in Section 5. Finally, Section 6 concludes with directions for future research.

2. α-RNNs

Given auto-correlated observations of covariates or predictors, ${\mathit{x}}_t$, and continuous responses ${\mathit{y}}_t$ at times $t=1,\dots ,N$, in the time series data $\mathcal{D}:={\left\{\left({\mathit{x}}_t,{\mathit{y}}_t\right)\right\}}_{t=1}^N$, our goal is to construct an m-step ($m>0$) ahead times series predictor, ${\widehat{\mathit{y}}}_{t+m}=F\left({\mathit{x}\_}_t\right)$, of an observed target, ${\mathit{y}}_{t+m}\in {\mathrm{ℝ}}^n$, from a p length input sequence ${\mathit{x}\_}_t$

${\mathit{y}}_{t+m}:=F\left({\mathit{x}\_}_t\right)+u_t,\text{where}{\mathit{x}\_}_t:=\left\{{\mathit{x}}_{t-p+1},\dots ,{\mathit{x}}_t\right\},$

${\mathit{x}}_{t-j}=:L^j\left[{\mathit{x}}_t\right]$ is the $j^{th}$ lagged observation of ${\mathbf{x}}_t\in {\mathrm{ℝ}}^d$, for $j=0,\dots ,p-1$ and $u_t$ is the homoscedastic model error at time t. We introduce the α-RNN model (as shown in Figure 1):

${\widehat{\mathit{y}}}_{t+m}=F_{W,b,\alpha }\left({\mathit{x}\_}_t\right)(1)$

where $F_{W,b,\alpha }\left({\mathit{x}\_}_t\right)$ is an $\alpha \in \left[\mathrm{0,1}\right]$ smoothed RNN with weight matrices $W:=\left(W_h,U_h,W_y\right)$, where the input weight matrix $W_h\in {\mathrm{ℝ}}^{H\times d}$, the recurrence weight matrix $U_h\in {\mathrm{ℝ}}^{H\times H}$, the output weight matrix $W_y\in {\mathrm{ℝ}}^{n\times H}$, and H is the number of hidden units. The hidden and output bias vectors are given by $\mathit{b}:=\left({\mathit{b}}_h,{\mathit{b}}_y\right)$.

FIGURE 1

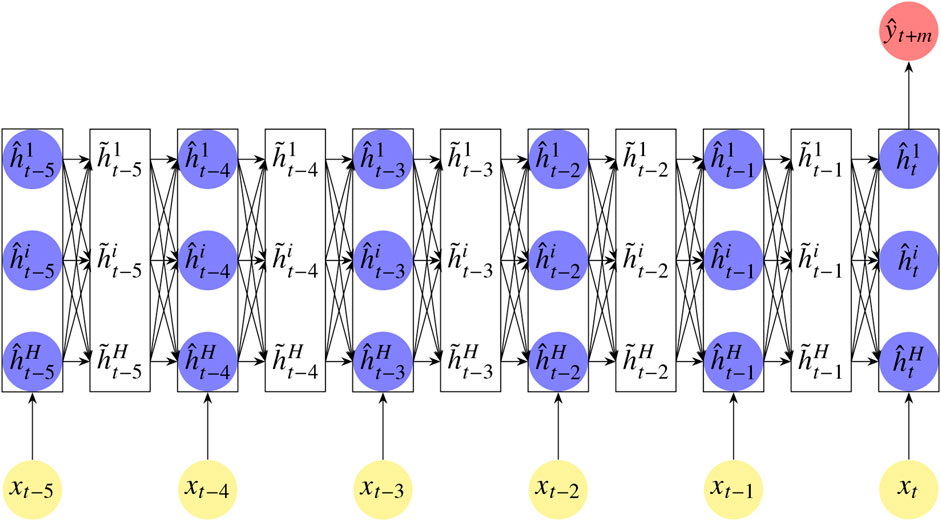
FIGURE 1. An illustrative example of an α-RNN with an alternating hidden recurrent layer (with blue nodes) and a smoothing layer (white block), “unfolded” over a sequence of six time steps. Each lagged feature ${\mathit{x}}_{t-i}$ in the sequence ${\mathit{x}\_}_t$ is denoted by the yellow nodes. The hidden recurrent layer contains H units (blue nodes) and the ith output, after smoothing, at time step t is denoted by ${\tilde{\mathit{h}}}_t^i$. At the last time step t, the hidden units connect to a single unactivated output unit to give ${\widehat{y}}_{t+m}$ (red node).

For each index in a sequence, s = t-p+2, … ,t, forward passes repeatedly update a hidden internal state ${\widehat{h}}_s\in {\mathrm{ℝ}}^H$, using the following model:

$\begin{array}{c}\left(\text{output}\right){\widehat{\mathit{y}}}_{t+m}=W_y{\widehat{\mathit{h}}}_t+{\mathit{b}}_y,\\ \left(\text{hidden state update}\right){\widehat{\mathit{h}}}_s=\sigma \left(U_h{\tilde{\mathit{h}}}_{s-1}+W_h{\mathit{x}}_s+{\mathit{b}}_h\right),s=t-p+2,\dots ,t\\ \left(\text{smoothing}\right){\tilde{\mathit{h}}}_s=\alpha {\widehat{\mathit{h}}}_s+\left(1-\alpha \right){\tilde{\mathit{h}}}_{s-1},\end{array}$

where $\sigma \left(\right):=tanh\left(\right)$ is the activation function and ${\tilde{\mathit{h}}}_s\in {\mathrm{ℝ}}^{\mathit{H}}$ is an exponentially smoothed version of the hidden state ${\widehat{\mathit{h}}}_s$, with the starting condition in each sequence, ${\widehat{\mathit{h}}}_{t-p+1}=\sigma \left(W_h{\mathit{x}}_{t-p+1}\right)$.

3. Univariate Times Series Modeling With Endogenous Features

This section bridges the time series modeling literature (Box and Jenkins, 1976; Kirchgässner and Wolters, 2007; Li and Zhu, 2020) and the machine learning literature. More precisely, we show the conditions under which plain RNNs are identical to autoregressive time series models and thus how RNNs generalize autoregressive models. Then we build on this result by applying time series analysis to characterize the behavior of static α-RNNs.

We shall assume here for ease of exposition that the time series data is univariate and the predictor is endogenous³, so that the data is $\mathcal{D}:={\left\{y_t\right\}}_{t=1}^N$.

We find it instructive to show that plain RNNs are non-linear AR(p) models. For ease of exposition, consider the simplest case of a RNN with one hidden unit, $H=1$. Without loss of generality, we set $U_h=W_h=\varphi$, $W_y=1$, $b_h=0$ and $b_y=\mu$. Under backward substitution, a plain-RNN, $F_{W,b}\left({\mathit{x}\_}_t\right)$, with sequence length p, is a non-linear auto-regressive, $NAR\left(p\right)$, model of order p: :

$\begin{array}{c}{\widehat{h}}_{t-p+1}=\sigma \left(\varphi y_{t-p+1}\right)\\ {\widehat{h}}_{t-p+2}=\sigma \left(\varphi {\widehat{h}}_{t-p+1}+\varphi y_{t-p+2}\right)\\ \dots =\dots \\ {\widehat{h}}_t=\sigma \left(\varphi {\widehat{h}}_{t-1}+\varphi y_t\right)\\ {\widehat{y}}_{t+m}={\widehat{h}}_t+\mu \end{array}$

then

${\widehat{y}}_{t+m}=\mu +\sigma (\varphi (1+\sigma (\varphi (L+\sigma (\varphi (L^2+\dots +\sigma \left(\varphi L^{p-1}\right)\dots )\left[y_t\right].(2)$

When the activation is the identity function $\sigma :=I_d$, then we recover the AR(p) model

${\widehat{y}}_{t+m}=\mu +{\displaystyle \sum }_{i=0}^{p-1}{\varphi }_{i+1}{L}^i\left[y_t\right],{\varphi }_i:={\varphi }^i.(3)$

with geometrically decaying autoregressive coefficients when $\left|\varphi \right|<1$.

The α-RNN(p) is almost identical to a plain RNN, but with an additional scalar smoothing parameter, α, which provides the recurrent network with “long-memory”⁴. To see this, let us consider a one-step ahead univariate α-RNN(p) in which the smoothing parameter is fixed and $H=1$.

This model augments the plain-RNN by replacing ${\widehat{h}}_{s-1}$ in the hidden layer with an exponentially smoothed hidden state ${\tilde{h}}_{s-1}$. The effect of the smoothing is to provide infinite memory when $\alpha \ne 1$. For the special case when $\alpha =1$, we recover the plain RNN with short memory of length $p\ll N$.

We can easily verify this informally by simplifying the parameterization and considering the unactivated case. Setting $b_y=b_h=0$, $U_h=W_h=\varphi \in \mathrm{ℝ}$ and $W_y=1$:

${\widehat{y}}_{t+1}={\widehat{h}}_t,(4)$

$=\varphi \left({\tilde{h}}_{t-1}+y_t\right),(5)$

$=\varphi \left(\alpha {\widehat{h}}_{t-1}+\left(1-\alpha \right){\tilde{h}}_{t-2}+y_t\right),(6)$

with the starting condition in each sequence, ${\widehat{h}}_{t-p+1}=\varphi y_{t-p+1}$. With out loss of generality, consider $p=2$ lags in the model so that ${\widehat{h}}_{t-1}=\varphi y_{t-1}$. Then

${\widehat{h}}_t=\varphi \left(\alpha \varphi y_{t-1}+\left(1-\alpha \right){\tilde{h}}_{t-2}+y_t\right)(7)$

and the model can be written in the simpler form

${\widehat{y}}_{t+1}={\varphi }_1{y}_t+{\varphi }_2{y}_{t-1}+\varphi \left(1-\alpha \right){\tilde{h}}_{t-2},(8)$

with auto-regressive weights ${\varphi }_1:=\varphi$ and ${\varphi }_2:=\alpha {\varphi }^2$. We now see that there is a third term on the RHS of Eq. 8 which vanishes when $\alpha =1$ but provides infinite memory to the model since ${\tilde{h}}_{t-2}$ depends on $y_1$, the first observation in the whole time series, not just the first observation in the sequence. To see this, we unroll the recursion relation in the exponential smoother:

${\tilde{h}}_{t+1}=\alpha {\displaystyle \sum }_{s=0}^{t-1}{\left(1-\alpha \right)}^s{\widehat{h}}_{t-s}+{\left(1-\alpha \right)}^t{y}_1.(9)$

where we used the property that ${\tilde{h}}_1=y_1$. It is often convenient to characterize exponential smoothing by the half-life⁵. To gain further insight on the memory of the network, Dixon (2021) study the partial auto-correlations of the process ${\widehat{y}}_{t+m}+u_t$ to characterize the memory and derive various properties and constraints needed for network stability and sequence length selection.

4. Multivariate Dynamic α-RNNS

We now return to the more general multivariate setting as in Section 2. The extension of RNNs to dynamical time series models, suitable for non-stationary time series data, relies on dynamic exponential smoothing. This is a time dependent, convex, combination of the smoothed output, ${\tilde{\mathit{h}}}_t$, and the hidden state ${\widehat{\mathit{h}}}_t$:

${\tilde{\mathit{h}}}_{t+1}={\mathit{\alpha }}_t\circ {\widehat{\mathit{h}}}_t+\left(1-{\mathit{\alpha }}_t\right)\circ {\tilde{\mathit{h}}}_t,(10)$

where $\circ$ denotes the Hadamard product between vectors and where ${\mathit{\alpha }}_t\in {\left[\mathrm{0,1}\right]}^H$ denotes the dynamic smoothing factor which can be equivalently written in the one-step-ahead forecast of the form

${\tilde{\mathit{h}}}_{t+1}={\tilde{\mathit{h}}}_t+{\mathit{\alpha }}_t\circ \left({\widehat{\mathit{h}}}_t-{\tilde{\mathit{h}}}_t\right).(11)$

Hence the smoothing can be viewed as a dynamic form of latent forecast error correction. When ${\left({\mathit{\alpha }}_t\right)}_i=0$, the $i^{th}$ component of the latent forecast error is ignored and the smoothing merely repeats the $i^{th}$ component of the current hidden state ${\left({\tilde{\mathit{h}}}_t\right)}_i$, which enforces the removal of the $i^{th}$ component from the memory. When ${\left({\mathit{\alpha }}_t\right)}_i=1$, the latent forecast error overwrites the current $i^{th}$ component of the hidden state ${\left({\tilde{\mathit{h}}}_t\right)}_i$. The smoothing can also be viewed as a weighted sum of the lagged observations, with lower or equal weights, ${\mathit{\alpha }}_{t-s}\circ {{{\displaystyle \prod }}^{\text{}}}_{r=1}^s\left(1-{\mathit{\alpha }}_{t-r+1}\right)$ at the $s\ge 1$ lagged hidden state, ${\widehat{\mathit{h}}}_{t-s}$:

${\tilde{\mathit{h}}}_{t+1}={\mathit{\alpha }}_t\circ {\widehat{\mathit{h}}}_t+{\displaystyle \sum }_{s=1}^{t-1}{\mathit{\alpha }}_{t-s}\circ \underset{r=1}{{\displaystyle \prod }^s}\left(1-{\mathit{\alpha }}_{t-r+1}\right)\circ {\widehat{\mathit{h}}}_{t-s}+g\left(\mathit{\alpha }\right),$

where $g\left(\mathit{\alpha }\right):={{{\displaystyle \prod }}^{\text{}}}_{r=0}^{t-1}\left(1-{\mathit{\alpha }}_{t-r}\right)\circ {\tilde{\mathit{y}}}_1$. Note that for any ${\left({\mathit{\alpha }}_{t-r+1}\right)}_i=1$, the $i^{th}$ component of the smoothed hidden state ${\left({\tilde{\mathit{h}}}_{t+1}\right)}_i$ will have no dependency on all the lagged $i^{th}$ components of hidden states ${\left\{{\left({\widehat{\mathit{h}}}_{t-s}\right)}_i\right\}}_{s\ge r}$. The model simply forgets the $i^{th}$ component of the hidden states at or beyond the $r^{th}$ lag.

4.1. Neural Network Exponential Smoothing

While the class of ${\alpha }_t$-RNN models under consideration is free to define how α is updated (including changing the frequency of the update) based on the hidden state and input, a convenient choice is use a recurrent layer. Remaining in the more general setup with a hidden state vector ${\widehat{\mathit{h}}}_t\in {\mathrm{ℝ}}^H$, let us model the smoothing parameter ${\widehat{\mathit{\alpha }}}_t\in {\left[\mathrm{0,1}\right]}^H$ to give a filtered time series

${\tilde{\mathit{h}}}_t={\widehat{\mathit{\alpha }}}_t\circ {\widehat{\mathit{h}}}_t+\left(1-{\widehat{\mathit{\alpha }}}_t\right)\circ {\tilde{\mathit{h}}}_{t-1}.(12)$

This smoothing is a vectorized form of the above classical setting, only here we note that when ${\left({\mathit{\alpha }}_t\right)}_i=1$, the $i^{th}$ component of the hidden variable is unmodified and the past filtered hidden variable is forgotten. On the other hand, when ${\left({\mathit{\alpha }}_t\right)}_i=0$, the $i^{th}$ component of the hidden variable is obsolete, instead setting the current filtered hidden variable to its past value. The smoothing in Eq. 12 can be viewed then as updating long-term memory, maintaining a smoothed hidden state variable as the memory through a convex combination of the current hidden variable and the previous smoothed hidden variable.

The hidden variable is given by the semi-affine transformation:

${\widehat{\mathit{h}}}_t=\sigma \left(U_h{\tilde{\mathit{h}}}_{t-1}+W_h{\mathit{x}}_t+{\mathit{b}}_h\right),(13)$

which in turn depends on the previous smoothed hidden variable. Substituting Eq. 13 into Eq. 12 gives a function of ${\tilde{\mathit{h}}}_{t-1}$ and ${\mathit{x}}_t$:

${\tilde{\mathit{h}}}_t=g\left({\tilde{\mathit{h}}}_{t-1},{\mathit{x}}_t;\mathit{\alpha }\right)(14)$

$:={\widehat{\mathit{\alpha }}}_t\circ \sigma \left(U_h{\tilde{\mathit{h}}}_{t-1}+W_h{\mathit{x}}_t+{\mathit{b}}_h\right)+\left(1-{\widehat{\mathit{\alpha }}}_t\right)\circ {\tilde{\mathit{h}}}_{t-1}.(15)$

We see that when ${\left({\mathit{\alpha }}_t\right)}_i=0$, the $i^{th}$ component of the smoothed hidden variable ${\left({\tilde{\mathit{h}}}_t\right)}_i$ is not updated by the input ${\mathit{x}}_t$. Conversely, when ${\left({\mathit{\alpha }}_t\right)}_i=1$, we observe that the $i^{th}$ hidden variable locally behaves like a non-linear autoregressive series. Thus the smoothing parameter can be viewed as the sensitivity of the smoothed hidden state to the input ${\mathit{x}}_t$.

The challenge becomes how to determine dynamically how much error correction is needed. As in GRUs and LSTMs, we can address this problem by learning $\widehat{\mathit{\alpha }}=F_{\left(W_{\alpha },U_{\alpha },b_{\alpha }\right)}\left({\mathit{x}\_}_t\right)$ from the input variables with the recurrent layer parameterized by weights and biases $\left(W_{\alpha },U_{\alpha },{\mathit{b}}_{\alpha }\right)$. The one-step ahead forecast of the smoothed hidden state, ${\tilde{\mathit{h}}}_t$, is the filtered output of another plain RNN with weights and biases $\left(W_h,U_h,{\mathit{b}}_h\right)$.

5. Results

This section describes numerical experiments using financial time series data to evaluate the various RNN models. All models are implemented in v1.15.0 of TensorFlow (Abadi et al., 2016). Times series cross-validation is performed using separate training, validation and test sets. To preserve the time structure of the data and avoid look ahead bias, each set represents a contiguous sampling period with the test set containing the most recent observations. To prepare the training, validation and testing sets for m-step ahead prediction, we set the target variables (responses) to the $t+m$ observation, $y_{t+m}$, and use the lags from $t-p+1,\dots t$ for each input sequence. This is repeated by incrementing t until the end of each set. In our experiments, each element in the input sequence is either a scalar or vector and the target variables are scalar.

We use the SimpleRNN Keras method with the default settings to implement a fully connected RNN. Tanh activation functions are used for the hidden layer with the number of units found by time series cross-validation with five folds to be $H\in \left\{\mathrm{5,10,20}\right\}$ and $L_1$ regularization, ${\lambda }_1\in \left\{0,{10}^{-3},{10}^{-2}\right\}$. The Glorot and Bengio uniform method (Glorot and Bengio, 2010) is used to initialize the non-recurrent weight matrices and an orthogonal method is used to initialize the recurrence weights as a random orthogonal matrix. Keras’s GRU method is implemented using version 1,406.1078v, which applies the reset gate to the hidden state before matrix multiplication. See Appendix 1.1 for a definition of the reset gate. Similarly, the LSTM method in Keras is used. Tanh activation functions are used for the recurrence layer and sigmoid activation functions are used for all other gates. The AlphaRNN and AlphatRNN classes are implemented by the authors for use in Keras. Statefulness is always disabled.

Each architecture is trained for up to 2000 epochs with an Adam optimization algorithm with default parameter values and using a mini-batch size of 1,000 drawn from the training set. Early stopping is implemented using a Keras call back with a patience of 50 to 100 and a minimum loss delta between ${10}^{-8}$ and ${10}^{-6}$. So, for example, if the patience is set to 50 and the minimum loss delta is ${10}^{-8}$, then fifty consecutive loss evaluations on mini-batch updates must each lie within ${10}^{-8}$ of each other before the training terminates. In practice, the actual number of epoches required varies between trainings due to the randomization of the weights and biases, and across different architectures and is typically between 200 and 1,500. The 2000 epoch limit is chosen as it provides an upper limit which is rarely encountered. No random permutations are used in the mini-batching sampling in order to preserve the ordering of the time series data. To evaluate the forecasting accuracy, we set the forecast horizon to up to ten steps ahead instead of the usual step ahead forecasts often presented in the machine learning literature—longer forecasting horizons are often more relevant due to operational constraints in industry applications and are more challenging when the data is non-stationary since the fixed partial auto-correlation of the process ${\widehat{y}}_{t+m}+u_t$ will not adequately capture the observed changing partial auto-correlation structure of the data. In the experiments below, we use $m=4$ and $m=10$ steps ahead. The reason we use less than $m=10$ in the first experiment is because we find that there is little memory in the data beyond four lags and hence it is of little value to predict beyond four time steps.

5.1. Bitcoin Forecasting

One minute snapshots of USD denominated Bitcoin mid-prices are captured from Coinbase over the period from January 1 to November 10, 2018. We demonstrate how the different networks forecast Bitcoin prices using lagged observations of prices. The predictor in the training and the test set is normalized using the moments of the training data only so as to avoid look-ahead bias or introduce a bias in the test data. We accept the Null hypothesis of the augmented Dickey-Fuller test as we can not reject it at even the 90% confidence level. The data is therefore stationary (contains at least one unit root). The largest test statistic is $-2.094$ and the p-value is 0.237 (the critical values are 1%: -3.431, 5%: -2.862, and 10%: -2.567). While the partial autocovariance structure is expected to be time dependent, we observe a short memory of only four lags by estimating the PACF over the entire history (see Figure 2).

FIGURE 2

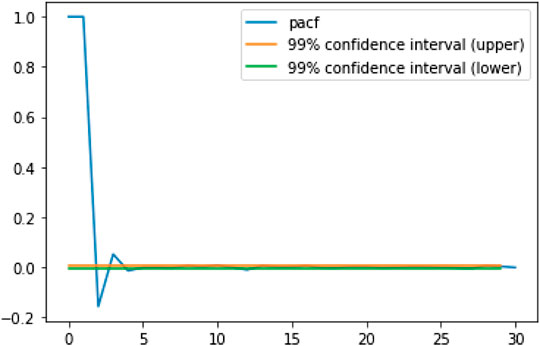
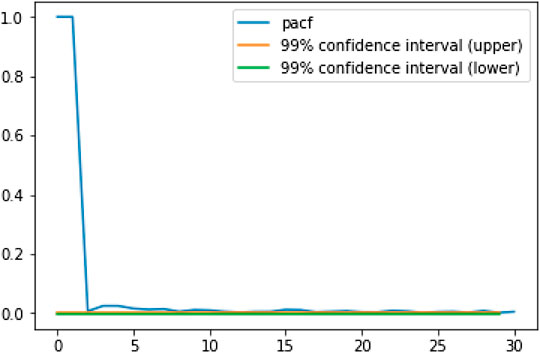
FIGURE 2. The partial autocorrelogram (PACF) for 1 min snapshots of Bitcoin mid-prices (USD) over the period January 1, 2018 to November 10, 2018.

We choose a sequence length of $p=4$ based on the PACF and perform a four-step ahead forecast. We comment in passing that there is little, if any, merit in forecasting beyond this time horizon given the largest significant lag indicated by the PACF. Figure 3 compares the performance of the various forecasting networks and shows that stationary models such as the plain RNN and the α-RNN least capture the price dynamics—this is expected because the partial autocorrelation is non-stationary.

FIGURE 3

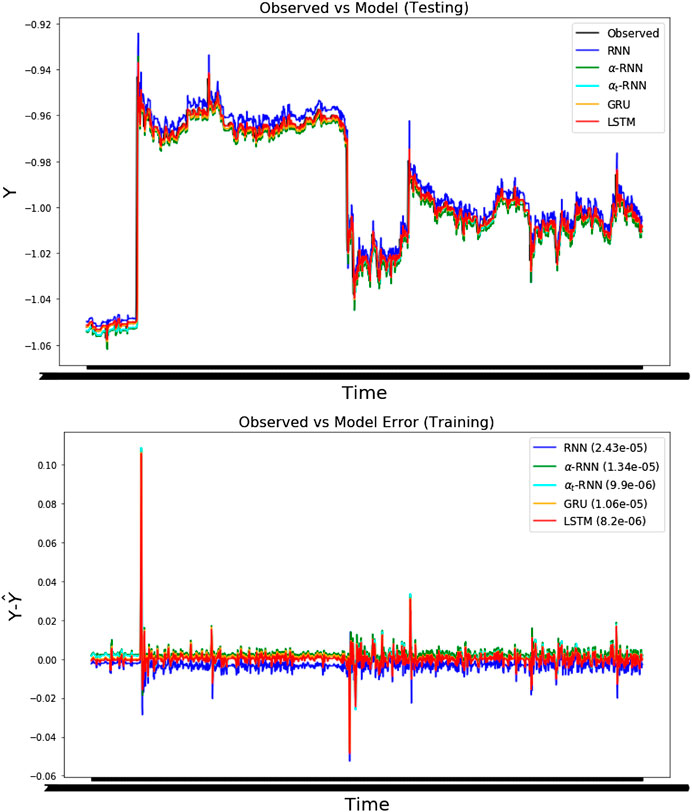
FIGURE 3. The four-step ahead forecasts of temperature using the minute snapshot Bitcoin prices (USD) with MSEs shown in parentheses. (top) The forecasts for each architecture and the observed out-of-sample time series. (bottom) The errors for each architecture over the same test period. Note that the prices have been standardized.

Viewing the results of time series cross validation, using the first 30,000 observations, in Table 1, we observe minor differences in the out-of-sample performance of the LSTM, GRU vs. the ${\alpha }_t$-RNN, suggesting that the reset gate and extra cellular memory in the LSTM provides negligible benefit for this dataset. In this case, we observe very marginal additional benefit in the LSTM, yet the complexity of the latter is approximately 50x that of the ${\alpha }_t$-RNN. Furthermore we observe evidence of strong over-fitting in the GRU and LSTM vs. the ${\alpha }_{\text{t}}$-RNN. The ratio of training to test errors are respectively 0.596 and 0.603 vs. 0.783. The ratio of training to validation errors are 0.863 and 0.862 vs. 0.898.

TABLE 1

TABLE 1. Thefour-stepahead Bitcoin forecasts are compared for various architectures using time series cross-validation. The half-life of the α-RNN is found to be 1.077 min ($\widehat{\alpha }=0.4744$).

5.2. High Frequency Trading Data

Our dataset consists of $N=\mathrm{1,033,468}$ observations of tick-by-tick Volume Weighted Average Prices (VWAPs) of CME listed ESU6 level II data over the month of August 2016 (Dixon, 2018; Dixon et al., 2019).

We reject the Null hypothesis of the augmented Dickey-Fuller test at the 99% confidence level in favor of the alternative hypothesis that the data is stationary (contains no unit roots. See for example (Tsay, 2010) for a definition of unit roots and details of the Dickey-Fuller test). The test statistic is $-5.243$ and the p-value is $7.16\times {10}^{-6}$ (the critical values are 1%: –3.431, 5%: –2.862, and 10%: –2.567).

The PACF in Figure 4 is observed to exhibit a cut-off at approximately 23 lags. We therefore choose a sequence length of $p=23$ and perform a ten-step ahead forecast. Note that the time-stamps of the tick data are not uniform and hence a step refers to a tick.

FIGURE 4

FIGURE 4. The PACF of the tick-by-tick VWAP of ESU6 over the month of August 2016.

Figure 5 compares the performance of the various networks and shows that plain RNN performs poorly, whereas and the ${\alpha }_t$-RNN better captures the VWAP dynamics. From Table 2, we further observe relatively minor differences in the performance of the GRU vs. the ${\alpha }_t$-RNN, again suggesting that the reset gate and extra cellular memory in the LSTM provides no benefit. In this case, we find that the GRU has 10x the number of parameters as the ${\alpha }_t$-RNN with very marginal benefit. Furthermore we observe evidence of strong over-fitting in the GRU and LSTM vs. the ${\alpha }_t$-RNN, although overall we observe stronger over-fitting on this dataset than the bitcoin dataset. The ratio of training to test errors are respectively 0.159 and 0.187 vs. 0.278. The ratio of training to validation errors are 0.240 and 0.226 vs. 0.368.

FIGURE 5

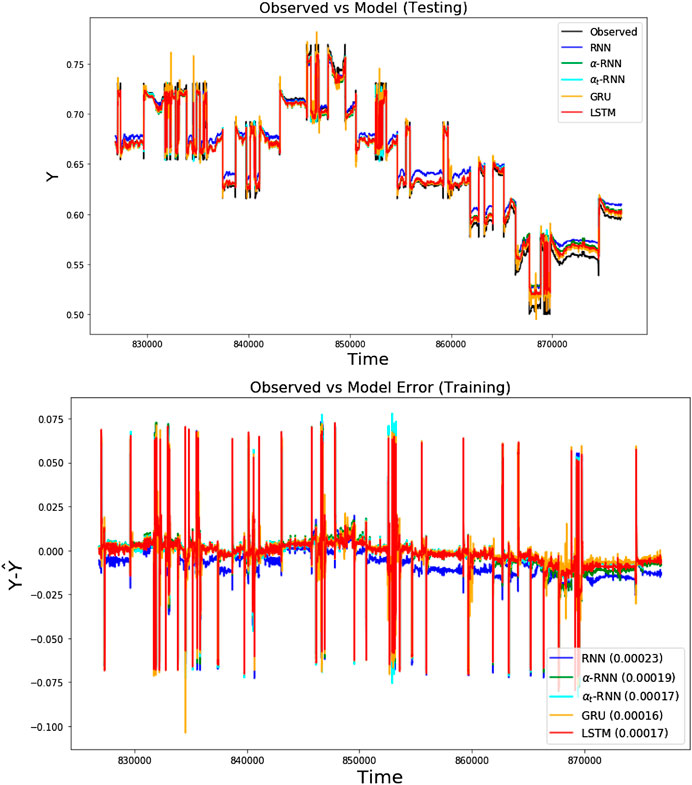
FIGURE 5. The ten-step ahead forecasts of VWAPs are compared for various architectures using the tick-by-tick dataset. (top) The forecasts for each architecture and the observed out-of-sample time series. (bottom) The errors for each architecture over the same test period.

TABLE 2

TABLE 2. Theten-stepahead forecasting models for VWAPs are compared for various architectures using time series cross-validation. The half-life of the α-RNN is found to be 2.398 periods ($\widehat{\alpha }=0.251$).

6. Conclusion

Financial time series modeling has entered an era of unprecedented growth in the size and complexity of data which require new modeling methodologies. This paper demonstrates a general class of exponential smoothed recurrent neural networks (RNNs) which are well suited to modeling non-stationary dynamical systems arising in industrial applications such as algorithmic and high frequency trading. Application of exponentially smoothed RNNs to minute level Bitcoin prices and CME futures tick data demonstrates the efficacy of exponential smoothing for multi-step time series forecasting. These examples show that exponentially smoothed RNNs are well suited to forecasting, exhibiting few layers and needing fewer parameters, than more complex architectures such as GRUs and LSTMs, yet retaining the most important aspects needed for forecasting non-stationary series. These methods scale to large numbers of covariates and complex data. The experimental design and architectural parameters, such as the predictive horizon and model parameters, can be determined by simple statistical tests and diagnostics, without the need for extensive hyper-parameter optimization. Moreover, unlike traditional time series methods such as ARIMA models, these methods are shown to be unconditionally stable without the need to pre-process the data.

Data Availability Statement

The datasets and Python codes for this study can be found at https://github.com/mfrdixon/alpha-RNN.

Author Contributions

MD contributed the methodology and results, and JL contributed to the results section.

Funding

The authors declare that this study received funding from Intel Corporation. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Appendix

1. GRUS and LSTMS1

1.1. GRUs

A GRU is given by:

$\begin{array}{c}\text{smoothing}:{\tilde{h}}_t={\widehat{\alpha }}_t\circ {\widehat{h}}_t+(1-{\widehat{\alpha }}_t)\circ {\tilde{h}}_{t-1}\\ \text{smoother update}:{\widehat{\alpha }}_t={\sigma }^{\left(1\right)}(U_{\alpha }{\tilde{h}}_{t-1}+W_{\alpha }{x}_t+b_{\alpha })\\ \text{hidden state update}:{\widehat{h}}_t=\sigma (U_h{\widehat{r}}_t\circ {\tilde{h}}_{t-1}+W_h{x}_t+b_h)\\ \text{reset update}:{\widehat{r}}_t={\sigma }^{\left(1\right)}(U_r{\tilde{h}}_{t-1}+W_r{x}_t+b_r).\end{array}$

When viewed as an extension of our ${\alpha }_t$ RNN model, we see that it has an additional reset, or switch, ${\widehat{r}}_t$, which forgets the dependence of ${\widehat{h}}_t$ on the smoothed hidden state. Effectively, it turns the update for ${\widehat{h}}_t$ from a plain RNN to a FFN and entirely neglect the recurrence. The recurrence in the update of ${\widehat{h}}_t$ is thus dynamic. It may appear that the combination of a reset and adaptive smoothing is redundant. But remember that ${\widehat{\alpha }}_t$ effects the level of error correction in the update of the smoothed hidden state, ${\tilde{h}}_t$, whereas ${\widehat{r}}_t$ adjusts the level of recurrence in the unsmoothed hidden state ${\widehat{h}}_t$. Put differently, ${\widehat{\alpha }}_t$ by itself can not disable the memory in the smoothed hidden state (internal memory), whereas ${\widehat{r}}_t$ in combination with ${\widehat{\alpha }}_t$ can. More precisely, when ${\alpha }_t=1$ and ${\widehat{r}}_t=0$, ${\tilde{h}}_t={\widehat{h}}_t=\sigma \left(W_h{x}_t+b_h\right)$ which is reset to the latest input, $x_t$, and the GRU is just a FFN. Also, when ${\alpha }_t=1$ and ${\widehat{r}}_t>0$, a GRU acts like a plain RNN. Thus a GRU can be seen as a more general architecture which is capable of being a FFN or a plain RNN under certain parameter values.

These additional layers (or cells) enable a GRU to learn extremely complex long-term temporal dynamics that a vanilla RNN is not capable of. Lastly, we comment in passing that in the GRU, as in a RNN, there is a final feedforward layer to transform the (smoothed) hidden state to a response:

${\widehat{y}}_t=W_Y{\tilde{h}}_t+b_Y.(\mathrm{A1})$

1.2. LSTMs

LSTMs are similar to GRUs but have a separate (cell) memory, $c_t$, in addition to a hidden state $h_t$. LSTMs also do not require that the memory updates are a convex combination. Hence they are more general than exponential smoothing. The mathematical description of LSTMs is rarely given in an intuitive form, but the model can be found in, for example, Hochreiter and Schmidhuber (1997).

The cell memory is updated by the following expression involving a forget gate, ${\widehat{\alpha }}_t$, an input gate ${\widehat{z}}_t$ and a cell gate ${\widehat{c}}_t$

$c_t={\widehat{\alpha }}_t\circ c_{t-1}+{\widehat{z}}_t\circ {\widehat{c}}_t.(\mathrm{A2})$

In the terminology of LSTMs, the triple $\left({\widehat{\alpha }}_t,{\widehat{r}}_t,{\widehat{z}}_t\right)$ are respectively referred to as the forget gate, output gate, and input gate. Our change of terminology is deliberate and designed to provided more intuition and continuity with RNNs and the statistics literature. We note that in the special case when ${\widehat{z}}_t=1-{\widehat{\alpha }}_t$ we obtain a similar exponential smoothing expression to that used in our ${\alpha }_t$-RNN. Beyond that, the role of the input gate appears superfluous and difficult to reason with using time series analysis.

When the forget gate, ${\widehat{\alpha }}_t=0$, then the cell memory depends solely on the cell memory gate update ${\widehat{c}}_t$. By the term ${\widehat{\alpha }}_t\circ c_{t-1}$, the cell memory has long-term memory which is only forgotten beyond lag s if ${\widehat{\alpha }}_{t-s}=0$. Thus the cell memory has an adaptive autoregressive structure.

The extra “memory”, treated as a hidden state and separate from the cell memory, is nothing more than a Hadamard product:

$h_t={\widehat{r}}_t\circ tanh\left(c_t\right),(\mathrm{A3})$

which is reset if ${\widehat{r}}_t=0$. If ${\widehat{r}}_t=1$, then the cell memory directly determines the hidden state.

Thus the reset gate can entirely override the effect of the cell memory’s autoregressive structure, without erasing it. In contrast, the ${\alpha }_t$-RNN and the GRU has one memory, which serves as the hidden state, and it is directly affected by the reset gate.

The reset, forget, input and cell memory gates are updated by plain RNNs all depending on the hidden state $h_t$.

$\begin{array}{c}\text{Reset gate}:{\widehat{r}}_t=\sigma (U_r{h}_{t-1}+W_r{x}_t+b_r)\\ \text{Forget gate}:{\widehat{\alpha }}_t=\sigma (U_{\alpha }{h}_{t-1}+W_{\alpha }{x}_t+b_{\alpha })\\ \text{Input gate}:{\widehat{z}}_t=\sigma (U_z{h}_{t-1}+W_z{x}_t+b_z)\\ \text{Cell memory gate}:{\widehat{c}}_t=\tanh (U_c{h}_{t-1}+W_c{x}_t+b_c).\end{array}$

The LSTM separates out the long memory, stored in the cellular memory, but uses a copy of it, which may additionally be reset. Strictly speaking, the cellular memory has long-short autoregressive memory structure, so it would be misleading in the context of time series analysis to strictly discern the two memories as long and short (as the nomenclature suggests). The latter can be thought of as a truncated version of the former.

Footnotes

¹Sample complexity bounds for RNNs have recently been derived by (Akpinar et al., 2019). Theorem 3.1 shows that for a recurrent units, inputs of length at most b, and a single real-valued output unit, the network requires only $\mathcal{O}\left(a^{4}b/{\mathit{ϵ}}^2\right)$ samples in order to attain a population prediction error of ε. Thus the more recurrent units required, the larger the amount of training data needed.

²By contrast, plain RNNs model stationary time series, and GRUs/LSTMs model non-stationary, but no hybrid exists which provides the modeler with the control to deploy either.

³The sequence of features is from the same time series as the predictor hence $n=d=1$.

⁴Long memory refers to autoregressive memory beyond the sequence length. This is also sometimes referred to as “stateful”. For avoidance of doubt, we are not suggesting that the α-RNN has an additional cellular memory, as in LSTMs.

⁵The half-life is the number of lags needed for the coefficient ${\left(1-\alpha \right)}^s$ to equal a half, which is $s=-1/lo{g}_2\left(1-\alpha \right)$.

References

Abadi, M., Barham, P., Chen, J., Chen, Z., Davis, A., Dean, J., et al. (2016). “TensorFlow: a system for large-scale machine learning,” in Proceedings of the 12th USENIX conference on operating systems design and implementation, Savannah, GA, November 2–4, 2016 (Berkeley, CA: OSDI’16) 265–283.

Google Scholar

Akpinar, N. J., Kratzwald, B., and Feuerriegel, S. (2019). Sample complexity bounds for recurrent neural networks with application to combinatorial graph problems. Preprint repository name [Preprint]. Available at: https://arxiv.org/abs/1901.10289.

Google Scholar

Bao, W., Yue, J., and Rao, Y. (2017). A deep learning framework for financial time series using stacked autoencoders and long-short term memory. PloS One 12, e0180944–e0180924. doi:10.1371/journal.pone.0180944

PubMed Abstract | CrossRef Full Text | Google Scholar

Bayer, J. (2015). Learning sequence representations. MS dissertation. Munich, Germany: Technische Universität München.

Google Scholar

Borovkova, S., and Tsiamas, I. (2019). An ensemble of LSTM neural networks for high‐frequency stock market classification. J. Forecast. 38, 600–619. doi:10.1002/for.2585

CrossRef Full Text | Google Scholar

Borovykh, A., Bohte, S., and Oosterlee, C. W. (2017). Conditional time series forecasting with convolutional neural networks. Preprint repository name [Preprint]. Available at: https://arxiv.org/abs/1703.04691.

Google Scholar

Box, G., and Jenkins, G. M. (1976). Time series analysis: forecasting and control. Hoboken, NJ: Holden Day, 575

Chen, S., and Ge, L. (2019). Exploring the attention mechanism in LSTM-based Hong Kong stock price movement prediction. Quant. Finance 19, 1507–1515. doi:10.1080/14697688.2019.1622287 \

CrossRef Full Text | Google Scholar

Chung, J., Gülçehre, Ç., Cho, K., and Bengio, Y. (2014). Empirical evaluation of gated recurrent neural networks on sequence modeling. Preprint repository name [Preprint]. Available at: https://arxiv.org/abs/1412.3555.

Google Scholar

Dixon, M. (2018). Sequence classification of the limit order book using recurrent neural networks. J. Comput. Sci. 24, 277. doi:10.1016/j.jocs.2017.08.018

CrossRef Full Text | Google Scholar

Dixon, M. F., Polson, N. G., and Sokolov, V. O. (2019). Deep learning for spatio‐temporal modeling: dynamic traffic flows and high frequency trading. Appl. Stoch. Model. Bus Ind 35, 788–807. doi:10.1002/asmb.2399

CrossRef Full Text | Google Scholar

Dixon, M. (2021). Industrial Forecasting with Exponentially Smoothed Recurrent Neural Networks, forthcoming in Technometrics.

Google Scholar

Dixon, M., and London, J. (2021b). Alpha-RNN source code and data repository. Available at: https://github.com/mfrdixon/alpha-RNN.

Google Scholar

Glorot, X., and Bengio, Y. (2010). “Understanding the difficulty of training deep feedforward neural networks,” in Proceedings of the international conference on artificial intelligence and statistics (AISTATS’10), Sardinia, Italy, Society for Artificial Intelligence and Statistics, 249–256

Google Scholar

Graves, A (2013). Generating sequences with recurrent neural networks. Preprint repository name [Preprint]. Available at: https://arxiv.org/abs/1308.0850.

Google Scholar

Hamilton, J. (1994). Time series analysis. Princeton, NJ: Princeton University Press, 592

Hochreiter, S., and Schmidhuber, J. (1997). Long short-term memory. Neural. Comput. 9, 1735–1780. doi:10.1162/neco.1997.9.8.1735

PubMed Abstract | CrossRef Full Text | Google Scholar

Kirchgässner, G., and Wolters, J. (2007). Introduction to modern time series analysis. Berlin, Heidelberg: Springer-Verlag, 277

Li, D., and Zhu, K. (2020). Inference for asymmetric exponentially weighted moving average models. J. Time Ser. Anal. 41, 154–162. doi:10.1111/jtsa.12464

CrossRef Full Text | Google Scholar

Mäkinen, Y., Kanniainen, J., Gabbouj, M., and Iosifidis, A. (2019). Forecasting jump arrivals in stock prices: new attention-based network architecture using limit order book data. Quant. Finance 19, 2033–2050. doi:10.1080/14697688.2019.1634277

CrossRef Full Text | Google Scholar

Pascanu, R., Mikolov, T., and Bengio, Y. (2012). “On the difficulty of training recurrent neural networks,” in ICML’13: proceedings of the 30th international conference on machine learning, 1310–1318. Available at: https://dl.acm.org/doi/10.5555/3042817.3043083.

Google Scholar

Sirignano, J., and Cont, R. (2019). Universal features of price formation in financial markets: perspectives from deep learning. Quant. Finance 19, 1449–1459. doi:10.1080/14697688.2019.1622295

CrossRef Full Text | Google Scholar

Tsay, R. S. (2010). Analysis of financial time series. 3rd Edn. Hoboken, NJ: Wiley

CrossRef Full Text