Optimal Maintenance for Degrading Assets in the Context of Asset Fleets-A Case Study

Decision-making for maintenance of engineering assets is a common challenge in the process industry due to ongoing degradation. With an increasing company-size, this problem becomes more complex from an operational and computational point of view. This paper introduces a case study to the academic community that represents the problem of optimal decision-making in the context of large asset fleets. The case study poses a large fleet of offshore compressors for gas production with a specific network structure. Two exemplary discrete-time mixed integer linear programming models following the Resource Task Network framework are presented. They address asset deterioration due to effects such as fouling by suggesting specific maintenance actions as a set of different countermeasures. Novel enumerator formulations are a computationally efficient and extendable way to model the various degradation types. Results show the benefit of optimal maintenance in the application to asset fleets. The decision-support that is delivered by the scheduling and planning approach helps to determine which maintenance type should be conducted and at what time. The paper demonstrates the benefits of optimal (long-term) schedules for maintenance, but indicate at the same time the need for efficient algorithms in the context of large asset fleets, in contrast to common industrial case studies that are rather small-scale.

1. Introduction

Industrial process plants have lifetimes of more than 30 years and they are prone to deterioration during their operation. These complex networks of physical pieces of equipment can encompass hundreds of linked assets. While greenfield investments implement state-of-the-art technology, existing plants need to be upgraded to maintain competitiveness. Therefore, advanced control technologies, monitoring of machinery condition, and data analytics are essential to enhance the operational profit of aging process plants. Efficient and sustainable operation of assets is the major challenge of this century. Next to operational profits, emission of carbon dioxide can be reduced while the reliability and safety in the plants can be improved.

The technical term maintenance refers to all actions that repair, replace or maintain assets when necessary. It makes sure that the plant condition is adequate to perform the required production tasks. While over time, and even more during production, the assets are deteriorating, they can be restored by maintenance activities. ISO 15926–1:2004 (en) describes it as one of the key activities within the life-cycle of a process plant (see Figure 1).

FIGURE 1

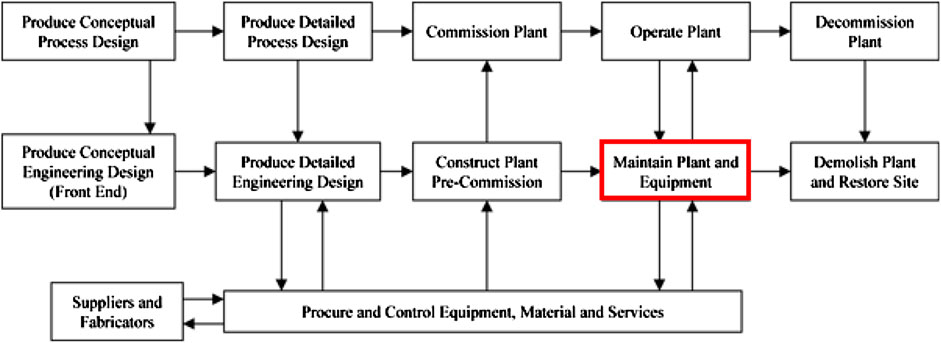
FIGURE 1. Main activities and data flows associated with the life-cycle of a plant, adapted from ISO 15926–1:2004 (en).

There are different maintenance strategies available. Figure 2 gives an overview of the different strategies that are mostly applied in industry and indicates the evolution of the strategies over time. The initial approach was corrective maintenance: As soon as an asset breaks, it is maintained or replaced. This maintenance approach may pose problems for safety-relevant assets or when avoidance of any production losses is necessary. Since it is uncertain when precisely an asset needs maintenance, maintenance was done regularly. The result is that there are additional (unnecessary) maintenance tasks performed or also that sometimes maintenance is not performed early enough. Condition-based maintenance, on the other hand, is only performed when needed. When an indicator suggests that the equipment is going to fail, maintenance is performed. Risk-based maintenance applies methods of risk management into maintenance, and by doing so, it assesses the probability of failure and the consequences. Reliability-centered maintenance is a systematic technique that tries to balance preventive and corrective maintenance. The goal is to find the most cost-efficient solution while maintaining reliability at the desired level. Maintaining a system with such an objective function is also called optimal maintenance [1].

FIGURE 2

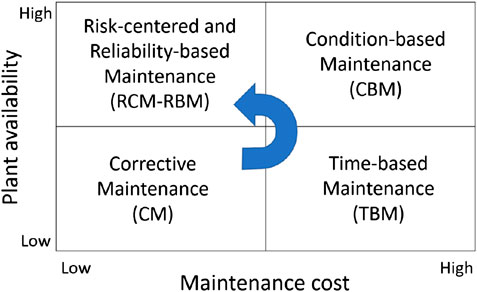
FIGURE 2. Maintenance strategies regarding their costs and the resulting plant availability; the arrow indicates the evolution of the strategies.

FIGURE 3

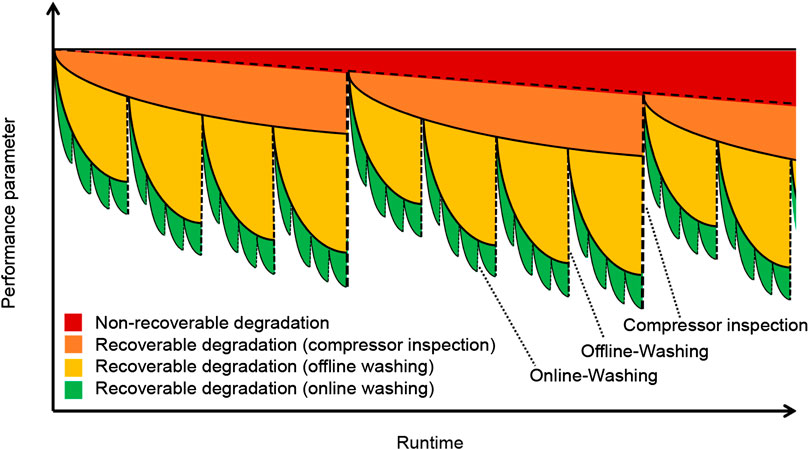
FIGURE 3. Example of the different types of degradation in a compressor and different types of maintenance to restore efficiency.

To increase the profit during the operation period in the life cycle of a plant, the different maintenance actions need to be scheduled and planned. However, the time scales of the maintenance actions should align with the time scale in which the decision to conduct a maintenance action is taken. Decisions about when to upgrade an asset to the state-of-the-art should be taken on a bigger time-scale, while decisions about when to conduct cheap and short maintenance should be taken on a shorter time-scale.

All process plants include engineering assets. Economies of scale encourage companies to aggregate and manage more substantial numbers of assets at the same time. By scaling the operations, a cost advantage is obtained, e.g., by decreased capital cost or increased knowledge management. The trend of the past years of multiple mergers and acquisitions [2] causes exactly this aggregation effect. If a company owns a large number of engineering assets of the same type or with a similar function, the sum of these assets is called an asset fleet. However, operating asset fleets poses new challenges for companies, such as the overwhelming complexity in the management of the fleet.

The deterioration of assets is well known and documented in the literature. Similarly, maintenance is acknowledged as an effective way to face this problem. The contribution of this work is to pose an industrial-sized case study to the academic community and propose formulations that are able to solve the maintenance scheduling and planning problem in feasible time scales. Other work of the authors, e.g., [3] Schulze Spüntrup F, Dalle Ave G. Integration of maintenance scheduling and planning for large-scale asset fleets. Submitted to: Comput Chem Eng (2019); focuses more on the development and integration of mathematical formulations, while the focus of this work is on the case study itself.

The next section gives an overview of the literature concerning the topics of compressor (and turbine) degradation and the planning and scheduling in large process systems, especially for maintenance actions. The problem statement in Section 3 follows this. Section 4 introduces a methodology to tackle this problem in both short-term and long-term horizons. Even though this problem is omnipresent in all kind of process industries, we focus on the case of an off-shore compressor fleet of an oil and gas company, which is introduced in Section 5. The results of the maintenance planning and scheduling are illustrated and discussed within the different subcases in Section 6. The conclusion gives an overview of the findings of this work and shows possible directions for future work.

2. Background

This section gives the necessary background about asset degradation, planning and scheduling in industrial settings, with a focus on maintenance, but also for production and other operational modes. The common challenge that is investigated is: How to operate and maintain my engineering assets in the best possible way. Specific goals may be the production profit, but also the reliability of the assets as well as the conjunct safety.

The degradation of engineering assets is manifold. Degradation is the process by which equipment gradually breaks down by a series of detrimental changes in its physical condition. These changes can be caused by time, use, or other external factors.

For the sake of this work, the focus for the literature review is on compressor degradation, as this type of asset is not only prevalent in the proposed case study of off-shore gas production, but also air separation plants, manufacturing of different kinds of goods, the construction industry or in HVAC units.

Reference 4 describe the degradation of gas turbine systems. Different mechanisms affect the degradation process: Increased tip clearance [5] and changes in the airfoil geometry [6] are interlinked with the effect of non-recoverable degradation. Recoverable degradation, which can be (partially) reversed by specific methods (e.g., washing) is described as changes in the airfoil surface quality [7]. Reference 4 summarize, that the effect of the degradation results in a lower capability to generate head pressure. However, they do not state the speed of deterioration, as it is a complex system of factors that influence it and therefore do not allow statements for unknown systems.

Reference 8 reported the power degradation for different gas turbine engines, ranging between 2 and 12% after 1 year of operation. This work proves the significance of fouling to the deterioration process.

Similarly, Ref. 9 analyze axial compressor fouling. After determining the key parameters that affect the level of fouling, a mathematical model is developed. The progressive compressor fouling model calculates the fouling stage by stage. Reference 9 introduce a specific deposit cleaning method. They propose to use regular washing (on- and off-line) to maintain a high level of efficiency.

In the work of Ref. 10 an overview of the technological developments in the field of gas turbine compressor washing is given. Foundation for his work are long-term field tests and observations. These results in a correlation between the rate of power degradation and the atmospheric conditions present where the compressor is working. An important outcome is an index of sensitivity to fouling, which includes gas turbines of different sizes and models. The conclusion of Ref. 10 is that the implementation of on-line and off-line washing is vital for a preventive turbine maintenance program, similar to the proposal of Ref. 9.

Reference 8 analyze the fouling mechanism in axial compressors. As the cause of fouling, they name adherence of particles to airfoils and annulus surfaces. A prevention method could be air filtration systems, but they also refer to detergent washing of components to reverse the fouling effect.

Reference 11 investigated further on the online-washing compressor cascade washing to restore the performance of gas turbines. While the on-line washing has been proposed to mitigate the effects of fouling, there has been little research from experience on how much washing can contribute to performance savings. With the case study of a 226 MW engine, the different cases of clean, fouled, and washed engines have been obtained. While the isentropic efficiency decreased by 6.6% in the fouled stated, the washing was able to recover 3.4% of this efficiency degradation. The authors conclude that washing can recover about 50% of the lost power of a compressor and that this not just improves the thermal efficiency of the compressor, but also ensures a safer operation since the compressor can operate further away from the surge line with good utilization of the shaft speed.

Reference 12 develop a scheduling model that incorporates maintenance activities into a machine schedule. The maintenance state of the machine is represented by an integer value which is decreases (based on the specific job) when a job is processed on the machine. This state accounts for a machine deterioration, which is dependent on the specific job performed. There is total flexibility about when to schedule the maintenance with the restriction that machine breakdowns are prevented at any time.

The scheduling of maintenance in a flow-shop proposed by Ref. 13 is formulated as a mixed integer linear model with maintenance operations on each production machine. This scheduling approach includes predictive maintenance, where each machine has a remaining useful life. The maintenance actions must be scheduled before this RUL is running out and a machine failure occurs.

Reference 14 optimize the power generation by applying parameter estimation via Kalman filtering combined with a hybrid dynamic model. Model predictive control is used with this hybrid dynamic model and compared to fixed washing schedules.

An integrated maintenance and production scheduling approach was developed by Ref. 15. Both decision processes are approached independently, keeping the close relation of both in mind. The approach is working on two time-scales. A vital feature of the research is to use asset health information as an input to generate a plan for optimal production. Residual useful life and the probability of failure are central components of the framework. The model is applied for a multipurpose process plant, and as an example case, a steel plant is used.

Reference 16 worked on production and maintenance planning in biopharmaceutical manufacturing with a performance decay. The mixed integer linear programming optimization model is trying to maximize the total operating profit. The yield decay depends on the number of batches and is piecewise-linear. For the first eight batches, there is no decay, afterward the yield is decaying by 5% percent per batch. The effects of maintenance duration, maintenance cost, and the resin’s lifetime (i.e., the profile of the decay) are discussed. A similar approach for a biopharmaceutical process with a continuous-time formulation is developed by Ref. 17. The MILP model is based on a Resource Task Network formulation, similar to this work, but with a continuous-time formulation. Since the presented process is a batch production process, the decay is defined by the number of batches produced since the last maintenance. The downstream process is considered as a black-box presentation and the decay affects only one specific resin in the process.

Another work focused on decaying performance exponentially and the cyclic scheduling of maintenance is presented in Ref. 18. Process information are used to find a cyclic schedule for feed processing. The main decisions that are taken in the optimized schedule are the assignments of feeds to units, the processing times and the number of subcycles on the different units. The resulting MINLP model is solved with a branch-and-bound method. The exponential decay stems from the catalyst and with every cleaning the performance is reset fully every time.

Reference 19 investigate an air separation plant. Optimal operation and the maintenance of compressor networks are part of the developed MILP model. On-line and off-line washing are considered as part of the condition-based maintenance approach. The degradation is considered in three different cases: Low, medium and high degradation. They are based on a study of industrial data. Offline-washing is not considered to be done during non-performance-related maintenance actions or regular shutdowns of the equipment. The degradation in the case study causes an increase in electrical power consumption of 2% per month, which leads to high saving potential.

3. Case Study

While many new process plants are built in regions where energy and raw material costs are substantially lower than in the former regions of high industrial density, plants that are in the middle of their life cycle and are operated in the regions with higher energy and raw material cost are facing a challenge: How to realize the efficient and sustainable operation of assets that are already installed with the technology of yesterday, running at the present time and the need for being competitive in the future?

This work aims to pose a case study to the academic community: In the off-shore gas production, large fleets of compressors are used. However, they are subject to continuous degradation. In order to ensure safety for the personnel on the platforms, but also to maintain reliable operations that meet the demand of the gas consumers on-shore, maintenance is essential. This article is supposed to establish a case study as a point of reference for future research in the field of maintenance scheduling and planning, especially for large asset fleets. During the research of the authors, it was evident that this type of case study has not been discussed in the literature before. Therefore, we seek to explain more details and enable other researchers from the process systems engineering and operations research community to contribute to this field by supplying a test bench for new formulations, algorithms, and approaches for planning and scheduling.

The case study is inspired by the operations of the company Equinor ASA on the Norwegian continental shelf, but is simplified and does not include any real data that could breach data protection. Figure 4 shows an overview of the network of compressors in the Norwegian Continental shelf. This is an example of how distributed these assets may be, which poses additional challenges for the logistics of maintenance crews. The distances that are required to travel are not part of the calculations of this work, but are reflected in the required time to perform specific maintenance types. Boundaries for specific values such as the degradation rates were set according to feasible ranges that were provided by literature and then randomized within these ranges. The data presented in this article cannot be used to re-construct or estimate the operations of this specific company. For the implementation into the operations of a specific company, these values can, however, be found quickly and the mathematical program can be adapted to match the prices and cost for a specific case.

FIGURE 4

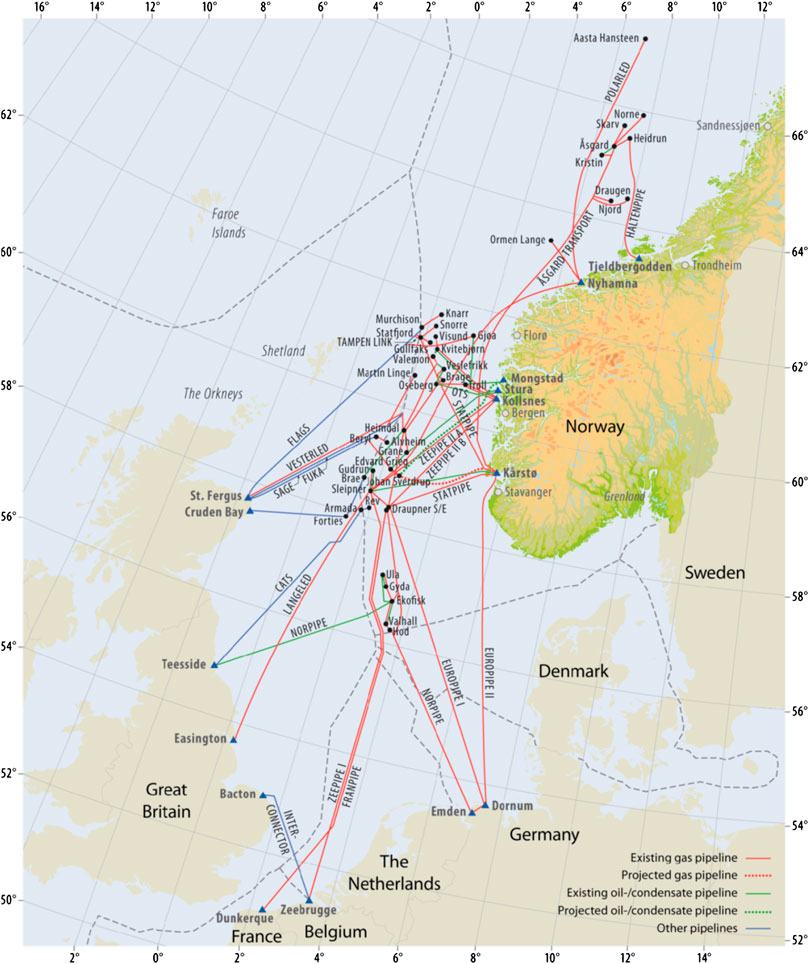
FIGURE 4. Platforms and pipelines on the Norwegian continental shelf. The picture shows assets of more than one company [20].

3.1. Description of the Process

In the following paragraphs, a description of the process is given. Similar operations can be found with any oil and gas company and platform layouts are usually similar. The case study concerns a fleet of recycle compressors, as introduced below. On an off-shore platform, three components are produced: Oil, gas, and water. They flow together from the production well-heads and manifolds to the first stage separator. As the separation process is not complete, streams of oil, gas, and water are not entirely pure yet and need further separation steps. For the gas stream, this happens via several stages of compressors and scrubbers. The scrubbers remove liquid parts from the gas and the compressors re-compress the gas before it enters the next scrubber. Figure 5 shows an example of the process configuration with a scrubber, a compressor, and the recycle. Usually, several of these compressors (with coolers and scrubbers) are in series, powered by a single gas turbine, as depicted in Figure 6. Once the gas is cleaned, it is transported to on-shore production facilities with the help of export compressors, which are not part of the compressor fleet that is part of the data set. The recycle gas compressors operate on different pressure levels. It is common to start with low pressure after the production separator and with every additional stage, the pressure of the gas is increased. As the gas contains oil and gas liquid drops, the compressors are subject to fouling and other degradation effects. Cleaning the gas from the liquids is required before it can be exported. Otherwise, it can lead to blockages in the export pipeline.

FIGURE 5

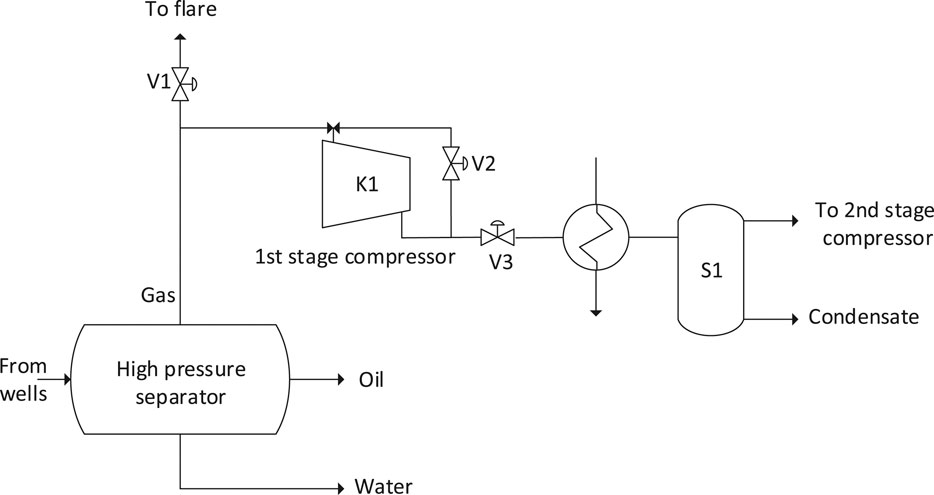
FIGURE 5. Schematic of the first stage gas compression process. K1 is the compressor, S1 the gas scrubber, V2 the recycle valve, which is normally closed.

FIGURE 6

FIGURE 6. Simplified schematic of a multistage gas compressor train powered by a gas turbine.

3.2. Description the Data Set

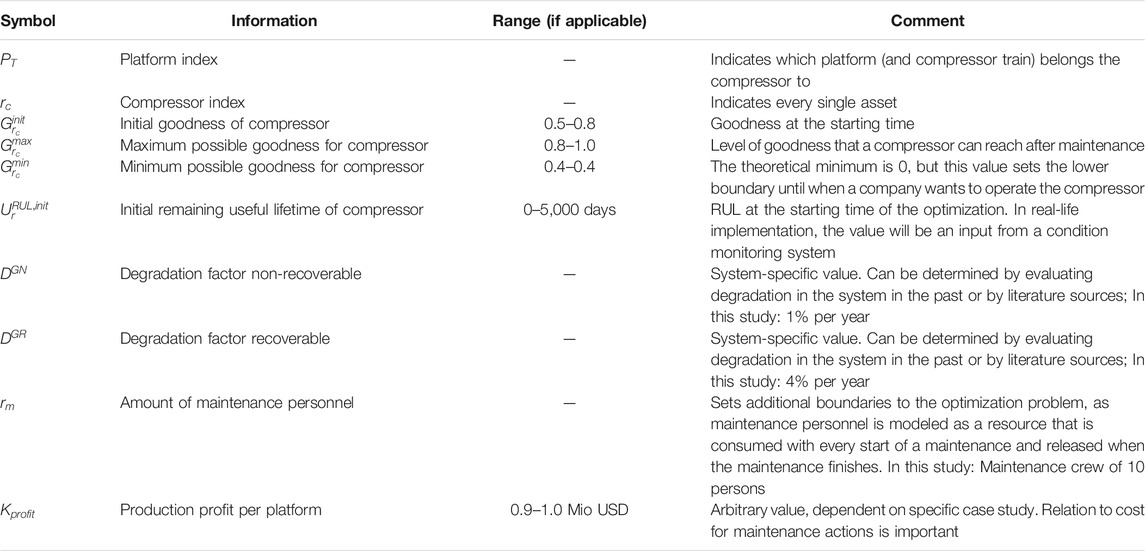
This section describes the data set in a way that it can be reconstructed and used for own implementation of scheduling and planning algorithms. Tables 1, 2 give an overview of the different parameters that are defined by the case study.

TABLE 1

TABLE 1. Overview of different parameters of the case study.

TABLE 2

TABLE 2. Overview of different maintenance types available in the case study.

The definition of the different compressors includes the platform they belong to, their initial goodness as well as the maximum and minimum goodness. The initial and the maximum goodness are hereby randomly distributed between a lower and an upper bound and the minimum goodness is a fixed value in order to resemble a company policy in which no compressor should be operated below a certain threshold. Similarly to the goodness of the compressor, the remaining useful lifetime of the compressor is defined with a value randomized within a given range. The production profit for every platform is defined, as a platform just produces if none of the compressors is maintained (compressors work in series, not in parallel). The maintenance personnel that can be used as a resource is defined and the amount of degradation (specified for recoverable and non-recoverable degradation) is defined, as well as the different types of maintenance actions that are available, including their associated duration, cost, maintenance personnel requirement, and effect on the degradation. The details are listed in Table 2.

The following maintenance actions are available in this case study:

• Short maintenance (e.g. fix a sealing; off-shore)

• Compressor inspection (off-shore)

• Long maintenance (full overhaul; on-shore)

• On-line washing

• Off-line washing

The base study is based on randomized data and the size can be increased or decreased as much as required. In this work, case study sizes up to 100 compressors are tested. As the data is randomized, it may happen that case studies are generated that cannot be solved. One example is, if too many compressors are initialized with a meager remaining useful lifetime, which forces all compressors into maintenance mode in the first time slot. As this would require more than the available maintenance personnel, no solution can be found. In this case, either the case study must be relaxed (more maintenance personnel available), or the initialization of the case study must be re-randomized to obtain a realistic starting point.

4. Mathematical Modeling

In this section, the mathematical formulation that builds the basis of a planning and a scheduling model is given. The mathematical foundation is similar for both models. Differences are within the choice of the relevant maintenance types for the specific model. The work is based on the results published in Refs. 21 and 22 but is refined and extended. The notation used in this work is explained in Table 3. The proposed formulation is one approach to tackle this problem. It is intended to give an example of how the problem can be encountered. First, the model is introduced.

TABLE 3

TABLE 3. Notation for the planning and scheduling formulation.

The chosen framework to model the problem is the Resource-Task Network (RTN) framework, which was developed by Ref. 23. Its capability to handle large problem sizes as they are present in industrial-sized problem was proven by Ref. 24.

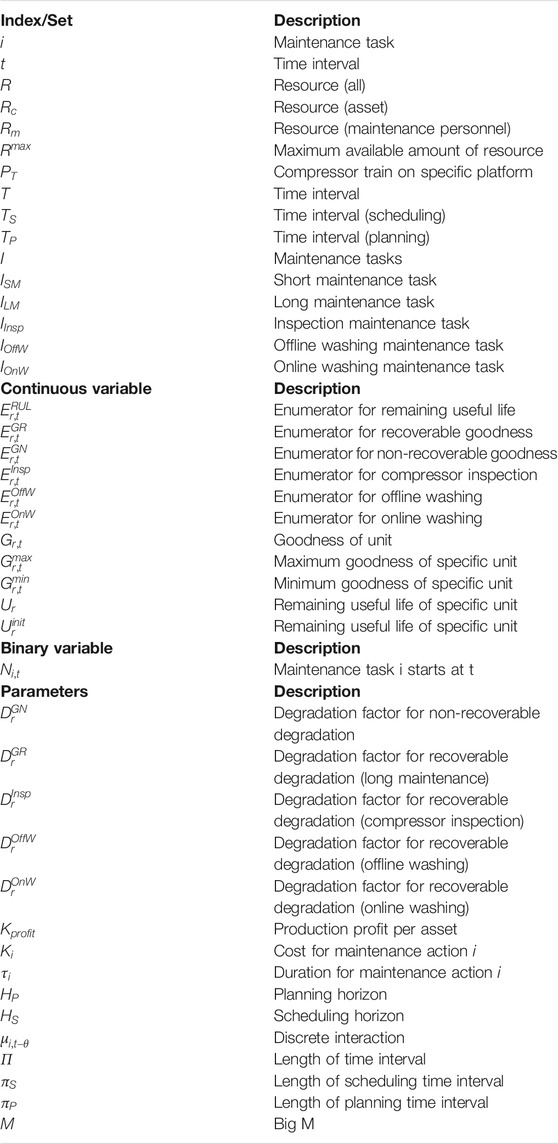
As the time-horizon of the problem is rather long and uncertainties such as weather conditions, shift schedules, and other factors will affect the exact timing when the maintenance actions are performed, a discrete-time model has been chosen for the problem representation. This allows to create a grid of time slots and for each time slot the decision of a specific maintenance task will be confirmed will be made computationally. This is denoted by the binary variable $N_{i,t}$. The time grid that is introduced here is defined in a generalizing manner with T as a time interval, while the actual models would refer to either $T_P$ for time intervals in the planning model or $T_S$ for time intervals in the scheduling model. Every time slot has a length of π, and therefore ${\pi }_S$ and ${\pi }_P$ for the length of the scheduling slots or planning slots, respectively. The following should hold true:

$T_S\cup T_P\subseteq T.(1)$

The index t refers to a specific time point in these intervals. Index i refers to a specific maintenance task in the superset I of maintenance tasks. The superset I has five subsets since there are three types of maintenance as explained in the problem statement: The short maintenance $I_{SM}$, the long maintenance $I_{LM}$, the on-line washing $I_{OnW}$, the off-line washing $I_{OffW}$ and the inspection $I_{Insp}$. More details about these maintenance tasks have been provided in the previous section. In time slots where maintenance is happening every type of maintenance (except on-line washing) the production is stopped, but the duration ${\tau }_i$ is individual for every compressor and type of maintenance. Another simplification has been done regarding the duration of maintenance tasks: The possible production losses due to a ramp-up and ramp-down of the production before and after the maintenance itself are included in the maintenance duration in order to account for all production losses due to the maintenance. The set of resources R has two subsets: compressors $R_C$ and maintenance personnel $R_M$. Each compressor is part of a compressor train on a specific platform $P_T$. For the example case study, each platform has one compressor train with five compressors in series. The amount of available resources is defined by the case study and modeled by the following equation:

$0\le R_{r,t}\le R_r^{max}\forall r\in R,t\in T.(2)$

For every compressor that is included in the data set, more information is given: For every compressor $R_C$ and at each time t we track the Remaining Useful Life (RUL) $U_{r,t}$ and the goodness $G_{r,t}$ of the unit.

The goodness of an asset is a measure of the performance which is affected by degradation effects. For every compressor, a maximum performance exists due to thermodynamical limitations due to the geometry of the compressor. Furthermore, many companies define a minimum acceptable efficiency of compressors. This defines the bounds of the goodness:

$G_r^{min}\le G_{r,t}\le G_r^{max}\forall r\in R_c,t\in T.(3)$

The goodness $G_{r,t}$ is calculated as follows:

$\begin{array}{c}{G}_{r,t}=G_r^{max}-D_r^{GR}\pi \left(E_{r,t}^{GR}-1\right)-D_r^{GN}\pi \left(E_{r,t}^{GN}-1\right)\\ -D_r^{Insp}\pi \left(E_{r,t}^{Insp}-1\right)-D_r^{OffW}\pi \left(E_{r,t}^{OffW}-1\right)\\ -D_r^{OnW}\pi \left(E_{r,t}^{OnW}-1\right)\\ \forall r\in R_c,t\in T.\end{array}(4)$

The notation of the different parameters and variables are specified in Table 3. Some terms may not be active if the specific maintenance type is not performed on the specific time horizon. The compressor washing-related terms are abundant for the planning model as an example. Every term of Eq. 4 refers to one specific enumerator. Depending on when a specific maintenance type was carried out the last time and therefore its enumerator was reset, a specific amount of goodness is substracted. This deterioration is dependent on the degradation factor for the specific degradation type and the length of the time intervals. The formulation of the enumerators is given later in this section.

The remaining useful lifetime $U_{r,t}$ is formulated as follows:

$U_{r,t}\le U_r^{max}-E_{r,t}^{RUL}\pi \forall r\in R_c,t\in T.(5)$

It linearly decreases with every passing time interval if a relevant maintenance action has not reset the enumerator. By doing so, the remaining useful lifetime decreased with every time slot and sets an artificial limit until the compressors need to be maintained to avoid a breakdown. In an industrial implementation, the compressor may have additional condition monitoring systems that can detect an approaching machine failure. This value delivered by a condition monitoring system should update the given value for the remaining useful lifetime.

In Eqs 4 and 8 different enumerators $E_{r,t}$ have been introduced. In the mathematical model used in this work, enumerators are several variables that track the time since a specific event occured, e.g., when a specific type of maintenance occured or one maintenance out of a relevant set of maintenances that have a common effect. In the following, the enumerator that is used to calculate the remaining useful lifetime, which is reset by both short and long maintenance types:

$E_{r,t}^{RUL}\ge E_{r,t-1}^{RUL}+1-M{\displaystyle \sum }_{i\in I_r{{\displaystyle \cap }}^{\text{}}\left(I_{SM}{{\displaystyle \cup }}^{\text{}}{I}_{LM}\right)}{N}_{i,t},\hspace{1em}\forall r\in R_c,t\in T,(6)$

$E_{r,t}^{RUL}\le E_{r,t-1}^{RUL}+1,\hspace{1em}\forall r\in R_c,t\in T,(7)$

$E_{r,t}^{RUL}\le 1+M\left(1-{\displaystyle \sum }_{i\in I_r{{\displaystyle \cap }}^{\text{}}\left(I_{SM}{{\displaystyle \cup }}^{\text{}}{I}_{LM}\right)}{N}_{i,t}\right),\hspace{1em}\forall r\in R_c,t\in T,(8)$

$E_{r,t}^{RUL}\ge 1,\hspace{1em}\forall r\in R_c,t\in T.(9)$

The enumerator will increase by 1 for every time slot that passed without a short or long maintenance. If a short or long maintenance was performed, the counter is reset. If there is no maintenance performed, the constraint in Eq. 9 becomes active and the enumerator will be incremented. Otherwise, the big-M term relaxes this constraint. In order to avoid that the enumerator increases by more than 1 per time interval Eq. 10 is restricting the possible increment per time slot. The upper bound is also specified in Eq. 11, where the enumerator is reset to 1 if maintenance is happening, otherwise the big-M term relaxes the upper bound. Equation 12 describes the lower bound of the enumerator, which is always 1.

In RTN formulations it is important to track the balance of the different resources. This includes that every time a specific maintenance is performed in a time slot, indicated by $N_{i,t}$ taking the value 1, a specific amount of resources ${\mu }_{r,i,t}$ is substracted from the initial amount of resources $R_{r0}$. This can be formulated as follows:

$R_{r,t}=R_{r,t-1}+R_{r,0}-{\displaystyle \sum }_i{\displaystyle \sum }_{\theta }{N}_{i,t-\theta }{\mu }_{i,r,t-\theta }\forall r\in R_c,t\in T.(10)$

The objective in this work is to try and optimize the operational production profit, as with optimal maintenance the production downtime is reduced and also the increased efficiency of the compressors leads to higher production rates and therefore higher profits. The production profit in this work is therefore defined as the sum of production profits from each compressor minus the overall cost for all maintenance conducted. The objective function is formulated as follows:

$\text{max}z=K_{profit}{\displaystyle \sum }_{r\in R_c}{G}_{r,t}-K_i{\displaystyle \sum }_{r\in R_c}{\displaystyle \sum }_i^{I_r}{\displaystyle \sum }_t^T{N}_{i,t}.(11)$

5. Results and Discussion

Based on the mathematical formulation in the previous section, a planning and a scheduling model have been created and cases of different sizes, as described in the case study section, have been solved using GAMS24.8.4/CPLEX 12.7.1.0 on an Intel(R) Core(TM) i7-6700HQ at 2.6 GHz and 16 GB RAM.

The cases that are considered encompass between 5 compressors and up to 100 compressors. In the planning model time horizons of either 4 or 8 years were chosen, with the time slots being either full months or half months. In the scheduling model, the same case study size were optimized for either one month or two months time horizons with time slots either being 3 or 6 h long.

In order to evaluate the operational improvement, as the base case for comparison was created for each model. In the planning model, the base case considers time-based maintenance in which every compressor is maintained every 24 months with a long maintenance. Additional short maintenance actions are performed, when required due to the remaining useful lifetime. The planning model considers long and short maintenance as well as compressor inspections. The scheduling model does include all mentioned maintenance types. However, the high prices of the longer lasting maintenance types in combination with their time duration that causes a production stop favors most of the time the short-term maintenance actions, namely on-line and off-line washing. Therefore, the base case of the scheduling model consists out of regular operations, but spares out the option of washing completely.

The results for the planning model are shown in Table 4. A total of 20 cases has been run and compared to the corresponding base case. Instead of showing the actual operating profits, the table shows the improvements in comparison to the base case. Additionally, the remaining optimization gap of the problem is shown. All cases are terminated after a maximum computation time of 20,000 s. Further calculation time might improve the objective function by finding an integer solution closer to the best bound. The results of the planning model show improvements to the operational profit of up to 8%. There are two trends visible: A finer time grid gives higher improvements and larger case studies show lower improvements. The first trend is logical as the smaller time grid allows maintenance to be closer to their optimal time point, as the time points are discrete and do not necessarily reflect the optimal time that could be achieved in a continuous-time formulation (Even though this would not reflect the real-world problem, as maintenance - especially in offshore-settings - will not be timed to be performed by a specific minute or second). The second trend does not appear logical on first sight. With increasing case studies one would assume at least similar improvements. However, there are constraints set by the amount of maintenance personnel available. As the fleet size increases, the amount of personnel does not increase and therefore the improvement rates are not constant.

TABLE 4

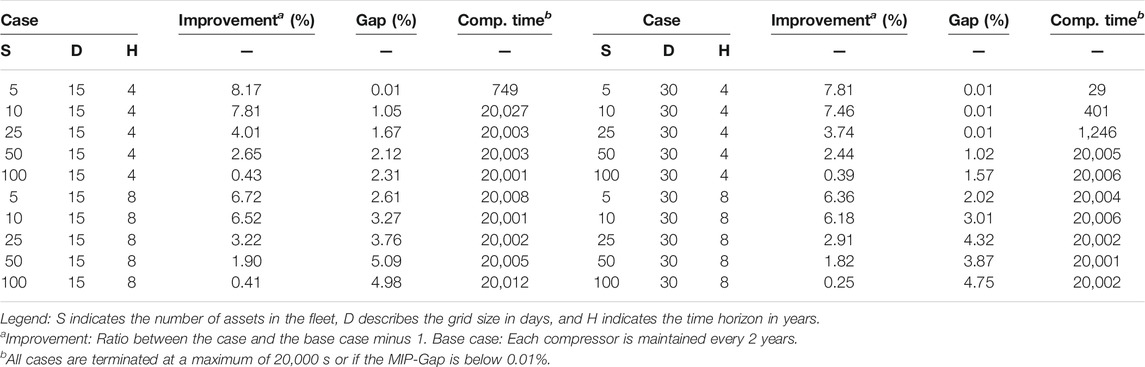
TABLE 4. Results of the planning optimization for different cases over a planning horizon of 4 or 8 years.

However, the optimization gap is increasing with larger fleet size, which may also cause lower improvement rates, as some additional improvement may be hidden in this gap.

The results for the scheduling model are shown in Table 5. Similar to the planning model, also a total of 20 cases has been run and compared to the corresponding base case. Again, improvement, the optimization gap and the computational time are listed in the table. Maximum computation time was again set to 20,000 s and the termination criterion 0.01% gap. The operational profits improved by up to 2%, with similar trends visible as before. A finer time grid gives higher improvements for the scheduling model and larger case studies show lower improvements that may again be affected by the increasing optimization gap. The optimization gaps in the scheduling model are in general larger than in the planning model. This can be explained by the larger problem size due to the number of time slots in the fine grid.

TABLE 5

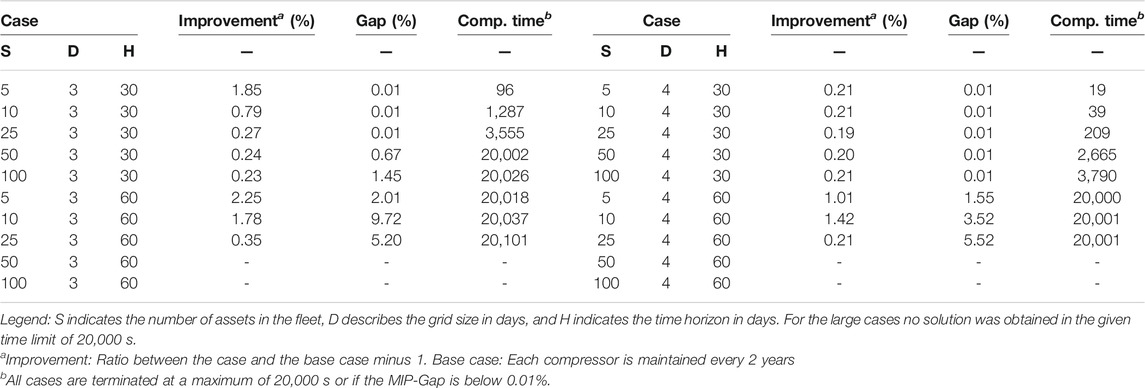
TABLE 5. Results of the scheduling optimization for different cases over a scheduling horizon (H) of 30 or 60 days.

6. Conclusion

This work presented a case study for the optimization of maintenance actions within a compressor fleet. A detailed description of the different parameters and ranges of those parameters enables the scientific community to use it as a test-bed for their own formulations. The fundamental hypothesis is that maintenance should not just be conducted because of approaching failures, but because the degradation is forcing the assets to perform at a suboptimal level and improvements of the operational profit can be realized by finding the optimal choice of maintenance type and time when these maintenance tasks should be performed.

As a first step, both a scheduling and a planning formulation have been individually presented. Both build on the RTN framework and are realized in a discrete-time fashion. Degradation has been considered by recoverable degradation, non-recoverable degradation and the remaining useful lifetime of an asset. Five different maintenance modes have been introduced and a combination of those is applied in the two models to counteract the linear degradation which is modeled via several enumerator formulations.

A range of cases has been run for both models and compared to base cases. The formulation used in the planning model enables improvements of the operational profit of up to 8%, while the scheduling formulation can improve profits in the short run by up to 2%.

By posing this example case study to the academic community, further work on solution strategies and formulation to handle this problem are strongly encouraged. First of all, existing planning and scheduling approaches other than the chosen discrete-time RTN can be tested. Further improvement may be achieved or more state-of-the-art approaches can be used, when research is done into the directions mentioned below.

In this work, a separate planning and scheduling formulation are presented. This is a pragmatical solution of the problem, as the different time dimensions require a different focus, especially regarding the available maintenance types, the time available for solving the problem, and the required level of detail. However, there is a major trend of integrating different layers of the control pyramid, as the communication between different systems is beneficial. Ref. 7 discuss this integration on the example of scheduling and advanced control.

In fact, maintenance planning is a highly stochastic problem. This concerns the input values from condition monitoring (e.g., The compressor will break in 30 days with a probability of 80%) but also the production outputs are rarely constant over the next years. The deterministic simplification in this work makes it possible to process large asset fleets, as stochastic approaches are mostly used for small case studies at the current time.

Other possible paths to explore regarding this case study are heuristics to rule out some solutions that are not optimal beforehand or apply a de-centralized approach. In fact, the problem can be decomposed into the decisions that are happening on a fleet level and need to be determined centrally. However, many decisions can also be decided on a lower level, for example on each individual platform. This will enable the formulation to include other information such as an approximation degradation, based on real-time information from the process. A steady communication between the platform-optimization model and the centralized fleet-model are key for communicating information about e.g., logistics or production demands.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

FS: Conceptualization, Methodology, Software, Writing - Original Draft, Visualization; GA: Conceptualization, Methodology, Software, Writing - Review Editing; LI: Resources, Supervision, Writing - Review Editing; IH: Conceptualization, Methodology, Supervision, Writing - Review Editing.

Conflict of Interest

Authors IH and GA were employed by the company Hitachi ABB Power Grids Research.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Financial support is gratefully acknowledged from the Marie Curie Horizon 2020 EID-ITN project “PROcess NeTwork Optimization for efficient and sustainable operation of Europe’s process industries taking machinery condition and process performance into account “PRONTO”, Grant agreement No 675215.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2020.528181/full#supplementary-material

References

1. Biondi, M, Sand, G, and Harjunkoski, I. Optimization of multipurpose process plant operations: a multi-time-scale maintenance and production scheduling approach. Comput Chem Eng (2017). 99:325–39. doi:10.1016/j.compchemeng.2017.01.007.

CrossRef Full Text | Google Scholar

2. Bock, S, Briskorn, D, and Horbach, A. Scheduling flexible maintenance activities subject to job-dependent machine deterioration. J Sched (2012). 15:565–78. doi:10.1007/s10951-011-0248-7.

CrossRef Full Text | Google Scholar

3. Cassady, CR, Pohl, EA, and Paul Murdock, W. Selective maintenance modeling for industrial systems. J Qual Mainten Eng (2001). 7:104–17. doi:10.1108/13552510110397412.

CrossRef Full Text | Google Scholar

4. Castro, PM, Sun, L, and Harjunkoski, I. Resource-task network formulations for industrial demand side management of a steel plant. Ind Eng Chem Res (2013). 52:13046–58. doi:10.1021/ie401044q.

CrossRef Full Text | Google Scholar

5. Deloitte. 2017 Global chemical industry mergers and acquisitions outlook: driving forward through global uncertainty (2017). p. 20, Technical Report.

Google Scholar

6. Elrod, WC, King, PI, and Poniatowski, EM. Effects of surface roughness, freestream turbulence, and incidence angle on the performance of a 2-D compressor cascade (1990). ASME. Technical Paper V001T01A061.

CrossRef Full Text | Google Scholar

7. Engell, S, and Harjunkoski, I. Optimal operation: scheduling, advanced control and their integration. Comput Chem Eng (2012). 47:121–33. doi:10.1016/j.compchemeng.2012.06.039.

CrossRef Full Text | Google Scholar

8. Hovland, G, and Antoine, M. Scheduling of gas turbine compressor washing. Intell Autom Soft Comput (2006). 12:63–73. doi:10.1080/10798587.2006.10642916.

CrossRef Full Text | Google Scholar

9. Igie, U, Pilidis, P, Fouflias, D, Ramsden, K, and Lambart, P. On-line compressor cascade washing for gas turbine performance investigation. In: ASME 2011 turbo expo: turbine technical conference and exposition; 2011 Jun 6–10; Vancouver, BC, Canada; New York, NY: ASME (2011). p. 221–31.

Google Scholar

10. Jain, V, and Grossmann, IE. Cyclic scheduling of continuous parallel-process units with decaying performance. AIChE J (1998). 44:1623–36. doi:10.1002/aic.690440714

CrossRef Full Text | Google Scholar

11. Khalid, SA, Khalsa, AS, Waitz, IA, Tan, CS, Greitzer, EM, Cumpsty, NA, et al. Endwall blockage in axial compressors. J Turbomach (1999). 121:499–509. doi:10.1115/1.2841344.

CrossRef Full Text | Google Scholar

12. Kurz, R, and Brun, K. Degradation in gas turbine systems. J Eng Gas Turbines Power (2001). 123:70. doi:10.1115/1.1340629.

CrossRef Full Text | Google Scholar

13. Kurz, R, and Brun, K. Fouling mechanisms in axial compressors. J Eng Gas Turbines Power (2012). 134:1–9. doi:10.1115/1.4004403.

CrossRef Full Text | Google Scholar

14. Liu, S, Yahia, A, and Papageorgiou, LG. Optimal production and maintenance planning of biopharmaceutical manufacturing under performance decay. Ind Eng Chem Res (2014). 53:17075–91. doi:10.1021/ie5008807.

CrossRef Full Text | Google Scholar

15. Norwegian Petroleum Directorate (2020). The oil and gas pipeline system-Norwegian petroleum. Available from: https://www.norskpetroleum.no/en/production-and-exports/the-oil-and-gas-pipeline-system/ (Accessed July 5, 2017).

Google Scholar

16. Pantelides, CC. Unified framework for optimal process planning and scheduling [PhD dissertation]. New Brunswick (NJ): Rutgers University (1994).

Google Scholar

17. Schulze Spüntrup, F, Dalle Ave, G, Imsland, L, and Harjunkoski, I. Optimal maintenance scheduling for washing of compressors to increase operational efficiency. In: Proceedings of the 29th European symposium on computer aided process engineering-ESCAPE29 (2019). p. 1513–8.

Google Scholar

18. Schulze Spüntrup, F, Dalle Ave, G, Imsland, L, and Harjunkoski, I. Performance-based maintenance planning for asset fleets. In: Proceedings of the 12th IFAC symposium on dynamics and control of process systems, including biosystems; 2019 Apr 23–26; Florianópolis, Brazil. New York, NY: IFAC (2019). p. 1–1024.

Google Scholar

19. Singh, D, Tabakoff, W, and Mechanics, E. Simulation of performance deterioration in eroded compressors. In: ASME 1996 international gas turbine and aeroengine congress and exhibition; 1996 Jun 10–13; Birmingham, UK. New York, NY: ASME (1996). p. 1–8.

Google Scholar

20. Stalder, J-P. Gas turbine compressor washing state of the art: field experiences. J Eng Gas Turbines Power (2001). 123:363. doi:10.1115/1.1361108.

CrossRef Full Text | Google Scholar

21. Tarabrin, AP, Schurovsky, VA, Bodrov, AI, and Stalder, JP. An analysis of axial compressors fouling and a cleaning method of their blading. In: ASME 1996 International gas turbine and aeroengine congress and exhibition; 1996 Jun 10–13; Birmingham, UK. New York, NY: ASME (1996). p. 1–7.

Google Scholar

22. Varnier, C, and Zerhouni, N. Scheduling predictive maintenance in flow-shop. In: Proceedings of IEEE 2012 prognostics and system health management conference; 2012 May 23–25; Beijing, China. IEEE (2012). p. 1–6.

Google Scholar

23. Vieira, M, Pinto-Varela, T, and Barbosa-Póvoa, AP. Production and maintenance planning optimisation in biopharmaceutical processes under performance decay using a continuous-time formulation: a multi-objective approach. Comput Chem Eng (2017). 107:111–39. doi:10.1016/j.compchemeng.2017.03.008.

CrossRef Full Text | Google Scholar

24. Xenos, DP, Kopanos, GM, Cicciotti, M, and Thornhill, NF. Operational optimization of networks of compressors considering condition-based maintenance. Comput Chem Eng (2016). 84:117–31. doi:10.1016/j.compchemeng.2015.08.008.

CrossRef Full Text | Google Scholar