- 1Department of Computer Science, Chiba Institute of Technology, Narashino, Japan
- 2Graduate School of Applied Informatics, University of Hyogo, Kobe, Japan
Multiple non-linear systems demonstrate the phenomenon where fluctuations enhance the synchronization and periodic behaviors of the system. In the phenomenon induced by stochastic additive noise, stochastic resonance, noise enhances the synchronization of system behaviors against weak input signals. Along with stochastic noise, deterministic chaos induces a phenomenon like stochastic resonance called chaotic resonance. This review summarizes the progress of studies on chaotic resonance over the most recent decade. First, the fundamental characteristics of chaotic resonance are reviewed. Second, chaotic resonance in brain informatics, including cerebellar learning and deterministic fluctuations observed in electroencephalography/magnetoencephalography examinations, are reviewed. Third, the “reduced region of orbit” method is reviewed for the potential application of chaotic resonance. This review emphasizes the potential importance of recapturing neural fluctuation functionality, previously considered in the framework of stochastic resonance (also called stochastic facilitation), through chaotic resonance and assesses the effectiveness of applying chaotic resonance.
1. Introduction
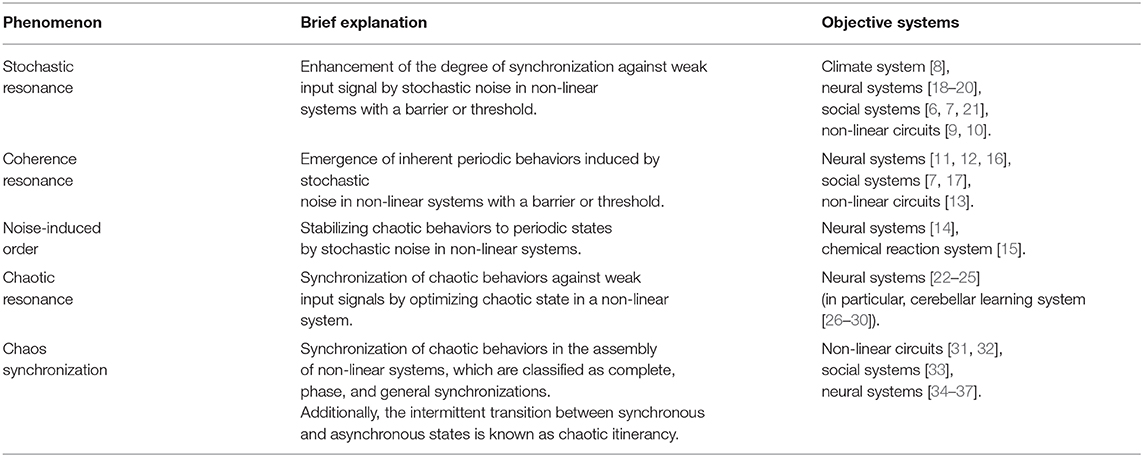
Various non-linear systems reportedly demonstrate a phenomenon where fluctuations enhance synchronization and periodic behaviors (reviewed in [1–5]) [6, 7]. Phenomena induced by stochastic additive noise, stochastic resonance [8–10] and coherence resonance/noise-induced order [11–17] are well-known. In stochastic resonance, the synchronization of system behaviors against weak input signal is enhanced by noise [8–10]. In coherence resonance/noise-induced order, the intrinsic periodic system behaviors are induced by noise [11–17]. In addition to stochastic noise, deterministic chaos induces stochastic resonance, also called chaotic resonance (reviewed in [3, 4]). These phenomena are summarized in Table 1.
Studies have assessed these phenomena and have identified various functionalities of fluctuations in neural activity (reviewed in [38–41]). These studies have primarily focused on two kinds of phenomena: sensitivity enhancement of sensory neural systems [38] and functionality enhancement of the central nervous system [39–42]. A study on sensory neural systems reported that crayfish and paddlefish use background noise to detect slight movements in the water made by predators and prey [38]. Another study on the central nervous system reported that the chaotic dynamics of electroencephalography (EEG) in the olfactory bulb of rabbits contributes to efficient memory search [43]. Moreover, studies on the cerebellar learning process (i.e., the inferior olive nucleus) showed transmission of teacher signals with rich error information in the form of a low-rate chaotic spiking pattern (~1.0 Hz) [26–30]. Furthermore, neuroimaging modalities, such as functional magnetic resonance imaging (fMRI) and EEG/magnetoencephalography (MEG) revealed the degrees of neural fluctuations are related to cognitive functions, aging, development, and psychiatric disorders [44–48] (reviewed in [40, 41]).
These resonance phenomena induced by fluctuations, especially stochastic resonance, have recently been applied to biomedical engineering [49–52]. Kurita et al. developed a wearable device that enhances the tactile sensitivity of surgeons' hands by applying appropriate vibrations [50, 51]. Enders et al. and Seo et al. further utilized this method by applying vibrotactile noise to study stochastic resonance in the human sensory systems and proposed a rehabilitation method to improve haptic sensations in patients with paralysis [49, 53]. In addition to the sensory neural systems at the cognitive levels of brain function, Van der Groen et al. developed a method to enhance perceptual decision-making using the stochastic resonance effect [52]. Specifically, applying the optimal amount of noise by transcranial random noise stimulation to the visual cortex can be used as a non-invasive brain stimulation technique to enhance the accuracy of perceptual decisions. Regarding chaotic resonance, although several studies reported that its sensitivity to a weak input signal is higher than that of stochastic resonance [23, 54], no study has reported any application of chaotic resonance. One possible reason for this might be the strength of additive noise, which can be easily controlled from the outside during stochastic resonance. Conversely, controlling the chaotic states to elicit chaotic resonance is difficult in many cases, especially in biological systems. To tackle this difficulty, we previously proposed a new chaos control method called the “reduced region of orbit (RRO)” method, where the chaotic signals are shifted to the appropriate chaotic state to elicit a chaotic resonance by external feedback signals [55]. First, the RRO-based method was adopted for a simple discrete chaotic system, such as the cubic map and its assembly [55, 56], as well as to a continuous chaotic system termed Chua's circuit [57]. Studies have now started applying the RRO-based method to neural systems [58, 59]. The RRO-based method is expected to open an avenue for utilizing chaotic resonance in biomedical engineering in addition to its application in stochastic resonance.
In this review, we summarize the progress of studies on chaotic resonance over the decade. First, the fundamental characteristics of chaotic resonance were reviewed. Second, chaotic resonance in brain informatics, including cerebellar learning and deterministic fluctuations observed in EEG/MEG, are reviewed. Finally, studies on the RRO-based method for controlling chaotic resonance are also reviewed. Through chaotic resonance, this review emphasizes the potential importance of recapturing neural fluctuation functionality, previously considered in the framework of stochastic resonance (also called stochastic facilitation), and assesses the effectiveness of applying chaotic resonance.
2. Mechanism and Fundamental Characteristics of Chaotic Resonance
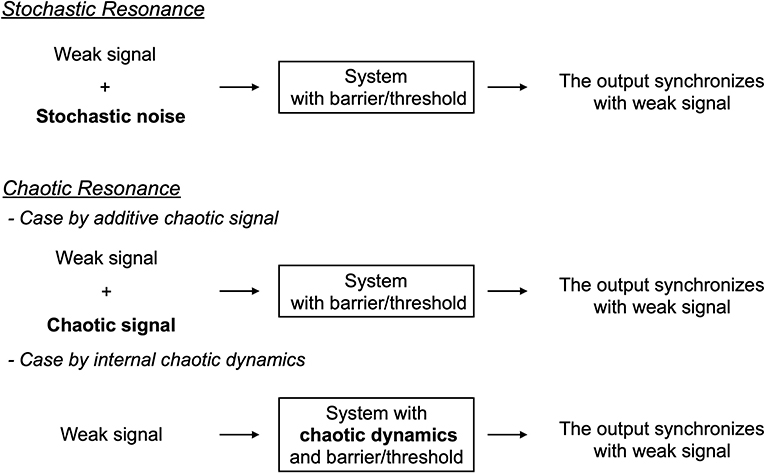
First, we review the mechanism of chaotic resonance in comparison with stochastic resonance (see the overview of these resonance phenomena in Figure 1). We assumed a condition in which the input signal is too weak for the system state to surpass the barrier or threshold. Under this condition, in case of stochastic resonance, the additive stochastic noise is applied to the system with appropriate strength; the system state surpasses the barrier or threshold due to the noise, especially when the input signal exhibits a peak. Consequently, the weak input signal and the system output synchronize with one another. Initially, the concept of stochastic resonance was devised to explain the mechanism of periodically recurrent ice ages, called the Milankovitch cycle [8]. Presently, it is widely recognized that stochastic resonance emerges in various kinds of systems with the following three factors: a barrier/threshold, a source of noise, and a weak input signal [8–10]. Moreover, the noise source is not restricted to additive stochastic noise; chaos also causes a phenomenon of stochastic resonance, i.e., chaotic resonance (reviewed in [3, 4]).
In chaotic resonance, two forms have been proposed to utilize chaotic dynamical fluctuation (reviewed in [3, 4]). In one form, the external additive chaotic signal is applied to the system instead of the stochastic noise [60, 61]; in the other form, an alternative intrinsic chaotic dynamics is utilized. Many of the recently published studies were classified as the latter form (reviewed in [3, 4]). In the following sections, we review this type of chaotic resonance. Initially, chaotic resonance was found in chaotic systems with chaos-chaos intermittency, in which the chaotic orbit hops among the several separated chaotic attractor regions, such as the cubic map and Chua's circuits [62–64] (reviewed in [3]). In these chaotic systems, an attractor merging crisis arises according to the adjustment of internal order parameters; through this crisis, chaos-chaos intermittency is induced. The degree of synchronization in chaotic resonance approximately maximizes, which is the bifurcation point for this attractor merging crisis. The underlying reason for this phenomenon is that, approximately at this bifurcation, the intrinsic hopping of chaotic attractor regions seldomly occurs under the absence of weak external signals. In this situation, the application of the external signal acts as a perturbation that switches the orbit among the attractors. Consequently, the induced chaos-chaos intermittency synchronizes with the external signal. Under conditions without chaos-chaos intermittency, the external signal is too weak to induce the chaos-chaos intermittency. Conversely, because of the inherent chaotic dynamics with a large disturbance, under high-frequency conditions of chaos-chaos intermittency, the hopping does not synchronize with a weak external signal. Another fundamental characteristic of chaotic resonance is that the degree of synchronization exhibits a unimodal maximum peak around an appropriate signal strength at the frequency of the input signal [54, 64, 65]. These characteristics are interpreted such that chaotic resonance has resonance frequency as the resonance phenomenon, and the stabilization of chaotic states by large signal strength degrades the degree of synchronization [65].
3. Chaotic Resonance in Neural Systems
Previous studies on the dynamic behaviors of neural activity have revealed that chaos exists at several hierarchical levels in neural systems, ranging from the electrical response of a single neuron to brain activity produced by neural assemblies [66–68]. To identify the functionalities of chaos in neural systems, previous studies evaluated chaotic resonance within them [22, 23, 54, 65]. Sinha constructed a neural population model composed of excitatory and inhibitory neural populations, and the neural activity of this model was indicated by the mean spiking rate [22]. This neural model exhibits chaos-chaos intermittency, which synchronizes with the weak external signal, i.e., it induces a chaotic resonance [22]. Moreover, we constructed chaos neural networks as per the mean spiking rate model with several embedded memory patterns; these networks exhibit chaos-chaos intermittency among the stored memory patterns [23, 54, 65]. The degree of synchronization of the period for recalling the memory against a weak input stimulus is maximized around the emergence of the attractor merging crises [23, 54, 65]. Additionally, comparing the sensitivity of chaotic resonance with that of stochastic resonance, chaotic resonance exhibits higher sensitivity than stochastic resonance [23, 54, 65].
In actual neural systems, various types of neural coding forms exist as well as the mean spiking rate coding, such as spike timing coding and spike population coding (reviewed in [69]). Spiking neural models have been widely utilized to describe the dynamic behaviors of these neural coding forms and to reveal the brain informatics mechanism [28, 70–72] (reviewed in [69, 73]). Previously, several studies have identified chaotic resonance in spiking neurons and spiking neural networks, such as in the inferior olive neural systems for cerebellar learning and in the Izhikevich neuron model [24–27, 30]. Spiking neural systems do not exhibit chaos-chaos intermittency but rather exhibit threshold characteristics for spike generation (reviewed in [74]). During chaotic resonance in spiking neural systems, the chaotic behavior against input signals induces spike-responses that do not occur at specific times but rather vary for each trial. In this manner, the distribution frequency of these spike timings against the input signal becomes congruent with the shape of the input signal [24–27, 30]. In addition to the mean spiking rate models, the chaotic resonance in spiking neural systems exhibits a unimodal maximum peak of signal response at the appropriate input frequency. The signal response of chaotic resonance is maintained under a weak strength of the input signal where the chaotic state is present [25, 30]. Moreover, chaotic resonance responses and their sensitivity maximize around the edge between the periodic spiking state and chaotic spiking state (called edge of chaos [75]) [25].
With large-scale neural fluctuations, observed as EEG, MEG, and fMRI signals, the complexity of temporal behaviors of brain activity reflects the ability of cognitive functions [76], development [47], aging [44, 77, 78], and the pathology of psychiatric disorders [45, 48, 79, 80] (reviewed in [40, 41, 81]). Previous studies considered the temporal complexity of brain activity under the framework of stochastic resonance (also called stochastic facilitation) (reviewed in [39]). Several studies reported that these complex brain activities involve the deterministic dynamical processes that reflect the internal brain informatics process rather than the stochastic process [47, 77, 82, 83]. In addition to these studies based on physiological data analysis, several model-based studies with spiking neural networks demonstrated that network structures (e.g., synaptic weight distribution and network topology) induce complex deterministic dynamical neural activities [72, 84]. These studies may indicate the existence of chaotic resonance in a wide range of brain activities and cognitive processes. Although it is difficult to examine chaos with experimental time-series of brain activity involving stochastic noise in high-dimensional dynamical systems [85], future studies that assess the complexity of neural activity will validate this speculation.
4. Controlling Chaotic Resonance by External Feedback Signals
Although the internal system parameters cannot be adjusted from outside the system, our proposed RRO-based method induces chaotic resonance by adjusting the attractor merging crisis [55]. This RRO-based method is expected to facilitate the biomedical application of chaotic resonance [58, 59]. In this section, we review the mechanisms for eliciting and controlling chaotic resonance using the RRO-based method and the recent progress in its application to neural systems.
Systems with chaos-chaos intermittency possess cubic map structures in their dynamics [86, 87]. RRO feedback signals control the conditions for the development of attractor merging crisis by adjusting the local maximum and minimum values of the map function [55, 59]. In particular, under the condition of high-frequency chaos-chaos intermittency, RRO feedback signals with positive feedback strength, including the effect of reducing the absolute values of local maximum and minimum of the map function, reduce the frequency of chaos-chaos intermittency. Without the chaos-chaos intermittency, the RRO feedback signals with negative feedback strength, including those with the effect of increasing the local maximum/minimum of the map function, induce chaos-chaos intermittency and enhance the frequency of chaos-chaos intermittency. Consequently, in both cases, the appropriate frequency of chaos-chaos intermittency for chaotic resonance is achieved. Previously, various methods were proposed for controlling the chaotic state by using external perturbations, such as the Ott-Grebogi-Yorke method [88], delayed feedback method [89, 90], and H∞ method [91] (reviewed in [92]). These conventional chaos control methods provide a transition for the conversion of chaotic states to stable periodic states or stable fixed points. The RRO-based method not only eliminates the chaotic state but also optimizes the chaotic state for chaotic resonance. Initially, the RRO-based method was adopted for a discrete cubic map system [55]; subsequently, the RRO-based method has been applied to coupled chaotic systems [56]. Moreover, in continuous chaotic systems, RRO feedback signals based on dynamical behavior on the Poincaré section have been developed, which can induce chaotic resonance [57].
As a potential application of the RRO-based method to neural systems, we applied RRO feedback signals to a discrete neural population model composed of excitatory and inhibitory neural populations [55]. This neural model, proposed by Sinha, possesses the cubic map structure in its dynamics and can elicit chaos-chaos intermittency behaviors [22]. Through this RRO mechanism, the frequency of chaos-chaos intermittency is adjusted, and a chaotic resonance is induced [55, 59]. Compared with conventional stochastic resonance induced by additive noise, chaotic resonance induced by RRO feedback signals exhibits a relatively high degree of synchronization against the input signal and a high sensitivity against weak input signals [59]. Moreover, additive noise for inducing stochastic resonance only causes the development of the attractor merging crisis in the non-chaos-chaos intermittency states, whereas the RRO feedback signals can either induce or prevent the attractor merging crisis by applying a negative or positive feedback strength, respectively [59]. For these reasons, the RRO-based method has higher adaptability to more varied attractor conditions than does additive noise in stochastic resonance. These advantages of the RRO-based method might facilitate the development of chaotic resonance instead of stochastic resonance in systems in which the internal system parameters cannot be adjusted, especially biological systems.
5. Conclusions
Based on the accumulation of studies over the past decades, we reviewed the fundamental characteristics of chaotic resonance. The recent studies, dealing with the complex neural activity caused by the deterministic process and multiple complex network structures, indicated the possibility that chaotic resonance, rather than stochastic resonance/stochastic facilitation, will become the framework for other studies to understand the functionality of neural fluctuations. Moreover, with regard to the application of chaotic resonance in biomedical regions, our proposed RRO-based method might be utilized for the enhancement of neural functionality, which, to date, has restricted the application of stochastic resonance. Although judging and controlling chaotic states is difficult in many systems, including actual neural systems, recently proposed analysis methods for predicting and judging chaos [93–95] and future studies will bring new insights to the functionality of neural fluctuation and biomedical application of chaotic resonance. Moreover, in future works, robust noise evaluation methods for chaos under noisy environments and the development of RRO-based methods against more physiological neural systems are needed. Furthermore, as the extension of the RRO-based method, the development of new methods for controlling intermittent chaotic behaviors in systems with more complex attractors, such as multiple structures for co-existing chaotic attractors and limit cycles [96] will be important topics for future studies. Not restricted to biomedical applications, chaotic neural oscillations have been widely used in bio-inspired informatics and robotics systems [97, 98]. In these systems, by not removing the chaotic states but rather transiting the chaotic states to the appropriate chaotic state according to each objective, the RRO-based method might be a candidate for these controlling methods. Therefore, as part of future studies, these aspects are also important.
Author Contributions
SN and HN discussed the progress of studies on chaotic resonance. SN drafted the main manuscript text and prepared all figures. All authors contributed to the article and approved the submitted version.
Funding
This work was supported by JSPS KAKENHI for Early-Career Scientists (grant number, 18K18124 to SN).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Harmer GP, Davis BR, Abbott D. A review of stochastic resonance: circuits and measurement. IEEE Trans Instr Meas. (2002) 51:299–309. doi: 10.1109/19.997828
2. Pikovsky A, Rosenblum M, Kurths J. Synchronization: A Universal Concept in Nonlinear Sciences, Vol. 12. Cambridge: Cambridge University Press (2003).
3. Anishchenko VS, Astakhov V, Neiman A, Vadivasova T, Schimansky-Geier L. Nonlinear Dynamics of Chaotic and Stochastic Systems: Tutorial and Modern Developments. Berlin; Heidelberg: Springer Science & Business Media (2007).
4. Rajasekar S, Sanjuán MAF. Nonlinear Resonances. Cham: Springer (2016). doi: 10.1007/978-3-319-24886-8
5. Strogatz SH. Nonlinear Dynamics and Chaos With Student Solutions Manual: With Applications to Physics, Biology, Chemistry, and Engineering. Boca Raton, FL; London; New York, NY: CRC Press (2018). doi: 10.1201/9780429399640
6. Li JC, Li C, Mei DC. Effects of time delay on stochastic resonance of the stock prices in financial system. Phys Lett A. (2014) 378:1997–2000. doi: 10.1016/j.physleta.2014.05.036
7. Nobukawa S, Hashimoto R, Nishimura H, Yamanishi T, Chiba M. Noise-induced phenomena in the Kaldor business cycle model. Trans Inst Syst Control Inform Eng. (2017) 30:459–66. doi: 10.5687/iscie.30.459
8. Benzi R, Sutera A, Vulpiani A. The mechanism of stochastic resonance. J Phys A Math Gen. (1981) 14:L453. doi: 10.1088/0305-4470/14/11/006
9. Anishchenko VS, Safonova M, Chua LO. Stochastic resonance in the nonautonomous Chua's circuit. J Circuits Syst Comput. (1993) 3:553–78. doi: 10.1142/S0218126693000344
10. Korneta W, Gomes I, Mirasso CR, Toral R. Experimental study of stochastic resonance in a Chua's circuit operating in a chaotic regime. Phys D Nonlin Phenom. (2006) 219:93–100. doi: 10.1016/j.physd.2006.05.016
11. Pikovsky AS, Kurths J. Coherence resonance in a noise-driven excitable system. Phys Rev Lett. (1997) 78:775. doi: 10.1103/PhysRevLett.78.775
12. Lee SG, Neiman A, Kim S. Coherence resonance in a Hodgkin-Huxley neuron. Phys Rev E. (1998) 57:3292. doi: 10.1103/PhysRevE.57.3292
13. Palenzuela C, Toral R, Mirasso CR, Calvo O, Gunton JD. Coherence resonance in chaotic systems. Europhys Lett. (2001) 56:347. doi: 10.1209/epl/i2001-00526-5
14. Katada N, Nishimura H. Noise effects on chaos in chaotic neuron model. In: Peper F, Umeo H, Matsui N, Isokawa T, editors. Natural Computing. Tokyo: Springer (2010). p. 209–17. doi: 10.1007/978-4-431-53868-4_24
15. Yoshimoto M, Shirahama H, Kurosawa S. Noise-induced order in the chaos of the Belousov-Zhabotinsky reaction. J Chem Phys. (2008) 129:014508. doi: 10.1063/1.2946710
16. Wu J, Ma S. Coherence resonance of the spiking regularity in a neuron under electromagnetic radiation. Nonlin Dyn. (2019) 96:1895–908. doi: 10.1007/s11071-019-04892-z
17. Zhong GY, Li HF, Li JC, Mei DC, Tang NS, Long C. Coherence and anti-coherence resonance of corporation finance. Chaos Solit Fract. (2019) 118:376–85. doi: 10.1016/j.chaos.2018.12.008
18. Wang Q, Perc M, Duan Z, Chen G. Delay-induced multiple stochastic resonances on scale-free neuronal networks. Chaos. (2009) 19:023112. doi: 10.1063/1.3133126
19. Yilmaz E, Uzuntarla M, Ozer M, Perc M. Stochastic resonance in hybrid scale-free neuronal networks. Phys A Stat Mech Appl. (2013) 392:5735–41. doi: 10.1016/j.physa.2013.07.011
20. Nobukawa S, Nishimura H. Enhancement of spike-timing-dependent plasticity in spiking neural systems with noise. Int J Neural Syst. (2016) 26:1550040. doi: 10.1142/S0129065715500409
21. Dong Y, Wen S, Hu X, Li JC. Stochastic resonance of drawdown risk in energy market prices. Phys A Stat Mech Appl. (2020) 540:123098. doi: 10.1016/j.physa.2019.123098
22. Sinha S. Noise-free stochastic resonance in simple chaotic systems. Phys A Stat Mech Appl. (1999) 270:204–14. doi: 10.1016/S0378-4371(99)00136-3
23. Nishimura H, Katada N, Aihara K. Coherent response in a chaotic neural network. Neural Process Lett. (2000) 12:49–58. doi: 10.1023/A:1009626028831
24. Nobukawa S, Nishimura H, Yamanishi T, Liu JQ. Analysis of chaotic resonance in Izhikevich neuron model. PLoS ONE. (2015) 10:e0138919. doi: 10.1371/journal.pone.0138919
25. Nobukawa S, Nishimura H, Yamanishi T. Chaotic resonance in typical routes to chaos in the Izhikevich neuron model. Sci Rep. (2017) 7:1331. doi: 10.1038/s41598-017-01511-y
26. Schweighofer N, Doya K, Fukai H, Chiron JV, Furukawa T, Kawato M. Chaos may enhance information transmission in the inferior olive. Proc Natl Acad Sci USA. (2004) 101:4655–60. doi: 10.1073/pnas.0305966101
27. Tokuda IT, Han CE, Aihara K, Kawato M, Schweighofer N. The role of chaotic resonance in cerebellar learning. Neural Netw. (2010) 23:836–42. doi: 10.1016/j.neunet.2010.04.006
28. Schweighofer N, Lang EJ, Kawato M. Role of the olivo-cerebellar complex in motor learning and control. Front Neural Circuits. (2013) 7:94. doi: 10.3389/fncir.2013.00094
29. Kawato M, Kuroda S, Schweighofer N. Cerebellar supervised learning revisited: biophysical modeling and degrees-of-freedom control. Curr Opin Neurobiol. (2011) 21:791–800. doi: 10.1016/j.conb.2011.05.014
30. Nobukawa S, Nishimura H. Chaotic resonance in coupled inferior olive neurons with the Llinás approach neuron model. Neural Comput. (2016) 28:2505–32. doi: 10.1162/NECO_a_00894
31. Pecora LM, Carroll TL. Synchronization in chaotic systems. Phys Rev Lett. (1990) 64:821. doi: 10.1103/PhysRevLett.64.821
32. Chua LO, Itoh M, Kocarev L, Eckert K. Chaos synchronization in Chua's circuit. J Circuits Syst Comput. (1993) 3:93–108. doi: 10.1142/S0218126693000071
33. Huang C, Cao J. Active control strategy for synchronization and anti-synchronization of a fractional chaotic financial system. Phys A Stat Mech Appl. (2017) 473:262–75. doi: 10.1016/j.physa.2017.01.009
34. Tsuda I, Fujii H, Tadokoro S, Yasuoka T, Yamaguti Y. Chaotic itinerancy as a mechanism of irregular changes between synchronization and desynchronization in a neural network. J Integr Neurosci. (2004) 3:159–82. doi: 10.1142/S021963520400049X
35. Yoshioka M. Chaos synchronization in gap-junction-coupled neurons. Phys Rev E. (2005) 71:065203. doi: 10.1103/PhysRevE.71.065203
36. Rossello JL, Canals V, Oliver A, Morro A. Studying the role of synchronized and chaotic spiking neural ensembles in neural information processing. Int J Neural Syst. (2014) 24:1430003. doi: 10.1142/S0129065714300034
37. Tsuda I. Chaotic itinerancy and its roles in cognitive neurodynamics. Curr Opin Neurobiol. (2015) 31:67–71. doi: 10.1016/j.conb.2014.08.011
38. Hänggi P. Stochastic resonance in biology how noise can enhance detection of weak signals and help improve biological information processing. ChemPhysChem. (2002) 3:285–90. doi: 10.1002/1439-7641(20020315)3:3<285::AID-CPHC285>3.0.CO;2-A
39. McDonnell MD, Ward LM. The benefits of noise in neural systems: bridging theory and experiment. Nat Rev Neurosci. (2011) 12:415–26. doi: 10.1038/nrn3061
40. Takahashi T. Complexity of spontaneous brain activity in mental disorders. Prog Neuropsychopharmacol Biol Psychiatry. (2013) 45:258–66. doi: 10.1016/j.pnpbp.2012.05.001
41. Garrett DD, Samanez-Larkin GR, MacDonald SW, Lindenberger U, McIntosh AR, Grady CL. Moment-to-moment brain signal variability: a next frontier in human brain mapping? Neurosci Biobehav Rev. (2013) 37:610–24. doi: 10.1016/j.neubiorev.2013.02.015
42. Moss F, Ward LM, Sannita WG. Stochastic resonance and sensory information processing: a tutorial and review of application. Clin Neurophysiol. (2004) 115:267–81. doi: 10.1016/j.clinph.2003.09.014
43. Freeman WJ. Simulation of chaotic EEG patterns with a dynamic model of the olfactory system. Biol Cybern. (1987) 56:139–50. doi: 10.1007/BF00317988
44. Takahashi T, Cho RY, Murata T, Mizuno T, Kikuchi M, Mizukami K, et al. Age-related variation in EEG complexity to photic stimulation: a multiscale entropy analysis. Clin Neurophysiol. (2009) 120:476–83. doi: 10.1016/j.clinph.2008.12.043
45. Takahashi T, Cho RY, Mizuno T, Kikuchi M, Murata T, Takahashi K, et al. Antipsychotics reverse abnormal EEG complexity in drug-naive Schizophrenia: a multiscale entropy analysis. Neuroimage. (2010) 51:173–82. doi: 10.1016/j.neuroimage.2010.02.009
46. Okazaki R, Takahashi T, Ueno K, Takahashi K, Ishitobi M, Kikuchi M, et al. Changes in EEG complexity with electroconvulsive therapy in a patient with autism spectrum disorders: a multiscale entropy approach. Front Hum Neurosci. (2015) 9:106. doi: 10.3389/fnhum.2015.00106
47. Hasegawa C, Takahashi T, Yoshimura Y, Nobukawa S, Ikeda T, Saito DN, et al. Developmental trajectory of infant brain signal variability: a longitudinal pilot study. Front Neurosci. (2018) 12:566. doi: 10.3389/fnins.2018.00566
48. Nobukawa S, Yamanishi T, Nishimura H, Wada Y, Kikuchi M, Takahashi T. Atypical temporal-scale-specific fractal changes in Alzheimer's disease eeg and their relevance to cognitive decline. Cogn Neurodyn. (2019) 13:1–11. doi: 10.1007/s11571-018-9509-x
49. Enders LR, Hur P, Johnson MJ, Seo NJ. Remote vibrotactile noise improves light touch sensation in stroke survivors' fingertips via stochastic resonance. J Neuroeng Rehabil. (2013) 10:105. doi: 10.1186/1743-0003-10-105
50. Kurita Y, Shinohara M, Ueda J. Wearable sensorimotor enhancer for fingertip based on stochastic resonance effect. IEEE Trans Hum Mach Syst. (2013) 43:333–7. doi: 10.1109/TSMC.2013.2242886
51. Kurita Y, Sueda Y, Ishikawa T, Hattori M, Sawada H, Egi H, et al. Surgical grasping forceps with enhanced sensorimotor capability via the stochastic resonance effect. IEEE/ASME Trans Mechatron. (2016) 21:2624–34. doi: 10.1109/TMECH.2016.2591591
52. Van der Groen O, Tang MF, Wenderoth N, Mattingley JB. Stochastic resonance enhances the rate of evidence accumulation during combined brain stimulation and perceptual decision-making. PLoS Comput Biol. (2018) 14:e1006301. doi: 10.1371/journal.pcbi.1006301
53. Seo NJ, Kosmopoulos ML, Enders LR, Hur P. Effect of remote sensory noise on hand function post stroke. Front Hum Neurosci. (2014) 8:934. doi: 10.3389/fnhum.2014.00934
54. Nobukawa S, Nishimura H, Yamanishi T. Evaluation of chaotic resonance by Lyapunov exponent in attractor-merging type systems. In: Hirose A, Ozawa S, Doya K, Ikeda K, Lee M, Liu D, editors. International Conference on Neural Information Processing. Cham: Springer (2016). p. 430–7. doi: 10.1007/978-3-319-46687-3_48
55. Nobukawa S, Nishimura H, Yamanishi T, Doho H. Controlling chaotic resonance in systems with chaos-chaos intermittency using external feedback. IEICE Trans Fundam Electron Commun Comput Sci. (2018) 101:1900–6. doi: 10.1587/transfun.E101.A.1900
56. Nobukawa S, Nishimura H, Yamanishi T, Doho H. Induced synchronization of chaos-chaos intermittency maintaining asynchronous state of chaotic orbits by external feedback signals. IEICE Trans Fundam Electron Commun Comput Sci. (2019) 102:524–31. doi: 10.1587/transfun.E102.A.524
57. Nobukawa S, Doho H, Shibata N, Nishimura H, Yamanishi T. Chaos-chaos intermittency synchronization controlled by external feedback signals in Chua's circuits. IEICE Trans Fundam Electron Commun Comput Sci. (2020) 103:303–12. doi: 10.1587/transfun.2019EAP1081
58. Nobukawa S, Shibata N. Controlling chaotic resonance using external feedback signals in neural systems. Sci Rep. (2019) 9:4990. doi: 10.1038/s41598-019-41535-0
59. Nobukawa S, Shibata N, Nishimura H, Doho H, Wagatsuma N, Yamanishi T. Resonance phenomena controlled by external feedback signals and additive noise in neural systems. Sci Rep. (2019) 9:1–15. doi: 10.1038/s41598-019-48950-3
60. Carroll T, Pecora L. Stochastic resonance as a crisis in a period-doubled circuit. Phys Rev E. (1993) 47:3941. doi: 10.1103/PhysRevE.47.3941
61. Carroll T, Pecora L. Stochastic resonance and crises. Phys Rev Lett. (1993) 70:576. doi: 10.1103/PhysRevLett.70.576
62. Crisanti A, Falcioni M, Paladin G, Vulpiani A. Stochastic resonance in deterministic chaotic systems. J Phys A Math Gen. (1994) 27:L597. doi: 10.1088/0305-4470/27/17/001
63. Nicolis G, Nicolis C, McKernan D. Stochastic resonance in chaotic dynamics. J Stat Phys. (1993) 70:125–39. doi: 10.1007/BF01053958
64. Sinha S, Chakrabarti BK. Deterministic stochastic resonance in a piecewise linear chaotic map. Phys Rev E. (1998) 58:8009. doi: 10.1103/PhysRevE.58.8009
65. Nobukawa S, Nishimura H, Katada N. Chaotic resonance by chaotic attractors merging in discrete cubic map and chaotic neural network. IEICE Trans A. (2012) 95:357–66. Available online at: https://search.ieice.org/bin/summary.php?id=j95-a_4_357&category=A&lang=E&year=2012&abst=j
66. Arbib MA. The Handbook of Brain Theory and Neural Networks. 2nd ed. Cambridge: MIT Press (2003). doi: 10.7551/mitpress/3413.001.0001
67. Freeman WJ. Evidence from human scalp electroencephalograms of global chaotic itinerancy. Chaos. (2003) 13:1067–77. doi: 10.1063/1.1596553
68. Korn H, Faure P. Is there chaos in the brain? II. Experimental evidence and related models. Comptes Rendus Biol. (2003) 326:787–840. doi: 10.1016/j.crvi.2003.09.011
69. Rabinovich MI, Varona P, Selverston AI, Abarbanel HD. Dynamical principles in neuroscience. Rev Mod Phys. (2006) 78:1213. doi: 10.1103/RevModPhys.78.1213
70. Mejias J, Longtin A. Optimal heterogeneity for coding in spiking neural networks. Phys Rev Lett. (2012) 108:228102. doi: 10.1103/PhysRevLett.108.228102
71. Hiratani N, Teramae JN, Fukai T. Associative memory model with long-tail-distributed hebbian synaptic connections. Front Comput Neurosci. (2013) 6:102. doi: 10.3389/fncom.2012.00102
72. Nobukawa S, Nishimura H, Yamanishi T. Temporal-specific complexity of spiking patterns in spontaneous activity induced by a dual complex network structure. Sci Rep. (2019) 9:1–12. doi: 10.1038/s41598-019-49286-8
73. Taherkhani A, Belatreche A, Li Y, Cosma G, Maguire LP, McGinnity TM. A review of learning in biologically plausible spiking neural networks. Neural Netw. (2020) 122:253–72. doi: 10.1016/j.neunet.2019.09.036
74. Izhikevich EM. Dynamical Systems in Neuroscience. Cambridge: MIT Press (2007). doi: 10.7551/mitpress/2526.001.0001
75. Langton CG. Computation at the edge of chaos: phase transitions and emergent computation. Phys D Nonlin Phenom. (1990) 42:12–37. doi: 10.1016/0167-2789(90)90064-V
76. McIntosh AR, Kovacevic N, Itier RJ. Increased brain signal variability accompanies lower behavioral variability in development. PLoS Comput Biol. (2008) 4:e1000106. doi: 10.1371/journal.pcbi.1000106
77. Nobukawa S, Kikuchi M, Takahashi T. Changes in functional connectivity dynamics with aging: a dynamical phase synchronization approach. Neuroimage. (2019) 188:357–68. doi: 10.1016/j.neuroimage.2018.12.008
78. Takahashi T, Yoshimura Y, Hiraishi H, Hasegawa C, Munesue T, Higashida H, et al. Enhanced brain signal variability in children with autism spectrum disorder during early childhood. Hum Brain Mapp. (2016) 37:1038–50. doi: 10.1002/hbm.23089
79. Ahmadlou M, Adeli H, Adeli A. Fractality and a wavelet-chaos-methodology for EEG-based diagnosis of Alzheimer disease. Alzheimer Dis Assoc Dis. (2011) 25:85–92. doi: 10.1097/WAD.0b013e3181ed1160
80. Nobukawa S, Yamanishi T, Kasakawa S, Nishimura H, Kikuchi M, Takahashi T. Classification methods based on complexity and synchronization of electroencephalography signals in Alzheimer's disease. Front Psychiatry. (2020) 11:255. doi: 10.3389/fpsyt.2020.00255
81. Yang AC, Tsai SJ. Is mental illness complex? from behavior to brain. Prog Neuropsychopharmacol Biol Psychiatry. (2013) 45:253–7. doi: 10.1016/j.pnpbp.2012.09.015
82. Andrzejak RG, Lehnertz K, Mormann F, Rieke C, David P, Elger CE. Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: dependence on recording region and brain state. Phys Rev E. (2001) 64:061907. doi: 10.1103/PhysRevE.64.061907
83. Kunhimangalam R, Joseph PK, Sujith O. Nonlinear analysis of EEG signals: surrogate data analysis. IRBM. (2008) 29:239–44. doi: 10.1016/j.rbmret.2007.09.006
84. Nobukawa S, Nishimura H, Yamanishi T. Skewed and long-tailed distributions of spiking activity in coupled network modules with log-normal synaptic weight distribution. In: International Conference on Neural Information Processing. Elsevier Ireland Ltd. (2018). p. 535–44. doi: 10.1007/978-3-030-04167-0_48
85. Pijn JP, Van Neerven J, Noest A, da Silva FHL. Chaos or noise in EEG signals; dependence on state and brain site. Electroencephalogr Clin Neurophysiol. (1991) 79:371–81. doi: 10.1016/0013-4694(91)90202-F
86. Ishii H, Fujisaka H, Inoue M. Breakdown of chaos symmetry and intermittency in the double-well potential system. Phys Lett A. (1986) 116:257–63. doi: 10.1016/0375-9601(86)90590-6
87. Franaszek M. Analyzing chaotic behavior via multitransient chaos. Phys Rev A. (1992) 46:6340. doi: 10.1103/PhysRevA.46.6340
88. Ott E, Grebogi C, Yorke JA. Controlling chaos. Phys Rev Lett. (1990) 64:1196. doi: 10.1103/PhysRevLett.64.1196
89. Pyragas K. Continuous control of chaos by self-controlling feedback. Phys Lett A. (1992) 170:421–8. doi: 10.1016/0375-9601(92)90745-8
90. Nakajima H. On analytical properties of delayed feedback control of chaos. Phys Lett A. (1997) 232:207–10. doi: 10.1016/S0375-9601(97)00362-9
91. Jiang W, Guo-Dong Q, Bin D. Hâẑ variable universe adaptive fuzzy control for chaotic system. Chaos Solit Fract. (2005) 24:1075–86. doi: 10.1016/j.chaos.2004.09.056
92. Schöll E, Schuster HG. Handbook of Chaos Control, Vol. 2. Weinheim: Wiley Online Library (2008).
93. Lamamra K, Vaidyanathan S, Azar AT, Salah CB. Chaotic system modelling using a neural network with optimized structure. In: Azar AT, Vaidyanathan S, Ouannas A, editors. Fractional Order Control and Synchronization of Chaotic Systems. Cham: Springer (2017). p. 833–56. doi: 10.1007/-3-319-50249-6_29
94. Han M, Zhong K, Qiu T, Han B. Interval type-2 fuzzy neural networks for chaotic time series prediction: a concise overview. IEEE Trans Cybern. (2018) 49:2720–31. doi: 10.1109/TCYB.2018.2834356
95. Cimen M, Garip Z, Pala M, Boz AF, Akgul A. Modelling of a chaotic system motion in video with artificial neural networks. Chaos Theory Appl. (2019) 1:38–50. Available online at: https://dergipark.org.tr/en/pub/chaos/issue/50396/653302
96. Lai Q, Akgul A, Varan M, Kengne J, Erguzel AT. Dynamic analysis and synchronization control of an unusual chaotic system with exponential term and coexisting attractors. Chin J Phys. (2018) 56:2837–51. doi: 10.1016/j.cjph.2018.09.015
97. Park J, Mori H, Okuyama Y, Asada M. Chaotic itinerancy within the coupled dynamics between a physical body and neural oscillator networks. PLoS ONE. (2017) 12:e0182518. doi: 10.1371/journal.pone.0182518
Keywords: chaotic resonance, stochastic resonance, neural system, spiking neural network, chaos control, synchronization
Citation: Nobukawa S and Nishimura H (2020) Synchronization of Chaos in Neural Systems. Front. Appl. Math. Stat. 6:19. doi: 10.3389/fams.2020.00019
Received: 31 March 2020; Accepted: 07 May 2020;
Published: 25 June 2020.
Edited by:
Vijay Kumar Yadav, Nirma University, IndiaReviewed by:
Mayank Srivastava, Veer Bahadur Singh Purvanchal University, IndiaAkif Akgul, Sakarya University, Turkey
Copyright © 2020 Nobukawa and Nishimura. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sou Nobukawa, bm9idWthd2FAY3MuaXQtY2hpYmEuYWMuanA=
 Sou Nobukawa
Sou Nobukawa Haruhiko Nishimura
Haruhiko Nishimura