- Department of Mathematics, University of California, Irvine, Irvine, CA, United States
Sparsification of neural networks is one of the effective complexity reduction methods to improve efficiency and generalizability. Binarized activation offers an additional computational saving for inference. Due to vanishing gradient issue in training networks with binarized activation, coarse gradient (a.k.a. straight through estimator) is adopted in practice. In this paper, we study the problem of coarse gradient descent (CGD) learning of a one hidden layer convolutional neural network (CNN) with binarized activation function and sparse weights. It is known that when the input data is Gaussian distributed, no-overlap one hidden layer CNN with ReLU activation and general weight can be learned by GD in polynomial time at high probability in regression problems with ground truth. We propose a relaxed variable splitting method integrating thresholding and coarse gradient descent. The sparsity in network weight is realized through thresholding during the CGD training process. We prove that under thresholding of ℓ1, ℓ0, and transformed-ℓ1 penalties, no-overlap binary activation CNN can be learned with high probability, and the iterative weights converge to a global limit which is a transformation of the true weight under a novel sparsifying operation. We found explicit error estimates of sparse weights from the true weights.
1. Introduction
Deep neural networks (DNN) have achieved state-of-the-art performance on many machine learning tasks such as speech recognition [1], computer vision [2], and natural language processing [3]. Training such networks is a problem of minimizing a high-dimensional non-convex and non-smooth objective function, and is often solved by first-order methods such as stochastic gradient descent (SGD). Nevertheless, the success of neural network training remains to be understood from a theoretical perspective. Progress has been made in simplified model problems. Blum and Rivest [4] showed that even training a three-node neural network is NP-hard, and Shamir [5] showed learning a simple one-layer fully connected neural network is hard for some specific input distributions. Recently, several works [6, 7] focused on the geometric properties of loss functions, which is made possible by assuming that the input data distribution is Gaussian. They showed that SGD with random or zero initialization is able to train a no-overlap neural network in polynomial time.
Another prominent issue is that DNNs contain millions of parameters and lots of redundancies, potentially causing over-fitting and poor generalization [8] besides spending unnecessary computational resources. One way to reduce complexity is to sparsify the network weights using an empirical technique called pruning [9] so that the non-essential ones are zeroed out with minimal loss of performance [10–12]. Recently a surrogate ℓ0 regularization approach based on a continuous relaxation of Bernoulli random variables in the distribution sense is introduced with encouraging results on small size image data sets [13]. This motivated our work here to study deterministic regularization of ℓ0 via its Moreau envelope and related ℓ1 penalties in a one hidden layer convolutional neural network model [7]. Moreover, we consider binarized activation which further reduces computational costs [14].
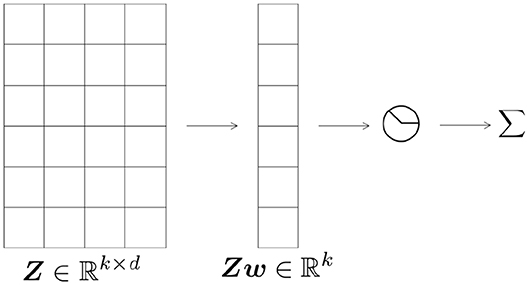
The architecture of the network is illustrated in Figure 1 similar to Brutzkus and Globerson [7]. We consider the convolutional setting in which a sparse filter w ∈ ℝd is shared among different hidden nodes. The input sample is Z ∈ ℝk×d. Note that this is identical to the one layer non-overlapping case where the input is x ∈ ℝk×d with k non-overlapping patches, each of size d. We also assume that the vectors of Z are i.i.d. Gaussian random vectors with zero mean and unit variance. Let denote this distribution. Finally, let σ denote the binarized ReLU activation function, σ(z): = χ{z>0} which equals 1 if z > 0, and 0 otherwise. The output of the network in Figure 1 is given by:
We address the realizable case, where the response training data is mapped from the input training data Z by Equation (1) with a ground truth unit weight vector w*. The input training data is generated by sampling m training points Z1, .., Zm from a Gaussian distribution. The learning problem seeks w to minimize the empirical risk function:
Due to binarized activation, the gradient of l in w is almost everywhere zero, hence in-effective for descent. Instead, an approximate gradient on the coarse scale, the so called coarse gradient (denoted as ) is adopted as proxy and is proved to drive the iterations to global minimum [14].
In the limit m ↑ ∞, the empirical risk l converges to the population risk:
which is more regular in w than l. However, the “true gradient” ∇wf is inaccessible in practice. On the other hand, the coarse gradient in the limit m ↑ ∞ forms an acute angle with the true gradient [14]. Hence the expected coarse gradient descent (CGD) essentially minimizes the population risk f as desired.
Our task is to sparsify w in CGD. We note that the iterative thresholding algorithms (IT) are commonly used for retrieving sparse signals [[15–19] and references therein]. In high dimensional setting, IT algorithms provide simplicity and low computational cost, while also promote sparsity of the target vector. We shall investigate the convergence of CGD with simultaneous thresholding for the following objective function
where f(w) is the population loss function of the network, and P is ℓ0, ℓ1, or the transformed-ℓ1 (Tℓ1) function: a one parameter family of bilinear transformations composed with the absolute value function [20, 21]. When acting on vectors, the Tℓ1 penalty interpolates ℓ0 and ℓ1 with thresholding in closed analytical form for any parameter value [19]. The ℓ1 thresholding function is known as soft-thresholding [15, 22], and that of ℓ0 the hard-thresholding [17, 18]. The thresholding part should be properly integrated with CGD to be applicable for learning CNNs. As pointed out in Louizos et al. [13], it is beneficial to attain sparsity during the optimization (training) process.
1.1. Contribution
We propose a Relaxed Variable Splitting (RVS) approach combining thresholding and CGD for minimizing the following augmented objective function
for a positive parameter β. We note in passing that minimizing in u recovers the original objective (4) with penalty P replaced by its Moreau envelope [23]. We shall prove that our algorithm (RVSCGD), alternately minimizing u and w, converges for ℓ0, ℓ1, and Tℓ1 penalties to a global limit with high probability. A key estimate is the Lipschitz inequality of the expected coarse gradient (Lemma 4). Then the descent of Lagrangian function (9) and the angles between the iterated w and w* follows. The is a novel shrinkage of the true weight w* up to a scalar multiple. The is a sparse approximation of w*. To our best knowledge, this result is the first to establish the convergence of CGD for sparse weight binarized activation networks. In numerical experiments, we observed that the limit of RVSCGD with the ℓ0 penalty recovers sparse w* accurately.
1.2. Outline
In section 2, we briefly overview related mathematical results in the study of neural networks and complexity reduction. Preliminaries are in section 3. In section 4, we state and discuss the main results. The proofs of the main results are in section 5, and conclusion in section 6.
2. Related Work
In recent years, significant progress has been made in the study of convergence in neural network training. From a theoretical point of view, optimizing (training) neural network is a non-convex non-smooth optimization problem. Blum and Rivest [4], Livni et al. [24], Shalev-Shwartz et al. and [25] showed that training a neural network is hard in the worst cases. Shamir [5] showed that if either the target function or input distribution is “nice,” optimization algorithms used in practice can succeed. Optimization methods in deep neural networks are often categorized into (stochastic) gradient descent methods and others.
Stochastic gradient descent methods were first proposed by Robbins and Monro [26]. The popular back-propagation algorithm was introduced in Rumelhart et al. [27]. Since then, many well-known SGD methods with adaptive learning rates were proposed and applied in practice, such as the Polyak momentum [28], AdaGrad [29], RMSProp [30], Adam [31], and AMSGrad [32].
The behavior of gradient descent methods in neural networks is better understood when the input has Gaussian distribution. Tian [6] showed that the population gradient descent can recover the true weight vector with random initialization for one-layer one-neuron model. Brutzkus and Globerson [7] proved that a convolution filter with non-overlapping input can be learned in polynomial time. Du et al. [33] showed (stochastic) gradient descent with random initialization can learn the convolutional filter in polynomial time and the convergence rate depends on the smoothness of the input distribution and the closeness of patches. Du et al. [34] analyzed the polynomial convergence guarantee of randomly initialized gradient descent algorithm for learning a one-hidden-layer convolutional neural network. A hybrid projected SGD (so called BinaryConnect) is widely used for training various weight quantized DNNs [35, 36]. Recently, a Moreau envelope based relaxation method (BinaryRelax) is proposed and analyzed to advance weight quantization in DNN training [37]. Also a blended coarse gradient descent method [14] is introduced to train fully quantized DNNs in weights and activation functions, and overcome vanishing gradients. For earlier work on coarse gradient (a.k.a. straight through estimator) (see [38–40] among others).
Non-SGD methods for deep learning include the Alternating Direction Method of Multipliers (ADMM) to transform a fully-connected neural network into an equality-constrained problem [41]; method of auxiliary coordinates (MAC) to replace a nested neural network with a constrained problem without nesting [42]. Zhang et al. [43] handled deep supervised hashing problem by an ADMM algorithm to overcome vanishing gradients.
For a similar model to (9) and treatment in a general context (see [44]); and in image processing (see [45]).
3. Preliminaries
3.1. The One-Layer Non-overlap Network
Consider the network introduced in Figure 1. Let σ denote the binarized ReLU activation function, σ(z): = χ{z>0}. The training sample loss is
where w* ∈ ℝd is the underlying (non-zero) teaching parameter. Note that (5) is invariant under scaling w → w/c, w* → w*/c, for any scalar c > 0. Without loss of generality, we assume ‖w*‖ = 1. Given independent training samples {Z1, …, ZN}, the associated empirical risk minimization reads
The empirical risk function in (6) is piece-wise constant and has i.e., zero partial w gradient. If σ were differentiable, then back-propagation would rely on:
However, σ has zero derivative i.e., rendering (7) inapplicable. We study the coarse gradient descent with σ′ in (7) replaced by the (sub)derivative μ′ of the regular ReLU function μ(x): = max(x, 0). More precisely, we use the following surrogate of :
with μ′(x) = σ(x). The constant represents a ReLU function μ with smaller slope, and will be necessary to give a stronger convergence result for our main findings. To simplify our analysis, we let N ↑ ∞ in (6), so that its coarse gradient approaches 𝔼Z[g(w, Z)]. The following lemma asserts that 𝔼Z[g(w, Z)] has positive correlation with the true gradient ∇f(w), and consequently, −𝔼Z[g(w, Z)] gives a reasonable descent direction.
Lemma 1. [14] If θ(w, w*) ∈ (0, π), and ‖w‖ ≠ 0, then the inner product between the expected coarse and true gradient w.r.t. w is
3.2. The Relaxed Variable Splitting Coarse Gradient Descent Method
Suppose we want to train the network in a way that wt converges to a limit in some neighborhood of w*, and we also want to promote sparsity in the limit . A classical approach is to minimize the Lagrangian: ϕ(w) = f(w) + λ‖w‖1, for some λ > 0. In practice, the ℓ1 penalty can also be replaced by ℓ0 or Tℓ1. Our proposed relaxed variable splitting (RVS) proceeds by first extending ϕ into a function of two variables f(w) + λ‖u‖1, and consider the augmented Lagrangian:
Let Sα be the soft thresholding operator, Sα(x) = sgn(x) max{|x| − α, 0}. The resulting RSVCGD method is described in Algorithm 1:
3.3. Comparison With ADMM
A well-known, modern method to solve the minimization problem ϕ(w) = f(w) + λ‖w‖1 is the Alternating Direction Method of Multipliers (or ADMM). In ADMM, we consider the Lagrangian
and apply the updates:
Although widely used in practice, the ADMM method has several drawbacks when it comes to regularizing deep neural networks: Firstly, the ℓ1 penalty is often replaced by ℓ0 in practice; but ‖·‖0 is non-differentiable and non-convex, thus current theory in optimization does not apply [46]. Secondly, the update is not applicable in practice on DNN, as it requires one to know fully how f(w) behaves. In most ADMM adaptations on DNN, this step is replaced by a simple gradient descent. Lastly, the Lagrange multiplier zt tends to reduce the sparsity of the limit of ut, as it seeks to close the gap between wt and ut.
In contrast, the RVSCGD method resolves all these difficulties presented by ADMM. Firstly, without the linear term 〈z, w − u〉, one has an explicit formula for the update of u, which can be easily implemented. Secondly, the update of wt is not an argmin update, but rather a gradient descent iteration itself, so our theory does not deviate from practice. Lastly, without the Lagrange multiplier term zt, there will be a gap between wt and ut at the limit. The ut is much more sparse than in the case of ADMM, and numerical results showed that f(wt) and f(ut) behave very similarly on deep networks. An intuitive explanation for this is that when the dimension of wt is high, most of its components that will be pruned off to get ut have very small magnitudes, and are often the redundant weights.
In short, the RVSCGD method is easier to implement (no need to keep track of the variable zt), can greatly increase sparsity in the weight variable ut, while also maintaining the same performance as the ADMM method. Moreover, RVSCGD has convergence guarantee and limit characterization as stated below.
4. Main Results
Theorem 1. Suppose that the initialization and penalty parameters of the RVSCGD algorithm satisfy:
(i) θ(w0, w*) ≤ π − δ, for some δ > 0;
(ii) , and ;
(iii) η is small such , where L is the Lipschitz constant in Lemma 4; and for all t, .
Then the Lagrangian decreases monotonically; and (ut, wt) converges sub-sequentially to a limit point , with , such that:
(i) Let and , then θ < δ;
(ii) The limit point satisfies and
where Sλ/β(·) is the soft-thresholding operator of ℓ1, for some constant ;
(iii) The limit point is close to the ground truth w* such that
Remark 1. As the sign of agrees with , Equation (12) implies that w* equals an expansion of or equivalently is (up to a scalar multiple) a shrinkage of w*, which explains the source of sparsity in . The assumption on η is reasonable, as will be shown below: is bounded away from zero, and thus is also bounded.
The proof is provided in details in section 5. Here we provide an overview of the key steps. First, we show that there exists a constant Lf such that
then we show that the Lipschitz gradient property still holds when replaced by the coarse gradient:
and subsequently show
These inequalities hold when ‖wt‖ ≥ M, for some M > 0. It can be shown that with bad initialization, one may have ‖wt‖ → 0 as t → ∞. We circumvent this problem by normalizing wt at each iteration.
Next, we show the iterations satisfy θt+1 ≤ θt, and . Finally, an analysis of the stationary point yields the desired bound.
In none of these steps do we use convexity of the ℓ1 penalty term. Here we extend our result to ℓ0 and transformed ℓ1 (Tℓ1) regularization [21].
Corollary 1.1. Suppose that the initialization of the RVSCGD algorithm satisfies the conditions in Theorem 1, and that the ℓ1 penalty is replaced by ℓ0 or Tℓ1. Then the RVSCGD iterations converge to a limit point satisfying Equation (12) with ℓ0's hard thresholding operator [18] or Tℓ1 thresholding [19] replacing Sλ/β, and similar bound (13) holds.
5. Proof of Main Results
The following Lemmas give an outline for the proof of Theorem 1.
Lemma 2. If every entry of Z is i.i.d. sampled from , and ‖w‖ ≠ 0, then the true gradient of the population loss f(w) is
for θ(w, w*) ∈ (0, π); and the expected coarse gradient w.r.t. w is
Lemma 3. (Properties of true gradient)
Given w1, w2 with min{‖w1‖, ‖w2‖} = c > 0 and max{‖w1‖, ‖w2‖} = C, there exists a constant Lf > 0 depends on c and C such that
Moreover, we have
Lemma 4. (Properties of expected coarse gradient)
If w1, w2 satisfy , and , then there exists a constant K such that
Moreover, there exists a constant L such that
Remark 2. The condition in Lemma 4 is to match the RVSCGD algorithm and to give an explicit value for K. The result still holds in general when 0 < c ≤ ‖w1‖, ‖w2‖ ≤ C. Compared to Lemma 3, when and , one has , which is a sharper bound than in the coarse gradient case.
Lemma 5. (Angle Descent)
Let θt: = θ(wt, w*). Suppose the initialization of the RVSCGD algorithm satisfies θ0 ≤ π − δ and , then θt+1 ≤ θt.
Lemma 6. (Lagrangian Descent)
Suppose the initialization of the RVSCGD algorithm satisfies , where L is the Lipschitz constant in Lemma 4, then .
Lemma 7. (Properties of limit point)
Suppose the initialization of the RVSCGD algorithm satisfies: θ(w0, w*) ≤ π − δ, for some δ > 0, λ is small such that , and η is small such that . Let and , then (ut, wt) converges to a limit point such that
Lemmas 2, 3 follow directly from Yin et al. [14]. The proof of Lemmas 4, 5, 6, 7 are provided below.
5.1. Proof of Lemma 4
First suppose ‖w1‖ = ‖w2‖ = 1. By Lemma 2, we have
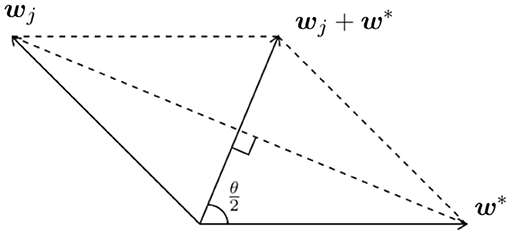
for j = 1, 2. Consider the plane formed by wj and w*, since ‖w*‖ = 1, we have an equilateral triangle formed by wj and w* (see Figure 2).
Simple geometry shows
Thus the expected coarse gradient simplifies to
which implies
with .
Now suppose . By Equation (15), we have , for all C > 0. Then,
where the first inequality follows from (19), and the second inequality is from the constraint , with equality when . Letting , the first claim is proved.
It remains to show the gradient descent inequality. By Yin et al. [14], we have
Let . Then
We will show
for ‖w1‖ = ‖w2‖ = 1 and θ2 ≤ θ1. By Equation (18),
It remains to show
or there exists a constant K1 such that
Notice that by writing , we have
where the last equality follows since ‖w1‖ = ‖w2‖ = 1 implies 〈w1 + w2, w2 − w1 〉 = 0. On the other hand,
so it suffices to show there exists a constant K2 such that
Notice the function θ ↦ θ + cosθ is monotonically increasing on [0, π]. For θ1, θ2 ∈ [0, π] with θ2 ≤ θ1, the LHS is non-positive, and the inequality holds. Thus, one can take , and .
5.2. Proof of Lemma 5
Due to normalization in the RVSCGD algorithm, ‖wt‖ = 1 for all t. By Equation (18), we have
and the update of u is the well-known soft-thresholding of w [15, 22]:
where Sλ/β(·) is the soft-thresholding operator:
and Sλ/β(w) applies the thresholding to each component of w. Then the update of w has the form
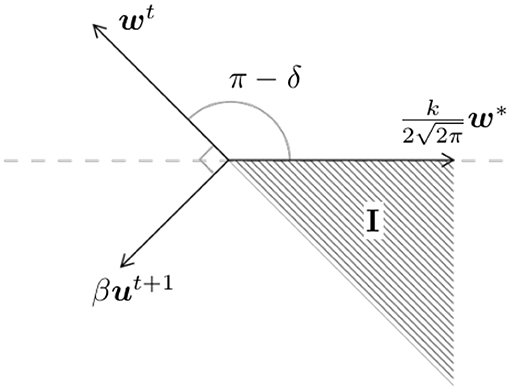
for some constant Ct > 0. Suppose the initialization satisfies θ(w0, w*) ≤ π − δ, for some δ > 0. It suffices to show that if θt ≤ π − δ, then θt+1 ≤ π − δ. To this end, since , we have . Consider the worst case scenario: wt, w*, ut+1 are co-planar with , and w*, ut+1 are on two sides of wt (see Figure 3). We need to be in region I. This condition is satisfied when β is small such that
or
since , we have ‖ut+1‖ ≤ 1. Thus, it suffices to have .
5.3. Proof of Lemma 6
By definition of the update on u, we have . It remains to show . First notice that since
where Ct > 0 is the normalizing constant, thus
For a fixed u: = ut+1 we have
Since ‖wt‖, ‖wt+1‖ = 1, we know (wt+1 − wt) bisects the angle between wt+1 and −wt. The assumption guarantees and θ(−wt, wt+1) < π. It follows that θ(wt+1 − wt, wt) and θ(wt+1 − wt, wt+1) are strictly less than . On the other hand, also lies in the plane bounded by wt+1 and −wt. Therefore,
This implies . Moreover, when Ct ≥ 1:
And when :
Thus, we have
Therefore, if η is small so that and , the update on w will decrease . Since Ct ≤ 2, the condition is satisfied when .
5.4. Proof of Lemma 7
Since is non-negative, by Lemma 5, 6, converges to some limit . This implies (ut, wt) converges to some stationary point . By the update of wt, we have
for some constant , where , c1 > 0 due to our assumption, and . For expression (20) to hold, we need
Expression (21) implies , and w* are co-planar. Let . From expression (21), and the fact that , we have
which implies Recall cos(a+b) = cos a cos b − sin a sin b. Thus,
which implies
By the initialization of β, we have . This implies θ < δ.
Finally, expression (20) can also be written as
From expression (23), we see that w*, after subtracting some vector whose signs agree with , and whose non-zero components are at most , is parallel to . This implies is some soft-thresholded version of w*, modulo normalization. Moreover, since , for small λ such that , we must have
On the other hand,
therefore, , for some constant C such that .
Finally, consider the equilateral triangle with sides , and . By the law of sines,
as θ is small, is near . We can assume . Together with expression (22), we have
5.5. Proof of Theorem 1
Combining Lemmas 2–7, Theorem 1 is proved.
5.6. Proof of Corollary
Lemma 8. [19] Let
where . Then is the Tℓ1 thresholding, equal to gλ(x) if |x| > t; zero elsewhere. Here if ; , elsewhere.
Lemma 9. [18] Let Then is the ℓ0 hard thresholding , if ; zero elsewhere.
We proceed by an outline similar to the proof of Theorem 1:
Step 1. First we show that and both decrease under the update of ut and wt. To see this, notice that the update on ut decreases and by definition. Then, for a fixed u = ut+1, the update on wt decreases and by a similar argument to that found in Theorem 1.
Step 2. Next, we show θ(wt, w*) ≤ π − δ, for some δ > 0, for all t, with initialization θ(w0, w*) = π − δ. For , by Lemma 8, we have
And for , by Lemma 9,
In both cases, each component of ut+1 is a thresholded version of the corresponding component of wt. This implies , and thus the argument in Theorem 1 follows through, and we have θ(wt, w*) ≤ π − θ, for all t.
Step 3. Finally, the equilibrium condition from Equation (21) still holds for the limit point, and a similar argument shows that .
6. Numerical Experiments
In this section, we demonstrate two simple experiments on implementing RVSCGD in practice.
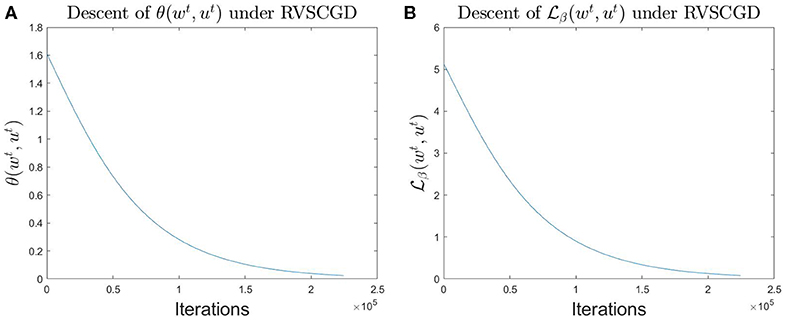
Firstly, we numerically verify our result on the one-layer, non-overlap network, using RVSCGD with ℓ0 penalty. The experiment was run with parameters k = 20, d = 50, β = 4.e − 3, λ = 1.e − 4, and η = 1.e − 5. Results are displayed in Figure 4. It can be seen that the RVSCGD converges quickly for this toy model; and the quantities , θ(wt, w*), decrease monotonically, as stated in Theorem 1.
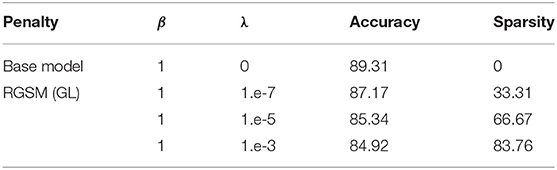
Secondly, we extend our method to a multi-layer network. Consider a variation of LeNet [47], where we replace all ReLU activations with the binarized ReLU function. The model is then trained on the MNIST dataset for 100 epochs using SGD with momentum 0.9, weight decay 5.e-4, and learning rate 1.e-3, which is decayed by a factor of 10 at epoch 60. The RVSCGD algorithm is applied on this model using the same training setting. The results are displayed in Table 1. Notice that the base model has an accuracy of 89.13%, which is lower than reported in Lecun [47]; this is because of the binarized ReLU replacement. Table 1 also shows that RVSCGD can effectively sparsify this variation of LeNet, with sparsity up to 83.76 and 4.39% loss in performance. We believe the loss in accuracy is mainly from 1-bit ReLU activation, which has too low a resolution to preserve important deep network information. We believe with higher bit quantization of weights and/or activations, networks can be more effectively pruned while still maintaining good performance (see [14]). This is a topic for our future studies.
7. Conclusion
We introduced a variable splitting coarse gradient descent method to learn a one-hidden layer neural network with sparse weight and binarized activation in a regression setting. The proof is based on the descent of a Lagrangian function and the angle between the sparse and true weights, and applies to ℓ1, ℓ0 and Tℓ1 sparse penalties. We plan to extend our work to a classification setting in the future.
Data Availability Statement
All datasets generated for this study are included in the article/supplementary material.
Author Contributions
TD performed the analysis. All authors contributed to the discussions and production of the manuscript.
Funding
The work was partially supported by NSF grants IIS-1632935 and DMS-1854434.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This manuscript has been released as a pre-print at http://export.arxiv.org/pdf/1901.09731 [48].
References
1. Hinton G, Deng L, Yu D, Dahl GE, Mohamed A, Jaitly N, et al. Deep neural networks for acoustic modeling in speech recognition: the shared views of four research groups. IEEE Signal Process Mag. (2012) 29:82–97. doi: 10.1109/MSP.2012.2205597
2. Krizhevsky A, Sutskever I, Hinton GE. ImageNet classification with deep convolutional neural networks. In: Bartlett PL, Pereira FCN, Burges CJC, Bottou L, Weinberger KQ, editors. Advances in Neural Information Processing Systems 25: 26th Annual Conference on Neural Information Processing Systems 2012 (2012). p. 1106–14. Available online at: http://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks
3. Dauphin YN, Fan A, Auli M, Grangier D. Language modeling with gated convolutional networks. In: Proceedings of the 34th International Conference on Machine Learning, Vol. 70. Sydney, NSW (2017). p. 933–41. doi: 10.5555/3305381.3305478
4. Blum AL, Rivest RL. Training a 3-node neural network is NP-complete. In: José HS, Werner R, Rivest RL, editors. Machine Learning: From Theory to Applications: Cooperative Research at Siemens and MIT. Berlin; Heidelberg: Springer (1993). p. 9–28. doi: 10.1007/3-540-56483-7_20
5. Shamir O. Distribution-specific hardness of learning neural networks. J Mach Learn Res. (2018) 19:1532–35. doi: 10.5555/3291125.3291157
6. Tian Y. An analytical formula of population gradient for two-layered ReLU network and its applications in convergence and critical point analysis. In: Proceedings of the 34th International Conference on Machine Learning, Vol. 70. Sydney, NSW: JMLR.org (2017). p. 3404–13. doi: 10.5555/3305890.3306033
7. Brutzkus A, Globerson A. Globally optimal gradient descent for a convnet with Gaussian inputs. In: Proceedings of the 34th International Conference on Machine Learning, Vol. 70. Sydney, NSW: JMLR.org (2017). p. 605–14.
8. Zhang C, Bengio S, Hardt M, Recht B, Vinyals O. Understanding deep learning requires rethinking generalization. In: 5th International Conference on Learning Representations, ICLR 2017. Toulon (2017). Available online at: https://openreview.net/forum?id=Sy8gdB9xx
9. LeCun Y, Denker J, Solla S. Optimal brain damage. In: Proceedings of the 2nd International Conference on Neural Information Processing Systems. Cambridge, MA: MIT Press (1989). p. 589–605. doi: 10.5555/109230.109298
10. Han S, Mao H, Dally WJ. Deep compression: compressing deep neural network with pruning, trained quantization and huffman coding. In: Bengio Y, LeCun Y, editors. 4th International Conference on Learning Representations, ICLR 2016. San Juan (2016). Available online at: http://arxiv.org/abs/1510.00149
11. Ullrich K, Meeds E, Welling M. Soft weight-sharing for neural network compression. In: 5th International Conference on Learning Representations, ICLR 2017. Toulon (2017). Available online at: https://openreview.net/forum?id=HJGwcKclx
12. Molchanov D, Ashukha A, Vetrov D. Variational dropout sparsifies deep neural networks. In: Proceedings of the 34th International Conference on Machine Learning, Vol. 70. Sydney, NSW: JMLR.org (2017). p. 2498–507. doi: 10.5555/3305890.3305939
13. Louizos C, Welling M, Kingma D. Learning sparse neural networks through L0 regularization. In: 6th International Conference on Learning Representations, ICLR 2018. Vancouver, BC (2018). Available online at: https://openreview.net/forum?id=H1Y8hhg0b
14. Yin P, Zhang S, Lyu J, Osher S, Qi Y, Xin J. Blended coarse gradient descent for full quantization of deep neural networks. Res Math Sci. (2019) 6:14. doi: 10.1007/s40687-018-0177-6
15. Daubechies I, Defrise M, Mol CD. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun Pure Appl Math. (2004) 57:1413–57. doi: 10.1002/cpa.20042
16. Candés E, Romberg J, Tao T. Stable signal recovery from incomplete and inaccurate measurements. Commun Pure Appl Math. (2006) 59:1207–23. doi: 10.1002/cpa.20124
17. Blumensath T, Davies M. Iterative thresholding for sparse approximations. J Fourier Anal Appl. (2008) 14:629–54. doi: 10.1007/s00041-008-9035-z
18. Blumensath T. Accelerated iterative hard thresholding. Signal Process. (2012) 92:752–6. doi: 10.1016/j.sigpro.2011.09.017
19. Zhang S, Xin J. Minimization of transformed l1 penalty: closed form representation and iterative thresholding algorithms. Commun Math Sci. (2017) 15:511–37. doi: 10.4310/CMS.2017.v15.n2.a9
20. Nikolova M. Local strong homogeneity of a regularized estimator. SIAM J Appl Math. (2000) 61:633–58. doi: 10.1137/S0036139997327794
21. Zhang S, Xin J. Minimization of transformed l1 penalty: theory, difference of convex function algorithm, and robust application in compressed sensing. Math Program Ser B. (2018) 169:307–36. doi: 10.1007/s10107-018-1236-x
22. Donoho D. Denoising by soft-thresholding. IEEE Trans Inform Theor. (1995) 41:613–27. doi: 10.1109/18.382009
23. Moreau JJ. Proximité et dualité dans un espace hilbertien. Bull Soc Math France. (1965) 93:273–99. doi: 10.24033/bsmf.1625
24. Livni R, Shalev-Shwartz S, Shamir O. On the computational efficiency of training neural networks. In: Proceedings of the 27th International Conference on Neural Information Processing Systems, Vol. 1. Cambridge, MA: MIT Press (2014). p. 855–63.
25. Shalev-Shwartz S, Shamir O, Shammah S. Failures of gradient-based deep learning. In: Precup D, Teh YW, editors. Proceedings of the 34th International Conference on Machine Learning, Vol. 70. Sydney, NSW: PMLR (2017). p. 3067–75. Available online at: http://proceedings.mlr.press/v70/shalev-shwartz17a.html
26. Robbins H, Monro S. A stochastic approximation method. Ann Math Stat. (1951) 22:400–7. doi: 10.1214/aoms/1177729586
27. Rumelhart D, Hinton G, Williams R. Learning representations by back-propagating errors. Nature. (1986) 323:533–6. doi: 10.1038/323533a0
28. Polyak B. Some methods of speeding up the convergence of iteration methods. USSR Comput Math Math Phys. (1964) 4:1–17. doi: 10.1016/0041-5553(64)90137-5
29. Duchi J, Hazan E, Singer Y. Adaptive subgradient methods for online learning and stochastic optimization. J Machine Learn Res. (2011) 12:2121–59. doi: 10.5555/1953048.2021068
30. Tieleman T, Hinton G. Divide the Gradient by a Running Average of Its Recent Magnitude. Technical report. Coursera: Neural networks for machine learning (2017).
31. Kingma D, Ba J. Adam: a method for stochastic optimization. In: Bengio Y, LeCun Y, editors. 3rd International Conference on Learning Representations, ICLR 2015. San Diego, CA (2015). Available online at: http://arxiv.org/abs/1412.6980
32. Reddi SJ, Kale S, Kumar S. On the convergence of adam and beyond. In: 6th International Conference on Learning Representations, ICLR 2018. Vancouver, BC (2018). Available online at: https://openreview.net/forum?id=ryQu7f-RZ
33. Du S, Lee J, Tian Y. When is a convolutional filter easy to learn? arXiv [preprint] arXiv:1709.06129. (2017).
34. Du S, Lee J, Tian Y, Singh A, Poczos B. Gradient descent learns one-hidden-layer CNN: don't be afraid of spurious local minima. In: Dy J, Krause A, editors. Proceedings of the 35th International Conference on Machine Learning, Vol. 80. Stockholm: PMLR (2018). p. 1339–48. Available online at: http://proceedings.mlr.press/v80/du18b.html
35. Courbariaux M, Bengio Y, David J-P. BinaryConnect: training deep neural networks with binary weights during propagations. In: Proceedings of the 28th International Conference on Neural Information Processing Systems, Vol. 2 (Cambridge, MA: MIT Press (2015). p. 3123–31.
36. Yin P, Zhang S, Qi Y, Xin J. Quantization and training of low bit-width convolutional neural networks for object detection. J Comput Math. (2019) 37:349–59. doi: 10.4208/jcm.1803-m2017-0301
37. Yin P, Zhang S, Lyu J, Osher S, Qi Y, Xin J. BinaryRelax: a relaxation approach for training deep neural networks with quantized weights. SIAM J Imag Sci. (2018) 11:2205–23. doi: 10.1137/18M1166134
39. Hubara I, Courbariaux M, Soudry D, El-Yaniv R, Bengio Y. Binarized neural networks: training neural networks with weights and activations constrained to +1 or −1. arXiv [preprint] arXiv:160202830. (2016).
40. Cai Z, He X, Sun J, Vasconcelos N. Deep learning with low precision by half-wave Gaussian quantization. In: 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu, HI (2017). p. 5406–14.
41. Taylor G, Burmeister R, Xu Z, Singh B, Patel A, Goldstein T. Training neural networks without gradients: a scalable ADMM approach. In: Proceedings of the 33rd International Conference on International Conference on Machine Learning, Vol. 48. New York, NY: JMLR.org (2016). p. 2722–31.
42. Carreira-Perpinan M, Wang W. Distributed optimization of deeply nested systems. In: Kaski S, Corander J, editors. Proceedings of the Seventeenth International Conference on Artificial Intelligence and Statistics. Reykjavik: PMLR (2014). p. 10–19. Available online at: http://proceedings.mlr.press/v33/carreira-perpinan14.html
43. Zhang Z, Chen Y, Saligrama V. Efficient training of very deep neural networks for supervised hashing. In: 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas, NV (2016). p. 1487–95.
44. Attouch H, Bolte J, Redont P, Soubeyran A. Proximal alternating minimization and projection methods for nonconvex problems: an approach based on the Kurdyka-Lojasiewicz inequality. Math Oper Res. (2010) 35:438–57. doi: 10.1287/moor.1100.0449
45. Wu T. Variable splitting based method for image restoration with impulse plus Gaussian noise. Math Probl Eng. (2016) 2016:3151303. doi: 10.1155/2016/3151303
46. Wang Y, Zeng J, Yin W. Global convergence of ADMM in nonconvex nonsmooth optimization. J Sci Comput. (2019) 78:29–63. doi: 10.1007/s10915-018-0757-z
47. Lecun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proc IEEE. (1998) 86:2278–324. doi: 10.1109/5.726791
Keywords: sparsification, 1-bit activation, regularization, convergence, coarse gradient descent
Citation: Dinh T and Xin J (2020) Convergence of a Relaxed Variable Splitting Coarse Gradient Descent Method for Learning Sparse Weight Binarized Activation Neural Network. Front. Appl. Math. Stat. 6:13. doi: 10.3389/fams.2020.00013
Received: 24 January 2020; Accepted: 14 April 2020;
Published: 06 May 2020.
Edited by:
Lucia Tabacu, Old Dominion University, United StatesReviewed by:
Jianjun Wang, Southwest University, ChinaYuguang Wang, University of New South Wales, Australia
Copyright © 2020 Dinh and Xin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Thu Dinh, dGh1ZDJAdWNpLmVkdQ==
 Thu Dinh
Thu Dinh Jack Xin
Jack Xin