Abstract
In this paper, we propose a fractional generalization of the well-known Laguerre differential equation. We replace the integer derivative by the conformable derivative of order 0 < α < 1. We then apply the Frobenius method with the fractional power series expansion to obtain two linearly independent solutions of the problem. For certain eigenvalues, the infinite series solution truncate to obtain the singular and non-singular fractional Laguerre functions. We obtain the fractional Laguerre functions in closed forms, and establish their orthogonality result. The applicability of the new fractional Laguerre functions is illustrated.
1. Introduction
In recent years, there are interests in studying fractional Sturm-Liouville eigenvalue problems. For instance, the fractional Bessel equation with applications was investigated in Okrasinski and Plociniczak [1, 2], where the fractional derivative is of the Riemann-Liouville type. In Abu Hammad and Khalil [3] the authors solved the fractional Legendre equation with conformable derivative and established the orthogonality property of the fractional Legendre functions. The applications of the fractional Legendre functions in solving fractional differential equations, were illustrated in Kazema et al. [4] and Syam and Al-Refai [5]. In this project we propose the following fractional generalization of the well-known Laguerre differential equation
where is the conformable derivative of order α. The conformable derivative was introduced recently in Khalil et al. [6], and below are the definition and main properties of the derivative.
Definition 1.1. For a function f :(0, ∞) → ℝ, the conformable derivative of order 0 < α ≤ 1 of f at x > 0, is defined by
and the derivative at x = 0 is defined by
The conformable derivative is a local derivative which has a physical and a geometrical interpretations and potential applications in physics and engineering [
7,
8]. It satisfies the nice properties of the integer derivative such as, the product rule, the quotient rule, and the chain rule, and it holds that
For more details about the conformable derivative we refer the reader to Abdeljawad [9] and Khalil et al. [6]. We mention here that even though the conformable is a nonlocal derivative (see [10, 11]), the simplicity and applications of the derivative make it of interests. Also, the applications of the obtained Fractional Leguerre functions are indicated in this manuscript. The rest of the paper is organized as follows: In section 2, we apply the Frobenius method together with the fractional series solution to solve the above equation and to obtain the fractional Laguerre functions. In section 3, we establish the orthogonality result of the fractional Laguerre functions and present the fractional Laguerre functions for several eigenvalues. Finally, we close up with some concluding remarks in section 4.
2. The Series Solution
The series solution is commonly used to solve various types of fractional differential equations (see [12–16]). Since x = 0, is α-regular singular point of Equation (1.1), see [17], we apply the well-known Frobenius method to obtain a solution of the form
where the values of r will be determined. We have
By substituting the above results in Equation (1.1) we have
The coefficients of xα(r−1) will lead to
Because α ≠ 0, and a0 = 0, will lead to the zero solution, we have
We start with r = 0, we have
or
Lemma 2.1.The coefficientsanin Equation (2.3) satisfy
Proof: The proof can be easily obtained by iterating the recursion in (2.3) and applying induction arguments. □
Remark 2.1.For α = 1, the recursion relation in (2.4) will reduce to
which is exactly the recursion relation that has been obtained in solving the Laguerre equation with integer derivative.
For we have for n ≥ 0,
By iterating the recursion in (2.6) and applying induction arguments, we have
Lemma 2.2.The coefficients an in Equation (2.6) satisfy
Remark 2.2.By applying the Frobenius method to the regular Laguerre equation with integer derivative α = 1, we obtain only one value of r = 0, which produces only one solution. Here with the fractional case, we obtain two values of, that will produce two linearly independent solutions of the problem as we will see later.
Now, in Equation (2.4), if we choose α = αm and λ = λm such that
for some integer m, then
and the infinite series solution will truncate to obtain the finite sum
where is the non-singular fractional Laguerre function of order m. Since
then
Analogously, in Equation (2.7), if we choose α = αm and λ = λm such that
then
and the infinite series solution will truncate to obtain the solution
where
is the fractional singular Laguerre function of order m − 1.
Remark 2.3.If we substitute αm = 1, then
Since, andwe have
which is the expansion of the Laguerre polynomialLm(x).
3. The Fractional Laguerre Functions
We start with the orthogonality property of the fractional Laguerre functions , m = 0, 1, 2, ⋯ . Here by we mean the non-singular and singular Laguerre functions obtained in (2.8) and (2.9).
Theorem 3.1.The fractional Laguerre functions, m = 0, 1, 2, ⋯ are orthogonal on (0, ∞) with respect to the weight functioni.e.,
Proof: One can easily prove that Equation (1.1) can be written as
Thus, the equation is of a special type of the fractional Sturm-liouville eigenvalue problem
where and . Using the fractional Lagrange Identity obtained in Al-Refai and Abdeljawad [18], we have
We have p(0) = 0, and
Thus the right hand side of Equation (3.2) equals zero which together with λm ≠ λn will lead to
and hence the result. □
Remark 3.1.Since the fractional Laguerre functions are orthogonal, they can be used as a basis of the spectral method to study fractional differential equations analytically and numerically. They also can be used as a basis of the fractional Gauss-Laguerre quadrature for approximating the value of integrals of the form
Remark 3.2.New types of improper integrals are determined using the orthogonality property which are not known before, such as
In the following we present the singular and non-singular fractional Laguerre functions of several orders.
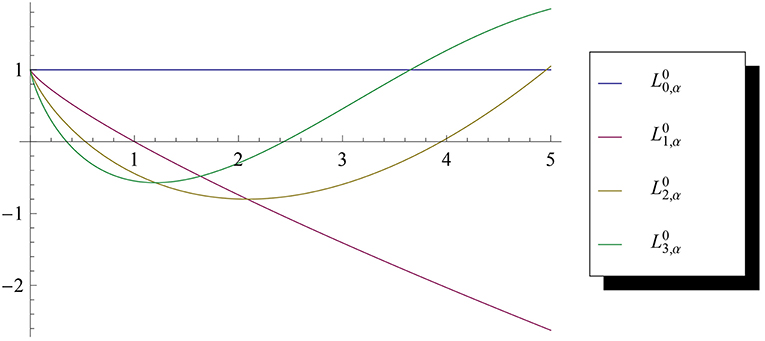
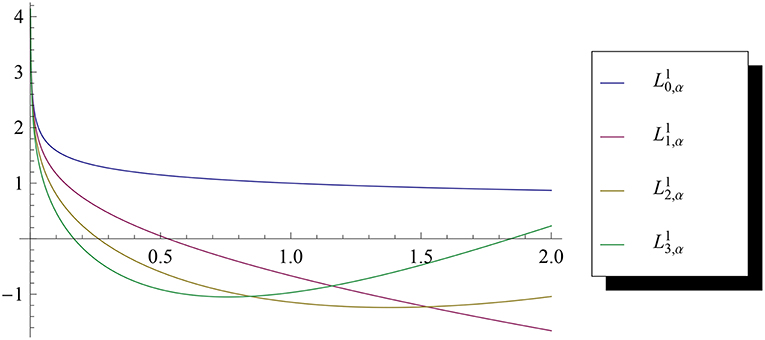
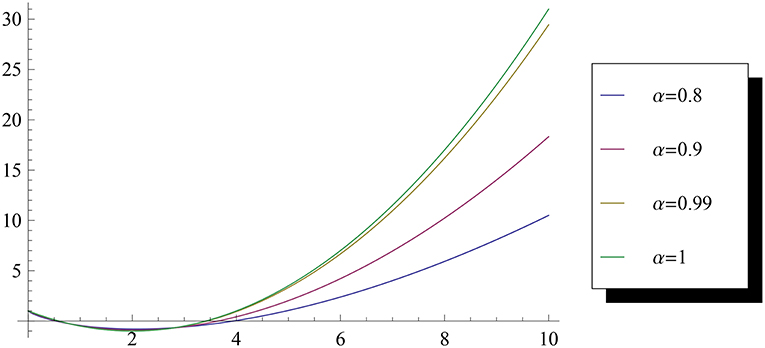
Figures 1, 2 depict the non-singular and singular fractional Laguerre functions of several orders for α = 0.8. Figure 3 depicts for several values of α. One can see that, as α approaches 1, the non-singular fractional Laguerre functions approach the Laguerre polynomial of degree 2.
Figure 1
Figure 2
Figure 3
4. Conclusion
We have considered the fractional Laguerre equation with conformable derivative. We obtained two linearly independent solutions using the fractional series solution and Frobenius method. The first non-singular solution is analytic on (0, ∞), and the second singular solution has a singularity at x = 0. For certain eigenvalues, these infinite solutions truncate to obtain the fractional Laguerre functions. Because of the orthogonality property of the fractional Laguerre functions, they can be used as a basis of the spectral method to study fractional differential equations, or as a basis of the Gauss-Laguerre quadrature for evaluating certain integrals. The obtained results coincide with the ones of the regular Laguerre polynomials as the derivative α approaches 1.
Statements
Author contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Acknowledgments
The authors gratefully acknowledge the support of the United Arab Emirates University under the SURE+ grant no. 31S291−26−2− SURE+2017.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1.
OkrasinskiWPlociniczakL. A note of fractional Bessel equation and its asymptotics. Fract Calc Appl Anal. (2013) 16:559–72. 10.2478/s13540-013-0036-5
2.
OkrasinskiWPlociniczakL. On fractional Bessel equation and the description of corneal topography. arXiv.1201.2526v2 [math.CA] (2012).
3.
Abu HammadMKhalilR. Legendre fractional differential equation and Legender fractional polynomials. Int J Appl Math Res. (2014) 3:214–9. 10.14419/ijamr.v3i3.2747
4.
KazemaSAbbasbandyaSKumarbS. Fractional-order Legendre functions for solving fractional-order differential equations. Appl Math Model. (2013) 37:5498–510. 10.1016/j.apm.2012.10.026
5.
SyamMAl-RefaiM. Solving fractional diffusion equation via the collocation method based on fractional Legendre functions. J Comput Methods Phys. (2014) 2014:381074. 10.1155/2014/381074
6.
KhalilRAl HoraniMYousefASababhehM. A new definition of fractional derivative. J Comput Appl Math. (2015) 264:65–70. 10.1016/j.cam.2014.01.002
7.
UstaFsarikayaM. Some improvements of conformable fractional integral inequalities. Int J Anal Appl. (2017) 14:162–6.
8.
ZhaoDLuoM. General conformable fractional derivative and its physical interpretation. Calcolo (2017) 54:903–17. 10.1007/s10092-017-0213-8
9.
AbdeljawadT. On conformable fractional calculus. J Comput Appl Math (2015) 279:57–66. 10.1016/j.cam.2014.10.016
10.
LiuCS. On the local fractional derivative of everywhere non-differentiable continuous functions on intervals. Commun Nonlin Sci Numer Simul. (2017) 42:229–35. 10.1016/j.cnsns.2016.05.029
11.
TarasovVE. No nonlocality. No fractional derivative. Commun Nonlin Sci Numer Simul. (2018) 62:157–63. 10.1016/j.cnsns.2018.02.019
12.
Al-RefaiMHajjiMSyamM. An efficient series solution for fractional differential equations. Abstr Appl Anal. (2014) 2014:891837. 10.1155/2014/891837
13.
Al-RefaiMSyamMAl-MdallalQ. On the fractional Legendre equation and fractional Legendre functions. Progr Fract Differ Appl. (2017) 3:93–102. 10.18576/pfda/030202
14.
BaleanuDIncMYusufAAliyoA. Space-time fractional Rosenou-Haynam equation: lie symmetry analysis, explicit solutions and conservation laws. Adv Differ Equat. (2018) 2018:64. 10.1186/s13662-018-1468-3
15.
BaleanuDIncMYusufAAliyoA. Lie symmetry analysis, exact solutions and conservation laws for the time fractional Caudrey-Dodd-Gibbon-Sawada-Kotera equation. Commun Nonlin Sci Numer Simul. (2018) 59:222–34. 10.1016/j.cnsns.2017.11.015
16.
IncMYusufAAliyoABaleanuD. Lie symmetry analysis, explicit solutions and conservation laws for the space-time fractional nonlinear evolution equations. Phys A (2018) 496:371–83. 10.1016/j.physa.2017.12.119
17.
UnalEGokdoganACelikE. Solutions around α singular point of a sequential conformable fractional differential equation. Kuwait J Sci. (2017) 44:9–16.
18.
Al-RefaiMAbdeljawadT. Fundamental results of conformable Sturm-Liouville eigenvalue problems. Complexity (2017) 2017:3720471. 10.1155/2017/3720471
Summary
Keywords
fractional differential equations, Laguerre equation, conformable fractional derivative, series solution, Frobenius method
Citation
Shat R, Alrefai S, Alhamayda I, Sarhan A and Al-Refai M (2019) The Fractional Laguerre Equation: Series Solutions and Fractional Laguerre Functions. Front. Appl. Math. Stat. 5:11. doi: 10.3389/fams.2019.00011
Received
10 February 2018
Accepted
04 February 2019
Published
20 February 2019
Volume
5 - 2019
Edited by
Dumitru Baleanu, University of Craiova, Romania
Reviewed by
Eqab Mahmoud Rabei, Al al-Bayt University, Jordan; Devendra Kumar, University of Rajasthan, India; Aliyu Isa Aliyu, Federal University, Dutse, Nigeria
Updates
Copyright
© 2019 Shat, Alrefai, Alhamayda, Sarhan and Al-Refai.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mohammed Al-Refai m_alrefai@yu.edu.jo
This article was submitted to Mathematical Physics, a section of the journal Frontiers in Applied Mathematics and Statistics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.