- 1Flight Research Laboratory Aerospace, National Research Council Canada, Ottawa, ON, Canada
- 2CRASH, Centre de Recherche Acoustique-Signal-Humain, Université de Sherbrooke, Boul de l’Université, Sherbrooke, QC, Canada
Introduction: Controlling broadband noise across the entire frequency spectrum, from low to high frequencies, remains a critical challenge in aerospace, transportation, and construction industries. Current acoustic metamaterials are effective primarily for low-frequency noise but suffer from narrow-band resonances that limit their application for broader-band noise attenuation.
Methods: This study introduces an innovative structured material system comprising a parallel assembly of structured materials and Helmholtz Resonators embedded within a fiberglass layer. A multi-objective optimization approach based on a surrogate model was employed to fine-tune the parameters of each structured material. The optimization process allowed precise grouping of individual resonant frequencies, thereby broadening the effective resonance frequency band to address low- and high-frequency noise.
Results: The proposed structured material system demonstrated significant broadband noise attenuation across a wide frequency range. The optimized configuration achieved effective noise reduction while adhering to practical implementation constraints, providing a feasible solution for industrial applications.
Discussion: This study underscores the importance of optimization in advancing noise control technologies. By overcoming the limitations of narrow-band resonances, the proposed approach achieves effective broadband noise attenuation, addressing critical challenges in aerospace, transportation, and construction. The integration of structured materials and Helmholtz Resonators, optimized using a surrogate model, broadens the resonance frequency band while meeting practical implementation requirements. These results highlight a viable and impactful solution for noise control across diverse industries.
1 Introduction
Attenuating a broad spectrum of noise sources, particularly at low frequencies within confined spaces, presents a significant challenge across various industries such as transportation, aeronautics, and building construction. The large wavelength characteristics of low-frequency noise impose fundamental design constraints, especially evident in the field of Unmanned Aerial Systems (UAS) noise mitigation. The primary noise source for UAS is propeller noise (Zhou and Fattah, 2017), which can be categorized into broadband noise and tonal noise (Kemp, 1932; Kurtz and Marte, 1970). Broadband noise arises from turbulence created by the interaction between the fluid and the propeller blade, while tonal noise results from rotor motion, with prominence at the harmonics of the propeller blade passing frequency.
While numerous techniques for controlling tonal noise exist, few simultaneously address both broadband and tonal noise effectively. For instance, the use of linear ducted propellers stands out as a method that enhances aerodynamic performance while protecting the blades from damage. Malgoezar et al. (2019) investigated propeller noise characteristics with a rigid duct through experimentation, revealing an increase in broadband noise, a decrease in the first harmonics, and an overall reduction in noise level upon duct introduction. Similarly Lu et al. (2016), explored the acoustic performance of both rigid and micro-perforated ducts, though the acoustic benefits were less significant than anticipated. Guo et al. (2021) developed a lined duct employing Helmholtz resonators with extended necks, achieving approximately 3 dB noise reduction within the 700–1,000 Hz range. In general, a well-designed ducted propeller can significantly enhance both aerodynamic and acoustic performances, particularly at high frequencies for broadband noise. However, the limited space available in propeller blade ducts restricts the integration of conventional materials such as Helmholtz Resonators (HRs). This type of liner is effective across a narrow frequency band, making it unsuitable for broadband noise reduction. Fortunately, new advancements in acoustic metamaterials offer greater potential for noise control.
Unlike traditional liners, which are limited to narrow frequency bands, the LEONAR (Simon, 2018; Simon, 2019; Jones et al., 2022) (Long Elastic Open Neck Acoustic Resonator) concept introduces an advanced design that can potentially extend the range of effective noise attenuation. This resonator consists of a perforated plate with holes connected to hollow, flexible, or rigid tubes that are inserted into a cavity and open at the end. The flexible tubes offer greater adaptability and allow for tuning of resonant frequencies, making the approach promising for applications requiring broadband noise control. Recent work by Simon (2024), Lafont et al. (2024) demonstrated the integration of the LEONAR concept in the acoustic coating applied to a hovering drone rotor, proposing optimized designs that achieved a wavelength-to-thickness ratio between 16 and 26, compared to the 4–8 range typical of classical resonators.
Kone et al. (2021a), Kone et al. (2022), Kone et al. (2021b), Kone et al. (2021c) proposed an alternative concept of structured materials, consisting of an assembly of four sub-metamaterials, each designed to group its lowest resonant frequencies together, forming a continuous frequency band for noise attenuation. This assembly effectively broadens the first resonant frequency band, attenuating up to 70% of noise levels. While other resonant frequency bands were also widened, the structured metamaterial achieved a noise attenuation of only 40% at these frequencies. Recent investigations (Kone et al., 2021c; Kone et al., 2020a) have shown that embedding these metamaterials within a layer of porous material, such as glass fiber, can further expand the absorption frequency ranges while maintaining good acoustic performance. Kone et al.'s studies revealed that the wavelength-to-thickness ratio for this type of metamaterial could exceed 30, providing an acoustic attenuation of 40% for frequencies above 200 Hz. Additionally, a second resonance frequency was observed with the structured materials, indicating potential for enhanced noise control.
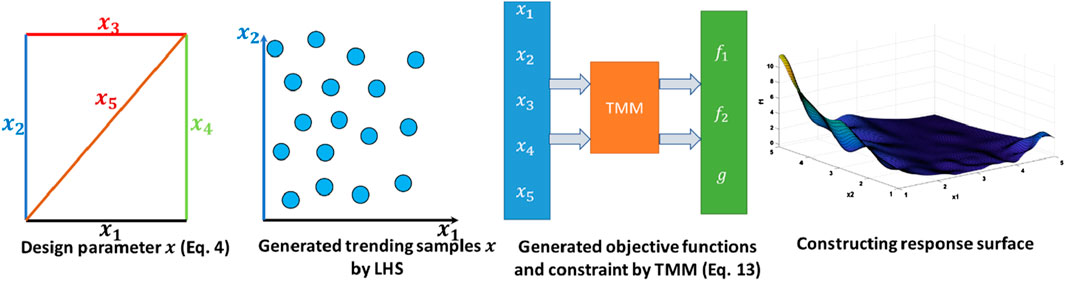
Building on the work of Kone et al. (2024c), Kone et al. (2023), Kone et al. (2024d), this paper aims to propose a metamaterial resulting from a careful assembly of structured materials (SMs) and Helmholtz resonators (HRs) capable of simultaneously attenuating tonal and broadband noise at low frequencies. The developed metamaterial solution should be incorporated into the thermo-acoustic insulation of existing aircraft for an improved reduction of cabin noise. Moreover, the proposed solution had to be optimized not only for acoustic performance but also for low weight, and low fabrication costs. The challenge was therefore to select a concept that, through multi-variable optimization, would produce a noise reduction improvement and would rapidly reach a technology readiness level for integration on-board aircraft. The optimization approach used is based on the construction of the surrogate model (metamodel) from the design parameters. A surrogate model is a simplified model that approximates the behavior of a more complex system, allowing for faster evaluations and analysis. This model is built by adjusting the input (design parameters) – output (sound absorption coefficient and first resonance frequency) relationships to obtain a fast, high-fidelity response surface approximation. Constructing an accurate surrogate model requires adequate input–output samples (training samples) that can properly capture the characteristics of the response surface. Conventionally, training samples are generated by space-filling designs including Latin hypercube sampling (LHS) (Swiler and Wyss, 2004). The transfer matrix method (TMM) (Kone et al., 2020b; Verdiere et al., 2013) is employed to characterize the sound absorption coefficient of the metamaterials. Once the response surface model is established, the multiobjective genetic algorithm approach (MOGA) (Deb, 2001) available in the open source software Dakota (2020) is used to idenfy for the optimum design parameters of the metamaterial.
The results obtained are compared with those obtained from numerical simulations using the finite element method, providing a comprehensive analysis of their effectiveness in noise attenuation.
2 Materials
The metamaterials investigated in this paper were meticulously designed as an intricate assembly, incorporating four structured materials (SMs) and eight Helmholtz Resonators (HRs). These elements were precisely arranged in parallel and embedded within a layer of fiberglass (FGL), providing the resulting configuration with unique sound attenuation properties. The metamaterial, without the porous layer, had a cylindrical form with a diameter
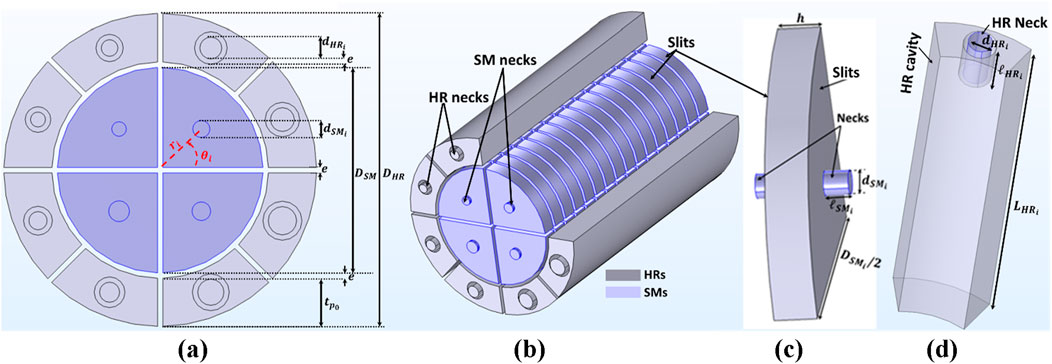
Figure 1. Metamaterial configuration under study: (A) Cross section, (B) Materials assembled without porous medium, (C) PUC of Structured Material, and (D) Inner HR.
This methodically designed and optimized metamaterial structure represents a novel and promising configuration for applications in aeronautics (propeller blade or aircraft cabin noise attenuation), ground transportation, and construction industries. The innovative integration of SMs and HRs, combined with the optimization process, provides a comprehensive and practical solution for broadband noise attenuation.
3 Modeling
Two complementary approaches were employed to characterize the acoustic properties of the materials described in Section 2. First, the analytical approach based on transfer matrix methods (TMM) is presented in this section. This method is used to calculate the objective functions implemented in the optimization algorithms. Subsequently, the numerical approach is discussed, serving to validate and complement the findings using the analytical method.
3.1 Analytical approach
In order to quickly characterize the acoustic performance of the metamaterial, the transfer matrix method (TMM) has been adopted. The TMMs presented and developed in the work of Kone et al. (2024d); (Equation 7, 10, 11) are used in this study. These TMMs were used to build the global transfer matrix of the metamaterial under study. This global transfer matrix will allow the calculation of the sound absorption coefficient (backed by a rigid wall).
3.1.1 Metamaterial TMM
Knowing the transfer matrix of each element constituting the parallel assembly of the metamaterial (Equations 7, 10, 11 in Kone et al. (2024d)); the overall transfer matrix of the metamaterial is deduced from the parallel matrix method (PTMM) (Kone et al. (2021b), Swiler and Wyss, 2004) and is given by:
where,
3.1.2 Metamaterial acoustic properties
By defining the global matrix as
3.2 Numerical approach
In this section only the model used to calculate the SAC is presented. Regarding the calculation of the STL, the reader will find a detailed description in Kone et al. (2024a). This subsection describes the analytical approach employed for SAC modeling. COMSOL Multiphysics was used for the prediction of the SAC of the metamaterial backed by a rigid wall at normal incidence. The frequency domain sound pressure modulus was used. The walls of each PUC were modelled as rigid. An impedance tube of diameter identical to the diameter of the metamaterial embedded in fiber glass, that is
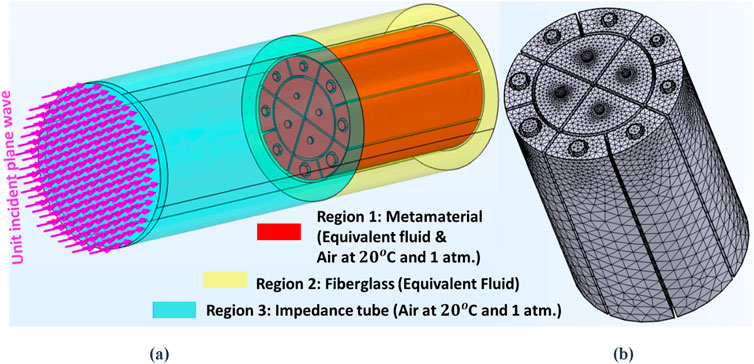
Figure 2. FEM model and mesh of the metamaterial connected to simulated impedance tubes for the hard-backed (SAC): (A) Model, and (B) mesh of Metamaterial without fiberglass layer.

Table 1. Johnson-Champoux-Allard (JCA) parameters of the slit and neck and fiberglass, where
4 Optimization approach
In this section only the methodology to optimize a structured material (SM) constituting the metamaterials is presented. The problem is to find design parameters that allow good sound absorption at the first desired resonance frequency of the SM under the constraint that the total thickness of the SM is less than the maximum length
where
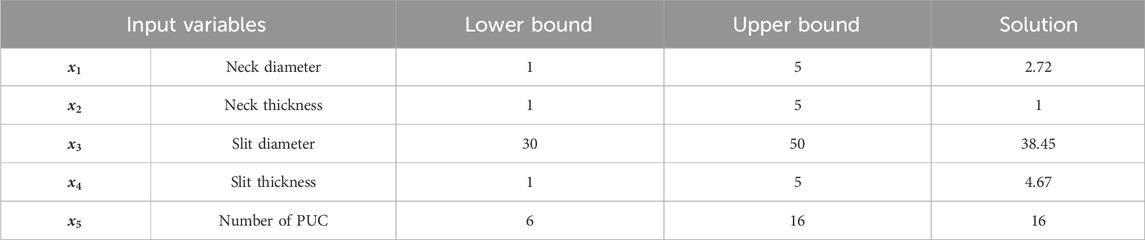
Five design parameters are necessary to design the SM described in section 2. These are the neck diameter
Each of the components of the design vector is limited according to the geometric constraints of the available space. These inequalities are linear constraints of the optimization variables. The constraint governing the maximum thickness, is the nonlinear function g(x) and is defined as:
The optimization problem to solve is to find the variable vector x which minimizes
were
Having defined the optimization problem, the next step involves constructing the response surface using surrogate modeling.
4.1 Surrogate model
The procedure of surrogate modeling is illustrated in Figure 3. This process begins with defining the input variables and target outputs. Input variables typically include the design parameters that influence the performance of the structured material (SM), such as neck diameter (
4.1.1 Kriging model
A Kriging model (Dakota, 2020), also known as Gaussian Process Regression, is a surrogate modeling technique used to predict the behavior of complex systems based on a limited number of observations. It creates a smooth approximation of a function by assuming that the unknown function follows a Gaussian process, characterized by a mean and a covariance function. A Kriging emulator,
4.1.2 Trend function
In a Kriging process, the trend function (
The constructed surrogate model is then used in the optimization process. By evaluating the surrogate model, the optimization algorithm can efficiently explore the design space to find the optimal set of parameters that minimizes the first objective function
4.2 Multiobjective genetic optimization algorithm using a surrogate model
In this subsection, the methodology for optimizing the structured material (SM) using a multiobjective genetic algorithm (MOGA) in conjunction with surrogate models described in subsection 4.1. The MOGA is an optimization technique inspired by the principles of natural evolution and genetic processes. Unlike traditional genetic algorithms that focuses on a single objective function, MOGA optimizes multiple conflicting objective functions simultaneously. This approach is particularly useful in engineering and design problems where trade-offs between different performance metrics are required. MOGA uses a population of candidate solutions to explore the search space. This allows the algorithm to maintain diversity and identify multiple Pareto optimal solutions in a single run. Solutions are selected based on their fitness, which is determined by their performance on multiple objectives. Techniques such as Pareto ranking and crowding distance are used to maintain a diverse set of high-quality solutions.
5 Results
In this section, the optimization results are analyzed and interpreted. First, the sound absorption coefficient (SAC) of the optimized structured material (SM) configuration is presented. Next, the SAC of the four assembled SMs and the eight assembled Helmholtz Resonators (HRs) is analyzed. Finally, the SAC of the complete metamaterial is evaluated.
5.1 Interpretation of optimization results
This section aims to solve the optimization problem defined in Equation 7, which seeks to identify the design parameters of a structured material (SM) that achieves high absorption performance at a first resonance frequency close to
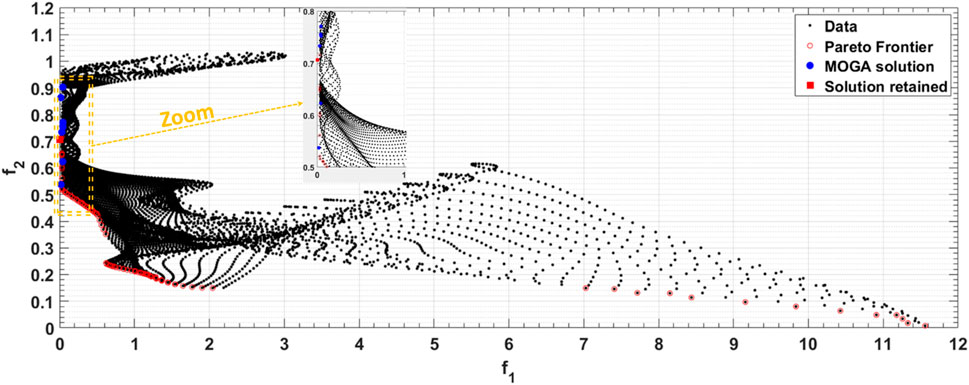
Figure 4. Samples of the objective functions, with the sound absorption coefficient (
The validation of the surrogate model was carried out using 100 samples, all derived from solutions predicted by the MOGA approach. This number of samples was selected to ensure a comprehensive evaluation of the surrogate model’s predictive capabilities across a diverse range of scenarios. The accuracy of the surrogate model is substantiated by an error threshold defined as
The results indicate that the optimized design parameters successfully achieve the desired absorption performance at the specified resonance frequency while adhering to the thickness constraint. This demonstrates the effectiveness of the surrogate modeling and optimization approach in designing structured materials with targeted acoustic properties.
The design parameter values from the solution, along with the variable ranges, were used to generate contour plots for both objective functions constructed using the surrogate model. Figures 5, 6 each displays a contour plot, illustrating the first SM’s resonance frequency and its absorption amplitude, respectively. In each subplot, two of the five design variables are varied, while the remaining variables are fixed at the values from the solution. These contour plots reveal the non-linear response surface of each objective function. The white dots on the subfigures represent the solutions of the optimization problem. The contour levels of the objective functions at these points are 0.005 for the first function (Figure 5) and 0.7 for the second objective function (Figure 6). These results demonstrate the reliability of the response surface model in addressing the optimization problem.
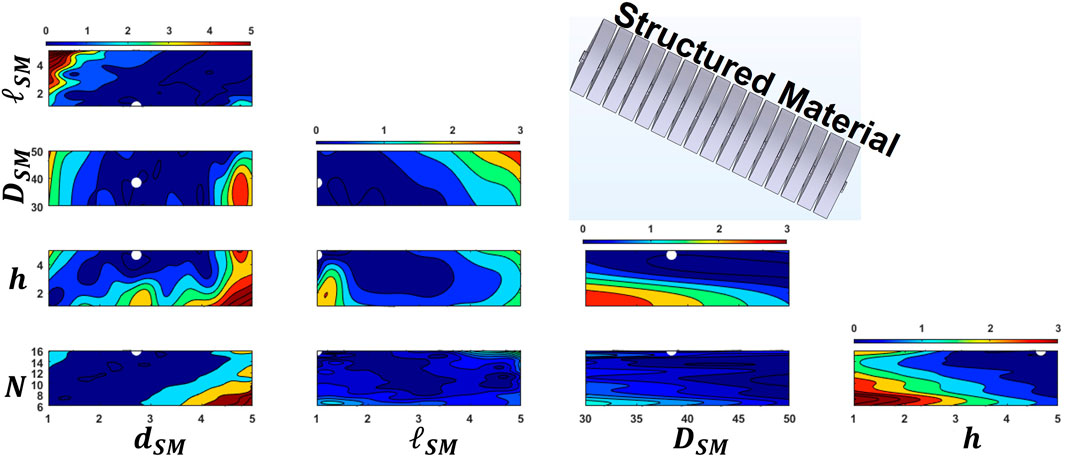
Figure 5. Non-dimensional resonnance frequency (
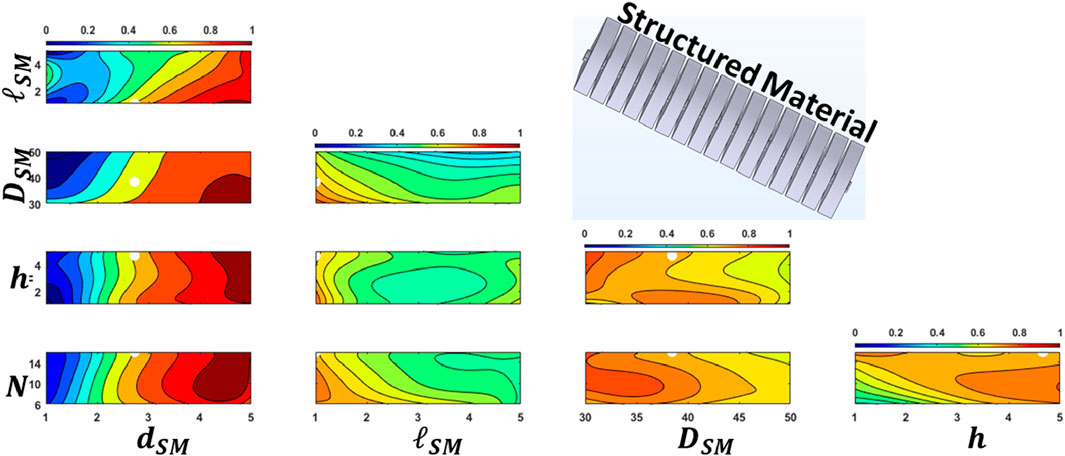
Figure 6. Sound Absorption Coefficient (
5.2 Sound absorption coefficient of optimized SM
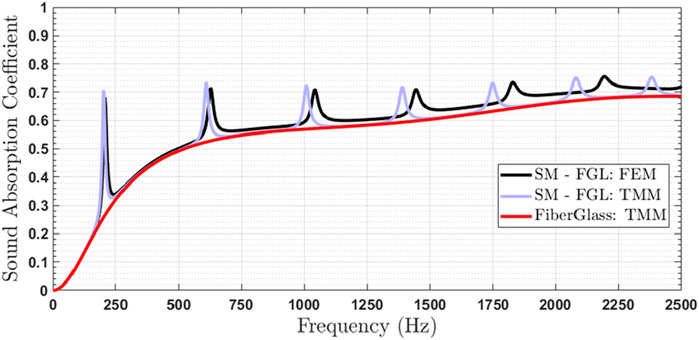
The structured material (SM), derived from solving the optimization problem and detailed in the last column of Table 2, was evaluated for its sound absorption performance validation. Figure 7 illustrates the sound absorption coefficient at normal incidence for the SM with a rigid bottom, as determined both analytically (using) and numerically (as described in Section 2). The results from both methods are in close agreement. A slight frequency shift is observed from the third resonance frequency onward of the SM. The authors believe that this is due to the approximation on the equivalent diameter of the SM slit made (Kone et al., 2024d). Since our objective is on the first resonance frequency, this influences very little our analysis. The first significant absorption frequency occurs around
5.3 Sound absorption coefficient of assembled SMs
The metamaterials consist of an assembly of four SMs in parallel, complemented by eight HRs. Each SM’s design parameters are identical except for the diameter of the neck of each Periodic Unit Cell (PUC). The objective is to have the first resonance frequencies of all four SMs closely spaced yet distinct. For instance, let SM1 represent the optimized configuration with the design parameters specified in the last column of Table 2, featuring a neck diameter of
Glass fiber is typically effective in attenuating high frequencies. In this study, its impact is observed at frequencies below 250 Hz (see Figures 7, 8), where it achieves an absorption performance of over 32%. Without the glass fiber layer, absorption at the second first resonance frequency (around 611 Hz) reaches only 21%, whereas the addition of the glass fiber increases it to 73%, resulting in a 52% improvement due to the contribution of the glass fiber.
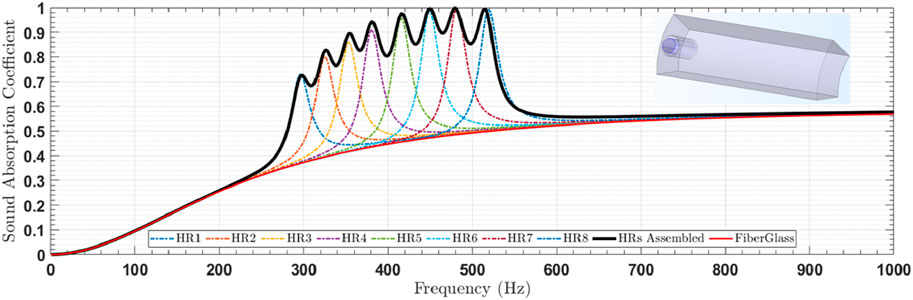
5.4 Sound absorption coefficient of assembled HRs
The Helmholtz resonators (HRs) incorporated into the design all have identical cavity volumes and the same neck length, defined by
5.5 Sound absorption coefficient of metamaterial
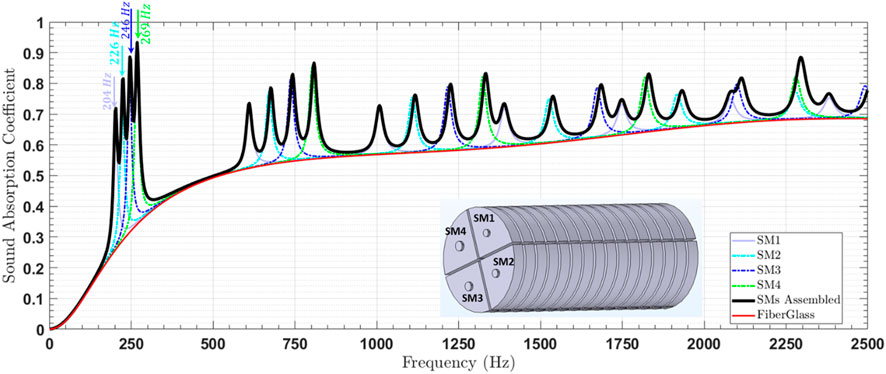
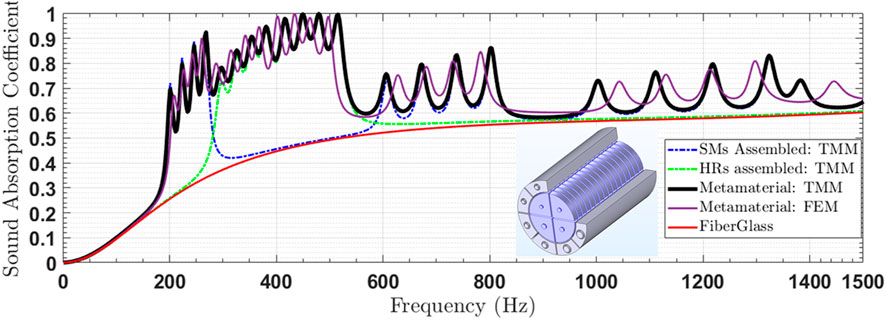
The structured materials (SMs) and Helmholtz resonators (HRs) were assembled in parallel to create the metamaterial for this study. The normal incidence sound absorption coefficient (SAC) of the metamaterial was determined using the TMM approach, as described by . These results were compared with those obtained from finite element method (FEM) simulations performed using COMSOL Multiphysics, as shown in Figure 10.
The SAC values derived from the analytical TMM model were found to be in close agreement with the FEM simulation results, validating the accuracy of the TMM approach. However, a slight frequency shift is observed from the resonance frequencies of the SM. The authors believe that this is due to the approximation on the equivalent diameter of the SM slit made (Kone et al., 2024d). Further investigation is needed to understand this discrepancy. However, it has very little impact on our study. This innovative configuration led to significantly improved acoustic performance, achieving an absorption rate of 60% for frequencies above 197 Hz. Furthermore, the metamaterial exhibited four distinct resonance frequencies, corresponding to the second resonance frequencies of each structured material, with these frequencies occurring around 596 Hz.
In the detailed analysis of the metamaterial’s acoustic properties, three distinct absorption frequency bands were identified, demonstrating the material’s capability to attenuate sound effectively across a broad frequency range (Figure 10). The first absorption band, which spans from 196 to 289 Hz, achieved performance levels above 50%, indicating significant sound attenuation in the lower frequency range. The third band, extending from 596 to 845 Hz with absorption performance exceeding 60%, was also linked to strong attenuation characteristics. Both of these bands emerged from the parallel assembly of three distinct structured metamaterial configurations, which worked in tandem to broaden the resonance frequencies, enabling more effective suppression of low-frequency noise. This arrangement facilitated the exploitation of multiple resonant mechanisms that overlapped to produce a more comprehensive attenuation profile, as illustrated in Figures 8, 10.
The intermediate absorption band, covering the range from 293 to 536 Hz, exhibited even higher absorption performance, with levels surpassing 70%. This enhanced absorption was primarily attributed to the parallel configuration of eight Helmholtz resonators. The design leveraged the individual resonance characteristics of each resonator, creating a cumulative effect that widened the frequency range of significant noise reduction. The resonators’ ability to target specific frequencies made them particularly suitable for addressing mid-range sound attenuation, as depicted in Figures 9, 10.
Moreover, the metamaterial demonstrated a wavelength-to-thickness ratio of approximately 18, placing it within the optimal range for acoustic metamaterial performance as proposed by Simon (2024), Lafont et al. (2024). This ratio indicates that the metamaterial achieves a compact form factor while maintaining high efficiency in sound absorption, aligning with the trend in modern acoustic engineering to develop thinner, lightweight materials that do not compromise on performance. The results underscore the potential of combining structured metamaterials with classical resonator designs to create hybrid configurations that offer superior noise control across a wide frequency spectrum, thus meeting stringent industrial requirements for low-frequency noise management.
6 Conclusion
In conclusion, this study has introduced and characterized thin acoustic metamaterials designed to effectively attenuate both tonal and broadband noise at low frequencies The optimization of the structured materials (SMs) and Helmholtz Resonators (HRs) has demonstrated significant potential for noise control across various industrial applications, including aeronautics, transportation, and construction.
The optimization approach successfully fine-tuned the design parameters of the SMs to achieve an absorption performance of at least 55% across a frequency range from
Analytical validation using the transfer matrix method (TMM) and comparative analysis with COMSOL simulations confirmed the robustness and computational efficiency of our approach. The TMM not only accurately predicted key metrics such as the Sound Absorption Coefficient (SAC) but also enabled rapid design optimization, which is crucial for tailoring metamaterials to meet specific acoustic performance requirements. The study underscores the dual benefits of these metamaterials in attenuating noise and enhancing sound transmission loss, making them versatile solutions for mitigating environmental noise pollution and improving acoustic comfort. The practical implications are significant, offering various industries a pathway to deploy efficient and customized noise control solutions rapidly and effectively.
Despite the acoustic advantages of this metamaterial, several aspects still require further investigation. One important factor is the weight of the metamaterial, which needs to be carefully studied to ensure its practicality in real-world applications.
Future research should focus on balancing acoustic performance with material density and structural design to achieve an optimal solution that meets both acoustic and weight constraints. Continued exploration of additional configurations and materials could optimize performance across broader frequency ranges and address specific industrial noise challenges more comprehensively.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
TK: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. SG: Investigation, Methodology, Resources, Supervision, Validation, Writing–review and editing. RP: Writing–review and editing. AG: Investigation, Methodology, Resources, Supervision, Validation, Writing–review and editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Champoux, Y., and Allard, J. (1991). Dynamic tortuosity and bulk modulus in air-saturated porous media. J. Appl. Phys. 70 (4), 1975–1979. doi:10.1063/1.349482
Dakota, A. Multilevel parallel object-oriented framework for design optimization, parameter estimation, uncertainty quantification, and sensitivity analysis: version 6.13 user’s manual, sand2020-12495 unlimited release (2020).
Deb, K. (2001). Multi-objective optimization using evolutionary algorithms. Hoboken, USA: John Wiley and Sons.
Guo, J., Zhou, T., Fang, Y., and Zhang, X. (2021). Experimental study on a compact lined circular duct for small-scale propeller noise reduction. Appl. Acoust. 179, 1–10. doi:10.1016/j.apacoust.2021.108062
Jones, M. G., Simon, F., and Roncen, R. (2022). Broadband and low-frequency acoustic liner investigations at NASA and ONERA. AIAA J. 60, 2481–2500. doi:10.2514/1.J060862
Kemp, C. F. B. (1932). Some properties of the sound emitted by airscrews. Proc. Phys. Soc. 44, 151–165. doi:10.1088/0959-5309/44/2/305
Kone, T. C., Ghinet, S., Dupont, T., Panneton, R., Grewal, A., and Wickramasinghe, V. (2020b). Characterization of the acoustic properties of complex shape metamaterials in Proceedings of INTER-NOISE, 23–26.
Kone, T. C., Ghinet, S., Panneton, R., Dupont, T., and Grewal, A. (2020b). Multi-tonal low frequency noise control using Helmholtz resonators with complex cavity designs for aircraft cabin noise improvement. Inter. Noise. Proc. Inter-Noise, 263(2), 3975–3986. doi:10.3397/in-2021-2569
Kone, T. C., Ghinet, S., Panneton, R., and Grewal, A. (2020a). Characterization of the acoustic properties of complex shape metamaterials in Proceedings of INTER-NOISE, 261.
Kone, T. C., Ghinet, S., Panneton, R., and Grewal, A. (2020c). Optimization of metamaterials with complex neck shapes for aircraft cabin noise improvement. Inter. Noise. Proc. INTER-NOISE, 263(2), 3963–3974. doi:10.3397/in-2021-2567
Kone, T. C., Ghinet, S., Panneton, R., and Grewal, A. (2023). Method for characterizing the acoustic properties of thin metamaterials capable of attenuating broadband noise at low frequencies in Proceedings of AWC 2023 conference, 51.3.
Kone, T. C., Ghinet, S., Panneton, R., and Grewal, A. (2024a). Mitigating low-frequency broadband aircraft noise through an assembly of structured acoustic materials. Proc. Mtgs. Acoust. 54, 030001. doi:10.1121/2.0001897
Kone, T. C., Ghinet, S., Panneton, R., and Grewal, A. (2024b). Structured acoustic materials for mitigating low-frequencybroadband aircraft noise: transfer matrix method in Proceedings of INTER-NOISE (Nante, France), 25–29 August.
Kone, T. C., Ghinet, S., Panneton, R., and Grewal, A. (2024c). Broadband low frequency noise attenuation using thin acoustic metamaterials for aircraft cabin noise mitigation in Inter-noise 2023 – 52nd international congress and exposition on noise control engineering, 2023, chiba, greater. Tokyo, Japan.
Kone, T. C., Ghinet, S., Panneton, R., and Grewal, A. (2024d). Broadband aircraft noise attenuation across low and high frequencies using structured materials in Proceedings of noise-con 2024 (New Orleand, LA: US).
Kone, T. C., Ghinet, S., Panneton, R., Grewal, A., Laly, Z., and Mechefske, C. (2022). Control and broadening of multiple noise frequencies using an assembly of sub-metamaterials connected by membranes for aircraft noise mitigation. Inter. Noise. Proc. INTER-NOISE, 265(3), 4607–4615. doi:10.3397/in_2022_0663
Kone, T. C., Lopez, M., Ghinet, S., Dupont, T., and Panneton, R. (2021a). Thermoviscous-acoustic metamaterials to damp acoustic modes in complex shape geometries at low frequencies. JASA 150 (3), 2272–2281. doi:10.1121/10.0006441
Kurtz, D. W., and Marte, J. E. (1970). A review of aerodynamic noise from propellers, rotors, and lift fans. California: California Institute of Technology.
Lafont, V., Sebbane, D., and Simon, F. (2024). “Feasibility of an acoustic liner applied to a fenestron: experimentation, inter-noise 2024,” in 53rd International Congress and Exposition on Noise Control Engineering, Nantes, France.
Lu, Z., Debiasi, M., and Khoo, B. C. (2016). “Acoustic characteristics of a multi-rotor MAV and its noise reduction technology,” in INTER-NOISE and NOISE-CON congress and conference proceedings, Hamburg, Germany.
Malgoezar, A. M., Vieira, A., Snellen, M., Simons, D. G., and Veldhuis, L. L. (2019). Experimental characterization of noise radiation from a ducted propeller of an unmanned aerial vehicle. Int. J. Aeroacoustics 18, 372–391. doi:10.1177/1475472x19852952
Simon, F. (2018). Long elastic open neck acoustic resonator for low frequency absorption. J. Sound. Vib. 421, 1–16. doi:10.1016/j.jsv.2018.01.044
Simon, F. (2024) Design and evaluation of an acoustic liner applied to a UAV ducted rotor in hover in Inter-noise 2024 – 53rd international Congress and Exposition on noise control engineering, 2024. Nantes France.
Swiler, L. P., and Wyss, G. D. (2004). A user’s guide to Sandia’s Latin hypercube sampling software: LHS UNIX library and standalone version. Albuquerque, NM: Sandia National Laboratories. Technical Report SAND04-2439.
Verdiere, K., Panneton, R., Elkoun, S., Dupont, T., and Leclaire, P. (2013). Transfer matrix method applied to the parallel assembly of sound absorbing materials. JASA 134, 4648–4658. doi:10.1121/1.4824839
Keywords: metamaterial, optimization, broadband-noise, aircraft-noise, cabin noise, low-frequency
Citation: Kone TC, Ghinet S, Panneton R and Grewal A (2025) Multi-objective optimization of structured material parameters for reducing broadband aircraft noise across various frequencies. Front. Acoust. 2:1498722. doi: 10.3389/facou.2024.1498722
Received: 19 September 2024; Accepted: 02 December 2024;
Published: 06 January 2025.
Edited by:
Minghui Lu, Nanjing University, ChinaReviewed by:
Frank Simon, Office National d'Études et de Recherches Aérospatiale, FranceEdith Roland Fotsing, Polytechnique Montréal, Canada
Copyright © 2025 Kone, Ghinet, Panneton and Grewal. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tenon Charly Kone, VGVub25DaGFybHkuS29uZUBucmMtY25yYy5nYy5jYQ==; Sebastian Ghinet, c2ViYXN0aWFuLmdoaW5ldEBucmMtY25yYy5nYy5jYQ==
 Tenon Charly Kone
Tenon Charly Kone Sebastian Ghinet
Sebastian Ghinet Raymond Panneton
Raymond Panneton Anant Grewal
Anant Grewal