- 1Centre for Mathematical Plasma Astrophysics, Department of Mathematics, KU Leuven, Leuven, Belgium
- 2Max-Planck-Institut für Sonnensystemforschung, Göttingen, Germany
Observations have revealed two regimes of kink oscillations of coronal loops. Large amplitude oscillations excited by impulsive energy releases such as coronal mass ejections are characterized by their strong damping by resonant absorption. Lower amplitude oscillations may also be excited and sustained by the ubiquitous motions present in the corona and so are characterized as being decayless. We perform numerical simulations to study the oscillation and evolution of coronal loops in a dynamical environment. We investigate the observational signatures of kink oscillations and the Kelvin-Helmholtz instability in terms of high-resolution seismological and spatial data analysis techniques. We find that low amplitude kink oscillations are capable of generating significant changes in the loop profile which can affect estimates of the transverse loop inhomogeneity based on seismological and forward modeling methods. The disparity between methods may be indicative of non-linear evolution of coronal loops. The influence on forward modeling estimates could also account for previous observational evidence favoring loops having wider inhomogeneous layers.
1. Introduction
Kink oscillations of coronal loops are periodic displacements of the loop axis. They were first observed using the Transition Region And Coronal Explorer (TRACE; Handy et al., 1999) in an active region perturbed by a solar flare (Aschwanden et al., 1999; Nakariakov et al., 1999). Hundreds of observations of standing kink modes have now been studied (e.g., catalogs by Goddard et al., 2016; Nechaeva et al., 2019), aided by the full disk coverage and enhanced temporal resolution of the Atmospheric Imaging Assembly (AIA) on board the Solar Dynamics Observatory (SDO; Lemen et al., 2012).
Large amplitude kink oscillations are observed to be strongly damped which is attributed to the process of resonant absorption (e.g., De Moortel et al., 2016, and references therein). This is a robust damping mechanism since it only requires that the transition between a higher density coronal loop and the lower density background plasma occurs over a finite spatial scale. In analytical and numerical models this transition is usually described in terms of a boundary layer surrounding the core of the loop. The inhomogeneous layer width (commonly normalized by the loop radius to produce the parameter ϵ) represents a transverse spatial scale which is also important for other physical processes such as phase mixing (Heyvaerts and Priest, 1983) and the Kelvin-Helmholtz instability. It is therefore a key physical parameter but difficult to observe directly, which motivates its seismological inference through the damping of kink oscillations.
The length L of a coronal loop is typically much larger than its radius R. Under this thin tube approximation, the phase speed of the kink mode is the kink speed Ck, which is a density-weighted average of the internal and external Alfvén speeds. Under the further thin boundary approximation corresponding to the limit ϵ → 0, the period of oscillation for the fundamental standing kink mode is then P = 2L/Ck. However, parametric studies (Van Doorsselaere et al., 2004; Soler et al., 2014; Pascoe et al., 2019a) find that the period of oscillation does also depend on the width of the boundary layer when it is sufficiently large.
The boundary layer of a coronal loop provides a continuous variation of the local Alfvén speed, and the resonance condition is satisfied where the kink mode frequency matches the local Alfvén frequency. A transfer of wave energy from collective kink motions to localized azimuthal perturbations (m = 1 Alfvén waves) will appear as a damping of the periodic loop displacement. The azimuthal motions will typically appear as unresolved Doppler velocity perturbations due to line-of-sight (LOS) integration of multiple waves and structures (e.g., De Moortel and Pascoe, 2012; Pant et al., 2019). Although this transfer is a linear and ideal process, subsequent phase-mixing of the Alfvén waves in the inhomogeneous layer can generate small spatial scales which enhance dissipative processes such as viscosity and resistivity (e.g., Pagano and De Moortel, 2017; Pagano et al., 2018).
Initial descriptions of the resonant absorption of kink oscillations took the form of exponential damping profiles (Goossens et al., 2002, 2012; Ruderman and Roberts, 2002; Arregui et al., 2007) based on analytical derivations for the asymptotic state of the system under the thin tube thin boundary (TTTB) approximation. Numerical simulations (Pascoe et al., 2012) found poor agreement with exponential damping behavior at early times, where a Gaussian damping profile appeared more suitable. The analytical description of Hood et al. (2013) accounted for this Gaussian damping regime as an approximation for the initial behavior of the kink mode, with exponential damping behavior at a later stage. The switch from Gaussian to exponential damping behavior was shown to depend on the loop density contrast ratio ζ, which was confirmed by the parametric study by Pascoe et al. (2013). It was also used to propose a general damping profile (GDP), combining both the Gaussian and exponential damping regimes, as a convenient approximation for seismology. The Gaussian damping behavior was initially studied for propagating kink waves but is also applicable to standing waves (e.g., Ruderman and Terradas, 2013; Magyar and Van Doorsselaere, 2016a; Pagano et al., 2018). In particular, Pascoe et al. (2019a) performed 300 numerical simulations to produce a lookup table (LUT) as a convenient means of estimating the damping profile beyond the applicability of the thin boundary approximation. Resonant absorption therefore accounts not only for the strong damping of kink oscillations but also the observational evidence for their non-exponential damping behavior (De Moortel et al., 2002; Ireland and De Moortel, 2002; Goddard et al., 2016; Morton and Mooroogen, 2016; Pascoe et al., 2016c), and allows the seismological inference of the transverse density profile of the loop (Pascoe et al., 2016b, 2017a, 2018).
The Kelvin-Helmholtz instability (KHI; e.g., Browning and Priest, 1984; Ofman et al., 1994) has been demonstrated by numerous numerical studies to cause redistribution of loop plasma during kink oscillations (e.g., Terradas et al., 2008a; Soler et al., 2010; Antolin et al., 2014; Karampelas and Van Doorsselaere, 2018). Since the rate of the instability depends on the shear flows it is also affected by the width of the inhomogeneous layer (e.g., Magyar and Van Doorsselaere, 2016a; Goddard et al., 2018). The “decayless” regime of kink oscillations refers to low amplitude oscillations which appear to be undamped (Anfinogentov et al., 2013, 2015; Nisticò et al., 2013) or even growing (Wang et al., 2012), in contrast with the large amplitude and strongly damped oscillations discussed above. Only coronal loops with a discontinuous boundary would not exhibit damping due to resonant absorption. However, the strong shear velocities that would be present in such a scenario would also lead to the rapid development of KHI and the establishment of an effective boundary layer by mixing of internal plasma. Forward modeling of EUV emission from coronal loops (e.g., Van Doorsselaere et al., 2016) suggests observational effects associated with KHI might contribute to the appearance of weak damping in some circumstances (Antolin et al., 2016, 2017), but generally the presence of damping by resonant absorption must be compensated by the driving mechanism, such as persistent footpoint oscillations (e.g., Afanasyev et al., 2019, 2020; Karampelas et al., 2019) or flows (Nakariakov et al., 2016; Karampelas and Doorsselaere, 2020). Decayless kink oscillations might be connected with the observation of propagating transverse velocity perturbations (e.g., Tomczyk et al., 2007; Tomczyk and McIntosh, 2009; Verth et al., 2010; Pascoe et al., 2015) since both appear to be ubiquitous and require a persistent source of wave energy, though spatial analysis of the decayless kink modes confirms they are indeed standing modes (Duckenfield et al., 2018) as does the period of oscillation being proportional to the loop length (Anfinogentov et al., 2015).
In this paper we consider the effect of the Kelvin-Helmholtz instability on the distortion of the loop density profile and its appearance in optically thin EUV images. Our simulation of a coronal loop experiencing multiple perturbations which excite and maintain standing kink oscillations approximating the decayless regime is presented in section 2. In section 3, we consider the observational signature of our simulation and compare the results with a statistical study of the density profiles of coronal loops. Conclusions are presented in section 4.
2. Numerical Simulation of Non-Linear Evolution
In this section, we describe our numerical simulation of a coronal loop which experiences multiple low-amplitude impulsive perturbations designed to excite the fundamental standing kink mode. Our use of multiple perturbations as opposed to a continuous driver facilitates analysis of the evolution of the loop and its oscillation in time by enabling us to use established techniques for the damping behavior of impulsively-generated decaying oscillations. The coronal loop is modeled as a straight flux tube embedded in a uniform magnetic field with no gravitational stratification. The only non-uniformity is thus provided by the coronal loop. We use a linear density profile in the inhomogeneous layer for comparison with previous work, in particular the parametric study by Pascoe et al. (2019a) which describes the effect of a thick inhomogeneous layer. We note that the numerical simulations in that paper studied the linear regime of kink oscillations and used cylindrical coordinates, with the assumption of m = 1 symmetry for the azimuthal dependence corresponding to the kink oscillation and Alfvén waves generated by resonant absorption (e.g., Pascoe et al., 2010). In this paper, we study non-linear evolution of the loop, which includes the breaking of m = 1 azimuthal symmetry by the development of KHI (e.g., the large deformations in Karampelas and Van Doorsselaere, 2018). We use LARE3D (Arber et al., 2001) which solves the non-linear MHD equations in Cartesian geometry.
The loop has a length of 100 Mm, radius of 1 Mm, and the uniform magnetic field strength corresponds to an external Alfvén speed of 1 Mm/s. The loop has a density contrast ratio of ζ = 3 for which the TTTB estimate for the period of oscillation of the fundamental kink mode is Pk ≈ 283 s, allowing several cycles of the oscillation to be observed between each perturbation (1, 000 s apart). However, each subsequent perturbation will be applied at a time which does not correspond to a zero in the oscillation of the current oscillation. The numerical domain extends to [−4, 4] Mm in the x and y directions perpendicular to the loop axis with a resolution of 400 × 400 × 200 grid points. Numerical tests indicate this is sufficient for the problem, and the need for significantly higher resolution in the transverse directions. Boundary conditions are periodic in the x- and y-directions, and line-tied in z. We consider a low-beta plasma (β = 0.001) and the loop is initially set in pressure balance, corresponding to a cooler loop. We do not consider non-adiabatic effects (e.g., Aschwanden and Terradas, 2008; Magyar et al., 2015; Ruderman et al., 2019).
An impulsive fundamental standing kink mode perturbation is applied to the x-component of the plasma velocity every 1, 000 s. Our aim is to demonstrate the evolution of the loop and oscillation parameters over several iterations of the perturbation. For this purpose we use a inhomogeneous layer width ϵ = 0.3 which is sufficiently large to provide significant (readily measurable) damping for the oscillation while not too large as to inhibit the development of KHI. Similarly, the amplitude of the velocity perturbations is approximately 1% of the Alfvén speed to allow KHI to develop at a moderate rate. Our density profile parameters ζ = 3 and ϵ = 0.3 are reasonable for a coronal loop, for example the loop analyzed on 2012-03-09 by Pascoe et al. (2017c) was estimated to have and (values correspond to the median and 95% credible interval). They are also similar to the values used in numerical simulations performed by Goddard et al. (2018) and Karampelas et al. (2019).
Our driver is intended to efficiently generate the fundamental standing kink mode in the loop, but does not correspond to the exact eigenfunction which would generally be unknown as the loop evolves during the simulation. We use the spatial form
with A = 0.015 Mm/s, k = π/L corresponding to the fundamental longitudinal harmonic, and ν = 3 providing an appropriate spatial scale in the radial () direction. We note that the form of our driver and loop also excludes higher harmonics which can be readily generated by a broadband footpoint driver (e.g., Afanasyev et al., 2020). A persistent footpoint driver is likely more realistic but makes it difficult to accurately measure the period of oscillation due to the presence of the driver spectrum in addition to the natural frequencies. The presence of longitudinal stratification due to gravity, expansion, or curvature leads to coupling of longitudinal harmonics (e.g., Pascoe et al., 2009; Pascoe and Nakariakov, 2016) and changes to the ratio of their periods (e.g., Andries et al., 2005; McEwan et al., 2006; Safari et al., 2007; Verth and Erdélyi, 2008; Arregui et al., 2013) but does not significantly affect the damping rate due to resonant absorption (Arregui et al., 2005; Dymova and Ruderman, 2006). The period ratio for harmonics has been observed in many studies of large-amplitude oscillations (e.g., Verwichte et al., 2004; De Moortel and Brady, 2007; Van Doorsselaere et al., 2007; Pascoe et al., 2016a, 2017a; Duckenfield et al., 2019) and recently in decayless oscillations (Duckenfield et al., 2018).
Figure 1 shows the evolution of the transverse loop density profile at the middle of the coronal loop, i.e., the anti-node for the fundamental standing kink mode. The panels show the density profile in normalized units (external density ρe = 1). The cross symbols in Figure 1 denote the center of mass of the loop. The dashed line represents the contour for which the local Alfvén speed matches the kink speed. Figure 2 demonstrates the evolution of the coronal loop and its oscillation during our simulation. The evolution of the loop profile is characterized by fitting the transverse density profile with a model based on a circular cross-section and linear density profile in the inhomogeneous layer, which is satisfied exactly for the initial condition but otherwise an approximation. They therefore correspond to a value which is averaged in the azimuthal direction, whereas it is known from previous work (e.g., Barbulescu et al., 2019; Hillier and Arregui, 2019) and our Figure 1 that KHI causes density perturbations to develop which exhibit the same m = 1 symmetry as the kink mode. For example, the loop becomes extended in the direction of its displacement (e.g., Karampelas and Van Doorsselaere, 2018). We note that this method for estimating loop parameters is only possible with simulation data, whereas the observational signatures will be considered in section 3.
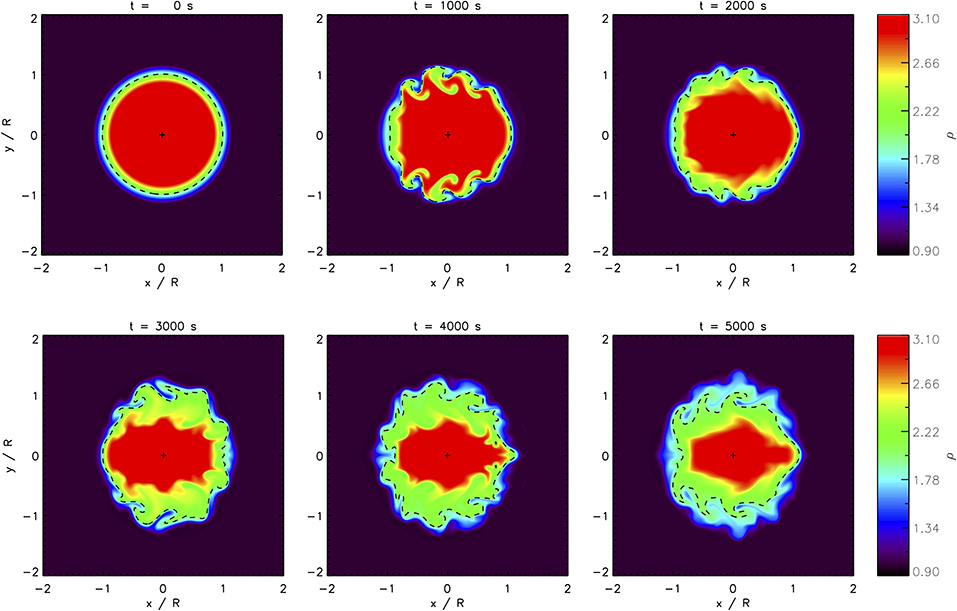
Figure 1. Evolution of the loop density profile in time. The panels show the density in normalized units at the middle (z = 50 Mm) of the coronal loop. The cross symbols denote the position of the loop. The dashed line represents the contour for which the local Alfvén speed matches the kink speed.
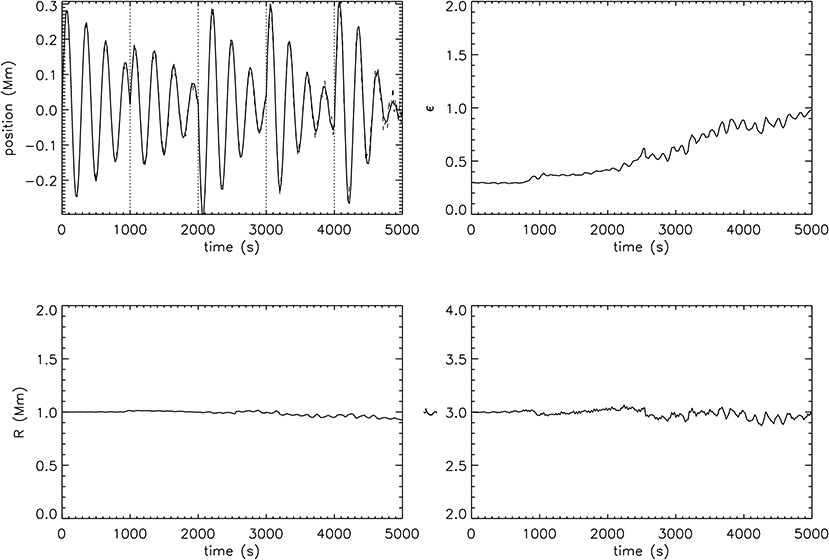
Figure 2. Oscillation of the coronal loop and evolution of the transverse loop density profile parameters taken at the middle of the loop during our numerical simulation; loop position (top left), normalized inhomogeneous layer width (top right), loop radius (bottom left), and density contrast ratio (bottom right).
The top left panel of Figure 2 shows the position of the coronal loop based on our fitting of the density profile (solid line). The dashed line is the position of the center of mass of the loop which is in good agreement. We apply a perturbation at t = 0 s and every 1, 000 s thereafter, indicated by the vertical dotted lines. The subsequent increase in amplitude of the oscillation depends on whether the perturbation is aligned with or opposed to the current direction of motion (which we choose arbitrarily to demonstrate both cases). We note that the abrupt changes in phase is a consequence of our driving mechanism, which is chosen for convenience of our analysis, and is not observed in decayless oscillations. The clear signature of damping and then an increase in amplitude also does not represent decayless oscillations with an approximately constant amplitude, although we have deliberately chosen a sufficiently long interval between perturbations to allow seismological analysis and this effect would be reduced by more frequent and lower amplitude perturbations.
The maximum amplitude of 0.3 Mm is consistent with the decayless regime of kink oscillations which is lower than 1 Mm and an average of approximately 0.2 Mm (Anfinogentov et al., 2015). It is evident that the damping rate at the end of the simulation is greater than that at the start of the simulation (further discussion below). The other panels in Figure 2 show the evolution of the loop parameters. There is no significant change in the loop radius R or density contrast ratio ζ. The main effect of KHI is the increase in the width of the inhomogeneous layer, from its initial value of 0.3 to approximately 1 at the end of our simulation. The onset of this increase occurs after several cycles of the oscillation due to the time required for KHI to develop. The widening inhomogeneous layer and unchanged loop radius are consistent with the study of non-linear evolution of loops by Goddard et al. (2018), although that paper considered the changes in the transverse intensity profile rather than the density profile here. Goddard et al. (2018) also reported a decrease in the peak intensity of the loop, whereas our analysis here indicates an unchanged density contrast ratio. There is no inconsistency in these two results since the decrease in intensity can also be associated with the mixing of plasmas of different temperatures by KHI, and numerical simulations such as those in Goddard et al. (2018) typically impose temperature profiles which decrease inside the loop to maintain pressure balance.
Figure 3 shows the oscillation of the coronal loop after the first applied perturbation and before the second. During this time there are minimal effects due to the non-linear evolution of the loop (see Figure 2) and so the damping rate is consistent with the black envelopes representing the linear solution calculated with the lookup table (LUT) of Pascoe et al. (2019a). The LUT envelope contains the correction for the boundary layer not being thin, whereas each of the colored envelopes are based on the thin boundary approximation and so overestimate the damping of the kink oscillation, particularly the exponential damping profile (red) which does not account for the Gaussian damping behavior during the first couple of cycles of the oscillation. For the general damping profile (GDP) the switch from a Gaussian profile (blue) to an exponential profile occurs after 2 cycles for a density contrast ratio of ζ = 3. The damping rate during subsequent cycles is increased due to KHI, as studied by Magyar and Van Doorsselaere (2016a). We also note that the fitted period of oscillation is P ≈ 1.01Pk, consistent with the small increase due to the presence of a non-thin boundary layer also found in numerical simulations by Pascoe et al. (2019a), and contrary to the decrease in period reported by Soler et al. (2013) and Soler et al. (2014).
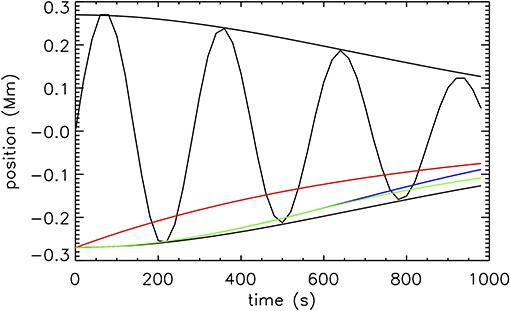
Figure 3. Damping of the kink oscillation after the first applied perturbation. The damping envelopes correspond to the LUT (black), GDP (green), Gaussian (blue), and exponential (red) damping profiles.
Figure 4 shows the results of wavelet analysis (Torrence and Compo, 1998) of the oscillation of the loop axis (left panel). The contours for the wavelet power suggests a small decrease in the period of oscillation in time. This effect is also found by fitting the oscillation as a series of damped perturbations with a time-varying period of oscillation and inhomogeneous layer width (right panel) based on the LUT damping profile. The fitted period of oscillation starts as slightly larger than the TTTB approximation (dashed line in left panel) due to the thickness of the inhomogeneous layer as discussed above. The period of oscillation then decreases during the simulation, due to the non-linear evolution, to a value slightly less than the TTTB approximation. Overall, the TTTB approximation remains a good approximation for the period of oscillation.
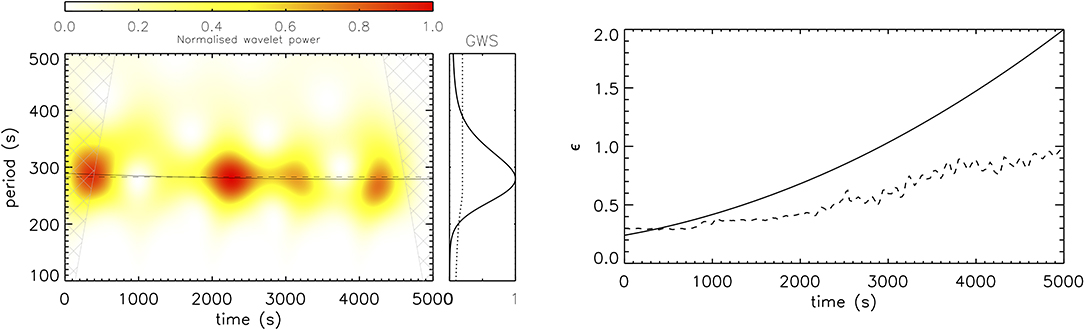
Figure 4. Wavelet analysis of the loop oscillation (left panel). The solid line in the normalized wavelet power represents the fitted variation of the period of oscillation in time. The dashed line denotes the estimate based on the TTTB approximation. The hatched region represents the cone of influence. The global wavelet spectrum (GWS) is shown with the dotted line corresponding to the 90% significance level. The right panel shows the seismologically determined variation in inhomogeneous layer width (compared with the estimate in Figure 2 shown as a dashed line).
The seismological estimate for ϵ is based on the damping due to resonant absorption calculated for different density profile parameters (ζ, ϵ) by Pascoe et al. (2019a) and summarized in the LUT1. This accounts for the effect of a thick inhomogeneous layer and the presence of the non-exponential damping regime. The loop model used in this paper is the same as that used to generate the LUT, and so the results may be directly compared with the relevant physical difference being the non-linear evolution due to finite amplitude kink oscillations. We fit our oscillation with a sinusoidal oscillation comprised of five segments (corresponding to each of the applied perturbations) but a period of oscillation and inhomogeneous layer width which vary (as quadratic polynomials) continuously across all segments. The solid lines in Figure 4 represent the fitted dependence of P(t) and ϵ(t) required to account for the period and damping in our simulation. Within each individual segment the damping profile is calculated from the LUT using ζ = 3 and the local average for P(t) and ϵ(t).
The increase in ϵ required to account for the increase in damping rate in time is much larger (approximately twice) than the estimate based on fitting the transverse density profile. On the other hand, it is evident from Figure 1 that the smaller estimate is more reasonable since the loop has not become fully inhomogeneous by the end of the simulation as the seismological analysis with ϵ → 2 suggests. We can therefore conclude that the non-linear evolution increases the damping rate of kink oscillations above the level suggested by the increasing inhomogeneous layer width. This is not unexpected since our estimate of the inhomogeneous layer width only describes the large scale broadening effect of KHI due to the mixing of loop plasma and external plasma, while KHI is also known to generate small scale structures (“TWIKH rolls”).
Figure 1 shows that these TWIKH rolls also modify the location where the condition for resonant absorption to occur is satisfied (dashed lines). In particular, near the locations of maximum mode coupling (x = 0, y = ±R), the TWIKH rolls cause the resonant contour to double back on itself, presenting additional locations at which resonant absorption can occur. Accordingly, we can caution that the seismologically-inferred value of ϵ is likely to be an overestimate in the case of loop oscillations with strong development of KHI. Previous studies have also estimated ϵ independently of seismological analysis using the transverse intensity profile of the loop. In the following section we consider how this estimate is also affected by the development of KHI.
The seismological model discussed above used a constant density contrast ratio and varying inhomogeneous width based on our understanding of the evolution of the loop due to KHI such as the results in Figure 2. However, approaching the oscillation from a purely seismological point of view, we could consider an alternative analysis of the increase in damping rate as due to a varying density contrast ratio with ϵ remaining constant. We find that this would require a significant increase to ζ > 15 and so could readily be refuted by a lack of brightening in EUV intensity images and due to a mechanism for large increases in loop mass (or decrease in surrounding plasma) to be theoretically accounted for. Such a large change in ζ would also significantly change the period of oscillation unless somehow balanced by a corresponding change in the magnetic field strength.
3. Observational Signature of Loop Evolution
In this section, we consider the evolution of our simulated coronal loop in terms of the established observational method to estimate the inhomogeneous layer width based on the shape of transverse intensity profile. The appearance of a coronal loop in optically thin EUV intensity images can be approximated using the square of the density integrated along the line-of-sight. This method was previously used by Aschwanden et al. (2003) and Aschwanden and Nightingale (2005) who modeled TRACE 171 data using a density profile with a sinusoidal inhomogeneous layer. It was extended by Aschwanden et al. (2007) to also consider rectangular (step) function and Gaussian density profiles, although these were found to typically be indistinguishable from the density profile with a sinusoidal inhomogeneous layer for TRACE data when including the smoothing effect of the instrumental point-spread function.
More recently, a similar method was applied by Pascoe et al. (2017b) to estimate the inhomogeneous layer width of a coronal loop observed using SDO/AIA 171. The density profiles used in that study included a step function, Gaussian profile, and a inhomogeneous layer with a linear profile. Bayesian analysis found very strong evidence for the linear transition over the step profile (and very strong evidence for the step profile over the Gaussian), indicative of a small but finite inhomogeneous layer in the loop, and consistent with the separate seismological studies of the same loop by Pascoe et al. (2016b, 2017a). A technique using both the seismological and intensity modeling methods simultaneously to estimate the inhomogeneous layer width of an oscillating coronal loop was produced by Pascoe et al. (2018).
Goddard et al. (2017) performed a statistical study of 233 coronal loops comparing the step, Gaussian, and linear inhomogeneous layer density profiles. For 58% of cases there was strong evidence for the existence of an inhomogeneous layer, and there were no cases of strong evidence against there being an inhomogeneous layer. The inhomogeneous layer widths observed covered the full range of 0 to 2 and had no correlation with the loop radius.
Figure 5 shows the value of inhomogeneous layer width inferred from our numerical simulation using the same method applied to observational data (Goddard et al., 2017; Pascoe et al., 2017b). This is calculated from the numerical data with the EUV intensity approximated as the square of the density integrated along the LOS, which we vary between 0 and 90 degrees relative to the plane of the loop oscillation. The observationally inferred value ϵobs increases with time due to the non-linear evolution of the loop by development of KHI, as in Goddard et al. (2018), and with the LOS angle since the density perturbations associated with this evolution reflect the m = 1 symmetry of the kink mode driving it (see Figure 1).
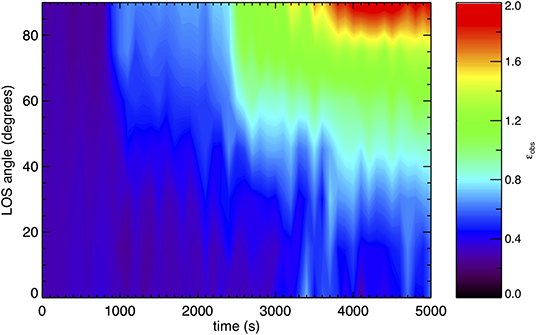
Figure 5. The inhomogeneous layer width based on the transverse intensity profile of the coronal loop in our numerical simulation. Near the start of the simulation the initial value of 0.3 is measured for all LOS angles, but at later times the observed value increases.
Large LOS angles show the strongest variation in ϵobs but would also exhibit the smallest transverse displacements. In such cases, the presence of kink oscillations could therefore be inferred indirectly by the increase of the inhomogeneous layer width in time, and directly using Doppler shift observations. For smaller LOS angles the increase in the inhomogeneous layer width is weaker but the transverse perturbations are larger, corresponding to the scenario for which decayless oscillations are detected by EUV imaging such as SDO/AIA. The estimate of ϵ presented in Figure 2 shows ϵ increasing to approximately 1 by the end of the simulation. This increase corresponds to an LOS angle of approximately 55 degrees in Figure 5. We can therefore expect that studies which consider the evolution of the loop coinciding with detectable oscillations (displacements) in EUV would typically underestimate the evolution which has actually taken place in terms of the evolution of the EUV intensity profile. This is in contrast to the results of the previous section which demonstrate how the seismologically-inferred value of ϵ would typically be an overestimate due to the generation of small scale density perturbations by KHI. Such a discrepancy between seismological and forward modeling estimates could therefore be indicative of non-linear evolution of the loop due to KHI, motivating further study to exclude other potential sources of discrepancy such as the influence of multiple loops along the LOS.
In Figure 6, we present a simple model to use the results of our numerical simulation to interpret an ensemble of observational data for a large number of loops such as the statistical study by Goddard et al. (2017). Those loops were chosen for a study of the transverse density profile with no consideration for oscillation. On the other hand, it has been established that decayless oscillations are ubiquitous in coronal loops (Anfinogentov et al., 2015). We can therefore consider that these loops will have undergone some range of non-linear evolution due to decayless oscillations, and that they also represent a range of LOS angles.
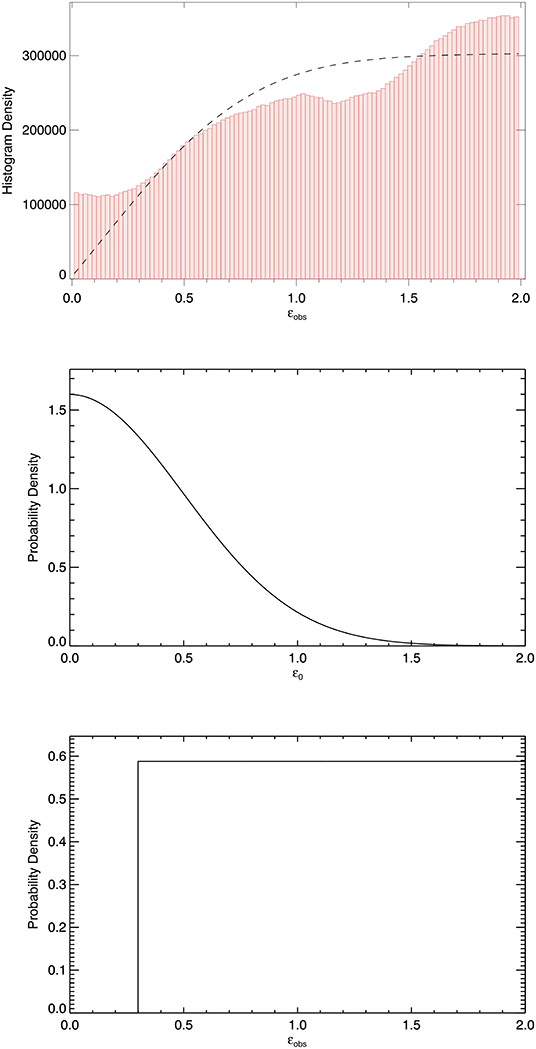
Figure 6. Histogram for the inhomogeneous layer width ϵobs based on observations of 233 coronal loops (top). The dashed line represents a model for the observed distribution of ϵobs based on loops being created with some initial distribution ϵ0 (middle), and ϵobs being some value greater than ϵ0 (shown in bottom panel for the case of ϵ0 = 0.3).
The top panel of Figure 6 shows a histogram of the observed value of the inhomogeneous layer width based on the study by Goddard et al. (2017). We note that in Figure 3 of that paper the values of ϵ correspond to the median value of the posterior probability distribution returned using Bayesian analysis with Markov chain Monte Carlo (MCMC) sampling (Anfinogentov et al., 2020). Here we also wish to consider the uncertainty associated with those values and so sum the full posterior probability distributions for all 233 loops. The study of each loop is based on 105 MCMC samples and the plotted histogram uses 100 bins hence the average histogram density being 233 × 105/100~200, 000.
Our model distribution for ϵobs, shown as the dashed line in the top panel, is the combination of two probability distributions described below. We consider that for a loop with initial inhomogeneous layer ϵ0, the observed value ϵobs may be any value greater than ϵ0 (up to 2 by definition) depending on the amount of non-linear evolution and LOS angle as demonstrated in Figure 5. This is shown in the bottom panel for the example of ϵ = 0.3, with a uniform distribution assumed for simplicity. The middle panel represents the initial distribution of ϵ0. This will be determined by the mechanism which creates coronal loops and is presently unknown. We assume a half-normal distribution with the width of the distribution taken to be a free parameter which we fit by comparing our final model distribution to that from our observational data. The fitted width of approximately 0.5 implies loops are only required to have small initial inhomogeneous layer widths to account for the observed values, assuming the observational results are influenced by non-linear evolution similar to that shown in Figure 5.
The largest difference between the model and observational data is in the limit ϵobs → 0. However, we note that the observational data is based on Bayesian analysis with a posterior probability density broadened to include values of 0 by observational error, whereas there is no consideration of errors in our model. The original statistical study by Goddard et al. (2017) found no cases for which the Bayesian evidence favored the step function density profile which corresponds to ϵ = 0. On the other hand, our assumption of a uniform probability distribution for ϵobs under-represents the expected peak at ϵ0 and especially penalizes the limit of ϵ0 → 0 for which the range ϵ0 ≤ ϵobs ≤ 2 is greatest.
This simple model therefore demonstrates how observational results supporting larger values of inhomogeneous layer width are compatible with loops being generated with initially small values of ϵ under the assumption that the non-linear evolution of loops due to decayless oscillations acts only to increase the observed value of ϵobs. This analysis also demonstrates how future observational studies might provide information about the mechanism by which coronal loops are generated if the probability distribution for ϵ0 could be related to a theoretical model as opposed to our assumption of a half-normal distribution.
4. Conclusions
In this paper we have simulated the non-linear evolution of a coronal loop due to KHI and investigated the effect on the corresponding observational signatures. To facilitate analysis of the results our driver is impulsive which is typically associated with large amplitude decaying kink oscillations. On the other hand, the low amplitude of our driver corresponds to the decayless regime of kink oscillations and the repetitive perturbations may be considered as an approximation of some intermittent driving mechanism, for example, random buffeting of loop footpoints by photospheric motions. However, it is unlikely that decayless oscillations are actually generated in this way since it introduces abrupt changes in the phase of the oscillation which are typically not observed. Our resulting oscillation is decayless over the longer term, as kink mode energy lost by resonant absorption is replaced by subsequent additional perturbations. We find that these low amplitude kink oscillations approximating the decayless regime are capable of generating significant changes in the loop profile which can affect both the seismological and spatial estimates for the inhomogeneous layer width by different amounts. This can potentially be used to infer the presence of non-linear evolution of loop profiles through any disparity in estimates, although care would be required to ensure the direction and magnitude of the disparity is consistent with the physical model and observational conditions. Furthermore, we demonstrate that this effect could account for the observed distribution of inhomogeneous layer widths favoring larger values even if the mechanism by which loops are generated were to favor thin layers. This is similar to the argument by Magyar and Van Doorsselaere (2016b) for the non-existence of multi-stranded coronal loops due to the mixing of plasma by KHI, but with the transverse plasma inhomogeneity being in the form of a boundary layer as opposed to a large number of small structures throughout the loop.
We can use the results of this paper to reconsider the case of a coronal loop which has been previously studied independently using seismological and spatial methods to determine to loop profile, and which exhibited both decayless and decaying kink oscillations. The seismological analysis of the loop, based on the large amplitude decaying oscillation, found an inhomogeneous layer width (Pascoe et al., 2017a) (the density contrast ratio was also estimated to be 3 as used in this paper). The spatial estimate based on forward modeling the transverse intensity profile produced a value of (Pascoe et al., 2017b). The loop was observed from the side, i.e., a LOS angle close to zero (see, e.g., Figure 1 of Pascoe et al., 2016b) and so a minimal increase in the width would be expected by studying the evolution of the intensity profile. The spatial study by Pascoe et al. (2017b) uses the loop intensity profile at the start of the large amplitude oscillation, however decayless oscillations were also detected in the same loop before, during and after the large amplitude oscillation; Nisticò et al. (2013) detected approximately 12 cycles of decayless oscillation before the onset of the large amplitude perturbation, while Pascoe et al. (2017a) estimated the amplitude of the decayless component as approximately 0.14 Mm (compared with a loop radius of approximately 3 Mm).
We can therefore consider two scenarios. Firstly, no KHI took place during the decayless regime, and so the spatial estimate of the inhomogeneous layer width is an accurate representation of the loop structure. Its consistency with the seismological estimate is due to the onset of any KHI arising from the large amplitude decaying oscillation being delayed by at least one cycle. Alternatively, KHI did take place during the decayless oscillations and in time to influence the results obtained for the large amplitude oscillation. The corresponding evolution of the loop profile means that the damping rate and inhomogeneous layer width would be overestimated by the seismological analysis, whereas the inhomogeneous layer width would be underestimated by the spatial analysis which has a very low LOS angle. The consistency of the two estimates for ϵ suggests the first scenario in which there was no KHI arising from the initial decayless stage of the oscillation. A recent study of the evolution of the temporal evolution of loops following large amplitude oscillations (Goddard and Nisticò, 2020) also found no clear evidence of KHI, but all loops analyzed did display changes after the onset of the oscillation. The extent to which this is due to observational issues, rather than genuine evolution of the loops, remains to be determined. That study was also based on DEM analysis which is known to produce overly broad spectra (e.g., Van Doorsselaere et al., 2018; Pascoe et al., 2019b) which may conceal the signatures of KHI.
The disparity between the abundant evidence for KHI in simulations compared to the lack of evidence in loop oscillations therefore remains to be accounted for. For the particular example considered above, the width of the loop being approximately three times larger than in our simulation may account for the apparent much slower evolution, with the non-linearity parameter being the displacement amplitude normalized by the loop radius (e.g., Van Doorsselaere et al., 2020). This reduces the 12 decayless cycles observed by Nisticò et al. (2013) to the equivalent of approximately 4 in our simulation, which is sufficiently early that the non-linear evolution would not influence either the seismological or spatial results, and so they would remain consistent with each other and an accurate representation of the actual loop structure.
Our simulation demonstrates that the development of KHI is associated with an increasing damping rate and decreasing period of oscillation. However, the variation in the period of oscillation is small (approximately 3% during our entire simulation) and likely to be surpassed in observations by additional effects, such as changes in loop length or plasma properties, which can cause larger changes and either increases or decreases (e.g., Ireland and De Moortel, 2002; Nisticò et al., 2013; White et al., 2013; Pascoe et al., 2017c). Recent analysis of standing kink oscillations excited by two solar flares found the later oscillations damped faster than the earlier ones, consistent with KHI, while the period of oscillation increased by approximately 20% during the observation (Pascoe et al., 2020). The insensitivity of the period of oscillation to the transverse loop structure is consistent with the kink oscillation being a collective fast magnetoacoustic mode (e.g., Díaz et al., 2005; Pascoe et al., 2007). Previous studies have demonstrated that the damping of kink oscillations by resonant absorption is also not sensitive to loops being multi-stranded (Terradas et al., 2008b; Pascoe et al., 2011). However, the presence of such structuring is of interest since it can lead to a significant underestimation of the wave energy estimated using Doppler measurements (De Moortel and Pascoe, 2012; Pant et al., 2019) or an overestimation of the broadness of DEM spectra (Van Doorsselaere et al., 2018). Due to LOS integration of optically thin EUV emission it is difficult to interpret fine structure in transverse intensity profiles, particularly when using a single channel as may be the case for coronal loops which are often identifiable only in the 171 channel of SDO/AIA. Observations using higher resolution instruments such as CRisp Imaging Spectro-Polarimeter (CRISP; Antolin et al., 2012; Scullion et al., 2014) and the High-Resolution Coronal Imager (Hi-C; Aschwanden and Peter, 2017; Williams et al., 2020) reveal that loop structuring indeed exists below the resolution of SDO/AIA. Our results demonstrate that the non-linear evolution of the loop profile by KHI produces a time-dependent (increasing) damping rate for kink oscillations that would not be expected for structuring due to loops being multi-stranded. This is due to KHI concentrating the changes to the loop profile in the inhomogeneous layer near the locations where resonant absorption occurs.
More generally, our results demonstrate the need for detailed comparison of non-linear numerical simulations and forward modeled observable signatures (preferably multi-channel) to assist in the interpretation of physical effects such as KHI. The confirmation, or otherwise, of such effects allows additional physical conditions to be revealed, for example the inhibition of KHI due to the presence of magnetic twist (Terradas et al., 2018).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
DP and TV contributed conception and design of the study. CG and DP performed the observational data analysis. DP wrote the first draft of the manuscript and received input from all co-authors.
Funding
DP and TV were supported by the GOA-2015-014 (KU Leuven) and the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. 724326).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnotes
References
Afanasyev, A., Karampelas, K., and Van Doorsselaere, T. (2019). Coronal loop transverse oscillations excited by different driver frequencies. Astrophys. J. 876:100. doi: 10.3847/1538-4357/ab1848
Afanasyev, A. N., Van Doorsselaere, T., and Nakariakov, V. M. (2020). Excitation of decay-less transverse oscillations of coronal loops by random motions. Astron. Astrophys. 633:L8. doi: 10.1051/0004-6361/201937187
Andries, J., Arregui, I., and Goossens, M. (2005). Determination of the coronal density stratification from the observation of harmonic coronal loop oscillations. Astrophys. J. Lett. 624, L57–L60. doi: 10.1086/430347
Anfinogentov, S., Nisticò, G., and Nakariakov, V. M. (2013). Decay-less kink oscillations in coronal loops. Astron. Astrophys. 560:A107. doi: 10.1051/0004-6361/201322094
Anfinogentov, S. A., Nakariakov, V. M., and Nisticò, G. (2015). Decayless low-amplitude kink oscillations: a common phenomenon in the solar corona? Astron. Astrophys. 583:A136. doi: 10.1051/0004-6361/201526195
Anfinogentov, S. A., Nakariakov, V. M., Pascoe, D. J., and Goddard, C. R. (2020). Solar Bayesian Analysis Toolkit – a new Markov chain Monte Carlo IDL code for Bayesian parameter inference. arXiv Preprints arXiv:2005.05365. Available online at: https://ui.adsabs.harvard.edu/abs/2020arXiv200505365A
Antolin, P., De Moortel, I., Van Doorsselaere, T., and Yokoyama, T. (2016). Modeling observed decay-less oscillations as resonantly enhanced kelvin-helmholtz vortices from transverse MHD waves and their seismological application. Astrophys. J. Lett. 830:L22. doi: 10.3847/2041-8205/830/2/L22
Antolin, P., De Moortel, I., Van Doorsselaere, T., and Yokoyama, T. (2017). Observational signatures of transverse magnetohydrodynamic waves and associated dynamic instabilities in coronal flux tubes. Astrophys. J. 836:219. doi: 10.3847/1538-4357/aa5eb2
Antolin, P., Vissers, G., and Rouppe van der Voort, L. (2012). On-Disk Coronal Rain. Solar Phys. 280, 457–474. doi: 10.1007/s11207-012-9979-7
Antolin, P., Yokoyama, T., and Van Doorsselaere, T. (2014). Fine strand-like structure in the solar corona from magnetohydrodynamic transverse oscillations. Astrophys. J. Lett. 787:L22. doi: 10.1088/2041-8205/787/2/L22
Arber, T., Longbottom, A., Gerrard, C., and Milne, A. (2001). A staggered grid, Lagrangian-Eulerian remap code for 3-d MHD simulations. J. Comput. Phys. 171, 151–181. doi: 10.1006/jcph.2001.6780
Arregui, I., Andries, J., Van Doorsselaere, T., Goossens, M., and Poedts, S. (2007). MHD seismology of coronal loops using the period and damping of quasi-mode kink oscillations. Astron. Astrophys. 463, 333–338. doi: 10.1051/0004-6361:20065863
Arregui, I., Asensio Ramos, A., and Diaz, A. J. (2013). Bayesian analysis of multiple harmonic oscillations in the solar corona. Astrophys. J. Lett. 765:L23. doi: 10.1088/2041-8205/765/1/L23
Arregui, I., Van Doorsselaere, T., Andries, J., Goossens, M., and Kimpe, D. (2005). Resonantly damped fast MHD kink modes in longitudinally stratified tubes with thick non-uniform transitional layers. Astron. Astrophys. 441, 361–370. doi: 10.1051/0004-6361:20053039
Aschwanden, M. J., Fletcher, L., Schrijver, C. J., and Alexander, D. (1999). Coronal loop oscillations observed with the transition region and coronal explorer. Astrophys. J. 520, 880–894. doi: 10.1086/307502
Aschwanden, M. J., and Nightingale, R. W. (2005). Elementary loop structures in the solar corona analyzed from TRACE triple-filter images. Astrophys. J. 633, 499–517. doi: 10.1086/452630
Aschwanden, M. J., Nightingale, R. W., Andries, J., Goossens, M., and Van Doorsselaere, T. (2003). Observational tests of damping by resonant absorption in coronal loop oscillations. Astrophys. J. 598, 1375–1386. doi: 10.1086/379104
Aschwanden, M. J., Nightingale, R. W., and Boerner, P. (2007). A statistical model of the inhomogeneous corona constrained by triple-filter measurements of elementary loop strands with TRACE. Astrophys. J. 656, 577–597. doi: 10.1086/510232
Aschwanden, M. J., and Peter, H. (2017). The width distribution of loops and strands in the solar corona–are we hitting rock bottom? Astrophys. J., 840:4. doi: 10.3847/1538-4357/aa6b01
Aschwanden, M. J., and Terradas, J. (2008). The effect of radiative cooling on coronal loop oscillations. Astrophys. J. Lett. 686:L127. doi: 10.1086/592963
Barbulescu, M., Ruderman, M. S., Van Doorsselaere, T., and Erdélyi, R. (2019). An analytical model of the Kelvin-Helmholtz instability of transverse coronal loop oscillations. Astrophys. J. 870:108. doi: 10.3847/1538-4357/aaf506
Browning, P. K., and Priest, E. R. (1984). Kelvin-Helmholtz instability of a phased-mixed Alfven wave. Astron. Astrophys. 131, 283–290.
De Moortel, I., and Brady, C. S. (2007). Observation of higher harmonic coronal loop oscillations. Astrophys. J. 664, 1210–1213. doi: 10.1086/518830
De Moortel, I., Hood, A. W., and Ireland, J. (2002). Coronal seismology through wavelet analysis. Astron. Astrophys. 381, 311–323. doi: 10.1051/0004-6361:20011659
De Moortel, I., and Pascoe, D. J. (2012). The effects of line-of-sight integration on multistrand coronal loop oscillations. Astrophys. J. 746:31. doi: 10.1088/0004-637X/746/1/31
De Moortel, I., Pascoe, D. J., Wright, A. N., and Hood, A. W. (2016). Transverse, propagating velocity perturbations in solar coronal loops. Plasma Phys. Controlled Fusion 58:014001. doi: 10.1088/0741-3335/58/1/014001
Díaz, A. J., Oliver, R., and Ballester, J. L. (2005). Fast magnetohydrodynamic oscillations in a multifibril Cartesian prominence model. Astron. Astrophys. 440, 1167–1175. doi: 10.1051/0004-6361:20052759
Duckenfield, T., Anfinogentov, S. A., Pascoe, D. J., and Nakariakov, V. M. (2018). Detection of the second harmonic of decay-less kink oscillations in the solar corona. Astrophys. J. Lett. 854:L5. doi: 10.3847/2041-8213/aaaaeb
Duckenfield, T. J., Goddard, C. R., Pascoe, D. J., and Nakariakov, V. M. (2019). Observational signatures of the third harmonic in a decaying kink oscillation of a coronal loop. Astron. Astrophys. 632:A64. doi: 10.1051/0004-6361/201936822
Dymova, M. V., and Ruderman, M. S. (2006). Resonantly damped oscillations of longitudinally stratified coronal loops. Astron. Astrophys. 457, 1059–1070. doi: 10.1051/0004-6361:20065051
Goddard, C. R., Antolin, P., and Pascoe, D. J. (2018). Evolution of the transverse density structure of oscillating coronal loops inferred by forward modeling of EUV intensity. Astrophys. J. 863:167. doi: 10.3847/1538-4357/aad3cc
Goddard, C. R., and Nisticò, G. (2020). Temporal evolution of oscillating coronal loops. Astron. Astrophys. 638:A89. doi: 10.1051/0004-6361/202037467
Goddard, C. R., Nisticò, G., Nakariakov, V. M., and Zimovets, I. V. (2016). A statistical study of decaying kink oscillations detected using SDO/AIA. Astron. Astrophys. 585:A137. doi: 10.1051/0004-6361/201527341
Goddard, C. R., Pascoe, D. J., Anfinogentov, S., and Nakariakov, V. M. (2017). A statistical study of the inferred transverse density profile of coronal loop threads observed with SDO/AIA. Astron. Astrophys. 605:A65. doi: 10.1051/0004-6361/201731023
Goossens, M., Andries, J., and Aschwanden, M. J. (2002). Coronal loop oscillations. An interpretation in terms of resonant absorption of quasi-mode kink oscillations. Astron. Astrophys. 394:L39–L42. doi: 10.1051/0004-6361:20021378
Goossens, M., Soler, R., Arregui, I., and Terradas, J. (2012). Analytic approximate seismology of propagating magnetohydrodynamic waves in the solar corona. Astrophys. J. 760:98. doi: 10.1088/0004-637X/760/2/98
Handy, B. N., Acton, L. W., Kankelborg, C. C., Wolfson, C. J., Akin, D. J., Bruner, M. E., et al. (1999). The transition region and coronal explorer. Solar Phys. 187, 229–260. doi: 10.1023/A:1005166902804
Heyvaerts, J., and Priest, E. R. (1983). Coronal heating by phase-mixed shear Alfven waves. Astron. Astrophys. 117, 220–234.
Hillier, A., and Arregui, I. (2019). Coronal cooling as a result of mixing by the nonlinear Kelvin-Helmholtz instability. Astrophys. J. 885:101. doi: 10.3847/1538-4357/ab4795
Hood, A. W., Ruderman, M., Pascoe, D. J., De Moortel, I., Terradas, J., and Wright, A. N. (2013). Damping of kink waves by mode coupling. I. Analytical treatment. Astron. Astrophys. 551:A39. doi: 10.1051/0004-6361/201220617
Ireland, J., and De Moortel, I. (2002). Application of wavelet analysis to transversal coronal loop oscillations. Astron. Astrophys. 391, 339–351. doi: 10.1051/0004-6361:20020643
Karampelas, K., and Doorsselaere, T. V. (2020). Generating transverse loop oscillations through a steady-flow driver. Astrophys. J. 897:L35. doi: 10.3847/2041-8213/ab9f38
Karampelas, K., and Van Doorsselaere, T. (2018). Simulations of fully deformed oscillating flux tubes. Astron. Astrophys. 610:L9. doi: 10.1051/0004-6361/201731646
Karampelas, K., Van Doorsselaere, T., Pascoe, D. J., Guo, M., and Antolin, P. (2019). Amplitudes and energy fluxes of simulated decayless kink oscillations. Front. Astron. Space Sci. 6:38. doi: 10.3389/fspas.2019.00038
Lemen, J. R., Title, A. M., Akin, D. J., Boerner, P. F., Chou, C., Drake, J. F., et al. (2012). The atmospheric imaging assembly (AIA) on the solar dynamics observatory (SDO). Solar Phys. 275, 17–40. doi: 10.1007/978-1-4614-3673-7_3
Magyar, N., and Van Doorsselaere, T. (2016a). Damping of nonlinear standing kink oscillations: a numerical study. Astron. Astrophys. 595:A81. doi: 10.1051/0004-6361/201629010
Magyar, N., and Van Doorsselaere, T. (2016b). The instability and non-existence of multi-stranded loops when driven by transverse waves. Astrophys. J. 823:82. doi: 10.3847/0004-637X/823/2/82
Magyar, N., Van Doorsselaere, T., and Marcu, A. (2015). Numerical simulations of transverse oscillations in radiatively cooling coronal loops. Astron. Astrophys. 582:A117. doi: 10.1051/0004-6361/201526287
McEwan, M. P., Donnelly, G. R., Díaz, A. J., and Roberts, B. (2006). On the period ratio P1/2P2 in the oscillations of coronal loops. Astron. Astrophys. 460, 893–899. doi: 10.1051/0004-6361:20065313
Morton, R. J., and Mooroogen, K. (2016). Model fitting of kink waves in the solar atmosphere: Gaussian damping and time-dependence. Astron. Astrophys. 593:A59. doi: 10.1051/0004-6361/201628613
Nakariakov, V. M., Anfinogentov, S. A., Nisticò, G., and Lee, D.-H. (2016). Undamped transverse oscillations of coronal loops as a self-oscillatory process. Astron. Astrophys. 591:L5. doi: 10.1051/0004-6361/201628850
Nakariakov, V. M., Ofman, L., Deluca, E. E., Roberts, B., and Davila, J. M. (1999). TRACE observation of damped coronal loop oscillations: implications for coronal heating. Science 285, 862–864. doi: 10.1126/science.285.5429.862
Nechaeva, A., Zimovets, I. V., Nakariakov, V. M., and Goddard, C. R. (2019). Catalog of decaying kink oscillations of coronal loops in the 24th solar cycle. Astrophys. J. Suppl. Ser. 241:31. doi: 10.3847/1538-4365/ab0e86
Nisticò, G., Nakariakov, V. M., and Verwichte, E. (2013). Decaying and decayless transverse oscillations of a coronal loop. Astron. Astrophys. 552:A57. doi: 10.1051/0004-6361/201220676
Ofman, L., Davila, J. M., and Steinolfson, R. S. (1994). Nonlinear studies of coronal heating by the resonant absorption of Alfvén waves. Geophys. Res. Lett. 21, 2259–2262. doi: 10.1029/94GL01416
Pagano, P., and De Moortel, I. (2017). Contribution of mode-coupling and phase-mixing of Alfvén waves to coronal heating. Astron. Astrophys. 601:A107. doi: 10.1051/0004-6361/201630059
Pagano, P., Pascoe, D. J., and De Moortel, I. (2018). Contribution of phase-mixing of Alfvén waves to coronal heating in multi-harmonic loop oscillations. Astron. Astrophys. 616:A125. doi: 10.1051/0004-6361/201732251
Pant, V., Magyar, N., Van Doorsselaere, T., and Morton, R. J. (2019). Investigating “dark” energy in the solar corona using forward modeling of MHD waves. Astrophys. J. 881:95. doi: 10.3847/1538-4357/ab2da3
Pascoe, D. J., Anfinogentov, S., Nisticò, G., Goddard, C. R., and Nakariakov, V. M. (2017a). Coronal loop seismology using damping of standing kink oscillations by mode coupling. II. additional physical effects and Bayesian analysis. Astron. Astrophys. 600:A78. doi: 10.1051/0004-6361/201629702
Pascoe, D. J., Anfinogentov, S. A., Goddard, C. R., and Nakariakov, V. M. (2018). Spatiotemporal analysis of coronal loops using seismology of damped kink oscillations and forward modeling of EUV intensity profiles. Astrophys. J. 860:31. doi: 10.3847/1538-4357/aac2bc
Pascoe, D. J., Goddard, C. R., Anfinogentov, S., and Nakariakov, V. M. (2017b). Coronal loop density profile estimated by forward modelling of EUV intensity. Astron. Astrophys. 600:L7. doi: 10.1051/0004-6361/201730458
Pascoe, D. J., Goddard, C. R., and Nakariakov, V. M. (2016a). Spatially resolved observation of the fundamental and second harmonic standing kink modes using SDO/AIA. Astron. Astrophys. 593:A53. doi: 10.1051/0004-6361/201628784
Pascoe, D. J., Goddard, C. R., Nisticò, G., Anfinogentov, S., and Nakariakov, V. M. (2016b). Coronal loop seismology using damping of standing kink oscillations by mode coupling. Astron. Astrophys. 589:A136. doi: 10.1051/0004-6361/201628255
Pascoe, D. J., Goddard, C. R., Nisticò, G., Anfinogentov, S., and Nakariakov, V. M. (2016c). Damping profile of standing kink oscillations observed by SDO/AIA. Astron. Astrophys. 585:L6. doi: 10.1051/0004-6361/201527835
Pascoe, D. J., Hood, A. W., de Moortel, I., and Wright, A. N. (2012). Spatial damping of propagating kink waves due to mode coupling. Astron. Astrophys. 539:A37. doi: 10.1051/0004-6361/201117979
Pascoe, D. J., Hood, A. W., De Moortel, I., and Wright, A. N. (2013). Damping of kink waves by mode coupling. II. Parametric study and seismology. Astron. Astrophys. 551:A40. doi: 10.1051/0004-6361/201220620
Pascoe, D. J., Hood, A. W., and Van Doorsselaere, T. (2019a). Coronal loop seismology using standing kink oscillations with a lookup table. Front. Astron. Space Sci. 6:22. doi: 10.3389/fspas.2019.00022
Pascoe, D. J., and Nakariakov, V. M. (2016). Standing sausage modes in curved coronal slabs. Astron. Astrophys. 593:A52. doi: 10.1051/0004-6361/201526546
Pascoe, D. J., Nakariakov, V. M., and Arber, T. D. (2007). Sausage oscillations in multishell coronal structures. Solar Phys. 246, 165–175. doi: 10.1007/s11207-007-9055-x
Pascoe, D. J., Nakariakov, V. M., Arber, T. D., and Murawski, K. (2009). Sausage oscillations in loops with a non-uniform cross-section. Astron. Astrophys. 494, 1119–1125. doi: 10.1051/0004-6361:200810541
Pascoe, D. J., Russell, A. J. B., Anfinogentov, S. A., Simões, P. J. A., Goddard, C. R., Nakariakov, V. M., et al. (2017c). Seismology of contracting and expanding coronal loops using damping of kink oscillations by mode coupling. Astron. Astrophys. 607:A8. doi: 10.1051/0004-6361/201730915
Pascoe, D. J., Smyrli, A., and Van Doorsselaere, T. (2019b). Coronal density and temperature profiles calculated by forward modeling EUV emission observed by SDO/AIA. Astrophys. J. 884:43. doi: 10.3847/1538-4357/ab3e39
Pascoe, D. J., Smyrli, A., and Van Doorsselaere, T. (2020). Tracking and seismological analysis of multiple coronal loops in an active region. Astrophys. J. 898:126. doi: 10.3847/1538-4357/aba0a6
Pascoe, D. J., Wright, A. N., and De Moortel, I. (2010). Coupled Alfvén and Kink oscillations in coronal loops. Astrophys. J. 711, 990–996. doi: 10.1088/0004-637X/711/2/990
Pascoe, D. J., Wright, A. N., and De Moortel, I. (2011). Propagating coupled Alfvén and Kink oscillations in an arbitrary inhomogeneous corona. Astrophys. J., 731:73. doi: 10.1088/0004-637X/731/1/73
Pascoe, D. J., Wright, A. N., De Moortel, I., and Hood, A. W. (2015). Excitation and damping of broadband kink waves in the solar corona. Astron. Astrophys. 578:A99. doi: 10.1051/0004-6361/201321328
Ruderman, M. S., and Roberts, B. (2002). The damping of coronal loop oscillations. Astrophys. J. 577, 475–486. doi: 10.1086/342130
Ruderman, M. S., Shukhobodskaya, D., and Shukhobodskiy, A. A. (2019). Resonant damping of propagating kink waves in non-stationary, longitudinally stratified, and expanding solar waveguides. Front. Astron. Space Sci. 6:10. doi: 10.3389/fspas.2019.00010
Ruderman, M. S., and Terradas, J. (2013). Damping of coronal loop kink oscillations due to mode conversion. Astron. Astrophys. 555:A27. doi: 10.1051/0004-6361/201220195
Safari, H., Nasiri, S., and Sobouti, Y. (2007). Fast kink modes of longitudinally stratified coronal loops. Astron. Astrophys. 470, 1111–1116. doi: 10.1051/0004-6361:20065997
Scullion, E., Rouppe van der Voort, L., Wedemeyer, S., and Antolin, P. (2014). Unresolved fine-scale structure in solar coronal loop-tops. Astrophys. J. 797:36. doi: 10.1088/0004-637X/797/1/36
Soler, R., Goossens, M., Terradas, J., and Oliver, R. (2013). The behavior of transverse waves in nonuniform solar flux tubes. I. Comparison of ideal and resistive results. Astrophys. J. 777:158. doi: 10.1088/0004-637X/777/2/158
Soler, R., Goossens, M., Terradas, J., and Oliver, R. (2014). The behavior of transverse waves in nonuniform solar flux tubes. II. Implications for coronal loop seismology. Astrophys. J. 781:111. doi: 10.1088/0004-637X/781/2/111
Soler, R., Terradas, J., Oliver, R., Ballester, J. L., and Goossens, M. (2010). Kelvin-Helmholtz instability in coronal magnetic flux tubes due to azimuthal shear flows. Astrophys. J. 712, 875–882. doi: 10.1088/0004-637X/712/2/875
Terradas, J., Andries, J., Goossens, M., Arregui, I., Oliver, R., and Ballester, J. L. (2008a). Nonlinear instability of kink oscillations due to shear motions. Astrophys. J. Lett. 687:L115. doi: 10.1086/593203
Terradas, J., Arregui, I., Oliver, R., Ballester, J. L., Andries, J., and Goossens, M. (2008b). Resonant absorption in complicated plasma configurations: applications to multistranded coronal loop oscillations. Astrophys. J. 679, 1611–1620. doi: 10.1086/586733
Terradas, J., Magyar, N., and Van Doorsselaere, T. (2018). Effect of magnetic twist on nonlinear transverse Kink oscillations of line-tied magnetic flux tubes. Astrophys. J. 853:35. doi: 10.3847/1538-4357/aa9d0f
Tomczyk, S., and McIntosh, S. W. (2009). Time-distance seismology of the solar corona with CoMP. Astrophys. J. 697, 1384–1391. doi: 10.1088/0004-637X/697/2/1384
Tomczyk, S., McIntosh, S. W., Keil, S. L., Judge, P. G., Schad, T., Seeley, D. H., et al. (2007). Alfvén waves in the solar corona. Science 317:1192. doi: 10.1126/science.1143304
Torrence, C., and Compo, G. P. (1998). A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 79, 61–78.
Van Doorsselaere, T., Andries, J., Poedts, S., and Goossens, M. (2004). Damping of coronal loop oscillations: calculation of resonantly damped Kink oscillations of one-dimensional nonuniform loops. Astrophys. J. 606, 1223–1232. doi: 10.1086/383191
Van Doorsselaere, T., Antolin, P., and Karampelas, K. (2018). Broadening of the differential emission measure by multi-shelled and turbulent loops. Astron. Astrophys. 620:A65. doi: 10.1051/0004-6361/201834086
Van Doorsselaere, T., Antolin, P., Yuan, D., Reznikova, V., and Magyar, N. (2016). Forward modelling of optically thin coronal plasma with the FoMo tool. Front. Astron. Space Sci. 3:4. doi: 10.3389/fspas.2016.00004
Van Doorsselaere, T., Li, B., Goossens, M., Hnat, B., and Magyar, N. (2020). Wave pressure and energy cascade rate of kink waves computed with Elsässer variables. Astrophys. J. 899:100. doi: 10.3847/1538-4357/aba0b8
Van Doorsselaere, T., Nakariakov, V. M., and Verwichte, E. (2007). Coronal loop seismology using multiple transverse loop oscillation harmonics. Astron. Astrophys. 473, 959–966. doi: 10.1051/0004-6361:20077783
Verth, G., and Erdélyi, R. (2008). Effect of longitudinal magnetic and density inhomogeneity on transversal coronal loop oscillations. Astron. Astrophys. 486, 1015–1022. doi: 10.1051/0004-6361:200809626
Verth, G., Terradas, J., and Goossens, M. (2010). Observational evidence of resonantly damped propagating Kink waves in the solar corona. Astrophys. J. Lett. 718:L102–L105. doi: 10.1088/2041-8205/718/2/L102
Verwichte, E., Nakariakov, V. M., Ofman, L., and Deluca, E. E. (2004). Characteristics of transverse oscillations in a coronal loop arcade. Solar Phys. 223, 77–94. doi: 10.1007/s11207-004-0807-6
Wang, T., Ofman, L., Davila, J. M., and Su, Y. (2012). Growing transverse oscillations of a multistranded loop observed by SDO/AIA. Astrophys. J. Lett. 751:L27. doi: 10.1088/2041-8205/751/2/L27
White, R. S., Verwichte, E., and Foullon, C. (2013). Anti-phase signature of flare generated transverse loop oscillations. Astrophys. J. 774:104. doi: 10.1088/0004-637X/774/2/104
Keywords: magnetohydrodynamics (MHD), sun - corona, sun - magnetic fields, sun - oscillations, waves and instabilities
Citation: Pascoe DJ, Goddard CR and Van Doorsselaere T (2020) Oscillation and Evolution of Coronal Loops in a Dynamical Solar Corona. Front. Astron. Space Sci. 7:61. doi: 10.3389/fspas.2020.00061
Received: 05 June 2020; Accepted: 03 August 2020;
Published: 09 September 2020.
Edited by:
Yihua Yan, National Astronomical Observatories (CAS), ChinaReviewed by:
Jose Luis Ballester, University of the Balearic Islands, SpainPetra Kohutova, University of Oslo, Norway
Copyright © 2020 Pascoe, Goddard and Van Doorsselaere. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: David J. Pascoe, ZGF2aWQucGFzY29lQGt1bGV1dmVuLmJl
 David J. Pascoe
David J. Pascoe Christopher R. Goddard2
Christopher R. Goddard2 Tom Van Doorsselaere
Tom Van Doorsselaere