Improvement of Plasma Sheet Neural Network Accuracy With Inclusion of Physical Information

The near-Earth plasma sheet is the source for electrons in the inner magnetosphere. The coupling between the solar wind and the near-Earth plasma sheet is dominated by non-linear processes, making any relationship difficult to infer. We report on the development of a neural network to capture the non-linear behavior between solar wind variations and the response of energetic electron flux in the plasma sheet. To train the neural network algorithm, we developed a data set with inputs from solar wind monitoring spacecraft. The targets come from three probes of the Time History of Events and Macroscale Interactions during Substorms mission as the spacecraft traversed the plasma sheet from years 2008–2019. Preliminary findings during the development of the neural network model show that tuning input parameters based on previously known physical properties is conducive to improving model performance.

1. Introduction

The fluxes of <200 keV electrons in the Earth's inner magnetosphere constitute the seed population, which is critically important for radiation belt dynamics. It is through cyclotron resonance with the electrons of energies between a few and tens of keV (Kennel and Petschek, 1966; Kennel and Thorne, 1967; Li et al., 2008, 2012) that chorus waves are generated outside the plasmapause in association with the injection of Plasma Sheet (PS) electrons into the inner magnetosphere (Tsurutani and Smith, 1974; Meredith et al., 2002). Whistler mode chorus waves play an important role in accelerating the seed electron population to relativistic energies in the outer radiation belt (Horne et al., 2005; Chen et al., 2007). Moreover, low-energy electrons (electrons with energies less than about 100 keV) are responsible for hazardous space weather phenomena such as surface charging (Garrett, 1981; Davis et al., 2008). The electron flux of low energies varies significantly with geomagnetic activity and even during quiet time periods. The source of the low-energy electrons is the PS. Much of the behavior of the PS is driven by variations in the solar wind (SW) and interplanetary magnetic field (IMF) upstream of Earth's bow shock (e.g., Aubry and McPherron, 1971; Nishida and Lyon, 1972; Tsutomu and Teruki, 1976; Terasawa et al., 1997; Wing et al., 2005; Nagata et al., 2008; Cao et al., 2013). It is therefore an important challenge to understand the distribution of energetic plasma entering the inner magnetosphere, as dependent upon SW driving.

Several studies have examined the link between SW variations and PS particles. For example, Borovsky et al. (1998) found that there are several PS properties that are highly correlated with upstream SW. Namely, the density, temperature, and total pressure of the PS are highly correlated with density, velocity, and dynamic pressure of the SW, respectively. Tsyganenko and Mukai (2003) used Geotail and Advance Composition Explorer (ACE) (Stone et al., 1998) data to develop an empirical model for PS ions dependent upon SW driving. Luo et al. (2011) additionally used Geotail and ACE to investigate the PS electron population with an empirical model for electron fluxes with energy >38 keV. Their model achieved good performance compared to observations; yet, it had limitations. Not being able to measure below 38 keV and using integrated flux made it impossible to accurately describe the behavior of electrons with lower energy. More recently, Dubyagin et al. (2019) estimated PS differential electron fluxes from Maxwellian and Kappa distribution functions derived from plasma moments obtained using an empirical model developed by Dubyagin et al. (2016). They found that for thermal and superthermal energies (≲1 keV) the estimations are accurate within a factor of two. Yet, for higher energy (≥10 keV), the estimates of electron flux diverge by more than an order of magnitude from observations. They suggest that to obtain a realistic representation of PS electrons at these energies, a flux based model should be developed.

Considering the limitations of previous empirical relationships to model plasma sheet properties from SW, an alternative method is to utilize machine learning (ML). ML is viable in the present era, yet there are challenges regarding the utility of using so-called “black- or gray-box” ML techniques. (e.g., Camporeale, 2019). We have a sufficiently large amount of observations (more than two 11-year solar cycles) of the SW and PS, and we have the necessary modern computational resources to process this amount of data. Bortnik et al. (2016) described a ML method to predict the value of some observable in the inner magnetosphere dependent upon a set of inputs and their time history. Using the methodology described by Bortnik et al. (2016), Chu et al. (2017) developed a neural network model of electron density in the inner magnetosphere with inputs of spacecraft location and time history of several geomagnetic indices. In a similar study, Zhelavskaya et al. (2017) used geomagnetic indices but included SW parameters as inputs to neural networks. They found their neural networks that included a combination of SW parameters and geomagnetic indices performed the best. Yue et al. (2015) used Support Vector Regression ML to develop an inner PS pressure model, during substorm growth phases only, based on inputs of SW dynamic pressure, sunspot number, Cross Polar Cap Potential, and the Auroral Electrojet Index. Their ML model was able to predict the observed pressure in the near-Earth PS during the substorm growth phase. In the present work, we used ML to develop an electron flux-based empirical model of the near-Earth PS during all times, using only the time history of upstream SW plasma and IMF parameters. The purpose of this brief report is to (1) establish that a machine learned model can, with some skill, predict the electron flux in the PS from SW input drivers only, and (2) demonstrate that using large amounts of data in a machine learning model is not as useful as using a limited dataset while applying established physical knowledge as inputs.

2. Methods

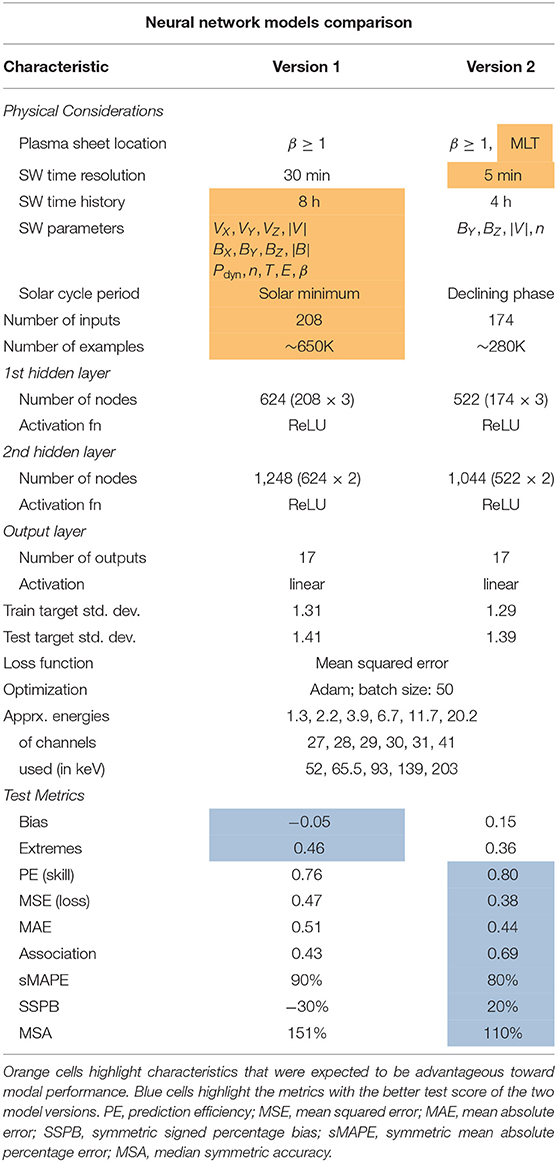
We used a feed-forward neural network (NN) to investigate the response of 1–200 keV energy electrons in the near-Earth PS to variations in the SW upstream of Earth's bow shock. There are two versions of a NN, which we label as Version 1 and Version 2, that we will describe. In both versions, there is an input layer, two hidden layers, and an output layer. The differences in both versions involve the number and types of inputs, the number of nodes in each hidden layer, and the amount of underlying physical information included as input.

2.1. Data Description

The data that were used in this study come from OMNI (King and Papitashvili, 2005) and Time History of Events and Macroscale Interactions during Substorms (THEMIS) (Angelopoulos, 2008). OMNI combines upstream SW measurements and calculated derivations for several plasma parameters. Measurements from multiple Lagrange L₁ spacecraft have been combined and propagated to the assumed Earth's bow shock at approximately 15 Earth radii (RE). An advantage of OMNI data, rather than data directly from the source spacecraft, is its continuity over several decades and multiple spacecraft. Each THEMIS satellite carries an Electrostatic Analyzer (ESA) (McFadden et al., 2008) and Solid State Telescope (SST) (Angelopoulos et al., 2008), which combined measure electrons in the energy range from a few eV to a few MeV. All OMNI and THEMIS data were obtained via the NASA Goddard Space Physics Data Facility.

2.1.1. Version 1 Target Data

The target data are PS electron flux of energies between approximately 1–200 keV. The THEMIS Science Team has combined measurements from the ESA and SST instruments into a single data product called GMOM (Ground combined MoMents). Altogether, there are 46 energy channels in the GMOM data set ranging from about 5 eV to ~300 keV. We chose 17 energy channels of electron flux between 1 and 200 keV because this energy range is most correlated with the generation of chorus waves and with spacecraft surface charging. The approximate energy of each channel is shown in Table 1. The log₁₀ of the energetic flux values make up the target vector, $\overrightarrow{y}$ (Equation 1a), which has 17 entries, one for each energy channel. Although there are several methods for filtering spacecraft observations to the PS (e.g., Roziers et al., 2009; Dubyagin et al., 2016), we adopt the method used by Ruan et al. (2005) that uses only a single criterion of plasma β ≥ 1. The β ≥ 1 criterion follows from average properties of the central PS described by Baumjohann et al. (1989).

TABLE 1

Table 1. Comparison of architecture and test metrics for Version 1 and Version 2 neural networks.

All of the data that we use for training the neural networks are from three probes, THEMIS-A, -D, and -E. The spacecraft have a nominal spin rate of 3 s, and thus have flux data with nominal time cadence of the same. However, electron flux enhancements resulting from magnetotail processes occur on minute time scales (e.g., Bame et al., 1967). We down-sampled the GMOM flux data to 1 min by taking the mean of intervals closed on the left and open on the right. From all observations marked by the THEMIS mission team with a good data quality flag from 1 February 2008 through 31 July 2019, we selected those that occurred when the spacecraft were between −9R_E ≥ XY_GSM ≥ −11R_E, had a measured plasma β ≥ 1, and were on the night side [between magnetic local times (MLTs) 18-06]. The spatial region chosen does not relate to any static structure in the magnetosphere. Rather, we presume that varying characteristics in the PS at these locations will be captured by the model since they are dependent upon SW driving. Combining observations that fit these criteria from all three spacecraft yielded around 830,000 one-minute observations. Note that not all of these were used in training due to missing data in the input data set, which is described next.

2.1.2. Version 1 Input Data

The inputs to the Version 1 NN are OMNI data from −0.5 to −8 h of each event identified in the target data set. Following evidence that the magnetosphere acts as a low-pass filter of the SW (Ilie et al., 2010), we used 30-min averaged OMNI data. Creating the input vector for each event is shown in Equations (1b) and (1c). We assumed a time delay of τ = 30 min to account for the time that it would take variations in the upstream SW to have an effect in the magnetotail. Thirteen OMNI parameters were used: SW proton number density, three velocity components and flow speed as well as IMF geocentric magnetic B_X, B_Y, B_Z, and |B|. Derived parameters included are SW proton temperature, electric field, dynamic pressure, and plasma beta. A full investigation quantifying the importance of these SW input drivers to PS electron flux is underway, however, such an investigation is beyond the scope of this brief report. As a preconditioning step, the values of each OMNI parameter were scaled to the range [−1, 1] by dividing all observations by the observed absolute maximum value between 2008 and 2019 for that particular parameter. With inclusion of these parameters and their time history, each input vector had 208 features. For each input vector ${\overrightarrow{x}}_i$, if there were any missing data, that input vector and its associated 1-min output vector ${\overrightarrow{y}}_i$ were discarded from the database. Approximately 26% of training examples were removed due to missing data, reducing the total number from about 830,000 to 613,952. We intentionally did not randomize our training and testing sets due to the time series nature of the observations in the PS. Rather, we selected February 2008 to February 2018 as the training data and March 2018 to July 2019 as the test data.

$\begin{array}{ll}{\overrightarrow{y}}_i={log}_{10}\left[{\text{eflux}}_1,\dots ,{\text{eflux}}_{17}\right]& (\mathrm{1a})\end{array}$

$\begin{array}{ll}\xi =\left[B_X,B_Y,B_Z,|B|,V_X,V_Y,V_Z,|V|,E,n,T,P_{\text{dyn}},\beta \right]& (\mathrm{1b})\end{array}$

$\begin{array}{ll}{\overrightarrow{x}}_i=\left[{\bar{\xi }}_{t_{y_i}-\tau },{\bar{\xi }}_{t_{y_i}-\tau -\Delta t},\dots ,{\bar{\xi }}_{t_{y_i}-\Delta T}\right]& (\mathrm{1c})\end{array}$

In Equations (1b) and (1c), $\bar{\xi }$ is the 30-min averaged ξ, τ = 30min is a time delay, t_yi is observation time of ${\overrightarrow{y}}_i$, Δt = 30min, and ΔT = 8h.

2.1.3. Version 2 Training Data

Based on physical understanding of the behavior of PS electrons to SW driving, we made changes to the input dataset. The Version 1 NN uses 30-min averaged OMNI data. However, 1–200 keV energy electron flux in the near-Earth PS can vary on timescales of minutes. By averaging out the smaller scale variations using the 30-min averaged SW, we had neglected to include information that could potentially increase the accuracy of the training. Moreover, many previous studies (e.g., Newell et al., 2007), have identified SW and IMF parameters that tend to influence the response of the magnetosphere, typically in some functional form. These studies have shown the most import contribution to magnetosphere response to be a combination of n, V, B_Y, and B_Z (e.g., Newell et al., 2007; Balikhin et al., 2010).

In the Version 2 NN, we restrict our input to include only these four parameters. The PS responds to solar wind variations through an increase in dayside reconnection and dynamic pressure, allowing plasma and energy to enter Earth's magnetosphere where it is stored in the magnetotail. The release of this stored energy both increases Earthward plasma flow and magnetic flux in the near-Earth PS, leading to increased energetic electron flux there. We chose these four parameters as indicators of how much reconnection and dynamic pressure will be impacting the dayside magnetosphere. We note that three of these parameters—V, B_Y, and B_Z—have long been shown to be an accurate predictor of energy input from the SW to the magnetosphere (e.g., Perreault and Akasofu, 1978).

2.1.3.1. Version 2 input data

For Version 2, we alter the input data to include only the four parameters from section 2.1.3. These parameters are averaged to 5 min and restricted to a time history of −0.5 to −4 h. To them, we add two inputs related to the spacecraft position. In a similar manner described by Bortnik et al. (2016), we encode spacecraft location by including the magnetic local time (MLT). For the purposes of this study only, we made a simplification that the characteristics of the PS within ±1 RE in radial distance at 10 RE are approximately consistent. Similar to the Version 1 input vector, the OMNI parameters that are included start at t₀ − 30min. The Version 2 input data is shown in Equation 2. Each input vector has 174 features; there are 172 OMNI inputs (4 parameters · (240−25) min/5 min) and 2 position inputs. The creation of the target vectors was unchanged.

$\begin{array}{ll}\varphi =\frac{\text{MLT}}{24}2\pi \xi =\left[B_Y,B_Z,|V|,n\right]& (\mathrm{2a})\end{array}$

$\begin{array}{ll}{\overrightarrow{x}}_i=\left[{\bar{\xi }}_{t_{y_i}-\tau },{\bar{\xi }}_{t_{y_i}-\tau -\Delta t},\dots ,{\bar{\xi }}_{t_{y_i}-\Delta T},cos{\varphi }_i,sin{\varphi }_i\right]& (\mathrm{2b})\end{array}$

In Equation 2, $\bar{\xi }$ is the 5-min averaged ξ, τ = 30min is a time delay, t_yi is observation time of ${\overrightarrow{y}}_i$, Δt = 5min, ΔT = 4h, and MLT is the magnetic local time of the spacecraft when each of the i observations were recorded. Unlike the Version 1 OMNI inputs, data in Version 2 were not scaled to the range [−1, 1]. Similar to the Version 1 input data, if there were any missing OMNI data in an input vector, then we discarded that (${\overrightarrow{x}}_i,{\overrightarrow{y}}_i$) example from the dataset. Since it is more likely to have missing data when averaging over 5 min than when averaging over 30 min, a much larger number, about 66%, of training examples were excluded in the Version 2 data. After removing examples with missing data, there were 282,294 total training examples remaining. As with Version 1, 10% of the examples were reserved for testing. The date ranges for Version 2 data are training: February 2008–August 2015 and testing: September 2015–May 2017. We note that these are not the same training/testing periods that were used for the Version 1 model. We discuss this discrepancy and its consequences in section 4.

2.2. Neural Network Description

A NN has the proven ability to fit any non-linear function between two sets of variables (Hornik et al., 1989). While we can be confident that some ambient SW plasma eventually finds its way to the PS, all of the non-linear methods involved for how it arrives there are not completely understood (e.g., Wing et al., 2014). To capture the unknown non-linear processes, we used the machine learning tool of a NN as a statistical mapping between upstream SW and PS observations.

2.2.1. Version 1 Neural Network

The Version 1 NN used an input layer, two hidden layers, and an output layer. The number of nodes in each hidden layer is based on a multiple of the number of inputs to that layer. The first hidden layer has 624 nodes, which is the number of inputs times three, and the second hidden layer has 1,248 nodes, which is 624 times two. All neurons in both layers are activated using the rectified linear unit function (ReLU, defined in Equation 3). In the output layer, a linear activation function is used to render the log of the flux values.

$\begin{array}{ll}\text{ReLU}:f(x)=\{\begin{array}{ll}0,\hfill & x<0\hfill \\ x,\hfill & x\ge 0\hfill \end{array}& (3)\end{array}$

2.2.2. Version 2 Neural Network

We made modifications to the NN by modifying both the inputs, targets, and NN architecture. See section 2.1.3.1 for descriptions of how the inputs were modified from the Version 1 model. The NN architecture modifications from Version 1 to Version 2 are as follows. The number of inputs to the Version 2 model is 174. The first hidden layer has 522 nodes, which is three times the number of inputs. The second hidden layer has 1,044 nodes which is twice the number of nodes in the first hidden layer. As in the Version 1 model, all nodes in both hidden layers are activated using ReLU, and the output layer is activated using a linear function.

2.3. Neural Network Training

We utilized Keras with Tensorflow (Abadi et al., 2015) software for our NN training. Weights and biases were updated using a loss function of mean squared error (MSE) and the Adam optimization algorithm (Kingma and Ba, 2014) with hyperparameters set to α(learning rate) = 0.001, β₁ = 0.9, β₂ = 0.999, and ϵ = 10⁻⁷. Although MSE was calculated using all 17 energy channels in the $\overrightarrow{y}-$ and $\hat{\overrightarrow{y}}$-vectors, the weights and biases for each channel were updated independently. For both versions, we stopped training when it was detected that the test loss had stopped decreasing after three consecutive epochs. This occurred after ten epochs for both versions. We trained both NNs in batches of 50 training examples, resulting in several thousand updates per epoch.

Figure 1 shows the training loss and test skill for both Version 1 and Version 2 neural networks. In Figures 1A–D, the black line was calculated using training data and the red line was calculated using the test data. Figure 1A is the MSE of predicted output vector vs. observed electron flux channels calculated after each epoch of training for model Version 1. We define a single epoch of training to be a complete pass through all training data. The curves do not look “smooth” because the weights were updated after each batch of 50 training examples and the loss was only recorded after each complete epoch (11,052 batches per epoch in Version 1 and 5,082 batches per epoch in Version 2). Figure 1B shows the skill of the model calculated after each epoch. Model skill was determined using the prediction efficiency (PE) metric, which was calculated as unity minus the ratio of the MSE to the observed variance. Figures 1C,D show the loss and skill of the Version 2 model for both train and test data after each epoch of training. In Version 1, the final training loss was 0.34, and the final training skill was 0.76. In Version 2, the training loss and skill are similar to Version 1, at 0.33 and 0.80, respectively. The test loss for both versions have final values of 0.47 for Version 1, and 0.38 for Version 2. The final test skill between the two versions are Version 1 PE is 0.76 and Version 2 PE is 0.80.

FIGURE 1

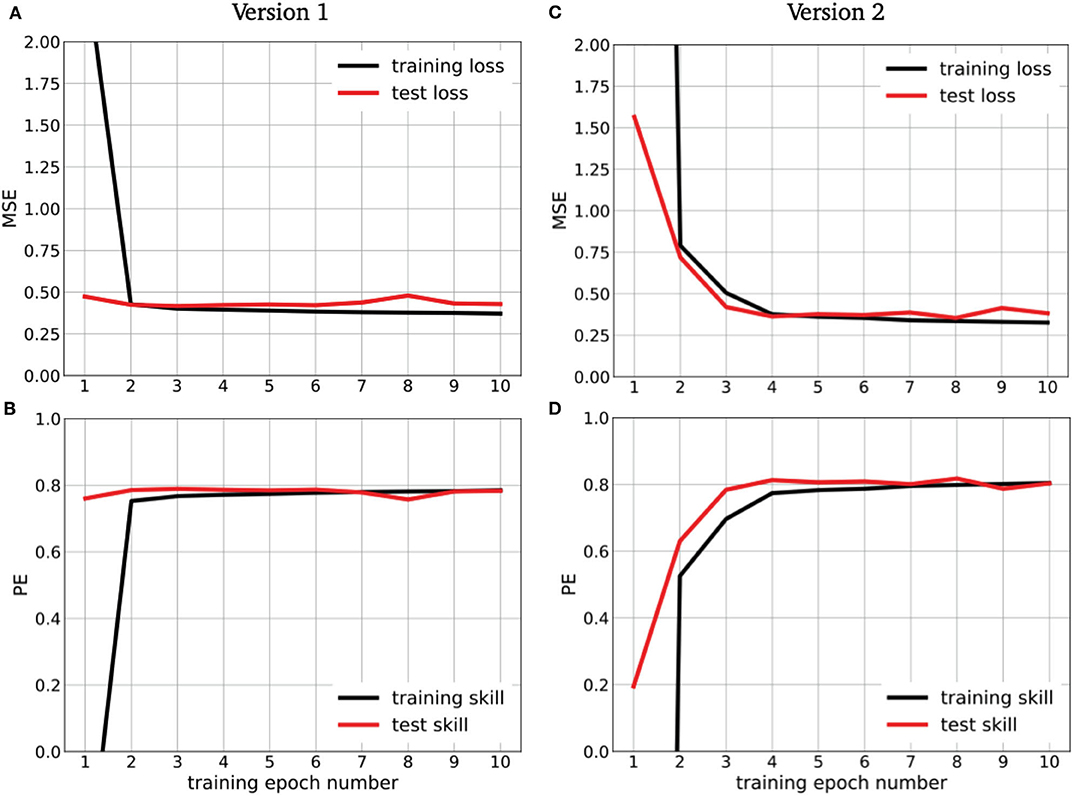
Figure 1. Training and test loss and skill for the two different model configurations. Panels (A,B) show the loss and skill metrics after each epoch of training the Version 1 model. Panels (C,D) show the same as (A,B) except they are from the Version 2 model.

3. Results

We have calculated several model-observation metrics for the two neural networks in order to evaluate their performance. Each metric was calculated using the data designated as test for both versions. Observations include the full set of $\overrightarrow{y}$, and model output, $\hat{\overrightarrow{y}}$, is obtained by applying the trained weights and biases to the test inputs, $\overrightarrow{x}$. The bottom section of Table 1, labeled Test section, shows all of the test metrics calculated for both versions of the NN. We use several different metrics for a more comprehensive model comparison (e.g., Liemohn et al., 2018). The first five (“Bias” through “MAE”) are calculated using the log of flux values and the last four (“Association” through “MSA”) are calculated using actual flux values. We highlighted in blue the metric between the two versions that more closely represents the observations. For all metrics calculated except Bias and Extremes, the Version 2 NN outperforms the Version 1 NN.

Bias is calculated as $\mathrm{\text{mean}}\left(\hat{\overrightarrow{y}}\right)-\mathrm{\text{mean}}(\overrightarrow{y})$. Version 1 has a slight negative bias of −0.05 and Version 2 has a larger, positive bias of 0.15. The Extremes are the ratio of the range of model flux to the range of observed flux. An Extreme score of 1 would indicate that the model output perfectly captures the observed range of flux values. Since the Version 1 score of 0.46 is closer to unity than the Version 2 score of 0.36, we can infer that the Version 1 model is better at capturing the range of observed flux values than Version 2. PE and MSE are defined in section 2.3, and for both, Version 2 outperforms Version 1. In training, the algorithm was attempting to minimize MSE on the training data, and PE was monitored to impede overfitting (see section 2.3). The MSE of Version 1 is 0.47 and the MSE of Version 2 is 0.38. The Version 2 PE of 0.80 is an improvement over the Version 1 PE of 0.76. We use Mean Absolute Error (MAE) as a second measure of the spread of the deviation between observed and modeled values. The Version 1 MAE is 0.51 and the Version 2 MAE is 0.44. If we take the square root of MSE to obtain the Root Mean Square Error (RMSE), then RMSE and MAE have the same units, in this case log₁₀(cm⁻²s⁻¹sr⁻¹). RMSE is larger than MAE for both models, which reveals that it is likely that there is a substantial spread of modeled flux values compared to the observed values.

The remaining metrics that are described were calculated using actual flux values. With Association, we use the standard textbook r² value commonly used for regression analysis. Our interpretation of Association is that the Version 1 model captures only 43% of the variance in the observed fluxes, while the Version 2 model is capturing nearly 70% of the variance in observed fluxes. The symmetric mean absolute percent error (sMAPE) ranges from 0 to 200 percent. The Version 1 model has a sMAPE of 90% and the Version 2 model has a sMAPE of 80%. The signed symmetric percent bias (SSPB) and the median symmetric accuracy (MSA) are two metrics described by Morley et al. (2018) that provide a more robust comparison of flux values that vary by orders of magnitude. SSPB is calculated using the median value of the log of flux, rather than the mean of the log of flux. Consistant with the Bias calculated using the mean of the log of flux values, The SSPB for Version 1 is negative, at −30% and the SSPB for Version 2 is positive at 20%. The fact that the absolute SSPB is lower for Version 2 than Version 1 implies that there is larger spread in the Version 1 modeled values than in the Version 2 modeled values compared to the observed values. This is consistant with the comparison of MAE and RMSE described in the previous paragraph. Despite the name, the MSA is a measure of error, and the values of MSA for Version 1 and Version 2 models indicates that there is less error in the Version 2 model. A percent error of 100% would imply that on average, there is a factor of two in the discrepancy between the observed flux and the modeled flux. The Version 2 NN achieves a MSA of 110%, which is better than the Version 1 MSA of 151%.

The comparison of observed to modeled electron flux using observations from the test data and modeled output from both versions of the NN is shown in Figure 2. Figure 2A shows the scatter for the Version 1 NN and Figure 2B shows the scatter for the Version 2 NN. The Version 1 scatter diagram shows a higher number of points overall than the Version 2 scatter diagram, because there was a larger amount of data in the Version 1 dataset (see section 2.1.2). The black diagonal dash-dotted line is a hypothetical ideal perfect correlation between observation and model. For both model versions, the scatter shows a clustering of the densest points close to the black line. The Version 2 model shows a larger portion of the points closer to the black line. Figure 2 is a general picture of model output and observational comparisons, and we are hesitant to draw conclusions regarding the behavior of plasma sheet electrons from it.

FIGURE 2

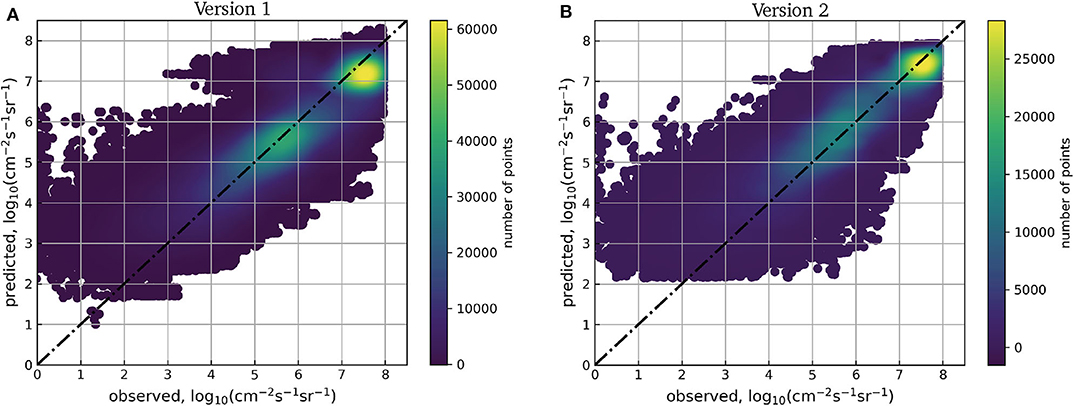
Figure 2. Scatter density correlation of modeled vs. observed electron flux at all 17 energy channels for (A) the Version 1 model and (B) the Version 2 model. The comparison for both models was performed on the data reserved for testing.

4. Discussion

The Version 1 model assumes no a priori knowledge about which quantities in the SW are important contributions to near-Earth PS variations. We made this choice in order to allow the NN to appropriately weight any parameters or combinations thereof that might have been overlooked by previous SW-magnetosphere coupling studies. There is a longer time history of the SW that is used in Version 1 than Version 2. The Version 1 NN is also trained on more than twice as many training examples than Version 2. These factors might suggest that the Version 1 NN would produce more accurate output than the Version 2 NN. However, despite the assumed advantages of the Version 1 model, the Version 2 model outperforms the Version 1 model in most model-data comparison metrics calculated (see Table 1). We propound that Version 2 outperforms Version 1 because of two modifications that were made based on physical information.

The first modification toward incorporating physical information relates to the time resolution of the inputs. When deciding to use 30-min averaged SW inputs, we used evidence that the magnetosphere acts as a low-pass filter of SW variations (e.g., Ilie et al., 2010). However, there is evidence that some higher time resolved information contained in the SW effects the PS (Lyons et al., 2009; Wang et al., 2017). Additionally, much of the behavior in the PS occurs on cycles of a few hours, i.e., substorm activity (e.g., Hones, 1972). By reducing the SW time history to 4 h, we neglect information that is likely relevant to predicting the electron flux in the PS. Others have found time delays of 6 h (Nagata et al., 2008) and 8 h (Borovsky et al., 1998) between SW/IMF variations and PS response. Even though the Version 2 model does not consider delays longer than 4 h, it still outperforms Version 1.

The second item of physical information that we introduced to the input set is the spatial distribution of observed electron flux. It is widely observed that there is a dawn-dusk asymmetry of electron fluxes in the PS (e.g., Walker and Farley, 1972; Lui and Rostoker, 1991; Sarafopoulos et al., 2001; Imada et al., 2008). We would expect both a higher flux and a larger number flux enhancements in the post local midnight, dawn section of the PS. Moreover, Wang et al. (2007) demonstrated that the spatial distribution of electrons within the PS is correlated with varying SW parameters. Wang et al. (2011) additionally show that the distribution of electron flux can be characterized by MLT as electrons drift closer toward the inner magnetosphere. Therefore, treating the PS as uniform in electron flux at a single radial distance, as modeled by the Version 1 NN, is physically inappropriate. By including the spacecraft location as an input for the Version 2 model, we are encoding the physical knowledge that the variation of electron flux is dependent upon spatial location within the PS.

Both model versions were trained using periods of the solar cycle that include quiet and active periods: Version 1, solar minimum through the declining phase and Version 2, solar minimum through solar maximum of solar cycle 24. However, Version 1 was tested on a period of solar quiet (solar minimum) and Version 2 was tested with data during a solar active period (declining phase). While we might expect the model to perform better during quiet SW conditions, this is not what we see when comparing Version 1 to Version 2. Moreover, there is not a substantial difference in the variance of training and testing target data between Versions 1 and 2. The Version 1 target data has standard deviations of 1.31 and 1.41 log₁₀(cm⁻²s⁻¹sr⁻¹) for train and test sets, respectively, while the Version 2 target data has standard deviations of 1.29 and 1.39 log₁₀(cm⁻²s⁻¹sr⁻¹), respectively. This further indicates that including physical information is more important than using a larger amount of data when training these neural networks.

5. Conclusion

In summary, this study showed that including additional physical understanding, even while reducing the data set and inputs in other ways, improved the quality of the NN predictive capability. With neural networks, tracing the contribution from inputs to outputs is difficult, hindering interpretability of results, i.e., determining which inputs contributed to which output, or finding a functional mapping between inputs and outputs. Azari et al. (2020) showed that incorporating physical knowledge into ML additionally improves scientific interpretability along with performance for certain models. Development of a robust NN model of PS electron flux from SW input using additional physical understanding shows promise for improving performance.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://spdf.gsfc.nasa.gov/pub/data/ (under identifiers OMNI and THEMIS). Model output data and specific observed data are available at the following link: https://doi.org/10.7302/559r-t639.

Author Contributions

We use the CRediT (Contributor Roles Taxonomy) categories (Brand et al., 2015) for providing the following contribution description. NG led the conceptualization and provided resources and supervision. ML assisted in conceptualization and formal analysis, provided the resources, funding acquisition, supervision, and aided in project administration. BS designed the methodology, conducted the investigation, performed data visualization and formal analysis, and wrote the original draft. All authors have contributed toward the revision and editing of the manuscript.

Funding

This work was funded in part by NASA Grant #NNX17AB87G. Work of NG was supported by NASA grants #NNX17AI48G (ROSES 2016), #80NSSC20K0353 (ROSES 2018), and Heliophysics Phase I DRIVE Science Center SOLSTICE (Solar Storms and Terrestrial Impacts Center) #80NSSC20K0600. BS was partially funded by Michigan Space Grant Consortium, NASA grant #NNX15AJ20H.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors thank the THEMIS mission team and OMNIWeb team for data availability. Matplotlib (matplotlib.org) plotting software was used to generate figures shown in this report. Neural network training was performed using Keras (https://keras.io) with Tensorflow (https://tensorflow.org). BS would like to thank useful discussions with A. R. Azari during manuscript preparation.

References

Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z., Citro, C., et al. (2015). TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. Technical report. Available online at: https://tensorflow.org

Google Scholar

Angelopoulos, V. (2008). The THEMIS mission. Space Sci. Rev. 141, 5–34. doi: 10.1007/s11214-008-9336-1

CrossRef Full Text | Google Scholar

Angelopoulos, V., Sibeck, D., Carlson, C. W., McFadden, J. P., Larson, D., Lin, R. P., et al. (2008). First results from the THEMIS mission. Space Sci. Rev. 141, 453–476. doi: 10.1007/s11214-008-9378-4

CrossRef Full Text | Google Scholar

Aubry, M. P., and McPherron, R. L. (1971). Magnetotail changes in relation to the solar wind magnetic field and magnetospheric substorms. J. Geophys. Res. 76, 4381–4401. doi: 10.1029/JA076i019p04381

CrossRef Full Text | Google Scholar

Azari, A. R., Lockhart, J. W., Liemohn, M. W., and Jia, X. (2020). Incorporating physical knowledge into machine learning for planetary space physics. Front. Astron. Space Sci. 7:36. doi: 10.3389/fspas.2020.00036

CrossRef Full Text | Google Scholar

Balikhin, M. A., Boynton, R. J., Billings, S. A., Gedalin, M., Ganushkina, N., Coca, D., et al. (2010). Data based quest for solar wind-magnetosphere coupling function. Geophys. Res. Lett. 37:L24107. doi: 10.1029/2010GL045733

CrossRef Full Text | Google Scholar

Bame, S. J., Asbridge, J. R., Felthauser, H. E., Hones, E. W., and Strong, I. B. (1967). Characteristics of the plasma sheet in the Earth's magnetotail. J. Geophys. Res. 72, 113–129. doi: 10.1029/JZ072i001p00113

CrossRef Full Text | Google Scholar

Baumjohann, W., Paschmann, G., and Cattell, C. A. (1989). Average plasma properties in the central plasma sheet. J. Geophys. Res. Space Phys. 94, 6597–6606. doi: 10.1029/JA094iA06p06597

CrossRef Full Text | Google Scholar

Borovsky, J. E., Thomsen, M. F., and Elphic, R. C. (1998). The driving of the plasma sheet by the solar wind. J. Geophys. Res. Space Phys. 103, 17617–17639. doi: 10.1029/97JA02986

CrossRef Full Text | Google Scholar

Bortnik, J., Li, W., Thorne, R. M., and Angelopoulos, V. (2016). A unified approach to inner magnetospheric state prediction. J. Geophys. Res. Space Phys. 121, 2423–2430. doi: 10.1002/2015JA021733

CrossRef Full Text | Google Scholar

Brand, A., Allen, L., Altman, M., Hlava, M., and Scott, J. (2015). Beyond authorship: attribution, contribution, collaboration, and credit. Learn. Publ. 28, 151–155. doi: 10.1087/20150211

CrossRef Full Text | Google Scholar

Camporeale, E. (2019). The challenge of machine learning in space weather: nowcasting and forecasting. Space Weather 17, 1166–1207. doi: 10.1029/2018SW002061

CrossRef Full Text | Google Scholar

Cao, J., Duan, A., Reme, H., and Dandouras, I. (2013). Relations of the energetic proton fluxes in the central plasma sheet with solar wind and geomagnetic activities. J. Geophys. Res. Space Phys. 118, 7226–7236. doi: 10.1002/2013JA019289

CrossRef Full Text | Google Scholar

Chen, Y., Reeves, G., and Friedel, R. (2007). The energization of relativistic electrons in the outer van allen radiation belt. Nat. Phys. 3, 614–617. doi: 10.1038/nphys655

CrossRef Full Text | Google Scholar

Chu, X., Bortnik, J., Li, W., Ma, Q., Denton, R., Yue, C., et al. (2017). A neural network model of three-dimensional dynamic electron density in the inner magnetosphere. J. Geophys. Res. Space Phys. 122, 9183–9197. doi: 10.1002/2017JA024464

CrossRef Full Text | Google Scholar

Davis, V. A., Mandell, M. J., and Thomsen, M. F. (2008). Representation of the measured geosynchronous plasma environment in spacecraft charging calculations. J. Geophys. Res. Space Phys. 113:A10204 doi: 10.1029/2008JA013116

CrossRef Full Text | Google Scholar

Dubyagin, S., Ganushkina, N., and Liemohn, M. (2019). On the accuracy of reconstructing plasma sheet electron fluxes from temperature and density models. Space Weather 17, 1704–1719. doi: 10.1029/2019SW002285

CrossRef Full Text | Google Scholar

Dubyagin, S., Ganushkina, N. Y., Sillanpää, I., and Runov, A. (2016). Solar wind-driven variations of electron plasma sheet densities and temperatures beyond geostationary orbit during storm times. J. Geophys. Res. Space Phys. 121, 8343–8360. doi: 10.1002/2016JA022947

CrossRef Full Text | Google Scholar

Garrett, H. B. (1981). The charging of spacecraft surfaces. Rev. Geophys. 19, 577–616. doi: 10.1029/RG019i004p00577

CrossRef Full Text | Google Scholar

Hones, E. W. (1972). Plasma sheet variations during substorms. Planet. Space Sci. 20, 1409–1431. doi: 10.1016/0032-0633(72)90048-7

CrossRef Full Text | Google Scholar

Horne, R. B., Thorne, R. M., Glauert, S. A., Albert, J. M., Meredith, N. P., and Anderson, R. R. (2005). Timescale for radiation belt electron acceleration by whistler mode chorus waves. J. Geophys. Res. Space Phys. 110:A03225. doi: 10.1029/2004JA010811

CrossRef Full Text | Google Scholar

Hornik, K., Stinchcombe, M., and White, H. (1989). Multilayer feedforward networks are universal approximators. Neural Netw. 2, 359–366. doi: 10.1016/0893-6080(89)90020-8

CrossRef Full Text | Google Scholar

Ilie, R., Liemohn, M. W., and Ridley, A. (2010). The effect of smoothed solar wind inputs on global modeling results. J. Geophys. Res. Space Phys. 115:A01213. doi: 10.1029/2009JA014443

CrossRef Full Text | Google Scholar

Imada, S., Hoshino, M., and Mukai, T. (2008). The dawn-dusk asymmetry of energetic electron in the earth's magnetotail: observation and transport models. J. Geophys. Res. Space Phys. 113:A11201. doi: 10.1029/2008JA013610

CrossRef Full Text | Google Scholar

Kennel, C. F., and Petschek, H. E. (1966). Limit on stably trapped particle fluxes. J. Geophys. Res. 71, 1–28. doi: 10.1029/JZ071i001p00001

CrossRef Full Text | Google Scholar

Kennel, C. F., and Thorne, R. M. (1967). Unstable growth of unducted whistlers propagating at an angle to the geomagnetic field. J. Geophys. Res. 72, 871–878. doi: 10.1029/JZ072i003p00871

CrossRef Full Text | Google Scholar

King, J. H., and Papitashvili, N. E. (2005). Solar wind spatial scales in and comparisons of hourly wind and ace plasma and magnetic field data. J. Geophys. Res. 110:A02104. doi: 10.1029/2004JA010649

CrossRef Full Text | Google Scholar

Kingma, D. P., and Ba, J. (2014). “Adam: a method for stochastic optimization, in 3rd International Conference on Learning Representations. Technical report.

Google Scholar

Li, W., Thorne, R., Bortnik, J., McPherron, R., Nishimura, Y., Angelopoulos, V., et al. (2012). Evolution of chorus waves and their source electrons during storms driven by corotating interaction regions. J. Geophys. Res. Space Phys. 117:A08209. doi: 10.1029/2012JA017797

CrossRef Full Text | Google Scholar

Li, W., Thorne, R. M., Meredith, N. P., Horne, R. B., Bortnik, J., Shprits, Y. Y., et al. (2008). Evaluation of whistler mode chorus amplification during an injection event observed on CRRES. J. Geophys. Res. Space Phys. 113:A09210. doi: 10.1029/2008JA013129

CrossRef Full Text | Google Scholar

Liemohn, M. W., McCollough, J. P., Jordanova, V. K., Ngwira, C. M., Morley, S. K., Cid, C., et al. (2018). Model evaluation guidelines for geomagnetic index predictions. Space Weather 16, 2079–2102. doi: 10.1029/2018SW002067

CrossRef Full Text | Google Scholar

Lui, W. W., and Rostoker, G. (1991). Effects of dawn-dusk pressure asymmetry on convection in the central plasma sheet. J. Geophys. Res. Space Phys. 96, 11501–11512. doi: 10.1029/91JA01173

CrossRef Full Text | Google Scholar

Luo, B., Tu, W., Li, X., Gong, J., Liu, S., Burin des Roziers, E., et al. (2011). On energetic electrons (>38 kev) in the central plasma sheet: data analysis and modeling. J. Geophys. Res. Space Phys. 116:A09220. doi: 10.1029/2011JA016562

CrossRef Full Text | Google Scholar

Lyons, L. R., Kim, H.-J., Xing, X., Zou, S., Lee, D.-Y., Heinselman, C., et al. (2009). Evidence that solar wind fluctuations substantially affect global convection and substorm occurrence. J. Geophys. Res. Space Phys. 114:A11306. doi: 10.1029/2009JA014281

CrossRef Full Text | Google Scholar

McFadden, J. P., Carlson, C. W., Larson, D., Ludlam, M., Abiad, R., Elliott, B., et al. (2008). The THEMIS ESA plasma instrument and in-flight calibration. Space Sci. Rev. 141, 277–302. doi: 10.1007/978-0-387-89820-9_13

CrossRef Full Text | Google Scholar

Meredith, N. P., Horne, R. B., Iles, R. H. A., Thorne, R. M., Heynderickx, D., and Anderson, R. R. (2002). Outer zone relativistic electron acceleration associated with substorm-enhanced whistler mode chorus. J. Geophys. Res. Space Phys. 107, SMP 29-1-SMP 29–14. doi: 10.1029/2001JA900146

CrossRef Full Text | Google Scholar

Morley, S. K., Brito, T. V., and Welling, D. T. (2018). Measures of model performance based on the log accuracy ratio. Space Weather 16, 69–88. doi: 10.1002/2017SW001669

CrossRef Full Text | Google Scholar

Nagata, D., Machida, S., Ohtani, S., Saito, Y., and Mukai, T. (2008). Solar wind control of plasma number density in the near-earth plasma sheet: three-dimensional structure. Ann. Geophys. 26, 4031–4049. doi: 10.5194/angeo-26-4031-2008

CrossRef Full Text | Google Scholar

Newell, P. T., Sotirelis, T., Liou, K., Meng, C.-I., and Rich, F. J. (2007). A nearly universal solar wind-magnetosphere coupling function inferred from 10 magnetospheric state variables. J. Geophys. Res. 112:A01206. doi: 10.1029/2006JA012015

CrossRef Full Text | Google Scholar

Nishida, A., and Lyon, E. F. (1972). Plasma sheet at lunar distance: structure and solar-wind dependence. J. Geophys. Res. 77, 4086–4099. doi: 10.1029/JA077i022p04086

CrossRef Full Text | Google Scholar

Perreault, P., and Akasofu, S. I. (1978). A study of geomagnetic storms. Geophys. J. Int. 54, 547–573. doi: 10.1111/j.1365-246X.1978.tb05494.x

CrossRef Full Text | Google Scholar

Roziers, E. B. D., Li, X., Baker, D. N., Fritz, T. A., Friedel, R., Onsager, T. G., et al. (2009). Energetic plasma sheet electrons and their relationship with the solar wind: a cluster and geotail study. J. Geophys. Res. Space Phys. 114:A02220. doi: 10.1029/2008JA013696

CrossRef Full Text | Google Scholar

Ruan, P., Fu, S. Y., Zong, Q.-G., Pu, Z. Y., Cao, X., Liu, W. L., et al. (2005). Ion composition variations in the plasma sheet observed by cluster/rapid. Geophys. Res. Lett. 32. doi: 10.1029/2004GL021266

CrossRef Full Text | Google Scholar

Sarafopoulos, D. V., Sidiropoulos, N. F., Sarris, E. T., Lutsenko, V., and Kudela, K. (2001). The dawn-dusk plasma sheet asymmetry of energetic particles: an interball perspective. J. Geophys. Res. Space Phys. 106, 13053–13065. doi: 10.1029/2000JA900157

CrossRef Full Text | Google Scholar

Stone, E. C., Frandsen, A. M., Mewaldt, R. A., Christian, E. R., Margolies, D., Ormes, J. F., et al. (1998). The advanced composition explorer. Space Sci. Rev. 86, 1–22. doi: 10.1007/978-94-011-4762-0_1

CrossRef Full Text | Google Scholar

Terasawa, T., Fujimoto, M., Mukai, T., Shinohara, I., Saito, Y., Yamamoto, T., et al. (1997). Solar wind control of density and temperature in the near-earth plasma sheet: Wind/geotail collaboration. Geophys. Res. Lett. 24, 935–938. doi: 10.1029/96GL04018

CrossRef Full Text | Google Scholar

Tsurutani, B. T., and Smith, E. J. (1974). Postmidnight chorus: a substorm phenomenon. J. Geophys. Res. 79, 118–127. doi: 10.1029/JA079i001p00118

CrossRef Full Text | Google Scholar

Tsutomu, T., and Teruki, M. (1976). Flapping motions of the tail plasma sheet induced by the interplanetary magnetic field variations. Planet. Space Sci. 24, 147–159. doi: 10.1016/0032-0633(76)90102-1

CrossRef Full Text | Google Scholar

Tsyganenko, N. A., and Mukai, T. (2003). Tail plasma sheet models derived from geotail particle data. J. Geophys. Res. Space Phys. 108:1136. doi: 10.1029/2002JA009707

CrossRef Full Text | Google Scholar

Walker, R. J., and Farley, T. A. (1972). Spatial distribution of energetic plasma sheet electrons. J. Geophys. Res. 77, 4650–4660. doi: 10.1029/JA077i025p04650

CrossRef Full Text | Google Scholar

Wang, C.-P., Gkioulidou, M., Lyons, L. R., Wolf, R. A., Angelopoulos, V., Nagai, T., et al. (2011). Spatial distributions of ions and electrons from the plasma sheet to the inner magnetosphere: comparisons between themis-geotail statistical results and the rice convection model. J. Geophys. Res. Space Phys. 116:A11216. doi: 10.1029/2011JA016809

CrossRef Full Text | Google Scholar

Wang, C.-P., Kim, C. Y., Weygand, J. M., Hsu, T.-S., and Chu, X. (2017). Effects of solar wind ultralow frequency fluctuations on plasma sheet electron temperature: regression analysis with support vector machine. J. Geophys. Res. Space Phys. 122, 4210–4227. doi: 10.1002/2016JA023746

CrossRef Full Text | Google Scholar

Wang, C.-P., Lyons, L. R., Nagai, T., Weygand, J. M., and McEntire, R. W. (2007). Sources, transport, and distributions of plasma sheet ions and electrons and dependences on interplanetary parameters under northward interplanetary magnetic field. J. Geophys. Res. Space Phys. 112:A10224. doi: 10.1029/2007JA012522

CrossRef Full Text | Google Scholar

Wing, S., Johnson, J. R., Chaston, C. C., Echim, M., Escoubet, C. P., Lavraud, B., et al. (2014). Review of solar wind entry into and transport within the plasma sheet. Space Sci. Rev. 184, 33–86. doi: 10.1007/s11214-014-0108-9

CrossRef Full Text | Google Scholar

Wing, S., Johnson, J. R., Newell, P. T., and Meng, C.-I. (2005). Dawn-dusk asymmetries, ion spectra, and sources in the northward interplanetary magnetic field plasma sheet. J. Geophys. Res. Space Phys. 110:A08205. doi: 10.1029/2005JA011086

CrossRef Full Text | Google Scholar

Yue, C., Wang, C.-P., Lyons, L., Wang, Y., Hsu, T.-S., Henderson, M., et al. (2015). A 2-d empirical plasma sheet pressure model for substorm growth phase using the support vector regression machine. J. Geophys. Res. Space Phys. 120, 1957–1973. doi: 10.1002/2014JA020787

CrossRef Full Text | Google Scholar

Zhelavskaya, I. S., Shprits, Y. Y., and Spasojevia, M. (2017). Empirical modeling of the plasmasphere dynamics using neural networks. J. Geophys. Res. Space Phys. 122, 11227–11244. doi: 10.1002/2017JA024406

CrossRef Full Text | Google Scholar