Collisionless Magnetic Reconnection and Waves: Progress Review

Magnetic reconnection is a fundamental process whereby microscopic plasma processes cause macroscopic changes in magnetic field topology, leading to explosive energy release. Waves and turbulence generated during the reconnection process can produce particle diffusion and anomalous resistivity, as well as heat the plasma and accelerate plasma particles, all of which can impact the reconnection process. We review progress on waves related to reconnection achieved using high resolution multi-point in situ observations over the last decade, since early Cluster and THEMIS observations and ending with recent Magnetospheric Multiscale results. In particular, we focus on the waves most frequently observed in relation to reconnection, ranging from low-frequency kinetic Alfvén waves (KAW), to intermediate frequency lower hybrid and whistler-mode waves, electrostatic broadband and solitary waves, as well as the high-frequency upper hybrid, Langmuir, and electron Bernstein waves. Significant progress has been made in understanding localization of the different wave modes in the context of the reconnection picture, better quantification of generation mechanisms and wave-particle interactions, including anomalous resistivity. Examples include: temperature anisotropy driven whistlers in the flux pileup region, anomalous effects due to lower-hybrid waves, upper hybrid wave generation within the electron diffusion region, wave-particle interaction of electrostatic solitary waves. While being clearly identified in observations, some of the wave processes remain challenging for reconnection simulations (electron Bernstein, upper hybrid, Langmuir, whistler), as the instabilities (streaming, loss-cone, shell) which drive these waves require high resolution of distribution functions in phase space, and realistic ratio of Debye to electron inertia scales. We discuss how reconnection configuration, i.e., symmetric vs. asymmetric, guide-field vs. antiparallel, affect wave occurrence, generation, effect on particles, and feedback on the overall reconnection process. Finally, we outline some of the major open questions, such as generation of electromagnetic radiation by reconnection sites and role of waves in triggering/onset of reconnection.

1. Introduction

Magnetic reconnection releases energy stored in the magnetic field via reconfiguration of the field topology (Biskamp, 2000). Such reconfiguration requires breaking of the ideal plasma frozen-in behavior. Magnetic reconnection is a fundamental plasma process, which operates in various plasma environments, such as the solar corona and chromosphere, planetary magnetospheres, solar wind, astrophysical plasmas, and well as in laboratory devices such as tokamaks (Yamada et al., 2010).

Waves and turbulence can be generated by the reconnection and provide feedback on the reconnection process, or preexisting waves and turbulence can affect the onset of reconnection. At the largest scales and lowest frequencies this corresponds to MHD turbulence (Lazarian et al., 2015). In collisionless plasmas kinetic processes become important, as they can lead to generation of waves over a wide range of scales and frequencies, in ion, hybrid, and electron ranges. Such waves and turbulence are present in all parts of the reconnection region, such as outflows (Osman et al., 2015), separatrix regions (Viberg et al., 2013), ion and electron diffusion region (Fu et al., 2017; Graham et al., 2017a). Reconnection leads to the generation of sharp gradients in both real and phase space. Waves and kinetic instabilities generally tend to relax such gradients leading to thermalization of the particle distribution, pitch-angle scattering, heating, and diffusion. Waves-particle interactions were also suggested as one of the ways to introduce dissipation into a collisionless system, via anomalous resistivity (Drake, 2003).

Kinetic wave processes in relation to reconnection can be studied in laboratory experiments (Ji et al., 2004; Fox et al., 2012). But only in situ space observations can provide the detailed information on both the electromagnetic fields and the particle distribution functions, so that both the generation and effect on particles can be studied. Recent Cluster (Escoubet et al., 2001), THEMIS (Angelopoulos, 2008) and Magnetospheric Multiscale (MMS) (Burch et al., 2016) missions provided unique data from near-Earth space. This allowed us to study plasma kinetic processes in a much more quantitative way than before. Here we review recent advances in the understanding the kinetic processes coupling collisionless magnetic reconnection and waves. We focus on the observational results over the last decade, since early Cluster observations (Vaivads et al., 2006; Fujimoto et al., 2011) and ending with recent MMS results.

2. Wave Types

Below we review the different waves types starting from the wave near the electron plasma frequency, f_pe, followed by lower frequency waves.

2.1. Upper Hybrid, Langmuir, Electron Bernstein Waves

In this section we discuss the waves near the electron plasma frequency f_pe, namely, Langmuir, upper hybrid (UH) and electron Bernstein, or equivalently electron cyclotron (EC), waves. The waves are generated by deformations in the electron distribution function, such as electron beams, ring, shell, or loss-cone distributions. These waves can grow at fast rates due to their high frequencies compared the other temporal scales associated with magnetic reconnection, and can thus act very quickly on electrons to dissipate unstable electron distributions or accelerate electrons, compared with timescales over which reconnection evolves. Moreover, these waves have typically relatively low group velocities compared with the electron thermal speed, and thus they are likely to be observed in or close to the source regions. This makes these wave perfect markers of the electron distribution function deformations, in particular of the fine electron boundaries resulting from ongoing magnetic reconnection. Such boundaries can be difficult to identify directly in particle data, due to insufficient temporal resolution of particle measurements compared to the fast time scales of wave growth. For example, these waves can be used to identify electron boundaries in the separatrix regions related to electron beams (Vaivads et al., 2004; Retinó et al., 2006) and loss-cone-like distributions created by the partial loss of hot magnetospheric electrons on reconnected field lines (Khotyaintsev et al., 2006; Graham et al., 2016c).

Spacecraft observations and numerical simulations have shown that fast electron beams are generated in the separatrix regions and that they are often unstable. For fast weak beams waves near the plasma frequency are favored, e.g., Langmuir, beam-mode, or UH waves. Both UH and Langmuir waves have been reported in magnetotail reconnection from Wind and Cluster observations. For example, Farrell et al. (2002) and Farrell et al. (2003) found UH generated in the separatrix region of magnetotail reconnection. Langmuir waves were also reported in the separatrix regions by Deng et al. (2004). Electron Bernstein waves have been reported at DFs by THEMIS (Zhou et al., 2009b). At Earth's magnetopause the plasma frequency line was found to be enhanced in the separatrices Vaivads et al. (2004); Retinó et al. (2006). Using a case study from MMS, Zhou et al. (2016) found Langmuir-like waves in the magnetospheric separatrix and electron Bernstein (EC) and beam-mode like waves in the magnetosheath separatrices. Beam-mode like waves have also been reported in the magnetospheric separatrices (Burch et al., 2018).

Multi-point observations by Cluster allowed detailed mapping of the HF waves in the reconnection diffusion region in the magnetail. These observations showed that Langmuir-like waves were found in the outer separatrices, where fast electron beams were simultaneously observed (Viberg et al., 2013). In addition, electron Bernstein waves and ESWs (discussed in the next section) were observed in the separatrix regions. New reconstruction methods can allow us to study waves in a more complex magnetic topology than a two-dimensional X line (Fu et al., 2015; Liu et al., 2019; Torbert et al., 2019).

Figure 1 shows an example of Langmuir waves observed in the separatrix of magnetotail reconnection reported by Viberg et al. (2013). Figure 1A shows a spectrogram of E, in which ESWs, EC (electron Bernstein) waves, and Langmuir waves are observed. Figure 1B shows an example of Langmuir waves and the associated electron distribution. The waves have peak frequency at f_pe and a clear electron beam was observed. The Langmuir waves tended to be observed in the outer separatrices, where the fastest electron beams are observed (Figure 1C).

FIGURE 1

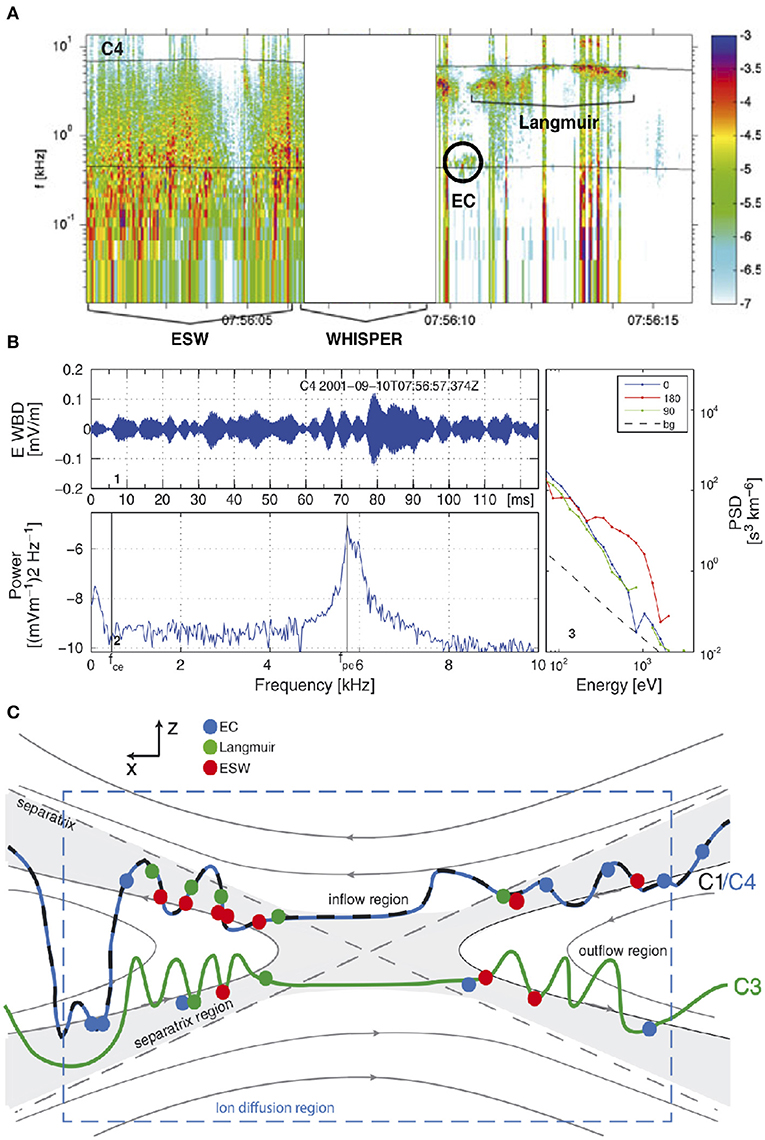
Figure 1. Example of waves observed in the separatrix of magnetotail reconnection observed by Cluster from Viberg et al. (2013). (A) Electric field spectrogram showing ESWs, EC waves, and Langmuir waves. (B) Example of Langmuir waves: 1 Waveform of Langmuir waves, 2 Power spectrum, and 3 electron phase-space densities at pitch angles 0° (blue), 90° (green), and 180° (red). (C) A schematic showing the paths of the Cluster spacecraft across the reconnection region and locations of the observed ESWs, EC waves, and Langmuir waves.

In weakly magnetized plasmas f_pe ≈ f_uh, so Langmuir and UH waves have very similar frequencies. Both Langmuir and UH waves have polarization close to linear, but can be distinguished by the electric field direction with respect to the ambient magnetic field. Langmuir waves (and beam-mode waves) are characterized by E_∥ ≫ E_⊥, while UH waves are characterized by E_⊥ ≫ E_∥. Like UH waves, electron Bernstein waves (or EC waves) are characterized by E_⊥ ≫ E_∥, but have frequencies between harmonics of the electron cyclotron frequency. Thus, Langmuir and UH waves are straightforward to distinguish when three-dimensional electric field data are available, as in the case of MMS.

Figure 2 shows an example of UH and electron Bernstein waves observed at Earth's magnetopause when reconnection is ongoing. The waveform (Figure 2a) shows that E_⊥ ≫ E_∥, consistent with UH and Bernstein waves. The power spectrum (Figure 2c) shows a series of spectral peaks between harmonics of f_ce, with the largest power observed near f_uh consistent with UH waves. The other spectral peaks above and below f_uh are consistent with Bernstein waves. Figure 2b shows the associated electron distribution at pitch angles θ = 0° (black), 90° (red), and 180° (blue), and a fit to the observed data. The distribution has a strong perpendicular temperature anisotropy at high energies, which is frequently observed in association with UH waves at the magnetopause (Graham et al., 2018). The dispersion relations of the UH and Bernstein waves are shown in Figure 2d. The peaks in the power spectra approximately correspond to the points of near-zero group velocity of the waves.

FIGURE 2

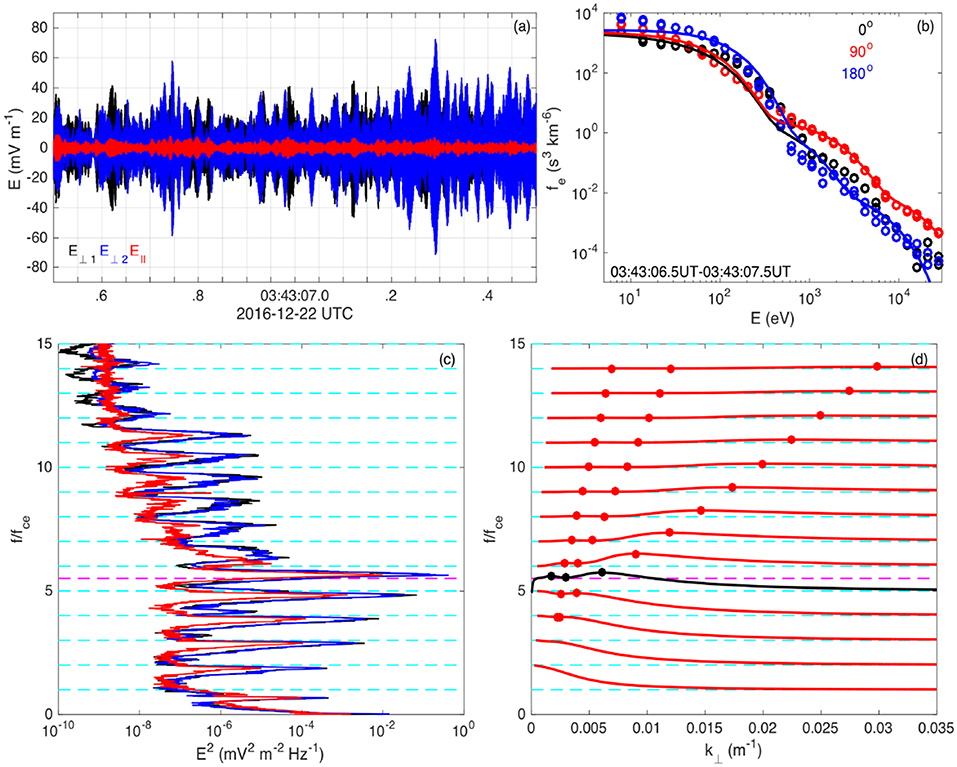
Figure 2. Example of UH and electron Bernstein waves observed by MMS at the reconnecting magnetopause from Graham et al. (2018). (a) Waveform in field-aligned coordinates. (b) Observed electron distribution associated with the waves (circles) and fitted distribution (solid lines). The black, red, and blue colors indicate the phase-space densities at pitch angles 0°, 90°, 180°, respectively. (c) Power spectra of the three electric field components. (d) Predicted dispersion relations of the UH waves (black), and electron Bernstein waves (red). The dots indicate points where the group velocity is zero. In (c,d) the cyan dashed lines indicate nf_ce and the magenta dashed line indicates f_uh.

Plasma frequency waves near the electron diffusion region (EDR) have recently been investigated by the MMS spacecraft. Graham et al. (2017a) showed for the first time that UH-like waves occur near the EDR, where agyrotropic electron beams and crescents develop, see Figure 3. Figure 3a shows the waveform of E. The electric field is characterized by E_⊥ ≫ E_∥ and is approximately one-dimensional. The peak amplitude of the wave is ~ 400 mV m⁻¹, making the waves amongst the largest amplitude observed at the magnetopause. The power spectrum (Figure 3b) shows that waves have peak power close to f_pe ≈ f_uh. So the waves are identified as UH waves. Figure 3c shows the electron velocity distribution function (VDF) observed at the same time as the waves. The VDF is characterized by a stationary core population and beam/crescent propagating perpendicular to the background magnetic field. This distribution exists in a spatial region of the local electron gyroradius size, and was found to be unstable to electron beam mode assuming the electrons are approximately unmagnetized (Figure 3d). The predicted wavelength of the unstable waves is well below the electron gyroradius size. Thus, the agyrotropic electron distributions (crescents) produced by reconnection within the EDR can be unstable to generation of UH waves, which in turn could modify the electron dynamics within the EDR.

FIGURE 3

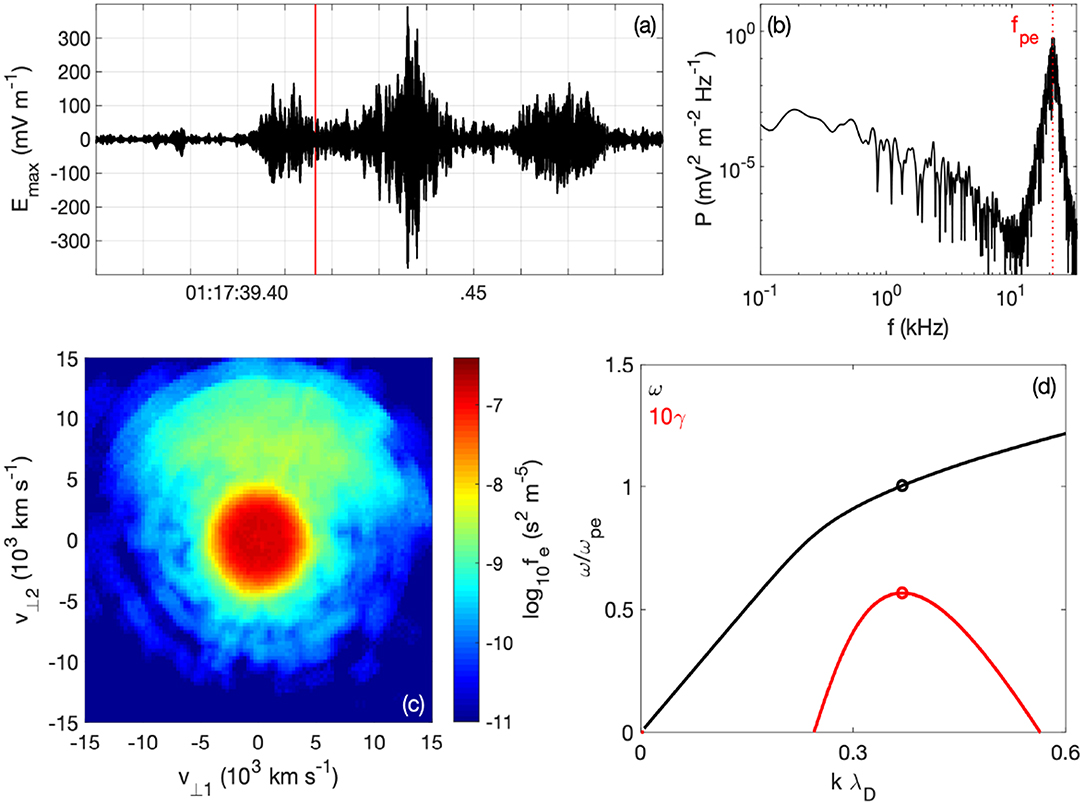
Figure 3. Example of UH waves observed near an EDR at Earth's magnetopause observed by MMS1 from Graham et al. (2017a). (a) Waveform of UH waves. (b) Power spectrum. (c) Two-dimensional reduced distribution in the plane perpendicular to the local magnetic field. (d) Dispersion relation (black) and growth rate (red) predicted by linear theory.

These results have been confirmed in subsequent studies. For example, Tang et al. (2019) found UH waves colocated with agyrotropic electron distributions at a narrow boundary at the magnetopause flank. Burch et al. (2019) found that the electron distributions associated with two EDRs in the magnetotail were unstable to large-amplitude Langmuir/beam-mode and UH waves. The observations showed that these wave reach large amplitudes (~ 100 mV m⁻¹), and nonlinear behavior in the form of electrostatic harmonics was observed (Dokgo et al., 2019). In each case a beam-plasma interaction was found to be the source of instability.

At present, there are very few simulations on plasma-frequency waves associated with magnetic reconnection, due to the difficulty in resolving at the same time Debye-scale high-frequency waves, low-density electron beams, and the overall reconnection structure. However, Fujimoto (2014) found beam-mode waves in the separatrices of symmetric reconnection. Recently, Dokgo et al. (2019) performed a local homogeneous simulation of UH waves generated by an agyrotropic electron crescent. They found that electrostatic beam-mode-like waves were generated, consistent with observations. Additionally, they found that weak electromagnetic waves were generated at the fundamental and second harmonic frequencies due to nonlinear processes.

Langmuir and UH waves are important because they are a source of coherent freely propagating electromagnetic waves (O and X modes in a magnetized plasma) near the local plasma frequency and harmonics (in the radio frequency range). The generation of radio waves has primarily been studied in the solar wind and at planetary foreshocks [e.g., Melrose (2017), and references therein]. For example, type III radio bursts are associated with fast electron beams originating from the Sun, and are likely accelerated by magnetic reconnection. There are several mechanisms proposed for electromagnetic waves, including three-wave decay and coalescence, three-wave electromagnetic decay, linear mode conversion, and antenna mechanisms associated with nonlinear currents. The recent observations of Langmuir and UH waves associated with reconnection suggests that radio waves may be generated in or near reconnection diffusion regions and the separatrices. The Langmuir and UH waves were observed at large-amplitudes, which suggests that nonlinear three-wave processes could occur. The waves observed in the separatrices and near the EDR, where density gradients are expected to occur, so linear mode conversion may be a viable source of radio emission. At present direct observations of electromagnetic waves generated at reconnection sites are currently lacking. Although studying radio emission source regions is challenging because the electrostatic waves at the plasma frequency and harmonics tend to dominate the electric field power, the observations provided by the four closely separated MMS spacecraft may provide a unique opportunity to study radio wave emission.

2.2. Broadband E_|| Waves

In this section we discuss broadband electrostatic waves (EWs) that propagate parallel to the ambient magnetic field. One subgroup of EWs are electrostatic solitary waves (ESWs), which are highly nonlinear solitary structures characterized by bipolar electric fields in the direction parallel to the ambient magnetic field. The bipolar electric field is associated with an electrostatic potential, and when this potential is positive, the ESWs are generally interpreted as propagating electron phase spaces holes (EHs) with inherently strong electron trapping. Following the initial work of Bernstein et al. (1957), a lot of attention has been spent on theoretical modeling of EHs. However, it was not until recently that MMS could make the first observations of the phase space depletion associated with ESWs (Mozer et al., 2018).

The frequencies of EWs and ESWs can extend from below the ion plasma frequency to the electron plasma frequency. Figure 4a shows an example of EW and ESW waveforms. Figure 4c shows a closeup of bipolar E_|| structures characteristic of ESWs, and Figure 4d shows a more periodic EW waveform. The corresponding spectral representation of waves is shown in Figure 4b, the wave spectrum is broadband, covering the frequency range between f_pi and above f_ce.

FIGURE 4

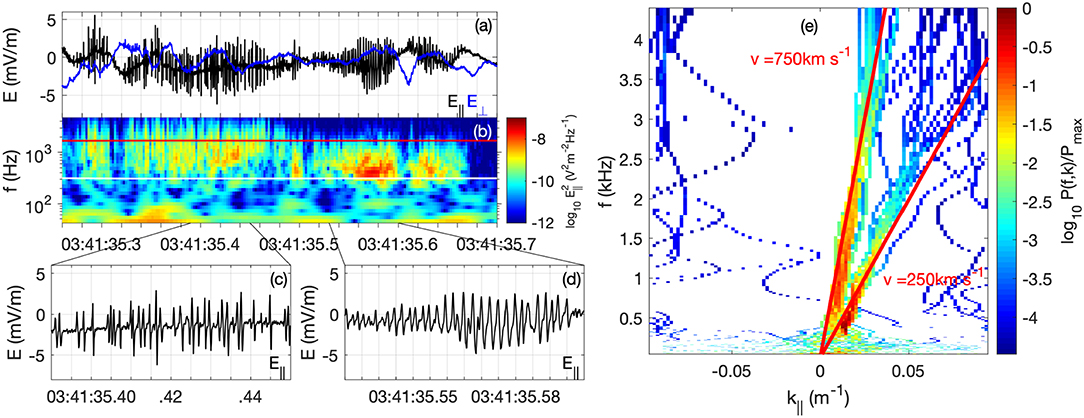
Figure 4. ESWs and electrostatic waves observed at a reconnecting magnetopause by Cluster (Graham et al., 2016b). (a) Waveforms of E_∥ and E_⊥. (b) Spectrogram of E_∥. The red and white lines are f_ce and f_pi. (c,d) E_∥ of the ESWs and more periodic electrostatic waves. (e) Frequency-wavenumber spectrum computed using multi-probe interferometry.

Already early Cluster observations have connected the appearances of ESWs with electron streaming at reconnection separatrices both in the magnetotail (Cattell, 2005) and the dayside magnetopause (Retinó et al., 2006). In the magnetotail, during individual reconnection events, ESWs have been observed in all four separatrix regions (Viberg et al., 2013); the ESWs were primarily observed at the inner side of separatrix regions, the side that is closest to the current sheet center, see Figure 1C. At the dayside magnetopause, EWs and ESWs were observed both at the magnetospheric and magnetosheath sides of the reconnection exhaust (Graham et al., 2015, 2016b). EWs and ESWs have also been routinely observed at dipolarization fronts (Le Contel et al., 2017) and inside magnetic islands produced by magnetic reconnection (Khotyaintsev et al., 2010).

The length scales of EWs and ESWs are on the order of several Debye lengths, and therefore they can develop at the smallest scales relevant to reconnection, i.e., within the EDR. Using multi-probe interferometry between the Cluster electric field probes separated by ~100 m, Graham et al. (2016b) found an average peak-to-peak length of 9λ_D at the magnetopause, with EWs having slightly smaller length scales than ESWs. This was later confirmed for ESWs by MMS using multi-spacecraft interferometry (Steinvall et al., 2019b). Also using multi-probe interferometry on Polar (Franz et al., 2005) found somewhat smaller length scales when investigating small-amplitude ESWs in the plasma sheet boundary layer. However, due to the limitations of single spacecraft interferometry (maximum probe separation ~100 m limiting the maximum speed which can be resolved), their study excluded the larger velocity structures, which may impact the perceived average length scales. The waves' phase speeds range from ~0 up to ≳v_Te and increased with increasing length scales (Franz et al., 2005; Graham et al., 2016b). The electric field amplitudes range from < 1 mV/m to a few hundreds mV/m in more rare cases (Graham et al., 2016b; Khotyaintsev et al., 2016), and are generally larger in the magnetotail than at the dayside magnetopause. Normalized to the electron temperature, the potential amplitude can span several orders of magnitude, from $e\varphi /k_B{T}_e=10^{-5}$ to above unity (Franz et al., 2005; Graham et al., 2016b; Norgren et al., 2019). At the magnetopause the potentials of EWs are in general lower than those of ESWs (Graham et al., 2016b). With MMS, four-spacecraft interferometry has become routinely applicable, resulting in unambiguous estimates of speeds and parallel length scales, and 3-D characterization of the wave structures (Holmes et al., 2018; Tong et al., 2018; Steinvall et al., 2019b).

Phase speeds of EWs and ESWs are highly dependent on their generation mechanism. For example, the Buneman instability which typically involves stationary ions and drifting electrons generates waves at low speeds, in general just above the ion thermal speed (Khotyaintsev et al., 2010; Norgren et al., 2015). Electron-electron streaming instabilities can generate waves at a large range of speeds, depending on the relative drift speed, temperature, and density of the electron populations (Omura et al., 1996). As such they have the potential to interact with a large part of the electron and ion populations and have generated considerable interest for their potential role in scattering and heating the plasma, and providing anomalous resistivity or drag.

Cluster showed that asymmetric reconnection was associated with EWs and ESWs propagating not only at different speeds, but also in different directions in close proximity to each other (Graham et al., 2015). The distinct wave speeds indicate the presence of complicated and/or evolving electron distributions, possibly related to complicated magnetic topologies and multiple source populations. Figure 4 shows observed waveforms together with the time-frequency and wavenumber-frequency spectrograms of two wave packages propagating at distinct speeds. On the magnetospheric side of the reconnection current layer, ESWs have been observed to propagate away from the X line (Khotyaintsev et al., 2016; Mozer et al., 2016). Khotyaintsev et al. (2016) observed a strong electron jet, also directed away from the X line, which was closely associated with the observed waves. The authors concluded that the waves were generated by the Buneman instability, and likely aided in the thermalization of the jet (Khotyaintsev et al., 2016). Another study from the magnetopause showed that the interaction of cold magnetospheric electrons with warm magnetosheath electrons made possible through magnetic reconnection can generate EWs (Ergun et al., 2016).

In symmetric antiparallel reconnection, the strongest field-aligned electron flows are formed at the four separatrices, by electrons streaming toward the X line (Fujimoto, 2014; Egedal et al., 2015; Norgren et al., 2019). Figure 5a shows the localized parallel bipolar electric fields developed as a consequence of these accelerated electron flows in a numerical simulation of symmetric magnetic reconnection (Fujimoto, 2014). The accelerated population and subsequent wave-particle interaction can be seen in the electron phase space in Figure 5b. The inflowing electrons are accelerated above the thermal energies toward the X line forming a beam, which gradually becomes more thermalized. The wave-particle interaction can be seen as modulations of the accelerated population. Figure 5c shows corresponding observations from a magnetic reconnection separatrix in the magnetotail made by MMS (Norgren et al., 2019). The colormap shows the 1-D reduced electron VDF, similar to Figure 5b. ESWs propagate toward the X line along the magnetic field with phase speeds v_ph (shown as dots) proportional to the beam speed. The bounding black lines show the range of speeds where the electrons can interact efficiently with the ESWs, defined as $v_{ph}\pm \sqrt{2e\varphi /m_e}$, where ϕ is the maximum potential of the ESWs. This interaction range is large enough to encompass the beam and indicates that the wave-particle interaction is strong and can contribute to thermalizing the beam. Through a numerical simulation, Hesse et al. (2018) found that the heating generated by the electrostatic turbulence at the separatrices led to macroscopic quasi-viscosity that contributed to the overall energy balance.

FIGURE 5

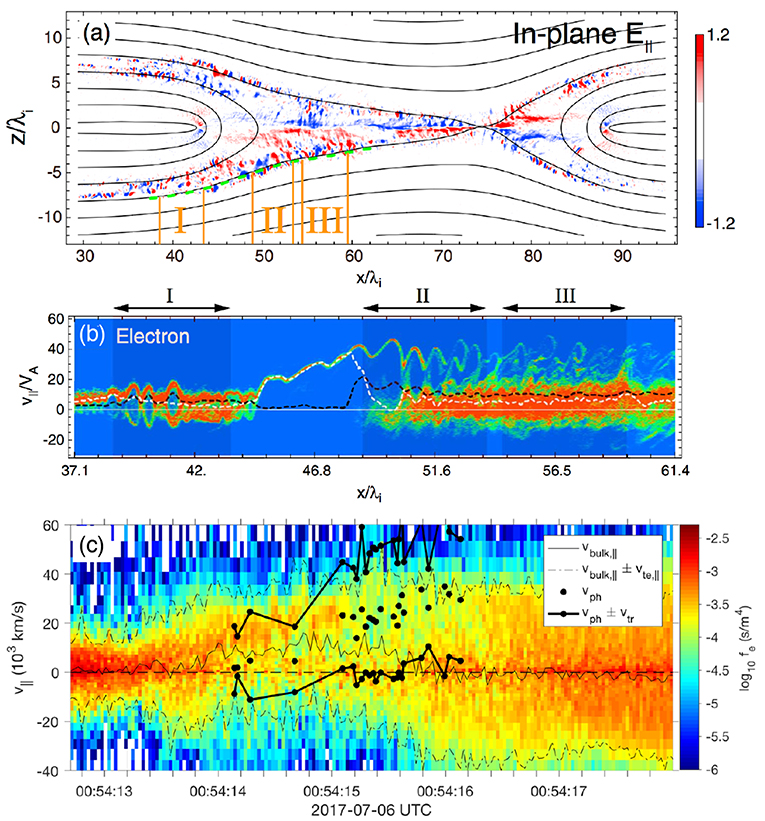
Figure 5. Electron phase space holes observed at the separatrix regions of magnetic reconnection. The electrons are accelerated toward the X line through a potential drop. The streaming electrons lead to instabilities and electron trapping. (a) Parallel electric fields and (b) reduced electron phase space density along the green dashed line in panel a of a numerical simulation of symmetric magnetic reconnection. The white dashed line shows the bulk velocity while the black line shows the thermal speed. Adapted from Fujimoto (2014). (c) MMS observations from a separatrix region in the magnetotail. The colormap shows the reduced electron VDF in which we can see how the lobe electrons become accelerated. The black dots show the speeds of individual ESWs, while the bounding black lines show the range of velocities in which the ESWs and particle distribution can interact efficiently.

In guide-field reconnection, the reconnection electric field has a component parallel to the magnetic field at the X line. This parallel electric field leads to enhanced field-aligned electron flows at two opposing of the four separatrices and merges them with the electron reconnection jet inside the EDR. At the same time the electron flows at the remaining two separatrices are suppressed. Numerical simulations showed that the intense field-aligned beams at the X line lead to electrostatic turbulence due to the relative drift between the ions and the electrons (Drake, 2003). The waves led to significant electron scattering and energization. However, while the anomalous drag associated with the waves was comparable in amplitude to the reconnection electric field, it was highly fluctuating and did not correlate spatially. Another numerical simulation predicted that the turbulence due to the electron jet in guide-field reconnection would evolve in two phases (Che et al., 2009). First, the Buneman instability would lead to the formation of electrostatic turbulence at low phase speeds and partially thermalize the beam. Eventually, the electron two-stream instability would take over, leading to higher phase speeds and continuing to thermalize the beam. This scenario was recently confirmed in an event study of guide-field reconnection at the dayside magnetopause by MMS (Khotyaintsev et al., 2019); it was shown that the electron reconnection jet was gradually thermalized due to the wave-particle interaction of broadband electrostatic turbulence.

While the thermalizing effect of ESWs on beams has been established, no quantitative estimates of anomalous resistivity, drag, cross field diffusion or momentum transfer due to ESWs have been made in association with magnetic reconnection. Vasko et al. (2017) derived diffusion coefficients based on ESWs observed in the inner magnetosphere, and found that the cross field diffusion due to the perpendicular electric fields was most efficient when the time scale of the ESWs as observed by the electrons were comparable to the local electron gyroperiod. As this should often the case for ESWs observed in magnetic reconnection regions, it is likely that cross field diffusion is also efficient here. The parallel electron beams generated by reconnection are closely associated with velocity shears, and at the separatrices also with density and pressure gradients. To quantify what effect these velocity shears and plasma gradients have on the wave instabilities, and how the wave-particle interaction affect the evolution of the plasma, wave quantities and gradients need to be measured simultaneously. This requires multi-scale separation of the spacecraft; separation on the order of electron kinetic scales to quantify the wave properties, and separation closer to ion kinetic scales to resolve plasma gradients. It is also necessary to compare the wave-particle interaction due to ESWs to that of the other wave modes commonly generated in the same regions, for example lower hybrid waves at the separatrices. In addition, to fully quantify the wave-particle interaction, even higher cadence velocity distribution function data than what are provided by MMS are required.

2.3. Whistlers

In the reconnection context, one of the most important properties of whistler waves is to provide fast and efficient pitch-angle scattering of electrons, which relaxes the temperature anisotropies and other non-thermal structures in the electron velocity distribution function (VDF). Whistlers can also transport energy in the form of Poynting flux, generally along the magnetic field. Whistlers have wavelength shorter than the ion inertial length, but much longer than the electron inertial lengths, so they are relevant for the scales larger than the typical EDR extent.

Whistlers are observed as fluctuations in E and B fields in the frequency range ~ 0.1f_ce < f < 1f_ce. The wave magnetic field polarization is right-handed and close to circular (Fu et al., 2019). Whistler magnetic fields typically have high degrees of polarization > 0.8, high ellipticity > +0.7, and high planarity > 0.8 (Taubenschuss et al., 2014). Figure 6 shows an example of whistlers with ~ 0.5f_ce < f < 1f_ce observed in the flux pileup region (FPR) at the front of a reconnection jet (Viberg et al., 2014). The waves can be clearly identified by the high degree of polarization (panel c) and ellipticity close to 1 (right-handed).

FIGURE 6

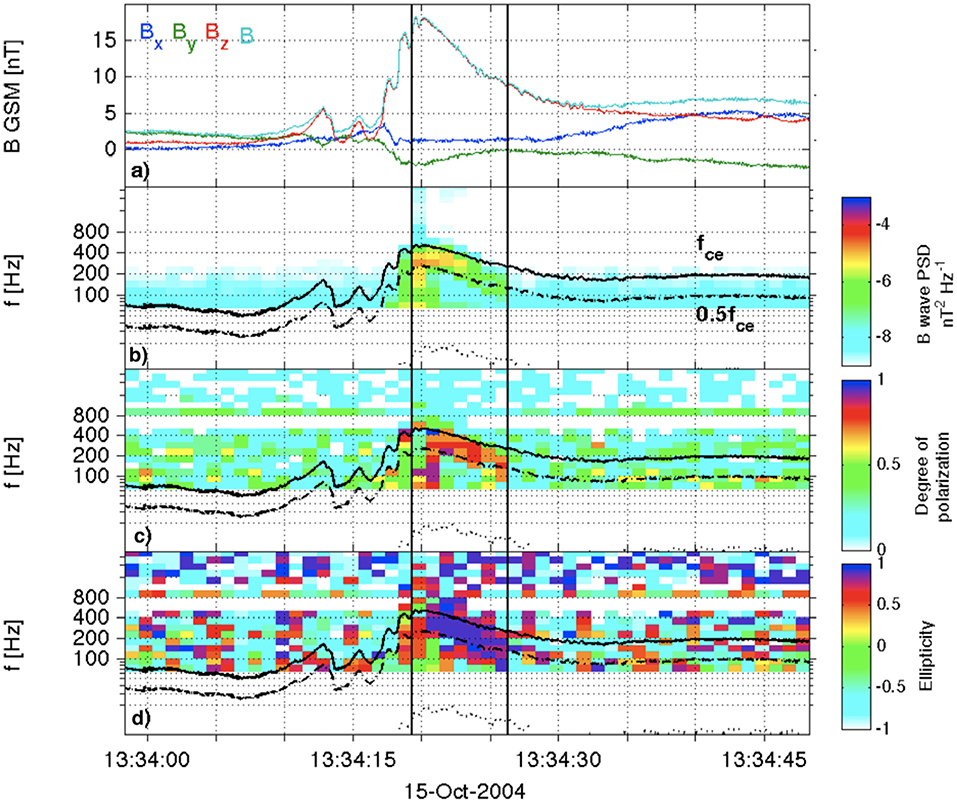
Figure 6. Example of whistler waves observed in the flux pileup region (FPR) at the front of a reconnection jet. (a) Magnetic field with clear increase in B_Z (FPR) characteristic for FPR (Sitnov et al., 2019). (b–d) Show power spectrum of magnetic fluctuations, degree of polarization and ellipticity all of which are enhanced in association with a whistler wave burst between 0.5 and 1 f_ce. Adapted from Viberg et al. (2014).

For quasi field-aligned wave vectors, small angle between the wave vector k and background B, whistlers are electromagnetic, while for larger angles approaching the resonance cone, the waves become quasi electrostatic. This change in wave characteristic with wave normal angle is illustrated in Figure 7B, which shows the E_long/E ratio, where E_long in the longitudinal (along k) component of the electric field.

FIGURE 7

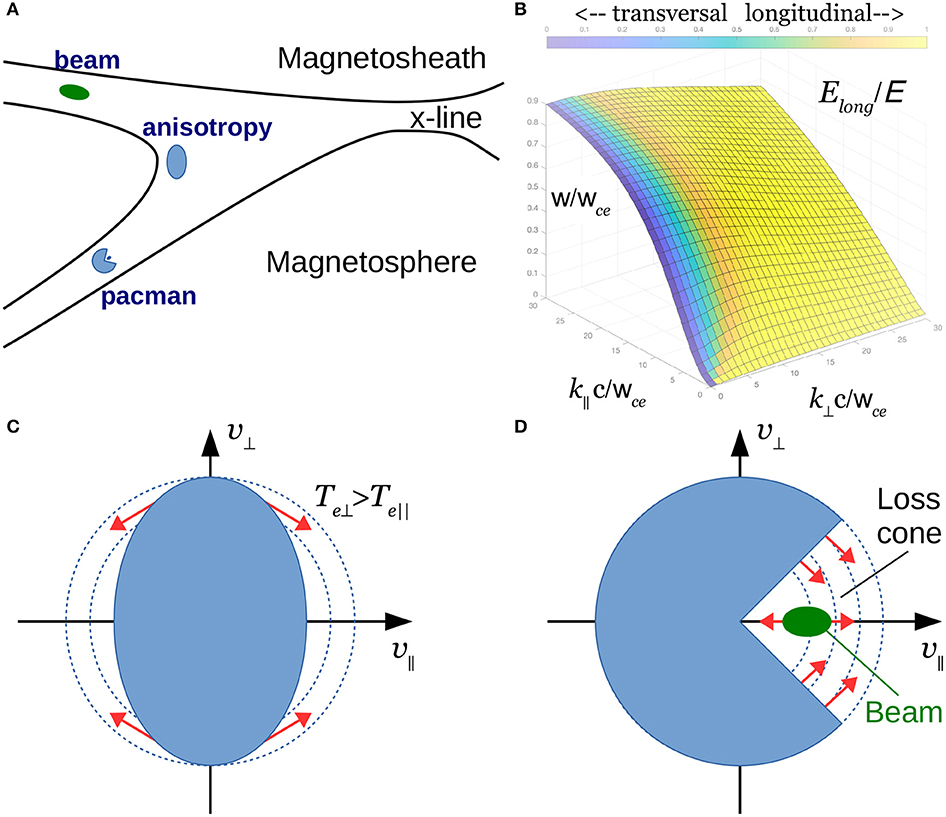
Figure 7. (A) Schematic of asymmetric (n_msh > n_sp, T_emsh < T_esp) magnetopause reconnection with 3 types of VDFs (anisotropy, beam, loss-cone+beam), (B) E_long/E on a whistler branch predicted from cold plasma theory, (C) anisotropic distribution with T_e⊥ > T_e||. (D) “Pacman” distribution—hot population with loss-cone and a cold beam. Red arrows in (C,D) illustrate pitch-angle scattering due to whistler generation.

In the context of reconnection whistlers were originally discussed in the frame of whistler mediated (Hall) reconnection (Mandt et al., 1994; Rogers et al., 2001), produced by the modified two-stream instability (MTSI) at ion kinetic scales within the reconnecting current sheet (Ji et al., 2004), or even as a means of triggering the reconnection (Wei et al., 2007). Whistlers were reported at reconnection sites using GEOTAIL and early Cluster data (Deng and Matsumoto, 2001; Khotyaintsev et al., 2004; Stenberg et al., 2005), without a clear conclusion on their role or generation mechanism. Since then good progress has been achieved in understanding where exactly the whistler appear in the reconnection picture. Detailed studies involving wave and electron data found that whistler generation can be attributed to unstable electron distributions, such as loss-cones, beams, and anisotropies, created by reconnection, see Figure 7.

Whistlers have been identified close to fronts of reconnection jets associated with regions of magnetic flux pileup (Le Contel et al., 2009; Khotyaintsev et al., 2011). This pileup occurs as the jet front region is squeezed in between the ambient plasma ahead of it and the jet itself. The pileup leads to betatron heating of electrons which creates a temperature anisotropy T_e⊥/T_e|| > 1, which becomes unstable to whistler generation. As a result, quasi field-aligned whistlers are generated by the cyclotron resonance. Whistlers introduce pitch-angle scattering at resonant energies which leads to relaxation of the anisotropy (Khotyaintsev et al., 2011). Figure 7C illustrates such an anisotropic distribution; red arrows show the direction of pitch-angle scattering. At energies above the resonant the behavior is close adiabatic (Fu et al., 2011, 2013). Based on a statistical study of dipolarization fronts (DF, likely reconnection jet fronts) in the magnetotail whistlers were found in 30–60% of studied DF cases, and that generally whistlers are 7 times more likely to be observed near a DF than at any random location in the magnetotail (Viberg et al., 2014). Statistically the waves were found close to the center of the current sheet and in association with anisotropic electron distributions. This confirms the case study by Khotyaintsev et al. (2011), where the location of the whistler source at the center of the current sheet has been determined from multi-spacecraft observations of the wave Poynting flux. However, in more complex reconnection configurations, as in the case of plasmoid coalescence (secondary reconnection), the source of pile-up driven whistlers can be located away from the center of the main current sheet (Fujimoto, 2017).

While the jet fronts are typically observed rather far (tens to hundreds of ion scales) from the X-line, the same FPR driven anisotropy can operate even within the diffusion region. A statistical survey of reconnection sites observed by Cluster have shown that the whistler waves are most often found in the pileup and separatrix regions (Huang et al., 2017). Using high resolution 2D PIC simulation, Fujimoto and Sydora (2008) have shown whistler generation in the downstream region of the electron outflow, where similar flux pileup is driven by the electron jet. The anisotropy is maximum in the center of the current sheet, and this is where the waves are generated and propagate away from the center in both directions and away from the X-line. Anisotropy driven whistlers in the vicinity of the EDR have been reported using THEMIS and MMS observations (Tang et al., 2013; Khotyaintsev et al., 2016). Cao et al. (2017) studied wave generation in an EDR using a kinetic dispersion solver and observed electron distributions, and concluded that generation is due to the perpendicular temperature anisotropy of the slightly suprathermal (300 eV) electrons.

Another source of whistler generation related to reconnection is the loss-cone distributions created by reconnection in the separatrix regions for current sheets with very different electron temperatures on the two sides of the current sheet. A typical example of such a current sheet is the dayside magnetopause, with hot plasmasheet population of one side, and significantly colder magnetosheath population on the other side. As reconnection proceeds, previously closed magnetospheric field lines become connected to the magnetosheath, which enables escape of hot plasmasheet electrons with small pitch angles forming a loss-cone distribution at the magnetospheric side of the boundary. Figure 7D (but without the beam) shows an example of such a loss-cone distribution. Graham et al. (2016c) and Uchino et al. (2017) reported whistlers in the magnetopheric separatrix region at the dayside magnetopause. The wave generation was consistent with the loss-cone mechanism, and the observed waves propagated toward the X-line and had small wave normal angles (Graham et al., 2016b). Such waves should not be confused with similar quasi-field-aligned whistlers observed close to the separatrix but on closed field lines (Contel et al., 2016), which are generated at the magnetic equator or in high-latitude B-minima (Vaivads et al., 2007).

Also electron beams, which are characteristic of the seperatrix regions, can generate whistlers. The generation in this case is by Landau resonance, and thus the waves have oblique wave normal angles (Fujimoto, 2014; Muñoz and Büchner, 2016). As mentioned above, such oblique waves are more electrostatic than the quasi-parallel waves. Such a generation mechanism has been suggested by observations based on the connection between whistlers and ESWs (Huang et al., 2016; Wilder et al., 2016; Zhou et al., 2018). Such waves have oblique wave normal angles of ~45°, have large amplitude electric fields with polarization close to linear, i.e., E_⊥ and E_|| of similar amplitude (Wilder et al., 2017; Khotyaintsev et al., 2019). Solving a kinetic dispersion solver using the observed electron distributions suggests whistler generation by electron beams is viable for both magnetotail and magnetopause conditions (Khotyaintsev et al., 2019; Ren et al., 2019).

In addition to direct generation by the beam, Goldman et al. (2014) suggested that whistlers can be generated by electron holes (ESWs) propagating along the separatrices via the Čherenkov mechanism. However, until now there were no observations supporting this picture. Recent MMS observations in the magnetotail show existence of EHs with associated right-hand polarized magnetic components consistent with whistlers (Steinvall et al., 2019a). The magnetic signature is rather localized to the EHs, i.e., no freely propagating whistler is observed as suggested by simulations (Goldman et al., 2014). However, this result can be specific to the studied plasma conditions, and other conditions need to be investigated.

Deeper into the separatrix regions on the magnetospheric side of the magnetopause the loss-cone can co-exist with a beam distribution, where the beam consists of the magnetosheath electrons accelerated by reconnection, forming a “pacman” distribution, Figure 7D. Such distributions can be unstable to both quasi-parallel and oblique whistlers at the same time. This is supported by reported events where the quasi-parallel and oblique whistlers co-exist in the separatrix regions on the magnetospheric side of the magnetopause (Zhou et al., 2018; Khotyaintsev et al., 2019).

Figure 7A summarizes different types of VDFs leading to whistler generation in the vicinity of the X-line. While the pile-up and beam generation operate in any current sheet configurations, the loss-cone requires large electron temperature difference across the current sheet.

Following these recent observational advances, we now need to more quantitatively understand the role of whistler waves for reconnection. What is the efficiency of wave-particle interaction, scattering/pitch-angle diffusion rates? How much does the Poynting flux transported by whistlers away from the reconnection site contribute to overall energy dissipation? We need to better understand the overall interaction between EHs and whistlers. Also the loss-cone driven whistlers have not been simulated, and will require new high-resolution simulations. While for the beam driven whistler more detailed observations are needed to better understand and characterize them.

2.4. Lower Hybrid Waves

In magnetic reconnection, lower hybrid (LH) waves are one of the most extensively studied wave modes. LH waves are found near the LH frequency $f_{LH}\approx \sqrt{f_{ce}{f}_{ci}}$. In this frequency range the electrons remain approximately frozen in, while ions are approximately unmagnetized. LH waves were proposed as a source of anomalous resistivity, as well as electron and ion heating, and particle transport Davidson and Gladd (1975); Treumann et al. (1991); Cairns and McMillan (2005). The source of these waves is most often attributed to the lower hybrid drift instability (LHDI), which becomes unstable due to density gradients and the associated diamagnetic current. The closely related modified two-stream instability, as well as complex ion VDFs, are also sources of LH waves. Thus, the waves are expected to occur at plasma boundaries, including those associated with magnetic reconnection, where cross-field currents and gradients occur.

Theoretically, the wave properties have been studied extensively and are generally well understood. Both theory and simulations show that the fastest growing modes are quasi-electrostatic waves, which develop at the edges of current sheets where the density gradient is largest. Slower growing electromagnetic modes develop closer to the neutral point (Daughton, 2003). These electromagnetic modes can modify the structure of the current sheet, and are closely related to kink and sausage modes (e.g., Yoon et al., 2002).

Early spacecraft observations found large-amplitude electric field fluctuations at plasma boundaries, such as at Earth's magnetopause and plasma sheet boundary layer. The fluctuations were found to be close to the lower hybrid frequency (e.g., Cattell and Mozer, 1986; Bale et al., 2002).

Cluster and THEMIS observations have furthered our understanding of the wave properties, in particular the electromagnetic properties of the waves. For example, Zhou et al. (2009b) found quasi-electrostatic LH waves at the edge of a magnetotail current sheet and more electromagnetic waves near the center. Similar electromagnetic drift waves have been reported near the EDR of asymmetric reconnection by MMS (Ergun et al., 2017). Using Cluster, Norgren et al. (2012) were able to determine the phase speed and wavelength of the waves using observations from two closely separated spacecraft. The waves were found to have kρ_e ~ 0.5−1, consistent with quasi-electrostatic LH waves. The magnetic field fluctuations associated with the waves were found to be due to the electron motion associated with the electrostatic potential of the waves. Figure 8 (top) shows the electric field vectors from two spacecraft and schematic of the electron motion associated with the wave potential. From these two spacecraft observations regions of diverging and converging fields were observed, corresponding to positive and negative electrostatic potentials, respectively. Magnetic field fluctuations δB_∥ parallel and antiparallel to the background magnetic field were found to be correlated with diverging and converging electric fields. Figure 8 (bottom) shows the electron motion associated the electrostatic potentials of lower hybrid waves. The E × B motion of the electrons around the potential, and negligible ion motion, results in δB_∥, according to Ampere's law. The relationship between E_⊥ and B_∥ fluctuations can be used to estimate the phase velocity of the waves (Norgren et al., 2012).

FIGURE 8

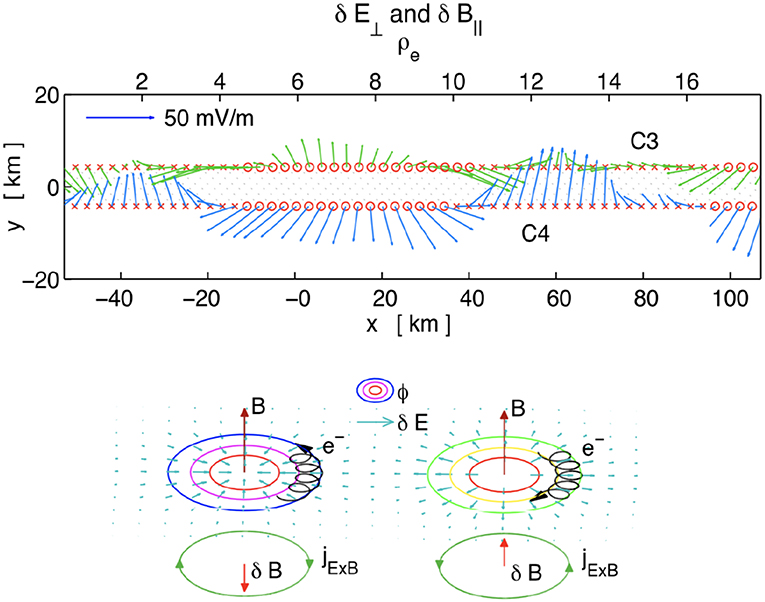
Figure 8. Example of lower hybrid waves observed by two Cluster spacecraft (Norgren et al., 2012). The waves had significant transverse electric fields forming alternating converging and diverging structures associated with corresponding negative and positive potentials, respectively. The potential structures and electric fields are associated with vortex-like electron motion as illustrated in the schematic.

Lower hybrid waves have often been observed at reconnection jet fronts/DFs (Zhou et al., 2009a; Khotyaintsev et al., 2011; Divin et al., 2015a; Greco et al., 2017; Pan et al., 2018). The cross-field current and density gradient associated with DFs provides the source of LH waves. The waves have properties similar to LH waves associated with reconnection, namely, they are quasi-electrostatic with kρ_e ~ 0.5. Pan et al. (2018) showed that the LH waves resulted in a rippling structure of a DF, which is seen as perturbations in B and n. Three-dimensional simulations have confirmed that LH waves are generated at DFs (Divin et al., 2015b). Some simulations show that DFs become rippled due to the kinetic interchange/ballooning instability (Pritchett and Coroniti, 2010; Vapirev et al., 2018), which is closely related to LHDI and produced waves with similar properties.

The anomalous contributions to magnetic reconnection have been evaluated with Cluster and THEMIS (Vaivads, 2004; Silin et al., 2005; Mozer et al., 2011), in particular the anomalous drag D = −〈δn_eδE〉/〈n_e〉 and the cross-field diffusion D_⊥, where 〈…〉 corresponds to spatial averaging. With these spacecraft only fields measurements are capable of resolving lower hybrid waves, so density perturbations were inferred using the spacecraft potential and electron velocity fluctuations were assumed to be moving at the convection velocity. These observations found that anomalous drag was small (Mozer et al., 2011), while cross-field diffusion can be significant (Vaivads, 2004).

Recently, lower hybrid waves have been frequently observed by MMS in the ion diffusion regions of magnetopause reconnection, where there is a large cross-field current and a density gradient (Graham et al., 2016a, 2017b; Khotyaintsev et al., 2016; Zhou et al., 2018). In each case the waves were found to be consistent with generation by LHDI and the estimated wavenumbers were kρ_e ~ 0.5, corresponding to the quasi-electrostatic mode. The waves were found at or adjacent to regions of intense parallel electron heating, reaching anisotropies up to T_∥/T_⊥ ~ 5 (Graham et al., 2017b). The wave properties were determined using the method in Norgren et al. (2012). In addition, Graham et al. (2017b) found a second group of LH waves in the magnetospheric inflow region driven by the interaction between cold magnetospheric ions and magnetosheath ions undergoing finite gyroradius motion on the magnetospheric side of the current sheet. These waves were suggested to be a source of heating of the cold ion population.

The anomalous fields associated with LH waves was recently investigated by Graham et al. (2017b) using the MMS spacecraft. Using four closely separated spacecraft enables a more reliable estimate of the anomalous terms associated with the LH waves. Figure 9 shows an example of LH waves observed at the reconnecting magnetopause and the estimated anomalous terms. Figures 9a,b show that the LH waves occur on the magnetospheric side of the current sheet. Figure 9c shows the electron density fluctuations inferred from the spacecraft potential. The density fluctuations are correlated with the electric field fluctuations of the waves. The anomalous drag D estimated from the four spacecraft peaks at close to 1 mV m⁻¹, similar to previous estimates. Figure 9e shows T_M = 〈δV_eNδB_L〉, which approximates the anomalous viscosity computed in numerical simulations (Price et al., 2016, 2017; Le et al., 2017, 2018). This term was found to be much smaller than D. Figure 9f shows that the cross-field diffusion coefficient D_⊥ reaches −0.8 × 10⁹ m² s⁻¹ and tends to be negative, corresponding to significant electron diffusion from the magnetosheath side of the current sheet to the magnetospheric side. These results are in good agreement with the earlier results of Cluster and THEMIS, and suggest that the anomalous fields do not contribute significantly to reconnection. However, like the Cluster and THEMIS observations, density perturbations were inferred from the spacecraft potential and the electron velocity fluctuations were inferred by assuming they undergo E × B drift motion, rather than direct particle measurements. Further work is therefore required to determine the precise role of LH waves in reconnection.

FIGURE 9

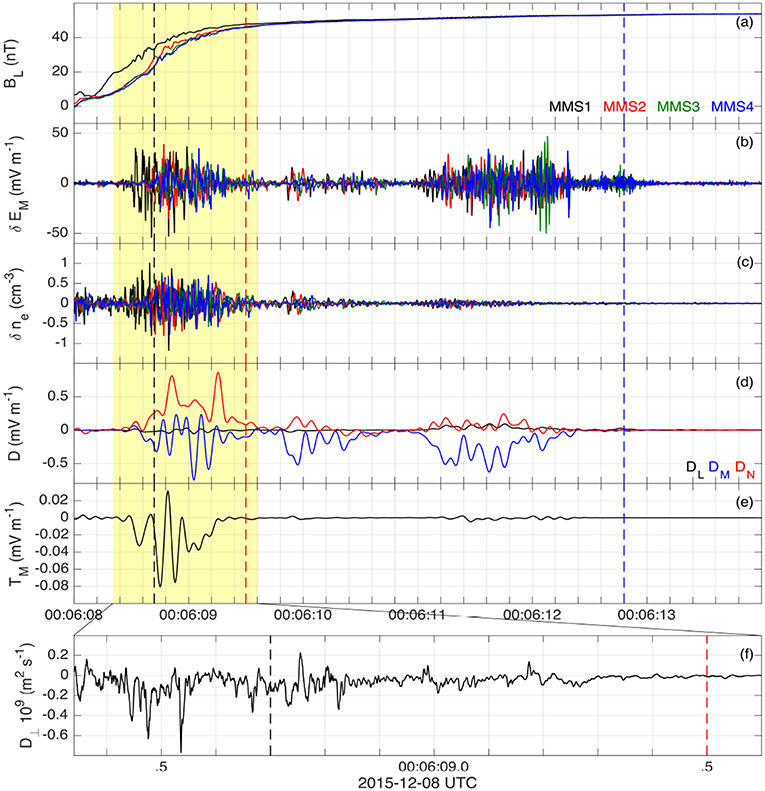
Figure 9. Anomalous terms associated with the LH waves at a reconnecting magnetopause. Figure is reproduced from Graham et al. (2017b). (a) B_L obtained from the four MMS spacecraft. (b) δE_M associated with LH waves. (c) δn_e associated with LH waves inferred from the spacecraft potential. (d,e) Anomalous drag D and anomalous viscosity T_M in the M direction estimated over the four spacecraft. (f) Cross-field diffusion coefficient D_⊥ associated with the diffusion region lower hybrid waves averaged over the four spacecraft. The black, red, and blue dashed lines mark the diffusion region, peak parallel electron heating, and ion edge, respectively (defined in Graham et al., 2017b).

The highest temporal resolution electron moments available on MMS are sufficiently high to resolve fluctuations at the lower hybrid frequency, enabling the wave properties to be studied in unprecedented detail. Recent observations by Graham et al. (2019) have confirmed that δE ≈ −δV_e × B for LH waves. In addition, large-amplitude δV_e,∥ were observed, indicating a finite k_∥ associated with the waves, which enables interaction with parallel propagating electrons via Landau resonance (Cairns and McMillan, 2005).

LH waves have been studied extensively with numerical simulations. However, only recently have three-dimensional simulations of magnetic reconnection been able investigate the role of LH waves. Recent simulations have investigated in detail the anomalous terms associated with LH waves generated by asymmetric reconnection (Price et al., 2016, 2017; Le et al., 2017, 2018). At present, the relative importance of the anomalous fields for ongoing reconnection is still debated. For example, Le et al. (2017) and Le et al. (2018) concluded that the anomalous terms were relatively unimportant, while Price et al. (2016) and Price et al. (2017) concluded that the anomalous terms were more important. Finally, Le et al. (2017) and Le et al. (2018) showed that parallel electron heating was enhanced in the magnetospheric inflow and separatrices when LH waves are present, compared with two-dimensional simulations, which suppress these waves. Lower hybrid waves can heat electron via Landau resonance if the waves have a finite parallel wave number (Cairns and McMillan, 2005). These intense regions of parallel heating have been observed by MMS (Graham et al., 2017b; Wang et al., 2017), although the relative importance of wave-particle interactions associated with LH waves vs. large-scale electric fields is still debated.

Further work is required to determine the role of anomalous contributions to reconnection, both with simulations and observations. Theoretical and numerical studies have shown that LH waves can heat electrons and ions. However, observational work is required to determine the role of lower hybrid waves in particle heating, and its relative importance to other processes associated with reconnection. Although observations have frequently been compared with theoretical predictions (typically in the local approximation), detailed comparisons of observations with simulations are generally lacking.

2.5. Ion Frequency Waves

At low frequencies below the lower hybrid frequency and particularly below the ion gyrofrequency, the ion dynamics start to dominate and ions are often the free energy source for those low frequency waves. Magnetic reconnection leads to ion distributions that are far from thermal equilibrium, such as temperature anisotropy, and which are thus potential free energy source for waves. The low frequency waves can be important for energy conversion, energy transport and structuring of the reconnection process. Despite the potential importance of these waves, they have not been extensively studied experimentally or in numerical simulations. Here we will first focus on one of the most important wave types—Kinetic Alfvén waves (KAWs), and at the end of the section mention also other types of plasma waves.

KAWs are known to be important in forming of the diffusion region (Rogers et al., 2001; Dai, 2009, 2018), in transporting energy away from the reconnection site (Shay et al., 2011; Liang et al., 2016), setting up field aligned currents and eventually also interacting with the ionosphere (Duan et al., 2016). There is no well defined way to identify KAWs in data. However, KAWs are characterized by wave vectors being close to perpendicular to the ambient magnetic field, electric/magnetic field ratio close to or above the local Alfvén speed, low values of magnetic field compression. KAWs have a characteristic scale size transverse to the ambient magnetic field that is comparable to or smaller than ion kinetic scales, while parallel scale that can be very large. KAWs transport energy along the magnetic field primarily through the Poynting flux, they are efficient in ion heating both perpendicular and parallel to the ambient magnetic field, as well as electron heating parallel to the magnetic field. In addition, parallel ion beams can form due to their Landau damping (Liang et al., 2017).

There are several mechanisms proposed for the generation of KAWs. One is the diffusion region itself where the setup of the Hall structure of the diffusion region directly corresponds to KAWs propagating away from the diffusion region along the separatrix regions (Shay et al., 2011; Zhang et al., 2017; Huang et al., 2018). Other mechanisms that have been suggested are the firehose instability leading to the generation of KAWs (Jiansen et al., 2018; Wang et al., 2018), KAW generation due to intermittent reconnection (Cao et al., 2013), KAWs being part of the turbulence generated in reconnection outflows (Huang et al., 2012). There has been progress in the understanding the relationship between KAWs and magnetic reconnection, but there are still many open questions.

On the observational side, in recent decades there have been KAW studies using Cluster, MMS and THEMIS data. The high resolution of the MMS data have enabled a very detailed analysis of KAWs within a reconnection outflow jet (Zhang et al., 2017), including KAW's dispersion properties and the associated wave-particle interactions (Gershman et al., 2017). Several studies have shown that significant earthward Poynting flux is carried by KAWs in the plasma sheet boundary layer (Stawarz et al., 2017) and in fast earthward flows within the plasma sheet (Chaston et al., 2012; Duan et al., 2016). It is widely accepted now that the fast flows in plasma sheet and active plasma sheet boundary layer are both result of magnetic reconnection. Figure 10 shows observations by THEMIS in fast earthward flows within plasma sheet where large energy fluxes in KAWs is observed. Observations show that ion energy flux dominates by more than a factor of ten the Poynting flux of KAWs indicating that ion flows are a potential source of KAWs. In addition, the Poynting flux intensity increases at distances below 15 R_E indicating that particularly reconnection jet breaking can be a source of KAWs. It is the consensus of most studies that the Poynting flux carried by KAW is sufficient to drive auroral acceleration processes down in the ionosphere (Angelopoulos et al., 2002; Chaston et al., 2012). Vaivads et al. (2010) have shown that in the case of asymmetric reconnection, the separatrix region on the low-density side (where Alfvén speed is higher) of the current sheet can develop a KAW edge in addition to well known electron and ion edges (Lindstedt et al., 2009), and the KAW edge lies in between ion and electron edges.

FIGURE 10

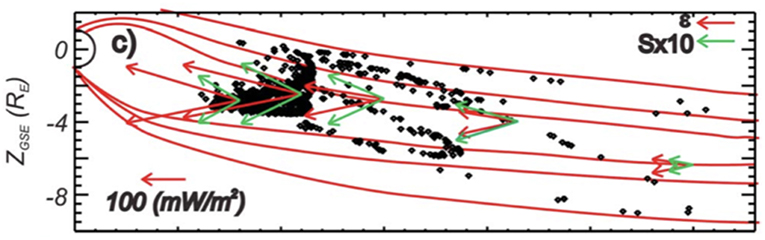
Figure 10. Average values of earthward ion energy flux (red arrows) and Poynting flux (green arrows) in the Earth's magnetotail (Chaston et al., 2012).

The progress on the theory/simulation side in the last decade has focused in several directions. One has been further development of the work by Rogers et al. (2001) showing the importance of KAWs in the structure of the reconnection diffusion region (Shay et al., 2011; Dai et al., 2017; Huang et al., 2018), particularly associating the Hall structure of magnetic reconnection diffusion and separatrix regions to KAWs propagating away from the reconnection site, see Figure 11. Another has been looking into the propagation of KAW along the separatrix region and showing that their damping is consistent with Landau damping (Sharma Pyakurel et al., 2018). Finally, there has been also work showing ion field-aligned acceleration due to KAWs (Liang et al., 2017).

FIGURE 11

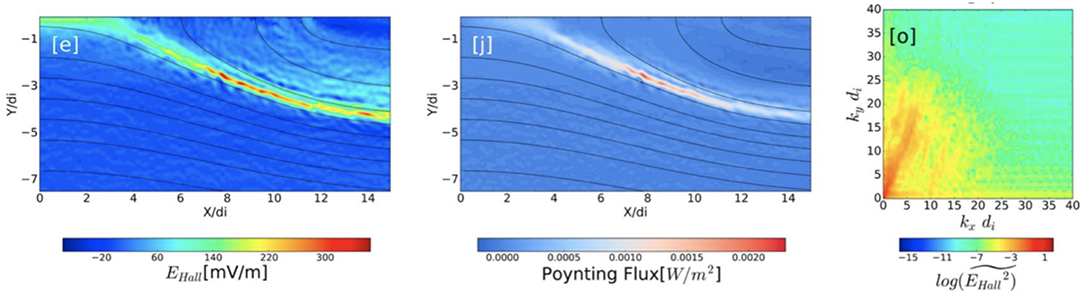
Figure 11. Kinetic Alfvén wave observations in the separatrix region using 2D PIC simulations (Huang et al., 2018). (Left) Hall electric field corresponding to KAW generated in reconnection diffusion region. (Middle) Poynting flux in X-direction showing large Poynting flux carried by KAW along the separatrix region away from the reconnection site. (Right) wave-number spectrum that shows that large amplitude electric fields are almost field aligned structures with perpendicular scale comparable to the ion kinetic scales and thus being consistent with KAW properties.

There are several open questions related to KAW and reconnection where we can expect significant progress in the nearest years. One is understanding KAW propagation to ionosphere, particularly using conjunction studies among spacecraft such as Cluster and MMS. Another is understanding electron field-aligned acceleration due to KAW, particularly non-linear mechanisms such as double layer formation. Another important question is the role of KAWs in ion heating including mass resolved observations. We know from low altitude ionospheric observations that KAWs can be very important for ion heating but similar systematic observations in relation to magnetic reconnection are lacking. Finally, we expect significant improvement in our understanding of KAW generation mechanisms in the reconnection jet outflow and breaking regions.

There are other low-frequency wave modes that have been recently addressed in several studies. One is firehose instability that requires large parallel anisotropy either due to the ion parallel heating or field aligned beams. Such anisotropies are observed in the reconnection outflow regions, particularly close to the separatrix region (Hietala et al., 2015). The firehose instability has been discussed also as a possible source of Pi2 pulsations that can occur in relation to the earthward reconnection jets (Wang et al., 2018). On the other hand, the statistical studies of fluctuations in reconnection jets have shown that, similar to the solar wind turbulence, the ion distribution functions show that their anisotropies are controlled by firehose, proton cyclotron and mirror instabilities (Vörös, 2011). More studies are needed, particularly kinetic scale studies using MMS data, to confirm the overall relationship between low-frequency modes and reconnection.

2.6. Discussion

Below we summarize our current understanding on how the wave occurrence and generation differ between the simplest symmetric antiparallel configuration of the reconnection site, and the ones with density and temperature asymmetries across the reconnecting layer, as well as with the presence of a guide field.

In symmetric antiparallel configurations the main agents driving waves are (1) electron dynamics in the EDR vicinity, (2) electron streaming in separatrix regions, (3) pileup of magnetic field, (4) cross-field currents at kinetic scales, and (5) ion dynamics in outflows.

(1) Complex electron dynamics in the EDR vicinity results in agyrotropic electron VDFs, such as crescents and agyrotropic beams. These distributions can be unstable to generation of large amplitude UH and Langmuir/beam-mode waves. The driving instabilities can be understood as non-magnetized beam-plasma instabilities, as they develop at scales below the electron gyroradius in weakly magnetized plasmas. And they lead to relaxation of the beams.

(2) Electron streaming in separatrix regions provides free energy for generation of Langmuir waves, EWs, ESWs, and oblique whistlers. The wave growth and subsequent nonlinear trapping of the streaming populations by large-amplitude waves leads to thermalization of the electron population, and generally couples the different streaming populations. For sufficiently slow wave speeds, the waves can couple the streaming electrons to ions (anomalous drag). Finite perpendicular extent of the waves and ESWs can also provide transfer of momentum across the velocity gradient (anomalous viscosity).

(3) Magnetic flux pileup leads to anisotropic distributions with T_e⊥ > T_e|| via the betatron mechanism. Such anisotropic distributions drive parallel whistlers. The whistlers then scatter the electron in pitch-angle, reducing the anisotropy. The scattering introduces non-adiabatic behavior into an otherwise adiabatic (betatron) electron response to the pileup, which results in overall electron heating (magnetic pumping).

(4) Cross-field currents at kinetic scales appear both in the ion diffusion region (Hall currents) as well as at the fronts of the reconnection jets where sharp gradients in density and the magnetic field exist. Such currents can drive LHDI, MTSI, and KAWs. LHDI is confined to the low-β side of the boundaries and its overall effect is to relax the driving gradient. This corresponds to cross-field diffusion of electrons. Despite the non-linear amplitudes typically observed at the magnetopause, LHDI does not provide substantial anomalous resistivity to support reconnection. LHDI can also lead to electron heating in the field-aligned direction. KAWs transport energy away from the reconnection region and heat ions (parallel and perpendicular to B) and electrons (parallel to B).

(5) Ion dynamics in the reconnection outflow jets results in development of strongly anisotropic ion VFDs. Like in the solar wind, the anisotropy range is controlled by firehose, proton cyclotron and mirror instabilities. Development of these instabilities leads to generation of low-frequency wave modes in the outflow and gradual thermalization of the ion VDFs.

In the general case, both the plasma density and temperature, as well as the magnetic field strength can be different on the two sides of the current sheet, which is usually the case at the magnetopause. The gradients in this case can be much more prominent than in the symmetric case. The gradient and the corresponding kinetic-scale cross-field currents drive LHDI and KAW.

(6) Large electron temperature asymmetry across the reconnection layer provides an additional driving agent, not present in symmetric reconnection. It can lead to unstable loss-cone distributions at the hotter side of the layer. Such loss-cones are created as the fast hot electrons escape to the other side of the layer once a field-line becomes reconnected. The unstable distributions can drive UH waves and field-aligned whistlers. The wave growth leads to pitch-angle scattering of resonant electrons, which fill the loss-cone. This reduces the ambipolar E_|| driven by the escape of the hot population and thus reduces acceleration by this E_|| of the colder component from the other side of the boundary.

(7) In a configuration with a guide field, the electron current at the X-line is a parallel current, with electrons being largely magnetized. Such fast electron flows at the X-line can become unstable, for example to the Buneman instability. The instabilities lead to thermalization of the electron distribution in the parallel to B direction, and thus to electron heating. The slow phase velocity of the Buneman instability allows it couple electrons to ions, and thus it can potentially introduce anomalous resistivity.

3. Summary and Outlook

In summary, there is great progress in understanding the waves in the context of collisionless magnetic reconnection over the last two decades, owing to the new data provided by the Cluster, THEMIS, and MMS missions. Localization of the different wave modes in the reconnection picture has been established. Reconnection jet fronts have been identified as important regions of energy conversion and wave generation. This new knowledge of waves can be particularly useful to study reconnection sites in planetary systems, in particular at kinetic scales, as planetary missions typically have comparable wave instruments to Cluster and MMS, but not the particle instruments.

There is substantial progress in quantification of the wave generation mechanisms and wave-particle interactions. While observed in the in-situ data, several waves modes (EC, UH, Langmuir, loss-cone whistler) are still challenging for simulations—instabilities which require fine coverage in phase space at the relevant energies, or Debye scales. More high-resolution simulations are needed to fully incorporate kinetic wave process into the reconnection theory.

Anomalous resistivity has been evaluated from the data for some waves (LHDI). To address the higher frequency waves new experimental data with faster electron measurements to resolve VDFs at the relevant time scale is needed.

There is little progress on understanding the electromagnetic radiation from reconnection sites using in situ observations, which is crucial for application to solar and astrophysical radio emissions. There is some indirect progress via better quantification of waves near the plasma frequency, but much more work is needed before one could use such in situ knowledge to better interpret radio emission from reconnection region at the Sun (Cairns et al., 2018).

Reconnection triggering/onset problem remains mostly theoretical, possibly because of difficulty of capturing the X-line formation in a dynamic unstable current sheet. Addressing this problem from an observational point of view can be done with a cross-scale multi-spacecraft configuration having a large number of points (more than 4), to simultaneously capture the large-scale current sheet evolution and the EDR. Cross-scale configurations of the existing space missions and new dedicated missions are needed to understand the coupling between the different parts of the reconnection region, the corresponding energy conversion, and particle acceleration.

Author Contributions

All authors participated in planning the paper and drafting the outline. Each of the authors had primary responsibility for at least one of the chapters, and secondary responsibility for several other chapters.

Funding

This work was supported by the Swedish National Space Agency, grant 128/17, and the Swedish Research Council, grant 2016-05507. Work at the University of Bergen was supported by the Research Council of Norway/CoE under contract 223252/F50.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work has been partially supported by International Space Science Institute (Bern).

References

Angelopoulos, V. (2008). The THEMIS mission. Space Sci. Rev. 141:5. doi: 10.1007/s11214-008-9336-1

CrossRef Full Text | Google Scholar

Angelopoulos, V., Chapman, J. A., Mozer, F. S., Scudder, J. D., Russell, C. T., Tsuruda, K., et al. (2002). Plasma sheet electromagnetic power generation and its dissipation along auroral field lines. J. Geophys. Res. Space Phys. 107, SMP 14–1–SMP 14–20. doi: 10.1029/2001JA900136

CrossRef Full Text | Google Scholar

Bale, S. D., Mozer, F. S., and Phan, T. (2002). Observation of lower hybrid drift instability in the diffusion region at a reconnecting magnetopause. Geophys. Res. Lett. 29, 33–1–33–4. doi: 10.1029/2002GL016113

CrossRef Full Text | Google Scholar

Bernstein, I. B., Greene, J. M., and Kruskal, M. D. (1957). Exact nonlinear plasma oscillations. Phys. Rev. 108, 546–550. doi: 10.1103/PhysRev.108.546

CrossRef Full Text | Google Scholar

Biskamp, D. (2000). Magnetic Reconnection in Plasmas (Cambridge Monographs on Plasma Physics). Cambridge: Cambridge University Press.

Google Scholar

Burch, J. L., Dokgo, K., Hwang, K. J., Torbert, R. B., Graham, D. B., Webster, J. M., et al. (2019). High-frequency wave generation in magnetotail reconnection: linear dispersion analysis. Geophys. Res. Lett. 46, 4089–4097. doi: 10.1029/2019GL082471

CrossRef Full Text | Google Scholar

Burch, J. L., Moore, T. E., Torbert, R. B., and Giles, B. L. (2016). Magnetospheric multiscale overview and science objectives. Space Sci. Rev. 199, 5–21. doi: 10.1007/s11214-015-0164-9

CrossRef Full Text | Google Scholar

Burch, J. L., Webster, J. M., Genestreti, K. J., Torbert, R. B., Giles, B. L., Fuselier, S. A., et al. (2018). Wave phenomena and beam-plasma interactions at the magnetopause reconnection region. J. Geophys. Res. Space Phys. 123, 1118–1133. doi: 10.1002/2017JA024789

PubMed Abstract | CrossRef Full Text | Google Scholar

Cairns, I. H., Lobzin, V. V., Donea, A., Tingay, S. J., McCauley, P. I., Oberoi, D., et al. (2018). Low altitude solar magnetic reconnection, type III solar radio bursts, and X-ray emissions. Sci. Rep. 8:1676. doi: 10.1038/s41598-018-19195-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Cairns, I. H., and McMillan, B. F. (2005). Electron acceleration by lower hybrid waves in magnetic reconnection regions. Phys. Plasmas 12:102110. doi: 10.1063/1.2080567

CrossRef Full Text | Google Scholar

Cao, D., Fu, H. S., Cao, J. B., Wang, T. Y., Graham, D. B., Chen, Z. Z., et al. (2017). MMS observations of whistler waves in electron diffusion region. Geophys. Res. Lett. 44, 3954–3962. doi: 10.1002/2017GL072703

CrossRef Full Text | Google Scholar

Cao, J. B., Wei, X. H., Duan, A. Y., Fu, H. S., Zhang, T. L., Reme, H., et al. (2013). Slow magnetosonic waves detected in reconnection diffusion region in the Earth's magnetotail. J. Geophys. Res. Space Phys. 118, 1659–1666. doi: 10.1002/jgra.50246

CrossRef Full Text | Google Scholar

Cattell, C. (2005). Cluster observations of electron holes in association with magnetotail reconnection and comparison to simulations. J. Geophys. Res. 110:A01211. doi: 10.1029/2004JA010519

CrossRef Full Text | Google Scholar

Cattell, C. A., and Mozer, F. S. (1986). Experimental determination of the dominant wave mode in the active near-Earth magnetotail. Geophys. Res. Lett. 13, 221–224. doi: 10.1029/GL013i003p00221

CrossRef Full Text | Google Scholar

Chaston, C. C., Bonnell, J. W., Clausen, L., and Angelopoulos, V. (2012). Correction to “Energy transport by kinetic-scale electromagnetic waves in fast plasma sheet flows”. J. Geophys. Res. Space Phys. 117:A09202. doi: 10.1029/2012JA018476

CrossRef Full Text | Google Scholar

Che, H., Drake, J. F., Swisdak, M., and Yoon, P. H. (2009). Nonlinear development of streaming instabilities in strongly magnetized plasma. Phys. Rev. Lett. 102:145004. doi: 10.1103/PhysRevLett.102.145004

PubMed Abstract | CrossRef Full Text | Google Scholar

Contel, O. L., Retinò, A., Breuillard, H., Mirioni, L., Robert, P., Chasapis, A., et al. (2016). Whistler mode waves and Hall fields detected by MMS during a dayside magnetopause crossing. Geophys. Res. Lett. 43, 5943–5952. doi: 10.1002/2016GL068968

CrossRef Full Text | Google Scholar

Dai, L. (2009). Collisionless magnetic reconnection via Alfvén eigenmodes. Phys. Rev. Lett. 102:245003. doi: 10.1103/PhysRevLett.102.245003

PubMed Abstract | CrossRef Full Text | Google Scholar

Dai, L. (2018). Structures of hall fields in asymmetric magnetic reconnection. J. Geophys. Res. Space Phys. 123, 7332–7341. doi: 10.1029/2018JA025251

CrossRef Full Text | Google Scholar

Dai, L., Wang, C., Zhang, Y., Lavraud, B., Burch, J., Pollock, C., et al. (2017). Kinetic Alfvén wave explanation of the Hall fields in magnetic reconnection. Geophys. Res. Lett. 44:2016GL071044. doi: 10.1002/2016GL071044

CrossRef Full Text | Google Scholar

Daughton, W. (2003). Electromagnetic properties of the lower-hybrid drift instability in a thin current sheet. Phys. Plasmas 10, 3103–3119. doi: 10.1063/1.1594724

CrossRef Full Text | Google Scholar

Davidson, R. C., and Gladd, N. T. (1975). Anomalous transport properties associated with the lower-hybrid-drift instability. Phys. Fluids 18, 1327–1335. doi: 10.1063/1.861021

CrossRef Full Text | Google Scholar

Deng, X. H., and Matsumoto, H. (2001). Rapid magnetic reconnection in the Earth's magnetosphere mediated by whistler waves. Nature 410, 557–560. doi: 10.1038/35069018

PubMed Abstract | CrossRef Full Text | Google Scholar

Deng, X. H., Matsumoto, H., Kojima, H., Mukai, T., Anderson, R. R., Baumjohann, W., et al. (2004). Geotail encounter with reconnection diffusion region in the Earth's magnetotail: evidence of multiple X lines collisionless reconnection? J. Geophys. Res. Space Phys. 109:A05206. doi: 10.1029/2004JA010632

CrossRef Full Text | Google Scholar

Divin, A., Khotyaintsev, Y. V., Vaivads, A., and André, M. (2015a). Lower hybrid drift instability at a dipolarization front. J. Geophys. Res. Space Phys. 120, 1124–1132. doi: 10.1002/2014JA020528

CrossRef Full Text | Google Scholar

Divin, A., Khotyaintsev, Y. V., Vaivads, A., André, M., Markidis, S., and Lapenta, G. (2015b). Evolution of the lower hybrid drift instability at reconnection jet front. J. Geophys. Res. Space Phys. 120, 2675–2690. doi: 10.1002/2014JA020503

CrossRef Full Text | Google Scholar

Dokgo, K., Hwang, K.-J., Burch, J. L., Choi, E., Yoon, P. H., Sibeck, D. G., et al. (2019). High-frequency wave generation in magnetotail reconnection: nonlinear harmonics of upper hybrid waves. Geophys. Res. Lett. doi: 10.1029/2019GL083361

PubMed Abstract | CrossRef Full Text | Google Scholar

Drake, J. F. (2003). Formation of electron holes and particle energization during magnetic reconnection. Science 299, 873–877. doi: 10.1126/science.1080333

PubMed Abstract | CrossRef Full Text | Google Scholar

Duan, S. P., Dai, L., Wang, C., Liang, J., Lui, A. T. Y., Chen, L. J., et al. (2016). Evidence of kinetic Alfvén eigenmode in the near-Earth magnetotail during substorm expansion phase. J. Geophys. Res. Space Phys. 121, 4316–4330. doi: 10.1002/2016JA022431

CrossRef Full Text | Google Scholar

Egedal, J., Daughton, W., Le, A., and Borg, A. L. (2015). Double layer electric fields aiding the production of energetic flat-top distributions and superthermal electrons within magnetic reconnection exhausts. Phys. Plasmas 22:101208. doi: 10.1063/1.4933055

CrossRef Full Text | Google Scholar

Ergun, R. E., Chen, L.-J., Wilder, F. D., Ahmadi, N., Eriksson, S., Usanova, M. E., et al. (2017). Drift waves, intense parallel electric fields, and turbulence associated with asymmetric magnetic reconnection at the magnetopause. Geophys. Res. Lett. 44, 2978–2986. doi: 10.1002/2016GL072493

CrossRef Full Text | Google Scholar

Ergun, R. E., Holmes, J. C., Goodrich, K. A., Wilder, F. D., Stawarz, J. E., Eriksson, S., et al. (2016). Magnetospheric multiscale observations of large-amplitude, parallel, electrostatic waves associated with magnetic reconnection at the magnetopause: waves associated with reconnection. Geophys. Res. Lett. 43, 5626–5634. doi: 10.1002/2016GL068992

CrossRef Full Text | Google Scholar

Escoubet, C. P., Fehringer, M., and Goldstein, M. (2001). The cluster mission. Ann. Geophys. 19, 1197–1200. doi: 10.5194/angeo-19-1197-2001

CrossRef Full Text | Google Scholar

Farrell, W. M., Desch, M. D., Kaiser, M. L., and Goetz, K. (2002). The dominance of electron plasma waves near a reconnection X-line region. Geophys. Res. Lett. 29, 8–1–8–4. doi: 10.1029/2002GL014662

CrossRef Full Text | Google Scholar

Farrell, W. M., Desch, M. D., Ogilvie, K. W., Kaiser, M. L., and Goetz, K. (2003). The role of upper hybrid waves in magnetic reconnection. Geophys. Res. Lett. 30:2259. doi: 10.1029/2003GL017549

CrossRef Full Text | Google Scholar

Fox, W., Porkolab, M., Egedal, J., Katz, N., and Le, A. (2012). Observations of electron phase-space holes driven during magnetic reconnection in a laboratory plasma. Phys. Plasmas 19:032118. doi: 10.1063/1.3692224

CrossRef Full Text | Google Scholar

Franz, J. R., Kintner, P. M., Pickett, J. S., and Chen, L.-J. (2005). Properties of small-amplitude electron phase-space holes observed by Polar. J. Geophys. Res. Space Phys. 110:A09212. doi: 10.1029/2005JA011095

CrossRef Full Text | Google Scholar

Fu, H. S., Khotyaintsev, Y. V., André, M., and Vaivads, A. (2011). Fermi and betatron acceleration of suprathermal electrons behind dipolarization fronts. Geophys. Res. Lett. 38:L16104. doi: 10.1029/2011GL048528

CrossRef Full Text | Google Scholar

Fu, H. S., Khotyaintsev, Y. V., Vaivads, A., Retinò, A., and Andre, M. (2013). Energetic electron acceleration by unsteady magnetic reconnection. Nat. Phys. 9, 426–430. doi: 10.1038/nphys2664

CrossRef Full Text | Google Scholar

Fu, H. S., Peng, F. Z., Liu, C. M., Burch, J. L., Gershman, D. G., and Le Contel, O. (2019). Evidence of electron acceleration at a reconnecting magnetopause. Geophys. Res. Lett. 46, 5645–5652. doi: 10.1029/2019GL083032

CrossRef Full Text | Google Scholar

Fu, H. S., Vaivads, A., Khotyaintsev, Y. V., André, M., Cao, J. B., Olshevsky, V., et al. (2017). Intermittent energy dissipation by turbulent reconnection. Geophys. Res. Lett. 44, 37–43. doi: 10.1002/2016GL071787

CrossRef Full Text | Google Scholar

Fu, H. S., Vaivads, A., Khotyaintsev, Y. V., Olshevsky, V., André, M., Cao, J. B., et al. (2015). How to find magnetic nulls and reconstruct field topology with MMS data? J. Geophys. Res. Space Phys. 120, 3758–3782. doi: 10.1002/2015JA021082

CrossRef Full Text | Google Scholar

Fujimoto, K. (2014). Wave activities in separatrix regions of magnetic reconnection. Geophys. Res. Lett. 41, 2721–2728. doi: 10.1002/2014GL059893

CrossRef Full Text | Google Scholar

Fujimoto, K. (2017). Bursty emission of whistler waves in association with plasmoid collision. Ann. Geophys. 35, 885–892. doi: 10.5194/angeo-35-885-2017

CrossRef Full Text | Google Scholar

Fujimoto, K., and Sydora, R. D. (2008). Whistler waves associated with magnetic reconnection. Geophys. Res. Lett. 35:L19112. doi: 10.1029/2008GL035201

CrossRef Full Text | Google Scholar

Fujimoto, M., Shinohara, I., and Kojima, H. (2011). Reconnection and waves: a review with a perspective. Space Sci. Rev. 160, 123–143. doi: 10.1007/s11214-011-9807-7

CrossRef Full Text | Google Scholar

Gershman, D. J., F-Viñas, A., Dorelli, J. C., Boardsen, S. A., Avanov, L. A., Bellan, P. M., et al. (2017). Wave-particle energy exchange directly observed in a kinetic Alfvén-branch wave. Nat. Commun. 8:14719. doi: 10.1038/ncomms14719

PubMed Abstract | CrossRef Full Text | Google Scholar

Goldman, M., Newman, D., Lapenta, G., Andersson, L., Gosling, J., Eriksson, S., et al. (2014). Čerenkov emission of quasiparallel whistlers by fast electron phase-space holes during magnetic reconnection. Phys. Rev. Lett. 112:145002. doi: 10.1103/PhysRevLett.112.145002

PubMed Abstract | CrossRef Full Text | Google Scholar

Graham, D., Khotyaintsev, Y., Vaivads, A., Norgren, C., André, M., Webster, J., et al. (2017a). Instability of agyrotropic electron beams near the electron diffusion region. Phys. Rev. Lett. 119:025101. doi: 10.1103/PhysRevLett.119.025101

PubMed Abstract | CrossRef Full Text | Google Scholar

Graham, D. B., Khotyaintsev, Y. V., Norgren, C., Vaivads, A., Andre, M., Drake, J. F., et al. (2019). Universality of lower hybrid waves at Earth's magnetopause. JGR Space Phys. doi: 10.1029/2019JA027155. [Epub ahead of print].

CrossRef Full Text | Google Scholar

Graham, D. B., Khotyaintsev, Y. V., Norgren, C., Vaivads, A., André, M., Lindqvist, P.-A., et al. (2016a). Electron currents and heating in the ion diffusion region of asymmetric reconnection. Geophys. Res. Lett. 43, 4691–4700. doi: 10.1002/2016GL068613

CrossRef Full Text | Google Scholar

Graham, D. B., Khotyaintsev, Y. V., Norgren, C., Vaivads, A., André, M., Toledo–Redondo, S., et al. (2017b). Lower hybrid waves in the ion diffusion and magnetospheric inflow regions. J. Geophys. Res. Space Phys. 122, 517–533. doi: 10.1002/2016JA023572

CrossRef Full Text | Google Scholar

Graham, D. B., Khotyaintsev, Y. V., Vaivads, A., and André, M. (2015). Electrostatic solitary waves with distinct speeds associated with asymmetric reconnection. Geophys. Res. Lett. 42, 215–224. doi: 10.1002/2014GL062538

CrossRef Full Text | Google Scholar

Graham, D. B., Khotyaintsev, Y. V., Vaivads, A., and André, M. (2016b). Electrostatic solitary waves and electrostatic waves at the magnetopause. J. Geophys. Res. Space Phys. 121, 3069–3092. doi: 10.1002/2015JA021527

CrossRef Full Text | Google Scholar

Graham, D. B., Vaivads, A., Khotyaintsev, Y. V., and André, M. (2016c). Whistler emission in the separatrix regions of asymmetric magnetic reconnection. J. Geophys. Res. Space Phys. 121, 1934–1954. doi: 10.1002/2015JA021239

CrossRef Full Text | Google Scholar

Graham, D. B., Vaivads, A., Khotyaintsev, Y. V., André, M., Le Contel, O., Malaspina, D. M., et al. (2018). Large-amplitude high-frequency waves at earth's magnetopause. J. Geophys. Res. Space Phys. 123, 2630–2657. doi: 10.1002/2017JA025034

CrossRef Full Text | Google Scholar

Greco, A., Artemyev, A., Zimbardo, G., Angelopoulos, V., and Runov, A. (2017). Role of lower hybrid waves in ion heating at dipolarization fronts. J. Geophys. Res. Space Phys. 122, 5092–5104. doi: 10.1002/2017JA023926

CrossRef Full Text | Google Scholar

Hesse, M., Norgren, C., Tenfjord, P., Burch, J. L., Liu, Y.-H., Chen, L.-J., et al. (2018). On the role of separatrix instabilities in heating the reconnection outflow region. Phys. Plasmas 25:122902. doi: 10.1063/1.5054100

CrossRef Full Text | Google Scholar

Hietala, H., Drake, J. F., Phan, T. D., Eastwood, J. P., and McFadden, J. P. (2015). Ion temperature anisotropy across a magnetotail reconnection jet. Geophys. Res. Lett. 42, 7239–7247. doi: 10.1002/2015GL065168

PubMed Abstract | CrossRef Full Text | Google Scholar

Holmes, J. C., Ergun, R. E., Newman, D. L., Ahmadi, N., Andersson, L., Contel, O. L., et al. (2018). Electron phase-space holes in three dimensions: multispacecraft observations by magnetospheric multiscale. J. Geophys. Res. Space Phys. 123, 9963–9978. doi: 10.1029/2018JA025750

CrossRef Full Text | Google Scholar

Huang, H., Yu, Y., Dai, L., and Wang, T. (2018). Kinetic alfvén waves excited in two-dimensional magnetic reconnection. J. Geophys. Res. Space Phys. 123, 6655–6669. doi: 10.1029/2017JA025071

CrossRef Full Text | Google Scholar

Huang, S. Y., Fu, H. S., Yuan, Z. G., Vaivads, A., Khotyaintsev, Y. V., Retino, A., et al. (2016). Two types of whistler waves in the hall reconnection region. J. Geophys. Res. Space Phys. 121, 6639–6646. doi: 10.1002/2016JA022650

CrossRef Full Text | Google Scholar

Huang, S. Y., Yuan, Z. G., Sahraoui, F., Fu, H. S., Pang, Y., Zhou, M., et al. (2017). Occurrence rate of whistler waves in the magnetotail reconnection region. J. Geophys. Res. Space Phys. 122, 7188–7196. doi: 10.1002/2016JA023670

CrossRef Full Text | Google Scholar

Huang, S. Y., Zhou, M., Sahraoui, F., Vaivads, A., Deng, X. H., André, M., et al. (2012). Observations of turbulence within reconnection jet in the presence of guide field. Geophys. Res. Lett. 39:L11104. doi: 10.1029/2012GL052210

CrossRef Full Text | Google Scholar

Ji, H., Terry, S., Yamada, M., Kulsrud, R., Kuritsyn, A., and Ren, Y. (2004). Electromagnetic fluctuations during fast reconnection in a laboratory plasma. Phys. Rev. Lett. 92:115001. doi: 10.1103/PhysRevLett.92.115001

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiansen, H., Xingyu, Z., Yajie, C., Chadi, S., Michael, S., Hui, L., et al. (2018). Plasma heating and alfvénic turbulence enhancement during two steps of energy conversion in magnetic reconnection exhaust region of solar wind. Astrophys. J. 856:148. doi: 10.3847/1538-4357/aab3cd

CrossRef Full Text | Google Scholar

Khotyaintsev, Y., Vaivads, A., Ogawa, Y., Popielawska, B., André, M., Buchert, S., et al. (2004). Cluster observations of high-frequency waves in the exterior cusp. Ann. Geophys. 22, 2403–2411. doi: 10.5194/angeo-22-2403-2004

CrossRef Full Text | Google Scholar

Khotyaintsev, Y. V., Cully, C. M., Vaivads, A., André, M., and Owen, C. J. (2011). Plasma jet braking: energy dissipation and nonadiabatic electrons. Phys. Rev. Lett. 106:165001. doi: 10.1103/PhysRevLett.106.165001

PubMed Abstract | CrossRef Full Text | Google Scholar

Khotyaintsev, Y. V., Graham, D. B., Norgren, C., Eriksson, E., Li, W., Johlander, A., et al. (2016). Electron jet of asymmetric reconnection. Geophys. Res. Lett. 43, 5571–5580. doi: 10.1002/2016GL069064

CrossRef Full Text | Google Scholar

Khotyaintsev, Y. V., Graham, D. B., Steinvall, K., Alm, L., Vaivads, A., Johlander, A., et al. (2019). Electron heating by debye-scale turbulence in guide-field reconnection. arXiv: 1908.09724.

Google Scholar

Khotyaintsev, Y. V., Vaivads, A., André, M., Fujimoto, M., Retinò, A., and Owen, C. J. (2010). Observations of slow electron holes at a magnetic reconnection site. Phys. Rev. Lett. 105:165002. doi: 10.1103/PhysRevLett.105.165002

PubMed Abstract | CrossRef Full Text | Google Scholar

Khotyaintsev, Y. V., Vaivads, A., Retinò, A., André, M., Owen, C. J., and Nilsson, H. (2006). Formation of inner structure of a reconnection separatrix region. Phys. Rev. Lett. 97:205003. doi: 10.1103/PhysRevLett.97.205003

PubMed Abstract | CrossRef Full Text | Google Scholar

Lazarian, A., Eyink, G., Vishniac, E., and Kowal, G. (2015). Turbulent reconnection and its implications. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 373:2041. doi: 10.1098/rsta.2014.0144

PubMed Abstract | CrossRef Full Text | Google Scholar

Le Contel, O., Nakamura, R., Breuillard, H., Argall, M. R., Graham, D. B., Fischer, D., et al. (2017). Lower hybrid drift waves and electromagnetic electron space-phase holes associated with dipolarization fronts and field-aligned currents observed by the magnetospheric multiscale mission during a substorm. J. Geophys. Res. Space Phys. 122, 12236–12257. doi: 10.1002/2017JA024550

CrossRef Full Text | Google Scholar

Le Contel, O., Roux, A., Jacquey, C., Robert, P., Berthomier, M., Chust, T., et al. (2009). Quasi-parallel whistler mode waves observed by THEMIS during near-earth dipolarizations. Ann. Geophys. 27, 2259–2275. doi: 10.5194/angeo-27-2259-2009

CrossRef Full Text | Google Scholar

Le, A., Daughton, W., Chen, L.-J., and Egedal, J. (2017). Enhanced electron mixing and heating in 3-D asymmetric reconnection at the Earth's magnetopause. Geophys. Res. Lett. 44, 2096–2104. doi: 10.1002/2017GL072522

CrossRef Full Text | Google Scholar

Le, A., Daughton, W., Ohia, O., Chen, L.-J., Liu, Y.-H., Wang, S., et al. (2018). Drift turbulence, particle transport, and anomalous dissipation at the reconnecting magnetopause. Phys. Plasmas 25:062103. doi: 10.1063/1.5027086

CrossRef Full Text | Google Scholar

Liang, J., Lin, Y., Johnson, J. R., Wang, X., and Wang, Z.-X. (2016). Kinetic Alfvén waves in three-dimensional magnetic reconnection. J. Geophys. Res. Space Phys. 121, 6526–6548. doi: 10.1002/2016JA022505

CrossRef Full Text | Google Scholar

Liang, J., Lin, Y., Johnson, J. R., Wang, Z.-X., and Wang, X. (2017). Ion acceleration and heating by kinetic Alfvén waves associated with magnetic reconnection. Phys. Plasmas 24:102110. doi: 10.1063/1.4991978

CrossRef Full Text | Google Scholar

Lindstedt, T., Khotyaintsev, Y. V., Vaivads, A., André, M., Fear, R. C., Lavraud, B., et al. (2009). Separatrix regions of magnetic reconnection at the magnetopause. Ann. Geophys. 27, 4039–4056. doi: 10.5194/angeo-27-4039-2009

CrossRef Full Text | Google Scholar

Liu, Y. Y., Fu, H. S., Olshevsky, V., Pontin, D. I., Liu, C. M., Wang, Z., et al. (2019). SOTE: a nonlinear method for magnetic topology reconstruction in space plasmas. Astrophys. J. Suppl. Ser. 244:31. doi: 10.3847/1538-4365/ab391a

CrossRef Full Text | Google Scholar

Mandt, M. E., Denton, R. E., and Drake, J. F. (1994). Transition to whistler mediated magnetic reconnection. Geophys. Res. Lett. 21, 73–76. doi: 10.1029/93GL03382

CrossRef Full Text | Google Scholar

Melrose, D. B. (2017). Coherent emission mechanisms in astrophysical plasmas. Rev. Mod. Plasma Phys. 1. doi: 10.1007/s41614-017-0007-0

CrossRef Full Text | Google Scholar

Mozer, F., Agapitov, O., Artemyev, A., Burch, J., Ergun, R., Giles, B., et al. (2016). Magnetospheric multiscale satellite observations of parallel electron acceleration in magnetic field reconnection by fermi reflection from time domain structures. Phys. Rev. Lett. 116:145101. doi: 10.1103/PhysRevLett.116.145101

PubMed Abstract | CrossRef Full Text | Google Scholar

Mozer, F., Agapitov, O., Giles, B., and Vasko, I. (2018). Direct observation of electron distributions inside millisecond duration electron holes. Phys. Rev. Lett. 121:135102. doi: 10.1103/PhysRevLett.121.135102

CrossRef Full Text | Google Scholar

Mozer, F. S., Wilber, M., and Drake, J. F. (2011). Wave associated anomalous drag during magnetic field reconnection. Phys. Plasmas 18:102902. doi: 10.1063/1.3647508

CrossRef Full Text | Google Scholar

Muñoz, P. A., and Büchner, J. (2016). Non-Maxwellian electron distribution functions due to self-generated turbulence in collisionless guide-field reconnection. Phys. Plasmas 23:102103. doi: 10.1063/1.4963773

CrossRef Full Text | Google Scholar

Norgren, C., André, M., Graham, D. B., Khotyaintsev, Y. V., and Vaivads, A. (2015). Slow electron holes in multicomponent plasmas. Geophys. Res. Lett. 42, 7264–7272. doi: 10.1002/2015GL065390

CrossRef Full Text | Google Scholar

Norgren, C., Hesse, M., Tenfjord, P., Graham, D. B., Khotyaintsev, Y. V., Vaivads, A., et al. (2019). Electron acceleration and thermalization at magnetotail separatrices. arXiv: 1908.11138.

Google Scholar

Norgren, C., Vaivads, A., Khotyaintsev, Y. V., and André, M. (2012). Lower hybrid drift waves: space observations. Phys. Rev. Lett. 109:055001. doi: 10.1103/PhysRevLett.109.055001

PubMed Abstract | CrossRef Full Text | Google Scholar

Omura, Y., Matsumoto, H., Miyake, T., and Kojima, H. (1996). Electron beam instabilities as generation mechanism of electrostatic solitary waves in the magnetotail. J. Geophys. Res. Space Phys. 101, 2685–2697. doi: 10.1029/95JA03145

CrossRef Full Text | Google Scholar

Osman, K. T., Kiyani, K. H., Matthaeus, W. H., Hnat, B., Chapman, S. C., and Khotyaintsev, Y. V. (2015). Multi-spacecraft measurement of turbulence within a magnetic reconnection jet. Astrophys. J. 815:L24. doi: 10.1088/2041-8205/815/2/L24

CrossRef Full Text | Google Scholar

Pan, D.-X., Khotyaintsev, Y. V., Graham, D. B., Vaivads, A., Zhou, X.-Z., André, M., et al. (2018). Rippled electron-scale structure of a dipolarization front. Geophys. Res. Lett. 45, 12116–12124. doi: 10.1029/2018GL080826

CrossRef Full Text | Google Scholar

Price, L., Swisdak, M., Drake, J. F., Burch, J. L., Cassak, P. A., and Ergun, R. E. (2017). Turbulence in three-dimensional simulations of magnetopause reconnection. J. Geophys. Res. Space Phys. 122, 11086–11099. doi: 10.1002/2017JA024227

CrossRef Full Text | Google Scholar

Price, L., Swisdak, M., Drake, J. F., Cassak, P. A., Dahlin, J. T., and Ergun, R. E. (2016). The effects of turbulence on three-dimensional magnetic reconnection at the magnetopause. Geophys. Res. Lett. 43, 6020–6027. doi: 10.1002/2016GL069578

CrossRef Full Text | Google Scholar

Pritchett, P. L., and Coroniti, F. V. (2010). A kinetic ballooning/interchange instability in the magnetotail. J. Geophys. Res. Space Phys. 115:A06301. doi: 10.1029/2009JA014752

CrossRef Full Text | Google Scholar

Ren, Y., Dai, L., Li, W., Tao, X., Wang, C., Tang, B., et al. (2019). Whistler waves driven by field-aligned streaming electrons in the near-earth magnetotail reconnection. Geophys. Res. Lett. 46, 5045–5054. doi: 10.1029/2019GL083283

CrossRef Full Text | Google Scholar

Retinó, A., Vaivads, A., André, M., Sahraoui, F., Khotyaintsev, Y., Pickett, J. S., et al. (2006). Structure of the separatrix region close to a magnetic reconnection X-line: cluster observations. Geophys. Res. Lett. 33:L06101. doi: 10.1029/2005GL024650

CrossRef Full Text | Google Scholar

Rogers, B. N., Denton, R. E., Drake, J. F., and Shay, M. A. (2001). Role of dispersive waves in collisionless magnetic reconnection. Phys. Rev. Lett. 87:195004. doi: 10.1103/PhysRevLett.87.195004

PubMed Abstract | CrossRef Full Text | Google Scholar

Sharma Pyakurel, P., Shay, M. A., Haggerty, C. C., Parashar, T. N., Drake, J. F., Cassak, P. A., et al. (2018). Super-Alfvénic propagation and damping of reconnection onset signatures. J. Geophys. Res. Space Phys. 123, 341–349. doi: 10.1002/2017JA024606

CrossRef Full Text | Google Scholar

Shay, M. A., Drake, J. F., Eastwood, J. P., and Phan, T. D. (2011). Super-Alfv\'enic propagation of substorm reconnection signatures and poynting flux. Phys. Rev. Lett. 107:065001. doi: 10.1103/PhysRevLett.107.065001

PubMed Abstract | CrossRef Full Text | Google Scholar

Silin, I., Büchner, J., and Vaivads, A. (2005). Anomalous resistivity due to nonlinear lower-hybrid drift waves. Phys. Plasmas 12:062902. doi: 10.1063/1.1927096

CrossRef Full Text | Google Scholar

Sitnov, M., Birn, J., Ferdousi, B., Gordeev, E., Khotyaintsev, Y., Merkin, V., et al. (2019). Explosive magnetotail activity. Space Sci. Rev. 215:31. doi: 10.1007/s11214-019-0599-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Stawarz, J. E., Eastwood, J. P., Varsani, A., Ergun, R. E., Shay, M. A., Nakamura, R., et al. (2017). Magnetospheric multiscale analysis of intense field-aligned Poynting flux near the Earth's plasma sheet boundary. Geophys. Res. Lett. 44, 7106–7113. doi: 10.1002/2017GL073685

CrossRef Full Text | Google Scholar

Steinvall, K., Khotyaintsev, Y. V., Graham, D. B., Vaivads, A., Contel, O. L., and Russell, C. T. (2019a). Observations of electromagnetic electron holes and evidence of cherenkov whistler emission. arXiv: 1908.11198.

Google Scholar

Steinvall, K., Khotyaintsev, Y. V., Graham, D. B., Vaivads, A., Lindqvist, P.-A., Russell, C. T., et al. (2019b). Multispacecraft analysis of electron holes. Geophys. Res. Lett. 46, 55–63. doi: 10.1029/2018GL080757

CrossRef Full Text | Google Scholar

Stenberg, G., Oscarsson, T., André, M., Vaivads, A., Morooka, M., Cornilleau-Wehrlin, N., et al. (2005). Electron-scale sheets of whistlers close to the magnetopause. Ann. Geophys. 23, 3715–3725. doi: 10.5194/angeo-23-3715-2005

CrossRef Full Text | Google Scholar

Tang, B.-B., Li, W. Y., Graham, D. B., Rager, A. C., Wang, C., Khotyaintsev, Y. V., et al. (2019). Crescent-shaped electron distributions at the nonreconnecting magnetopause: magnetospheric multiscale observations. Geophys. Res. Lett. 46, 3024–3032. doi: 10.1029/2019GL082231

CrossRef Full Text | Google Scholar

Tang, X., Cattell, C., Dombeck, J., Dai, L., Wilson, L. B., Breneman, A., et al. (2013). THEMIS observations of the magnetopause electron diffusion region: large amplitude waves and heated electrons. Geophys. Res. Lett. 40, 2884–2890. doi: 10.1002/grl.50565

CrossRef Full Text | Google Scholar

Taubenschuss, U., Khotyaintsev, Y. V., Santolík, O., Vaivads, A., Cully, C. M., Contel, O. L., et al. (2014). Wave normal angles of whistler mode chorus rising and falling tones. J. Geophys. Res. Space Phys. 119, 9567–9578. doi: 10.1002/2014JA020575

CrossRef Full Text | Google Scholar

Tong, Y., Vasko, I., Mozer, F. S., Bale, S. D., Roth, I., Artemyev, A. V., et al. (2018). Simultaneous multispacecraft probing of electron phase space holes. Geophys. Res. Lett. 45, 11513–11519. doi: 10.1029/2018GL079044

CrossRef Full Text | Google Scholar

Torbert, R. B., Dors, I., Argall, M. R., Genestreti, K. J., Burch, J. L., Farrugia, C. J., et al. (2019). A new method of 3d magnetic field reconstruction. arXiv: 1909.11255.

Google Scholar

Treumann, R. A., LaBelle, J., and Pottelette, R. (1991). Plasma diffusion at the magnetopause: the case of lower hybrid drift waves. J. Geophys. Res. Space Phys. 96, 16009–16013. doi: 10.1029/91JA01671

CrossRef Full Text | Google Scholar

Uchino, H., Kurita, S., Harada, Y., Machida, S., and Angelopoulos, V. (2017). Waves in the innermost open boundary layer formed by dayside magnetopause reconnection. J. Geophys. Res. Space Phys. 122, 3291–3307. doi: 10.1002/2016JA023300

CrossRef Full Text | Google Scholar

Vaivads, A. (2004). Cluster observations of lower hybrid turbulence within thin layers at the magnetopause. Geophys. Res. Lett. 31:L03804. doi: 10.1029/2003GL018142

CrossRef Full Text | Google Scholar

Vaivads, A., Khotyaintsev, Y., André, M., Retinò, A., Buchert, S., Rogers, B., et al. (2004). Structure of the magnetic reconnection diffusion region from four-spacecraft observations. Phys. Rev. Lett. 93:105001. doi: 10.1103/PhysRevLett.93.105001

PubMed Abstract | CrossRef Full Text | Google Scholar

Vaivads, A., Khotyaintsev, Y., André, M., and Treumann, R. (2006). “Plasma waves near reconnection sites,” in Geospace Electromagnetic Waves and Radiation, Lecture Notes in Physics, eds J. W. LaBelle and R. A. Treumann (Berlin; Heidelberg: Springer), 251–269.

Google Scholar

Vaivads, A., Retinò, A., Khotyaintsev, Y. V., and André, M. (2010). The Alfvén edge in asymmetric reconnection. Ann. Geophys. 28, 1327–1331. doi: 10.5194/angeo-28-1327-2010

CrossRef Full Text | Google Scholar

Vaivads, A., Santolík, O., Stenberg, G., André, M., Owen, C. J., Canu, P., et al. (2007). Source of whistler emissions at the dayside magnetopause. Geophys. Res. Lett. 34:L09106. doi: 10.1029/2006GL029195

CrossRef Full Text | Google Scholar

Vapirev, A., Lapenta, G., Divin, A., Markidis, S., Henri, P., Goldman, M., et al. (2018). Formation of a transient front structure near reconnection point in 3-D PIC simulations. J. Geophys. Res. Space Phys. 118, 1435–1449. doi: 10.1002/jgra.50136

CrossRef Full Text | Google Scholar

Vasko, I. Y., Agapitov, O. V., Mozer, F. S., Artemyev, A. V., Krasnoselskikh, V. V., and Bonnell, J. W. (2017). Diffusive scattering of electrons by electron holes around injection fronts. J. Geophys. Res. Space Phys. 122, 3163–3182. doi: 10.1002/2016JA023337

CrossRef Full Text | Google Scholar

Viberg, H., Khotyaintsev, Y. V., Vaivads, A., André, M., Fu, H. S., and Cornilleau-Wehrlin, N. (2014). Whistler mode waves at magnetotail dipolarization fronts. J. Geophys. Res. Space Phys. 119, 2605–2611. doi: 10.1002/2014JA019892

CrossRef Full Text | Google Scholar

Viberg, H., Khotyaintsev, Y. V., Vaivads, A., André, M., and Pickett, J. S. (2013). Mapping HF waves in the reconnection diffusion region. Geophys. Res. Lett. 40, 1032–1037. doi: 10.1002/grl.50227

CrossRef Full Text | Google Scholar

Vörös, Z. (2011). Magnetic reconnection associated fluctuations in the deep magnetotail: ARTEMIS results. Nonlin. Process. Geophys. 18, 861–869. doi: 10.5194/npg-18-861-2011

CrossRef Full Text | Google Scholar

Wang, C.-P., Xing, X., Liu, Y.-H., and Runov, A. (2018). A case study of connection between ground magnetic field perturbations and tail current sheet bursty flows at X = -60 RE. J. Geophys. Res. Space Phys. 123, 1822–1833. doi: 10.1002/2017JA024972

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, S., Chen, L.-J., Hesse, M., Wilson, L. B., Bessho, N., Gershman, D. J., et al. (2017). Parallel electron heating in the magnetospheric inflow region. Geophys. Res. Lett. 44, 4384–4392. doi: 10.1002/2017GL073404

CrossRef Full Text | Google Scholar

Wei, X. H., Cao, J. B., Zhou, G. C., Santolík, O., Rème, H., Dandouras, I., et al. (2007). Cluster observations of waves in the whistler frequency range associated with magnetic reconnection in the Earth's magnetotail. J. Geophys. Res. Space Phys. 112:A10225. doi: 10.1029/2006JA011771

CrossRef Full Text | Google Scholar

Wilder, F. D., Ergun, R. E., Goodrich, K. A., Goldman, M. V., Newman, D. L., Malaspina, D. M., et al. (2016). Observations of whistler mode waves with nonlinear parallel electric fields near the dayside magnetic reconnection separatrix by the Magnetospheric Multiscale mission. Geophys. Res. Lett. 43, 5909–5917. doi: 10.1002/2016GL069473

CrossRef Full Text | Google Scholar

Wilder, F. D., Ergun, R. E., Newman, D. L., Goodrich, K. A., Trattner, K. J., Goldman, M. V., et al. (2017). The nonlinear behavior of whistler waves at the reconnecting dayside magnetopause as observed by the Magnetospheric Multiscale mission: a case study. J. Geophys. Res. Space Phys. 122, 5487–5501. doi: 10.1002/2017JA024062

CrossRef Full Text | Google Scholar

Yamada, M., Kulsrud, R., and Ji, H. (2010). Magnetic reconnection. Rev. Mod. Phys. 82, 603–664. doi: 10.1103/RevModPhys.82.603

CrossRef Full Text | Google Scholar

Yoon, P. H., Lui, A. T. Y., and Sitnov, M. I. (2002). Generalized lower-hybrid drift instabilities in current-sheet equilibrium. Phys. Plasmas 9, 1526–1538. doi: 10.1063/1.1466822

CrossRef Full Text | Google Scholar

Zhang, Y. C., Lavraud, B., Dai, L., Wang, C., Marchaudon, A., Avanov, L., et al. (2017). Quantitative analysis of a Hall system in the exhaust of asymmetric magnetic reconnection. J. Geophys. Res. Space Phys. 122, 5277–5289. doi: 10.1002/2016JA023620

CrossRef Full Text | Google Scholar

Zhou, M., Ashour-Abdalla, M., Berchem, J., Walker, R. J., Liang, H., El-Alaoui, M., et al. (2016). Observation of high-frequency electrostatic waves in the vicinity of the reconnection ion diffusion region by the spacecraft of the Magnetospheric Multiscale (MMS) mission. Geophys. Res. Lett. 43, 4808–4815. doi: 10.1002/2016GL069010

CrossRef Full Text | Google Scholar

Zhou, M., Ashour-Abdalla, M., Deng, X., Schriver, D., El-Alaoui, M., and Pang, Y. (2009a). THEMIS observation of multiple dipolarization fronts and associated wave characteristics in the near-Earth magnetotail. Geophys. Res. Lett. 36:L20107. doi: 10.1029/2009GL040663

CrossRef Full Text | Google Scholar

Zhou, M., Berchem, J., Walker, R. J., El-Alaoui, M., Goldstein, M. L., Lapenta, G., et al. (2018). Magnetospheric multiscale observations of an ion diffusion region with large guide field at the magnetopause: current system, electron heating, and plasma waves. J. Geophys. Res. Space Phys. 123, 1834–1852. doi: 10.1002/2017JA024517

CrossRef Full Text | Google Scholar

Zhou, M., Deng, X. H., Li, S. Y., Pang, Y., Vaivads, A., Rème, H., et al. (2009b). Observation of waves near lower hybrid frequency in the reconnection region with thin current sheet. J. Geophys. Res. Space Phys. 114:A02216. doi: 10.1029/2008JA013427

CrossRef Full Text | Google Scholar