Progress in Global Helioseismology: A New Light on the Solar Modeling Problem and Its Implications for Solar-Like Stars

Since the first observations of solar oscillations in 1960, helioseismology has probably been one of the most successful fields of astrophysics. Data of unprecedented quality were obtained through the implementation of networks of ground-based observatories such as the GONG project or the BiSON network, coupled with space-based telescopes such as SOHO and SDO missions and more data is expected from the Solar Orbiter mission. Besides the improvement of observational data, solar seismologists developed sophisticated techniques to infer the internal structure of the Sun from its eigenfrequencies. These methods, then already extensively used in the field of Geophysics, are called inversion techniques. They allowed to precisely determine the position of the solar convective envelope, the helium abundance in this region and the internal radial profiles of given thermodynamic quantities. Back in 1990s these comparisons showed a very high agreement between solar models and the Sun. However, the downward revision of the CNO surface abundances in the Sun in 2005, confirmed in 2009, induced a drastic reduction of this agreement leading to the so-called solar modeling problem. More than 10 years later, in the era of the space-based photometry missions which have established asteroseismology of solar-like stars as a standard approach to obtain their masses, radii and ages, the solar modeling problem still awaits a solution. In this paper, we will present the results of new helioseismic inversions, discuss the current uncertainties of solar models as well as some possible solutions to the solar modeling problem. We will show how helioseismology can help us grasp what is amiss in our solar models. We will also show that, far from being an argument about details of solar models, the solar problem has significant implications for seismology of solar-like stars, on the main sequence and beyond, impacting asteroseismology as a whole as well as the fields requiring precise and accurate knowledge of stellar masses, radii and ages, such as Galactic archaeology and exoplanetology.

1. Introduction

For the past decades, helioseismology has been a thriving field, enjoying numerous successes and paving the way for asteroseismology of solar-like oscillators. These achievements are a consequence of the very high-quality seismic data obtained thanks to ground-based observation networks (Brookes et al., 1978; Harvey et al., 1988; Isaak et al., 1989) and space based observatories such as the SOHO satellite (Domingo et al., 1995).

These excellent data enabled the precise determination of the position of the base of the convective envelope (Christensen-Dalsgaard et al., 1991; Kosovichev and Fedorova, 1991; Basu and Antia, 1997), the determination of the solar rotation (Brown and Morrow, 1987; Kosovichev, 1988; Schou et al., 1998; Christensen-Dalsgaard and Thompson, 2007; García et al., 2007), density and sound speed profile (Antia and Basu, 1994) as well as an estimation of the helium abundance in the convective envelope through the use of sophisticated seismic analysis techniques (Vorontsov et al., 1991; Antia and Basu, 1994; Basu and Antia, 1995; Richard et al., 1998). The importance of helioseismology as a test of fundamental physics was also highlighted with the so-called solar neutrino problem, which was first thought to stem from inaccurate modeling of the solar core but was ultimately solved with the discovery of neutrino oscillations (Fukuda et al., 1999; Ahmad et al., 2002; Eguchi et al., 2003) and its impact for solar models (Turck-Chieze et al., 1988; Elsworth et al., 1990; Bahcall and Peña-Garay, 2004; Turck-Chièze, 2005; Turck-Chièze and Couvidat, 2011; Haxton et al., 2013). These successes led to the elaboration of stellar models well-suited for helioseismic studies and valided by seismic inversions (see for example Christensen-Dalsgaard et al., 1996) and served as a validation of the depiction of the solar structure and evolution to an excellent degree of accuracy.

However, the downward revision by about 30% of the abundances of carbon, nitrogen and oxygen determined in Asplund et al. (2004), Asplund et al. (2005b) revealed a new problem for standard models, the so-called solar metallicity, or solar modeling problem. This revision stems from the use of 3D atmospheric models instead of outdated 1D empirical models, from the inclusion of NLTE effects and from a careful selection of spectral lines. As C, N, and O are key contributors to the opacity in solar conditions, standard solar models built using the revised abundances from Asplund et al. (2005a) strongly disagreed with helioseismology (e.g., Turck-Chièze et al., 2004; Guzik, 2008). Further studies were performed in 2009, 2011, and 2015 (Asplund et al., 2009; Caffau et al., 2011; Grevesse et al., 2015; Scott et al., 2015a,b), showing that the 3D models agreed with each other and that the remaining differences were due to line selection effects. Recent re-investigations using spectroscopy further confirmed the results of 2009 and recent helioseismic determinations of the solar metallicity also agreed with a rather “low” value (Vorontsov et al., 2013; Buldgen et al., 2017d).

Quickly, it became clear that the solution to the solar metallicity problem was not purely a question of chemical abundances but could also be linked to other ingredients of the models. Investigations on various possible modifications to the solar models were rapidly performed following the publication of the revised abundances (see e.g., Bahcall et al., 2005a,b,c, 2006; Guzik et al., 2005, 2006; Delahaye and Pinsonneault, 2006; Montalban et al., 2006; Basu and Antia, 2008; Pinsonneault and Delahaye, 2009; Serenelli et al., 2009). These studies showed that a higher opacity could help solving the current discrepancies between solar models and helioseismology. This hypothesis gained some credence with the first experimental measurements of iron opacity in conditions close to those of the base of the solar convective envelope, showing strong disagreement with theoretical opacity computations (Bailey et al., 2015).

At the same time, new theoretical opacity computations became available for solar and stellar modeling (Le Pennec et al., 2015; Mondet et al., 2015; Colgan et al., 2016). Various groups showed that the modifications stemming from these recomputations were insufficient to solve the solar modeling problem and could even lead to larger discrepancies than before. Recently, Pradhan and Nahar (2018) and Zhao et al. (2018) presented new computations of iron opacity showing an increase compatible with experimental measurements. Yet, an opacity increase for a specific element will not necessarily be sufficient to solve the solar problem (Iglesias and Hansen, 2017) and other sources of uncertainties are present in the models.

Ultimately, the solar problem encompasses a wide variety of uncertain physical processes and key ingredients whose impacts are often neglected in standard stellar modeling. In this study, we will list some of the key contributors to the solar issue in section 2 and illustrate their impact on helioseismic constraints in section 3. We discuss the usual suspects of the micro- and macrophysics of the solar models but also briefly present some non-standard scenarios including accretion of material during the early stages of solar evolution as well as the hypothesis of an initial solar mass higher than the currently measured value. In addition, the solar modeling problem, despite its very specific nature, cannot be easily overlooked by stellar modelers. In the current era of high-quality asteroseismic data, stellar modelers are asked to provide very precise and accurate fundamental parameters for solar-like stars. This race to precision is however meaningless if the accuracy of the stellar models is not ensured. Currently, it is well known that the main limitations of stellar physics are the shortcomings of the theoretical models. Consequently, the solar modeling problem is still a very timely issue, as the recipe applied for the Sun is replicated for most of the solar-like oscillators. To illustrate the relevance of the solar modeling problem in asteroseismology, we briefly discuss in section 4 the impact of a potential solution to the solar problem on the seismic parameters of the 16Cyg binary system, one of the most observationally constrained solar-like oscillator, and discuss the potential use of seismic inversions to further constrain this system using asteroseismology. In section 5, we discuss some future prospects for solar models and further tracks for improving the physical accuracy of solar and stellar models. This discussion is then followed by a brief conclusion in section 6.

2. The solar modeling problem and its various contributors

While the solar modeling problem has at first been linked to the revision of the solar metallicity, its clear origin is still disputed and could well be the result of multiple small contributions from various micro- and macrophysical ingredients of the solar models. As such, the definition of the standard solar models derived by Bahcall et al. (1982) 30 years ago imposes a strict framework which does not take into account all the information we have on the solar structure.

A standard solar model is a one solar mass model, evolved to the solar age, taking microscopic diffusion into account and reproducing the current photospheric ratio of heavy elements over hydrogen, the current solar luminosity (or effective temperature) and the solar photospheric radius. To fulfill these constraints, the models are built using the initial abundance ratio of the heavy elements to hydrogen and the mixing length parameter for convection as free parameters of a minimization process. With this definition, the mathematical problem of reproducing the Sun is well-posed for a given set of constraints.

While this methodology leads to a simple approach for producing solar models using standard stellar evolution codes, it does not take into account all observational constraints. For example, standard solar models do not reproduce neither the rotation profile inside the Sun, nor the photospheric lithium abundance. Both constraints are well determined and point toward the absence or inaccurate implementation of various transport processes of both angular momentum and chemical elements in the current solar models.

Moreover, it is also clear that the mixing-length formalism of convection is inherently flawed and leads to an inaccurate depiction of both the upper layer of the solar convective envelope and its lower boundary, where additional chemical mixing is supposed to occur.

Finally, it should also be pointed out that standard solar model properties are strongly dependent on fundamental physical ingredients such as nuclear reaction rates, radiative opacities, chemical abundances, and the equation of state used for the stellar material.

Consequently, when discussing the inadequacy between standard solar models and helioseismic constraints, various contributors can be listed and could be held responsible for the observed disagreements. In the next sections, we will briefly discuss some of these contributors and their potential impact.

2.1. Chemical Abundances

The chemical abundances are the first and perhaps most important contributors to the solar modeling problem. The determination of the photospheric abundances of most elements heavier than helium is performed using spectroscopic data. For decades, spectroscopists used 1D empirical models of the solar atmosphere to determine the solar metallicity (e.g., Holweger and Mueller, 1974; Vernazza et al., 1976). These abundance tables are the so-called GN93 abundances from Grevesse and Noels (1993), which were used in the standard solar models of the 90s and led to the tremendous successes of helioseismology. They were slightly revised a couple of years later and recompiled in the so-called GS98 abundance tables (Grevesse and Sauval, 1998) still used today in helio- and asteroseismology.

The first solar abundance tables using 3D atmospheric models were the so-called AGS05 abundances (Asplund et al., 2005a) which initiated the solar modeling problem. These tables were revised in 2009 and became the AGSS09 abundance tables. Further determinations were made in 2011 and 2015 (Caffau et al., 2011; Grevesse et al., 2015; Scott et al., 2015a,b), one leading to an intermediate value between the GS98 and AGSS09 and the most recent confirming the results of 2009. Ultimately the remaining differences are related to the important aspects of line selection and blends (Allende Prieto et al., 2001), which can lead to different values for key chemical elements.

In a series of paper Bahcall et al. (2005c, 2006), Serenelli et al. (2009), and Vinyoles et al. (2017) discussed comparisons between standard solar models using photospheric and meteoritic abundances for the refractory elements. Comparisons between photospheric and meteoritic values for these elements have shown slight differences. Vinyoles et al. (2017) suggest that the meteoritic scale could be used as a higher precision substitute to the solar photospheric values. The main argument is that in recent revisions of solar abundances by Scott et al. (2015a,b) and Grevesse et al. (2015), the differences between photospheric and meteoritic values have been further reduced. However, this approach makes the assumption that the CI chondrites used to infer the meteoritic scale have not undergone any differentiation and represent a realistic sample of mean solar system materials. Recent investigations seem to indicate that this is not the case and that meteoritic abundances cannot be used as such substitutes for solar materials (N. Grevesse, private communication).

While spectroscopy is the most famous approach to determine the solar metallicity, helioseismology has also been used to derive this key ingredient of solar models. The first of such studies was performed by Takata and Shibahashi (2001), who favored a low value for the metallicity, in agreement with the results of AGS05. However, the precision of these results did not allow them to conclude, as the uncertainties were large enough to agree with all abundance tables. Antia and Basu (2006) used a different seismic technique and found an agreement with the GS98 abundance tables whereas Houdek and Gough (2011) found an intermediate value. Recently, Vorontsov et al. (2013) and Buldgen et al. (2017d) used different techniques and concluded that helioseismic methods favored a low metallicity in the solar envelope, more in agreement with the AGSS09 determination. Both studies stressed the strong dependency of these inferences on the equation of state, which dominates the uncertainties.

It is also worth noticing that the abundance of some elements cannot be directly inferred from spectroscopy of the solar photosphere. One of such elements is neon, which is derived from quiet regions of the solar corona (see Young, 2018, and references therein). Varying the neon abundance has a significant impact on opacity. Quickly after the revision of the solar abundances, Antia and Basu (2005) and Bahcall et al. (2005b) investigated the impact of changing the neon abundances to reconcile the AGS05 models with helioseismology. They found that a large increase was required. Recently, two independent studies (Landi and Testa, 2015; Young, 2018) have demonstrated that the abundance ratio of neon over oxygen should be increased by 40%, which leads to significant changes in solar models, but still well below the values found by previous studies.

The reason for this large impact of the abundances of elements heavier than helium is due to their large contribution to the radiative opacity inside the Sun (Blancard et al., 2012; Mondet et al., 2015). Despite their low abundance, they significantly shape the transport of energy in the radiative layers of the Sun, which represent most of its structure. This implies that they have a significant impact on the stratification of solar models and therefore on their (dis)agreement with observational constraints.

2.2. Opacity Tables

Since the transport of energy in most of the solar structure is carried out by radiation, it is unsurprising that the radiative opacities have a large impact on solar models. As the solar modeling problem was unveiled in 2004, the opacities were quickly pointed out as one of the potential causes of the discrepancies between the models and helioseismology (Basu and Antia, 2004).

Today, they remain one of the most uncertain elements of the solar models. Indeed, various tables disagree with each other and lead to significantly different solar models at the level of precision of helioseismic constraints. Moreover, none of the current tables provides a satisfactory agreement with helioseismic constraints with recent abundances. In this paper, we will present results using the OPAL (Iglesias and Rogers, 1996), OP (Badnell et al., 2005), OPAS (Mondet et al., 2015), and OPLIB (Colgan et al., 2016) tables which have been computed by different groups at different times. Moreover, purely numerical considerations are also relevant, related to the various approaches chosen for the interpolation procedure of the opacity tables (Houdek and Rogl, 1996).

These disagreements have motivated attempts to measure experimentally the opacity of key elements in physical conditions as close to solar as possible. The first of such measurements using a Z machine at the Sandia National Laboratories have been recently published for iron (Bailey et al., 2015) and showed large discrepancies with theoretical calculations of iron spectral opacities, between 30 and 400%. The origin of these discrepancies is still unclear and these experimental results still await independent confirmation. Nevertheless, various studies have been carried out to try to close the gap between theoretical calculations and the experiments (Iglesias, 2015; Blancard et al., 2016; Nahar and Pradhan, 2016; Iglesias and Hansen, 2017; Pain et al., 2018; Pradhan and Nahar, 2018; Zhao et al., 2018), some of which finding opacity increases compatible with the experimental results (Bailey et al., 2015). The debate is, however, still very much open and will probably require further extensive theoretical computations and comparisons with experiments.

2.3. Equation of State

Another key elements of solar models is the equation of state. Throughout the years, refinements to the equation of state have also contributed to improve the agreements of solar models with helioseismic constraints.

Two different approaches are used to compute an equation of state for stellar models. The first and most common approach is the so-called “chemical picture,” where the thermodynamical quantities are computed from a free-energy minimization approach. The chemical picture has been used in the computation of the CEFF (Christensen-Dalsgaard and Däppen, 1992), FreeEOS (Irwin, 2012), SAHA-S (Gryaznov et al., 2004; Gryaznov et al., 2006, 2013; Baturin et al., 2013), and MHD (Däppen et al., 1988; Hummer and Mihalas, 1988; Mihalas et al., 1988, 1990) equations of state. Moreover, in the regimes of astrophysical applications, effects as those of radiation pressure, relativistic corrections and electron degeneracy, amongst other, have to be included in the free energy and included consistently in the equation of state. Slight differences between various equations of state using the “chemical picture” might however result from different hypotheses made when taking into account these effects.

The other approach used in equation of state calculations is the so-called “physical picture,” which uses fundamental constituents and computes their interactions ab initio. Namely, this formalism considers separately atomic nuclei and electrons and describes their states using quantum wavefunctions. Again, additional corrections are included for astrophysical considerations. This approach has been used to compute the OPAL equation of state (Rogers et al., 1996; Rogers and Nayfonov, 2002).

The equation of state is a fundamental constituent of solar models, as it impacts indirectly multiple processes acting in solar and stellar interiors. For example, it influences the ionization levels of the chemical elements, which impacts the opacity at various temperatures. In some cases, differences between opacity tables do actually stem from the fact that a different equation of state has been associated with the computations. Consequently, one should in principle use opacity tables with the same equation of state employed in their computation. This is however unfortunately not always possible. The impact of the equation of state can also be directly seen in the sound-speed profile of solar models. This is particularly important when comparing models with various constituents with helioseismic inferences, as the equation of state will impact the results in a significant manner. The induced variations are such that it is often stated that inversions of density profile should not be done using kernels such as the (ρ, Y) kernels, as they lead to biases in the inferred profiles (see Basu et al., 2009, for a discussion and an illustration of this effect).

Moreover, differences in ionization level will impact diffusion velocities and hence the transport of chemicals during the evolution of the Sun. The equation of state also affects the adiabatic temperature gradient, which will influence the onset of convective transport and hence macroscopic mixing in solar and stellar models.

Various studies have been performed to improve the current equation of state in the solar models by carrying out inversions of the profile of the adiabatic exponent, ${\Gamma }_1=\frac{\partial lnP}{\partial ln\rho }{|}_S$ (e.g., Elliott, 1996; Basu and Christensen-Dalsgaard, 1997; Vorontsov et al., 2013).

2.4. Mixing of Chemical Elements

2.4.1. Microscopic Diffusion

It is well-known from first principle that a slow transport of the chemical elements is present in stellar radiative layers. This transport process is called microscopic diffusion and is linked to the various effects of temperature, pressure and composition gradients as well as the effects of ionization and radiation pressure with the various chemical elements of the stellar plasma. These effects induce chemical composition gradients in the stellar radiative regions and thus drastically change the expected initial chemical composition of solar models and their structure. In terms of nomenclature, solar models including the effects of microscopic diffusion are called “standard solar models” whereas models not including this transport process are called “classical solar models.” It was one of the big successes in the early days of helioseismology to show that diffusion was acting in the Sun and thus had to be included in stellar model computations (e.g., Christensen-Dalsgaard et al., 1993; Basu and Antia, 1994; Basu et al., 1996).

While it has been proven that solar models including microscopic diffusion are by far superior to models neglecting it, there are still some uncertainties linked to details in the physical processes underlying the generic term “microscopic diffusion” described in textbooks such as Burgers (1969), Chapman and Cowling (1970), Ferziger and Kaper (1972), and Michaud et al. (2015). As such, various approaches for its implementation exist in the literature (Michaud et al., 1976; Noerdlinger, 1977; Paquette et al., 1986; Michaud and Proffitt, 1993; Thoul et al., 1994), with various hypotheses linked to the components of the stellar plasma and the physical processes considered. It is also worth noticing that many standard solar models do not consider the effects of partial ionization nor the effects of radiation pressure when computing the transport of chemicals by microscopic diffusion. Including radiation pressure can be done in various ways; a simple approximate formula has been derived by Alecian and LeBlanc (2002), to avoid the full computation of radiative accelerations for each element, which is very expensive numerically. Indeed, computing the effects of radiation in a fully consistent manner requires to compute the opacities for each chemical element on the fly at the given conditions of the layer of stellar material. This requires to interpolate in the individual opacity tables whenever these are made available and is computationally very expensive. In the solar case, Turcotte et al. (1998) have demonstrated that these effects are negligible for the solar case. However, other studies have shown that slight modifications should be expected (Schlattl, 2002; Gorshkov and Baturin, 2008, 2010) while the radiative accelerations for certain elements will of course be ultimately influenced by potential significant opacity modifications. Other effects, such as quantum corrections on diffusion coefficients will also slightly affect the transport of chemical elements in the Sun and thus alter the (dis)agreement with helioseismic constraints (Schlattl and Salaris, 2003). Recently, careful investigations of the numerical integrations of the resistance coefficients have also been undertaken by Zhang (2017). This study found slight but significant modifications to the properties of solar models, resulting from singularities in the case of an attractive screened Coulomb potential. In addition, while many of these effects might well be of small importance, when not completely negligible for the Sun, this hypothesis does not hold for other stars (see e.g., Richard et al., 2002a,b; VandenBerg et al., 2002; Théado et al., 2005; Michaud and Richer., 2008; Theado and Vauclair, 2010; Deal et al., 2018).

2.4.2. Macroscopic Chemical Mixing at the Base of the Convective Zone

Besides microscopic diffusion, macroscopic motions of the solar plasma are also responsible for alterations of the chemical stratification inside the Sun. The most well-known process is turbulent convection, which occurs in the upper layers of the solar envelope. The modeling of convection is one of the most central problem in stellar astrophysics, as most of the current stellar evolution codes use the so-called mixing length theory (MLT) which is a very crude representation of the turbulent motions occurring in stellar conditions (Böhm-Vitense, 1958; Cox and Giuli, 1968). For the solar modeling problem, the shortcomings of the MLT are especially crucial for the positioning of the base of the convective zone and the transition from convective to radiative transport of energy. Indeed, the largest differences between the Sun and standard models are found right below the base of the convective zone.

The problem is linked to the criterion used to determine the extension of convective region, the so-called Schwarzschild criterion (Schwarzschild, 1906). This criterion is based on the cancelation of the convective flux, which translates into a local criterion for the temperature gradients inside the star. However, the cancelation of the flux does not necessarily imply a cancelation of the velocity of the convective elements, which is the parameter determining the extent of the mixed region. This extra-mixed region and its thermal stratification are still uncertain, although hydrodynamical simulations can provide some guidelines in the computation of this so-called “overshooting” or “penetrative convection” at the base of the solar convective zone (Xiong and Deng, 2001; Rempel, 2004; Li and Yang, 2007; Yang and Li, 2007; Viallet et al., 2015; Hotta, 2017). Helioseismology can also be used to provide some insights on the transition of the temperature gradient from adiabatic to radiative in this region (Monteiro et al., 1994; Christensen-Dalsgaard et al., 2011) but unfortunately, it is difficult to disentangle the effects of overshoot from the effects of opacities which can also alter the temperature gradient in these layers.

Besides the effects of overshooting, the base of the solar convective zone is also affected by the effects of rotation in a thin region called the tachocline (Spiegel and Zahn, 1992). In this region of around 0.04R_⊙ wide (Corbard et al., 1999; Elliott and Gough, 1999), the rotational profile of the Sun changes from differentally rotating in latitude to solid body rotating. This transition implies shear-induced mixing of the chemical elements. However, comparisons of helioseismic inversions of the solar rotation profile to rotating models have shown that the effects of meridional circulation and shear-induced turbulence were insufficient to reproduce the inferred properties. Hence, additional processes linked to magnetism or internal gravity waves have to be invoked to reproduce the solar rotation profile (Gough and McIntyre, 1998; Charbonnel and Talon, 2005; Eggenberger et al., 2005). These effects impact the chemical evolution of the Sun, being for example thought to be responsible for the observed lithium depletion and influencing the evolution of the solar convective zone. These effects, while localized, also slightly influence the calibration procedure and hence the initial chemical composition of the standard solar models (Proffitt and Michaud, 1991; Richard et al., 1996; Gabriel, 1997; Brun et al., 2002). It should be noted, however, that including these processes in a calibration procedure is extremely difficult and somewhat dangerous as they introduce additional parameters which are not constrained from first principles. Hence, further theoretical work is required to avoid the artificial fine-tuning of correlated parameters which could lead to spurious solutions. The recent detection of gravity modes by Fossat et al. (2017) could prove to be a game changer in that respect, by providing an average rotation of the solar core. This would provide a link between mean molecular weight and potential rotation gradients, providing very stringent constraints on the nature of the physical process responsible for the flat rotation profile of the upper radiative layers (Eggenberger et al., 2005). This detection, however, still needs to be confirmed independently as it has already triggered some controversy (Schunker et al., 2018).

The extra-mixing below the envelope is often treated in a parametric way, by introducing an additional turbulent diffusion coefficient depending on various parameters. In our study, we parametrize this diffusion coefficient as a function of ρ_cz, the density value at the base of the convective zone

$\begin{array}{ll}{D}_{Turb}=D{\left(\frac{{\rho }_{\text{cz}}}{\rho (r)}\right)}^N,& (1)\end{array}$

with the free parameters D [cm²s⁻¹], and N which were fixed to 7500 and 3 respectively in the work of Proffitt and Michaud (1991).

2.5. Early Evolution

In the previous sections, we discussed mainly effects that occurred largely on the main sequence and consisted in the “usual suspects” of the solar modeling problem. There are, however, other sources of uncertainties in the early solar evolution that could have an impact on the present-day solar structure as seen from helioseismic constraints.

These include accretion of material during the early stages of the formation of the solar system. This would lead to a contrast in the models, where the internal structure would behave as if the model had a high metallicity, whereas the upper layers would have the observed photospheric abundances. Accretion of low metallicity material was considered by Winnick et al. (2002), Guzik et al. (2006), or Castro et al. (2007). The proposed scenario was that 98% in mass of the Sun could have formed from metal-rich material, in agreement with the GS98 or GN93 abundances, while the last 2% of material would be metal-poor or metal-free and would have been accreted after the apparition of the radiative core of the Sun, to avoid a full mixing of the elements. This scenario provided some improvement in the position of the base of the convective envelope, the helium abundance in the convective zone and to some extent in the sound speed profile [at least in Guzik et al. (2006), whereas Castro et al. (2007) still find large discrepancies just below the convective zone].

Serenelli et al. (2011) have tested the accretion scenario using various metallicities, masses and times at which accretion took place. They found that accretion alone could not solve the solar problem, as metal-rich accretion led to a good agreement in the position of the base of the convective zone and sound speed profile, but reduced the agreement in helium abundance. Metal-poor accretion only provided a good agreement in helium abundance in the convective zone in their tests. They also noted that accretion of material could easily lead to a strong disagreement in lithium abundances, implying that at least additional mixing would be required to reproduce the proper lithium depletion.

Besides accretion, the so-called "faint young Sun paradox" has also motivated non-standard computations of the evolution of the Sun, including exponentially decaying mass loss on the main-sequence. The paradox resides in the fact the solar luminosity on the zero-age main sequence, according to a standard model evolution, would be around 70% of its current luminosity, which is insufficient to explain the presence of liquid water on Mars and the Earth at an early stage of the evolution of the solar system. Other solutions have been suggested to explain these discrepancies, such as greenhouse gases (see Forget et al., 2013; Airapetian et al., 2016; Wordsworth, 2016; Bristow et al., 2017; Turbet et al., 2017), a revision of the carbon cycle in the early Earth's atmosphere (Charnay et al., 2017) or a slightly more massive young Sun (Sackmann and Boothroyd, 2003; Minton and Malhotra, 2007; Turck-Chièze et al., 2011; Weiss and Heners, 2013).

Physically, one makes the hypothesis that large mass loss on the pre-main sequence could still be present at the very beginning of the main-sequence. Indeed Wood et al. (2005) have observed large winds on young solar-like stars. Increasing the mass loss on the early main sequence implies that the mass and hence the solar luminosity at the zero-age main sequence would be slightly higher and could then provide the physical conditions required for the presence of liquid water. Typically, this effect is erased as the models including mass loss recover the standard evolution of luminosity at about 2 Gy. Of course, such a non-standard evolution leaves traces on observational constraints. Early works by Guzik et al. (1987) and Graedel et al. (1991) studied its impact on the lithium depletion problem and recently, Guzik and Mussack (2010) and Wood et al. (2018) investigated its impact on seismic properties and neutrino fluxes. It appears that such massive models improve the agreement of low metallicity models in the upper radiative layers but not in the core. The disagreement in the central regions has to be mitigated by modifying other physical ingredients such as the screening factors of nuclear reaction. Following Wood et al. (2018), this can be done using the dynamical screening factor of Mussack and Däppen (2011). As for the rotational profile of the Sun, the potential detection of solar gravity modes would provide stringent constraints on the solar core, which could eventually require to question key ingredients linked to the nuclear reactions. Spalding et al. (2018) suggest another way to test this hypothesis by analyzing terrestrial or martian sediments to look for traces of specific Milankovitch cycle imprints scaling with the solar mass. Detecting such frequencies at different epochs could provide a direct hint at the history of the Sun and thus insights on the “young massive Sun hypothesis.”

Following the neutrino measurements by Davis et al. (1968) and their disagreement with the solar models of the time, Dilke and Gough (1972), adapting the formalism of (Defouw, 1970), suggested a mechanism that could alter the core properties of the Sun in its early evolution and provide a solar explanation for the some climate cycles on Earth. The mechanism received some criticism by Ulrich and Rood (1973), Ulrich (1974) and Ulrich (1975) and was further investigated by Unno (1975) and also discussed by various other authors (Christensen-Dalsgaard et al., 1974; Ledoux, 1974; Boury et al., 1975; Scuflaire et al., 1975; Shibahashi et al., 1975; Gabriel et al., 1976; Noels et al., 1976). The original idea was called the “solar spoon” and was linked to the potential intermittent mixing of the solar core as a result of gravity modes, which would be excited by a form of ϵ mechanism due to ³He burning. In practice, the first appearance of overstability is favored by some form of mixing such as the aftermath of the intermittent convective core at early stages of solar evolution, some amount of rotational mixing or other unknown processes such as magnetic convection (Schatten, 1973). Once a favorable condition for overstability is provided at some point during the solar evolution, the oscillations can be excited by the intermittent burning of ³He, which starts once the first oscillations have grown large enough. However, since the gravity modes are stabilized by radiative damping, a trapping condition has to be ensured so that they can grow large enough in the deep layers to trigger the intermittent burning and self-sustain the cycle.

Provided an adequate trapping of the modes, mixing of ³He will occur as a result of the oscillation and the Brunt-Visl profile of the solar model will be altered. After a sufficient nuclear time linked to the ³He, the depletion of nuclear fuel will induce the disappearance of the overstability. However, the overstability will propagate toward lower temperatures and thus subsist in regions where its timescale will be greater, provided that the ³He profile is adequate for its development. The whole process will thus be quasi-periodic, as the different timescales involved will change over the course of the solar evolution.

In a recent paper Gough (2015) discussed the process and considered it ruled out. However, a steep ³He is suggested by non-linear inversions of the solar core (Marchenkov et al., 2000), which could drive the overstable oscillations described by Dilke and Gough (1972) and Unno (1975). Roxburgh (1976, 1984) suggested that the instability would break down into mild turbulence and locally modify the sound-speed gradient. Various computations have been undertaken to investigate the stability of g modes to this form of ϵ mechanism. Christensen-Dalsgaard et al. (1974), Boury et al. (1975), and Shibahashi et al. (1975) found, using the quasi-adiabatic approximation, that some low order g modes could be unstable. Christensen-Dalsgaard and Gough (1975) investigated the issue using fully non-adiabatic computations and found the modes to be likely stable, as a result of significant damping in the upper layers of the convective envelope. Saio (1980), using a linear non-adiabatic analysis taking into account time-dependent convection, confirmed the instability of some g modes in early stages of the solar evolution. Moreover, Saio (1980) confirmed the potential instability of the g₂ ℓ = 1 mode in the present Sun and suggested that some higher degree modes could also be non-linearly coupled with the g₂ ℓ = 1 mode. The issue was later investigated by Kosovichev and Severnyi (1985), which confirmed that mixing and a low-metallicity of the solar models would enhance the instability of the gravity modes with respect to the ϵ mechanism. The main difficulty in reaching a definitive answer on the issue is linked to the treatment of the behavior of the convective envelope in the stability analysis. Moreover, a fully non-linear analysis of the development of the instability is required to prove that it would lead to a significant transport of chemical elements which would self-sustain the process. Ulrich and Rood (1973) and Ulrich (1974) have stated that an additional agent was required to provide the necessary chemical mixing, as the non-radial oscillation would be insufficient to do so. Non-linear calculations of resonant coupling of gravity modes by Dziembowski (1983), using the approach of Dziembowski (1982), confirmed this criticism of the original formalism of Dilke and Gough (1972). Finally, the absence of undisputed detection and identification of gravity modes does not allow to close the debate. In the quest for solar g-modes, other excitation mechanisms have been suggested and investigated (see Appourchaux et al., 2010, for a review on solar gravity modes), predicting various detectability levels for these highly-sought pulsations.

In recent years, the ϵ mechanism has been reinvestigated in metal-poor low-mass main-sequence stars (Sonoi and Shibahashi, 2012a,b). In this case, the reduced size of the outer convective zone simplifies the treatment of the stability analysis, as it is thought to play a minor role in the total energy budget.

Other more subtle effects, like the low-temperature opacities (Guzik et al., 2006), the equation of state or the properties of the chemical mixing at the base of the convective zone in the early phases of the solar evolution (Baturin et al., 2015) could affect the observed properties of the current Sun and the conclusion we may draw from them. At first, these effects may seem negligible but they would actually impact the initial conditions of a solar calibration, hence leading to overall changes in the structure that cannot be fully neglected. A very stringent constraint on such effects is the lithium depletion observed in the solar photosphere, which is strongly affected by micro- and macrophysical effects in the solar models.

3. Combined Structural Inversions and Structural Diagnostics

In this section, we will present inversion results of solar models built with various physical ingredients. All models have been computed with the Lige stellar evolution code (CLES, Scuflaire et al., 2008b). Their oscillations have been computed using the Lige adiabatic oscillation code (LOSC, Scuflaire et al., 2008a) and the inversions have been carried out using the SOLA method (Pijpers and Thompson, 1994) implemented in the InversionKit software (Reese et al., 2012).

We followed the guidelines of Rabello-Soares et al. (1999) to adjust the trade-off parameters of the inversion techniques and used the data of Basu et al. (2009) supplemented by an extension of BiSON observations of Davies et al. (2014) (as used in Buldgen et al., 2018). We computed inversions of the squared adiabatic sound speed $c^2=\frac{{\Gamma }_{1}P}{\rho }$, an entropy proxy, denoted $S_{5/3}=\frac{P}{{\rho }^{5/3}}$ presented in Buldgen et al. (2017e); and the Ledoux discriminant, defined as $A=\frac{dln\rho }{dlnr}-\frac{1}{{\Gamma }_1}\frac{dlnP}{dlnr}$ as in Buldgen et al. (2017c).

We start in sections 3.1, 3.2, and 3.3 by presenting inversion results for solar models built using different physical ingredients. To test the dependency of standard solar models on chemical composition and opacities, we used models built using the AGSS09 and GS98 abundances tables, the OPAS, OPAL, and OPLIB opacity tables and models including the revision of the neon abundance found in Landi and Testa (2015) and Young (2018), hereafter AGSS09Ne. We also present results for various implementations of the mixing of chemical elements, namely the use of the Paquette et al. (1986) collision integrals in the diffusion coefficients, the effects of considering the partial ionization of the heavy elements in the computation of microscopic diffusion. Besides microscopic effects, we also consider macroscopic mixing, in the form of an adiabatic overshoot and in the form of turbulent diffusion. All models presented here have been built using the FreeEOS equation of state and the Adelberger et al. (2011) nuclear reaction rates, except for the model taking into account partial ionization in the computation of microscopic diffusion which used the SAHA-S equation of state (Gryaznov et al., 2004; Gryaznov et al., 2013; Baturin et al., 2013).

In Figure 1, we illustrate the effect of the changes in the properties of the chemical mixing on the metallicity profile of the solar models. Most of the trends can be easily understood. For example, taking into account partial ionization of the metals when computing microscopic diffusion as in the AGSS09-OPAL-PartIon model (blue) will lead to a slightly more efficient diffusion of these elements, as they encounter less repulsion near the base of the convective zone and thus will more easily fall down toward central layers. Using the screened Coulomb potentials in the diffusion coefficients, as in Paquette et al. (1986), in the AGSS09-OPAL-Paquette model, leads to a less efficient diffusion during the evolution, as the ions will experience more repulsion than in the case of the cut-off hypothesis over a Debye sphere used in the original Thoul et al. (1994) formalism. The models including turbulent diffusion, denoted “AGSS09-OPAL-DT” and “AGSS09-OPAL-Proffitt” in Table 1, show a much more different behavior. In the “AGSS09-OPAL-DT” model, we have fixed the D and N parameter of Equation (1) to respectively 50 and 2 and to 7500 and 3 the “AGSS09-OPAL-Proffitt” model. The peak stemming from the variations of diffusion velocity near the base of the convective envelope is erased by the turbulent mixing, which induces a very different metallicity profile. The disappearance of this metal-peak is actually seen in the Ledoux discriminant inversion through its impact on the temperature gradient around 0.65 solar radii (see section 3.3). It is also worth noticing that including the prescription of Proffitt and Michaud (1991) for turbulent diffusion has a sufficiently large impact on the calibration to alter the initial chemical composition of model “AGSS09-OPAL-Paquette,” as can also be seen from Table 1, whereas the coefficients used in Buldgen et al. (2017c) have a negligible impact on the initial conditions.

FIGURE 1

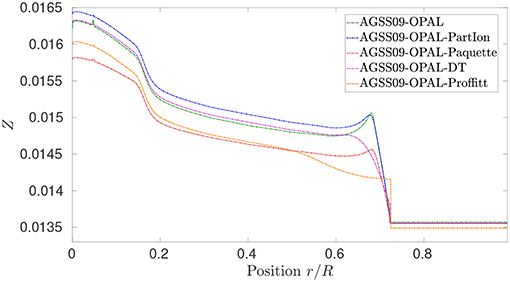
Figure 1. Metallicity profile of the standard solar models of Table 1 including various prescriptions for the transport of chemicals.

TABLE 1

Table 1. Physical ingredients of the standard solar models used in this study.

3.1. Sound Speed Inversions

We start with classical sound speed inversions, presented in Figure 2. In the left panel of Figure 2, we present results for standard solar models built with various abundances and opacities. We can see the illustration of the well-known solar modeling problem when comparing the standard AGSS09 models, in green, with the GS98 standard model, in orange. However, it appears that considering the 40% increase of the Ne/O ratio derived independently by Landi and Testa (2015) and Young (2018) provides a significant improvement of the agreement between AGSS09 models and helioseismic inversions. This is not a surprise, since a neon increase, although much larger, was already suggested by Antia and Basu (2005), Zaatri et al. (2007), and Basu and Antia (2008) as a potential solution to the solar modeling problem. Similarly, using the more recent OPAS or OPLIB opacity tables also leads to a non-negligible improvement of the agreement of low-metallicity models and helioseismic results. However, this significant improvement is restricted to the radiative layers. Indeed, large discrepancies in sound speed in the convective envelope are still present for all the AGSS09 models. This is likely due to the large discrepancies in helium in the convective envelope, since, as we will see in section 3.4, none of the models presented in Figure 2 shows a good agreement with the helioseismic helium abundance.

FIGURE 2

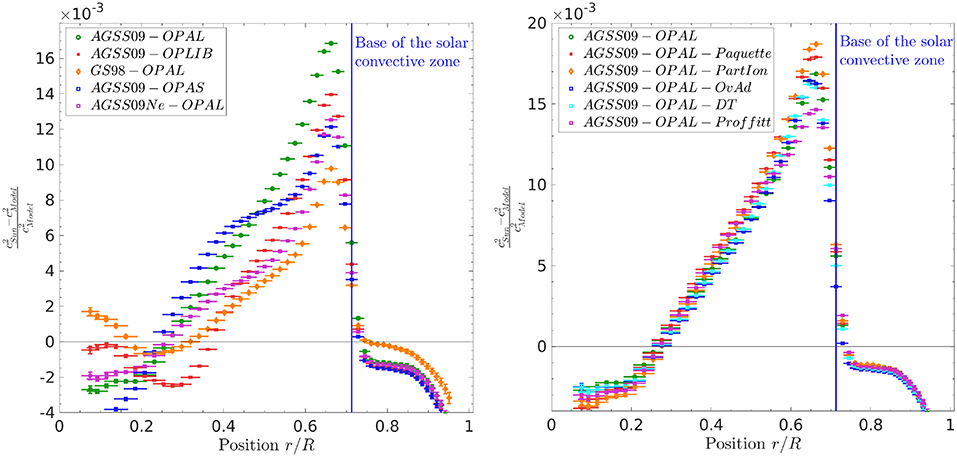
Figure 2. (Left) Relative squared sound speed differences between standard solar models using various abundance and opacity tables and helioseismic results. (Right) Relative squared sound speed differences between models including various prescriptions for the mixing of the chemical elements and helioseismic results.

In the right panel of Figure 2, we illustrate squared adiabatic sound speed inversions for models including various prescriptions for the mixing of the chemical elements. Using the Paquette et al. (1986) collision integrals or considering partial ionization in the computation of microscopic diffusion leads to an increase of the disagreements in the sound speed profile just below the convective envelope (orange and red symbols in the right panel of Figure 2). Adding a form of macroscopic mixing improves the agreement of AGSS09 models and helioseismic inversions, as can be seen from the models including either turbulent diffusion or a form of overshooting. The best agreement is found for the polynomial formulation of turbulent diffusion used in Proffitt and Michaud (1991) to reproduce the solar lithium abundances (purple symbols in the right panel of Figure 2). However, the improvement is very localized and the mixing has little to no impact on the deeper radiative layers. This demonstrates, as is now well-known, that the solar modeling problem cannot stem only from an inaccuracy of the mixing of the chemical elements, but that other ingredients such as the radiative opacities, may be partially responsible for the discrepancies.

3.2. Entropy Proxy Inversions

In addition to squared adiabatic sound speed, other structural quantities can be inverted, such as for example the density, using the (ρ, Γ₁) structural pair (see e.g., Antia and Basu, 1994) or the squared isothermal sound speed (see e.g., Dziembowski et al., 1990; Gough and Thompson, 1991). Recently, we presented in Buldgen et al. (2017b) approaches to change the structural variables of the variational equations which could in turn be used in helio- and asteroseismology. In Buldgen et al. (2017e), we presented inversion results of an entropy proxy, denoted $S_{5/3}=\frac{P}{{\rho }^{5/3}}$ which provides interesting insights on the solar structure. In Figure 3, we show the inversion results of this structural quantity for the models discussed in section 3.1.

FIGURE 3

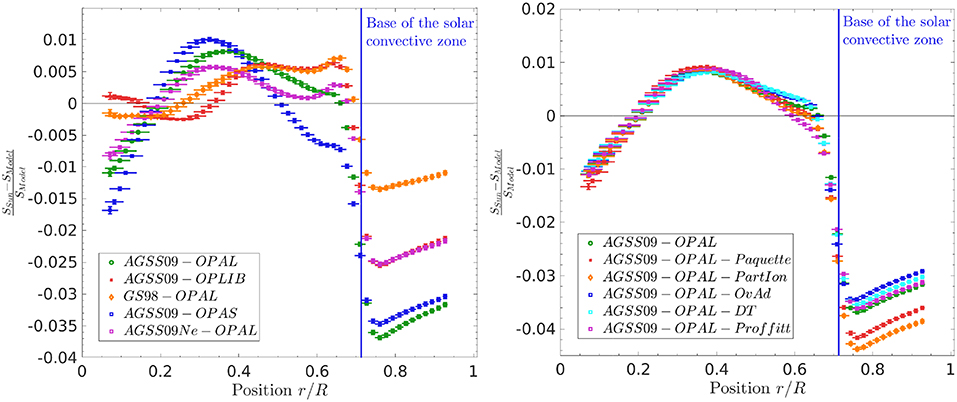
Figure 3. (Left) Relative entropy proxy differences between standard solar models using various abundance and opacity tables and helioseismic results. (Right) relative entropy proxy differences between models including various prescriptions for the mixing of the chemical elements and helioseismic results.

From Figure 3, a slightly different picture of the problem is drawn. In the left panel, the model built with the OPAS opacity tables which performed quite well in the sound speed inversion does not provide a good agreement in the entropy proxy, whereas the OPLIB opacities provide a very significant improvement over the OPAL opacities, similar to the effect of the neon revision. Nevertheless, it is clear that the performance of the AGSS09 models is still very far from the agreement obtained using the GS98 abundances. The performance of the models built with the OPLIB opacities and the revision of the neon abundance is due to the steeper temperature gradient of these models below the convective envelope due to either the behavior of the opacity profile (see Colgan et al., 2016; Guzik et al., 2016, for a discussion) or simply the increase of neon which leads to an increased opacity. Indeed, from Blancard et al. (2012), it appears that neon is the third most important contributor to the opacity at the base of the solar convective zone.

In the right panel of Figure 3, we can see again that none of the modifications of the transport of chemical elements have led to a large improvement of the performance of low-metallicity solar models. Slight modifications to the S_5/3 profile are seen, with the model including adiabatic overshooting performing slightly better than the models including turbulent diffusion. Again, we also see that the models including the Paquette et al. (1986) collision integrals or partial ionization when computing microscopic diffusion lead to an increase of the disagreements with helioseismic results. Overall, this inversion confirms that the solution to the solar modeling problem is not to be found from the mixing of the chemical elements alone, but also that some distinction can be made over the type of mixing if one refines the diagnostic by combining it to a quantity more sensitive to local variations. This will be further discussed in section 3.3, when presenting the results of the Ledoux discriminant inversions.

3.3. Ledoux Discriminant Inversions

In section 3.2, we discussed the results of inversions of an entropy proxy and showed the importance of combining the information from various inversion techniques to lift potential degeneracies that could hinder our understanding of the solar modeling problem. This thinking can be pushed even further by carrying out inversions of the Ledoux discriminant. These inversions were already presented in Gough and Kosovichev (1993b), Elliott (1996), Kosovichev (1999), and Takata and Montgomery (2002) but have not been exploited to analyse the discrepancies found for models built with the recent abundance tables of Asplund et al. (2009). This analysis was carried out in Buldgen et al. (2017e, 2018), where in this last paper, an extended set of models is analyzed.

In Figure 4, we present inversion results for the models of sections 3.1 and 3.2. The first striking feature of these inversions is the large disagreements at the base of the convective zone which is found for any opacity tables, chemical abundances and mixing considered. These discrepancies illustrate clearly the fact that the standard solar models are unable to reproduce the transition in both temperature and chemical composition gradient at the base of the convective envelope. The main difficulty is to separate each of their contributions to the A inversion.

FIGURE 4

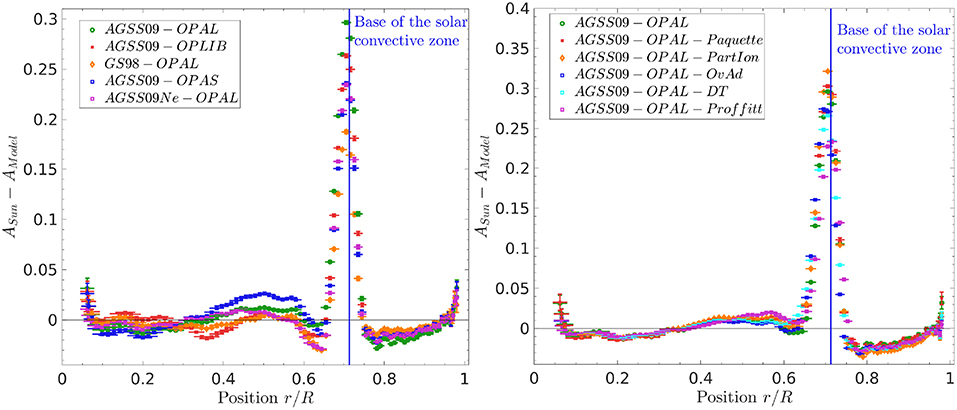
Figure 4. (Left) Ledoux discriminant differences between standard solar models using various abundance and opacity tables and helioseismic results. (Right) Ledoux discriminant differences between models including various prescriptions for the mixing of the chemical elements and helioseismic results.

Overall, the results are again quite mixed. In the left panel of Figure 4, we find that the increase in neon provides the largest improvement, bringing the models to an agreement nearly as good as that found in the GS98 models. The OPAS and OPLIB opacity tables also significantly improve the behavior of the AGSS09 models. Nevertheless, the results are far from convincing. Moreover, even the GS98 models show large deviations below the convective zone, as deep as 0.6 solar radii, thus in a region supposedly fully radiative. This emphasizes that while the potentially missing macroscopic mixing process is certainly very localized, it can still have an impact in deeper radiative layers. Indeed, it will influence the initial chemical abundances required to reproduce the solar surface metallicity, luminosity and temperature (or radius) at a solar age and thus the whole structure to a level that is detectable with helioseismic data.

This is confirmed by the right panel of Figure 4, where we can see the impact of extra-mixing below the convective zone. Again, the parametrization of Proffitt and Michaud (1991) provides the largest improvement for the low-metallicity models, while the second parametrization used in Buldgen et al. (2017c) provides a similar agreement to that of using a convective overshoot and the use of Paquette et al. (1986) collision integrals and considering partial ionization in the computation of microscopic diffusion leads to larger deviations. This does not mean, however, that turbulent mixing is not occurring at the base of the convective zone and that such approaches should not be explored. However, it clearly shows that mixing alone is not sufficient to solve the solar modeling problem and other ingredients have to be revised. Hence, it is of crucial importance to compare physical ingredients, formalisms and numerical techniques to fully assess their importance for the current issue, in a similar fashion to what has been done in Boothroyd and Sackmann (2003), Lebreton et al. (2007), and Montalbán et al. (2007).

On a sidenote, we would like to emphasize the degeneracy at play in the analysis of helioseismic inversions. Even when combining the results of sound speed, entropy proxy, and Ledoux discriminant, we cannot fully distinguish between thermal and compositional effects. Moreover, the inverted results are not independent. They could in principle all be deduced from the solar density profile. In that sense, they all provide the same information about the solar structure. For example, if one uses the Ledoux discriminant inversion to correct the A profile of a standard solar model and integrate the other variables, assuming Γ₁ known, the agreement in both sound speed and entropy proxy is very significantly improved. However, combining the inversions is useful when trying to link an improvement with respect to the helioseismic inversions to a change in the physical ingredients of the models, as the degeneracy at play between compositional and thermal effects will not act in the same way for all structural variables.

Despite these differences in their behaviors, one cannot fully separate thermal and compositional effects without further assumptions linked to the equation of state of stellar material and the chemical composition or the temperature stratification. This degeneracy is a consequence of the physical dependencies of the quantities for which inversions can be carried out, and of the fact that the changes considered in the models will always impact both temperature and chemical gradients. For example, changing the opacity tables will alter the position of the base of the convective zone in the models and thus alter the diffusion history, thus the chemical gradients. Similarly, adding an additional mixing at the base of the convective zone will alter the chemical history of the model and thus the temperature gradients, near the base of the convective zone but also deeper, as seen from the A inversion of the model including turbulent diffusion following Proffitt and Michaud (1991). In that sense, one should emphasize the value of independent constraints such as neutrino measurements, which provide crucial additional informations about the deep layers of the Sun particularly the temperature.

3.4. Convective Envelope Properties and Frequency Separation Ratios

Besides looking at seismic inversions, it is also interesting to analyse other complementary constraints. Indeed, solar models do not have only to show a good agreement in terms of inferred quantities, but should also reproduce the correct position of the base of the convective zone (Christensen-Dalsgaard et al., 1991; Kosovichev and Fedorova, 1991; Basu and Antia, 1997), determined to be around 0.713 solar radii and the helium abundance in the convective envelope, determined by (Vorontsov et al., 1991, 2013) and found to be above 0.245¹. In addition, a classical seismic diagnostic of the solar models are the so-called frequency separation ratios

$\begin{array}{ll}{r}_{0,2}=\frac{{\nu }_{n,0}-{\nu }_{n-1,2}}{{\nu }_{n,1}-{\nu }_{n-1,1}},& (2)\end{array}$

$\begin{array}{ll}{r}_{1,3}=\frac{{\nu }_{n,1}-{\nu }_{n-1,3}}{{\nu }_{n+1,0}-{\nu }_{n,0}},& (3)\end{array}$

following the definitions of Roxburgh and Vorontsov (2003b). They showed that these ratios are very sensitive to the deep layers of stellar structure. In this section, we present in Table 2 the above properties of the solar models presented in the preceding sections and illustrate in Figure 5 the frequency separation ratios of some of our models and those obtained from BiSON data.

TABLE 2

Table 2. Parameters of the standard solar models used in this study.

FIGURE 5

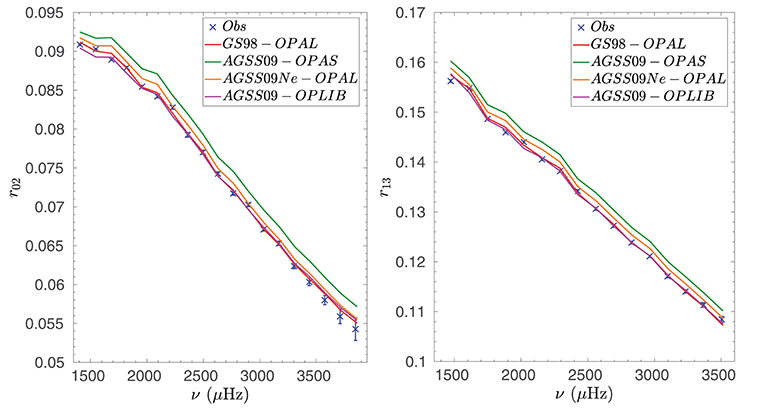
Figure 5. Comparison between the observed frequency separation ratios r_0,2 and r_1,3 from the BiSON data and those of solar models built with various abondance and opacity tables.

From Table 2, we can see that models with the AGSS09 abundances all have a surface helium abundance well below the seismically determined intervals and a too shallow convective envelope. A more worrying result is found for the models built with the latest OPLIB and OPAS opacity tables, as their helium abundance is even lower than those built using the OPAL tables. This is a consequence of the reduction of the opacity in an extended part of the solar radiative zone, which implies a higher initial hydrogen abundance of the model to allow them to reproduce the solar luminosity at the solar age.

The only AGSS09 model to show a significant improvement in the helium abundance is the one using the Proffitt and Michaud (1991) parametrization of turbulent diffusion. However, this is made at the expense of a larger disagreement of the position of the base of the convective zone. The model including the revised neon abundance, for example, does not significantly improve the helium abundance problem while it reduced the discrepancies observed in structural inversions. All other modifications lead to somewhat similar conclusions, with neither the macroscopic mixing nor the modifications to microscopic diffusion implying a decisive improvement of the models. However, the similarities between the parameters of the models including partial ionization in the computation of microscopic diffusion and those including macroscopic mixing illustrate the importance of combining the structural inversions, since they could differentiate between both effects.

In Figure 5, we compare the frequency separation ratios of theoretical models including revised abundance and opacity tables. In previous papers, the good agreement between the frequency separation ratios of the GS98 and the solar data was considered as a strong argument against the revised abundances. We see in Figure 5 that a similar agreement can be obtained by using the OPLIB opacities in AGSS09 models and that the neon revision also provided a significant improvement of the agreement. This results from the fact that the frequency separation ratios are sensitive to the sound-speed derivative. Hence, they are sensitive to both the temperature and chemical composition gradients and not only to the chemical composition of the solar radiative layers.

Consequently, the frequency separation ratios cannot be used as a direct constraint on the solar chemical composition. However, they certainly provide some additional information to dissect the current solar modeling problem. For example, the fact that the model built with the OPAS opacity tables, while it provided a quite good improvement in the squared sound speed inversion, demonstrates that there is a clear issue. Similarly, since the AGSS09 OPLIB model reproduces quite well the ratios implies that the gradient of the ratio of temperature over mean molecular weight must be quite close to the solar one, but clearly fails at reproducing the mean molecular weight itself, since the helium abundance in the convective envelope is far too low.

3.5. Modified Solar Models

In addition to the models presented in the previous sections, we also carried out inversions for models built using a modified profile of the mean Rosseland opacity and taking into account the recent revision of the neon abundance. The modification is implemented as a combination of a polynomial and a Gaussian peaked around logT = 6.35. The general behavior of the considered alteration of the opacity profile is motivated by the current discussions in the opacity community regarding uncertainties in conditions similar to those of the base of the solar convective envelope. These models also include an additional macroscopic mixing of the chemical elements at the base of the convective zone in the form of either turbulent diffusion or overshoot.

The opacity modification is implemented as a multiplicative factor to the mean Rosseland opacity

$\begin{array}{ll}{\kappa }^{\prime }=(1+f_{\kappa }(T))\kappa ,& (4)\end{array}$

with κ the original value of the mean Rosseland opacity, κ′ the modified value and f_κ(T) the parametric function considered. An illustration of f_κ(T) is provided in Figure 6, the modification is cut at lower temperatures than those of the position of the base of the convective zone, as these regions will not affect the solar modeling problem. However, in stars other than the Sun, modifications can also be expected in other regimes and their amplitude might be higher than what is found in the solar case. As can be seen, most of the alteration is localized below the base of the solar convective zone, and the order of magnitude is similar to the value given by Pradhan and Nahar (2018) and Zhao et al. (2018)² whereas at higher temperatures, the modification quickly drops to values of the same order of magnitude as the various standard opacity tables. From a physical point of view, the sharp decrease in opacity uncertainties at higher temperatures due to the higher ionization state of the various chemical elements and the reduced contribution of photon absorption to the total opacity budget. In our study, the opacity modification is applied throughout the evolution and each of these “corrected” models is recalibrated individually.

FIGURE 6

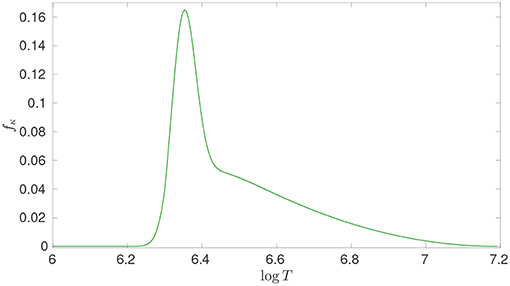
Figure 6. Modification to the opacity profile used in the solar models denoted as “Poly.” f_κ(T) is the increase in relative opacity applied during the evolution.

We considered models built with the AGSS09 abundance tables, including the corrected neon abundance, the OPAL opacity tables and the SAHA-S equation of state. The motivation behind the use of the SAHA-S EOS was to include the most recent version of an EOS relying on the chemical picture. We summarize the physical ingredients of these modified solar models in Table 3. All these models have been built with the idea of seeing how well the agreement with all the seismic diagnostics could be improved and what we could learn about the degeneracies of the solar modeling problem. A more extended study can be found in Buldgen et al. (2018) where we have investigated various modifications to the opacity profile using various standard opacity tables as a starting point. Similar studies using modified models can also be found in Montalban et al. (2006), Christensen-Dalsgaard et al. (2009), Christensen-Dalsgaard and Houdek (2010), Ayukov and Baturin (2011), Ayukov and Baturin (2017), and Christensen-Dalsgaard et al. (2018).

TABLE 3

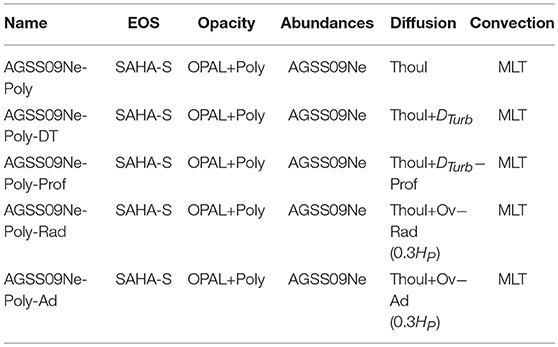
Table 3. Physical ingredients of the solar models with modified opacities and additional mixing used in this study.

We illustrate in Figure 7 the results of the c², S_5/3 and A inversions for these various modified models. In Figure 8, we compare the frequency separation ratios of these models to those of BiSON data and in Table 4, we give the values of various parameters of these solar models of direct interest for helioseismology. We have used the following naming convention for the additional mixing at the base of the convective envelope: “AGSS09Ne-Poly-DT” denotes a model where we used Equation (1) with the values of 50 and 2 for the D and N coefficients respectively, whereas “AGSS09Ne-Poly-Prof” denotes the use of the values 7500 and 3 for these coefficients. “AGSS09Ne-Poly-Rad” denotes the uses of a step overshoot function of 0.3H_P using the radiative temperature gradient in the overshooting region and an instantaneous mixing of the chemical elements whereas “AGSS09Ne-Poly-Ad” denotes the uses of the same step overshoot function but fixing the temperature gradient to the adiabatic gradient.

FIGURE 7

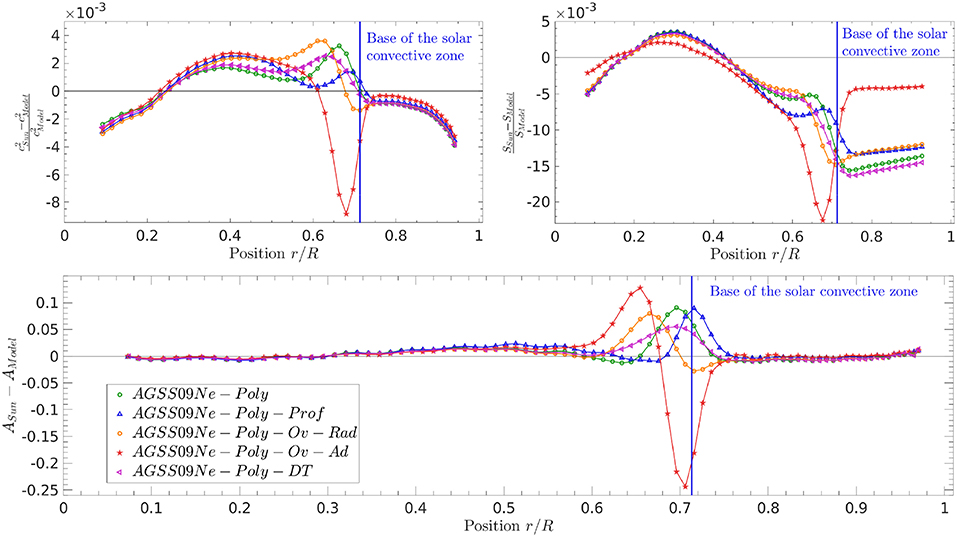
Figure 7. (Upper-left) Squared adiabatic sound speed inversions for the solar models including a modified mean Rosseland opacity and additional macroscopic mixing. (Upper-right) Entropy proxy inversions for the solar models including a modified mean Rosseland opacity and additional macroscopic mixing. (Lower) Ledoux discriminant inversions for the solar models including a modified mean Rosseland opacity and additional macroscopic mixing. The error bars have the same amplitude as for the standard models but were left out to ease of readibility of the figure.

FIGURE 8

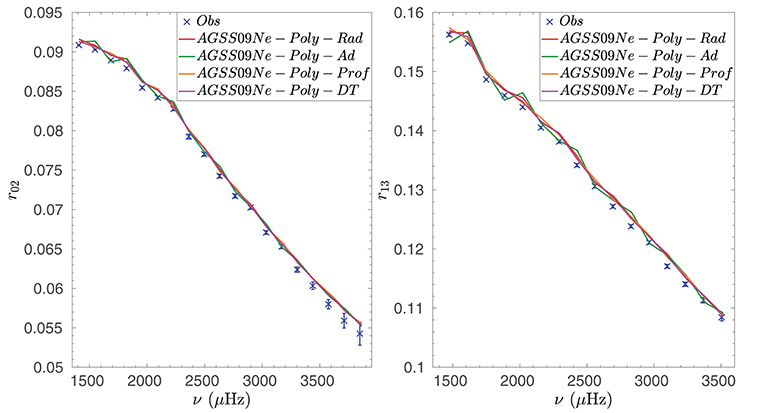
Figure 8. Comparison between the observed frequency separation ratios and those of the solar models including modified opacity tables and additional macroscopic mixing.

TABLE 4

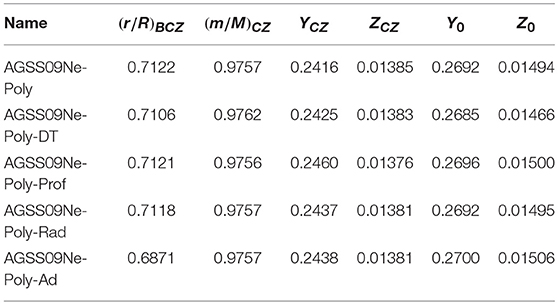
Table 4. Parameters of the solar models with modified opacities and additional mixing used in this study.

As can be seen from Table 4, the parameters of these models are in much better agreement with helioseismology. For nearly all models, the position of the base of the convective zone is in near perfect agreement with helioseismic constraints. The only exception being the model including adiabatic overshoot, which leads to an extension of the base of the convective zone far beyond what is expected from helioseismology and generates an glitch in the sound speed profile due to the too steep position of the transition in temperature gradients. This is perfectly illustrated in the c² and A profiles (in red in Figure 7) which show large deviations in the transition region.

All models also present a significant increase in the helium abundance in the convective zone. This is a direct consequence of the extended region over which the opacity is increased, which leads to a reduced initial hydrogen abundance and thus a higher initial helium abundance. However, the values still remain slightly lower than the helioseismic value³, implying that, while the base of the convective zone is placed at the right position, something is still amiss in the solar models. This is confirmed by a closer analysis of the inversion results and the frequency separation ratios.

From the upper-left panel of Figure 7, we can see that the sound speed profile is in very good agreement with helioseismic results. However, considering the amount of ingredients that have been fine-tuned, the presence of very significant deviations below 0.6 solar radii indicate that something still needs to be corrected in these models. Similarly, the height of the entropy plateau is still off by more than 1% for all models, except the model including adiabatic overshoot which strongly disagrees with the base of the convective zone. Such disagreements give weight to the hypothesis that, beyond corrections to the radiative opacities, the modeling of the transition in temperature gradient at the base of the convective region will have a strong impact on the inversion results. This is a well-known fact, which has been analyzed and discussed by Christensen-Dalsgaard et al. (2011, 2018). However, the current results show in a new way the potential of helioseismic data to provide very stringent constraints on the solar structure.

The Ledoux discriminant inversions also illustrate the full potential of these diagnostics. In the lower panel of Figure 7, we can see that the inversions clearly show the different behaviors of various types of chemical mixing unlike the results illustrated in Figure 4. The reason why these different behaviors were not visible in Figure 4 is due to the fact that the mixed region was actually compared to a region that is fully mixed in the Sun. It seems that any type of mixing could provide a significant improvement in the Ledoux discriminant, especially the adiabatic overshooting. In the modified models, since the fully mixed region in the models more closely resembles that of the Sun, the Ledoux discriminant is far more useful in disentangling the various types of macroscopic mixing occurring below the transition in temperature gradient.

In Figure 8, we compare the values of the frequency separation ratios from our to observations. From a comparison between Figures 5, 8, we can see that the opacity modification induces a slight improvement in comparison with the standard AGSS09Ne model, especially at lower frequencies. However, it appears that the model built with the GS98 abundances still performs better. This also advocates for change in opacity over a wider range of temperature, which could be linked to a revision of the equation of state used in the opacity computations in such regimes. In practice, opacity computations are expected to be more robust at higher temperatures, as less transitions come into play. The equation of state used by different groups to compute the tables may explain some of the differences⁴. However, the large differences observed in the Bailey et al. (2015) experiment results may also be linked to other issues in current opacity computations (Krief et al., 2016; Nahar and Pradhan, 2016; Pain and Gilleron, 2019). (Krief et al., 2016; Nahar and Pradhan, 2016; Pain and Gilleron, 2019).

Indeed, changes of even a few percent at higher temperatures could significantly affect the frequency separation ratios, as well as the agreement with the helioseismic helium abundance in the convective envelope. Modifications of such amplitude are within the uncertainties of the opacity tables (Guzik et al., 2005, 2006) and thus do not imply significant revisions of the physics in opacity computations, unlike the modifications required at the base of the solar convective zone. Amongst the modified models, the addition of macroscopic mixing of the chemical elements does not have a significant impact on the ratios, with the exception of the adiabatic overshoot, which adds an oscillatory signal due to the large mismatch in the position of the base of the convective zone in this model.

In Figure 9, we illustrate the gradient of the natural logarithm of temperature with respect to the natural logarithm of pressure $(\nabla =\frac{dlnT}{dlnP})$ for the various modified solar models considered in our study. As can be seen, the combination of both opacity modifications and chemical mixing allows to place the base of the convective zone in very good agreement with helioseismology, with the exception of course of the adiabatic overshoot. One can also note the slight differences in temperature gradient near the base of the convective zone for the various mixing. As the mean molecular weight gradients will be also very different, it can also be easily understood why the Ledoux discriminant inversions offer a great opportunity to probe chemical mixing just below the base of the convective zone. In the Appendix section, we discuss how the Ledoux discriminant can be separated in its chemical and thermal components and how additional insights could be gained from these inversions. It also appears that the temperature gradient quickly follows a very similar behavior at 0.5 solar radii for all models, as expected from the small amplitude of the considered opacity modifications at higher temperatures. These small shifts are however of constant sign over the whole radiative layers and thus still impact the initial hydrogen abundance of the calibrated model and its present-day helium abundance in the convective zone.

FIGURE 9

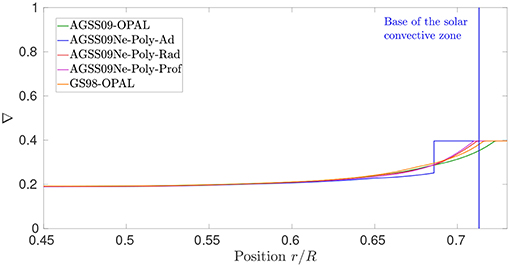
Figure 9. Gradient of the natural logarithm of temperature with respect to the natural logarithm of pressure for the modified solar models considered in this study.

4. Impact of Solar Model Modifications on the 16Cyg Binary System

4.1. From Global Helioseismology to Asteroseismology

With the advent of the CoRoT (Baglin et al., 2009) and Kepler missions (Borucki et al., 2010), asteroseismology of solar-like oscillators has become the golden path to characterize other stars than the Sun. Today, asteroseismic modeling is considered a standard tool to derive precise values of stellar fundamental parameters of stars, namely mass, radius and age which are of particular interest for fields such as exoplanetology and Galactic archaeology. While the high precision of these determinations is undisputable, as they result from the high precision of the seismic data, their accuracy will of course depend on the actual accuracy of the underlying stellar evolution models.

Consequently, efforts have recently been made to quantify the impact of physical ingredients on the determination of these fundamental parameters. In parallel, the wealth of seismic and non-seismic data led to the development of sophisticated modeling tools (Bazot et al., 2012; Gruberbauer et al., 2012; Rendle et al., 2019) and new analyses techniques (see for example Verma et al., 2014; Roxburgh, 2016; Farnir et al., 2019). Most notably, the advent of space-based photometric data allowed the extension of seismic inversion techniques to other targets than the Sun. The use of these methods had been discussed with artificial data in a few pioneering works (see for example Gough and Kosovichev, 1993a,b; Roxburgh et al., 1998; Roxburgh and Vorontsov, 2002).

From a seismic point of view, the first obvious targets to attempt seismic inversions are low-mass main-sequence solar-like oscillating stars observed by Kepler during the whole duration of the nominal mission. These stars have been assembled in a single catalog, called the Kepler LEGACY sample (Lund et al., 2017; Silva Aguirre et al., 2017). Amongst these stars, the most constrained targets are the components of the 16Cyg binary systems. In addition to high-quality seismic data, interferometric, photometric, and spectrocopic constraints are also available, providing an unprecedented dataset for such solar twins. Various studies have been dedicated to their modeling using forward and inverse approaches.

Given its extensive datasets, the 16Cyg binary systems offers an excellent opportunity to test the ingredients of stellar models to a degree of sophistication similar to helioseismic investigations. From a physical point of view, one can consider the targets of the Kepler LEGACY sample as additional experimental points to understand the solar modeling problem. In this section, we will carry out the academic exercise of considering the impact of the solar modeling problem on the seismic constraints of the 16Cyg binary system.

In our exercise, we computed different sets of models for the 16Cyg binary systems using the same initial conditions, summarized in Table 5, but various physical ingredients. These values have been taken from a preliminary modeling of the 16Cyg binary system presented in Farnir et al. (2019)⁵. The first set of models is composed of standard models of both stars built using the AGSS09 abundances, the FreeEOS equation of state, the OPAL opacities, following the diffusion formalism of Thoul et al. (1994), the classical mixing-length theory of convection and using an Eddington gray atmosphere. First, we test opacity modifications, considering that a re-investigation of the 16Cyg binary system would be required should updated opacity tables be made available⁶. Hence, we computed a second set of models of 16CygA&B that includes the polynomial opacity modification that we considered for model “AGSS09Ne-Poly” of section 3.5„ represented in Figure 6. Finally, the third set of models considers both this opacity modification and the parametric macroscopic mixing of Proffitt and Michaud (1991) as in model “AGSS09Ne-Poly-Prof” of section 3.5. The properties of the models of the various sets are summarized in Table 6. The models have been calibrated by evolving them until they reach the radius values determined using interferometry (White et al., 2013). Hence, each has a different age, as a result of the differences in their physical ingredients. All ages are however consistent between the components of the binary system.

TABLE 5

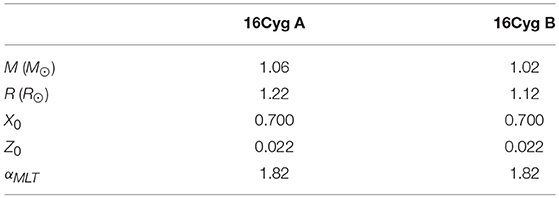
Table 5. Parameters of the 16Cyg models with modified opacities and additional mixing used in this study.

TABLE 6

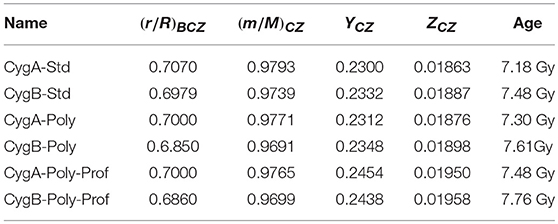
Table 6. Parameters of the 16Cyg models with modified opacities and additional mixing used in this study.

The goal of this exercise is fairly simple: to illustrate the impact a potential solution to the solar modeling problem could have on the determination of stellar fundamental parameters such as mass, radius, and age for stars other than the Sun. Hence, it also serves the purpose of reminding the model-dependence of asteroseismic investigations, but also how the high-quality asteroseismic data can help us better understand the physical processes acting inside stars by providing other experimental conditions to those at hand in helioseismology. A good illustration of the limitations of stellar models, and thus a central point for which a revision of their ingredients could have a significant impact is found for example in the current discussions related to the transport of angular momentum on both the main-sequence and the red giant branch (Eggenberger et al., 2017, 2019; Benomar et al., 2018; Ouazzani et al., 2018). In those cases, the sensitivity of the proposed mechanisms to the chemical composition gradients, and thus their validity, could be influenced by revisions of some of the physical ingredients at play when studying the solar modeling problem.

4.2. Impact of the Solar Problem on Classical Seismic Indices

Forward seismic modeling techniques can vary quite extensively depending on the quality of the data. The crudest approach uses the so-called scaling laws to infer stellar properties, whereas the most sophisticated techniques use various combinations of the individual frequencies. Amongst them, the use of the r_0,2 and r_1,3 ratios defined by Roxburgh and Vorontsov (2003b) and defined in Equations (2, 3) allow to infer the internal structure without too much dependency on the upper layers. Indeed, the direct use of the individual frequencies is not optimal for solar-like oscillators, as they are strongly influenced by the “surface effect” problem and lead to unrealistic precisions on stellar parameters⁷.

In Figure 10, we compare the frequency separation ratios of the various models with respect to the observations. As can be seen, none of the models fit very well the seismic data at hand, although the agreement is not catastrophic either. This is not surprising, as they have not been fitted to the individual frequency ratios. However, what is more striking is that the variations between the theoretical models that are induced by the opacity modifications and the additional turbulent mixing is significant with respect to the observational uncertainties for most of the data. This is not really surprising but emphasizes the model-dependence of seismic modeling results. As expected, the variations observed here are also reflected in the fundamental parameters. However, this behavior should be inspected for a given fit of the seismic constraints to be certain that the accuracy of the inferences is so significantly affected.

FIGURE 10

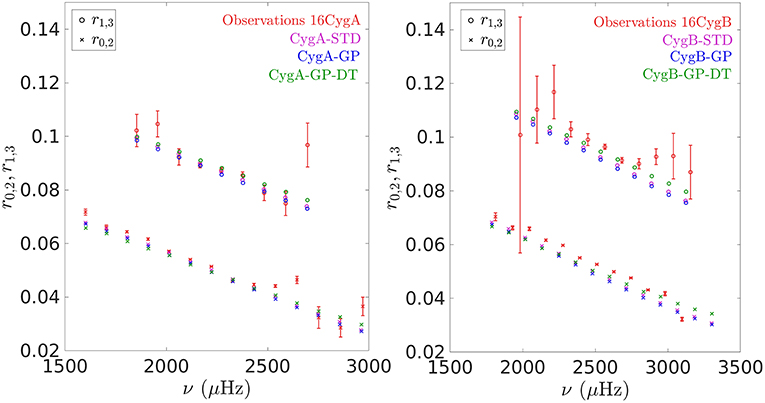
Figure 10. Comparison between the observed frequency ratios and those of the 16Cyg A and B models considered in this study.

Unsurprisingly, the most affected parameter is the age, for which variations between the standard models and the models including opacity modifications and additional mixing can reach around 4%, whereas including only the opacity modifications only induces a variation of almost 2%. These variations are of course quite small. However, they are as large as the uncertainties on the fundamental parameters derived from seismic modeling studies using the whole Kepler dataset (see for example Metcalfe et al., 2015; Silva Aguirre et al., 2017) and are of course only indicative of the impact of the changes of given ingredients for a given set of initial conditions for the evolutionary models. Taking into account the uncertainties on the other fundamental parameters for a given set of constraints could lead to a larger spread in age.

In Buldgen et al. (2016a), we demonstrated that a similar spread in age could also be seen by altering the efficiency of microscopic diffusion. Hence, we can state that modifying the formalism of microscopic diffusion, using the Paquette et al. (1986) approach and considering partial ionization when computing microscopic diffusion would also cause a change in age of the order of one per cent. Consequently, we can confirm that for the current best Kepler targets (Borucki et al., 2010), as well as for future TESS and PLATO targets (Rauer et al., 2014; Ricker et al., 2015), the main contributors to the fundamental parameters will not be the propagation of the observational uncertainties onto the inferred parameters, but the physical ingredients of the underlying grids of evolutionary models. In such a context, very high precision results, for example as those of Metcalfe et al. (2015) or (Buldgen et al., 2016a,b) for the 16Cyg binary system, should only be taken as valid for a given set of physical ingredients.

To illustrate some of the differences between the various models considered here, we show in Figure 11 the temperature gradients inside the models. As can be seen, the modification of the mean Rosseland opacity does not induce any significant variations in the deep layers. The main variation is unsurprisingly located at the base of the convective zone. A small modification is also seen in luminosity but well below the observational error bars. Interestingly, the inclusion of turbulent diffusion has altered the deep layers of the model. The variations are actually due to a change of the hydrogen abundance in the central layers. Indeed, X_C is 0.038 in the model including turbulent diffusion and 0.029 in the standard model. This could be due to the inhibition of microscopic diffusion that is induced by the turbulent mixing.

FIGURE 11

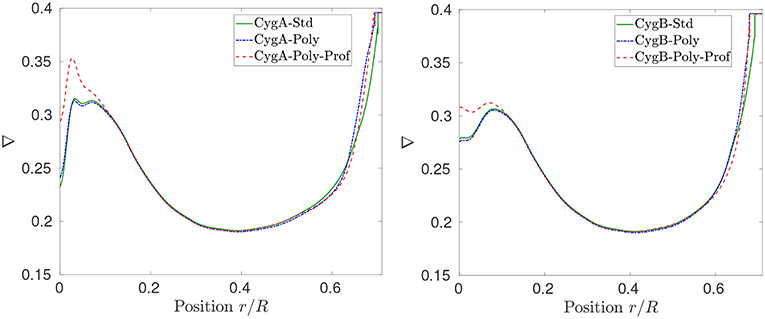
Figure 11. Temperature gradient profiles as of function of r/R for the 16Cyg A and B models considered in this study.

The extreme impact of the Proffitt and Michaud (1991) parametric approach to turbulent diffusion can also be seen in Figure 12, where we illustrate the metallicity profile of the models of the 16Cyg binary system. One can see the influence of turbulent diffusion on the surface abundance of metals that is significantly higher than in the standard model and the model including modified opacity. It is also interesting to note the slight differences between these two models. We emphasize here that there is no modification to the mixing of chemicals. However, there is an indirect impact of the opacity modification on chemicals through the modification of the position of the base of the convective envelope. Here, the higher opacity leads to a larger convective envelope, extending at higher temperatures. This implies that microscopic diffusion will be slightly less efficient and thus, that a higher metallicity will be found in the envelope but also just below the envelope, where metals tend to accumulate over the duration of the evolution. This is particularly well seen in the left panel of Figure 12 in the case of 16CygA.

FIGURE 12

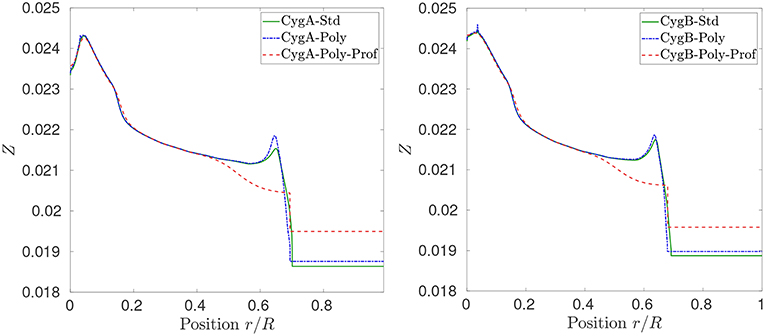
Figure 12. Metallicity profiles as of function of r/R for the 16Cyg A and B models considered in this study.

Overall, the modifications we see in the models of both components remain quite small. They could, however, be modified by the seismic optimization procedure which will alter the initial conditions of the evolutionary sequence. Therefore, some variations seen in the models assuming the same initial parameters but different approaches for the mixing of the chemical elements might be erased at the expense of a change of fundamental parameters such as mass, radius and age, as was noted in Buldgen et al. (2016b). On this matter, the case of 16Cyg is particularly interesting and promising, as both stars form a binary system. This adds another level of constraint on their initial composition and their age, further reducing the amplitude of the changes one can make to the models.

4.3. Impact of the Solar Problem on Indicator Inversions

In addition to classical seismic forward modeling, Reese et al. (2012), Buldgen et al. (2015b), Buldgen et al. (2015a), and Buldgen et al. (2018) developed inversions of so-called structural indicators, defined as integrated quantities, which can offer additional constraints beyond the use of classical seismic indices. In this section, we briefly discuss the potential variations in these seismic indicators that can be expected from the modifications of the physical ingredients of the 16Cyg binary system models. It should however be noted that these results are preliminary and that the true diagnostic potential of the inversions might be further improved. For example, the use of non-linear inversions, following the formalism of Roxburgh and Vorontsov (2003a) may provide an excellent complement, less sensitive to surface effects, to the classical formalism used in global helioseismology.

Here, we limit ourselves to a brief discussion on the diagnostic potential of structural indicators, namely the t_u indicator from Buldgen et al. (2015a), defined as

$\begin{array}{ll}{t}_u={\displaystyle {\int }_0^R}f(r){\left(\frac{du}{dr}\right)}^{2}dr,& (5)\end{array}$

with u = P/ρ, R the stellar radius and f(r) a suitably chosen parametric weight function (see Buldgen et al., 2015a, for details).

The impact of the changes in physics on the t_u indicator can be seen in Figure 13, where we recreate the figures from Buldgen et al. (2016a,b) presenting the inversion results. As can be seen, the variations are quite small compared to the uncertainties of the inversions. However, the variations of the fundamental parameters will strongly affect the values of the structural indicators. As the t_u indicator scales with M², its value is also strongly dependent on the mass and radii inferred from the forward modeling procedure. Including a small mixing at the base of the envelope of 16CygB, Buldgen et al. (2016b) found a variation of the t_u indicator between 12 and 20% between some models. However, it is very unlikely that this variation only results from changes in the structure of the models, but rather stems also from inaccuracies in the stellar fundamental parameters. This is illustrated in Figure 13, since the models are built using the same mass and evolved until they have the same radius. From these tests, we can see that the maximum variations in t_u at a given mass and radius are of approximately 6%; this is well below the uncertainties of the t_u indicator that can reach values around 16%. On a sidenote, it also appears that the mean density value is not well reproduced for 16CygB, with a difference of around 2% between the reference models and the inverted value. The t_u value seems however to be in very good agreement with the inversions, but it remains to be seen whether one can obtain a good agreement for all inverted quantities. In addition to the t_u and $\bar{\rho }$ inversions, additional indicators presented in Buldgen et al. (2018) can be used to constrain the internal structure of the star. Moreover, taking into account the lithium and beryllium abundances, whenever measured, are also key additional observations to accurately depict the evolution of solar-like stars (Deal et al., 2015; Thévenin et al., 2017). In the case of the 16Cyg binary system, the lithium abundance for both stars has been determined (King et al., 1997; Tucci Maia et al., 2014), finding the lithium abundance to be more depleted in the B component by approximately a factor 5. Deal et al. (2015) suggested that those differences could have been provoked by an accretion of planetary matter on 16CygB which would have triggered thermohaline mixing. Following these results, the differences observed in both the indicator inversions and the lithium abundance motivated the study of Buldgen et al. (2016b) who assessed the impact of extra-mixing on the inversion results. However, since various physical ingredients could affect the inversion result, Buldgen et al. (2016b) concluded that the problem might be degenerate and required a careful re-study. Moreover, it is still unclear whether the process leading to the far more significant lithium depletion in the B component would still leave a mark on its present-day structure.

FIGURE 13

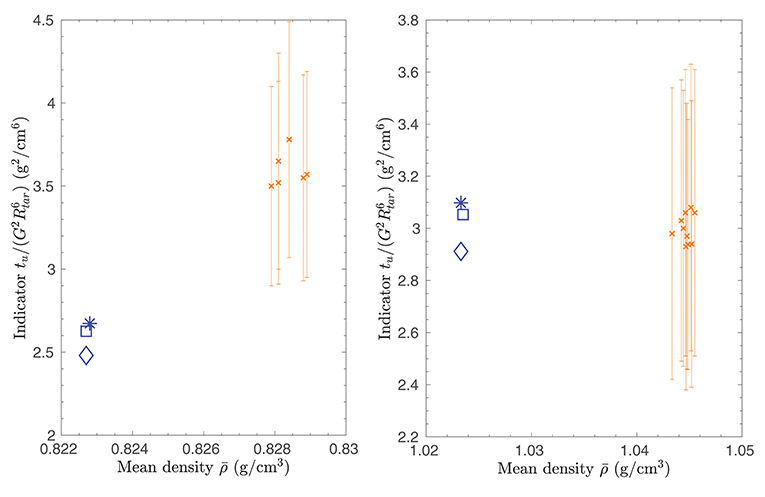
Figure 13. Comparison of t_u and $\bar{\rho }$ inversions for 16CygA and B for the models considered in this study. The blue symbols refer to the reference models: * for the standard models, □ for the models with modified opacity and ♢ for the models including both the opacity modification and turbulent diffusion.

Results for some Kepler LEGACY stars have already been presented in Buldgen et al. (2017a), showing the diagnostic potential of these additional indicators. However, Appourchaux et al. (2015) demonstrated the potential of the method of Roxburgh and Vorontsov (2003a) by providing an inversion of the whole hydrostatic structure of a Kepler target. There is no doubt that the use of such an approach on the targets of the Kepler LEGACY sample in the Gaia era will provide invaluable information for stellar modelers, allowing to test with unprecedented thoroughness our depiction of stellar structure in a much more model-independent way than what is achievable with linear asteroseismic inversions.

5. Prospects and Discussion

In the previous sections, we presented the current state of the solar modeling problem, with a strong emphasis on helioseismic diagnostics and their capabilities. While it is obvious that global helioseismology is an essential tool to probe the internal structure of the Sun, it does not imply that other fields cannot also reshape the picture of the current solar issue. As mentioned earlier, constraints provided by helioseismic inversions are somewhat degenerate. Indeed, they do not give direct constraints on the temperature gradients inside the Sun as they also probe variables related to a combination of temperature and mean molecular weight.

For example, measurements of neutrinos fluxes also provide stringent complementary constraints on the temperature of the most central regions of the solar core, probing a zone inaccessible to global helioseismology. Recent simultaneous measurements of all neutrinos of the pp-chain (Borexino Collaboration et al., 2018) provide a very complete picture of the solar core. In the future, measurements of the CNO neutrinos could provide more direct constraints on the chemical composition of the solar core (see Gough, 2019, for a recent discussion), in particular, its oxygen abundance, offering strong constraints on the chemical mixing during the evolution of the Sun. However, it is also clear that the neutrino fluxes measurements could also be significantly affected by a revision of the electronic screening formulas used in stellar models (Mussack and Däppen, 2011), as mentioned by Vinyoles et al. (2017).

Similarly, the solar lithium and beryllium abundances also play a key role in understanding the evolution of the Sun (Richard et al., 1996; Piau and Turck-Chièze, 2001). They are closely linked to the intensity and the extent of the mixing at the base of the convective zone, thus constraining the physical processes that can be at play in this narrow region. As such, a key point for the future of solar modeling is understanding the nature and impact of so-called “non-standard” processes often treated using ad-hoc prescriptions. The stakes of the solar modeling problem are not so much to validate a value of the solar metallicity, but to trigger the development of new generations of stellar models.

In this perspective, the advent of space-based photometry missions and the rapid development of asteroseismology offers an unprecedented opportunity for stellar modelers. Today, we can use seismology to precisely probe the interior of thousands of stars, providing stellar modelers with additional experimental measurements to refine their understanding of the theory of stellar structure and evolution, from the microscopic scales of nuclear reactions and radiative transfer to the large scale of turbulent hydrodynamical motions.

In a provocative way, one could state that stellar physics is far from being reduced to an optimization problem and that the main concerns of asteroseismic modelers should not be on providing extremely precise stellar fundamental parameters. Indeed, those will always be model-dependent. Thus, their precision will always be overestimated, as the systematic differences that can result from inaccurate physical ingredients are difficult to estimate. On the contrary, stellar and solar seismologists should focus on the quality and relevance of their inferences and the connection between their data and the actual physical constraints that they contain. With this mindset, asteroseismology will truly fulfill its role of complementary, “experimental” domain of theoretical stellar physics.

Of course, the progress of stellar physics will require a strong effort on the modeling side. Improvements of the physical ingredients of stellar models are the keys to the solution of the solar modeling problem. From a macrophysical point of view for example, the development of hydrodynamical simulations also offers great potential for our understanding of turbulence in stellar conditions (see for example Jørgensen et al., 2018, for an application in the solar case). Linking these simulations to a formalism that can be used in stellar evolution codes is one of the key challenges of the coming years, especially for our depiction of the evolution of convective cores. From a microphysical point of view, further improvements of radiative opacities, microscopic diffusion, or the equation of state will also lead to revolutions in the field and will certainly play a key role for the solar problem.

A first step in this direction is to compare various evolution codes to separate the numerical contributions to the uncertainties to those that clearly result from physical inaccuracies. This approach, although time-consuming and not very rewarding, is also crucial to motivate further developments and improvements of stellar evolution codes from a numerical point of view. In that respect, it is of course pointless to claim the superiority of one code over others, as much as it is useless to use them as blackboxes. It is clear that the numerical development of some codes has been focused on implementing thoroughly specific aspects (e.g., rotation, magnetic instabilities and internal gravity waves for the GENEC code Eggenberger et al., 2008, microscopic diffusion including a complete treatment of radiative acceleration for the Montral-Montpellier code Turcotte et al., 1998; Richer et al., 2000; Richard et al., 2001 and the Toulouse-Geneva evolution code Théado et al., 2012, or the consistent evolution of convective boundary and quality of the models for seismology of the Liége code Scuflaire et al., 2008b).

6. Conclusion

This paper has focused on providing a brief review of the solar modeling problem, mainly from a helioseismic perspective. We have discussed in section 2 the various contributors to the current issue. Unsurprisingly, the opacity remains the usual suspect and probably the most significant contributor to the disagreements between standard solar models and helioseismic constraints. Beside the opacities, the mixing of the chemical element and the equation of state are the other usual suspects who could have a significant impact on the solar structure. In section 2.5, we also briefly presented some additional processes that could impact the present-day solar structure and thus the current discrepancies. While they are not commonly presented in the literature, they should perhaps not be totally dismissed.

In section 3, we presented inversion results, frequency separation ratios and convective envelope properties of a sample of solar models built with various physical ingredients. The constraining nature of combining this entire set of information into one consistent study is very clear, as it allows to isolate the effect of the various contributors to the solar problem. We showed the impact of an extended modification of the mean Rosseland opacity, for which the largest amplitude of the correction lay in the conditions of the iron opacity peak at logT = 6.35. We also show that the increased neon abundance found by Landi and Testa (2015) and Young (2018) significantly reduces the discrepancies of the low-metallicity solar models. In addition, we show that the combined inversions could provide stringent constraints on the type of mixing at the base of the solar convective zone. Further extensions of this study using a non-linear inversion technique and/or the phase shift of the mode frequencies to properly reproduce the transition in temperature gradients will provide key constraints for the physical implementation of overshooting at the base of stellar envelopes.

In section 4, we have briefly discussed the impact of the solar modeling problem on the structure of the best Kepler targets, the components of the 16Cyg binary system. To do so, we have computed models with a given set of physical ingredients using the standard solar model framework, including the opacity modification we used for our modified solar models or including both the opacity modification and turbulent diffusion using the parametric approach of Proffitt and Michaud (1991). We demonstrated that the impact of such modifications would be significant at the level of precision required from asteroseismic investigations. In that respect, improving the current seismic inference techniques is crucial to better exploit the constraints on these uncertain processes and, by providing more stringent analyses, to ensure the success of future space missions such as PLATO and to bring theoretical stellar physics to a new level of accuracy. Improving indicator inversions but also generalizing the use of non-linear inversions can be foreseen as the most promising way to fully exploit the data. However, new approaches to treat the seismic information in forward modeling methods also provide important insights in the limitations of seismic information and define the necessary reference models for seismic inversions (Farnir et al., 2019).

Ultimately, the extension of such advanced modeling strategies further away from the solar conditions will allow to truly probe the limitations of the current state of theoretical stellar physics. In conclusion, the future of asteroseismology is deeply rooted in its history and the early developments of helioseismology. From these solid grounds, asteroseismologists can further develop this young and successful research field. This requires to solve the solar modeling problem, to promote synergies between stellar physicists, seismic modelers and experts in hydrodynamical simulations without perhaps falling into the trap of a race to precision of stellar parameters that are intrisically model-dependent.

Data Availability

Publicly available datasets were analyzed in this study. This data can be found here: https://academic.oup.com/mnras/article/446/3/2959/2893058#supplementary-data.

Author Contributions

GB, SS, and AN contributed equally to the paper.

Funding

GB acknowledges support from the ERC Consolidator Grant funding scheme (project ASTEROCHRONOMETRY, G.A. n. 772293). This work is sponsored the Swiss National Science Foundation (project number 200020-172505). S.J.A.J.S. is funded by the Wallonia-Brussels Federation ARC grant for Concerted Research Actions.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^We consider here a conservative approach given the differences in the precision of the helium determination found by various studies.

2. ^A. Pradhan, private communication.

3. ^We consider here a conservative interval between 0.245 and 0.26 in agreement with recent studies (Vorontsov et al., 2013).

4. ^This statement is however, difficult to assess, as the equation of state used for opacity computations is often not available, at least for the recent OPAS and OPLIB tables.

5. ^Namely, the results are only presented for the A component in Table 2, second column of Farnir et al. (2019), but the modeling was carried out for both components.

6. ^Buldgen et al. (2016b) also investigated the use of the OPAS opacities in their modeling, but this should be done more thoroughly.

7. ^Indeed, early studies already discussed the fact that individual frequencies did not constitute independent constraints on stellar structure and should not be used directly as inputs of stellar forward modeling.

References

Adelberger, E. G., García, A., Robertson, R. G. H., Snover, K. A., Balantekin, A. B., Heeger, K., et al. (2011). Solar fusion cross sections. II. The pp chain and CNO cycles. Rev. Mod. Phys. 83, 195–246. doi: 10.1103/RevModPhys.83.195

CrossRef Full Text | Google Scholar

Ahmad, Q. R., Allen, R. C., Andersen, T. C., Anglin, J. D., Barton, J. C., Beier, E. W., et al. (2002). Direct evidence for neutrino flavor transformation from neutral-current interactions in the sudbury neutrino observatory. Phys. Rev. Lett. 89:011301. doi: 10.1103/PhysRevLett.89.011301

PubMed Abstract | CrossRef Full Text | Google Scholar

Airapetian, V. S., Glocer, A., Gronoff, G., Hébrard, E., and Danchi, W. (2016). Prebiotic chemistry and atmospheric warming of early Earth by an active young Sun. Nat. Geosci. 9, 452–455. doi: 10.1038/ngeo2719

CrossRef Full Text | Google Scholar

Alecian, G., and LeBlanc, F. (2002). New approximate formulae for radiative accelerations in stars. Mon. Notices R. Astron. Soc. 332, 891–900. doi: 10.1046/j.1365-8711.2002.05352.x

CrossRef Full Text | Google Scholar

Allende Prieto, C., Lambert, D. L., and Asplund, M. (2001). The forbidden abundance of oxygen in the Sun. Astrophys. J. Lett. 556, L63–L66. doi: 10.1086/322874

CrossRef Full Text | Google Scholar

Antia, H. M., and Basu, S. (1994). Nonasymptotic helioseismic inversion for solar structure. Astron. Astrophys. Suppl. Ser. 107, 421–444.

Google Scholar

Antia, H. M., and Basu, S. (2005). The Discrepancy between Solar Abundances and Helioseismology. Astrophys. J. Lett. 620, L129–L132. doi: 10.1086/428652

CrossRef Full Text | Google Scholar

Antia, H. M., and Basu, S. (2006). Determining solar abundances using helioseismology. Astrophys. J. 644, 1292–1298. doi: 10.1086/503707

CrossRef Full Text | Google Scholar

Appourchaux, T., Antia, H. M., Ball, W., Creevey, O., Lebreton, Y., Verma, K., et al. (2015). A seismic and gravitationally bound double star observed by Kepler. Implication for the presence of a convective core. Astron. Astrophys. 582:A25. doi: 10.1051/0004-6361/201526610

CrossRef Full Text | Google Scholar

Appourchaux, T., Belkacem, K., Broomhall, A.-M., Chaplin, W. J., Gough, D. O., Houdek, G., et al. (2010). The quest for the solar g modes. Astron. Astrophys. Rev. 18, 197–277. doi: 10.1007/s00159-009-0027-z

CrossRef Full Text | Google Scholar

Asplund, M., Grevesse, N., and Sauval, A. J. (2005a). “The solar chemical composition,” in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, Vol. 336 of Astronomical Society of the Pacific Conference Series, eds T. G. Barnes III and F. N. Bash (Austin, TX: Astronomical Society of the Pacific), 25.

Asplund, M., Grevesse, N., Sauval, A. J., Allende Prieto, C., and Blomme, R. (2005b). Line formation in solar granulation. VI. [C I], C I, CH and C₂ lines and the photospheric C abundance. Astron. Astrophys. 431, 693–705. doi: 10.1051/0004-6361:20041951

CrossRef Full Text | Google Scholar

Asplund, M., Grevesse, N., Sauval, A. J., Allende Prieto, C., and Kiselman, D. (2004). Line formation in solar granulation. IV. [O I], O I and OH lines and the photospheric O abundance. Astron. Astrophys. 417, 751–768. doi: 10.1051/0004-6361:20034328

CrossRef Full Text | Google Scholar

Asplund, M., Grevesse, N., Sauval, A. J., and Scott, P. (2009). The chemical composition of the Sun. Annu. Rev. Astron. Astrophys. 47, 481–522. doi: 10.1146/annurev.astro.46.060407.145222

CrossRef Full Text | Google Scholar

Ayukov, S. V., and Baturin, V. A. (2011). Low-Z solar model: sound speed profile under the convection zone. J. Phys. Conf. Ser. 271:012033. doi: 10.1088/1742-6596/271/1/012033

CrossRef Full Text | Google Scholar

Ayukov, S. V., and Baturin, V. A. (2017). Helioseismic models of the sun with a low heavy element abundance. Astron. Rep. 61, 901–913. doi: 10.1134/S1063772917100018

CrossRef Full Text | Google Scholar

Badnell, N. R., Bautista, M. A., Butler, K., Delahaye, F., Mendoza, C., Palmeri, P., et al. (2005). Updated opacities from the Opacity Project. Mon. Notices R. Astron. Soc. 360, 458–464. doi: 10.1111/j.1365-2966.2005.08991.x

CrossRef Full Text | Google Scholar

Baglin, A., Auvergne, M., Barge, P., Deleuil, M., Michel, E., and CoRoT Exoplanet Science Team (2009). “CoRoT: Description of the Mission and Early Results,” in Transiting Planets, Vol. 253 of IAU Symposium, eds F. Pont, D. Sasselov, and M. J. Holman, 71–81.

Google Scholar

Bahcall, J. N., Basu, S., Pinsonneault, M., and Serenelli, A. M. (2005a). Helioseismological implications of recent solar abundance determinations. Astrophys. J. 618, 1049–1056. doi: 10.1086/426070

CrossRef Full Text | Google Scholar

Bahcall, J. N., Basu, S., and Serenelli, A. M. (2005b). What is the Neon abundance of the Sun? Astrophys. J. 631, 1281–1285. doi: 10.1086/431926

CrossRef Full Text | Google Scholar

Bahcall, J. N., Huebner, W. F., Lubow, S. H., Parker, P. D., and Ulrich, R. K. (1982). Standard solar models and the uncertainties in predicted capture rates of solar neutrinos. Rev. Mod. Phys. 54, 767–799. doi: 10.1103/RevModPhys.54.767

CrossRef Full Text | Google Scholar

Bahcall, J. N., and Peña-Garay, C. (2004). Solar models and solar neutrino oscillations. New J. Phys. 6:63. doi: 10.1088/1367-2630/6/1/063

CrossRef Full Text | Google Scholar

Bahcall, J. N., Serenelli, A. M., and Basu, S. (2005c). New solar opacities, abundances, helioseismology, and neutrino fluxes. Astrophys. J. Lett. 621, L85–L88. doi: 10.1086/428929

CrossRef Full Text | Google Scholar

Bahcall, J. N., Serenelli, A. M., and Basu, S. (2006). 10,000 Standard solar models: a monte carlo simulation. Astron. Astrophys. Suppl. Ser. 165, 400–431. doi: 10.1086/504043

CrossRef Full Text | Google Scholar

Bailey, J. E., Nagayama, T., Loisel, G. P., Rochau, G. A., Blancard, C., Colgan, J., et al. (2015). A higher-than-predicted measurement of iron opacity at solar interior temperatures. Nature 517, 56–59. doi: 10.1038/nature14048

PubMed Abstract | CrossRef Full Text | Google Scholar

Basu, S., and Antia, H. M. (1994). Effects of diffusion on the extent of overshoot below the solar convection zone. Mon. Notices R. Astron. Soc. 269:1137. doi: 10.1093/mnras/269.4.1137

CrossRef Full Text | Google Scholar

Basu, S., and Antia, H. M. (1995). Helium abundance in the solar envelope. Mon. Notices R. Astron. Soc., 276:1402–1408.

Google Scholar

Basu, S., and Antia, H. M. (1997). Seismic measurement of the depth of the solar convection zone. Mon. Notices R. Astron. Soc. 287, 189–198.

Google Scholar

Basu, S., and Antia, H. M. (2004). Constraining solar abundances using helioseismology. Astrophys. J. Lett. 606, L85–L88. doi: 10.1086/421110

CrossRef Full Text | Google Scholar

Basu, S., and Antia, H. M. (2008). Helioseismology and solar abundances. Phys. Rep. 457, 217–283. doi: 10.1016/j.physrep.2007.12.002

CrossRef Full Text | Google Scholar

Basu, S., Chaplin, W. J., Elsworth, Y., New, R., and Serenelli, A. M. (2009). Fresh insights on the structure of the solar core. Astrophys. J. 699, 1403–1417. doi: 10.1088/0004-637X/699/2/1403

CrossRef Full Text | Google Scholar

Basu, S., and Christensen-Dalsgaard, J. (1997). Equation of state and helioseismic inversions. Astron. Astrophys. 322, L5–L8.

Google Scholar

Basu, S., Christensen-Dalsgaard, J., Schou, J., Thompson, M. J., and Tomczyk, S. (1996). Solar structure as revealed by 1 year LOWL data. Bull. Astron. Soc. India 24:147.

Google Scholar

Baturin, V. A., Ayukov, S. V., Gryaznov, V. K., Iosilevskiy, I. L., Fortov, V. E., and Starostin, A. N. (2013). “The Current Version of the SAHA-S Equation of State: Improvement and Perspective,” in Progress in Physics of the Sun and Stars: A New Era in Helio- and Asteroseismology, volume 479 of Astronomical Society of the Pacific Conference Series, eds H. Shibahashi, and A. E. Lynas-Gray, 11.

Google Scholar

Baturin, V. A., Gorshkov, A. B., and Oreshina, A. V. (2015). Formation of a chemical-composition gradient beneath the convection zone and the early evolution of the sun. Astron. Rep. 59, 46–57. doi: 10.1134/S1063772915010023

CrossRef Full Text | Google Scholar

Bazot, M., Bourguignon, S., and Christensen-Dalsgaard, J. (2012). A Bayesian approach to the modelling of α Cen A. Mon. Notices R. Astron. Soc. 427, 1847–1866. doi: 10.1111/j.1365-2966.2012.21818.x

CrossRef Full Text | Google Scholar

Benomar, O., Bazot, M., Nielsen, M. B., Gizon, L., Sekii, T., Takata, M., et al. (2018). Asteroseismic detection of latitudinal differential rotation in 13 Sun-like stars. Science 361, 1231–1234. doi: 10.1126/science.aao6571

PubMed Abstract | CrossRef Full Text | Google Scholar

Blancard, C., Colgan, J., Cossé, P., Faussurier, G., Fontes, C. J., Gilleron, F., et al. (2016). Comment on “large enhancement in high-energy photoionization of Fe XVII and missing continuum plasma opacity”. Phys. Rev. Lett. 117:249501. doi: 10.1103/PhysRevLett.117.249501

PubMed Abstract | CrossRef Full Text | Google Scholar

Blancard, C., Cossé, P., and Faussurier, G. (2012). Solar mixture opacity calculations using detailed configuration and level accounting treatments. Astrophys. J. 745:10. doi: 10.1088/0004-637X/745/1/10

CrossRef Full Text | Google Scholar

Böhm-Vitense, E. (1958). Über die Wasserstoffkonvektionszone in Sternen verschiedener Effektivtemperaturen und Leuchtkräfte. Mit 5 Textabbildungen. Z. Astrophys. 46:108.

Google Scholar

Boothroyd, A. I., and Sackmann, I.-J. (2003). Our Sun. IV. The standard model and helioseismology: consequences of uncertainties in input physics and in observed solar parameters. Astrophys. J. 583, 1004–1023. doi: 10.1086/345407

CrossRef Full Text | Google Scholar

Borexino Collaboration, Agostini, M., Altenmüller, K., Appel, S., Atroshchenko, V., Bagdasarian, Z., et al. (2018). Comprehensive measurement of pp-chain solar neutrinos. Nature 562, 505–510. doi: 10.1038/s41586-018-0624-y

CrossRef Full Text | Google Scholar

Borucki, W. J., Koch, D., Basri, G., Batalha, N., Brown, T., Caldwell, D., et al. (2010). Kepler planet-detection mission: introduction and first results. Science 327:977. doi: 10.1126/science.1185402

PubMed Abstract | CrossRef Full Text | Google Scholar

Boury, A., Gabriel, M., Noels, A., Scuflaire, R., and Ledoux, P. (1975). Vibrational instability of a 1 solar mass star towards non-radial oscillations. Astron. Astrophys. 41, 279–285.

Google Scholar

Bristow, T. F., Haberle, R. M., Blake, D. F., Des Marais, D. J., Eigenbrode, J. L., Fairén, A. G., et al. (2017). Low Hesperian PCO2 constrained from in situ mineralogical analysis at Gale Crater, Mars. Proc. Natl. Acad. Sci. U.S.A. 114, 2166–2170. doi: 10.1073/pnas.1616649114

PubMed Abstract | CrossRef Full Text | Google Scholar

Brookes, J. R., Isaak, G. R., and van der Raay, H. B. (1978). A resonant-scattering solar spectrometer. Mon. Notices R. Astron. Soc. 185, 1–18. doi: 10.1093/mnras/185.1.1

CrossRef Full Text | Google Scholar

Brown, T. M., and Morrow, C. A. (1987). “Observations of solar p-mode rotational splittings,” in The Internal Solar Angular Velocity, Vol. 137 of Astrophysics and Space Science Library, eds B. R. Durney and S. Sofia (Sunspot: Reidel), 7–17.

Google Scholar

Brun, A. S., Antia, H. M., Chitre, S. M., and Zahn, J.-P. (2002). Seismic tests for solar models with tachocline mixing. Astron. Astrophys. 391, 725–739. doi: 10.1051/0004-6361:20020837

CrossRef Full Text | Google Scholar

Buldgen, G., Reese, D., and Dupret, M.-A. (2017a). Asteroseismic inversions in the Kepler era: application to the Kepler Legacy sample. Euro. Phys. J. Web Conf. 160:03005. doi: 10.1051/epjconf/201716003005

CrossRef Full Text | Google Scholar

Buldgen, G., Reese, D. R., and Dupret, M. A. (2015a). Using seismic inversions to obtain an indicator of internal mixing processes in main-sequence solar-like stars. Astron. Astrophys. 583:A62. doi: 10.1051/0004-6361/201526390

CrossRef Full Text | Google Scholar

Buldgen, G., Reese, D. R., and Dupret, M. A. (2016a). Constraints on the structure of 16 Cygni A and 16 Cygni B using inversion techniques. Astron. Astrophys. 585:A109. doi: 10.1051/0004-6361/201527032

CrossRef Full Text | Google Scholar

Buldgen, G., Reese, D. R., and Dupret, M. A. (2017b). Analysis of the linear approximation of seismic inversions for various structural pairs. Astron. Astrophys. 598:A21. doi: 10.1051/0004-6361/201629485

CrossRef Full Text | Google Scholar

Buldgen, G., Reese, D. R., and Dupret, M. A. (2018). Constraining convective regions with asteroseismic linear structural inversions. Astron. Astrophys. 609:A95. doi: 10.1051/0004-6361/201730693

CrossRef Full Text | Google Scholar

Buldgen, G., Reese, D. R., Dupret, M. A., and Samadi, R. (2015b). Stellar acoustic radii, mean densities, and ages from seismic inversion techniques. Astron. Astrophys. 574:A42. doi: 10.1051/0004-6361/201424613

CrossRef Full Text | Google Scholar

Buldgen, G., Salmon, S. J. A. J., Godart, M., Noels, A., Scuflaire, R., Dupret, M. A., et al. (2017c). Inversions of the Ledoux discriminant: a closer look at the tachocline. Mon. Notices R. Astron. Soc. 472, L70–L74. doi: 10.1093/mnrasl/slx139

CrossRef Full Text | Google Scholar

Buldgen, G., Salmon, S. J. A. J., Noels, A., Scuflaire, R., Dupret, M. A., and Reese, D. R. (2017d). Determining the metallicity of the solar envelope using seismic inversion techniques. Mon. Notices R. Astron. Soc. 472, 751–764. doi: 10.1093/mnras/stx2057

CrossRef Full Text | Google Scholar

Buldgen, G., Salmon, S. J. A. J., Noels, A., Scuflaire, R., Reese, D. R., Dupret, M.-A., et al. (2017e). Seismic inversion of the solar entropy. A case for improving the standard solar model. Astron. Astrophys. 607:A58. doi: 10.1051/0004-6361/201731354

CrossRef Full Text | Google Scholar

Buldgen, G., Salmon, S. J. A. J., Reese, D. R., and Dupret, M. A. (2016b). In-depth study of 16CygB using inversion techniques. Astron. Astrophys. 596:A73. doi: 10.1051/0004-6361/201628773

CrossRef Full Text | Google Scholar

Burgers, J. M. (1969). Flow Equations for Composite Gases (New York, NY: Academic Press).

Google Scholar

Caffau, E., Ludwig, H.-G., Steffen, M., Freytag, B., and Bonifacio, P. (2011). Solar chemical abundances determined with a CO5BOLD 3D model atmosphere. Sol. Phys. 268, 255–269. doi: 10.1007/s11207-010-9541-4

CrossRef Full Text | Google Scholar

Castro, M., Vauclair, S., and Richard, O. (2007). Low abundances of heavy elements in the solar outer layers: comparisons of solar models with helioseismic inversions. Astron. Astrophys. 463, 755–758. doi: 10.1051/0004-6361:20066327

CrossRef Full Text | Google Scholar

Chapman, S., and Cowling, T. G. (1970). The Mathematical Theory of Non-uniform Gases. An Account of the Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases (Cambridge: University Press).

Google Scholar

Charbonnel, C., and Talon, S. (2005). Influence of gravity waves on the internal rotation and Li abundance of solar-type stars. Science 309, 2189–2191. doi: 10.1126/science.1116849

PubMed Abstract | CrossRef Full Text | Google Scholar

Charnay, B., Le Hir, G., Fluteau, F., Forget, F., and Catling, D. C. (2017). A warm or a cold early Earth? New insights from a 3-D climate-carbon model. Earth Planet. Sci. Lett. 474, 97–109. doi: 10.1016/j.epsl.2017.06.029

CrossRef Full Text | Google Scholar

Christensen-Dalsgaard, J., and Däppen, W. (1992). Solar oscillations and the equation of state. Astron. Astrophys. Rev. 4, 267–361. doi: 10.1007/BF00872687

CrossRef Full Text | Google Scholar

Christensen-Dalsgaard, J., Däppen, W., Ajukov, S. V., Anderson, E. R., Antia, H. M., Basu, S., et al. (1996). The current state of solar modeling. Science 272, 1286–1292.

PubMed Abstract | Google Scholar

Christensen-Dalsgaard, J., di Mauro, M. P., Houdek, G., and Pijpers, F. (2009). On the opacity change required to compensate for the revised solar composition. Astron. Astrophys. 494, 205–208. doi: 10.1051/0004-6361:200810170

CrossRef Full Text | Google Scholar

Christensen-Dalsgaard, J., Dilke, F. W. W., and Gough, D. O. (1974). The stability of a solar model to non-radial oscillations. Mon. Notices R. Astron. Soc. 169, 429–445.

Google Scholar

Christensen-Dalsgaard, J., and Gough, D. O. (1975). Nonadiabatic nonradial oscillations of a solar model. Memoir. Soc. R. Sci. Liege 8, 309–316.

Google Scholar

Christensen-Dalsgaard, J., Gough, D. O., and Knudstrup, E. (2018). On the hydrostatic stratification of the solar tachocline. Mon. Notices R. Astron. Soc. 477, 3845–3852. doi: 10.1093/mnras/sty752

CrossRef Full Text | Google Scholar

Christensen-Dalsgaard, J., Gough, D. O., and Thompson, M. J. (1991). The depth of the solar convection zone. Astrophys. J. 378, 413–437. doi: 10.1086/170441

CrossRef Full Text | Google Scholar

Christensen-Dalsgaard, J., and Houdek, G. (2010). Prospects for asteroseismology. Astrophys. Space Sci. 328, 51–66. doi: 10.1007/s10509-009-0227-z

CrossRef Full Text | Google Scholar

Christensen-Dalsgaard, J., Monteiro, M. J. P. F. G., Rempel, M., and Thompson, M. J. (2011). A more realistic representation of overshoot at the base of the solar convective envelope as seen by helioseismology. Mon. Notices R. Astron. Soc. 414, 1158–1174. doi: 10.1111/j.1365-2966.2011.18460.x

CrossRef Full Text | Google Scholar

Christensen-Dalsgaard, J., Proffitt, C. R., and Thompson, M. J. (1993). Effects of diffusion on solar models and their oscillation frequencies. Astrophys. J. Lett. 403, L75–L78. doi: 10.1086/186725

CrossRef Full Text | Google Scholar

Christensen-Dalsgaard, J., and Thompson, M. J. (2007). “Observational results and issues concerning the tachocline,” in The Solar Tachocline, eds D. W. Hughes, R. Rosner, and N. O. Weiss (Cambridge: Cambridge University Press), 53.

Google Scholar

Colgan, J., Kilcrease, D. P., Magee, N. H., Sherrill, M. E., Abdallah, J. Jr., Hakel, P., et al. (2016). A new generation of Los Alamos opacity tables. Astrophys. J. 817:116. doi: 10.3847/0004-637X/817/2/116

CrossRef Full Text | Google Scholar

Corbard, T., Blanc-Féraud, L., Berthomieu, G., and Provost, J. (1999). Non linear regularization for helioseismic inversions. Application for the study of the solar tachocline. Astron. Astrophys. 344, 696–708.

Google Scholar

Cox, J. P., and Giuli, R. T. (1968). Principles of Stellar Structure (New York, NY: Gordon and Breach).

Google Scholar

Däppen, W., Mihalas, D., Hummer, D. G., and Mihalas, B. W. (1988). The equation of state for stellar envelopes. III - Thermodynamic quantities. Astrophys. J. 332, 261–270.

Google Scholar

Davies, G. R., Broomhall, A. M., Chaplin, W. J., Elsworth, Y., and Hale, S. J. (2014). Low-frequency, low-degree solar p-mode properties from 22 years of Birmingham Solar Oscillations Network data. Mon. Notices R. Astron. Soc. 439, 2025–2032. doi: 10.1093/mnras/stu080

CrossRef Full Text | Google Scholar

Davis, R., Harmer, D. S., and Hoffman, K. C. (1968). Search for neutrinos from the Sun. Phys. Rev. Lett. 20, 1205–1209.

Google Scholar

Deal, M., Alecian, G., Lebreton, Y., Goupil, M. J., Marques, J. P., LeBlanc, F., et al. (2018). Impacts of radiative accelerations on solar-like oscillating main-sequence stars. Astron. Astrophys. 618:A10. doi: 10.1051/0004-6361/201833361

CrossRef Full Text | Google Scholar

Deal, M., Richard, O., and Vauclair, S. (2015). Accretion of planetary matter and the lithium problem in the 16 Cygni stellar system. Astron. Astrophys. 584:A105. doi: 10.1051/0004-6361/201526917

CrossRef Full Text | Google Scholar

Defouw, R. J. (1970). Thermal-convective instability. Astrophys. J. 160:659.

Google Scholar

Delahaye, F., and Pinsonneault, M. H. (2006). The solar heavy-element abundances. I. Constraints from stellar interiors. Astrophys. J. 649, 529–540. doi: 10.1086/505260

CrossRef Full Text | Google Scholar

Dilke, F. W. W., and Gough, D. O. (1972). The Solar spoon. Nature 240, 262–294.

Google Scholar

Domingo, V., Fleck, B., and Poland, A. I. (1995). The SOHO mission: an overview. Sol. Phys. 162, 1–37.

Google Scholar

Dziembowski, W. (1982). Nonlinear mode coupling in oscillating stars. I - Second order theory of the coherent mode coupling. Acta Astron. 32, 147–171.

Google Scholar

Dziembowski, W. (1983). Resonant coupling between solar gravity modes. Sol. Phys. 82, 259–266.

Google Scholar

Dziembowski, W. A., Pamyatnykh, A. A., and Sienkiewicz, R. (1990). Solar model from helioseismology and the neutrino flux problem. Mon. Notices R. Astron. Soc. 244, 542–550.

Google Scholar

Eggenberger, P., Deheuvels, S., Miglio, A., Ekström, S., Georgy, C., Meynet, G., et al. (2019). Asteroseismology of evolved stars to constrain the internal transport of angular momentum. I. Efficiency of transport during the subgiant phase. Astron. Astrophys. 621:A66. doi: 10.1051/0004-6361/201833447

CrossRef Full Text | Google Scholar

Eggenberger, P., Lagarde, N., Miglio, A., Montalbán, J., Ekström, S., Georgy, C., et al. (2017). Constraining the efficiency of angular momentum transport with asteroseismology of red giants: the effect of stellar mass. Astron. Astrophys. 599:A18. doi :10.1051/0004-6361/201629459

Google Scholar

Eggenberger, P., Maeder, A., and Meynet, G. (2005). Stellar evolution with rotation and magnetic fields. IV. The solar rotation profile. Astron. Astrophys. 440, L9–L12. doi: 10.1051/0004-6361:200500156

CrossRef Full Text | Google Scholar

Eggenberger, P., Meynet, G., Maeder, A., Hirschi, R., Charbonnel, C., Talon, S., et al. (2008). The Geneva stellar evolution code. Astrophys. Space Sci. 316, 43–54. doi: 10.1007/s10509-007-9511-y

CrossRef Full Text | Google Scholar

Eguchi, K., Enomoto, S., Furuno, K., Goldman, J., Hanada, H., Ikeda, H., et al. (2003). First results from KamLAND: evidence for reactor antineutrino disappearance. Phys. Rev. Lett. 90:021802. doi: 10.1103/PhysRevLett.90.021802

PubMed Abstract | CrossRef Full Text | Google Scholar

Elliott, J. R. (1996). Equation of state in the solar convection zone and the implications of helioseismology. Mon. Notices R. Astron. Soc. 280, 1244–1256. doi: 10.1093/mnras/280.4.1244

CrossRef Full Text | Google Scholar

Elliott, J. R., and Gough, D. O. (1999). Calibration of the thickness of the solar tachocline. Astrophys. J. 516, 475–481.

Google Scholar

Elsworth, Y., Howe, R., Isaak, G. R., McLeod, C. P., and New, R. (1990). Evidence from solar seismology against non-standard solar-core models. Nature 347, 536–539.

Google Scholar

Farnir, M., Dupret, M.-A., Salmon, S. J. A. J., Noels, A., and Buldgen, G. (2019). Comprehensive stellar seismic analysis. New method exploiting the glitches information in solar-like pulsators. Astron. Astrophys. 622:A98. doi: 10.1051/0004-6361/201834044

CrossRef Full Text | Google Scholar

Ferziger, J. H., and Kaper, H. G. (eds.) (1972). Mathematical Theory of Transport Processes in Gases. Amsterdam: North-Holland Pub. Co.

Google Scholar

Forget, F., Wordsworth, R., Millour, E., Madeleine, J.-B., Kerber, L., Leconte, J., et al. (2013). 3D modelling of the early martian climate under a denser CO₂ atmosphere: temperatures and CO₂ ice clouds. Icarus 222, 81–99. doi: 10.1016/j.icarus.2012.10.019

CrossRef Full Text | Google Scholar

Fossat, E., Boumier, P., Corbard, T., Provost, J., Salabert, D., Schmider, F. X., et al. (2017). Asymptotic g modes: evidence for a rapid rotation of the solar core. Astron. Astrophys. 604:A40. doi: 10.1051/0004-6361/201730460

CrossRef Full Text | Google Scholar

Fukuda, Y., Hayakawa, T., Ichihara, E., Inoue, K., Ishihara, K., Ishino, H., et al. (1999). Constraints on neutrino oscillation parameters from the measurement of day-night solar neutrino fluxes at super-kamiokande. Phys. Rev. Lett. 82, 1810–1814. doi: 10.1103/PhysRevLett.82.1810

CrossRef Full Text | Google Scholar

Gabriel, M. (1997). Influence of heavy element and rotationally induced diffusions on the solar models. Astron. Astrophys. 327, 771–778.

Google Scholar

Gabriel, M., Noels, A., Scuflaire, R., and Boury, A. (1976). On the evolution of a one-solar-mass star with a periodically mixed core. Astron. Astrophys. 47, 137–141.

Google Scholar

García, R. A., Turck-Chièze, S., Jiménez-Reyes, S. J., Ballot, J., Pallé, P. L., Eff-Darwich, A., et al. (2007). Tracking solar gravity modes: the dynamics of the Solar core. Science 316:1591. doi: 10.1126/science.1140598

PubMed Abstract | CrossRef Full Text | Google Scholar

Gorshkov, A. B., and Baturin, V. A. (2008). Diffusion settling of heavy elements in the solar interior. Astron. Rep. 52, 760–771. doi: 10.1134/S1063772908090072

CrossRef Full Text | Google Scholar

Gorshkov, A. B., and Baturin, V. A. (2010). Elemental diffusion and segregation processes in partially ionized solar plasma. Astrophys. Space Sci. 328, 171–174. doi: 10.1007/s10509-010-0277-2

CrossRef Full Text | Google Scholar

Gough, D. O. (2015). Some glimpses from helioseismology at the dynamics of the deep solar interior. Space Sci. Rev. 196, 15–47. doi: 10.1007/s11214-015-0159-6

CrossRef Full Text | Google Scholar

Gough, D. O. (2019). Anticipating the Sun's heavy-element abundance. Mon. Notices R. Astron. Soc. 485, L114–L115. doi: 10.1093/mnrasl/slz044

CrossRef Full Text | Google Scholar

Gough, D. O., and Kosovichev, A. G. (1993a). “Initial asteroseismic inversions,” in Inside the stars; Proceedings of the 137th IAU Colloquium, Vol. 40 of Astronomical Society of the Pacific Conference Series, eds W. W. Weiss and A. Baglin (Vienna: University of Vienna), 541.

Google Scholar

Gough, D. O., and Kosovichev, A. G. (1993b). The Influence of Low-Degree P-Mode Frequencies on the Determination of the Structure of the Solar Interior. Mon. Notices R. Astron. Soc. 264:522. doi: 10.1093/mnras/264.2.522

CrossRef Full Text | Google Scholar

Gough, D. O., and McIntyre, M. E. (1998). Inevitability of a magnetic field in the Sun's radiative interior. Nature 394, 755–757. doi: 10.1038/29472

CrossRef Full Text | Google Scholar

Gough, D. O., and Thompson, M. J. (1991). The Inversion Problem (Tucson, AZ: University of Arizona Press), 519–561.

Google Scholar

Graedel, T. E., Sackmann, I.-J., and Boothroyd, A. I. (1991). Early solar mass loss - A potential solution to the weak sun paradox. Geophys. Res. Lett. 18, 1881–1884. doi: 10.1029/91GL02314

CrossRef Full Text | Google Scholar

Grevesse, N., and Noels, A. (1993). “Cosmic abundances of the elements,” in Origin and Evolution of the Elements, eds N. Prantzos, E. Vangioni-Flam, and M. Casse, 15–25.

Google Scholar

Grevesse, N., and Sauval, A. J. (1998). Standard solar composition. Space Sci. Rev. 85, 161–174.

Google Scholar

Grevesse, N., Scott, P., Asplund, M., and Sauval, A. J. (2015). The elemental composition of the Sun. III. The heavy elements Cu to Th. Astron. Astrophys. 573:A27. doi: 10.1051/0004-6361/201424111

CrossRef Full Text | Google Scholar

Gruberbauer, M., Guenther, D. B., and Kallinger, T. (2012). Toward a new kind of asteroseismic grid fitting. Astrophys. J. 749:109. doi: 10.1088/0004-637X/749/2/109

CrossRef Full Text | Google Scholar

Gryaznov, V., Iosilevskiy, I., Fortov, V., Starostin, A., Roerich, V., Baturin, V. A., et al. (2013). Saha's thermodynamic model of solar plasma. Contrib. Plasma Phys. 53, 392–396. doi: 10.1002/ctpp.201200109

CrossRef Full Text | Google Scholar

Gryaznov, V. K., Ayukov, S. V., Baturin, V. A., Iosilevskiy, I. L., Starostin, A. N., and Fortov, V. E. (2004). “SAHA-S model: equation of State and Thermodynamic Functions of Solar Plasma,” in Equation-of-State and Phase-Transition in Models of Ordinary Astrophysical Matter, vol. 731 of American Institute of Physics Conference Series, eds V. Celebonovic, D. Gough, and W. Däppen, 147–161.

Google Scholar

Gryaznov, V. K., Ayukov, S. V., Baturin, V. A., Iosilevskiy, I. L., Starostin, A. N., and Fortov, V. E. (2006). Solar plasma: calculation of thermodynamic functions and equation of state. J. Phys. A Math. Gen. 39:4459. doi: 10.1088/0305-4470/39/17/S22

CrossRef Full Text | Google Scholar

Guzik, J. A. (2008). Problems for the standard solar model arising from the new solar mixture. Memor. Soc. Astron. Ital. 79:481.

Google Scholar

Guzik, J. A., Fontes, C. J., Walczak, P., Wood, S. R., Mussack, K., and Farag, E. (2016). Sound speed and oscillation frequencies for solar models evolved with Los Alamos ATOMIC opacities. IAU Focus Meet. 29, 532–535. doi: 10.1017/S1743921316006062

CrossRef Full Text | Google Scholar

Guzik, J. A., and Mussack, K. (2010). Exploring mass lOSS, low-Z accretion, and convective overshoot in solar models to mitigate the solar abundance problem. Astrophys. J. 713, 1108–1119. doi: 10.1088/0004-637X/713/2/1108

CrossRef Full Text | Google Scholar

Guzik, J. A., Watson, L. S., and Cox, A. N. (2005). Can Enhanced diffusion improve helioseismic agreement for solar models with revised abundances? Astrophys. J. 627, 1049–1056. doi: 10.1086/430438

CrossRef Full Text | Google Scholar

Guzik, J. A., Watson, L. S., and Cox, A. N. (2006). Implications of revised solar abundances for helioseismology. Memor. Soc. Astron. Ital. 77:389.

Google Scholar

Guzik, J. A., Willson, L. A., and Brunish, W. M. (1987). A comparison between mass-losing and standard solar models. Astrophys. J. 319, 957–965.

Google Scholar

Harvey, J., Abdel-Gawad, K., Ball, W., Boxum, B., Bull, F., Cole, J., et al. (1988). “The GONG instrument,” in Seismology of the Sun and Sun-Like Stars, Vol. 286 of ESA Special Publication, ed E. J. Rolfe.

Google Scholar

Haxton, W. C., Hamish Robertson, R. G., and Serenelli, A. M. (2013). Solar neutrinos: status and prospects. Annu. Rev. Astron. Astrophys 51, 21–61. doi: 10.1146/annurev-astro-081811-125539

CrossRef Full Text | Google Scholar

Holweger, H., and Mueller, E. A. (1974). The photospheric barium spectrum - Solar abundance and collision broadening of BA II lines by hydrogen. Sol. Phys. 39, 19–30.

Google Scholar

Hotta, H. (2017). Solar overshoot region and small-scale dynamo with realistic energy flux. Astrophys. J. 843:52. doi: 10.3847/1538-4357/aa784b

CrossRef Full Text | Google Scholar

Houdek, G., and Gough, D. O. (2011). On the seismic age and heavy-element abundance of the Sun. Mon. Notices R. Astron. Soc. 418, 1217–1230. doi: 10.1111/j.1365-2966.2011.19572.x

CrossRef Full Text | Google Scholar

Houdek, G., and Rogl, J. (1996). On the accuracy of opacity interpolation schemes. Bull. Astron. Soc. India 24, 317–320.

Google Scholar

Hummer, D. G., and Mihalas, D. (1988). The equation of state for stellar envelopes. I - an occupation probability formalism for the truncation of internal partition functions. Astrophys. J. 331, 794–814.

Google Scholar

Iglesias, C. A. (2015). Iron-group opacities for B stars. Mon. Notices R. Astron. Soc. 450, 2–9. doi: 10.1093/mnras/stv591

CrossRef Full Text | Google Scholar

Iglesias, C. A., and Hansen, S. B. (2017). Fe XVII opacity at solar interior conditions. Astrophys. J. 835:284. doi: 10.3847/1538-4357/835/2/284

CrossRef Full Text | Google Scholar

Iglesias, C. A., and Rogers, F. J. (1996). Updated opal opacities. Astrophys. J. 464:943.

Google Scholar

Irwin, A. W. (2012). FreeEOS: Equation of State for Stellar Interiors Calculations. Astrophysics Source Code Library.

Google Scholar

Isaak, G. R., McLeod, C. P., Palle, P. L., van der Raay, H. B., and Roca Cortes, T. (1989). Solar oscillations as seen in the NaI and KI absorption lines. Astron. Astrophys. 208, 297–302.

Google Scholar

Jørgensen, A. C. S., Mosumgaard, J. R., Weiss, A., Silva Aguirre, V., and Christensen-Dalsgaard, J. (2018). Coupling 1D stellar evolution with 3D-hydrodynamical simulations on the fly - I. A new standard solar model. Mon. Notices R. Astron. Soc. 481, L35–L39. doi: 10.1093/mnrasl/sly152

CrossRef Full Text | Google Scholar

King, J. R., Deliyannis, C. P., Hiltgen, D. D., Stephens, A., Cunha, K., and Boesgaard, A. M. (1997). Lithium abundances in the solar twins 16 CYG A and B and the solar analog alpha CEN A, calibration of the 6707 angstrom Li region linelist, and implications. Astron. J. 113:1871. doi: 10.1086/118399

CrossRef Full Text | Google Scholar

Kosovichev, A. G. (1988). The internal rotation of the sun from helioseismological data. Soviet Astron. Lett. 14:145.

Google Scholar

Kosovichev, A. G. (1999). Inversion methods in helioseismology and solar tomography. J. Comput. Appl. Math. 109, 1–39.

Google Scholar

Kosovichev, A. G., and Fedorova, A. V. (1991). Construction of a seismic model of the Sun. Sov. Astron. 35:507.

Google Scholar

Kosovichev, A. G., and Severnyi, A. B. (1985). The influence of chemical composition on the stability of solar gravity-mode oscillations. Izvestiya Ordena Trudovogo Krasnogo Znameni Krymskoj Astrofizicheskoj Observatorii 72, 188–198.

Google Scholar

Krief, M., Feigel, A., and Gazit, D. (2016). Line broadening and the solar opacity problem. Astrophys. J. 824:98. doi: 10.3847/0004-637X/824/2/98

CrossRef Full Text | Google Scholar

Landi, E., and Testa, P. (2015). Neon and oxygen abundances and abundance ratio in the solar corona. Astrophys. J. 800:110. doi: 10.1088/0004-637X/800/2/110

CrossRef Full Text | Google Scholar

Le Pennec, M., Turck-Chièze, S., Salmon, S., Blancard, C., Cossé, P., Faussurier, G., et al. (2015). First new solar models with OPAS opacity tables. Astrophys. J. Lett. 813:L42. doi: 10.1088/2041-8205/813/2/L42

CrossRef Full Text | Google Scholar

Lebreton, Y., Montalbán, J., Christensen-Dalsgaard, J., Théado, S., Hui-Bon-Hoa, A., Monteiro, M. J. P. F. G., et al. (2007). “Microscopic Diffusion in Stellar Evolution Codes: First Comparisons Results of ESTA-Task 3,” in EAS Publications Series, Vol. 26 of EAS Publications Series, eds C. W. Straka, Y. Lebreton, and M. J. P. F. G. Monteiro, 155–165.

Google Scholar

Ledoux, P. (1974). “Non-radial oscillations,” in Stellar Instability and Evolution, Vol. 59 of IAU Symposium, eds P. Ledoux, A. Noels, and A. W. Rodgers (Canberra, ACT: International Astronomical Union Dordrecht; D. Reidel Publishing), 135–173.

Google Scholar

Li, Y., and Yang, J. Y. (2007). Testing turbulent convection theory in solar models - I. Structure of the solar convection zone. Mon. Notices R. Astron. Soc. 375, 388–402. doi: 10.1111/j.1365-2966.2006.11319.x

CrossRef Full Text | Google Scholar

Lund, M. N., Silva Aguirre, V., Davies, G. R., Chaplin, W. J., Christensen-Dalsgaard, J., Houdek, G., et al. (2017). Standing on the shoulders of dwarfs: the kepler asteroseismic LEGACY sample. I. oscillation mode parameters. Astrophys. J. 835:172. doi: 10.3847/1538-4357/835/2/172

CrossRef Full Text | Google Scholar

Marchenkov, K., Roxburgh, I., and Vorontsov, S. (2000). Non-linear inversion for the hydrostatic structure of the solar interior. Mon. Notices R. Astron. Soc. 312, 39–50. doi: 10.1046/j.1365-8711.2000.03059.x

CrossRef Full Text | Google Scholar

Metcalfe, T. S., Creevey, O. L., and Davies, G. R. (2015). Asteroseismic Modeling of 16 Cyg A B using the Complete Kepler Data Set. Astrophys. J. Lett. 811:L37. doi: 10.1088/2041-8205/811/2/L37

CrossRef Full Text | Google Scholar

Michaud, G., Alecian, G., and Richer, J. (2015). Atomic Diffusion in Stars. Springer International Publishing.

Google Scholar

Michaud, G., Charland, Y., Vauclair, S., and Vauclair, G. (1976). Diffusion in main-sequence stars - Radiation forces, time scales, anomalies. Astrophys. J. 210, 447–465. doi: 10.1086/154848

CrossRef Full Text | Google Scholar

Michaud, G., and Proffitt, C. R. (1993). “Particle transport processes,” in Inside the Stars; Proceedings of the 137th IAU Colloquium, eds W. W. Weiss and A. Baglin (Vienna: University of Vienna), 246–259.

Google Scholar

Michaud, G., and Richer, J. (2008). Radiative accelerations in stellar evolution. Memor. Soc. Astron. Ital. 79:592.

Google Scholar

Mihalas, D., Däppen, W., and Hummer, D. G. (1988). The equation of state for stellar envelopes. II - Algorithm and selected results. Astrophys. J. 331, 815–825.

Google Scholar

Mihalas, D., Hummer, D. G., Mihalas, B. W., and Däppen, W. (1990). The equation of state for stellar envelopes. IV - Thermodynamic quantities and selected ionization fractions for six elemental mixes. Astrophys. J. 350, 300–308. doi: 10.1086/168383

CrossRef Full Text | Google Scholar

Minton, D. A., and Malhotra, R. (2007). Assessing the massive young sun hypothesis to solve the warm young Earth puzzle. Astrophys. J. 660, 1700–1706. doi: 10.1086/514331

CrossRef Full Text | Google Scholar

Mondet, G., Blancard, C., Cossé, P., and Faussurier, G. (2015). Opacity calculations for solar mixtures. Astron. Astrophys. Suppl. Ser. 220:2. doi: 10.1088/0067-0049/220/1/2

CrossRef Full Text | Google Scholar

Montalban, J., Miglio, A., Theado, S., Noels, A., and Grevesse, N. (2006). The new solar abundances - Part II: the crisis and possible solutions. Commun. Asteroseismol. 147, 80–84. doi: 10.1553/cia147s80

CrossRef Full Text | Google Scholar

Montalbán, J., Théado, S., and Lebreton, Y. (2007). “Comparisons for ESTA-Task3: CLES and CESAM,” in EAS Publications Series, volume 26 of EAS Publications Series, C. W. Straka, Y. Lebreton, and M. J. P. F. G. Monteiro, 167–176.

Google Scholar

Monteiro, M. J. P. F. G., Christensen-Dalsgaard, J., and Thompson, M. J. (1994). Seismic study of overshoot at the base of the solar convective envelope. Astron. Astrophys. 283, 247–262.

Google Scholar

Mussack, K., and Däppen, W. (2011). Dynamic screening correction for solar p-p reaction rates. Astrophys. J. 729:96. doi: 10.1088/0004-637X/729/2/96

CrossRef Full Text | Google Scholar

Nahar, S. N., and Pradhan, A. K. (2016). Large enhancement in high-energy photoionization of Fe XVII and missing continuum plasma opacity. Phys. Rev. Lett. 116:235003. doi: 10.1103/PhysRevLett.116.235003

PubMed Abstract | CrossRef Full Text | Google Scholar

Noels, A., Boury, A., Gabriel, M., and Scuflaire, R. (1976). Vibrational stability towards non-radial oscillations during central hydrogen burning. Astron. Astrophys. 49:103.

Google Scholar

Noerdlinger, P. D. (1977). Diffusion of helium in the sun. Astron. Astrophys. 57, 407–415.

Google Scholar

Ouazzani, R.-M., Marques, J. P., Goupil, M., Christophe, S., Antoci, V., and Salmon, S. J. A. J. (2018). {\gamma} Doradus stars as test of angular momentum transport models. arXiv e-prints.

Pain, J.-C., and Gilleron, F. (2019). Opacity calculations for stellar astrophysics. arXiv e-prints.

Google Scholar

Pain, J.-C., Gilleron, F., and Comet, M. (2018). “Detailed opacity calculations for stellar models,” in Workshop on Astrophysical Opacities, Vol. 515 of Astronomical Society of the Pacific Conference Series eds C. Mendoza, S. Turck-Chiéze, and J. Colgan (Kalamazoo, MI: Astronomical Society of the Pacific), 35.

Google Scholar

Paquette, C., Pelletier, C., Fontaine, G., and Michaud, G. (1986). Diffusion coefficients for stellar plasmas. Astron. Astrophys. Suppl. Ser. 61, 177–195. doi: 10.1086/191111

CrossRef Full Text | Google Scholar

Piau, L., and Turck-Chièze, S. (2001). “Lithium burning in the early evolution of the Sun and Sun-like Stars,” in From Darkness to Light: Origin and Evolution of Young Stellar Clusters, Vol. 243 of Astronomical Society of the Pacific Conference Series, eds T. Montmerle and P. André (San Francisco, CA: Astronomical Society of the Pacific), 639.

Google Scholar

Pijpers, F. P., and Thompson, M. J. (1994). The SOLA method for helioseismic inversion. Astron. Astrophys. 281, 231–240.

Google Scholar

Pinsonneault, M. H., and Delahaye, F. (2009). The shoiolar heavy element abundances. II. Constraints from stellar atmospheres. Astrophys. J. 704, 1174–1188. doi: 10.1088/0004-637X/704/2/1174

CrossRef Full Text | Google Scholar

Pradhan, A. K., and Nahar, S. N. (2018). “Recalculation of astrophysical opacities: overview, methodology, and atomic calculations,” in Workshop on Astrophysical Opacities, Vol. 515 of Astronomical Society of the Pacific Conference Series, 79.

Google Scholar

Proffitt, C. R., and Michaud, G. (1991). Gravitational settling in solar models. Astrophys. J. 380, 238–250. doi: 10.1086/170580

CrossRef Full Text | Google Scholar

Rabello-Soares, M. C., Basu, S., and Christensen-Dalsgaard, J. (1999). On the choice of parameters in solar-structure inversion. Mon. Notices R. Astron. Soc. 309, 35–47.

Google Scholar

Rauer, H., Catala, C., Aerts, C., Appourchaux, T., Benz, W., Brandeker, A., et al. (2014). The PLATO 2.0 mission. Exp. Astron. 38, 249–330. doi: 10.1007/s10686-014-9383-4

CrossRef Full Text | Google Scholar

Reese, D. R., Marques, J. P., Goupil, M. J., Thompson, M. J., and Deheuvels, S. (2012). Estimating stellar mean density through seismic inversions. Astron. Astrophys. 539:A63. doi: 10.1051/0004-6361/201118156

CrossRef Full Text | Google Scholar

Rempel, M. (2004). Overshoot at the base of the solar convection zone: a semianalytical approach. Astrophys. J. 607, 1046–1064. doi: 10.1086/383605

CrossRef Full Text | Google Scholar

Rendle, B. M., Buldgen, G., Miglio, A., Reese, D., Noels, A., Davies, G. R., et al. (2019). AIMS - a new tool for stellar parameter determinations using asteroseismic constraints. Mon. Notices R. Astron. Soc. 484, 771–786. doi: 10.1093/mnras/stz031

CrossRef Full Text | Google Scholar

Richard, O., Dziembowski, W. A., Sienkiewicz, R., and Goode, P. R. (1998). On the accuracy of helioseismic determination of solar helium abundance. Astron. Astrophys. 338, 756–760.

Google Scholar

Richard, O., Michaud, G., and Richer, J. (2001). Iron convection zones in B, A, and F stars. Astrophys. J. 558, 377–391. doi: 10.1086/322264

CrossRef Full Text | Google Scholar

Richard, O., Michaud, G., and Richer, J. (2002a). Models of metal-poor stars with gravitational settling and radiative accelerations. III. Metallicity dependence. Astrophys. J. 580, 1100–1117. doi: 10.1086/343733

CrossRef Full Text | Google Scholar

Richard, O., Michaud, G., Richer, J., Turcotte, S., Turck-Chièze, S., and VandenBerg, D. A. (2002b). Models of metal-poor stars with gravitational settling and radiative accelerations. I. Evolution and abundance anomalies. Astrophys. J. 568, 979–997. doi: 10.1086/338952

CrossRef Full Text | Google Scholar

Richard, O., Vauclair, S., Charbonnel, C., and Dziembowski, W. A. (1996). New solar models including helioseismological constraints and light-element depletion. Astron. Astrophys. 312, 1000–1011.

Google Scholar

Richer, J., Michaud, G., and Turcotte, S. (2000). The Evolution of AMFM stars, abundance anomalies, and turbulent transport. Astrophys. J. 529, 338–356. doi: 10.1086/308274

CrossRef Full Text | Google Scholar

Ricker, G. R., Winn, J. N., Vanderspek, R., Latham, D. W., Bakos, G. Á., Bean, J. L., et al. (2015). Transiting Exoplanet Survey Satellite (TESS). J. Astron. Telesc. Instrum. Syst. 1:014003. doi: 10.1117/1.JATIS.1.1.014003

CrossRef Full Text | Google Scholar

Rogers, F. J., and Nayfonov, A. (2002). Updated and expanded OPAL equation-of-state tables: implications for helioseismology. Astrophys. J. 576, 1064–1074. doi: 10.1086/341894

CrossRef Full Text | Google Scholar

Rogers, F. J., Swenson, F. J., and Iglesias, C. A. (1996). OPAL equation-of-state tables for astrophysical applications. Astrophys. J. 456:902.

Google Scholar

Roxburgh, I., Audard, N., Basu, S., Christensen-Dalsgaard, J., and Vorontsov, S. (1998). “Inversion for the internal structure of an evolved small mass star using modes with l=0-3 in proceedings,” in Sounding Solar and Stellar Interiors, eds F. Schmider and J. Provost (Nice: IAU Coll. 181), 245.

Roxburgh, I., and Vorontsov, S. (2003a). Diagnostics of the internal structure of stars using the differential response technique. Astrophys. Space Sci. 284, 187–191. doi: 10.1051/0004-6361:20031318

CrossRef Full Text | Google Scholar

Roxburgh, I. W. (1976). “The internal structure of the Sun and solar type stars,” in Basic Mechanisms of Solar Activity, Vol. 71 of IAU Symposium, eds V. Bumba and J. Kleczek (Prague, Czechoslovakia), 453.

Google Scholar

Roxburgh, I. W. (1984). “On turbulent mixing,” in Observational Tests of the Stellar Evolution Theory, Vol. 105 of IAU Symposium, eds A. Maeder and A. Renzini (Geneva: D. Reidel Publishing Company), 519.

Google Scholar

Roxburgh, I. W. (2016). Asteroseismic model fitting by comparing ϵ_n values. Astron. Astrophys. 585:A63. doi: 10.1051/0004-6361/201526593

CrossRef Full Text | Google Scholar

Roxburgh, I. W., and Vorontsov, S. V. (2002). “Inversion for a 0.8 Msolar star using differential-response technique,” in Proceedings of the First Eddington Workshop on Stellar Structure and Habitable Planet Finding, Vol. 485 of ESA Special Publication, eds B. Battrick, F. Favata, I. W. Roxburgh, and D. Galadi (Córdoba: ESA Publications Division), 337–339.

Google Scholar

Roxburgh, I. W., and Vorontsov, S. V. (2003b). The ratio of small to large separations of acoustic oscillations as a diagnostic of the interior of solar-like stars. Astron. Astrophys. 411, 215–220.

Google Scholar

Sackmann, I.-J., and Boothroyd, A. I. (2003). Our Sun. V. A bright young sun consistent with helioseismology and warm temperatures on Ancient Earth and Mars. Astrophys. J. 583, 1024–1039. doi: 10.1086/345408

CrossRef Full Text | Google Scholar

Saio, H. (1980). Stability of nonradial g/+/-mode pulsations in 1 solar mass models. Astrophys. J. 240, 685–692.

Google Scholar

Schatten, K. H. (1973). Magnetic convection. Sol. Phys. 33, 305–318.

Google Scholar

Schlattl, H. (2002). Microscopic diffusion of partly ionized metals in the Sun and metal-poor stars. Astron. Astrophys. 395, 85–95. doi: 10.1051/0004-6361:20021212

CrossRef Full Text | Google Scholar

Schlattl, H., and Salaris, M. (2003). Quantum corrections to microscopic diffusion constants. Astron. Astrophys. 402, 29–35. doi: 10.1051/0004-6361:20030230

CrossRef Full Text | Google Scholar

Schou, J., Antia, H. M., Basu, S., Bogart, R. S., Bush, R. I., Chitre, S. M., et al. (1998). Helioseismic studies of differential rotation in the solar envelope by the solar oscillations investigation using the michelson doppler imager. Astrophys. J. 505, 390–417.

Google Scholar

Schunker, H., Schou, J., Gaulme, P., and Gizon, L. (2018). Fragile detection of solar g-Modes by Fossat et al. Sol. Phys. 293:95. doi: 10.1007/s11207-018-1313-6

CrossRef Full Text | Google Scholar

Schwarzschild, K. (1906). On the equilibrium of the Sun's atmosphere. Nachrichten von der Königlichen Gesellschaft der Wissenschaften zu Göttingen 195, 41–53.

Google Scholar

Scott, P., Asplund, M., Grevesse, N., Bergemann, M., and Sauval, A. J. (2015a). The elemental composition of the Sun. II. The iron group elements Sc to Ni. Astron. Astrophys. 573:A26. doi: 10.1051/0004-6361/201424110

CrossRef Full Text | Google Scholar

Scott, P., Grevesse, N., Asplund, M., Sauval, A. J., Lind, K., Takeda, Y., et al. (2015b). The elemental composition of the Sun. I. The intermediate mass elements Na to Ca. Astron. Astrophys. 573:A25. doi: 10.1051/0004-6361/201424109

CrossRef Full Text | Google Scholar

Scuflaire, R., Gabriel, M., Noels, A., and Boury, A. (1975). Oscillatory periods in the sun and theoretical models with or without mixing. Astron. Astrophys. 45, 15–18.

Google Scholar

Scuflaire, R., Montalbán, J., Théado, S., Bourge, P.-O., Miglio, A., Godart, M., et al. (2008a). The Liège oscillation code. Astrophys. Space Sci. 316, 149–154. doi: 10.1007/s10509-007-9577-6

CrossRef Full Text | Google Scholar

Scuflaire, R., Théado, S., Montalbán, J., Miglio, A., Bourge, P.-O., Godart, M., et al. (2008b). CLÉS, code liégeois d'Évolution stellaire. Astrophys. Space Sci. 316, 83–91. doi: 10.1007/s10509-007-9650-1

CrossRef Full Text | Google Scholar

Serenelli, A. M., Basu, S., Ferguson, J. W., and Asplund, M. (2009). New solar composition: the problem with solar models revisited. Astrophys. J. Lett. 705, L123–L127. doi: 10.1088/0004-637X/705/2/L123

CrossRef Full Text | Google Scholar

Serenelli, A. M., Haxton, W. C., and Peña-Garay, C. (2011). Solar models with accretion. I. Application to the solar abundance problem. Astrophys. J. 743:24. doi: 10.1088/0004-637X/743/1/24

CrossRef Full Text | Google Scholar

Shibahashi, H., Osaki, Y., and Unno, W. (1975). Nonradial g-mode oscillations and the stability of the sun. Publ. Astron. Soc. Jpn 27, 401–410.

Google Scholar

Silva Aguirre, V., Lund, M. N., Antia, H. M., Ball, W. H., Basu, S., Christensen-Dalsgaard, J., et al. (2017). Standing on the shoulders of dwarfs: the kepler asteroseismic LEGACY sample. II.Radii, masses, and ages. Astrophys. J. 835:173. doi: 10.3847/1538-4357/835/2/173

CrossRef Full Text | Google Scholar

Sonoi, T., and Shibahashi, H. (2012a). Dipole low-order g-mode instability of metal-poor low-mass main-sequence stars due to the ϵ mechanism. Mon. Notices R. Astron. Soc. 422, 2642–2647. doi: 10.1111/j.1365-2966.2012.20827.x

CrossRef Full Text | Google Scholar

Sonoi, T., and Shibahashi, H. (2012b). Fully nonadiabatic analysis of vibrational instability of population III stars due to the varepsilon-Mechanism. Publ. Astron. Soc. Jpn 64:2. doi: 10.1093/pasj/64.1.2

CrossRef Full Text | Google Scholar

Spalding, C., Fischer, W. W., and Laughlin, G. (2018). An Orbital window into the Ancient Suns Mass. Astrophys. J. Lett. 869:L19. doi: 10.3847/2041-8213/aaf219

CrossRef Full Text | Google Scholar

Spiegel, E. A., and Zahn, J.-P. (1992). The solar tachocline. Astron. Astrophys. 265, 106–114.

Google Scholar

Takata, M., and Montgomery, M. H. (2002). “Seismic inversions for white dwarf stars,” in IAU Colloq. 185: Radial and Nonradial Pulsationsn as Probes of Stellar Physics, Vol. 259 of Astronomical Society of the Pacific Conference Series, eds C. Aerts, T. R. Bedding, and J. Christensen-Dalsgaard (San Francisco, CA: Astronomical Society of the Pacific), 606.

Google Scholar

Takata, M., and Shibahashi, H. (2001). “Solar metal abundance inferred from helioseismology,” in Recent Insights into the Physics of the Sun and Heliosphere: Highlights from SOHO and Other Space Missions, Vol. 203 of IAU Symposium, eds P. Brekke, B. Fleck, and J. B. Gurman, 43.

Google Scholar

Théado, S., Alecian, G., LeBlanc, F., and Vauclair, S. (2012). The new Toulouse-Geneva stellar evolution code including radiative accelerations of heavy elements. Astron. Astrophys. 546:A100. doi: 10.1051/0004-6361/201219610

CrossRef Full Text | Google Scholar

Theado, S., and Vauclair, S. (2010). Radiative accelerations, accumulation of iron and thermohaline convection inside stars. Theado 328, 209–212. doi: 10.1007/s10509-009-0221-5

CrossRef Full Text | Google Scholar

Théado, S., Vauclair, S., Castro, M., Charpinet, S., and Dolez, N. (2005). Asteroseismic tests of element diffusion in solar type stars. Astron. Astrophys. 437, 553–560. doi: 10.1051/0004-6361:20042328

CrossRef Full Text | Google Scholar

Thévenin, F., Oreshina, A. V., Baturin, V. A., Gorshkov, A. B., Morel, P., and Provost, J. (2017). Evolution of lithium abundance in the Sun and solar twins. Astron. Astrophys. 598:A64. doi: 10.1051/0004-6361/201629385

CrossRef Full Text | Google Scholar

Thoul, A. A., Bahcall, J. N., and Loeb, A. (1994). Element diffusion in the solar interior. Astrophys. J. 421, 828–842.

Google Scholar

Tucci Maia, M., Meléndez, J., and Ramírez, I. (2014). High precision abundances in the 16 Cyg binary system: a signature of the rocky core in the giant planet. Astrophys. J. Lett. 790:L25. doi: 10.1088/2041-8205/790/2/L25

CrossRef Full Text | Google Scholar

Turbet, M., Forget, F., Head, J. W., and Wordsworth, R. (2017). 3D modelling of the climatic impact of outflow channel formation events on early Mars. Icarus 288, 10–36. doi: 10.1016/j.icarus.2017.01.024

CrossRef Full Text | Google Scholar

Turck-Chièze, S. (2005). How does helioseismology constrain solar neutrino properties? Nucl. Phys. B Proc. Suppl. 143, 35–42. doi: 10.1016/j.nuclphysbps.2005.01.085

CrossRef Full Text | Google Scholar

Turck-Chieze, S., Cahen, S., Casse, M., and Doom, C. (1988). Revisiting the standard solar model. Astrophys. J. 335, 415–424.

Google Scholar

Turck-Chièze, S., and Couvidat, S. (2011). Solar neutrinos, helioseismology and the solar internal dynamics. Rep. Prog. Phys. 74:086901. doi: 10.1088/0034-4885/74/8/086901

CrossRef Full Text | Google Scholar

Turck-Chièze, S., Couvidat, S., Piau, L., Ferguson, J., Lambert, P., Ballot, J., et al. (2004). Surprising sun: a new step towards a complete picture? Phys. Rev. Lett. 93:211102. doi: 10.1103/PhysRevLett.93.211102

PubMed Abstract | CrossRef Full Text | Google Scholar

Turck-Chièze, S., Piau, L., and Couvidat, S. (2011). The solar energetic balance revisited by young solar analogs, helioseismology, and neutrinos. Astrophys. J. Lett. 731:L29. doi: 10.1088/2041-8205/731/2/L29

CrossRef Full Text | Google Scholar

Turcotte, S., Richer, J., Michaud, G., Iglesias, C. A., and Rogers, F. J. (1998). Consistent solar evolution model including diffusion and radiative acceleration effects. Astrophys. J. 504, 539–558.

Google Scholar

Ulrich, R. K. (1974). Solar models with low neutrino fluxes. Astrophys. J. 188, 369–378.

Google Scholar

Ulrich, R. K. (1975). Solar neutrinos and variations in the solar luminosity. Science 190, 619–624.

Google Scholar

Ulrich, R. K., and Rood, R. T. (1973). Mixing in stellar models. Nat. Phys. Sci. 241, 111–112.

Google Scholar

Unno, W. (1975). On the stability of the solar core. Publ. Astron. Soc. Jpn 27, 81–99.

Google Scholar

VandenBerg, D. A., Richard, O., Michaud, G., and Richer, J. (2002). Models of metal-poor stars with gravitational settling and radiative accelerations. II. the age of the oldest stars. Astrophys. J. 571, 487–500. doi: 10.1086/339895

CrossRef Full Text | Google Scholar

Verma, K., Faria, J. P., Antia, H. M., Basu, S., Mazumdar, A., Monteiro, M. J. P. F. G., et al. (2014). Asteroseismic estimate of helium abundance of a solar analog binary system. Astrophys. J. 790:138. doi: 10.1088/0004-637X/790/2/138

CrossRef Full Text | Google Scholar

Vernazza, J. E., Avrett, E. H., and Loeser, R. (1976). Structure of the solar chromosphere. II - The underlying photosphere and temperature-minimum region. Astron. Astrophys. Suppl. Ser. 30, 1–60.

Google Scholar

Viallet, M., Meakin, C., Prat, V., and Arnett, D. (2015). Toward a consistent use of overshooting parametrizations in 1D stellar evolution codes. Astron. Astrophys. 580:A61. doi: 10.1051/0004-6361/201526294

CrossRef Full Text | Google Scholar

Vinyoles, N., Serenelli, A. M., Villante, F. L., Basu, S., Bergström, J., Gonzalez-Garcia, M. C., et al. (2017). A new generation of standard solar models. Astrophys. J. 835:202. doi: 10.3847/1538-4357/835/2/202

CrossRef Full Text | Google Scholar

Vorontsov, S. V., Baturin, V. A., Ayukov, S. V., and Gryaznov, V. K. (2013). Helioseismic calibration of the equation of state and chemical composition in the solar convective envelope. Mon. Notices R. Astron. Soc. 430, 1636–1652. doi: 10.1093/mnras/sts701

CrossRef Full Text | Google Scholar

Vorontsov, S. V., Baturin, V. A., and Pamiatnykh, A. A. (1991). Seismological measurement of solar helium abundance. Nature 349, 49–51.

Google Scholar

Weiss, A., and Heners, N. (2013). Low-mass stars: Open problems all along their evolution. Eur. Phys. J. Web Conf. 43:01002. doi: 10.1051/epjconf/20134301002

CrossRef Full Text | Google Scholar

White, T. R., Huber, D., Maestro, V., Bedding, T. R., Ireland, M. J., Baron, F., et al (2013). Interferometric radii of bright Kepler stars with the CHARA Array: Cygni and 16 Cygni A and B. Mon. Notices R. Astron. Soc. 433, 1262–1270. doi: 10.1093/mnras/stt802

CrossRef Full Text | Google Scholar

Winnick, R. A., Demarque, P., Basu, S., and Guenther, D. B. (2002). Seismic test of solar models, solar neutrinos, and implications for metal-rich accretion. Astrophys. J. 576, 1075–1084. doi: 10.1086/341795

CrossRef Full Text | Google Scholar

Wood, B. E., Müller, H.-R., Zank, G. P., Linsky, J. L., and Redfield, S. (2005). New mass-loss measurements from astrospheric lyα absorption. Astrophys. J. Lett. 628, L143–L146. doi: 10.1086/432716

CrossRef Full Text | Google Scholar

Wood, S. R., Mussack, K., and Guzik, J. A. (2018). Solar models with dynamic screening and early mass loss tested by helioseismic, astrophysical, and planetary constraints. Sol. Phys. 293:111. doi: 10.1007/s11207-018-1334-1

CrossRef Full Text | Google Scholar

Wordsworth, R. D. (2016). The climate of Early mars. Annu. Rev. Earth Planet. Sci. 44, 381–408. doi: 10.1146/annurev-earth-060115-012355

CrossRef Full Text | Google Scholar

Xiong, D. R., and Deng, L. (2001). The structure of the solar convective overshooting zone. Mon. Notices R. Astron. Soc. 327, 1137–1144. doi: 10.1046/j.1365-8711.2001.04820.x

CrossRef Full Text | Google Scholar

Yang, J. Y., and Li, Y. (2007). Testing turbulent convection theory in solar models - II. Solar p-mode oscillations. Mon. Notices R. Astron. Soc. 375, 403–414. doi: 10.1111/j.1365-2966.2006.11320.x

CrossRef Full Text | Google Scholar

Young, P. R. (2018). Element abundance ratios in the quiet sun transition region. Astrophys. J. 855:15. doi: 10.3847/1538-4357/aaab48

CrossRef Full Text | Google Scholar

Zaatri, A., Provost, J., Berthomieu, G., Morel, P., and Corbard, T. (2007). Sensitivity of low degree oscillations to the change in solar abundances. Astron. Astrophys. 469, 1145–1149. doi: 10.1051/0004-6361:20077212

CrossRef Full Text | Google Scholar

Zhang, Q. S. (2017). Numerical integral of resistance coefficients in diffusion. Astrophys. J. 834:132. doi: 10.3847/1538-4357/834/2/132

CrossRef Full Text | Google Scholar

Zhao, L., Eissner, W., Nahar, S. N., and Pradhan, A. K. (2018). “Converged R-matrix calculations of the photoionization of fexvii in astrophysical plasmas: from convergence to completeness,” in Workshop on Astrophysical Opacities, Vol. 515 of Astronomical Society of the Pacific Conference Series, eds C. Mendoza, S. Turck-Chiéze, and J. Colgan (Kalamazoo, MI: Astronomical Society of the Pacific), 89.

Google Scholar

Appendix

FIGURE A1

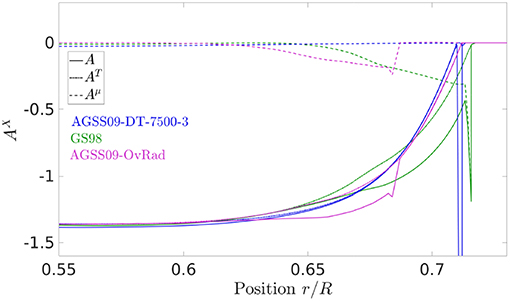
Figure A1. Decomposition of the Ledoux discriminant in its thermal and chemical composition gradients contributions for a model built with the GS98 abundances, and other models including modified opacity tables and macroscopic chemical mixing.

To have a closer look at the impact of extra mixing at the base of the convective zone, we illustrate in Figure A1 the various contributions to the Ledoux discriminant, A. We use the following definition

$\begin{array}{ll}A=-\frac{r\delta }{H_P}\left({\nabla }_{Ad}-\nabla +\frac{\varphi }{\delta }{\nabla }_{\mu }\right),& (\mathrm{A1})\end{array}$

with H_P the pressure scale height, μ the mean molecular weight, P the pressure and $\delta =-{\left(\frac{\partial ln\rho }{\partial lnT}\right)}_{P,\mu }$, $\varphi ={\left(\frac{\partial ln\rho }{\partial ln\mu }\right)}_{P,T}$, $\nabla =\frac{dlnT}{dlnP}$, ${\nabla }_{Ad}={\left(\frac{\partial lnT}{\partial lnP}\right)}_S$, with S the entropy, ${\nabla }_{\mu }=\frac{dln\mu }{dlnP}$. We define the thermal and chemical contributions to the Ledoux discriminant, A^T and A^μ as

$\begin{array}{ll}{A}^{\mu }=-\frac{r\varphi }{H_P}{\nabla }_{\mu },& (\mathrm{A2})\end{array}$

$\begin{array}{ll}{A}^T=-\frac{r\delta }{H_P}({\nabla }_{Ad}-\nabla ).& (\mathrm{A3})\end{array}$

From Figure A1, we see that the thermal contribution largely dominates the behavior of the Ledoux discriminant, with the exception of the last percent of the radiative regions. There is a clear difference between a fully mixed overshoot and that of turbulent diffusion. This opens up the possibility to combine seismic diagnostics to distinguish the form of the macroscopic mixing at the base of the solar convective zone and explains the observed differences in Figure 7. Using non-linear inversions, as in Corbard et al. (1999), may also help to further constrain the profile of the Ledoux discriminant between 0.67 and 0.71 solar radii. There also appears to be a clear difference in the temperature contribution, A^T, between the various models, around 0.65 solar radii. This difference is due to the too steep temperature gradient at this position, seen for the GS98 model and the model built using radiative overshoot. A parametric modeling of the transition in both temperature and chemical gradients should shed new light the existing degeneracies and provide seismic constraints to works aiming at including hydrodynamical prescriptions in stellar evolutionary codes. To that end, a combination of the analysis of the phase-shift of frequencies, as carried out by Christensen-Dalsgaard et al. (2011) or the use of a non-linear RLS method following the approach of Corbard et al. (1999) would allow to probe the sharp transition in Ledoux discriminant at the base of the convective zone.