- 1Centre for Fundamental Research in Photosynthesis, Vergiate, Italy
- 2Photosynthesis Research Unit, Centro Studi sulla Biologia Cellulare e Molecolare delle Piante, Milan, Italy
- 3Istituto di Biologia e Biotecnologia Agraria, Consiglio Nazionale delle Ricerche, Milan, Italy
Two phylloquinone molecules (A1), one being predominantly coordinated by PsaA subunit residues (A1A) the other by those of PsaB (A1B), act as intermediates in the two parallel electron transfer chains of Photosystem I. The oxidation kinetics of the two phyllosemiquinones by the iron-sulfur cluster FX differ by approximately one order of magnitude, with being oxidized in about 200 ns and in about 20 ns. These differences are generally explained in terms of asymmetries in the driving force for FX reduction on the two electron transfer chains. Site directed mutations of conserved amino acids composing the A1 binding site have been engineered on both reaction center subunits, and proved to affect selectively the oxidation lifetime of either , for PsaA mutants, or , for PsaB mutants. The mutation effects are here critically reviewed, also by novel modeling simulations employing the tunneling formalism to estimate the electron transfer rates. Three main classes of mutation effects are in particular addressed: (i) those leading to an acceleration, (ii) those leading to a moderated slowing (~5-folds), and (iii) those leading to a severe slowing (>20-folds) of the kinetics. The effect of specific amino acid perturbations contributing to the poising of the phylloquinones redox potential and, in turn, to PSI functionality, is discussed.
Overview of Electron Transfer IN Photosystem I
Photosystem I (PSI) is a key component of both the linear and the cyclic electron transport chains of oxygenic photosynthesis. Electron transfer (ET) reactions take place in a protein-cofactor super-complex known as the core, which is overall well conserved throughout evolution. The core complex of PSI is composed by over 20 protein subunits, the exact number being species-specific. Most of the cofactors involved both in light harvesting and ET reactions are bound by the heterodimer composed of the PsaA and PsaB protein subunits (Jordan et al., 2001; Qin et al., 2015; Mazor et al., 2017). The most notable exception are two iron-sulfur clusters, named FA and FB, which are bound by the PsaC subunit instead. Structural studies indicate that the cofactors involved in ET reactions are related to a C2 (mirror) symmetry (Figure 1) with respect to an axis perpendicular to the putative membrane plane (Jordan et al., 2001; Qin et al., 2015; Mazor et al., 2017), which is a common structural motif of photosynthetic reaction centers. However, a large body of evidences has been gathered leading to the conclusion that, differently from the other well-characterized systems such as the purple bacteria RC and Photosystem II, in PSI both cofactors chains are ET active (Joliot and Joliot, 1999; Guergova-Kuras et al., 2001; Muhiuddin et al., 2001; Santabarbara et al., 2005a, 2010a; Rappaport et al., 2006; Redding and van der Est, 2006; Srinivasan and Golbeck, 2009; Makita and Hastings, 2016).
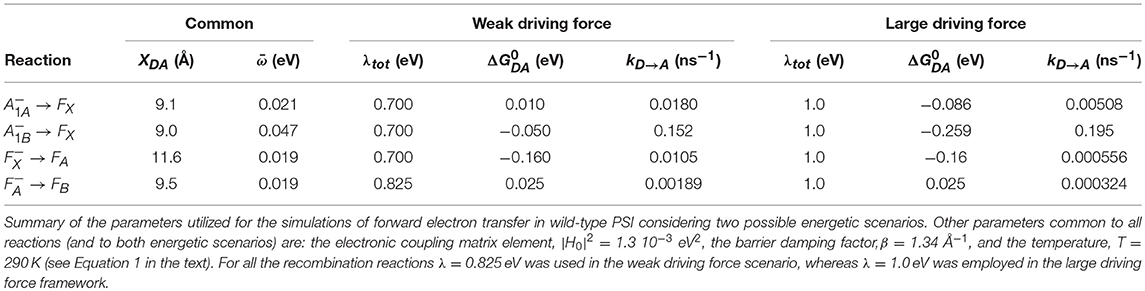
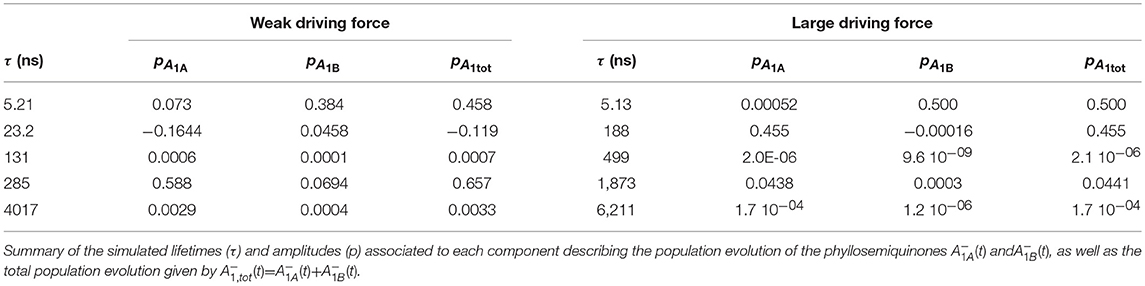
Figure 1. (A) Structural organization of the co-factors composing the electron transfer chains in Photosystem I from Jordan et al. (2001), PDB file # 1JB0. Shown are: the terminal electron donor (P700) considered as Chl a/Chl a′ hetero-dimer (black); the so-called accessory Chl a are unlabeled (gray); the primary Chl a electron acceptors A0(A/B) (green); the phylloquinones A1A (red) and A1B (blue) and the terminal 4Fe-4S clusters, FX (gold), FA (orange), and FB (burgundy). (B) Phylloquinone binding niche of the PsaA reaction center subunit. The phylloquinone molecule (A1A) is shown in brown. The atom color-coded (C: yellow, O: red, N: blue) side chains represent the principal protein residues interacting with the redox moiety. Mutations of these specific residues are discussed in the text. Side chains shown in gray also have a role in controlling ET properties but will not be specifically discussed here.
Electron transfer reactions are initiated from the lowest singlet excited state of the chromophores composing the photochemically active center, giving rise to the population, via one or more intermediate steps, of a radical pair consisting of a chlorophyll (Chl) cation, residing on the metastable electron donor (), and a phyllosemiquinone anion (). Two specific radical pairs, attributed to and (the subscript refers to the subunit harboring the phylloquinone), were identified in PSI, demonstrating the photochemical functionality of both ET branches (Poluektov et al., 2005; Santabarbara et al., 2005b, 2006, 2010c; Berthold et al., 2012). Successive ET reactions involve the cascade oxidation of initially by the PsaA:PsaB coordinated cluster FX, and successively by the PsaC-coordinated clusters FA and FB, that are oxidized by diffusible electron carries, the most common of which is ferredoxin. Noticeably, FX represents a point of convergence of the two active ET branches, as it is shared by both, and so are the terminal acceptors FA and FB (Figure 1).
In place of a remarkable structural symmetry of the active ET chains, they also show clear functional differences, the most evident being the approximately one order of magnitude slower oxidation lifetime of with respect to at room temperature. These two reactions are characterized by apparent lifetimes in the 200–350 and 5–30 ns intervals, respectively (e.g., Brettel, 1997; Santabarbara et al., 2005a, 2010a; Rappaport et al., 2006; Srinivasan and Golbeck, 2009; Makita and Hastings, 2016 for reviews). The assignment of these oxidation components to ET events involving either or was based on the study of site-selective mutants of the phylloquinone binding niches of either the PsaA or the PsaB subunit, leading to specific alterations of either the “slow” (~250 ns) or the “fast” (~20 ns) lifetime (Guergova-Kuras et al., 2001; Xu et al., 2003; Byrdin et al., 2006; Santabarbara et al., 2008, 2010b, 2015; Srinivasan et al., 2011). Moreover, not only the apparent oxidation lifetimes of and differ significantly, but they also have distinct temperature dependences, with ~250 ns showing a significant thermal activation (100–130 meV, Schlodder et al., 1998; Agalarov and Brettel, 2003; Santabarbara et al., 2009) and the ~20 ns being only weakly temperature dependent (7–43 meV, Agalarov and Brettel, 2003; Santabarbara et al., 2009). The complexity of oxidation at physiological temperature is also highlighted by the presence of an additional kinetic phase, sometimes referred to as “intermediate,” having lifetimes in the 150–180 ns range. This component was first observed in investigations of the reaction temperature dependence (Agalarov and Brettel, 2003) and successively in mutants of the PsaA subunit affecting the binding niche (Byrdin et al., 2006; Santabarbara et al., 2008). It has been tentatively assigned to ET involving the 4Fe-4S clusters. The above discussed differences in the kinetic behavior of and represent a nice example of the specific involvement of protein binding and coordination in tuning the redox properties of cofactors active in ET reactions. This is a well-recognized phenomenon which is also apparent for the 4Fe-4S clusters bound to PSI, that although being chemically indistinguishable, display differences in the redox potentials well exceeding 150 mV, based on titrations, which pose FA and FB in the –(500–550) mV range (Ke et al., 1973, 1977; Evans et al., 1974; Lozier and Butler, 1974; Heathcote et al., 1978; Evans and Heathcote, 1980; Nugent et al., 1981) and FX in the –(670–730) mV interval [(Ke et al., 1977; Chamorowsky and Cammack, 1982; Parrett et al., 1989) and the detailed discussion by Brettel (1997) on the limits of these estimations]. On the other hand, direct titration of has proven to be very difficult because of its very negative redox midpoint potential. Henceforth, to acquire information on the redox properties of and , alternative approaches based either on theoretical chemical methods (Ishikita and Knapp, 2003; Karyagina et al., 2007; Ptushenko et al., 2008; Kawashima and Ishikita, 2017) or on modeling of the ET reactions kinetics in the framework of non-adiabatic ET tunneling theory (Santabarbara et al., 2005a; Moser and Dutton, 2006; Makita et al., 2015; Santabarbara and Zucchelli, 2016; Cherepanov et al., 2017; Makita and Hastings, 2017; Milanovsky et al., 2017) have been adopted.
Still, the predictions from these two approaches do not generally agree, despite showing some common traits, the most relevant of which being that the estimated redox potential (E0) of the pair is more negative than that of . Structure-based theoretical calculations tend to predict a difference in potential between the two phylloquinone (PhQ) molecules exceeding 100 mV, whereas kinetic modeling predicts the difference to be in the order to 40–60 mV.
Although the latter approach appears more indirect, it is constrained to satisfactorily reproduce the ET kinetics, at least to a semi-quantitative level. Comparing different energetic landscapes, it was concluded that a scenario involving a weakly endergonic oxidation of (standard free energy difference, of +10 meV) and a larger ( = −50 meV) exergonic oxidation of provided a good description of both the room temperature kinetics as well as their temperature dependences (Santabarbara and Zucchelli, 2016). Scenarios involving largely exergonic oxidation of both and (e.g., = −86 meV and = −259 meV from Ptushenko et al. (2008); note the subscript indicates the electron donor) were also shown to be compatible with the experimental results, although they required a larger value of the (total) reorganization energy and concomitantly predicted a rather slow oxidation of reduced FX (Santabarbara and Zucchelli, 2016). At the same time Makita and Hastings (2017), based on analogous kinetic approaches but also considering the effect of replacing the naturally occurring PhQ with exogenous redox moieties having inherently different redox midpoint potentials, obtained results comparable with the weak driving force scenario, but with differences in the best-describing driving force estimation as = 45 meV and = −10 meV (Makita et al., 2015; Makita and Hastings, 2017). Moreover, these authors showed that considering the effect of different ET processes, for instance the forward oxidation kinetics and the charge recombination reaction between the ET intermediates (i.e., reduced FA and FB) and the terminal electron donor , imposed some critical constrain to the model parameters other than the Gibbs free energy (Makita and Hastings, 2017). In their modeling framework, large reorganization energies such as those necessary to describe forward ET in the “largely exergonic” scenario, did not lead to acceptable descriptions of the recombination kinetics. Moreover, their arguments imply that all ET reactions downstream of and need to be considered in order to properly account for the charge recombination processes.
As highlighted in a recent critical review (Santabarbara et al., 2019) specific choices of parameter sets can have significant impact on the back estimation of (and therefore on the ) from kinetic modeling. Yet, a consensus energetic scenario was retrieved in which oxidation fell in the weakly exergonic to weakly endergonic picture (−5 < <35 meV) and oxidation was generally exergonic, with the associated driving force being larger than −10 meV (−50 < < -10 meV).
To further resume the potentiality of theory-bound kinetic modeling in uncovering the ET energetics in PSI, in the following paragraphs the basic principles of ET rates description and of kinetic simulations will be briefly introduced. This will be done in association to a semi-quantitative modeling of both the energetics and the kinetics of oxidation in wild-type PSI reaction center. The effect of mutations affecting the PhQ binding sites, in particular at the level of the PsaA subunit, will then be discussed, and, in this context, kinetic simulations will also be presented for the mutant scenarios.
Basic Principles of Electron Transfer Theory
The ET rates between a donor-acceptor cofactor pair can be described by the following equation, which represents a simplified form of the expression originally derived by Hopfield (1974); Devault (1980), but considering a single (mean) nuclear mode coupled to the ET event:
In Equation (1), is the electronic coupling term described by , its maximal value at wavefunction overlap, β, a damping term associated to the probability of tunneling the potential barrier and XDA, the edge-to-edge cofactor distance. The 3.6 factor is a correction for the van der Waals radii. λ is the (total) reorganization energy, is the angular frequency of the mean coupled nuclear mode, ℏ is the Dirac constant, kB is the Boltzman constant and T is the temperature. When < < kBT the expression simplifies to: , yielding the semi-classical one derived by Marcus (Marcus and Sutin, 1985). An expression which considers multiple modes and specific electron-phonon coupling and that provides a more accurate description of temperature dependence over a broad temperature range was derived by Jortner (1976). However, employing Jortner formalism leads inevitably to a large increase in the number of parameters to be considered, and most of the deviations with respect to Equation 1 are predicted at low and intermediate temperatures. Hence, the Hopfield-Marcus expressions represent a good approximation, at least at physiological temperatures. Noticeably, Equation 1 has been parameterised by Moser and Dutton (1992) and Moser and Dutton (1996) in a linearised form on logarithmic scale that at room temperature is: . The parameterised values are equivalent to ~10−3 eV2, β = 1.38 Å−1 and = 56 meV in Equation 1. Similar values will be adopted in the forthcoming calculations ( = 1.3 10−3 eV2, β = 1.34 Å−1) but will instead be taken from the analysis of the temperature dependences of these electron transfer reactions (Mula et al., 2012), i.e., = 21 meV and = 47 meV. The values of and λ will be discussed below (see Table 1 for compilation of the input parameters).
From Equation (1) (and equivalently from the parameterised “ET ruler” expression) the maximal rate of ET (for any given ) is obtained when . Under these conditions the temperature dependence of the reaction is minimal. The absolute maximal rate is attained not only when but also when = , i.e., at minimal distance.
Kinetic Simulations
Once the ET rates are computed (Equation 1) they can be inserted in an appropriate kinetic model which depends on the reaction scheme considered (Figure 2). In case ET involves only one-electron oxido-reductions, like in the case of PSI, the temporal evolution of the ET cofactor populations can be described by a system of coupled ordinary differential equations having, in compact matrix notation, the general form: D(t) = Ki·D(t). D(t) is a vector describing the temporal evolution of the redox intermediate populations and D(t) is its first derivative with respect to time. Both vectors have the same dimension equalling the number of ET steps in the redox chain, i. Ki is a square matrix containing the molecular rate constants between couples of donors-acceptors as its elements and is often called the rate matrix. Elements on the diagonal include the depopulation of redox intermediates whereas the off-diagonal ones are the formation/population rates. This system has general solutions of the form: , where ζj and Vj are, the eigenvalues and the eigenvectors, respectively, necessary to diagonalise Ki. The eigenvalues are univocally determined and relates to the experimentally observed lifetimes () by the simple relation . It is very commonly assumed that the inverse of the experimentally determined lifetimes () describes to a good approximation the ET rate constants. This is however reasonable only as long as the off-diagonal terms of Ki are much smaller than the diagonal ones. In general the eigenvalues, and therefore the observed lifetimes, will depend on all the rate constants coupling the different intermediates. In order to unambiguously define the pre-exponential amplitude, scaling constants (cj) weighting the eigenvectors of Ki need to be determined. This requires solving a boundary problem, which is most commonly determined by the initial conditions (e.g., the concentration of the intermediates at t → 0). As discussed for the eigenvalues/lifetime relation, also the eigenvectors elements (amplitudes) cannot be directly associated to specific ET events, because their values will depend on all of the rate constant composing the Ki matrix, as well as on the boundary conditions (see Santabarbara et al., 2014 for further discussion). The statistical utilization of the two active ET chains in PSI, which ideally defines the boundary, is still somewhat debated and might be dependent on the class of organisms considered. Whereas, in model green algae the two branches appear to be almost equally active in ET reactions (e.g., Guergova-Kuras et al., 2001; Santabarbara et al., 2005a,b, 2015), more asymmetric utilization, in favor of the PsaA branch (up to 0.8:0.2), have been reported for model cyanobacterial species (e.g., Xu et al., 2003; Cohen et al., 2004; Dashdorj et al., 2005; Milanovsky et al., 2014; Sun et al., 2014; Makita and Hastings, 2015), although more even utilization has been also reported for these organism too (e.g., Santabarbara et al., 2006, 2010c). For the modeling described here we consider even initial populations on the phylloquinones (0.5) and no population in all other intermediates. This scenario is more representative, in general, to the one most commonly encountered in green algae. It was chosen because some of the site-directed mutants discussed below were raised only in the PSI of C. reinhardtii. It is worth mentioning, however, that changes in the initial populations would only affect the relative amplitudes of oxidation phases, but not their lifetimes.
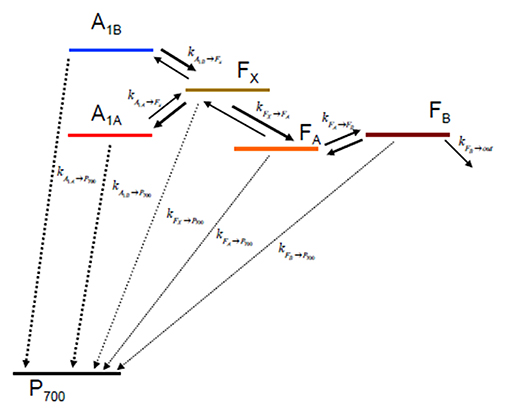
Figure 2. Kinetic scheme describing the electron transfer reactions downstream of A1 and the recombination paths to considered in the simulations.
Kinetic Description of A1 Oxidation
Kinetic modeling of electron transfer reactions, coupled to theory-based ET rate description, represents an useful tool to extract the energetics associated to reactions whose chemical-physical properties are cumbersome to address by other biophysical and biochemical methodologies. Yet, as discussed in the previous paragraphs, the description of the ET rates also requires the knowledge of a set of parameters (e.g., , λDA, tot, , and ). These are not always straightforwardly extractable from the experimental data and need therefore to be fixed in the calculation, often to some consensus values stemming from the parameterisation developed by Moser and Dutton (1992) and Moser and Dutton (1996). Because of these limitations, it appears sensible to limit the tuning of adjustable parameters to reach a good semi-quantitative description of the results rather than aiming at an exact reproduction of the experimental data.
In the following paragraphs the discussion will be focused on the kinetics of oxidation in PSI, and in particular on the driving force (standard free energy differences, ) associated to these reactions, while limiting to a minimum the tuning of all other adjustable parameters, particularly the reorganization energies. Thus, the description presented shall be considered to only semi-quantitatively describe these ET reaction kinetics, and whenever possible the values of parameters, unless taken from independent studies, will be rounded to the closer decade interval. It is arguable that this is a reasonable approach, not only because of the uncertainties on some of the parameters already addressed but also because, whereas the modeling provides information on the population evolutions (changes in cofactor redox-state concentration over time), the experimentally measured kinetics also depend on other properties of the cofactors. For instance, in transient absorption, which is possibly the most popular experimental approach, the experimental data also reflects the differential (reduced/oxidized) extinction coefficient of the cofactors (Δε). This is expected to be similar, but not necessarily identical, for the case of the phylloquinones considered here. Moreover, contributions of other redox centers, such as the iron-sulfur centers, and the occurrence of spectral changes associated with electrogenic reactions (electrochromism), would also give rise to kinetically overlapped optical transients, so that an exact correspondence between the population evolution and the experimental shall not be, in principle, expected.
Moreover, recent reinvestigations have shown that ET oxidation kinetics display significant dispersive character even at room temperature (Malferrari et al., 2016; Kurashov et al., 2018), i.e., are better described by lifetime distributions rather than a sum of discrete exponentials. This implies some distributed character also for the microscopic parameters employed in the ET rate description. Instead, in the modeling approach described in Paragraph 3, the parameters are accounted by a single, well-defined, value instead. Hence, the retrieved values for the parameter of interest (, in this case) shall better be considered as an estimation of its mean value, provided that the underlying distribution is symmetric and reasonably narrow.
Thus, within this semi-quantitative limit, two alterative energetic scenarios for oxidation in PSI will be discussed: (i) the one involving a “weak driving force” for, particularly, oxidation (ii) the one considering “large driving force” for the oxidation of both and .
Wild-Type Reaction Centers
Weak Driving Force Case
The energetic scenario describing the oxidation kinetics of and in a wild-type PSI reaction center, within the weak driving force framework, is schematically illustrated in Figure 3A. It is considered that = 10 meV, = −50 meV, = −160 meV, and = 25 meV, values that fall within the range originally suggested, within the bidirectional ET framework, by Santabarbara et al. (2005a) and which validity has been recently rediscussed (Santabarbara et al., 2019). However, similar scenarios for oxidation were previously suggested by Brettel (1997). Setting the redox midpoint potential of FB to −555 mV, which is compatible with the direct redox titration (see Brettel, 1997 for a compilation of literature values), the redox potentials of the other considered cofactors are: = −680 meV, = −740 mV, = −690 mV, and = −530 mV. The redox midpoint potential of is taken as 450 mV. In order to reduce to a minimum the number of adjustable parameters, a common value of the total reoganization energy (λ) equal to 0.7 eV was employed for all forward reactions involving , , and FX. A larger reorganization energy (0.825 eV) was utilized for ET reactions between the remaining metal centers (FA and FB) instead and for all the recombination reactions with . This reorganization energy might appear low, as Density Function Theory (DFT) calculations performed on Ferredoxin, which is highly homologous to the FA/FB-binding PsaC subunit of PSI, predicted it to be as high as 0.64 for the internal reorganization component alone (Sigfridsson et al., 2001). Hence, calculations were also performed by employing total reorganizations of 1 and 1.3 eV (~twice the internal) for the ET between FA and FB. These simulations, shown in Figure S1, indicate that the oxidation kinetics remain virtually unchanged, but significant kinetic slowdown is modeled for the downstream cofactors kinetics. Whereas, a value of λFA→FB = 1 eV still provides acceptable descriptions, raising its value to 1.3 eV resulted in a too slow oxidation of the terminal iron-sulfur cluster acceptors (without changing any of the other parameters). The only rate constant which was not modeled according to theory was FB oxidation, as this represents just an output from the system. The value of this rate was set to (1 μs)−1 corresponding to the fastest phase of Ferredoxin reduction (Setif, 2001). The list of all parameters used in the simulations is reported in Table 1.
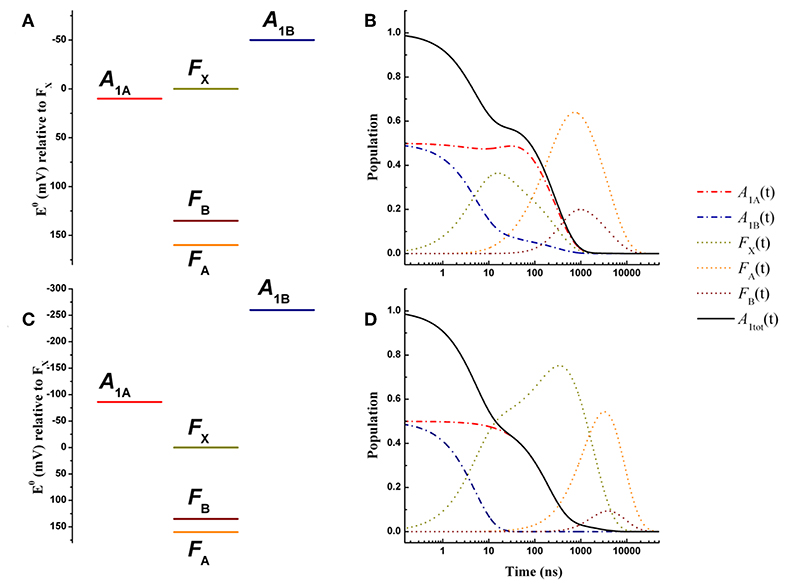
Figure 3. Energetics (A,C) and kinetic simulations (B,D) of the electron transfer reactions downstream of A1 for a wild-type PSI reaction center, according to the “weak” (A,B) and the “large” (C,D) driving force scenarios. Dash-dotted blue lines: A1B; dash-dotted red lines: A1A; dotted golden lines: FX; dotted orange lines: FA; dotted burgundy lines: FB. Black solid line: A1tot = A1A+A1B.
The simulated ET kinetics of all the intermediates considered employing the just described parameters are shown in Figure 3B. The A1A and A1B oxidation kinetics are characterized by four main exponential decay components described by lifetimes of 5.2, 23.1, 131, and 285 ns (Table 2), whereas an additional lifetime component of ~4 μs has extremely low amplitude (note that the lifetimes are common to all intermediates, but not the amplitudes). The relative amplitudes of these components, for the total oxidation of , which is the only experimental accessible one and which is given by the straight summation of modeled and , are 0.45, −0.12, 0.0007, and 0.66 (Table 2). This indicates that the fastest and slowest components are largely dominant. As discussed in previous studies (Santabarbara et al., 2010a, 2015; Santabarbara and Zucchelli, 2016), the number of simulated components is larger than those retrieved experimentally. This is because the simulations will yield a number of lifetimes equal to the number of ET steps considered. Still, predicted lifetimes which fall closely spaced in time (e.g., ~5 and 25 ns) would be hardly distinguishable experimentally. Similar considerations could be extended to the ~130 and 280 ns component, due also to the differences in relative amplitudes. Nonetheless an oxidation phase characterized by a lifetime of 140–180 ns became observable in mutants in which the ~250 ns phase was lengthened as a result of specific amino-acid side chain substitutions (Byrdin et al., 2006; Santabarbara et al., 2008, 2015). Moreover, this phase was also observed in temperature dependence studies of oxidation of wild-type PSI (Agalarov and Brettel, 2003; Santabarbara et al., 2009), suggesting it was not the result of mutations of the PhQ binding site. The simulated lifetime of 131 ns corresponds therefore rather nicely to the experimentally retrieved values. Noteworthy, whereas the ~5, 25, and 250 ns are simulated also in minimal models considering only A1A and A1B and FX (e.g., Santabarbara et al., 2010a, 2015; Santabarbara and Zucchelli, 2016), the 131 ns is not, indicating it is associated to ET reactions involving the terminal 4Fe-4S cluster acceptors. In fact, although this component has rather weak amplitude on it is a dominant one in oxidation of FB. Moreover, it is the lifetime associated to this component, together with its relative amplitude in the Fe-S clusters oxidation, which is primarily affected by varying the value of λFA→FB, becoming ~500 ns and ~1 μs for total reorganizations of 1 and 1.3 eV, respectively (Figure S1). Grouping the lifetimes of <50 ns and more than 50 ns into macroscopic “fast” and “slow” oxidation phases, respectively, a proportion of 0.34:0.66 between them is found, corresponding to an average lifetime of 188 ns, which is in good agreement with the experimental reports, particularly concerning PSI of green algae (Santabarbara et al., 2005a, 2010a; Rappaport et al., 2006).
Recombination reactions (from all considered co-factors) were modeled simply suppressing the output from the system. Under these conditions the only possible oxidation path for electrons that have reached the terminal acceptors is that of recombining with the cation located on P700. It is obtained that under these simulation conditions, FA and FB are oxidized with mean lifetimes of ~75 ms, equalling reduction. This value is also in excellent agreement with experimental estimations, from which a rather broad range of 20–100 ms is reported (Brettel, 1997; Shinkarev et al., 2002). Importantly, the recombination lifetime is much faster than the predicted rates for direct recombination between either FA and FB and P700 (which are in the hours-to-days span due to large distances between the redox centers). Thus, the modeled recombination has to proceed by back-population (reduction) of the co-factors upstream to terminal iron-sulfur clusters, and is therefore kinetically limited by the large energy gap between FA and FX.
Large Driving Force Case
An energetic scheme and the associated kinetic simulations representative of the large driving force scenario for the oxidation of both of and in a wild-type PSI are presented in Figures 3C,D, respectively. The values of = −86 meV, = −259 meV were taken from the study of Ptushenko et al. (2008). To allow a straightforward comparison, all other parameters, with the exception of λ, were the same as in the simulations of Figure 3B. In order to semi-quantitatively describe oxidation, a value of λ = 1 eV (rather than 0.7 eV used for the weak driving force scenario) needed to be considered, and to limit the number of tuneable parameters this value was adopted for all others reaction (forward and recombination) considered (Table 1). Simulations for the values proposed by Milanovsky et al. (2017), = −55 meV, = −220 meV, in which the driving forces are lower but remain significant, are presented in Figure S2, and with all other relevant parameters listed in Table S1. Semi-quantitative agreement was reached just by using a slightly lower value of the total reorganization energy (0.925 eV), common to all considered reactions.
The kinetics are described by three sub-microsecond components of 5.1, 194, and 499 ns, and two microsecond phases of 1.9 and 6 μs, with the longest one representing the outcome from the system (Table 2). The two fastest components have by far the largest amplitude on the total oxidation, corresponding to 0.5 and 0.45, respectively, with the residual 0.05 being associated to the 1.9 μs phase, which is not reported in experimental measurements, but it may simply escape detection because of its very small amplitude (Table 2). The 499 ns phase corresponds to inter Fe-S ET. Its lifetime matches the one also predicted for the weak-driving force scenario when using the same value of 1 eV for λFA→FB, and it can be accelerated to resemble the experimental reported phase of ~160 ns by decreasing the reorganization to ~0.85 (not shown). However, this would assume that λFA→FB has a lower value than λA1→FX, which is not reasonable as ET between metal cluster is expected to be associated with larger reorganization energies. Differently from the weak driving force scenario, the relative amplitudes of the fast and slow oxidation phases, match the initial populations.
Hence, both the weak driving force and the large driving force scenarios appear to provide an overall consistent description of the ET kinetics of forward reactions in wild-type PSI reaction center. Within this simple framework, however, the weak driving force model reproduce more satisfactorily the recombination reactions from the terminal Fe-S cluster [see discussion in the Supplementary information of Santabarbara et al. (2019)]. Thus, this energetic scheme can be considered as a good starting point to address the effect of specific mutations at the level of the phylloquinone binding site. A comparison with the shifts in driving force necessary to account for the kinetic alterations observed in the mutants within the large driving force scenario, will however be discussed.
Effect of Mutations of the Phylloquinone Binding Pockets
The energetics of oxidation has been altered by two complementary approaches, one involving the perturbation of PhQ-protein interactions by mutations of key residues in the redox center binding niches (Santabarbara et al., 2005a, 2010a; Rappaport et al., 2006; Srinivasan and Golbeck, 2009), the other involving the replacement of the naturally occurring PhQ with exogenous quinones, possessing inherently different redox potentials (Iwaki et al., 1996; Itoh et al., 2001; Makita et al., 2015; Milanovsky et al., 2017). One of the principal differences between the two strategies is that whereas in the “mutational” approach the properties of A1A and A1B can be tested separately by specific mutations of either the PsaA or the PsaB subunit (moreover mutants of both subunits have also been reported (Guergova-Kuras et al., 2001; Rappaport et al., 2006; Santabarbara et al., 2010a), in the “quinone replacement” approach, the energertics of both ET branches are simultaneously affected, as it is the redox properties of the exogenous moiety which governs the perturbation. Results from the quinone-exchange approach have been recently reviewed in detail by Makita and Hastings (2016), Makita and Hastings (2017), and Milanovsky et al. (2017). Therefore, here we focus the discussion on the effect of site directed mutants of the A1 binding pocket.
Site-directed mutations altering the PhQ binding niches of both the PsaA and PsaB subunits have been investigated in a rather large number of studies, using as model organisms mainly Synechocystis sp. PCC6803 for cyanobacteria and Chlamydomonas reinhardtii for green algae (see Santabarbara et al., 2005a, 2010a; Rappaport et al., 2006; Redding and van der Est, 2006; Srinivasan and Golbeck, 2009 for reviews). In general, mutants of the PsaA subunit, and therefore perturbations of A1A, appear to be better characterized, because of the slower apparent “natural” oxidation kinetics at room temperature and also because recombination reactions with at cryogenic temperatures (Brettel, 1997; Shinkarev et al., 2002), at least under ambient redox conditions (Poluektov et al., 2005; Santabarbara et al., 2005b, 2006, 2010c), are dominated by the . Henceforth, the discussion and the accompanying numerical simulations will be focused on mutations of the PsaA subunit, although similar arguments could be applied to the mutants of PsaB affecting principally A1B. The effect of specific amino-acid substitutions in the A1A binding niche can be classified in three main “kinetic phenotypes”.
Most mutants were designed to target residues which appear to closely interact with the PhQ moiety, according to structural models (Figure 1B). The main interactions are predicted to be due to aromatic π-stackings (such as Trp697) and, more indirectly, from the H-bond network amongst residues composing the binding niche [e.g., Met688, Ser692, Trp697, numbering as in Thermosynechococcus elongatus structural model of Jordan et al. (2001)]. Substitutions of these residue side chains led to a slowing down of the 200–300 ns oxidation lifetime observed in the wild-type to 600–1,200 ns in mutants of both green algae (e.g., Guergova-Kuras et al., 2001; Muhiuddin et al., 2001; Purton et al., 2001; Ali et al., 2006; Byrdin et al., 2006; Santabarbara et al., 2008) and cyanobacteria (e.g., Xu et al., 2003). Yet, the relative amplitudes of “fast” and “slow” phases of oxidation were hardly affected by these mutations (Guergova-Kuras et al., 2001; Byrdin et al., 2006; Rappaport et al., 2006; Santabarbara et al., 2008, 2010a). This group of mutants, which comprises a large number of specific residue substitutions, will be considered, also in the accompanying calculations, as a single class and referred to as “moderately slowing down” scenario.
An extreme slowing down effect was observed in a specific mutant of the PsaA subunit of C. reinhardtii, PsaA-F689N (Santabarbara et al., 2015). This residue is likely involved in “distal” π-stacking and its substitution with an amino-acid bearing a polar side chain resulted in an apparent oxidation lifetime of ~17 μs, i.e., 20 times slower than the wild-type. This rather unique, at least so far, mutation effect will be considered as an independent class, referred hereafter as “extreme slow-down” scenario.
The last class of mutants which will be considered comprises substitutions of residues putatively involved in the asymmetric H-bond to the PhQ moiety. According to the structural models, H-bonding will take place through Leu722 peptide bond (Santabarbara et al., 2010b; Srinivasan et al., 2011; Mula et al., 2012). Henceforth, side-chains substitutions, excluding the one with Proline, are not expected to directly perturb the protein-cofactor interactions. Yet, because of the tight-packing of the side chains, mutations of Psa-L722 might indirectly perturb the H-bond donation to A1A as a result of steric hindrance and consequent micro-reconfigurations of the binding-pocket. Indeed, mutations of the Leu722 residue of the PsaA subunit in both cyanobacteria (Srinivasan et al., 2011) and green algae (Santabarbara et al., 2010b) led to alterations of the oxidation kinetics that, differently from all mutations discussed above, decreased the oxidation lifetime to 160–180 ns. Moreover, a redistribution of the “fast”:“slow” phase amplitudes was detected resulting in a relative increase of the rapid phase and therefore in a significant acceleration of the overall oxidation kinetics (Santabarbara et al., 2010b; Srinivasan et al., 2011). This third class of mutants will be hereafter referred to as “moderately speed up” scenario.
In order to rationalize the kinetic perturbations in the three classes of mutants discussed above, simulations were performed starting from the wild-type scenarios, presented in Figure 3. It is here considered that the main impact of the mutations is on the redox midpoint potential of , thereby determining a variation of the Gibbs free energy . Thus, we introduce the term to specifically highlight the effect of the amino-acid substitutions. Figures 4A,B show the alterations to the system energetics necessary to simulate the kinetics for the PsaA-L722 mutants belonging to the moderately accelerating mutant class when starting from the weak driving force scenario (Figure 3A). By considering = −25 meV, i.e., a net increase in the driving force, the acceleration of oxidation kinetics with respect to the WT is reproduced rather well, as the simulated lifetimes become 5.2, 22.5, 141, and 182 ns. Interestingly, also the redistribution in amplitudes between the “fast” and the “slow” phases of oxidation is semi-quantitatively reproduced in the simulation. The shift in reported here is similar to that already discussed by Santabarbara et al. (2010b) with small differences related to adopting an extended kinetic model as well as specific values of in the present calculations. Thus, whereas the acceleration of the kinetics can be straightforwardly linked to the increase in the driving force, the apparent amplitude redistribution results from the suppression of the transient inter-quinone electron transfer driven by the asymmetry in and that is present in the wild-type and that is reduced in the mutants, as the redox gap between the two quinones becomes less significant (Santabarbara et al., 2010b). The same shift in the reaction free energy, = −25 meV, satisfactorily describes the faster lifetime in the PsaA-L722 also within the large driving force framework. However, in this case, it does not account for the just discussed amplitude redistribution. The simulations for the mutants starting from the wild-type scenario discussed by Ptushenko et al. (2008) and Milanovsky et al. (2017) are presented in Figures S3A,B, S4A,B, respectively.
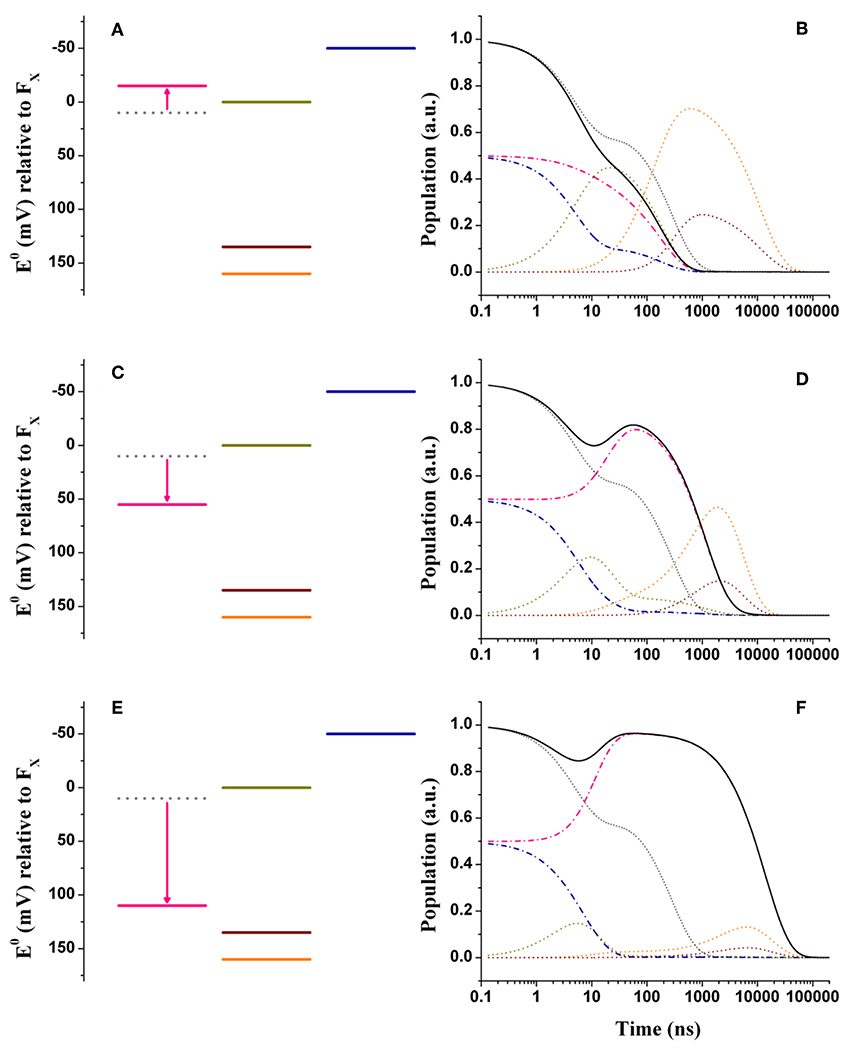
Figure 4. Energetics (A,C,E) and kinetic simulations (B,D,F) of the electron transfer reactions downstream of A1 in the three classes of mutants of the PsaA reaction center subunit discussed in the text. (A,B) Simulate the “moderately speed up” scenario; (C,D) The “moderately slowing down” scenario; (E,F) The “extreme slow-down” scenario. In all energetics panels the shifted redox midpoint potential induced by the specific mutation is indicated in pink, whereas the wild-type potential is shown as gray dotted lines. In the kinetic simulations the same color-coding as in Figure 3 is used (dash-dotted blue lines: A1B; dotted golden lines: FX; dotted orange lines: FA; dotted burgundy lines: FB; black solid line: A1tot = A1A+A1B) for the exception of the “mutated” A1A kinetics which are shown in pink. The gray dotted lines show the simulations of A1tot relaxation in the wild-type for ease of comparison.
Figures 4C,D show the simulations for the class of “moderately slowing down” mutants, targeted to obtain a main oxidation lifetime for of about 1,000 ns. The effect of the mutations can be rather well-simulated by considering = +45 meV. For this alteration of , lifetimes of 4.9, 16, 131, and 968 ns were simulated, which correspond rather well with experimental observations especially considering that those should be taken as representative of several different specific mutations. One interesting observation is that the ~131 ns component predicted in the wild-type is hardly affected by the shift in . However, whereas this component falls quite close to the 150 ns oxidation phase in the wild-type, it becomes temporally well-separated in the mutants. This agrees with the observation that an intermediate phase of similar lifetime (~150 ns) could be also retrieved in mutants that slowed down oxidation (Byrdin et al., 2006; Santabarbara et al., 2008). The simulations predict however a redistribution (~15%) of the amplitudes in favor of the slower decay phases, which somewhat exceeds the virtual absence of redistribution reported for experimental data. From a semi-quantitative point of view, these simulations can nonetheless be considered satisfactory.
The effect of mutants that moderately slow down the oxidation phase is more difficult to reproduce in the large driving force scenario. Lowering the driving force leads to both a lengthening of the ~200 ns phase observed in the wild-type as well as a sizable increase of the ~2 μs contribution, which is instead negligible in the unperturbed system. In this case we opted then to match the lengthening in the average oxidation lifetime which is accounted by considering +35 < <55 meV (Figures S3C,D, S4C,D) similarly to what derived from the weak driving force model.
In Figures 4E,F are shown the energetic scenario and the simulated kinetics describing the “extreme slowing” of oxidation reported for the PsaA-F689N mutant. A remarkable = +120 meV is required to describe this class of mutants, yielding lifetimes of 3.8, 9.2, 131 ns, and 3.6, 11.2 μs. In this scenario, the slowest (11.2 μs) component carries significant amplitude and needs therefore to be considered. In fact, its simulated value corresponds rather well with the one observed experimentally. As already discussed in Santabarbara et al. (2015) however, when considering only a shift in , an excessive redistribution of the relative amplitudes with respect to those observed experimentally is simulated. This discrepancy can be compensated when taking into account possible effects of the mutation also on the reorganization energy, because of the very polarisable nature of this particular substitution. Since an exact description goes beyond the scope of the present survey, it shall be argued that a decrease of about 100 meV in the oxidation driving force shall be considered as an upper limit for the mutation-induced perturbation.
When considering shifts in the driving force in the +110 < <130 meV interval, a good description of the PsaA-F689N mutation effect is obtained also within the large driving force wild-type scenarios (Figures S3E,F, S4E,F). Also starting from these initial models a large redistribution of amplitudes is simulated, since, in the mutant, oxidation becomes energetically unfavorable, thereby promoting inter-quinone initial population transfer.
General Perspectives
From the above reported simulations it can be concluded that, when considering initial energetic scenarios in which oxidation is associated with either weak or rather large driving forces, the effect of mutations of key residues participating to the binding site can be reasonably rationalized assuming that alterations of the phylloquinone redox properties represent the dominant factor. Substitutions of conserved residues in the binding niche accounted for a shift of about ~+40 mV of the phylloquinone potential, as long these involved conservative side chain exchanges that did not include additional highly polar or possibly charge-bearing side chains. The latter can lead instead to much larger perturbations, as observed in the PsaA-F689N mutant of C. reinhardtii. Mutations of the residues involved in H-bond donation to PhQ can lead to similar, absolute value, potential shift but toward a higher reducing potential ( = −25 meV). This can result from a combination of eventually antagonistic effects due to changes in both the H-bond strength (likely a weakening) as well as to more indirect perturbations of the binding site. Interestingly, whereas these mutants showed faster oxidation kinetics, which could be seen as an improvement of the overall reaction center performance, they displayed, at the same time, a lowering of the PhQ binding strength, manifesting as a RC sub-population with empty binding sites. Recombination reactions leading to triplet state formation were detected in this fraction of center (Santabarbara et al., 2010b; Srinivasan et al., 2011). Since this can lead to oxidative stress because of singlet oxygen sensitization, a tighter PhQ binding appears as a weak penalty in place of an overall marginal kinetic slowing.
Still, although a good semi-quantitative description of both the ET kinetics in the wild-type as well as in mutations affecting PhQ binding interactions is obtained, further elucidation concerning the precise energetics of A1 oxidation as well as of the successive ET reactions, particularly those involving the iron-sulfur clusters which are instead significantly different depending on the initial energetic scenarios adopted for the wild-type description, is still need. It can be foreseen that this shall be accomplished by a combination of experimental approaches, ranging from quantum-chemical methods to spectroscopic ones. Concerning the latter, considering that a wide range of mutations has been already engineered, and that quinone moiety substitutions represent a power tool to alter the PhQ energetics as well, a systemic joint experimental and kinetic modeling analysis, not only of forward electron transfer reactions at room temperature, but also of their temperature dependence, that has been very seldom explored, and of the recombination reactions with , together with their temperature dependence, would not only almost certainly result in a far more precise description of the system energetics but also in a better understanding of the protein-mediated tuning of ET co-factors.
Author Contributions
SS and AC wrote the paper. SS performed the kinetic simulations.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
SS and AC acknowledge Fondazione Cariplo that supported this research through the project Cyanobacterial Platform Optimized for Bioproductions (ref. 2016-0667). SS also acknowledge support from the S.a.C program of the CFRP (SaC2018.mkII/b). SS thanks Prof. Gary Hastings (Georgia State University) for stimulating discussion.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fpls.2019.00852/full#supplementary-material
References
Agalarov, R., and Brettel, K. (2003). Temperature dependence of biphasic forward electron transfer from the phylloquinone(s) A1 in photosystem I: only the slower phase is activated. Biochim. Biophys. Acta 1604, 7–12. doi: 10.1016/S0005-2728(03)00024-0
Ali, K., Santabarbara, S., Heathcote, P., Evans, M. C. W., and Purton, S. (2006). Bidirectional electron transfer in photosystem I: replacement of the symmetry-breaking tryptophan close to the PsaB-bound phylloquinone A1B with a glycine residue alters the redox properties of A1B and blocks forward electron transfer at cryogenic temperatures. Biochim. Biophys. Acta 1757, 1623–1633. doi: 10.1016/j.bbabio.2006.07.006
Berthold, T., von Gromoff, E. D., Santabarbara, S., Stehle, P., Link, G., Poluektov, O. G., et al. (2012). Exploring the electron transfer pathways in photosystem I by high-time-resolution electron paramagnetic resonance: observation of the B-side radical pair in whole cells of the deuterated green alga Chlamydomonas reinhardtii at cryogenic temperatures. J. Am. Chem. Soc. 134, 5563–5576. doi: 10.1021/ja208806g
Brettel, K. (1997). Electron transfer and arrangement of the redox cofactors in photosystem I. Biochim. Biophys. Acta 1318, 322–373. doi: 10.1016/S0005-2728(96)00112-0
Byrdin, M., Santabarbara, S., Gu, F., Fairclough, V. W., Heathcote, P., Redding, K. E., et al. (2006). Assignment of a kinetic component to electron transfer between iron-sulfur clusters FX and FA/B of Photosystem I. Biochim. Biophys. Acta 1757, 1529–1538. doi: 10.1016/j.bbabio.2006.06.016
Chamorowsky, S. K., and Cammack, R. (1982). Direct determination of the midpoint potential of the acceptor X in chloroplast Photosystem I by electrochemical reduction and electron spin resonance. Photochem. Photobiophys. 4, 195–200.
Cherepanov, D. A., Milanovsky, G. E., Petrova, A. A., Tikhonov, A. N., and Semenov, A. Y. (2017). Electron transfer through the acceptor side of photosystem I: interaction with exogenous acceptors and molecular oxygen. Biochemistry (Moscow) 82, 1249–1268. doi: 10.1134/S0006297917110037
Cohen, R. O., Shen, G., Golbeck, J. H., Xu, W., Chitnis, P. R., Valieva, A. I., et al. (2004). Evidence for asymmetric electron transfer in cyanobacterial photosystem I: analysis of a methionine-to-leucine mutation of the ligand to the primary electron acceptor A0. Biochemistry 43, 4741–4754. doi: 10.1021/bi035633f
Dashdorj, N., Xu, W., Cohen, R. O., Golbeck, J. H., and Savikhin, S. (2005). Asymmetric electron transfer in cyanobacterial Photosystem I: charge separation and secondary electron transfer dynamics of mutations near the primary electron acceptor A0. Biophys. J. 88, 1238–12349. doi: 10.1529/biophysj.104.050963
Devault, D. (1980). Quantum mechanical tunnelling in biological systems. Q. Rev. Biophys. 13, 387–564. doi: 10.1017/S003358350000175X
Evans, M. C. W., and Heathcote, P. (1980). Effects of glycerol on the redox properties of the electron acceptor complex in spinach photosystem I particles. Biochim. Biophys. Acta 590, 89–96. doi: 10.1016/0005-2728(80)90148-6
Evans, M. C. W., Reeves, S. G., and Cammack, R. (1974). Determination of the oxidation-reduction potential of the bound iron–sulphur proteins of the primary electron acceptor complex of Photosystem I in spinach chloroplasts. FEBS Lett. 49, 111–114. doi: 10.1016/0014-5793(74)80644-7
Guergova-Kuras, M., Boudreaux, B., Joliot, A., Joliot, P., and Redding, K. E. (2001). Evidence for two active branches for electron transfer in photosystem I. Proc. Natl. Acad. Sci. U.S.A 98, 4437–4442. doi: 10.1073/pnas.081078898
Heathcote, P., Williams-Smith, D. L., Sihra, C. K., and Evans, M. C. W. (1978). The role of the membrane-bound iron-sulphur centres A and B in the Photosystem I reaction centre of spinach chloroplasts. Biochim. Biophys. Acta 503, 333–342. doi: 10.1016/0005-2728(78)90192-5
Hopfield, J. J. (1974). Electron transfer between biological molecules by thermally activated tunnelling. Proc. Natl. Acad. Sci. U.S.A 71, 3640–3644. doi: 10.1073/pnas.71.9.3640
Ishikita, H., and Knapp, E. W. (2003). Redox potential of quinones in both electron transfer branches of photosystem I. J. Biol. Chem. 278, 52002–52011. doi: 10.1074/jbc.M306434200
Itoh, S., Iwaki, M., and Ikegami, I. (2001). Modification of Photosystem I reaction center by extraction and exchange of chlorophylls and quinone. Biochim. Biophys. Acta 1507, 115–138. doi: 10.1016/S0005-2728(01)00199-2
Iwaki, M., Kumazaki, S., Yoshihara, K., Erabi, T., and Itoh, S. (1996). ΔG0 dependence of the electron transfer rate in the photosynthetic reaction center of plant photosystem I: natural optimization of reaction between chlorophyll a A0 and quinone. J. Phys. Chem. 100, 10802–10809. doi: 10.1021/jp960221k
Joliot, P., and Joliot, A. (1999). In vivo analysis of the electron transfer within photosystem I: are the two phylloquinones involved? Biochemistry 38, 11130–11136. doi: 10.1021/bi990857c
Jordan, P., Fromme, P., Witt, H. T., Klukas, O., Saenger, W., and Krauss, N. (2001). Three dimensional structure of cyanobacterial Photosystem I at 2.5 Å resolution. Nature 411, 909–917. doi: 10.1038/35082000
Jortner, J. (1976). Temperature dependent activation energy for electron transfer between biological molecules. J. Chem. Phys. 64, 4860–4867. doi: 10.1063/1.432142
Karyagina, I., Pushkar, Y., Stehlik, D., van der Est, A., Ishikita, H., Knapp, E. W., et al. (2007). Contributions of the protein environment to the midpoint potentials of the A1 phylloquinones and the Fx iron-sulfur cluster in photosystem I. Biochemistry 46, 10804–10816. doi: 10.1021/bi700846z
Kawashima, K., and Ishikita, H. (2017). Structural factors that alter the redox potential of quinones in cyanobacterial and plant Photosystem I. Biochemistry 56, 3019–3028. doi: 10.1021/acs.biochem.7b00082
Ke, B., Dolan, E., Sugahara, K., Hawkridge, F. M., Demeter, S., and Shaw, E. (1977). Electrochemical and kinetic evidence for a transient electron transfer acceptor in the photochemical charge separation in photosystem I. Plant Cell Physiol. 3–7, 187–199.
Ke, B., Hansen, R. E., and Beinert, H. (1973). Oxidation-reduction potentials of bound iron-sulfur proteins of photosystem I. Proc. Natl. Acad. Sci. U.S.A 70, 2941–2945. doi: 10.1073/pnas.70.10.2941
Kurashov, V., Gorka, M., Milanovsky, G. E., Johnson, T. W., Cherepanov, D. A., Semenov, A. Y., et al. (2018). Critical evaluation of electron transfer kinetics in P700-FA/FB, P700-FX, and P700-A1 Photosystem I core complexes in liquid and in trehalose glass. Biochim. Biophys. Acta 1859, 1288–1301. doi: 10.1016/j.bbabio.2018.09.367
Lozier, R. H., and Butler, W. L. (1974). Light-induced absorbance changes in chloroplasts mediated by photosystem I and photosystem II at low temperature. Biochim. Biophys. Acta 333, 465–480. doi: 10.1016/0005-2728(74)90131-5
Makita, H., and Hastings, G. (2015). Directionality of electron transfer in cyanobacterial photosystem I at 298 and 77K. FEBS Lett. 589, 1412–1417. doi: 10.1016/j.febslet.2015.04.048
Makita, H., and Hastings, G. (2016). Modeling electron transfer in photosystem I. Biochim. Biophys. Acta 1857, 723–733. doi: 10.1016/j.bbabio.2016.03.015
Makita, H., and Hastings, G. (2017). Inverted-region electron transfer as a mechanism for enhancing photosynthetic solar energy conversion efficiency. Proc. Natl. Acad. Sci. U.S.A 114, 9267–9272. doi: 10.1073/pnas.1704855114
Makita, H., Zhao, N., and Hastings, G. (2015). Time-resolved visible and infrared difference spectroscopy for the study of photosystem I with different quinones incorporated into the A1 binding site. Biochim. Biophys. Acta 1847, 343–354. doi: 10.1016/j.bbabio.2014.12.007
Malferrari, M., Savitsky, A., Mamedov, M. D., Milanovsky, G. E., Lubitz, W., Möbius, K., et al. (2016). Trehalose matrix effects on charge-recombination kinetics in Photosystem I of oxygenic photosynthesis at different dehydration levels. Biochim. Biophys. Acta 1857, 1440–1454. doi: 10.1016/j.bbabio.2016.05.001
Marcus, R. A., and Sutin, N. (1985). Electron transfer in chemistry and biology. Biochim. Biophys. Acta 811, 265–322. doi: 10.1016/0304-4173(85)90014-X
Mazor, Y., Borovikova, A., Caspy, I., and Nelson, N. (2017). Structure of the plant photosystem I supercomplex at 2.6 Å resolution. Nat. Plants 3:17014. doi: 10.1038/nplants.2017.14
Milanovsky, G. E., Petrova, A. A., Cherepanov, D. A., and Semenov, A. Y. (2017). Kinetic modeling of electron transfer reactions in photosystem I complexes of various structures with substituted quinone acceptors. Photosynth. Res. 133, 185–199. doi: 10.1007/s11120-017-0366-y
Milanovsky, G. E., Ptushenko, V. V., Golbeck, J. H., Semenov, A. Y., and Cherepanov, D. A. (2014). Molecular dynamics study of the primary charge separation reactions in Photosystem I: effect of the replacement of the axial ligands to the electron acceptor A0. Biochim. Biophys. Acta 1837, 1472–1483. doi: 10.1016/j.bbabio.2014.03.001
Moser, C., and Dutton, P. L. (1996). “Outline of theory of protein electron transfer,” in Protein Electron Transfer, ed D. S. Bendall (Oxford: BIOS Scientific Publishers, 1–18.
Moser, C. C., and Dutton, P. L. (1992). Engineering protein structure for electron transfer function in photosynthetic reaction centers. Biochim. Biophys. Acta 1101, 171–176. doi: 10.1016/S0005-2728(05)80012-X
Moser, C. C., and Dutton, P. L. (2006). “Application of marcus theory to photosystem I electron transfer,” in Photosystem I: The Light–Driven Plastocyanin:Ferredoxin Oxidoreductase, ed J. H. Golbeck (Dordrecht, Kluwer Academic Publishers), 583–594. doi: 10.1007/978-1-4020-4256-0_34
Muhiuddin, I. P., Heathcote, P., Carter, S., Purton, S., Rigby, S. E. J., and Evans, M. C. W. (2001). Evidence from time resolved studies of the / radical pair for photosynthetic electron transfer on both the PsaA and PsaB branches of the photosystem I reaction centre. FEBS Lett. 503, 56–60. doi: 10.1016/S0014-5793(01)02696-5
Mula, S., McConnell, M. D., Ching, A., Zhao, N., Gordon, H. L., Hastings, G., et al. (2012). Introduction of a hydrogen bond between phylloquinone PhQA and a threonine side-chain OH group in photosystem I. J. Phys. Chem. B 116, 14008–14016. doi: 10.1021/jp309410w
Nugent, J. H., Moller, B. L., and Evans, M. C. W. (1981). Comparison of the EPR properties of Photosystem I iron–sulphur centres A and B in spinach and barley. Biochim. Biophys. Acta 634, 249–255. doi: 10.1016/0005-2728(81)90143-2
Parrett, K. G., Mehari, T., Warren, P. G., and Golbeck, J. H. (1989). Purification and properties of the intact P700- and Fx-containing Photosystem I core protein. Biochim. Biophys. Acta 973, 324–332. doi: 10.1016/S0005-2728(89)80439-6
Poluektov, O. G., Paschenko, S. V., Utschig, L. M., Lakshmi, K. V., and Thurnauer, M. C. (2005). Bidirectional electron transfer in photosystem I: direct evidence from high-frequency time-resolved EPR spectroscopy. J. Am. Chem. Soc. 127, 11910–11911. doi: 10.1021/ja053315t
Ptushenko, V. V., Cherepanov, D. A., Krishtalik, L. I., and Semenov, A. Y. (2008). Semi-continuum electrostatic calculations of redox potentials in photosystem I. Photosynth. Res. 97, 55–74. doi: 10.1007/s11120-008-9309-y
Purton, S., Stevens, D. R., Muhiuddin, I. P., Evans, M. C., Carter, S., Rigby, S. E., et al. (2001). Site-directed mutagenesis of PsaA residue W693 affects phylloquinone binding and function in the photosystem I reaction center of Chlamydomonas reinhardtii. Biochemistry 40, 2167–2175. doi: 10.1021/bi0019489
Qin, X., Suga, M., Kuang, T., and Shen, J. R. (2015). Photosynthesis. Structural basis for energy transfer pathways in the plant PSI-LHCI supercomplex. Science 348, 989–995. doi: 10.1126/science.aab0214
Rappaport, F., Diner, B. A., and Redding, K. E. (2006). “Optical measurements of secondary electron transfer in photosystem I,” in Photosystem I: The Light–Driven Plastocyanin:Ferredoxin Oxidoreductase, ed J. H. Golbeck (Dordrecht, Kluwer Academic Publishers), 223–244. doi: 10.1007/978-1-4020-4256-0_16
Redding, K. E., and van der Est, A. (2006). “The directionality of electron transport in photosystem I,” in Photosystem I: The Light–Driven Plastocyanin:Ferredoxin Oxidoreductase, ed J. H. Golbeck (Dordrecht, Kluwer Academic Publishers), 413–437. doi: 10.1007/978-1-4020-4256-0_25
Santabarbara, S., Bullock, B., Rappaport, F., and Redding, K. E. (2015). Controlling electron transfer between the two cofactor chains of photosystem I by the redox state of one of their components. Biophys. J. 108, 1537–1547. doi: 10.1016/j.bpj.2015.01.009
Santabarbara, S., Casazza, A. P., and Hastings, G. (2019). Modelling electron transfer in photosystem I: limits and perspectives. Physiol. Plant. 166, 73–87. doi: 10.1111/ppl.12959
Santabarbara, S., Galuppini, L., and Casazza, A. P. (2010a). Bidirectional electron transfer in the reaction centre of photosystem I. J. Integr. Plant. Biol. 52, 735–749. doi: 10.1111/j.1744-7909.2010.00977.x
Santabarbara, S., Heathcote, P., and Evans, M. C. W. (2005a). Modelling of the electron transfer reactions in Photosystem I by electron tunnelling theory. Biochim. Biophys. Acta 1708, 283–310. doi: 10.1016/j.bbabio.2005.05.001
Santabarbara, S., Jasaitis, A., Byrdin, M., Gu, F., Rappaport, F., and Redding, K. E. (2008). Additive effect of mutations affecting the rate of phylloquinone reoxidation and directionality of electron transfer within photosystem I. Photochem. Photobiol. 84, 1381–1387. doi: 10.1111/j.1751-1097.2008.00458.x
Santabarbara, S., Jennings, R. C., and Zucchelli, G. (2014). “Effects of quasi-equilibrium states on the kinetics of electron transfer and radical pair stabilisation in photosystem I,” in The Biophysics of Photosynthesis, eds J. H. Golbeck, A. van der Est (New York, NY: Springer-Verlag), 241–274. doi: 10.1007/978-1-4939-1148-6_8
Santabarbara, S., Kuprov, I., Fairclough, W. V., Purton, S., Hore, P. J., Heathcote, P., et al. (2005b). Bidirectional electron transfer in photosystem I: determination of two distances between and in spin-correlated radical pairs. Biochemistry 44, 2119–2128. doi: 10.1021/bi048445d
Santabarbara, S., Kuprov, I., Hore, P. J., Casal, A., Heathcote, P., and Evans, M. C. W. (2006). Analysis of the spin-polarized electron spin echo of the [] radical pair of photosystem I indicates that both reaction center subunits are competent in electron transfer in cyanobacteria, green algae, and higher plants. Biochemistry 45, 7389–7403. doi: 10.1021/bi060330h
Santabarbara, S., Kuprov, I., Poluektov, O. G., Casal, A., Russell, C. A., Purton, S., et al. (2010b). Directionality of electron-transfer reactions in photosystem I of prokaryotes: universality of the bidirectional electron-transfer model. J. Phys. Chem. B 114, 15158–15171. doi: 10.1021/jp1044018
Santabarbara, S., Redding, K. E., and Rappaport, F. (2009). Temperature dependence of the reduction of P700+ by tightly bound plastocyanin in vivo. Biochemistry 48, 10457–10466. doi: 10.1021/bi901052c
Santabarbara, S., Reifschneider, K., Jasaitis, A., Gu, F., Agostini, G., Carbonera, D., et al. (2010c). Interquinone electron transfer in photosystem I as evidenced by altering the hydrogen bond strength to the phylloquinone(s). J. Phys. Chem. B 114, 9300–9312. doi: 10.1021/jp1038656
Santabarbara, S., and Zucchelli, G. (2016). Comparative kinetic and energetic modelling of phyllosemiquinone oxidation in Photosystem I. Phys. Chem. Chem. Phys. 18, 9687–9701. doi: 10.1039/C5CP06590A
Schlodder, E., Falkenberg, K., Gergeleit, M., and Brettel, K. (1998). Temperature dependence of forward and reverse electron transfer from , the reduced secondary electron acceptor in photosystem I. Biochemistry 37, 9466–9476. doi: 10.1021/bi973182r
Setif, P. (2001). Ferredoxin and flavodoxin reduction by photosystem I. Biochim. Biophys. Acta 1507, 161–179. doi: 10.1016/S0005-2728(01)00205-5
Shinkarev, V. P., Zybailov, B., Vassiliev, I. R., and Golbeck, J. H. (2002). Modelling of the charge recombination kinetics with phylloquinone and plastoquinone-9 in the A1 site of photosystem I. Biophys. J. 83, 2885–2897. doi: 10.1016/S0006-3495(02)75298-3
Sigfridsson, E., Olsson, M. H. M., and Ryde, U. (2001). A comparison of the inner-sphere reorganization energies of cytochromes, iron–sulfur clusters, and blue copper proteins. J. Phys. Chem. B 105, 5546–5552. doi: 10.1021/jp0037403
Srinivasan, N., and Golbeck, J. H. (2009). Protein-cofactor interactions in bioenergetic complexes: the role of the A1A and A1B phylloquinones in Photosystem I. Biochim. Biophys. Acta 1787, 1057–1088. doi: 10.1016/j.bbabio.2009.04.010
Srinivasan, N., Santabarbara, S., Rappaport, F., Carbonera, D., Redding, K. E., van der Est, A., et al. (2011). Alteration of the H–bond to the A1A phylloquinone in Photosystem I: influence on the kinetics and energetics of electron transfer. J. Phys. Chem. B 115, 1751–1759. doi: 10.1021/jp109531b
Sun, J., Hao, S., Radle, M., Xu, W., Shelaev, I., Nadtochenko, V., et al. (2014). Evidence that histidine forms a coordination bond to the A0A and A0B chlorophylls and a second H-bond to the A1A and A1B phylloquinones in M688HPsaA and M668HPsaB variants of Synechocystis sp. PCC 6803. Biochim. Biophys. Acta 1837, 1362–1375. doi: 10.1016/j.bbabio.2014.04.004
Xu, W., Chitnis, P. R., Valeva, A., van der Est, A., Brettel, K., Guergova-Kuras, M., et al. (2003). Electron transfer in cyanobacterial photosystem I: II. determination of forward electron transfer rates of site-directed mutants in a putative electron transfer pathway from A0 through A1 to FX. J. Biol. Chem. 278, 27876–27887. doi: 10.1074/jbc.M302965200
Keywords: photosystem I, electron transfer, phylloquinone, kinetic modeling, bioenergetics, redox tuning
Citation: Santabarbara S and Casazza AP (2019) Kinetics and Energetics of Phylloquinone Reduction in Photosystem I: Insight From Modeling of the Site Directed Mutants. Front. Plant Sci. 10:852. doi: 10.3389/fpls.2019.00852
Received: 25 March 2019; Accepted: 13 June 2019;
Published: 02 July 2019.
Edited by:
Julian Eaton-Rye, University of Otago, New ZealandReviewed by:
Alexey Yu Semenov, Lomonosov Moscow State University, RussiaArt Van Der Est, Brock University, Canada
Copyright © 2019 Santabarbara and Casazza. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Stefano Santabarbara, c3RlZmFuby5zYW50YWJhcmJhcmFAY25yLml0
 Stefano Santabarbara
Stefano Santabarbara Anna Paola Casazza
Anna Paola Casazza