- 1Research School of Biology, Australian National University, ANU College of Science, Canberra, ACT, Australia
- 2Department of Chemistry and Biochemistry, College of Computer, Mathematical and Natural Sciences, University of Maryland, College Park, MD, United States
A commentary on
Directions for Optimization of Photosynthetic Carbon Fixation: RuBisCO's Efficiency May Not Be So Constrained After All
by Cummins, P. L., Kannappan, B., and Gready, J. E. (2018). Front. Plant Sci. 9:183. doi: 10.3389/fpls.2018.00183
Introduction
Ribulose 1,5-bisphosphate carboxylase/oxygenase (Rubisco, EC 4.1.1.39) catalyzes the fixation of CO2 and O2 onto ribulose 1,5-bisphosphate (RuBP) during photosynthesis and photorespiration, respectively. This enzyme is required by nearly all photosynthetic organisms and its expression, structure, and mechanism have been intensively studied, with the ultimate objective of engineering a more “efficient” enzyme (i.e., faster and more specific to CO2). The reaction proceeds via a step-wise mechanism whereby RuBP is converted to an enediolate and then CO2 is added and the resulting 6-carbon (carboxyketone) intermediate is hydrated and cleaved (Figure 1A). Nevertheless, our current understanding of the chemical mechanism is limited and thus best ways to optimize the rate of CO2 fixation or affinity for CO2 are not totally clear. Therefore, comparisons of Rubisco kinetics from different organisms have been used to infer general rules that dictate variations in turn-over for carboxylation (k), apparent Michaelis constant for CO2 (Kc), and specificity (Sc/o). In their recent paper, Cummins et al. (2018) looked at published kinetic constants for a range of photosynthetic organisms and using linear regressions, concluded that “dissociation constants” for CO2 and O2 (rate constants for decarboxylation and deoxygenation) were relatively high and break the generally assumed relationship between kcat and Sc/o. Despite substantial variation in the chemical strategies of Rubiscos from different taxonomic groups that may exist, we believe that this analysis misinterprets implicit relationships between Rubisco rate constants, and overlooks experimental evidence (Table 1) for feeble rates of deoxygenation and decarboxylation.
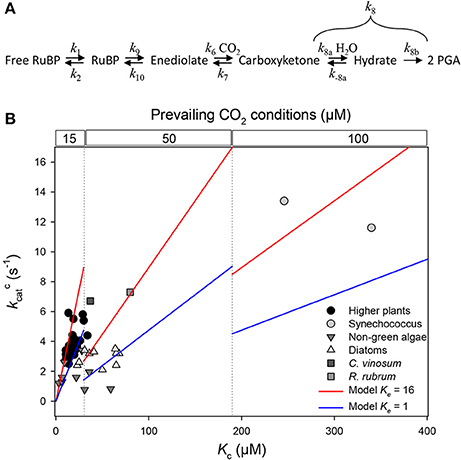
Figure 1. Relationship between Rubisco's turn-over rate for carboxylation (k) and the apparent Michaelis constant for CO2 (Kc) using the same dataset tabulated by (Cummins et al., 2018). (A) Formal representation of the mechanism for carboxylation, with rate constants mentioned in main text. (B) Representation of k against Kc using a linear scale on both axes. Steady-state kinetics are so that k = Kc·k6·c·Ke/[(1 + c)·(1 + Ke)] where Ke is enolization equilibrium constant k9/k10 and c is commitment to catalysis k8/k7 (Farquhar, 1979). It should be noted that k6 is not in s−1 but in μM−1 s−1 and thus not on the same scale for all organisms since it depends on prevailing subcellular CO2 concentration. The two linear models shown (blue and red lines) represent numerical examples of the relationship and assume that k6·[CO2] is fixed at 5 s−1 while k6 is subdivided into three domains of prevailing CO2 conditions varying with Kc (10, 50 and 100 μM). Calculations assume that enolization is efficient (Ke = 16, red) or poor (Ke = 1, blue) and that the commitment to catalysis is c = 95/5 = 19 (Lorimer et al., 1986).
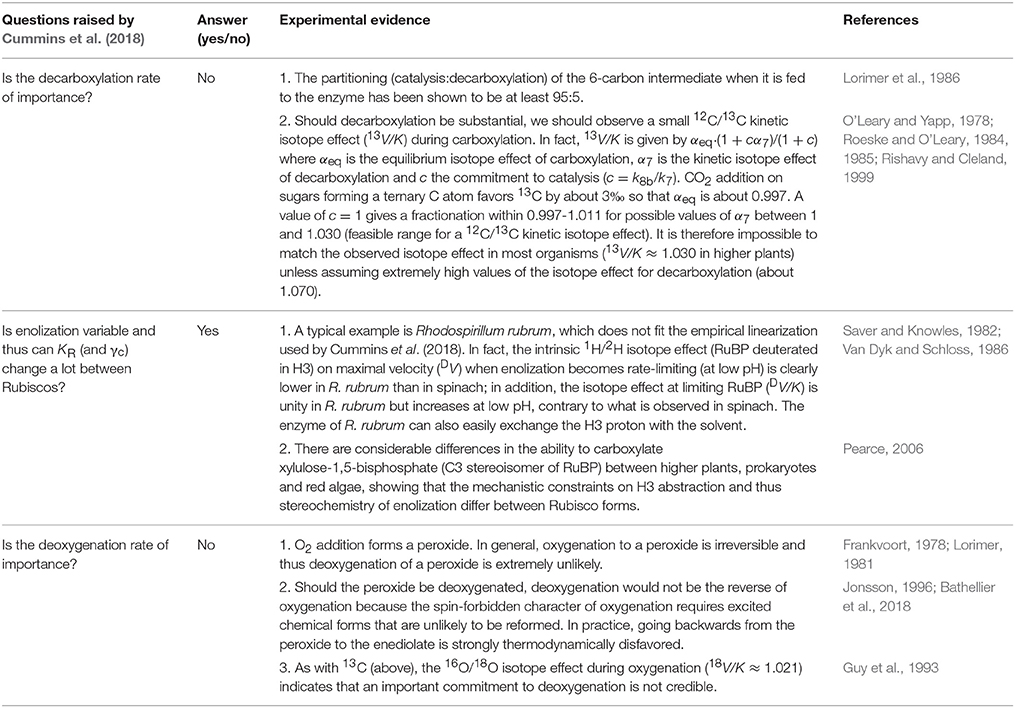
Table 1. Direct evidence that the enolization equilibrium differs between Rubisco forms, and that decarboxylation and deoxygenation are negligible.
Simple Linear Regression is Unlikely to be Representative
It is common practice to use linear relationships between kinetic parameters in order to facilitate our understanding of the implicit linkage between rate constants of the mechanism. However, this technique is difficult to apply to Rubisco kinetics because no combination of experimentally accessible kinetic parameters (k, Kc, Sc/o) gives access to individual rate constants. Basically, Cummins et al. (2018) use the relationship Kc = (k + γck7)/KRk6 (where k6 and k7 are the rate constants associated with CO2 addition [carboxylation per se] and decarboxylation, respectively1; γc is a complex parameter that integrates rate constants of enolization as well as hydration and cleavage) in order to find 1/KRk6 and γck7/KRk6 by linear regression across enzymes from a variety of photosynthetic organisms. As they recognize themselves, there is no linear relationship between Kc and k (replotted in Figure 1B). Therefore, they used either (i) a selection of points (typically, one taxonomic group) to minimize non-linearity or (ii) used a log-transformation with subsequent re-linearization by Taylor expansion. The first method gives a considerable range of values between taxonomic groups (negative or positive slope), and the second method disregards conditions of validity to perform a Taylor expansion (i.e. to neglect second-order terms). Computed coefficients 1/KRk6 and γck7/KRk6 are in fact very unlikely to be constant because: (i) KR directly depends on RuBP enolization equilibrium constant (Ke) since KR = Ke/(1 + Ke), which varies between Rubisco forms (Table 1); (ii) the rate constant for carboxylation (k6) and/or decarboxylation (k7) may vary between Rubisco forms; and (iii) γc comprises rate constants of enolization as well as hydration and cleavage.
There is experimental evidence that hydration is a very efficient process, that is, the on-enzyme hydration equilibrium of the carboxyketone substantially favors the hydrated form (Lorimer et al., 1986). Furthermore, (stereo)chemical constraints on the mechanism indicate that CO2 addition and hydration may be concerted (Cleland et al., 1998). Mathematically, this means that γc must be a relatively small number, close to k/k8a where k8a denotes the rate constant associated with hydration [denoted as k7 in Cummins et al. (2018)]. Also, k can be rearranged to k9k8b/(k9 + k8b), making apparent the rate constant of enolization (k9). There is also direct evidence that the enolization equilibrium varies between Rubisco forms, and this probably contributes to explaining the non-linearity of the k/Kc relationship, as explained in Table 1 and (Tcherkez, 2013). In other words, the commitment to, and the transition state involved in enolization differ significantly between Rubisco forms such that the enolization equilibrium is an important variable in the landscape of Rubisco kinetic parameters, in addition to carboxylation (k6) and processing (k8).
Decarboxylation and Deoxygenation are Negligible in Wild-Type Rubisco
Linear regressions carried out by Cummins et al. (2018) provide an estimate of γck7 (the product of γc and the decarboxylation rate constant, k7) which is found to be of the same order of magnitude (3–4 s−1) as k itself, meaning a low commitment of the enzyme to catalysis (k/γck7 ≈ 1). Such a high decarboxylation rate clearly contradicts experimental evidence (Table 1). We nevertheless recognize that mutant Rubisco forms can be impacted on decarboxylation, as we previously assumed in the L335V mutant to explain the typically low 12C/13C isotope effect on V/K (McNevin et al., 2007). Kinetic fitting of Rubisco velocity carried out by McNevin et al. (2006) suggested modest-to-high values of decarboxylation but these authors explicitly mentioned that computations were unable to give a reliable value, with no improvement of residuals whatever k7 may be. Deoxygenation is even less likely than decarboxylation for fundamental reasons summarized in Table 1.
Kinetic Parameters are Constrained by Both Chemistry and Environment
Taken as a whole, while we recognize that the attempt of Cummins et al. (2018) is valuable in trying to extract implicit rate constants from readily observable kinetic parameters, we believe that concluding that decarboxylation and deoxygenation are quantitatively important is not plausible. Our assumption published in Tcherkez et al. (2006) that Rubisco's evolutionary strategy involves complementarity of the active site to the transition-state, referred to as “tight-binding hypothesis” by Cummins et al. (2018), does not necessarily include a preferential change in the rate constant for carboxylation (k6) instead of k7 (decarboxylation), contrary to their claim. Rubisco adaptive value integrates not only catalytic “efficiency” (k/Kc) but also specificity (Sc/o), in the prevailing environmental CO2/O2 conditions. Even in diatoms which show variation in Kc while having a rather constant k (Young et al., 2016), there is a relationship with CCM protein abundance and composition (such as the occurrence of carbonic anhydrase isoform δ) and thus subcellular CO2 concentrations (Young and Hopkinson, 2017) (see also Figure 1B). Also, it should be kept in mind that some residues of the active site are involved in several steps, such as R. rubrum Lys 166 which is involved in both enolization and hydration + cleavage, providing a chemical basis for the interdependence of kinetic parameters (Harpel et al., 2002). Therefore, the analysis described in Cummins et al. (2018) does not provide evidence that Rubisco kinetics are “not so constrained.”
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
The authors thank the Australian Research Council for its support through a Future Fellowship grant, under contract FT140100645.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnotes
1. ^Here, we use the original rate constant numbering used to describe Rubisco kinetics in (Farquhar 1979).
References
Bathellier, C., Tcherkez, G., Lorimer, G. H., and Farquhar, G. D. (2018). Rubisco is not really so bad. Plant Cell Environ. 41, 705–716. doi: 10.1111/pce.13149
Cleland, W. W., Andrews, T. J., Gutteridge, S., Hartman, F. C., and Lorimer, G. H. (1998). Mechanism of Rubisco: the carbamate as general base. Chem. Rev. 98, 549–562. doi: 10.1021/cr970010r
Cummins, P. L., Kannappan, B., and Gready, J. E. (2018). Directions for optimization of photosynthetic carbon fixation: Rubisco's efficiency may not be so constrained after all. Front. Plant Sci. 9:183. doi: 10.3389/fpls.2018.00183
Farquhar, G. D. (1979). Models describing the kinetics of ribulose biphosphate carboxylase-oxygenase. Arch. Biochem. Biophys. 193, 456–468. doi: 10.1016/0003-9861(79)90052-3
Frankvoort, W. (1978). The reaction between diacetyl and hydrogen peroxide: its mechanism and kinetic constants. Thermochim. Acta 25, 35–49. doi: 10.1016/0040-6031(78)80038-0
Guy, R. D., Fogel, M. L., and Berry, J. A. (1993). Photosynthetic rractionation of the stable isotopes of oxygen and carbon. Plant Physiol. 101:37. doi: 10.1104/pp.101.1.37
Harpel, M. R., Larimer, F. W., and Hartman, F. C. (2002). Multifaceted roles of Lys166 of ribulose-bisphosphate carboxylase/oxygenase as discerned by product analysis and chemical rescue of site-directed mutants. Biochemistry 41, 1390–1397. doi: 10.1021/bi011828g
Jonsson, M. (1996). Thermochemical properties of peroxides and peroxyl radicals. J. Phys. Chem. 100, 6814–6818. doi: 10.1021/jp9601126
Lorimer, G. H. (1981). The carboxylation and oxygenation of ribulose 1,5-bisphosphate: the primary events in photosynthesis and photorespiration. Annu. Rev. Plant Physiol. 32, 349–382. doi: 10.1146/annurev.pp.32.060181.002025
Lorimer, G. H., Andrews, T. J., Pierce, J., and Schloss, J. V. (1986). 2′-carboxy-3-keto-D-arabinitol 1,5-bisphosphate, the six-carbon intermediate of the ribulose bisphosphate carboxylase reaction. Philos. Trans. Roy. Soc. Lond. B Biol. Sci. 313, 397–407. doi: 10.1098/rstb.1986.0046
McNevin, D., von Caemmerer, S., and Farquhar, G. (2006). Determining Rubisco activation kinetics and other rate and equilibrium constants by simultaneous multiple non-linear regression of a kinetic model. J. Exp. Bot. 57, 3883–3900. doi: 10.1093/jxb/erl156
McNevin, D. B., Badger, M. R., Whitney, S. M., von Caemmerer, S., Tcherkez, G. G., and Farquhar, G. D. (2007). Differences in carbon isotope discrimination of three variants of D-ribulose-1,5-bisphosphate carboxylase/oxygenase reflect differences in their catalytic mechanisms. J. Biol. Chem. 282, 36068–36076. doi: 10.1074/jbc.M706274200
O'Leary, M. H., and Yapp, C. J. (1978). Equilibrium carbon isotope effect on a decarboxylation reaction. Biochem. Biophys. Res. Commun. 80, 155–160. doi: 10.1016/0006-291X(78)91117-8
Pearce, F. G. (2006). Catalytic by-product formation and ligand binding by ribulose bisphosphate carboxylases from different phylogenies. Biochem. J. 399, 525–534. doi: 10.1042/BJ20060430
Rishavy, M. A., and Cleland, W. W. (1999). 13C, 15N, and 18O equilibrium isotope effects and fractionation factors. Can. J. Chem. 77, 967–977.
Roeske, C. A., and O'Leary, M. H. (1984). Carbon isotope effects on enzyme-catalyzed carboxylation of ribulose bisphosphate. Biochemistry 23, 6275–6284. doi: 10.1021/bi00320a058
Roeske, C. A., and O'Leary, M. H. (1985). Carbon isotope effect on carboxylation of ribulose bisphosphate catalyzed by ribulose bisphosphate carboxylase from Rhodospirillum rubrum. Biochemistry 24, 1603–1607. doi: 10.1021/bi00328a005
Saver, B. G., and Knowles, J. R. (1982). Ribulose 1,5-bisphosphate carboxylase: enzyme-catalyzed appearance of solvent tritium at carbon 3 of ribulose 1,5-bisphosphate reisolated after partial reaction. Biochemistry 21, 5398–5403. doi: 10.1021/bi00265a003
Tcherkez, G. (2013). Modelling the reaction mechanism of ribulose-1,5-bisphosphate carboxylase/oxygenase and consequences for kinetic parameters. Plant Cell Environ. 36, 1586–1596. doi: 10.1111/pce.12066
Tcherkez, G. G., Farquhar, G. D., and Andrews, T. J. (2006). Despite slow catalysis and confused substrate specificity, all ribulose bisphosphate carboxylases may be nearly perfectly optimized. Proc. Natl. Acad. Sci. U.S.A. 103, 7246–7251. doi: 10.1073/pnas.0600605103
Van Dyk, D. E., and Schloss, J. V. (1986). Deuterium isotope effects in the carboxylase reaction of ribulose-1,5-bisphosphate carboxylase/oxygenase. Biochemistry 25, 5145–5156. doi: 10.1021/bi00366a024
Young, J. N., Heureux, A. M., Sharwood, R. E., Rickaby, R. E., Morel, F. M., and Whitney, S. M. (2016). Large variation in the Rubisco kinetics of diatoms reveals diversity among their carbon-concentrating mechanisms. J. Exp. Bot. 67, 3445–3456. doi: 10.1093/jxb/erw163
Keywords: enzymatic activity, rubisco, isotope fractionation, enzyme kinetics and specificity, trade-offs
Citation: Tcherkez GG, Bathellier C, Farquhar GD and Lorimer GH (2018) Commentary: Directions for Optimization of Photosynthetic Carbon Fixation: RuBisCO's Efficiency May Not Be So Constrained After All. Front. Plant Sci. 9:929. doi: 10.3389/fpls.2018.00929
Received: 04 May 2018; Accepted: 11 June 2018;
Published: 27 June 2018.
Edited by:
Hartmut Stützel, Leibniz Universität Hannover, GermanyReviewed by:
Thomas D. Sharkey, Michigan State University, United StatesGrant Pearce, University of Canterbury, New Zealand
Copyright © 2018 Tcherkez, Bathellier, Farquhar and Lorimer. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Guillaume G. Tcherkez, Z3VpbGxhdW1lLnRjaGVya2V6QGFudS5lZHUuYXU=
 Guillaume G. Tcherkez
Guillaume G. Tcherkez Camille Bathellier1
Camille Bathellier1 George H. Lorimer
George H. Lorimer