Quantification of Beat-To-Beat Variability of Action Potential Durations in Langendorff-Perfused Mouse Hearts

Background: Beat-to-beat variability in action potential duration (APD) is an intrinsic property of cardiac tissue and is altered in pro-arrhythmic states. However, it has never been examined in mice.

Methods: Left atrial or ventricular monophasic action potentials (MAPs) were recorded from Langendorff-perfused mouse hearts during regular 8 Hz pacing. Time-domain, frequency-domain and non-linear analyses were used to quantify APD variability.

Results: Mean atrial APD (90% repolarization) was 23.5 ± 6.3 ms and standard deviation (SD) was 0.9 ± 0.5 ms (n = 6 hearts). Coefficient of variation (CoV) was 4.0 ± 1.9% and root mean square (RMS) of successive differences in APDs was 0.3 ± 0.2 ms. The peaks for low- and high-frequency were 0.7 ± 0.5 and 2.7 ± 0.9 Hz, respectively, with percentage powers of 39.0 ± 20.5 and 59.3 ± 22.9%. Poincaré plots of APD_n+1 against APD_n revealed ellipsoid shapes. The ratio of the SD along the line-of-identity (SD2) to the SD perpendicular to the line-of-identity (SD1) was 8.28 ± 4.78. Approximate and sample entropy were 0.57 ± 0.12 and 0.57 ± 0.15, respectively. Detrended fluctuation analysis revealed short- and long-term fluctuation slopes of 1.80 ± 0.15 and 0.85 ± 0.29, respectively. When compared to atrial APDs, ventricular APDs were longer (ANOVA, P < 0.05), showed lower mean SD and CoV but similar RMS of successive differences in APDs and showed lower SD2 (P < 0.05). No difference in the remaining parameters was observed.

Conclusion: Beat-to-beat variability in APD is observed in mouse hearts during regular pacing. Atrial MAPs showed greater degree of variability than ventricular MAPs. Non-linear techniques offer further insights on short-term and long-term variability and signal complexity.

Introduction

Beat-to-beat variations in the repolarization time-course represent an intrinsic property of cardiac electrophysiological function. This may be manifested as variability of action potential durations (APDs) at the cellular level (Nanasi et al., 2017), or of QT durations at the organism level (Niemeijer et al., 2014; Phadumdeo and Weinberg, 2018). This variability may be affected by distinct physiological states, such as the degree of intercellular coupling (Zaniboni et al., 2000), redox states (Kistamas et al., 2015a), altered intracellular calcium handling (Kistamas et al., 2015b) or APD itself (Abi-Gerges et al., 2010). Clinical studies have shown that higher variability in QT intervals can predict pro-arrhythmic outcomes in the context of non-ischemic heart failure (Hinterseer et al., 2010), as well as long QT syndrome (Hinterseer et al., 2009).

Mouse models are widely used to study cardiac electrophysiological and arrhythmogenic properties, owing to their amenability to pharmacological or genetic manipulation (Nerbonne, 2014; Choy et al., 2016). However, despite the importance of APD variability, it has never been examined in this species. In this study, we quantified beat-to-beat variability in APDs by applying time-domain and non-linear techniques for the first time to monophasic action potential recordings (MAPs) obtained from Langendorff-perfused mouse hearts during regular pacing.

Materials and Methods

Solutions

Krebs-Henseleit solution (composition in mM: NaCl 119, NaHCO₃ 25, KCl 4, KH₂PO₄ 1.2, MgCl₂ 1, CaCl₂ 1.8, glucose 10 and sodium pyruvate 2, pH 7.4), which has been bicarbonate-buffered and bubbled with 95% O₂-5% CO₂, was used in the experiments described in this study.

Preparation of Langendorff-Perfused Mouse Hearts

This study was approved by the Animal Welfare and Ethical Review Body at the University of Cambridge. Wild-type mice of 129 genetic background between 5 and 7 months of age were used. They were maintained at room temperature (21 ± 1°C) and were subjected to a 12:12 h light/dark cycle with free access to sterile rodent chow and water in an animal facility. Mice were terminated by dislocation of the cervical spine in accordance with Sections 1(c) and 2 of Schedule 1 of the UK Animals (Scientific Procedures) Act 1986. The technique for Langendorff perfusion has been used by our group and described previously (Tse et al., 2016a,d, 2017). After removal from their chest cavities, the hearts were submerged in ice-cold Krebs-Henseleit solution. The aortas were cannulated using a custom-made 21-gauge cannula prefilled with ice-cold buffer. A micro-aneurysm clip (Harvard Apparatus, UK) was used to secure the hearts onto the Langendorff perfusion system. Retrograde perfusion was carried out at a flow rate of 2 to 2.5 ml min⁻¹ by use of a peristaltic pump (Watson–Marlow Bredel pumps model 505S, Falmouth, Cornwall, UK). The perfusate passed through successively 200 and 5 μm filters and warmed to 37°C using a water jacket and circulator before arriving at the aorta. Approximately 90% of the hearts regained their pink color and spontaneous rhythmic activity. These were therefore studied further. The remaining 10% did not and were discarded. The hearts were perfused for a further 20 min to minimize residual effects of endogenous catecholamine release, before their electrophysiology properties were characterized.

Stimulating Procedures

Paired platinum electrodes (1 mm interpole distance) were used to stimulate the right ventricular epicardium electrically. This took place at 8 Hz, using square wave pulses of 2 ms in duration, with a stimulation voltage set to three times the diastolic threshold (Grass S48 Stimulator, Grass-Telefactor, Slough, UK) immediately after the start of perfusion.

Atrial and Ventricular Map Recording Procedures

For atrial MAP recordings, the atrio-ventricular nodes of the Langendorff perfused hearts were first mechanically ablated as previously described (Tse et al., 2016b). This eliminated ventricular far-field activity at the recording electrode. The MAP electrode was placed at the left atrial or ventricular epicardium (Linton Instruments, Harvard Apparatus). The stimulating and recording electrodes were maintained at constant positions separated approximately by a distance of 3 mm. All recordings were performed using a baseline cycle length (BCL) of 125 ms (8 Hz) to exclude rate-dependent differences in action potential durations (APDs). MAPs were pre-amplified using a NL100AK head stage, amplified with a NL 104A amplifier and band pass filtered between 0.5 Hz and 1 kHz using a NL125/6 filter (Neurolog, Hertfordshire, UK) and then digitized (1401plus MKII, Cambridge Electronic Design, Cambridge, UK) at 5 kHz. Waveforms were analyzed using Spike2 software (Cambridge Electronic Design, UK). MAP waveforms that did not match established criteria for MAP signals were rejected (Knollmann et al., 2001; Tse et al., 2016c). They must have stable baselines, fast upstrokes, with no inflections or negative spikes, and a rapid first phase of repolarization. Zero Percent repolarization was measured at the peak of the MAP and Hundred Percent repolarization was measured at the point of return of the potential to baseline (Gussak et al., 2000; Knollmann et al., 2001; Fabritz et al., 2003).

APD Variability Analysis

APD variability analysis was performed using Kubios HRV Standard software (Version 3.0.2) over a 60 s period. Time-domain analysis yielded the (1) standard deviation (SD) of APDs, which represents the overall (short-term and long-term) variability, and (2) root mean square (RMSSD) of successive differences of APDs, which represents the short-term variability:

$\begin{array}{cc}\text{SDAPD}=\sqrt{\frac{1}{N-1}{\displaystyle \sum _{j=1}^N{\left({\text{APD}}_j-\text{ A}\overline{\text{PD}}\right)}^2}}& (1)\end{array}$

$\begin{array}{cc}\text{RMSSD}=\sqrt{\frac{1}{N-1}{\displaystyle \sum _{j=1}^{N-1}{\left({\text{APD}}_{j+1}-{\text{APD}}_j\right)}^2}}& (2)\end{array}$

Frequency-domain analysis was conducted using the Fast Fourier Transform method. For frequency domain parameters, spectral analysis was performed by using fast-Fourier transform method. The sampling frequency was set to 8 Hz. The power in the repolarization spectrum between 0.04 and 4 Hz was defined as total power (TP). The power in the repolarization spectrum was divided into three different frequency bands: very low frequency power (VLF, 0 to 0.04 Hz), low frequency power (LF, 0.04 to 1.5 Hz) and high frequency power (HF, 1.5 to 4 Hz).

The above frequency analysis does not provide any information on the time evolution of the frequencies. To achieve, this, time-frequency analysis was conducted using two different techniques. Firstly, short-time Fourier transform (STFT) was used to break the signal into small time segments using an appropriate sliding-window function, and then apply a Fourier transformation to the successive sliding-window segments. The Hanning window with a Fast Fourier Transform length of 256 and overlap of 128 were selected.

Secondly, continuous wavelet transform (CWT) was used to divide a continuous-time function into wavelets given by:

$\begin{array}{cc}\text{CWT}(\text{a},\text{b})=\frac{\text{1}}{\sqrt{\text{a}}}{\displaystyle {\int }_{-\infty }^{\text{+}\infty }\text{x}\left(\text{t}\right)\cdot {\psi }^{\ast }}(\frac{\text{t}-\text{b}}{\text{a}})\text{dt}& (3)\end{array}$

Where the superscript, *, is the complex conjugate and ψ_a,b* represents a translated and scaled complex conjugated mother wavelet. The mother wavelet ψ is invertible when it verifies the condition of admissibility which is stated as:

$\begin{array}{cc}{\displaystyle {\int }_{-\infty }^{\text{+}\infty }\frac{\left|\widehat{\psi }(\omega )\right|}{\omega }}\text{ d}\omega <\infty & (4)\end{array}$

The Morlet wavelet was selected, which uses a Gaussian-modulated sinusoid:

$\begin{array}{cc}\psi \left(t\right)=\frac{1}{\sqrt[4]{\pi }}\left({\text{e}}^{\text{i}{\omega }_{o}t}-{\text{e}}^{-\frac{{\omega }_o^2}{2}}\right){\text{e}}^{-\frac{t^2}{2}}& (5)\end{array}$

where ω_o is the central frequency of the mother wavelet. The second term in the brackets corrects for the non-zero mean of the complex sinusoid of the first term. This becomes negligible for values of ω_o > 5, which we selected in our case:

$\begin{array}{cc}\psi \left(t\right)=\frac{1}{\sqrt[4]{\pi }}{\text{e}}^{\text{i}{\omega }_{o}t}{\text{e}}^{-\frac{t^2}{2}}& (6)\end{array}$

Non-linear properties of APD variability were studied as follow. Poincaré plots are graphical representations of the correlation between successive APD values, in which APD_n+1 is plotted against APD_n. This enables determination of the SD of the points perpendicular to the line-of-identity (SD1). Different points along this perpendicular axis represent a beat-to-beat variation between the initial (n) and subsequent (n + 1) contraction, representing multiple two-beat “snapshots” with little correlation to a progressive time parameter. Therefore, SD1 is associated with instantaneous or short-term variability. As for the points along the line-of-identity (SD2), it shows beat-to-beat consistency between the initial (n) and subsequent (n + 1) RR interval. Hence, deviation of the clustered SD2 points away from the average RR interval, taken with reference to the centroid, represents long-term variability. The ratio SD2 to SD1 then gives an indication of the degree of long-term variability in relation to the short-term variability.

Coined in 1991 by Pincus et al., the concept of approximate entropy was introduced to provide approximations on the degree of regularity when applied to a short-duration epoch, which cannot be achieved with moment statistics such as mean and variance. This is applied to non-stationary biomedical data such as heart rate variability, which commonly presents with non-linearity and complexity. Logarithmically, the approximate entropy takes into account the imputed threshold “r” under which a recurrence is identified. With this it expresses the likelihood of repeated signals within the threshold for m and m + 1 points. It is computed as follows:

Firstly, a set of length m vectors u_j is formed:

$\begin{array}{cc}{\text{u}}_{\text{j}}=({\text{APD}}_{\text{j}};{\text{APD}}_{\text{j+1}},\dots ,{\text{APD}}_{\text{j+m}-\text{1}});\text{j=1};2;\dots \text{N}-\text{m}+\text{1}& (7)\end{array}$

where, m is the embedding dimension and N is the number of measured APDs. The distance between these vectors is defined as the maximum absolute difference between the corresponding elements:

$\begin{array}{cc}\text{d}({\text{u}}_{\text{j}},{\text{u}}_{\text{k}})=\text{max}\{{\text{|APD}}_{\text{j+n}}-{\text{APD}}_{\text{k+n}}\text{||n}=\text{0},\dots ,\text{m}-\text{1}\}& (8)\end{array}$

for each u_j the relative number of vectors u_k for which d(u_j, u_k) ≤ r is calculated. This index is denoted with Cmj (r) and can be written in the form

$\begin{array}{cc}{C}_j^m\left(r\right)=\frac{\text{nbr of}\left\{u_k|d\left(u_j,u_k\right)\le r\right\}}{N-m+1}\forall k& (9)\end{array}$

Taking the natural logarithms gives:

$\begin{array}{cc}{\Phi }^m\left(r\right)=\frac{1}{N-m+1}{\displaystyle \sum _{j=1}^{N-m+1}\text{ln}{C}_j^m\left(r\right).}& (10)\end{array}$

The approximate entropy is then defined as:

$\begin{array}{cc}\text{ApEn}\left(m,r,N\right)={\Phi }^m\left(r\right)-{\Phi }^{m+1}(r)& (11)\end{array}$

Approximate entropy measures the likelihood that certain patterns of observations are followed by different patterns of observations. As such, a lower approximate entropy values reflect a more regular signal, whereas higher values reflect a more irregular signal (Pincus, 1991; Mesin, 2018).

The sample entropy also provides a measure of signal irregularity but is less susceptible to bias than approximate entropy (Richman and Moorman, 2000; Nayak et al., 2018). This is done by eliminating the counting of self-matches; hence the count of the number of similar vector lengths is always one less than that of ApEn. Furthermore, sample entropy uses the logarithm of the sum of conditional properties rather than each conditional property individually, illustrated by the negative natural logarithm for conditional properties. Both sample entropy and approximate entropy are able to differentiate between experimental and theoretical data sets. However, it has been demonstrated that sample entropy yielded better relative consistency compared to approximate entropy, reflecting independence from data length and choice of m or r (Molina-Pico et al., 2011).

This is given by:

$\begin{array}{cc}{C}_j^m\left(r\right)=\frac{\text{nbr of}\left\{u_k|d\left(u_j,u_k\right)\le r\right\}}{N-m}\forall k\ne j& (12)\end{array}$

Averaging then gives:

$\begin{array}{cc}{C}^m\left(r\right)=\frac{1}{N-m+1}{\displaystyle \sum _{j=1}^{N-m+1}{C}_j^m(r)}& (13)\end{array}$

The sample entropy is then given by:

$\begin{array}{cc}\text{SampEn}\left(m,r,N\right)=\ln (\frac{C^m\left(r\right)}{C^{m+1}\left(r\right)})& (14)\end{array}$

Finally, detrended fluctuation analysis (DFA) was performed to determine long-range correlations in non-stationary physiological time series (Peng et al., 1995), yielding both short-term fluctuation (α1) and long-term fluctuation (α2) slopes. The point at which the slopes α1 and α2 is the crossover point.

Statistical Analysis

All values were expressed as mean ± standard error of the mean (SEM). Numerical data were compared by one-way analysis of variance (ANOVA), a statistical technique that utilizes the F-distribution to compare the means or two or more samples. P < 0.05 was considered statistically significant and was denoted by * in the figures.

Results

Atrial and Ventricular Action Potential Duration Variability Determined Using Time-Domain and Frequency-Domain Methods

Representative stable MAP recordings were obtained from the left atrial (Figure 1A) or ventricular (Figure 1B) epicardium of Langendorff-perfused mouse hearts during regular 8 Hz pacing. Typical time series of atrial and ventricular APDs at 90% repolarization (APD₉₀) are shown in Figures 1C,D, respectively and their corresponding histograms are shown in Figures 1E,F, respectively. Atrial APD₉₀ took a mean value of 23.5 ± 6.3 ms (Figure 2A) with a mean standard deviation (SD) 0.9 ± 0.5 ms (Figure 2B) (n = 6 hearts). The coefficient of variation (CoV), a measure of relative variability calculated by dividing SD by the mean and subsequently multiplying by 100%, was 4.0 ± 1.9% (Figure 2C) and the root mean square (RMS) of successive differences in APDs was 0.3 ± 0.2 ms (Figure 2D). By contrast, ventricular APD₉₀ (n = 6 hearts) were longer than atrial APD₉₀ (44.0 ± 9.1 ms; ANOVA, P < 0.05), with lower mean SD (0.4 ± 0.2 ms, P < 0.05), CoV (0.8 ± 0.3%, P < 0.01) but similar RMS of successive differences in APD₉₀ (0.2 ± 0.3%, P > 0.05).

FIGURE 1

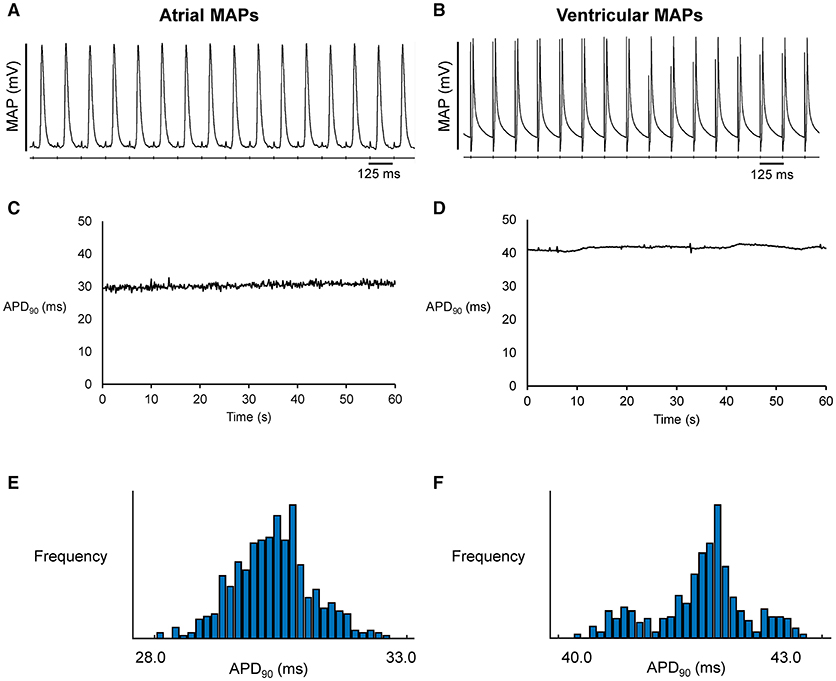
Figure 1. Representative MAP traces from a single heart obtained over a ten-second period during regular 8 Hz pacing from the left atrium (A) or left ventricle (B). The corresponding time-series (C,D) and histograms (E,F) for action potential duration at 90% repolarization (APD₉₀).

FIGURE 2

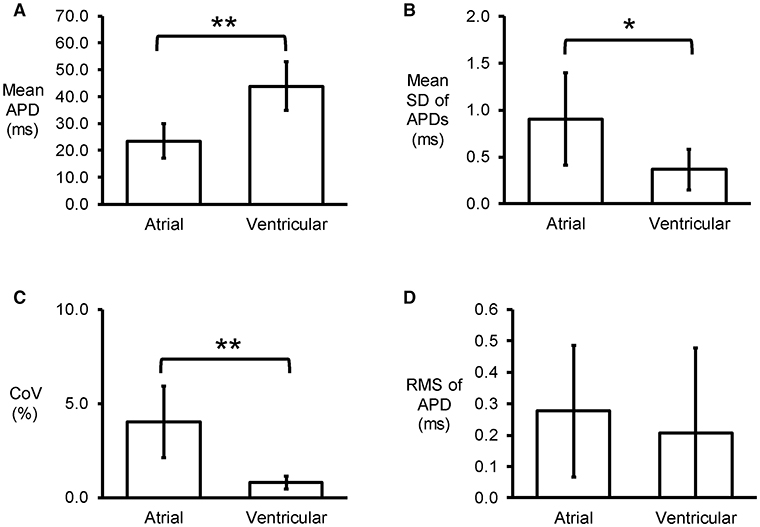
Figure 2. Time-domain analysis yielding mean APD (A), standard deviation (SD) of APDs (B), coefficient of variation (CoV) (C), and root mean square (RMS) of successive differences of APDs (D) (n = 6; *P < 0.05; **P < 0.01).

An example of a frequency spectrum using the Fast Fourier Transform method is shown in Figure 3A. Frequency-domain analysis revealed that the peaks for very low-, low- and high-frequency for atrial MAPs were 0.04 ± 0.00, 0.7 ± 0.5 and 2.7 ± 0.9 Hz, respectively (Figures 3B–D), with percentage powers of 1.7 ± 2.6, 39.0 ± 20.5, and 59.3 ± 22.9% (Figures 3E–G). For the ventricles, similar peak frequencies (0.04 ± 0.00, 0.2 ± 0.0 and 3.0 ± 0.6%) and percentage powers (0.9 ± 1.1, 66.0 ± 27.8, and 32.5 ± 27.0) were observed (ANOVA, P > 0.05).

FIGURE 3

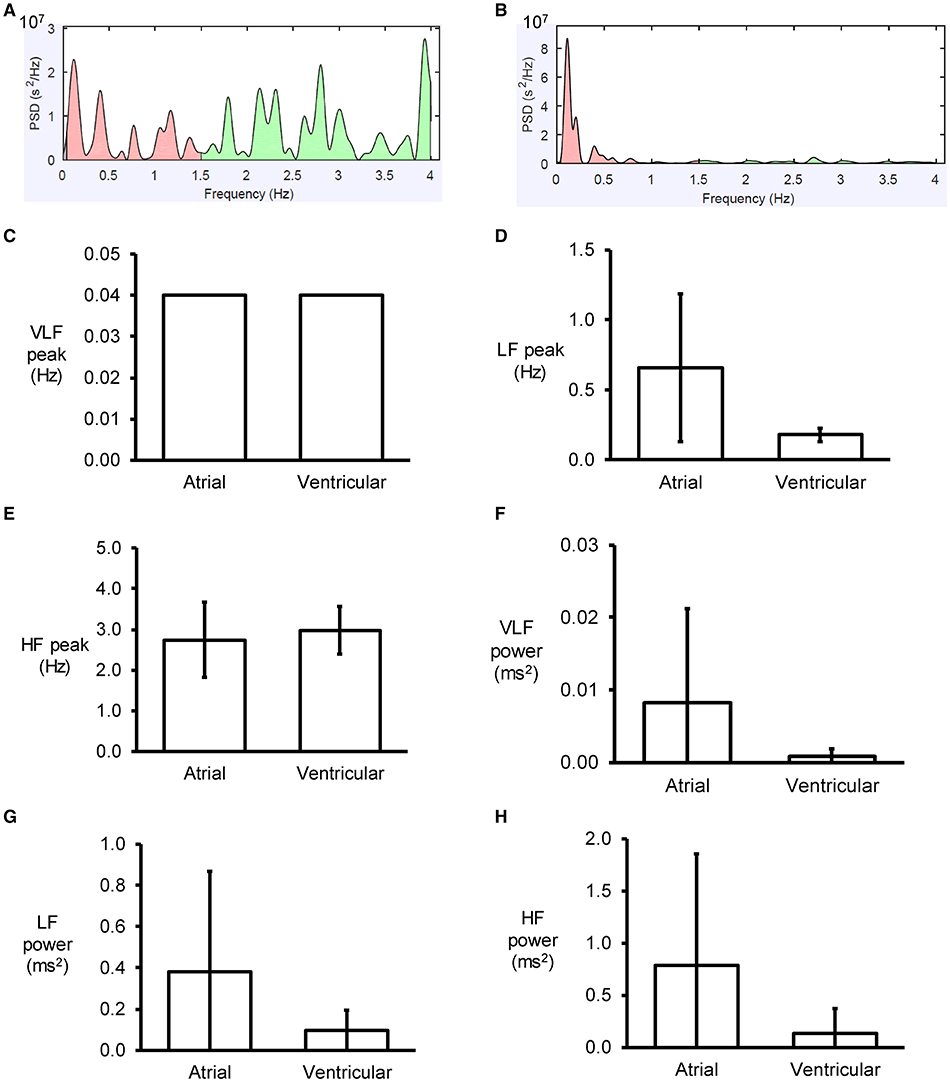
Figure 3. Examples of frequency spectra using the Fast Fourier Transform method for atrial (A) and ventricular (B) MAP recordings. Peaks for very low- (C), low- (D) and high-frequency (E) for atrial and ventricular MAPs, and their percentage powers (F–H).

Simultaneous time-frequency analysis was subsequently performed using short-time Fourier transform (STFT) and continuous wavelet transform (CWT). Application of STFT yielded plots demonstrating frequency against time for atrial and ventricular APD₉₀ (Figures 4A,B), and their corresponding three-dimensional representations (Figures 4C,D). CWT with Morlet wavelets as basis functions of atrial and ventricular APD₉₀ yielded image plots shown in Figures 4E,F, respectively.

FIGURE 4

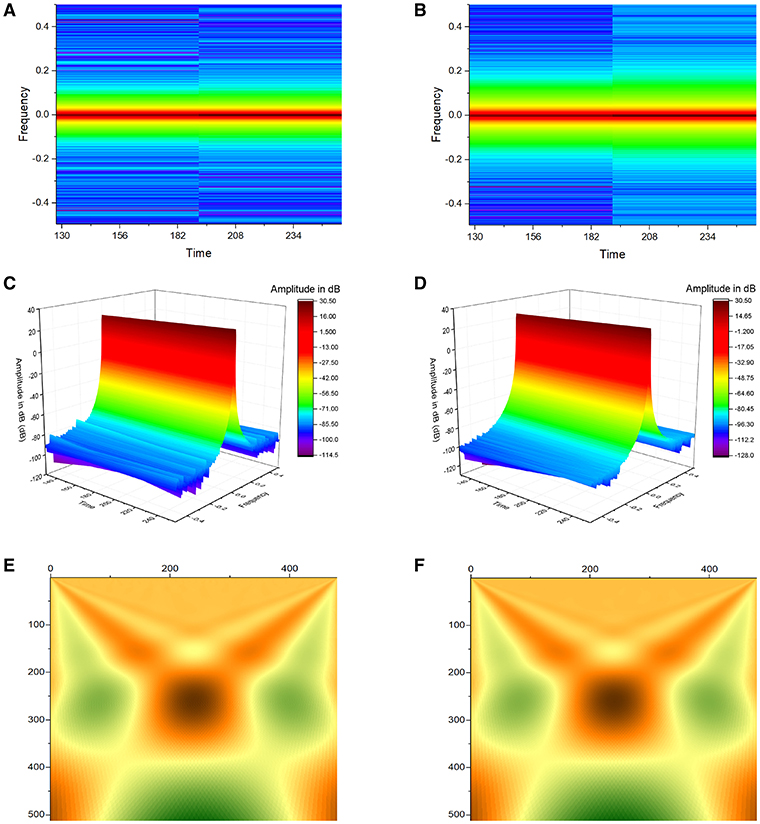
Figure 4. Application of Short-Time Fourier Transform (STFT) yielded plots demonstrating frequency against time for atrial (A) and ventricular APD₉₀ (B), and their corresponding three-dimensional representations (C,D). Continuous wavelet transform (CWT) with Morlet wavelets as basis functions of atrial (E) and ventricular APD₉₀ (F).

Action Potential Duration Variability Determined Using Non-linear Methods

Poincaré plots expressing APD_n+1 as a function of APD_n were constructed for the atrial and ventricular MAPs (Figures 5A,B). In all of the hearts studied, ellipsoid shapes of the data points were evident. The SD perpendicular to the line-of-identity (SD1) and SD along the line-of-identity (SD2) are shown in Figures 5C,D, respectively. For atrial recordings, the mean SD1 and SD2 were 0.20 ± 0.15 and 1.26 ± 0.67, respectively. The SD2 to SD1 ratio took a mean value of 8.28 ± 4.78 (Figure 5E). The approximate and sample entropy took values of 0.57 ± 0.12 (Figure 5F) and 0.57 ± 0.15 (Figure 5G), respectively. For ventricular MAPs, Poincaré plots of APD_n+1 against APD_n revealed similar ellipsoid shapes. They showed similar SD1 (0.15 ± 0.19, P > 0.05) and lower SD2 (0.49 ± 0.26, P < 0.05). Nevertheless, there was no difference in SD2/SD1 ratio (6.19 ± 3.03, P > 0.05). Moreover, approximate entropy (0.69 ± 0.27, P > 0.05), and sample entropy (0.75 ± 0.54, P > 0.05) were statistically indistinguishable when compared to the atrial parameters.

FIGURE 5

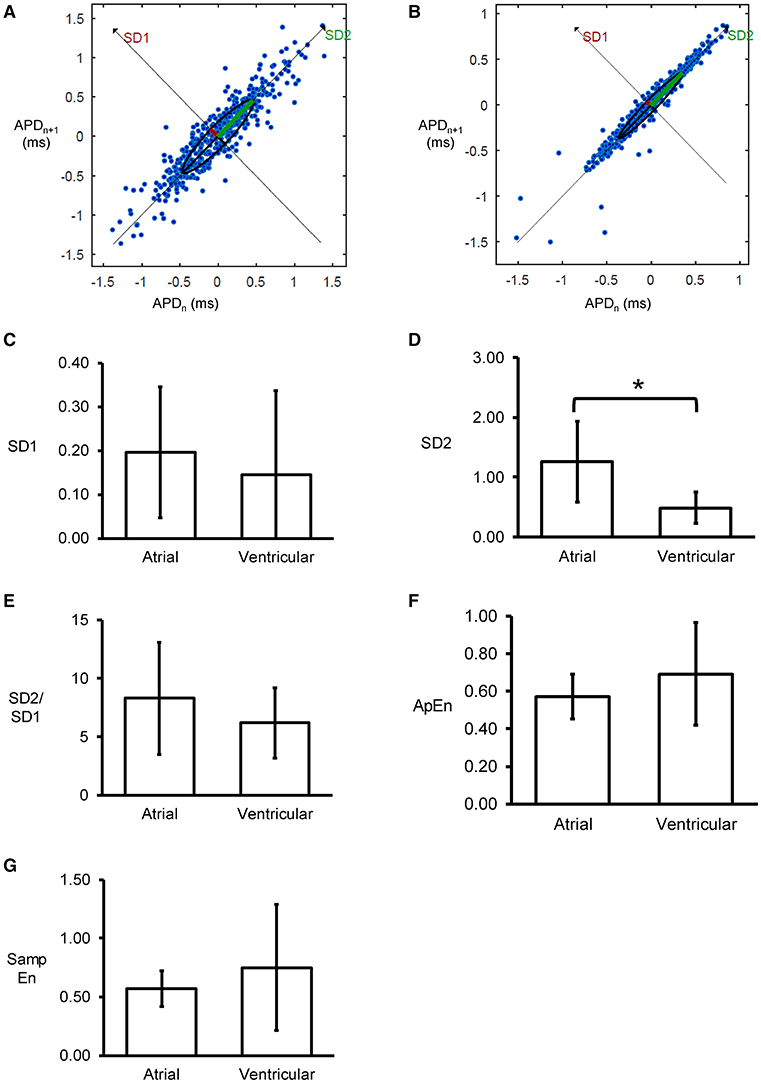
Figure 5. Representative Poincaré plots of APD_n+1 against APD_n from the left atrium (A) or left ventricle (B) from a single heart. SD along the line-of-identity (SD1) (C) and SD perpendicular to the line-of-identity (SD2) (D), and the SD2/SD1 ratio (E), approximate entropy (F), and sample entropy (G) (*P < 0.05).

Detrended fluctuation analysis plotting the detrended fluctuations F(n) as a function of n in a log-log scale was performed for the atrial and ventricular MAPs (Figures 6A,B). This revealed short- (α1) and long-term (α2) fluctuation slopes of 1.80 ± 0.15 (Figure 6C) and 0.85 ± 0.29 (Figure 6D), respectively for the atria, which were not significantly different from the values obtained from the ventricles (1.32 ± 0.49 and 1.15 ± 0.28, respectively, both P > 0.05). α1 was significantly larger than α2 in the atria (ANOVA, P < 0.001) but not in the ventricles (ANOVA, P > 0.05).

FIGURE 6

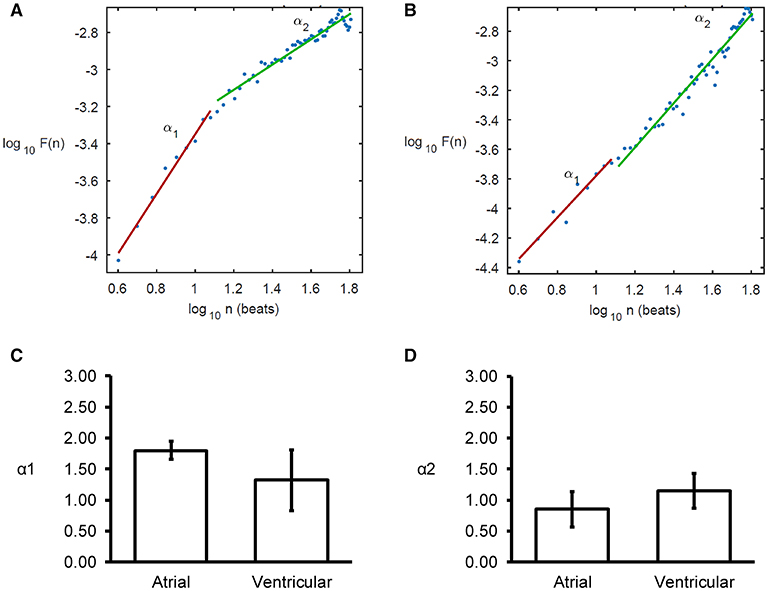
Figure 6. Detrended fluctuation analysis (DFA) plots expressing detrended fluctuations F(n) as a function of n in a log-log scale for the atria (A) and ventricles (B), yielding short-term (C), and long-term (D) fluctuation slopes (α1 and α2, respectively).

The variability data for APD₇₀, APD₅₀, and APD₃₀ are shown in Supplementary Appendices 1–3, respectively.

Discussion

This is the first proof-of-concept study investigating the beat-to-beat variability in repolarization time-courses of atrial and ventricular MAP recordings in whole hearts of mice. The main findings are that (1) variability in APDs can be detected using time-domain, frequency-domain, combined time-frequency, and non-linear methods; (2) the atria and ventricles show similar low- and high-frequency peaks; (3) but the atria showed predominantly low-frequency components whereas the ventricles showed predominantly high-frequency components; (4) Poincaré plot showed ellipsoid shapes from all of the hearts; (5) the SD perpendicular to the line-of-identity (SD2) was significantly larger than the SD along the line-of-identity (SD1), leading to SD2/SD1 ratios greater than unity; (6) a degree of disorder was identified by approximate and sample entropy analyses, (7) short-term fluctuation slopes were steeper than long-term fluctuation slopes.

Variability in recorded signals is an intrinsic property of excitable media in biological systems. In the heart, heart rate variability (HRV) is normally observed in the healthy state (Shaffer and Ginsberg, 2017), whereas alterations in HRV have been associated with adverse outcomes such as arrhythmogenesis that may be mediated through generation of APD variability (Mcintyre et al., 2014). Similarly, beat-to-beat variability in the repolarization time-course can be present and can be observed electrocardiographically as QT interval variability (Baumert et al., 2016; Orini et al., 2016). Naturally occurring beat-to-beat variations in APDs have been observed in isolated cardiomyocytes (Kiyosue and Arita, 1989; Shryock et al., 2013), even when pacing rate and temperature are held constant (Zaniboni et al., 2000). It has been studied in detail in canine ventricular cardiomyocytes (Abi-Gerges et al., 2010; Kistamas et al., 2015a,b; Szentandrassy et al., 2015; Magyar et al., 2016), but never in mouse models whether in single cells or isolated hearts. Our study adds to the literature by demonstrating that such variabilities are also present in Langendorff-perfused mouse hearts under similar constant rate pacing conditions. Computational modeling has previously identified the molecular mechanisms underlying such beat-to-beat variability in APDs (Heijman et al., 2013). These include stochastic gating of ion channels, in particular that of sodium and delayed rectifier potassium channels. Although fluctuations in APDs was present in our experimental mouse model, the variability was very small, with standard deviation of around 1.4 ms for the atria and 0.2 ms for the ventricles. This may be due to the differing morphology of the cardiac action potentials in this species. Consistent with these findings, modeling studies suggests that variability is higher in species that have more pronounced plateau phase during repolarization, such as guinea pigs and rabbits (Heijman et al., 2013), than those with a triangular action potential morphology such as mice. Indeed, the standard deviation is around 10 ms in guinea pig ventricular cardiomyocytes (Zaniboni et al., 2000) and 7 ms in rabbit sinoatrial nodal cells (Wilders and Jongsma, 1993). This variability is dependent on the APD. Therefore, one way to express this is the coefficient of variation (CoV), given by the percentage of SD divided by the mean APD. The CoV is around 2% in both the guinea pig and the rabbit ventricles. From our study, we found CoV to be 4.0% in the atria and 0.8% in the ventricles. It should be noted that our model used intact hearts whereas single cells were used in the other studies. Multicellular preparations are known to show lower levels of variability than in single cells because of electrical coupling, which dampens the differences between cells (Magyar et al., 2015).

Time-domain analysis allowed the quantification of the variability using standard deviations, coefficients of variations and root mean squares of successive APDs in both the atria and ventricles. It was noted that atrial APDs were significantly shorter than ventricular APDs, in keeping with our previous findings (Tse et al., 2016a,b). Moreover, we report for the first time higher degrees of variability in the atria as reflected by higher mean SD, CoV and RMS of APDs when compared to the ventricles. Frequency-domain analysis using the Fast Fourier Transform-based method produced power spectrum density estimates for the APD₉₀ time series. This provides the basic information on how power is distributed as a function of frequency. We observed that both atrial and ventricular MAPs were predominantly in the low-frequency domain. LF and HF rhythms in repolarization variability are important as they reflect QT rate adaptation (Merri et al., 1993). Variability assessed in the frequency domain represents an index of temporal dispersion of ventricular repolarization (Lombardi et al., 1998) which is an important determinant of arrhythmogenesis. However, the above frequency analysis does not provide any information on the time evolution of the frequencies. To achieve, this, time-frequency analysis was conducted using both short-time Fourier transform (STFT) and continuous wavelet transform (CWT). Previously, time-frequency analysis has been applied to electrograms to detect regional cardiac repolarization alternans that occur transiently (Orini et al., 2013, 2014).

Significantly, non-linear analyses of APDs yielded further insights. Thus, Poincaré plots of APDs showed ellipsoid shapes in all of the hearts studied, and together with a SD2/SD1 ratio >1, indicated that variability in the long-term was greater than variability in the short-term. This ratio was around 6 to 8 and did not significantly differ between the atria and ventricles. In a canine model, higher short-term variability calculated from Poincaré plots being associated with the occurrence of drug-induced torsade de pointes (Thomsen et al., 2004). Furthermore, the present findings also found a degree of entropy present in the atria and ventricles. Entropy refers to the degree of disorder in a system and has been used to quantify the regularity or complexity of biological signals (Pincus, 1991; Pincus and Goldberger, 1994). These entropy calculations are based on the state space reconstruction of time series data (Richman and Moorman, 2000; Bandt and Pompe, 2002; Li et al., 2015). Our study quantified for the first time approximate entropy in the atria and ventricles. This is an appropriate method for time series with more than 50 points, a condition that we have satisfied (Pincus, 2001). Similar, this study determined sample entropy, which is a refined version of approximate entropy. It can quantify the irregularity of APD time series without biasing (Richman and Moorman, 2000) and has the advantage of eliminating self-matches and being less dependent on time-series length (Li et al., 2009). Entropy has been identified as a pro-arrhythmic indicator (Cervigon et al., 2016). High entropy in repolarization was shown to predict arrhythmic or mortality outcomes in patients receiving implantable-cardioverter defibrillator for primary prevention of sudden cardiac death (Demazumder et al., 2016). Further studies are needed to confirm or refute the hypothesis that increased approximate or sample entropy predicts the onset of atrial or ventricular arrhythmias in mouse hearts. However, its use has some important limitations. For example, it should not be applied to long duration signals because more computations are required for real-time implementation (Tripathy et al., 2017).

Fractional calculus has been applied to investigate physiological time series such as heart rate variability (González et al., 2012; Sturmberg and West, 2013; Sturmberg et al., 2015). Some techniques assume stationary signals whilst others do not make such assumptions (Gao et al., 2013). This study applied for the first time detrended fluctuation analysis (DFA) to reveal complex fractal fluctuation patterns by delineating them into long- and short-term fluctuation for the first time in the mouse heart. DFA is a method for quantifying long-range correlations in non-stationary physiological time series (Peng et al., 1995). DFA enables correct estimation of the power law scaling, the Hurst exponent, in the presence of extrinsic non-stationaries while eliminating spurious detection of long-range dependence (West et al., 2008). The average fluctuation is plotted against the number of beats on a log-log scale, yielding short- and long-term fluctuation slopes, or scaling exponents (α1 and α2, respectively). α of 0.5 indicates uncorrelated data, and deviations from 0.5 indicates the presence of correlation. For example, in the atria, we found α1 to be around 1.7, suggesting the presence of short-term correlation, but α2 was around 0.7, suggesting the minimal long-term correlations. In the ventricles, α1 and α2 took similar values to those observed in the atria.

Previously, decreases in the short-term exponent of HRV, has been associated with arrhythmic and mortality outcomes in heart failure after acute myocardial infarction (Huikuri et al., 2000) and in end-stage renal failure patients receiving peritoneal dialysis (Chiang et al., 2016). Decreases in the short-term exponent have also been detected prior to the onset of atrial arrhythmias (Vikman et al., 1999). In a rabbit hypertrophic cardiomyopathy model, DFA of maximum QT intervals showed higher scaling exponent in diseased compared to control groups (Sanbe et al., 2005). In human induced pluripotent stem cell-derived cardiomyocytes, fractal correlations as determined by α1 was observed (Kuusela et al., 2016). In humans, a significant decrease in α1 was observed during sympathetic activation suggesting a breakdown of the short-term fractal organization of heart rate (Tulppo et al., 2005). Moreover, normal α1 but lower α2 was observed in patients with atrial fibrillation compared to those without AF (Kalisnik et al., 2015).

Previous work has demonstrated that HRV time series have a crossover phenomenon (Havlin et al., 1999; Penzel et al., 2003). In this study, DFA also found scaling trends with two distinct values. This is interesting because it may be related to bi-fractality, where fractal patterns can emerge from random fluctuations via allometric filtering mechanisms (Scafetta and West, 2007). Thus, APD time series are potentially crossover-fractals with two fractal dimensions. This could be validated by using empirical mode decomposition to construct crossover-fractals from two monofractals (Liaw and Chiu, 2010). However, although DFA is useful for exploring the structure of correlations in physiological time series, tracking the local evolution of the exponent by a recursive least-squares method can yield structures of correlations that can provide additional details on the dynamics of these series (Bojorges-Valdez et al., 2007). Our findings suggest that repolarization characteristics exhibit fractal behavior and may be better represented using concepts from fractional calculus, for example by using fractal dynamical equations (Marculescu and Bogdan, 2011). Such an approach has successfully been used to optimize control for implantable pacemakers (Bogdan et al., 2012, 2013).

Moreover, fractional differintegration was used to characterize HRV, allowing determination of the standard deviation of the fractionally differintegrated RR time series for a fractional differintegration of order α [SDFDINN(α)]. α_c, the order of the fractional differintegration that provide the minimum standard deviation of the fractionally differintegrated RR set, showed a linear correlation with the Hurst exponent. Interestingly this method for estimating the exponent showed less bias and lower variance when compared to DFA (García-González et al., 2013). Also, α_c was closely related to α₁ but they were not equal. Future studies are needed to explore the predictive values of these fluctuation exponents, and to evaluate the efficacy of fractal dynamical state equation to describe the spatial and temporal dependency structure of repolarization properties in mouse models of cardiac arrhythmias (Xue and Bogdan, 2017).

Conclusions

The present findings provide a proof-of-concept that APD variability is present at baseline conditions and can be detected using time-domain, frequency-domain and non-linear techniques. Atrial MAPs showed greater degree of variability than ventricular MAPs. Non-linear techniques offer further insights on short-term and long-term variability and signal complexity.

Author Contributions

GT: study conception, data analysis and interpretation, manuscript drafting, critical revision of manuscript. YD, FC, TL, GH, KHCL, GL, GB, and SC: data interpretation, critical revision of manuscript. KL, WKW, and WTW: study supervision, data interpretation, critical revision of manuscript.

Funding

The Biotechnology and Biological Sciences Research Council (GT). Economic and Social Research Council (FC). The National Nature Science Foundation of China (No. 81470421 and No. 81770328 to YD).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

GT received research funding from the BBSRC for this research and is currently supported by a Clinical Assistant Professorship from the Croucher Foundation of Hong Kong. WTW is supported by the Direct Grant for Research from the Research Committee of the Chinese University of Hong Kong, China. YD is supported by the National Nature Science Foundation of China (No. 81470421 and No. 81770328).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2018.01578/full#supplementary-material

References

Abi-Gerges, N., Valentin, J. P., and Pollard, C. E. (2010). Dog left ventricular midmyocardial myocytes for assessment of drug-induced delayed repolarization: short-term variability and proarrhythmic potential. Br. J. Pharmacol. 159, 77–92. doi: 10.1111/j.1476-5381.2009.00338.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Bandt, C., and Pompe, B. (2002). Permutation entropy: a natural complexity measure for time series. Phys. Rev. Lett. 88:174102. doi: 10.1103/PhysRevLett.88.174102

PubMed Abstract | CrossRef Full Text | Google Scholar

Baumert, M., Porta, A., Vos, M. A., Malik, M., Couderc, J.-P., Laguna, P., et al. (2016). QT interval variability in body surface ECG: measurement, physiological basis, and clinical value: position statement and consensus guidance endorsed by the European Heart Rhythm Association jointly with the ESC working group on cardiac cellular electrophysiology. Europace 18, 925–944. doi: 10.1093/europace/euv405

PubMed Abstract | CrossRef Full Text | Google Scholar

Bogdan, P., Jain, S., Goyal, K., and Marculescu, R. (2012). “Implantable pacemakers control and optimization via fractional calculus approaches: a cyber-physical systems perspective,” in 2012 IEEE/ACM Third International Conference on Cyber-Physical Systems (Beijing), 23–32. doi: 10.1109/ICCPS.2012.11

CrossRef Full Text | Google Scholar

Bogdan, P., Jain, S., and Marculescu, R. (2013). Pacemaker control of heart rate variability: a cyber physical system perspective. ACM Trans. Embed. Comput. Syst. 12, 1–22. doi: 10.1145/2435227.2435246

CrossRef Full Text | Google Scholar

Bojorges-Valdez, E. R., Echeverría, J. C., Valdés-Cristerna, R., and Peña, M. A. (2007). Scaling patterns of heart rate variability data. Physiol. Meas. 28, 721–730. doi: 10.1088/0967-3334/28/6/010

PubMed Abstract | CrossRef Full Text | Google Scholar

Cervigon, R., Moreno, J., Garcia-Quintanilla, J., Perez-Villacastin, J., and Castells, F. (2016). Entropy at the right atrium as a predictor of atrial fibrillation recurrence outcome after pulmonary vein ablation. Biomed. Tech. 61, 29–36. doi: 10.1515/bmt-2014-0172

PubMed Abstract | CrossRef Full Text | Google Scholar

Chiang, J.-Y., Huang, J.-W., Lin, L.-Y., Chang, C.-H., Chu, F.-Y., Lin, Y.-H., et al. (2016). Detrended fluctuation analysis of heart rate dynamics is an important prognostic factor in patients with end-stage renal disease receiving peritoneal dialysis. PLoS ONE 11:e0147282. doi: 10.1371/journal.pone.0147282

PubMed Abstract | CrossRef Full Text | Google Scholar

Choy, L., Yeo, J. M., Tse, V., Chan, S. P., and Tse, G. (2016). Cardiac disease and arrhythmogenesis: mechanistic insights from mouse models. Int. J. Cardiol. Heart Vasc. 12, 1–10. doi: 10.1016/j.ijcha.2016.05.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Demazumder, D., Limpitikul, W. B., Dorante, M., Dey, S., Mukhopadhyay, B., Zhang, Y., et al. (2016). Entropy of cardiac repolarization predicts ventricular arrhythmias and mortality in patients receiving an implantable cardioverter-defibrillator for primary prevention of sudden death. EP Europace 18, 1818–1828. doi: 10.1093/europace/euv399

PubMed Abstract | CrossRef Full Text | Google Scholar

Fabritz, L., Kirchhof, P., Franz, M. R., Eckardt, L., Mönnig, G., Milberg, P., et al. (2003). Prolonged action potential durations, increased dispersion of repolarization, and polymorphic ventricular tachycardia in a mouse model of proarrhythmia. Basic Res. Cardiol. 98, 25–32. doi: 10.1007/s00395-003-0386-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, J., Gurbaxani, B., Hu, J., Heilman, K., Emauele, V., Lewis, G., et al. (2013). Multiscale analysis of heart rate variability in non-stationary environments. Front. Physiol. 4:119. doi: 10.3389/fphys.2013.00119

PubMed Abstract | CrossRef Full Text | Google Scholar

García-González, M. A., Fernández-Chimeno, M., Capdevila, L., Parrado, E., and Ramos-Castro, J. (2013). An application of fractional differintegration to heart rate variability time series. Comput. Methods Programs Biomed. 111, 33–40. doi: 10.1016/j.cmpb.2013.02.009

PubMed Abstract | CrossRef Full Text | Google Scholar

González, M. A. G., Castro, J. J. R., and Fernández-Chimeno, M. (2012). “A novel index based on fractional calculus to assess the dynamics of heart rate variability: changes due to Chi or Yoga meditations,” in 2012 Computing in Cardiology (Krakow), 925–928.

Google Scholar

Gussak, I., Chaitman, B. R., Kopecky, S. L., and Nerbonne, J. M. (2000). Rapid ventricular repolarization in rodents: electrocardiographic manifestations, molecular mechanisms, and clinical insights. J. Electrocardiol. 33, 159–170. doi: 10.1016/S0022-0736(00)80072-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Havlin, S., Amaral, L. A. N., Ashkenazy, Y., Goldberger, A. L., Ivanov, P. C., and Stanley, H. E. (1999). Application of statistical physics to heartbeat diagnosis. Physica A Stat. Mech. Appl. 274, 99–110. doi: 10.1016/S0378-4371(99)00333-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Heijman, J., Zaza, A., Johnson, D. M., Rudy, Y., Peeters, R. L., Volders, P. G., et al. (2013). Determinants of beat-to-beat variability of repolarization duration in the canine ventricular myocyte: a computational analysis. PLoS Comput. Biol. 9:e1003202. doi: 10.1371/journal.pcbi.1003202

PubMed Abstract | CrossRef Full Text | Google Scholar

Hinterseer, M., Beckmann, B. M., Thomsen, M. B., Pfeufer, A., Dalla Pozza, R., Loeff, M., et al. (2009). Relation of increased short-term variability of QT interval to congenital long-QT syndrome. Am. J. Cardiol. 103, 1244–1248. doi: 10.1016/j.amjcard.2009.01.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Hinterseer, M., Beckmann, B. M., Thomsen, M. B., Pfeufer, A., Ulbrich, M., Sinner, M. F., et al. (2010). Usefulness of short-term variability of QT intervals as a predictor for electrical remodeling and proarrhythmia in patients with nonischemic heart failure. Am. J. Cardiol. 106, 216–220. doi: 10.1016/j.amjcard.2010.02.033

PubMed Abstract | CrossRef Full Text | Google Scholar

Huikuri, H. V., Makikallio, T. H., Peng, C. K., Goldberger, A. L., Hintze, U., and Moller, M. (2000). Fractal correlation properties of R-R interval dynamics and mortality in patients with depressed left ventricular function after an acute myocardial infarction. Circulation 101, 47–53. doi: 10.1161/01.CIR.101.1.47

PubMed Abstract | CrossRef Full Text | Google Scholar

Kalisnik, J. M., Hrovat, E., Hrastovec, A., Avbelj, V., Zibert, J., and Gersak, B. (2015). Severe cardiac autonomic derangement and altered ventricular repolarization pave the way to postoperative atrial fibrillation. Innovations 10, 398–405. doi: 10.1097/IMI.0000000000000203

PubMed Abstract | CrossRef Full Text | Google Scholar

Kistamas, K., Hegyi, B., Vaczi, K., Horvath, B., Banyasz, T., Magyar, J., et al. (2015a). Oxidative shift in tissue redox potential increases beat-to-beat variability of action potential duration. Can. J. Physiol. Pharmacol. 93, 563–568. doi: 10.1139/cjpp-2014-0531

PubMed Abstract | CrossRef Full Text | Google Scholar

Kistamas, K., Szentandrassy, N., Hegyi, B., Vaczi, K., Ruzsnavszky, F., Horvath, B., et al. (2015b). Changes in intracellular calcium concentration influence beat-to-beat variability of action potential duration in canine ventricular myocytes. J. Physiol. Pharmacol. 66, 73–81. Available online at: https://pdfs.semanticscholar.org/9776/967cc719dbcc52982ac82cc3f400074aa601.pdf

PubMed Abstract | Google Scholar

Kiyosue, T., and Arita, M. (1989). Late sodium current and its contribution to action potential configuration in guinea pig ventricular myocytes. Circ. Res. 64, 389–397. doi: 10.1161/01.RES.64.2.389

PubMed Abstract | CrossRef Full Text | Google Scholar

Knollmann, B. C., Katchman, A. N., and Franz, M. R. (2001). Monophasic action potential recordings from intact mouse heart: validation, regional heterogeneity, and relation to refractoriness. J. Cardiovasc. Electrophysiol. 12, 1286–1294. doi: 10.1046/j.1540-8167.2001.01286.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuusela, J., Kim, J., Rasanen, E., and Aalto-Setala, K. (2016). The effects of pharmacological compounds on beat rate variations in human long QT-syndrome cardiomyocytes. Stem Cell Rev. 12, 698–707. doi: 10.1007/s12015-016-9686-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, H., Han, W., Hu, C., and Meng, M. Q. H. (2009). “Detecting ventricular fibrillation by fast algorithm of dynamic sample entropy,” in 2009 IEEE International Conference on Robotics and Biomimetics (ROBIO) (Guilin), 1105–1110.

Google Scholar

Li, P., Liu, C., Li, K., Zheng, D., Liu, C., and Hou, Y. (2015). Assessing the complexity of short-term heartbeat interval series by distribution entropy. Med. Biol. Eng. Comput. 53, 77–87. doi: 10.1007/s11517-014-1216-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Liaw, S.-S., and Chiu, F.-Y. (2010). Constructing crossover-fractals using intrinsic mode functions. Adv. Adapt. Data Anal. 2, 509–520. doi: 10.1142/S1793536910000598

CrossRef Full Text | Google Scholar

Lombardi, F., Colombo, A., Porta, A., Baselli, G., Cerutti, S., and Fiorentini, C. (1998). Assessment of the coupling between RTapex and RR interval as an index of temporal dispersion of ventricular repolarization. Pacing Clin. Electrophysiol. 21, 2396–2400. doi: 10.1111/j.1540-8159.1998.tb01189.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Magyar, J., Banyasz, T., Szentandrassy, N., Kistamas, K., Nanasi, P. P., and Satin, J. (2015). Role of gap junction channel in the development of beat-to-beat action potential repolarization variability and arrhythmias. Curr. Pharm. Des. 21, 1042–1052. doi: 10.2174/1381612820666141029102443

PubMed Abstract | CrossRef Full Text | Google Scholar

Magyar, J., Kistamas, K., Vaczi, K., Hegyi, B., Horvath, B., Banyasz, T., et al. (2016). Concept of relative variability of cardiac action potential duration and its test under various experimental conditions. Gen. Physiol. Biophys. 35, 55–62. doi: 10.4149/gpb_2015019

PubMed Abstract | CrossRef Full Text | Google Scholar

Marculescu, R., and Bogdan, P. (2011). Cyberphysical systems: workload modeling and design optimization. IEEE Design Test Comput. 28, 78–87. doi: 10.1109/MDT.2010.142

CrossRef Full Text | Google Scholar

Mcintyre, S. D., Kakade, V., Mori, Y., and Tolkacheva, E. G. (2014). Heart rate variability and alternans formation in the heart: the role of feedback in cardiac dynamics. J. Theor. Biol. 350, 90–97. doi: 10.1016/j.jtbi.2014.02.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Merri, M., Alberti, M., and Moss, A. J. (1993). Dynamic analysis of ventricular repolarization duration from 24-hour Holter recordings. IEEE Trans. Biomed. Eng. 40, 1219–1225. doi: 10.1109/10.250577

PubMed Abstract | CrossRef Full Text | Google Scholar

Mesin, L. (2018). Estimation of complexity of sampled biomedical continuous time signals using approximate entropy. Front. Physiol. 9:710. doi: 10.3389/fphys.2018.00710

PubMed Abstract | CrossRef Full Text | Google Scholar

Molina-Pico, A., Cuesta-Frau, D., Aboy, M., Crespo, C., Miro-Martinez, P., and Oltra-Crespo, S. (2011). Comparative study of approximate entropy and sample entropy robustness to spikes. Artif. Intell. Med. 53, 97–106. doi: 10.1016/j.artmed.2011.06.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Nanasi, P. P., Magyar, J., Varro, A., and Ordog, B. (2017). Beat-to-beat variability of cardiac action potential duration: underlying mechanism and clinical implications. Can. J. Physiol. Pharmacol. 95, 1230–1235. doi: 10.1139/cjpp-2016-0597

PubMed Abstract | CrossRef Full Text | Google Scholar

Nayak, S. K., Bit, A., Dey, A., Mohapatra, B., and Pal, K. (2018). A review on the nonlinear dynamical system analysis of electrocardiogram signal. J. Healthc. Eng. 2018:6920420. doi: 10.1155/2018/6920420

PubMed Abstract | CrossRef Full Text | Google Scholar

Nerbonne, J. M. (2014). Mouse models of arrhythmogenic cardiovascular disease: challenges and opportunities. Curr. Opin. Pharmacol. 15, 107–114. doi: 10.1016/j.coph.2014.02.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Niemeijer, M. N., Van Den Berg, M. E., Eijgelsheim, M., Van Herpen, G., Stricker, B. H., Kors, J. A., et al. (2014). Short-term QT variability markers for the prediction of ventricular arrhythmias and sudden cardiac death: a systematic review. Heart 100, 1831–1836. doi: 10.1136/heartjnl-2014-305671

PubMed Abstract | CrossRef Full Text | Google Scholar

Orini, M., Hanson, B., Monasterio, V., Martinez, J. P., Hayward, M., Taggart, P., et al. (2014). Comparative evaluation of methodologies for T-wave alternans mapping in electrograms. IEEE Trans. Biomed. Eng. 61, 308–316. doi: 10.1109/TBME.2013.2289304

PubMed Abstract | CrossRef Full Text | Google Scholar

Orini, M., Hanson, B., Taggart, P., and Lambiase, P. (2013). Detection of transient, regional cardiac repolarization alternans by time-frequency analysis of synthetic electrograms. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2013, 3773–3776. doi: 10.1109/EMBC.2013.6610365

PubMed Abstract | CrossRef Full Text | Google Scholar

Orini, M., Taggart, P., and Lambiase, P. D. (2016). “A multivariate time-frequency approach for tracking QT variability changes unrelated to heart rate variability,” in 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) (Orlando, FL), 924–927.

Google Scholar

Peng, C. K., Havlin, S., Stanley, H. E., and Goldberger, A. L. (1995). Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos 5, 82–87. doi: 10.1063/1.166141

PubMed Abstract | CrossRef Full Text | Google Scholar

Penzel, T., Kantelhardt, J. W., Grote, L., Peter, J. H., and Bunde, A. (2003). Comparison of detrended fluctuation analysis and spectral analysis for heart rate variability in sleep and sleep apnea. IEEE Trans. Biomed. Eng. 50, 1143–1151. doi: 10.1109/TBME.2003.817636

PubMed Abstract | CrossRef Full Text | Google Scholar

Phadumdeo, V. M., and Weinberg, S. H. (2018). Heart rate variability alters cardiac repolarization and electromechanical dynamics. J. Theor. Biol. 442, 31–43. doi: 10.1016/j.jtbi.2018.01.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Pincus, S. M. (1991). Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. U.S.A. 88, 2297–2301. doi: 10.1073/pnas.88.6.2297

PubMed Abstract | CrossRef Full Text | Google Scholar

Pincus, S. M. (2001). Assessing serial irregularity and its implications for health. Ann. N. Y. Acad. Sci. 954, 245–267. doi: 10.1111/j.1749-6632.2001.tb02755.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Pincus, S. M., and Goldberger, A. L. (1994). Physiological time-series analysis: what does regularity quantify? Am. J. Physiol. 266, H1643–H1656.

PubMed Abstract | Google Scholar

Richman, J. S., and Moorman, J. R. (2000). Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 278, H2039–H2049. doi: 10.1152/ajpheart.2000.278.6.H2039

PubMed Abstract | CrossRef Full Text | Google Scholar

Sanbe, A., James, J., Tuzcu, V., Nas, S., Martin, L., Gulick, J., et al. (2005). Transgenic rabbit model for human troponin I-based hypertrophic cardiomyopathy. Circulation 111, 2330–2338. doi: 10.1161/01.CIR.0000164234.24957.75

PubMed Abstract | CrossRef Full Text | Google Scholar

Scafetta, N., and West, B. J. (2007). Emergence of bi-fractal time series from noise via allometric filters. EPL 79:30003. doi: 10.1209/0295-5075/79/30003

CrossRef Full Text | Google Scholar

Shaffer, F., and Ginsberg, J. P. (2017). An overview of heart rate variability metrics and norms. Front. Pub. Health 5:258. doi: 10.3389/fpubh.2017.00258

PubMed Abstract | CrossRef Full Text | Google Scholar

Shryock, J. C., Song, Y., Rajamani, S., Antzelevitch, C., and Belardinelli, L. (2013). The arrhythmogenic consequences of increasing late INa in the cardiomyocyte. Cardiovasc. Res. 99, 600–611. doi: 10.1093/cvr/cvt145

PubMed Abstract | CrossRef Full Text | Google Scholar

Sturmberg, J. P., Bennett, J. M., Picard, M., and Seely, A. J. E. (2015). The trajectory of life. Decreasing physiological network complexity through changing fractal patterns. Front. Physiol. 6:169. doi: 10.3389/fphys.2015.00169

PubMed Abstract | CrossRef Full Text | Google Scholar

Sturmberg, J. P., and West, B. J. (2013). “Fractals in physiology and medicine,” in Handbook of Systems and Complexity in Health, eds J. P. Sturmberg and C. M. Martin (New York, NY: Springer New York), 171–192. doi: 10.1007/978-1-4614-4998-0_11

CrossRef Full Text | Google Scholar

Szentandrassy, N., Kistamas, K., Hegyi, B., Horvath, B., Ruzsnavszky, F., Vaczi, K., et al. (2015). Contribution of ion currents to beat-to-beat variability of action potential duration in canine ventricular myocytes. Pflugers Arch. 467, 1431–1443. doi: 10.1007/s00424-014-1581-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Thomsen, M. B., Verduyn, S. C., Stengl, M., Beekman, J. D., De Pater, G., Van Opstal, J., et al. (2004). Increased short-term variability of repolarization predicts d-sotalol-induced torsades de pointes in dogs. Circulation 110, 2453–2459. doi: 10.1161/01.CIR.0000145162.64183.C8

PubMed Abstract | CrossRef Full Text | Google Scholar

Tripathy, R. K., Deb, S., and Dandapat, S. (2017). Analysis of physiological signals using state space correlation entropy. Healthcare Technol. Lett. 4, 30–33. doi: 10.1049/htl.2016.0065

PubMed Abstract | CrossRef Full Text | Google Scholar

Tse, G., Liu, T., Li, G., Keung, W., Yeo, J. M., Fiona Chan, Y. W., et al. (2017). Effects of pharmacological gap junction and sodium channel blockade on S1S2 restitution properties in Langendorff-perfused mouse hearts. Oncotarget 8, 85341–85352. doi: 10.18632/oncotarget.19675

PubMed Abstract | CrossRef Full Text | Google Scholar

Tse, G., Sun, B., Wong, S. T., Tse, V., and Yeo, J. M. (2016a). Anti-arrhythmic effects of hypercalcemia in hyperkalemic, Langendorff-perfused mouse hearts. Biomed. Rep. 5, 301–310. doi: 10.3892/br.2016.735

PubMed Abstract | CrossRef Full Text | Google Scholar

Tse, G., Tse, V., Yeo, J. M., and Sun, B. (2016b). Atrial anti-arrhythmic effects of heptanol in langendorff-perfused mouse hearts. PLoS ONE 11:e0148858. doi: 10.1371/journal.pone.0148858

PubMed Abstract | CrossRef Full Text | Google Scholar

Tse, G., Wong, S. T., Tse, V., and Yeo, J. M. (2016c). Monophasic action potential recordings: which is the recording electrode? J. Basic Clin. Physiol. Pharmacol. 27, 457–462. doi: 10.1515/jbcpp-2016-0007

PubMed Abstract | CrossRef Full Text | Google Scholar

Tse, G., Yeo, J. M., Tse, V., Kwan, J., and Sun, B. (2016d). Gap junction inhibition by heptanol increases ventricular arrhythmogenicity by reducing conduction velocity without affecting repolarization properties or myocardial refractoriness in Langendorff-perfused mouse hearts. Mol. Med. Rep. 14, 4069–4074. doi: 10.3892/mmr.2016.5738

PubMed Abstract | CrossRef Full Text | Google Scholar

Tulppo, M. P., Kiviniemi, A. M., Hautala, A. J., Kallio, M., Seppanen, T., Makikallio, T. H., et al. (2005). Physiological background of the loss of fractal heart rate dynamics. Circulation 112, 314–319. doi: 10.1161/CIRCULATIONAHA.104.523712

PubMed Abstract | CrossRef Full Text | Google Scholar

Vikman, S., Makikallio, T. H., Yli-Mayry, S., Pikkujamsa, S., Koivisto, A. M., Reinikainen, P., et al. (1999). Altered complexity and correlation properties of R-R interval dynamics before the spontaneous onset of paroxysmal atrial fibrillation. Circulation 100, 2079–2084. doi: 10.1161/01.CIR.100.20.2079

PubMed Abstract | CrossRef Full Text | Google Scholar

West, B. J., Geneston, E. L., and Grigolini, P. (2008). Maximizing information exchange between complex networks. Phys. Rep. 468, 1–99. doi: 10.1016/j.physrep.2008.06.003

CrossRef Full Text | Google Scholar

Wilders, R., and Jongsma, H. J. (1993). Beating irregularity of single pacemaker cells isolated from the rabbit sinoatrial node. Biophys. J. 65, 2601–2613. doi: 10.1016/S0006-3495(93)81289-X

PubMed Abstract | CrossRef Full Text | Google Scholar

Xue, Y., and Bogdan, P. (2017). “Constructing compact causal mathematical models for complex dynamics,” in Proceedings of the 8th International Conference on Cyber-Physical Systems (Pittsburgh, PA: ACM). doi: 10.1145/3055004.3055017

CrossRef Full Text | Google Scholar

Zaniboni, M., Pollard, A. E., Yang, L., and Spitzer, K. W. (2000). Beat-to-beat repolarization variability in ventricular myocytes and its suppression by electrical coupling. Am. J. Physiol. Heart Circ. Physiol. 278, H677–H687. doi: 10.1152/ajpheart.2000.278.3.H677

PubMed Abstract | CrossRef Full Text | Google Scholar