The Resting Potential and K+ Currents in Primary Human Articular Chondrocytes

Human transplant programs provide significant opportunities for detailed in vitro assessments of physiological properties of selected tissues and cell types. We present a semi-quantitative study of the fundamental electrophysiological/biophysical characteristics of human chondrocytes, focused on K⁺ transport mechanisms, and their ability to regulate to the resting membrane potential, E_m. Patch clamp studies on these enzymatically isolated human chondrocytes reveal consistent expression of at least three functionally distinct K⁺ currents, as well as transient receptor potential (TRP) currents. The small size of these cells and their exceptionally low current densities present significant technical challenges for electrophysiological recordings. These limitations have been addressed by parallel development of a mathematical model of these K⁺ and TRP channel ion transfer mechanisms in an attempt to reveal their contributions to E_m. In combination, these experimental results and simulations yield new insights into: (i) the ionic basis for E_m and its expected range of values; (ii) modulation of E_m by the unique articular joint extracellular milieu; (iii) some aspects of TRP channel mediated depolarization-secretion coupling; (iv) some of the essential biophysical principles that regulate K⁺ channel function in “chondrons.” The chondron denotes the chondrocyte and its immediate extracellular compartment. The presence of discrete localized surface charges and associated zeta potentials at the chondrocyte surface are regulated by cell metabolism and can modulate interactions of chondrocytes with the extracellular matrix. Semi-quantitative analysis of these factors in chondrocyte/chondron function may yield insights into progressive osteoarthritis.

Introduction

Articular cartilage is a major component of the flexible connective tissue that covers the opposed ends of articular joints. It is essential for the stability and low friction movement of the associated long bones (Huber et al., 2000). This tissue is populated predominately by only one type of cell—the chondrocyte, and it lacks any significant vascular, or lymphatic elements. Each chondrocyte, together with its immediate pericellular coat or glycocalyx, forms a functional unit that has been named a “chondron” (Poole, 1997; Guilak et al., 2006; Nguyen et al., 2010; McLane et al., 2013). Under physiological circumstances, cyclical mechanical forces within the joint capsule create a dynamic environment that modulates cellular metabolism and maintains overall health (Wu and Chen, 2000; Guilak et al., 2006; Chen et al., 2013).

Although chondrocytes occupy only ~1–10% of the total volume of mammalian articular cartilage (Hall et al., 1996; Archer and Francis-West, 2003), they play essential roles in the homeostasis of the extracellular matrix (ECM). In part, this is because these cells synthesize and secrete most of the essential lubricants within the joint, including hyaluronan and lubricin (Ogawa et al., 2014). The ECM is composed of: (i) collagen fibers that give the tissue the ability to resist tension, (ii) negatively charged gel-like proteoglycans that are trapped within the collagen mesh and allow the tissue to bear compression, and (iii) synovial fluid which acts as a lubricant, thus ensuring low friction movement of the bones. The primary role of the chondrocyte is to maintain viable cartilage by regulating macromolecular synthesis and breakdown of its essential constituents and to produce lubricants (Huber et al., 2000; Guilak et al., 2006; Ogawa et al., 2014).

In a variety of progressive chronic diseases, or as a consequence of injury, there is chondrocyte damage and related dysfunction (Bush et al., 2003; Martin and Buckwalter, 2003; Bush and Hall, 2005; Mobasheri et al., 2015). In these situations, the dynamic balance between matrix synthesis and degradation is altered and the low friction environment within the joint may also be reduced (Urban et al., 1993). Frequently, there also is an inflammatory response within the articular joint (Pelletier et al., 2001). These factors can increase the early development of osteoarthritis, and attendant thinning of the cartilage layer, thus resulting in painful, bone-against-bone friction (Bush et al., 2003; Mobasheri et al., 2015). The progression of osteoarthritis and the reduced ability of chondrocyte ion transport systems to respond to perturbations in the extracellular environment (Pelletier et al., 2001) have also been associated with deficiencies in volume regulation (Urban et al., 1993; Lewis et al., 2011). It is known that damage to cartilage is more prominent in the setting of co-incident changes in osmolarity in the chondron. In part, this may be because these volume changes are linked to an abnormal resting membrane potential in chondrocytes (Lewis et al., 2011) caused by altered ion transport, e.g., changes in K⁺ and/or Cl⁻ channel activity. However, uncertainty and some disagreements remain concerning the fundamental ionic mechanisms for this progressive loss of function of the affected chondrocytes in chronic disease settings.

Detailed experimental investigations that address possible functional relationships between chondrocyte electrophysiology and pathophysiology are technically challenging. This is mainly due to the very small size of a mature chondrocyte and the associated limitations of in vitro electrophysiological/biophysical studies. In fact, it is not certain that conventional patch pipette methods (Lewis et al., 2011) can accurately determine the resting potential of isolated single chondrocytes (Ince et al., 1986; Mason et al., 2005; Wilson et al., 2011). Partly for this reason, and also to allow us to integrate our patch clamp results with other experimental data we have developed a mathematical model based on the fundamental components responsible for K⁺ transport in the human chondrocyte. This model is based mainly on experimental data obtained from human chondrocyte preparations.

The goals of this paper are: (i) to identify the main K⁺ currents that contribute to the resting membrane potential (ii) to develop the first mathematical model of essential electrophysiological principles exhibited by human chondrocytes, (iii) to illustrate the utility of this model by simulating the dependence of the chondrocyte resting membrane potential on identified electrolytes and osmolarity in synovial fluid (iv) to put our findings in the context of depolarization-secretion coupling in the chondrocyte based on data from recordings of TRP channel-mediated cation (Na⁺ and Ca²⁺) influx in chondrocytes (cf. Lewis et al., 2013; O'Conor et al., 2014).

Methods

Mammalian chondrocytes express a number of different voltage- and ligand-gated ion channels, together with ion-selective pumps and exchangers as well as intercellular coupling proteins (cf. Barrett-Jolley et al., 2010; Asmar et al., 2016). In this study, we have extended this published data set using two different experimental preparations for recordings of ion selective currents in unstimulated chondrocytes. We have also complemented and extended these findings with the development of a mathematical model to account for regulation of the resting membrane potential, E_m, in human chondrocytes. The new data sets presented in this paper are based mainly on patch clamp experiments which were done using enzymatically isolated individual human chondrocytes obtained from a knee replacement program (The Southern Alberta Transplant Service). These cells, held in 2D culture for 1–3 days, were not passaged and are therefore classified as “primary.”

Experimental Conditions

In the experimental conditions employed in this study, isolated human chondrocytes had E_m values ranging from −30 to −60 mV when superfused with normal Tyrode's solution and studied using standard whole-cell patch clamp methods (Clark et al., 2011). This range of resting membrane potential values may reflect the intrinsic heterogeneous physiological states of these cells. However, as we have reported previously, some of this variability is very likely to result from the fact that in these very small, approximately spherical cells (diameter, ~7 microns; capacitance, ~6–12 pF), the patch pipette recording method is being applied very near its maximal technical capabilities (Wilson et al., 2011). That is, the input resistance of the chondrocyte is very large (5–10 GΩ), and the maximum seal resistance between the surface membrane of the chondrocytes and the polished surface of the glass pipette is comparable to 5–15 GΩ. The consequence is that the actual chondrocyte membrane potential may be underestimated due to the current flow through the seal resistance. In most circumstances this results in a depolarization, as noted in our previous work (Wilson et al., 2011).

Electrophysiological Studies

For these electrophysiological studies, selected populations of chondrocytes were first plated on pieces of glass coverslips, which were then transferred from the culture dishes to our superfusion chamber at the start of each experiment. Only single isolated cells with a smooth surface rounded appearance were selected for these recordings using standard patch-clamp methods (Clark et al., 2011).

Patch pipettes were fabricated from non-heparinized hematocrit capillaries. Patch pipette-filling solutions were either (i) K⁺-rich (KCl) or (ii) Cs⁺-rich (CsCl), depending on the protocol. In most experiments, free Ca²⁺ concentration in the pipette solutions was buffered to very low levels (<10 nM) by 10 mM EGTA, without added Ca²⁺. The D.C. resistance of the pipettes when filled with internal solutions was in the range ~2–4 MΩ. The seal resistance before breaking into the chondrocyte to begin whole-cell recording ranged from 4.8 to 72.3 GΩ (mean ± s.e.m.; 16.1 ± 1.5 GΩ, n = 66). Successful seals formed very rapidly (~1–2 s), and the subsequent break-in to the cells for whole-cell recording was “clean”; access resistance was generally about twice the value of the pipette resistance. (cf. Clark et al., 2011).

All electrophysiological measurements were made with a Multi-Clamp 700 A patch clamp amplifier (Molecular Devices). Membrane currents and potentials were digitized with a 1,322 A data acquisition system, stored on a microcomputer and analyzed off-line with PClamp (version 8). The “standard” voltage-clamp protocols consisted of (i) 1 s voltage ramp from −100 to +100 mV (holding potential generally −80 mV), repeated at a frequency of 0.2–0.5 Hz, and (ii) a “step” protocol, consisting of 500 ms steps from a holding potential of −80 mV membrane to potentials between −100 and +100 mV. In some experiments, a “P/n” protocol was used to correct “step” currents for linear leakage and capacity transient currents. Since the ramp and step protocols gave very similar current-voltage (I–V) relationships, the ramp protocol was used to obtain rapid, repetitive measurement of the I–V, e.g., during drug applications.

Transmembrane current values were normalized to cell capacitance, which was measured from the area under the capacitative current transient produced by a +5 mV step in membrane potential. Capacitance was recorded before and after break-in to the cell; the capacitance of each single chondrocyte was taken as the difference in these capacitance values. Drugs were delivered to cells with a multi-barreled local superfusion device that changed the solution around a cell within <1 s. All experiments were carried out at room temperature (20–22°C).

In the second experimental part of this study, after obtaining the data that characterized the predominant K⁺ currents in enzymatically isolated human chondrocytes, we analyzed TRP channel mediated currents (Figures 8, 9) using a different source human articular chondrocytes. These cells were from a chondrocyte preparation made available by Glaxo Smith Kline Ltd (GSK) (Balakrishna et al., 2014). GSK cells that were cultured from frozen samples of primary cells (batches #1060, #1274). The culture medium was DMEM/F12, supplemented with 10% fetal calf serum, 2 mM L-glutamine and penicillin/streptomycin (1:10). These chondrocytes were used up to a maximum of 6 days after plating and were not passaged. TRP channels were activated or blocked using proprietary compounds that were obtained from Glaxo Smith Kline; GSK Ltd. (Thorneloe et al., 2008; Hilfiker et al., 2013).

The Atypical Microenvironment of the Chondrocyte

In adult mammals, the chondrocyte cell population is in a physiological environment, the articular joint fluid that differs significantly from that of most other cells in healthy human tissues. A number of these important differences are listed in Table 1. Note that the extracellular fluid within the articular joint is hypertonic (~320 mOsm vs. blood plasma, ~280 mOsm). In addition, the extracellular pH, i.e., that of the synovial fluid that bathes the chondrocyte is somewhat acidic, pH 7.2; and the extracellular [K⁺]_o levels are significantly elevated measuring ~10–15 mM, as opposed to 4.0–5.4 mM [K⁺]_o in normal mammalian plasma (Huber et al., 2000; Wilkins et al., 2000a). Nevertheless, the main large transmembrane electrochemical gradients for Na⁺, K⁺, and Cl⁻ in chondrocytes are quite similar to those in other mammalian cells. Establishment and maintenance of these gradients leads to the requirement for an ATP-dependent Na⁺/K⁺ pump mechanism (assumed to be electrogenic). This maintains ionic homeostasis and stabilizes cell volume. Evidence for expression of a Na⁺/K⁺ ATPase has been obtained in bovine articular chondrocytes (Mobasheri et al., 1997). It is also known that glucose is the major energy substrate for articular chondrocytes and that these cells express Glut1 and Glut3 glucose transporter (Phillips et al., 2005). The Mobasheri Group (Mobasheri et al., 2008) have also reported that the expression, distribution and function of these facilitative glucose transporters are regulated significantly by hypoxia, inflammation, or altered complements of articular joint growth factors.

TABLE 1

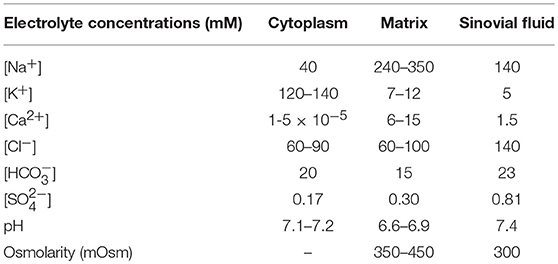
Table 1. Ion concentrations in compartments within the mammalian knee joint (see Ref. Hall et al., 1996) (adapted from Table 1 in Wilkins et al., 2000a).

The fixed negative charges on proteoglycans of the extracellular matrix are in the immediate vicinity of the chondrocyte and can attract cations (e.g., Na⁺), while also excluding anions. As a result, localized cation accumulation occurs (Table 1), and for this reason there is a significant osmotically driven water influx (Urban et al., 1993; Wilkins et al., 2000a; Lewis et al., 2011). In addition, intrinsic characteristics of the “pericellular matrix” on the immediate surface of each chondrocyte can serve as a significant diffusion barrier, as demonstrated recently with the use of optical trap methods (McLane et al., 2013). It is also important to note that the literature now suggests that the relevant functional unit of the chondrocyte is the chondron. It includes the cell (chondrocyte) and its glycocalyx or pericellular coat (Muir, 1995; Poole, 1997; Guilak et al., 2006).

The articular joint receives only very limited blood supply. Accordingly, the synovial fluid must supply adult articular cartilage with the required (small amounts of) nutrients, as well as sufficient oxygen to maintain Na⁺/K⁺ pump activity and ensure intracellular Ca²⁺, [Ca²⁺]_i, homeostasis (Mobasheri et al., 1997; Mobasheri, 1998; Chao et al., 2006). Metabolic byproducts are removed mainly by diffusion (Urban et al., 1993; Wilkins et al., 2000b). An important consequence of the “avascular” nature of this articular joint tissue is that chondrocytes generate ATP by substrate-level phosphorylation during anaerobic respiration (Guilak et al., 1997). This generates H⁺ ions as a byproduct, and this tends to acidify the pH in this micro-environment. The dynamic changes in mechanical loading within the knee joint during activity also expose chondrocytes to very significant fluctuations in vector and shear forces. The resulting mechanical changes can activate mechano-or shear-sensitive ion channels (Hall et al., 1996; Lane Smith et al., 2000; Mouw et al., 2006).

Model Development

We have developed a new, first generation mathematical model for the resting membrane potential, E_m, of the chondrocyte, based partly on the experimental data obtained and described in section Electrophysiological Studies. This includes (a) K⁺ currents, (b) time-independent currents, (c) pump and exchanger currents, and (d) intracellular Ca²⁺ buffering. These components are illustrated in Figure 1 and are described in detail in following sections. The transmembrane ion transport processes include: I_K−DR, a voltage-dependent delayed rectifier K⁺ channel; I_K−Ca, voltage and internal Ca²⁺-dependent K⁺ channel; I_K−2p, a two-pore K⁺ channel; I_K−ATP, ATP-dependent K⁺ channel; I_Na,b, a time-independent “background” Na⁺ channel; I_K,b, a time-independent “background” K⁺ channel; I_Cl,b, a time-independent “background” Cl⁻ channel; I_NaK, ATP-dependent electrogenic Na⁺-K⁺ pump; I_NaCa, electrogenic Na⁺-Ca²⁺ exchanger; I_NaH, the transmembrane Na⁺ flux of the electroneutral Na⁺-H⁺ antiporter; I_Ca,ATP, electroneutral ATP-dependent Ca pump; and I_TRPV4, cation permeable TRPV4 ion channel. In this model, intracellular Ca²⁺ is buffered by binding to calmodulin.

FIGURE 1

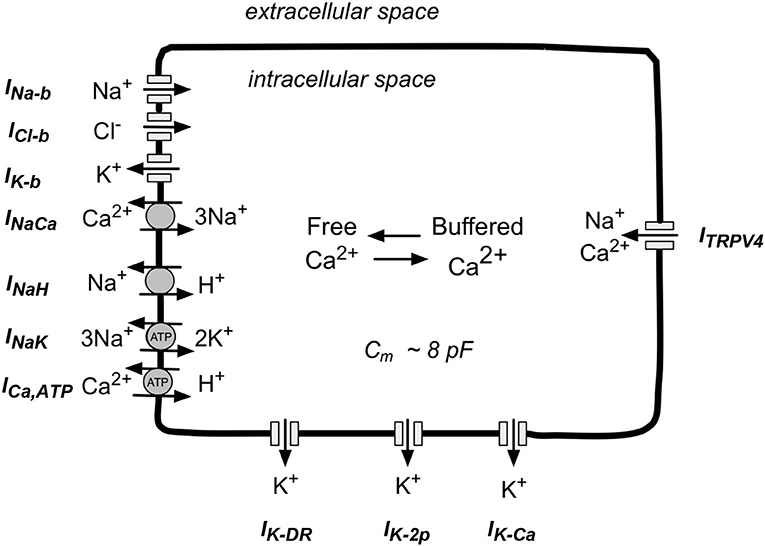
Figure 1. Schematic illustration of the main ion selective channels, ion exchange proteins, and ATP-dependent ion pumps that are known to be expressed in human chondrocytes. This information forms the basis for our mathematical model of chondrocyte K⁺ transport and resting potential, E_m. The three ion selective channels labeled at the top left of this diagram are so-called background channels; these currents show no time dependence. The three types of ion channels shown on the bottom are the focus of this paper. These K⁺-selective channels in human chondrocytes, have been studied in detail in our Laboratory and by other groups (see section Results). The ion-selective pumps and exchangers shown at the bottom left are necessary to maintain volume, and contribute to electrolyte homeostasis in the human chondrocyte. The TRPV4 channels shown on the right can allow Na⁺ and Ca²+ influx. In addition, (see section Discussion) chondrocytes can exhibit cell-to-cell coupling via connexin-mediated ion and metabolite transfer, and/or “hemichannel behavior” (see section Discussion).

The equation governing the transmembrane potential, V, of the chondrocyte is

$\begin{array}{l}{C}_m\frac{dV}{dt}=-(I_{K-DR}+I_{K-Ca}+I_{K-2p}+I_{K-ATP}+I_{Na,b}+I_{K,b}\\ +I_{Cl,b}+I_{NaK}+I_{NaCa}+I_{TRPV4})& (1)\end{array}$

where C_m is chondrocyte capacitance (8 pF). This equation includes all transport processes that are electrogenic i.e., generate net transmembrane current(s).

The intracellular concentrations of Na⁺, [Na⁺]_i and K⁺, [K⁺]_i, are governed by two transport equations, namely,

$\begin{array}{ll}\frac{d{\left[N{a}^{+}\right]}_i}{dt}=\frac{-(I_{Na,b}+3I_{NaK}+{3I}_{NaCa}-I_{NaH})}{vo{l}_{i}F}& (2)\end{array}$

and

$\begin{array}{ll}\frac{d{\left[K^{+}\right]}_i}{dt}=\frac{-(I_{K,b}-2I_{NaK}+I_{K-DR}+I_{K-2p}+I_{K-Ca}+I_{K-ATP})}{vo{l}_{i}F}& (3)\end{array}$

where vol_i is the internal volume of the chondrocyte (calculated to be 0.005884 mL), and F is the Faraday constant, 96,485 C/mol. Note that Equation (1) does not include I_NaH, since this is the Na⁺ flux generated by the electroneutral Na⁺-H⁺ antiporter, but this term is included in the Na⁺ homeostasis Equation (2). Equations (2) and (3) specify how the intracellular concentrations of Na⁺ and K⁺ evolve with time, and also how the Nernst potentials for Na⁺, and for K⁺, change with time. R = 8.314 J K⁻¹ mol⁻¹ is the universal gas constant, T = 310.15 is body temperature in deg. Kelvin, and z_Na = 1 and z_K = 1 are ionic valances for Na⁺ and K⁺, respectively. The extracellular concentrations of Na⁺, [Na⁺]_o, and K⁺, [K⁺]_o, are held constant during each simulation. However, some simulations were done after changing these values to those that are more representative of the physiological milieu of the chondrocyte, (shown in Table 1), rather than those set by our experimental superfusate for the patch-clamp experiments.

Intracellular Ca²⁺ concentration, [Ca²⁺]_i, also changes with time, due to transmembrane transport of Ca²⁺ by the Na⁺-Ca²⁺ exchanger and ATP-dependent Ca²⁺ pump, and intracellular calmodulin binding, according to the equation:

$\begin{array}{ll}\frac{d{\left[C{a}^{2+}\right]}_i}{dt}=\frac{(I_{NaCa}-I_{Ca,ATP})}{vo{l}_{i}F}-0.045\frac{d{O}_c}{dt}& (4)\end{array}$

where O_c is the fraction of intracellular calmodulin bound to Ca²⁺ (see Equation 39).

Differential equations (1–4) and those for I_K,Ca and calmodulin buffering were solved numerically. All data simulations and processing was performed off-line using both noncommercial and commercial software packages (Radhakrishnan and Hindmarsh, 1993; Maleckar et al., 2009; Eaton et al., 2014), as well as custom, in-house scripts. The software that is the basis of our model of the chondrocyte resting membrane potential is available on request.

Results

Ion-Selective Transmembrane Currents

Potassium Currents

We have identified and partially characterized three different K⁺ currents in mammalian chondrocytes. In principle, each of these can contribute to the resting membrane potential, E_m, either at baseline or following selective activation/enhancement by physiological stimuli or pathophysiological conditions. These K⁺ currents are: (i) a time-and voltage dependent delayed rectifier K⁺ current, I_K−DR; (ii) a K⁺ current due to 2-pore K⁺ channels, I_K−2p; and (iii) a large conductance voltage and Ca²⁺-activated K⁺ current, I_K−Ca, have been studied in some detail in our laboratory (Wilson et al., 2004; Clark et al., 2010, 2011, respectively) and also by other groups (for reviews, see Grandolfo et al., 1992; Mobasheri et al., 2007, 2012; Barrett-Jolley et al., 2010; Asmar et al., 2016). An ATP-dependent K⁺ current (I_K−ATP) has also been identified in patch clamp studies published by other investigators (cf. Mobasheri et al., 2007).

A typical pattern of K⁺ currents from our patch clamp recordings using single isolated human articular chondrocytes (denoted HAC) is illustrated in Figure 2A. This chondrocyte first held at −80 mV, and then the membrane potential was stepped to selected levels between −100 and +110 mV, in 10 mV increments at a rate of 0.2 Hz. Three consistent features are noteworthy: (i) over much of this membrane potential range, the currents showed no obvious time- and voltage dependence, (ii) after being activated, these currents became much greater in amplitude and showed larger fluctuations with increasingly depolarized membrane voltages; (iii) large, very noisy outward currents began to appear at about +60 mV.

FIGURE 2

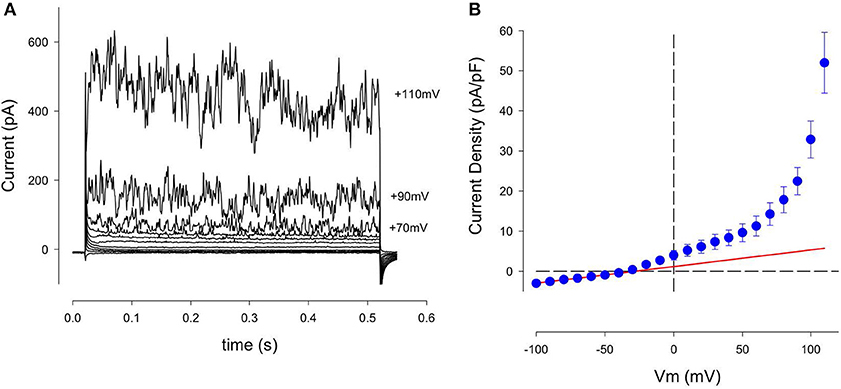
Figure 2. Family of K⁺ currents recorded from an isolated human chondrocyte maintained in primary 2D culture conditions. (A) These currents were recorded from a chondrocyte that was held at −80 mV, and then stepped to membrane potentials between −100 and +110 mV, in 10 mV increments. Current records are shown between −90 and +100 mV, (in 20 mV increments). This chondrocyte had been in culture for 3 days; its capacitance, C_m, was 7.3 pF. Panel (B) is an averaged current-voltage (I–V) relation for 13 cells, (1 day in culture). Currents recorded from each cell were normalized to cell capacitance before averaging. Solid red trace is the best-fit straight line between −100 and −50 mV. Its slope is 0.042 nS/pF. Mean ± s.e.m. C_m of 13 cells was 7.4 ± 0.8 pF.

Figure 2B consists of an averaged isochronal current-voltage (I–V) relationship based on data obtained from 13 human chondrocytes, each studied after 1 day in cell culture. The magnitude of these K⁺ currents was normalized to the capacitance of each cell in order to compensate for differences in cell size. Note that this I–V relationship is approximately linear at membrane potentials negative to about −50 mV but becomes non-linear at more depolarized voltages. The solid red trace shows the best-fit straight line for the data between −50 and −100 mV, extrapolated over the entire potential range of the I–V plot. The nonlinearity at depolarized membrane potentials is mainly due to increases in the noisy outward current. This feature is very evident at membrane potentials positive to about +60 mV. Note also that there is a small non-linearity in the I–V between ~−40 and +50 mV. This suggests that another component of outward current might be present in these single HAC preparations.

Delayed rectifier K⁺ current: I_K-DR

A conventional time- and voltage-dependent delayed rectifier K⁺ current has been identified in mouse, canine, rabbit, and human articular chondrocytes under primary culture conditions (Wilson et al., 2004; Barrett-Jolley et al., 2010; Clark et al., 2010). Our previous analysis of ion selectivity, as judged by reversal potential measurements, has shown that this current, denoted I_K−DR, is carried mainly by K⁺ (Wilson et al., 2004; Clark et al., 2010). Moreover, the biophysical properties of this current and its pharmacological blockade suggested that it is generated by a well-known Kv1.x conductance family, perhaps Kv1.5 or Kv1.6.

The presence of this small time- and voltage-dependent current in these human chondrocyte (HAC) preparations was revealed more clearly when the linear leak and capacity currents were removed from the raw current records (see Methods section). An example of current records from one HAC preparation in which these correction procedures were used is shown in Figure 3. The records in Figure 3A clearly reveal the time- and voltage-dependent properties of the relatively small component of outward current that is activated at membrane potentials positive to ~-40 mV. The rate of activation of this current increases significantly with progressively larger depolarizations. Note, however, these K⁺ currents showed no inactivation during the 500 ms voltage-clamp steps. In summary, the properties of this current resembled the “delayed rectifier” K⁺ current, I_K−DR that we and others have reported previously from studies in chondrocytes from other species (Wilson et al., 2004; Clark et al., 2010). Not all isolated human chondrocytes expressed this type of “delayed-rectifier” K⁺ current. As an example, in one group of 13 HAC studied after 1 day in culture, only 8 cells expressed a detectable I_K−DR. In a second group of 12 HAC studied after 3 days in culture, only 4 cells expressed I_K−DR. These findings suggest that there is intrinsic variability in the expression of this K⁺ current; and/or that its expression may decrease with time in culture (see section Discussion). Figure 3B shows a plot of I_K−DR conductance vs. membrane voltage, E_m, for 16 cells. The I_K−DR conductance values were obtained by dividing peak I_K−DR by the electrochemical driving force. (EMF), which is defined as the membrane potential, V, minus the Nernst potential for K⁺, E_k (~−83 mV under the experimental recording conditions). The best-fit Boltzmann relationship (red line) in Figure 3B yields a descriptor of the voltage dependent activation of this K⁺ current. I_K−DR was described by the following expression, as we have published previously (Maleckar et al., 2009);

$\begin{array}{ll}{I}_{K-DR}=g_{K-DR}{\alpha }_{KDr}(\text{V}-{\text{E}}_{\text{K}})& (5)\end{array}$

where

FIGURE 3

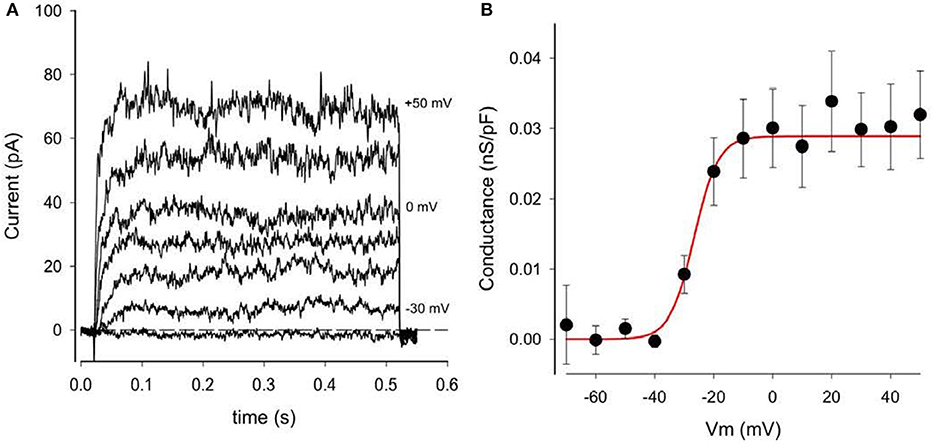
Figure 3. Delayed rectifier K⁺ currents, I_K−DR, in a human chondrocyte. (A) Examples of I_K−DR activated by voltage-clamp steps from holding potential of −80 mV to membrane potentials of −40, −30, −20, −10, 0, +20, and +50 mV. Records have been corrected for capacity and linear leak currents. (B) Plot of I_K−DR peak conductance (per pF) vs. membrane voltage, V. Conductance was obtained by dividing peak I_K−DR by (V-E_K), where E_K is K⁺ Nernst potential (−83 mV). Data from 16 cells (mean ± SEM). The best-fit Boltzmann relationship (red line) is the factor αK-DR (Equation 2).

g_K−DR is the maximal I_K−DR conductance, namely 0.0289 nS/pF from Figure 3B, and

α_KDr is a voltage-dependent activation factor, given by the expression

$\begin{array}{ll}{\alpha }_{KDr}=\frac{1.0}{(1.0+e^{\frac{-(V+26.7)}{4.1}}}& (6)\end{array}$

Note that the extracellular potassium concentration, [K⁺]_o, was initially set to 5.4 mM under “typical” physiological conditions. In fact, however, [K⁺]_o is likely to be in the 5–15 mM range in the microenvironment of the chondrocyte in situ (see Table 1). Intracellular K⁺ concentration was initially set to 140 mM in this parameterization of the model, but evolves through time, governed by Equation (3).

Ca²⁺-activated K⁺ current: I_K−Ca

The prominent fluctuations in outward current traces recorded from all human chondrocytes at strongly depolarized membrane potentials suggested the expression of this “large” variant of Ca²⁺-activated K⁺ channels (“BK,” KCa1.1). It is well-known that the voltage dependent gating of these BK channels is strongly modulated by the intracellular Ca²⁺ concentration, [Ca²⁺]_i (cf. Horrigan and Aldrich, 2002; Magleby, 2003; Berkefeld et al., 2006, 2010; Barrett-Jolley et al., 2010; Mobasheri et al., 2012; Asmar et al., 2016). In the experimental results in Figure 2 [Ca²⁺]_i was held very low (<10 nM) by using a patch pipette solution containing no added Ca²⁺, combined with a strong Ca²⁺ buffer (10 mM EGTA). In the presence of this very low [Ca²⁺]_i, these BK channels can be activated only by very strong voltage clamp depolarizations (e.g., >+40 mV).

To more clearly reveal the functionally important properties of this BK current, additional experiments were carried out using a pipette solution containing 3 mM Ca²⁺ and 10 mM EGTA, which yielded a nominal free Ca²⁺ concentration of ~175 nM. Data from these experiments are summarized in Figure 4. Currents from two groups of HAC's, one with “low” internal Ca²⁺ solution, and one with “high” Ca²⁺, are shown in Figures 4A,B, respectively. It is clear that the “noisy” outward currents were much larger in the presence of “high” [Ca²⁺]_i compared with “low.” Figure 4C compares pooled I–V data from subsets of HAC preparations perfused internally with either “low” or “high” internal [Ca²⁺]_i. All of these chondrocytes were from the same batch, and recordings were made after 1 day in conventional 2D cell culture. As expected for currents generated by BK channels the large, fluctuating outward currents recorded from chondrocytes with “high” [Ca²⁺]_i were activated at considerably more negative membrane potentials than from chondrocytes with “low” [Ca²⁺]_i (Horrigan and Aldrich, 2002; Berkefeld et al., 2010). Moreover, the maximum current (measured at +100 mV) was several times larger in the “high” [Ca²⁺]_i chondrocytes. These results strongly suggest that a Ca²⁺-activated current I_K−Ca, produced by the so-called BK channels, is an important component of K⁺ current in these cultured HAC cells (Magleby, 2003; cf. Sun et al., 2009).

FIGURE 4

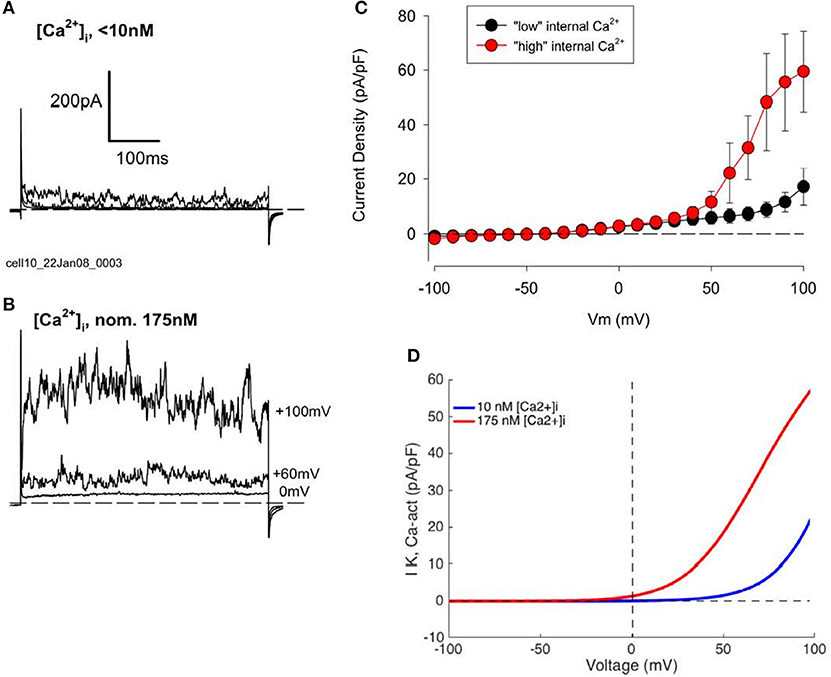
Figure 4. Effect of changes in intracellular Ca²⁺, [Ca²⁺]_i, concentration on K⁺ currents in human articular chondrocytes. (A) Example of currents from a HAC with “low” internal [Ca²⁺]_i (0 [Ca²⁺]_i, 10 mM EGTA). Currents produced by voltage steps to 0, +60, and +100 mV from a holding potential of −80 mV are shown. C_m = 9.72 pF. (B) Currents from a cell with “high” internal [Ca²⁺]_i (3 mM added Ca²⁺, 10 mM EGTA; nominal Ca²⁺ concentration = 175 nM). Voltage-clamp steps were to 0, +60, and +100 mV. C_m = 6.24 pF. Currents in (A,B) were not leak or capacity current corrected. (C) I–V relations for groups of HAC with “low” (n = 5, blue) and “high” (n = 4, red) [Ca²⁺]_i patch-clamp solution. These chondrocytes were all from same batch, 1 day in culture. (D) Model I–Vs for I_K−Ca, with different internal [Ca²⁺] levels (from Equation 4).

It is well-known that the molecular properties and biophysical characteristics of the extensive Ca²⁺ activated K⁺ channel family can be used to divide them into three sub-groups (Berkefeld et al., 2010). Defining characteristics include: (i) the specific biophysical properties of the current (e.g., its voltage dependence), (ii) their pharmacological profile (e.g., sensitivity to block by apamin or tetraethylammonium, TEA), or (iii) the single channel conductance. In the case of human chondrocytes (as shown in Figures 2, 3) the pronounced current fluctuations (noise) strongly suggest the presence of the variant of Ca²⁺ activated K⁺ channels known as the large conductance subtype, BK. The major properties of this current (cf. Horrigan and Aldrich, 2002) have been incorporated into a detailed mathematical model developed by Sun et al. (2009).

The mathematical description for this Ca²⁺-activated K⁺ current is a 10-state kinetic Markov-type model, including four calcium-binding steps, with all the voltage dependence assigned to the transitions between closed and open states, i.e., the C-O equilibrium:

$\begin{array}{ll}\frac{d{C}_O}{dt}={\beta }_O{O}_o-{\alpha }_O{C}_o+K_c{C}_1-{4CaC}_o& (7)\end{array}$

$\begin{array}{ll}\frac{d{C}_1}{dt}={\beta }_1{O}_1-{\alpha }_1{C}_1-K_c{C}_1+{4CaC}_o-{3CaC}_1+{2K_{c}C}_2& (8)\end{array}$

$\begin{array}{ll}\frac{d{C}_2}{dt}={\beta }_2{O}_2-{\alpha }_2{C}_2-{2K}_c{C}_2+{3CaC}_1-{2CaC}_2+{3K_{c}C}_3& (9)\end{array}$

$\begin{array}{ll}\frac{d{C}_3}{dt}={\beta }_3{O}_3-{\alpha }_3{C}_3-{3K}_c{C}_3+{2CaC}_2-{CaC}_3+{4K_{c}C}_4& (10)\end{array}$

$\begin{array}{ll}\frac{d{C}_4}{dt}={\beta }_4{O}_4-{\alpha }_4{C}_4-{4K}_c{C}_4+{CaC}_3& (11)\end{array}$

$\begin{array}{ll}\frac{d{O}_0}{dt}={-\beta }_0{O}_0+{\alpha }_0{C}_0+K_0{O}_1-4{CaO}_0& (12)\end{array}$

$\begin{array}{ll}\frac{d{O}_1}{dt}={-\beta }_1{O}_1+{\alpha }_1{C}_1-K_o{O}_1+{4CaO}_o-{3CaO}_1+{2K_{o}O}_2& (13)\end{array}$

$\begin{array}{ll}\frac{d{O}_1}{dt}={-\beta }_2{O}_2+{\alpha }_2{C}_2-{2K}_o{O}_2+{3CaO}_1-{2CaO}_2+{2K_{o}O}_3& (14)\end{array}$

$\begin{array}{ll}\frac{d{O}_3}{dt}={-\beta }_3{O}_3+{\alpha }_3{C}_3-{3K}_o{O}_3+{2CaO}_2-{CaO}_3+{4K_{o}O}_4& (15)\end{array}$

$\begin{array}{ll}\frac{d{O}_4}{dt}={-\beta }_4{O}_4+{\alpha }_4{C}_4-{4K}_o{O}_4+{CaO}_3& (16)\end{array}$

where C_{n = 0,1,2,3,4} and O_{n = 0,1,2,3,4} are closed and open states 1 through 4, respectively, with the total open probability corresponding to the sum of the open states, O; α_{n = 0,1,2,3,4} represent rates corresponding to transition from a closed to an open state and β_{n = 0,1,2,3,4} represent rates corresponding to transition from an open to a closed state; K_o and K_c are off-rates from open and closed states, respectively, and Ca is the calcium on-rate, where

$\begin{array}{ll}{\alpha }_n={A_{n}e}^{\frac{z_{CO}VF}{RT}}& (17)\end{array}$

$\begin{array}{ll}{\beta }_n={B_{n}e}^{\frac{z_{OC}VF}{RT}}& (18)\end{array}$

A₀ = 0.659, A₁ = 3.955, A₂ = 25.05, A₃ = 129.2, A₄ = 261.1;

B₀ = 2651.7, B₁ = 1767.8, B₂ = 1244.0, B₃ = 713.0, B₄ = 160.0;

z_CO = 0.718, z_OC = 0.646, K_c = 13.5, K_O = 1.5,

and the Ca²⁺ on-rates per site are 10⁹ M⁻¹s⁻¹, Ca²⁺ off-rates from C_n per binding site are 10⁹ K_C (13,500 s⁻¹) and Ca²⁺ off-rates from O_n per binding site are 10⁹ K_O (1,500 s⁻¹), and R is the universal gas constant, = 8.314 J K⁻¹ mol⁻¹ and T = 310.15 is body temperature in Kelvin.

I_K−Ca is then defined by:

$\begin{array}{ll}{I}_{K-Ca}={\text{g}}_{K-Ca}\text{O}(\text{V}-{\text{E}}_{\text{K}})& (19)\end{array}$

where g_K−Ca is the maximal conductance of the channel, equal to 2.50 nS/pF, O is the total open probability as given above, V is the transmembrane potential, and E_K is the Nernst potential for potassium.

We have used this mathematical formalism to compute I–V relationships for BK currents that can assumed to have been recorded from isolated human chondrocytes under conditions in which the composition of the pipette solution was adjusted (buffered) so that the [Ca²⁺]_i was ~10⁻⁸ M. In this situation, this K⁺ current can be activated at only very positive membrane potentials. In contrast, when [Ca²⁺]_i was increased to ~175 nM this Ca²⁺-activated K⁺ current activates at much less strongly depolarized membrane potentials, as shown by the computations summarized in Figure 4D.

Further information regarding the functional properties of this BK channel-mediated current was obtained using conventional pharmacological approaches. As shown in Figure 5 this K⁺ current can be blocked completely by concentrations of TEA that are known to quite selectively inhibit these BK channels. This pattern of results provides further evidence for the consistent and potentially prominent expression of this K⁺ current in human articular chondrocytes.

FIGURE 5

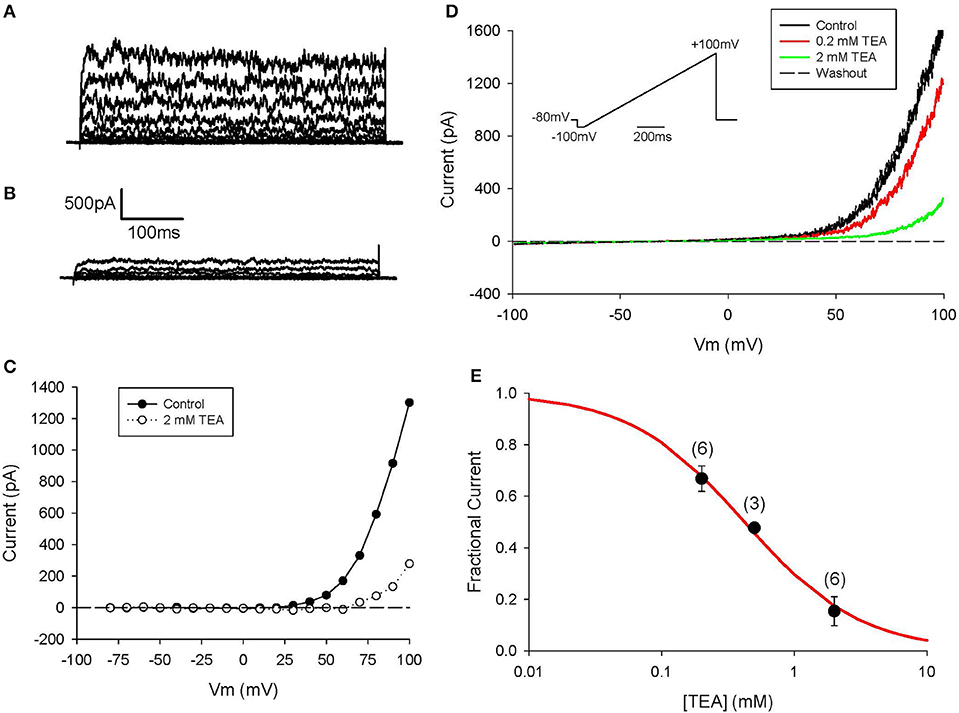
Figure 5. Block of I_K−Ca in human chondrocyte by TEA. (A) Control currents. The voltage-clamp protocol consisted of 500 ms steps from h.p. −80 to +100 mV. Linear leak and capacitive currents were removed using a P/3 protocol. (B) Currents in presence of 2 mM TEA. (C) I–V relations for control and TEA currents in (A,B). (D) Currents in response to a ramp protocol (inset), in control and in presence of 0.2 and 2 mM TEA. Same cell as (A,B). Cell capacitance was 12.0 pF; 3 days in culture. (E) Dose-response for TEA pooled from 3 to 6 cells (indicated above each data point). Each current amplitude was measured at +100 mV. Solid line is best-fit binding equation, with K_m = 0.42 mM.

Although, I_K−Ca is a major outward current in human chondrocytes, it apparently does not contribute substantially to the resting potential under our conditions. This is because of the following: the input resistance of the human chondrocyte is very high (~5–10 GΩ); and under this circumstance, activation of a small number of these Ca²⁺ activated K⁺ channels would give rise to a resting potential that would be characterized by significant fluctuations in membrane voltage. Activation of these large conductance K⁺ channels is not consistent with recordings of resting membrane potential in the region of −40 mV (see Discussion section).

2-Pore K⁺ current: I_K−2P

Our previous work (Clark et al., 2011) defined recording conditions under which a K⁺ current generated by the TASK family of two-pore K⁺ channels could be identified consistently in single chondrocytes. This apparently very small current, that we denote I_K−2p, exhibits no detectable time dependence (Goldstein et al., 2001). It is known that certain 2-pore K⁺ currents (including the TASK variants) are augmented by an increase in pH (alkalinization) of the extracellular medium (Patel and Honoré, 2001; Cid et al., 2013) and can be blocked by some local anesthetics (Kindler and Yost, 2005; Webb and Ghosh, 2009).

We have recorded this K⁺ current under high [K⁺]_o conditions, to ensure that the current changes are relatively large, so that their biophysical properties can be resolved. However, before these results can be put into a functional context, or incorporated into a mathematical model of human chondrocyte electrophysiology, they need to be corrected (scaled) to physiological conditions (i.e., normal [K⁺]_o levels). This can be done based on the Eisenman principle (cf. Hille, 2001): the conductance of an ion-selective channel scales according to the square root of the extracellular concentration of the permeant ion. Accordingly, I_K−2p is described by the classical Goldman-Hodgkin-Katz equation for a single ion species, with a square-root scaling factor to account for [K⁺]_o:

$\begin{array}{ll}{I}_{K-2p}=\frac{P_k{z}^{2}V{F}^2}{RT}\frac{\left({\left[K^{+}\right]}_i-{\left[K^{+}\right]}_o{e}^{\frac{-zVF}{RT}}\right)}{\left(1-e^{\frac{-zVF}{RT}}\right)}& (20)\end{array}$

where P_K is a [K⁺]-dependent scaling factor that describes the permeability (conductance) for this K⁺ current, namely 3.1x10⁻⁶ √([K⁺]_i/[K⁺]_o), and z = 1 is the ionic valence for potassium.

The I–V relationship in Figure 6A shows that our primary data (Wilson et al., 2004) recorded in isotonic [K⁺] (~145 mM), has the expected reversal potential (of 0 mV). The I–V relationship based on Equation (20) was fitted to the data. This fit determined the magnitude of P_K. Figure 6B shows the model I–V when [K⁺]_o is an assumed normal [K⁺]_o of 5.4 mM, with a corresponding reversal potential of ~−83 mV.

FIGURE 6

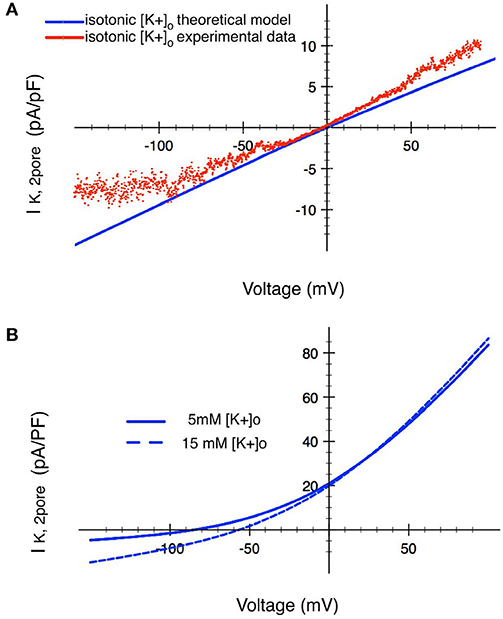
Figure 6. Analysis of the ion transfer function (I–V relationship) for a 2-pore K⁺ current in human chondrocytes. (A) Raw experimental data plotted as an I–V curve together with a superimposed I–V relationship (red trace) based on the mathematical formulation given in the text. These results were obtained in isotonic [K⁺]o conditions. The two traces in (B) show corresponding I–V relationships derived using the Eisenman Principle, so that this K⁺ current can be studied in conditions ([K⁺]o of 5 mM and 15 mM) that are in the physiological range. The blue trace shows the I–V relationship for this 2-pore K⁺ channel when [K⁺]o is 15 mM. The black trace shows the change in this ion transfer relationship when [K⁺]o is decreased to 5 mM. (see Table 1 and section Discussion).

As illustrated in Table 1, the extracellular milieu of the chondrocyte is somewhat unusual, since it has been reported to have a [K⁺]_o level of ~7–12 mM. Accordingly, a I–V curve for the 2-pore or TASK K⁺ current was also calculated assuming a [K⁺]_o of 15 mM, as shown by the broken trajectory in Figure 6B. We have previously reported (Wilson et al., 2004) that this K⁺ current is strongly inhibited by the anesthetic bupivacaine; and that an effective concentration of bupivacaine resulted in a significant depolarization of the resting potential (see section Discussion and Kindler and Yost, 2005; Webb and Ghosh, 2009).

ATP-sensitive K⁺ current: I_K−ATP

An ATP-sensitive K⁺ current I_K−ATP has been identified in chondrocytes that were isolated from the knee joint of a number of different mammalian species (Barrett-Jolley et al., 2010; Mobasheri et al., 2012; Asmar et al., 2016). Our previous experimental work in human articular chondrocytes (Clark et al., 2011) did not reveal any significant I_K−ATP. A likely reason for this is that the intracellular ATP/ADP ratio is set by the “internal pipette solution” in these electrophysiological experiments, and these conditions are such that I_K−ATP is unlikely to be activated. However, a relatively low ATP/ADP ratio that is prevalent in the somewhat hypoxic environment of the chondrocyte in articular joints makes it likely that I_K−ATP in fact will be activated during physiological biomechanical activity. Thus, a validated but general mathematical expression for this time-independent current (I_K−ATP) has been included in our mathematical model of the chondrocyte resting potential. This expression scaled to the I_K−ATP experimental data published by Mobasheri et al. (2007, 2012). An ATP-dependent K⁺ current simulated using to Equation (21) below is illustrated in Figure S1.

$\begin{array}{ll}{I}_{K-,ATP}=\sigma g_o{p}_o{f}_{ATP}(V-E_K)& (21)\end{array}$

where σ = 0.6 is the channel density, g_o is the unitary channel conductance, p_o = 0.91 is the maximum open channel probability, and f_ATP is the fraction of activated channels, given by:

$\begin{array}{ll}{f}_{ATP}=\frac{1.0}{1.0+{\left[\frac{AT{P}_i}{K_m}\right]}^H}& (22)\end{array}$

$\begin{array}{ll}H=1.3+0.74e^{-H_{K_{ATP}}AD{P}_i}& (23)\end{array}$

$\begin{array}{ll}{K}_m=35.8+17.9{AD{P}_i}^{K_{m,ATP}}& (24)\end{array}$

$\begin{array}{ll}{\text{ADP}}_{\text{i}}={\text{C}}_{\text{A}}-{\text{ATP}}_{\text{i}}& (25)\end{array}$

where C_A = 8 mM is the total concentration of adenine nucleotides, ADP_i and ATP_i are the intracellular concentrations of adenosine diphosphate, (ADP) and adenosine triphosphate, (ATP) respectively, H_K,ATP = −0.001, and K_m,ATP = 0.56.

Note that this ATP-sensitive K⁺ current is not utilized in our initial description of the ionic basis for the HAC resting potential. That is, its channel density, σ, has been set to zero in our initial or first order model parameterization.

Time-Independent or Background Ionic Currents

Three distinct time-independent background (or leakage) conductances corresponding to “resting” Na⁺, K⁺, and Cl⁻ fluxes, have been included in this model. Simple mathematical descriptors for each conductance have been formulated, and each yields a linear I–V relationship.

The background (inward) Na⁺ and (outward) K⁺ currents, are described by.

$\begin{array}{ll}{I}_{Na,b}=G_{Na,b}(V-E_{Na})& (26)\end{array}$

$\begin{array}{ll}{I}_{K,b}=G_{K,b}(V-E_K)& (27)\end{array}$

where G_Na,b = 0.1 nS/pF is the maximum conductance for the background sodium channel, and G_K,b = 0.07 nS/pF is the maximum conductance for the background potassium channel. [Na⁺]_o was initially set to 130 mM under “typical” physiological conditions, but in the environs of the chondrocyte may be in the range shown in Table 1. [Na⁺]_i, was initially set to 8 mM in this parameterization of the model, and evolves through time, governed by Equation (2), hence E_Na also changes with time. Similarly, [K⁺]_o was set to “typical” physiological conditions, 5.4 mM, but is likely to be higher in the chondrocyte's environment (Table 1). [K⁺]_i was initially set to 140 mM, but this concentration evolved according to Equation (3), thus also changing E_K.

In mammalian chondrocytes from a number of different species, a significant background Cl⁻ conductance has also been identified (cf. Tsuga et al., 2002; Barrett-Jolley et al., 2010; Funabashi et al., 2010a; Kurita et al., 2015). We have incorporated this type of Cl⁻ current by formulating it as a linear time-independent current, specified by the equations below:

$\begin{array}{ll}{I}_{Cl,b}=G_{Cl,b}(V-E_{\text{Cl}})& (28)\end{array}$

where G_Cl,b = 0.05 pS/pF is the maximum conductance for the background Cl⁻ channel, and where the reversal potential, is −65 mV. The I–V relationships for these three background currents are shown in Figure S2.

Ion Pump and Exchanger Currents

Electrogenic Na⁺/K⁺ pump: I_NaK

Active (ATP requiring) extrusion of Na⁺ from chondrocytes is assumed to be achieved by the combined expression level and turnover rate of a conventional electrogenic Na⁺/K⁺ pump. Mobasheri et al. (1997, 1998) have characterized some of the functional properties of an electrogenic Na⁺/K⁺ pump in bovine articular chondrocytes. Our model makes use of the Na⁺/K⁺ pump formulation from Nygren et al. (1998):

$\begin{array}{l}{I}_{NaK}={\overline{I}}_{NaK}\left(\frac{{\left[K^{+}\right]}_o}{{\left[K^{+}\right]}_o+k_{Na{K}_K}}\right)\left(\frac{{\left[N{a}^{+}\right]}_i^{1.5}}{{\left[N{a}^{+}\right]}_i^{1.5}+k_{Na{K}_{Na}}^{1.5}}\right)\\ \left(\frac{V+150}{V+200}\right)& (29)\end{array}$

where ${\overline{I}}_{NaK}$ is the maximal current density 1.58 pA/pF [K⁺]_o is the extracellular potassium concentration. It has been initially set to 140 mM for “typical” values; Table 1), [Na⁺]_i is the intracellular sodium concentration, as defined previously, and given by equation (2), k_NaK,K is the half-maximum K⁺ binding concentration, and k_NaK,Na is half-maximum Na⁺ binding concentration, with values of 1.0 and 11.0 mmol/L, respectively.

This Na⁺/K⁺ pump activity (the product of expression density and turnover rate) generates a small outward electrogenic current. In this simplified model (cf. Trujillo et al., 1999) this Na⁺/K⁺ pump magnitude has been scaled to achieve a steady-state [Na⁺]_i of 10–12 mM. Representative ion transfer relationships for this I_Nak are shown in Figure 7A.

FIGURE 7

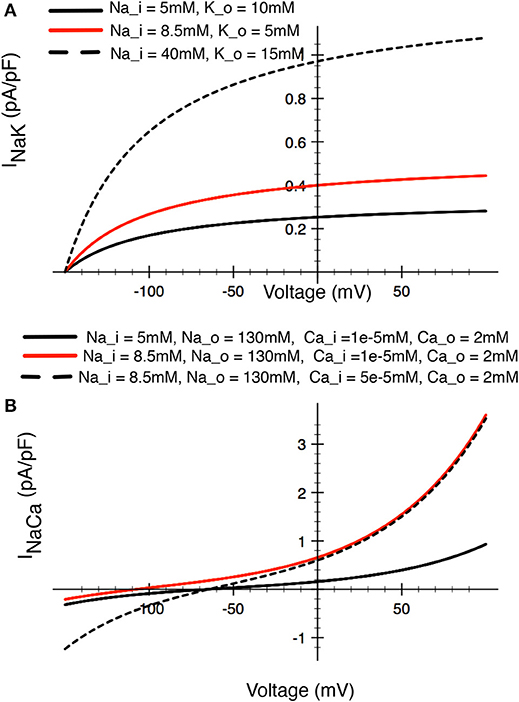
Figure 7. Illustrations of the relative sizes of net currents produced by (A) the Na⁺/K⁺ pump, and (B) the Na⁺/Ca²⁺ exchanger in a human chondrocyte. The three superimposed I–V curves for the Na⁺/K⁺ pump illustrated in (A) bracket the [Na⁺] and [K⁺] levels that have been reported in the literature (see Table 1). The red trace would approximately correspond to baseline conditions for [Na⁺] and [K⁺] in other mammalian cells. The three superimposed I–V curves for the Na⁺/Ca²⁺ exchanger in (B) illustrated the relative magnitudes for this current, with the red trace again approximating the resting or baseline I_Na−Ca current in most other mammalian cells.

Na⁺/Ca²+ Exchanger: I_NaCa

The activity of the Na⁺/Ca²⁺ exchanger plays a key role in Ca²⁺ homeostasis in articular chondrocytes (Sánchez et al., 2006) as it does in most other cell types. We have modeled this electrogenic exchange process using a mathematical expression that we have developed from our work on human atrial myocytes. Its overall properties (ion transfer characteristics, dependence on [Na⁺]_i and [Ca²⁺]_i have been validated previously (Nygren et al., 1998):

$\begin{array}{ll}{I}_{NaCa}=k_{NaCa}\frac{{\left[N{a}^{+}\right]}_i^3{[C{a}^{2+}]}_o{e}^{\frac{\gamma VF}{RT}}-{\left[N{a}^{+}\right]}_o^3{[C{a}^{2+}]}_i{e}^{\frac{(\gamma -1.0)VF}{RT}}}{1.0+d_{NaCa}\{{\left[N{a}^{+}\right]}_o^3{[C{a}^{2+}]}_i+{\left[N{a}^{+}\right]}_i^3{[C{a}^{2+}]}_o\}}& (30)\end{array}$

Where k_NaCa is a scaling factor for this current, set to 0.0374842 pA/(mmol/L)⁴, γ is the position of the energy barrier that modulates the voltage dependence of I_NaCa, set to 0.45, and d_NaCa is the denominator constant for the current, set to 0.0003 (mmol/L)^−4., [Na⁺]_o is the extracellular Na⁺ concentration; [Na⁺]_i is the intracellular Na⁺ concentration as given by Equation (2), [Ca²⁺]_o is extracellular Ca²⁺ concentration (1.8 mM in a “typical” parameterization; see Table 1), and [Ca²⁺]_i is the evolving intracellular calcium concentration given by Equation (4).

This electrogenic ion exchange mechanism has been scaled based on a baseline or resting [Na⁺]_i of 12 mM, and [Ca²⁺]_i of 3 x 10⁻⁸ M (see Table 1 and section Discussion). The resulting I–V relationship under these conditions is shown in Figure 7B.

Na⁺/H⁺ exchanger: I_NaH

Chondrocytes express a Na⁺/H⁺ antiporter (Trujillo et al., 1999; Barrett-Jolley et al., 2010) that contributes importantly to pH regulation. By analogy with its role in many other cells and tissues, this antiporter is responsible for establishing and maintaining the transcellular pH gradient that is essential for maintaining baseline [Na⁺]_i levels and optimizing several different intracellular enzyme activities. In addition, intracellular pH indirectly regulates a number of the ion channels that are expressed (e.g., 2-pore K⁺ channels). pH can modulate essential enzymatic processes (e.g., Na⁺/K⁺ pump) in both physiological and pathophysiological settings.

We have used the equations originally developed by Crampin and Smith (2006) to model this electroneutral antiporter:

$\begin{array}{ll}{I}_{NaH}=N_{NaH}{I}_{Na{H}_{mod}}{I}_{Na{H}_{exch}}& (31)\end{array}$

$\begin{array}{ll}{I}_{NaHmod}=\frac{1}{1+(K_i^{n_H}/{\left[H^{+}\right]}_i^{n_H}}& (32)\end{array}$

$\begin{array}{ll}{I}_{Na{H}_{exch}}=\frac{t_1{t}_2-t_3{t}_4}{t_1+t_2+t_3+t_4}& (33)\end{array}$

$\begin{array}{ll}{t}_1=\frac{k_1^{+}{\left[N{a}^{+}\right]}_o/K_{Na}^o}{\begin{array}{c}1+\frac{{\left[N{a}^{+}\right]}_o}{K_{Na}^o}+\frac{{\left[H^{+}\right]}_o}{K_H^o}\\ \end{array}}& (34)\end{array}$

$\begin{array}{ll}{t}_2=\frac{k_2^{+}{\left[H^{+}\right]}_i/K_H^i}{\begin{array}{c}1+\frac{{\left[N{a}^{+}\right]}_i}{K_{Na}^i}+\frac{{\left[H^{+}\right]}_i}{K_H^i}\\ \end{array}}& (35)\end{array}$

$\begin{array}{ll}{t}_3=\frac{k_1^{-}{\left[N{a}^{+}\right]}_i/K_{Na}^i}{\begin{array}{c}1+\frac{{\left[N{a}^{+}\right]}_i}{K_{Na}^i}+\frac{{\left[H^{+}\right]}_i}{K_H^i}\\ \end{array}}& (36)\end{array}$

$\begin{array}{ll}{t}_4=\frac{k_2^{-}{\left[H^{+}\right]}_o/K_H^o}{\begin{array}{c}1+\frac{{\left[N{a}^{+}\right]}_o}{K_{Na}^o}+\frac{{\left[H^{+}\right]}_o}{K_H^o}\end{array}}& (37)\end{array}$

where, N_NaH = 4899, $k_1^{+}$ = 10.5, $k_1^{-}$ = 0.201, $k_2^{+}$ = 15.8, $k_2^{-}$ = 183, $k_{H,mod}^i$ = 3.07e-5,$K_{H,mod}^{°}$ = 4.8e-7, $k_{Na}^i$ = 16.2, $K_{Na}^{°}$ = 195, $K_H^i$ = 6.05e-4, $K_H^{°}$ = 1.62e-3, n_H = 1, m_H = 3, [Na⁺]_i and [Na⁺]_o are the intracellular and extracellular Na⁺ concentrations as given by Equation (2) respectively. [H⁺]_i and [H⁺]_o are the intracellular and extracellular proton concentrations. [H⁺]_i is an evolving concentration, initialized at pH 7.2. In any given simulation [H⁺]_o is selected and then held at this but constant value, typically set to pH 7.4.

Intracellular [Ca²⁺]_i Homeostasis: ATP-Dependent Ca Pump: I_Ca,ATP

In human chondrocytes, [Ca²⁺]_i is regulated by a combination of ion transporters, ion pumps, and intrinsic intracellular Ca²⁺ buffering mechanisms. As noted, there is evidence that Na⁺/Ca²⁺ exchanger is functionally expressed in mammalian chondrocytes (Sánchez et al., 2006). Accordingly, Equation (4) in our model that accounts for overall [Ca²⁺]_i dynamics includes this antiporter mechanism: an electroneutral, sarcolemmal ATP-requiring Ca²⁺ pump (Nygren et al., 1998), as well as intracellular Ca²⁺ buffering.

The Ca²⁺ pump ion transporter is electroneutral as a consequence of its ability to allow two H⁺ ions to move into the cell for each Ca²⁺ ion that is extruded per transport cycle. We have assumed that the major Ca²⁺ buffer in the cytosol (both in terms of its Ca²⁺ binding capacity and its kinetics) is calmodulin. The cytosolic calmodulin concentration has been adapted from our previous work (Nygren et al., 1998) adjusted for the much smaller intracellular volume of the human chondrocyte. The relevant equations for this electroneutral Ca²⁺ pump and for Ca²⁺ buffering by calmodulin are given by:

$\begin{array}{ll}{I}_{Ca,ATP}=Ima{x}_{Ca,ATP}\frac{{[Ca2+]}_i}{{[Ca2+]}_i+k_{Ca,ATP}}& (38)\end{array}$

and

$\begin{array}{ll}\frac{d{O}_C}{dt}=2x{10}^5{[Ca2+]}_i(1-O_C)-476 O_C& (39)\end{array}$

where Imax_Ca,ATP = 0.6349 pA/pF is the maximal Ca²⁺ pump current density, k_Ca,ATP is the half-maximum Ca²⁺ binding concentration, (0.0002 mmol/L), [Ca²⁺]_i is the intracellular calcium concentration as described by Equation (4), and O_C is the fractional occupancy of the calmodulin buffer by Ca²⁺.

Transient Receptor Potential (TRP) Current: I_TRPV4

A fundamental question concerning the electrophysiology of non-excitable cells is: how do they sense the external environment and what ion flux mechanism(s) are responsible for this “trigger/transducer” signal? Ligand-gated cation-selective channels that have properties very similar to those exhibited by some members of the transient receptor potential or TRP family of ion channels (Nilius and Oswianik, 2011; Kaneko and Szallasi, 2014) are expressed in mammalian chondrocytes (cf. Gavenis et al., 2009; Phan et al., 2009; Clark et al., 2010; Asmar et al., 2016). Specifically, TRPV4 is prominently expressed in mouse (Clark et al., 2010) and porcine (Phan et al., 2009) chondrocytes. Previous work on endothelial cells suggests that this type of conductance is the basis for the small Ca²⁺ influx that then “triggers” a much larger release of Ca²⁺ from intracellular stores (the endoplasmic reticulum, Sonkusare et al., 2012) and thus can even produce “Ca²⁺ waves” (Guilak et al., 1999; Han et al., 2012). This important chain of events can initiate dynamic Ca²⁺-dependent intracellular signaling pathways, as well as modulating much longer-term processes such as transcription (Berridge, 1997; Dolmetsch et al., 1997; Berridge et al., 2000; Parekh and Muallem, 2011). Some of these initial sensing/signaling pathways rely on specific integrin isoforms (Wright et al., 1997; Millward-Sadler et al., 2000; Mobasheri et al., 2002; Han et al., 2012).

We have identified significant TRP currents in human articular chondrocyte (HAC) preparations after superfusion with novel “TRPV4 activator” compounds synthesized by Glaxo Smith Kline (GSK) (Thorneloe et al., 2008; Hilfiker et al., 2013). These experimental results and related mathematical analysis/simulations are shown in Figures 8, 9. Based on this and a variety of other published results we have formulated the working hypothesis that, in the human chondrocyte, there is a multicomponent signaling complex that includes: TRP channels, Ca²⁺-activated K⁺ channels, connexins/pannexins, and purinergic receptors (Loeser et al., 2000; Millward-Sadler et al., 2004; Elliott et al., 2009; Knight et al., 2009; Chekeni et al., 2010; Garcia and Knight, 2010). By analogy with a number of other non-excitable cells this may form the basis for some of the ligand and stretch-sensitive responses in chondrocytes, including the initiation and modulation of intra- and intercellular Ca²⁺ waves.

FIGURE 8

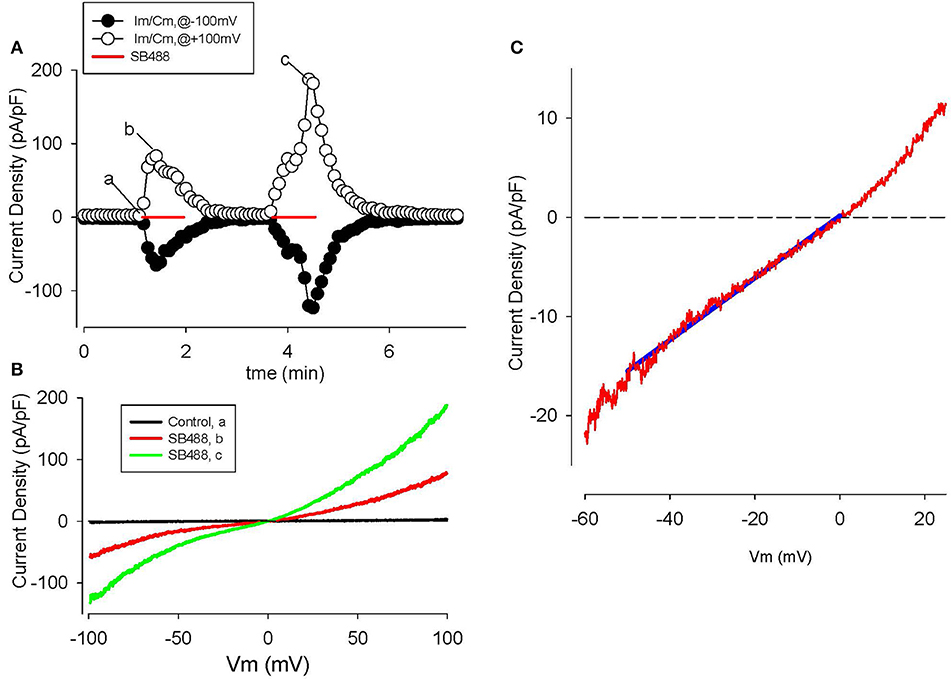
Figure 8. Activation of TRPV4 channel currents by the GSK agonist, SB488, in human articular chondrocytes. (A) Time course of membrane current density changes at +100 (open circles) and −100 mV (closed circles) during repeated ramp voltage-clamp protocols. Red bars indicate the application of 1 μM SB488. (B) I–V relations before (trace “a,” black) and during application of SB488 (b,c) as illustrated in (A). (C) I–V for SB488 induced current on reduced membrane voltage and current scales i.e., in the voltage range of the chondrocyte resting membrane potential. The solid blue line is a linear fit to the I–V over the potential range from 0 to −50 mV.

FIGURE 9

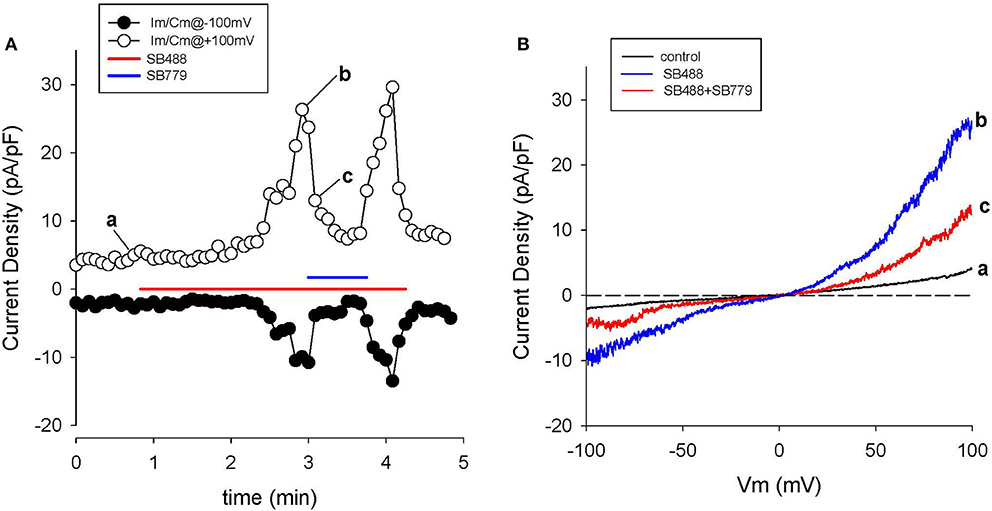
Figure 9. Block of SB488-induced currents through TRPV4 channels by SB779. (A) Time course of membrane current changes at +100 (open circles) and −100 mV (closed circles) during repeated ramp voltage-clamp protocols. Colored bars indicate application of 1 μM SB488 (red), or SB488 +1 μM SB779 (blue). Note the nearly complete inhibition of SB488-induced current by SB779. I-V relations before (a), during SB488 (b) and during SB488 + SB779 (c). Panel (B) shows 3 superimposed I-V curves: (a) baseline, (b) in the agonist (SB488), and (c) in the combined presence of SB488 and SB779.

GSK SB488-induced currents in voltage-clamped human chondrocytes

The GSK compound SB488 is a potent agonist for TRPV4 channels (Nilius and Oswianik, 2011; Hilfiker et al., 2013). Our preliminary work has shown that SB488 (1 μM) can induce large non-selective cation currents in primary mouse articular chondrocytes (Giles and Clark, unpublished). Since the inward current due to TRPV4 channels is carried by Ca²⁺ and Na⁺ ions (Nilius and Oswianik, 2011) these non-selective cation channels could constitute one of the essential triggers for intracellular Ca²⁺ release and Ca²⁺-dependent signal transduction in HAC preparations. Figure 8 shows a representative example of the time course and I-V relationships of the SB488-induced currents in a voltage-clamped HAC. Figure 8A consists of a plot of these membrane currents measured at +100 and −100 mV, in response to a ramp voltage-clamp protocol (see Methods section). SB488 (1 μM) application activated a quasi linear current that exhibited both transient and maintained components and declined very slowly after removal of this compound (taking ~1.5 min to return to control levels).

Examples of HAC I-V relations recorded before and during SB488 application are shown in Figure 8B. The baseline or control current was very small and its I–V was essentially linear over the entire potential range that was tested. However, the pipette solution was CsCl-rich, so K⁺ currents were completely blocked. In contrast, after SB488 application a relatively large transmembrane current developed. These two I–V curves intersect very near 0 mV, as shown in the inset. The mean (± s.e.m.) of this reversal potential value for SB488-induced currents in 13 different HAC preparations was 1.8 ± 0.4 mV consistent with the known properties of the TRPV4 family of ion channels.

A different GSK compound, SB779, (Hilfiker et al., 2013) can potently block the currents induced by SB488. It was also studied in our HAC preparations. The data in Figure 9 confirm that SB 799 is an effective blocker of the SB488-induced currents. Figure 9A shows the time course of membrane current at +100 and −100 mV in response to a multiple ramp voltage-clamp protocol. In this HAC, application of SB488 (1 μM) resulted in a slow increase in current i.e., taking about 1 min before currents increased significantly above control levels. This SB488-induced current was quickly blocked by application of SB779 (even in the presence of SB488). This marked reduction of the SB488-induced current by SB779 is consistent with either block of a SB488 “receptor,” or direct, potential-independent block of the SB488-activated ion channels by SB779. Figure 9B illustrates I–V relations recorded at base line, during SB488 alone, and in the presence of SB488 and SB779. The similarity of these I–V relationships and reversal potentials suggest that these compounds do in fact act as selective TRPV4 agonists and antagonists in these HAC preparations.

Discussion

The Resting Membrane Potential in Human Chondrocytes

The new electrophysiological data and first order mathematical model provided by this study add significantly to the previously published papers on fundamental mechanisms of human chondrocyte biology and pathophysiology (cf. Barrett-Jolley et al., 2010; Mobasheri et al., 2012; Asmar et al., 2016). Our main goal was to define the ionic basis for the resting membrane potential, E_m. Detailed knowledge of the basis for E_m of the chondrocyte is especially important since it is a non-excitable cell. In these preparations e.g., endothelial cells, glia, it is known that even very small changes in E_m can strongly modulate [Ca²⁺]_i (Bouchard et al., 1993; Baczkó et al., 2003; Poon et al., 2014). Either transient or maintained changes in [Ca²⁺]_i can modulate Ca²⁺-dependent signaling, as well as the related homeostatic and gene transcription mechanisms (Chao et al., 2006; Lin et al., 2008). In chondrocytes there is also evidence that relatively small alterations in E_m can contribute to dynamic regulation of cell volume (Barrett-Jolley et al., 2010; Lewis et al., 2011).

Given the technical difficulty of making accurate, reproducible recordings of transmembrane ionic currents in small cells that have large input resistances, our mathematical model provides an additional basis for understanding the physiological roles of each of the distinct K⁺ currents that have been characterized in human chondrocytes. It is evident from the results in Figures 2–6 that any one, or a combination, of these K⁺ currents could: (i) significantly hyperpolarize the resting potential, and/or (ii) repolarize the chondrocyte after it had been depolarized (Funabashi et al., 2010b). It is also apparent that significant, cyclic depolarization can result from the effects of mechanical activity (stretch or shear), as well as via ligand-gated conductances, (e.g., ATP) or activation of TRP channels.

At this stage of model development our simulations do not fully reveal the ionic basis for E_m in isolated human chondrocytes. However, they provide further insight into the consistent finding that a range of membrane potential values (−30 to −50 mV) are obtained in single cell patch clamp experiments on human chondrocytes, even after ensuring that ‘multi-GΩ’ seal resistances are obtained. This is because the net outward current that sets the resting membrane potential at steady-state is very small as shown in Figures 2, 7; and is expected from the very large (5–10 GΩ) input resistance (cf. Wilson et al., 2011). Improvement on the work reported here will require extensive additional experimental data, perhaps recorded at physiological temperatures. Additional data analyses and model development will also need to consider alternate approaches for accounting for the interactions among Na⁺/K⁺ pump activity, background Cl⁻ fluxes, and overall cellular osmotic homeostasis (Armstrong, 2003).

The Physiological Milieu of the Chondrocyte

Classical knowledge of unusual physiologic milieu (see Table 1) within the articular joint yields the expectation that these conditions would be expected to regulate the E_m, e.g., by altering the conductance or gating properties of intrinsic K⁺ currents that expressed at baseline; through modulation ligand-gated currents; or by changing cell metabolism. For example, the extracellular synovial fluid is somewhat hypertonic (320–340 mOsM vs. approximately 280 mOsM in most mammalian tissues). The effects of osmolarity on voltage gated K⁺ currents have been studied quite extensively, and chondrocytes also express volume-sensitive K⁺ and Cl⁻ currents (Lewis et al., 2011).

We were very interested in an additional mechanism through which changes in the osmolarity of the superfusate or extracellular solution may manifest themselves. It is well-known that changes in osmolarity can alter the “screening or shielding” of discrete membrane surface charges on the plasma membrane and that such changes can regulate channel gating displacement or shifting by altering the voltage-dependence of gating. The main effect of this has been identified as a shift in the voltage-dependence of gating variables, due to altered surface charge or zeta potential (Kell and DeFelice, 1988; Hille, 2001). It is also known that divalent or trivalent cations, (as well as charged osmolytes) can effectively reduce the zeta potential component of the overall membrane potential (Hille, 2001). Although surface potential cannot be measured directly by conventional transmembrane potential recordings, changes in it can be mimicked in silico (as shown in Figure 10). Accordingly, in our final set of computations we have shifted the activation curve for I_K−DR by 10 mV in either the depolarizing or hyperpolarizing direction (Figure 10A). As expected, this maneuver alters the size of this K⁺ current by changing the fraction that is “available” within the membrane potential range that is near the estimated HAC resting potential (Figure 10B). In the case of the human chondrocyte (as shown in Table 1), surface charge screening resulting from increased osmolarity, would be expected to shift the activation curve to the right (in the depolarized direction), therefore decreasing I_K−DR at membrane potentials near E_m. An important functional consequence would be a tendency to depolarize the resting potential of the chondrocyte (Figure 10C).

FIGURE 10

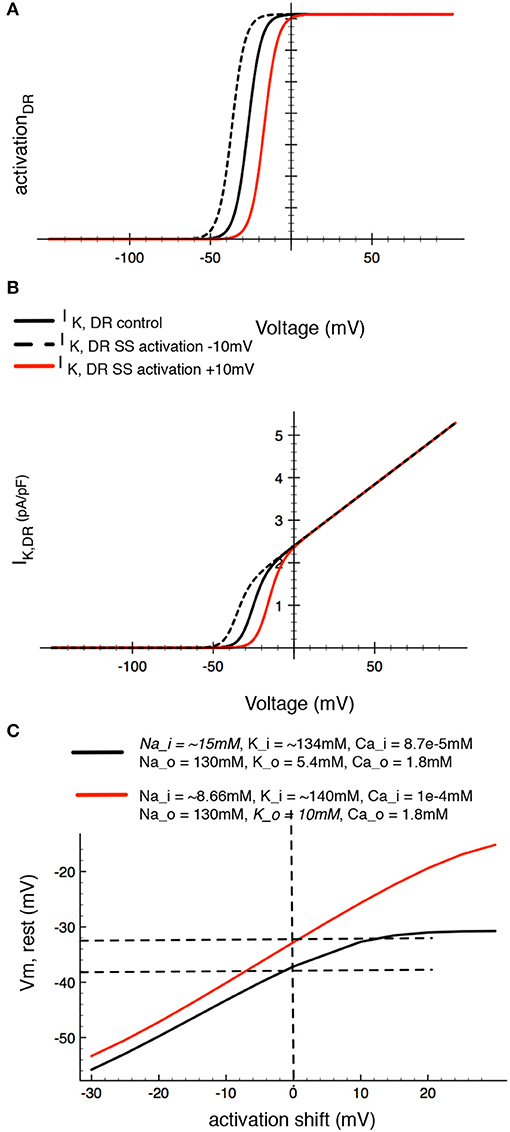
Figure 10. Demonstration of the effects of in silico changes in the voltage-dependence for activation of the delayed rectifier K⁺ current, I_K−DR, Panels (A,B), illustrate the altered activation curves and I-V relationships, respectively. Panel (A) shows the derived activation curve for I_K−DR (black line) at baseline and after shifting its midpoint ±10 mV to begin an analysis of the effects of changes in surface potential on chondrocyte E_m. Panel (B) shows the (black line computed chondrocyte I–V curves for I_K−DR at baseline and after the activation of I_K−DR is shifted ±10 mV. Panel (C) shows the corresponding changes in resting membrane potential in the baseline model and after [Na⁺]_i. The red line in (C) was computed assuming that intracellular [Na⁺]_i is 15 mM. The resulting augmentation/stimulation of the Na⁺/K⁺ pump provides an electrogenic outward current that can significantly hyperpolarize E_m (see Discussion section) at all membrane potentials.

Perhaps the strongest evidence that in situ the chondrocyte can exhibit significant surface membrane delimited zeta potentials (and restricted diffusion profiles) has been provided by both classical and recent studies that have defined important properties of the chondrocyte pericellular matrix (Poole et al., 1987; Pfander and Gelse, 2007). As mentioned previously, these papers argue in favor of the chondrocyte and its pericellular matrix being defined as an integral functional unit denoted the chondron (Poole et al., 1987; Nguyen et al., 2010; Wilusz et al., 2014). The microanatomy of the chondron, specifically its likelihood for promoting restricted diffusion of e.g., K⁺ and metabolites is likely to be significant factors regulating the chondrocyte “microenvironment.” Within this functional space emerging knowledge of glucose transport (and hence cellular energetics), as well as paracrine and inflammatory factor profiles, will need to be further defined and accounted for (c.f. Mobasheri et al., 1998).

As noted in the Introduction, the pH in the extracellular matrix can be somewhat acidic, ~6.9 as opposed to 7.2 (see Table 1). Changes in [H⁺]_o measured in terms of pH alteration can also have “surface change effects” similar to those described above (cf. Hille, 2001). Specifically, lowering pH_o (acidification) would result in a decrease in I_KDR and therefore an independent and additional tendency to depolarize the chondrocyte resting membrane potential.

Other conditions that characterize the milieu mammalian articular chondrocyte would also be expected to have very significant electrophysiological consequences, mainly by altering E_m. Perhaps the main one of these in chondrocytes is the significant elevation of intracellular [Na⁺]_i levels to (perhaps) as much as 20 mM as opposed to values of 8–10 mM in most other mammalian cells. This elevated [Na⁺]_i may partly explain the somewhat atypical pH_i values, since intrinsic Na⁺/H⁺ exchange activity and thus pH regulation would be altered. What is likely more important, [Na⁺]_i levels in the 15–30 mM range would strongly regulate (activate) the electrogenic Na⁺/K⁺ pump. The resulting increase in outward electrogenic pump current (see Figure 7A) would provide a significant hyperpolarizing influence to the chondrocyte E_m. This possibility is illustrated by the black traces in Figure 10C. Note that when [Na⁺]_i is increased (8.6 to 15 mM) the extra outward Na⁺/K⁺ pump current can significantly hyperpolarize the chondrocyte E_m. After key principles of chondrocyte Ca²⁺ transport are further understood, it may be possible to revise and improve related aspects of our chondrocyte model as has been done for the PC 12 cell (Duman et al., 2008). One reason for working toward these changes/improvements is the possibility of gaining new insights into [Ca²⁺]_i regulated apoptosis and autophagy (Harr and Distelhorst, 2010) as well as senescence (Mobasheri et al., 1998).

Ca²⁺-Influx and Ca²⁺-Dependent Currents

As noted, activation of TRPV4 channels would be expected to result in a significant influx of Ca²⁺ and Na⁺, and a related depolarization, when the chondrocyte membrane potential is negative to approximately −20 mV, the reversal potential (see Figures 8, 9) for ion flux through these channels. However, any such TRP channel-induced depolarization would be transient, and relatively small. This is because depolarization and/ or Ca²⁺ influx would be expected to be quickly followed by a K⁺ efflux. This would result in repolarization back to E_m or even beyond (a hyperpolarization). This K⁺ efflux/outward current would be due to a combination of: (i) the depolarization-induced activation of the delayed rectifier K⁺ currents, I_K−DR, and/or (ii) turning on of the BK and/or other Ca²⁺-activated K⁺ current (cf. Horrigan and Aldrich, 2002; Magleby, 2003; Sun et al., 2009). In other nonexcitable cells, even a very small Ca²⁺ influx can trigger a large Ca²⁺ release from the ER, thus producing a significant increase in intracellular Ca²⁺, [Ca²⁺]_i. Moreover, the extent to which [Ca²⁺]_i in the ER changes can trigger a secondary but significant net Ca²⁺ influx mediated by I_CRAC channels expressed in the surface membrane (c.f. Shaw et al., 2013). In a human chondrocyte-derived cell line, Funabashi et al. (2010b) have shown that histamine can strongly enhance a Ca²⁺-activated K⁺ current, and thus hyperpolarize the chondrocyte membrane potential. This relatively hyperpolarized transmembrane voltage, E_m, is maintained until [Ca²⁺]_i and/or Ca²⁺-dependent signaling mechanisms reset to “resting” values. This Ca²⁺ dependent hyperpolarization may also contribute to chondrocyte differentiation (Muramatsu et al., 2007).

Connexin-Mediated Current Flow and Electrotonic Interactions

As mentioned in the Introduction, chondrocytes in articular joints from adult humans function as isolated, single cells. Interestingly, however, Cell Physiological data from early adolescent articular joint preparations suggest that the growth plate of articular joints includes small groups of closely opposed chondrocytes. In these preparations, expression of selected members of the connexin family of intercellular communication proteins (e.g., Cx43) has been detected using standard immunohistochemical approaches (Chi et al., 2004; Mayan et al., 2013a,b; Asmar et al., 2016).

We also note that is Cx43 increased expression in isolated adult chondrocytes can result in release ATP in response to e.g. mechanical perturbations (Millward-Sadler et al., 2004; Knight et al., 2009; Garcia and Knight, 2010). One plausible mechanism for this, is the occurrence of transient openings of these “hemi-channels” that consist of either pannexin or connexin subunits (Saez et al., 2003; Garcia and Knight, 2010; Penuela et al., 2013). Given this important functionality, our mathematical model also includes a connexin-mediated conductance (Figure 4). However, since this initial model development was focused on simulating adult chondrocyte behavior under a restricted set of physiological conditions, these connexin single-cell channels were shut off (assigned a conductance value of 0 pS) in all simulations that form the basis of this paper. We acknowledge that this choice does not allow this model to account for any of the interesting function properties that arise from the so-called connexon-43 hemichannel behavior in chondrocytes (Knight et al., 2009). This “hemichannel activity” in chondrocytes can also be mediated by the pannexin family of integral membrane proteins (Bond et al., 2011; Matta et al., 2015).

Limitations of the Mathematical Model of the Human Chondrocyte Resting Membrane Potential

The mathematical model that we have developed is an important advance. However, we recognize that it has significant limitations. These include:

a) It is apparent that Ca²⁺ is an essential signaling molecule in the chondrocyte. Expression of L-type Ca²⁺ channels has been reported in growth plate chondrocytes (Sugimoto et al., 1996; Zuscik et al., 1997), but not in other single cell adult chondrocyte preparations. In the future, more detailed consideration of the details of (i) Ca²⁺ channels (ii) TRP channels (iii) CRAC channels (iv) the Na⁺/Ca²⁺ exchanger and (v) the Ca²⁺ pumps in both the endoplasmic reticulum and the surface membrane must be included in the model. In fact systematic experimental and modeling studies of each functional element in chondrocyte [Ca²⁺] homeostasis are needed, perhaps with an emphasis on the so-called Ca²⁺ signalosome with emphasis on the Ca²⁺ pump in the endoplasmic reticulum, (Kranias and Hajjar, 2012).

b) Mathematical expressions that would allow simulations of what has been termed “the AM and FM modes of Ca²⁺ signaling” (Berridge, 1997; Berridge et al., 2000), will require consideration of [Ca²⁺]_i-dependent phosphorylation and dephosphorylation reactions, the involvement of IP-3 in Ca²⁺ release, (Mak and Foskett, 2015) as well as accounting for the Ca²⁺-dependence involved in transcriptional regulation of ion channel, antiporter and pump target molecules.

c) There is evidence that cell culture conditions can alter both chondrocyte phenotype and gene expression profiles (Spitzer et al., 2000; Chen et al., 2012; but see Asmar et al., 2016). These patterns of changes will need to be taken into account for attempting to either interpolate or extrapolate findings from this model. This limitation can be addressed when new data sets are available from isolated chondrocytes that have been isolated from defined ‘zone’ (Berridge, 2007; Amanatullah et al., 2014) cultures in 3-D scaffold or substrates with known stiffness (Chen et al., 2012).

Summary

This mathematical model of chondrocyte electrophysiology provides a reliable platform for integrating and evaluating both recent and well-established experimental data that is relevant to the generation of the resting potential. At a minimum, given that the chondrocyte is in a unique but relatively inaccessible, environment, our model provides new insights into: the biophysical effects of alterations in ionic strength of synovial fluid on ion channel voltage-dependent gating (zeta potential effects). Key elements of the zeta potential working hypothesis can be tested if recent advances in voltage-dependent dye methods are implemented to provide a means of separating the various components of the signal that underlies the “transmembrane potential” in small nonexcitable cells (Cohen and Venkatachalam, 2014). It will also be necessary to account for the effects of cyclic stretch on chondrocyte ion channels by defining the main strain dependent alterations in channel gating voltage dependence or kinetics (cf. Hille, 2001; Maleckar et al., 2009). Approaches for detecting and determining the limitations of present patch clamp methods that can bias key electrophysiological data sets and influence their interpretation must continue to be utilized and refined. However, even in its present form this first-order model will continue to be useful for rationalizing and bringing together genomic data from microarray expression profiles, and understanding ion channel/antiporter drug target initiatives.

Author Contributions

RBC carried out all of the experimental work in this paper, and provided valuable input into the development and validation of the mathematical model. MM when supervising Dr. H. Narayanan at Simula Research Inc in Oslo, Norway lead the mathematical modeling component of this study. BV, a Senior Scientist at Glaxo Smith Kline, Philadelphia, USA provided valuable input into experimental design and facilitated transfer of the GSK properiarty cell lines and pro-drugs. WRG lead the project and wrote the manuscript. All authors have read and revised the manuscript, and are in agreement with its main findings and conclusions.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

An Alberta Innovates—Health Solutions (AI-HS) Scientist Award (WRG), an AI-HS Starter Grant, and a Canadian Institutes of Health Research Grant were combined to support this experimental work and related model development in the Giles laboratory at the University of Calgary. We are grateful to the Southern Alberta Tissue Transplant Facility (Dr. R. Krawetz) for supply of human articular joint (knee) tissue. Ms. Colleen Kondo prepared and maintained the human chondrocyte cultures and was responsible for project management in the Giles laboratory. Postdoctoral Fellowship funding for Dr. Harish Narayanan from both the Simula Research Laboratory, Oslo, Norway and the AI-HS is gratefully acknowledged. Dr. Narayanan provided input into early aspects of the computational work in this paper. Glaxo Smith Kline Laboratories in Philadelphia, Pennsylvania supplied the human chondrocyte cell line and TRPV4 agonists/antagonists that were used to generate some of the data.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2018.00974/full#supplementary-material

References

Amanatullah, D. F., Yamane, S., and Reddi, A. H. (2014). Distinct patterns of gene expression in the superficial, middle and deep zones of bovine articular cartilage. J. Tiss. Eng. Regen. Med. 8, 505–514. doi: 10.1002/term.1543

PubMed Abstract | CrossRef Full Text | Google Scholar

Archer, C. W., and Francis-West, P. (2003). The chondrocyte. Int. J. Biochem. Cell Biol. 35, 401–404. doi: 10.1016/S1357-2725(02)00301-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Armstrong, C. M. (2003). The Na/K pump, Cl ion, and osmotic stabilization of cells. Proc. Natl. Acad. Sci. U.S.A. 100, 6257–6262. doi: 10.1073/pnas.0931278100

PubMed Abstract | CrossRef Full Text | Google Scholar

Asmar, A., Barrett-Jolley, R., Werner, A., Kelly, R. Jr, and Stacey, M. (2016). Membrane channel gene expression in human costal and articular chondrocytes. Organogenesis 12, 94–107. doi: 10.1080/15476278.2016.1181238

PubMed Abstract | CrossRef Full Text | Google Scholar

Baczkó, I., Giles, W. R., and Light, P. E. (2003). Resting membrane potential regulates Na⁺-Ca²⁺ exchange-mediated Ca²⁺ overload during hypoxia-reoxygenation in rat ventricular myocytes. J. Physiol. 550, 889–898. doi: 10.1113/jphysiol.2003.043372

PubMed Abstract | CrossRef Full Text | Google Scholar

Balakrishna, S., Song, W., Achanta, S., Doran, S. F., Liu, B., and Kaelberer, M. M. (2014). TRPV4 inhibition counteracts edema and inflammation and improves pulmonary function and oxygen saturation in chemically induced acute lung injury. Am. J. Physiol. Lung Cell. Mol. Physiol. 307, L158–L172. doi: 10.1152/ajplung.00065.2014

PubMed Abstract | CrossRef Full Text | Google Scholar

Barrett-Jolley, R., Lewis, R., Fallman, R., and Mobasheri, A. (2010). The emerging chondrocyte channelome. Front. Physiol. 223:135. doi: 10.3389/fphys.2010.00135

CrossRef Full Text

Berkefeld, H., Falker, B., and Schulte, U. (2010). Ca²⁺+-activated K⁺ channels: from protein complexes to function. Physiol. Rev. 90, 1437–1459. doi: 10.1152/physrev.00049.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

Berkefeld, H., Sailer, C. A., Bildi, W., Rohde, V., Thumfart, J. O., Eble, S., et al. (2006). BKCa-Cav channel complexes mediate rapid and localized Ca²⁺-activated K⁺ signaling. Science 314, 615–620. doi: 10.1126/science.1132915

PubMed Abstract | CrossRef Full Text | Google Scholar

Berridge, M. J. (1997). The AM and FM of calcium signalling. Nature 386, 759–760. doi: 10.1038/386759a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Berridge, M. J. (2007). Inositol triphosphate and calcium osciallations. Biochem. Soc. Symp. 74, 1–7. doi: 10.1042/BSS2007c01

CrossRef Full Text

Berridge, M. J., Lipp, P., and Bootman, M. D. (2000). The versatility and universitality of calcium signalling. Nat. Rev. Mol. Cell Biol. 1, 11–21. doi: 10.1038/35036035

PubMed Abstract | CrossRef Full Text | Google Scholar

Bond, S. R., Lau, A., Penuela, S., Sampaio, A. V., Underhill, T. M., Laird, D. W., et al. (2011). Pannexin 3 is a novel target for Runx2 expressed by osteoblasts and mature growth plate chondrocytes. J. Bone Miner. Res. 26, 2911–2922. doi: 10.1002/jbmr.509

PubMed Abstract | CrossRef Full Text | Google Scholar

Bouchard, R. A., Clark, R. B., and Giles, W. R. (1993). Regulation of unloaded cell shortening by sarcolemmal sodium-calcium exchange in isolated rat ventricular myocytes. J. Physiol. 469, 583–599. doi: 10.1113/jphysiol.1993.sp019831

PubMed Abstract | CrossRef Full Text | Google Scholar

Bush, P. G., and Hall, A. C. (2005). Passive osmotic properties of in situ human articular chondrocytes within non-degenerate and degenerate cartilage. J. Cell. Physiol. 204, 309–319. doi: 10.1002/jcp.20294

PubMed Abstract | CrossRef Full Text | Google Scholar

Bush, P. G., Huntley, J. S., Brenkel, I. J., and Hall, A. C. (2003). The shape of things to come: chondrocytes and osteoarthritis. Clin. Invest. Med. 26, 249–251.

PubMed Abstract | Google Scholar

Chao, P. H., West, A. C., and Hung, C. T. (2006). Chondrocyte intracellular calcium, cytoskeletal organization, and gene expression responses to dynamic osmotic loading. Am. J. Physiol. Cell Physiol. 291, C718–C725. doi: 10.1152/ajpcell.00127.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

Chekeni, F. B., Elliott, M. R., Sandilos, J. K., Walk, S. F., Kinchen, J. M., Lazarowski, E. R., et al. (2010). Pannexin 1 channels mediate ‘find-me’ signals ATP release and membrane permeability during apoptosis. Nature 467, 863–867. doi: 10.1038/nature09413

CrossRef Full Text

Chen, C., Tambe, D. T., Deng, L., and Yang, L. (2013). Biomechanical properties and mechanobiology of the articular chondrocyte. Am. J. Physiol. Cell Physiol. 305, C1202–C1208. doi: 10.1152/ajpcell.00242.2013

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, J., Irianto, J., Inamdar, S., Pravincumar, P., Lee, D. A., Bader, D. L., et al. (2012). Cell mechanics, structure, and function are regulated by the stiffness of the three-dimensional microenvironment. Biophys. J. 103, 1188–11997. doi: 10.1016/j.bpj.2012.07.054

PubMed Abstract | CrossRef Full Text | Google Scholar

Chi, S. S., Rattner, J. B., and Matyas, J. R. (2004). Communication between paired chondrocytes in the superficial zone of articular cartilage. J. Anat. 205, 363–370. doi: 10.1111/j.0021-8782.2004.00350.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Cid, L. P., Roa-Rojas, H. A., Niemeyer, M. I., González, W., Araki, M., and Sepúlveda, K. F. V. (2013). TASK-2: a K_2P K⁺ channel with complex regulation and diverse physiological functions. Front. Physiol. 4:198. doi: 10.3389/fphys.2013.00198

PubMed Abstract | CrossRef Full Text | Google Scholar

Clark, A. L., Votta, B. J., Kumar, S., Liedtke, W., and Guilak, F. (2010). Chondroprotective role of the osmotically sensitive ion channel transient receptor potential vanilloid 4: age- and sex-dependent progression of osteoarthritis in TRPV 4-deficient mice. Arthritis Rheumatol. 62, 2973–2983. doi: 10.1002/art.27624

CrossRef Full Text

Clark, R. B., Kondo, C., and Giles, W. R. (2011). Two-pore K⁺ channels contribute to membrane potential of isolated human articular chondrocytes. J. Physiol. 589, 5071–5089. doi: 10.1113/jphysiol.2011.210757

CrossRef Full Text

Cohen, A. E., and Venkatachalam, V. (2014). Bringing bioelectricity to light. Annu. Rev. Biophys. 43, 211–232. doi: 10.1146/annurev-biophys-051013-022717

PubMed Abstract | CrossRef Full Text | Google Scholar

Crampin, E. J., and Smith, N. P. (2006). A dynamic model of excitation-contraction coupling during acidosis in cardiac ventricular myocytes. Biophys. J. 90, 3074–3090. doi: 10.1529/biophysj.105.070557

PubMed Abstract | CrossRef Full Text | Google Scholar

Dolmetsch, R. E., Lewis, R. S., Goodnow, C. C., and Healy, J. I. (1997). Differential activation of transcription factors induced by Ca²⁺ response amplitude and duration. Nature 386, 855–858. doi: 10.1038/386855a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Duman, J. G., Chen, L., and Hille, B. (2008). Calcium transport mechanisms of PC12 cells. J. Gen. Physiol. 131, 307–323. doi: 10.1085/jgp.200709915

PubMed Abstract | CrossRef Full Text | Google Scholar

Eaton, J. W., Bateman, D., Hauberg, S., and Wehbring, R. (2014). GNU Octave Version 3.8.1 Manual: A High-Level Interactive Language for Numerical Computations. CreateSpace Independent Publishing Platform. Available online at: http://www.gnu.org/software/octave/doc/interpreter/

Elliott, M. R., Chekeni, F. B., Trampont, P. C., Lazarowski, E. R., Kadl, A., Walk, S. F., et al. (2009). Nucleotides released by apoptotic cells act as a find-me signal to promote phagocytic clearance. Nature 461, 282–286. doi: 10.1038/nature08296

PubMed Abstract | CrossRef Full Text | Google Scholar

Funabashi, K., Fujii, M., Yamamura, H., Ohya, S., and Imaizumi, Y. (2010a). Contribution of chloride channel conductance to the regulation of resting membrane potential in chondrocytes. J. Pharmacol. Sci. 113, 94–99. doi: 10.1254/jphs.10026SC

PubMed Abstract | CrossRef Full Text | Google Scholar

Funabashi, K., Ohya, S., Yamamura, H., Hatano, N., Muraki, K., and Giles, W. R. (2010b). Accelerated Ca²⁺ entry by membrane hyperpolarization due to Ca²⁺-activated K⁺ channel activation in response to histamine in chondrocytes. Am. J. Physiol. Cell Physiol. 298, C786–C797. doi: 10.1152/ajpcell.00469.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

Garcia, M., and Knight, M. M. (2010). Cyclic loading opens hemichannels to release ATP as part of a chondrocyte mechanotransduction pathway. J. Orthop. Res. 28, 510–515. doi: 10.1002/jor.21025

PubMed Abstract | CrossRef Full Text | Google Scholar

Gavenis, K., Schumacher, C., Schneider, U., Eisfeld, J., Mollenhauer, J., and Schmidt-Rohlfing, B. (2009). Expression of ion channels of the TRP family in articular chondrocytes from osteoarthritic patients: changes between native and in vitro propagated chondrocytes. Mol. Cell. Biochem. 321, 135–143. doi: 10.1007/s11010-008-9927-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Goldstein, S. A. N., Bockenhauer, D., and Zilberberg, N. (2001). Potassium leak channels and the KCNK family of two-P-domain subunits. Nat. Rev. Neurosci. 2, 175–184. doi: 10.1038/35058574

PubMed Abstract | CrossRef Full Text | Google Scholar

Grandolfo, M., D'Andrea, P., Martina, M., Ruzzier, F., and Vittur, F. (1992). Calcium-activated potassium channels in chondrocytes. Biochem. Biophys. Res. Commun. 182, 1429–1434. doi: 10.1016/0006-291X(92)91893-U

PubMed Abstract | CrossRef Full Text | Google Scholar

Guilak, F., Alexopoulos, L. G., Upton, M. L., Youn, I., Choi, J. B., Cao, L., et al. (2006). The pericellular matrix as a transducer of biomechanical and biochemical signals in articular cartilage. Ann. N.Y. Acad. Sci. 1068, 498–512. doi: 10.1196/annals.1346.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Guilak, F., Sah, R. L., and Setton, L. A. (1997). “Physical regulation of cartilage metabolism,” in Basic Orthopaedic Biomechanics, eds V. C. Mow and W. C. Hayes (Philadelphia, PA: Lippincott-Raven), 179–207.

Guilak, F., Zell, R. A., Erickson, G. R., Grande, D. A., Rubin, C. T., and McLeod, K. J. (1999). Mechanically induced calcium waves in articular chondrocytes are inhibited by gadolinium and amiloride. J. Orthop. Res. 17, 421–429. doi: 10.1002/jor.1100170319

PubMed Abstract | CrossRef Full Text | Google Scholar

Hall, A., Horwitz, E. R., and Wilkins, R. J. (1996). The cellular physiology of articular cartilage. Exp. Physiol. 81, 535–545. doi: 10.1113/expphysiol.1996.sp003956

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, S. K., Wouters, W., Clark, A., and Herzog, W. (2012). Mechanically induced calcium signaling in chondrocytes in situ. J. Orthop. Res. 30, 475–481. doi: 10.1002/jor.21536

PubMed Abstract | CrossRef Full Text | Google Scholar

Harr, M. W., and Distelhorst, C. W. (2010). Apoptosis and autophagy: decoding calcium signals that mediate life or death. Cold Spring Harb. Perspect. Biol. 2, 1–18. doi: 10.1101/cshperspect.a005579

CrossRef Full Text

Hilfiker, M. A., Hoang, T. H., Cornil, J., Eidam, H. S., Matasic, D. S., and Roethke, T. J. (2013). Optimization of a novel series of TRPV4 antagonists with in vivo activity in a model of pulmonary edema. ACS Med. Chem. Lett. 4, 293–296. doi: 10.1021/ml300449k

PubMed Abstract | CrossRef Full Text | Google Scholar

Hille, B. (2001). Ion Channels of Excitable Membranes. Sunderland, MA: Sinauer Associates.

Horrigan, F. T., and Aldrich, R. W. (2002). Coupling between voltage sensor activation, Ca²⁺ binding and channel opening in large conductance (BK) potassium channels. J. Gen. Physiol. 120, 267–305. doi: 10.1085/jgp.20028605

PubMed Abstract | CrossRef Full Text | Google Scholar

Huber, M., Trattnig, S., and Lintner, F. (2000). Anatomy, biochemistry and physiology of articular cartilage. Invest. Radiol. 35, 573–580. doi: 10.1097/00004424-200010000-00003

PubMed Abstract | CrossRef Full Text | Google Scholar

Ince, C., van Bavel, E., van Duijn, B., Donkersloot, K., Coremans, A., and Ypey, D. L. (1986). Intracellular microelectrode measurements in small cells evaluated with the patch clamp technique. Biophys. J. 50, 1203–1209. doi: 10.1016/S0006-3495(86)83563-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaneko, Y., and Szallasi, A. (2014). Transient receptor potential (TRP) channels: a clinical perspective. Br. J. Pharmacol. 171, 2474–2507. doi: 10.1111/bph.12414

PubMed Abstract | CrossRef Full Text | Google Scholar

Kell, M. J., and DeFelice, L. J. (1988). Surface charge near the cardiac inward-rectifier channel measured from single-channel conductance. J. Membr. Biol. 102, 1–10. doi: 10.1007/BF01875348

PubMed Abstract | CrossRef Full Text | Google Scholar

Kindler, C. H., and Yost, C. S. (2005). Two-pore domain potassium channels: new sites of local anesthetic action and toxicity. Reg. Anesth. Pain Med. 30, 260–274. doi: 10.1016/j.rapm.2004.12.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Knight, M. M., McGlashan, S. R., Garcia, M., Jensen, C. G., and Poole, C. A. (2009). Articular chondrocytes express connexin 43 hemichannels and P2 receptors - a putative mechanoreceptor complex involving the primary cilium? J. Anat. 214, 275–283. doi: 10.1111/j.1469-7580.2008.01021

PubMed Abstract | CrossRef Full Text | Google Scholar

Kranias, E. G., and Hajjar, R. J. (2012). Modulation of cardiac contractility by the phopholamban/SERCA2a regulatome. Circ. Res. 110, 1646–1660. doi: 10.1161/CIRCRESAHA.111.259754

CrossRef Full Text

Kurita, T., Yamamura, H., Suziki, Y., Giles, W. R., and Imaizumi, Y. (2015). The CIC-7 chloride channel is down regulated by hypo-osmotic stress in human chondrocytes. Mol. Pharmacol. 1, 113–120. doi: 10.1124/mol.115.098160

CrossRef Full Text

Lane Smith, R., Trindade, M. C., Ikenoue, T., Mohtai, M., Das, P., Carter, D. R., et al. (2000). Effects of shear stress on articular chondrocyte metabolism. Biorheology 37, 95–107.

PubMed Abstract | Google Scholar

Lewis, R., Asplin, K. E., Bruce, G., Dart, C., Mobasheri, A., and Barrett-Jolley, R. (2011). The role of the membrane potential in chondrocyte volume regulation. J. Cell. Physiol. 226, 2979–2986. doi: 10.1002/jcp.22646

PubMed Abstract | CrossRef Full Text | Google Scholar

Lewis, R., May, H., Mobasheri, A., and Barrett-Jolley, R. (2013). Chondrocyte channel transcriptomics: do microarray data fit with expression and functional data? Channels 7, 459–467. doi: 10.4161/chan.26071

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, Z., Fitzgerald, J. B., Xu, J., Willers, C., Wood, D., Grodzinsky, A. J., et al. (2008). Gene expression profiles of human chondrocytes during passaged monolayer cultivation. J. Orthop. Res. 26, 1230–1237. doi: 10.1002/jor.20523

PubMed Abstract | CrossRef Full Text | Google Scholar

Loeser, R. F., Sadiev, S., Tan, L., and Goldring, M. B. (2000). Integrin expression by primary and immortalized human chondrocytes: evidence of a differential role for α1β1 and α2β1 integrins in mediating chondrocyte adhesion to types II and VI collagen. Osteoarthr. Cartil. 8, 96–105. doi: 10.1053/joca.1999.0277

PubMed Abstract | CrossRef Full Text | Google Scholar

Magleby, K. L. (2003). Gating mechanism of BK (Slo1) channels: so near, yet so far. J. Gen. Physiol. 121, 81–96. doi: 10.1085/jgp.20028721

PubMed Abstract | CrossRef Full Text | Google Scholar

Mak, D. O., and Foskett, J. K. (2015). Inositol 1,4,5-trisphosphate receptors in the endoplasmic reticulum: a single-channel point of view. Cell Calcium 58, 67–78. doi: 10.1016/j.ceca.2014.12.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Maleckar, M. M., Greenstein, J. L., Giles, W. R., and Trayanova, N. A. (2009). K⁺ current changes account for the rate dependence of the action potential in the human atrial myocyte. Am. J. Physiol. Heart Circ. Physiol. 297, 1398–1410. doi: 10.1152/ajpheart.00411.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

Martin, J. A., and Buckwalter, J. A. (2003). The role of chondrocyte senescence in the pathogenesis of osteoarthritis and in limiting cartilage repair. J. Bone Joint Surg. Am. 85, 106–110. doi: 10.2106/00004623-200300002-00014

PubMed Abstract | CrossRef Full Text | Google Scholar

Mason, M. J., Simpson, A. K., Mahaut-Smith, M. P., and Robinson, H. P. C. (2005). The interpretation of current-clamp recordings in the cell-attached patch-clamp configuration. Biophys. J. 88, 739–750. doi: 10.1529/biophysj.104.049866

PubMed Abstract | CrossRef Full Text | Google Scholar

Matta, C., Fodor, J., Miosge, N., Takacs, R., Juhasz, T., Rybaltovszki, H., et al. (2015). Purinergic signaling is required for calcium oscillations in migratory chondrogenic progenitor cells. Pflugers Arch. Eur. J. Physiol. 467, 429–442. doi: 10.1007/s00424-014-1529-8

CrossRef Full Text

Mayan, M. D., Carpintero-Fernandez, P., Gago-Fuentes, R., Fernandez-Puente, P., and Filguiera-Fernandez, P. (2013a). Articular chondrocytes are physically connected through a cellular network that is responsible of the metabolic coupling between chondroctifs located in different layers of the tissue. Osteoarthr. Cartil. 21, S18–S19. doi: 10.1016/j.joca.2013.02.060

CrossRef Full Text

Mayan, M. D., Carpintero-Fernandez, P., Gago-Fuentes, R., Martinez-de-Ilarduya, O., Wang, H. Z., Valiunas, V., et al. (2013b). Human articular chondrocytes express multiple gap junction proteins differential expression of connexins in normal and osteoarthritic cartilage. Am. J. Pathol. 182, 137–1346. doi: 10.1016/j.ajpath.2012.12.018

PubMed Abstract | CrossRef Full Text | Google Scholar

McLane, L. T., Chang, P., Granquist, A., Boehm, H., Kramer, A., Scrimgeour, J., et al. (2013). Spatial organization and mechanical properties of the pericellular matrix on chondrocytes. Biophys. J. 104, 986–996. doi: 10.1016/j.bpj.2013.01.028

PubMed Abstract | CrossRef Full Text | Google Scholar

Millward-Sadler, S. J., Wright, M. O., Flatman, P. W., and Salter, D. M. (2004). ATP in the mechanotransduction pathway of normal human chondrocytes. Biorheology 41, 567–575.

PubMed Abstract | Google Scholar

Millward-Sadler, S. J., Wright, M. O., Lee, H. S., Caldwell, H., Nuki, G., and Salter, D. M. (2000). Altered electrophysiological responses to mechanical stimulation and abnormal signaling through alpha 5 beta 1 integrin in chondrocytes from osteoarthritic cartilage. Osteoarthr. Cartil. 8, 272–278. doi: 10.1053/joca.1999.0301

CrossRef Full Text

Mobasheri, A. (1998). Correlation between [Na⁺], glycosaminoglycan and Na⁺/K⁺ pump density in the extracellular matrix of bovine articular cartilage. Physiol. Res. 47, 47–52.

PubMed Abstract | Google Scholar

Mobasheri, A., Bondy, C. A., Moley, K., Mendes, A. F., Rosa, S. C., and Richardson, S. M. (2008). Facilitative glucose transporters in articular chondrocytes. Expression, distribution and functional regulation of GLUT isoforms by hypoxia, hypoxia mimetics, growth factors and proinflammatory cytokines. Adv. Anat. Embryol. Cell Biol. 200, 1–84. doi: 10.1007/978-3-540-78899-7

CrossRef Full Text

Mobasheri, A., Carter, S. D., Martín-Vasallo, P., and Shakibaei, M. (2002). Integrins and stretch activated ion channels; putative components of functional cell surface mechanoreceptors in articular chondrocytes. Cell Biol. 26, 1–18. doi: 10.1006/cbir.2001.0826

PubMed Abstract | CrossRef Full Text | Google Scholar

Mobasheri, A., Errington, R. J., Golding, S., Hall, A. C., and Urban, J. P. G. (1997). Characterization of the Na⁺K⁺-ATPase in isolated bovine articular chondrocytes; molecular evidence for multiple α and β isoforms. Cell Biol. Int. 21, 201–212. doi: 10.1006/cbir.1997.0137

PubMed Abstract | CrossRef Full Text | Google Scholar

Mobasheri, A., Gent, T. C., Nash, A. I., Womack, M. D., Moskaluk, C. A., and Barrett-Jolley, R. (2007). Evidence for functional ATP-sensitive (K_ATP) potassium channels in human and equine articular chondrocytes. Osteoarthr. Cartil. 15, 1–8. doi: 10.1016/j.joca.2006.06.017

CrossRef Full Text

Mobasheri, A., Lewsi, R., Ferreira-Mendes, A., Rufino, A., Dart, C., and Barrett-Jolley, R. (2012). Potassium channels in articular chondrocytes. Channels 6, 416–425. doi: 10.4161/chan.22340

PubMed Abstract | CrossRef Full Text | Google Scholar

Mobasheri, A., Matta, C., Zakany, R., and Musumeci, G. (2015). Chondrosenescence: definition, hallmarks and potential role in the pathogenesis of osteoarthritis. Maturitas 80, 237–244. doi: 10.1016/j.maturitas.2014.12.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Mobasheri, A. R., Mobasheri, M. J. O., Francis, E., Trujillo, D., Alvarez de la Rosa, D., and Martin-Vasallo, P. (1998). Ion transport in chondrocytes: membrane transporters involved in intracellular ion homeostasis and the regulation of cell volume, free [Ca²⁺] and pH. Histol. Histopathol. 13, 893–910. doi: 10.14670/HH-13.893

PubMed Abstract | CrossRef Full Text | Google Scholar

Mouw, J. K., Imler, S. M., and Levenston, M. E. (2006). Ion-channel regulation of chondrocyte matrix synthesis in 3D culture under static and dynamic compression. Biomech. Model. Mechanobiol. 6, 33–41. doi: 10.1007/s10237-006-0034-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Muir, H. (1995). The chondrocyte, architect of cartilage. Biomechanics, structure, function and molecular biology of cartilage matrix macromolecules. Bioessays 17, 1039–1048. doi: 10.1002/bies.950171208

PubMed Abstract | CrossRef Full Text | Google Scholar

Muramatsu, S., Wakabayashi, M., Ohno, T., Amano, K., Ooishi, R., and Sugahara, T. (2007). Functional gene screening system identified TRPV4 as a regulator of chondrogenic differentiation. J. Biol. Chem. 282, 32158–32167. doi: 10.1074/jbc.M706158200

PubMed Abstract | CrossRef Full Text | Google Scholar

Nguyen, B. V., Wang, Q. G., Kuiper, N. J., El Haj, A. J., Thomas, C. R., and Zhang, Z. (2010). Biomechanical properties of single chondrocytes and chondrons determined by micromanipulation and finite-element modeling. J. Rheumat. Soc. Interface 7, 1723–1733. doi: 10.1098/rsif.2010.0207

CrossRef Full Text

Nilius, B., and Oswianik, G. (2011). The transient receptor potential family of ion channels. Genome Biol. 12, 218–224. doi: 10.1186/gb-2011-12-3-218

PubMed Abstract | CrossRef Full Text | Google Scholar

Nygren, A., Fiset, C., Firek, L., Clark, W., Lindblad, D. S., Clark, R. B., et al. (1998). Mathematical model of an adult human atrial cell: the role of K⁺ currents in repolarization. Circ. Res. 82, 63–81. doi: 10.1161/01.RES.82.1.63

PubMed Abstract | CrossRef Full Text | Google Scholar

O'Conor, C. J., Leddy, H. A., Benefield, H. C., Liedtke, W. B., and Guilak, F. (2014). TRPV4-mediated mechanotransduction regulates the metabolic response of chondrocytes to dynamic loading. Proc. Natl. Acad. Sci. U.S.A. 111, 1316–1321. doi: 10.1073/pnas.1319569111

PubMed Abstract | CrossRef Full Text | Google Scholar

Ogawa, H., Kozhemyakina, E., Hung, H. H., Grodzinsky, A. J., and Lassar, A. B. (2014). Mechanical motion promotes expression of Prg4 in articular cartilage via multiple CREB-dependent, fluid flow shear stress-induced signaling pathways. Genes Dev. 28, 127–139. doi: 10.1101/gad.231969.113

PubMed Abstract | CrossRef Full Text | Google Scholar

Parekh, A. B., and Muallem, S. (2011). Ca²⁺ signaling and gene regulation. Cell Calcium 49:279. doi: 10.1016/j.ceca.2011.01.002

CrossRef Full Text

Patel, A. J., and Honoré, E. (2001). Properties and modulation of mammalian 2P domain K⁺ channels. Trends Neurosci. 24, 339–346. doi: 10.1016/S0166-2236(00)01810-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Pelletier, J. P., Martel-Pelletier, J., and Abramson, S. B. (2001). Osteoarthritis, an inflammatory disease: potential implication for the selection of new therapeutic targets. Arthrit. Rheumatol. 44, 1237–1247. doi: 10.1002/1529-0131(200106)44:6<1237::AID-ART214>3.0.CO;2-F

PubMed Abstract | CrossRef Full Text | Google Scholar

Penuela, S., Gehi, R., and Laird, D. W. (2013). The biochemistry and function of pannexin channels. Biochim. Biophys. Acta 1828, 15–22. doi: 10.1016/j.bbamem.2012.01.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Pfander, D., and Gelse, K. (2007). Hypoxia and osteoarthritis: how chondrocytes survive hypoxic environments. Curr. Opin. Rheumatol. 19, 457–462. doi: 10.1097/BOR.0b013e3282ba5693

PubMed Abstract | CrossRef Full Text | Google Scholar

Phan, M. N., Leddy, H. A., Votta, B. J., Kumar, S., Levy, D. S., Lipshutz, D. B., et al. (2009). Functional characterization of TRPV4 as an osmotically sensitive ion channel in porcine articular chondrocytes. Arthritis Rheumatol. 60, 3028–3037. doi: 10.1002/art.24799

PubMed Abstract | CrossRef Full Text | Google Scholar

Phillips, T., Ferraz, I., Bell, S., Clegg, P. D., Carter, D., and Mobasheri, A. (2005). Differential regulation of the GLUT1 and GLUT3 glucose transporters by growth factors and pro-inflammatory cytokines in equine articular chondrocytes. Vet. J. 169, 216–222. doi: 10.1016/j.tvjl.2004.01.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Poole, A. C., Flint, M. H., and Beaumont, B. W. (1987). Chondrons in cartilage: ultrastructural analysis of the pericellular microenvironment in adult human articular cartilages. J. Orthop. Res. 5, 509–522. doi: 10.1002/jor.1100050406

PubMed Abstract | CrossRef Full Text | Google Scholar

Poole, C. A. (1997). Articular cartilage chondrons: form, function and failure. J. Anat. 191, 1–13. doi: 10.1046/j.1469-7580.1997.19110001.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Poon, I. K., Chiu, Y. H., Armstrong, A. J., Kinchen, J. M., Juncadella, I. J., Bayliss, D. A., et al. (2014). Unexpected link between an antibiotic, pannexin channels and apoptosis. Nature 507, 329–334. doi: 10.1038/nature13147

PubMed Abstract | CrossRef Full Text | Google Scholar

Radhakrishnan, K., and Hindmarsh, A. C. (1993). Description and Use of LSODE, the Livermore Solver for Ordinary Differential Equations. NASA, Office of Management, Scientific and Technical Information Program. UCRL-ID-113855.

Saez, J. C., Berthoud, V. M., Brañes, M. C., Martínez, A. D., and Beyer, E. C. (2003). Plasma membrane channels formed by connexins: their regulation and functions. Physiol. Rev. 83, 1359–1400. doi: 10.1152/physrev.00007.2003

PubMed Abstract | CrossRef Full Text | Google Scholar

Sánchez, J. C., Powell, T., Staines, H. M., and Wilkins, R. J. (2006). Electrophysiological demonstration of Na⁺/Ca²⁺ exchange in bovine articular chondrocytes. Biorheology 43, 83–94.

PubMed Abstract | Google Scholar

Shaw, P. J., Qu, B., Hoth, M., and Feske, S. (2013). Molecular regulation of CRAC channels and their role in lymphocyte function. Cell Mol. Life Sci. 70, 2637–2656. doi: 10.1007/s00018-012-1175-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Sonkusare, S. K., Bonev, A. D., Ledoux, J., Liedtke, W., Kotlikoff, M. I., Heppner, T. J., et al. (2012). Elementary Ca²⁺ signals through endothelial TRPV4 channels regulate vascular function. Science 336, 597–601. doi: 10.1126/science.1216283

PubMed Abstract | CrossRef Full Text | Google Scholar

Spitzer, N. C., Lautermilch, N. J., Smith, R. D., and Gomez, T. M. (2000). Coding of neuronal differentiation by calcium transients. Bioessays 22, 811–817. doi: 10.1002/1521-1878(200009)22:9<811::AID-BIES6>3.0.CO;2-G

PubMed Abstract | CrossRef Full Text | Google Scholar

Sugimoto, T., Yoshino, M., Nagao, M., Ishii, S., and Yabu, H. (1996). Voltage-gated ionic channels in cultured rabbit articular chondrocytes. Comp. Biochem. Physiol. 115, 223–232. doi: 10.1016/S0742-8413(96)00091-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, L., Xiong, Y., Zeng, X., Wu, Y., Pan, N., Lingle, C. J., et al. (2009). Differential regulation of action potentials by inactivating and nonactivating BK channels in rat adrenal chromaffin cells. Biophys. J. 97, 1832–1842. doi: 10.1016/j.bpj.2009.06.042

PubMed Abstract | CrossRef Full Text | Google Scholar

Thorneloe, K. S., Sulpizio, A. C., and Westfall, T. D. (2008). N-((1S)-1-{[4-((2S)-2-{[2,4-Dichlorophenyl)sulfonyl]amino}-3-hydroxypropanoyl)-1-piperazinyl]carbonyl}-3-methylbutyl)-1-benzothiophene-2-carboxamide (GSK1016790A), a novel and potent transient receptor potential vanilloid 4 channel agonist induces urinary bladder contraction and hyperactivity: part 1. J. Pharm. Exp. Ther. 326, 432–442. doi: 10.1124/jpet.108.139295

CrossRef Full Text

Trujillo, E., Alvarez de la Rosa, D., Mobasheri, A., Gonzalez, T., Canessa, C. M., and Martín-Vasallo, P. (1999). Sodium transport systems in human chondrocytes II. Expression of ENaC, Na⁺/K⁺ /2Cl⁻ cotransporter and Na⁺/H⁺ exchangers in healthy and arthritic chondrocytes. Histol. Histopathol. 14, 1023–1031.

PubMed Abstract | Google Scholar

Tsuga, K., Tohse, N., Yoshino, M., Sugimoto, T., Yamashita, T., Ishii, S., et al. (2002). Chloride conductance determining membrane potential of rabbit articular chondrocytes. J. Membr. Biol. 185, 75–81. doi: 10.1007/s00232-001-0112-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Urban, J. P., Hall, A. C., and Gehl, K. A. (1993). Regulation of matrix synthesis rates by the ionic and osmotic environment of articular chondrycytes. J. Cell. Physiol. 154, 262–270. doi: 10.1002/jcp.1041540208

PubMed Abstract | CrossRef Full Text | Google Scholar

Webb, S. T., and Ghosh, S. (2009). Intra-articular bupivacaine: potentially chondrotoxic? Br. J. Anaes. 102, 439–441. doi: 10.1093/bja/aep036

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilkins, R. J., Browning, J. A., and Ellory, J. C. (2000a). Surviving in a matrix: membrane transport in articular chondrocytes. J. Membr. Biol. 177, 95–108. doi: 10.1007/s002320001103

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilkins, R. J., Browning, J. A., and Urban, J. P. (2000b). Chondrocyte regulation by mechanical load. Biorheology 37, 67–74.

PubMed Abstract | Google Scholar

Wilson, J. R., Clark, R. B., Banderali, U., and Giles, W. R. (2011). Measurement of the membrane potential in small cells using patch clamp methods. Channels 5, 530–537. doi: 10.4161/chan.5.6.17484

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilson, J. R., Duncan, N. A., Giles, W. R., and Clark, R. B. (2004). A voltage-dependent K⁺ current contributes to membrane potential of acutely isolated canine articular chondrocytes. J. Physiol. 557, 93–104. doi: 10.1113/jphysiol.2003.058883

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilusz, R. E., Sanchez-Adams, J., and Guilak, F. (2014). The structure and function of the pericellular matrix of articular cartilage. Matrix Biol. 39, 25–32. doi: 10.1016/j.matbio.2014.08.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Wright, M. O., Nishida, K., Bavington, C., Godolphin, J. L., Dunne, E., Walmsley, S., et al. (1997). Hyperpolarisation of cultured human chondrocytes following cyclical pressure-induced strain: evidence of a role for alpha 5 beta 1 integrin as a chondrocyte mechanoreceptor. J. Orthop. Res. 15, 742–747. doi: 10.1002/jor.1100150517

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Q. Q., and Chen, Q. (2000). Mechanoregulation of chondrocyte proliferation, maturation, and hypertrophy: ion-channel dependent transduction of matrix deformation signals. Exp. Cell Res. 256, 383–391. doi: 10.1006/excr.2000.4847

PubMed Abstract | CrossRef Full Text | Google Scholar

Zuscik, M. J., Gunter, T. E., Puzas, J. E., and Rosier, R. N. (1997). Characterization of voltage-sensitive calcium channels in growth plate chondrocytes. Biochem. Biophys. Res. Commun. 234, 432–438. doi: 10.1006/bbrc.1997.6661

PubMed Abstract | CrossRef Full Text | Google Scholar