Propagation Properties of a Twisted Hermite-Gaussian Correlated Schell-Model Beam in Free Space

We introduce a novel type of twisted partially coherent beams with a nonconventional correlation function, named the twisted Hermite-Gaussian correlated Schell-model (THGCSM) beam. The condition that a twist phase can be imposed on a partially coherent beam is addressed for Schell-model fields endowed with rectangular symmetry. Further, the analytical formula for the THGCSM beam propagating in free space has been derived with the help of the generalized Collins formula. The propagation properties, such as the spectral density and the spectral degree of coherence (SDOC) of the THGCSM beam, also have been studied in detail by some numerical examples. The numerical results show that the twist phase plays a role in resisting beam splitting, caused by the correlation structure, and induces the rotation of the distribution of the SDOC on propagation. Moreover, it is interesting to find that when the beam carries a twist phase, this will endow the beam the ability to maintain its distribution of the SDOC on propagation and enhance the self -reconstruction capability of the SDOC. Our results may provide new insights into nonconventional partially coherent beams with twisted phase and may be useful in some applications, such as optical communications and information recovery.

Introduction

Coherence is one of the most notable features of a laser beam. These light beams (i.e., partially coherent beam) have attracted intensive attentions due to their wide applications in inertial confinement fusion, ghost imaging, sub-Rayleigh imaging, particle trapping, free space optical communications and optical scattering [1–8]. Furthermore, Gori et al. [9, 10] proposed the sufficient conditions for designing a real genuine cross-spectral density function or matrix of a partially coherent beam. Based on the above works, a variety of partially coherent beams with nonconventional correlation functions (i.e., the correlation function doesn’t satisfy the Gaussian distribution) have been introduced theoretically and generated experimentally [11–27]. It is found that beams with nonconventional correlation functions will exhibit unique properties on propagation, such as self-splitting, self-reconstruction, locally sharpened and laterally shifted intensity maxima [13, 22, 27], which are useful in multi-particles trapping, atoms guiding, image transfer and recovery. Moreover, the beam profiles in the focal plane (or far fields) can be controlled by endowing the beam with a specific correlation function [15–19, 26], for example, dark-hollow beam profiles (or an optical cage) can be formed near the focal plane when the correlation function satisfies a Laguerre–Gaussian distribution [18]. A Multi-Gaussian correlated Schell-model beam would generate a rectangular intensity profile in the focal plane, and a ring-shaped beam and controllable intensity lattices also can be achieved with the help of the correlation functions [15, 26]. In addition, partially coherent beams with prescribed correlation functions can be applied to reduce scintillation in turbulence [28], overcome the classical Rayleigh diffraction limit [29], coherence-based optical encryption [30], robust microscopy imaging [31], robust far-field imaging [32], and optical beam shaping [33].

On the other hand, partially coherent beams with a twist phase (i.e., twisted partially coherent beam) carry orbital angular momentum (OAM) [34]. Twist phase as a “genuinely two-dimensional” phase can’t exist in a coherent beam and its value is bounded in strength. Twist phase was introduced by Simon et al. in 1993 and has been demonstrated in an experiment by Friberg [35, 36]. Due to the intrinsic chiral property of the twist phase the rotation of the beam spot on propagation is induced, and both the distribution of the SDOC, the degree of polarization and the state of polarization of the beam on propagation are affected [37, 38]. Besides, light beams with a twist phase have advantages in resisting coherence (or turbulence)-induced degeneration, depolarization and overcoming the classical Rayleigh limit [37, 39]. It is shown in [40, 41] that using a twist phase can greatly increase the amount of OAM of a partially coherent vortex beam and enhance its self-reconstruction capability.

Recently, some new ways have been introduced to generate twisted Gaussian Schell-model beams and measure their orbital angular momentum [42, 43]. The problem of when a twist phase can be imposed on a partially coherent beam, generated from a Schell-model source with axial symmetries, was explored in [44, 45]. Two approaches have been proposed to devise genuine twist beams with and without symmetry [46, 47]. In this paper, we devised a newly twisted partially coherent beam named the twisted Hermite-Gaussian correlated Schell-model (THGCSM) beam. The condition that the THGCSM beam will be bona fide is met, and the propagation properties of the THGCSM beam have been investigated in detail. Our results show that the twist phase plays a role of preventing deterioration of the intensity distribution and induces rotation of the distribution of the SDOC around the axis on propagation. Furthermore, the twist phase also will enhance the ability of the beam to maintain the distribution of the SDOC and its self-reconstruction capability, which will be useful for optical information processing and recovery.

Theory of the Twisted Hermite-Gaussian Correlated Schell-Model Beam

Twisted Schell-Model Beams With Rectangular Symmetry

Based on the unified theory of coherence and polarization, the statistical properties of a partially coherent beam can be characterized by the cross-spectral density (CSD) [48]. For Schell-model fields, endowed with rectangular symmetry, the cross-spectral density (CSD) of the beam can be expressed as

$W_0 \left({\mathit{r}}_{\mathbf{1}},{\mathit{r}}_{\mathbf{2}}\right)={\tau }^{\ast }\left({\mathit{r}}_{\mathbf{1}}\right)\tau \left({\mathit{r}}_{\mathbf{2}}\right) u\left(\left|x_1-x_2\right|\right) u\left(\left|y_1-y_2\right|\right),(1)$

where r₁ = (x₁, y₁), r₂ = (x₂, y₂) are two arbitrary transverse position vectors, τ (r_i) denotes the transmission function of an arbitrary (complex) amplitude filter and u (|x₁-x₂|)u (|y₁-y₂|) is the spectral degree of coherence. When the beam carries a twist phase, the CSD is defined as

$W_{0u} \left({\mathit{r}}_{\mathbf{1}},{\mathit{r}}_{\mathbf{2}}\right)={\tau }^{\ast }\left({\mathit{r}}_{\mathbf{1}}\right)\tau \left({\mathit{r}}_{\mathbf{2}}\right) u\left(\left|x_1-x_2\right|\right) u\left(\left|y_1-y_2\right|\right)\mathit{exp}\left(-ik{\mu }_0{\mathit{r}}_{\mathbf{1}}\times {\mathit{r}}_{\mathbf{2}}\right), (2)$

where the last exponential term represents the twist phase, with μ₀ being the twist factor. According to the Refs. [44, 45], the CSD will be bona fide, if and only if the corresponding uniform source, defined as

$W_u \left({\mathit{r}}_{\mathbf{1}},{\mathit{r}}_{\mathbf{2}}\right)= u\left(\left|x_1-x_2\right|\right) u\left(\left|y_1-y_2\right|\right)\mathit{exp}\left(-ik{\mu }_0{\mathit{r}}_{\mathbf{1}}\times {\mathit{r}}_{\mathbf{2}}\right),(3)$

is bona fide too. Then, we find that the uniform source satisfies the following formal integral relationship

${\displaystyle \int d^2\rho W_u\left({\mathit{r}}_{\mathbf{1}},\mathit{\rho }\right)T_u\left(\mathit{\rho },{\mathit{r}}_{\mathbf{2}}\right)}= {\displaystyle \int d^2\rho T_u\left({\mathit{r}}_{\mathbf{1}},\mathit{\rho }\right)W_u\left(\mathit{\rho },{\mathit{r}}_{\mathbf{2}}\right)}, (4)$

for any pair (r₁, r₂), ρ = (ρ_x, ρ_y) is an arbitrary transverse position vector, and $T_u=exp\left(-ik{\mu }_0{\mathit{r}}_1\times {\mathit{r}}_2\right)$ denotes the twist phase. To prove this, on substituting Eq. 3 into Equation 4, the l. h. s of Eq. 4 reads as follows

${\displaystyle \int d^2\rho W_u\left({\mathit{r}}_{\mathbf{1}},\mathit{\rho }\right)T_u\left(\mathit{\rho },{\mathit{r}}_{\mathbf{2}}\right)}= {\displaystyle \int d^2\rho u\left(\left|x_1-{\rho }_x\right|\right) u\left(\left|y_1-{\rho }_y\right|\right)\mathit{exp}\left(-ik{\mu }_0\left({\mathit{r}}_{\mathbf{1}}-{\mathit{r}}_{\mathbf{2}}\right)\times \mathit{\rho }\right)}, (5)$

For the r. h. s of Eq. 4 we obtain:

${\displaystyle \int d^2\rho T_u\left({\mathit{r}}_{\mathbf{1}},\mathit{\rho }\right)W_u\left(\mathit{\rho },{\mathit{r}}_{\mathbf{2}}\right)}={\displaystyle \int d^2\rho u\left(\left|{\rho }_x-x_2\right|\right) u\left(\left|{\rho }_y-y_2\right|\right)\mathit{exp}\left(-ik{\mu }_0\left({\mathit{r}}_{\mathbf{1}}-{\mathit{r}}_{\mathbf{2}}\right)\times \mathit{\rho }\right)},(6)$

Then, taking into account that $\exp \left[-ik{\mu }_0\left({\mathit{r}}_{\mathbf{1}}-{\mathit{r}}_{\mathbf{2}}\right)\times \mathit{\rho }\right]=\exp \left[-ik{\mu }_0\left({\mathit{r}}_{\mathbf{1}}-{\mathit{r}}_{\mathbf{2}}\right)\times \left(\mathit{\rho }-\left({\mathit{r}}_{\mathbf{2}}-{\mathit{r}}_{\mathbf{1}}\right)\right)\right],$ Eq. 6 can be expressed as follows

${\displaystyle \int d^2\rho T_u\left({\mathit{r}}_{\mathbf{1}},\mathit{\rho }\right)W_u\left(\mathit{\rho },{\mathit{r}}_{\mathbf{2}}\right)}={\displaystyle \int d^2\rho u\left(\left|{\rho }_x-\left(x_2-x_1\right)-x_1\right|\right) u\left(\left|{\rho }_y-\left(y_2-y_1\right)-y_1\right|\right)} \times \mathit{exp}\left[-ik{\mu }_0\left({\mathit{r}}_{\mathbf{1}}-{\mathit{r}}_{\mathbf{2}}\right)\times \left(\mathit{\rho }-\left({\mathit{r}}_{\mathbf{2}}-{\mathit{r}}_{\mathbf{1}}\right)\right)\right].(7)$

On letting ρ = ρ − (r₂−r₁), Eq. 7 can be recast as

${\displaystyle \int d^2\rho T_u\left({\mathit{r}}_{\mathbf{1}},\mathit{\rho }\right)W_u\left(\mathit{\rho },{\mathit{r}}_{\mathbf{2}}\right)=}{\displaystyle \int d^2\rho u\left(\left|{\rho }_x-x_1\right|\right) u\left(\left|{\rho }_y-y_1\right|\right)\mathit{exp}\left[-ik{\mu }_0\left({\mathit{r}}_{\mathbf{1}}-{\mathit{r}}_{\mathbf{2}}\right)\times \mathit{\rho }\right]}.(8)$

Thus, the Equation 4 has been proved. Moreover, it has been mentioned in [45], when the Equation 4 is satisfied, the uniform source W_u defined by Eq. 3 and the twist phase T_u share the same coherent modes, defined as

${\mathrm{\Phi }}_{j,m}\left(r\right)=\sqrt{\frac{u}{\pi }}{\left[\frac{\left(j-\left|m\right|\right)!}{\left(j+\left|m\right|\right)!}\right]}^{\mathbf{1}/\mathbf{2}}{\left(r\sqrt{u}\right)}^{2\left|m\right|}\mathit{exp}\left(i2m\phi \right)L_{j-\left|m\right|}^{2\left|m\right|}\left(u{r}^2\right)\mathit{exp}\left(-\frac{u{r}^2}{2}\right),(9)$

with u = kμ₀, k = 2π/λ is the wavenumber with wavelength λ, and j = 0, 1/2, 1, … , m = -j, j+1, … , j. Here, $L_{j-\left|m\right|}^{2\left|m\right|}$ is the Laguerre polynomials with the radial index j-|m| and the angular index 2|m|, while exp (i2mφ) represents the vortex phase.

If the uniform source W_u is bona fide, the sufficient condition is that the eigenvalue sequence {λ_j,m} should be nonnegative. These eigenvalues are defined as

${\lambda }_{j,m}={\displaystyle \iint d^2{\mathit{r}}_{\mathbf{1}}{\mathit{r}}_{\mathbf{2}}{W}_u\left({\mathit{r}}_{\mathbf{1}},{\mathit{r}}_{\mathbf{2}}\right){\mathrm{\Phi }}_{j,m}\left({\mathit{r}}_{\mathbf{1}}\right){\mathrm{\Phi }}_{j,m}^{\ast }\left({\mathit{r}}_{\mathbf{2}}\right)}.(10)$

On substituting equations 3 and (9) into Equation 10, and on letting ${\mathit{r}}_1-{\mathit{r}}_2\mathit{ }= \mathit{r}$, we have

${\lambda }_{j,m}={\displaystyle \int d^{2}ru\left(x\right)u\left(y\right)}{\displaystyle \int d^2{\mathit{r}}_{\mathbf{2}}\mathit{exp}\left(-ik{\mu }_0\mathit{r}\times {\mathit{r}}_{\mathbf{2}}\right){\mathrm{\Phi }}_{j,m}\left(\mathit{r}+{\mathit{r}}_{\mathbf{2}}\right){\mathrm{\Phi }}_{j,m}^{\ast }\left({\mathit{r}}_{\mathbf{2}}\right)}.(11)$

Use the Following Expression [45]

${\displaystyle \int d^2{\mathit{r}}_{\mathbf{2}}\mathit{exp}\left(-ik{\mu }_0\mathit{r}\times {\mathit{r}}_{\mathbf{2}}\right){\mathrm{\Phi }}_{j,m}\left(\mathit{r}+{\mathit{r}}_{\mathbf{2}}\right){\mathrm{\Phi }}_{j,m}^{\ast }\left({\mathit{r}}_{\mathbf{2}}\right)}={\mathrm{ℒ}}_{j+m}\left(u{r}^2\right),(12)$

with ${\mathrm{ℒ}}_n\left(x\right)=L_n\left(x\right)\mathit{exp}\left(-x/2\right)$ , and ${\lambda }_{j,m}={\lambda }_{j+m}={\mathrm{\Lambda }}_b$. After some operation, we have

${\mathrm{\Lambda }}_b={\displaystyle \sum _{k0=0}^b{\displaystyle \int u\left(x\right)L_{k0}^{-1/2}\left(u{x}^2\right)\mathit{exp}\left(-\frac{u{x}^2}{2}\right)}dx{\displaystyle \int u\left(y\right)L_{b-k0}^{-1/2}\left(u{y}^2\right)\mathit{exp}\left(-\frac{u{y}^2}{2}\right)dy}}.(13)$

Eq. 13 is one of the main results of this paper, which can be used to assess the conditions when the Schell-model beams with rectangular symmetry can carry the twist phase.

Analytical Formula for a Twisted Hermite-Gaussian Correlated Schell-Model Beam

In this section, we introduce a new kind of twisted partially coherent beam with nonconventional correlation function, named the twisted Hermite-Gaussian correlated Schell-model (THGCSM) beam. As a natural extension of the Hermite-Gaussian correlated Schell-model (HGCSM) beam [22], the CSD in the source plane (z = 0) is defined as

$W\left({\mathit{r}}_{\mathbf{1}},{\mathit{r}}_{\mathbf{2}}\right)=\exp \left(\frac{{\mathit{r}}_{{\mathbf{1}}^{\mathbf{2}}}+{\mathit{r}}_{{\mathbf{2}}^{\mathbf{2}}}}{4{\sigma }_0^2}\right)\frac{H_{2m}\left[\left(x_2-x_1\right)/\sqrt{2}{\mathrm{\delta }}_0\right]}{H_{2m}\left[0\right]}\exp \left[-\frac{{\left(x_2-x_1\right)}^2}{2{\mathrm{\delta }}_0^2}\right]\times \frac{H_{2n}\left[\frac{\left(y_2-y_1\right)}{\sqrt{2}{\mathrm{\delta }}_0}\right]}{H_{2n}\left[0\right]}\exp \left[-\frac{{\left(y_2-y_1\right)}^2}{2{\mathrm{\delta }}_0^2}\right]\exp \left(-ik{\mu }_0{\mathit{r}}_{\mathbf{1}}\times {\mathit{r}}_{\mathbf{2}}\right),(14)$

where r₁ = (x₁, y₁), r₂ = (x₂, y₂) are two arbitrary transverse position vectors in the source plane, σ₀ and δ₀ represent the beam width and the spatial coherence width, respectively. H_2m and H_2n are the Hermite polynomial of order 2m and 2n, respectively. After some algebra, Equation 14 can be expressed in the following alternative form

$W\left({\mathit{r}}_{\mathbf{1}},{\mathit{r}}_{\mathbf{2}}\right)=\frac{m!\sqrt{\pi }}{\mathrm{\Gamma }\left(m+1/2\right)}\frac{n!\sqrt{\pi }}{\mathrm{\Gamma }\left(n+1/2\right)}\mathit{exp}\left(\frac{r_1^2+r_2^2}{4{\sigma }_0^2}\right)L_m^{-1/2}\left[-\frac{{\left(x_2-x_1\right)}^2}{2{\mathrm{\delta }}_0^2}\right]\mathit{exp}\left[-\frac{{\left(x_2-x_1\right)}^2}{2{\mathrm{\delta }}_0^2}\right]\times L_n^{-1/2}\left[-\frac{{\left(y_2-y_1\right)}^2}{2{\mathrm{\delta }}_0^2}\right]\mathit{exp}\left[-\frac{{\left(y_2-y_1\right)}^2}{2{\mathrm{\delta }}_0^2}\right]\mathit{exp}\left(-ik{\mu }_0{\mathit{r}}_{\mathbf{1}}\times {\mathit{r}}_{\mathbf{2}}\right).(15)$

As mentioned in section 2.1, the THGCSM beam will be bona fide, if and only if the corresponding uniform source, defined as

$W_{u0}\left({\mathit{r}}_{\mathbf{1}},{\mathit{r}}_{\mathbf{2}}\right)=L_m^{-1/2}\left[-\frac{{\left(x_2-x_1\right)}^2}{2{\mathrm{\delta }}_0^2}\right]\mathit{exp}\left[-\frac{{\left(x_2-x_1\right)}^2}{2{\mathrm{\delta }}_0^2}\right]\times L_n^{-1/2}\left[-\frac{{\left(y_2-y_1\right)}^2}{2{\mathrm{\delta }}_0^2}\right]\mathit{exp}\left[-\frac{{\left(y_2-y_1\right)}^2}{2{\mathrm{\delta }}_0^2}\right]\mathit{exp}\left(-ik{\mu }_0{\mathit{r}}_{\mathbf{1}}\times {\mathit{r}}_{\mathbf{2}}\right).(16)$

is bona fide too. On substituting Equation 15 into Equation 10, and after some tedious integrations and algebraic manipulations, we have

$\begin{array}{l}{\mathrm{\Lambda }}_b={\displaystyle \sum }_{k0=0}^b\frac{2{\mathrm{\delta }}_0^2}{1+u{\mathrm{\delta }}_0^2}\frac{\mathrm{\Gamma }\left(m+k0+1/2\right)\mathrm{\Gamma }\left(n+b-k0+1/2\right)}{m!k!n!\left(b-k0\right)!}\\ {\left(\frac{u{\mathrm{\delta }}_0^2}{1+u{\mathrm{\delta }}_0^2}\right)}^{m+n}{\left(\frac{1-u{\mathrm{\delta }}_0^2}{1+u{\mathrm{\delta }}_0^2}\right)}^b{\times }_2\\ F_1\left[-m,-k0;-m-k0+\frac{1}{2};-\frac{\left(1+u{\mathrm{\delta }}_0^2\right)}{\left(1-u{\mathrm{\delta }}_0^2\right)}\right]{\times }_2\\ F_1\left[-n,k0-b;k0-b-n+\frac{1}{2},-\frac{\left(1+u{\mathrm{\delta }}_0^2\right)}{1-u{\mathrm{\delta }}_0^2}\right],\end{array}(17)$

where ₂F₁ is a hypergeometric function. So, in order for W_u to be bona fide (i.e., λ_j,m should be nonnegative), the parameter u = kμ₀ in Eq. 17 must be bounded by the following inequality:

$u{\mathrm{\delta }}_0^2\le 1.(18)$

Thus, the THGCSM beam will be bona fide, if and only if the Equation 18 is satisfied. Then, the propagation of the THGCSM beam through an ABCD optical system can be investigated with the help of the generalized Collins formula [38, 40].

$W\left({\mathit{\rho }}_{\mathbf{1}},{\mathit{\rho }}_{\mathbf{2}};z\right)=\frac{1}{{\left(\lambda B\right)}^2}\mathit{exp}\left[-\frac{ikD}{2B}\left({\rho }_1^2-{\rho }_2^2\right)\right]{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}W\left({\mathit{r}}_{\mathbf{1}},{\mathit{r}}_{\mathbf{2}}\right)}}\times \mathit{exp}\left[-\frac{ikA}{2B}\left({\mathit{r}}_{\mathbf{1}}^{\mathbf{2}}-{\mathit{r}}_{\mathbf{2}}^{\mathbf{2}}\right)\right]\mathit{exp}\left[\frac{ik}{B}\left({\mathit{r}}_{\mathbf{1}}\cdot {\mathit{\rho }}_{\mathbf{1}}-{\mathit{r}}_{\mathbf{2}}\cdot {\mathit{\rho }}_{\mathbf{2}}\right)\right]d^2{\mathit{r}}_{\mathbf{1}}{d}^2{\mathit{r}}_{\mathbf{2}},(19)$

where ρ₁ = (ρ_x1, ρ_y1) and ρ₂ = (ρ_x2, ρ_y2) are two arbitrary transverse position vectors in the observation plane, and A, B, C, D are the transfer matrix elements of an optical system. On substituting Equation 14 into Equation 19, we obtain the analytical formulae for the CSD of a THGCSM beam in the output plane as follows:

$\begin{array}{l}W\left({\rho }_1,{\rho }_2;z\right)=\frac{{\pi }^2}{{\lambda }^2{B}^2{\alpha }_1{\alpha }_2}\exp \left[-\frac{{\beta }_x^2+{\beta }_y^2}{4{\alpha }_2}\right]\exp \left[-\frac{ikD}{2B}\left({\rho }_1^2-{\rho }_2^2\right)\right]\exp \left[-\frac{k^2}{4{\alpha }_1{B}^2}{\left({\rho }_1-{\rho }_2\right)}^2\right]\\ \times {\displaystyle \sum _{k_1=0}^m{\displaystyle \sum _{k_2=0}^n{\displaystyle \sum _{p_1=0}^{k_1}{\displaystyle \sum _{p_2=0}^{k_2}\frac{m!\sqrt{\pi }}{\Gamma \left(m+1/2\right)}\frac{n!\sqrt{\pi }}{\Gamma \left(n+1/2\right)}\frac{\left(2k_1\right)}{\left(2k_1-2p_1\right)!p_1!}\frac{\left(2k_2\right)}{\left(2k_2-2p_2\right)!p_2!}\frac{{\left(-1\right)}^{k_1+k_2}}{k_1!k_2!}}}}}\\ \times \left(\begin{array}{c}n-\frac{1}{2}\\ n-k_2\end{array}\right)\left(\begin{array}{c}m-\frac{1}{2}\\ m-k_1\end{array}\right){\left(\frac{1}{2{\delta }_0^2}\right)}^{k_1+k_2}{\left(\frac{{\beta }_x}{2{\alpha }_2}\right)}^{2k_1}{\left(\frac{{\beta }_y}{2{\alpha }_2}\right)}^{2k_2}{\left(\frac{{\alpha }_2}{{\beta }_x^2}\right)}^{p_1}{\left(\frac{{\alpha }_2}{{\beta }_y^2}\right)}^{p_2},\end{array}(20)$

with

${\alpha }_1=\frac{1}{2{\sigma }_0^2};{\alpha }_2=\frac{1}{8{\sigma }_0^2}+\frac{1}{2{\mathrm{\delta }}_0^2}+\frac{k^2{\mu }_0^2}{4{\alpha }_1}+\frac{k^2{A}^2}{4{\alpha }_1{B}^2},(21)$

${\beta }_x=\frac{ik\left({\rho }_{x1}+{\rho }_{x2}\right)}{2B}+\frac{k^2{\mu }_0\left({\rho }_{y1}-{\rho }_{y2}\right)}{2{\alpha }_{1}B}+\frac{k^{2}A\left({\rho }_{x1}-{\rho }_{x2}\right)}{2{\alpha }_1{B}^2}(22)$

${\beta }_y=\frac{ik\left({\rho }_{y1}+{\rho }_{y2}\right)}{2B}-\frac{k^2{\mu }_0\left({\rho }_{x1}-{\rho }_{x2}\right)}{2{\alpha }_{1}B}+\frac{k^{2}A\left({\rho }_{y1}-{\rho }_{y2}\right)}{2{\alpha }_1{B}^2}(23)$

The spectral density of the THGCSM beam at point ρ in the receiver plane is defined as

$S\left(\mathit{\rho },z\right)=W\left(\mathit{\rho },\mathit{\rho },z\right).(24)$

The spectral degree of coherence (SDOC) of the THGCSM beam at a pair of transverse points with position vectors ρ₁ and ρ₂ in the output plane can be expressed by the formula

$\eta \left({\mathit{\rho }}_{\mathbf{1}},{\mathit{\rho }}_{\mathbf{2}};z\right)=\frac{W\left({\mathit{\rho }}_{\mathbf{1}},{\mathit{\rho }}_{\mathbf{2}};z\right)}{\sqrt{W\left({\mathit{\rho }}_{\mathbf{1}},{\mathit{\rho }}_{\mathbf{1}};z\right)W\left({\mathit{\rho }}_{\mathbf{2}},{\mathit{\rho }}_{\mathbf{2}};z\right)}}(25)$

Based on the obtained formulae above, we can study the propagation properties of a THGCSM beam in a convenient way.

Numerical Simulation of a THGCSM Beam

Paraxial Propagation of the THGCSM Beam Through an ABCD Optical System.

In this section, we study the paraxial propagation of the THGCSM beam through an ABCD optical system by applying the formulae derived in section 2. In the following examples, we consider the beam propagating in free space after passing through a lens with focal length f = 400mm, which is located at $z = 0$. The parameters of the beam and the transfer matrix are defined as λ = 632.8 nm, σ₀ = 1 mm, δ₀ = 0.5 mm, $A = 1-z/f, B = z$ , $C = -1/f$ , and $D = 1$. According to Equation 24, we calculate the normalized spectral density of a focused THGCSM beam at several propagation distances with different values of the twist factor μ₀, as shown in Figures 1, 2. One can find that when μ₀ = 0 m⁻¹ (see the first row), the THGCSM beam reduces to a HGCSM beam, and with the increase of the propagation distance, the intensity distributions of the HGCSM beam gradually change from one beam spot into two spots or four beam spots as expected [22]. From the second and third rows of Figures 1, 2, it is interesting to find that a twist phase does not seem to cause the beam to rotate during the transmission, no matter what the value of the parameters m n is. This result is quite different from that obtained in former works [37, 38], where it was shown that the twist phase would induce the beam to rotate on propagation. This phenomenon will be explained in Figure 8, by investigating the self-reconstruction characteristics of the beam spectral density. In addition, the twist phase has the effect of hindering the beam spot to split on propagation, and the larger the value of the twist factor is, the beam spot will split more difficult. This means that the twist phase plays a role preventing deterioration of the intensity distribution. Thus, the twist phase can be used to control the intensity distribution of a THGCSM beam on propagation in free space.

FIGURE 1

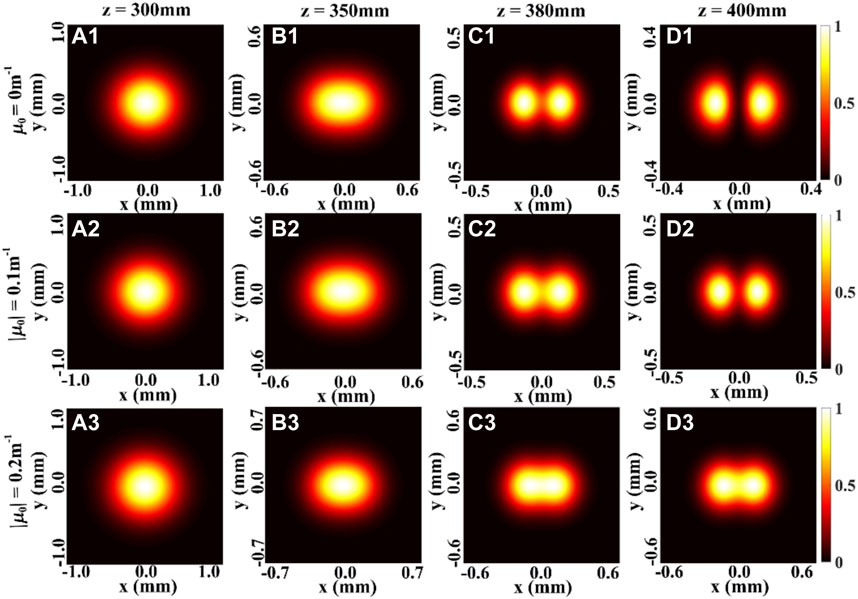
FIGURE 1. Density plot of the normalized spectral density of a focused THGCSM beam with m = 1, n = 0 for different values of the twist factor μ₀ at several propagation distances.

FIGURE 2

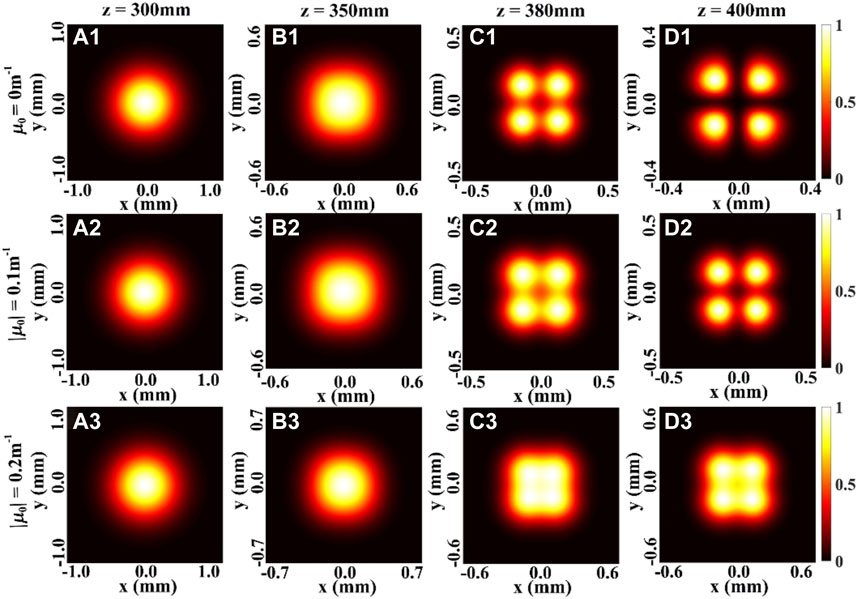
FIGURE 2. Density plot of the normalized spectral density of a focused THGCSM beam with m = 1, n = 1 for different values of the twist factor μ₀ at several propagation distances.

Then, the evolution properties the SDOC of a focused THGCSM beam on propagation also have been investigated. Figures 3, 4 show the modulus of the SDOC between two points ρ and -ρ (i.e., |η(ρ,-ρ)|), at several propagation distances with different values of the twist factor μ₀. The first row of the Figures 3, 4 show the variation of the SDOC of a focused HGCSM beam versus the propagation distances z. It is found that the distribution of the SDOC of the HGCSM beam exhibits an array distribution in the source plane (i.e., z = 0 mm), and the number of the beamlets increase as the values of the beam order m or n increase.

FIGURE 3

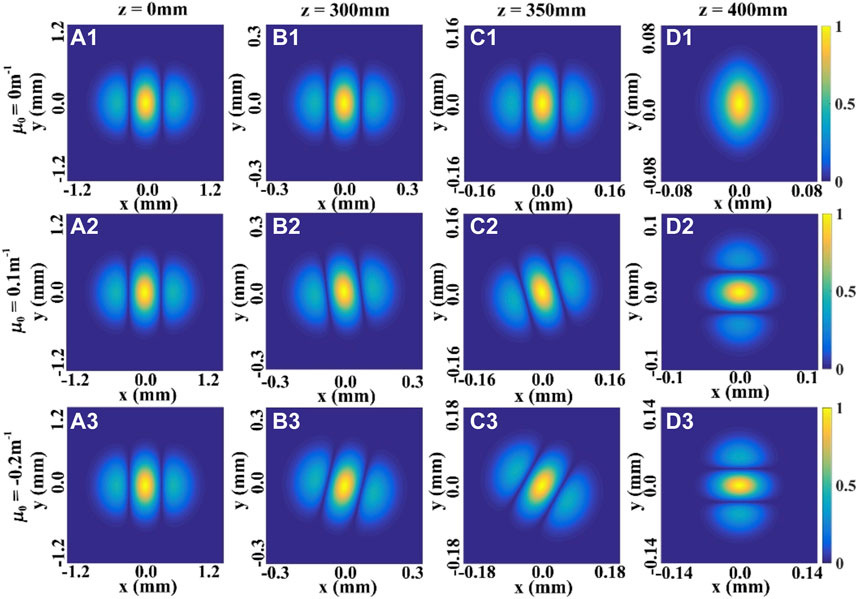
FIGURE 3. Modulus of the SDOC between two points ρ and−ρ of the THGCSM beam with m = 1, n = 0 for different values of the twist factor μ₀ at several propagation distances.

FIGURE 4

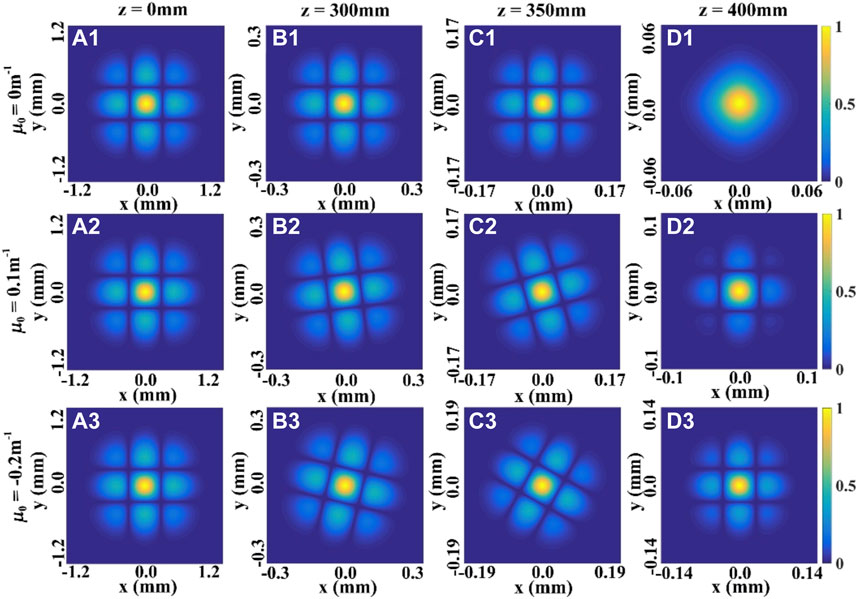
FIGURE 4. Modulus of the SDOC between two points ρ and −ρ of the THGCSM beam with m = 1, n = 1 for different values of the twist factor μ₀ at several propagation distances.

When the propagation distance z increases, the profile of the SDOC firstly remains invariant, and then becomes one beam spot in the focal plane. This means that the information regarding the SDOC is increasingly lacking with increasing propagation distance. The second and the third rows of the Figures 3, 4 show the influence of the twist phase on the evolution properties of the SDOC. We find that the twist phase induces a rotation of the SDOC on propagation, such that when μ₀ > 0, the distribution of the SDOC rotates anti-clockwise, and when μ₀ < 0, the distribution of the SDOC rotates clockwise. The SDOC rotates faster with increasing twist factor μ₀, and the rotation angle varies between −π/2 or π/2 in the focal plane. These phenomena can be explained by the fact that the twist phase imposes angular momentum on the beam. Further, one can still determine the structure of the SDOC even in the focal plane. Thus, the twist phase can be used to maintain the beam’s information of the correlation function.

In order to investigate the influence of the spatial coherence width and the twist phase on the beam propagation properties, the density plots of the normalized spectral density and the modulus of the SDOC have been studied, as shown in Figures 5, 6. In Figure 5, we calculated the density plots of the normalized spectral density and the modulus of the SDOC (|η(ρ,−ρ)|) of a focused HGCSM beam (i.e., THGCSM beam with μ₀ = 0) for different values of the spatial coherence width δ₀ in the focal plane. One can find that with the increase of the spatial coherence width, the beam profile of the HGCSM beam will evolve from the original array beam shape to a Gaussian beam profile (i.e., the self-splitting properties of the HGCSM beam on propagation gradually disappear) as expected in [22].

FIGURE 5

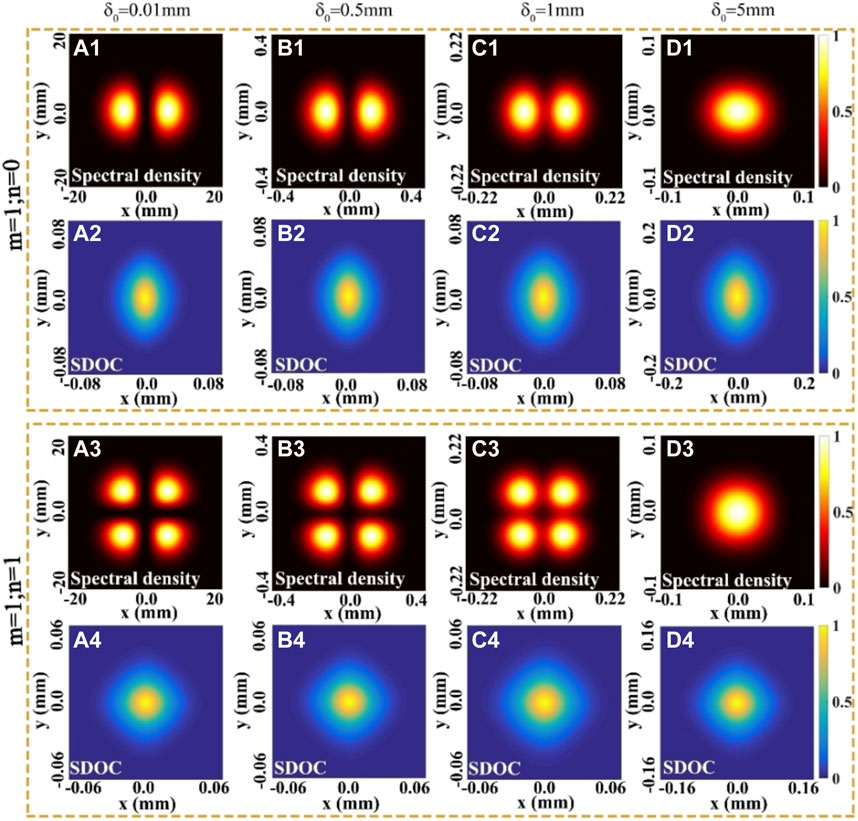
FIGURE 5. Density plots of the normalized spectral density and the modulus of the SDOC (|η(ρ,−ρ)|) of a focused HGCSM beam for different values of the spatial coherence width δ₀ in the focal plane.

FIGURE 6

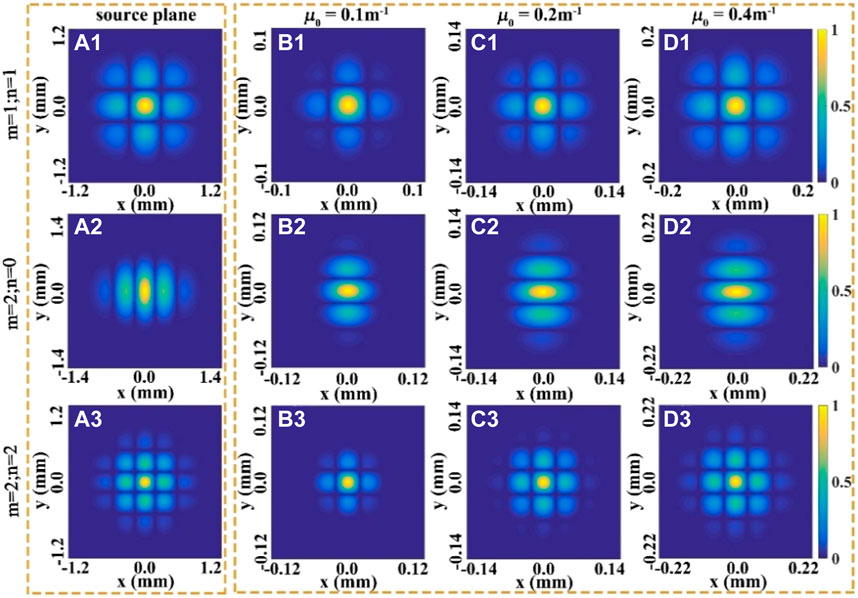
FIGURE 6. Modulus of the SDOC (|η(ρ,−ρ)|) of the THGCSM beam for different values of the twist factor μ₀ in the source and focal plane, respectively.

Moreover, regardless of the value of the spatial coherence width, the distribution of the SDOC is always maintained as a beam spot. Therefore, the ability to obtain information about the correlation function of the beam in the far field (or focal plane) cannot be improved by changing the coherence length or the order m n of the beam.

Further, we calculated the modulus of the SDOC (|μ(ρ,-ρ)|) of the THGCSM beam in the source and focal plane, respectively. It is interesting to find that with the increase of the twist factor, the strength of the sidelobes of the SDOC are enhanced. This exciting new finding may help us to find a new way to improve the reliability of the correlation function.

Self-Reconstruction Characteristics of the THGCSM Beam

In this section, we focus on the Self-reconstruction behavior of the THGCSM beam when the THGCSM beam is partially blocked by a sector-shaped opaque obstacle (SSOO) in the source plane. Figure 7 shows the illustration of a THGCSM beam self-healing process. A beam in the input plane (z = 0) is disturbed by a partially opaque obstacle in the input plane and is propagating through an ABCD optical system consisting of a lens and the free space behind the lens.

FIGURE 7

FIGURE 7. Illustration of a THGCSM beam self-healing process.

Figure 8 shows the changes of the density plot of the normalized spectral density of a focused THGCSM beam obstructed by a SSOO for different values of the twist factor at several propagation distances. From the first row of the Figure 8, one can see that with the increase of the propagation distance z, due to the effect of the correlation function, the beam splits into four beamlets as expected in [22]. The second and third row of the Figure 8 show the effect of the twist phase on the normalized spectral density. By comparing the condition μ₀ = 0.2 m⁻¹ and the condition μ₀ = −0.2 m⁻¹, we can find that the twist phase would induce the rotation of the beam on propagation: the distribution of the spectral density rotates clockwise when μ₀ > 0, the distribution of the spectral density rotates anti-clockwise when μ₀ < 0. This phenomenon is consistent with former results [37, 38]. Therefore, the twist phase actually still causes the beam to rotate during propagation, but it is not noticeable when the beam is intact (Figures 1, 2).

FIGURE 8

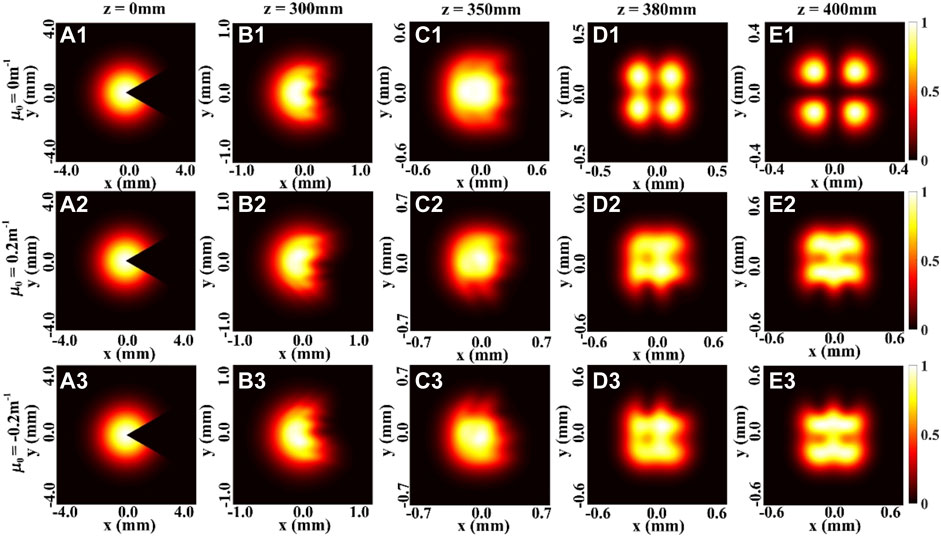
FIGURE 8. Density plot of the normalized spectral density of a focused THGCSM beam with m = 1, n = 1 obstructed by a SSOO with center angle α = π/3 for different values of the twist factor μ₀ at several propagation distances.

Moreover, Figure 9 shows the Self-reconstruction characteristics of the normalized spectral density and the modulus of the SDOC (|ηρ,−ρ)|) when the beam is obstructed by a SSOO for different values of the center angle α in the focal plane. To assess the influences of the twist parameter on the self-reconstruction capability quantitatively, a parameter named the degree of self-reconstruction D_P (i.e., $D_p=\frac{{\left[{\displaystyle \iint \langle I_{wt}\left(\mathit{\rho }\right)\rangle \langle I_{ob}\left(\mathit{\rho }\right)\rangle d^2\mathit{\rho }}\right]}^2}{{\displaystyle \iint \langle I_{wt}{\left(\mathit{\rho }\right)}^2\rangle d^2\mathit{\rho }}{\displaystyle \iint \langle I_{ob}{\left(\mathit{\rho }\right)}^2\rangle d^2\mathit{\rho }}}$ , with I_wt and I_ob stand for the beam intensities without and with obstruction, respectively) is used to characterize it [41]. It is interesting to find that even if the beam has been obstructed by a SSOO, one still can determine the information of the correlation function of an obstructed THGCSM from its SDOC distribution in the focal plane. In addition, with the increase of the center angle, the self-reconstruction capability also decreased (see the evolution of the quantity D_P in the left upper corner of the figure). Our results can find application in information transmission and recovery.

FIGURE 9

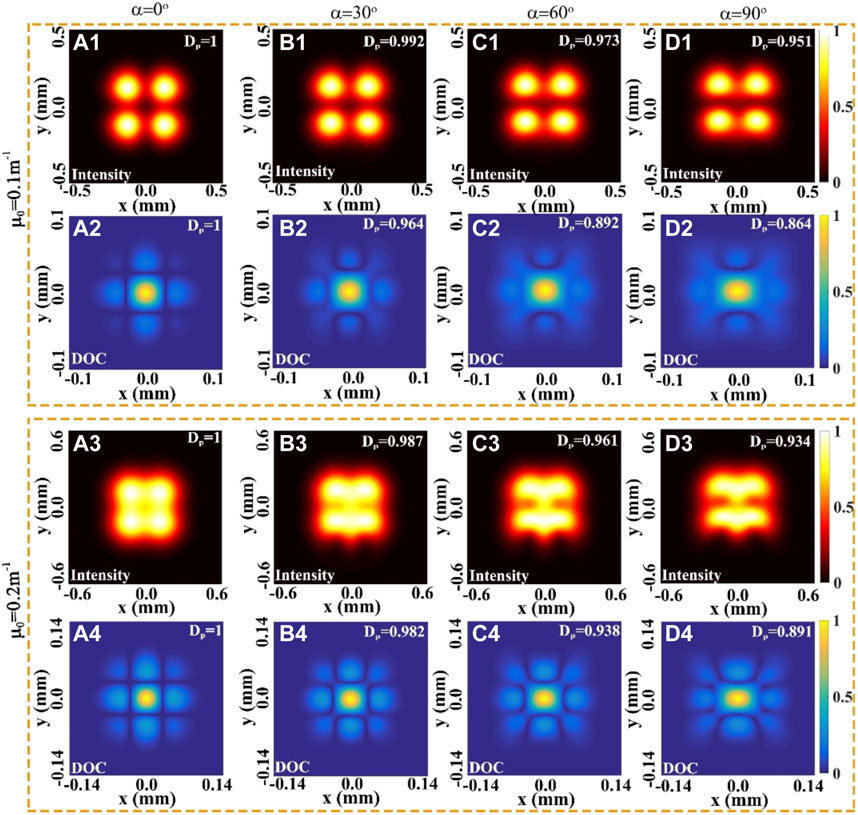
FIGURE 9. Density plot of the normalized spectral density and the modulus of the SDOC (|η(ρ,−ρ)|) of a focused THGCSM beam with m = 1, n = 1 obstructed by a SSOO for different values of twist factor μ₀ and center angle α in the focal plane.

Conclusion

In summary, we have introduced a new class of partially coherent twisted beam, named twisted Hermite-Gaussian correlated Schell-model (THGCSM) beam, and investigated its propagation properties through an ABCD optical system. The problem of when a twist phase can be imposed on Schell-model source fields with rectangular symmetries was solved. Based on the derived assessment condition, the condition that the THGCSM beam will be a bona fide one, also has been explored. The analytical expression for the CSD function of the THGCSM propagation through an ABCD optical system has been derived with the help of the generalized Collins integral formula. Based on the derived formula we have examined the evolution properties of the THGCSM beam. Our simulation results indicate that the evolution properties of the beam are closely related to the twist phase, e.g., with an increasing twist phase, the self-splitting properties of the beam gradually weaken on propagation. Further, the evolution of the SDOC also has been studied. Apart from inducing the rotation of the SDOC on propagation, the twist phase can greatly enhance the ability of the SDOC to maintain its profile on propagation, even in the focal plane. This provides a way to improve the reliability of the correlation function. Moreover, the self-reconstruction characteristics of the THGCSM beam have been explored in detail, and one can find that even if the beam has been obstructed by an opaque obstacle, one still can determine the information relating to the correlation function of an obstructed THGCSM from its SDOC distribution in the focal plane. Our results are anticipated to find applications in optical communications and information recovery.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

LeL and XP proposed the idea. LeL wrote the original manuscript. HW, LiL, YD, and FW gave suggestions in numerical simulation. XP, YC, and BH supervised the project. All authors contributed to the revision of the manuscript and approved the final version.

Funding

This work was supported by the National Natural Science Foundation of China (Nos 12192254, 11774251, 11874046, 11904247, 11974218, 12104263, 12174279); National Key Research and Development Program of China (2019YFA0705000); Natural Science Foundation of Shandong Province (ZR2021QA093); Local Science and Technology Development Project of the Central Government (Grant No. YDZX20203700001766); Innovation Group of Jinan (2018GXRC010).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Kato Y, Mima K, Miyanaga N, Arinaga S, Kitagawa Y, Nakatsuka M, et al. Random Phasing of High-Power Lasers for Uniform Target Acceleration and Plasma-Instability Suppression. Phys Rev Lett (1984) 53:1057–60. doi:10.1103/PhysRevLett.53.1057

CrossRef Full Text | Google Scholar

2. Ferri F, Magatti D, Gatti A, Bache M, Brambilla E, Lugiato LA. High-resolution Ghost Image and Ghost Diffraction Experiments with thermal Light. Phys Rev Lett (2005) 94:183602. doi:10.1103/PhysRevLett.94.183602

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Oh J-E, Cho Y-W, Scarcelli G, Kim Y-H. Sub-Rayleigh Imaging via Speckle Illumination. Opt Lett (2013) 38:682–4. doi:10.1364/OL.38.000682

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Auñón JM, Nieto-Vesperinas M. Partially Coherent Fluctuating Sources that Produce the Same Optical Force as a Laser Beam. Opt Lett (2013) 38:2869–72. doi:10.1364/OL.38.002869

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Zhao C, Cai Y. Trapping Two Types of Particles Using a Focused Partially Coherent Elegant Laguerre-Gaussian Beam. Opt Lett (2011) 36:2251–3. doi:10.1364/OL.36.002251

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Ricklin JC, Davidson FM. Atmospheric Optical Communication with a Gaussian Schell Beam. J Opt Soc Am A (2003) 20:856–66. doi:10.1364/josaa.20.000856

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Beams R, Cançado LG, Oh S-H, Jorio A, Novotny L. Spatial Coherence in Near-Field Raman Scattering. Phys Rev Lett (2014) 113:186101. doi:10.1103/PhysRevLett.113.186101

PubMed Abstract | CrossRef Full Text | Google Scholar

8. van Dijk T, Fischer DG, Visser TD, Wolf E. Effects of Spatial Coherence on the Angular Distribution of Radiant Intensity Generated by Scattering on a Sphere. Phys Rev Lett (2010) 104:173902. doi:10.1103/PhysRevLett.104.173902

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Gori F, Santarsiero M. Devising Genuine Spatial Correlation Functions. Opt Lett (2007) 32:3531–3. doi:10.1364/ol.32.003531

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Gori F, Ramírez-Sánchez V, Santarsiero M, Shirai T. On Genuine Cross-Spectral Density Matrices. J Opt A: Pure Appl Opt (2009) 11:085706. doi:10.1088/1464-4258/11/8/085706

CrossRef Full Text | Google Scholar

11. Cai Y, Chen Y, Yu J, Liu X, Liu L. Generation of Partially Coherent Beams. Prog Opt (2017) 62:157–223. doi:10.1016/bs.po.2016.11.001

CrossRef Full Text | Google Scholar

12. Cai Y, Chen Y, Wang F. Generation and Propagation of Partially Coherent Beams with Nonconventional Correlation Functions: A Review [invited]. J Opt Soc Am A (2014) 31:2083–96. doi:10.1364/JOSAA.31.002083

CrossRef Full Text | Google Scholar

13. Lajunen H, Saastamoinen T. Propagation Characteristics of Partially Coherent Beams with Spatially Varying Correlations. Opt Lett (2011) 36:4104–6. doi:10.1364/OL.36.004104

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Wang F, Liu X, Yuan Y, Cai Y. Experimental Generation of Partially Coherent Beams with Different Complex Degrees of Coherence. Opt Lett (2013) 38:1814–6. doi:10.1364/OL.38.001814

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Mei Z, Korotkova O. Random Sources Generating Ring-Shaped Beams. Opt Lett (2013) 38:91–3. doi:10.1364/OL.38.000091

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Mei Z, Korotkova O. Cosine-Gaussian Schell-Model Sources. Opt Lett (2013) 38:2578–80. doi:10.1364/OL.38.002578

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Liang C, Wang F, Liu X, Cai Y, Korotkova O. Experimental Generation of Cosine-Gaussian-Correlated Schell-Model Beams with Rectangular Symmetry. Opt Lett (2014) 39:769–72. doi:10.1364/OL.39.000769

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Chen Y, Cai Y. Generation of a Controllable Optical Cage by Focusing a Laguerre-Gaussian Correlated Schell-Model Beam. Opt Lett (2014) 39:2549–52. doi:10.1364/OL.39.002549

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Korotkova O. Random Sources for Rectangular Far fields. Opt Lett (2014) 39:64–7. doi:10.1364/OL.39.000064

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Chen Y, Wang F, Liu L, Zhao C, Cai Y, Korotkova O. Generation and Propagation of a Partially Coherent Vector Beam with Special Correlation Functions. Phys Rev A (2014) 89:13801. doi:10.1103/PhysRevA.89.013801

CrossRef Full Text | Google Scholar

21. Ma L, Ponomarenko SA. Free-space Propagation of Optical Coherence Lattices and Periodicity Reciprocity. Opt Express (2015) 23:1848–56. doi:10.1364/OE.23.001848

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Chen Y, Gu J, Wang F, Cai Y. Self-splitting Properties of a Hermite-Gaussian Correlated Schell-Model Beam. Phys Rev A (2015) 91:13823. doi:10.1103/PhysRevA.91.013823

CrossRef Full Text | Google Scholar

23. Zhu S, Chen Y, Wang J, Wang H, Li Z, Cai Y. Generation and Propagation of a Vector Cosine-Gaussian Correlated Beam with Radial Polarization. Opt Express (2015) 23:33099–155. doi:10.1364/OE.23.033099

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Chen Y, Ponomarenko SA, Cai Y. Experimental Generation of Optical Coherence Lattices. Appl Phys Lett (2016) 109:061107. doi:10.1063/1.4960966

CrossRef Full Text | Google Scholar

25. Liu X, Yu J, Cai Y, Ponomarenko SA. Propagation of Optical Coherence Lattices in the Turbulent Atmosphere. Opt Lett (2016) 41:4182–5. doi:10.1364/OL.41.004182

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Liang C, Mi C, Wang F, Zhao C, Cai Y, Ponomarenko SA. Vector Optical Coherence Lattices Generating Controllable Far-Field Beam Profiles. Opt Express (2017) 25:9872–85. doi:10.1364/OE.25.009872

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Xu Z, Liu X, Chen Y, Wang F, Liu L, Monfared YE, et al. Self-healing Properties of Hermite-Gaussian Correlated Schell-Model Beams. Opt Express (2020) 28:2828–37. doi:10.1364/OE.383805

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Gu Y, Gbur G. Scintillation of Nonuniformly Correlated Beams in Atmospheric Turbulence. Opt Lett (2013) 38:1395–7. doi:10.1364/OL.38.001395

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Liang C, Wu G, Wang F, Li W, Cai Y, Ponomarenko SA. Overcoming the Classical Rayleigh Diffraction Limit by Controlling Two-point Correlations of Partially Coherent Light Sources. Opt Express (2017) 25:28352–62. doi:10.1364/OE.25.028352

CrossRef Full Text | Google Scholar

30. Peng D, Huang Z, Liu Y, Chen Y, Wang F, Ponomarenko SA, et al. Optical Coherence Encryption with Structured Random Light. PhotoniX (2021) 2:6–15. doi:10.1186/s43074-021-00027-z

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Shen Y, Sun H, Peng D, Chen Y, Cai Q, Wu D, et al. Optical Image Reconstruction in 4f Imaging System: Role of Spatial Coherence Structure Engineering. Appl Phys Lett (2021) 118:181102. doi:10.1063/5.0046288

CrossRef Full Text | Google Scholar

32. Liu Y, Chen Y, Chen Y, Wang F, Cai Y, Liang C, et al. Robust Far-Field Imaging by Spatial Coherence Engineering. Opto-Electron Adv (2021) 4:210027. doi:10.29026/oea.2021.210027

CrossRef Full Text | Google Scholar

33. Chen Y, Wang F, Cai Y. Partially Coherent Light Beam Shaping via Complex Spatial Coherence Structure Engineering. Adv Phys X (2022) 7:2009742. doi:10.1080/23746149.2021.2009742

CrossRef Full Text | Google Scholar

34. Serna J, Movilla JM. Orbital Angular Momentum of Partially Coherent Beams. Opt Lett (2001) 26:405–7. doi:10.1364/OL.26.000405

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Simon R, Mukunda N. Twisted Gaussian Schell-Model Beams. J Opt Soc Am A (1993) 10:95. doi:10.1364/JOSAA.10.000095

CrossRef Full Text | Google Scholar

36. Friberg AT, Tervonen E, Turunen J. Interpretation and Experimental Demonstration of Twisted Gaussian Schell-Model Beams. J Opt Soc Am A (1994) 11:1818–26. doi:10.1364/JOSAA.11.001818

CrossRef Full Text | Google Scholar

37. Peng X, Liu L, Yu J, Liu X, Cai Y, Baykal Y, et al. Propagation of a Radially Polarized Twisted Gaussian Schell-Model Beam in Turbulent Atmosphere. J Opt (2016) 18:125601. doi:10.1088/2040-8978/18/12/125601

CrossRef Full Text | Google Scholar

38. Wu G. Propagation Properties of a Radially Polarized Partially Coherent Twisted Beam in Free Space. J Opt Soc Am A (2016) 33:345–50. doi:10.1364/JOSAA.33.000345

CrossRef Full Text | Google Scholar

39. Tong Z, Korotkova O. Beyond the Classical Rayleigh Limit with Twisted Light. Opt Lett (2012) 37:2595–7. doi:10.1364/OL.37.002595

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Peng X, Liu L, Wang F, Popov S, Cai Y. Twisted Laguerre-Gaussian Schell-Model Beam and its Orbital Angular Moment. Opt Express (2018) 26:33956–69. doi:10.1364/OE.26.033956

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Peng X, Wang H, Liu L, Wang F, Popov S, Cai Y. Self-reconstruction of Twisted Laguerre-Gaussian Schell-Model Beams Partially Blocked by an Opaque Obstacle. Opt Express (2020) 28:31510–23. doi:10.1364/OE.408357

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Wang H, Peng X, Liu L, Wang F, Cai Y, Ponomarenko SA. Generating Bona Fide Twisted Gaussian Schell-Model Beams. Opt Lett (2019) 44:3709–12. doi:10.1364/OL.44.003709

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Wang H, Peng X, Zhang H, Liu L, Chen Y, Wang F, et al. Experimental Synthesis of Partially Coherent Beam with Controllable Twist Phase and Measuring its Orbital Angular Momentum. Nanophotonics (2021). doi:10.1515/nanoph-2021-0432

CrossRef Full Text | Google Scholar

44. Borghi R. Twisting Partially Coherent Light. Opt Lett (2018) 43:1627–30. doi:10.1364/OL.43.001627

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Borghi R, Gori F, Guattari G, Santarsiero M. Twisted Schell-Model Beams with Axial Symmetry. Opt Lett (2015) 40:4504. doi:10.1364/OL.40.004504

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Mei Z, Korotkova O. Random Sources for Rotating Spectral Densities. Opt Lett (2017) 42:255–8. doi:10.1364/OL.42.000255

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Gori F, Santarsiero M. Devising Genuine Twisted Cross-Spectral Densities. Opt Lett (2018) 43:595–8. doi:10.1364/OL.43.000595

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Wolf E. Introduction to the Theory of Coherence and Polarization of Light [M]. Cambridge: Cambridge University Press (2007).

Google Scholar