- Department of Scientific Computing, Florida State University, Tallahassee, FL, United States
For ecoSLM—an ultra coarse-grained slip link model—the ability to use a time-step that increases with chain molecular weight is an important source of efficiency in modeling the linear rheology of monodisperse chains. This feature is labeled “temporal coarse-graining” in this paper. It is compromised for blends of linear chains, where the time-step is set by the short chains, but the length of the simulation run is determined by the long chains. The problem is present for any polydisperse sample, and is particularly acute for binary blends with widely separated molecular weights. To recover temporal coarse-graining, we propose an adaptive time-step algorithm, where the time-step is determined by the shortest unrelaxed chains in the ensemble, which increases as the simulation proceeds. It involves two additional steps: recalibration, which is triggered when any component relaxes completely, and re-equilibration, in which slip links on completely relaxed components are renewed. We obtain reasonable settings for these steps, and validate the adaptive time-step algorithm by comparing it with the original, constant time-step ecoSLM for binary, ternary, and polydisperse blends. Speedups ranging from 50 to 1,500% are obtained when molecular weights of the components are widely separated, without a significant loss of accuracy. Conversely, the adaptive time-step algorithm is not recommended when molecular weights are not well-separated, since it can be slower than the constant time-step method.
1. Introduction
Despite the popularity of the tube model (TM), the list of its shortcomings keeps getting longer when it is subjected to strong tests [1–3], and its assumptions are scrutinized more closely [4–6]. Many of these issues stem from the difficulty in accounting for the process of constraint release (CR), which is a relaxation mechanism by which stress on an internal portion of a test chain is relaxed as a neighboring chain slips away.
This is quite conspicuous even in the linear viscoelasticity (LVE) of a bidisperse mixture of long and short chains. Upon complete relaxation of the short component, does the subsequent relaxation of the long chains occur in a “skinny tube” composed of entanglements with both short and long chains, a “fat tube” composed of long-lived entanglements with other long chains, or something in between [7–9]? This question, and its implications, have sparked a long discussion on which tube to use, and when and how to switch from one to the other [3, 10–17].
Fortunately, the class of slip spring and slip link models (SLMs), despite their numerous individual differences, do not suffer from these drawbacks [2, 17–23]. They discard the notion of a tube and treat entanglements between chains in the ensemble as slip links or slip springs. SLMs reimagine CR using a simple, yet powerful, insight: when a slip link is destroyed on one of the chains due to reputation or contour length fluctuations, it is simultaneously eliminated on the “partner chain.” This gives them a structural advantage over the TM.
The catch, however, is that SLMs are computationally expensive. In this regard, they are no match for the TM, which typically predicts the LVE of linear or star polymers in a fraction of a second. This led us to pursue a “barebones” SLM, and culminated in the ecoSLM—a lightweight, ultra coarse-grained SLM, resolved at the level of an entanglement strand [24]. For many polymers, this level of coarse-graining leads to several orders of magnitude reduction in computational cost. Despite its simplicity, ecoSLM provides quantitative descriptions of the LVE of symmetric and asymmetric stars, H-polymers, and bidisperse linear blends with widely separated molecular weights [24–26].
1.1. Temporal Coarse-Graining in ecoSLM
ecoSLM's combination of speed and accuracy is attractive, and keeps alive the dream of model-based analytical rheology, which involves thousands of trials and model evaluations [27–32]. For a long time, ecoSLM remained as an effective, albeit informal, Markov Chain Monte Carlo (MCMC) algorithm. The underlying mathematical model was not explicitly specified. Recently however, this deficiency was rectified by articulating the master equation animating the Monte Carlo algorithm, and a microscopic model with repulsive interactions between adjacent slip links, which justifies the quadratic fluctuation potential used (the MCMC algorithm and potential are described in section 2.1) [33]. As a result, ecoSLM rests on firmer mathematical ground, which exposes an interface that allows fine-grained SLMs to systematically couple with it.
Due to the level of coarse-graining, it comes as no surprise that the ecoSLM is far from a zero-parameter model. Besides inputs like the entanglement molecular weight Me and plateau modulus G0, it needs additional parameters that are not required for other SLMs. As a kinetic Monte Carlo algorithm, ecoSLM links real and Monte Carlo time using a “time shift” parameter τ0 ≈ τe, the equilibration time of an entanglement strand. More importantly [33], the dependence of friction on chain length in the underlying Fokker-Planck equation has to be specified. It can be obtained from fine-grained SLMs, or from experiments by fitting viscosity data on monodisperse chains [24]. It is loosely related to the average time required to equilibrate slack along its axis [24]. As an approximation, the dependence of the friction coefficient on chain length (expressed as the average number of slip links per chain) can be folded into the scaling between real and Monte Carlo time via a time shift factor . Fits to experimental data on linear polymers suggest γ ≈ 1.4 ± 0.1 [24, 33].
The time shift factor σt results in “temporal coarse-graining.” As shown in section 2.1, the time-step Δt corresponding to a Monte Carlo trial increases with chain length as . Since relaxation time increases with chain length, roughly as , the ability to use a larger time-step is an important source of efficiency for the ecoSLM. It allows the ecoSLM to model ensembles of thousands of monodisperse linear chains with hundreds of entanglements each, in under a minute.
1.2. The Problem With Polydispersity
Typical industrial polymers have broad molecular weight distributions (MWD) that are determined by the method of synthesis [34]. In contrast, model polymers, often synthesized using living polymerizations [35, 36], have relatively low polydispersity. Popular implementations of the TM deal with polydispersity by creating an ensemble of chains from the MWD [37–39]. The same approach can be employed with multi-chain SLMs, although it is less common due to increased computational cost [26, 40–42]. Recent work on discretizing nearly monodisperse MWD (polydispersity index ≲ 1.1) recommends using a “blend of monodisperse fractions” of f = 5−10 suitably selected chain lengths [43].
Blends of polymers with widely separated molecular weights hamper the boost provided by temporal coarse-graining in ecoSLM. For example, in a bidisperse blend of short () and long () chains, the time-step is controlled by the short chains , even though the final simulation time is set by the terminal relaxation time of long chains, which may be crudely approximated as . The total computational cost increases with Tsim/Δt, and can get quite expensive for . The problem may be exacerbated for polydisperse samples represented using f fractions , since the final simulation time is set by the longest chain, while the time-step is set by the shortest chain. Due to this bottle-neck, it is easier for ecoSLM to model a monodisperse polymer with using a large time-step, than a mildly polydisperse sample with , where is the weight-averaged number of slip links, and Δt is set by the shortest chains in the ensemble.
1.3. Motivation and Scope
In blends of monodisperse fractions, the constant time-step in ecoSLM is governed by the shortest chains in the ensemble. This principal goal of this work is to explore whether we can release this constraint. It considers the possibility of pursuing an adaptive time-step kinetic Monte Carlo strategy, where Δt increases as the simulation proceeds. Strangely, this harkens back to the idea of tube dilation or dynamic dilution used in the TM, where CR in entangled polymers is modeled as an effective widening of the tube [9, 44, 45]. As stress-bearing strands relax, they are viewed as “solvent,” whose primary action on the remaining unrelaxed fraction is mediated through a frictional drag that effectively rescales time. A conceptually similar approach may be considered in the ecoSLM to mitigate the loss of temporal coarse-graining in polydisperse mixtures. Once the shortest chains in the ensemble have completely relaxed, the time-step is increased, and determined by the chain length of the shortest unrelaxed chains. In the absence of CR, when the chains are decoupled, this idea is perfectly sound (see section 3). However, such relaxation in a “thin tube” is cannot explain the speeding up of long chains diluted with short chains [9–11, 13, 46, 47], when CR is switched on.
Instead of resorting to theory to determine the extent of acceleration a priori [3, 17], we adopt an empirical approach in the spirit of adaptive time-step solvers for ordinary differential equations [48]. For illustration, consider a bidisperse blend. Upon complete relaxation of short chains, we separately evolve the dynamics using two different timesteps: corresponding to the short chains, and corresponding the longer chains. That is, we repeat a small stretch of the simulation using both fine-grained and coarse-grained time-steps. We compare the evolution using the two different time-steps to figure out the correction or acceleration to be applied to the coarse-grained timestep. This is still to be understood as an approximation, where we hope to trade a small amount of accuracy for the potential of a sizable improvement in speed.
In section 2.3, the proof-of-concept idea of adaptive time-step (ATS) ecoSLM is fleshed out, and tested thoroughly on bidisperse blends in section 3.1. It involves two steps, recalibration and re-equilibration, that are absent in the standard or constant time-step (CTS) version of ecoSLM. In section 3.2, we extend this analysis to ternary blends, and show how this method enables us to compute the linear rheology of model polymers with modest polydispersity at a reasonable computational cost. Throughout, we treat the original CTS ecoSLM as the gold standard, and measure changes in accuracy and speed with reference to it.
2. Methods
ecoSLM is a multi-chain (uses an ensemble of hundreds to thousands of chains), virtual-space (spatial coordinates of slip links are not explicitly tracked) SLM, that records the evolution of a small number of state variables. It assumes that chains adopt Gaussian conformations, which implies that it cannot be used to predict nonlinear rheology, where this assumption is violated. Nevertheless, it can be used to compute the LVE of arbitrary mixtures of polymers, by monitoring macroscopically measurable time-correlation functions such as stress and dielectric relaxation [25].
In the following, the standard constant time-step algorithm (CTSA) is first recapitulated for monodisperse linear polymers. Next, generalization of the CTSA to polydisperse polymers is described, with an emphasis on bidisperse mixtures. Subsequently, an adaptive time-step algorithm (ATSA) for polydisperse polymers is described. This method entails recalibration (RC) and reequilibration (RE) steps to account for fast relaxing components.
2.1. CTSA: Monodisperse Linear Chains
Consider an ensemble of n chains with an average of slip links per chain, where M is the molecular weight, and Me is the entanglement molecular weight. Each chain experiences Brownian motion that can destroy or create new slip links at chain ends. The instantaneous number of slip links on chain i, denoted by Zi, fluctuates around the average value (marked with an overbar). Note that Zi is an integer, even though can take non-integer values. These fluctuations are governed by changes in total potential energy,
where the quadratic fluctuation potential for chain i is given by,
Throughout this work, energy is expressed in units of kBT, where kB is Boltzmann's constant, and T is the absolute temperature. This potential was originally derived by balancing the Gaussian spring force compressing a chain, with a fictitious force pulling on its ends [49]. The quadratic form of the potential with ν = 3/2 arises from the assumption of a Gaussian chain [49–51].
On the other hand, Schieber considered a single chain SLM [52], where the number of slip links was treated as a stochastic variable controlled by an effective chemical potential. Uneyama and Masubuchi subsequently used the label “non-interacting” slip links to describe this microscopic model [53], because the slip links were treated as phantom objects that could pass through one another. For sufficiently long chains near equilibrium, this model also leads to a quadratic fluctuation potential with ν = 1/2, instead of 3/2. This formalism can be extended to include repulsive interaction between adjacent slip links so that they cannot pass through one another [52]. This results in higher values of ν [53]. Under reasonable assumptions, it takes the form used currently in the ecoSLM with a weak dependence on that converges to 3/2 for long chains [33],
A constant value of ν = 3/2 was used in most previous studies using the ecoSLM [24–26]. Fortunately, for monodisperse linear polymers, comparison of simulations with ν = 3/2, and those using Equation (3) indicate that when terminal relaxation is not governed by deep retraction of chain ends, predictions of LVE are somewhat insensitive to the precise value of ν [33]. A vivid example where this is not true is the relaxation of a well-entangled star in a permanent network.
In the ecoSLM, slip links represent a physical entanglement between two chains. The state of pair-wise entanglement between slip links is described using a connectivity map C(·, ·). Let (i, j) represent the jth slip link on chain i, which is paired with the slip link (i′, j′). Duality stipulates that,
where 1 ≤ j ≤ Zi, and . Self-entanglements are forbidden, 1 ≤ i ≠ i′ ≤ n. Thus, the state of the system at any instant can be described by specifying the number of slip links on each chain {Zi}, and the connectivity map C. The underlying master equation and microscopic model are specified in [33].
To compute time-correlation functions such as stress relaxation, it is necessary to track auxiliary properties of slip links. Under the assumption of Gaussian chain conformations, stress arises from unrelaxed chain segments between slip links [54–56]. The normalized stress relaxation function ϕ(t) is the fraction of original segments that survive at time t [24]. Therefore, it is helpful to tag each slip link as “original” (surviving from time t = 0), or “new” (resulting from a creation move during the simulation).
ecoSLM is initialized by creating an ensemble of n chains with slip links each. The connectivity map C is initialized by pairing slip links randomly. A short “burn-in” run is performed to equilibrate the system. All the slip links in the ensemble are initially tagged as “original.” The MCMC algorithm used to propagate the dynamics is fleshed out as Algorithm 1 (Supplementary Material). Since no comparisons are made with experiments or other simulations in this work, we set τ0 = 1, G0 = 1, and γ = 1.4 throughout this paper, without any loss of generality. The timestep, defined as , is normalized by the number of chains to make simulations independent of system size.
The coupling between slip links on different chains accounts for CR. If desired CR can be turned off by breaking this association, and setting C(i, j) = null. This is useful to study dynamics of a chain in a fixed or permanent network, or to isolate the effects of CR. When CR is turned off, the dynamics are modified to an average of n independent, non-interacting, single chain simulations. During the creation and destruction moves, there is no partner slip link (i′, j′) to consider, and the change in energy ΔU = ΔUi (instead of ) reflects this.
2.2. CTSA: Polydisperse Blends
Let us now generalize this method to a polydisperse blend with f distinct components or fractions. That is, the ensemble consists of n1 chains with slip links, n2 chains with slip links, and so on until f chains with slip links each. Throughout this work, we shall assume that components are listed in increasing order of chain lengths (). To simplify the description, we shall also provisionally assume that this is the order in which the components relax, although we can work around this requirement by simply reordering the components. The weight fraction of component c is,
The CTSA is presented as Algorithm 2 (Supplementary Material); its overall structure is similar to Algorithm 1.
Since there is more than one component, we have to generalize three choices: (i) the timestep Δt, (ii) the probability ρc of picking component c for creation or destruction of slip links, and (iii) the probability of selecting a partner chain during a creation step. For monodisperse chains described earlier, (i) , (ii) ρ1 = 1 (single component), and (iii) the probability of selecting “component 1” as a partner is also 1.
For polydisperse polymers, it can be shown that the time step Δt [24],
where is the time-step associated with component c. To understand its ramifications, it is illustrative to consider an equimolar bidisperse blend (n1 = n2), where component 1 (2) corresponds to the short (long) chains. If, for example, and , Δt2 ≈ 25Δt1, assuming γ = 1.4. Since Δt in Equation (6) is controlled by the smallest timestep, we find Δt ≈ Δt1. This is what we mean by “time-step is controlled by short chains.”
The probability ρc of picking component c for creation or destruction of slip links can be shown to be [24],
From Equation (6), it is clear that . For the equimolar bidisperse blend with and , this implies ρ1 ≈ 0.96. This combination of large ρ1, which means the short chain is usually selected for a creation or destruction move, and small Δt ≈ Δt1 conspire to slow the simulation down enormously. In this example, ecoSLM takes ≈ 0.1 s and ≈ 23 s of CPU time to compute the LVE of n = 1, 000 monodisperse chains with 10 and 100 slip links, respectively. For an equimolar bidisperse blend with n1 = n2 = 500, the computational time increases 6x to ≈120 s.
Finally, during a creation step the probability of selecting a chain belonging to the cth component is proportional to its weight fraction wc [24]. Note that for monodisperse chains, these choices collapse to the usual settings considered in Algorithm 1 (Supplementary Material). Another limiting case (and indeed the method used to originally justify these choices) is the no CR case, where the calculation simplifies to a series of independent simulations.
2.3. ATSA: Polydisperse Blends
The goal of the ATS algorithm (ATSA) is to mimic the response [ϕ(t)] of the CTSA for polydisperse blends at a lower computational cost. This is accomplished by mitigating the primary factor (size of time-step) responsible for the loss of ecoSLM's “temporal coarse-graining” feature for monodisperse polymers. Unsurprisingly, the ATSA is similar to the CTSA described previously, with two additional ingredients: recalibration (RC) and re-equilibration (RE). It takes the same inputs as the CTSA, viz. an ensemble of f monodisperse fractions where nc (number of chains) and (average number of slip links) corresponding to component c = 1, 2, ⋯ , f are specified at the outset.
For a polydisperse sample, the ATSA initially proceeds just like the CTSA, with timestep Δt and ρc given by Equations (6) and (7), respectively. Consequently, the normalized stress relaxation ϕ(t) is initially identical. At some point , all the original slip links on the shortest chains (component 1 with slip links) are replaced with new ones. The stress associated with chains belonging to this component is completely relaxed. In the language of the tube model, it is now effectively a “solvent.”
Let us illustrate the subsequent steps in the ATSA without considering the RC and RE steps. As shown later in Figure 4A, this setting is appropriate when CR is switched off, and the f components in the polydisperse mixture relax independently. In this setting, for , where is the time at which the stress corresponding to component k has completely relaxed, the timestep Δt is reset according to,
Comparing with Equation (6), we note that the time-step is governed only by fractions that have not completely relaxed yet. The probability of picking component c for creation or destruction steps ρc is adjusted so that ρc = 0 for all fractions that are completely relaxed. We renormalize the other probabilities so that,
Note that only unrelaxed components are selected for creation or destruction steps. Let us examine how this applies to the equimolar bidisperse case with and considered previously (but with CR switched off for now). Upon relaxation of the short polymers, the timestep is switched to Δt = Δt2 according to Equation (8). This implies a 25x increase in the time step from Δt ≈ Δt1 to Δt = Δt2, and a corresponding decrease in computational cost. Equation (9) implies that we reset ρ1 = 0 and ρ2 = 1, so that only long chains are selected for creation and destruction moves.
When CR is switched on, the interaction between components has to be accounted for, as alluded to earlier. Note that for , while only unrelaxed chains (c > k) are selected for creation and destruction moves, completely relaxed short chains (c ≤ k) may still be selected as partner chains. The probability of selecting a partner chain belonging to component c is wc, as before. The acceleration in the dynamics due to the relaxed fraction (“fat tube” vs. “thin tube”) is modeled by the RC step. In contrast to the CTSA, completely relaxed components are not explicitly chosen for creation or destruction; we attempt to indirectly account for the renewal of slip links on these shorter chains by periodic RE steps (see Figure 1).
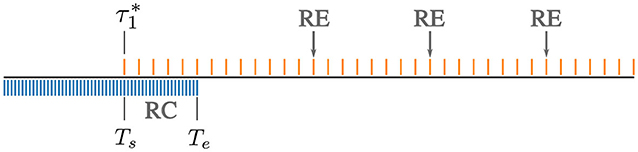
Figure 1. Structure of ATSA. For a bidisperse blend of short and long chains, the fine-grained time-step Δtfg (blue grid) is initially controlled by the short chains. Recalibration (RC) is triggered at time , when the short chains completely relax. For times Ts ≤ t ≤ Te, the dynamics are evolved using two time-steps Δtfg (blue) and a larger coarse-grained Δtcg (orange). Beyond, Te the suitably adjusted larger time-step is used to further evolve the dynamics. Re-equilibration (RE) is performed periodically, approximately at intervals of starting from time Te.
2.3.1. Recalibration
RC is triggered when all the original slip links belonging to component k are completely replaced. Let us denote the start of a RC step by , where the subscript “s” denotes the “start” time. It is easiest to illustrate this method for a bidisperse blend as depicted schematically in Figure 1. To anchor to a specific example, we go back to the equimolar (n1 = n2= 500) bidisperse blend with and . Here, the initial time-step Δt ≈ Δt1 ≈ 0.05, which is about 25x smaller than Δt2 ≈ 1.26. Recall that time is reported in units of τ0 throughout this work. Using this small time-step (depicted by the fine grid in Figure 1), we find that 15,000.
Let Te > Ts denote the time corresponding to the “end” of the RC step. Here we set Te = 2Ts ≈ 30,000. We propagate the dynamics in the time interval Ts ≤ t ≤ Te using two different timesteps: a fine-grained (or “current”) time step Δtfg, and a coarse-grained timestep Δtcg. In our example, Δtfg ≈ Δt1 ≈ 0.05, and Δtcg = Δt2 ≈ 1.26. In general, upon complete relaxation of component k for a polydisperse mixture,
In the first pass, we continue calculating ϕ(t) over the interval Ts ≤ t ≤ Te with time step Δtfg (fine grid in Figure 1). Let us denote this ϕ(t) with a subscript as ϕfg(t). In the second pass, we recompute dynamics over the interval Ts ≤ t ≤ Te with the larger time step Δtcg, and label the corresponding response as ϕcg(t). For our particular bidisperse example, the relevant portion of the relaxation window (marked by Ts and Te) is shown in Figure 2. The blue and orange curves correspond to ϕfg(t) and ϕcg(t), respectively.
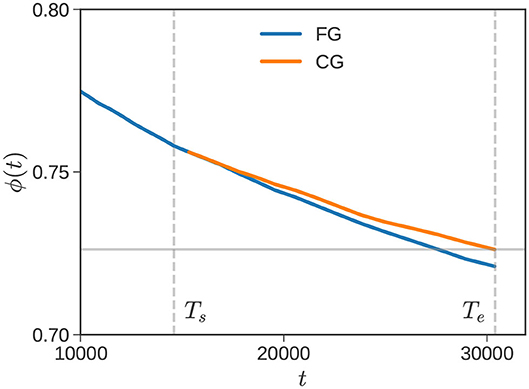
Figure 2. Recalibration. Vertical dashed lines mark Ts and Te for an equimolar mixture of , where dynamics are propagated using a fine-grained (blue) and coarse-grained (orange) time-step. The horizontal line marks ϕcg(Te), which is used to find the RC scaling factor frc.
With CR switched on, the coarse-grained calculation results in slower relaxation, because it ignores the acceleration in dynamics due to the relaxed fraction. In this work, we quantify the extent of acceleration using a scalar factor frc. We define , where is defined by asserting . The temporally coarse-grained timestep is then set to,
In the bidisperse blend example considered in Figure 2, ϕcg(Te) = 0.726, which is shown by the gray horizontal line. The time at which it intersects the ϕfg curve is , so that frc = 0.94. The calculation for t > Te is performed with a time-step recalibrated as Δt = 0.94Δtcg ≈ 1.18, in this example. This is still of order Δt2, but is subtly corrected to account for accelerated dynamics. It is evident from Figure 2 that the scaling factor frc depends on Te. It increases with Te initially, approaching a constant value for sufficiently large Te. We section 3, we revisit this issue quantitatively.
A recalibration step is initiated when one of the components completely relaxes. Thus, for a binary blend, there is a single recalibration step that occurs, when the short chains relax. For a polydisperse blend with f fractions, there may be up to f − 1 RC steps. The time-step after each RC event increases, and is set by the smallest unrelaxed fraction, suitably modified to account for acceleration via frc.
2.3.2. Re-equilibration
In the ATSA, the identity of a completely relaxed species is retained after all its slip links are replaced. In particular, relaxed components continue to serve as partner chains for the remaining unrelaxed components. The RE step, which refreshes the connectivity information of all the completely relaxed species, by sampling from the equilibrium distribution, is initiated periodically (see schematic in Figure 1). This connectivity altering step has no instantaneous effect on the stress, since it does not affect original slip links. However, it can alter the subsequent course of evolution.
Again, it is easiest to describe the RE step for a bidisperse blend with short and long chains. We shall discuss the frequency of re-equilibration after we discuss what a RE step entails. Consider a time , when the short chains have completely relaxed, but the long chains still bear significant amount of residual stress. If a RE step is initiated, the number distribution of slip links on the short chains and their connectivity is resampled from the equilibrium distribution in three steps:
1. all the existing slip links on the short chains are destroyed;
2. using the fluctuation potential (Equation 2), the number of new slip links on these short chains Zi are directly sampled;
3. partner chains for these newly created slip links are selected as in the creation step, i.e., in proportion to the weight fraction of all chains.
The time interval between RE steps, Tre, may be approximated in several ways. The simplest method is to set . However, we recognize that is the result of one numerical experiment, and like all extreme value measurements, it is noisy. Therefore, it is perhaps useful to sample Tre from a distribution. From numerical experiments, results are found to be somewhat insensitive to the precise method used, with a few caveats that are discussed in section 3. Thus, here, we describe a simple method (based on assumptions that we know are not strictly valid) that is easy to implement. Surprisingly, it appears to work as well as other, more sophisticated, methods.
Suppose the relaxation time of the component 1 is τ1, so that the probability that a chain is unrelaxed at time t may be approximated by the survival probability, . Now consider an ensemble of n1 similar chains; if we assume that the relaxation of these chains proceeds independently, then the probability that all the chains in the ensemble have relaxed at time t is given by,
We assume that is one observation from this cumulative probability distribution. Subsequent RE times Tre may also be sampled from this distribution. The probability density function (PDF) is obtained by differentiating Equation (12) with respect to t as,
Figure 3 plots πens(t) as a function of the number of chains n1. The distribution gets wider as the number of chains n1 decreases, reflecting the increased uncertainty in overinterpreting a single observed value of . We identify the observed value with the most probable value of the PDF (the maxima of the PDF). With this approximation, it can be shown that . Armed with this information, we can sample Tre from πens(Tre) using standard sampling techniques.
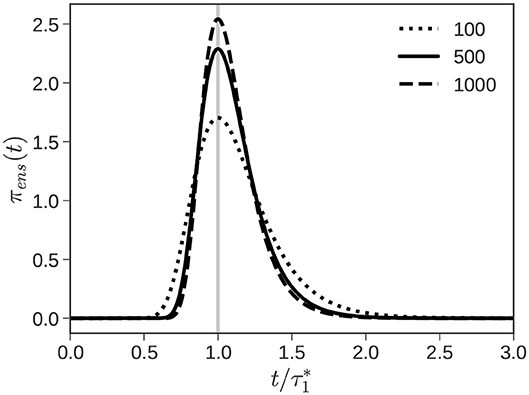
Figure 3. Reequilibration. The PDF (Equation 13) from which the RE time Tre is sampled narrows as the number of chains n1 increases from 100 to 1,000.
To complete the discussion, we tie couple of loose threads. First, the time elapsed since the last RE step Telapse is tracked, and a new RE step is carried out when it exceeds Tre. The clock is reset (Telapse = 0), and a new Tre is drawn from πens(Tre). For a binary blend, RE is performed “most probably” around , as shown in Figure 3. Second, the extension to the polydisperse case is straightforward. We record the time for the last component to completely relax , and the time elapsed since the previous RE step, Telapse, as before. A RE step in which all the relaxed components i ≤ k are re-equilibrated is carried out when Telapse exceeds Tre. Salient modifications to the CTSA are highlighted in Algorithm 3 (Supplementary Material).
3. Results and Discussion
The two main features of the ATSA are (i) partial recovery of temporal coarse-graining due to larger time-steps upon complete relaxation of a component, and (ii) corrections due to RC and RE steps that account for accelerated dynamics in the presence of CR. When CR is switched off, the second feature becomes irrelevant as the chains relax independently. To test this, we first perform a simulation in which CR is suppressed.
As a base case, we consider a bidisperse blend with at a weight fraction of w1 = 0.5. We use n1 = 800 and n2 = 200 chains for an ensemble of 1,000 total chains. Figure 4A compares the ϕ(t) obtained from the CTSA and ATSA, averaged over five independent replicas. The agreement between the two curves is excellent. The dashed and dotted lines depict the ϕ(t) of the monodisperse short and long chains, respectively. The terminal relaxation of the bidisperse blend is controlled by the relaxation of the long chains.

Figure 4. CR switched off and on. Normalized stress relaxation of a bidisperse blend () with w1 = w2 = 0.50 using the CTSA (solid blue) and ATSA (dashed orange). The dashed and dotted gray lines mark the normalized stress relaxation of the monodisperse and components, respectively. The vertical gray line marks , when the stress associated with the short chains is completely relaxed. CR is switched off in (A), but switched on in (B), where the dashed, dotted, and solid black lines show the ATS calculation without RC, RE, and both RC and RE, respectively.
In the CTSA, a constant time-step of Δt ≈ 0.03 (via Equation 6) is held fixed through the simulation. The ATSA starts with this small value for Δt. At , the short chains completely relax, shown by vertical gray line in Figure 4A. Since CR is suppressed, the RC step is irrelevant (even if it is artificially triggered it leads to frc ≈ 1). Thus, for , Δt is temporally coarse-grained to Δt = Δt2 ≈ 0.875, according to Equation (11). Again, since CR is suppressed, the RE step is irrelevant, and does not affect the evolution of the system, even if it is artificially triggered.
In this particular example, the final simulation time where ϕ(t) falls below the threshold 10−4, is . The ATSA thus uses the smaller Δt = Δt1 for the first 0.1% of the simulation, and switches to a time-step that is 30x larger for the remaining 99.9% of the simulation. This is reflected in the significantly faster runtimes: on a single modern CPU, the ATSA takes 0.23 s, while the CTSA takes 3.03 s. Due to (common) overhead associated with operations like initialization, file input and output etc., the gain is smaller than the theoretical maximum of 30x.
Figure 4B repeats the calculation on this bidisperse blend, but with CR switched on. As before, the dashed and dotted gray lines depict the response of the monodisperse constituents. It should be noted that these responses are not the same as in Figure 4A, because CR is active even in the monodisperse samples. The CTSA response is shown as a solid blue line, and when the short chains completely relax is marked with a vertical gray line. The ATSA response with both RC and RE steps included is shown by the dashed orange line, and is in excellent agreement with the CTSA. Since a larger time-step is used, the ATS calculation is ~6x faster than the CTS calculation (0.27 vs. 1.63 s).
Figure 4B also shows the impact of not incorporating the RC or RE steps. When neither RC nor RE steps are included, the response obtained is shown by the solid black line. This response is much slower than response of the CTSA. This shows why the RC and RE steps are important when CR is switched on; in contrast, Figure 4A in unaffected by the inclusion or exclusion of the RE or RC steps. The effect of including RC (RE) while excluding RE (RC) is shown by the dotted (dashed) black line in Figure 4B. Note that in the “no RC” case, we assume frc = 1. As expected, including either of these steps accelerates dynamics, and pushes the response toward the CTSA; when both steps are included simultaneously, the ATS calculation essentially overlaps with the CTS response.
Next, we isolate and study different aspects and choices of the ATSA, primarily for binary blends. Based on calculations on a number of different binary blend systems, we study the speed versus accuracy tradeoff. We then show that the method still works for ternary blends, and finish by computing the LVE of a polydisperse sample.
3.1. Bidisperse Blend
We start by exploring the choices made in the RC and RE steps for the “base case” bidisperse blend (, with w1 = 0.5) studied above. For the RC step, we study the effect of the size of the interval Te − Ts on the recalibration factor frc. For the RE step, we study the effect of RE frequency Tre on the dynamics.
3.1.1. RC Overlap Duration
In the ATSA, the RC step involves repeating a FG and CG calculation over a time period Ts ≤ t ≤ Te (see Figures 1, 2 for example). For binary blends, is the time when the short chains completely relax. The stress relaxation for the bidisperse blend () with w1 = 0.50, previously shown in Figure 4B, is zoomed into in Figure 5. The CTS (solid blue), ATS (dashed orange), and (vertical gray) lines are the same.
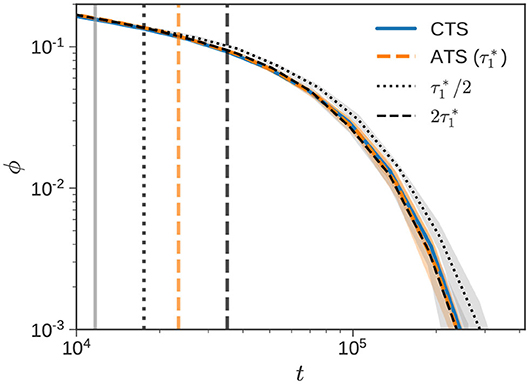
Figure 5. Recalibration duration. Normalized stress relaxation of the bidisperse blend () with w1 = 0.50 reported in Figure 4B is zoomed into. The CTS (solid blue), ATS (dashed orange), and (vertical gray) lines are identical. The dotted and dashed black curves denote ATS simulations performed where Te is selected according to and , respectively. Vertical lines of the same kind mark Te. In the standard ATSA, (dashed orange).
We use three different choices for the duration of the RC step, namely , , and . The default choice in the ATSA corresponds to , which is shown by the dashed orange curve. The interval over which the RC step is carried out corresponds to the distance between the vertical gray line (Ts) and the vertical dashed orange line (Te). The other two choices explore what happens when we increase or decrease Te around this choice. When the RC time interval is doubled (dashed black) to , the effect of the resulting ϕ(t) is essentially negligible. However, when the RC time interval is halved (dotted black) to , the predicted response is noticeably slower.
The origin of this slow response can be traced back to frc. For , frc ≈ 0.9, whereas for the two longer RC intervals frc ≈ 0.8. This difference may be understood through the lens of Figure 2. When RC interval is small, the “distance” between the FG and CG curves is small. In this regime, increasing the interval, leads to a decrease in frc. Beyond a certain point (comparable with ), frc approximately settles to a constant value. This phenomenon is also on display in Figure 4B, when we consider the curves corresponding to “no RC” (frc = 1) and the CTSA. In this particular figure, we can think of the CTSA as the FG calculation, and the “no RC” case as the CG calculation with a long Te. On a log-log plot, frc corresponds to the “horizontal distance” between the no RC and CTSA curves. After the short chains completely collapse (vertical gray line), the two curves separate out. Beyond a certain point comparable with , this distance becomes approximately constant, and corresponds to a constant value of frc.
For this reason, it is better to err on the side of using a longer RC interval. However, the computational cost increases with Te − Ts, since two different calculations (FG and CG) are performed over the same interval. In practice, we find that using offers a reasonable trade-off. It is simpler to justify, since we seek to approximate processes faster than the timescale at which the short chains have completely relaxed into a simple scalar factor. Indeed, it is possible to develop more sophisticated estimates of frc by monitoring the evolution of frc as a function of the RC interval. In particular, we could track the first derivative dfrc/dTe to further optimize the algorithm. Since this is a proof-of-concept paper, we do not perform this analysis here. However, it might definitely be a worthwhile idea to pursue.
3.1.2. RE Frequency
In the ATSA, we sample the RE time Tre from the PDF πens given by 13. As shown in Figure 3, for bidisperse blends, the PDF has a maxima at , and its width depends on the number of short chains n1 in the ensemble. As n1 → ∞, the PDF converges to a Dirac delta function .
Figure 6 zooms in on the CTSA and ATSA results depicted in Figure 4B to highlight the relaxation response around (denoted by vertical gray line), and beyond. As observed previously, the agreement between the ATSA and CTSA is excellent. We first consider the alternative of using a constant frequency of (solid black line), instead of sampling stochastically from πens. We note from the figure, that this simple choice also performs quite well, especially considering the uncertainty associated with the simulation. From experience with a number of different bidisperse samples, it appears that using a constant leads to slightly slower relaxation than sampling from the PDF πens. If we artificially set a higher RE frequency , we obtain the dotted line in Figure 6, which provides a better correspondence with the CTS calculation. Decreasing the frequency to (dashed line), results in significantly slower relaxation, as expected.
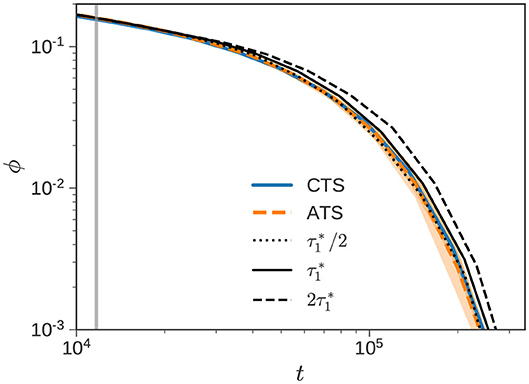
Figure 6. Re-equilibration frequency. Normalized stress relaxation of the bidisperse blend () with w1 = 0.50 reported in Figure 4B is zoomed in. The CTS (solid blue), ATS (dashed orange), and (vertical gray) lines are identical. The dashed, solid, and dotted black lines denote ATS simulations performed with constant , and , respectively.
It is interesting that stochastically sampling Tre from a PDF with a maxima at has roughly the same effect as choosing a constant for this example. It is possible to conceive of different RE algorithms. For example, instead of completely re-equilibrating all the short chains at a constant or stochastic RE time Tre, we could re-equilibrate a fraction of the slip links on the completely relaxed chains more frequently. We did not explore this direction in this work, since the ATSA, as specified, appears to offer a good compromise between simplicity and effectiveness.
3.1.3. Speed and Accuracy
Thus far, we have primarily focused on a single bidisperse blend with . In this part, we vary the molecular weight of the long chain = 20, 40, and 80, and the composition of the blend w1 = 0.25, 0.5, 0.75. The array of panels in Figure 7 compares the ATSA and CTSA for these 9 cases. Note that the base case is plotted at the center.
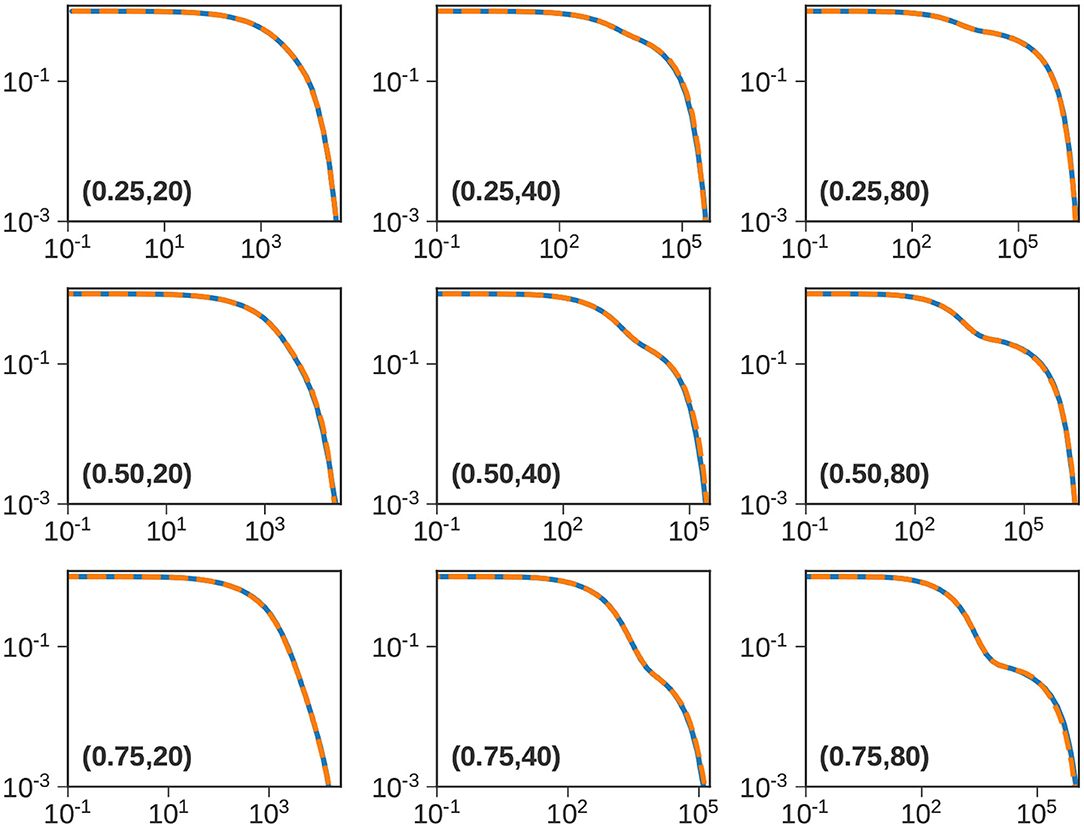
Figure 7. Bidisperse blends. Normalized stress relaxation predictions [ϕ(t) vs. t] using the CTS (solid blue) and ATS (dashed orange) methods with . The composition (w1) and long chain length () are indicated in parenthesis. Note that the figure in the center corresponds to the base case studied in Figure 4B.
From left to right, the length of the long chain increases, and from top to bottom, the fraction of the short chain w1 increases. When , the lengths of the two components are comparable, and we do not observe a distinct shoulder. For and 80, however, we can distinguish the relaxation of the short and the long chains. As w1 increases, the height of the shoulder which arises primarily from entanglements between long chains, decreases (approximately as ) [24]. It is clear from Figure 7 that the ATSA does a remarkable job of approximating the ϕ(t) obtained from the CTSA.
Figure 8 studies trends in these systems more quantitatively. The four subfigures explore (Figure 8A) the variation of the scaling factor frc, (Figure 8B) the time at which the short chains completely collapse , (Figure 8C) the speedup obtained by using the ATS approximation, and (Figure 8D) the error incurred in the approximation. These factors are plotted as a function of w1, with as a parameter.
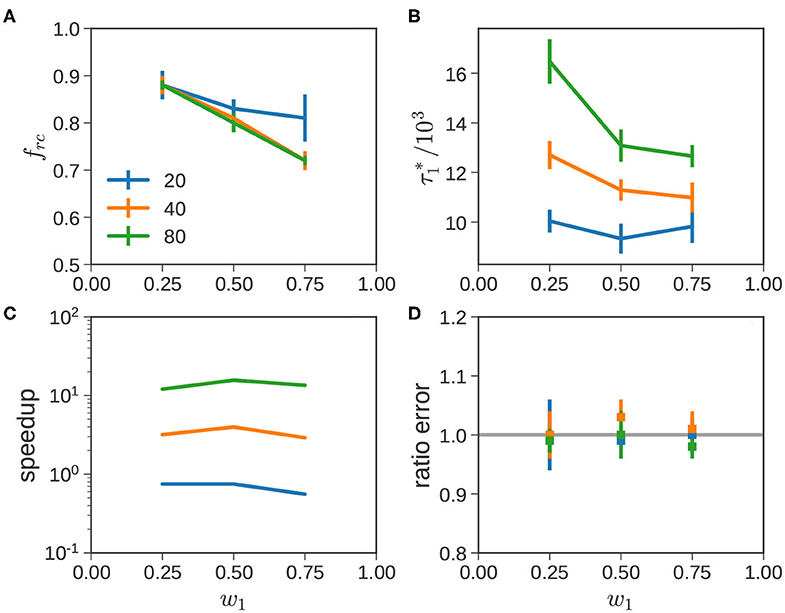
Figure 8. Bidisperse blends quantitative analysis. The acceleration factor frc (A), (B), speedup due to ATSA (C), and the difference between the ATS and CTS responses (D) are shown for the blends considered in Figure 7. In each subfigure, the blue, orange, and green lines depict , 40, and 80, respectively.
From Figure 8A, we note that frc decreases with increasing fraction of short chains w1. This indicates a stronger acceleration of the dynamics of the long chains, as they are diluted with an increasing amount of short chains. This trend may be justified using the lens of tube dilation in the TM. While the correspondence is not perfect, fs = 1 roughly corresponds to relaxation of the long chain in a thin tube. As w1 increases, the tube dilates, leading to progressively faster dynamics. For monodisperse long chains, corresponding to w1 = 0, we expect frc = 1.0, independent of . Thus, we would expect the three curves to approximately overlap at small w1. Beyond this early regime, frc appears to decrease with initially at a fixed w1, but appears to settle to a constant value for = 40 and 80.
In Figure 8B, increases as or w2 increase. When increases, the relaxation of the short chains is slowed because the lifetime of slip links associated with long chains increases. When w2 increases, the fraction of short-long slip links increase thereby increasing the average lifetime of slip links on short chains, leading to a slowdown in relaxation. It is useful to compare these to that in Figure 4A when CR is completely suppressed and the dynamics of the short chains are decoupled from both long chains and other short chains. In this scenario, , is independent of or w2. It represents an upper-threshold; when CR is turned back on, begins to approach this level as increases. This is especially pronounced near w1 → 0 for long , where nearly all the slip links on the short chains are paired with relatively long-lived slip links on longer chains.
We measure speed up in Figure 8C using the ratio of the CPU times required for the ATSA and CTSA calculations. When the computational cost is same or comparable, the speedup is approximately one; larger (smaller) values denotes improvement (deterioration) in computational efficiency. The first thing that is visible from Figure 8C is that the ATSA improves as increases. In comparison, the variation with blend composition at a given value of is relatively modest. For = 40 and 80, speedups of 3–6x and 10–15x are obtained, respectively. Interestingly, the speedup is in the range of 0.55–0.8x for . Since this is less than one, it implies that we are actually worse off with the approximate method. How does this happen? ATSA requires additional overhead during the recalibration process including repeating the calculation with two different timesteps, besides additional file operations. This fixed cost cannot be amortized over the relatively short remainder of the simulation, with only a marginally larger Δt corresponding to . In general, speedups from the ATSA for binary blends are greatest, when the terminal relaxation time is much greater than (or ), where the cost of the overhead can be spread over a long simulation run with a much larger timestep.
We measure accuracy of the ATSA by comparing it with the CTSA, which is treated as a gold-standard. Let the response of the CTS and ATS calculations be labeled as ϕcts(t) and ϕats(t), respectively. In the best case scenario, the two curves are identical, and their ratio r(t) = ϕats(t)/ϕcts(t) ≡ 1. However, since ecoSLM is a stochastic simulation, we would not expect this equality to hold even for two independent runs using the CTSA. The variability between different runs has to be accounted for. We use the ratio as an error measure instead of the difference |ϕats(t) − ϕcts(t)| for two reasons. First, the ATS calculation initially (when ϕ values are largest) exactly follows the CTS calculation and does not contribute to error. Often after a RC event a substantial fraction of the initial stress has relaxed, and the values of ϕ are small, which might potentially understate the possible deviations between ATSA and CTSA. Second, since ϕ(t) typically displayed on a log-log plot, a ratio is a geometric better measure of the difference between two curves.
In Figure 8D, we incorporate the variability between different runs, and plot the mean value of the ratio . We observe is tightly clustered around its expected value. This indicates that the ATSA provides a reasonably approximation to the CTSA, across all blends. Overall, this presents the advantages and disadvantages of the ATSA. For , which present the hardest cases for the CTSA, the ATSA provides speed ups of an order of magnitude or more without much loss in accuracy. Conversely, when is not significantly greater than , it is preferable to use the CTSA. This will manifest itself again, when we consider polydisperse samples below.
3.2. Ternary and Polydisperse Blends
We briefly consider extensions to ternary blends (f = 3), and a single polydisperse sample with f = 8. For the ternary blend, we consider chains with , and a total of ~2,000 chains in the ensemble. We consider two different compositions: (i) equal number fraction so that the same number of chains (n1 = n2 = n3 = 667) are used for each component, and (ii) equal weight fraction, so that w1 = w2 = w3 ≈ 1/3. This case corresponds to n1 = 1, 450, n2 = 362, and n3 = 186.
Figure 9 plots the ϕ(t) using the CTSA and ATSA. As before, the ATSA offers a good approximation to the ϕ(t) obtained from the CTSA for both cases. The corresponding to the component is approximately 17.4 × 103 and 16.4 × 103 for the equal number and weight fraction calculations, respectively. This decrease is directionally consistent with Figure 8B, where for a given blend decreases as w1 increases. A similar decrease is also observed for the component, with for the equal number fraction case, decreasing to 1.1 × 106 for the equal weight fraction case.
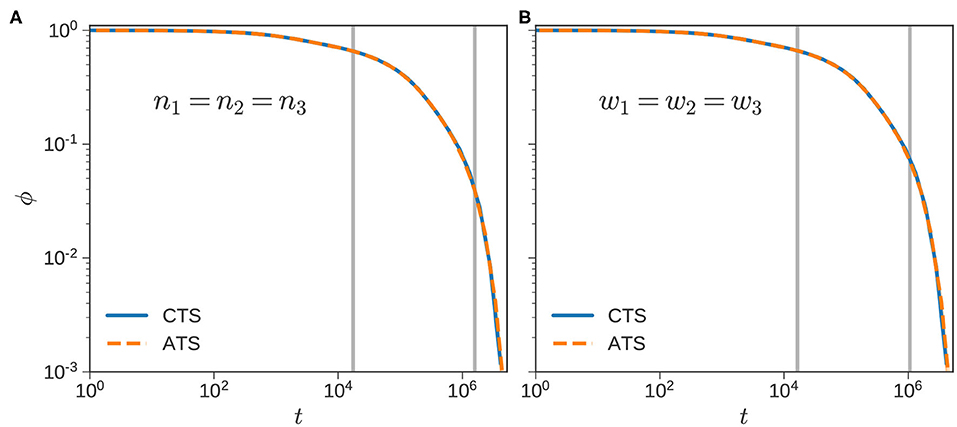
Figure 9. Ternary blends. Normalized stress relaxation curves using the CTS (blue) and ATS (dashed orange) algorithms for ternary blends with . The number and weight fractions of the components are equal in (A,B), respectively. The gray lines mark and in both subfigures mark the times at which components 1 and 2 relax completely.
The speedups obtained using the ATSA are 2.7x and 6.5x for the equal number and weight fraction calculations, respectively. Note that varies inversely with the number of chains of a particular species in the ensemble. In the equal weight fraction case, the time step following the first RC step increases to 0.34 compared to 0.18 for the equal number fraction case. After the second RC step, the corresponding numbers for Δt are 2.0 and 0.67, respectively. Thus, the difference in the speed-ups is largely explained by the larger time-steps in the equal weight fraction case.
Finally, Figure 10 uses a blend of f = 8 monodisperse fractions to represent a polydisperse sample with weight-averaged number of slip links and polydispersity index of 1.2. A log-normal distribution is assumed, and the method outlined in [43] is used to obtain the chain lengths and weight fractions of the components. The average number of slip links of the components range from to 138. Note that the time-steps (Equation 6) corresponding to the shortest and longest chains differ by a factor of 30.
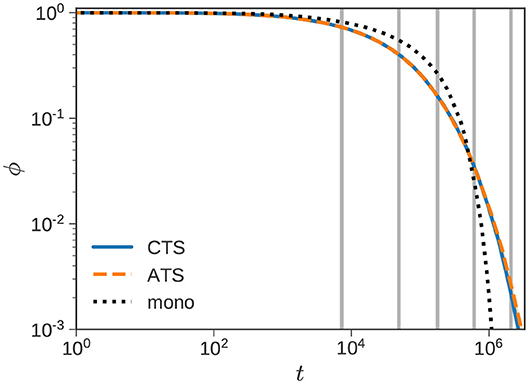
Figure 10. Polydisperse sample. Normalized stress relaxation of a sample with , and polydispersity index of 1.2 using f = 8 fractions. Gray lines indicate complete relaxation of shorter components. The dotted line shows ϕ(t) of a monodisperse polymer with .
The dotted line shows the sharp stress decay of a monodisperse polymer with . The response of the polydisperse sample shows a wider spread of timescales as expected. The agreement between the CTSA and the ATSA is quite good. Due to the smooth unimodal distribution, we do not observe multiple shoulders in the figure following the complete relaxation (indicated by vertical gray lines) of faster components. On average it took 13.5 s of CPU time to compute the ATSA response. While this is indeed faster than the CTSA, it represents speedup of a modest factor of 1.5. While a 50% improvement in speed is quite substantial, it is far from the order of magnitude improvement in computational efficiency observed for binary blends with widely separated chain lengths.
The polydisperse example is also significant because it shows both the promise and limits of the ATSA. We obtain a substantial improvement in speed (50%) without sacrificing accuracy too much. However, the improvement in speed is nevertheless underwhelming. The underlying reason is not dissimilar from the blend studied in Figure 8. The RC step following the complete relaxation of a species requires an investment of resources that is recouped subsequently. Small or modest increases in the time step, impairs the potential speedup of the ATSA, and as observed previously, it is indeed possible for the ATSA to underperform the CTSA.
When a polydisperse sample is discretized the chain lengths of consecutive components are not widely separated. In this case, the number of slip links are , and the corresponding number of chains are {ni} = {6, 66, 296, 626, 630, 300, 68, 8}. There is of course room for improvement of the ATSA. In the current version, a RC step is triggered when any component completely collapses. It is possible to imagine an algorithm in which an RC step is triggered only when a significant jump in time-step (Δtcg/Δtfg) is on the table. Such an algorithm, or some variation thereof, would essentially revert to CTSA, and avoid situations like the blend studied previously. It also has the potential to improve performance on polydisperse samples where the change in timestep may not always be significant.
4. Summary
For monodisperse polymers, the standard or CTSA algorithm for ecoSLM has a desirable property of temporal coarse graining which permits larger time-steps for longer chains, thereby expediting the simulation. However, this property is compromised for blends of polymers, and is keenly evident in binary blends with widely separated molecular weights. Here, the time-step is limited by the short chains, while terminal relaxation is governed by the long chains. The primary contribution of this paper is an ATSA for ecoSLM which recovers, at least partially, this lost property of temporal coarse-graining. The goal of the ATSA is to mimic the CTSA at a significantly lower computational cost.
In the ATSA, the time-step is determined by the shortest unrelaxed chains in the ensemble, which increases as the simulation proceeds. It involves two additional steps: recalibration and re-equilibration. During recalibration, which is triggered when any component completely relaxes, we repeat a segment of the simulation with fine-grained and coarse-grained time-steps, to figure out the appropriate Δt. A re-equilibration step, in which slip links on completely relaxed components are renewed, is triggered periodically. Both steps are necessary to get the ATSA to match the CTSA. Since this is a proof-of-concept paper, we did not fully optimize the recalibration and re-equilibration steps. For RC, we found that setting the duration of the RC step to Te ≈ 2Ts or slightly larger is sufficient. For RE, we found that stochastically drawing provides reasonable results.
For binary blends, we validated the ATSA by comparing it with the CTSA for a variety of different chain lengths and blend compositions. As an approximation, the accuracy of the ATSA was found to be within an acceptable range, without any systematic deviations. From an efficiency standpoint, the sweet spot for the ATSA is when , where speedups of orders of magnitude are possible. On the flip side, when , the ATSA can actually be slower than the CTSA, as the overhead associated with the RC and RE steps cannot be sufficiently amortized over a short simulation run with a marginally larger time-step.
For a ternary blend with two different blend compositions, we again observed a reasonable tradeoff between speed and accuracy, with speedups between 2.5 and 6x for the two cases studied. We also studied a polydisperse sample with f = 8 fraction, seeking to mimic the response of a log-normal distribution with a modest polydispersity index. For this case, the ATSA was found to be 50% faster than the CTSA. While significant, this is somewhat muted because the chain lengths of the fractions are not spaced sufficiently apart, and the change in Δt following a RC step is not always significant. We discussed potential ways to improve the performance of the ATSA further. The ATSA resembles to the idea of dynamic tube dilation in the tube model. However, instead of using theory to determine the extent of “tube dilation,” it determines it empirically by matching the response with that of the CTSA. It might be most useful for star-linear, star-star blends, or other branched polymers like H-polymers or combs where the disparity in relaxation times can be wider.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
SS designed the study, wrote the code, performed calculations, and assembled results for this paper.
Funding
This work was based in part upon work supported by the National Science Foundation under grant no. NSF DMR-1727870.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.579499/full#supplementary-material
References
1. Wang SQ. The tip of iceberg in nonlinear polymer rheology: entangled liquids are solids. J Polym Sci B. (2008) 46:2660–5. doi: 10.1002/polb.21588
2. Desai PS, Kang BG, Katzarova M, Hall R, Huang Q, Lee S, et al. Challenging tube and slip-link models: predicting the linear rheology of blends of well-characterized star and linear 1,4-polybutadienes. Macromolecules. (2016) 49:4964–77. doi: 10.1021/acs.macromol.5b02641
3. Read DJ, Shivokhin ME, Likhtman AE. Contour length fluctuations and constraint release in entangled polymers: slip-spring simulations and their implications for binary blend rheology. J Rheol. (2018) 62:1017–36. doi: 10.1122/1.5031072
4. Shanbhag S, Park SJ, Zhou Q, Larson RG. Implications of microscopic simulations of polymer melts for mean-field tube theories. Mol Phys. (2007) 105:249–60. doi: 10.1080/00268970601143333
5. Wang SQ. Nonlinear rheology of entangled polymers at turning point. Soft Matter. (2015) 11:1454–8. doi: 10.1039/C4SM02664K
6. Schweizer KS, Sussman DM. A force-level theory of the rheology of entangled rod and chain polymer liquids. I. Tube deformation, microscopic yielding, and the nonlinear elastic limit. J Chem Phys. (2016) 145:214903. doi: 10.1063/1.4968516
7. Marrucci G. Relaxation by reptation and tube enlargement: a model for polydisperse polymers. J Polym Sci. (1985) 23:159–77. doi: 10.1002/pol.1985.180230115
8. Doi M, Graessley WW, Helfand E, Pearson DS. Dynamics of polymers in polydisperse melts. Macromolecules. (1987) 20:1900. doi: 10.1021/ma00174a035
9. Viovy JL, Rubinstein M, Colby RH. Constraint release in polymer melts - tube reorganization versus tube dilation. Macromolecules. (1991) 24:3587–96. doi: 10.1021/ma00012a020
10. Park SJ, Larson RG. Tube dilation and reptation in binary blends of monodisperse linear polymers. Macromolecules. (2004) 37:597–604. doi: 10.1021/ma0343683
11. Watanabe H, Ishida S, Matsumiya Y, Inoue T. Test of full and partial tube dilation pictures in entangled blends of linear polyisoprenes. Macromolecules. (2004) 37:6619–31. doi: 10.1021/ma0495689
12. Lee JH, Fetters LJ, Archer LA, Halasa AF. Tube dynamics in binary polymer blends. Macromolecules. (2005) 38:3917–32. doi: 10.1021/ma040080h
13. Park SJ, Larson RG. Long-chain dynamics in binary blends of monodisperse linear polymers. J Rheol. (2006) 50:21–39. doi: 10.1122/1.2127907
14. van Ruymbeke E, Masubuchi Y, Watanabe H. Effective value of the dynamic dilution exponent in bidisperse linear polymers: from 1 to 4/3. Macromolecules. (2012) 45:2085–98. doi: 10.1021/ma202167q
15. Watanabe H, Matsumiya Y, van Ruymbeke E. Component relaxation times in entangled binary blends of linear chains: reptation/CLF along partially or fully dilated tube. Macromolecules. (2013) 46:9296–312. doi: 10.1021/ma4018795
16. van Ruymbeke E, Shchetnikava V, Matsumiya Y, Watanabe H. Dynamic dilution effect in binary blends of linear polymers with well-separated molecular weights. Macromolecules. (2014) 47:7653–65. doi: 10.1021/ma501566w
17. Read DJ, Jagannathan K, Sukumaran SK, Auhl D. A full-chain constitutive model for bidisperse blends of linear polymers. J Rheol. (2012) 56:823–73. doi: 10.1122/1.4707948
18. Nair DM, Schieber JD. Linear viscoelastic predictions of a consistently unconstrained brownian slip-link model. Macromolecules. (2006) 39:3386–97. doi: 10.1021/ma0519056
19. Masubuchi Y, Watanabe H, Ianniruberto G, Greco F, Marrucci G. Comparison among slip-link simulations of bidisperse linear polymer melts. Macromolecules. (2008) 41:8275–80. doi: 10.1021/ma800954q
20. Khaliullin RN, Schieber JD. Application of the slip-link model to bidisperse systems. Macromolecules. (2010) 43:6202–12. doi: 10.1021/ma902823k
21. Langeloth M, Masubuchi Y, Böhm MC, Müller-Plathe F. Reptation and constraint release dynamics in bidisperse polymer melts. J Chem Phys. (2014) 141:194904-1–7. doi: 10.1063/1.4901425
22. Shivokhin ME, van Ruymbeke E, Bailly C, Kouloumasis D, Hadjichristidis N, Likhtman AE. Understanding constraint release in star/linear polymer blends. Macromolecules. (2014) 47:2451–63. doi: 10.1021/ma402475a
23. Katzarova M, Kashyap T, Schieber JD, Venerus DC. Linear viscoelastic behavior of bidisperse polystyrene blends: experiments and slip-link predictions. Rheol Acta. (2018) 57:327–38. doi: 10.1007/s00397-018-1079-7
24. Shanbhag S. Fast slip link model for bidisperse linear polymer melts. Macromolecules. (2019) 52:3092–103. doi: 10.1021/acs.macromol.8b02367
25. Shanbhag S, Larson RG, Takimoto J, Doi M. Deviations from dynamic dilution in the terminal relaxation of star polymers. Phys Rev Lett. (2001) 87:195502. doi: 10.1103/PhysRevLett.87.195502
26. Shanbhag S, Larson RG. A slip link model of branch-point motion in entangled polymers. Macromolecules. (2004) 37:8160–6. doi: 10.1021/ma034532m
27. Janzen J, Colby RH. Diagnosing long-chain branching in polyethylenes. J Mol Struct. (1999) 486:569–84. doi: 10.1016/S0022-2860(99)00097-6
28. Wood-Adams PM, Dealy JM. Using rheological data to determine the branching level in metallocene polyethylenes. Macromolecules. (2000) 33:7481–8. doi: 10.1021/ma991534r
29. Shanbhag S. Analytical rheology of blends of linear and star polymers using a Bayesian formulation. Rheol Acta. (2010) 49:411–22. doi: 10.1007/s00397-010-0443-z
30. Shanbhag S. Analytical rheology of branched polymer melts: Identifying and resolving degenerate structures. J Rheol. (2011) 55:177–94. doi: 10.1122/1.3523627
31. Takeh A, Worch J, Shanbhag S. Analytical rheology of metallocene-catalyzed polyethylenes. Macromolecules. (2011) 44:3656–65. doi: 10.1021/ma2004772
32. Shanbhag S. Analytical rheology of polymer melts: state of the art. ISRN Mater Sci. (2012) 2012:732176. doi: 10.5402/2012/732176
33. Shanbhag S. Mathematical foundations of an ultra coarse-grained slip link model. J Chem Phys. (2019) 151:044903. doi: 10.1063/1.5111032
34. Peebles LH. Molecular Weight Distributions in Polymers. Vol. 18. New York, NY: Interscience Publishers (1971).
36. Webster OW. Living polymerization methods. Science. (1991) 251:887–93. doi: 10.1126/science.251.4996.887
37. Das C, Inkson NJ, Read DJ, Kelmanson MA, McLeish TCB. Computational linear rheology of general branch-on-branch polymers. J Rheol. (2006) 50:207–34. doi: 10.1122/1.2167487
38. Park SJ, Shanbhag S, Larson RG. A hierarchical algorithm for predicting the linear viscoelastic properties of polymer melts with long-chain branching. Rheol Acta. (2005) 44:318–30. doi: 10.1007/s00397-004-0415-2
39. Wang ZW, Chen X, Larson RG. Comparing tube models for predicting the linear rheology of branched polymer melts. J Rheol. (2010) 54:223–60. doi: 10.1122/1.3301246
40. Valadez-Pérez NE, Taletskiy K, Schieber JD, Shivokhin M. Efficient determination of slip-link parameters from broadly polydisperse linear melts. Polymers. (2018) 10:908. doi: 10.3390/polym10080908
41. Taletskiy K, Tervoort TA, Schieber JD. Predictions of the linear rheology of polydisperse, entangled linear polymer melts by using the discrete slip-link model. J Rheol. (2018) 62:1331–8. doi: 10.1122/1.5033858
42. Katzarova M, Andreev M, Sliozberg YR, Mrozek RA, Lenhart JL, Andzelm JW, et al. Rheological predictions of network systems swollen with entangled solvent. AIChE J. (2014) 60:1372–80. doi: 10.1002/aic.14370
43. Shanbhag S. How many monodisperse fractions are required to discretize polydisperse polymers? Macromol Theory Simul. (2020) 29:2000020-1–8. doi: 10.1002/mats.202000020
44. Ball RC, Mcleish TCB. Dynamic dilution and the viscosity of star polymer melts. Macromolecules. (1989) 22:1911–3. doi: 10.1021/ma00194a066
45. McLeish TCB. Why, and when, does dynamic tube dilation work for stars? J Rheol. (2003) 47:177–98. doi: 10.1122/1.1529174
46. Watanabe H, Matsumiya Y, Inoue T. Dielectric and viscoelastic relaxation of highly entangled star polyisoprene: quantitative test of tube dilation model. Macromolecules. (2002) 35:2339–57. doi: 10.1021/ma011782z
47. Matsumiya Y, Masubuchi Y, Inoue T, Urakawa O, Liu CY, van Ruymbeke E, et al. Dielectric and viscoelastic behavior of star-branched polyisoprene: two coarse-grained length scales in dynamic tube dilation. Macromolecules. (2014) 47:7637–52. doi: 10.1021/ma501561y
48. Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical Recipes. 3rd Edn. The Art of Scientific Computing. New York, NY: Cambridge University Press (2007).
49. Doi M, Kuzuu NY. Rheology of star polymers in concentrated-solutions and melts. J Polym Sci C. (1980) 18:775–80. doi: 10.1002/pol.1980.130181205
50. Pearson DS, Helfand E. Viscoelastic properties of star-shaped polymers. Macromolecules. (1984) 17:888–95. doi: 10.1021/ma00134a060
51. Shanbhag S, Larson RG. Chain retraction potential in a fixed entanglement network. Phys Rev Lett. (2005) 94:076001. doi: 10.1103/PhysRevLett.94.076001
52. Schieber JD. Fluctuations in entanglements of polymer liquids. J Chem Phys. (2003) 118:5162–6. doi: 10.1063/1.1553764
53. Uneyama T, Masubuchi Y. Detailed balance condition and effective free energy in the primitive chain network model. J Chem Phys. (2011) 135:184904. doi: 10.1063/1.3658775
54. Larson RG. Structure and Rheology of Complex Fluids. New York, NY: Oxford University Press (1998).
55. Uneyama T. Single chain slip-spring model for fast rheology simulations of entangled polymers on GPU. Nihon Reoroji Gakkaishi. (2011) 39:135–52. doi: 10.1678/rheology.39.135
Keywords: slip links, coarse-graining, Monte Carlo, adaptive time step, algorithm
Citation: Shanbhag S (2020) Temporal Coarse-Graining in a Slip Link Model for Polydisperse Polymer Melts. Front. Phys. 8:579499. doi: 10.3389/fphy.2020.579499
Received: 02 July 2020; Accepted: 03 September 2020;
Published: 14 October 2020.
Edited by:
Chunggi Baig, Ulsan National Institute of Science and Technology, South KoreaReviewed by:
Jay Schieber, Illinois Institute of Technology, United StatesYuichi Masubuchi, Nagoya University, Japan
Copyright © 2020 Shanbhag. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sachin Shanbhag, c3NoYW5iaGFnQGZzdS5lZHU=
 Sachin Shanbhag
Sachin Shanbhag