Synchronizability of Multilayer Networks With K-nearest-neighbor Topologies

In this paper, the synchronizability of multilayer K-nearest-neighbor networks is studied by using the master stability function method. The analytical expressions for the eigenvalues of the supra-Laplacian matrix are given for two-layer and multilayer K-nearest-neighbor networks. In addition, the impacts of various topological parameters (such as the network size, the node degree, the number of layers, the intra-layer and the inter-layer coupling strengths) on the network synchronizability are discussed. Finally, the theoretical results are verified through numerical simulation.

1. Introduction

Since the appearance of small-world networks and scale-free networks [1, 2], complex networks have attracted much attention due to their pervading through various scientific fields. Till now, complex networks have been applied in nature and society, such as scientific cooperation networks, information networks, biological networks, power grids, social networks, and so on [3, 4]. Recently, a new description of the complex network called the multilayer network, where nodes interact with more than one type of links, was put forward and gradually became an important branch of complex networks [5–8].

Synchronization, as a significative collective behavior on complex networks, has been widely and extensively discussed during the past two decades [9–14]. Further, there has been an increasing interest focusing on the finite-time synchronization, especially when the synchronization is required to be realized in finite time because of practical need [15, 16]. On the other hand, scholars have done a lot of work to analyze the synchronization of multilayer networks. A general framework for studying the diffusion processes on multiplex networks was proposed in [17, 18]. In 2014, Aguirre et al. revealed that the connector nodes between layers play an important role in the synchronizability of interconnected networks [19]. Further, intra-layer synchronization, inter-layer synchronization, counterpart synchronization, and generalized synchronization in multiplex networks have been investigated [20–24]. Tang et al. proposed three necessary regions to describe the different types of coherent behaviors (such as complete synchronization, intra-layer synchronization, and inter-layer synchronization) in multiplex networks based on the master stability function method [25].

However, most of the existing works focused on the effects of network structures on the synchronizability of multilayer networks through numerical simulation. To better understand the relationships between topological parameters and synchronizability, it is necessary to give a more rigorous theoretical analysis. Recently, the analytical expressions for the eigenvalues of multilayer fully-connected networks, star networks, chain networks, and star-ring networks were derived to analyze the synchronizability [26–30]. To the best of our knowledge, very little work has been devoted to studying the synchronizability of multilayer K-nearest-neighbor networks. Due to the complexity of the multilayer networks, it is still a real challenge to derive the analytical expressions for the eigenvalue spectrum of the supra-Laplacian matrix.

Motivated by the above discussion, we study the synchronizability of multilayer networks with K-nearest-neighbor topologies. The present study uses the master stability function method to investigate the relationships between various topological parameters and network synchronizability. With this framework, we strictly derive the analytical expressions for the eigenvalues of two-layer and multilayer K-nearest-neighbor networks. Analytical and numerical results show that the network size, the node degree, the number of layers, the intra-layer and the inter-layer coupling strengths can have important effects on the synchronizability of multilayer K-nearest-neighbor networks.

The structure of this paper is organized as follows. The model of multilayer networks and some preliminaries are given in section 2. Section 3 studies the synchronizability of two-layer and multilayer K-nearest-neighbor networks. Numerical examples in section 4 illustrate the effectiveness of theoretical results. The conclusion is finally drawn in section 5.

2. Problem Formulation and Preliminaries

The dynamics of multilayer networks consisting of M layers are described as follows [25]:

$\begin{array}{ll}\frac{d{X_i}^{\alpha }}{dt}=f\left({X_i}^{\alpha }\right)-a{\displaystyle \sum _{j=1}^N}{w_{ij}}^{\alpha }H\left({X_j}^{\alpha }\right)-d{\displaystyle \sum _{\beta =1}^M}{d_i}^{\alpha \beta }\Gamma \left({X_i}^{\beta }\right),& (1)\end{array}$

where $X_i^{\alpha }\in R^n$ is the state of the i-th node in the α-th layer, 1 ≤ i ≤ N, 1 ≤ α ≤ M. f :Rⁿ→Rⁿ is a smooth non-linear vector function. The continuous function H : Rⁿ→Rⁿ and a are the intra-layer coupling function and coupling strength, respectively. Γ : Rⁿ→Rⁿ and d are the inter-layer coupling function and coupling strength, respectively. For simplicity, let $H({X_j}^{\alpha })=H{X_j}^{\alpha }$, $\Gamma ({X_i}^{\alpha })=\Gamma {X_i}^{\alpha }$ and H = Γ. In the α-th layer, if the i-th node is connected with the j-th (j ≠ i) node, ${w_{ij}}^{\alpha }\mathrm{\text{=}}-1$, otherwise, ${w_{ij}}^{\alpha }\mathrm{\text{=}}0$, and ${w_{ii}}^{\alpha }=-{\sum }_{j=1,j\ne i}^N{w_{ij}}^{\alpha }$ (i, j = 1, 2, ..., N and α = 1, 2, ..., M). $L^{(\alpha )}=(a{w_{ij}}^{\alpha })\in R^{N\times N}$ is the Laplacian matrix of the α-th layer. Similarly, if the i-th node, in the α-th layer, is connected with its replica in the β-th (α ≠ β) layer, $d_i^{\alpha \beta }=-1$, otherwise $d_i^{\alpha \beta }=0$, and ${d_i}^{\alpha \alpha }=-{\sum }_{k=1,k\ne \alpha }^M{d_i}^{\alpha k}$ (α, β = 1, 2, ..., M (α ≠ β)). It is obvious that $L^I=(d{d}_i^{\alpha \beta })\in R^{M\times M}$ is the interlayer Laplacian matrix.

Denote

$\begin{array}{l}{X}^{(\alpha )}=\left(\begin{array}{c}{X_1}^{\alpha }\\ {X_2}^{\alpha }\\ ⋮\\ {X_N}^{\alpha }\end{array}\right),X=\left(\begin{array}{c}{X}^{(1)}\\ X^{(2)}\\ ⋮\\ X^{(M)}\end{array}\right),\\ \tilde{f}(X^{(\alpha )})=\left(\begin{array}{c}f({X_1}^{\alpha })\\ f({X_2}^{\alpha })\\ ⋮\\ f({X_N}^{\alpha })\end{array}\right),F(X)=\left(\begin{array}{c}\tilde{f}(X^{(1)})\\ \tilde{f}(X^{(2)})\\ ⋮\\ \tilde{f}(X^{(M)})\end{array}\right),\end{array}$

then we can rewrite the evolution of the multilayer network (1) as following form:

$\begin{array}{ll}\frac{dX}{dt}=F(X)-(({{L}}^L+{{L}}^I)\otimes \Gamma )X,& (2)\end{array}$

where

$\begin{array}{ll}{{L}}^L=\left(\begin{array}{cccc}{L}^{(1)}& 0& \cdots & 0\\ 0& L^{(2)}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & L^{(M)}\end{array}\right)={\displaystyle \underset{\alpha =1}{\overset{M}{\oplus }}}{L}^{(\alpha )},& (3)\end{array}$

$\begin{array}{ll}{{L}}^I=L^I\otimes I_N.& (4)\end{array}$

Here, ⊗ is the Kronecker product, ⊕ is the direct sum operation, I_N is the N × N identity matrix. Then we can get the supra-Laplacian matrix of multilayer networks (1),

$\begin{array}{ll}{L}={{L}}^L+{{L}}^I.& (5)\end{array}$

The decomposition of the supra-Laplacian matrix given in Equation (5) is fundamental for the discovery of several spectral performances of the multilayer networks [17]. According to the master stability function (MSF) framework [31], the synchronized regions of dynamical systems can be classified into four classes: empty, bounded, unbounded and the union of some bounded and unbounded regions. Here, we only focus on the bounded and unbounded synchronized regions. If the synchronized region is unbounded, the network synchronizability is positively correlated to the non-zero minimum eigenvalue (λ₂) of the supra-Laplacian matrix. On the other hand, if the synchronized region is bounded, the eigenratio of the maximum eigenvalue and the non-zero minimum eigenvalue (r = λ_max/λ₂) characterizes the network synchronizability. A smaller r value means that there is a stronger synchronizability of the network.

Throughout the rest of this paper, a useful lemma is presented as follows.

Lemma 1. (see [28]) Let A and B are two square matrices with the same size, then

$\begin{array}{ll}|\begin{array}{cccc}A& B& \cdots & B\\ B& A& \cdots & B\\ ⋮& ⋮& \ddots & ⋮\\ B& B& \cdots & A\end{array}{|}_{M\times M}=|A-B{|}^{M-1}·|A+(M-1)B|,& (6)\end{array}$

where M is a positive integer greater than 1.

3. Synchronizability of Multilayer Networks

In this section, analytical results are presented for the synchronizability of multilayer networks with K-nearest-neighbor topologies.

3.1. Two-Layer K-nearest-neighbor Networks

We consider a two-layer model, each layer is a K-nearest-neighbor network with N nodes (K is an even number) and every node in one layer is connecting with its counterpart in the other layer. The corresponding structure can be shown in Figure 1.

FIGURE 1

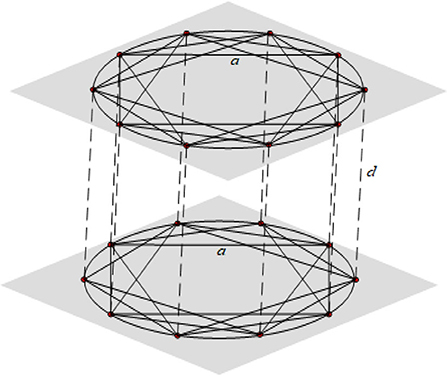
Figure 1. Two-layer networks with K-nearest-neighbor topologies, where d is the inter-layer coupling strength and a is the intra-layer coupling strength.

So the supra-Laplacian matrix can be written as follows:

$\begin{array}{ll}{L}=\left(\begin{array}{cc}A+d{I}_N& -d{I}_N\\ -d{I}_N& A+d{I}_N\end{array}\right),& (7)\end{array}$

where

$\begin{array}{l}A=\left(\begin{array}{cccccc}Ka& \stackrel{\frac{K}{2}}{\overbrace{-a\cdots -a}}& 0& \cdots & 0& \stackrel{\frac{K}{2}}{\overbrace{-a\cdots -a}}\\ -a& Ka& \stackrel{\frac{K}{2}}{\overbrace{-a\cdots -a}}& 0& \cdots 0& \stackrel{\frac{K}{2}-1}{\overbrace{-a\cdots -a}}\\ -a& -a& Ka& \stackrel{\frac{K}{2}}{\overbrace{-a\cdots -a}}& 0\cdots 0& \stackrel{\frac{K}{2}-2}{\overbrace{-a\cdots -a}}\\ ⋮& \ddots & \ddots & \ddots & \ddots & ⋮\\ \stackrel{\frac{K}{2}-1}{\overbrace{-a\cdots -a}}& 0\cdots & 0& \stackrel{\frac{K}{2}}{\overbrace{-a\cdots -a}}& Ka& -a\\ \stackrel{\frac{K}{2}}{\overbrace{-a\cdots -a}}& 0& \cdots & 0& \stackrel{\frac{K}{2}}{\overbrace{-a\cdots -a}}& Ka\end{array}\right).\end{array}$

According to Lemma 1, we can get the characteristic polynomial of ${L}$:

$\begin{array}{l}|\lambda I_{2N}-{L}|=\left|\begin{array}{cc}\lambda I_N-(A+d{I}_N)& d{I}_N\\ d{I}_N& \lambda I_N-(A+d{I}_N)\end{array}\right|\\ =\begin{array}{c}|(\lambda -2d)I_N-A|·|\lambda I_N-A|\end{array}.& (8)\end{array}$

Let |λI_N − A| = 0, the eigenvalues of the K-nearest neighbor network can be written as [32]:

$\begin{array}{l}{\lambda }_l=Ka-2a{\displaystyle \sum _{j=1}^{K/2}}cos\left(\frac{2\pi \left(l-1\right)j}{N}\right),l=1,2,...,N.\end{array}$

Let |(λ − 2d)I_N−A| = 0, it follows that

$\begin{array}{l}{\lambda }_l-2d=Ka-2a{\displaystyle \sum _{j=1}^{K/2}}cos\left(\frac{2\pi \left(l-1\right)j}{N}\right),l=1,2,...,N.\end{array}$

Then, the eigenvalues of ${L}$ are

$\begin{array}{l}0,Ka-2a{\displaystyle \sum _{j=1}^{K/2}}cos\left(\frac{2\pi \left(l-1\right)j}{N}\right),2d,Ka\\ +2d-2a{\displaystyle \sum _{j=1}^{K/2}}cos\left(\frac{2\pi \left(l-1\right)j}{N}\right),\\ l=2,3,...,N.& (9)\end{array}$

When 1 ≪ K ≪ N, we can obtain the smallest non-zero eigenvalue λ₂ and the largest eigenvalue λ_max based on the series expansion,

$\begin{array}{ll}{\lambda }_2\approx min\left\{\frac{a{\pi }^{2}K(K+1)(K+2)}{6N^2},2d\right\},& (10)\end{array}$

$\begin{array}{ll}{\lambda }_{max}\approx a(K+1)\left(1+\frac{2}{3\pi }\right)+2d.& (11)\end{array}$

The relationships between λ₂, r = λ_max/λ₂ and the network parameters are shown in Table 1.

TABLE 1

Table 1. Change of a, d, K, N for λ₂, r = λ_max/λ₂ of two-layer K-nearest-neighbor networks.

Remark 1. When K = 2, the eigenvalues of single networks are ${\lambda }_l=2a-2acos\left(\frac{2\pi \left(l-1\right)}{N}\right)$ $=4a{sin}^2\left(\frac{\left(l-1\right)\pi }{N}\right),l=1,2,...,N.$ Then, the eigenvalues of supra-Laplacian matrix ${L}$ are $4a{sin}^2\left(\frac{\left(l-1\right)\pi }{N}\right),2d+4a{sin}^2\left(\frac{\left(l-1\right)\pi }{N}\right),l=1,2,...,N.$ In [26], synchronizability of duplex ring networks was investigated. Obviously, the network model of this paper is more general.

3.2. Multilayer K-nearest-neighbor Networks

Similarly, we consider the multilayer network with M layers, the corresponding structure is shown in Supplementary Figure 1.

We obtain the supra-Laplacian matrix ${L}$,

$\begin{array}{ll}{L}={\left(\begin{array}{cccc}A+(M-1)d{I}_N& -d{I}_N& \cdots & -d{I}_N\\ -d{I}_N& A+(M-1)d{I}_N& \cdots & -d{I}_N\\ ⋮& ⋮& \ddots & ⋮\\ -d{I}_N& -d{I}_N& \cdots & A+(M-1)d{I}_N\end{array}\right)}_{M\times M},& (12)\end{array}$

where A is given in section 3.1.

According to Lemma 1, the characteristic polynomial of ${L}$ is:

$\begin{array}{l}|\lambda I_{MN}-{L}|\\ =\left|\begin{array}{cccc}(\lambda -(M-1)d)I_N-A& d{I}_N& \cdots & d{I}_N\\ d{I}_N& (\lambda -(M-1)d)I_N-A& \cdots & d{I}_N\\ ⋮& ⋮& \ddots & ⋮\\ d{I}_N& d{I}_N& \cdots & (\lambda -(M-1)d)I_N-A\\ \end{array}\right|\\ =\begin{array}{c}|(\lambda -Md)I_N-A{|}^{M-1}·|\lambda I_N-A|\end{array}.& (13)\end{array}$

Then, the eigenvalues of ${L}$ are

$\begin{array}{l}0,Ka-2a{\displaystyle \sum _{j=1}^{K/2}}cos\left(\frac{2\pi \left(l-1\right)j}{N}\right),{\displaystyle \underset{M-1}{{\displaystyle \underbrace{Md,...,Md}}}},\hfill \\ {\displaystyle \underset{M-1}{{\displaystyle \underbrace{\begin{array}{c}Ka+Md-2a{\displaystyle \sum _{j=1}^{K/2}}cos\left(\frac{2\pi \left(l-1\right)j}{N}\right),...,Ka+Md\hfill \\ -2a{\displaystyle \sum _{j=1}^{K/2}}cos\left(\frac{2\pi \left(l-1\right)j}{N}\right)\hfill \end{array}}}}},\hfill \\ l=2,3,...,N.& (14)\end{array}$

When 1 ≪ K ≪ N, we can obtain the smallest non-zero eigenvalue λ₂ and the largest eigenvalue λ_max based on the series expansion,

$\begin{array}{ll}{\lambda }_2\approx min\left\{\frac{a{\pi }^{2}K(K+1)(K+2)}{6N^2},Md\right\},& (15)\end{array}$

$\begin{array}{ll}{\lambda }_{max}\approx a(K+1)\left(1+\frac{2}{3\pi }\right)+Md.& (16)\end{array}$

The relationships between λ₂, r = λ_max/λ₂ and the network parameters are shown in Supplementary Table 1.

Remark 2. When M = 2, the smallest non-zero eigenvalue ${\lambda }_2\approx min\left\{\frac{a{\pi }^{2}K(K+1)(K+2)}{6N^2},2d\right\}$ and the largest eigenvalue ${\lambda }_{max}\approx a(K+1)\left(1+\frac{2}{3\pi }\right)+2d$, which are equal to the eigenvalues in Equations (10) and (11). Actually, the two-layer network is a special case of the multilayer network.

4. Numerical Simulations

In this section, numerical examples are presented to study the synchronizability of the multilayer K-nearest-neighbor networks.

4.1. The Synchronizability of Two-Layer Networks

(1) Let N = 200, K = 50, d = 1, the impact of the intra-layer coupling strength a on network synchronizability is shown in Figures 2A,B. When the synchronized region is unbounded, Figure 2A displays that λ₂ increases with small a ($a<a_0=\frac{12N^{2}d}{{\pi }^{2}K(K+1)(K+2)}\approx 0.3668$), and then reaches a certain value λ₂ = 2d = 2. This implies that the synchronizability of two-layer networks is first enhanced with small values of increasing a and then held constant with ever-increasing a. When the synchronized region is bounded, it can be observed from Figure 2B that the eigenratio r = λ_max/λ₂ first decreases with small a (a < a₀) and then increases monotonically. It means that the synchronizability is enhanced firstly, then gets weakened after reaching the maximum. The synchronizability of two-layer networks is maximized at $a_0=\frac{12N^{2}d}{{\pi }^{2}K(K+1)(K+2)}$.

(2) Let N = 200, K = 50, a = 0.5, the impact of the inter-layer coupling strength d on network synchronizability is shown in Figures 2C,D. When $0.5<d<d_0=\frac{a{\pi }^{2}K(K+1)(K+2)}{12N^2}\approx 1.3632$, Figure 2C depicts that λ₂ increases linearly with small d. When d > d₀, it reaches a certain value λ₂ = 2d₀. This implies that, with an unbounded synchronized region, the synchronizability is first enhanced with small d and then kept invariant. In Figure 2D, it can be observed that the eigenratio r = λ_max/λ₂ first decreases with small d (d < d₀) and then increases slowly. It means that, with a bounded synchronized region, the synchronizability is enhanced firstly and then slowly gets weakened after reaching the maximum. The synchronizability of two-layer networks is maximized at $d_0=\frac{a{\pi }^{2}K(K+1)(K+2)}{12N^2}$.

(3) Let N = 200, d = 5, a = 0.5, the relationship between the synchronizability and the node degree K is shown in Figures 3A,B. When the synchronized region is unbounded, as shown in Figure 3A, λ₂ increases sharply with increasing K (50 < K < K₀ = 77), and then reaches a λ₂ = 2d = 10. This implies that the synchronizability of two-layer networks is first enhanced and enhanced and then kept invariant. When the synchronized region is bounded, it can be observed from from Figure 3B that the eigenratio r = λ_max/λ₂ first decreases with increasing K (50 < K < K₀ = 77) and then increases monotonically. It means that the synchronizability is enhanced sharply with increasing K, then reaches its maximum, and finally gets weakened. The two-layer networks is maximized at K₀ = 77.

(4) Let K = 50, a = d = 1, the relationship between the synchronizability and the network size N is shown in Figures 3C,D. When 300 < N < 330, it depicts that λ₂ and the eigenratio r = λ_max/λ₂ remain invariant with increasing N. When N > 330, λ₂ decreases with increasing N, and the eigenratio r = λ_max/λ₂ increases with increasing N. This implies that, with unbounded or bounded synchronized regions, the synchronizability is first kept invariant and then gets weakened with increasing the network size N.

FIGURE 2

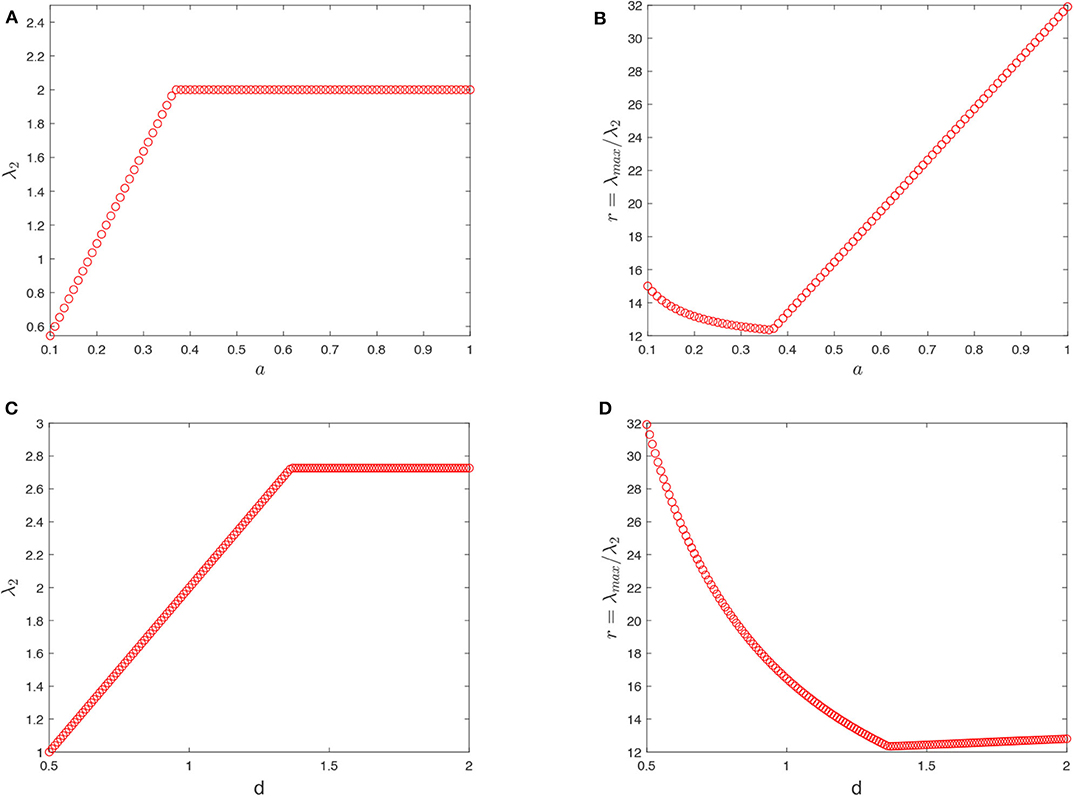
Figure 2. Synchronizability of two-layer K-nearest-neighbor networks. Panels (A,B) display λ₂ and r = λ_max/λ₂ vs. the intra-layer coupling strength a (N = 200, K = 50, d = 1). Panels (C,D) display λ₂ and r = λ_max/λ₂ vs. the inter-layer coupling strength d (N = 200, K = 50, a = 0.5).

FIGURE 3

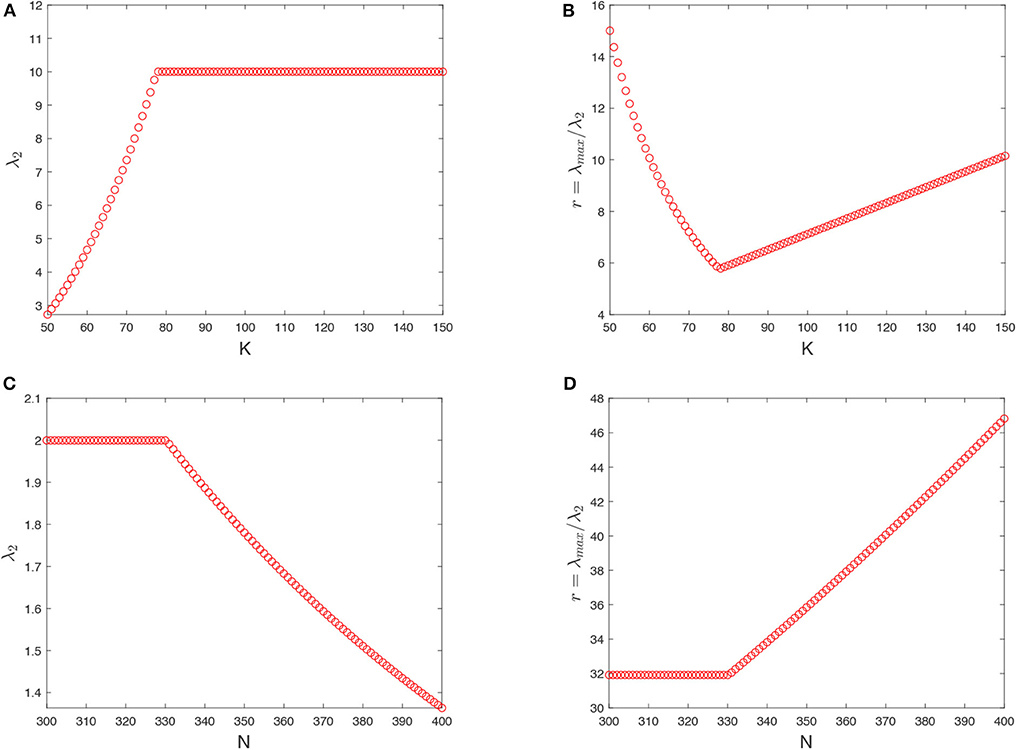
Figure 3. Synchronizability of two-layer K-nearest-neighbor networks. Panels (A,B) display λ₂ and r = λ_max/λ₂ vs. the node degree K (N = 200, d = 5, a = 0.5). Panels (C,D) display λ₂ and r = λ_max/λ₂ vs. the network size N (K = 50, a = d = 1).

4.2. The Synchronizability of Multilayer Networks

Here, we investigate the synchronizability of multilayer K-nearest-neighbor networks. As shown in Supplementary Figures 2,3, the impact of the intra-layer coupling strength a, the inter-layer coupling strength d, the node degree K and the network size N on network synchronizability are similar to the two-layer K-nearest-neighbor networks.

It can be seen from Supplementary Figure 2 that λ₂ increases nearly linearly at the beginning and then reaches a upper bounded value, the eigenratio r = λ_max/λ₂ first decreases and then increases monotonically. It reveals that the synchronizability is enhanced firstly, and then reaches its maximum. Furthermore, the optimal parameters $a_0=\frac{6M{N}^{2}d}{{\pi }^{2}K(K+1)(K+2)}\approx 1.8339$, $d_0=\frac{a{\pi }^{2}K(K+1)(K+2)}{6M{N}^2}\approx 0.2726$ and K₀ = 133 are obtained to maximize the synchronizability of multilayer networks. Supplementary Figures 3A,B depict that λ₂ and the eigenratio r = λ_max/λ₂ remain invariant with increasing N (100 < N < 147). When N > 147, λ₂ decreases and the eigenratio r = λ_max/λ₂ increases with increasing N. This implies that, the synchronizability is first kept invariant and then gets weakened with increasing the network size N. Let N = 200, K = 50, a = d = 0.5, Supplementary Figures 3C,D show that λ₂ increases at the beginning and then keeps invariant, the eigenratio r = λ_max/λ₂ first decreases and then increases slowly with increasing the number of layers M. The observation reveals that the synchronizability of multilayer networks is maximized at M₀ = 6.

5. Conclusion

This paper aims to investigate the synchronizability of multilayer networks with K-nearest-neighbor topologies. The master stability function method allows one to analyze how various topological parameters influence network synchronizability. Here, the analytical expressions for the eigenvalues of two-layer and multilayer K-nearest-neighbor networks have been obtained. Further, we have discussed the impacts of the network size, the node degree, the number of layers, the intra-layer and the inter-layer coupling strengths on the synchronizability of multilayer K-nearest-neighbor networks. Recently, network coherence [33, 34] is an interesting but challenging topic, and coherence analysis of multilayer networks is a part of our future work.

Data Availability Statement

All datasets generated for this study are included in the article/Supplementary Material.

Author Contributions

LZ and YW contributed to the conception and design of the study. YW organized the literature. LZ performed the design of figures and wrote the first draft of the manuscript. All authors contributed to the manuscript revision and read and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 61304173), and Foundation of Liaoning Educational Committee (Grant No. LJ2017QL021).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.571507/full#supplementary-material

References

1. Watts DJ, Strogatz SH. Collective dynamics of ‘small-world' networks. Nature. (1998) 393:440–2. doi: 10.1038/30918

CrossRef Full Text | Google Scholar

2. Barabási AL, Albert R. Emergence of scaling in random networks. Science. (1999) 286:509–12. doi: 10.1126/science.286.5439.509

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Boccaletti S, Latora V, Moreno Y, Chavez M, Hwang DU. Complex networks: structure and dynamics. Phys Rep. (2006) 424:175–308. doi: 10.1016/j.physrep.2005.10.009

CrossRef Full Text | Google Scholar

4. Newman MEJ. Networks: An Introduction. Oxford: Oxford University Press (2010).

Google Scholar

5. Mucha PJ, Richardson T, Macon K, Porter MA, Onnela JP. Community structure in time-dependent, multiscale, and multiplex networks. Science. (2010) 328:876–8. doi: 10.1126/science.1184819

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Lee K, Kim JY, Lee S, Goh K. Multiplex networks. In: D'Agostino G, Scala A, editors. Networks of Networks: The Last Frontier of Complexity. Berlin: Springer International Publishing (2014). p.53–72.

Google Scholar

7. Kivelä M, Arenas A, Barthelemy M, Gleeson JP, Moreno Y, Porter MA. Multilayer networks. J Complex Netw. (2014) 2:203–71. doi: 10.1093/comnet/cnu016

CrossRef Full Text | Google Scholar

8. Boccaletti S, Bianconi G, Criado R, del Genio CI, Gómez-Gardeñes J, Romance M, et al. The structure and dynamics of multilayer networks. Physics Reports. (2014) 544:1-C122. doi: 10.1016/j.physrep.2014.07.001

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Wang XF, Chen GR. Synchronization in small-world dynamical networks. Int J Bifurcat Chaos. (2002) 12:187–92. doi: 10.1142/S0218127402004292

CrossRef Full Text | Google Scholar

10. Wang XF, Chen GR. Synchronization in scale-free dynamical networks: robustness and fragility. IEEE Trans Circ Syst I Fundament Theory Appl. (2002) 49:54–62. doi: 10.1109/81.974874

CrossRef Full Text | Google Scholar

11. Arenas A, Díaz-Guilera A, Kurths J, Moreno Y, Zhou CS. Synchronization in complex networks. Phys Rep. (2008) 469:93–153. doi: 10.1016/j.physrep.2008.09.002

CrossRef Full Text | Google Scholar

12. Li CP, Sun WG, Kurths J. Synchronization between two coupled complex networks. Physical Review E. (2007) 76:046204. doi: 10.1103/PhysRevE.76.046204

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Yu WW, Chen GR, Lü JH, Kurths J. Synchronization via pinning control on general complex networks. SIAM J Control Optimizat. (2013) 51:1395–416. doi: 10.1137/100781699

CrossRef Full Text | Google Scholar

14. Xu J, Li N, Zhang XL, Qin XL. Fuzzy synchronization control for fractional-order chaotic systems with different structures. Front Phys. (2020) 8:155. doi: 10.3389/fphy.2020.00155

CrossRef Full Text | Google Scholar

15. Liu XY, Lam J, Yu WW, Chen GR. Finite-time consensus of multiagent systems with a switching protocol. IEEE Trans Neural Netw Learn Syst. (2016) 27:853–62. doi: 10.1109/TNNLS.2015.2425933

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Liu XY, Su HS, Chen MZQ. A switching approach to designing finite-time synchronization controllers of coupled neural networks. IEEE Trans Neural Netw Learn Syst. (2016) 27:471–82. doi: 10.1109/TNNLS.2015.2448549

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Gómez S, Diaz-Guilera A, Gómez-Gardeñes J, Perez-Vicente CJ. Diffusion dynamics on multiplex networks. Phys Rev Lett. (2013) 110:028701. doi: 10.1103/PhysRevLett.110.028701

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Solé-Ribalta A, De Domenico M, Kouvaris NE, Diaz-Guilera A, Gomez S, Arenas A. Spectral properties of the Laplacian of multiplex networks. Phys Rev E. (2013) 88:032807. doi: 10.1103/PhysRevE.88.032807

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Aguirre J, Sevilla-Escoboza R, Gutiérrez R, Papo D, Buldú JM. Synchronization of interconnected networks: the role of connector nodes. Phys Rev Lett. (2014) 112:248701. doi: 10.1103/PhysRevLett.112.248701

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Gambuzza LV, Frasca M, Gómez-Gardeñes J. Intra-layer synchronization in multiplex networks. Europhys Lett. (2015) 110:20010. doi: 10.1209/0295-5075/110/20010

CrossRef Full Text | Google Scholar

21. Sevilla-Escoboza R, Sendiña-Nadal I, Leyva I, Gutierrez R, Buldu JM, Boccaletti S. Inter-layer synchronization in multiplex networks of identical layers. Chaos. (2016) 26:065304. doi: 10.1063/1.4952967

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Leyva I, Sevilla-Escoboza R, Sendiña-Nadal I, Gutierrez R, Buldu JM, Boccaletti S. Inter-layer synchronization in non-identical multi-layer networks. Sci Rep. (2017) 7:45475. doi: 10.1038/srep45475

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Wei X, Wu XQ, Lu JA, Zhao JC. Counterpart synchronization of duplex networks with delayed nodes and noise perturbation. J Stat Mech Theory Exp. (2015) 2015:P11021. doi: 10.1088/1742-5468/2015/11/P11021

CrossRef Full Text | Google Scholar

24. Ning D, Wu XQ, Lu JA, Lü JH. Driving-based generalized synchronization in two-layer networks via pinning control. Chaos. (2015) 25:113104. doi: 10.1063/1.4935069

CrossRef Full Text | Google Scholar

25. Tang LK, Wu XQ, Lü JH, Lu JA, D'Souza RM. Master stability functions for complete, intralayer, and interlayer synchronization in multiplex networks of coupled Rössler oscillators. Phys Rev E. (2019) 99:012304. doi: 10.1103/PhysRevE.99.012304

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Wei J, Wu XQ, Lu JA, Wei X. Synchronizability of duplex regular networks. Europhys Lett. (2017) 120:20005. doi: 10.1209/0295-5075/120/20005

CrossRef Full Text | Google Scholar

27. Xu MM, Lu JA, Zhou J. Synchronizability and eigenvalues of two-layer star networks. Acta Phys Sin. (2016) 65:028902. doi: 10.7498/aps.65.028902

CrossRef Full Text | Google Scholar

28. Sun J, Li XX, Zhang JH, Shen YZ, Li YY. Synchronizability and eigenvalues of multilayer star networks through unidirectionally coupling. Acta Phys Sin. (2017) 66:188901 (in Chinese). doi: 10.7498/aps.66.188901

CrossRef Full Text | Google Scholar

29. Deng Y, Jia Z, Deng GM, Zhang QF. Eigenvalue spectrum and synchronizability of multiplex chain networks. Phys A. (2020) 537:122631. doi: 10.1016/j.physa.2019.122631

CrossRef Full Text | Google Scholar

30. Deng Y, Jia Z, Yang FM. Synchronizability of multilayer star and star-ring networks. Discrete Dyn Nat Soc. (2020) 2020:9143917. doi: 10.1155/2020/9143917

CrossRef Full Text | Google Scholar

31. Pecora LM, Carroll TL. Master stability functions for synchronized coupled systems. Phys Rev Lett. (1998) 80:2109. doi: 10.1103/PhysRevLett.80.2109

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Wang XF, Li X, Chen GR. Network Science: An Introduction. Beijing: High Education Press (2012) (in Chinese).

Google Scholar

33. Hong MD, Sun WG, Liu SY, Xuan TF. Coherence analysis and Laplacian energy of recursive trees with controlled initial states. Front Inf Technol Electron Eng. (2020) 21:931-8. doi: 10.1631/FITEE.1900133

CrossRef Full Text | Google Scholar

34. Sun WG, Sun MT, Guan JB, Jia Q. Robustness of coherence in noisy scale-free networks and applications to identification of influential spreaders. IEEE Trans Circ Syst II Express Briefs. (2020) 67:1274–8. doi: 10.1109/TCSII.2019.2929139

CrossRef Full Text | Google Scholar