The Quantitative Comparison Between the Neuronal Network and the Cosmic Web

We investigate the similarities between two of the most challenging and complex systems in Nature: the network of neuronal cells in the human brain, and the cosmic network of galaxies. We explore the structural, morphological, network properties and the memory capacity of these two fascinating systems, with a quantitative approach. In order to have an homogeneous analysis of both systems, our procedure does not consider the true neural connectivity but an approximation of it, based on simple proximity. The tantalizing degree of similarity that our analysis exposes seems to suggest that the self-organization of both complex systems is likely being shaped by similar principles of network dynamics, despite the radically different scales and processes at play.

Introduction

Central to our vision of Nature are two fascinating systems: the network of neurons in the human brain and the cosmic web of galaxies.

The human brain is a complex temporally and spatially multiscale structure in which cellular, molecular and neuronal phenomena coexist. It can be modeled as a hierarchical network (i.e., “the human connectome” [1]), in which neurons cluster into circuits, columns, and different interconnected functional areas. The structure of the neuronal network allows the linking between different areas, all devoted to process specific spatiotemporal activities over their neurons, forming the physical and biological basis of cognition [e.g., Ref. 2]. Some of major challenges of contemporary neuroscience are to disentangle the structure of the connectome (e.g., the complete map of the neural connections in a brain), to understand how this structure can produce complex cognitive functions, and to define the role of glial cells and of the microenvironment in the interneuronal physiology.

The Universe, according to the large collection of telescope data gathered over many decades, seems to be reasonably well described by a “consensus” physical model called the $\text{Λ}$CDM model (Lambda Cold Dark Matter), which accounts for gravity from ordinary and dark matter (i.e., very weakly interacting particles), for the expanding space-time described by General Relativity, and for the anti-gravitational energy associated to the empty space, called the “dark energy”. Such model presently gives the best picture of how cosmic structures have emerged from the expanding background and have formed the cosmic web [e.g., Refs. 3 and 4]. The most important building blocks of the cosmic web are self-gravitating dark matter dominated halos, in which ordinary matter has collapsed to form galaxies (and all stars within them). The initial distribution of matter density fluctuations was early amplified by the action of gravity, and has developed into larger groups or clusters of galaxies, filaments, matter sheets, and voids, in a large-scale web in all directions in space. Among the main challenges that cosmology still faces, are the physical nature of dark energy, the composition of dark matter (or the realm of alternative scenarios for it), the apparent tension between different measurements of the expansion rate of the Universe, the exact sequence of processes responsible for the variety of galaxy morphology and their co-evolution with supermassive black holes [e.g., Ref. 5, for a recent review].

Although the relevant physical interactions in the above two systems are completely different, their observation through microscopic and telescopic techniques have captured a tantalizing similar morphology, to the point that it has often been noted that the cosmic web and the web of neurons look alike [e.g., Refs. 6 and 7].

In this work, we apply methods from cosmology, neuroscience, and network analysis to explore this thought-provoking question quantitatively for the first time, to our knowledge.

Materials and Methods

Immunohistochemistry and Microscopy

We analyzed several independent samples of cerebral and of cerebellar human cortex were formalin-fixed and paraffin-embedded [8], sampling slices of depth $4\mu \text{m}$, with magnification factors of $4\times$, $10\times$ and $40\times$. Neurofilaments were labeled using the Neurofilament (2F11) Mouse Monoclonal Antibody (Ventana/CellMarque/Roche). Samples were automatically processed by Ventana BenchMark Ultra Immunostainers. A Nikon eclipse 50i microscope was then used to visualize the samples. Magnifications larger than $40\times$ was avoided in order to obtain a better optical depth resolution, as well as to minimize the non-linear response of the optic microscopy.

Cosmological Simulations

We used synthetic samples of the cosmic web from a high-resolution (${2400}^3$ cells and dark matter particles) simulation of a cubic ${100}^3{\text{ Mpc}}^3$ cosmic volume ($1\text{ Mpc}=3.085\cdot {10}^{24}\text{ cm}$), performed with the grid code ENZO [9] as detailed in Ref. 10. The simulation produces a realistic distribution of dark matter, ordinary matter, and magnetic fields at the present epoch. In order to mimic the “slicing” procedure of brain tissues, we produced 12 different thin slices (with thickness $25\text{ Mpc}$) from the simulated volume, by extracting four slices in perpendicular directions with respect to each of the independent axes of the simulation. We give public access to our cosmic web images, as well as to the brain samples and to the images of other natural networks discussed below at this URL https://cosmosimfrazza.myfreesites.net/cosmic-web-and-brain-network-datasets.

Results

Absolute Numbers, Internal Proportions, and Composition

We first quote data available from the literature, which allow us a first sketchy comparison of the absolute sizes of both systems. The radius of the observable Universe is $R_U\sim 13.9\text{ Gpc}$ [11]. The extrapolation of recent observations posits that a total of $N_g\sim 2.6\cdot {10}^{12}$ galaxies may be present in within the sphere of the observable Universe [12], with up to $\sim 5\cdot {10}^{10}$ galaxies with masses equal or larger to the one of the Milky Way. The largest clusters of galaxies total a mass exceeding ${10}^{15}$ solar masses (1 solar mass $=1.989\cdot {10}^{33}\text{ g}$). Long filaments of ordinary and dark matter, with extension of several tens of Megaparsecs, connect clusters and groups of galaxies and are separated by mostly empty space [e.g., Ref. 4].

According to recent estimates, the adult human brain contains $N_{\text{neu}}\approx 8.6\pm 0.8\cdot {10}^{10}$ neurons in total, and almost an equal number of non-neuronal cells. Only $\sim 20-25\text{\%}$ of all neurons are located in the cortical gray matter (representing $\sim 80\text{\%}$ percent of brain mass), while the cerebellum has about $\sim 6.9\cdot {10}^{10}$ neurons ($\sim 80\text{\%}$ of brain neurons) [13, 14].

It can be noticed that the two systems are organized in well defined networks, with $\sim {10}^{10}-{10}^{11}$ nodes interconnected through filaments (if we consider as nodes all galaxies with masses comparable or larger to that of the Milky Way, see above), whose typical extent is only a tiny fraction ($\le {10}^{-3}$) of their host system size. Also, galaxies and neurons have a typical scale radius, which is only a very small fraction of the typical length of filaments they are connected to. Moreover, available data suggest that the flow of information and energy in the two networks is mostly confined to $\le 25\text{\%}$ of the mass/energy content of each system.

In the case of the Universe we refer to the present-day composition, based on Planck Collaboration et al. [15], as the relative energy distribution is a function of time in the $\text{Λ}$CDM cosmological model; for the human brain, we referred to the published researches about human brain composition [e.g., Refs. 16 and 17].

In summary: 1) the brain is composed by water ($77-78\text{\%}$), lipids ($10-12\text{\%}$), proteins ($8\text{\%}$), carbohydrates ($1\text{\%}$), soluble organic substances ($2\text{\%}$), salt ($1\text{\%}$); 2) the Universe is made for a $73\sim \text{\%}$ by Dark Energy (a scalar energy field of the empty space), for a $22.5\text{\%}$ by Dark Matter, for $4.4\text{\%}$ by ordinary baryonic matter and for less than $\le 0.1\text{\%}$ by photons and neutrinos.

Strikingly, in both cases $\sim 75\text{\%}$ of the mass/energy distribution is made of an apparently passive material, that permeates both systems and has an only indirect role in their internal structure: water in the case of the brain, and dark energy in cosmology, which to a large extent does not affect the internal dynamics of cosmic structures [e.g., Ref. 18].

Morphological Comparison

Small samples of the human cerebral and cerebellar cortex were harvested during corticectomy to approach subcortical tumors (Section 2.1). The neuronal cells have been then stained with clone 2F11 monoclonal antibody against neurofilaments, which are neuron-specific intermediate filaments in the cytoplasm of neurons that provide structural support to the neuronal cytoskeleton, along with microtubules and microfilaments. It has been shown that the number, spacing, and areal density of neurofilaments in neurons are measures with a strong dependency on axon caliber [e.g., Refs. 19–21]. Although also microtubules density depends on axon caliber, it has been shown that microtubules often form small clusters in the vicinity of membranous organelles [22]. For this reason we consider neurofilaments might be more homogeneously arranged in the neuron, and likely to be a better target to visualize the spatial distribution of neurons in the slices. For the cosmic web, we analyzed each one of the 12 thin slices from the simulated volume (Section 2.2), to assess the effect of cosmic variance. Such 2-dimensional approach mimics what is done with brain samples, and due to the large degree of isotropy of the cosmic web on such large scales this approach can also be used to readily translate our statistics into the 3-dimensional case.

Figure 1 gives an overview of the details of structures observed at various scales (from $4\times$, $10\times$ and $40\times$ magnifications in the case of brain tissues, and on corresponding steps in zoom in the case of the cosmic web) in our dataset. Especially on large scales, the various samples do not show any spectacular degree of similarity. In particular, the predominant role of the large overdensities marked by clusters of galaxies is evident in the cosmic web sample, while the finer structure of neurofilaments in the brain samples produces richer small-scale patterns. At the highest magnification achieved in our brain slices, however, the refined network of neuronal bodies and of filaments start presenting some similarity with the cosmic web on $\le 20\text{ Mpc}$ scales. When focusing on histological slices, some variability can be noticed that depends on different neuronal subtypes in brain and cerebellar cortex. In the first slice, small neurons in the granular layer are shown, along with the transition to the gangliar layer with some Purkinje cells at the bottom of the picture. Conversely, the second slice depicts large pyramidal cells interspersed with small neuronal cells of the brain gray matter (granular cells).

FIGURE 1

FIGURE 1. Maps of normalized density contrast, $\delta \rho$ for examples of slices of the cerebellum (top row), of the brain cortex (middle row) and of the dark matter distribution of the cosmic web (lower row), for various levels of magnification. The spectral and network analysis presented in this work will mostly focus on $40\times$ samples as in the right panels.

We will use in this work statistical tools to 1) compare the distribution of structure across the entire continuum range of spatial scales of our samples, also compared to other natural complex systems (Section 3.3); 2) measure the properties of connectivity between nodes in the network, estimating the tendency to form highly clustered configurations (see Section 3.4).

Spectral Analysis

We used here a statistics commonly used in cosmology: the density power spectrum, $P\left(k\right)$, which directly measures the contributions of different spatial frequencies, $k=2\pi L/l$ (where l is the spatial scale and L is the maximum scale of each system), to the density contrast, defined as $\delta \rho =\rho /\overline{\rho }-1$, where ρ is the density and $\overline{\rho }$ is the average density of each sample. We measured $P\left(k\right)$ for our 2-dimensional samples, by decomposing $\delta \rho$ into a series of discrete spatial frequencies, $\delta \left(\overrightarrow{k}\right)$: $\langle \delta \left(\overrightarrow{k}\right)\delta \left(\overrightarrow{k^{\prime }}\right)\rangle =2{\pi }^{3}P\left(k\right){\delta }_D^2\left(\overrightarrow{k}+\overrightarrow{k^{\prime }}\right)$, where ${\delta }_D^2$ is the 2-dimensional Dirac delta function.

In the case of the cosmological simulation, $\langle \rho \rangle$ is uniquely constrained by the initial conditions of the simulation, while in the sample of the cortex and cerebellum we define it based on the average measured within the sample itself. While accurately knowing the local density contrast is trivial in the simulation, it shall be noticed that a precise mapping of the recorded pixel intensity to a projected matter density is far from trivial in microscope observation, due to the non-linear response of the microscopic imaging process. As noted in Section 2.1, our choice of using very thin tissue samples and a magnification not higher than $\times 40$ is indeed motivated by the goal of minimizing the non-linear response of the optic microscopy, by keeping the optical depth small compared to the aperture of the image. For this reason, $\delta \rho$ in our brain samples strictly is a measure of the contrast of optical absorptions along the line of sight, which we assume to be a proxy for the density contrast for the sake of comparing with cosmological samples. We applied standard Fast Fourier Transform with periodic boundary conditions to compute the power spectra of cosmic web samples (as the domains are truly periodic), while in the case of the brain samples we used a standard zero-padding technique to embed the observed samples into a $2\times 2$ larger and empty area, and applied apodisation at the interfaces between the empty area and the data, in order to minimize spurious edge effects, as commonly done in simulations [e.g., Ref. 23].

The resulting power spectra are shown in Figure 2. It shall be stressed that power spectra are free to be slid horizontally in the plot, in the sense that the reference scale L related to $k=1$ is decided a-posteriori. In the following, after a preliminary comparison of spectra we adjusted the horizontal scale so that $k=1$ corresponds to $L=1.6$ mm in brain samples, and to $L=100\text{ Mpc}$ in the cosmic web. This corresponds to a scaling ratio of $1.875\cdot {10}^{27}$ between the two systems. The amplitude of spectra in the vertical direction, instead, is self-normalized to the total variance of $\delta \rho$ within each sample. As a consequence, the brain samples are differently normalized at $k=1$, since when a lower magnification is used and larger spatial scales are sampled, $\le 1.6$ mm scales contribute proportionally less to the variance of $\delta \rho$ within the entire sample. In the first panel, we compare the spectra of a random cosmic web slice with random brain slices obtained with different magnifications. The comparison strikingly shows (in line with what suggested on Figure 1) that a remarkable similarity with spectra is obtained when comparing $\le 1$ mm scales in brain samples to $\le 100$ Mpc scales of the cosmic web. Most of the neuronal cells observed in our cerebellar samples are granule cells, with somata having a $\sim 5\mu \text{m}$ diameter, while their dendrites have dendrites with a typical $\sim 13\mu m$ length. The axon length (although variable depending on the cortical areas) is on average in the range of several millimeters [e.g., Ref. 24]. Considering that the slices used for microscopic inspection most often are not parallel to the axis of axons, it is likely that fragments of these fibers around $\sim 1-2\text{ mm}$ in length are visible in the slices. Therefore, the excess power of neural power spectra in this spatial regime reflects the abundance of structures with this typical size distribution.

FIGURE 2

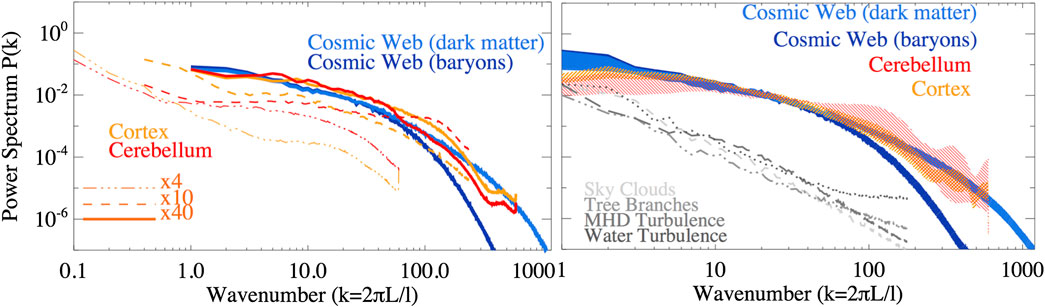
FIGURE 2. Left: power spectra of density fluctuations in all samples (in the case of brain samples, spectra from slices of different size and magnification factors are shown). Right: power spectra of density fluctuations (in the case of brain tissues, only the $40\times$ slices are used here), with shaded areas enclosing the entire distribution of spectra for all samples (12 slices for cosmic web samples and four for the brain samples). Comparison power spectra from other samples natural systems are shown with gray lines.

On the other hand, the fluctuations measured on $\ge 1-2$ mm scales in brain samples present a steeper spectral shape than in cosmic web spectra. For this reason, in the remainder of the analysis we focused on datasets of $40\times$ brain samples for a close comparison with cosmic web slices. In the second panel, we show $P\left(k\right)$ both for the dark matter and gas distribution of all slices, which are almost identical on large scales ($\ge$ Mpc) and more diffuse on smaller scales due to smoothing effect of gas pressure. As for the cosmic web spectra, we show the envelope containing all spectra of all $40\times$ samples with shaded areas. We find a large agreement across nearly $\sim 2$ decades in spatial scales. The similarity between the cerebellum on $0.01-1.6\text{ mm}$ scales and the dark matter distribution of the cosmic web on $1-{10}^2\text{ Mpc}$ scales is remarkable. On smaller scales, the cortex sample displays significant more power than the cerebellum, owing to the distribution of small neurons in the granular layer described above, while the baryon distribution of the cosmic web has less power, due to the (well-known) effect of gas pressure in smoothing out the fluctuations of baryon gas density on small enough scale for hydrodynamical effects to be relevant. In all cases we measure broken power laws, unlike what is expected for (simpler) fractal distributions [e.g., Ref. 25]. This is in line with several works, which have shown that at small scales, $r\le 20\text{ Mpc}$ the galaxy correlation function scales as $\propto r^{-1}$ (where r is the spatial scale in the 2-point correlation function) while on larger scales the density only weakly (logarithmically) depends on the system size [e.g., Refs. 26 and 27].

Lastly, we produced control power spectra for other randomly drawn samples of natural networks (sky clouds, tree branches, water turbulence, and magneto-hydrodynamic turbulence - all available at https://cosmosimfrazza.myfreesites.net/cosmic-web-and-brain-network-datasets), with the goal of double checking that our method is not biased to produce similarity between truly different physical systems. As shown by the gray lines in the right panel of Figure 2, such systems display a more regular power-law spectral behavior, clearly at variance with what found in the main networks analyzed in this work - even if in the latter case we did not perform a full analysis across the entire dynamical range of such systems, looking for the emergence of possible spectral features as in the case of the brain and the cosmic samples.

However, power spectra are blind to phase correlations in the continuous field, hence two morphologically different distributions can still produce similar spectra [28]. In the following section we will thus also rely on non-spectral methods to compare the different samples.

Network Analysis

Network science have proliferated into various physical disciplines, including neuroscience [e.g., Ref. 29–32] as well as cosmology [e.g., Refs. 33 and 34]. Complex network analysis can partially soften the problem of not having perfectly consistent density estimators across our samples, in the sense that defining the nodes of the various networks is less sensitive to the exact mapping details of the images. We focus here on two simple network parameters commonly used in graph theory and network analysis [e.g., Refs. 35 and 36]. The first is the degree centrality, $C_d$, which measures the degree of connectivity of a network within the localized area (determined by a maximum linking length, $l_{\text{link}}$):

$C_d\left(j\right)=\frac{k_j}{n-1}(1)$

where $k_j$ is the number of (undirected) connections to/from each j-node and n is the total number of nodes in the entire network. The second parameter is the clustering coefficient, C, which quantifies the existence of structure within the local vicinity of nodes, compared to a network of random points (i.e., the ratio of connected triangles of nodes to all possible triples in a given connected cluster). It is measured as

$C\left(j\right)=\frac{2y_j}{k_j\left(k_j-1\right)},(2)$

in which $y_j$ is the number of links between neighboring nodes of the j-node.

While sophisticated methods to identify nodes and filaments in the simulated cosmic network [e.g., Ref. 4] or in the neuronal network [e.g., Ref. 37] have been proposed, here we explore a simpler approach with the advantage of being readily applicable to both networks. The method is inspired by standard “halo finding” procedures in cosmology to identify the self-gravitating halos in the cosmic web [38]. In detail: 1) we marke the highest intensity peaks in all maps (i.e., pixels in the top $10\text{\%}$ of the intensity distribution of each map); 2) we compute the enclosed average intensity of pixels within circles of increasing radius, until a low threshold value, $\text{Δ}$, is matched. The radius of the circle reaching the $\text{Δ}$ value defines the radius of each node in the network ($r_{\text{Δ}}$); 3) all pixels at a distance $\le r_{\text{Δ}}$ are assumed to belong to that node. In the case of the cosmic web we tailored the procedure so that $\text{Δ}=330\overline{\rho }$, while in the case of the brain networks we tailored the values of $\text{Δ}$ so that the radius of nodes in the networks reasonably matches the size suggested by visual inspection.

We then built the adjacent matrix of nodes, $M_{ij}$, i.e., a matrix with rows/columns equal to the number of detected nodes, with value $M_{ij}=1$ if the nodes are separated by a distance $\le l_{\text{link}}$, or $M_{ij}=0$ otherwise. The choice of $l_{\text{link}}$ is arbitrary, but a full scan of network parameters as a function of $l_{\text{link}}$ is beyond the goals of this first exploratory work. We thus focused on one specific choice for the linking length, motivated by the recent analysis of observed galaxies by de Regt et al. [33], who suggested $l_{\text{link}}=1.2\text{ Mpc}$ as the reference “linking length” for matter halos in the cosmic web (i.e., $\sim L/100$ in Figure 2). Based on the similarity of power spectra after opportunely renormalizing the spatial scales presented in Section 3.3, we thus consistently rescaled the linking length in $40\times$ brain samples to $l_{\text{link}}=16\mu \text{m}$. Figure 3 gives close up view of the nodes and networks reconstructed for three slices of our dataset.

FIGURE 3

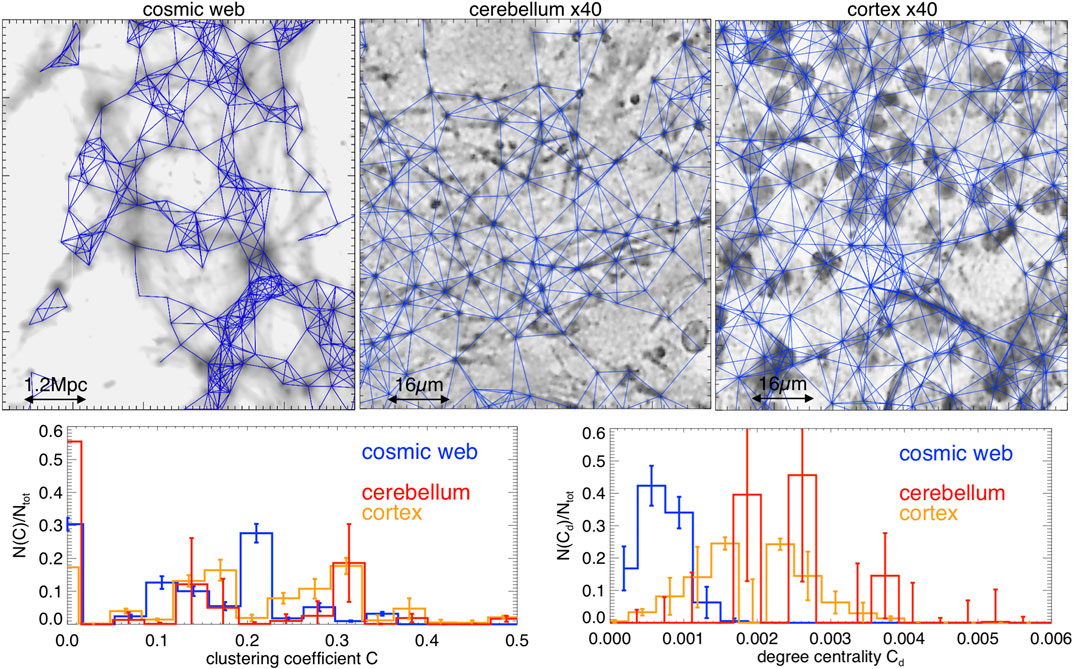
FIGURE 3. Top panels: zoomed details of the reconstructed connections between nodes for three example of networks in our sample (blue lines, superimposed to the density contrast maps). Bottom panels: distributions of clustering coefficient and of degree centrality for all slices (the error bars give the scatter within each investigated sample of slices). The reconstructed connections do not take into account the long-range neural connections, and the clusters shown are purely spatial.

This method selects from $N\sim 3800-4700$ nodes in our cosmic web slices, with an average number of $\langle k\rangle \sim 3.8-4.1$ connections per node. For the cerebellum slices we measured $\langle k\rangle \sim 1.9-3.7$, while for the cortex we measured $\langle k\rangle \sim 4.6-5.4$ for the $N\sim 1800-2000$ identified nodes. On the other hand, the estimated average number of nodes for the simulated cosmic web is $\sim 40\text{\%}$ smaller of the results reported from real galaxy surveys by de Regt et al. [33], which is understood because of the much smaller thickness of our model slices (a factor $\sim 4$ thinner in comoving depth compared to observations).

Both statistics clearly show that the brain and cosmic web networks are very different from Erdös–Rényi random networks of the same size, which would instead predict for the two parameters $C_{\text{random}}\approx \langle k\rangle /N$ ($\le 2\cdot {10}^{-3}$ in our case) and $C_{\text{d},\text{random}}\approx C_{\text{random}}\left(1-C_{\text{random}}\right)/N$ ($\le {10}^{-7}-{10}^{-6}$ in our case), in the limit of large N [e.g., Ref. 39]. We can see that instead all measured distributions of C measure a few different peaks in the $C\sim 0.1-0.4$ range, clearly indicating that all networks are highly correlated, i.e., their links tend to be highly clustered together. In the case of the cosmic web, similar sparse peaks were measured in real data by de Regt et al. [33], and are ascribed to galaxies in moderate ($C\sim 0.1$) or rich ($C\sim 0.3$) environments, like filaments or large clusters of galaxies. Only the residual part of the distributions, with $C\le {10}^{-2}$, marks instead regions of the network in which the connectivity is close to random (e.g., nodes in void regions). The networks also have values of degree centrality clearly much larger (by three to four orders of magnitude) than corresponding random networks. In the cosmic network, the distributions of $C_d$ are approximately Poissonian and in line with the galaxy network studied by Ref. 33, even if the peaks of the distribution are at lower values than the brain samples. The latter is compatible with the enhanced presence of small neurons in the granular layer, already discussed above, which leads to the presence of more closely packed clusters of nodes.

We point out that in this study we analyzed only a fraction of the cortex, and not the whole Central Nervous System, whose architecture is obviously different. Actually, while proximity can accurately describe the cosmic web, neural webs are based on connections and therefore our analysis is not sensitive to long-range connectivity. But indeed long-range connectivity is known to be a crucial feature of neural webs. We defer the application of more complex network statistics [e.g., Ref. 40]) to future work.

Discussion

We have presented a detailed comparison between the neuronal network and the cosmic web, two of the most fascinating and complex networks in Nature, with the goal of assessing the level of similarity between these two physical systems in an objective way.

We have also applied homogeneous statistical approaches to real lab samples of both the brain and the cerebellar cortex (Section 2.1), and to slices of the simulated distribution of dark matter and ordinary in the cosmic web (Section 2.2), and quantified their morphological and network properties using spectral analysis (Section 3.3) as well as network parameters from graph theory (Section 3.4). Within the range of simplifying assumptions we used to define both networks (e.g., based on the proximity of nodes identified from the continuous matter distribution rendered by different imaging techniques) our findings hint at the fact that similar network configurations can emerge from the interaction of entirely different physical processes, resulting in similar levels of complexity and self-organization, despite the dramatic disparity in spatial scales (i.e., $\sim {10}^{27}$) of these two systems.

We are aware that this approach has several limitations. First, our comparison focused on density of matter. The selection of neurofilaments to outline the neuronal network was based on the fact that they are quite evenly expressed in the cytoplasmic compartment of the neurons. Our results should be further validated with different markers, as microfilaments or microtubules. Second, we assumed that the highest stain density is located at the level of neuronal Soma, which is an approximation, leading to a non-standard definition of nodes. Further studies are required to validate our results with functional neural network data and without losing anatomical-visual definition. Third, our study has been based on histological slices, which can obviously show only a tiny portion of the brain network itself. Moreover, while the cosmic web uses proximity to define its network, neural webs are based on connections that can be significantly long-range spatially, and which could not be properly assessed through our analysis due to technical limitation of the method. For the above limitations, we could not present a systematic and complete connectivity analysis of networks, as we focused on simple proximity and not on long-range connectivity. A key Frontier of this line of comparative research is the possibility of measuring the memory capacity of both networks, a task presently made challenging by the radically different approaches presently available to measure to monitor the flow of information within them. An interesting factoid well illustrates that possible similarities also exist in this respect. The total memory capacity of the human brain has been recently estimated using section electron microscopy to reconstruct the 3D distribution of dendritic spines and of their synapses, and finding 26 distinct synaptic strengths, which accounts to an average of $\sim 4.7$ bits of information per neuronal cell [41]. Extrapolated to the total average number of nodes in the neuronal network, this yields $\approx 2\cdot {10}^{16}\text{ bits}$, i.e., $\sim 2.5$ Petabytes as the memory capacity of the human brain. For the cosmic web, a radically different idea based on Information Theory can been used to quantify how much information is encoded by the 3-dimensional structure of the cosmic web [42, 43]. Through the computation of the “statistical complexity” that characterizes the dynamical evolution of simulated universes, it has been argued that $\sim 3.5\cdot {10}^{16}$ bits (i.e., $\approx 4.3$ Petabytes of memory) are necessary to store the information of cosmic structure within the entire observable Universe ($\approx 13.8\text{ Gpc}$). Such close agreement may appear as a mere coincidence, considering that, given ambiguities in defining both networks, particularly the cosmic web, these numbers are known only approximately.

Together with the rest of the analysis presented in this work, such similarities are meant to motivate the development of more powerful and discriminating algorithms to pinpoint analogies and differences of these fascinating systems, almost at the conceivable extremes of spatial scales in the Universe.

Data Availability Statement

All brain samples analysed in this work, as well as relevant samples of the simulated cosmic web and the reconstructed network connectivity are publicly accessible at this URL: https://cosmosimfrazza.myfreesites.net/cosmic-web-and-brain-network-datasets.

Ethics Statement

This study was carried out in accordance with the recommendations of the University Hospital of Modena. All subjects gave written informed consent in accordance with the Declaration of Helsinki.

Author Contributions

Both authors contributed to the writing of the manuscript and to the interpretation of results. FV is responsible for the production of the cosmological simulations and for numerical methods adopted in the paper. AF is responsible for the extraction of the brain samples used in this work.

Funding

FV acknowledges financial support from the ERC Starting Grant “MAGCOW”, no. 714196.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We gratefully acknowledge Elena Zunarelli (Department of Anatomic Pathology, University Hospital Policlinico di Modena, Modena, Italy) for producing the slices used in Figure 1. The cosmological simulation of this work have been produced using the ENZO code (http://enzo-project.org), which is the product of a collaborative effort of scientists at many universities and national laboratories. The simulations/analysis of this work have been produced on Piz Daint supercomputer at CSCS-ETHZ (Lugano, Switzerland) and on Marconi at CINECA (Bologna, Italy) under projects s805 and INA17_C4A28 with (FV as Principal Investigator). FV acknowledges the usage of online storage tools kindly provided by the INAF Astronomical Archive (IA2) initiave (http://www.ia2.inaf.it). We gratefully acknowledge careful reading of this manuscript by D. Wittor.

References

1. Sporns O. The human connectome: a complex network. Ann N Y Acad Sci. (2011). 1224:109–25. doi:10.1111/j.1749-6632.2010.05888.x

CrossRef Full Text | Google Scholar

2. Battaglia D, Witt A, Wolf F, Geisel T. Dynamic effective connectivity of inter-areal brain circuits. PLoS Comput Biol. (2012). 8:1–20. doi:10.1371/journal.pcbi.1002438

CrossRef Full Text | Google Scholar

3. Schneider P. Extragalactic astronomy and cosmology: an introduction. Berlin, Heidelberg: Springer (2015). doi:10.1007/978-3-642-54083-7

CrossRef Full Text | Google Scholar

4. Libeskind NI, van de Weygaert R, Cautun M, Falck B, Tempel E, Abel T, et al. Tracing the cosmic web. Mon Not R Astron Soc Lett. (2018). 473:1195–217. doi:10.1093/mnras/stx1976

CrossRef Full Text | Google Scholar

5. Doré O, Hirata C, Wang Y, Weinberg D, Eifler T, Foley RJ, et al. WFIRST: the essential cosmology space observatory for the coming decade. arXiv:1904.01174. arXiv e-prints (2019)., https://arxiv.org/abs/1904.01174

Google Scholar

6. Lima M, Brain + Universe (2009). Visual complexity. http://www.visualcomplexity.com/vc/blog/?p=234

Google Scholar

7. Neyrinck M, Elul T, Silver M, Mallouh E, Aragón-Calvo M, Banducci S, et al. Exploring Connections Between Cosmos & Mind Through Six Interactive Art Installations in “As Above As Below”. arXiv:2008.05942. arXiv e-prints (2020).

Google Scholar

8. Hsu SM. [39] immunohistochemistry. M Wilchek, and EA Bayer, editors Avidin-biotin technology. Methods in enzymology. Vol. 184. Cambridge, MA: Academic Press (1990). p. 357–63. doi:https://doi.org/10.1016/0076-6879(90)84293-P

CrossRef Full Text | Google Scholar

9. Bryan GL, Norman ML, O’Shea BW, Abel T, Wise JH, Turk MJ, et al. ENZO: an adaptive mesh refinement code for astrophysics. Astrophys J. (2014). 211:19. doi:10.1088/0067-0049/211/2/19

CrossRef Full Text | Google Scholar

10. Vazza F, Brueggen M, Gheller C, Hackstein S, Wittor D, Hinz PM. Simulations of extragalactic magnetic fields and of their observables. Class Quant Grav. (2017). 34:234001. doi:10.1088/1361-6382/aa8e60

CrossRef Full Text | Google Scholar

11. Condon JJ, Matthews AM. $\text{Λ}$CDM cosmology for astronomers. Publ Astron Soc Pac. (2018). 130:073001. doi:10.1088/1538-3873/aac1b2

CrossRef Full Text | Google Scholar

12. Conselice CJ, Wilkinson A, Duncan K, Mortlock A. The evolution of galaxy number density at z < 8 and its implications. Astrophys J. (2016). 830:83. doi:10.3847/0004-637X/830/2/83

CrossRef Full Text | Google Scholar

13. Azevedo FA, Carvalho LR, Grinberg LT, Farfel JM, Ferretti RE, Leite RE, et al. Equal numbers of neuronal and nonneuronal cells make the human brain an isometrically scaled-up primate brain. J Comp Neurol. (2009). 513:532–41. doi:10.1002/cne.21974

CrossRef Full Text | Google Scholar

14. Herculano-Houzel S. The remarkable, yet not extraordinary, human brain as a scaled-up primate brain and its associated cost. Proc Natl Acad Sci USA. (2012). 109:10661–8. doi:10.1073/pnas.1201895109

CrossRef Full Text | Google Scholar

15.Planck Collaboration, Ade PAR, Aghanim N, Arnaud M, Ashdown M, Aumont J, et al. Planck 2015 results. XIII. Cosmological parameters. Astron Astrophys. (2016). 594:63. doi:10.1051/0004-6361/201525830

CrossRef Full Text | Google Scholar

16. O’brien JS, Sampson EL. Lipid composition of the normal human brain: gray matter, white matter, and myelin. J Lipid Res. (1965). 6(4):537–44.

Google Scholar

17.Biochemistry and the central nervous system. A.M.A. Archives Neurol Psychiatry. (1957). 77:56. doi:10.1001/archneurpsyc.1957.02330310066012

CrossRef Full Text | Google Scholar

18. Pfeifer S, McCarthy IG, Stafford SG, Brown ST, Font AS, Kwan J, et al. The Bahamas project: effects of dynamical dark energy on large-scale structure. arXiv e-prints (2020) arXiv:2004.07670.

Google Scholar

19. Maxwell W, Graham D. Loss of axonal microtubules and neurofilaments after stretch-injury to guinea pig optic nerve fibers. J Neurotrauma. (1997). 14:603–14. doi:10.1089/neu.1997.14.603

CrossRef Full Text | Google Scholar

20. Jafari SS, Nielson M, Graham DI, Maxwell WL. Axonal cytoskeletal changes after nondisruptive axonal injury. ii. intermediate sized axons. J Neurotrauma. (1998). 15:955–66. doi:10.1089/neu.1998.15.955. PMID: 9840768

CrossRef Full Text | Google Scholar

21. Fournier AJ, Hogan JD, Rajbhandari L, Shrestha S, Venkatesan A, Ramesh KT. Changes in neurofilament and microtubule distribution following focal axon compression. PLoS One. (2015). 10:1–21. doi:10.1371/journal.pone.0131617

CrossRef Full Text | Google Scholar

22. Price R, Lasek R, Katz M. Microtubules have special physical associations with smooth endoplasmic reticula and mitochondria in axons. Brain Res. (1991). 540:209–16. doi:https://doi.org/10.1016/0006-8993(91)90509-T

CrossRef Full Text | Google Scholar

23. Vazza F, Brunetti G, Gheller C, Brunino R, Brüggen M. Massive and refined. II. The statistical properties of turbulent motions in massive galaxy clusters with high spatial resolution. Astron Astrophys. (2011). 529:A17. doi:10.1051/0004-6361/201016015

CrossRef Full Text | Google Scholar

24. Manto M, Gruol D, Schmahmann J, Koibuchi N, Rossi F. Handbook of the cerebellum and cerebellar disorders. Berlin, Heidelberg: Springer (2013). p. 1–24. doi:10.1007/978-94-007-1333-8

Google Scholar

25. Sylos Labini F, Vasilyev NL, Baryshev YV. Power law correlations in galaxy distribution and finite volume effects from the sloan digital sky survey data release four. Astron Astrophys. (2007). 465:23–33. doi:10.1051/0004-6361:20065321

CrossRef Full Text | Google Scholar

26. Sylos Labini F, Vasilyev NL, Baryshev YV. Large-scale fluctuations in the distribution of galaxies from the two-degree galaxy redshift survey. Astron Astrophys. (2009). 496:7–23. doi:10.1051/0004-6361:200810575

CrossRef Full Text | Google Scholar

27. Sylos Labini F Inhomogeneities in the universe. Class Quant Grav. (2011). 28:164003. doi:10.1088/0264-9381/28/16/164003

CrossRef Full Text | Google Scholar

28. Coles P. Phase correlations and topological measures of large-scale structure. Data Anal. (2009). 665:493–522. doi:10.1007/978-3-540-44767-2_15

CrossRef Full Text | Google Scholar

29. Bassett DS, Bullmore E. Small-world brain networks. Neuroscientist. (2006). 12:512–23. doi:10.1177/1073858406293182. PMID: 17079517

CrossRef Full Text | Google Scholar

30. Meng L, Xiang J. Brain network analysis and classification based on convolutional neural network. Front Comput Neurosci. (2018). 12:95. doi:10.3389/fncom.2018.00095

CrossRef Full Text | Google Scholar

31. Joyce KE, Laurienti PJ, Burdette JH, Hayasaka S. A new measure of centrality for brain networks. PLoS One. (2010). 5:1–13. doi:10.1371/journal.pone.0012200

CrossRef Full Text | Google Scholar

32. Sporns O, Honey CJ, Ktter R. Identification and classification of hubs in brain networks. PLoS One. (2007). 2:e1049. doi:10.1371/journal.pone.0001049

CrossRef Full Text | Google Scholar

33. de Regt R, Apunevych S, von Ferber C, Holovatch Y, Novosyadlyj B. Network analysis of the COSMOS galaxy field. Mon Not R Astron Soc Lett. (2018). 477:4738–448. doi:10.1093/mnras/sty801

CrossRef Full Text | Google Scholar

34. Tsizh M, Novosyadlyj B, Holovatch Y, Libeskind NI. Large-scale structures in the $\text{Λ}$CDM Universe: network analysis and machine learning. arXiv e-prints (2019) arXiv:1910.07868.

Google Scholar

35. Hansen DL, Shneiderman B, Smith MA, Himelboim I. Social network analysis: measuring, mapping, and modeling collections of connections. In: DL Hansen, B Shneiderman, MA Smith, and I Himelboim, editors Analyzing social media networks with NodeXL. 2nd ed. Chap. 3, Morgan Kaufmann (2020). p. 31–51. doi:https://doi.org/10.1016/B978-0-12-817756-3.00003-0

CrossRef Full Text | Google Scholar

36. Golbeck J. Network structure and measures. In: J Golbeck, editor Analyzing the social web. Chap. 2. Boston: Morgan Kaufmann (2013). p. 25–44. doi:https://doi.org/10.1016/B978-0-12-405531-5.00003-1

CrossRef Full Text | Google Scholar

37. Stanley M, Moussa M, Paolini B, Lyday R, Burdette J, Laurienti P. Defining nodes in complex brain networks. Front Comput Neurosci. (2013). 7:169. doi:10.3389/fncom.2013.00169

CrossRef Full Text | Google Scholar

38. Knebe A, Knollmann SR, Muldrew SI, Pearce FR, Aragon-Calvo MA, Ascasibar Y, et al. Haloes gone MAD14: the halo-finder comparison project. Mon Not Roy Astron Soc. (2011). 415:2293–318. doi:10.1111/j.1365-2966.2011.18858.x

CrossRef Full Text | Google Scholar

39. Albert R, Barabási AL. Statistical mechanics of complex networks. Rev Mod Phys. (2002). 74:47–97. doi:10.1103/RevModPhys.74.47

CrossRef Full Text | Google Scholar

40. van den Heuvel MP, Sporns O. Rich-club organization of the human connectome. J Neurosci. (2011). 31:15775–86. doi:10.1523/JNEUROSCI.3539-11.2011

CrossRef Full Text | Google Scholar

41. Bartol TM, Bromer C, Kinney J, Chirillo MA, Bourne JN, Harris KM, et al. Nanoconnectomic upper bound on the variability of synaptic plasticity. Elife. (2015). 4:e10778. doi:10.7554/eLife.10778

CrossRef Full Text | Google Scholar

42. Vazza F On the complexity and the information content of cosmic structures. Mon Not R Astron Soc: Lett. (2017). 465:4942–55. doi:10.1093/mnras/stw3089

CrossRef Full Text | Google Scholar

43. Vazza F How complex is the cosmic web?. Mon Not R Astron Soc: Lett. (2019). 491:5447–63. doi:10.1093/mnras/stz3317

CrossRef Full Text | Google Scholar