Chemical Design Model for Emergent Synthetic Catch Bonds

All primary chemical bonds inherently weaken under increasing tension. Interestingly, nature is able to combine such bonds into protein complexes that accomplish the opposite behavior: they strengthen with increasing tensional force. These complexes known as catch bonds are increasingly considered a general feature in biological systems subjected to mechanical stress. Despite their prevalence in nature however, no truly synthetic realizations of catch bonds have been accomplished so far, as it is a profound challenge to synthetically mimic the allosteric mechanisms employed by protein catch bonds. In this work we propose a computational model that shows how a synthetic catch bond could be accomplished with the help of existing supramolecular motifs and mechanophores, each of which individually act as slip bonds. This model allows us to identify the limits of catch bonding in terms of a number of experimentally measurable parameters. This knowledge could be used to suggest potential molecular candidates, thereby providing a foothold in the ongoing pursuit to realize synthetic catch bonds.

1. Introduction

All primary bonds, covalent or supramolecular, weaken under the action of mechanical load. Such primary chemical bonds, whose dissociation rate grows with increasing force, are known as slip bonds. Interestingly, many protein bonds found in Nature defy this fundamental rule and show the opposite behavior: up to a certain peak force these bonds only strengthen as the applied tensile force grows. Bonds that display this property are known as catch bonds [1]. This behavior is intriguing, as the primary molecular interactions these catch bonding complexes employ each individually act as slip bonds. Catch bonding thus appears to be an emergent phenomenon that occurs when multiple slip bonds work together collectively.

Catch bonds were first discovered experimentally in the cell adhesion protein P-selectin in 2003 [2], and since then a wide range of proteins with mechanical functions have been found to act as catch bonds. Besides the best known examples in biological adhesion proteins such as P-selectin and FimH [3], these include proteins involved in blood clot formation in injured blood vessels, such as the binding between glycoproteins and human von Willebrand Factor [4]. Other examples are membrane proteins involved in mechanotransduction between the extracellular matrix and the intracellular actin skeleton, such as vinculin and integrin [5]. Catch bonding occurs in intracellular applications, such as in myosin-dynein bond formation [6] and in the kinetochore protein machinery that connects microtubules to chromosomes during cell division [7]. More recently, also the membrane bound stator component of flagella was found to display catch bond behavior [8].

Ever since their first discovery, studies have attempted to answer how catch bond proteins manage to achieve this counterintuitive force-induced bond strengthening behavior. Many catch bonds can allosterically switch conformations as a tensile force is applied to them. A prominent example is the mechanism of the FimH catch bond [9, 10]. In this catch bond, the FimH binding domain is closely associated with an autoinhibiting pilin domain that keeps the binding domain in a low-affinity state. When tensile forces pull the two domains apart, the binding domain tightens, which results in a stronger bond [9]. Force-induced conformational switching has also been observed in selectin catch bonds. Selectins contain a ligand-binding lectin domain positioned at an angle relative to an epidermal growth factor domain. Depending on this angle, the selectin catch bond can be in either a weakly bound bent conformation or a more strongly bound extended conformation. Tensile forces applied to selectin catch bonds induce a conformational change from the bent to the extended form, increasing the number of lectin-ligand interactions in the binding pocket [11, 12].

Despite these successes in elucidating the mechanisms of the FimH and selectin catch bonds, directly observing the structural changes in catch bonding proteins remains a challenge in most cases. For this reason, most efforts to characterize catch bond mechanisms have instead focussed on capturing the force response in conceptual physical models [1]. Over the past few years, several models have been applied successfully to a variety of known catch bonds. From a conceptual point of view, the simplest of these energy landscape models is the one state two-pathway model [13]. This model assumes the bond to be in only one state, from which two competing paths of dissociation exist. One of the energy barriers associated with these dissociation paths increases with increasing force, while the other decreases. At low forces, the increasing barrier is rate-limiting, resulting in an increasing bond lifetime as a function of force: catch bond behavior. As the force exceeds a critical value however, the decreasing barrier becomes rate-limiting and the bond reverts back to a slip bond. This catch-to-slip transition is a general feature in biological catch bonds identified so far.

Although the one-state two-pathway model successfully describes catch bond behavior in protein bonds such as those of P-selectin, the fact that it contains an energy barrier that increases with force is a simplification: After all, each of the primary supramolecular interactions employed by the protein individually behave as slip bonds and hence have an energy barrier that decreases with force. This means that the energy barrier in the one-state two-pathway model that increases with force cannot describe a single bond dissociation or reorganization within the protein. Rather, it has to describe a more complex transition, such as the dissociation of a weak supramolecular bond and subsequent formation of a stronger bond. A slightly more complex model that takes into account the fact that the individual bonds weaken with force is the two-state two-pathway model [14, 15]. This model treats the catch bond as a balance between a weakly bound state with a short lifetime and a strongly bound state with a long lifetime (Figure 1A). In contrast to the one-state two-pathway model, application of force only lowers each of the energy barriers in the system, but the force affects the height of these barriers to a varying extent. This asymmetry in the force-response “tilts” the energy landscape, which makes occupation of the long lifetime state more likely with respect to the short lifetime state. The net result is an increasing bond lifetime at intermediate forces. As the force increases further, the weakening of both states eventually reduces the bond lifetime again. This model has successfully described catch bonding behavior in biological systems that show transitions between strong and weak states, such as selectin catch bonds [15]. Critically, the two-state two-pathway model provides a physical explanation for the paradox of how a protein complex that can only employ slip bonds as its primary bonds can still behave as a catch bond as a whole.

FIGURE 1

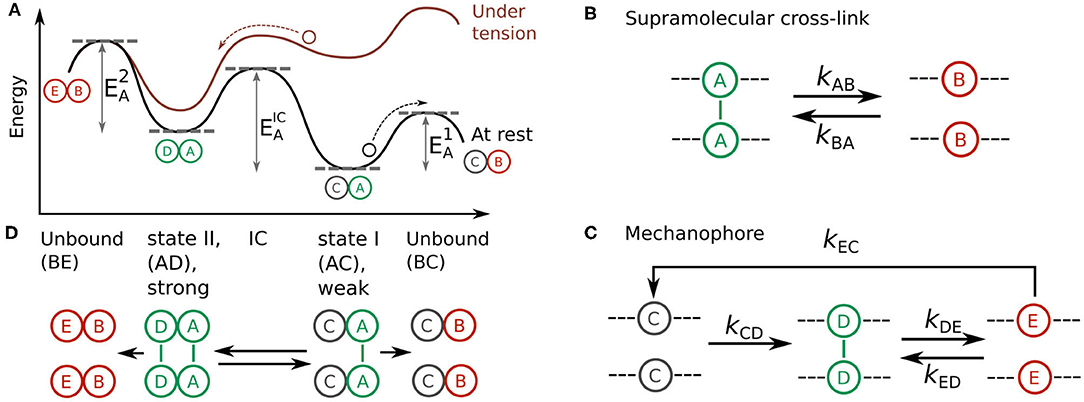
Figure 1. (A) Energy landscape of a two-state, two-pathway catch bond at rest (black) and under tension (red). The activation energies of dissociation from state I, dissociation from state II, and interconversion between these states are shown as $E_A^1$, $E_A^2$, and $E_A^{IC}$, respectively. (B,C) Design model of a synthetic catch bond that consists of (B) a supramolecular cross-link and (C) a mechanophore capable of forming a supramolecular cross-link under force-activation. (D) Schematic representation of a catch bond consisting of one supramolecular cross-link and one mechanophore in weak state I (AC) and strong state II (AD), along with the two unbound states BC and BE that could be reached from these states.

These insights into the mechanisms of catch bonds beg the question whether it is possible to design synthetic catch bonds that, like FimH and selectin, can switch reversibly between weakly bound and strongly bound states. Such synthetic catch bonds could prove valuable model systems to study the collective effects catch bonds can provide to biological networks and interfaces. An example of such collective effects are the selectin catch bonds found on the surfaces of leukocytes. The catch bond nature of selectin allows these leukocytes to roll on the endothelium surfaces specifically in areas where a fast blood flow exerts shear stresses on the leukocytes, while staying detached when the blood flow is slow [16]. More recent computational studies on nanoparticle networks cross-linked with catch bonds also found enhanced network toughness compared to networks that only utilized slip bonds [17, 18]. The lack of synthetic catch bonds leaves the vast possibility these unique bonds have in shaping material mechanics unexplored for bio-mimetic synthetic materials.

Designing a synthetic realization of a catch bond is no trivial task. The mechanically-induced conformational changes that give rise to catch bonding in proteins are so complex that they cannot be directly mimicked synthetically. However, this does not imply that the concept of a catch bond, a bond that strengthens under tension, is out-of-reach for the synthetic chemist. This paper addresses the question whether a catch bond, separate from its biological reality, can be constructed in a minimal chemical design.

We aim to provide a generic chemical design, as a guide for synthetic chemists, that creates a minimal realization of the conceptual two-state two-pathway model described above. Out of the existing phenomenological catch bond models, this provides the most convenient starting point: it is the only model that explains how a system that consists exclusively of slip bonds can still behave as a catch bond on a collective level, and each of the synthetic building blocks we can employ individually behave as slip bonds.

Here, we propose a minimal design model for a synthetic two-state catch bond, which demonstrates how catch bonding can be achieved by combining mechanophores and supramolecular motifs. Using the conceptual two-state two-pathway model as a foundation, we derive a number of design criteria such a supramolecular construct should fulfill in order to display catch bond activity, and we test these criteria with kinetic monte carlo simulations. Our results allow us to identify a phase diagram showing a transition between a slip bonding and a catch bonding regime as a function of three control parameters which can be determined experimentally. These findings could be used to suggest potential molecular candidates to make the first true synthetic catch bond a reality, and bring us one step closer to utilizing synthetic catch bonds as model systems to investigate collective effects of catch bonding in biology. Furthermore, such a synthetic catch bond would serve as a novel building block in material science, opening up new avenues to design bio-inspired materials with enhanced properties.

2. Conceptual Design of a Synthetic Catch Bond

To design a synthetic catch bond based on the two-state two-pathway model, we first need to get a conceptual picture of the criteria that must be fulfilled to make such a catch bond work. In the two-state, two-pathways model, a catch bond can transition between two states. The first is a weak, inactivated state I with a short lifetime and the second is a stronger, activated state II with a much longer lifetime. The catch bond relies on the principle that the relative occupancy of these two states changes as a function of force: As the force exerted on the catch bond is increased, the likelihood increases that the bond becomes trapped in the activated state II before it dissociates. As a result, the average bond lifetime of an ensemble of such catch bonds will increase as a function of force.

To obtain a deeper insight in how we can tune the probabilities between states I and II, we can visualize the two-state two-pathway model as an energy landscape (Figure 1A) [15]. Two energy minima in this landscape represent the weak, inactivated state I and the strong, activated state II. Bond dissociation is possible from both of these states, and the rates of these processes are governed by energy barriers $E_A^1$ and $E_A^2$, respectively. A third energy barrier $E_A^{IC}$ governs the rate of interconversion between states I and II. In the absence of tension, dissociation from the weakly bound state I is more likely than interconversion toward the strong state II, which results in a short bond lifetime. Tension applied to the bond tilts the energy landscape, which lowers the energy barrier for interconversion toward the strong state $E_A^{IC}$ relative to $E_A^1$. This increases the probability that the system ends up in the strong state II before dissociation, which results in a longer bond lifetime.

This increase in bond lifetime under tension, signaling catch behavior, continues until $E_A^{IC}$ is so low compared to $E_A^1$ that any further increase in force will not substantially affect the probability to reach state II. If the force is increased beyond this point, the progressive lowering of barriers $E_A^1$ and $E_A^2$ only weakens the bond, which makes the system transition from a catch bond to a slip bond at high forces. We note that this catch behavior at low and intermediate forces, and its transition to slip bonding at high forces, is also a feature of all known biological catch bonds, which therefore should be referred to as catch-slip bonds.

Based on this conceptual picture we can reason that the following three criteria must be met to make the catch bond work:

1. $E_A^2$ should be higher than the energy barrier $E_A^1$. This criterion ensures that it is more difficult to dissociate from state II than from state I. As a result, the bond lifetime increases as the probability of visiting state II relative to state I increases at greater forces.

2. At low forces, we require that dissociation from the weak state I occurs more quickly than interconversion to the stronger state II. This criterion ensures a short bond lifetime, dictated by the dissociation time of the weak state I. This means that the energy barrier $E_A^1$ must be substantially lower than the energy barrier $E_A^{IC}$ at low forces.

3. At greater forces however, we require the opposite behavior. Here, dissociation from the weak state I should occur more slowly than interconversion to the stronger state II. This ensures a long lifetime, because the chance of visiting state II before bond dissociation becomes greater. Therefore, energy barrier $E_A^1$ must be higher than the energy barrier $E_A^{IC}$ at high forces.

The apparent contradiction between the latter two criteria can only be resolved if the height of the barriers $E_A^1$ and $E_A^{IC}$ scale differently as a function of force. This asymmetry in the response of the kinetic barriers to force is pivotal in the function of the two-state, two-pathway catch bond.

3. Molecular Design Model

Now that we have a conceptual picture of the theoretical requirements of a two-state two-pathway catch bond, we set out to develop a molecular design model that fulfills these criteria in order to realize a chemical design for a synthetic catch bond. Our design consists of an oligomeric construct composed of two types of supramolecular interactions (Figures 1B,C). The first of these monomers is a “simple” supramolecular slip bond A that dissociates into its unbound state B (Figure 1B). The reaction equilibrium of this reaction is governed by the forward rate k_AB and reverse rate k_BA. In the inactive, weakly bound state I of the catch bond, only these simple slip bonds A are engaged.

Our two-state, two-pathway catch bond also requires the ability to switch to a more strongly bound state II under force in order to fulfill criteria 1, 2, and 3 we have identified above. To this end, we include a second type of force-responsive monomer in our supramolecular oligomer. This monomer is a so-called mechanophore: a molecule that consists in an inactive state C at rest and undergoes a force-induced conformational change k_CD that allows it to form a supramolecular slip bond D (Figure 1C). The formation of this supramolecular slip bond D corresponds to the activated state II of the catch bond. In turn, this slip bond D reversibly dissociates into the unbound state E with forward and backwards rates k_DE and k_ED respectively. As the formation of the supramolecular bond stabilizes the active state of the mechanophore, deactivation to state C occurs exclusively via the debonded state E at reaction rate k_EC.

The catch-bonding oligomer is constructed of N = N_A + N_C monomers. Let the symbols n_i with i = A, B..E denote the number of monomers in their respective conformational state, with the condition Σ_in_i = N. Since the states A and D form supramolecular bonds, only these contribute to the mechanical stability of the construct, so that the total number of bonds equals n_bonds = n_A + n_D. The overall picture of this catch bond design is as follows (Figure 1D): in the absence of applied force, the oligomer exists in the inactivated state I with all N_A monomers in the bound (A) state and all mechanophores N_C in the inactivated state C. In this inactivated state of the catch bond, the bond lifetime is thus governed by the weak slip bonds A. Application of small stretching forces increases the probability of activating the C → D bonds relative to the probability of rupturing some A → B bonds. This pushes the system into the activated state II where the bond lifetime is governed by the D supramolecular interactions. Provided that the bond strength of the D bonds is greater than that of the A bonds, we can expect state II to be a stronger overall bond than state I. In short, this means that we can fulfill the criterion 1 of a two-state two-pathway catch bond ($E_A^2>E_A^1$) by ensuring that the bond strength of the D bonds is greater than the bond strength of the A bonds.

We note that the activated state II is a multivalent state, as it is comprised of both A − A and D − D interactions. As a result, dissociation from state II is possible via multiple pathways, in which these interactions break either simultaneously or sequentially. This makes the overall energy landscape of the proposed catch bond slightly more complex as compared to a monovalent two-state catch bond. In spite of this more complicated picture, the system can achieve catch bonding as long as the lifetime of the multivalent state II is longer than the life time of state I.

To ensure that this design model also fulfills the second and third criteria of a two-state two-pathway catch bond, we have to consider the kinetics of the system. In our catch bond design, we can write out the following set of kinetic equations that govern the occupation of the states over time:

$\begin{array}{ll}\frac{d{n}_A}{dt}=-k_{AB}·n_A+k_{BA}(N_A-n_A)& (1)\end{array}$

$\begin{array}{ll}\frac{d{n}_C}{dt}=-k_{CD}·n_C+k_{EC}(N_C-n_C-n_D)& (2)\end{array}$

$\begin{array}{ll}\frac{d{n}_D}{dt}=k_{CD}·n_C-k_{DE}·n_D+k_{ED}(N_C-n_C-n_D)& (3)\end{array}$

As discussed above, criteria 2 and 3 of a two-state, two-pathway model dictate that the height of the energy barrier of dissociation from the inactive state I should be lower than the height of the barrier of interconversion between the inactive state I and the active state II at small forces, but higher at large forces. Given that in our case the inactive state I is a state with predominantly A bonds (high n_A) and the active state II is the state with predominantly D bonds (high n_D), this can be achieved if the rate constants k_AB and k_CD are force-dependent and scale differently as a function of force. We incorporate the effect of applied force in our system by presuming that the rate constants of supramolecular bond rupture (A → B and D → E) and mechanophore-activation (C → D) display Kramers-Bell type thermally-activated and mechanically-enhanced kinetics [19]. For these reaction steps, the rate constants can then be written as:

$\begin{array}{ll}{k}_{ij}=k_{ij,0}·\text{exp}\left[\beta f\delta x_i\right]& (4)\end{array}$

Here, (ij) = (AB), (CD), and (DE), β = 1/k_BT, k_ij,0 is the reaction rate at zero force and δx_i is the activation length. This activation length δx_i denotes the length change of the bond in the activated state relative to the bond at rest, and determines the susceptibility of the bond to mechanical activation. The rate constants of all other transitions are assumed to be independent of the applied force. According to the Kramers-Bell model, energy barriers are exponentially lowered as a function of force, and the degree to which they do so depends on the activation length δx_i. If supramolecular bond A and mechanophore C are chosen such that k_AB,0 > k_CD,0 and δx_A < δx_C, we ensure that k_AB > k_CD at small forces, while k_AB < k_CD at large forces. Hence, design criteria 2 and 3 are both met. Within this argument based on rate constants, design criterion 1 ($E_A^2>E_A^1$) can be expressed as k_AB > k_DE. This can be realized if k_AB,0 > k_DE,0, assuming that δx_A is similar to δx_D.

In essence, the synthetic catch bond we propose exists as a balance between two subpopulations: a weakly bound state I from which dissociation is slow and a more strongly bound state II from which dissociation is faster. Meeting criteria 2 and 3 ensures that increasing the force shifts the balance between these two subpopulations toward the more strongly bound state II. This force-induced shifting between subpopulations is the key mechanism by which many relevant biological two-state catch bonds have been identified to work, such as the interaction between von Willebrand factor and platelet glycoprotein Ibα [20], and P-selectin [15].

We note in passing that the Kramers-Bell description of force-enhanced thermal barrier transitions does not take into account the directionality of the applied force. Rather, in the catch bond we propose (Figure 1D) it is assumed that a fixed magnitude of force is applied to cross-links (A − A and D − D) and the mechanophore (C). In practice however, the dissociation of the A − A and D − D bonds might require a different force directionality than the activation of the mechanophore C → D. For example, activation of mechanophore C could require the rupture of intramolecular bonds within C oriented in a different direction than the intermolecular cross-link A − A. Depending on the direction in which the force is applied to the catch bond as a whole, the magnitude of the applied tensional load might be distributed differently in each of the relevant directions, which could cause cross-link C to experience a different magnitude of force than supramolecular bonds A − A and D − D. We do not account for this effect in our simplified design model. Moreover, the Kramers-Bell description (Equation 4) assumes that the applied force only affects the height of the energy barrier for bond dissociation, but does not affect its curvature [21]. This assumption is only valid if the barrier is sufficiently steep, that is, if the activation length is comparatively short with respect to the barrier height, which is the case for most mechanically stable supramolecular motifs.

4. Results

To test whether our molecular design model displays catch bonding, we solve the system of kinetic equations (1–3) with a Gillespie Kinetic Monte Carlo (KMC) algorithm, which takes into account the effect of thermal fluctuations, as discussed in [22]. We run a simulation until n_bonds = n_A + n_D = 0, which signifies rupture of the oligomer. For each of the designs and loading condition we test, we run 1,000 independent simulations to ensure sufficient statistics. We simulate these rupture events in the limit of constant strain. Since the supramolecular bonds (A-A and D-D) that connect two unimers act as springs, the condition of constant strain implies a constant force f on each of the supramolecular bonds in parallel. As a result, the force per bond f is time-invariant in the limit of constant strain, while the cumulative load on the dimer F(t) = fn_bonds varies over time.

We first consider the simplest case of our supramolecular oligomer, which is a dimer composed of only a supramolecular slip bond A-A without mechanophores: N = N_A and N_C = 0. For a single supramolecular bond (N_A = 1), we observe Poisson statistics, where the dimensionless bond lifetime $\tilde{\tau }=\tau k_{BA,0}$ decays exponentially as a function of the dimensionless force $\tilde{f}=f\delta x_A/k_{B}T$ (Figure 2A). Each data point in Figure 2A is averaged over 10,000 simulations per force. For multivalent dimers (N_A > 1), we observe two exponential decay regimes in the bond lifetime. This effect was previously explained for failure of multivalent colloidal aggregates [23]. For small forces, rupture of the multivalent dimer is cooperative. Here, dissociation occurs relatively slowly compared to reassociation (k_AB << k_BA). As a result, dissociated bonds within the dimer have ample time to reform as long as other bonds within the dimer are still present, preventing dissociation of the dimer as a whole. Due to this multivalency effect, one expects an exponential slope that scales with N_A. Indeed, we find that increasing N_A strongly increases the slope of the bond lifetime at small forces. By contrast, at large forces we observe a slope that is independent of N_A. Here, dissociation occurs substantially faster than association (k_AB >> k_BA), so that bond rupture is simply a sequence of rupturing all bonds in succession. In this regime, adding more bonds N_A would have little effect on the bond lifetime, so that one would indeed expect the slope to be insensitive to N_A. Due to this force-dependent transition from cooperative to non-cooperative behavior, the degree to which the rupture rate is affected by the force decreases as a function of force. This multivalency effect is a useful tool in designing a synthetic catch bond, because it could help the rate of mechanophore activation (k_CD) overtake the dissociation of the A-A bonds (k_AB) more easily at large forces.

FIGURE 2

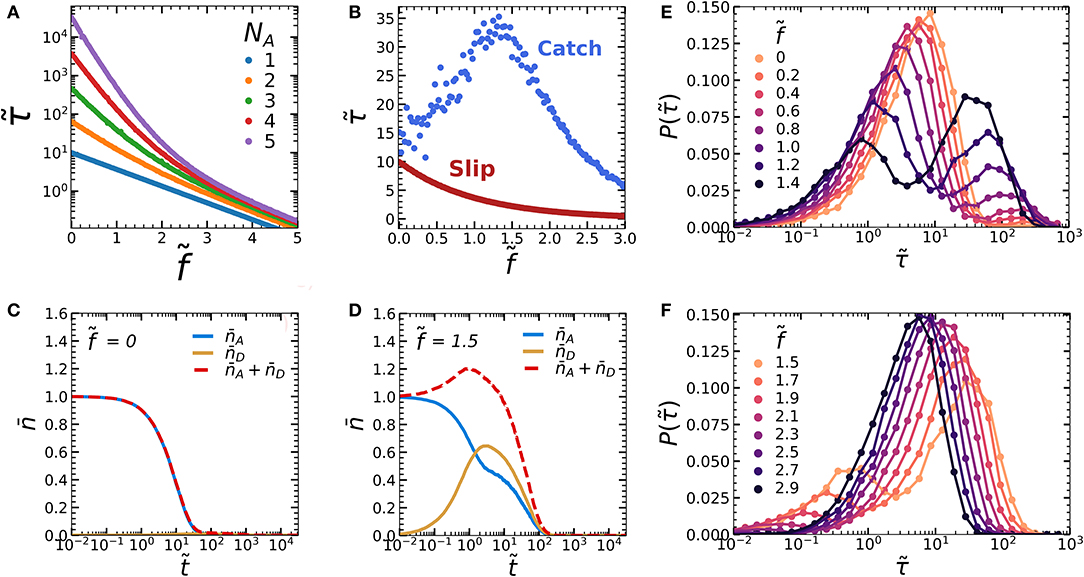
Figure 2. (A) Force-lifetime curve of an oligomer consisting of a varying number of subunits (N_A), without a mechanophore (N_C = 0). (B) Force lifetime curves of a single N_A = 1 oligomer displays slip bond behavior in the absence of a mechanophore (red curve, N_C = 0) and catch bond behavior in the presence of a mechanophore (blue curve, N_C = 1). (C,D) Kinetic diagrams of the blue curve in figure b showing the average number of bonds in the A and D states (${\overline{n}}_A$ and ${\overline{n}}_D$) over simulation time steps $\tilde{t}$ at $\tilde{f}=0$ (C) and around maximum lifetime, at $\widetilde{f=1.5}$ (D). (E,F) Logarithmically binned histograms of the bond dissociation times $\tilde{\tau }$ at different forces for (E) $\tilde{f}<1.5$ and (F) $\tilde{f}>1.5$. Simulations were run with zero-force rate constants k_AB,0 = 0.1, k_CD,0 = 0.001, k_DE,0 = 0.01 and activation lengths δx_c = 4.6, and δx_D = δx_A = 1.

We now introduce a mechanophore into our dimer to explore the possibility to create a catch bond. The simplest catch bond we can consider consists of one A-A dimer and one mechanophore (N_A = N_C = 1). We choose our kinetic parameters such that they fulfill the three criteria of a two-state two-pathway catch bond: k_DE,0 < k_AB,0 (criterion 1), k_AB,0 > k_CD,0 (criterion 2), and dx_A < dx_C (criterion 3). The bond reformation rates k_BA and k_ED are controlled by diffusion and thus considered of similar magnitude, so that k_BA = k_ED = 1. As a simplification we assume that the spontaneous conversion of the activated to the inactivated chromophore is slow compared to the other rates in the system, so that it can be ignored (k_EC = 0).

Interestingly, we find that adding a single mechanophore to one A-A dimer bond already yields convincing catch bonding behavior (Figure 2B, averaged over 1,000 simulations per force). We can understand how this occurs by studying the average number of bonds in the A-A and D-D states over time (Figures 2C,D). At $\tilde{f}=0$, we find that almost exclusively the weak A-A bonds are present, while only a small number of the mechanophores activate due to thermal activation (Figure 2C). By contrast, under tension at the maximum of the force-lifetime curve $\tilde{f}=1.5$, the strong mechanical scaling of the mechanophore activation rate increases k_CD relative to the A-A dimer rupture rate k_AB. This causes an increasing amount of oligomers to become trapped in the stronger, activated D-D state before rupture (Figure 2D). In the latter case we also find that the A-A dissociation (${\overline{n}}_A$) occurs in two stages: After a quick initial decay, the dissociation rate slows down dramatically as soon as ${\overline{n}}_D$ increases. We can attribute this to a multivalency effect: as soon as both the A-A and D-D dimers are formed, the A-A bond can dissociate without breaking the dimer. This allows the bond to reform via rate constant k_BA. Due to this reassociation, we can expect ${\overline{n}}_A$ to drop more slowly.

All data we have discussed so far are averaged over at least 1,000 simulations per datapoint. While such averaged properties can inform us whether a population of bonds display catch bonding as a whole, they provide no information on the lifetime distribution at the level of the individual bonds. To obtain such insight, we constructed logarithmically binned histograms of the bond dissociation time $\tilde{\tau }$ for varying forces in the regime of increasing bond lifetime, $\tilde{f}<1.5$ (Figure 2E) and in the regime of decreasing bond lifetime $\tilde{f}>1.5$ (Figure 2F). At force $\tilde{f}=0$, bond dissociation occurs from a single population. As we increase the force toward $\tilde{f}=1.5$, we observe that an increasing fraction of bonds dissociates from a second population with a higher lifetime. Simultaneously, the lifetimes of both these populations decrease with increasing force. This trend continues as we increase the force beyond $\tilde{f}>1.5$ as shown in Figure 2F, until only the long-lifetime population is left at $\tilde{f}=2.3$. In short, the lifetime enhancement as seen in the catch bond force-lifetime curve in Figure 2B is only visible as a collective effect. On the level of the individual bonds however, dissociation proceeds from two populations, and the lifetimes of each of these populations are in fact lowered by the applied force. The increasing average bond lifetime is thus caused by a shift in probability between two states, rather than by a increase in the lifetimes of the states themselves. These observations are in line with the two-state, two pathway model.

We have now established that catch bonding can be achieved in our model system by combining a simple oligomer and a mechanophore. However, the phase space for synthetic design is vast, and the tunability of the kinetic parameters depends on the availability of supramolecular motifs and mechanophores. For a more complete picture, we thus set out on a systematic exploration of the parameter space. Although we have previously reasoned that a certain range in the parameters k_AB,0/k_CD,0, δx_C/δx_A, and k_AB,0/k_DE,0 is required to achieve catch bonding, the question remains where the boundaries of this catch bonding regime lie exactly. Furthermore, we can wonder how different aspects of our catch bond can be tuned by these parameters, such as the relative increase in bond lifetime under force or the location of the optimum of our force-bond lifetime curve. Such knowledge would be especially useful in the rational design of artificial catch bonds.

To answer these questions, we systematically vary each of the parameters k_AB,0/k_CD,0, δx_C/δx_A, and k_AB,0/k_DE,0 while recording their force-lifetime curves (Figure 3). First, we vary the ratio of activation lengths between the process of mechanophore activation and A-A bond rupture δx_C/δx_A, by varying δx_C at constant δx_A = 1 (Figure 3A). When the activation lengths are similar (δx_C/δx_A = 1), we find clear slip-bond behavior. As we increase δx_C/δx_A, we find a transition from slip bonding to catch bonding behavior, paired with an increasing lifetime at intermediate forces. At greater values of δx_C/δx_A, k_CD becomes greater than k_AB at intermediate forces, which increases the chance the mechanophore activates and forms the D-D bond before rupture of the A-A slip bond occurs. At the boundary between the slip and catch regimes, we observe a case of ideal bonding at (δx_C/δx_A = 3.1) where the lifetime $\tilde{\tau }$ remains constant for a sizeable range of forces $0<\tilde{f}<1$. In short, we can increase δx_C/δx_A to increase the fraction of bonds that reach the activated state II before dissociation from state I. This allows us to tune the average force-lifetime curve between slip bonding, ideal bonding and catch bonding.

FIGURE 3

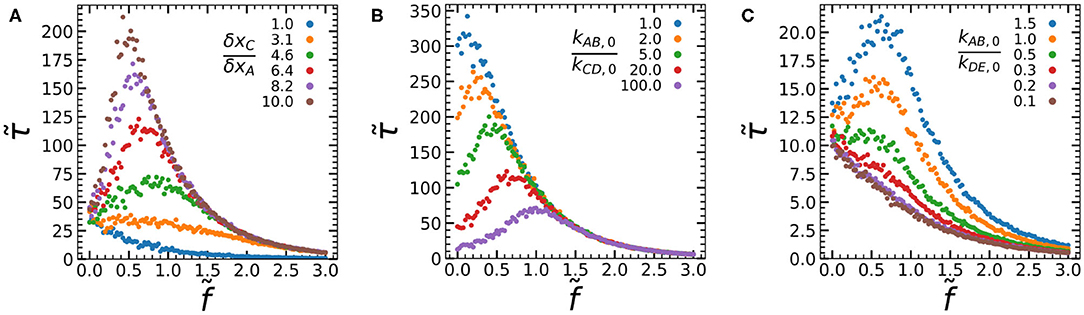
Figure 3. Force-lifetime curves simulated at varying δx_C/δx_A (A), k_AB,0/k_CD,0 (B), and k_AB,0/k_DE,0 (C). Data was recorded at δx_C/δx_A = 6.4 (B,C), k_AB,0/k_CD,0 = 20 (A,C), and k_AB,0/k_DE,0 = 10 (A,B). All data are averages of 1,000 simulations per force, at N_A = N_C = 1, dx_DE = dx_AB = 1, k_ED,0 = k_BA,0 = 1, and k_AB,0 = 0.1.

When we vary k_AB,0/k_CD,0 by changing k_CD,0, we observe an altogether different effect on the catch bond curve (Figure 3B). In the limit k_AB,0/k_CD,0 → 0 the kinetic equations dictate that the catch bond will be universally activated even at $\tilde{f}=0$, which results in slip bond behavior governed by the bond lifetime of the strong D-D bond (k_DE). We indeed observe a force-lifetime curve that tends toward a slip bond at low values of k_AB,0/k_CD,0. As k_AB,0/k_CD,0 increases, the bond lifetimes at low forces and at the force maximum drop consistently, while the force maximum itself shifts toward greater forces. This tunability of the force maximum is an interesting feature which could be exploited in the design of artificial catch bonds. It can be explained as follows: At high values of k_AB,0/k_CD,0, the initial offset in rate constants k_CD and k_AB is greater, which means that greater forces are required before the rate of mechanophore activation overtakes the rate of A-A bond rupture, activating the catch bond. Finally, the bond lifetime at large forces appears unaffected by k_AB,0/k_CD,0. At such large forces the catch bond will be universally activated, which means that further changes in k_AB,0/k_CD,0 will have little effect. In short, k_AB,0/k_CD,0 can be used to strongly tune the lifetime at small forces and the force at which the maximum lifetime is reached, without affecting the lifetime at large forces. The effect of k_AB,0/k_CD,0 can also be understood in terms of our conceptual model: Increasing k_AB,0/k_CD,0 lowers the energy barrier $E_A^1$ relative to barrier $E_A^{IC}$ at low forces. This lowers the bond lifetime, because an increasing fraction of bonds dissociate from state I without reaching activated state II. At large forces beyond the lifetime maximum however, the chance of reaching state II is high regardless of k_AB,0/k_CD,0, since δx_C > δx_A. When most catch bonds reach state II, the bond lifetime is governed by barrier $E_A^2$. This barrier is unaffected by k_AB,0/k_CD,0 and hence the lifetime at large forces is unaffected by k_AB,0/k_CD,0.

However, varying the ratio of the initial bond A-A and D-D bond strengths k_AB,0/k_DE,0 (Figure 3C) has a large effect on the bond lifetime at large forces. The lifetime at the force maximum is also strongly affected, while the lifetime at low forces is unaffected. As we increase the value of k_AB,0/k_DE,0, we find a clear transition from slip bond behavior to catch bond behavior with increasing bond lifetimes. At low k_AB,0/k_DE,0, the mechanophore might be activated, but this activation does not lead to the formation of a stronger bond. As such, the lifetime of the construct as a whole remains governed by the weak A-A cross-link, and we observe slip bond behavior. For larger k_AB,0/k_DE,0 on the other hand, activation of the mechanophore leads to an increasingly strong D-D bond and hence a longer bond lifetime at the force maximum and larger forces. An interesting observation is that some catch bonding can already be observed before the D-D bond is stronger than the A-A bond, at k_AB,0/k_DE,0 = 1. If the A-A and D-D bond are of comparable strength, we can expect the lifetime of the activated catch bond as a whole to increase due to multivalency. This has interesting implications for the effort to create an artificial catch bond, as it means that it is not necessary for the mechanophore to form a very strong D-D cross-link. Rather, it is sufficient if the activated state contains multiple bonds of a similar strength as the bonds in the inactivated state. In terms of the conceptual two-state, two-pathway picture, increasing k_AB,0/k_DE,0 increases the energy barrier $E_A^2$ relative to barrier $E_A^1$. This increases the bond lifetime in the activated state II relative to state I but has little effect on the chance of reaching state II. As a result, we find an increasing bond lifetime at high forces, where the chance of reaching state II is high, but little increase in lifetime at low forces, where the chance of reaching state II is low.

Combined, these results show how different aspects of our catch bond can be tuned by varying three parameters. Specifically, we can tune the location of the force maximum and the bond lifetime at low force by varying k_AB,0/k_CD,0; we can tune the bond lifetime at large forces by varying k_AB,0/k_DE,0, and we can tune the lifetime of our catch bond at the force maximum by varying all three parameters. To also obtain quantitative insight in the minimal conditions required to achieve catch bonding, we can define a parameter that quantifies the degree of catch bonding and study how this parameter varies as a function of our three control parameters. We define the parameter $\Delta \tilde{\tau }/\tilde{\tau }$, which denotes the mechanical enhancement: the increase of the bond lifetime at the force maximum relative to the bond lifetime in the absence of force (Figure 4A, inset). $\Delta \tilde{\tau }/\tilde{\tau }$ is equal to 0 for slip bonds and ideal bonds, and increases with more pronounced catch-bonding.

FIGURE 4

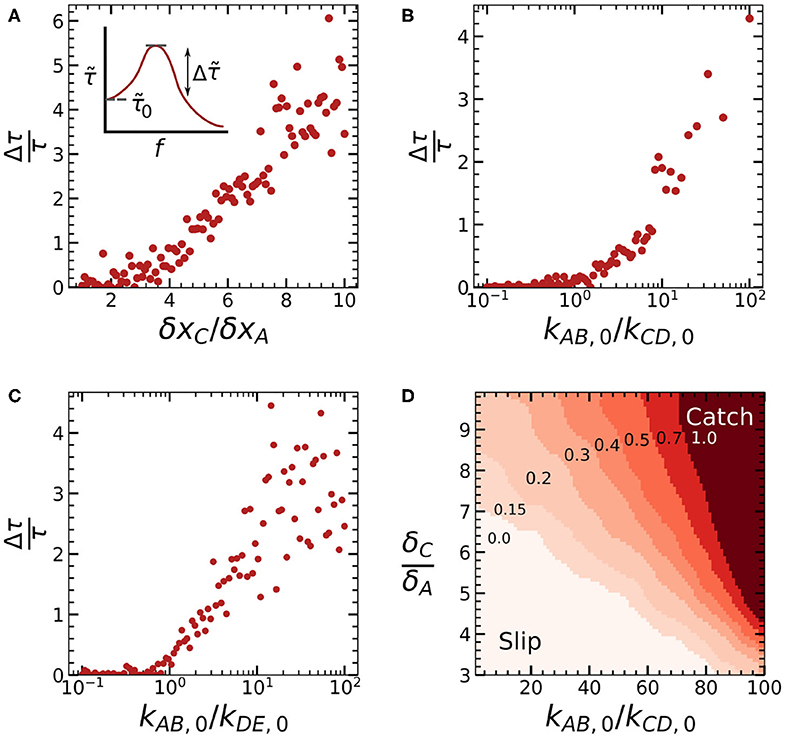
Figure 4. Plots of the mechanical enhancement $\Delta \tilde{\tau }/\tau$ [(A), inset] as a function of the three control parameters δx_C/δx_A (A), k_AB,0/k_CD,0 (B), and k_AB,0/k_DE,0 (C) calculated for the series of force-lifetime curves shown in Figure 3. (D) Contour plot of $\Delta \tilde{\tau }/{\tau }^0$ as a function of both δx_C/δx_A and k_AB,0/k_CD,0.

We calculated $\Delta \tilde{\tau }/\tilde{\tau }$ for each of the three simulation series we discussed above, as shown in Figures 4A–C. We observe that increasing δx_C/δx_A leads to a linear increase in the mechanical enhancement above a critical value δx_C/δx_A ≈ 2. Catch bonding increases logarithmically as k_AB,0/k_CD,0 and k_AB,0/k_DE,0 both increase beyond a critical value of ≈ 1, although some catch bonding can already be observed for k_AB,0/k_DE,0 < 1, due to the multivalency effect we discussed above. The parameters k_AB,0/k_CD,0 and δx_C/δx_A together determine whether criteria 2 and 3 of a two-state, two-pathways model are met. This means that we can expect the greatest effect on the mechanical enhancement if both parameters are increased together. To study the combined effect of these two parameters, we carried out a range of simulations where we varied both k_AB,0/k_CD,0 and k_AB,0/k_CD,0. As a result, we obtained a gaussian-binned phase diagram (Figure 4D) showing a gradual transition from a clear slip-regime at low k_AB,0/k_CD,0 and low δx_C/δx_A to a regime which shows distinct catch bond behavior at high k_AB,0/k_CD,0 and δx_C/δx_A.

5. Discussion

In this work, we have presented a minimal chemical design model for a synthetic catch bond. This model provides a theoretical picture of how synthetic catch bonding could be achieved in an oligomer consisting of supramolecular moieties (A) and mechanophores (C), each of which individually act as slip bonds. We can tune the characteristic force-lifetime curve of these catch bonds with three kinetic control parameters derived from the energy landscape of the two-state two-pathway model. Specifically, we can tune the lifetime at zero force with k_AB,0/k_CD,0, the lifetime in the activated state with k_AB,0/k_DE,0, and the lifetime at the force maximum with the ratio of the activation lengths δx_C/δx_A as well as the previous two parameters. These parameters might therefore offer a foothold to not only build a synthetic catch bond, but also tune its characteristics.

We have determined the limits of the range these parameters should take in order to achieve catch bond behavior by quantifying the bond lifetime enhancement at the force maximum relative to the bond lifetime at zero force. These findings have allowed us to identify a phase diagram of catch bond behavior that could form a theoretical framework. With this framework in hand, the next step is to predict potential molecular candidates to fulfill the role of our supramolecular cross-link (A) and mechanophore (C). Theoretically, many primary supramolecular bonding types can be considered for the supramolecular bond A, such as those based on hydrogen bonds, hydrophobic interactions or electrostatic interactions, for which a wide variety of molecular realizations are available to the supramolecular chemist (Figure 5A).

FIGURE 5

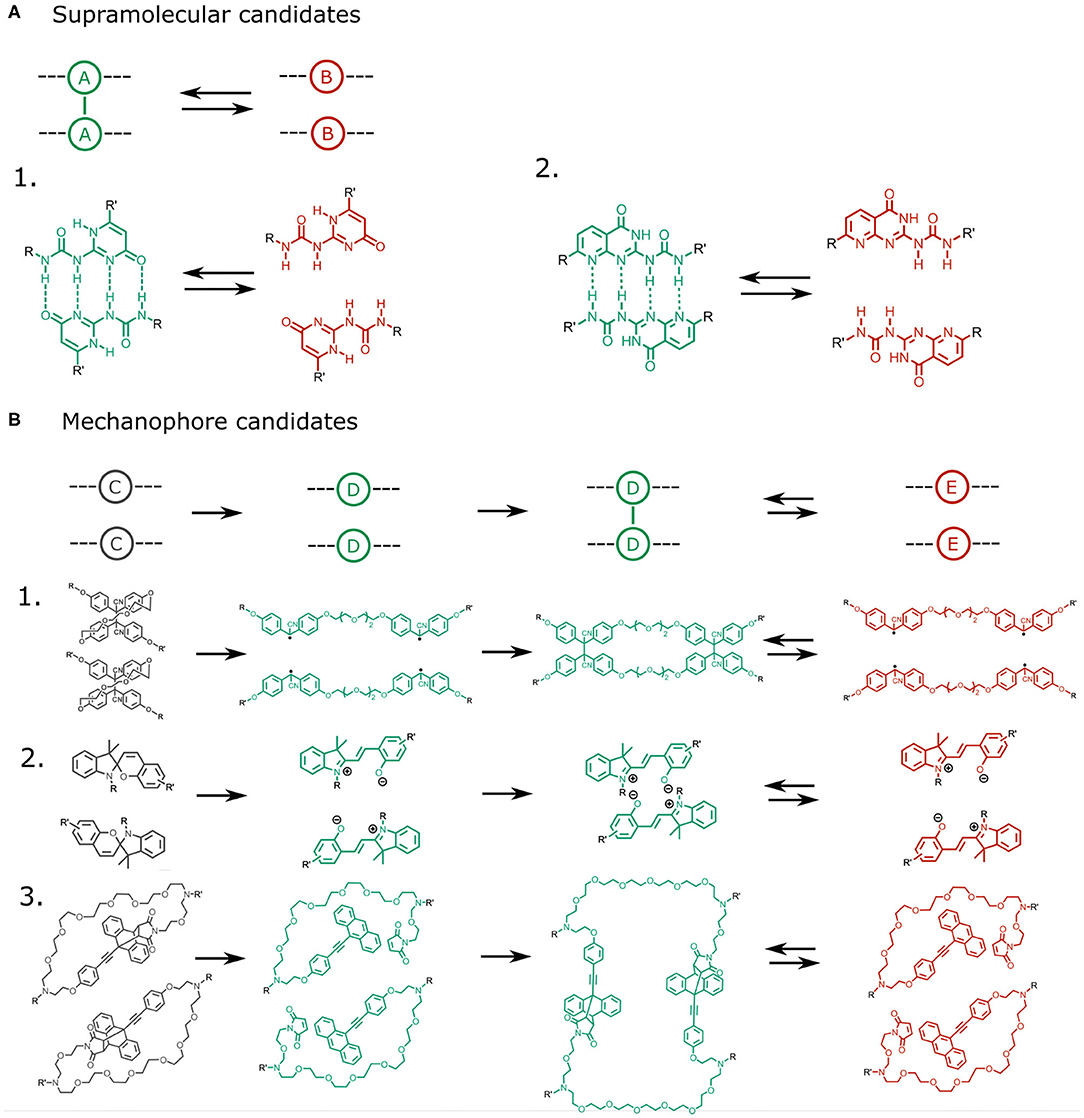
Figure 5. (A) Potential quadruple hydrogen bonding candidates for the supramolecular interaction A − A. Two examples based on 2-ureido-4[1H]-pyrimidone are shown [24, 25]. (B) Potential mechanophore candidates should be capable of converting an intramolecular bond (C) into an intermolecular bond (D − D). Hypothetical examples are: 1. a bridged tetraphenyl succinonitrile molecule containing a reversibly cleavable C-C bond [26, 27], 2. spiropyran, which converts into zwitterionic merocyanine after rupture of an intramolecular C-C bond, allowing it to dimerize through electrostatic interactions and π − π stacking [28–31], and 3. Diels-Alder adducts, which can dissociate through a mechanically induced retro-Diels-Alder reaction, and subsequently reassociate to form intermolecular Diels-Alder bonds [32].

The choice for the mechanophore C requires more attention, as the suitable molecule should be capable of a force-induced transition from an intramolecular to an intermolecular bond, for which several candidates are available (Figure 5B). One potential realization of molecule C is spiropyran, which can undergo a reversible covalent bond dissociation [29] converting it into the zwitterionic merocyanin molecule capable of dimerization through π − π stacking and electrostatic interactions [30, 31]. Other candidates include Diels-Alder adducts of aromatic molecules, which can be activated by a mechanically-triggered retro Diels-Alder reaction [32]. In a Diels-Alder mechanophore, force-induced dissociation of an intramolecular Diels-Alder adduct can trigger the formation of an intermolecular Diels-Alder adduct or the exposure of an aromatic group capable of undergoing pi-bonding. Finally, succinonitrile compounds may be considered. These contain labile covalent bonds that can dissociate reversibly into radicals, whose recombination with adjacent moieties can trigger intermolecular bonding from a labile intramolecular bond [26, 27].

In selecting a suitable supramolecular unit/mechanophore pair, care should be taken that these satisfy the criteria we have identified. The criterion that k_AB,0/k_CD,0 >> 1 should be viable as many mechanophore activations rely on the dissociation of covalent bonds, whereas the supramolecular cross links rely on weaker interactions. Similarly, the criterion that k_AB,0/k_DE,0 >> 1 should be viable as the bonds formed upon mechanophore activation are generally stronger than the supramolecular interactions, especially in the case of diels alder adducts and succinonitrile compounds. However, one of the greatest bottlenecks in selecting a suitable A and C pair is likely to ensure a sufficiently large activation length ratio δx_C/δx_A. Our simulations reveal that δx_C/δx_A must be greater than 3 to obtain a catch bond. However, experimental evidence reveals that activation lengths of many mechanophores are in fact similar to those of many supramolecular interactions. For example, the activation length of the spiropyran ring opening is around 1.93 [28], which does not exceed the activation length of the commonly used supramolecular unit 2-ureido-4[1H]-pyrimidone (2.3 Å) [24].

A potential solution to this challenge is to make use of the force geometry. While our model does not take into account the effect of molecular groups surrounding the mechanophore, experimental results show the effective activation length of mechanophores can depend strongly on the surrounding chemical environment. For example, single molecule force spectroscopy studies on a mechanophore embedded in a polymer show that the activation length of a mechanophore can be enhanced by the surrounding polymer backbone [33]. In this case, the activation length is interpreted as the effective contour length difference between the mechanophore at rest and in its activated state in the direction of the applied force. This suggests that by making clever use of the way in which force is distributed over the bond, it is perhaps possible to achieve an effective activation length difference without employing exotic molecules with intrinsically large activation lengths. This might also offer an explanation on how natural proteins can act as catch bonds in spite of the fact that they mostly employ common supramolecular interactions.

Another avenue that could be explored in the future is the effect of multivalency in achieving catch bond behavior. In this work, we have only looked at multivalency in the number of supramolecular (A) units, but multivalency in the number of mechanophores (C) might also have important implications: In the limit of constant strain, we could predict that incorporating multiple mechanophore units increases the collective work applied to the bond as n_Cfδx. Under constant tension force, this means that the effect of the activation length of the interconversion between the inactive and active states is multiplied by n_C. We can imagine this as follows: as soon as one of the mechanophores activates, the lifetime of the bond is increased, which in turn increases the likelihood that other mechanophores are activated before the catch bond dissociates as a whole. This effect might allow catch bonds to be made out of mechanophores that otherwise would not have a sufficiently large activation length. It could also have implications for biological catch bonds. Despite having only a limited pool of amino acids and thus interactions to choose from, catch bonding protein complexes could employ multivalency to obtain large effective activation lengths for the transitions between their inactive and active states.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

JS conceived the project. JG and MG wrote the simulation code. MG performed the simulations and the data analysis. All authors discussed the data and their interpretation and co-wrote the manuscript.

Funding

The research presented in this article was financially supported by VLAG Graduate School. JG acknowledges the European Research Council for financial support (ERC CoG SOFTBREAK).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.00361/full#supplementary-material

References

1. Thomas WE, Vogel V, Sokurenko E. Biophysics of catch bonds. Annu Rev Biophys. (2008) 37:399–416. doi: 10.1146/annurev.biophys.37.032807.125804

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Marshall B, Long M, Piper J, Yago T, McEver R, Zhu C. Direct observation of catch bonds involving cell-adhesion molecules. Nature. (2003) 423:190–3. doi: 10.1038/nature01605

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Thomas W, Nilsson L, Forero M, Sokurenko E, Vogel V. Shear-dependent ‘stick-and-roll’ adhesion of type 1 fimbriated Escherichia coli. Mol Microbiol. (2004) 53:1545–57. doi: 10.1111/j.1365-2958.2004.04226.x

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Yago T, Lou J, Wu T, Yang J, Miner JJ, Coburn L, et al. Platelet glycoprotein lb alpha forms catch bonds with human WT vWF but not with type 2B von Willebrand disease vWF. J Clin Investig. (2008) 118:3195–207. doi: 10.1172/JCI35754

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Huang DL, Bax NA, Buckley CD, Weis WI, Dunn AR. Vinculin forms a directionally asymmetric catch bond with f-actin. Science. (2017) 357:703–6. doi: 10.1126/science.aan2556

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Rai AK, Rai A, Ramaiya AJ, Jha R, Mallik R. Molecular adaptations allow dynein to generate large collective forces inside cells. Cell. (2013) 152:172–82. doi: 10.1016/j.cell.2012.11.044

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Akiyoshi B, Sarangapani KK, Powers AF, Nelson CR, Reichow SL, Arellano-Santoyo H, et al. Tension directly stabilizes reconstituted kinetochore-microtubule attachments. Nature. (2010) 468:576–U255. doi: 10.1038/nature09594

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Nord AL, Gachon E, Perez-Carrasco R, Nirody JA, Barducci A, Berry RM, et al. Catch bond drives stator mechanosensitivity in the bacterial flagellar motor. Proc Natl Acad Sci USA. (2017) 114:12952–7. doi: 10.1073/pnas.1716002114

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Trong IL, Aprikian P, Kidd BA, Forero-Shelton M, Tchesnokova V, Rajagopal P, et al. Structural basis for mechanical force regulation of the adhesin fimh via finger trap-like sheet twisting. Cell. (2010) 141:645–55. doi: 10.1016/j.cell.2010.03.038

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Sauer MM, Jakob RP, Eras J, Baday S, Eris D, Navarra G, et al. Catch-bond mechanism of the bacterial adhesin FimH. Nat Commun. (2016) 7:10738. doi: 10.1038/ncomms10738

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Waldron TT, Springer TA. Transmission of allostery through the lectin domain in selectin-mediated cell adhesion. Proc Natl Acad Sci USA. (2009) 106:85–90. doi: 10.1073/pnas.0810620105

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Preston RC, Jakob RP, Binder FPC, Sager CP, Ernst B, Maier T. E-selectin ligand complexes adopt an extended high-affinity conformation. J Mol Cell Biol. (2016) 8:62–72. doi: 10.1093/jmcb/mjv046

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Pereverzev YV, Prezhdo OV, Forero M, Sokurenko EV, Thomas WE. The two-pathway model for the catch-slip transition in biological adhesion. Biophys J. (2005) 89:1446–54. doi: 10.1529/biophysj.105.062158

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Evans E, Leung A, Heinrich V, Zhu C. Mechanical switching and coupling between two dissociation pathways in a P-selectin adhesion bond. Proc Natl Acad Sci USA. (2004) 101:11281–6. doi: 10.1073/pnas.0401870101

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Barsegov V, Thirumalai D. Dynamics of unbinding of cell adhesion molecules: Transition from catch to slip bonds. Proc Natl Acad Sci USA. (2005) 102:1835–9. doi: 10.1073/pnas.0406938102

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Ley K, Laudanna C, Cybulsky MI, Nourshargh S. Getting to the site of inflammation: the leukocyte adhesion cascade updated. Nat Rev Immunol. (2007) 7:678–89. doi: 10.1038/nri2156

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Zhang T, Mbanga BL, Yashin VV, Balazs AC. Tailoring the mechanical properties of nanoparticle networks that encompass biomimetic catch bonds. J Polym Sci Part B. (2018) 56:105–18. doi: 10.1002/polb.24542

CrossRef Full Text | Google Scholar

18. Iyer BVS, Yashin VV, Balazs AC. Harnessing biomimetic catch bonds to create mechanically robust nanoparticle networks. Polymer. (2015) 69:310–20. doi: 10.1016/j.polymer.2015.01.015

CrossRef Full Text | Google Scholar

19. Bell G. Models for the specific adhesion of cells to cells. Science. (1978) 200:618–27. doi: 10.1126/science.347575

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Ju L, Dong JF, Cruz MA, Zhu C. The N-terminal flanking region of the A1 domain regulates the force-dependent binding of von Willebrand factor to platelet glycoprotein Ib alpha. J Biol Chem. (2013) 288:32289–301. doi: 10.1074/jbc.M113.504001

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Evans E, Ritchie K. Strength of a weak bond connecting flexible polymer chains. Biophys J. (1999) 76:2439–47. doi: 10.1016/S0006-3495(99)77399-6

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Gillespie D. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J Comput Phys. (1976) 22:403–34. doi: 10.1016/0021-9991(76)90041-3

CrossRef Full Text | Google Scholar

23. Sprakel J, Lindstroem SB, Kodger TE, Weitz DA. Stress enhancement in the delayed yielding of colloidal gels. Phys Rev Lett. (2011) 106:248303. doi: 10.1103/PhysRevLett.106.248303

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Hosono N, Kushner AM, Chung J, Palmans ARA, Guan Z, Meijer EW. Forced unfolding of single-chain polymeric nanoparticles. J Am Chem Soc. (2015) 137:6880–8. doi: 10.1021/jacs.5b02967

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Corbin P, Zimmerman S. Self-association without regard to prototropy. A heterocycle that forms extremely stable quadruply hydrogen-bonded dimers. J Am Chem Soc. (1998) 120:9710–1. doi: 10.1021/ja981884d

CrossRef Full Text | Google Scholar

26. Sakai H, Sumi T, Aoki D, Goseki R, Otsuka H. Thermally stable radical-type mechanochromic polymers based on difluorenylsuccinonitrile. ACS Macro Lett. (2018) 7:1359–63. doi: 10.1021/acsmacrolett.8b00755

CrossRef Full Text | Google Scholar

27. Kato S, Ishizuki K, Aoki D, Goseki R, Otsuka H. Freezing-induced mechanoluminescence of polymer gels. ACS Macro Lett. (2018) 7:1087–91. doi: 10.1021/acsmacrolett.8b00521

CrossRef Full Text | Google Scholar

28. Gossweiler GR, Kouznetsova TB, Craig SL. Force-rate characterization of two spiropyran-based molecular force probes. J Am Chem Soc. (2015) 137:6148–51. doi: 10.1021/jacs.5b02492

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Davis DA, Hamilton A, Yang J, Cremar LD, Van Gough D, Potisek SL, et al. Force-induced activation of covalent bonds in mechanoresponsive polymeric materials. Nature. (2009) 459:68–72. doi: 10.1038/nature07970

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Achilleos DS, Hatton TA, Vamvakaki M. Light-regulated supramolecular engineering of polymeric nanocapsules. J Am Chem Soc. (2012) 134:5726–9. doi: 10.1021/ja212177q

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Zhang L, Dai L, Rong Y, Liu Z, Tong D, Huang Y, et al. Light-triggered reversible self-assembly of gold nanoparticle oligomers for tunable SERS. Langmuir. (2015) 31:1164–71. doi: 10.1021/la504365b

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Gostl R, Sijbesma RP. pi-extended anthracenes as sensitive probes for mechanical stress. Chem Sci. (2016) 7:370–5. doi: 10.1039/C5SC03297K

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Klukovich HM, Kouznetsova TB, Kean ZS, Lenhardt JM, Craig SL. A backbone lever-arm effect enhances polymer mechanochemistry. Nat Chem. (2013) 5:110–4. doi: 10.1038/nchem.1540

PubMed Abstract | CrossRef Full Text | Google Scholar