Estimating the Serial Interval of the Novel Coronavirus Disease (COVID-19): A Statistical Analysis Using the Public Data in Hong Kong From January 16 to February 15, 2020

Background: The emerging virus, severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), has caused a large outbreak of novel coronavirus disease (COVID-19) since the end of 2019. As of February 15, there were 56 COVID-19 cases confirmed in Hong Kong since the first case with symptom onset on January 23, 2020.

Methods: Based on the publicly available surveillance data in Hong Kong, we identified 21 transmission events as of February 15, 2020. An interval censored likelihood framework is adopted to fit three different distributions including Gamma, Weibull, and lognormal, that govern the serial interval (SI) of COVID-19. We selected the distribution according to the Akaike information criterion corrected for small sample size (AICc).

Findings: We found the lognormal distribution performed slightly better than the other two distributions in terms of the AICc. Assuming a lognormal distribution model, we estimated the mean of SI at 4.9 days (95% CI: 3.6–6.2) and SD of SI at 4.4 days (95% CI: 2.9–8.3) by using the information of all 21 transmission events.

Conclusion: The SI of COVID-19 may be shorter than the preliminary estimates in previous works. Given the likelihood that SI could be shorter than the incubation period, pre-symptomatic transmission may occur, and extra efforts on timely contact tracing and quarantine are crucially needed in combating the COVID-19 outbreak.

Introduction

The coronavirus disease 2019 (COVID-19) is caused by the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2, formerly known as the “2019-nCoV”), which has emerged at the end of 2019 [1–5]. COVID-19 cases were soon exported to many Chinese cities and overseas [6], and the travel-related risk of disease spread was suggested in previous studies [4, 7–9]. The risks of rapid spreading were evaluated based on the early surveillance data and also compared to other previous respiratory infectious diseases [5, 10–14]. Since the first confirmed imported case in Hong Kong on January 23 [15], the local government has implemented a series of control and prevention measures for COVID-19, including enhanced border screening and traffic restrictions [16, 17].

The COVID-19 pandemic has affected most of the regions around the world, including places with less developed healthcare systems. Hong Kong was the hardest hit region in the severe acute respiratory syndrome (SARS) outbreaks in 2003 [18, 19], and thus it is expected to be more prepared in mitigation of emerging infectious disease outbreaks [20]. The lesson in Hong Kong shall be an example for other regions, in particular those less developed places with poor settings [21–24]. As of February 15, there were 56 COVID-19 cases confirmed in Hong Kong [16], and local transmission was also recognized by the contact tracing investigation. Given the risk of human-to-human transmission, the serial interval (SI), which refers to the time interval from illness onset in a primary case (i.e., infector) to that in a secondary case (i.e., infectee) [25–28], was of interest to the iterative rate of transmission generations of COVID-19. SI could be used to assist strategic decision-making of public health policies and construct analytical frameworks for studying the transmission dynamics of SARS-CoV-2.

In this study, we examined the publicly available materials released by the Center for Health Protection (CHP) of Hong Kong. Adopting the case-ascertained design [29], we identified the transmission chain from index cases to secondary cases. We estimated the SI of COVID-19 based on 21 identified transmission chains from the surveillance data and contact tracing data in Hong Kong.

Data and Methods

As of February 15, there were 56 confirmed COVID-19 cases in Hong Kong [16], which followed the case definition in official diagnostic protocol released by the World Health Organization (WHO) [30]. To identify the pairs of infector (i.e., primary case) and infectee (i.e., secondary case), we scanned all news press released by the CHP of Hong Kong between January 16 and February 15, 2020 [17]. The exact symptom onset dates of all individual patients were released by CHP [16], which were publicly available, and used to match each transmission chain. For those infectees associated with multiple infectors, we recorded the range of onset dates of all associated infectors, i.e., lower and upper bounds. With all publicly available information from CHP, we constructed the transmission events by subjectively screening the exposure link between consecutive COVID-19 infections. We identified 21 transmission events, including 12 infectees matched with only one infector, that were used for SI estimation. Note that all the 21 transmission events occurred in Hong Kong, and most of the cases involved Hong Kong residents.

Following previous studies [25], we adopted a distribution function with mean μ and standard deviation (SD) σ, denoted by g(|μ, σ), to govern the distribution of SI. We defined g(|μ, σ) as three different distributions; Gamma, Weibull, and lognormal distribution. The interval censored likelihood [31], denoted by L₀, of SI estimates is defined in Equation (1). It happens in the practical analyses of serial interval (as well as incubation period), observations are typically integer while the population mean can be a real value.

$\begin{array}{ll}{L}_0\left(\mu ,\sigma |\tau ,T^{\text{low}},T^{\text{up}}\right)={\displaystyle \prod _i}\left[\underset{T_i^{\text{low}}}{\stackrel{T_i^{\text{up}}}{\int }}h\left(t|T_i^{\text{low}},T_i^{\text{up}}\right)g({\tau }_i-t|\mu ,\sigma )\text{d}t\right]& (1)\end{array}$

The h(·) was the probability density function (PDF) of exposure following a uniform distribution with a range from T^low to T^up. The terms T_i^low and T_i^up denoted the lower and upper bounds, respectively, for the range of onset dates of multiple infectors linked to the i-th infectee. The τ_i was the observed onset date of the i-th infectee. Hence, the likelihood function in Equation (1) can be interpreted as the probability of the SI being observed with uncertain onset dates of infectors but a fixed onset date of the infectee [25, 31]. We calculated the maximum likelihood estimates of μ and σ. Their 95% confidence interval (95% CI) were calculated by using the profile likelihood estimation framework with a cutoff threshold determined by a Chi-square quantile [32]. We select the distribution of g(·|μ, σ) according to the Akaike information criterion corrected for small sample size, denoted by AICc. We employed both Pearson's correlation and coefficient of determination, i.e., R-squared, to measure the goodness-of-fit of the selected model.

In addition, as pointed out in [31], it was possible that the naive likelihood in Equation (1) underestimated the SI due to sampling biases. Hence, we adjusted for the right truncation observation bias due to isolation by using an alternative likelihood function, L, in Equation (2), which is based on the non-truncated version in Equation (1). The truncation scheme in Nishiura et al. [31], as well as adopted in Kwok et al. [21], is relying on prior knowledge of an additional parameter, i.e., the intrinsic growth rate of the epidemic, which is commonly assumed and fixed in the likelihood framework. The truncation scheme adopted in this work was previously discussed in Zhao [33], which considers both likelihood of occurrence and likelihood of being observed subjected to the implementation of isolation.

$\begin{array}{ll}L\left(\mu ,\sigma |\tau ,T^{\text{low}},T^{\text{up}}\right)={\displaystyle \prod _i}\frac{\left[\underset{T_i^{\text{low}}}{\stackrel{T_i^{\text{up}}}{\int }}h(t|T_i^{\text{low}},T_i^{\text{up}}).g({\tau }_i-t|\mu ,\sigma )\text{d}t\right]}{G(d_i-T_i^{low}|\mu ,\sigma )}& (2)\end{array}$

Here, the G(·) was the cumulative distribution function of g(·|μ, σ). The d_i was the isolation date of the infector associated with the i-th infectee. All other notations were the same as those in Equation (1). The maximum likelihood estimates were calculated, and AICc was employed for model selection.

Results and Discussion

The observed SIs of all 21 samples have a mean of 4.3 days, median of 4 days, interquartile range (IQR) between 2 and 5, and a range from 1 to 13 days. For the 12 “infector- infectee” pairs, the observed SIs have a mean of 3 days, median of 2 days, IQR between 2 and 4, and range from 1 to 8 days. Figure 1 shows the likelihood profiles of varying SI with respect to μ and σ of SI. In Table 1, for the non-truncated scenario [i.e., using Equation [1]], we found the three distributions have almost equivalent fitting performance in terms of the AICc. The lognormal distribution has the lowest AICc, and thus it is presented as the main result for the SI estimation. By using all 21 samples, we estimated the mean of SI at 3.9 days (95% CI: 2.8–7.2) and SD of SI at 2.6 days (95% CI: 1.6–9.3). Between the observed and the fitted distributions, the Pearson's correlation is 0.98, and the R-squared is 0.97. These estimates largely matched the results in the existing literature [31, 34, 35]. Considering only the 12 “infector-infectee” pairs, we found the lognormal distribution also outperformed, and we estimated the mean of SI at 3.0 days (95% CI: 1.9–6.8) and SD of SI at 2.0 days (95% CI: 1.0–10.5). In this case, the Pearson's correlation is 0.96, and the R-squared is 0.92. The fitted lognormal distributions were shown in Figure 2.

FIGURE 1

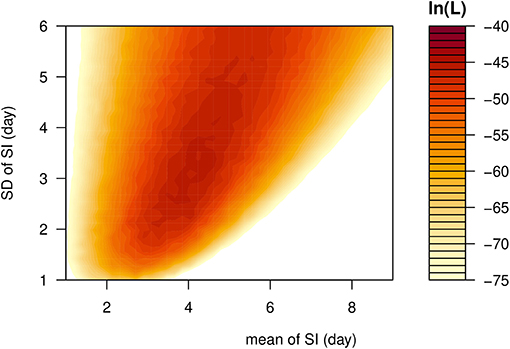
Figure 1. The likelihood profile of the varying serial interval (SI) of COVID-19 by using all samples. The color scheme is shown on the right-hand side, and a darker color indicates a larger log-likelihood, i.e., ln(L), value.

TABLE 1

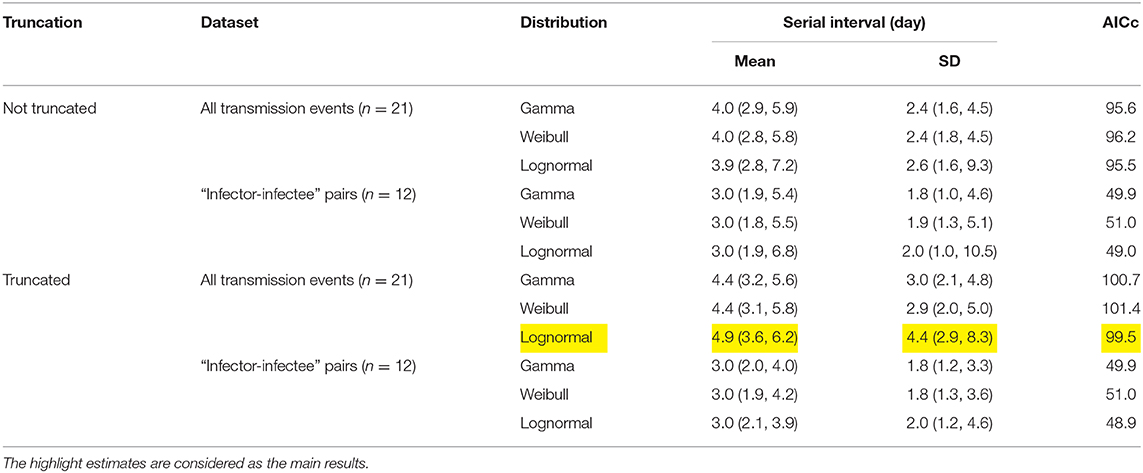
Table 1. Summary of the estimates of the serial interval (SI) mean and standard deviation (SD) from three different distributions.

FIGURE 2

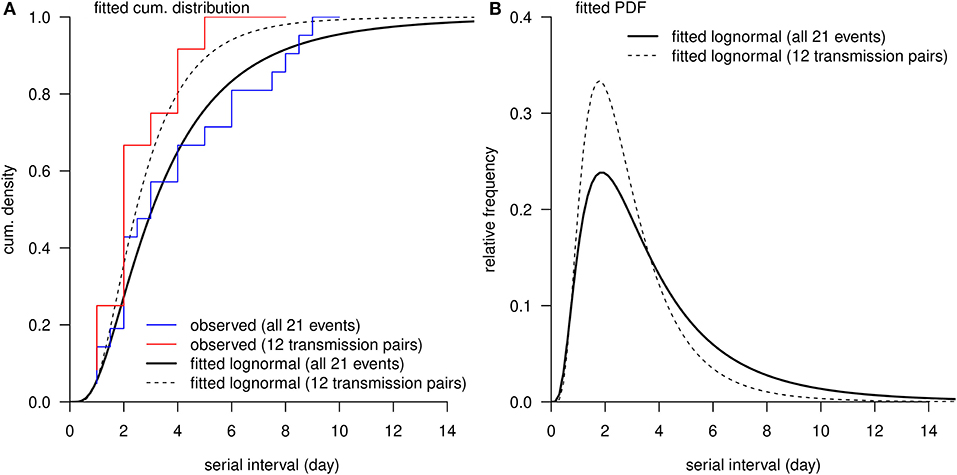
Figure 2. The distribution of serial interval (SI). (A), the red curve is the observed cumulative distribution of SI from 12 transmission pairs, and the blue curve is the observed cumulative distribution of SI from all 21 transmission events. (A,B), the black bold curve is the fitted lognormal distribution using all 21 transmission events, and the dashed thin curve is the fitted lognormal distribution using 12 transmission pairs without truncation.

For the right-truncated scenario [i.e., using Equation (2)], the lognormal distribution also outperformed in terms of the AICc, see Table 1. By using all 21 samples, we estimated the mean of SI at 4.9 days (95% CI: 3.6–6.2) and SD of SI at 4.4 days (95% CI: 2.9–8.3). By only using the 12 “infector-infectee” pairs, we estimated the mean of SI at 3.0 days (95% CI: 2.1–3.9) and SD of SI at 2.0 days (95% CI: 1.2–4.6). The Pearson's correlation and coefficient of determination were no longer applicable here since the likelihood function was adjusted and thus not solely depended on the SI observations.

Comparing to the SI of SARS with a mean of 8.4 days and SD of 3.4 days [36], the estimated 4.9-day SI for COVID-19 indicated rapid cycles of generation replacement in the transmission chain. Hence, highly efficient public health control measures, including contact tracing, isolation, and screening, were strongly recommended to mitigate the epidemic size. The timely supply and delivery of healthcare resources, e.g., facemasks, alcohol sterilizer, and manpower and equipment for treatment, were required in response to the rapid growing incidences of COVID-19 [4, 37]. In the places with less developed healthcare systems and limited medical resources, such a rapid growth of the epidemic may cause a burden to the public health system. Therefore, preparedness and cautiousness for the risk of COVID-19 are crucial to minimize impacts [38, 39].

As also pointed out by recent works [31, 34, 35, 40], the mean of SI at 4.9 days is slightly smaller than the mean incubation period, roughly 5 days, estimated by many previous studies [41–44]. The pre-symptomatic transmission may occur when the SI is shorter than the incubation period. If isolation can be conducted immediately after the symptom onset, the pre-symptomatic transmission is likely to contribute to most of SARS-CoV-2 infections. This situation has been recognized by a recent epidemiological investigation [45], and has been implemented in the mechanistic modeling studies of the COVID-19 epidemic [4, 46], where the pre-symptomatic cases were contagious. As such, merely isolating the symptomatic cases will lead to a considerable proportion of secondary cases, and thus contact tracing and immediately quarantine were crucial to reduce the risk of infection. In addition, we would like to point out that minor negative SI observations were reported in recent studies [34, 35, 47–49]. The negativity in the SI may occur when the incubation period is short with a large variance. However, negative value was not observed in our dataset, which may be due to the small sample size. We further remark that this is unlikely to bias the estimation of mean SI, but may lead to a slight underestimation of the SD of SI. The purpose of estimating SI is to approximate the generation interval (time lag of infections of successive cases) which is strictly positive. Caution should be taken when dealing with negative SI.

A recently epidemiological study used 5 “infector-infectee” pairs from contact tracing data in Wuhan, China during the early outbreak to estimate the mean SI at 7.5 days (95% CI: 5.3–19.0) [42], which appeared larger than our SI estimate of 4.9 days. Although the 95% CIs of SI estimates in this study, consistent with previous studies [21, 31, 33–35], and those in Li et al. [42] were not significantly separated, the difference in the SI estimates might exist. If this difference was not due to sampling chance, one of the possible explanations could be enhanced public awareness and swift control measures including the contact tracing and isolation implemented in Hong Kong. Since Hong Kong was the hardest hit in the SARS outbreaks in 2003 [18, 19], the local public health control was one of the most effective in the world. In the initial phase of the outbreak in Wuhan, the transmission occurred without sufficient awareness and effective intervention, thus the SI estimate in Li et al. [42] may be regarded as the intrinsic (wild) SI, as defined in Champredon et al. [50], of COVID-19. Whereas, the SI estimate in Hong Kong may be regarded as the effective SI, in more practical situations where timely action (quarantining cases and their close contacts) is in place [23], such that one case could be isolated before having the chance to further infect others. If timely action was not in place, infections of longer serial interval may occur. Thus, shorter SI observations might be an outcome of effectiveness in control in a location. The practice in Hong Kong is an example for other regions, including less developed countries.

The SI estimate can benefit from larger sample size. The estimates in our study were based on 21 identified transmission events including 12 “infector-infectee” pairs. Although the sample size was smaller than 28 transmission events in Nishiura et al. [31], 71 in You et al. [35] and 468 in Du et al. [34], the advantage of this analysis is that all the 21 transmission events were identified in Hong Kong. Hence, the surveillance data were under consistent reporting and recording standards, which further reduced the heterogenicity in the observations. Our analysis can be improved if larger records on the local transmission events can be produced. Furthermore, a comparison between different localities is important, which sheds light on the effects of different external factors on SI.

Accurate and consistent records on dates of illness onset were essential to the estimation of the SI. All samples used in this analysis were identified in Hong Kong and collected consistently from the CHP [16, 17]. Hence, the reporting criteria were most likely to be the same for all COVID-19 cases, which potentially made our findings more robust.

Clusters of cases can occur by person-to-person transmission within a cluster, e.g.,

• scenario (I): person A infected B, C, and D; or

• scenario (II): A to B to C to D; or

• scenario (III): a mixture of (I) and (II), e.g., A to B, B to C and D;

or they can occur through common exposure to an unrecognized source of infection, e.g.,

• scenario (IV): an unknown person X infected A, B, C, and D; or

• scenario (V): a mixture of (IV) and (I) or (II), e.g., X to A and B, B to C and D.

The lack of information in the publicly available dataset made it difficult to disentangle such complicated situations. The scenarios (I) and (II) can be covered by a pair of “infector-infectee” such that we could identify the link between two unique consecutive infections. Under the scenario (III), we cannot clearly identify the pairwise match between the infector and infectee, which means there were multiple candidates for the infector of one infectee. As such, we employed the PDF h(·) in Equation (1) to account for the possible time of exposure ranging from T^low to T^up. There is no information available on the SI for scenarios (IV) as well as (V) due to the onset date of person X being unknown, and thus our analysis was limited in the scenarios (I)-(III). We note that we should be extra cautious in interpreting the clusters of cases because of this potential limitation. Although we used interval censoring likelihood to deal with the multiple-infector matching issue, more detailed information of the exposure history and clue on “who acquires infection from whom” (WAIFW) would improve our estimates.

Longer SI might be difficult to confirm in reality due to the isolation of confirmed infections [51, 52], or to identify and link together due to the less accurate information associated with memory error which occurred in the backward contact tracing exercise [34]. The issue associated with isolation could possibly bias the SI estimates and lead to an underestimated result [31]. It is possible that at the initial stage the SI is longer than later when strict isolation takes place [23]. Nevertheless, a comparison of estimated SI for SARS and COVID-19 in Hong Kong is still meaningful. We found that the estimated SI of COVID-19 appears shorter than that of SARS. It would be hard to imagine that isolation is responsible for the difference. It is unlikely that the isolation is more rapid in cases of COVID-19 than cases in SARS in Hong Kong, as well as other limitations, which would have happened for both. Thus, the difference we observed for COVID-19 and SARS is likely intrinsic. Given the rapid spreading of COVID-19, effective contact tracing and quarantine/isolation were even more crucial for successful control.

Conclusion

Together with the basic reproduction number, the serial interval is one of the most important epidemiological parameters, although is difficult to estimate and garners less attention than the former. Here, we found that the SI of COVID-19 may be shorter than the preliminary estimates seen in previous works. Since SI could be shorter than the incubation period among some cases, pre-symptomatic transmission may occur, and extra efforts on timely contact tracing and quarantine are crucially needed in combating the COVID-19 outbreak.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author's Note

We note the preprint version of this study is posted in the medRxiv with doi: 10.1101/2020.02.21.20026559 [53], and in the ResearchSquare with doi: 10.21203/rs.3.rs-18805/v3 [54].

Author Contributions

SZ conceived the study and carried out the analysis. SZ and DH drafted the first manuscript. All authors discussed the results, critically read, revised the manuscript, and gave final approval for publication.

Funding

DH was supported by General Research Fund (grant number: 15205119) of the Research Grants Council (RGC) of Hong Kong, China and Alibaba (China) Co. Ltd. Collaborative Research project. WW was supported by National Natural Science Foundation of China (grant number: 61672013) and Huaian Key Laboratory for Infectious Diseases Control and Prevention (grant number: HAP201704), Huaian, Jiangsu, China.

Conflict of Interest

DH received funding from Alibaba (China) Co. Ltd. Collaborative Research project.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer STA declared a shared affiliation with one of the authors, JR to the handling editor at time of review.

References

1. World Health Organization. 'Pneumonia of unknown cause – China', Emergencies preparedness, response, Disease outbreak news, World Health Organization (WHO). (2020). Available online at: https://www.who.int/csr/don/05-january-2020-pneumonia-of-unkown-cause-china/en/ (accessed March 8, 2020).

PubMed Abstract | Google Scholar

2. Li R, Pei S, Chen B, Song Y, Zhang T, Yang W, et al. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV2). Science. (2020) 368:489–93. doi: 10.1126/science.abb3221

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Sun K, Chen J, Viboud C. Early epidemiological analysis of the coronavirus disease 2019 outbreak based on crowdsourced data: a population-level observational study. Lancet Digital Health. (2020) 2:e201–8. doi: 10.1016/S2589-7500(20)30026-1

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Wu JT, Leung K, Leung GM. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet. (2020) 395:689–97. doi: 10.1016/S0140-6736(20)30260-9

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Zhao S, Musa SS, Lin Q, Ran J, Yang G, Wang W, et al. Estimating the unreported number of novel coronavirus (2019-nCoV) cases in China in the first half of january 2020: a data-driven modelling analysis of the early outbreak. J Clin Med. (2020) 9:388. doi: 10.3390/jcm9020388

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Wells CR, Sah P, Moghadas SM, Pandey A, Shoukat A, Wang Y, et al. Impact of international travel and border control measures on the global spread of the novel 2019 coronavirus outbreak. Proc Natl Acad Sci USA. (2020) 117:7504–9. doi: 10.1073/pnas.2002616117

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Bogoch II, Watts A, Thomas-Bachli A, Huber C, Kraemer MU, Khan K. Pneumonia of unknown etiology in Wuhan, China: potential for international spread via commercial air travel. J Travel Med. (2020) 27:taaa008. doi: 10.1093/jtm/taaa008

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Zhao S, Zhuang Z, Cao P, Ran J, Gao D, Lou Y, et al. Quantifying the association between domestic travel and the exportation of novel coronavirus (2019-nCoV) cases from Wuhan, China in 2020: a correlational analysis. J Travel Med. (2020) 27:taaa022. doi: 10.1093/jtm/taaa022

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Zhao S, Zhuang Z, Ran J, Lin J, Yang G, Yang L, et al. The association between domestic train transportation and novel coronavirus outbreak in China, from 2019 to 2020: a data-driven correlational report. Travel Med Infect Dis. (2020) 33:101568. doi: 10.1016/j.tmaid.2020.101568

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Kang D, Choi H, Kim J-H, Choi J. Spatial epidemic dynamics of the COVID-19 outbreak in China. Int J Infect Dis. (2020) 94:96–102. doi: 10.1016/j.ijid.2020.03.076

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Kucharski AJ, Russell TW, Diamond C, Liu Y, Edmunds J, Funk S, et al. Early dynamics of transmission and control of COVID-19: a mathematical modelling study. Lancet Infect Dis. (2020) 20:553–8. doi: 10.1016/S1473-3099(20)30144-4

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Liang K. Mathematical model of infection kinetics and its analysis for COVID-19, SARS and MERS. Infect Genet Evol. (2020) 82:104306. doi: 10.1016/j.meegid.2020.104306

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Zhao S, Lin Q, Ran J, Musa SS, Yang G, Wang W, et al. Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, from 2019 to 2020: a data-driven analysis in the early phase of the outbreak. Int J Infect Dis. (2020). 92:214–7. doi: 10.1016/j.ijid.2020.01.050

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Riou J, Althaus CL. Pattern of early human-to-human transmission of Wuhan 2019 novel coronavirus (2019-nCoV), December 2019 to January 2020. Eurosurveillance. (2020) 25:2000058. doi: 10.2807/1560-7917.ES.2020.25.4.2000058

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Kwok KO, Wong V, Wei VWI, Wong SYS, Tang JW-T. Novel coronavirus (2019-nCoV) cases in Hong Kong and implications for further spread. J Infect. (2020) 80:671–93. doi: 10.1016/j.jinf.2020.02.002

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Centre for Health Protection. Summary of data and outbreak situation of the Severe Respiratory Disease associated with a Novel Infectious Agent, Centre for Health Protection, the government of Hong Kong. (2020). Available online at: https://www.chp.gov.hk/en/features/102465.html (accessed March 8, 2020).

Google Scholar

17. Centre for Health Protection. The collection of Press Releases by the Centre for Health Protection (CHP) of Hong Kong. (2020). Available online at: https://www.chp.gov.hk/en/media/116/index.html (accessed March 8, 2020).

PubMed Abstract | Google Scholar

18. Bauch CT, Lloyd-Smith JO, Coffee MP, Galvani AP. Dynamically modeling SARS and other newly emerging respiratory illnesses: past, present, and future. Epidemiology. (2005) 16:791–801. doi: 10.1097/01.ede.0000181633.80269.4c

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Leung GM, Hedley AJ, Ho L-M, Chau P, Wong IOL, Thach TQ, et al. The epidemiology of severe acute respiratory syndrome in the 2003 Hong Kong epidemic: an analysis of all 1755 patients. Ann Intern Med. (2004) 141:662–73. doi: 10.7326/0003-4819-141-9-200411020-00006

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Ran J, Zhao S, Zhuang Z, Chong MKC, Cai Y, Cao P, et al. Quantifying the improvement in confirmation efficiency of the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) during the early phase of outbreak in Hong Kong in 2020. Int J Infect Dis. (2020) 96:284–7. doi: 10.1016/j.ijid.2020.05.015

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Kwok KO, Wong VWY, Wei WI, Wong SYS, Tang JW-T. Epidemiological characteristics of the first 53 laboratory-confirmed cases of COVID-19 epidemic in Hong Kong, 13 February 2020. Eurosurveillance. (2020) 25:2000155. doi: 10.2807/1560-7917.ES.2020.25.16.2000155

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Leung GM, Cowling BJ, Wu JT. From a sprint to a marathon in Hong Kong. N Engl J Med. (2020) 382:e45. doi: 10.1056/NEJMc2009790

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Zhao S, Cao P, Chong MKC, Gao D, Lou Y, Ran J, et al. COVID-19 and gender-specific difference: Analysis of public surveillance data in Hong Kong and Shenzhen, China, from January 10 to February 15, 2020. Infect Control Hosp Epidemiol. (2020) 41:750–1. doi: 10.1017/ice.2020.64

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Wong SYS, Kwok KO, Chan FKL. What can countries learn from Hong Kong's response to the COVID-19 pandemic? CMAJ. (2020) 192:E511–5. doi: 10.1503/cmaj.200563

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Cowling BJ, Fang VJ, Riley S, Peiris JM, Leung GM. Estimation of the serial interval of influenza. Epidemiology. (2009) 20:344–7. doi: 10.1097/EDE.0b013e31819d1092

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Fine PEM. The interval between successive cases of an infectious disease. Am J Epidemiol. (2003) 158:1039–47. doi: 10.1093/aje/kwg251

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Nishiura H, Chowell G, Heesterbeek H, Wallinga J. The ideal reporting interval for an epidemic to objectively interpret the epidemiological time course. J R Soc Interf . (2010) 7:297–307. doi: 10.1098/rsif.2009.0153

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Wallinga J, Lipsitch M. How generation intervals shape the relationship between growth rates and reproductive numbers. Proc R Soc B: Biol Sci. (2007) 274:599–604. doi: 10.1098/rspb.2006.3754

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Yang Y, Longini I, Halloran ME. Design and evaluation of prophylactic interventions using infectious disease incidence data from close contact groups. J R Stat Soc Ser C-Appl Stat. (2006) 55:317–30. doi: 10.1111/j.1467-9876.2006.00539.x

PubMed Abstract | CrossRef Full Text | Google Scholar

30. World Health Organization. Laboratory Testing for 2019 Novel Coronavirus (2019-nCoV) in Suspected Human Cases, World Health Organization (WHO). (2020). Available online at: https://www.who.int/health-topics/coronavirus/laboratory-diagnostics-for-novel-coronavirus (accessed March 8, 2020).

Google Scholar

31. Nishiura H, Linton NM, Akhmetzhanov AR. Serial interval of novel coronavirus (COVID-19) infections. Int J Infect Dis. (2020) 93:284–6. doi: 10.1016/j.ijid.2020.02.060

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Fan J, Huang T. Profile likelihood inferences on semiparametric varying-coefficient partially linear models. Bernoulli. (2005) 11:1031–57. doi: 10.3150/bj/1137421639

CrossRef Full Text | Google Scholar

33. Zhao S. Estimating the time interval between transmission generations when negative values occur in the serial interval data: using COVID-19 as an example. Math Biosci Eng. (2020) 17:3512–9. doi: 10.2807/1560-7917.ES.2020.25.17.2000257

CrossRef Full Text | Google Scholar

34. Du Z, Xu X, Wu Y, Wang L, Cowling BJ, Meyers LA. Serial interval of COVID-19 among publicly reported confirmed cases. Emerg Infect Dis J. (2020) 26:1341–43. doi: 10.3201/eid2606.200357

PubMed Abstract | CrossRef Full Text | Google Scholar

35. You C, Deng Y., Hu W., Sun J., Lin Q., Zhou F, et al. Estimation of the time-varying reproduction number of COVID-19 outbreak in China. Int J Hygiene Environ Health. 228:113555. doi: 10.1016/j.ijheh.2020.113555

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Lipsitch M, Cohen T, Cooper B, Robins JM, Ma S, James L, et al. Transmission dynamics and control of severe acute respiratory syndrome. Science. (2003) 300:1966–70. doi: 10.1126/science.1086616

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Zhao S, Stone L, Gao D, Musa SS, Chong MKC, He D, et al. Imitation dynamics in the mitigation of the novel coronavirus disease (COVID-19) outbreak in Wuhan, China from 2019 to 2020. Ann Transl Med. (2020) 8:488. doi: 10.21037/atm.2020.03.168

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Chong KC, Cheng W, Zhao S, Ling F, Mohammad KN, Wang MH, et al. Monitoring disease transmissibility of 2019 novel coronavirus disease in Zhejiang, China. Int J Inf Dis. (2020) 96:128–130. doi: 10.1016/j.ijid.2020.04.036

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Lin Q, Zhao S, Gao D, Lou Y, Yang S, Musa SS, et al. A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action. Int J Infect Dis. (2020) 93:211–6. doi: 10.1016/j.ijid.2020.02.058

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Wang K, Zhao S, Liao Y, Zhao T, Wang X, Zhang X, et al. Estimating the serial interval of the novel coronavirus disease (COVID-19) based on the public surveillance data in Shenzhen, China from January 19 to February 22, 2020. Transbound Emerg Dis. (2020). doi: 10.1111/tbed.13647. [Epub ahead of print].

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Backer JA, Klinkenberg D, Wallinga J. Incubation period of 2019 novel coronavirus (2019-nCoV) infections among travellers from Wuhan, China, 20–28 January 2020. Eurosurveillance. (2020) 25:2000062. doi: 10.2807/1560-7917.ES.2020.25.5.2000062

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Li Q, Guan X, Wu P, Wang X, Zhou L, Tong Y, et al. Early Transmission Dynamics in Wuhan, China, of novel coronavirus–infected pneumonia. N Engl J Med. (2020) 382:1199–207. doi: 10.1056/NEJMoa2001316

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Linton MN, Kobayashi T, Yang Y, Hayashi K, Akhmetzhanov RA, Jung S-M, et al. Incubation period and other epidemiological characteristics of 2019 novel coronavirus infections with right truncation: a statistical analysis of publicly available case data. J Clin Med. (2020) 9:538. doi: 10.3390/jcm9020538

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Lauer SA, Grantz KH, Bi Q, Jones FK, Zheng Q, Meredith H, et al. The incubation period of 2019-nCoV from publicly reported confirmed cases: estimation and application. medRxiv [Preprint]. (2020). doi: 10.1101/2020.02.02.20020016

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Rothe C, Schunk M, Sothmann P, Bretzel G, Froeschl G, Wallrauch C, et al. Transmission of 2019-nCoV infection from an asymptomatic contact in Germany. N Engl J Med. (2020) 382:970–1. doi: 10.1056/NEJMc2001468

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Chowell G, Dhillon R, Srikrishna D. Getting to zero quickly in the 2019-nCov epidemic with vaccines or rapid testing. medRxiv [Preprint]. (2020). doi: 10.1101/2020.02.03.20020271

CrossRef Full Text | Google Scholar

47. Ferretti L, Wymant C, Kendall M, Zhao L, Nurtay A, Abeler-Dörner L, et al. Quantifying SARS-CoV-2 transmission suggests epidemic control with digital contact tracing. Science. (2020) 368:eabb6936. doi: 10.1126/science.abb6936

PubMed Abstract | CrossRef Full Text | Google Scholar

48. He X, Lau EHY, Wu P, Deng X, Wang J, Hao X, et al. Temporal dynamics in viral shedding and transmissibility of COVID-19. Nat Med. (2020) 26:672–5. doi: 10.1038/s41591-020-0869-5

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Ma S, Zhang J, Zeng M, Yun Q, Guo W, Zheng Y, et al. Epidemiological parameters of coronavirus disease 2019: a pooled analysis of publicly reported individual data of 1155 cases from seven countries. medRxiv [Preprin]. (2020). doi: 10.1101/2020.03.21.20040329

CrossRef Full Text | Google Scholar

50. Champredon D, Dushoff J. Intrinsic and realized generation intervals in infectious-disease transmission. Proc R Soc B: Biol Sci. (2015) 282:20152026. doi: 10.1098/rspb.2015.2026

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Park SW, Champredon D, Dushoff J. Inferring generation-interval distributions from contact-tracing data. J R Soc Interf . (2020) 17:20190719. doi: 10.1098/rsif.2019.0719

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Yan P. Separate roles of the latent and infectious periods in shaping the relation between the basic reproduction number and the intrinsic growth rate of infectious disease outbreaks. J Theoret Biol. (2008) 251:238–52. doi: 10.1016/j.jtbi.2007.11.027

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Zhao S, Gao D, Zhuang Z, Chong M, Cai Y, Ran J, et al. Estimating the serial interval of the novel coronavirus disease (COVID-19): a statistical analysis using the public data in Hong Kong from January 16 to February 15, 2020. medRxiv [Preprint]. (2020). doi: 10.1101/2020.02.21.20026559

CrossRef Full Text | Google Scholar

54. Zhao S, Gao D, Zhuang Z, Chong M, Cai Y, Ran J, et al. Estimating the serial interval of the novel coronavirus disease (COVID-19): a statistical analysis using the public data in Hong Kong from January 16 to February 15, 2020. Res Square. (2020). doi: 10.21203/rs.3.rs-18805/v1. [Epub ahead of print].

CrossRef Full Text | Google Scholar