- 1Department of Chemistry and Physics, Purdue University, West Lafayette, IN, United States
- 2Department of Chemistry and Chemical Biology, Harvard University Cambridge, Cambridge, MA, United States
We present a simple interpolation formula using dimensional limits D = 1 and D = ∞ to obtain the D = 3 ground-state energies of atoms and molecules. For atoms, these limits are linked by first-order perturbation terms of electron-electron interactions. This unorthodox approach is illustrated by ground-states for two, three, and four electron atoms, with modest effort to obtain fairly accurate results. Also, we treat the ground-state of H2 over a wide range of the internuclear distance R, and compares well with the standard exact results from the Full Configuration Interaction method. Similar dimensional interpolations may be useful for complex many-body systems.
1. Introduction
Dimensional scaling, as applied to chemical physics, offers promising computational strategies and heuristic perspectives to study electronic structures and obtain energies of atoms, molecules, and extended systems [1–4]. Taking a spatial dimension other than D = 3 can make a problem much simpler and then use perturbation theory or other techniques to obtain an approximate result for D = 3. Years ago, a D-scaling technique used with quantum chromodynamics [5] was prompted for helium [2–4]. The approach began with the D → ∞ limit and added terms in powers of δ = 1/D. It was arduous and asymptotic but by summation techniques attained very high accuracy for D = 3 [6]. Other dimensional scaling approaches were extended to N-electron atoms [7], renormalization with 1/Z expansions [8], random walks [9], interpolation of hard sphere virial coefficients [10], resonance states [11], and dynamics of many-body systems in external fields [12, 13].
Recently, a simple analytical interpolation formula emerged using both the D = 1 and D → ∞ limits for helium [14]. It makes use of only the dimensional dependence of a hydrogen atom, together with the exactly known first-order perturbation terms with λ = 1/Z for the dimensional limits of the electron-electron 〈1/r12〉 interaction. In the D = 1 limit, the Coulombic potentials are replaced by delta functions in appropriately scaled coordinates [15]. In the D → ∞ limit, the electrons assume positions fixed relative to another and to the nucleus, with wave functions replaced by delta functions [16]. Then at D = 3, the ground state energy of helium ϵ3 can be obtained by linking ϵ1 and ϵ∞ together with the first-order perturbation coefficients and of the 1/Z expansion. The first-order terms actually provide much of the dimension dependence. This article exhibits the applicability of an unorthodox formula, a blend of dimensions with first-order perturbations, to more complex many-body systems.
We outline the following sections: in section 2 the interpolation formula; in section 3 treat helium; in section 4 lithium; in section 5 beryllium; in section 6 hydrogen molecule. Each atom section 3–5 has four subsections: A for D = 1; B for D → ∞; C for , the first-order perturbation terms; D for ϵ3, the ground-state energy at D = 3 is obtained from the interpolation formula. For the hydrogen molecule section 6, the subsections deal how the internuclear distance R varies in the D = 1 and D → ∞ dimensions and mesh into D = 3. Finally, in section 7 we comment on prospects for blending dimensional limits to serve other many-body problems.
2. Dimensional Interpolation
For dimensional scaling of atoms and molecules the energy erupts to infinity as D → 1 and vanishes as D → ∞. Hence, we adopt scaled units (with hartree atomic units) whereby and , so the reduced energy ϵD remains finite in both limits. When expressed in a 1/Z perturbation expansion, the reduced energy is given by
with λ = 1/Z, where Z is the total nuclear charge of the corresponding atom. The first-order perturbation coefficient is (1, 6):
It represents the expectation value, , of the electron-electron repulsion evaluated with the zeroth-order hydrogenic wave function, exp(−r1 − r2). Accordingly, is universal. For D = 1, 3, ∞ the corresponding term , respectively.
Our interpolation for atoms, developed in [14], weights the dimensional limits by δ = 1/D, providing δϵ1 and (1 − δ)ϵ∞ in a simple analytic formula
We aim to illustrate the interpolation formula more fully, presenting results with modest calculations having respectable accuracy for two, three, and four electrons.
For the hydrogen molecule, a different scaling scheme will be used and illustrated. The rescaling of the internuclear distance R→R′ is given by:
An approximation for D = 3 (where R = R′) emerges:
on interpolating linearly between the dimensional limits, developed by Loeser in [17–19]; especially see the paragraphs around Equations (23) and (24) of [17] for more details.
3. Two-Electrons: Helium
The formula worked very well for D = 3, helium with λ = 1/2:
The input ingredients are exact limit energies: ϵ1 = −0.788843 from Ref. [15]; ϵ∞ = −0.684442 from [4]; and the three first-order perturbation terms displayed in Equation (2). The interpolation delivered ϵ3 = −0.725780, a result very close to the exact ground-state energy −0.725931 [4]. The interpolation accuracy of 2 millihartrees is better than current density functional theory.
3.1. One-Dimension: D = 1
We will calculate the ground-state energy of the Hamiltonian operator using the variational principle. It is less accurate than [15], but much easier to deal with two and more electrons [20]. The Hamiltonian with electrons in delta functions is:
with λ = 1/Z. The electronic wave function is as follows:
where the normalized wave functions χ1 and χ2 are defined as:
and
We optimize the parameter ξ, defined in (9, 10), and calculate the minimum value of the operator Eϕ(ξ) defined as:
We divide the above Hamiltonian into three parts, where
is the kinetic energy of the two electrons,
is the potential energy of the two electrons due to nuclear attraction, and
is the interaction energy for electron-electron repulsion in the system.
We minimize the Hamiltonian operator Eϕ(ξ) with respect to ξ, with
such that
and obtain ξ0 = 0.875, which put into Equation (15) gives the ground-state energy, ϵ1 = −0.765625. This result is found in [20–22], but it is approximated by 2.9% since noted the exact value is ϵ1 = −0.788843.
3.2. Infinite-Dimension: D → ∞
At large-D limit, the effective ground state Hamiltonian for a two electron atom, with inter-electronic correlation can be written as:
with
where θ is the angle between r1 and r2; see [7] for more details.
We minimize the above effective-Hamiltonian with respect to the parameters r1, r2, and θ respectively, and obtain the corresponding ground state energy to be: ϵ∞ = −0.684442 (see Table 1 in [14], and [22]).
3.3. First-Order Perturbations:
In a two-electron atom, with nuclear charge Z, the exact Hamiltonian in D-dimension using atomic units can be written as:
where the Laplacian operator in D-dimension is defined as:
For helium-like atoms we consider the two electrons are in a 1s-like state with spatial part being symmetric (both electrons are in the same state) and the spin part in the antisymmetric spin singlet. The spatial part of the electronic wave function can be written as:
where the normalized wave functions χ1(r1) and χ2(r2) are defined as:
and
The normalization constant is calculated as:
with
is the surface area of an unit sphere in D-dimension.
In D-dimension, with the above wave functions, we obtain the following first-order coefficient [14]:
As shown in Equation (2) and for D = 1, 3, ∞, respectively .
3.4. Interpolation for D = 3
We use the formula shown in Equation (6), already noting that the exact limit energies and first-order perturbation terms, gave ϵ3 = −0.725780; accurate to 0.02%. If we replace the variational result ϵ1 = −0.765625 (from section 3.1), the formula would give ϵ3 = −0.71839, accurate to 2.9%. However, if we evaluate ϵ1 by using Equation (3), a subformula is
with D = 1. This yielded a good approximation of 0.11% for ϵ1 = −0.787996, near the exact ϵ1 = −0.788843. With this better ϵ1 we obtain ϵ3 = −0.725496, with accuracy of 0.06%.
In conventional quantum chemistry textbooks treating D = 3 helium, the electron-electron interaction, 〈1/r12〉, is evaluated by first-order perturbation theory. The result is ϵ3 = −0.687529 with accuracy of 5.29%.
4. Three-Electrons: Lithium
The ground-state of the lithium atom had been calculated a long ago by using the variational method with complicated wave functions [23–25]. Here we present the interpolation formula, using the D = 1 and D = ∞ limits and the first-order perturbation terms. For the ground-state of the lithium atom our formula gave ϵ3 = −0.839648, with approximation 1.04% compared the exact result ϵ3 = −0.830896 [26].
4.1. One-Dimension: D=1
In a three-electron atom, with nuclear charge Z, the exact Hamiltonian in one-dimension using atomic units can be written as:
with λ = 1/Z.
In the lithium atom we consider that two electrons are in the 1s state and the third electron is in a 2s state, with the spatial part being symmetric (both electrons are in the same state) and the spin part in the antisymmetric state. We write spatial part of the electronic wave function as:
The two normalized wave functions χ1(r1), χ2(r2) are described in Equations (9) and (10). We assume that the 1s wave functions are orthogonal to the 2s wave function:
We calculate the ground state energy of a three-electron atom using variational principle. We optimize the parameter ξ, defined in the wave functions χ1(r1), χ2(r2), χ3(r3), and obtain the minimum value of the Hamiltonian operator Eϕ(ξ), which is defined as
We divide the above Hamiltonian (31) into five parts, where
is the kinetic energy of the three electrons,
is the potential energy of the three electrons due to nuclear attraction, and
are the interaction energies for inter-electronic repulsions in the system.
We minimize the Hamiltonian operator Eϕ(ξ) with respect to ξ, with
such that
and obtain ξ0 = 0.697856, which put into Equation (37) gives the ground-state energy, ϵ1 = −0.693979.
4.2. Infinite-Dimension: D → ∞
At large-D-limit the effective ground state Hamiltonian for three-electron atoms, with correlation can be written as:
where
with γij = γij = cos θij, and θij is the angle between ri and rj. The quantities Γ(i) and Γ are called the Gramian determinants. In Equation (39) the quantity is effectively defined as:
See page 111, Equation (35) in [7] for more details.
We minimize the above effective-Hamiltonian with respect to the parameters r1, r2, r3, and θ12, θ13, θ23, respectively and obtain the corresponding ground state energy ϵ∞ = −0.795453.
4.3. First-Order Perturbations:
As the electrons reside in two orbits, 1s22s, there are three electron-electron pairs: one from 1s2, the two others and from 1s2s. Thus, each coefficient is comprised from the three electron pairs:
The D = 1 item is obtained via section 4.1. The D = 3 item is attained from [27]. Here we will develop both D = 3 and D → ∞ bringing the third electron akin with the two-electron treatment in section 3.3. As the Hamiltonian is evident in Equations (19) and (20), we start with the electronic wave function:
The two normalized functions χ1(r1), χ2(r2) are taken care of in Equations (22), (23), (24), and (25). We assume that the 1s wave functions are orthogonal to the 2s wave function:
The normalization is:
with .
To obtain the first-order terms for D = 3 and D → ∞ we need to assemble some integrals associated with the key f (D) function shown in Equations (2) and (26). The output is:
with
and the hypergeometric function enters in (26).
The parent integral is,
and
From GD(a, b) we compute the following integral:
In the integrals, we used the normalized wave functions χ1(r1), χ2(r2), and χ3(r3) already specified, such a typical term:
From Equation (53), we see that we have to put a = 2 and b = 1, so y = 1/9. In Equations (48) and (55) the hypergeometric function is available in tabulations [28]. We computed up to D = 106 to see that the function converges to
At the D → ∞ limit
For D = 3, the function gives
and,
4.4. Interpolation for D = 3
Again we use the interpolation formula shown in Equation (6),
now with λ = 1/Z = 1/3. The input from our A, B, C subsections was:
and
Our interpolation gave the Li atom ground-state energy with error 1%: ϵ3 = −0.839648, compared with the exact result ϵ3 = −0.830896 [26].
5. Four-Electron: Beryllium
The electronic structure of the beryllium atom is highly interesting because it's implication in different areas of modern science, for e.g. stellar astrophysics and plasmas, high-temperature physics, etc. The ground-state energy for the Be-atom has been calculated by applying various methods for e.g., the Configuration Interaction (CI) method with Slater-type orbitals (STOs) [29], the Hylleraas method (Hy) [30], the Hylleraas-Configuration Interaction method (Hy-CI) [31], and the Exponential Correlated Gaussian (ECG) method [32, 33]. In this section, we present the dimensional interpolation formula, by using the results from D = 1 and D = ∞ limit, to obtain the ground state energy of the four-electron atoms. With dimensional interpolation we obtain the ground state energy of beryllium atom to be ϵ3 = −0.910325, compared to the exact energy ϵ3 = −0.916709, with a percentage error of 0.6%.
5.1. One-Dimension: D=1
In Four-electron atoms, with nuclear charge Z = 1/λ, the exact Hamiltonian in one-dimension using atomic units can be written as:
In beryllium atom we consider that two electrons are in the 1s state, and the other two electrons are in the 2s state with the spatial part being symmetric (both electrons are in the same state) and the spin part in the antisymmetric state. We write spatial part of the electronic wave function as follows:
The three normalized wave functions χ1(r1), χ2(r2), χ3(r3) are described in Equations (9), (10), and (30). We assume that the 1s wave functions are orthogonal to the two 2s wave functions χ3(r3) and
We calculate the ground state energy of a four-electron atom with variational principle. We optimize the parameter ξ, defined in the wave functions χ1(r1), χ2(r2), χ3(r3), χ4(r4), and obtain the minimum value of the Hamiltonian operator Eϕ(ξ), which is defined as:
We divide the above Hamiltonian into five parts, where
is the kinetic energy of the four electrons,
is the potential energy of the four electrons due to nuclear attraction, and
are the interaction energies for inter-electronic repulsions in the system.
We minimize the Hamiltonian operator Eϕ(ξ) with respect to ξ, with
such that
and obtain ξ0 = 0.590850, which put into Equation (68) gives the ground-state energy, ϵ1 = −0.645842.
5.2. Infinite-Dimension: D → ∞
In large-D-limit the effective ground state Hamiltonian for four-electron atoms, with inter-electronic correlation can be written as:
where
with γij = γij = cos θij, and θij are the angle between ri and rj. The quantities Γ(i) and Γ are the Gramian determinants. In Equation (70) the quantity is effectively defined as follows:
See page 111, Equation (35) in [7] for more details.
We minimize the above effective-Hamiltonian with respect to the parameters r1, r2, r3, r4, and θ12, θ13, θ14, θ23, θ24, θ34 respectively and obtain the corresponding ground state energy ϵ∞ = −0.875837.
5.3. First-Order Perturbations:
As the electrons reside in two orbits, 1s22s2, there are six electron-electron pairs: one from 1s2, four others , , , from 1s2s; and another lonely from 2s2. Each coefficient is comprised from the six electron pairs:
The D = 1 item is obtained via section 5.1. Here we will develop both D = 3 and D → ∞ bringing the fourth electron akin with the three-electron treatment in section 4.3. As the Hamiltonian is evident in Equations (19) and (20), we start with the electronic wave function:
The two normalized 1s wave functions χ1(r1), χ2(r2) are taken care of in Equations (22), (23), (24), and (25). We assume that the 1s wave functions are orthogonal to the 2s wave functions χ2(r2), defined in (46), and:
with normalization constant defined in (47).
We take the same approach as section 4.3 to calculate the first-order term (the 2s2 electron-electron repulsion term) at D → ∞ limit with the help of Equations (50, 52):
with and f (D) function shown in Equations (2) and (26). This is the same functional expression as in lithium atom (53), but the arguments are different.
To calculate the first-order perturbation coefficient for beryllium we use the normalized wave functions χ1(r1), χ2(r2), χ3(r3), and χ4(r4) already specified, which gives rise to a typical term like
From the above Equation (79), we see that we have to put a = 1 and b = 1, so y = 0. In Equation (78) the hypergeometric function
and f (D) → 2−1/2 at D → ∞ limit.
At D → ∞ limit (78) gives
For D = 3 we use the following formula from [1] and [28]:
From the above relation (82) we can compute the following integral:
At D = 3 the 2s wave function
with α = 1 such that
To calculate the inter-electronic repulsion energy from (85) we use the above type of integrals in Equation (82) and K3(i, j, k) in Equation (83), with a = 1, b = 1, and k = 0.
With the help of (82, 83) we calculate the first-order coefficient (2s-2s part) for the beryllium atom in three dimension:
5.4. Interpolation for D=3
We again use the interpolation formula shown in Equation (6),
now with λ = 1/Z = 1/4. The input from our A, B, C subsections was:
and
Our interpolation gives the Be atom ground-state energy with error 0.6%: ϵ3 = −0.910325, compared with the exact result ϵ3 = −0.916709.
6. Hydrogen Molecule
The ground state potential energy function, V(R), of the hydrogen molecule has been calculated by many methods [34–37]. Recently, Olivares-Pilón and Turbiner [38] presented a general theory for obtaining the V(R) function for diatomic molecules. They dealt with the Born-Oppenheimer approximation, based on matching R in short and long distances via a two-point Padé approximation. Here, we present a simpler approach obtaining V(R) for H2 at D = 3 by using interpolation between D = 1 and D → ∞ dimensional limits. Key aspects of dimensional scaling had been developed years ago by Tan and Loeser [18], Lòpez-Cabrera et al. [19] and Frantz and Herschbach [17]. They did an excellent treatment on and partial on H2. Now we will complete V(R) for H2 by interpolation.
6.1. One-Dimension: D=1
In H2, with nuclear charge of each atom Z, the electronic part of the Hamiltonian in one-dimension using atomic units can be written as [20, 39]:
with a = R/2, where R is the distance between the two nuclei located at r = ±a; also λ = 1/Z = 1. The Hamiltonian energy eigenvalues provide symmetric and antisymmetric states under exchange of the electrons. The symmetric state pertains to the ground-state potential energy [20]:
The total binding energy is obtained by adding the nucleus-nucleus-interaction term (1/R) with the electronic energy.
6.2. Infinite-Dimension: D → ∞
Many important features of the H2 molecule are calculated in cylindrical coordinates because this problem has a natural cylindrical symmetry about the z-axis. The D-dimensional space in cylindrical coordinates is described by a linear coordinate z and a (D − 1)-dimensional subspace specified by spherical coordinates, which are orthogonal to each other. The coordinate ρ is the radius of a (D − 1)-dimensional sphere; see section 2 of [17] for more details.
For H2, convention locates the two nuclei A and B on the z-axis at −R/2 and R/2, respectively, with equal charges ZA = ZB = Z. The electrons are located at (ρ1, z1) and (ρ2, z2), with a dihedral angle ϕ specifying their relative azimuthal orientation about the molecular axis. The effective Hamiltonian for large-D limit in cylindrical coordinates is [17, 40]:
with a = R/2 and
In the D → ∞ limit, the Hamiltonian has two locations for electrons, namely: symmetric, with ρ1 = ρ2 and z1 = z2, and antisymmetric, with ρ1 = ρ2 and z1 = −z2. When R has the nuclei well apart, in the symmetric case, both electrons cluster near one of the nuclei ; in the antisymmetric case, each electron resides near just one of the nuclei (H2 → H + H). Thus, the antisymmetric case is much more favorable for the ground-state energy.
We minimize the Hamiltonian (90) with respect to ρ's and z's to obtain the ground state energy, ϵ∞(R); we numerically evaluate the corresponding optimized parameters , and ϕ* for different values of R.
The total binding energy is obtained by adding to ϵ∞(R) the internuclear-interaction term (1/R).
6.3. Interpolation for D=3
Unlike the atoms, our interpolation will be different for a molecule. An atom has only one nucleus, with the electrons orbiting about the positive charge; our interpolation with the first-order perturbation works well for atoms but not for a molecule. For a diatomic molecule, V(R) is fundamental, with the internuclear distance R. As mentioned in Equations (4) and (5), our interpolation for H2 uses a modified rescaling scheme developed by [17–19] with the D = 1 and D → ∞ dimensional limits:
The rescaled distances are:
The rescaled Hamiltonians have distinct factors in the kinetic and potential energy parts: In D = 1: Hamiltonian (88) becomes:
In D → ∞: Hamiltonian (90) becomes:
with a = R/2 and
We minimized these rescaled Hamiltonians (93) with respect to the rescaled distances (92).
In Figure 1, we have plotted the binding energies of H2 as functions of R, in the three dimensions (91), adding the nuclear repulsion term, 1/R. The curves are colored: red for D = 1, green for D → ∞, and blue for D = 3, the interpolation. It compares fairly well with the nominally exact V(R) curve, colored orange, for H2 obtained from the full configuration interaction (FCI) method [41, 42]. We have obtained the FCI by using the OpenFermion quantum computational chemistry software [43].
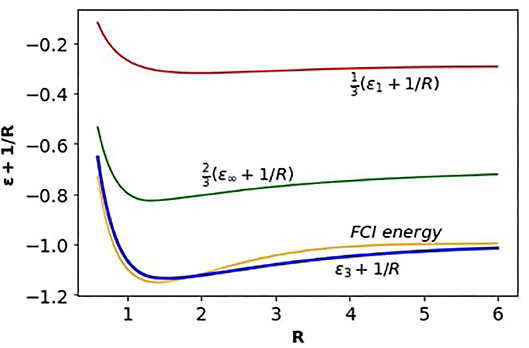
Figure 1. The binding V(R) curves for H2, shown from different dimensions. The red and green curves pertain to D = 1 and D → ∞, respectively, parts from Equations (92) and (93) of the interpolaiton. The blue curve, ϵ3(R) + 1/R, represents D = 3, the interpolation result at Equation (91). The orange curve is a highly accurate result obtained from computation [43].
7. Conclusion and Prospects
The formula used for atoms we consider unorthodox, as it recently emerged [14] whereas other D-interpolations are elderly [44, 45]. The fresh aspect links the energies ϵ1 and ϵ∞ together with the first-order perturbation coefficients and plus from their 1/Z expansions. Those perturbations arise from of electron-electron pair interactions, 〈1/rij〉; they actually provide much of the dimension dependence. For H2 we used a different scaling than with the atoms, since H2 links the distance R between the two nuclei. Then the rescaling is: R → 1/3R′ for D → 1; R → 2/3R′ for D → ∞. Interpolating between the dimensional limits gave a fair approximation of the binding energy for D = 3, when compared with the full configuration interaction (FCI).
In tally, our sections 3, 4, and 5 treat He, Li, Be; in section 6 dealt with H2. In subsections we describe the D = 1 limit, the D = ∞ limit, the first-order perturbations, and the interpolation output.
The ingredients of the interpolation are well suited for computing. In our calculation we treat the electrons exclusively in s states with spherical or, in the molecular case, cylindrical symmetry. However, we expect the possibility to extend our method to encompass atoms with electrons of finite angular momentum, although this could be more challenging. We also expect the method to hold true for larger atomic, molecular and extended systems. More than ground-state energies are accessible. However, there are prospects for combining dimensional limits to serve other many-body problems. One is examining dimensional dependence of quantum entanglement [46, 47]. Another is the isomorphism between the Ising model [48] and two-level quantum mechanics [49]. Long ago the Ising model was solved in one, two and infinite dimensions [50–52], as well much activity near four dimensions [53]. The unknown solution at D = 3 remains a challenge even by quantum computing [54, 55]. More light on the solution might come by blending of dimensions akin to our unorthodox interpolated formula.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors (SK and KG) acknowledge the partial financial support by the U.S. Department of Energy (Office of Basic Energy Sciences) under Award No. DE-SC0019215 and the Integrated Data Science Initiative Grant (IDSI F.90000303), Purdue University. This manuscript has been released as a pre-print at arXiv:2004.11489 [quant-ph] [56].
References
1. Herrick DR, Stillinger FH. Variable dimensionality in atoms and its effect on the ground state of the helium isoelectronic sequence. Phys Rev A. (1975) 11:42–53. doi: 10.1103/PhysRevA.11.42
2. Mlodinow LD, Papanicolaou N. SO(2,1) algebra and the large N expansion in quantum mechanics. Ann Phys. (1980) 128:314–334.
4. Herschbach DR. Dimensional interpolation for two-electron atoms. J Chem Phys. (1986) 84:838–51. doi: 10.1063/1.450584
6. Goodson DZ, López-Cabrera M, Herschbach DR, Morgan III JD. Large-order dimensional perturbation theory for two-electron atoms. J Chem Phys. (1992) 97:8481–96.
7. Zhen Z, Loeser J. In: Herschbach DR, Avery J, Goscinski O. (eds.). Large-D Limit for N-Electron Atoms. Dordrecht: Springer Netherlands (1993). p. 83–114.
8. Kais S, Herschbach DR. The 1/Z expansion and renormalization of the large-dimension limit for many-electron atoms. J Chem Phys. (1994) 100:4367–76.
10. Loeser JG, Zhen Z, Kais S, Herschbach DR. Dimensional interpolation of hard sphere virial coefficients. J Chem Phys. (1991) 95:4525–44.
11. Kais S, Herschbach DR. Dimensional scaling for quasistationary states. J Chem Phys. (1993) 98:3990–8.
12. Wei Q, Kais S, Herschbach DR. Dimensional scaling treatment of stability of simple diatomic molecules induced by superintense, high-frequency laser fields. J Chem Phys. (2008) 129:214110. doi: 10.1063/1.3027451
13. Wei Q, Kais S, Herschbach DR. Dimensional scaling treatment of stability of atomic anions induced by superintense, high-frequency laser fields. J Chem Phys. (2007) 127:094301. doi: 10.1063/1.2768037
14. Herschbach DR, Loeser JG, Virgo WL. Exploring unorthodox dimensions for two-electron atoms. J Phys Chem A. (2017) 121:6336–40. doi: 10.1021/acs.jpca.7b06148
15. Rosenthal CM. Solution of the delta function model for heliumlike ions. J Chem Phys. (1971) 55:2474–83. doi: 10.1063/1.1676436
16. Loeser JG, Herschbach DR. Dimension dependence of correlation energies in two-electron atoms. J Chem Phys. (1987) 86:3512–21. doi: 10.1063/1.451954
17. Frantz DD, Herschbach DR. Lewis electronic structures as the large-dimension limit for and H2 molecules. Chem Phys. (1988) 126:59–71.
18. Tan AL, Loeser JG. In: Herschbach DR, Avery J, Goscinski O, editors. Simple molecules and variant scalings. Dimensional Scaling in Chemical Physics. Dordrecht: Springer Netherlands (1993). p. 230–55. doi: 10.1007/978-94-011-1836-1_3
19. López-Cabrera M, Tan AL, Loeser JG. Scaling and interpolation for dimensionally generalized electronic structure. J Phys Chem. (1993) 97:2467–78.
20. Lapidus IR. One-dimensional models for two-electron systems. Am J Phys. (1975) 43:790–2. doi: 10.1119/1.9708
21. White RJ, Stillinger FH. Analytic approach to electron correlation in atoms. J Chem Phys. (1970) 52:5800–14. doi: 10.1063/1.1672862
22. Loeser JG, Herschbach DR. Hylleraas-Pekeris treatment of D-dimensional two-electron atoms. J Chem Phys. (1986) 84:3882–92. doi: 10.1063/1.450099
25. Larsson S, Burke EA. Variational calculation of the ground state of the lithium atom. Phys Rev. (1969) 184:248.
26. Scherr CW, Silverman JN, Matsen FA. Perturbation energy coefficients and ionization potentials of the ground state of three-to ten-electron isoelectronic atomic series. Phys Rev. (1962) 127:830.
27. Wilson Jr EB. Wave functions for the ground state of lithium and three-electron ions. J Chem Phys. (1933) 1:210–8.
28. Abramowitz M, Stegun IA. Handbook of Mathematical Functions With Formulas, Graphs, and Mathematical Tables, Vol. 55. US Government Printing Office (1948).
29. Bunge CF. Configuration interaction benchmark for Be ground state. Theor Chem Acc. (2010) 126:139–50. doi: 10.1007/s00214-009-0601-5
30. Büsse G, Kleindienst H, Lüchow A. Nonrelativistic energies for the Be atom: double-linked Hylleraas-CI calculation. Int J Quantum Chem. (1998) 66:241–7.
31. Sims JS, Hagstrom SA. Hylleraas-configuration-interaction study of the 1s ground state of neutral beryllium. Phys Rev A. (2011) 83:032518. doi: 10.1103/PHYSREVA.83.032518
32. Puchalski M, Komasa J, Pachucki K. Testing quantum electrodynamics in the lowest singlet states of the beryllium atom. Phys Rev A. (2013) 87:030502. doi: 10.1103/PhysRevA.87.030502
33. Stanke M, Komasa J, Bubin S, Adamowicz L. Five lowest S 1 states of the Be atom calculated with a finite-nuclear-mass approach and with relativistic and QED corrections. Phys Rev A. (2009) 80:022514. doi: 10.1103/PhysRevA.80.022514
34. James HM, Coolidge AS. The ground state of the hydrogen molecule. J Chem Phys. (1933) 1:825–35. doi: 10.1063/1.1749252
35. Kolos W, Roothaan CCJ. Accurate electronic wave functions for the H2 molecule. Rev Mod Phys. (1960) 32:219. doi: 10.1103/RevModPhys.32.219
36. Svidzinsky AA, Scully MO, Herschbach DR. Simple and surprisingly accurate approach to the chemical bond obtained from dimensional scaling. Phys Rev Lett. (2005) 95:080401. doi: 10.1103/PhysRevLett.95.080401
37. Chen G, Chin SA, Dou Y, Kapale KT, Kim M, Svidzinsky AA, et al. The two electron molecular bond revisited: from Bohr orbits to two-center orbitals. Adv At Mol Opt Phys. (2005) 51:93–238. doi: 10.1016/S1049-250X(05)51015-2
38. Olivares-Pilón H, Turbiner AV. Towards the theory of Potential Energy Curves for diatomic molecular ions: case. arXiv [preprint]. arXiv:1904.06614. (2019). Available online at: https://arxiv.org/abs/1904.06614
39. Lapidus IR. One-dimensional hydrogen molecule revisited. Am J Phys. (1982) 50:453–6. doi: 10.1119/1.12833
40. Herrick DR. Degeneracies in energy levels of quantum systems of variable dimensionality. J Math Phys. (1975) 16:281–3. doi: 10.1063/1.522538
41. Bauschlicher CW, Langhoff SR, Taylor PR. Accurate quantum chemical calculations. Adv Chem Phys. (1990) 77:103–61.
42. Sherrill CD, Schaefer HF III. The configuration interaction method: advances in highly correlated approaches. In: Löwdin P-O, Sabin JR, Zerner MC, Brändas E, editors. Advances in Quantum Chemistry. Vol. 34. San Diego, CA: Elsevier (1999). p. 143–269.
43. McClean JR, Rubin NC, Sung KJ, Kivlichan ID, Monroig XB, Cao Y, et al. OpenFermion: the electronic structure package for quantum computers. Quant Sci Technol. (2020) 5:034014. doi: 10.1088/2058-9565/ab8ebc
44. Kais S, Sung SM, Herschbach DR. Large-Z and-N dependence of atomic energies from renormalization of the large-dimension limit. Int J Quantum Chem. (1994) 49:657–74. doi: 10.1002/qua.560490511
45. Cardy J. Scaling and Renormalization in Statistical Physics. Vol. 5. Cambridge, UK: Cambridge University Press (1996).
46. Kais S. Entanglement, electron correlation, and density matrices. Adv Chem Phys. (2007) 134:493. doi: 10.1002/9780470106600.ch18
47. Huang Z, Wang H, Kais S. Entanglement and electron correlation in quantum chemistry calculations. J Mod Opt. (2006) 53:2543–58. doi: 10.1080/09500340600955674
48. Chandler D. Introduction to Modern Statistical Mechanics. Oxford: Oxford University Press (1987).
49. Loeser JG, Herschbach DR. In: Tsipis CA, Popov VS, Herschbach DR, Avery JS, editors. Dimensional Scaling. New Methods in Quantum Theory. 1st Edn. Dordrecht: Kluwer Academic Pub (1996) 1–32.
50. Ising E. Beitrag zur theorie des ferromagnetismus. Z Phys. (1925) 31:253–8. doi: 10.1007/BF02980577
51. Stanley HE. Spherical model as the limit of infinite spin dimensionality. Phys Rev. (1968) 176:718–22. doi: 10.1103/PhysRev.176.718
52. Berlin TH, Kac M. The spherical model of a ferromagnet. Phys Rev. (1952) 86:821–35. doi: 10.1103/PhysRev.86.821
53. Herschbach DR. Dimensional scaling and renormalization. Int J Quantum Chem. (1996) 57:295–308. doi: 10.1002/(SICI)1097-461X(1996)57:3<295::AID-QUA3>3.0.CO;2-T
54. Xia R, Bian T, Kais S. Electronic structure calculations and the Ising Hamiltonian. J Phys Chem B. (2017) 122:3384–95. doi: 10.1021/acs.jpcb.7b10371
55. Nielsen MA, Chuang IL. Quantum Computation and Quantum Information: 10th Anniversary Edition. Cambridge, UK: Cambridge University Press (2010).
56. Ghosh KJB, Kais S, Herschbach DR. Unorthodox dimensional interpolations for He, Li, Be atoms and hydrogen molecule. arXiv [preprint]. arXiv:2004.11489. (2020). Available online at: https://arxiv.org/abs/2004.11489
Keywords: dimensional interpolation, dimensional scaling, large-d limit, one-dimension, hydrogen molecule, ground state energy and ground state binding energy
Citation: Ghosh KJB, Kais S and Herschbach DR (2020) Unorthodox Dimensional Interpolations for He, Li, Be Atoms and Hydrogen Molecule. Front. Phys. 8:331. doi: 10.3389/fphy.2020.00331
Received: 08 June 2020; Accepted: 16 July 2020;
Published: 27 August 2020.
Edited by:
Bretislav Friedrich, Fritz-Haber-Institut, GermanyReviewed by:
John Stuart Briggs, University of Freiburg, GermanyDavid A. Mazziotti, University of Chicago, United States
Copyright © 2020 Ghosh, Kais and Herschbach. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dudley R. Herschbach, ZGhlcnNjaGJhY2hAZ21haWwuY29t
 Kumar J. B. Ghosh
Kumar J. B. Ghosh Sabre Kais
Sabre Kais Dudley R. Herschbach
Dudley R. Herschbach