Nuclear Collective Dynamics in Transport Model With the Lattice Hamiltonian Method

We review recent progress in studying nuclear collective dynamics by solving the Boltzmann-Uehling-Uhlenbeck (BUU) equation with the lattice Hamiltonian method, treating the collision term with the full-ensemble stochastic collision approach. This lattice BUU (LBUU) method has recently been developed and implemented with a GPU parallel computing technique, and achieves rather stable nuclear ground-state evolution and high accuracy in evaluating the nucleon-nucleon (NN) collision term. This new LBUU method has been applied to investigate nuclear isoscalar giant monopole resonances and isovector giant dipole resonances. While calculations using the LBUU method without the NN collision term (i.e., the lattice Hamiltonian Vlasov method) provide a reasonable description of the excitation energies of nuclear giant resonances, the full LBUU calculations can well reproduce the width of the giant dipole resonance of ²⁰⁸Pb by including a collisional damping from NN scattering. The observed strong correlation between the width of the nuclear giant dipole resonance and the NN elastic cross-section suggests that the NN elastic scattering plays an important role in nuclear collective dynamics, and the width of the nuclear giant dipole resonance provides a good probe of the in-medium NN elastic cross-section.

1. Introduction

Transport models deal with the time evolution of the Wigner function or phase-space distribution function $f(\overrightarrow{r},\overrightarrow{p},t)$ that arises from the Wigner representation of the Schrödinger equation [1, 2], and provide a successful semi-classical time-dependent approach to studying nuclear dynamics, especially with regard to heavy-ion collisions (HICs). One of the main ingredients of transport models is the mean-field potential, which embodies information on the nuclear equation of state (EOS) or the in-medium effective nuclear interaction. Therefore, transport models serve as an important theoretical tool for investigating the EOS of asymmetric nuclear matter from observables in HICs. A good deal of information on the nuclear EOS, from sub-saturation [3–5] to supra-saturation densities of about 3–5 times saturation density [6–18], has been obtained from transport model analyses of various observables, such as collective flows and particle production, in intermediate- and high-energy HICs. Exact information about the nuclear EOS is crucial for describing reaction dynamics of exotic nuclei [19, 20], various properties of both finite nuclei (e.g., neutron skin thickness [21–23] and drip lines [24, 25]) and neutron stars (e.g., masses and cooling mechanisms [26–30]), and astrophysical processes, such as supernova explosion scenarios [31–33]. In particular, it should be mentioned that the first gravitational wave signal GW170817 [34] of a binary neutron star merger has recently been observed and localized by the LIGO and Virgo observatories, inaugurating a new era of multimessenger astronomy and supplying important constraints on the dense nuclear matter EOS [35–39]. Moreover, very recently, using X-ray data from NASA's Neutron Star Interior Composition Explorer (NICER), the mass and radius of the millisecond pulsar PSR J0030+0451 have been simultaneously estimated [40, 41] and the implications for the dense nuclear matter EOS analyzed [42]. In addition, a new record for the maximum mass of neutron stars, namely a millisecond pulsar J0740+6620 with mass $2.14_{-0.09}^{+0.10}{M}_{\odot }$ (68.3% credibility interval), has been reported recently [43]; this heaviest neutron star observed so far can rule out many soft nuclear matter equations of state, and in particular, the supersoft high-density symmetry energy [44].

The time-dependent Hartree-Fock (TDHF) theory provides a very successful quantum many-body framework at the mean-field level for describing low-energy nuclear reaction dynamics, including the nuclear collective dynamics (see e.g., references [45, 46] for a review of recent work). Given that the Vlasov equation, i.e., the Boltzmann-Uehling-Uhlenbeck (BUU) equation without the nucleon-nucleon (NN) collision term, corresponds to the semi-classical limit of the TDHF equation, transport models can thus be seen as an efficient semi-classical approach to studying nuclear collective dynamics. In particular, the two-particle-two-hole (2p-2h) correlation beyond the mean-field approximation, which dominates the collisional damping of nuclear giant resonances, can be effectively taken into account in transport models via binary collisions. The literature contains many works that study nuclear giant resonances based on the pure Vlasov equation [47–49], the Vlasov equation with a collision relaxation time [50], and the full transport model with both the mean-field and the NN scatterings [51–53]. For example, based on simulations of transport models, the excitation energies of nuclear giant resonances have been used to extract information on the nuclear EOS and neutron-proton effective mass splitting [54], while the width of nuclear giant dipole resonance (GDR) has been proposed as an effective probe of the in-medium NN elastic cross-section [55]. The width of the nuclear GDR can also serve as a fingerprint of α-particle clustering configurations in nuclei [56].

Although transport models have been extensively used in the study of nuclear giant resonances, the accurate description of giant resonances within transport models is still a challenge. In transport models, unlike in simulations of HICs at intermediate and high energies, the calculation of nuclear giant resonances, which are the collective excitation states with an excitation energy of about 20 MeV, requires a more proper description of nuclear ground states and an accurate implementation of Pauli blocking. In particular, Pauli blocking is intimately related to the collisional damping and hence the width of nuclear giant resonances in the transport model calculations. In this sense, studying the nuclear collective motion provides an ideal way to examine and improve transport models, since the effects of several deficiencies, such as the inaccurate treatment of Pauli blocking, are more pronounced in nuclear collective dynamics with small-amplitude oscillations. Transport models for HICs can be roughly divided into two categories, the BUU equation (see e.g., reference [2]) and the quantum molecular dynamics (QMD) model (see e.g., reference [57]). From the viewpoint of transport models, the essential difference between these two types is that the BUU-type models mimic $f(\overrightarrow{r},\overrightarrow{p},t)$ by having a large number of ensembles or test particles for each nucleon, while the QMD-type models use a Gaussian wave packet for each nucleon. Recently, the transport model community started a code comparison project [58–60] to try to understand the source of the discrepancies between various transport model codes and thus eventually reduce the uncertainties in transport models. For the issue of Pauli blocking, the QMD-type transport models seem not to be as good as the BUU-type models [59]; therefore the BUU-type transport models are more suitable for the study of nuclear collective motions, especially for the calculation of the spreading width, in which the accurate treatment of Pauli blocking is essential.

In order to study (near-)equilibrium nuclear dynamics within the framework of transport models, a BUU-type transport model, namely the lattice BUU (LBUU) method [55, 61], has recently been developed, which can achieve good stability for the ground-state evolution [61] and treat Pauli blocking with very high accuracy [55]. The resulting LBUU framework has the following features: (1) a smearing of the local density, which is commonly used in transport models to obtain a smooth mean field, is included self-consistently in the equations of motion through the lattice Hamiltonian (LH) method; (2) the ground state of a nucleus is obtained by varying the total energy with respect to the nucleon density distribution based on the same Hamiltonian that governs the system evolution; (3) the NN collision term in the BUU equation is implemented through a full-ensemble stochastic collision approach. The above features, as well as a sufficiently large number of ensembles, make it possible to solve the BUU equation almost exactly, and thus one can obtain very accurate results for the nuclear collective motions within the BUU equation. We note that the high accuracy of the LBUU method relies on a large amount of computational resources; therefore, high-performance GPU parallel computing [62] has been employed in the LBUU implementation to improve the computational efficiency.

This paper is organized as follows. In section 2, we first introduce the LBUU method for solving the BUU equation, including the mean field, the collision integral, and the initialization for the nuclear ground state, and then describe how to deal with the nuclear giant resonances within transport models. In section 3, we present results on the peak energies of the nuclear giant resonances obtained from lattice Hamiltonian Vlasov (LHV) calculations, i.e., LBUU calculations without the NN collision term, and then compare these with results from the random-phase approximation (RPA). In section 4, we give results on the strength function and the width of the GDR from the full LBUU calculations, and compare these with experimental data from the ${}^{[208]}\text{P}\text{b}(\overrightarrow{p},{\overrightarrow{p}}^{ \prime })$ reaction carried out at the Research Center for Nuclear Physics (RCNP) in Osaka, Japan [63]. Finally we give a brief summary and outlook in section 5.

2. Model Description

The starting point for calculating the nuclear collective motion is the BUU equation with a momentum-dependent mean-field potential $U(\overrightarrow{r},\overrightarrow{p})$:

$\begin{array}{ll}\frac{\partial f}{\partial t}+\frac{\overrightarrow{p}}{E}·{\nabla }_{\overrightarrow{r}}f+{\nabla }_{\overrightarrow{p}}U(\overrightarrow{r},\overrightarrow{p})·{\nabla }_{\overrightarrow{r}}f-{\nabla }_{\overrightarrow{r}}U(\overrightarrow{r},\overrightarrow{p})·{\nabla }_{\overrightarrow{p}}f=I_{\text{c}},& (1)\end{array}$

where f (the Wigner function) is the Fourier transform of the one-body density matrix $\rho (\overrightarrow{r}+\overrightarrow{s}/2,\overrightarrow{r}-\overrightarrow{s}/2)$, i.e.,

$\begin{array}{ll}f(\overrightarrow{r},\overrightarrow{p})=\frac{1}{{(2\pi \hslash )}^3}{\displaystyle \int \text{exp}}(-i\frac{\overrightarrow{p}}{\hslash }·\overrightarrow{s})\rho (\overrightarrow{r}+\overrightarrow{s}/2,\overrightarrow{r}-\overrightarrow{s}/2)d^{3}s.& (2)\end{array}$

In the local density approximation, $f(\overrightarrow{r},\overrightarrow{p})$ is reduced to the classical one-body phase-space distribution function. The collision term I_c, which takes into account the Pauli principle due to nucleons' Fermi statistics, reads

$\begin{array}{l}{I}_{\text{c}}=-g{\displaystyle \int \frac{d^2{p}_2}{{(2\pi \hslash )}^3}}\frac{d^3{p}_3}{{(2\pi \hslash )}^3}\frac{d^3{p}_4}{{(2\pi \hslash )}^3}|{{M}}_{12\to 34}{|}^2{(2\pi )}^4\\ {\delta }^4(p_1+p_2-p_3-p_4)\times [f_1{f}_2(1-f_3)(1-f_4)-f_3{f}_4(1\text{}-f_1)(1\text{}-f_2)],& (3)\end{array}$

where g = 2 is the spin degeneracy factor and ${{M}}_{12\to 34}$ is the in-medium transition matrix element. Note that we have ignored the isospin index in the above three equations, but it can be restored easily. The BUU equation without the collision term I_c is referred to as the Vlasov equation, which is the semi-classical limit of the quantum transport theory with the system described by the one-body phase-space distribution function [1, 2], whereas the quantum corrections can be included perturbatively [64, 65].

We use the LH method, originally proposed by Lenk and Pandharipande [66] in 1989, to solve the BUU equation. The LH method has been successfully employed in the study of HICs [67, 68]. It improves the sample smoothing technique of the usual test particle approach [69] and conserves the total energy almost exactly. In the LH method, the phase-space distribution function $f_{\tau }(\overrightarrow{r},\overrightarrow{p},t)$ is mimicked by A × N_E test nucleons with a form factor S in the coordinate space to modify the relation between the test nucleons and the Wigner function, i.e.,

$\begin{array}{ll}{f}_{\tau }(\overrightarrow{r},\overrightarrow{p},t)=\frac{1}{g}\frac{{(2\pi \hslash )}^3}{N_{\text{E}}}{\displaystyle \sum _i^{A{N}_{\text{E}},\tau }S}[{\overrightarrow{r}}_i(t)-\overrightarrow{r}]\delta [{\overrightarrow{p}}_i(t)-\overrightarrow{p}],& (4)\end{array}$

where A is the mass number of the system and N_E is the number of ensembles or number of test particles, usually a very large number, used in the calculation. The sum in the above expression runs over all test nucleons with isospin τ. The form factor S can take a Gaussian form, or a certain form with a finite range that ensures the particle number conservation. By giving each test nucleon a form factor, the movement of a test nucleon leads to a continuous variation of the local nucleon density of nearby lattice sites, which is useful for smoothing the nucleon distribution functions in phase space. A similar form factor in momentum space [here the δ-function is used in Equation (4)] could be introduced and might help to reduce fluctuations if a momentum-dependent mean-field potential is employed, and in the future it would be interesting to carry out a systematic investigation of the effects of a form factor in momentum space. The equations of motion of the test nucleons are governed by the total Hamiltonian, and we approximate the latter by the lattice Hamiltonian, i.e.,

$\begin{array}{ll}H={\displaystyle \int {H}}(\overrightarrow{r})d\overrightarrow{r}\approx l_x{l}_y{l}_z{\displaystyle \sum _{\alpha }{H}}({\overrightarrow{r}}_{\alpha })\equiv H_L,& (5)\end{array}$

where ${\overrightarrow{r}}_{\alpha }$ denotes the coordinates of lattice site α, and l_x, l_y, and l_z are the lattice spacings. Therefore, in the LH method only the values of the phase-space distribution function at lattice sites $f_{\tau }({\overrightarrow{r}}_{\alpha },\overrightarrow{p},t)$ need to be calculated.

By solving the BUU equation or Vlasov equation using the LH method, one obtains the time evolution of $f(\overrightarrow{r},\overrightarrow{p},t)$, or the test nucleons' coordinates ${\overrightarrow{r}}_i$ and momenta ${\overrightarrow{p}}_i$, and then the time evolution of other physical quantities can be calculated accordingly.

2.1. Mean Fields

We employ the Skyrme pseudopotential to calculate the lattice Hamiltonian in Equation (5). The next-to-next-to-next leading order (N3LO) Skyrme pseudopotential [70], which is a mapping of the N3LO local energy density functional [71], generalizes the standard Skyrme interaction [72] and can reproduce the empirical nuclear optical potential up to about 1 GeV in kinetic energy [73], which the standard Skyrme interactions fail to describe. The Hamiltonian density from the N3LO Skyrme pseudopotential contains the kinetic term ${{H}}^{\text{kin}}(\overrightarrow{r})$, the local term ${{H}}^{\text{loc}}(\overrightarrow{r})$, the momentum-dependent term ${{H}}^{\text{MD}}(\overrightarrow{r})$, the density-dependent term ${{H}}^{\text{DD}}(\overrightarrow{r})$, and the gradient term ${{H}}^{\text{grad}}(\overrightarrow{r})$. The kinetic term

$\begin{array}{ll}{{H}}^{\text{kin}}(\overrightarrow{r})={\displaystyle \sum _{\tau =n,p}{\displaystyle \int d^3}}p\frac{p^2}{2m_{\tau }}{f}_{\tau }(\overrightarrow{r},\overrightarrow{p})& (6)\end{array}$

and the local term

$\begin{array}{ll}{{H}}^{\text{loc}}(\overrightarrow{r})=\frac{t_0}{4}[(2+x_0){\rho }^2-(2x_0+1){\displaystyle \sum _{\tau =n,p}{\rho }_{\tau }^2}]& (7)\end{array}$

are the same as those from the standard Skyrme interaction. The momentum-dependent term is written in the form

$\begin{array}{l}{{H}}^{\text{MD}}(\overrightarrow{r})={\displaystyle \int d^3}p{d}^3{p}^{\prime }{K}_s(\overrightarrow{p},{\overrightarrow{p}}^{\prime })f(\overrightarrow{r},\overrightarrow{p})f(\overrightarrow{r},{\overrightarrow{p}}^{\prime })\\ +{\displaystyle \sum _{\tau =n,p}{\displaystyle \int d^3}}p{d}^3{p}^{\prime }{K}_v(\overrightarrow{p},{\overrightarrow{p}}^{\prime })f_{\tau }(\overrightarrow{r},\overrightarrow{p})f_{\tau }(\overrightarrow{r},{\overrightarrow{p}}^{\prime }),& (8)\end{array}$

with $f(\overrightarrow{r},\overrightarrow{p})=f_n(\overrightarrow{r},\overrightarrow{p})+f_p(\overrightarrow{r},\overrightarrow{p})$. The quantities ${{K}}_{\text{s}}(\overrightarrow{p},{\overrightarrow{p}}^{\prime })$ and ${{K}}_{\text{v}}(\overrightarrow{p},{\overrightarrow{p}}^{\prime })$ in Equation (8) represent the isoscalar and isovector kernels of the momentum-dependent part of the mean-field potential, respectively; ${{K}}_{\text{s}}(\overrightarrow{p},{\overrightarrow{p}}^{\prime })$ and ${{K}}_{\text{v}}(\overrightarrow{p},{\overrightarrow{p}}^{\prime })$ for the N3LO Skyrme pseudopotential are expressed as

$\begin{array}{ll}{K}_{\text{s}}(\overrightarrow{p},{\overrightarrow{p}}^{\prime })=\frac{C^{[2]}}{16{\hslash }^2}{(\overrightarrow{p}-{\overrightarrow{p}}^{\prime })}^2+\frac{C^{[4]}}{32{\hslash }^2}{(\overrightarrow{p}-{\overrightarrow{p}}^{\prime })}^4+\frac{C^{[6]}}{16{\hslash }^2}{(\overrightarrow{p}-{\overrightarrow{p}}^{\prime })}^6,& (9)\end{array}$

$\begin{array}{ll}{K}_{\text{v}}(\overrightarrow{p},{\overrightarrow{p}}^{\prime })=\frac{D^{[2]}}{16{\hslash }^2}{(\overrightarrow{p}-{\overrightarrow{p}}^{\prime })}^2+\frac{D^{[4]}}{32{\hslash }^2}{(\overrightarrow{p}-{\overrightarrow{p}}^{\prime })}^4+\frac{D^{[6]}}{16{\hslash }^2}{(\overrightarrow{p}-{\overrightarrow{p}}^{\prime })}^6.& (10)\end{array}$

If we keep only the C^[2] and D^[2] terms, the N3LO Skyrme pseudopotential reduces to the standard Skyrme effective interaction. For the sake of simplicity in performing numerical derivatives, we truncate at the second order of the spatial gradient of $\rho (\overrightarrow{r})$,

$\begin{array}{l}{{H}}^{\text{grad}}(\overrightarrow{r})=\frac{1}{8}{E}^{[2]}\left\{\rho (\overrightarrow{r}){\nabla }^2\rho (\overrightarrow{r})-{\left[\nabla \rho (\overrightarrow{r})\right]}^2\right\}\\ +\frac{1}{8}{F}^{[2]}{\displaystyle \sum _{\tau =n,p}}\left\{{\rho }_{\tau }(\overrightarrow{r}){\nabla }^2{\rho }_{\tau }(\overrightarrow{r})-{\left[\nabla {\rho }_{\tau }(\overrightarrow{r})\right]}^2\right\}\\ =\frac{1}{8}{g}^{[2]}\left\{\rho (\overrightarrow{r}){\nabla }^2\rho (\overrightarrow{r})-{\left[\nabla \rho (\overrightarrow{r})\right]}^2\right\}\\ +\frac{1}{8}{g}_{\text{iso}}^{[2]}\left\{{\rho }_{\delta }(\overrightarrow{r}){\nabla }^2{\rho }_{\delta }(\overrightarrow{r})-{\left[\nabla {\rho }_{\delta }(\overrightarrow{r})\right]}^2\right\}.& (11)\end{array}$

In the second line we have introduced $g^{\left[2\right]}=E^{\left[2\right]}+\frac{1}{2}{F}^{\left[2\right]}$, $g_{\text{iso}}^{\left[2\right]}=\frac{1}{2}{F}^{\left[2\right]}$, and ρ_δ = ρ_n − ρ_p. We neglect the second term in Equation (11) since it is much smaller than the first term; in other words, we keep only the second-order spatial derivative of the total nucleon density $\rho (\overrightarrow{r})$. The density-dependent term for the N3LO Skyrme pseudopotential takes its form in the standard Skyrme interaction,

$\begin{array}{ll}{{H}}^{\text{DD}}(\overrightarrow{r})=\frac{t_3}{24}[(2+x_3){\rho }^2-(2x_3+1){\displaystyle \sum _{\tau =n,p}{\rho }_{\tau }^2}]{\rho }^{\alpha }.& (12)\end{array}$

One can see that the Hamiltonian density ${H}(\overrightarrow{r})$, expressed as the sum of Equations (6)–(8), (11), and (12), is explicitly dependent on $f_{\tau }(\overrightarrow{r},\overrightarrow{p})$ as well as on the densities ${\rho }_{\tau }(\overrightarrow{r})$ and their derivatives.

In the above expressions, the parameters C^[n], D^[n], E^[n], and F^[n] are recombinations of the Skyrme parameters $t_1^{\left[n\right]}$, $t_2^{\left[n\right]}$, $x_1^{\left[n\right]}$ and $x_2^{\left[n\right]}$, which are related to the derivative terms of the Skyrme two-body potential $v_{\text{Sk}}({\overrightarrow{r}}_1,{\overrightarrow{r}}_2)$, i.e.,

$\begin{array}{ll}{C}^{[n]}=t_1^{[n]}(2+x_1^{[n]})+t_2^{[n]}(2+x_2^{[n]}),& (13)\end{array}$

$\begin{array}{ll}{D}^{[n]}=-t_1^{[n]}(2x_1^{[n]}+1)+t_2^{[n]}(2x_2^{[n]}+1),& (14)\end{array}$

$\begin{array}{ll}{E}^{[n]}=\frac{i^n}{2^n}[t_1^{[n]}(2+x_1^{[n]})-t_2^{[n]}(2+x_2^{[n]})],& (15)\end{array}$

$\begin{array}{ll}{F}^{[n]}=-\frac{i^n}{2^n}[t_1^{[n]}(2x_1^{[n]}+1)+t_2^{[n]}(2x_2^{[n]}+1)].& (16)\end{array}$

Specifically, we obtain the coefficient of the gradient term,

$\begin{array}{ll}{g}^{[2]}=E^{[2]}+\frac{1}{2}{F}^{[2]}=-\frac{1}{8}[3t_1^{[2]}-t_2^{[2]}(5+4x_2^{[2]})].& (17)\end{array}$

Substituting $f(\overrightarrow{r},\overrightarrow{p},t)$ as expressed in Equation (4) into Equations (6)–(12) and noting that the local nucleon density ${\rho }_{\tau }(\overrightarrow{r})$ is given by the integral of $f_{\tau }(\overrightarrow{r},\overrightarrow{p},t)$ with respect to momentum,

$\begin{array}{ll}{\rho }_{\tau }(\overrightarrow{r},t)=g{\displaystyle \int f_{\tau }}(\overrightarrow{r},\overrightarrow{p},t)\frac{d^{3}p}{{(2\pi \hslash )}^3}=\frac{1}{N_{\text{E}}}{\displaystyle \sum _i^{\alpha ,\tau }S}[{\overrightarrow{r}}_i(t)-\overrightarrow{r}],& (18)\end{array}$

we can express the lattice Hamiltonian H_L in Equation (5) in terms of the coordinates and momenta of the test nucleons. Since the coordinates and momenta of the test nucleons ${\overrightarrow{r}}_i$ and ${\overrightarrow{p}}_i$ can be regarded as the canonical variables of the lattice Hamiltonian, their time evolution is then governed by the Hamilton equation for all ensembles,

$\begin{array}{l}\frac{d{\overrightarrow{r}}_i}{dt}=N_{\text{E}}\frac{\partial H_L[{\overrightarrow{r}}_1(t),\dots ,{\overrightarrow{r}}_{A\times N_{\text{E}}}(t);{\overrightarrow{p}}_1(t),\dots ,{\overrightarrow{p}}_{A\times N_{\text{E}}}(t)]}{\partial {\overrightarrow{p}}_i}\\ =\frac{{\overrightarrow{p}}_i(t)}{m}+N_{\text{E}}{l}_x{l}_y{l}_z{\displaystyle \sum _{\alpha \in V_i}\frac{\partial {{H}}_{\alpha }^{\text{MD}}}{\partial {\overrightarrow{p}}_i}},& (19)\end{array}$

$\begin{array}{l}\frac{d{\overrightarrow{p}}_i}{dt}=-N_{\text{E}}\frac{\partial H_L[{\overrightarrow{r}}_1(t),\dots ,{\overrightarrow{r}}_{A\times N_{\text{E}}}(t);{\overrightarrow{p}}_1(t),\dots ,{\overrightarrow{p}}_{A\times N_{\text{E}}}(t)]}{\partial {\overrightarrow{r}}_i}\\ =-N_{\text{E}}{l}_x{l}_y{l}_z\\ \times {\displaystyle \sum _{\alpha \in V_i}\{}{\displaystyle \sum _{\tau }^{n,p}[}\frac{\partial ({{H}}_{\alpha }^{\text{loc}}+{{H}}_{\alpha }^{\text{Cou}}+{{H}}_{\alpha }^{\text{DD}})}{\partial {\rho }_{\tau ,\alpha }}\\ +{\displaystyle \sum _{n=0}{(-1)}^n}{\nabla }^n\frac{\partial {{H}}_{\alpha }^{\text{grad}}}{\partial {\nabla }^n{\rho }_{\tau ,\alpha }}]\frac{\partial {\rho }_{\tau ,\alpha }}{\partial {\overrightarrow{r}}_i}+\frac{\partial {{H}}_{\alpha }^{\text{MD}}}{\partial {\overrightarrow{r}}_i}\}& (20)\end{array}$

In the above two equations, the subscript α refers to values at lattice site α. The V_i under the summation sign represents the volume that the form factor of the ith test nucleon covers, and the sums run over all lattice sites inside V_i. The Coulomb interaction contributes to the Hamiltonian density through the term

$\begin{array}{l}{{H}}^{\text{Cou}}({\overrightarrow{r}}_{\alpha })=e^2{\rho }_p({\overrightarrow{r}}_{\alpha })\left\{\frac{1}{2}{\displaystyle \int \frac{{\rho }_p({\overrightarrow{r}}^{\prime })}{|{\overrightarrow{r}}_{\alpha }-{\overrightarrow{r}}^{\prime }|}}d{\overrightarrow{r}}^{\prime }-\frac{3}{4}{\left[\frac{3{\rho }_p({\overrightarrow{r}}_{\alpha })}{\pi }\right]}^{1/3}\right\}\\ \approx e^2{\rho }_p({\overrightarrow{r}}_{\alpha })\left\{\frac{1}{2}{\displaystyle \sum _{{\alpha }^{\prime }\ne \alpha }\frac{{\rho }_p({\overrightarrow{r}}_{{\alpha }^{\prime }})l_x{l}_y{l}_z}{|{\overrightarrow{r}}_{\alpha }-{\overrightarrow{r}}_{{\alpha }^{\prime }}|}}-\frac{3}{4}{\left[\frac{3{\rho }_p({\overrightarrow{r}}_{\alpha })}{\pi }\right]}^{1/3}\right\},& (21)\end{array}$

where the second term represents the contribution from the Coulomb exchange energy. Further tests show that the Coulomb energy ${{H}}^{\text{Cou}}({\overrightarrow{r}}_{\alpha })$ converges at the lattice spacing of l_x = l_y = l_z = 0.5 fm used in the present LBUU simulations. The gradient term ${{H}}_{\alpha }^{\text{grad}}$ in Equation (20) is obtained by considering

$\begin{array}{l}\delta \text{}{\displaystyle \int \text{}}{{H}}^{\text{grad}}(\overrightarrow{r})d^{3}r={\displaystyle \sum _{\tau }^{n,p}{\displaystyle \int \text{}}}[\frac{\partial {{H}}^{\text{grad}}(\overrightarrow{r})}{\partial {\rho }_{\tau }(\overrightarrow{r})}\delta {\rho }_{\tau }(\overrightarrow{r})\\ +\frac{\partial {{H}}^{\text{grad}}(\overrightarrow{r})}{\partial \nabla {\rho }_{\tau }(\overrightarrow{r})}\delta \nabla {\rho }_{\tau }(\overrightarrow{r})+\frac{\partial {{H}}^{\text{grad}}(\overrightarrow{r})}{\partial {\nabla }^2{\rho }_{\tau }(\overrightarrow{r})}\delta {\nabla }^2{\rho }_{\tau }(\overrightarrow{r})+\cdots ]d^{3}r\\ ={\displaystyle \sum _{\tau }^{n,p}{\displaystyle \int {\displaystyle \sum _{n=0}{(-1)}^n}}}{\nabla }^n\frac{\partial {{H}}^{\text{grad}}(\overrightarrow{r})}{\partial {\nabla }^n{\rho }_{\tau }(\overrightarrow{r})}\delta {\rho }_{\tau }(\overrightarrow{r})d^{3}r,& (22)\end{array}$

where we have integrated by parts to obtain the second line. The spatial derivative of ρ_τ,α in Equation (20) is related to the spatial derivative of S through

$\begin{array}{ll}\frac{\partial {\rho }_{\tau ,\alpha }}{\partial {\overrightarrow{r}}_i}=\frac{\partial }{\partial {\overrightarrow{r}}_i}{\displaystyle \sum _{{\overrightarrow{r}}_j\in V_{\alpha }}^{{\tau }_j=\tau }S}({\overrightarrow{r}}_j-{\overrightarrow{r}}_{\alpha })=\{\begin{array}{ll}\frac{\partial S({\overrightarrow{r}}_i-{\overrightarrow{r}}_{\alpha })}{\partial {\overrightarrow{r}}_i},\hfill & {\tau }_i=\tau ,\hfill \\ 0,\hfill & {\tau }_i\ne \tau .\hfill \end{array}& (23)\end{array}$

Substituting the $f_{\tau }(\overrightarrow{r},\overrightarrow{p})$ from Equation (4) into Equation (8), we obtain the momentum-dependent parts of the equation of motion for the test nucleons, and these are expressed in terms of the sums over the test nucleons as

$\begin{array}{l}\frac{\partial {{H}}^{\text{MD}}({\overrightarrow{r}}_{\alpha })}{\partial {\overrightarrow{r}}_i}=2\frac{\partial S[{\overrightarrow{r}}_i(t)-{\overrightarrow{r}}_{\alpha }]}{\partial {\overrightarrow{r}}_i}\\ \times \text{ }\{{\displaystyle \sum _{j\in V_{\alpha }}S}[{\overrightarrow{r}}_j(t)-{\overrightarrow{r}}_{\alpha }]K_{\text{s}}[{\overrightarrow{p}}_i(t),{\overrightarrow{p}}_j(t)]\\ +{\displaystyle \sum _{j\in V_{\alpha }}^{{\tau }_j={\tau }_i}S}[{\overrightarrow{r}}_j(t)-{\overrightarrow{r}}_{\alpha }]K_{\text{v}}[{\overrightarrow{p}}_i(t),{\overrightarrow{p}}_j(t)]\},& (24)\end{array}$

$\begin{array}{l}\frac{\partial {{H}}^{\text{MD}}({\overrightarrow{r}}_{\alpha })}{\partial {\overrightarrow{p}}_i}=2S[{\overrightarrow{r}}_i(t)-{\overrightarrow{r}}_{\alpha }]\\ \times \text{ }\{{\displaystyle \sum _{j\in V_{\alpha }}S}[{\overrightarrow{r}}_j(t)-{\overrightarrow{r}}_{\alpha }]\frac{\partial K_{\text{s}}[{\overrightarrow{p}}_i(t),{\overrightarrow{p}}_j(t)]}{\partial {\overrightarrow{p}}_i}\\ +{\displaystyle \sum _{j\in V_{\alpha }}^{{\tau }_j={\tau }_i}S}[{\overrightarrow{r}}_j(t)-{\overrightarrow{r}}_{\alpha }]\frac{\partial K_{\text{v}}[{\overrightarrow{p}}_i(t),{\overrightarrow{p}}_j(t)]}{\partial {\overrightarrow{p}}_i}\}& (25)\end{array}$

Using Equations (19)–(25), one can evaluate the time evolution of the coordinates ${\overrightarrow{r}}_i(t)$ and momenta ${\overrightarrow{p}}_i(t)$ of the test nucleons, and then obtain $f(\overrightarrow{r},\overrightarrow{p},t)$ from Equation (4), based on which physical observables can be calculated.

The choice of the form factor $S({\overrightarrow{r}}_i-\overrightarrow{r})$ should ensure particle number conservation,

$\begin{array}{ll}{\displaystyle \sum _{\alpha }\rho }({\overrightarrow{r}}_{\alpha })l_x{l}_y{l}_z=\frac{1}{N_{\text{E}}}{\displaystyle \sum _{\alpha }{\displaystyle \sum _{i}S}}({\overrightarrow{r}}_i-{\overrightarrow{r}}_{\alpha })l_x{l}_y{l}_z=A.& (26)\end{array}$

In the present LBUU framework, we use a triangular form

$\begin{array}{l}S({\overrightarrow{r}}_i-\overrightarrow{r})=\frac{1}{{(nl/2)}^6}g(\Delta x)g(\Delta y)g(\Delta z),\\ g(q)=\left(\frac{nl}{2}-|q|\right)\theta \left(\frac{nl}{2}-|q|\right),& (27)\end{array}$

where θ is the Heaviside function and n is an integer that determines the range of S. Generally speaking, calculations on lattices violate momentum conservation since they break Galilean invariance. Early studies have shown that the total momentum can be conserved to a high degree of accuracy if n ≥ 4 [66].

It should be mentioned that compared with the conventional test particle method, in which the equations of motion for the test nucleons are derived from single-particle Hamiltonians, the equations of motion for the test nucleons in the LH method, Equations (19) and (20), are derived from the total Hamiltonian of the system. In the former approach it is difficult to conserve energy exactly [2, 66], while the latter approach can ensure exact energy conservation in the dynamic process [66].

2.2. Collision Integral

In the present LBUU method, the stochastic collision method [74], instead of the commonly used geometric method, is implemented for the NN collision term in the BUU equation. In the stochastic collision approach, the collision probability of two test nucleons can be derived directly from the NN collision term, I_c in Equation (3), as follows. Considering nucleons around lattice site ${\overrightarrow{r}}_{\alpha }$ from two momentum space volume elements $V_{{\overrightarrow{p}}_1}={\overrightarrow{p}}_1\pm \frac{1}{2}{\Delta }^3{\overrightarrow{p}}_1$ and $V_{{\overrightarrow{p}}_2}={\overrightarrow{p}}_2\pm \frac{1}{2}{\Delta }^3{\overrightarrow{p}}_2$, one can average over momentum space volume $V_{{\overrightarrow{p}}_i}$ to obtain the distribution function $f({\overrightarrow{r}}_{\alpha },{\overrightarrow{p}}_i)$ according to Equation (4):

$\begin{array}{ll}f({\overrightarrow{r}}_{\alpha },{\overrightarrow{p}}_i)\approx \frac{1}{{\Delta }^3{\overrightarrow{p}}_i}\frac{{(2\pi \hslash )}^3}{g{N}_{\text{E}}}{\displaystyle \sum _j^{{\overrightarrow{p}}_j\in V_{{\overrightarrow{p}}_i}}S}({\overrightarrow{r}}_j-{\overrightarrow{r}}_{\alpha }).& (28)\end{array}$

The number of collisions between nucleons from these two momentum space volumes that happen in a time interval Δt is

$\begin{array}{l}\Delta N^{\text{coll}}({\overrightarrow{r}}_{\alpha },{\overrightarrow{p}}_1,{\overrightarrow{p}}_2)=g\frac{{\Delta }^3{\overrightarrow{p}}_1}{{(2\pi \hslash )}^3}{\left|\frac{df({\overrightarrow{r}}_{\alpha },{\overrightarrow{p}}_1)}{dt}\right|}_{{\overrightarrow{p}}_2}^{\text{coll}}{l}_x{l}_y{l}_z\Delta t\\ =g\frac{{\Delta }^3{\overrightarrow{p}}_2}{{(2\pi \hslash )}^3}{\left|\frac{df({\overrightarrow{r}}_{\alpha },{\overrightarrow{p}}_2)}{dt}\right|}_{{\overrightarrow{p}}_1}^{\text{coll}}{l}_x{l}_y{l}_z\Delta t.& (29)\end{array}$

The quantities $|\frac{df({\overrightarrow{r}}_{\alpha },{\overrightarrow{p}}_1)}{dt}{|}_{{\overrightarrow{p}}_2}^{\text{coll}}$ and $|\frac{df({\overrightarrow{r}}_{\alpha },{\overrightarrow{p}}_2)}{dt}{|}_{{\overrightarrow{p}}_1}^{\text{coll}}$ are the changing rates of $f({\overrightarrow{r}}_{\alpha },{\overrightarrow{p}}_1)$ and $f({\overrightarrow{r}}_{\alpha },{\overrightarrow{p}}_2)$, respectively, caused by two-body scatterings between the nucleons in $V_{{\overrightarrow{p}}_1}$ and $V_{{\overrightarrow{p}}_2}$. These terms can be obtained directly from Equation (3), i.e., the NN collision term in the BUU equation, as

$\begin{array}{l}{\left|\frac{df({\overrightarrow{r}}_{\alpha },{\overrightarrow{p}}_1)}{dt}\right|}_{{\overrightarrow{p}}_2}^{\text{coll}}=g\frac{{\Delta }^3{\overrightarrow{p}}_2}{{(2\pi \hslash )}^3}f({\overrightarrow{r}}_{\alpha },{\overrightarrow{p}}_1)f({\overrightarrow{r}}_{\alpha },{\overrightarrow{p}}_2)\\ {\displaystyle \int \frac{d^3{p}_3}{{(2\pi \hslash )}^3}}\frac{d^3{p}_4}{{(2\pi \hslash )}^3}|{{M}}_{12\to 34}{|}^2{\left(2\pi \right)}^4\\ {\delta }^4(p_1+p_2-p_3-p_4)\\ =g\frac{{\Delta }^3{\overrightarrow{p}}_2}{{(2\pi \hslash )}^3}f({\overrightarrow{r}}_{\alpha },{\overrightarrow{p}}_1)f({\overrightarrow{r}}_{\alpha },{\overrightarrow{p}}_2)v_{\text{rel}}{\sigma }_{\text{NN}}^{*},& (30)\end{array}$

where we have substituted in the definition of the cross-section,

$\begin{array}{l}{\sigma }_{\text{NN}}^{*}=\frac{1}{v_{\text{rel}}}\int \frac{d^3{p}_3}{{(2\pi \hslash )}^3}\frac{d^3{p}_4}{{(2\pi \hslash )}^3}|{{M}}_{12\to 34}{|}^2{\left(2\pi \right)}^4\\ {\delta }^4(p_1+p_2-p_3-p_4),& (31)\end{array}$

with v_rel being the relative velocity of the test nucleons in the two momentum space volumes and ${\sigma }_{\text{NN}}^{*}$ the scattering cross-section in the two-nuclei center-of-mass frame. Here, we obtain the in-medium NN cross-section ${\sigma }_{\text{NN}}^{*}$ by multiplying the free NN cross-section ${\sigma }_{\text{NN}}^{\text{free}}$ by a medium-correction factor. The NN elastic scattering cross-section in free space, ${\sigma }_{\text{NN}}^{\text{free}}$, is taken from the parameterization in reference [75] with a cutoff of ${\sigma }_{\text{NN}}^{\text{free}}(p_{\text{lab}}\le 0.1\text{ GeV}/c)={\sigma }_{\text{NN}}^{\text{free}}(p_{\text{lab}}=0.1\text{ GeV}/c)$ for neutron-neutron (nn) or proton-proton (pp) scatterings and a cutoff of ${\sigma }_{\text{NN}}^{\text{free}}(p_{\text{lab}}\le 0.05\text{ GeV}/c)={\sigma }_{\text{NN}}^{\text{free}}(p_{\text{lab}}=0.05\text{ GeV}/c)$ for neutron-proton (np) scatterings, since the parameterization is shown to be valid for nucleon momentum p_lab down to the corresponding cutoff [75]. We note that the p_lab cutoff actually corresponds to only a few MeV of incident kinetic energy (i.e., 1.3 MeV for p_lab = 0.05 GeV/c and 5.3 MeV for p_lab = 0.1 GeV/c), and these very low-energy scatterings are not important in the present transport model calculations. Since this parameterization of ${\sigma }_{\text{NN}}^{*}$ is given in the two-nucleon center-of-mass frame, its value in the two-nuclei center-of-mass frame can be obtained through the Lorentz invariant quantity $E_1{E}_2{v}_{\text{rel}}{\sigma }_{\text{NN}}^{*}$. From Equations (28)–(30) one obtains

$\begin{array}{l}\Delta N^{\text{coll}}({\overrightarrow{r}}_{\alpha },{\overrightarrow{p}}_1,{\overrightarrow{p}}_2)={\displaystyle \sum _{i,j}^{\begin{array}{c}{\overrightarrow{p}}_i\in V_{{\overrightarrow{p}}_1}\\ {\overrightarrow{p}}_j\in V_{{\overrightarrow{p}}_2}\end{array}}\Delta }{N}_{ij}^{\text{coll}}\\ ={\displaystyle \sum _{i,j}^{\begin{array}{c}{\overrightarrow{p}}_i\in V_{{\overrightarrow{p}}_1}\\ {\overrightarrow{p}}_j\in V_{{\overrightarrow{p}}_2}\end{array}}\frac{1}{N_{\text{E}}^2}}{v}_{\text{rel}}{\sigma }_{\text{NN}}^{*}S({\overrightarrow{r}}_i-{\overrightarrow{r}}_{\alpha })S({\overrightarrow{r}}_j-{\overrightarrow{r}}_{\alpha })l_x{l}_y{l}_Z\Delta t,& (32)\end{array}$

where $\Delta N_{ij}^{\text{coll}}$ denotes the number of physical collisions from the scattering of the ith and jth test nucleons. Given that every test nucleon is 1/N_E of a physical nucleon, one obtains the collision probability of the ith and jth test nucleons as

$\begin{array}{ll}{P}_{ij}=\frac{\Delta N_{ij}^{\text{coll}}}{{(1/N_{\text{E}})}^2}=v_{\text{rel}}{\sigma }_{\text{NN}}^{*}S({\overrightarrow{r}}_i-{\overrightarrow{r}}_{\alpha })S({\overrightarrow{r}}_j-{\overrightarrow{r}}_{\alpha })l_x{l}_y{l}_z\Delta t.& (33)\end{array}$

One can reduce statistical fluctuations of the collision events by allowing collisions of test nucleons that come from different ensembles. In this case the collision probability is reduced, P_ij → P_ij/N_E, via the scaling ${\sigma }_{\text{NN}}^{*}\to {\sigma }_{\text{NN}}^{*}/N_{\text{E}}$. In our case, the NN scattering probabilities are very small within one time step, so instead of evaluating the probabilities of all possible collisions of test nucleons, we randomly divide the test nucleons that are available for scattering around the lattice site α into many pairs for scattering, and amplify the corresponding scattering probabilities accordingly, which is a common practice when one allows the scattering of test nucleons from different ensembles [74, 76]. The amplified scattering probabilities are given by

$\begin{array}{ll}{P}_{i{j}^{\prime }}=P_{ij}\frac{N_{\alpha }(N_{\alpha }-1)/2}{N_{\alpha }^{\prime }/2},& (34)\end{array}$

where N_α is the number of test nucleons that contribute to lattice site ${\overrightarrow{r}}_{\alpha }$ and $N_{\alpha }^{\prime }$ is the number of test nucleons available for scattering. Since we choose a finite-range form factor for coordinates in the LBUU framework, one test nucleon can be involved in different collision events at different lattice sites. Those test nucleons that have already collided at another lattice site are excluded from the scattering at the present lattice site, so $N_{\alpha }^{\prime }$ is not necessarily equal to N_α. The time step Δt needs to be sufficiently small to pin down the effect of such an exclusion by suppressing the chance of multi-scattering attempts, as well as to keep $P_{ij}^{\prime }$ less than unity. In the present LBUU framework, we choose Δt = 0.2 fm/c for the full LBUU calculations and Δt = 0.4 fm/c for the Vlasov calculations (i.e., the LBUU calculations without the NN scatterings).

To verify the accuracy of the stochastic collision treatment within the present LBUU framework, we simulate collisions of nucleons confined in a cubic box of volume V = 10 × 10 × 10 fm³ with periodic boundary conditions. In this simulation, we ignore the nuclear mean-field potential and the quantum nature of nucleons. Initially, 80 neutrons and 80 protons are uniformly distributed over the box, corresponding to a nucleon density of ρ = 0.16 fm³. Their momenta are generated according to the relativistic Boltzmann distribution,

$\begin{array}{ll}P(p)\propto p^2\exp \text{}\left[\frac{\sqrt{m^2+p^2}}{T}\right],& (35)\end{array}$

where m = 939 MeV is the free nucleon mass. Here, the temperature T is taken to be 14.24 MeV so that the system has the same kinetic energy density as the zero-temperature isospin-symmetric Fermi gas of nucleons.

Using the NN elastic scattering cross-section in free space [75], we simulate the time evolution of this system up to 1 fm/c with a time step of 0.2 fm/c and N_E = 1, 000. It is constructive to see the collision rate as a function of the center-of-mass energy $\sqrt{s}$ of the colliding nucleon pair. The $\sqrt{s}$ distributions of the collision rates for np and for nn plus pp are plotted as red circles in the left and right panels of Figure 1, respectively. Theoretically, considering two species of particles following relativistic Boltzmann distributions, the $\sqrt{s}$ distributions of their collision rates can be derived as

$\begin{array}{ll}\frac{d{N}_{\text{coll}}}{dtd{s}^{1/2}}=\frac{1}{1+{\delta }_{ij}}\frac{N_i{N}_j}{V}\frac{s(s-4m^2)K_1(s^{1/2}/T)\sigma (s^{1/2})}{4m^4{T}_{\text{B}}{K}_2^2(m/T)},& (36)\end{array}$

where K_n is the nth order modified Bessel function, N_i (N_j) is the number of particles i (j) in the volume V, and σ is their scattering cross-section. The expected distributions are shown as black solid lines in Figure 1 for comparison. It is seen that the LBUU calculations are in excellent agreement with the expected results.

FIGURE 1

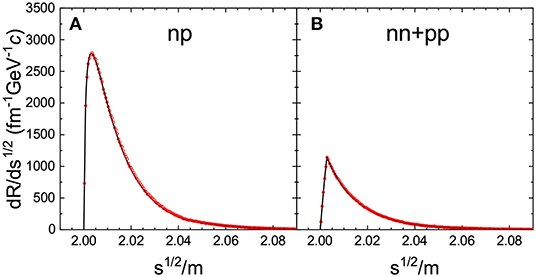
Figure 1. The $\sqrt{s}$ distribution of (A) np and (B) nn + pp elastic collision rates for the Boltzmann distribution at T = 14.24 MeV, with 80 neutrons and 80 protons in a cube of volume V = 10 × 10 × 10 fm³, for theoretical predictions (black solid line) and LBUU calculations (red circles). In both calculations, we choose free NN cross-sections as parameterized in reference [75].

Given the quantum nature of nucleons, we handle Pauli blocking in the LBUU method as follows. If the NN scattering between the ith and jth test nucleons happens at the lattice site ${\overrightarrow{r}}_{\alpha }$ according to P_ij or $P_{ij}^{\prime }$, the directions of their final momenta ${\overrightarrow{p}}_3$ and ${\overrightarrow{p}}_4$ are determined by the differential cross-section given in reference [75], and then the Pauli blocking factor $\left[1-f({\overrightarrow{r}}_{\alpha },{\overrightarrow{p}}_3)\right]\times \left[1-f({\overrightarrow{r}}_{\alpha },{\overrightarrow{p}}_4)\right]$ is used to determine whether the collision is blocked by the Pauli principle. The distribution function $f_{\tau }({\overrightarrow{r}}_{\alpha },\overrightarrow{p})$ is calculated according to Equation (28). For the momentum space volume ${\Delta }^3{\overrightarrow{p}}_i$, we take a sphere with radius $R_{\tau }^p({\overrightarrow{r}}_{\alpha },\overrightarrow{p})$ centered at ${\overrightarrow{p}}_i$. In typical BUU transport models, $R_{\tau }^p({\overrightarrow{r}}_{\alpha },\overrightarrow{p})$ is a constant of about a hundred MeV. For the calculation of small-amplitude nuclear collective dynamics near the ground state, a specifically proposed $R_{\tau }^p({\overrightarrow{r}}_{\alpha },\overrightarrow{p})$ is more suitable [51], i.e.,

$\begin{array}{ll}{R}_{\tau }^p({\overrightarrow{r}}_{\alpha },\overrightarrow{p})=\max [\Delta p,p_{\tau }^F({\overrightarrow{r}}_{\alpha })-|\overrightarrow{p}|],& (37)\end{array}$

where Δp is a constant that should be sufficiently small and $p_{\tau }^F=\hslash {(3{\pi }^2{\rho }_{\tau })}^{1/3}$ is the nucleon Fermi momentum.

2.3. Ground State Initialization and Evolution Stability

In the present LBUU method, we obtain the ground state of nuclei at zero temperature by varying the Hamiltonian with respect to the nuclear radial density, which is sometimes called Thomas-Fermi (TF) initialization [51, 66, 77, 78] in the one-body transport model. We assume that for a ground-state nucleus at zero temperature, its Wigner function satisfies

$\begin{array}{ll}{f}_{\tau }(\overrightarrow{r},\overrightarrow{p})=\frac{2}{{(2\pi \hslash )}^3}\theta [|\overrightarrow{p}|-p_{\tau }^F(\overrightarrow{r})],& (38)\end{array}$

where $p_{\tau }^F(\overrightarrow{r})$ is the local Fermi momentum given by

$\begin{array}{ll}{p}_{\tau }^F(\overrightarrow{r})=\hslash {[3{\pi }^2{\rho }_{\tau }(\overrightarrow{r})]}^{1/3}.& (39)\end{array}$

It should be noted that, in principle, with the inclusion of NN scatterings, which goes beyond mean-field correlations, the nucleon momentum distribution in the ground state may differ slightly from the zero-temperature Fermi distribution. If we assume for simplicity that the nucleus is spherical, the total energy of a ground-state nucleus at zero temperature can be regarded as a functional of the radial density ρ_τ(r) and its spatial gradients,

$\begin{array}{ll}E={\displaystyle \int {H}}[r,{\rho }_{\tau }(r),\nabla {\rho }_{\tau }(r),{\nabla }^2{\rho }_{\tau }(r),\dots ]dr.& (40)\end{array}$

The neutron (proton) radial density in a ground-state nucleus can be obtained, by varying the total energy with respect to ρ_τ(r) [note that for protons the contribution from the Coulomb interaction in Equation (21) should also be included in the Hamiltonian density], as

$\begin{array}{ll}\frac{1}{2m}{\left\{p_{\tau }^F[{\rho }_{\tau }(r)]\right\}}^2+U_{\tau }\{p_{\tau }^{\text{F}}[{\rho }_{\tau }(r)],r\}={\mu }_{\tau },& (41)\end{array}$

where μ_τ is the chemical potential of a proton or neutron inside the nucleus, with value determined by the given proton number Z or neutron number N. The quantity $U_{\tau }\{p_{\tau }^{\text{F}}[{\rho }_{\tau }(r)],r\}$ refers to the single nucleon potential of the nucleon with local Fermi momentum. The single nucleon potential is derived by varying the Hamiltonian density in Equations (6)–(12) with respect to the phase-space distribution function and density gradients, and its detailed expression for the N3LO Skyrme pseudopotential is given in reference [73]. The physical significance of Equation (41) is very intuitive: in a classical picture, in a ground-state nucleus at zero temperature, the nucleons in the Fermi surface at different radial positions have the same chemical potential. The local density ${\rho }_{\tau }(\overrightarrow{r})$ for a ground-state spherical nucleus is obtained by solving Equation (41) subject to the following boundary conditions on the total local density ρ(r) = ρ_n(r)+ρ_p(r):

$\begin{array}{ll}\frac{\partial \rho (r)}{\partial r}{|}_{r=0}=\frac{\partial \rho (r)}{\partial r}{|}_{r=r_{\text{B}}}=0.& (42)\end{array}$

Here, r_B is the boundary of the nucleus and it satisfies ρ(r_B) = 0.

In the present LBUU framework, the initial coordinates of test nucleons are generated according to the obtained ${\rho }_{\tau }(\overrightarrow{r})$, while their initial momenta are generated from a zero-temperature Fermi distribution with the Fermi momentum given in Equation (39). Owing to the presence of the form factor $S(\overrightarrow{r}-{\overrightarrow{r}}^{\prime })$ introduced in Equation (4), the density is smeared slightly in the LBUU calculations compared with the realistic local density. Thus the initial ground-state radial density distribution is slightly different from the solution of Equation (41). Unlike the Gaussian wave packet that is used to mimic the Wigner function in QMD model [57], the form factor $S(\overrightarrow{r}-{\overrightarrow{r}}^{\prime })$ does not have any physical meaning; it can be regarded as a numerical technique introduced in the test-particle approach so that one can obtain well-defined densities and mean fields. As shown in the following, an additional gradient term in the local density can compensate for the effects caused by the smearing of the local density due to the form factor. In this subsection, we will denote by $\tilde{\rho }(\overrightarrow{r})$ the local density in the LBUU calculation and by $\rho (\overrightarrow{r})$ the realistic local density. The local density $\tilde{\rho }(\overrightarrow{r})$ can be regarded as a convolution of the realistic local density with the form factor,

$\begin{array}{ll}\tilde{\rho }(\overrightarrow{r})={\displaystyle \int \rho }({\overrightarrow{r}}^{\prime })S(\overrightarrow{r}-{\overrightarrow{r}}^{\prime })d^3{r}^{\prime }.& (43)\end{array}$

To express $\rho (\overrightarrow{r})$ in terms of $\tilde{\rho }(\overrightarrow{r})$, we have formally

$\begin{array}{l}\rho (\overrightarrow{r})={\displaystyle \int \tilde{\rho }}({\overrightarrow{r}}^{\prime })S^{-1}({\overrightarrow{r}}^{\prime }-\overrightarrow{r})d^3{r}^{\prime }\\ ={\displaystyle \int }\left[{\displaystyle \sum _{n=0}^{\infty }\frac{1}{n!}}{\nabla }^n\tilde{\rho }(\overrightarrow{r}){({\overrightarrow{r}}^{\prime }-\overrightarrow{r})}^n\right]S^{-1}({\overrightarrow{r}}^{\prime }-\overrightarrow{r})d^3{r}^{\prime }\\ \approx \tilde{\rho }(\overrightarrow{r})+c{\nabla }^2\tilde{\rho }(\overrightarrow{r}),& (44)\end{array}$

where we have truncated at next-to-leading order [the $\nabla \tilde{\rho }(\overrightarrow{r})$ term vanishes because of the symmetry of the integral] and $S^{-1}(\overrightarrow{r}-{\overrightarrow{r}}^{\prime })$ is the inverse of $S(\overrightarrow{r}-{\overrightarrow{r}}^{\prime })$, which satisfies

$\begin{array}{ll}{\displaystyle \int S}(\overrightarrow{r}-{\overrightarrow{r}}^{\prime \prime })S^{-1}({\overrightarrow{r}}^{\prime \prime }-{\overrightarrow{r}}^{\prime })d^3{r}^{″}=\delta (\overrightarrow{r}-{\overrightarrow{r}}^{\prime }).& (45)\end{array}$

The parameter c, defined by

$\begin{array}{ll}c\equiv {\displaystyle \int \frac{1}{2}}{({\overrightarrow{r}}^{\prime }-\overrightarrow{r})}^2{S}^{-1}({\overrightarrow{r}}^{\prime }-\overrightarrow{r})d^3{r}^{\prime },& (46)\end{array}$

is a small constant that depends only on the form of S. In the LBUU framework, to obtain $\rho (\overrightarrow{r})$ by direct correction of $\tilde{\rho }(\overrightarrow{r})$ is not feasible since numerically the density in Equation (44) is not always positive. If we substitute Equation (44) into the total Hamiltonian, with several necessary approximations, we obtain an additional term that is proportional to $c\tilde{\rho }(\overrightarrow{r}){\nabla }^2\tilde{\rho }(\overrightarrow{r})$. This term leads to an additional gradient term ${Ẽ}^{\left[2\right]}{\nabla }^2\tilde{\rho }$ in the equations of motion (20). Therefore, in practice we can add the extra gradient terms ${Ẽ}^{\left[2\right]}{\nabla }^2\tilde{\rho }$ to the equations of motion, to compensate for the smearing of density due to the form factor. In principle, the parameter Ẽ^[2] should contain higher-order effects, so we adjust it to roughly obtain the ground-state root-mean-square (rms) radius evolution with the smallest oscillation, since the rms radius in the exact ground state should not change with time. Normally Ẽ^[2] is a small parameter, around 15 MeV for various (N3LO) Skyrme parameter sets. It should be mentioned that this correction of the density gradient term improves the stability of the ground-state evolution (rms radius and radial density profile) only slightly, and does not lead to much difference in the results for collective motions. In ideal cases with N_E → ∞ and l_x, l_y, l_z → 0, the local density in the LBUU calculation will approach the physical local density, and Ẽ^[2] will become zero. Since all the LBUU calculations are based on $\tilde{\rho }(\overrightarrow{r})$, we do not distinguish between $\tilde{\rho }(\overrightarrow{r})$ and $\rho (\overrightarrow{r})$, and $\rho (\overrightarrow{r})$ should be interpreted as $\tilde{\rho }(\overrightarrow{r})$ in the rest of the article.

We first examine the ground-state evolution stability of the LHV calculation, i.e., the LBUU calculation without the collision term, since in principle all NN scatterings should be blocked in the ground state. We show in Figure 2 the time evolution of the radial density profile from the LHV calculation for the nucleus ²⁰⁸Pb in ground state up to 1, 000 fm/c, obtained with N_E = 10, 000 and a time step of Δt = 0.4 fm/c by using the N3LO Skyrme pseudopotential SP6m. We notice from Figure 2 that the profile of the radial density exhibits only very small variations with time, which indicates the success of the above initialization method. It also shows that the smearing of the local density caused by the inclusion of the form factor S does not affect the dynamic evolution significantly. Such features indicate that the present LBUU method of solving the BUU equation can be used to study long-time nuclear processes, such as nuclear spallation and heavy-ion fusion reactions.

FIGURE 2

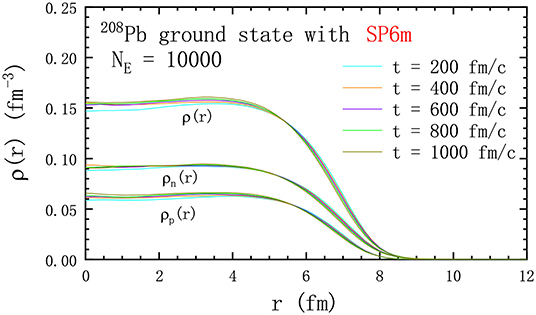
Figure 2. Time evolution of the radial density profile of the ground state of ²⁰⁸Pb based on the LHV calculation (i.e., the LBUU calculation without NN scatterings) with the N3LO Skyrme pseudopotential SP6m up to 1, 000 fm/c. Reproduced from reference [61] with permission from the American Physical Society.

Apart from the radial density profile, other properties of the ground-state evolution stability are also examined. In Figure 3 we present the time evolution of the rms radius, the fraction of bound nucleons, and the binding energy of the LHV calculation (i.e., the LBUU calculation without NN scatterings). The calculations are performed with time step Δt = 0.4 fm/c and with N_E = 5, 000 and 10, 000. The test nucleons for which the form factor does not overlap with that of others are considered free test nucleons, and they are excluded when calculating the fraction of bound nucleons and the rms radius. We notice from Figure 3A that although in the N_E = 5, 000 case the rms radius starts to decrease after about 800 fm/c, the LHV calculation gives a fairly stable time evolution of the rms radius. The observed decrease is due to the evaporation of test nucleons from the bound nuclei, which is illustrated in Figure 3B. Such evaporation of test nucleons is inevitable in transport model calculations because of the limited precision of the numerical realization, but it can be suppressed by increasing N_E, as seen in Figure 3B, though the result with E_E = 5, 000 is already satisfactory [61]. As Figure 3C shows, the LH method ensures the energy conservation to a very high degree. The difference between the cases of N_E = 5, 000 and N_E = 10, 000 is mainly due to the numerical precision of the gradient term in the Hamiltonian. It is seen from Figure 3 that the present LBUU framework can give a fairly stable ground-state time evolution. Owing to the high efficiency of GPU parallel computing, it becomes possible to include more ensembles or test particles in the LBUU calculation. As one will see in the following, to obtain the correct GDR width, as many as 30, 000 ensembles are needed in the full LBUU calculation with NN scatterings.

FIGURE 3

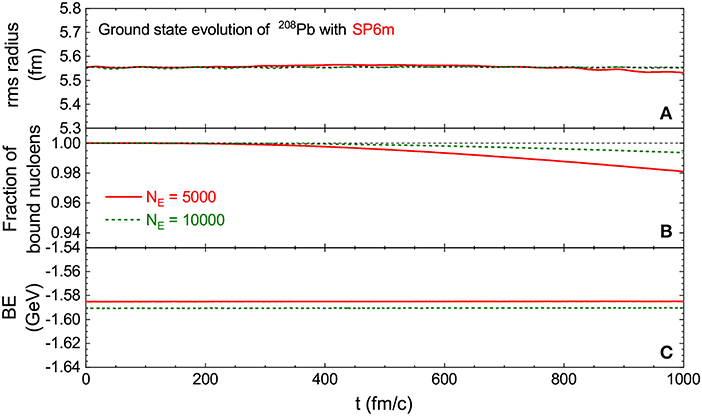
Figure 3. Time evolution of (A) rms radius, (B) fraction of bound nucleons, and (C) binding energy of the ²⁰⁸Pb ground state from the LHV calculation (i.e., the LBUU calculation without NN scatterings) with the N3LO Skyrme pseudopotential SP6m up to 1, 000 fm/c. Calculations are performed with a time step of Δt = 0.4 fm/c and with N_E = 5, 000 and 10, 000. Reproduced from reference [61] with permission from the American Physical Society.

For the stability of the ground-state evolution in the full LBUU calculation, we note that for ${\sigma }_{\text{NN}}^{\text{free}}$ with N_E = 30, 000, the rms radius and the ground-state energy of ²⁰⁸Pb vary <3.6% (0.2 fm) and 3.2% (50 MeV), respectively, during the time evolution of 0–500 fm/c [55]. The stability of the rms radius in the full LBUU calculation is not as good as in the LHV case, and this may be due to the fact that with the inclusion of NN scatterings, i.e., beyond mean-field correlations, the nucleon momentum distribution in the ground state may differ slightly from the zero-temperature Fermi distribution. Apart from this, although the LH method can conserve the energy almost exactly for the mean-field evolution without NN collisions, the non-perfect energy conservation in the LBUU calculation could be caused by the NN scattering processes, which usually violate energy conservation when the momentum-dependent mean-field potentials are used. Both problems require further investigation of transport model calculations in the future.

2.4. Nuclear Giant Resonances Within Transport Models

We consider a small excitation of the Hamiltonian,

$\begin{array}{ll}{\widehat{H}}_{\text{ex}}(t)=\lambda \widehat{Q}\delta (t-t_0),& (47)\end{array}$

where $\widehat{Q}$ is the excitation operator for a given mode and λ is the initial excitation parameter, which is assumed to be small. In linear response theory [79], the response of the excitation operator $\widehat{Q}$ as a function of time is given by

$\begin{array}{l}\Delta \langle \widehat{Q}\rangle (t)=\langle 0^{\prime }|\widehat{Q}|0^{\prime }\rangle (t)-\langle 0|\widehat{Q}|0\rangle (t)\\ =-\frac{2\lambda \theta (t)}{\hslash }{\displaystyle \sum _F|}\langle F|\widehat{Q}|0\rangle {|}^2\sin \frac{(E_F-E_0)t}{\hslash },& (48)\end{array}$

where |0〉 is the unperturbed nuclear ground state with energy E₀, |0′〉 is the nuclear state after the perturbation, and |F〉 is the energy eigenstate of the excited nucleus with eigen-energy E_F. The strength function, which is defined as

$\begin{array}{ll}S(E)={\displaystyle \sum _F|}\langle F|\widehat{Q}|0\rangle {|}^2\delta (E-E_F+E_0),& (49)\end{array}$

can be expressed as a Fourier integral of $\Delta \langle \widehat{Q}\rangle (t)$ in Equation (48):

$\begin{array}{ll}S(E)=-\frac{1}{\pi \lambda }{\displaystyle {\int }_0^{\infty }d}t\Delta \langle \widehat{Q}\rangle (t)\sin \frac{Et}{\hslash }.& (50)\end{array}$

By evaluating the time evolution of $\Delta \langle \widehat{Q}\rangle (t)$ within the transport model, we can obtain the strength function and, subsequently, other quantities, such as the peak energy, width, and energy-weighted sum rules. The time evolution of $\Delta \langle \widehat{Q}\rangle (t)$ can be expressed in terms of the Wigner function $f(\overrightarrow{r},\overrightarrow{p})$ as follows.

If we assume that $\widehat{Q}$ is a one-body operator, then it can be written as the sum of single-particle operators $\widehat{q}$ acting on each nucleon, $\widehat{Q}=\sum _i^A\widehat{q}$, and the expectation value of $\widehat{Q}$ for a given state is evaluated as

$\begin{array}{l}\langle \widehat{Q}\rangle =\langle \Phi |\widehat{Q}|\Phi \rangle ={\displaystyle \int \langle \Phi |{\overrightarrow{r}}_1\cdots {\overrightarrow{r}}_N\rangle \langle {\overrightarrow{r}}_1\cdots {\overrightarrow{r}}_N|\widehat{Q}|{\overrightarrow{r}}_1^{\prime }\cdots {\overrightarrow{r}}_N^{\prime }\rangle }\\ \langle {\overrightarrow{r}}_1^{\prime }\cdots {\overrightarrow{r}}_N^{\prime }|\Phi \rangle d^3{r}_1\cdots d^3{r}_N{d}^3{r}_1^{\prime }\cdots d^3{r}_N^{\prime },& (51)\end{array}$

where we have added two identity operators. Considering the definition of the one-body density matrix,

$\rho ({\overrightarrow{r}}_1,{\overrightarrow{r}}_1^{\prime })=A{\displaystyle \int \langle {\overrightarrow{r}}_1{\overrightarrow{r}}_2\cdots {\overrightarrow{r}}_N|\Phi \rangle \langle \Phi |{\overrightarrow{r}}_1^{\prime }{\overrightarrow{r}}_2\cdots {\overrightarrow{r}}_N\rangle }{d}^3{r}_2\cdots d^3{r}_N,$

and combining it with the one-body operator condition $\widehat{Q}=\sum _i^A\widehat{q}$, we can rewrite Equation (51) as

$\begin{array}{ll}\langle \widehat{Q}\rangle ={\displaystyle \int \rho }({\overrightarrow{r}}_1^{\prime },{\overrightarrow{r}}_1)\langle {\overrightarrow{r}}_1|\widehat{q}|{\overrightarrow{r}}_1^{\prime }\rangle d^3{r}_1{d}^3{r}_1^{\prime }.& (52)\end{array}$

The density matrix can be expressed in coordinate space as the inverse Fourier transform of $f(\overrightarrow{r},\overrightarrow{p})$,

$\begin{array}{ll}\rho (\overrightarrow{r}-\frac{\overrightarrow{s}}{2},\overrightarrow{r}+\frac{\overrightarrow{s}}{2})={\displaystyle \int f}(\overrightarrow{r},\overrightarrow{p})\text{exp}\left(i\frac{\overrightarrow{p}}{\hslash }\overrightarrow{s}\right)d^{3}p.& (53)\end{array}$

In the above equation we have changed the integration variables: ${\overrightarrow{r}}_1=\overrightarrow{r}+\frac{\overrightarrow{s}}{2}$ and ${\overrightarrow{r}}_1^{\prime }=\overrightarrow{r}-\frac{\overrightarrow{s}}{2}$. We define the Wigner transform of $\widehat{q}$ in coordinate space,

$\begin{array}{ll}q(\overrightarrow{r},\overrightarrow{p})\equiv {\displaystyle \int \exp }(-i\frac{\overrightarrow{p}}{\hslash }·\overrightarrow{s})q(\overrightarrow{r}+\frac{\overrightarrow{s}}{2},\overrightarrow{r}-\frac{\overrightarrow{s}}{2})d^{3}s,& (54)\end{array}$

where $q(\overrightarrow{r}+\frac{\overrightarrow{s}}{2},\overrightarrow{r}-\frac{\overrightarrow{s}}{2})=\langle \overrightarrow{r}+\frac{\overrightarrow{s}}{2}|\widehat{q}|\overrightarrow{r}-\frac{\overrightarrow{s}}{2}\rangle$ represents the matrix element of $\widehat{q}$ in coordinate space. By substituting Equation (53) and the inverse transform of Equation (54) into Equation (52), the expectation of $\widehat{Q}$ can be written in the form

$\begin{array}{ll}\langle \widehat{Q}\rangle ={\displaystyle \int f}(\overrightarrow{r},\overrightarrow{p})q(\overrightarrow{r},\overrightarrow{p})d^{3}r{d}^{3}p,& (55)\end{array}$

which means that the time evolution of $\langle \widehat{Q}\rangle$ can be calculated through the time evolution of $f(\overrightarrow{r},\overrightarrow{p})$.

In the transport model, different external excitations $\lambda \widehat{Q}\delta (t-t_0)$ can be generated by changing the positions and momenta of the test nucleons as follows [47]:

$\begin{array}{ll}{\overrightarrow{r}}_i\to {\overrightarrow{r}}_i+\lambda \frac{\partial q({\overrightarrow{r}}_i,{\overrightarrow{p}}_i)}{\partial {\overrightarrow{p}}_i},{\overrightarrow{p}}_i\to {\overrightarrow{p}}_i-\lambda \frac{\partial q({\overrightarrow{r}}_i,{\overrightarrow{p}}_i)}{\partial {\overrightarrow{r}}_i}.& (56)\end{array}$

The detailed forms of $q({\overrightarrow{r}}_i,{\overrightarrow{p}}_i)$ for different collective modes and their corresponding initializations in the transport model will be given later.

3. Lattice Hamiltonian Vlasov Calculations

In this section we compare the peak energy of nuclear giant resonances obtained from LBUU calculations without the NN scatterings, i.e., LHV calculations, with that obtained from the RPA, since the 2p-2h correlation is absent in both cases. Both the isoscalar monopole and isovector dipole modes of ²⁰⁸Pb are examined.

3.1. Isoscalar Monopole Mode

Since the isoscalar giant monopole resonance (ISGMR) provides information about the nuclear matter incompressibility [80–85], which is a fundamental quantity that characterizes the EOS of symmetric nuclear matter, it is interesting to study the ISGMR within the transport model to make a cross-check with the incompressibility extracted from the HICs.

From the point of view of the one-body transport model, the isoscalar monopole mode is regarded as a compressional breathing of the nuclear fluid. The excitation operator ${\widehat{Q}}_{\text{ISM}}$ for the isoscalar monopole mode and its one-body operator ${\widehat{q}}_{\text{ISM}}$ take the forms

$\begin{array}{ll}{\widehat{Q}}_{\text{ISM}}=\frac{1}{A}{\displaystyle \sum _i^{\text{A}}{\widehat{r}}_i^2},{\widehat{q}}_{\text{ISM}}=\frac{{\widehat{r}}^2}{A}.& (57)\end{array}$

From Equation (54) we obtain the Wigner transform of ${\widehat{q}}_{\text{ISM}}$ as

$\begin{array}{ll}{q}_{\text{ISM}}(\overrightarrow{r},\overrightarrow{p})=\frac{{\overrightarrow{r}}^2}{A}.& (58)\end{array}$

According to Equation (56), we can generate in the transport model the initial isoscalar monopole excitation by changing the initial phase-space information of test nucleons with respect to that of the ground state:

$\begin{array}{ll}{\overrightarrow{p}}_i\to {\overrightarrow{p}}_i-2\lambda \frac{{\overrightarrow{r}}_i}{A}.& (59)\end{array}$

The spatial coordinates of the test nucleons remain unchanged since q_ISM in Equation (58) is independent of momentum. Note that the rms radius of a nucleus, shown in Figure 3, is given by the square root of the expectation value of ${\widehat{Q}}_{\text{ISM}}$.

We show in Figure 4 the time evolution of $\Delta \langle {\widehat{Q}}_{\text{ISM}}\rangle$, i.e., the difference between the expectation values of $\langle {\widehat{Q}}_{\text{ISM}}\rangle$ for the excited state and the ground state from the LHV calculations. The results are from one conventional Skyrme interaction MSL1 and three N3LO Skyrme pseudopotentials, SP6s, SP6m, and SP6h. In the calculation, we set the number of ensembles N_E to 5, 000, and the initial excitation parameter λ is taken to be 100 MeV · fm⁻¹/c. One sees from the figure that the time evolution of $\Delta \langle {\widehat{Q}}_{\text{ISM}}\rangle$, or equivalently the rms radius, displays a very regular oscillation, and the rapid increase of the radius with time that is generally seen in most BUU calculations using the conventional test particle method does not show up here. Besides that, since the only damping mechanism in the LHV calculation is Landau damping, the amplitude of the oscillation only decreases slightly. Landau damping is caused by one-body dissipation, which is governed by a coupling of single-particle and collective motions. It should be mentioned that in the RPA framework, the damping also comes only from one-body dissipation, since the coupling to more complex states, such as 2p-2h states, is missing in RPA [86]. We obtain the peak energy of the giant monopole resonance through Fourier transform of the time evolution of $\Delta \langle {\widehat{Q}}_{\text{ISM}}\rangle$ shown in Figure 4. The obtained peak energy is 13.8 MeV for SP6s, 13.6 MeV for SP6m, 13.9 MeV for SP6h, and 13.5 MeV for MSL1. In order to compare the result from the LHV calculation with that from RPA, we calculate the strength function of the giant monopole resonance using the Skyrme-RPA code of Colo et al. [87] with the MSL1 interaction. The obtained peak energy of 14.1 MeV is comparable to that from the LHV calculation with MSL1, and the small discrepancy may reflect the difference between their semi-classical and quantum natures.

FIGURE 4

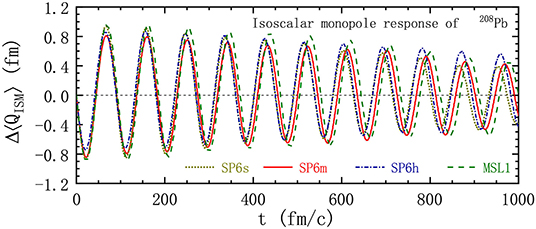
Figure 4. Time evolution of $\Delta \langle {\widehat{Q}}_{\text{ISM}}\rangle$ of ²⁰⁸Pb after a perturbation by ${Ĥ}_{\text{ex}}(t)=\lambda {\widehat{Q}}_{\text{ISM}}\delta (t-t_0)$ with λ = 100 MeV · fm⁻¹/c in the LHV calculations. The results correspond to three N3LO Skyrme pseudopotentials, SP6s, SP6m, and SP6h, and one conventional Skyrme interaction MSL1. Reproduced from reference [61] with permission from the American Physical Society.

3.2. Isovector Dipole Mode

The isovector giant dipole resonance (IVGDR) of finite nuclei is the earliest observed nuclear collective excitation. Systematic experimental investigation of the IVGDR with photon-nuclear reactions was conducted decades ago [88]. Recent precise measurements of the isovector dipole response have been performed at the RCNP for ⁴⁸Ca [89], ¹²⁰Sn [90], and ²⁰⁸Pb [63] with inelastic proton scattering, as well as at GSI for ⁶⁸Ni [91] by using Coulomb excitation in inverse kinematics. Recently, a low-lying mode called pygmy dipole resonance (PDR) has been observed experimentally [92–95], and this effect has already been studied based on the Vlasov equation [47]. The IVGDR [54, 96, 97], PDR [98, 99], and electric dipole polarizability α_D [100–103], which are dominated by these isovector dipole modes, provide sensitive probes to constrain the density dependence of the nuclear symmetry energy.

For the isovector dipole mode, the external perturbation can be written in the form

$\begin{array}{ll}{\widehat{Q}}_{\text{IVD}}=\frac{N}{A}{\displaystyle \sum _i^Z{\widehat{z}}_i}-\frac{Z}{A}{\displaystyle \sum _i^N{\widehat{z}}_i}.& (60)\end{array}$

The coefficients in front of the single-particle position operator are chosen so as to keep the center of mass of the nucleus at rest. According to Equation (56), in transport models the excited nucleus can be obtained by changing the initial phase-space coordinates of test nucleons:

$\begin{array}{ll}{p}_z\to \{\begin{array}{ll}{p}_z-\lambda \frac{N}{A}\hfill & \text{for protons},\hfill \\ p_z+\lambda \frac{Z}{A}\hfill & \text{for neutrons}.\hfill \end{array}& (61)\end{array}$

We show in Figure 5 the time evolution of $\Delta \langle {\widehat{Q}}_{\text{IVD}}\rangle$ for ²⁰⁸Pb with the interactions SP6s, SP6m, SP6h, and MSL1 of the LHV calculations. The number of ensembles N_E and the initial excitation parameter λ are set to 5, 000 and 25 MeV/c, respectively. Based on the time evolution of $\Delta \langle {\widehat{Q}}_{\text{IVD}}\rangle$ shown in Figure 5, the obtained peak energies for SP6s, SP6m, SP6h, and MSL1 are 13.4 MeV, 13.5 MeV, 13.7 MeV, and 13.1 MeV, respectively. The peak energy of MSL1 from the RPA calculation is 13.3 MeV, which is comparable to that obtained from the LBUU calculation without the NN collision term.

FIGURE 5

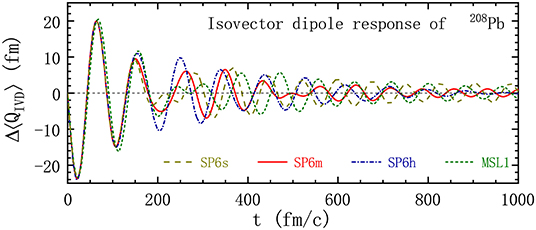
Figure 5. Same as Figure 4 but for the isovector dipole mode with λ = 25 MeV/c. Reproduced from reference [61] with permission from the American Physical Society.

4. Spreading Width of the Giant Dipole Resonance and Collisional Damping

It is generally thought that in low-energy HICs with incident energies of only a few MeV/nucleon, the NN scatterings can be safely neglected since they are mostly blocked by the Pauli principle. However, when it comes to the width of the GDR, the collisional damping caused by NN scatterings is an essential mechanism for enhancing the insufficient GDR width obtained through the pure Vlasov calculation [55]. Nevertheless, to properly implement the damping mechanism caused by NN scatterings in transport models requires a rather accurate treatment of the Pauli blocking, which is a challenge in transport model calculations. The main difficulty lies in accurately calculating local momentum distributions $f_{\tau }({\overrightarrow{r}}_{\alpha },\overrightarrow{p})$ in transport models. Inaccuracy of $f_{\tau }({\overrightarrow{r}}_{\alpha },\overrightarrow{p})$ negatively affects the accuracy of the Pauli blocking and leads to spurious collisions, which enhance the collisional damping and thus overestimate the width of nuclear giant resonances. There are three main origins of the inaccuracy of the calculated $f_{\tau }({\overrightarrow{r}}_{\alpha },\overrightarrow{p})$ and hence the spurious collisions in transport models:

(1) fluctuations in calculating $f_{\tau }({\overrightarrow{r}}_{\alpha },\overrightarrow{p})$ through Equation (28) caused by too-small N_E;

(2) a spurious temperature caused by a finite Δp in calculating $f_{\tau }({\overrightarrow{r}}_{\alpha },\overrightarrow{p})$ (also see reference [51]);

(3) the finite lattice spacing l causing diffusion in local momentum space due to the averaging of different local lattice densities in the nuclear surface region.

In order to obtain the spreading width with high accuracy from the BUU equation, one should choose a large N_E together with sufficiently small l and Δp. After a careful test, it is found [55] that to get a convergent GDR width, l should be smaller than 0.5 fm, Δp smaller than 0.05 GeV, and N_E larger than 30, 000. Further reducing Δp and l or increasing N_E leads to only a negligible decrease of the calculated GDR width. Therefore, in the following full LBUU calculations of the GDR width, we take l = 0.5 fm, Δp = 0.05 GeV, and N_E = 30, 000.

The collisional damping or NN scattering can have a significant effect on the width of nuclear giant resonances. Figure 6 shows the time evolution of the isovector dipole response $\Delta \langle {\widehat{Q}}_{\text{IVD}}\rangle$ of ²⁰⁸Pb and its strength function obtained from the LHV calculation and the full LBUU calculation with the free NN elastic scattering cross-section [55]. In both cases, the N3LO Skyrme pseudopotential SP6h is adopted, and the same initial excitation with λ = 15 MeV/c is employed (we note that varying λ by 2/3 leads to almost the same value of the GDR width). The dotted line in the left panel of Figure 6 is the time evolution of the expectation value $\langle 0|{\widehat{Q}}_{\text{IVD}}|0\rangle$ in the ground state of ²⁰⁸Pb as obtained from the LBUU calculation with the free-space NN cross-section. The expectation value $\langle 0|{\widehat{Q}}_{\text{IVD}}|0\rangle$ in the ground state of ²⁰⁸Pb is negligible compared with that in the GDR cases with and without NN scatterings. It is seen that including NN scatterings significantly increases the damping of the oscillations and leads to a much larger width. From the strength functions, the obtained GDR width of ²⁰⁸Pb is 1.5 MeV in the Vlasov calculation and 6.5 MeV in the LBUU calculation with NN scatterings. We also notice from the right panel of Figure 6 that the peak shifts to a higher energy when the NN scatterings are included. The impact that the NN scatterings have on the width indicates that they may also affect some particular observables in low-energy HICs, such as the nuclear stopping of HICs in the Fermi energy region, which merit further study.

FIGURE 6

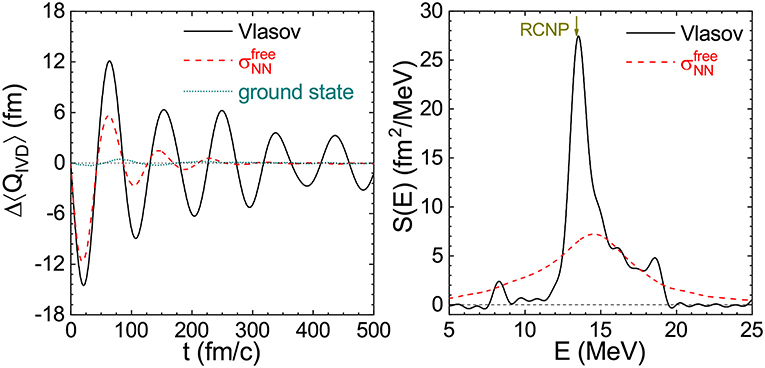
Figure 6. Time evolution of $\Delta \langle {\widehat{Q}}_{\text{IVD}}\rangle$ (left) and its strength function (right) for ²⁰⁸Pb after a perturbation ${Ĥ}_{\text{ex}}=\lambda {\widehat{Q}}_{\text{IVD}}\delta (t-t_0)$ with λ = 15 MeV/c obtained from the LHV (Vlasov) calculation and the LBUU calculation with the free NN cross-section ${\sigma }_{\text{NN}}^{\text{free}}$. The dotted line in the left panel is the expectation value of ${\widehat{Q}}_{\text{IVD}}$ in the ground state from the LBUU calculation with ${\sigma }_{\text{NN}}^{\text{free}}$. Reproduced from reference [55] under the Creative Commons CCBY license.

Recent experiments performed at the RCNP on the ${}^{208}\text{P}\text{b}(\overrightarrow{p},{\overrightarrow{p}}^{\prime })$ reaction [63] have measured the GDR width of ²⁰⁸Pb accurately, giving a value of 4.0 MeV. Therefore, the LBUU calculation with the free NN elastic cross-section (which predicts a GDR width of 6.5 MeV) significantly overestimates the GDR width of ²⁰⁸Pb. It is well-known that the NN elastic cross-section is suppressed in the nuclear medium, so the overestimation of the GDR width with ${\sigma }_{\text{NN}}^{\text{free}}$ is understandable since the medium effects on the NN elastic cross-section will weaken the collisional damping and thus result in smaller GDR width. As shown in reference [55], in order to reproduce the experimental GDR width of ²⁰⁸Pb obtained at the RCNP, a strong medium reduction of the NN cross-section is needed. There are many parameterizations for the medium reduction of the NN cross-section [104–107], which could be dependent on density, collision energy, or isospin. As an example, we choose the FU4FP6 parameterization [107] for the medium reduction of the cross-section to calculate the strength function and width of the GDR in ²⁰⁸Pb. The FU4FP6 parameterization of the medium reduction is density-, momentum-, and isospin-dependent; it is preferred by the nucleon induced nuclear reaction cross-section data [107] and predicts a very strong in-medium reduction of NN scattering cross-sections. The strength function of the GDR in ²⁰⁸Pb from the LBUU calculation is shown in Figure 7 and compared with the RCNP data [63]. The GDR width obtained from the LBUU calculation through the full width at half maximum (FWHM) of the strength function is 4.32 MeV, which is consistent with the value of 4.0 MeV found in the RCNP experiment. However, the Skyrme pseudopotential SP6h used in the calculation overestimates the peak energy by about 1.5 MeV. Using effective interactions with a different symmetry energy slope parameter L or different nuclear effective masses can easily reproduce the correct peak energy [54]. In order to compare the shape of the strength function and the value of the width of the GDR in ²⁰⁸Pb, we shift the strength function from the LBUU calculation to match the experimental peak energy. We conclude from Figure 7 that the present LBUU method with the FU4FP6 parameterization [107] for the medium reduction of the NN scattering cross-section can well reproduce the measured shape of the strength function and the width of the GDR in ²⁰⁸Pb. It should be stressed that the FU4FP6 parameterization suggests a very strong in-medium reduction of NN scattering cross-sections, consistent with the conclusions obtained in reference [55].

FIGURE 7

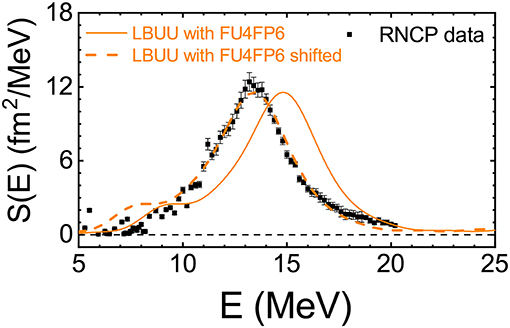
Figure 7. Strength function of the GDR in ²⁰⁸Pb after a perturbation ${Ĥ}_{\text{ex}}=\lambda {\widehat{Q}}_{\text{IVD}}\delta (t-t_0)$ with λ = 15 MeV/c obtained from the LBUU calculation using the FU4FP6 parameterization [107] for the in-medium NN scattering cross-section. The strength function measured in the RCNP experiment [63] is also shown for comparison.

5. Summary and Outlook

We have reviewed recent progress in calculating nuclear collective motions by solving the BUU equation with the LH method. In order to calculate the nuclear collective motions accurately with the BUU equation, the present LBUU framework includes the following features: (1) the smearing of the local density is incorporated in the equations of motion self-consistently through the lattice Hamiltonian method; (2) the initialization of a ground state nucleus is carried out according to a nucleon radial density distribution obtained by varying the same Hamiltonian that governs the evolution; (3) the NN collision term in the BUU equation is implemented through a full-ensemble stochastic collision approach; (4) high-performance GPU parallel computing is employed to increase the computational efficiency. The present LBUU framework with these features affords a new level of precision in solving the BUU equation.

Within the LBUU framework, it has been shown that the peak energies of the ISGMR and IVGDR obtained from the pure Vlasov calculation are consistent with those from the RPA calculation, and the full LBUU calculation can yield a reasonable GDR strength function compared with the experimental data. The peak energies can be used to extract information about the nuclear EOS, while the width of the GDR can constrain the medium reduction of the elastic NN scattering cross-section. The success of the present LBUU framework in describing the nuclear collective motions has demonstrated its capability in treating the stability of ground-state nuclei and the nuclear dynamics near equilibrium. Thus the present LBUU framework provides a solid foundation for studying long-time processes of heavy-ion reactions at low energies, such as heavy-ion fusion and multi-nucleon transfer reactions at near-barrier energies, based on solving the BUU equation. The significant effects of the collisional damping on the width of the nuclear GDR indicate that NN scatterings should play a crucial role in nuclear collective dynamics with small-amplitude oscillations.

The present LBUU framework has been shown to significantly reduce the uncertainties in transport model simulations of HICs in various respects, especially with regard to the stability of the nuclear ground-state evolution and the accurate treatment of NN scatterings as well as the Pauli blocking. This is very important for various studies of HICs based on transport model calculations, such as the extraction of the nuclear EOS and the in-medium NN scattering cross-sections. Further studies of HICs from low to intermediate energies within the present LBUU framework are in progress, and it is expected that more reliable information on the nuclear EOS, the in-medium NN scattering cross-sections, and the effective nuclear interactions will be gained in near future.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This work was partially supported by the National Natural Science Foundation of China under Contracts Nos. 11947214, 11905302, 11890714, 11625521, and 11421505, the Key Research Program of Frontier Sciences of the CAS under Grant No. QYZDJ-SSW-SLH002, the Strategic Priority Research Program of the CAS under Grants Nos. XDB16 and XDB34000000, and the Major State Basic Research Development Program (973 Program) in China under Contract No. 2015CB856904.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Pawel Danielewicz, Che Ming Ko, Bao-An Li, and Jun Su for helpful discussions, as well as Meisen Gao, Jie Pu, Xiaopeng Zhang, Chen Zhong, and Ying Zhou for setting up and maintaining the GPU servers.

References

1. Carruthers P, Zachariasen F. Quantum collision theory with phase-space distributions. Rev Mod Phys. (1983) 55:245–85. doi: 10.1103/RevModPhys.55.245

CrossRef Full Text | Google Scholar

2. Bertsch G, Das Gupta S. A guide to microscopic models for intermediate energy heavy in collisions. Phys Rep. (1988) 160:189–233. doi: 10.1016/0370-1573(88)90170-6

CrossRef Full Text | Google Scholar

3. Li BA. Neutron-proton differential flow as a probe of isospin-dependence of the nuclear equation of state. Phys Rev Lett. (2000) 85:4221–4. doi: 10.1103/PhysRevLett.85.4221

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Chen LW, Ko CM, Li BA. Determination of the stiffness of the nuclear symmetry energy from isospin diffusion. Phys Rev Lett. (2005) 94:032701. doi: 10.1103/PhysRevLett.94.032701

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Tsang MB, Zhang Y, Danielewicz P, Famiano M, Li Z, Lynch WG, et al. Constraints on the density dependence of the symmetry energy. Phys Rev Lett. (2009) 102:122701. doi: 10.1103/PhysRevLett.102.122701

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Danielewicz P, Lacey RA, Gossiaux PB, Pinkenburg C, Chung P, Alexander JM, et al. Disappearance of elliptic flow: a new probe for the nuclear equation of state. Phys Rev Lett. (1998) 81:2438. doi: 10.1103/PhysRevLett.81.2438

CrossRef Full Text | Google Scholar

7. Li BA. Probing the high density behavior of the nuclear symmetry energy with high energy heavy-ion collisions. Phys Rev Lett. (2002) 88:192701. doi: 10.1103/PhysRevLett.88.192701

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Danielewicz P, Lacey R, Lynch WG. Determination of the equation of state of dense matter. Science. (2002) 298:1592–6. doi: 10.1126/science.1078070

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Xiao Z, Li BA, Chen LW, Yong GC, Zhang M. Circumstantial evidence for a soft nuclear symmetry energy at suprasaturation densities. Phys Rev Lett. (2009) 102:062502. doi: 10.1103/PhysRevLett.102.062502

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Feng ZQ, Jin GM. Probing high-density behavior of symmetry energy from pion emission in heavy-ion collisions. Phys Lett B. (2010) 683:140–4. doi: 10.1016/j.physletb.2009.12.006

CrossRef Full Text | Google Scholar

11. Russotto P, Wu PZ, Zoric M, Chartier M, Leifels Y, Lemmon RC, et al. Symmetry energy from elliptic flow in ¹⁹⁷Au + ¹⁹⁷Au. Phys Lett B. (2011) 697:471–6. doi: 10.1016/j.physletb.2011.02.033

CrossRef Full Text | Google Scholar

12. Xie WJ, Su J, Zhu L, Zhang FS. Symmetry energy and pion production in the Boltzmann–Langevin approach. Phys Lett B. (2013) 718:1510–4. doi: 10.1016/j.physletb.2012.12.021

CrossRef Full Text | Google Scholar

13. Cozma MD, Leifels Y, Trautmann W, Li Q, Russotto P. Toward a model-independent constraint of the high-density dependence of the symmetry energy. Phys Rev C. (2013) 88:044912. doi: 10.1103/PhysRevC.88.044912

CrossRef Full Text | Google Scholar

14. Russotto P, Gannon S, Kupny S, Lasko P, Acosta L, Adamczyk M, et al. Results of the ASY-EOS experiment at GSI: the symmetry energy at suprasaturation density. Phys Rev C. (2016) 94:034608. doi: 10.1103/PhysRevC.94.034608

CrossRef Full Text | Google Scholar

15. Cozma MD. Feasibility of constraining the curvature parameter of the symmetry energy using elliptic flow data. Eur Phys J A. (2018) 54:40. doi: 10.1140/epja/i2018-12470-1

CrossRef Full Text | Google Scholar

16. Feng ZQ. Nuclear dynamics and particle production near threshold energies in heavy-ion collisions. Nucl Sci Tech. (2018) 29:40. doi: 10.1007/s41365-018-0379-z

CrossRef Full Text | Google Scholar

17. Li PC, Wang YJ, Li QF, Zhang HF. Collective flow and nuclear stopping in heavy ion collisions in Fermi energy domain. Nucl Sci Tech. (2018) 29:177. doi: 10.1007/s41365-018-0510-1

CrossRef Full Text | Google Scholar

18. Wolter H. The high-density symmetry energy in heavy-ion collisions and compact stars. Universe. (2018) 4:72. doi: 10.3390/universe4060072

CrossRef Full Text | Google Scholar

19. Baran V, Colonna M, Greco V, Di Toro M. Reaction dynamics with exotic nuclei. Phys Rep. (2005) 410:335–466. doi: 10.1016/j.physrep.2004.12.004

CrossRef Full Text | Google Scholar

20. Li BA, Chen LW, Ko CM. Recent progress and new challenges in isospin physics with heavy-ion reactions. Phys Rep. (2008) 464:113–281. doi: 10.1016/j.physrep.2008.04.005

CrossRef Full Text | Google Scholar

21. Brown BA. Neutron radii in nuclei and the neutron equation of state. Phys Rev Lett. (2000) 85:5296. doi: 10.1103/PhysRevLett.85.5296

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Typel S, Brown BA. Neutron radii and the neutron equation of state in relativistic models. Phys Rev C. (2001) 64:027302. doi: 10.1103/PhysRevC.64.027302

CrossRef Full Text | Google Scholar

23. Yoshida S, Sagawa H. Neutron skin thickness and equation of state in asymmetric nuclear matter. Phys Rev C. (2004) 69:024318. doi: 10.1103/PhysRevC.69.024318

CrossRef Full Text | Google Scholar

24. Oyamatsu K, Iida K, Koura H. Neutron drip line and the equation of state of nuclear matter. Phys Rev C. (2010) 82:027301. doi: 10.1103/PhysRevC.82.027301

CrossRef Full Text | Google Scholar

25. Wang R, Chen LW. Positioning the neutron drip line and the r-process paths in the nuclear landscape. Phys Rev C. (2015) 92:031303. doi: 10.1103/PhysRevC.92.031303

CrossRef Full Text | Google Scholar

26. Prakash M, Ainsworth TL, Lattimer JM. Equation of state and the maximum mass of neutron stars. Phys Rev Lett. (1988) 61:2518–21. doi: 10.1103/PhysRevLett.61.2518

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Lattimer JM, Pethick CJ, Prakash M, Haensel P. Direct URCA process in neutron stars. Phys Rev Lett. (1991) 66:2701–4. doi: 10.1103/PhysRevLett.66.2701

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Lattimer JM, Prakash M. The physics of neutron stars. Science. (2004) 304:536. doi: 10.1126/science.1090720

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Steiner A, Prakash M, Lattimer J, Ellis P. Isospin asymmetry in nuclei and neutron stars. Phys Rep. (2005) 411:325–75. doi: 10.1016/j.physrep.2005.02.004

CrossRef Full Text | Google Scholar

30. Lattimer J, Prakash M. Neutron star observations: prognosis for equation of state constraints. Phys Rep. (2007) 442:109–65. doi: 10.1016/j.physrep.2007.02.003

CrossRef Full Text | Google Scholar

31. Sumiyoshi K, Toki H. Relativistic equation of state of nuclear matter for the supernova explosion and the birth of neutron stars. Astrophys J. (1994) 422:700. doi: 10.1086/173763

CrossRef Full Text | Google Scholar

32. Oertel M, Hempel M, Klähn T, Typel S. Equations of state for supernovae and compact stars. Rev Mod Phys. (2017) 89:015007. doi: 10.1103/RevModPhys.89.015007

CrossRef Full Text | Google Scholar

33. Pais H, Gulminelli F, Providencia C, Ropke G. Light and heavy clusters in warm stellar matter. Nucl Sci Tech. (2018) 29:181. doi: 10.1007/s41365-018-0518-6

CrossRef Full Text | Google Scholar

34. Abbott BP, et al. GW170817: Observation of gravitational waves from a binary neutron star inspiral. Phys Rev Lett. (2017) 119:161101. doi: 10.1103/PhysRevLett.119.161101

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Zhou EP, Zhou X, Li A. Constraints on interquark interaction parameters with GW170817 in a binary strange star scenario. Phys Rev D. (2018) 97:083015. doi: 10.1103/PhysRevD.97.083015

CrossRef Full Text | Google Scholar

36. De S, Finstad D, Lattimer JM, Brown DA, Berger E, Biwer CM. Tidal deformabilities and radii of neutron stars from the observation of GW170817. Phys Rev Lett. (2018) 121:091102. doi: 10.1103/PhysRevLett.121.091102

CrossRef Full Text | Google Scholar

37. Zhang NB, Li BA. Astrophysical constraints on a parametric equation of state for neutron-rich nucleonic matter. Nucl Sci Tech. (2018) 29:178. doi: 10.1007/s41365-018-0515-9

CrossRef Full Text | Google Scholar

38. Li BA, Krastev PG, Wen DH, Zhang NB. Towards understanding astrophysical effects of nuclear symmetry energy. Eur Phys J A. (2019) 55:117. doi: 10.1140/epja/i2019-12780-8

CrossRef Full Text | Google Scholar

39. Zhou Y, Chen LW, Zhang Z. Equation of state of dense matter in the multimessenger era. Phys Rev D. (2019) 99:121301. doi: 10.1103/PhysRevD.99.121301

CrossRef Full Text | Google Scholar

40. Riley TE, Watts AL, Bogdanov S, Ray PS, Ludlam RM, Guillot S, et al. A NICER view of PSR J0030+0451: millisecond pulsar parameter estimation. Astrophys J Lett. (2019) 887:L21. doi: 10.3847/2041-8213/ab481c

CrossRef Full Text | Google Scholar

41. Miller MC, Lamb FK, Dittmann AJ, Bogdanov S, Arzoumanian Z, Gendreau KC, et al. PSR J0030+0451 mass and radius from NICER data and implications for the properties of neutron star matter. Astrophys J Lett. (2019) 887:L24. doi: 10.3847/2041-8213/ab50c5

CrossRef Full Text | Google Scholar

42. Raaijmakers G, Riley TE, Watts AL, Greif SK, Morsink SM, Hebeler K, et al. A NICER view of PSR J0030+0451: implications for the dense matter equation of state. Astrophys J Lett. (2019) 887:L22. doi: 10.3847/2041-8213/ab451a

CrossRef Full Text | Google Scholar

43. Cromartie HT, et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. (2019) 4:72–6. doi: 10.1038/s41550-019-0880-2

CrossRef Full Text | Google Scholar

44. Zhou Y, Chen LW. Ruling out the supersoft high-density symmetry energy from the discovery of PSR J0740+6620 with mass $2.14_{-0.09}^{+0.10}{M}_{\odot }$. Astrophys J. (2019) 886:52. doi: 10.3847/1538-4357/ab4adf

CrossRef Full Text | Google Scholar

45. Simenel C, Umar AS. Heavy-ion collisions and fission dynamics with the time-dependent Hartree-Fock theory and its extensions. Prog Part Nucl Phys. (2018) 103:19–66. doi: 10.1016/j.ppnp.2018.07.002

CrossRef Full Text | Google Scholar

46. Stevenson PD, Barton MC. Low-energy heavy-ion reactions and the Skyrme effective interaction. Prog Part Nucl Phys. (2019) 104:142–64. doi: 10.1016/j.ppnp.2018.09.002

CrossRef Full Text | Google Scholar

47. Urban M. Pygmy resonance and torus mode within Vlasov dynamics. Phys Rev C. (2012) 85:034322. doi: 10.1103/PhysRevC.85.034322

CrossRef Full Text | Google Scholar

48. Baran V, Colonna M, Di Toro M, Frecus B, Croitoru A, Dumitru D. Nuclear collective dynamics within Vlasov approach. Eur Phys J D. (2014) 68:356. doi: 10.1140/epjd/e2014-50171-x

CrossRef Full Text | Google Scholar

49. Zheng H, Burrello S, Colonna M, Baran V. Dipole response in neutron-rich nuclei with new Skyrme interactions. Phys Rev C. (2016) 94:014313. doi: 10.1103/PhysRevC.94.014313

CrossRef Full Text | Google Scholar

50. Smerzi A, Bonasera A, DiToro M. Damping of giant resonances in hot nuclei. Phys Rev C. (1991) 44:1713–6. doi: 10.1103/PhysRevC.44.1713

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Gaitanos T, Larionov AB, Lenske H, Mosel U. Breathing mode in an improved transport approach. Phys Rev C. (2010) 81:054316. doi: 10.1103/PhysRevC.81.054316

CrossRef Full Text | Google Scholar

52. Tao C, Ma YG, Zhang GQ, Cao XG, Fang DQ, Wang HW, et al. Isoscalar giant monopole resonance in Sn isotopes using a quantum molecular dynamics model. Phys Rev C. (2013) 88:064615. doi: 10.1103/PhysRevC.88.064615

CrossRef Full Text | Google Scholar

53. Wang K, Ma YG, Zhang GQ, Cao XG, He WB, Shen WQ. Giant dipole resonance in proton capture reactions using an extended quantum molecular dynamics model. Phys Rev C. (2017) 95:014608. doi: 10.1103/PhysRevC.95.014608

CrossRef Full Text | Google Scholar

54. Kong HY, Xu J, Chen LW, Li BA, Ma YG. Constraining simultaneously nuclear symmetry energy and neutron-proton effective mass splitting with nucleus giant resonances using a dynamical approach. Phys Rev C. (2017) 95:034324. doi: 10.1103/PhysRevC.95.034324

CrossRef Full Text | Google Scholar

55. Wang R, Zhang Z, Chen LW, Ko CM, Ma YG. Constrains on the in-medium nucleon-nucleon cross-section from the width of nuclear giant dipole resonance. Phys Lett B. (2020) 807:135532. doi: 10.1016/j.physletb.2020.135532

CrossRef Full Text | Google Scholar

56. He WB, Ma YG, Cao XG, Cai XZ, Zhang GQ. Giant dipole resonance as a fingerprint of α clustering configurations in ¹²C and ¹⁶O. Phys Rev Lett. (2014) 113:032506. doi: 10.1103/PhysRevLett.113.032506

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Aichelin J. “Quantum” molecular dynamics—a dynamical microscopic n-body approach to investigate fragment formation and the nuclear equation of state in heavy ion collisions. Phys Rep. (1991) 202:233–360. doi: 10.1016/0370-1573(91)90094-3

CrossRef Full Text | Google Scholar

58. Xu J, Chen LW, Tsang MB, Wolter H, Zhang YX, Aichelin J, et al. Understanding transport simulations of heavy-ion collisions at 100A and 400A MeV: comparison of heavy-ion transport codes under controlled conditions. Phys Rev C. (2016) 93:044609. doi: 10.1103/PhysRevC.93.044609

CrossRef Full Text | Google Scholar

59. Zhang YX, Wang YJ, Colonna M, Danielewicz P, Ono A, Tsang MB, et al. Comparison of heavy-ion transport simulations: collision integral in a box. Phys Rev C. (2018) 97:034625. doi: 10.1103/PhysRevC.97.034625

CrossRef Full Text | Google Scholar

60. Ono A, Xu J, Colonna M, Danielewicz P, Ko CM, Tsang MB, et al. Comparison of heavy-ion transport simulations: collision integral with pions and Δ resonances in a box. Phys Rev C. (2019) 100:044617. doi: 10.1103/PhysRevC.100.044617

CrossRef Full Text | Google Scholar

61. Wang R, Chen LW, Zhang Z. Nuclear collective dynamics in the lattice Hamiltonian Vlasov method. Phys Rev C. (2019) 99:044609. doi: 10.1103/PhysRevC.99.044609

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Ruetsch G, Fatica M. CUDA Fortran for Scientists and Engineers: Best Practices for Efficient CUDA Fortran Programming. Waltham, MA: Morgan Kaufmann (2013).

Google Scholar

63. Tamii A, Poltoratska I, von Neumann-Cosel P, Fujita Y, Adachi T, Bertulani CA, et al. Complete electric dipole response and the neutron skin in ²⁰⁸Pb. Phys Rev Lett. (2011) 107:062502. doi: 10.1103/PhysRevLett.107.062502

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Bonasera A, Kondratyev VN, Smerzi A, Remler EA. Nuclear dynamics in the Wigner representation. Phys Rev Lett. (1993) 71:505–8. doi: 10.1103/PhysRevLett.71.505

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Kondratyev V, Smerzi A, Bonasera A. Dynamics of a quantal system. Nucl Phys A. (1994) 577:813–28. doi: 10.1016/0375-9474(94)90946-6

CrossRef Full Text | Google Scholar

66. Lenk RJ, Pandharipande VR. Nuclear mean field dynamics in the lattice Hamiltonian Vlasov method. Phys Rev C. (1989) 39:2242–9. doi: 10.1103/PhysRevC.39.2242

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Xu HM, Lynch WG, Danielewicz P, Bertsch GF. Disappearance of fusionlike residues and the nuclear equation of state. Phys Rev Lett. (1990) 65:843–6. doi: 10.1103/PhysRevLett.65.843

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Xu HM. Disappearance of flow in intermediate-energy nucleus-nucleus collisions. Phys Rev Lett. (1991) 67:2769–72. doi: 10.1103/PhysRevLett.67.2769

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Wong CY. Dynamics of nuclear fluid. VIII. Time-dependent Hartree-Fock approximation from a classical point of view. Phys Rev C. (1982) 25:1460–75. doi: 10.1103/PhysRevC.25.1460

CrossRef Full Text | Google Scholar

70. Raimondi F, Carlsson BG, Dobaczewski J. Effective pseudopotential for energy density functionals with higher-order derivatives. Phys Rev C. (2011) 83:054311. doi: 10.1103/PhysRevC.83.054311

CrossRef Full Text | Google Scholar

71. Carlsson BG, Dobaczewski J, Kortelainen M. Local nuclear energy density functional at next-to-next-to-next-to-leading order. Phys Rev C. (2008) 78:044326. doi: 10.1103/PhysRevC.78.044326

CrossRef Full Text | Google Scholar

72. Chabanat E, Bonche P, Haensel P, Meyer J, Schaeffer R. A Skyrme parametrization from subnuclear to neutron star densities. Nucl Phys A. (1997) 627:710–46. doi: 10.1016/S0375-9474(97)00596-4

CrossRef Full Text | Google Scholar

73. Wang R, Chen LW, Zhou Y. Extended Skyrme interactions for transport model simulations of heavy-ion collisions. Phys Rev C. (2018) 98:054618. doi: 10.1103/PhysRevC.98.054618

CrossRef Full Text | Google Scholar

74. Danielewicz P, Bertsch GF. Production of deuterons and pions in a transport model of energetic heavy-ion reactions. Nucl Phys A. (1991) 533:712–48. doi: 10.1016/0375-9474(91)90541-D

CrossRef Full Text | Google Scholar

75. Cugnon J, L'Hôte D, Vandermeulen J. Simple parametrization of cross-sections for nuclear transport studies up to the GeV range. Nucl Instrum Methods Phys Res Sect B Beam Interact Mater At (1996) 111:215–20. doi: 10.1016/0168-583X(95)01384-9

CrossRef Full Text | Google Scholar

76. Xu Z, Greiner C. Thermalization of gluons in ultrarelativistic heavy ion collisions by including three-body interactions in a parton cascade. Phys Rev C. (2005) 71:064901. doi: 10.1103/PhysRevC.71.064901

CrossRef Full Text | Google Scholar

77. Danielewicz P. Determination of the mean-field momentum-dependence using elliptic flow. Nucl Phys A. (2000) 673:375–410. doi: 10.1016/S0375-9474(00)00083-X

CrossRef Full Text | Google Scholar

78. Lin H, Danielewicz P. One-body Langevin dynamics in heavy-ion collisions at intermediate energies. Phys Rev C. (2019) 99:024612. doi: 10.1103/PhysRevC.99.024612

CrossRef Full Text | Google Scholar

79. Fetter A, Walecka JD. Quantum Theory of Many-Particle Systems. New York, NY: McGraw-Hill (1971).

Google Scholar

80. Youngblood DH, Clark HL, Lui YW. Incompressibility of nuclear matter from the giant monopole resonance. Phys Rev Lett. (1999) 82:691–4. doi: 10.1103/PhysRevLett.82.691

CrossRef Full Text | Google Scholar

81. Shlomo S, Youngblood DH. Nuclear matter compressibility from isoscalar giant monopole resonance. Phys Rev C. (1993) 47:529–36. doi: 10.1103/PhysRevC.47.529

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Li T, Garg U, Liu Y, Marks R, Nayak BK, Rao PVM, et al. Isotopic dependence of the giant monopole resonance in the even-A^112−124Sn isotopes and the asymmetry term in nuclear incompressibility. Phys Rev Lett. (2007) 99:162503. doi: 10.1103/PhysRevLett.99.162503

PubMed Abstract | CrossRef Full Text | Google Scholar

83. Patel D, Garg U, Fujiwara M, Akimune H, Berg GPA, Harakeh MN, et al. Giant monopole resonance in even-A Cd isotopes, the asymmetry term in nuclear incompressibility, and the “softness” of Sn and Cd nuclei. Phys Lett B. (2012) 718:447–450. doi: 10.1016/j.physletb.2012.10.056

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Patel D, Garg U, Fujiwara M, Adachi T, Akimune H, Berg G, et al. Testing the mutually enhanced magicity effect in nuclear incompressibility via the giant monopole resonance in the 204,206,208Pb isotopes. Phys Lett B. (2013) 726:178–81. doi: 10.1016/j.physletb.2013.08.027

CrossRef Full Text | Google Scholar

85. Gupta YK, Garg U, Howard KB, Matta JT, Şenyiğit M, Itoh M. Are there nuclear structure effects on the isoscalar giant monopole resonance and nuclear incompressibility near A~90? Phys Lett B. (2016) 760:482–5. doi: 10.1016/j.physletb.2016.07.021

CrossRef Full Text | Google Scholar

86. Bertsch GF, Bortignon PF, Broglia RA. Damping of nuclear excitations. Rev Mod Phys. (1983) 55:287–314. doi: 10.1103/RevModPhys.55.287

CrossRef Full Text | Google Scholar

87. Colò G, Cao L, Van Giai N, Capelli L. Self-consistent RPA calculations with Skyrme-type interactions: the skyrme_rpa program. Comput Phys Commun. (2013) 184:142–61. doi: 10.1016/j.cpc.2012.07.016

CrossRef Full Text | Google Scholar

88. Berman BL, Fultz SC. Measurements of the giant dipole resonance with monoenergetic photons. Rev Mod Phys. (1975) 47:713–61. doi: 10.1103/RevModPhys.47.713

CrossRef Full Text | Google Scholar

89. Birkhan J, Miorelli M, Bacca S, Bassauer S, Bertulani CA, Hagen G, et al. Electric dipole polarizability of ⁴⁸Ca and implications for the neutron skin. Phys Rev Lett. (2017) 118:252501. doi: 10.1103/PhysRevLett.118.252501

PubMed Abstract | CrossRef Full Text | Google Scholar

90. Hashimoto T, Krumbholz AM, Reinhard PG, Tamii A, von Neumann-Cosel P, Adachi T, et al. Dipole polarizability of ¹²⁰Sn and nuclear energy density functionals. Phys Rev C. (2015) 92:031305. doi: 10.1103/PhysRevC.92.031305

CrossRef Full Text | Google Scholar

91. Rossi DM, Adrich P, Aksouh F, Alvarez-Pol H, Aumann T, Benlliure J, et al. Measurement of the dipole polarizability of the unstable neutron-rich nucleus ⁶⁸Ni. Phys Rev Lett. (2013) 111:242503. doi: 10.1103/PhysRevLett.111.242503

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Ryezayeva N, Hartmann T, Kalmykov Y, Lenske H, von Neumann-Cosel P, Ponomarev VY, et al. Nature of low-energy dipole strength in nuclei: the case of a resonance at particle threshold in ²⁰⁸Pb. Phys Rev Lett. (2002) 89:272502. doi: 10.1103/PhysRevLett.89.272502

PubMed Abstract | CrossRef Full Text | Google Scholar

93. LAND-FRS Collaboration, Adrich P, Klimkiewicz A, Fallot M, Boretzky K, Aumann T, et al. Evidence for Pygmy and giant dipole resonances in ¹³⁰Sn and ¹³²Sn. Phys Rev Lett. (2005) 95:132501. doi: 10.1103/PhysRevLett.95.132501

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Wieland O, Bracco A, Camera F, Benzoni G, Blasi N, Brambilla S, et al. Search for the Pygmy dipole resonance in ⁶⁸Ni at 600MeV/nucleon. Phys Rev Lett. (2009) 102:092502. doi: 10.1103/PhysRevLett.102.092502

PubMed Abstract | CrossRef Full Text | Google Scholar

95. Endres J, Litvinova E, Savran D, Butler PA, Harakeh MN, Harissopulos S, et al. Isospin character of the Pygmy dipole resonance in ¹²⁴Sn. Phys Rev Lett. (2010) 105:212503. doi: 10.1103/PhysRevLett.105.212503

PubMed Abstract | CrossRef Full Text | Google Scholar

96. Yildirim S, Gaitanos T, Toro MD, Greco V. Relativistic transport approach to collective nuclear dynamics. Phys Rev C. (2005) 72:064317. doi: 10.1103/PhysRevC.72.064317

CrossRef Full Text | Google Scholar

97. Trippa L, Colò G, Vigezzi E. Giant dipole resonance as a quantitative constraint on the symmetry energy. Phys Rev C. (2008) 77:061304. doi: 10.1103/PhysRevC.77.061304

CrossRef Full Text | Google Scholar

98. Carbone A, Colò G, Bracco A, Cao LG, Bortignon PF, Camera F, et al. Constraints on the symmetry energy and neutron skins from pygmy resonances in ⁶⁸Ni and ¹³²Sn. Phys Rev C. (2010) 81:041301. doi: 10.1103/PhysRevC.81.041301

CrossRef Full Text | Google Scholar

99. Baran V, Colonna M, Di Toro M, Croitoru A, Dumitru D. Connecting the pygmy dipole resonance to the neutron skin. Phys Rev C. (2013) 88:044610. doi: 10.1103/PhysRevC.88.044610

CrossRef Full Text | Google Scholar

100. Piekarewicz J, Agrawal BK, Colò G, Nazarewicz W, Paar N, Reinhard PG, et al. Electric dipole polarizability and the neutron skin. Phys Rev C. (2012) 85:041302. doi: 10.1103/PhysRevC.85.041302

CrossRef Full Text | Google Scholar

101. Roca-Maza X, Brenna M, Colò G, Centelles M, Viñas X, Agrawal BK, et al. Electric dipole polarizability in ²⁰⁸Pb: insights from the droplet model. Phys Rev C. (2013) 88:024316. doi: 10.1103/PhysRevC.88.024316

CrossRef Full Text | Google Scholar

102. Roca-Maza X, Viñas X, Centelles M, Agrawal BK, Colò G, Paar N, et al. Neutron skin thickness from the measured electric dipole polarizability in ⁶⁸Ni, ¹²⁰Sn, and ²⁰⁸Pb. Phys Rev C. (2015) 92:064304. doi: 10.1103/PhysRevC.92.064304

CrossRef Full Text | Google Scholar

103. Zhang Z, Chen LW. Electric dipole polarizability in Pb 208 as a probe of the symmetry energy and neutron matter around ρ 0/3. Phys Rev C. (2015) 92:031301. doi: 10.1103/PhysRevC.92.031301

CrossRef Full Text | Google Scholar

104. Lopez O, Durand D, Lehaut G, Borderie B, Frankland JD, Rivet MF, et al. In-medium effects for nuclear matter in the Fermi-energy domain. Phys Rev C. (2014) 90:064602. doi: 10.1103/PhysRevC.90.064602

CrossRef Full Text | Google Scholar

105. Li P, Wang Y, Li Q, Guo C, Zhang H. Effects of the in-medium nucleon-nucleon cross-section on collective flow and nuclear stopping in heavy-ion collisions in the Fermi-energy domain. Phys Rev C. (2018) 97:044620. doi: 10.1103/PhysRevC.97.044620

CrossRef Full Text | Google Scholar

106. Barker B, Danielewicz P. Shear viscosity from nuclear stopping. Phys Rev C. (2019) 99:034607. doi: 10.1103/PhysRevC.99.034607

CrossRef Full Text | Google Scholar

107. Ou L, He Xy. In-medium nucleon-nucleon elastic cross-sections determined from the nucleon induced reaction cross-section data. Chinese Phys C. (2019) 43:044103. doi: 10.1088/1674-1137/43/4/044103

CrossRef Full Text | Google Scholar