- 1Faculty of Mechanical Engineering, Czech Technical University in Prague, Prague, Czechia
- 2Condensed Matter Physics Department, Jožef Stefan Institute, Ljubljana, Slovenia
- 3Institute of Nanoscience and Nanotechnology, National Centre for Scientific Research “Demokritos”, Aghia Paraskevi, Greece
- 4Department of Physics, National and Kapodistrian University of Athens, Zografou, Greece
- 5Biomolecular Physics Laboratory, National Centre for Scientific Research “Demokritos”, Aghia Paraskevi, Greece
Liquid crystals hosting nanoparticles comprise a fascinating research field, ranging from fundamental aspects of phase transitions to applications in optics and photonics. Liquid-crystalline phases exhibit topological defects that can be used for assembly of nanoparticles in periodical arrays, and at the same time, the nanoparticles can increase the stability range of liquid-crystalline phases. This has been experimentally demonstrated over the past few years in the case of blue phases that are present in some strongly chiral liquid crystals. Experimental results in quantum dot-driven blue phase stabilization are presented here by means of high-resolution calorimetry and polarizing optical microscopy. It is demonstrated that quantum dots essentially stabilize the macroscopically amorphous blue phase III. There are discussed similarities and differences between the effects of spherical and anisotropic nanoparticles on blue phase stabilization; moreover, future prospects and trends in the field are addressed.
Introduction
Liquid crystals (LCs) form a fascinating class of soft materials exhibiting a plethora of mesophases between the isotropic liquid and the crystal phases. Being discovered in the end of the 19th century [1], LCs made inroads into optical display technologies in the second half of the 20th century [2]. Upon reducing temperature, LCs undergo several phase transitions along which they progressively obtain a long-range orientational and partial positional order. The competition between the incompatible structures of adjacent mesophases often results in the appearance of topological defects such as disclinations and screw and edge dislocations. In addition, LCs exhibit anisotropy in their elastic, dielectric, and optical properties. Hence, they form a multidisciplinary scaffold, where fundamental science, and envisioned applications meet [3–7]. The former consists of studies of quenched-random disorder and inclusions on symmetry-braking phase transitions [8–11], critical phenomena, and universality classes [12–16]. The latter is related to attempts for assembly and orientation of nanoparticles (NPs) [17], as well as to search of tunable photonic crystals and lasers [18, 19], soft magnetoelectrics [20–22], and metamaterials [23]. Moreover, liquid-crystalline cholesteric and blue phases comprise a testing ground for the study of active materials [24, 25], with rapidly increasing interest in physics and biology [26].
Among the most interesting liquid-crystalline phases for applications in optics and photonics are the so-called blue phases (BPs). These phases are inherently present in some strongly chiral LCs and only within a narrow temperature range (in most cases from 1 to 3 K) between the isotropic (I) and chiral nematic (N*) phases. Three such phases have been identified, denoted as blue phase III (BPIII), blue phase II (BPII), and blue phase I (BPI), upon reducing temperature. The extension of the BP range as a function of increased chirality was demonstrated in phase diagrams of racemic-chiral mixtures [27]. Their thermodynamic stability was confirmed by identifying the distinct thermal signatures of I-BPIII, BPIII-BPII, BPII-BPI, and BPI-N* transitions for cholesteryl non-anoate [28]. In the late 90s, the BP phase diagrams were revisited and the critical behavior as a function of chirality was well-understood [29, 30]. Regarding structure, BPI and BPII consist of double-twisted cylinders, with the director being parallel to the cylinder axis in the center and gradually changing from −45° to +45°, as it can be schematically depicted in Figure 1. This structure emanates from a continuous competition between two factors: the chirality and the packing topology. The double-twisted cylinders are packed in such a way that BPII and BPI exhibit three-dimensional simple cubic and body-centered cubic defect lattices, respectively [31–33]. Between these cylinders, there is no LC molecular alignment, i.e., the cylinders coexist with lines of −1/2 disclinations as seen in Figure 1. The structure of BPIII, in particular, remained elusive for many years [34]. Though it was initially considered to be locally similar to BPII [35], recent systematic theoretical work by Henrich et al. [36, 37] yields a macroscopically amorphous network of disclination lines. These lines are interconnected in BPIII and BPII, whereas they do not intersect in the case of BPI.
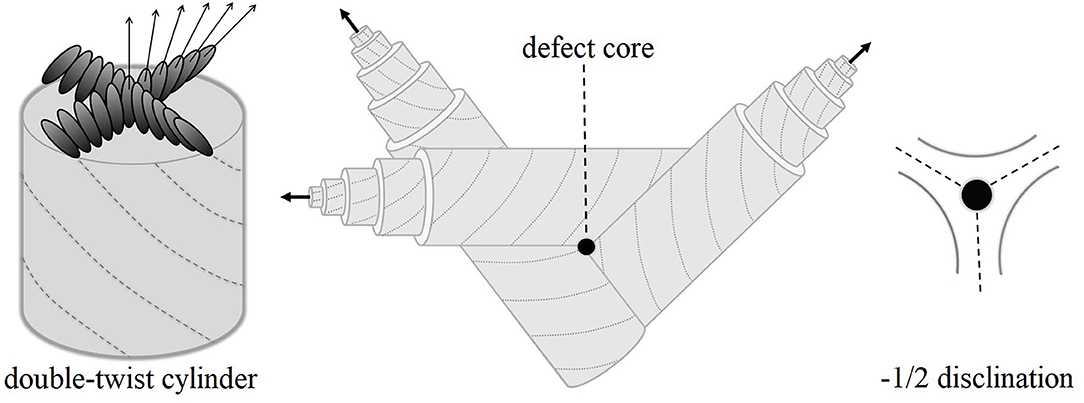
Figure 1. At the left-hand side, the molecular orientation is shown along the cross section of a double-twist cylinder of the blue phase structure. The director (marked by arrows) is parallel to the cylinder axis in the center and gradually changes toward ±45° at the periphery. Defects appear in the volume between double-twist cylinders, as seen in the center. The topology enforces −1/2 disclinations as shown at the right-hand side.
The cubic lattice of BPs with periodicity in visible wavelengths could be exploited toward the fabrication of tunable photonic crystals, as proposed by Etchegoin [38]. Following work of Cao et al. [18] reported lasing in a three-dimensional photonic-bandgap BPII sample. Nevertheless, the narrow temperature stability range of BPs remained a long-standing, unsurpassed obstacle. The envisioning of applications revived the interest of the scientific community in exploring strategies to extend the BP temperature stability range. Kikuchi et al. [39] exploited bi-continuous phase separation phenomena in LC and polymer composites that, in case of a BPI defect lattice, could drive the polymer chains in the space between the double-twist cylinders, i.e., assemble them along the disclination lines. Indeed, this work resulted in the first experimental demonstration of BP stabilization. Posterior stabilization strategies were based on mixing of chiral and non-chiral molecules [40] and fast quenching in super-cooled states [41, 42]. The use of surface-functionalized NPs is a more recent, yet very effective strategy toward expanding the temperature range of BPs. The first reports came out almost simultaneously for spherical Au nanoparticles dispersed in a LC/chiral dopant mixture [43] and CdSe quantum dots (QDs) [44, 45] dispersed in single LC compounds. Subsequent studies used additional types of spherical NPs and QDs, by varying the core composition and diameter, as well as the surface functionalization [46–52]. Apart from the stabilization effect, it has been also reported that NPs could improve the electro-optical performance of blue phase-based optical displays [53].
Experimental results are presented here on two mixtures of CdSxSe1−x quantum dots (QDs) dispersed in the chiral LC compound S-(+)-4-(2′-methylbutyl) phenyl-4′-n-octylbiphenyl-4 carboxylate), henceforth referred to as CE8. The thermal and optical properties of the mixtures have been investigated by means of high-resolution ac calorimetry and polarizing optical microscopy. It is shown that the presence of CdSSe increases the total BP range and especially promotes the BPIII stabilization. In the succeeding sections, the materials and methods are presented, followed by the presentation of experimental results and discussion with respect to other recent advances and trends.
Materials and Methods
CE8 of high purity has been purchased from Merck and exhibits all three BPs within a total range of 5 K [44]. QDs of the CdSxSe1−x core (where x = 0.5) have been synthesized in the National Center for Scientific Research “Demokritos” (Greece). They have a core diameter of 3.4 nm, and they are surface-functionalized by flexible oleyl amine and tri-octyl phosphine molecules [54]. The oleyl amine-based functionalization has proven very effective in obtaining high-quality dispersions of spherical and anisotropic NPs in LCs [44, 45, 54–57]. Two mixtures of CE8 and CdSSe QDs have been prepared, with concentrations χ = 0.01 and χ = 0.05, where χ is defined as the ratio of the mass of QDs over the total sample mass (QDs and CE8). The mixing protocol has been described in previous studies [44, 45]. High-resolution ac calorimetry and polarizing optical microscopy have been used to study the mixtures' properties.
The calorimetric apparatus at Jožef Stefan Institute (Slovenia) is home-made and fully automatized. It achieves an excellent thermal stability (better than 50 μK) and operates at slow scanning rates. This way, the samples are kept close to thermal equilibrium and the temperature profiles of heat capacity Cp(T) are accurately derived. For calorimetric measurements, quantities of ~30 mg of the mixtures are placed immediately after preparation in home-made, high-purity silver cells. A glass bead thermistor and a heater are attached to the cell prior to measurements.
Polarizing optical microscopy yields the characteristic textures of liquid-crystalline phases. The apparatus in National and Kapodistrian University of Athens (Greece) consists of a Leica DM2500P microscope equipped with a Leica DFG420 digital image-acquisition camera. An Instec HCS402 heating stage with temperature stability better than 10 mK is attached to the microscope, allowing for temperature scans. The samples were placed between glass slides of 10-μm thickness.
The combination of ac calorimetry and polarizing optical microscopy provides a solid picture for the mixtures' phase transition behavior. By checking the thermal and optical properties with two methods, upon heating and cooling, the possibility that BPs are super-cooled, i.e., thermodynamically unstable, is ruled out. Moreover, calorimetry provides robust evidence that these phases exist in bulk (thick) samples and are not induced or stabilized by the interfaces in thin samples. The latter has been recently demonstrated by means of microscopy as a function of the cell thickness, the anchoring conditions, and the effective anchoring strength [58].
Results
The Cp(T) profiles of the two mixtures, χ = 0.01 and χ = 0.05, have been obtained at the same scanning rates of 0.25 Kh−1 upon cooling from the I down to the N* phase. They are shown in Figure 2, at the middle and top layers, respectively. At the bottom layer, the Cp(T) profile of pure CE8 [44] is shown at the same temperature range for comparison. The presence of CdSSe QDs has a strong impact on the phase transition behavior of the mixtures with respect to pure CE8. In particular, a widening of the total BP range is observed, from 5.0 K for CE8 to 7.2 K for χ = 0.05. Although the increase of the total BP range is moderate, an impressive increase of the BPIII range by a factor of six times is found.
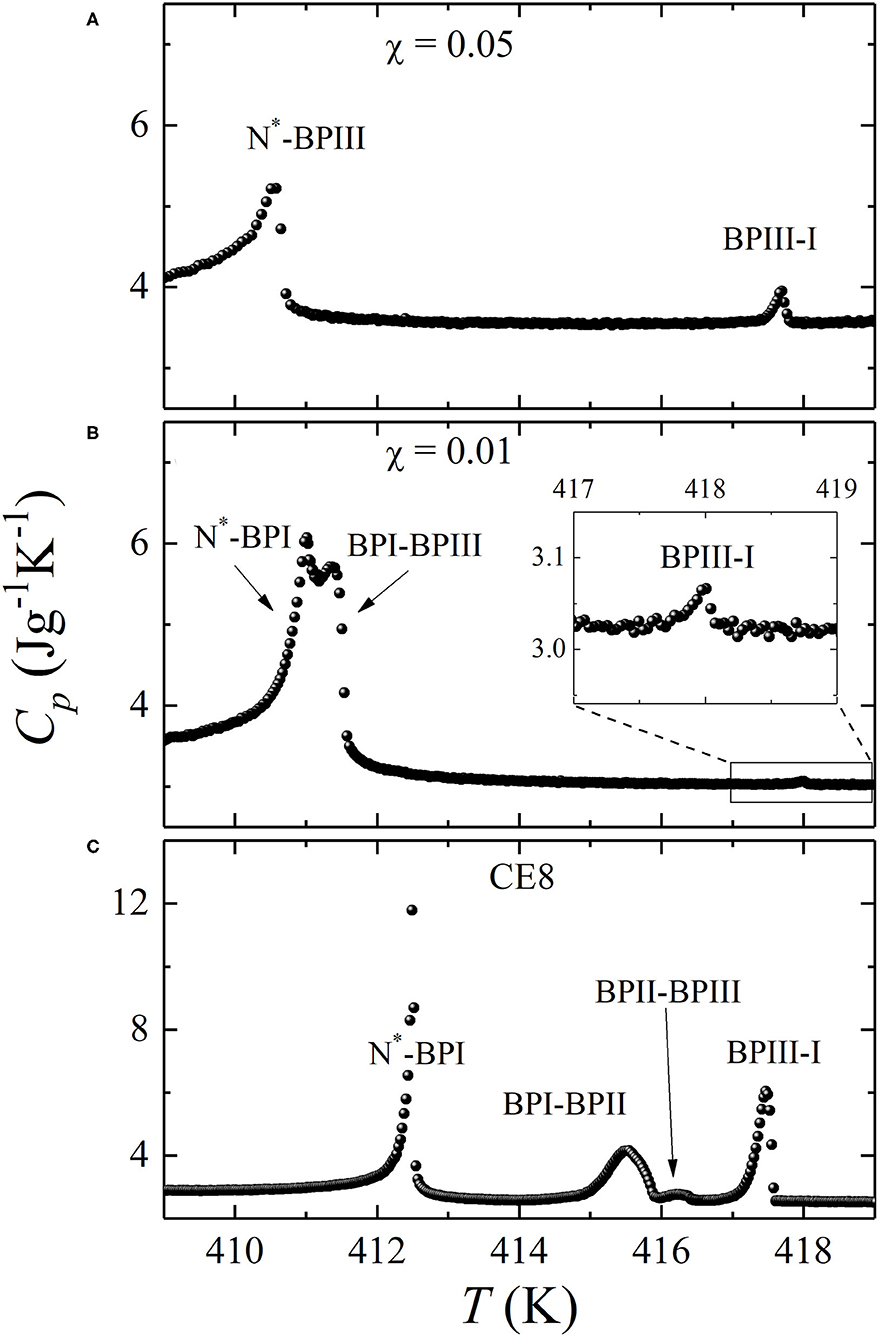
Figure 2. Heat capacity temperature profiles Cp(T) obtained by ac calorimetry for two mixtures of chiral liquid crystal CE8 and CdSSe QDs. Top layer (A): χ = 0.05. Middle layer (B): χ = 0.01. Bottom layer (C): pure CE8 (from Ref. [44]). The inset in layer (B) shows a blow-up of the temperature regime around BPIII-I anomaly, which is greatly suppressed and barely visible in the full-scale plot.
All phase transitions appear suppressed in the presence of QDs. An interesting feature is the apparent stronger suppression of I-BPIII anomaly for χ = 0.01 with respect to χ = 0.05. This does not imply any abnormality regarding the enthalpic content of phase transition behavior, taking into account that ac calorimetry in the conventional (so-call ac) mode of operation senses only the continuous part of enthalpy change. In case of first-order transitions (such as the I-BPIII) latent heat is present, being the major contribution to the total enthalpy. The latter can be in this case measured by operating the calorimeter in a different, so-called relaxation or non-adiabatic scanning mode [59]. Note that ac runs are more precise for the determination of the transition temperatures, and they have been chosen for the construction of the temperature-concentration phase diagram. Nevertheless, only the size of the anomalies obtained by relaxation runs can be used for a comparison of the total enthalpic content of first-order I-BPIII transition between pure CE8 and the mixtures. Such types of runs have not been performed, since the determination of enthalpy values is not the focus of the present work.
Another interesting feature of the phase transition behavior is that BPII is already absent at χ = 0.01. The phase sequence I-BPIII-BPII-BPI-N* of pure CE8 has given its place to I-BPIII-BPI-N* in the case of χ = 0.01. By additionally increasing the QD concentration to χ = 0.05, BPI also disappears and BPIII occupies the full temperature range of 7.2 K between the I and N* phases. Hence, the presence of CdSSe QDs strongly promotes the stabilization of BPIII and yields an I-BPIII-N* sequence, with an extended BPIII range.
In order to additionally confirm the phase sequence derived by ac calorimetry, the optical textures have been examined upon sequential heating and cooling cycles. The temperature is slowly changed, using average scanning rates from 0.1 to 0.2 Kmin−1. The images are captured at several temperatures in the transmission mode and under crossed polarizers, for the χ = 0.01 mixture. Well-reproducible foggy blue textures of BPIII and vivid turquoise-green, large-size platelets attributed to BPI appearing on both heating and cooling. Oily streaks, characteristic of the N* phase in planar anchoring conditions, are also found. All the aforementioned textures remain stable when leaving the sample for longer time scales at a fixed temperature.
In Figure 3, the temperature-concentration (T-χ) phase diagram of the CE8 and CdSSe nanocomposites is presented, based on the combined results from calorimetry and microscopy which agree well with each other. The three insets show the characteristic textures of the BPIII, BPI, and N* phases for χ = 0.01. The phase diagram clearly demonstrates that by increasing the QD concentration, the range of the amorphous BPIII structure prevails over BPII and BPI.
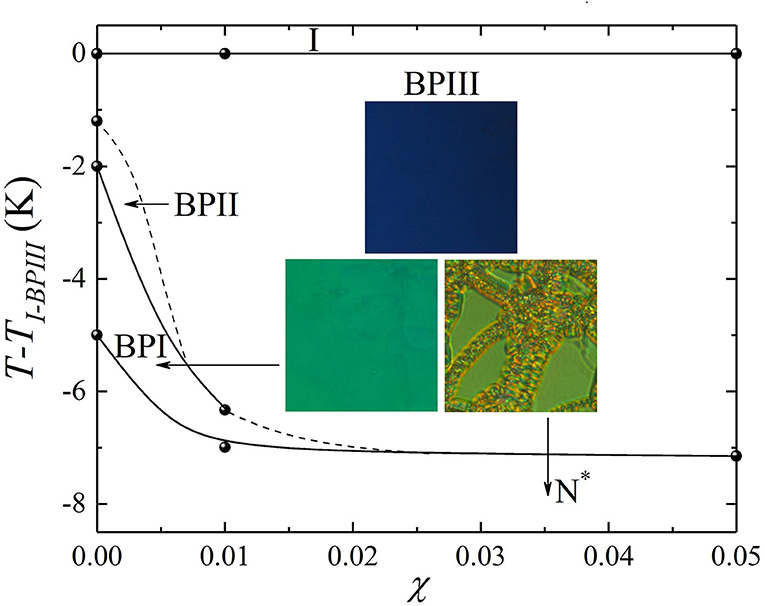
Figure 3. Temperature vs. concentration (T-χ) phase diagram obtained for CE8 and CdSSe nanocomposites, upon cooling, by ac calorimetry and polarizing optical microscopy. The I-BPIII transition temperature (TI−BPIII) has been subtracted from absolute values in all cases. The solid circles represent the phase transition temperatures obtained by ac calorimetry, and the solid lines that connect them serve as guides to the eye. The dotted lines indicate the termination of the BPIII-BPII and the BPIII-BPI phase transition lines. The images (insets) show the foggy blue BPIII texture, the turquoise-green BPI platelets and the N* oily streaks for the χ = 0.01 mixture.
Discussion
This work shows that BPII and BPI gradually disappear and BPIII prevails, exhibiting a six-fold extended range in the presence of CdSSe QDs. BPIII has been also strongly stabilized in the case of CdSe QDs of almost identical size (3.5 nm) and similar surface treatment dispersed in CE8 [44], as well as in another chiral LC compound CE6 [45]. In both these cases, BPII already disappeared for small concentrations of QDs (below χ = 0.02 for CE8 and below χ = 0.01 for CE6). However, BPI was mildly affected and remained present for higher QD concentrations than in the current work. In particular, in the case of CE8 the CdSe-driven stabilization reaches saturation in concentrations well above χ = 0.05 [44]. On the contrary, the CdSSe-driven stabilization effect of this work essentially saturates around χ = 0.01. With the LC compound being the same and the QD core size almost identical, the different impact must be related to density changes and surface functionalization. Indeed, as mentioned above, the composition of the QDs used here is CdSxSe1−x (where x = 0.5). In addition, oleyl amine binds on both Cd and S, whereas tri-octyl phosphine only on Se. Hence, the partial replacement of Se by S yields a larger coverage of the CdSSe surface with oleyl amine combined with reduced core density. The latter is reflected in slower kinetics of CdSSe QDs in the LC volume, since they sense a more viscous medium with respect to their heavier CdSe counterparts. Hence, their trapping to the defect cores is slightly less effective and the overall stabilization milder. This reveals the great importance of NP chemistry, related to the modification of core composition and surface functionalization, in their trapping efficiency.
The adaptive character of NPs is related to their size and coating; both play an important role in the NP entrapment within the cores of defects. The trapping mechanism has been originally proposed by Kikuchi et al. [39] for polymer-stabilized BPs, focusing on the energy gain when part of the defect volume is replaced by the guest (polymer) molecules. It was later on generalized for NPs [44, 60], focusing on the adaptive character of the latter that should not significantly disrupt the surrounding LC ordering. This implies that the energy gain from the defect core replacement prevails over the energy cost for non-favorable boundary conditions in the interfaces between NPs and LC molecules [61]. Both CdSSe and CdSe QDs surface-functionalized with flexible molecules are highly adaptive to the defect lattices of LC structures. Apart from stabilizing BPs, it is also shown that they induce a stable twist-grain boundary phase, characterized by screw dislocations, in the cases of CE8 [54] and CE6 LCs [61]. Au NPs with oleyl amine coating are also reported to stabilize BPIII and induce a twist-grain boundary phase in CE8 [54, 62]. Note that the aforementioned mechanism for NP assembly in the defect cores could be extended by including the contribution of saddle-splay elasticity; preliminary efforts to create a more general phenomenological model can be found in our recent study [62], and additional work is in progress. A new theoretical approach has been recently proposed by Machon and Alexander [63] and by Selinger [64] for analyzing the director deformations in liquid-crystalline phases, based on splay, twist, bend, and saddle-splay contributions in the free energy.
BP stabilization driven by spherical NPs is reported in several other studies in literature. The NP cores are composed of ZnS, Ni, MnO2, Fe3O4, and SiO2, and the sizes range from 2 nm to over 100 nm [46–52]. The effect is mostly on LC materials exhibiting BPI and, in few cases, BPII. According to theoretical predictions, BPI and BPII defect lattices could be used as matrices for large-scale, stable assembly of large (up to 100 nm) NPs that should remain unaffected by thermal fluctuations [65]. Nevertheless, most of the existing size-dependent studies [46, 48] suggest that the trapping becomes less effective and the stabilization effect milder as the NP size grows. When the size of particles becomes essentially larger, approaching the μm scale, the stabilizing effect may be associated with their assembly within the interfaces between platelets [66]. Moreover, it is worth investigating how the NPs affect the relaxation of a double-twist cylinder structure and if the larger sizes suppress the fluctuations, as theory suggests [65]. In the present ac calorimetric measurements, the frequency has been chosen to achieve a thermally thin sample, i.e., a sample without temperature gradients. In such slow timescales, the impact of QDs on the relaxation times of double-twist cylinder structures could not be assessed.
The small spherical QDs of the present and previous studies [44, 45] exhibit a minor shift of the BPIII-I transition temperature to slightly higher or lower values (depending on the QDs size, surface functionalization, and the LC host). On the contrary, large anisotropic NPs, such as graphene, laponite, and MoS2 nanosheets, systematically upshift the BPIII-I transition temperature even at minute concentrations [55–57, 67]. This trend confirmed by other studies [68, 69] is attributed to the ordering of LC molecules induced within the I phase by the large surfaces of nanosheets. It also explains why large anisotropic NPs with similar surface functionalization promote the stabilization of the more ordered BPI structure over the less ordered, macroscopically amorphous BPIII [55–57, 67].
Summary
Soft nanocomposites of LCs and NPs constitute an exciting field of ongoing research. BPs hold a prominent position among liquid-crystalline phases due to their high potential for applications [70, 71]. The defect lattices could be used for assembly of NPs in regular templates or tuned by external fields [37, 50, 71]. Among various approaches, the nanoparticle-driven BP stabilization has attracted considerable interest over the last 10 years. Spherical quantum dots and nanoparticles, as well as anisotropic nanosheets, have been tested as stabilization agents. In this study, we have shown that small spherical QDs, surface-functionalized with flexible molecules, extend the total blue phase range of CE8 and strongly increase the stability of BPIII. The outcomes of this work have been compared to other studies on QDs and other spherical and anisotropic NPs. The role of chemistry is very important since even moderate changes in the core composition and surface functionalization [56] have a noticeable impact on the stabilization effect. The results obtained so far have revealed certain trends, as well as the key mechanisms behind the BP stabilization. These mechanisms could be reformed to clearly include the saddle-splay contribution, using recently proposed mathematical formulations [63, 64]. It is anticipated that additional studies, both experimental and theoretical, will clarify the precise role of nanoparticle size, shape, core density, and coating.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
ML, MT, and GC prepared the samples, performed the calorimetric measurements, and data analysis. GC and IL performed the optical measurements. VT synthesized and provided the quantum dots. GN and ZK conceived the idea and planned the work on blue phase stabilization. GC, MD, IL, GN, and ZK discussed and interpreted the results. GC, ML, and MT have prepared the figures. The manuscript was written by GC and reviewed by all authors.
Funding
GC acknowledges the support of Project CZ.02.2.69/0.0/0.0/16_027/0008465 for Mobility of Researchers under the Operational Programme Research, Development and Education. ML and MT acknowledge the support of Project P1-0125 of the Slovenian Research Agency. GN and IL acknowledge the support of THALES Project of the Operational Strategic Plan Education and Lifelong Learning, co-financed by the European Social Fund and the State of Greece.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Reinitzer F. Beitrage zur kenntniss des cholesterins. Monatch Chem. (1888) 9:421–441. [English translation: Weiss A. Contributions to the knowledge of cholesterol. Liq Cryst. (1989) 5:7–18. doi: 10.1080/02678298908026349]
2. Heilmeier GH. Liquid-crystal display devices. Sci Am. (1970) 222:100–6. doi: 10.1038/scientificamerican0470-100
3. Poulin P, Stark H, Lubensky TC, Weitz DA. Novel colloidal interactions in anisotropic fluids. Science. (1997) 275:1770–3. doi: 10.1126/science.275.5307.1770
4. Goodby JW, Saez IM, Cowling SJ, Görtz V, Draper M, Hall AW, et al. Transmission and amplification of information and properties in nanostructured liquid crystals. Angew Chem Int Ed. (2008) 47:2754–5787. doi: 10.1002/anie.200701111
5. Humar M. Liquid-crystal-droplet optical microcavities. Liq Cryst. (2016) 43:1937–50. doi: 10.1080/02678292.2016.1221151
6. Kim DS, Copar S, Tkalec U, Yoon DK. Mosaics of topological defects in micropatterned liquid crystal textures. Sci Adv. (2018) 4:eaau8064. doi: 10.1126/sciadv.aau8064
7. Riahinasab ST, Keshavarz A, Melton CN, Elbaradei A, Warren GI, Selinger RLB, et al. Nanoparticle-based hollow microstructures formed by two-stage nematic nucleation and phase separation. Nat Commun. (2019) 10:894. doi: 10.1038/s41467-019-08702-3
8. Bellini T, Clark NA, Schaeffer DW. Dynamic light-scattering study of nematic and smectic-A liquid-crystal ordering in silica aerogel. Phys Rev Lett. (1995) 74:2740–3. doi: 10.1103/PhysRevLett.74.2740
9. Iannacchione GS, Garland CW, Mang JT, Rieker TP. Calorimetric and small angle x-ray scattering study of phase transitions in octylcyanobiphenyl-aerosil dispersions. Phys Rev E. (1998) 58:5966–81. doi: 10.1103/PhysRevE.58.5966
10. Clegg PS, Birgeneau RJ, Park S, Garland CW, Iannacchione GS, Leheny RL, et al. High-resolution x-ray study of the nematic-smectic-A and smectic-A-smectic-C transitions in liquid-crystal-aerosil gels. Phys Rev E. (2003) 68:031706. doi: 10.1103/PhysRevE.68.031706
11. Cordoyiannis G, Nounesis G, Bobnar V, Kralj S, Kutnjak Z. Confinement-induced orientational order in a ferroelectric liquid crystal containing dispersed aerosils. Phys Rev Lett. (2005) 94:027801. doi: 10.1103/PhysRevLett.94.027801
12. Halperin BI, Lubensky TC, Ma SK. First-order phase transitions in superconductors and smectic-A liquid crystals. Phys Rev Lett. (1974) 47:292–5. doi: 10.1103/PhysRevLett.32.292
13. Anisimov MA, Cladis PA, Gorodetskii EE, Huse DA, Podneks VE, Taratuta VG, et al. Experimental test of a fluctuation-induced 1st order phase transition - the nematic-smectic-A transition. Phys Rev A. (1990) 41:6749–62. doi: 10.1103/PhysRevA.41.6749
14. Garland CW, Nounesis G. Critical behavior at nematic smectic-A phase transitions. Phys Rev E. (1995) 49:2964–71. doi: 10.1103/PhysRevE.49.2964
15. Bellini T, Radzihovsky L, Toner J, Clark NA. Universality and scaling in the disordering of a smectic liquid crystal. Science. (2001) 294:1074–9. doi: 10.1126/science.1057480
16. Cordoyiannis G, Tripathi CSP, Glorieux C, Thoen J. Order of phase transitions and tricriticality in mixtures of octylocycyanobiphenyl and nonylocycyanobiphenyl liquid crystals: a high-resolution study by adiabatic scanning calorimetry. Phys Rev E. (2010) 82:031707. doi: 10.1103/PhysRevE.82.031707
17. Lagerwall JPF, Scalia G, Haluska M, Dettlaff-Weglikowska U, Roth S, Giesselmann F. Nanotube alignment using lyotropic liquid crystals. Adv Mater. (2007) 19:359–64. doi: 10.1002/adma.200600889
18. Cao WY, Muñoz A, Palffy-Muhoray P, Taheri B. Lasing in a three-dimensional photonic crystal of the liquid crystal blue phase II. Nat Mater. (2002) 1:111–3. doi: 10.1038/nmat727
19. Wang M, Zou C, Sun J, Zhang L, Wang L, Xiao J, et al. Asymmetric tunable photonic bandgaps in self-organized 3D nanostructure of polymer-stabilized blue phase I modulated by voltage polarity. Adv Func Mater. (2017) 27:1702261. doi: 10.1002/adfm.201702261
20. Reznikov Y, Buchnev O, Tereshchenko O, Reshetnyak V, Glushchenko A. Ferroelectric nematic suspension. Appl Phys Lett. (2003) 82:1917–9. doi: 10.1063/1.1560871
21. Mertelj A, Osterman N, Lisjak D, Copič. Magneto-optic and converse magnetoelectric effects in a ferromagnetic liquid crystal. Soft Matter. (2014) 10:9065–72. doi: 10.1039/c4sm01625d
22. Cordoyiannis G, Gyergyek S, RoŽič B, Kralj S, Kutnjak Z, Nounesis G. The effect of magnetic nanoparticles upon the smectic-A to smectic-C* phase transition. Liq Cryst. (2016) 43:314–9. doi: 10.1080/02678292.2015.1108464
23. Pendery JS, Merchiers O, Coursault D, Grand J, Ayeb H, Greget R, et al. Gold nanoparticle self-assembly moderated by a cholesteric liquid crystal. Soft Matter. (2013) 9:9366–75. doi: 10.1039/c3sm51736e
24. Metselaar L, Doostmohammadi A, Yeomans J. Topological states in chiral active matter: dynamic blue phases and active half-skyrmions. J. Chem. Phys. (2019) 150:064909. doi: 10.1063/1.5085282
25. Carenza LN, Gonnella G, Marenduzzo D, Negro G. Rotation and propulsion in 3D active chiral droplets. Proc Natl Acad Sci USA. (2019) 116:22065–70. doi: 10.1073/pnas.1910909116
26. Prost J, Jülicher F, Joanny J-F. Active gel physics. Nat Phys. (2015) 11:111-117. doi: 10.1038/NPHYS3224
27. Collings PJ. Chiral-racemic phase diagram of a blue-phase liquid crystal – comment. Phys Rev A. (1986) 33:2153–4. doi: 10.1103/PhysRevA.33.2153
28. Thoen J. Adiabatic scanning calorimetric results for the blue phases of cholesteryl nonanoate. Phys Rev A. (1988) 37:1754–9. doi: 10.1103/PhysRevA.37.1754
29. Kutnjak Z, Garland CW, Schatz CG, Collings PJ, Booth CJ, Goodby JW. Critical point for the blue-phase-III-isotropic phase transition in chiral liquid crystals. Phys Rev E. (1996) 53:4955–63. doi: 10.1103/PhysRevE.53.4955
30. Anisimov MA, Agayan VA, Collings PJ. Nature of the blue-phase-III-isotropic critical point: an analog with the liquid-gas transition. Phys Rev E. (1998) 57:582–95. doi: 10.1103/PhysRevE.57.582
31. Grebel H, Hornreich RM, Shtrikman S. Landau theory of cholesteric blue phases – the role of higher harmonics. Phys Rev A. (1984) 30:3264–78. doi: 10.1103/PhysRevA.30.3264
32. Dubois-Violette E, Pansu B, Pieranski P. Infinite periodic minimal-surfaces – a model for blue phases. Mol Cryst Liq Cryst. (1990) 192:221–37 (1990). doi: 10.1080/00268949008035634
33. Koistinen EP, Keyes PH. Light-scattering study of the structure of blue phase-III. Phys Rev Lett. (1995) 74:4460–3. doi: 10.1103/PhysRevLett.74.4460
34. Rokhsar DS, Sethna JP. Quasicrystalline textures of cholesteric liquid crystals: blue phase III. Phys Rev Lett. (1986) 56:1727–30. doi: 10.1103/PhysRevLett.56.1727
35. Coles H, Gleeson HF. Electric field induced phase transitions and color switching in the blue phases of chiral nematic liquid crystals. Mol Cryst Liq Cryst. (1989) 167:213–125. doi: 10.1080/00268948908037178
36. Henrich O, Stratford K, Cates ME, Marenduzzo D. Structure of blue phase III of cholesteric liquid crystals. Phys Rev Lett. (2011) 106:107801. doi: 10.1103/PhysRevLett.106.107801
37. Henrich O, Marenduzzo D. The secret of the blue fog. Phys World. (2017) 30:25–9. doi: 10.1088/2058-7058/30/4/34
38. Etchegoin P. Blue phase of cholesteric liquid crystals as thermotropic photonic crystals. Phys Rev E. (2000) 62:1435–7. doi: 10.1103/PhysRevE.62.1435
39. Kikuchi H, Yokota M, Hisakado Y, Yang H, Kajiyama T. Polymer-stabilized liquid crystal blue phases. Nat Mater. (2002) 1:64–8. doi: 10.1038/nmat712
40. Nakata M, Takanishi Y, Watanabe J, Takezoe H. Blue phases induced by doping chiral nematic liquid crystals with nonchiral molecules. Phys Rev E. (2003) 68:041710. doi: 10.1103/PhysRevE.68.041710
41. Yoshizawa A, Kogawa Y, Kobayashi K, Takanishi Y, Yamamoto J. A binaphthyl derivative with a wide range of a blue phase. J Mater Chem. (2009) 19:5759–64. doi: 10.1039/b902898f
42. Choi H, Hiruchi H, Ogawa Y, Kikuchi H. Polymer-stabilized supercooled blue phase. Appl Phys Lett. (2012) 101:131904. doi: 10.1063/1.4752461
43. Yoshida H, Tanaka Y, Kawamoto K, Kubo H, Tsuda T, Fujii A, et al. Nanoparticle-stabilized cholesteric blue phases. Appl Phys Express. (2009) 2:121501. doi: 10.1143/APEX.2.121501
44. Karatairi E, RoŽič B, Kutnjak Z, Tzitzios V, Nounesis G, Cordoyiannis G, et al. Nanoparticle-induced widening of the temperature range of liquid-crystalline blue phases. Phys Rev E. (2010) 81:041703. doi: 10.1103/PhysRevE.81.041703
45. Cordoyiannis G, Losada-Pérez P, Tripathi CSP, RoŽič B, Tkalec U, Tzitzios V, et al. Blue phase III widening in CE6-dispersed surface functionalised CdSe nanoparticles. Liq Cryst. (2010) 37:1419–26. doi: 10.1080/02678292.2010.519057
46. Dierking I, Blenkhorn W, Gredland E, Drake W, Kociuruba R, Kayser B, et al. Stabilising liquid crystalline blue phases. Soft Matter. (2012) 8:4355–62. doi: 10.1039/c2sm07155j
47. Wang L, He W, Ziao Z, Meng F, Zhang Y, Yang P, et al. Hysteresis-free blue phase liquid-crystal-stabilized by ZnS nanoparticles. Small. (2012) 8:2189–93. doi: 10.1002/smll.201200052
48. Sharma A, Worden M, Hegmann T. Nanoparticle-promoted thermal stabilization of room temperature cholesteric blue phase mixtures. Ferroelectrics. (2012) 431:154–63. doi: 10.1080/00150193.2012.684980
49. Gharbi MA, Manet S, Lhermitte J, Brown S, Milette J, Toader V, et al. Reversible nanoparticle cubic lattices in blue phase liquid crystals. ACS Nano. (2016) 10:3410–5. doi: 10.1021/acsnano.5b07379
50. He W-L, Zhang W-K, Xu H, Li L-H, Yang Z, Cao H, et al. Preparation and optical properties of Fe3O4 nanoparticles-doped blue phase liquid crystal. Phys Chem Chem Phys. (2016) 18:29028–32. doi: 10.1039/c6cp05421h
51. Liu FS, Ma GS, Zhao DY. Nickel nanoparticle-stabilized room-temperature blue-phase liquid crystals. Nanotechnology. (2018) 29:285703. doi: 10.1088/1361-6528/aabaa4
52. Hsu CJ, Huang MK, Tsai PC, Hsieh CT, Kuo KL, You CF, et al. The effects of silica nanoparticles on blue-phase liquid crystals. Liq Cryst. (2018) 45:303–9. doi: 10.1080/02678292.2017.1324645
53. Wang L, He W, Xiao M, Wang M, Yang P, Zhou Z, et al. Low voltage and hysteresis-free blue phase liquid crystal dispersed by ferroelectric nanoparticles. J Mater Chem. (2012) 22:19629–33. doi: 10.1039/c2jm34013e
54. Trček M, Cordoyiannis G, Tzitzios V, Kralj S, Nounesis G, Lelidis I, et al. Nanoparticle-induced twist-grain boundary phase. Phys Rev E. (2014) 90:032501. doi: 10.1103/PhysRevE.90.032501
55. Lavrič M, Tzitzios V, Kralj S, Cordoyiannis G, Lelidis I, Nounesis G, et al. The effect of graphene on liquid-crystalline blue phases. Appl Phys Lett. (2013) 103:143116. doi: 10.1063/1.4824424
56. Lavrič M, Cordoyiannis G, Tzitzios V, Lelidis I, Kralj S, Nounesis G, et al. Liquid-crystalline blue phase stabilization by CoPt-decorated reduced-graphene oxide nanosheets dispersed in a chiral liquid crystal. J Appl Phys. (2020) 127:095101. doi: 10.1063/1.5141930
57. Lavrič M, Cordoyiannis G, Kralj S, Tzitzios V, Nounesis G, et al. Effect of anisotropic MoS2 nanoparticles on the blue phase range of a chiral liquid crystal. Appl Opt. (2013) 52:E47–52. doi: 10.1364/AO.52.000E47
58. Trček M, Cordoyiannis G, Nounesis G, Kutnjak Z, Lelidis I. Twist-grain-boundary-A*-phase stabilization in confined geometry by the interfaces. Liq Cryst. (2016) 43:1437–47. doi: 10.1080/02678292.2016.1175675
59. Yao H, Kenji E, Garland CW. Nonadiabatic scanning calorimeter. Rev Sci Instrum. (1998) 69:172–8. doi: 10.1063/1.1148492
60. RoŽič B, Tzitzios V, Karatairi E, Tkalec U, Nounesis G, Kutnjak Z, et al. Theoretical and experimental study of the nanoparticle-driven blue phase stabilization. Eur Phys J E. (2011) 34:17. doi: 10.1140/epje/i2011-11017-8
61. Cordoyiannis G, Jampani VSR, Kralj S, Dhara S, Tzitzios V, Basina G, et al. Different modulated structures of topological defects stabilized by adaptive targeting nanoparticles. Soft Matter. (2013) 9:3956–64. doi: 10.1039/c3sm27644a
62. Gudimalla A, Lavrič M, Trček M, Harkai S, RoŽič B, Cordoyiannis G, et al. Nanoparticle-stabilized lattices of topological defects in liquid crystals. Int J Thermodyn. (2020) 41:51. doi: 10.1007/s10765-020-02631-w
63. Machon T, Alexander GP. Umbilic lines in orientational order. Phys Rev X. (2016) 6:01103. doi: 10.1103/PhysRevX.6.011033
64. Selinger JV. Interpretation of saddle-splay and the Oseen-Frank free energy in liquid crystals. Liq Cryst Reviews. (2018) 6:129–42. doi: 10.1080/21680396.2019.1581103
65. Ravnik M, Alexander GP, Yeomans JM, Žumer S. Three-dimensional colloidal crystals in liquid crystalline blue phases. Proc Natl Acad Sci USA. (2011) 108:5188–92. doi: 10.1073/pnas.1015831108
66. Draude AP, Kalavalapalli TY, Iliut M, McConnell B, Dierking I. Stabilization of liquid crystal blue phases by carbon nanoparticles of varying dimensionality. Nanoscale Adv. (2020) 2:2404–9. doi: 10.1039/d0na00276c
67. Lavrič M, Tzitzios V, Cordoyiannis G, Kralj S, Nounesis G, Lelidis I, et al. Blue phase range widening induced by laponite nanoplatelets in the chiral liquid crystal CE8. Mol Cryst Liq Cryst. (2015) 615:14–8. doi: 10.1080/15421406.2015.1066554
68. Zhang W-K, Wang X, Wang D, Yang Z, Gao H, Xing Y, et al. Blue phase liquid crystals affected by graphene oxide modified with aminazobenzol group. Liq Cryst. (2016) 43:573–80. doi: 10.1080/02678292.2015.1126862
69. Zhao YZ, Qiao X, Li KX, Ding SY, Tian SP, Ren HP, et al. Blue phase liquid crystals stabilized by graphene oxide modified with aminoalkyl group. Mol Cryst Liq Cryst. (2018) 664:1–8. doi: 10.1080/15421406.2018.1442706
70. Gandhi SS, Kim MS, Hwang JY, Chien LC. Electro-optical memory of a nanoengineered amorphous blue-phase-III polymer scaffold. Adv Mater. (2016) 28:8998–9005. doi: 10.1002/adma.201603226
Keywords: liquid crystals, blue phases, topological defects, disclination lines, nanoparticles, quantum dots
Citation: Cordoyiannis G, Lavrič M, Trček M, Tzitzios V, Lelidis I, Nounesis G, Daniel M and Kutnjak Z (2020) Quantum Dot-Driven Stabilization of Liquid-Crystalline Blue Phases. Front. Phys. 8:315. doi: 10.3389/fphy.2020.00315
Received: 12 February 2020; Accepted: 09 July 2020;
Published: 31 August 2020.
Edited by:
Giancarlo Ruocco, Center for Life NanoScience (IIT), ItalyReviewed by:
Haifeng Yu, Peking University, ChinaGiuseppe Gonnella, University of Bari Aldo Moro, Italy
Copyright © 2020 Cordoyiannis, Lavrič, Trček, Tzitzios, Lelidis, Nounesis, Daniel and Kutnjak. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: George Cordoyiannis, Z2Vvcmdpb3Mua29yZG9naWFubmlzQGZzLmN2dXQuY3o=
 George Cordoyiannis
George Cordoyiannis Marta Lavrič
Marta Lavrič Maja Trček2
Maja Trček2 Vasileios Tzitzios
Vasileios Tzitzios Ioannis Lelidis
Ioannis Lelidis George Nounesis
George Nounesis Matej Daniel
Matej Daniel