- Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
A variety of superconducting materials exhibit multi-band behavior in a form of multicomponent Fermi surfaces. By using a two-band model with a pair hopping, we explain how the interband coupling affects the physical properties of multi-band superconductors. We determine the temperature dependence of the superconducting gap and the specific heat, which strongly diverge from the BCS-type behavior. The anisotropic gap for the system with the mixed gap symmetry is found. Additionally, the spectral function and density of states are significantly modified by the inter-orbital interactions. The results obtained for different symmetries of the order parameter are in a good agreement with the experimental findings for the iron-based superconductors and other multi-band systems.
1. Introduction
The discovery of superconductivity in multi-band materials opened a period of intensive studies of these systems [1, 2]. Superconductivity in such multi-band systems was first considered within the BCS-type formulation by Moskalenko [3] and by Suhl et al. [4]. As a consequence of multi-band properties one can observe several order parameters of different magnitude [5, 6]. The multi-band nature of superconductivity was experimentally observed in many compounds such as NbSe2 [7], YNi2B2C [8], fullerities A3C60 [9], MgB2 [10], and high-temperature iron-based systems [11, 12]. In spite of numerous experimental and theoretical studies, the role of the interplay between order parameters in different bands is not well-understood and requires further studies.
Theoretical description of iron-based materials remains a challenge and the nature of pairing interactions in these compounds is still under debate [13–16]. In a standard formulation, the general two-particle on-site interaction is given by intra- and inter-orbital Hubbard repulsion, Hund's exchange, and pair hopping [17]. These interactions are generated automatically in the multiorbital models with two-body interactions using a Hubbard-type approach restricted to intrasite processes [18–20]. The pairing interaction responsible for the occurrence of superconductivity arises probably from an exchange of spin, orbital, or charge fluctuations. In a case of spin fluctuations the pairing vertex can be calculated using the fluctuation exchange approximation (FLEX) [21].
The difficulties with a correct description of iron-based superconductors are connected with a relatively large number of bands emerging at the Fermi surface [5]. Generally, the Fermi surfaces and characteristic band structure of the iron-based superconductors are the consequences of the layered structure of these compounds. In many cases the Fermi surface consists of hole- and electron-like pockets near the Γ and M points of the first Brillouin zone, respectively. Moreover, the Fermi surface strongly depends on doping [22, 23]. It can lead to the Lifshitz transitions induced by doping [24, 25], pressure [26], or external magnetic field [27]. It also modifies the physical properties of supeconductors [28], such as the pairing symmetry. Therefore, the development and investigation of various microscopic models is essential to explain the normal-state and superconducting properties, which can capture the main features of electronic structure near the Fermi level [29].
The conventional multi-band BCS-type and iron-based superconductors differ also in their symmetry of the order parameter. In conventional systems, the order parameter has the same sign on the Fermi pockets, what is observed e.g., in MgB2 [6]. However, in nearly magnetic Fe-based layered systems mediated by antiferromagnetic spin fluctuations, the s± symmetry with a sign reversal of the order parameter between different Fermi surface sheets can be favored [13, 30]. As a consequence, the unconventional properties are observed experimentally [31], e.g., in the measurements of energy gap or specific heat. These observations can provide the information about the effective interactions in each band and the symmetry of the order parameter. Therefore, it is important to investigate how different properties of the multi-band systems are affected by these microscopic quantities.
For the reasons mentioned above, in the present paper we investigate a two-band model of iron-based superconductors. We assume the coupling between bands in a form of the pair hopping interaction. The main objective of these studies is to explain how the inter-band coupling and the symmetry of order parameters influence the basic superconducting properties. For different values of the model parameters we predict and discuss the behavior of energy gap, specific heat, electron density of states and spectral function. The rest of the paper is organized as follows. In section 2, we present the model under consideration and the method of calculation. Section 3 is devoted to the numerical results and their discussion. Finally, a summary is included in section 4.
2. Model and Method
For a description of iron-based materials (in the absence of superconductivity) we choose a minimal two-orbital model [32], taking into account only two degenerated dxz and dyz orbitals in a case of the unit cell with one Fe atom. This choice is sufficient to describe the low-energy states near the Fermi level [29]. In practice, due to two Fe atoms in the unit cell, the model describes four bands in the case of the folded first Brillouin zone. The model Hamiltonian is given in a general form:
where (cαkσ) is creation (annihilation) operator of an electron in orbital α with momentum k and spin σ, whereas describes the kinetic energy of a particle changing the orbital from β to α and they are explicitly given by
The hopping integrals (t1, t2, t3, t4) = (−1.0, 1.3, −0.85, −0.85) are given in energy units of |t1|. The chemical potential is set as μ = 1.54|t1|. The band structure is given by diagonalization of the above Hamiltonian. Thus, one gets
where Eεkσ are eigenvalues of the Hamiltonian [Equation (1)] given as
where bands are labelled by index ±. This model reproduces the characteristic Fermi surfaces of iron-based superconductors [5, 22, 23] in a case of two Fe-ions in the unit cell – for the folded first Brillouin zone, shown in Figure 1B, it contains two hole-like and two electron-like pockets around the Γ' and M' points, respectively.
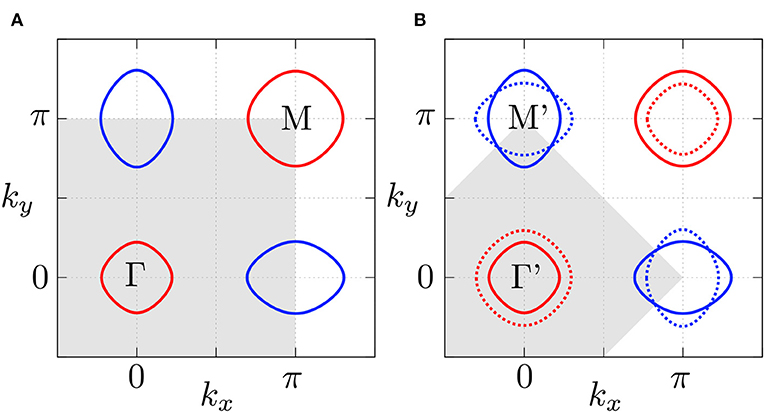
Figure 1. The Fermi surface given by the model used for a case of one (A) and two (B) Fe atoms in unit cell. Blue (red) line corresponds to the Fermi surface associated with the band ε labelled by 1 (2). In both panels the gray area shows parts of the unfolded and folded first Brouillon zone (FBZ), respectively. We also indicate the high-symmetry points of the FBZ: Γ = (0, 0) and M=(π, π) (or Γ' and M' for a case of folded FBZ).
We should notice, that the minimal two-band model used by Raghu et al. [32] concerns only dxz and dyz orbitals. In some situations, additional dxy orbital should be also included, what leads in natural way to three-orbital models [33, 34]. Inclusion of additional orbitlals can be reasonable due to some particular lattice symmetries [35, 36]. Moreover, in some crucial cases, the tight binding models based on exact DFT calculations should also be used [37–39]. More detailed description, discussion and comparison of different types of tight binding models can be found in the review by Fernandes and Chubukov [29].
2.1. Superconducting State
A realistic description of the interactions in iron–based superconductors contains all possible two-body on-site interactions between electrons in Fe(3d) orbitals (description in the real space) [19, 40]. In a general case, we can distinguish the intra- and interorbital Coulomb repulsions as well as the Hund's rule exchange and the pair hopping term [14, 29]. However, due to the spin fluctuations an interplay between these interaction terms can lead to an effective paring as a source of superconductivity [13]. For a sake of simplicity, in our calculation, we assume a phenomenological form of the interaction in the momentum space [41, 42], where the superconductivity is introduced by a BCS-like term of the following form:
where Uε < 0 denotes an effective pairing potential in the band ε (intra-band pairing), and in a general case it can be different in both bands. The pair hopping J couples both the bands (inter-band interaction). Values of Uε and J can be associated with the coupling constants in the Ginzburg-Landau theory [43, 44]. In the mean-field approximation one gets:
where χεk = χεηε(k) is the superconducting order parameter (SOP) in the band ε. Here, χε denotes the amplitude of the SOP in a given band, whereas ηε(k) are form factors describing the gap symmetry, i.e., dependence of the SOP on the momentum [42].
The relation describing the symmetry of the superconducting order parameter in the momentum space is a consequence of the paring interactions in the real space existing in the system [14]. By Fourier transforming of these interactions one can find the form factor η(k) corresponding to a given symmetry. In the standard situations the form factors are given as:
The s-wave symmetry for the iron-based superconductors is denoted by s± [13]. The form factors η(k) for different symmetries and for two dimensional momentum space are schematically shown in Figure 2. For symmetries other than s-wave, one can notice a change of a sign of η (blue and red shadows in the figure correspond to negative and positive values of η, respectively). Moreover, one can find momenta, where η = 0, which are called the nodal lines. The mutual relation between η and the shape of the Fermi surface (given in our case by the model) leads to an occurrence of the nodal lines in the superconducting gap at the Fermi surface [e.g., Figures 2A,C,D].
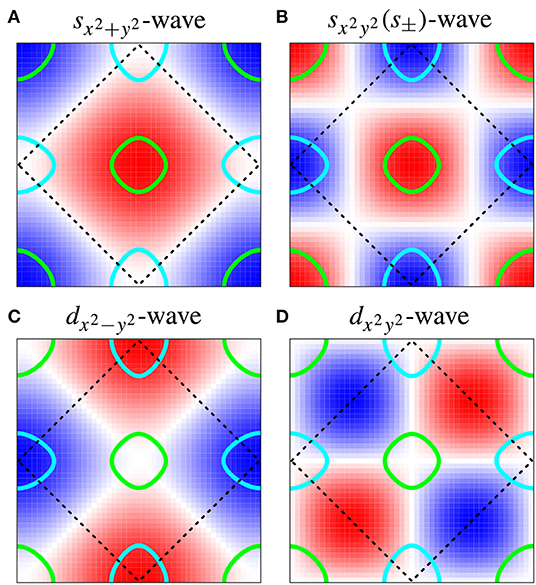
Figure 2. The comparison of different symmetries of the superconducting order parameter (in the momentum space kx × ky): (A) s-wave, (B) s- (s±)-wave, (C) d-wave, (D) d-wave. Blue and red regions denote negative and positive values of the form factor η(k) for a given symmetry, whereas nodal lines are white. The Fermi surfaces of the iron-based superconductors in the model used are also shown - cyan and green lines correspond to the electron-like and hole-like pockets, respectively.
The basic possible symmetries of the SOP are mentioned above, while the mixed symmetries of the gap are discussed in section 3.5 (cf. also section 3.4). We should also notice, that in cases investigated in the present work, values of Uε and J, as well as the ratio between them, are chosen in such a way to have different ratios between amplitudes of the order parameter χε in different bands ε (cf. Table 1 or Figures 3, 4).
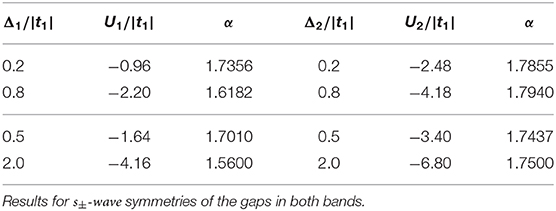
Table 1. Values of the pairing interaction Uε for chosen gaps Δε at T = 0 and fitted values of α in Equation (13), describing temperature dependence of the superconducting gap in the absence of the pair hopping coupling (J = 0).
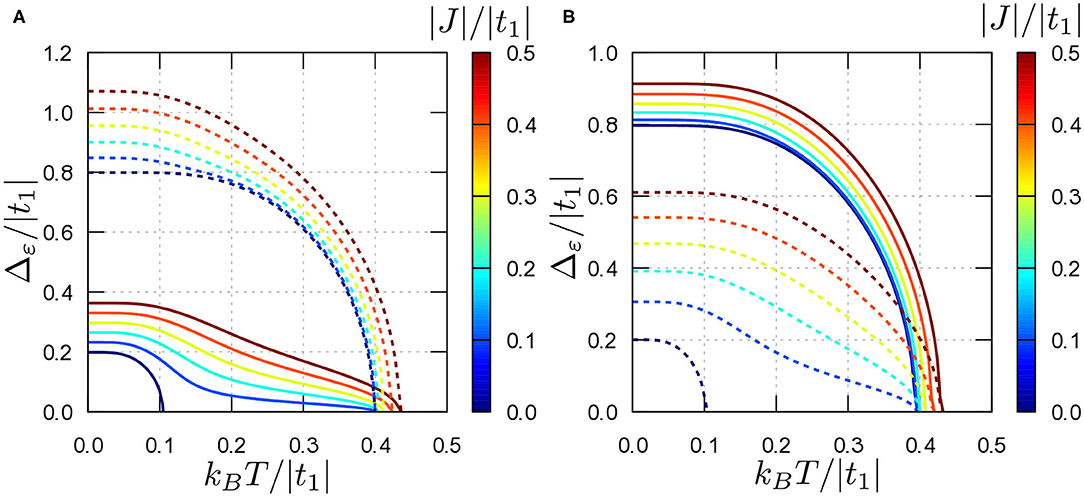
Figure 3. Superconducting energy gap as a function of temperature T for different values of the pair hopping J (scale on the left, J = 0.0, 0.1, 0.2, 0.3, 0.4, 0.5, respectively). Solid (dashed) lines denote the gaps in 1st (2nd) band. Results for (Δ1; Δ2) equal (0.2;0.8) and (0.8;0.2) are presented in (A,B), respectively (cf. Table 1).
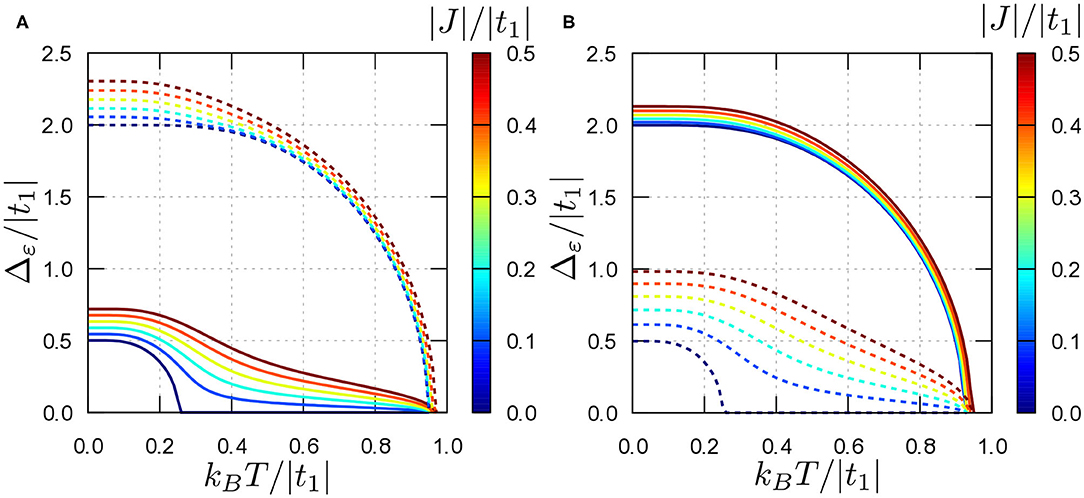
Figure 4. The same as in Figure 3, but for (Δ1; Δ2) equal (A) (0.5;2.0) and (B) (2.0;0.5) (cf. Table 1).
The full Hamiltonian in the Nambu notation is rewritten in the form:
with
where are the Nambu spinors. The Hamiltonian (Equation 5) can be diagonalized by the unitary Bogoliubov transformation:
Then, the full Hamitonian H can be rewritten in a diagonal form: , where the quasiparticle spectrum in the superconducting state takes a BCS-like form:
with the transformation's coefficients:
One needs to be aware that the non-zero pair hopping coupling J between both bands leads to an effective SOP in a band ε = 1, 2 (last term in Equation 8) given by:
Theoretical description of the interaction in the momentum space is formally given by the form factor ηε(k). As we know, one of the most important experimental manifestation of the superconductivity is the energy gap in the density of state (DOS), typically defined as a distance between two coherence peaks. Because only the effective SOPs at the Fermi surface (FS) have a real impact on the gap in the DOS, the superconducting gap 2Δε depends on a maximal value of for the momentum k at the FS of the ε band:
We will show numerically that this definition is in a good agreement with the DOS properties (cf. sections 3.3, 3.4).
Finally, the grand canonical potential is given by Ω≡−kBTln (Tr[exp(−H/kBT)]) and
whereas the equilibrium values of the variational parameters χε at a given temperature T are defined by the global minimum of Ω.
3. Numerical Results and Discussion
The ground state of the system can be obtained from a minimization of the grand canonical potential Ω (Equation 12) with respect to the SOP amplitude χε in both bands ε, at fixed values of other parameters. The calculations have been performed in the momentum space using a square lattice grid kx × ky = 300 × 300 and periodic boundary conditions, with the help of the graphic processor unit (GPU) acceleration described in [45]. Such a dense k-point grid strongly reduces the finite-size effects [46]. In the next sections, we present and discuss the temperature dependence of the gaps (section 3.1) and specific heat (section 3.2). In these sections we chose the s±-wave gap symmetry in both bands, what corresponds to the standard assumption for the iron-based superconductors. Additionally, for the chosen model parameters we study the gap anisotropy and spectral functions for the cases of the same and different gap symmetry in each band (sections 3.3, 3.4, respectively).
3.1. The Temperature Dependence of the Effective Superconducting Gaps
We start from the description of the temperature dependence of the effective superconducting gap in two cases of different values of gaps in each band (the specific values of model parameters are given in Table 1). We compare results for the fixed ratio between gaps in both bands obtained in two cases: (i) of the relatively small gaps (weak coupling) and (ii) large gaps (strong coupling). The chosen ratio corresponds to the typical relation between gaps in iron-based superconductors (examples of those materials will be described in the subsequent paragraphs). Numerical results for these cases are shown in Figures 3, 4, respectively. Here, we assume the s±-wave symmetry of the superconducting gap in both bands. This assumption corresponds to a typical situation considered in the iron-based materials.
In the absence of coupling between the bands (J = 0) we can find two independent transition temperatures. The temperature dependencies of the superconducting gap Δε(T) in each band show a standard BCS behavior as expected from the mean-field theory (cf. the curves for J = 0 in Figures 3, 4). In this case, the gap value as a function of temperature can be interpolated as [47]:
where α is a constant (α = 1.74 in the weak coupling limit, i.e., in the BCS theory) [48]. The fitted values of α for the cases considered in this work are also collected in Table 1. For the first band one observes an increasing deviation from the BCS value with increasing U1, while in the second band the value of α does change only slightly, even for large U2. We should have in mind that the BCS formula (13) has been defined for the isotropic s-wave superconductivity, while presented numerical results correspond to the s±-wave gap symmetry in both bands, what can be the source of the disagreement with the BCS value of α. Δε(T) and Tc are associated not only with the pairing interaction Uε and symmetry of the SOP [given a priori by the form factor ηε(k)] but also with the band filling nε. It should be noted that the bands of considered model have different widths (half-widths: D1≃1.5|t1|, D2≃6|t1|, D2/D1≃4 [32, 49]). Different filling in both bands and band widths can also influence the value of α.
For a non-zero inter-band coupling (J ≠ 0) only a single transition from the superconducting to normal phase occurs in the system. At the transition temperature Tc both gaps Δ1 and Δ2 as well as the SOP amplitudes χ1 and χ2 go to zero continuously. Tc is rather close to the value of the transition temperature for the band with the larger gap. The lower transition temperature (connected with the band with the smaller gap) disappears. In the case of J ≠ 0, a deflection of Δε(T) from its typical BCS-like temperature dependence (13) is clearly visible (cf. also [4, 50]). The deflection is larger in the band with the smaller gap, while in the band with the larger gap it is almost not noticeable (apart from the fact that it is increased by J ≠ 0)—compare Figures 3, 4. Notice also that Δε(T) (in the band with the small gap) changes its curvature at the intermediate temperatures (if J is relatively small—cf. Figures 3A,B), whereas in the other band Δε(T) shows its typical BCS behavior. Additionally, we notice a relatively small increase of the critical temperature with increasing J. This change is more pronounced when J is strongly enlarged.
Similar deflection of the gap from the BCS-like shape has been observed experimentally for, e.g., 111 [51], 122 [52], and 1111 [53] families of the iron-based superconductors (in a more realistic three band model, there is the pair of leading bands with similar but unresolved gaps coupled by spin fluctuations and the weakly coupled third band [54, 55]) as well as in other multi-band superconductors such as PuCoGa5 [56], (Li1−xFex)OHFeSe [57], LnOFeAs [58], Sn(Pb)Mo6S8 [59], or classical two-band MgB2 [60–63]. In a case of MgB2 one has detected also a similar character of the interplay between intra- and inter-band quantities, which has been observed in a temperature dependence of the critical Josephson currents from one band to the other of the MgB2–insulator–MgB2 tunnel junctions [61, 64], or in a more general case of the two–band Josephson junction [65].
3.2. Specific Heat
Expanding the approach described in [66], we find numerically the specific heat for the multi-band system with the equilibrium values of the variational parameters χε [67]. From the grand canonical potential Ω(χε) (Equation 12), we determine the entropy as S = −dΩ/dT and the specific heat as C = −T∂2Ω/∂T2 (at fixed temperature T). Thus, the entropy can be formally rewritten as:
where the subscript e labels the equilibrium values of the SOP amplitudes χε. Because the system is in the state corresponding to the global minimum of Ω, we have ∂Ω/∂χε|e = 0 for any band ε. As a consequence, we obtain:
where f(ω) = 1/(1+exp(ω/kBT)) is the Fermi-Dirac distribution. In a similar way one can find the specific heat as . However, one needs to remember that the SOP depends on temperature in a non-trivial way, as it has been described in the previous section.
The numerical results of the specific heat C are shown in Figure 5 (similarly as previously we assume the s±-wave symmetry of the superconducting gap in both bands). In each of the presented cases, in the absence of pair hopping coupling J = 0 (dashed thin black lines) one gets two finite jumps of C, what is a consequence of the existence of two phase transitions from the superconducting to normal phase in each band at two different Tc, separately.
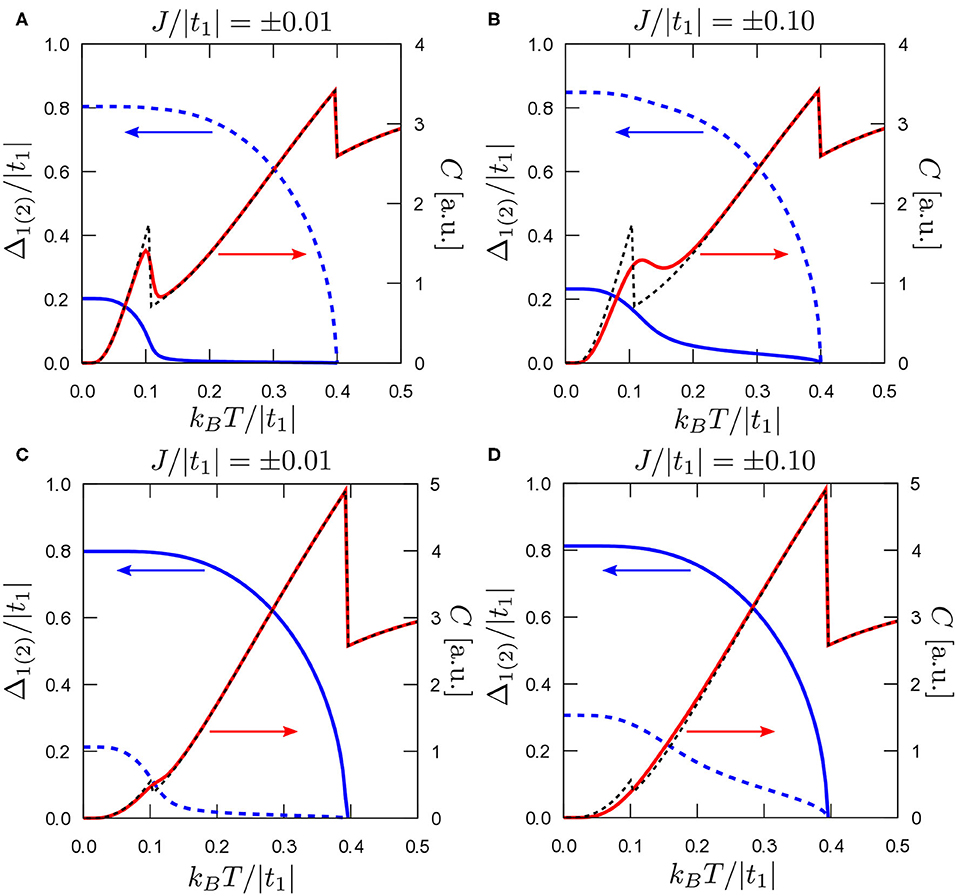
Figure 5. Temperature dependence of the superconducting gap Δε (blue lines) and the specific heat C (red lines). Solid (dashed) blue lines show superconducting gap Δε in the first (second) band. For a comparison also C for J = 0 is shown (dashed black line). Results for different values of pair hopping coupling |J| = 0.01, 0.1 (as labeled) in two cases of (Δ1; Δ2): (0.2;0.8) and (0.8;0.2) (A–D, respectively; cf. Table 1).
Non-zero J leads to a deflection with respect to the non-coupled case, which is relatively well visible near the first phase transition, i.e., that at lower temperature in the non-coupled case. Moreover, this deflection is greater for J larger than the average pairing in the system, what is well visible in Figures 5B,D. For (Figures 5A,C), the deflection is well visible only near the first phase transition in the non-coupled case (at lower temperature), whereas at temperatures near the phase transition, where the superconductivity vanishes in the system, results for J = 0 and J ≠ 0 are not distinguishable. Obviously the heat capacity in the normal phase is not dependent on J. Similar behavior has been described theoretically using α model e.g., in MgB2 [68–70], where interactions are described by the electron-phonon coupling.
The behavior of heat capacity observed here was found experimentally in many multi-band materials like iron-based superconductors from 11 [71, 72], 111 [73–75], or 122 family [52, 76–87], MgB2—classical two band superconductor [88] and many others (e.g., 2H-PdxTaSe2 [89], Lu2Fe3Si5 [90] or NbS2 [91]). One needs to stress that the unconventional superconductors (with the gap symmetry other than s-wave) is characterized by a different dependence of C vs. T/Tc.
3.3. The Spectral Functions for Iron-Based Superconductors (Realistic Case of Both Bands of s±-Wave Symmetry)
At the beginning, let us start from a definition of the spectral function, as a tool to study superconducting systems. This theoretical quantity is important from experimental point of view due to its correspondence to the angle-resolved photoemission spectroscopy (ARPES) results [92]. Additionally, it is worthwhile to mention that the shape of the gap at the Fermi surface has an important influence on the spectral function and the density of states in the superconducting state.
Firstly, we define the Green function in the form Ĝ(ω) = 1/(ω−H), and . Formally, it can be rewritten in the form:
where matrix ℍεk is given by Equation (6). Then we define the spectral function as and the DOS as . Using an expression (Equation 7) for electron annihilation and creation operators in the language of the Bogoliubov quasiparticle operators we can find [92, 93]:
where δ(ω) is the Dirac delta function. Numerically δ(ω) is approximated by ζ/[π(ω2 + ζ2)], with the damping parameter ζ taken as 0.01. Coherence factors of the Bogoliubov quasiparticles and are nontrivial functions of the SOP (Equation 9).
In the absence of the interactions (i.e., U1 = U2 = 0 and J = 0), the spectral function reproduces the non-interacting band structure of the system. It consists of two branches forming the FSs around X and Y points (the first band) and around Γ and M points (the second band). In our case the non-interacting spectral functions (Figure 6B) are in a good agreement with the band structure of the mentioned model [32, 49]. As a consequence of the absence of superconductivity, we do not observe any gap at the Fermi level (Figure 6A). The total DOS is a sum of the DOSs in the bands and this result well agrees with the previous studies [49, 94].
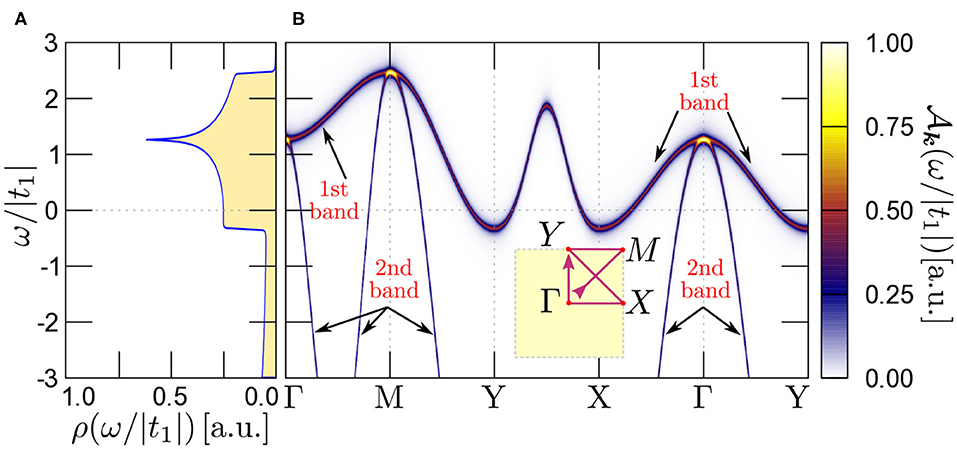
Figure 6. The density of states ρ(ω) (A) and spectral function (B) along high symmetry directions (show in inset) in the absence of superconductivity.
The temperature dependence of the gap and specific heat presented in previous sections (sections 3.1, 3.2, respectively), do not changes qualitatively for other gap symmetries. Here, we will discuss in detail the case when gaps in both bands have the s±-wave symmetry. Similarly to the previous analyses, we have chosen the s±-wave gap symmetry, which is a characteristic feature of many iron-based superconductors.
The results for the spectral functions are shown in Figure 7. As a consequence of nonzero pairing interaction, which leads to particle-hole mixing [92, 95], we observe typical BCS behavior of the band branches around the Fermi level. In the DOS we can distinguish coherent peaks corresponding to the superconducting gaps Δ1 and Δ2. This feature is indeed independent of the chosen model parameters (cf. upper and lower panels). As it was written previously in section 3.1, increasing J leads to larger values of the gaps. This effect of J ≠ 0 is also present for non-isotropic nodeless gaps (what is also well visible in Figure 8).
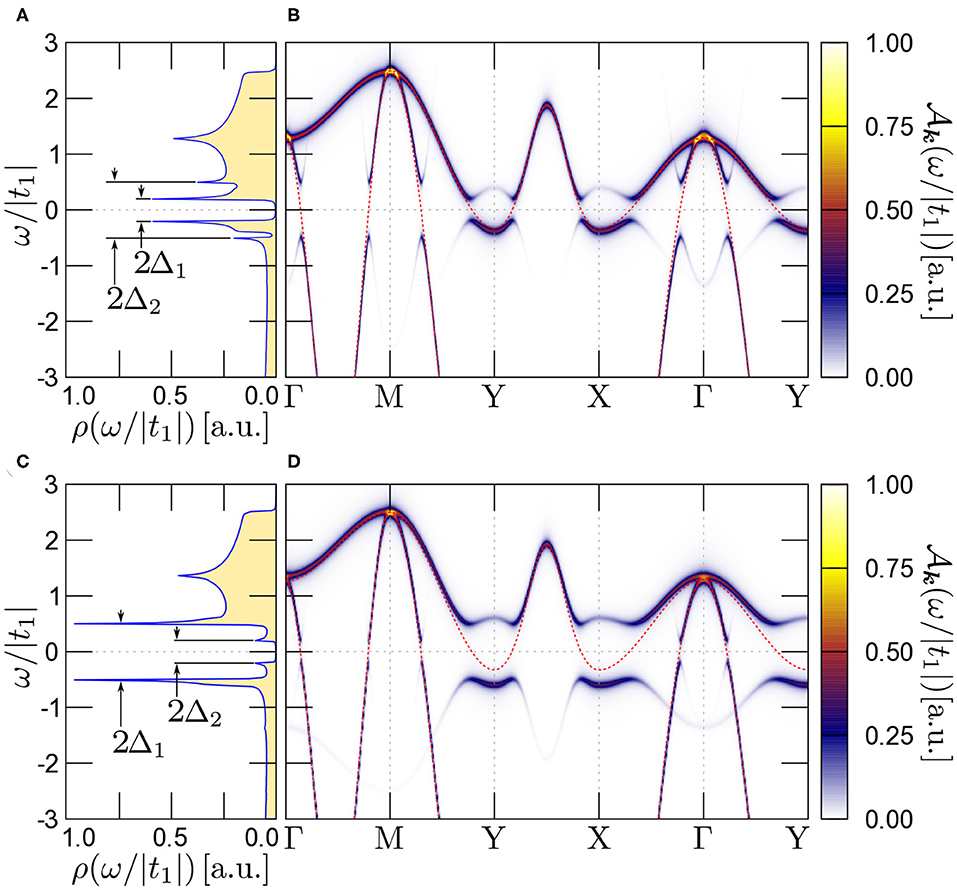
Figure 7. Density of states ρ(ω) [left panels: (A,C)] and spectral function along the high symmetry directions [right panels: (B,D)] in the presence of superconductivity with the s±-wave symmetry in both bands. Results for (Δ1; Δ2) equal to (0.2;0.5) [the top panels: (A,B)] and (0.5;0.2) [the bottom panels: (C,D)] at T = 0 and in the absence of the pair hopping coupling (J = 0). The dashed red lines corresponds to the results in the absence of superconductivity presented in Figure 6.
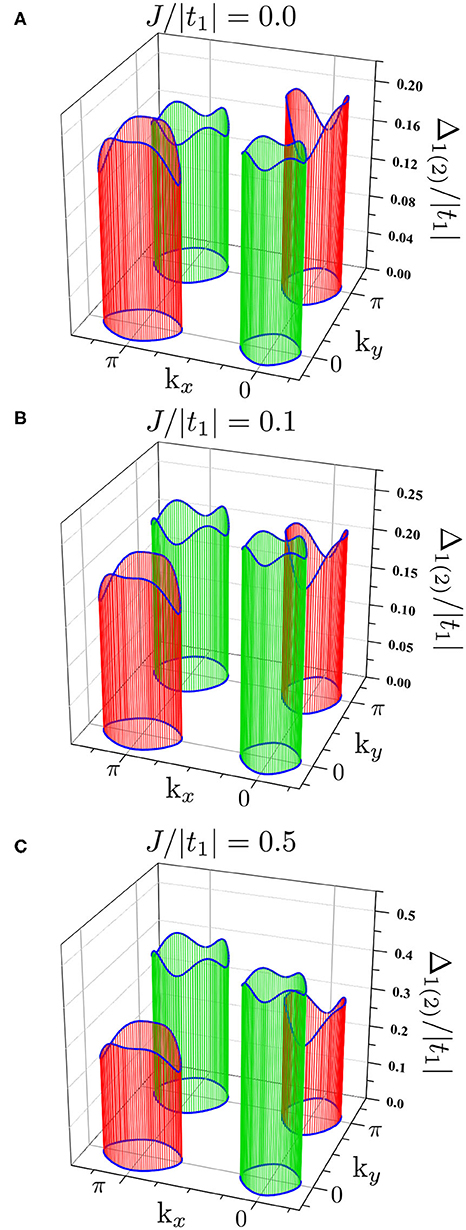
Figure 8. The momentum dependence of the superconducting gap (at the Fermi level) in the first (around X and Y points—red lines) and second (around Γ and M points—green lines) band. Results for s±-wave symmetry in both bands (and for (Δ1; Δ2) equal to (0.2;0.2) at T = 0) for different values of the pair hopping coupling: J/|t1| = 0.0 (A), J/|t1| = 0.1 (B), and J/|t1| = 0.5 (C).
The numerical results of gap anisotropy (i.e., the momentum dependence of the energy gaps at the Fermi level) are shown in Figure 8. In the absence of the pair hopping (J = 0), in both bands one can observe the anisotropic gaps (Figure 8A). Increasing J leads only to the modification of the gap values in both bands (Figures 8B,C) without changing the “symmetry” in both bands.
3.4. Spectral Functions in the Case of Bands With Different Gap Symmetry (s- and d-Wave Symmetries)
Theoretically, we can assume that a few gaps with different symmetries can exist in a superconducting material. As a consequence, for J ≠ 0 one can find interesting features of the DOS and the untypical anisotropies of the gaps at the Fermi surface. Now, we will discuss the case when the gap in the first band is of s-wave symmetry and the gap in the second band is of d-wave symmetry (J ≠ 0 mixes the gap symmetries). Here we do not consider the s±-wave symmetry, for better description of effects of one band with strongly anisotropic gap on the second band with constant gap. The gap in the band with d-wave symmetry exhibits nodal points and thus the mutual relations between nodal and nodeless gaps are investigated.
The results of spectral function are shown in Figure 9. First, we will discuss the case in the absence of pair hopping coupling (top panels). In the first band we can find well visible gap structure, while in a second band as a consequence of the nodal lines, in some regions along the high symmetry directions, we can find places without the gap (shown by red arrows in Figure 9B). It has a direct impact on the DOS (Figure 9A)—we can find a conventional s-wave gap structure [96] and second non-empty gap with a characteristic -shape (similar like in the case of d-wave high temperature superconductors [97–99]).
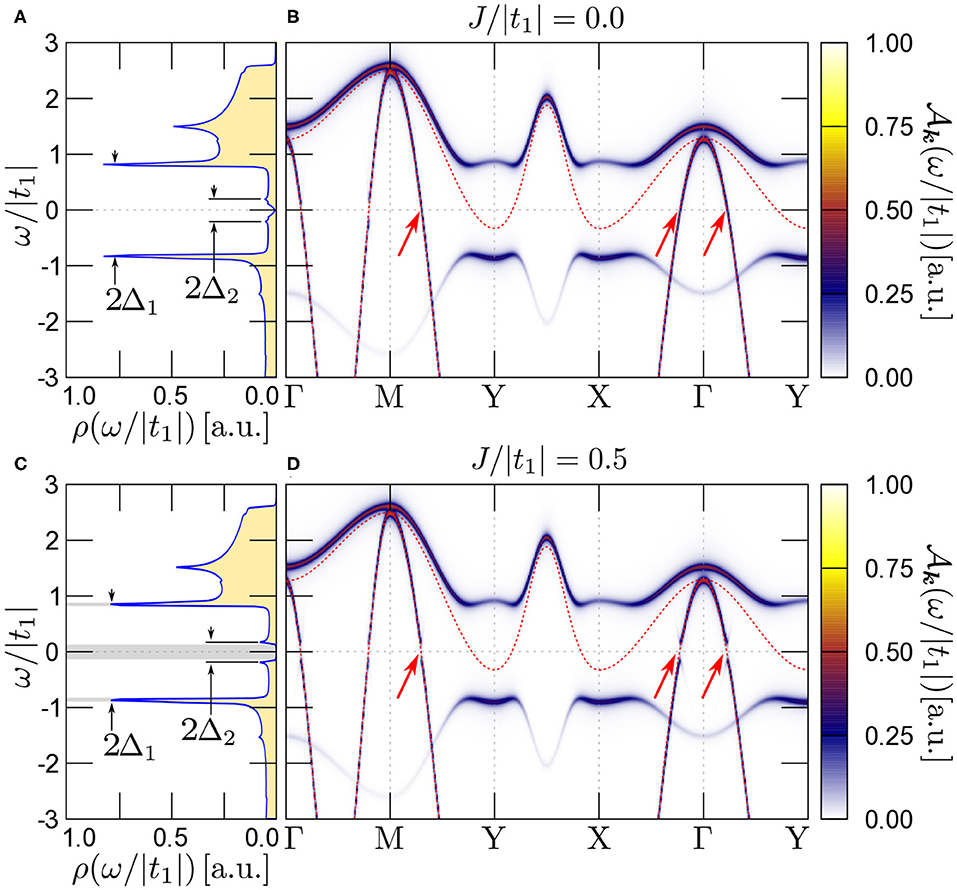
Figure 9. Density of states ρ(ω) [left panels: (A,C)] and spectral function along the high symmetry directions [right panels: (B,D)] in the presence of superconductivity. In the first (second) band the superconducting gap is of the s-wave (d-wave) symmetry. Results for (Δ1; Δ2) equal to (0.8;0.2) at T = 0 in the absence [(A,B), J = 0] and the presence [(C,D), J/t1 = 0.5] of the pair hopping coupling J. The dashed red lines corresponds to the results in the absence of superconductivity presented in Figure 6. Red arrows show places, where the coupling J between bands opens additional gaps [cf. (B,D)].
As we have shown in section 3.3, increasing J leads to the change of the gap shape in the momentum space. For the chosen symmetry (conventional s-wave symmetry and d-type symmetry with nodal lines), the gap opening is well visible along the nodal lines (shown by red arrows in Figure 9D). As a consequence, we can observe also modification of the gap structures in the DOS—initially non-empty small gap is modified by the part of the isotropic symmetry and it leads to opening of the conventional gap (marked by the gray are in Figure 9C).
The momentum dependence of the superconducting gap for the considered case are shown in Figure 10. For J = 0, in the first band the gap is isotropic (red lines), while in the second band the gap is anisotropic (green lines) with the nodal lines (Figure 10A). Similarly as in the previous case, increasing J leads to the modification of the gap values. However, due to the different symmetries, the gaps change also their shapes (Figures 10B,C). Due to J ≠ 0 initially isotropic gap in the first band is modified by the anisotropic gap in the second band and vice versa. This is particularly well visible for the second band (green lines), where the influence of J results in vanishing of the gap in some parts of the FS (shown by arrow in Figure 10C).
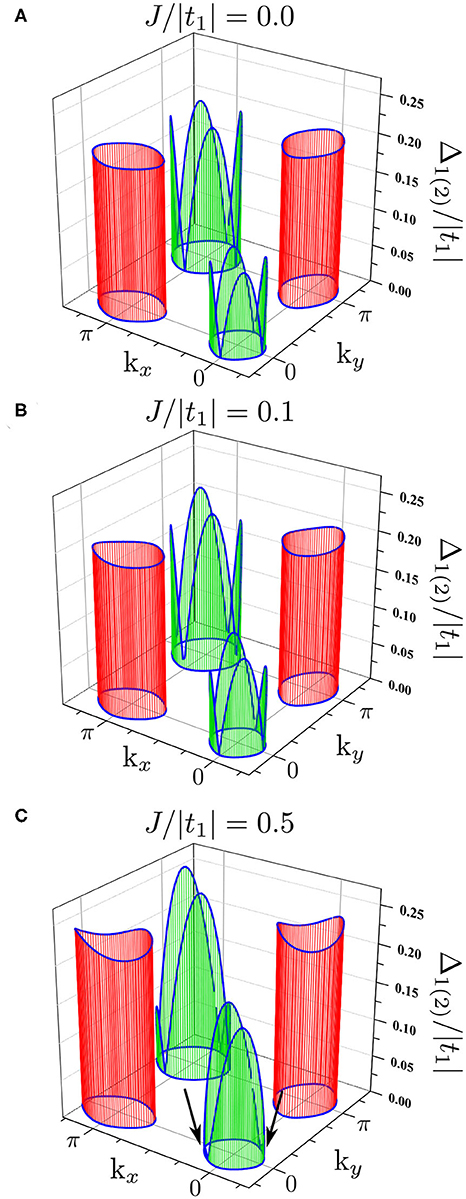
Figure 10. The same as in Figure 8 for two different symmetries of the gap: the s-wave and d-wave symmetries in the first and second band, respectively. Results for (Δ1; Δ2) equal to (0.2;0.2) at T = 0 for different values of the pair hopping coupling: J/|t1| = 0.0 (A), J/|t1| = 0.1 (B), and J/|t1| = 0.5 (C).
Mutual interplay between two gaps with different symmetries can be important for a realization of a gap anisotropy in multi-band materials like iron-based superconductors that have been observed in these compounds [100–104]. In these materials the results similar to those shown in Figure 10 have been observed experimentally. Moreover, the results presented here reveal the situation when one band has a nodal line in the gap structure. Results, similar to those presented for anisotropic gaps, have been also found in other theoretical studies using the fluctuation exchange approximation (FLEX) [105–110] or ab initio calculations [111]. However, it is possible to change a nodal gap into nodless one by disorder [112].
3.5. Additional Remarks and Comments
One should be aware that the structure of the DOS between the coherence peaks can be different in cases of nodal and nodeless symmetry [113, 114]. In the case of the s-wave symmetry, we observe a full-gaped structure. Any additional anisotropy of the gap symmetry (e.g., in a case of the s±-wave) leads to emergence of additional structure around the coherence peaks. Finally, for the symmetry with nodal lines we observe the (mentioned) -shape DOS structure. From a shape of the in-gap states in the DOS that can be experimentally observed by, e.g., the scanning tunneling microscopy (STM) [115], one can deduce the information about the gap symmetry. Similarly like in the cuprates [116], the gap in the presence of disorder strongly depends on a impurity configuration. This effect can be also observed in the iron-based materials and can lead to the modification of the double-gap structure of the DOS [113, 117].
The experimental results indicate the existence of the two anisotropic s-wave gaps in 11 [118–120] or 122 family compounds [113, 120–122], (Li1−xFex)OHFeSe [57], SmFeAsO0.9F0.1 [123]. However, the interplay of coherence peaks in the DOS shows an existence of some kind of interaction between the bands [124], what can be visible as the disappearance of the double-gap structure of the DOS. Similar behavior can be also observed in MgB2 [125, 126], where the interplay between two (conventional) gaps in the DOS occurs.
We should also have in mind the possibility of mixing gap symmetries other than that investigated in section 3.4, e.g., like s+id symmetry. This scenario was firstly proposed in a context of the cuprates by Ruckenstein et al. [127] and by Kotliar [128]. In such a case, due to a mutual competition between two different symmetries like s and d, for some range of parameters a state with form factor η(k) = ηs(k)+αηd(k) can be stable [129], where ηi(k) are the form factors and α defines the ratio between amplitudes of the order parameters with symmetry s and d. This competition can be expected in Ba1−xKxFe2As2, where doping leads to change of the gap symmetry. In such a case, in some range of parameters the mixing gap symmetry s+is± can be expected [130, 131]. Recent experiments based on the muon spin rotation (μSR) measurements suggest a realization of this state in Ba1−xKxFe2As2, around x~0.7 [132]. Similar measurements suggest also a realization of s+d symmetry in CsCa2Fe4As4F2 [133] and KCa2Fe4As4F [134].
The possibility of the realization of a state with the mixing symmetry was suggest in the system with time-reversal symmetry-breaking [107, 135, 136]. This is possible due to lowering spontaneously the fourfold rotational symmetry C4 to C2 symmetry, e.g., by a transition from tetragonal to orthorhombic phase [137]. This transition can be also associated with nematicity of the system [138].
Concluding, competition between two different types of the gap symmetry can lead to a state with mixed symmetry gap. In a context of our study, a role of the interband interaction is important [139], which can lead to an effective modification of the momentum-dependent gap value (cf. section 3.4). In our case, the interplay between different types of the symmetries at Γ- and M-centered FSs leads to a modification of the gap value dependently on J strength.
4. Summary
The multi-band nature of many superconducting materials make them very interesting for experimental and theoretical studies. A mutual influence between bands leads to the unconventional behavior of various physical properties. In this paper, using the two-band model of the iron-based superconductors we have studied a role of the pair-hopping coupling between bands on the physical properties such as superconducting gap, specific heat, spectral function and density of states. We show that the arbitrary small but finite pair-hopping coupling between the bands strongly influence the temperature dependence of superconducting gap and heat capacity, which significantly deflect from the BCS-type behavior. Also the spectral function and electron density of states demonstrate the unconventional nature of superconductivity in the two-band system. These results can be helpful to obtain the information about the symmetry of the gap [72, 140, 141] and the relations between effective interactions in the multi-band systems. The unconventional behavior found in the present work can be observed in many experiments and are in a good agreement with the predictions of the Ginzburg-Landau theory [44]. More recently, similar results have been also found in the case of the two-band superfluid system in the BCS-BEC crossover regime [142].
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
AP initialized the project and performed numerical calculation. AP and KK prepared the first version of the manuscript. All authors analyzed and discussed the results and contributed to the final version of the manuscript.
Funding
This work was supported by the National Science Centre (NCN, Poland) under grants OPUS no. 2017/25/B/ST3/02586 (AP and PP) and SONATINA no. 2017/24/C/ST3/00276 (KK). AP and KK appreciate also founding in the frame of scholarships of the Minister of Science and Higher Education (Poland) for outstanding young scientists (2019 edition, nos. 818/STYP/14/2019 and 821/STYP/14/2019, respectively).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors are thankful to S.-L. Drechsler for very fruitful discussions and comments.
References
1. Johnston DC. The puzzle of high temperature superconductivity in layered iron pnictides and chalcogenides. Adv Phys. (2010) 59:803. doi: 10.1080/00018732.2010.513480
2. Stewart GR. Superconductivity in iron compounds. Rev Mod Phys. (2011) 83:1589. doi: 10.1103/RevModPhys.83.1589
3. Moskalenko VA. Superconductivity of metals taking into account overlapping of the energy bands. Phys Met Metallogr. (1959) 8:25.
4. Suhl H, Matthias BT, Walker LR. Bardeen-Cooper-Schrieffer theory of superconductivity in the case of overlapping bands. Phys Rev Lett. (1959) 3:552. doi: 10.1103/PhysRevLett.3.552
5. Ding H, Richard P, Nakayama K, Sugawara K, Arakane T, Sekiba Y, et al. Observation of Fermi-surface-dependent nodeless superconducting gaps in Ba0.6K0.4Fe2As2. EPL. (2008) 83:47001. doi: 10.1209/0295-5075/83/47001
6. Margine ER, Giustino F. Two-gap superconductivity in heavily n-doped graphene: ab initio Migdal-Eliashberg theory. Phys Rev B. (2014) 90:014518. doi: 10.1103/PhysRevB.90.014518
7. Kohsaka Y, Taylor C, Fujita K, Schmidt A, Lupien C, Hanaguri T, et al. An intrinsic bond-centered electronic glass with unidirectional domains in underdoped cuprates. Science. (2007) 315:1380. doi: 10.1126/science.1138584
8. Cava RJ, Zandbergen HW, Batlogg B, Eisaki H, Takagi H, Krajewski JJ, et al. Superconductivity in lanthanum nickel boro-nitride. Nature. (1994) 372:245. doi: 10.1038/372245a0
9. Hebard AF, Rosseinsky MJ, Haddon RC, Murphy DW, Glarum SH, Palstra TTM, et al. Superconductivity at 18 K in potassium-doped C60. Nature. (1991) 350:600–601. doi: 10.1038/350600a0
10. Nagamatsu J, Nakagawa N, Muranaka T, Zenitani Y, Akimitsu J. Superconductivity at 39 K in magnesium diboride. Nature. (2001) 410:63. doi: 10.1038/35065039
11. Kamihara Y, Hiramatsu H, Hirano M, Kawamura R, Yanagi H, Kamiya T, et al. Iron-based layered superconductor: LaOFeP. J Am Chem Soc. (2006) 128:10012. doi: 10.1021/ja063355c
12. Kamihara Y, Watanabe T, Hirano M, Hosono H. Iron-based layered superconductor La[O1−xFx]FeAs (x = 0.05-0.12) with Tc = 26 K. J Am Chem Soc. (2008) 130:3296. doi: 10.1021/ja800073m
13. Mazin II, Singh DJ, Johannes MD, Du MH. Unconventional superconductivity with a sign reversal in the order parameter of LaFeAsO1−xFx. Phys Rev Lett. (2008) 101:057003. doi: 10.1103/PhysRevLett.101.057003
14. Hirschfeld PJ, Korshunov MM, Mazin II. Gap symmetry and structure of Fe-based superconductors. Rep Prog Phys. (2011) 74:124508. doi: 10.1088/0034-4885/74/12/124508
15. Scalapino DJ. A common thread: the pairing interaction for unconventional superconductors. Rev Mod Phys. (2012) 84:1383. doi: 10.1103/RevModPhys.84.1383
16. Hosono H, Kuroki K. Iron-based superconductors: current status of materials and pairing mechanism. Physica C. (2015) 514:399. doi: 10.1016/j.physc.2015.02.020
17. Graser S, Maier TA, Hirschfeld PJ, Scalapino DJ. Near-degeneracy of several pairing channels in multiorbital models for the Fe pnictides. N J Phys. (2009) 11:025016. doi: 10.1088/1367-2630/11/2/025016
18. Castellani C, Natoli CR, Ranninger J. Magnetic structure of V2S3 in the insulating phase. Phys Rev B. (1978) 18:4945. doi: 10.1103/PhysRevB.18.4945
19. Oleś AM. Antiferromagnetism and correlation of electrons in transition metals. Phys Rev B. (1983) 28:327. doi: 10.1103/PhysRevB.28.327
20. Kubo K. Pairing symmetry in a two-orbital Hubbard model on a square lattice. Phys Rev B. (2007) 75:224509. doi: 10.1103/PhysRevB.75.224509
21. Bickers NE, Scalapino DJ, White SR. Conserving approximations for strongly correlated electron systems: bethe-salpeter equation and dynamics for the two-dimensional hubbard model. Phys Rev Lett. (1989) 62:961. doi: 10.1103/PhysRevLett.62.961
22. Yin ZP, Haule K, Kotliar G. Kinetic frustration and the nature of the magnetic and paramagnetic states in iron pnictides and iron chalcogenides. Nat Mater. (2011) 10:932. doi: 10.1038/nmat3120
23. Kordyuk AA. Iron-based superconductors: magnetism, superconductivity, and electronic structure (Review Article). Low Temp Phys. (2012) 38:888. doi: 10.1063/1.4752092
24. Liu C, Kondo T, Fernandes RM, Palczewski AD, Mun ED, Ni N, et al. Evidence for a Lifshitz transition in electron-doped iron arsenic superconductors at the onset of superconductivity. Nat Phys. (2010) 6:419. doi: 10.1038/nphys1656
25. Liu C, Palczewski AD, Dhaka RS, Kondo T, Fernandes RM, Mun ED, et al. Importance of the Fermi-surface topology to the superconducting state of the electron-doped pnictide Ba(Fe1−xCox)2As2. Phys Rev B. (2011) 84:020509. doi: 10.1103/PhysRevB.84.020509
26. Quader K, Widom M. Lifshitz and other transitions in alkaline-earth 122 pnictides under pressure. Phys Rev B. (2014) 90:144512. doi: 10.1103/PhysRevB.90.144512
27. Ptok A, Kapcia KJ, Cichy A, Oleś AM, Piekarz P. Magnetic Lifshitz transition and its consequences in multi-band iron-based superconductors. Sci Rep. (2017) 7:41979. doi: 10.1038/srep41979
28. Rodriguez JP. Collective mode at Lifshitz transition in iron-pnictide superconductors. J Phys Condens Matter. (2016) 28:375701. doi: 10.1088/0953-8984/28/37/375701
29. Fernandes RM, Chubukov AV. Low-energy microscopic models for iron-based superconductors: a review. Rep Prog Phys. (2017) 80:014503. doi: 10.1088/1361-6633/80/1/014503
30. Mazin II. Superconductivity gets an iron boost. Nature. (2010) 464:183. doi: 10.1038/nature08914
31. Richard P, Qian T, Ding H. ARPES measurements of the superconducting gap of Fe-based superconductors and their implications to the pairing mechanism. J Phys Condens Matter. (2015) 27:293203. doi: 10.1088/0953-8984/27/29/293203
32. Raghu S, Qi XL, Liu CX, Scalapino DJ, Zhang SC. Minimal two-band model of the superconducting iron oxypnictides. Phys Rev B. (2008) 77:220503. doi: 10.1103/PhysRevB.77.220503
33. Lee PA, Wen XG. Spin-triplet p-wave pairing in a three-orbital model for iron pnictide superconductors. Phys Rev B. (2008) 78:144517. doi: 10.1103/PhysRevB.78.144517
34. Daghofer M, Nicholson A, Moreo A, Dagotto E. Three orbital model for the iron-based superconductors. Phys Rev B. (2010) 81:014511. doi: 10.1103/PhysRevB.81.014511
35. Hu J, Hao N. S4 Symmetric microscopic model for iron-based superconductors. Phys Rev X. (2012). 2:021009. doi: 10.1103/PhysRevX.2.021009
36. Cvetkovic V, Vafek O. Space group symmetry, spin-orbit coupling, and the low-energy effective Hamiltonian for iron-based superconductors. Phys Rev B. (2013) 88:134510. doi: 10.1103/PhysRevB.88.134510
37. Kuroki K, Onari S, Arita R, Usui H, Tanaka Y, Kontani H, et al. Unconventional pairing originating from the disconnected fermi surfaces of superconducting LaFeAsO1−xFx. Phys Rev Lett. (2008) 101:087004. doi: 10.1103/PhysRevLett.101.087004
38. Miyake T, Nakamura K, Arita R, Imada M. Comparison of ab initio low-energy models for LaFePO, LaFeAsO, BaFe2As2, LiFeAs, FeSe, and FeTe: electron correlation and covalency. J Phys Soc Japan. (2010) 79:044705. doi: 10.1143/JPSJ.79.044705
39. Ptok A, Kapcia KJ, Piekarz P, Oleś AM. The ab initio study of unconventional superconductivity in CeCoIn5 and FeSe. N. J Phys. (2017) 19:063039. doi: 10.1088/1367-2630/aa6d9d
40. Andersen OK, Boeri L. On the multi-orbital band structure and itinerant magnetism of iron-based superconductors. Ann Phys. (2011) 523:8–50. doi: 10.1002/andp.201000149
41. Zhang P, Richard P, Qian T, Shi X, Ma J, Zeng LK, et al. Observation of momentum-confined in-gap impurity state in Ba0.6K0.4Fe2As2: evidence for antiphase s± pairing. Phys Rev X. (2014) 4:031001. doi: 10.1103/PhysRevX.4.031001
42. Ptok A, Crivelli D, Kapcia KJ. Change of the sign of superconducting intraband order parameters induced by interband pair hopping interaction in iron-based high-temperature superconductors. Supercond Sci Technol. (2015) 28:045010. doi: 10.1088/0953-2048/28/4/045010
43. Shanenko AA, Milošević MV, Peeters FM, Vagov AV. Extended Ginzburg-Landau formalism for two-band superconductors. Phys Rev Lett. (2011) 106:047005. doi: 10.1103/PhysRevLett.106.047005
44. Komendová L, Chen Y, Shanenko AA, Milošević MV, Peeters FM. Two-band superconductors: hidden criticality deep in the superconducting state. Phys Rev Lett. (2012) 108:207002. doi: 10.1103/PhysRevLett.108.207002
45. Januszewski M, Ptok A, Crivelli D, Gardas B. GPU-based acceleration of free energy calculations in solid state physics. Comput Phys Commun. (2015) 192:220. doi: 10.1016/j.cpc.2015.02.012
46. Ptok A, Crivelli D. Influence of finite size effects on the Fulde-Ferrell-Larkin-Ovchinnikov state. Commun Comput Phys. (2017) 21:748. doi: 10.4208/cicp.OA-2016-0041
47. Bardeen J, Cooper LN, Schrieffer JR. Theory of superconductivity. Phys Rev. (1957) 108:1175. doi: 10.1103/PhysRev.108.1175
48. Yerin YS, Omelyanchouk AN. Coherent current states in a two-band superconductor. Low Temp Phys. (2007) 33:401–7. doi: 10.1063/1.2737547
49. Ptok A. Influence of s±symmetry on unconventional superconductivity in pnictides above the Pauli limit-two-band model study. Eur Phys J B. (2014) 87:2. doi: 10.1140/epjb/e2013-41007-2
50. Dóra B, Virosztek A. Thermodynamics and optical conductivity of unconventional spin density waves. Eur Phys J B. (2001) 22:167. doi: 10.1007/PL00011140
51. Kuzmichev SA, Shanygina TE, Morozov IV, Boltalin AI, Roslova MV, Wurmehl S, et al. Investigation of LiFeAs by means of “break-junction” technique. JETP Lett. (2012) 95:537. doi: 10.1134/S0021364012100086
52. Muratov AV, Kuzmicheva TE, Sadakov AV, Gavrilkin SY, Knyazev DA, Kuzmichev SA, et al. Probing bulk superconducting order parameter in Ba(K)Fe2As2 by four complementary techniques. arXiv [preprint], arXiv:1612.05540 (2016).
53. Kuzmichev SA, Kuzmicheva TE, Tchesnokov SN, Pudalov VM, Vasiliev AN. Estimation of intraband and interband relative coupling constants from temperature dependences of the order parameter for two-gap superconductors. J Supercond Nov Mag. (2016) 29:1111. doi: 10.1007/s10948-016-3386-5
54. Yerin Y, Drechsler SL, Fuchs G. Ginzburg-Landau analysis of the critical temperature and the upper critical field for three-band superconductors. J Low Temp Phys. (2013) 173:247. doi: 10.1007/s10909-013-0903-9
55. Wang Y, Berlijn T, Hirschfeld PJ, Scalapino DJ, Maier TA. Glide-plane symmetry and superconducting gap structure of iron-based superconductors. Phys Rev Lett. (2015) 114:107002. doi: 10.1103/PhysRevLett.114.107002
56. Daghero D, Tortello M, Ummarino GA, Griveau JC, Colineau E, Eloirdi R, et al. Strong-coupling d-wave superconductivity in PuCoGa5 probed by point-contact spectroscopy. Nat Commun. (2012) 3:786. doi: 10.1038/ncomms1785
57. Du Z, Yang X, Lin H, Fang D, Du G, Xing J, et al. Scrutinizing the double superconducting gaps and strong coupling pairing in (Li1−xFexOH)FeSe. Nat Commun. (2015) 7:10565. doi: 10.1038/ncomms10565
58. Kuzmicheva TE, Kuzmichev SA, Mikheev MG, Ponomarev YG, Tchesnokov SN, Pudalov VM, et al. Andreev spectroscopy of iron-based superconductors: temperature dependence of the order parameters and scaling of ΔL, S withTc. Phys Usp. (2014) 57:819. doi: 10.3367/UFNe.0184.201408i.0888
59. Petrović AP, Lortz R, Santi G, Berthod C, Dubois C, Decroux M, et al. Multiband superconductivity in the Chevrel phases SnMo6S8 and PbMo6S8. Phys Rev Lett. (2011) 106:017003. doi: 10.1103/PhysRevLett.106.017003
60. Iavarone M, Karapetrov G, Koshelev AE, Kwok WK, Crabtree GW, Hinks DG, et al. Two-band superconductivity in MgB2. Phys Rev Lett. (2002) 89:187002. doi: 10.1103/PhysRevLett.89.187002
61. Brinkman A, Golubov AA, Rogalla H, Dolgov OV, Kortus J, Kong Y, et al. Multiband model for tunneling in MgB2 junctions. Phys Rev B. (2002) 65:180517. doi: 10.1103/PhysRevB.65.180517
62. Kristoffel N, Örd T, Rägo K. MgB2 two-gap superconductivity with intra- and interband couplings. EPL. (2003) 61:109. doi: 10.1209/epl/i2003-00256-8
63. Askerzade I. Unconventional Superconductors. Berlin; Heidelberg: Springer-Verlag (2012) doi: 10.1007/978-3-642-22652-6
64. Brinkman A, Rowell JM. MgB2 tunnel junctions and SQUIDs. Phys C. (2007) 456:188. doi: 10.1016/j.physc.2007.01.019
65. Yerin Y, Omelyanchouk AN. Proximity and Josephson effects in microstructures based on multiband superconductors (Review Article). Low Temp Phys. (2017) 43:1013–37. doi: 10.1063/1.5004444
66. Wysokinski MM, Spalek J. Properties of an almost localized Fermi liquid in an applied magnetic field revisited: a statistically consistent Gutzwiller approach. J Phys Condens Matter. (2014) 26:055601. doi: 10.1088/0953-8984/26/5/055601
67. Ptok A. Multiple phase transitions in Pauli-limited iron-based superconductors. J Phys Condens Matter. (2015) 27:482001. doi: 10.1088/0953-8984/27/48/482001
68. Bouquet F, Wang Y, Fisher RA, Hinks DG, Jorgensen JD, Junod A, et al. Phenomenological two-gap model for the specific heat of MgB2. EPL. (2001) 56:856. doi: 10.1209/epl/i2001-00598-7
69. Maksimov EG, Karakozov AE, Gorshunov BP, Zhukova ES, Ponomarev YG, Dressel M. Electronic specific heat of two-band layered superconductors: analysis within the generalized two-band α model. Phys Rev B. (2011) 84:174504. doi: 10.1103/PhysRevB.84.174504
70. Vargunin A, Rägo K, Örd T. Two-gap superconductivity: interband interaction in the role of an external field. Supercond Sci Technol. (2013) 26:065008. doi: 10.1088/0953-2048/26/6/065008
71. Lin JY, Hsieh YS, Chareev DA, Vasiliev AN, Parsons Y, Yang HD. Coexistence of isotropic and extended s-wave order parameters in FeSe as revealed by low-temperature specific heat. Phys Rev B. (2011) 84:220507. doi: 10.1103/PhysRevB.84.220507
72. Konno T, Adachi T, Imaizumi M, Noji T, Kawamata T, Koike Y. Superconducting gap and symmetry in FeSe1−xTex studied by specific heat in magnetic fields. J Phys Soc Jpn. (2014) 83:094721. doi: 10.7566/JPSJ.83.094721
73. Fletcher JD, Serafin A, Malone L, Analytis JG, Chu JH, Erickson AS, et al. Evidence for a nodal-line superconducting state in LaFePO. Phys Rev Lett. (2009) 102:147001. doi: 10.1103/PhysRevLett.102.147001
74. Stockert U, Abdel-Hafiez M, Evtushinsky DV, Zabolotnyy VB, Wolter AUB, Wurmehl S, et al. Specific heat and angle-resolved photoemission spectroscopy study of the superconducting gaps in LiFeAs. Phys Rev B. (2011) 83:224512. doi: 10.1103/PhysRevB.83.224512
75. Wang AF, Luo XG, Yan YJ, Ying JJ, Xiang ZJ, Ye GJ, et al. Phase diagram and calorimetric properties of NaFe1−xCoxAs. Phys Rev B. (2012) 85:224521. doi: 10.1103/PhysRevB.85.224521
76. Fukazawa H, Yamada Y, Kondo K, Saito T, Kohori Y, Kuga K, et al. Possible multiple gap superconductivity with line nodes in heavily hole-doped superconductor KFe2As2 studied by 75As nuclear quadrupole resonance and specific heat. J Phys Soc Jpn. (2009) 78:083712. doi: 10.1143/JPSJ.78.083712
77. Fukazawa H, Saito T, Yamada Y, Kondo K, Hirano M, Kohori Y, et al. NMR/NQR and specific heat studies of iron pnictide superconductor KFe2As2. J Phys Soc Jpn. (2011) 80:SA118. doi: 10.1143/JPSJS.80SA.SA118
78. Abdel-Hafiez M, Aswartham S, Wurmehl S, Grinenko V, Hess C, Drechsler SL, et al. Specific heat and upper critical fields in KFe2As2 single crystals. Phys Rev B. (2012) 85:134533. doi: 10.1103/PhysRevB.85.134533
79. Wang AF, Pan BY, Luo XG, Chen F, Yan YJ, Ying JJ, et al. Calorimetric study of single-crystal CsFe2As2. Phys Rev B. (2013) 87:214509. doi: 10.1103/PhysRevB.87.214509
80. Grinenko V, Efremov DV, Drechsler SL, Aswartham S, Gruner D, Roslova M, et al. Superconducting specific-heat jump (β ≈ 2) for K1−xNaxFe2As2. Phys Rev B. (2014) 89:060504. doi: 10.1103/PhysRevB.89.060504
81. Hardy F, Eder R, Jackson M, Aoki D, Paulsen C, Wolf T, et al. Multiband superconductivity in KFe2As2: evidence for one isotropic and several lilliputian energy gaps. J Phys Soc Jpn. (2014) 83:014711. doi: 10.7566/JPSJ.83.014711
82. Johnston S, Abdel-Hafiez M, Harnagea L, Grinenko V, Bombor D, Krupskaya Y, et al. Specific heat of Ca0.32Na0.68Fe2As2 single crystals: unconventional s± multiband superconductivity with intermediate repulsive interband coupling and sizable attractive intraband couplings. Phys Rev B. (2014) 89:134507. doi: 10.1103/PhysRevB.89.134507
83. Zhang S, Singh YP, Huang XY, Chen XJ, Dzero M, Almasan CC. Orbital and Pauli limiting effects in heavily doped Ba0.05K0.95Fe2As2. Phys Rev B. (2015) 92:174524. doi: 10.1103/PhysRevB.92.174524
84. Rotundu CR, Forrest TR, Phillips NE, Birgeneau RJ. Specific heat of Ba0.59K0.41Fe2As2, an Fe-Pnictide superconductor with Tc = 36.9 K, and a new method for identifying the electron contribution. J Phys Soc Jpn. (2015) 84:114701. doi: 10.7566/JPSJ.84.114701
85. Hardy F, Böhmer AE, de' Medici L, Capone M, Giovannetti G, Eder R, et al. Strong correlations, strong coupling, and s-wave superconductivity in hole-doped BaFe2As2 single crystals. Phys Rev B. (2016) 94:205113. doi: 10.1103/PhysRevB.94.205113
86. Khim S, Aswartham S, Grinenko V, Efremov D, Blum CGF, Steckel F, et al. A calorimetric investigation of RbFe2As2 single crystals. Phys Status Solidi. (2016) 254:1600208. doi: 10.1002/pssb.201600208
87. Drechsler SL, Johnston S, Grinenko V, Tomczak JM, Rosner H. Constraints on the total coupling strength to bosons in the iron based superconductors. Phys Status Solidi. (2017) 254:1700006. doi: 10.1002/pssb.201700006
88. Bud'ko SL, Canfield PC. Superconductivity of magnesium diboride. Phys C. (2015) 514:142. doi: 10.1016/j.physc.2015.02.024
89. Bhoi D, Khim S, Nam W, Lee BS, Kim C, Jeon BG, et al. Interplay of charge density wave and multiband superconductivity in 2H-PdxTaSe2. Sci Rep. (2016) 6:24068. doi: 10.1038/srep24068
90. Nakajima Y, Nakagawa T, Tamegai T, Harima H. Specific-heat evidence for two-gap superconductivity in the ternary-iron silicide Lu2Fe3Si5. Phys Rev Lett. (2008) 100:157001. doi: 10.1103/PhysRevLett.100.157001
91. Kačmarčík J, Pribulová Z, Marcenat C, Klein T, Rodière P, Cario L, et al. Specific heat measurements of a superconducting NbS2 single crystal in an external magnetic field: energy gap structure. Phys Rev B. (2010) 82:014518. doi: 10.1103/PhysRevB.82.014518
92. Matsui H, Sato T, Takahashi T, Wang SC, Yang HB, Ding H, et al. BCS-like bogoliubov quasiparticles in High-Tc superconductors observed by angle-resolved photoemission spectroscopy. Phys Rev Lett. (2003) 90:217002. doi: 10.1103/PhysRevLett.90.217002
93. Okazaki K, Ito Y, Ota Y, Kotani Y, Shimojima T, Kiss T, et al. Superconductivity in an electron band just above the Fermi level: possible route to BCS-BEC superconductivity. Sci Rep. (2014) 4:4109. doi: 10.1038/srep04109
94. Nomura T. Perturbation Theory of High- Tc Superconductivity in Iron Pnictides. J Phys Soc Jpn. (2009) 78:034716. doi: 10.1143/JPSJ.78.034716
95. LeBlanc JPF, Carbotte JP, Nicol EJ. Effects of a particle-hole asymmetric pseudogap on Bogoliubov quasiparticles. Phys Rev B. (2011) 83:184506. doi: 10.1103/PhysRevB.83.184506
97. Wei JYT, Yeh NC, Garrigus DF, Strasik M. Directional tunneling and Andreev Reflection on YBa2Cu3O7−δ single crystals: predominance of d-wave pairing symmetry verified with the generalized Blonder, Tinkham, and Klapwijk Theory. Phys Rev Lett. (1998) 81:2542. doi: 10.1103/PhysRevLett.81.2542
98. Lee WS, Shen ZX. Superconductivity: bring on the real resonance. Nat Phys. (2008) 4:95. doi: 10.1038/nphys849
99. Kuang L, Zhao H, Feng S. Pseudogap-induced asymmetric tunneling in cuprate superconductors. Phys C. (2014) 501:62. doi: 10.1016/j.physc.2014.04.003
100. Shimojima T, Sakaguchi F, Ishizaka K, Ishida Y, Kiss T, Okawa M, et al. Orbital-independent superconducting gaps in iron pnictides. Science. (2011) 332:564. doi: 10.1126/science.1202150
101. Allan MP, Rost AW, Mackenzie AP, Xie Y, Davis JC, Kihou K, et al. Anisotropic energy gaps of iron-based superconductivity from intraband quasiparticle interference in LiFeAs. Science. (2012) 336:563. doi: 10.1126/science.1218726
102. Okazaki K, Ota Y, Kotani Y, Malaeb W, Ishida Y, Shimojima T, et al. Octet-line node structure of superconducting order parameter in KFe2As2. Science. (2012) 337:1314. doi: 10.1126/science.1222793
103. Umezawa K, Li Y, Miao H, Nakayama K, Liu ZH, Richard P, et al. Unconventional anisotropic s-wave superconducting gaps of the LiFeAs iron-pnictide superconductor. Phys Rev Lett. (2012) 108:037002. doi: 10.1103/PhysRevLett.108.037002
104. Borisenko SV, Zabolotnyy VB, Kordyuk AA, Evtushinsky DV, Kim TK, Morozov IV, et al. One-sign order parameter in iron based superconductor. Symmetry. (2012) 4:251. doi: 10.3390/sym4010251
105. Maier TA, Graser S, Scalapino DJ, Hirschfeld PJ. Origin of gap anisotropy in spin fluctuation models of the iron pnictides. Phys Rev B. (2009) 79:224510. doi: 10.1103/PhysRevB.79.224510
106. Thomale R, Platt C, Hanke W, Bernevig BA. Mechanism for explaining differences in the order parameters of FeAs-based and FeP-based Pnictide superconductors. Phys Rev Lett. (2011) 106:187003. doi: 10.1103/PhysRevLett.106.187003
107. Platt C, Thomale R, Honerkamp C, Zhang SC, Hanke W. Mechanism for a pairing state with time-reversal symmetry breaking in iron-based superconductors. Phys Rev B. (2012) 85:180502. doi: 10.1103/PhysRevB.85.180502
108. Wang Y, Kreisel A, Zabolotnyy VB, Borisenko SV, Büchner B, Maier TA, et al. Superconducting gap in LiFeAs from three-dimensional spin-fluctuation pairing calculations. Phys Rev B. (2013) 88:174516. doi: 10.1103/PhysRevB.88.174516
109. Yang Y, Wang WS, Lu HY, Xiang YY, Wang QH. Electronic structure and d-wave superconductivity in FeS. Phys Rev B. (2016) 93:104514. doi: 10.1103/PhysRevB.93.104514
110. Benfatto L, Valenzuela B, Fanfarillo L. Nematic pairing from orbital-selective spin fluctuations in FeSe. NPJ Quant Mater. (2018) 3:56. doi: 10.1038/s41535-018-0129-9
111. Essenberger F, Sanna A, Buczek P, Ernst A, Sandratskii L, Gross EKU. Ab initio theory of iron-based superconductors. Phys Rev B. (2016) 94:014503. doi: 10.1103/PhysRevB.94.014503
112. Mizukami Y, Konczykowski M, Kawamoto Y, Kurata S, Kasahara S, Hashimoto K, et al. Disorder-induced topological change of the superconducting gap structure in iron pnictides. Nat Commun. (2014) 5:5657. doi: 10.1038/ncomms6657
113. Shan L, Wang YL, Shen B, Zeng B, Huang Y, Li A, et al. Observation of ordered vortices with Andreev bound states in Ba0.6K0.4Fe2As2. Nat Phys. (2011) 7:325. doi: 10.1038/nphys1908
114. Guterding D, Altmeyer M, Jeschke HO, Valentí R. Near-degeneracy of extended and dxy order parameters in quasi-two-dimensional organic superconductors. Phys Rev B. (2016) 94:024515. doi: 10.1103/PhysRevB.94.024515
115. Hoffman JE. Spectroscopic scanning tunneling microscopy insights into Fe-based superconductors. Rep Prog Phys. (2011) 74:124513. doi: 10.1088/0034-4885/74/12/124513
116. Maśka MM, Śledź Z, Czajka K, Mierzejewski M. Inhomogeneity-induced enhancement of the pairing interaction in cuprate superconductors. Phys Rev Lett. (2007) 99:147006. doi: 10.1103/PhysRevLett.99.147006
117. Hanaguri T, Niitaka S, Kuroki K, Takagi H. Unconventional s-wave superconductivity in Fe(Se,Te). Science. (2010) 328:474. doi: 10.1126/science.1187399
118. Song CL, Wang YL, Cheng P, Jiang YP, Li W, Zhang T, et al. Direct observation of nodes and twofold symmetry in FeSe superconductor. Science. (2011) 332:1410. doi: 10.1126/science.1202226
119. Li W, Ding H, Deng P, Chang K, Song C, He K, et al. Phase separation and magnetic order in K-doped iron selenide superconductor. Nat Phys. (2012) 8:126. doi: 10.1038/nphys2155
120. Jing G, Xing-Yuan H, Jun Z, Yun-Yin J, Ya-Dong G, Bing S, et al. Observation of mode-like features in tunneling spectra of iron-based superconductors. Chinese Phys B. (2015) 24:077402. doi: 10.1088/1674-1056/24/7/077402
121. Terashima K, Sekiba Y, Bowen JH, Nakayama K, Kawahara T, Sato T, et al. Fermi surface nesting induced strong pairing in iron-based superconductors. Proc Natl Acad Sci USA. (2009) 106:7330. doi: 10.1073/pnas.0900469106
122. Teague ML, Drayna GK, Lockhart GP, Cheng P, Shen B, Wen HH, et al. Measurement of a sign-changing two-gap superconducting phase in electron-doped Ba(Fe1−xCox)2As2 single crystals using scanning tunneling spectroscopy. Phys Rev Lett. (2011) 106:087004. doi: 10.1103/PhysRevLett.106.087004
123. Wang YL, Shan L, Fang L, Cheng P, Ren C, Wen HH. Multiple gaps in SmFeAsO0.9F0.1 revealed by point-contact spectroscopy. Supercond Sci Technol. (2009) 22:015018. doi: 10.1088/0953-2048/22/1/015018
124. Yang X, Du Z, Du G, Gu Q, Lin H, Fang D, et al. Strong-coupling superconductivity revealed by scanning tunneling microscope in tetragonal FeS. Phys Rev B. (2016) 94:024521. doi: 10.1103/PhysRevB.94.024521
125. Szabó P, Samuely P, Kačmarčík J, Klein T, Marcus J, Fruchart D, et al. Evidence for two superconducting energy gaps in MgB2 by point-contact spectroscopy. Phys Rev Lett. (2001) 87:137005. doi: 10.1103/PhysRevLett.87.137005
126. Chen K, Dai W, Zhuang CG, Li Q, Carabello S, Lambert JG, et al. Momentum-dependent multiple gaps in magnesium diboride probed by electron tunnelling spectroscopy. Nat Commun. (2012) 3:619. doi: 10.1038/ncomms1626
127. Ruckenstein AE, Hirschfeld PJ, Appel J. Mean-field theory of high-Tc superconductivity: The superexchange mechanism. Phys Rev B. (1987) 36:857. doi: 10.1103/PhysRevB.36.857
128. Kotliar G. Resonating valence bonds and d-wave superconductivity. Phys Rev B. (1988) 37:3664. doi: 10.1103/PhysRevB.37.3664
129. Liu M, Xing DY, Wang ZD. Mixed (s+id)-wave order parameters in the Van Hove scenario. Phys Rev B. (1997) 55:3181. doi: 10.1103/PhysRevB.55.3181
130. Khodas M, Chubukov AV. Interpocket pairing and gap symmetry in Fe-based superconductors with only electron pockets. Phys Rev Lett. (2012) 108:247003. doi: 10.1103/PhysRevLett.108.247003
131. Maiti S, Chubukov AV. s+is state with broken time-reversal symmetry in Fe-based superconductors. Phys Rev B. (2013). 87:144511. doi: 10.1103/PhysRevB.87.144511
132. Grinenko V, Sarkar R, Kihou K, Lee CH, Morozov I, Aswartham S, et al. Emerging superconductivity with broken time reversal symmetry inside a superconductings-wave state. Nat. Phys. (2020) 16:789. doi: 10.1038/s41567-020-0886-9
133. Kirschner FKK, Adroja DT, Wang ZC, Lang F, Smidman M, Baker PJ, et al. Two-gap superconductivity with line nodes in CsCa2Fe4As4F2. Phys Rev B. (2018) 97:060506. doi: 10.1103/PhysRevB.97.060506
134. Smidman M, Kirschner FKK, Adroja DT, Hillier AD, Lang F, Wang ZC, et al. Nodal multigap superconductivity in KCa2Fe4As4F2. Phys Rev B. (2018) 97:060509. doi: 10.1103/PhysRevB.97.060509
135. Lee WC, Zhang SC, Wu C. Pairing state with a time-reversal symmetry breaking in FeAs-based superconductors. Phys Rev Lett. (2009) 102:217002. doi: 10.1103/PhysRevLett.102.217002
136. Kang J, Chubukov AV, Fernandes RM. Time-reversal symmetry-breaking nematic superconductivity in FeSe. Phys Rev B. (2018) 98:064508. doi: 10.1103/PhysRevB.98.064508
137. Livanas G, Aperis A, Kotetes P, Varelogiannis G. Nematicity from mixed s±+d states in iron-based superconductors. Phys Rev B. (2015) 91:104502. doi: 10.1103/PhysRevB.91.104502
138. Fernandes RM, Millis AJ. Nematicity as a probe of superconducting pairing in iron-based superconductors. Phys Rev Lett. (2013) 111:127001. doi: 10.1103/PhysRevLett.111.127001
139. Maiti S, Korshunov MM, Chubukov AV. Gap symmetry in KFe2As2 and the cos(4θ) gap component in LiFeAs. Phys Rev B. (2012) 85:014511. doi: 10.1103/PhysRevB.85.014511
140. Zaki SN, Maeno Y, Mao Z. Changes in the Superconducting State of Sr2RuO4 under Magnetic Fields Probed by Specific Heat. J Phys Soc Jpn. (2000) 69:572. doi: 10.1143/JPSJ.69.572
141. Nomura T, Yamada K. Detailed investigation of gap structure and specific heat in the p-wave superconductor Sr2RuO4. J Phys Soc Jpn. (2002) 71:404. doi: 10.1143/JPSJ.71.404
Keywords: iron-based superconductors, specific heat, two-band model, pair-hopping coupling, gap symmetry
Citation: Ptok A, Kapcia KJ and Piekarz P (2020) Effects of Pair-Hopping Coupling on Properties of Multi-Band Iron-Based Superconductors. Front. Phys. 8:284. doi: 10.3389/fphy.2020.00284
Received: 14 November 2019; Accepted: 23 June 2020;
Published: 19 August 2020.
Edited by:
Jun Zhao, Fudan University, ChinaCopyright © 2020 Ptok, Kapcia and Piekarz. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Andrzej Ptok, YXB0b2smI3gwMDA0MDttbWoucGw=
†ORCID: Andrzej Ptok https://orcid.org/0000-0002-5566-2656
Konrad Jerzy Kapcia https://orcid.org/0000-0001-8842-1886
Przemysław Piekarz https://orcid.org/0000-0001-6339-2986
 Andrzej Ptok
Andrzej Ptok Konrad Jerzy Kapcia
Konrad Jerzy Kapcia Przemysław Piekarz†
Przemysław Piekarz†