- Université du Luxembourg, Luxembourg, Luxembourg
The main purpose of this paper is to study time operators associated with cylindrical elements, i.e., generalized functions with values in locally convex spaces. It is given the characterization of the domains of the constructed time operators and partially resolved the problem of decomposability of random elements.
1. Introduction
The paper is devoted to extensions of internal time operators on the spaces of functions with values in topological vector spaces and on the spaces of generalized functions of this type associated with K-systems. The main reason of the introduction of time operators was the Lambda transformation theory formulated by I. Prigogine and his collaborators (see [1–3]) as a new approach to the theory of irreversibility in statistical physics. Precisely, to the problem of the relation between the reversible laws of dynamics and the observed irreversible (stochastic) evolution. Let us remind, that the classical view point was that irreversible behavior of the observed time evolution in a dynamical system can only arise from deterministic dynamics as the result of averaging (coarse-graining). The new approach can be formulated, in simplified terms, as a task to relate a given unitary evolution group {Ut}t∈ℝ acting on a Hilbert space of Gibbs' square integrable densities with an entropy increasing evolution semigroup {Wt}t∈ℝ+ through a similarity transformation called the transformation Λ (Lambda) (see [3]) as follows:
Almost all known constructions of Λ transformations have been done so far for the dynamical systems which admit time operators (see [4] for another approach). Such dynamical systems allow the existence of Lyapunov variables, defined as functions of time operators, representing non-equilibrium entropy [1]. This is also a possible way to the task of defining time operator in quantum mechanics which in turn could allow to determine entropy operator. However, the class of dynamical systems for which time operators can be defined is very narrow, in fact, it is limited to K-systems.
Time operators were initially defined on the Hilbert space of square integrable functions. The problem of an extension of the concept of time operator was motivated by a need to extend the Λ transformation theory beyond square integrable probability densities. Indeed, it is natural to ask about a possibility to extend Λ and Wt on a larger class of states, including probability measures. Particularly interesting, from the physical point of view, is the possibility of extension on singular measures concentrated at single points of the phase space [2, 5–7].
Another motivation for the introduction and study of time operators is due to the recently discovered fact that time operators can be also associated with non-invertible dynamics and used as a new tool in the spectral analysis of evolution semigroups of unstable dynamical systems (see e.g., [8–13]). In this case time operators and evolution semigroups are defined on various topological vector spaces. The relation between the time operator T and the evolution semigroup {Ut} is such that each Ut preserves the domain of T and satisfies the relation
The idea behind the spectral analysis of the evolution semigroup {Ut} on a Hilbert space with the help of the time operator T is to decompose T in terms of a complete system of its eigenvectors {en,k}, Ten,k = nen,k, such that Uten,k = en+t,k, as follows
Similar spectral decompositions but in terms of Schauder bases or frames can be obtained in other topological vector spaces.
In this paper we will focus on the construction of time operators associated with K-systems acting on the spaces of cylindrical elements. A cylindrical element is an object which is a generalization of an E valued function, where E is a locally convex space. More precisely, p-cylindrical element, which will be defined in the next section, is a generalization of a weakly p-integrable function with values in E.
Although such extensions of time operators concern various topological vector spaces we will elaborate a unified approach based on the idea of stochastic integral with respect to cylindrical martingales (see [14]). We will also study the related problem of decomposability of cylindrical elements. It can happen that the action of a time operator or even a conditional expectation does not leave the space of vector valued functions invariant but leads to cylindrical elements instead. The decomposability of cylindrical elements allows to represent them again as measurable functions.
The paper is organized as follows. In section 2, we gathered the basic facts on cylindrical elements, cylindrical measures and cylindrical martingales. We focus on the Pettis integrability of vector valued functions and cylindrical elements. We also characterize vector spaces of Pettis integrable cylindrical elements. Section 3 is devoted to the construction of time operators with respect to cylindrical processes and to the solution of the problem of decomposability in two particular cases.
2. Cylindrical Elements and Cylindrical Martingales
Throughout this paper, by a locally convex space (l.c.s.) or a topological vector space (t.v.s) we mean a Hausdorff l.c.s. (respectively t.v.s.) not equal to {0} over the field of real or complex scalars. If E is an l.c.s. then E′ denotes its topological dual and 〈x, x′〉 stands for the value of a functional x′ ∈ E′ at x ∈ E. For subsets A ⊂ E and B ⊂ E′ the symbols A◦ and B◦ denote the polars with respect to the duality 〈E, E′〉 and 〈E′, E〉 respectively, i.e., A◦ = {x′ ∈ E′:|〈x, x′〉| ≤ 1, for each x ∈ A} and B◦ = {x ∈ E:|〈x, x′〉| ≤ 1, for each x′ ∈ B}. By σ(E′, E) we shall denote the weak topology on E′ and by τ(E′, E) the Mackey topology, i.e., is the topology of uniform convergence on all σ(E, E′)–compact, convex, circled subsets of E. will denote the space E′ with the Mackey topology. An l.c.s. E is quasi-complete if each bounded closed subset of E is complete.
Let be a probability space, , p ≥ 0, and let E be an l.c.s. By a p-cylindrical element, or simply cylindrical element, we mean a linear operator X : E′ → Lp. Notice that any function x(·) : Ω → E such that 〈x(·), x′〉 ∈ Lp determines the cylindrical element
Let us now introduce the concept of Pettis integrability of cylindrical elements. The reason of doing this is the following. In statistical physics the main object of interest is the time evolution of statistical ensembles, represented mathematically as probability distributions. However, for technical reasons we often take only some classes of probability distributions as the states of the system. In our case we confine to those probability measures which are absolutely continuous with respect to some reference measure. This allows to replace measures by their densities (Radon-Nikodyn derivatives) or by classes of integrable functions in general. Nevertheless, for a given integrable function f we can recover the corresponding measure μf putting
Replacing f by a vector valued function we should be able to recover the corresponding measure like in (3) but this is not always possible. For example, if E is a Banach space and a measurable function such that is integrable then (3) holds and defines E-valued measure. However this is not true, in general, under the weaker assumption of integrability of , for all x′ ∈ E. Additional assumptions have to be imposed on such as the Pettis integrability defined below. The same can happen when we replace vector valued functions by cylindrical elements.
We say that a cylindrical element X : E′ → L0 is Pettis integrable if X(E′) ⊂ L1 and for each there exists xA ∈ E such that
We write
and call it the Pettis integral of the cylindrical element X. Replacing in (4) and (5) X by a vector valued function we obtain the classical definition of the Pettis integral (see [15]).
General properties of Pettis integrable cylindrical elements are in ref. ([16]). Here we will show relations between Pettis integrability and continuity of cylindrical elements.
We have
Proposition 1. ([16, 17]) Let E be a sequentially complete l.c.s. space and X : E′ → L1 a cylindrical element. Then the following conditions are equivalent
(1) T is Pettis integrable
(2) T is continuous.
Actually, the implication (2) ⇒ (1) in the above Proposition is valid without the assumption of sequential completeness (see [17]).
Let us also mention about two properties of Pettis integrable cylindrical elements which will be used later:
Proposition 2. If E and F are l.c.s., S : E → F is a continuous linear operator and X : E′ → L1 is a Pettis integrable cylindrical element, then the linear operator X ◦ S* : F′ → L1 is Pettis integrable and
Proposition 3. If X is a Pettis integrable cylindrical element then for each absolutely convex neighborhood of 0 in E
The proofs of the above properties can be found in [17].
It follows from Proposition 3 that if E is a normed space then X is a bounded linear operator form E′ to L1 with the operator norm
Notice that σ(L1, L∞) compactness of a family of functions in L1 is equivalent to its uniform integrability (Dunford-Pettis Theorem) thus using the Vallèe-Poussin Theorem (see e.g., [18]) we obtain
Corollary. If p > 1, E is a reflexive Banach space and X : E′ → Lp a continuous cylindrical element then X is Pettis integrable.
Let E be an l.c.s. and let , p ≥ 1, denote the space of all separably valued and weakly p-integrable functions x(·) : Ω → E with the topology generated by the family of seminorms
where U are convex and circled neighborhoods of zero in E.
It follows from ([16], Prop. 3.2, Th. 3.1 and Th. 3.2) that if E is a locally convex Fréchet space and p = 1 then the completion consists of all cylindrical elements X : E′ → L1 which are continuous and compact linear maps. In general, we will denote by the completion of .
If then for each fixed g ∈ Lq, , the map
from E′ to L1 is a Pettis integrable cylindrical element.
Let us also recall some relations between cylindrical elements and cylindrical measures on a locally convex space E. Denote by the σ-field generated by cylindrical sets in E, i.e., the sets of the form
where n ∈ ℕ, , ( denotes the Borel σ-field in ℝn).
Let μ be a finitely additive measure on and let
The measure μ is called cylindrical if for each n ∈ ℕ and is a probability measure on .
Each cylindrical element X determines a cylindrical measure μ defined as
Conversely, if μ is a cylindrical measure on then there exist a probability space and a cylindrical element satisfying the above equality (see [19]). The correspondence between cylindrical measures and cylindrical elements is one-to-one.
If μ is a cylindrical measure and Xμ the corresponding cylindrical element such that
and some p > 0, then we say that μ has a weak p-order.
An important property of a cylindrical measure is its concentration on some families of sets. Namely, let 𝔖 be a family of subsets of E and μ a cylindrical measure on . We say that μ is scalarly concentrated on 𝔖 if for each ε > 0 there is A ∈ 𝔖 such that
for each x′ ∈ E′, where ∗ denotes the inner measure.
Assume that 𝔖 is the family of all compact circled subsets of E and denote by the space E′ with the topology of uniform convergence on the sets from 𝔖. One of the basic relations between Pettis integrable cylindrical elements and the corresponding cylindrical measures is contained in the following Proposition.
Proposition 4. Let E be a complete l.c.s., 𝔖 the family of all compact circled subsets of E and X a cylindrical element. If , p ≥ 1, then the corresponding cylindrical measure μ is scalarly concentrated on 𝔖.
The proof of this Proposition is based on the fact that X is continuous cylindrical element from E′ to Lp which transforms equicontinuous subsets of E′ into relatively compact sets in Lp, p > 1 (see also the proof of Th.4.1 in [16]).
The converse implication is not true in general even for Radon measures but is true for cylindrical Gaussian measures and corresponding L2–valued cylindrical elements (see [16] for details).
3. Time Operator
Before defining time operator acting on cylindrical elements let us remind the classical construction which is based on the idea of Misra-Prigogine-Courbage [3]. Let us consider an abstract dynamical system given by the quadruple , where {St} is a group of one-to-one μ invariant transformations of Ω and either t ∈ ℤ or t ∈ ℝ.
A K-flow (we will say K-system) is a probability space with a group of measure preserving transformations St, t ∈ ℝ, of Ω. We assume that there exists a σ-algebra such that the family , has the properties
(i) , for s < t
(ii)
(iii) – the trivial σ-algebra, i.e., the algebra of sets of measure 0 or 1.
where stands for σ-algebra generated by , t ∈ ℝ.
We replace deterministic evolution of phase space points by the Liouville evolution of probability density functions putting
where ρ is measurable function on Ω. The invariance of the measure μ implies that the transformations Ut considered as operators on form a unitary group.
In this setting a possible approach to the problem of irreversibility can be formulated as in section 1. Namely it is constructed the Lambda operator connecting the reversible group {Ut}t∈ℝ with an entropy increasing evolution semigroup {Wt}t≥0. It is assumed that Λ is a bounded linear operator on with densely defined inverse Λ−1 such that defines, for t ≥ 0, a continuous one-parameter group of contractions. For physical reasons it is also additionally assumed that Λ is positivity preserving, Λ1 = 1 and ||Wt(ρ − 1)|| decreases strictly monotonically to 0, as t → +∞, for all densities ρ ≢ 1. The last condition means that the entropy of the system tends strictly monotonically to zero when the system approaches equilibrium.
In classical dynamical systems Lambda transformations have been constructed on the Lp spaces associated with K-systems as functions of time operators. The main idea of such construction is ([3] see also [20–22]) that each K-system determines the family {Et}t∈ℝ of conditional expectations,
which in turn defines the operator T on each space , p ≥ 1,
which is called the time operator.
In the case of discrete time, t ∈ ℤ, we consider the group {Sn}n∈ℤ generated by a single measure preserving transformation S, i.e., , for n ≠ 0, and S0 = I. The time operator T is then defined as
If p = 2 then the above integral, or sum, defining T is just the spectral resolution of a selfadjoint operator. In this case {Ut}t∈ℝ defined in (6) is a unitary group on L2 satisfying the following relation with T
which is equivalent to (2).
The transformation Λ is defined, up to constants, as an operator function Λ = Λ(T). Namely
where E−∞ is the projection on the space . The function f is assumed to be positive, decreasing on ℝ, f (−∞) = 1, f (+∞) = 0 and such that ln f is concave on ℝ. Then, for any such function f the corresponding operator Λ is injective on L2, one-to-one with densely defined inverse (see ref. [21]). Moreover the semigroup
is Markovian and decreases to 0, for each density ρ ≠ 1 and together with {Ut} satisfies the relation (1).
The time operator as defined in (7) uses the family of conditional expectations {Et} which can be treated as a spectral family of projectors on the Hilbert space L2 which defines a selfadjoint operator or, for a given ρ ∈ L2, {Etρ} can be considered as a martingale with respect to the filtration . In the latter case the integral defining T can be understood as a stochastic integral with respect to a martingale. Such approach allows to define time operators on larger classes of function, for example on L1. Moreover the stochastic integral technique allows to replace the family of projectors {Et} by a family of operators {Mt} such that for a given ρ {Mtρ} is a martingale with respect to . In fact, such a generalization of the definition of time operators has been proposed in [22]. The extension of the definition of T on L1 spaces can be found in [23].
It should be stressed that the above mentioned extension of the time operator concerns such states (probability measures) which have densities. However, in statistical physics the class of states can be larger and contain, for example, singular measures. There were successful attempts of such extension of the domain of time operators (see [2, 5, 6]).
We will define now a time operator acting on p-cylindrical elements. As we have seen in section 2 p-cylindrical element is actually a generalization of a weakly p-integrable function with values in a topological vector space. Equivalently, time operators will act on cylindrical measures on a topological vector spaces. This is a significant step beyond the classical Lp space.
We have to define first the conditional expectation of a cylindrical element. Let denote the usual operator of the conditional expectation (see [18]), and let , p ≥ 1, be a p-cylindrical element obtained as the composition of operators and X. Note that if is continuous, then is also continuous. Thus, if is continuous, 1 ≤ p < ∞, then for each sub σ-field the 1-cylindrical element satisfies
for each .
The above definition of conditional expectation applies, in particular, to Banach space valued functions. Indeed, each function x(·) : Ω → E, where E is a Banach space, which has a weak p-order defines a cylindrical element . Thus we can define the conditional expectation of x(·)
It should be noticed that it is not always possible to define the conditional expectation of a Banach space valued function which is not strongly integrable. Indeed one can find (see [24]) a Pettis integrable function x(·) with values in a reflexive Banach space E and a sub σ-algebra for which does not exist any measurable function y(·) : Ω → E such that
However, we have shown above that this conditional expectation exists as a cylindrical element although not generated by a measurable function. Thus the replacement of Pettis integrable functions by the corresponding cylindrical elements allows to give a meaning to a generalization of the concept of conditional expectation.
Let us assume that E is a complete l.c.s. and a linear ordered set. A family of cylindrical elements , , will be called the p-cylindrical process. If each Xt is Pettis integrable then the process will be also called Pettis integrable. Recall that Pettis integrability is equivalent continuity - Proposition 1.
Let be a family of σ-fields such that and , for t1 < t2. A p-cylindrical process , where p ≥ 1, is called p-cylindrical martingale if it is adapted with respect to , each Xt is continuous, and , for s < t.
It is easy to show that a τ-continuous p-cylindrical process is p-cylindrical martingale if and only if is a real martingale for each x′ ∈ E′. The proposition below shows that for cylindrical martingales we have an analog of the classical convergence theorem (see [25]).
Proposition 5. Let be a discrete time p-cylindrical martingale with respect to , p > 1, and assume that is barreled Barreled space. If
then there exists a continuous cylindrical element such that
and Xt converges to X in Lp norm.
This proposition is not true in the case p = 1. However assuming that
we obtain an analog of Proposition 5.
In the case of continuous time we can obtain similar results under the additional assumption of right continuity of the considered martingales. The assumption of right continuity of a martingale {mt} allows to define the stochastic integral ∫f (t)dmt, where f (t) is a Borel measurable function (see [26]).
The object of our interest will be the cylindrical martingales generated by a single cylindrical element, like in the thesis of Proposition 5, associated with the filtration determined by a given. K-flow.
Let be a family of σ-algebras of a given K-flow and {Mt} an associated operator valued martingale i.e., a family of bounded operators on Lp, p ≥ 1, such that {Mt} is a right continuous martingale with respect to . In the classical approach (see [22] for the details) it was assumed that {Mt} acts on L2, has orthogonal increments: for s1 ≤ s2 < t1 ≤ t2 (Ms2 − Ms1)(Mt2 − Mt1) = 0 and that M∞ is a positive one-to-one operator satisfying
where Ut is given by (6). It was shown that for a fixed monotonic function f on ℝ the transformation
is well-defined on the domain Df which is dense in L2. Taking f (t) = t we obtain the time operator. If we assume that f is a positive non-increasing function on ℝ with , and such that for each t ∈ ℝ the quotient f (s)/f (s − t) is a bounded and non-increasing function of s then (11) defines the discussed above similarity transformation Λ which in turn defines the Markov semigroup (9).
Note that taking Mt = Et, where , we obtain an operator valued martingale satisfying the required properties. Moreover, a cylindrical element X with values in Lp defines the p-cylindrical martingale {EtX}. Therefore, in the case p = 2 we can apply directly the above construction putting in (11) Xx′, x′ ∈ E′, instead of ρ. Replacing the space L2 by L2 ⊖ 1 we can omit the second component in (11) obtaining the following operator f (T) acting on cylindrical elements
We can not apply directly the above approach in the case p ≥ 1, p ≠ 2. Here we have to use a different approach to stochastic integration. The theory of integrals ∫f (t)dmt, where {mt} is a p-integrable martingale can be found in Bichteler's paper [26]. This integral is defined first for simple functions (or processes) f (t). Then it is said that {mt} is an Lp-integrator if {mt} is p-integrable and the linear operator f ↦ ∫f (t)dmt from the space of elementary integrands to Lp has an extension satisfying the dominated convergence theorem (see Def.1 in [26]).
Theorem 1. Let E be an l.c.s. and a K-flow. If 1 < p < ∞ then for any simple function f with a bounded support the linear operator on L(E′, Lp)
is correctly defined, for each x ′ ∈ E′, the martingale is an Lp-integrator and we have
where τ is such that f (t) = 0, for |t| > τ and Cp is a constant which depends only on p.
If p = 1 then the above integral exists and the martingale is an L1-integrator under the additional assumption that
Proof. If p > 1 we can apply (3.8) from [26] which says that a p-intergrable martingale is an Lp-integrator. If p = 1 we use Th. 7.2 from [26] and the additional assumption (13) to show that for each x′ ∈ E” the martingale is an L1 integrator. Note that because the martingales satisfy the assumption (13), in the latter case, they are elements of the Hardy space H1, i.e., (10) is satisfied.
It follows from Theorem 1 that f (T) can be defined for simple functions with bounded support. However, because of the dominated convergence theorem we can extend the class of functions taking, for example, f (t) = t to obtain the operator
which acts on the space L(E′, Lp).
Let {Ut} be the evolution group on L(E′, Lp) associated with the transformations {St}, i.e., for X ∈ L(E′, Lp), UtX is a cylindrical element of the form
Using the relation Es+tUt = UtEs valid for conditional expectations associated with the K-system and the evolution {St} on the ordinary Lp-space (see e.g., [21]) we obtain that also
This leads to the following
Corollary. The operator T is a time operator on the space L(E′, Lp) associated with the evolution {Ut}.
We can also take as f a bounded monotonic function with the listed above properties to obtain an analog of the operator Lambda, Λ = f (T). An important example of applications the above construction of T is the possibility to define time operators on the spaces of weakly integrable E-valued functions. This is because the constructed above stochastic integral transforms cylindrical elements into cylindrical elements. If we take as an argument of T the cylindrical element generated by an E valued function then after the transformation it need not to remain a function (see remarks concerning the conditional expectation of Pettis integrable functions). However f (T) leaves the space L(E′, Lp) invariant.
An important question is: When a cylindrical element is generated by a measurable function defined on Ω with values in the vector space E? Similar question concerns martingales: When the integral transformation of a p-cylindrical martingale generated by a vector valued function will be still a function generated martingale? The rest of this section is devoted to an answer to these questions.
Let us introduce first the following definition:
We say that X is p-decomposable, p > 0, if there exists a measurable function x(·) : Ω → E such that
10 Xx′ = 〈x(·), x′〉, for each x′ ∈ E′
20 , for each continuous seminorm ||·|| on E.
Decomposability of a cylindrical element depends both on properties of X as a linear operator and on the topological properties of the vector space E. We will consider the problem of decomposability in both cases. We begin with the dependence of the decomposability of a cylindrical element X : E′ → L1 on the properties of E. It is obvious that if E is finite dimensional then each 1-cylindrical element is 1-decomposable. If E is infinite dimensional then the space of Pettis integrable functions on Ω with values in E, introduced in section 2, is not complete in general and its completion may contain cylindrical elements which are not associated with any measurable function. However, the transformations like conditional expectation or time operator leave invariant. Thus we can ask if there are locally convex spaces for which this completion remains a function space. The next theorem shows such a possibility.
Theorem 2. Let E be a locally convex nuclear Fréchet space. Then each element of is 1-decomposable.
Proof. In the proof we will use some results concerning tensor products of l.c.s. Let us first introduce the notation and remind the relevant facts (see [27]). Let E be an l.c.s., F a Banach space and E ⊗ F the algebraic tensor product. We define two basic topologies on E ⊗ F. First is the ε-topology generated by the seminorms
where U runs over a basis of convex and circled neighborhoods of 0 in E and B is the unit ball in F. By we denote the completion of E ⊗ F in the ε-topology.
The second topology, called the projective topology, is generated by the seminorms
where the infinitum is taken over all representations of the element and U is an absolutely convex neighborhood of 0 in E. By we denote the completion of E ⊗ F in the projective topology.
Note that the ε-topology and the projective topology are respectively the weakest and the strongest topology on the tensor product of two l.c.s. which are generated by cross-seminorms (see [27]).
It is known that if E is a Banach space then is norm isomorphic to the space L1(E) of all E valued Bochner integrable functions f on Ω endowed with the norm . If E is just an l.c.s. then is isomorphic with L1(E) defined as the space of all strongly measurable functions f such that ||f (·)|| is integrable for each semi-norm ||·|| on E.
We have shown in [16] that if E is a separable l.c.s. Fréchet space then can be identified (is isomorhic) with . However, when E is a complete nuclear l.c.s. the latter space is isomorphic to (see [27]). Therefore, each element from is represented by a Bochner integrable function which ends the proof.
It follows from the above theorem that for a nuclear space valued functions the Pettis integrability is equivalent to the Bochner integrability like in the finite dimensional case.
Let now consider the dependence between decomposability and operator properties of cylindrical elements. It is known that if E = H – is a Hilbert space then a 2-cylindrical martingale X : H′ → L2 is 2-decomposable if and only if the mapping
is a Hilbert-Schmidt operator for any t (see [14]).
We can also decompose cylindrical elements by composing them with Hilbert-Schmidt operators or, more generally, with absolutely summing operators. The problem of decomposability of a cylindrical element acting on a Banach space through a composition with an absolutely summing operator has been already resolved (see [25, 28] and references therein). Here, we will resolve this problem in the case of cylindrical elements acting on locally convex spaces.
If E and F are normed spaces and 0 < p < ∞ then a linear operator S : E → F is said to be p-absolutely summing if there exists a constant C such that for each x1, …, xn ∈ E
In the sequel we will use the following Pietsch Majorization Theorem:
Proposition 6. ([29], p. 232) Let E and F be normed spaces. An operator S : E → F is p-absolutely summing, 0 < p < ∞, if there exist a constant C and a Radon probability measure μ on the unit ball U◦ of E′, where U◦ is equipped with the σ(E′, E) - topology, such that
We shall now extend the definition of the p-absolutely summing operatoron operators acting on an l.c.s. with values in a t.v.s. Consider first the case of an operator S : E → F, where F is a quasi-normed space. Recall that a quasi-norm on F is a non-negative positively defined homogenous function ||·|| such that for some r, 0 < r ≤ 1, we have
We then say that the space F is r-normed.
Remark:
(i) An r-normed space is s-normed for 0 < s ≤ r ≤ 1
(ii) If 0 < r ≤ 1 then the space Lr is r-normed.
The definition of a p-absolutely summing operator S : E → F, for E normed and F quasi-normed space, is the same as in the case of normed spaces. Moreover, the Proposition 6 remains true and we have
Proposition 7. ([29]) Let Ω be a compact Hausdorff space and ν a probability measure on Ω. Then the canonical embedding of the space C(Ω) (continuous functions on Ω) into Lp(Ω, ν) is p-absolutely summing for 0 < p < ∞.
Before we turn to the further generalization of the concept of p-absolutely summing operators we shall introduce first some auxiliary normed spaces and decompositions of bounded operators on topological vector spaces.
Let E be an l.c.s. and U an absolutely convex neighborhood of 0 in E. By EU we denote the normed space where pU(·) is the Minkowski functional of U. Let ÊU denotes the completion of EU in the norm pU(·) and ΦU the canonical map from E into EU (or into ÊU). Of course ΦU is continuous. Now, let F be a t.v.s. A subset B of F is said to be p-absolutely convex if whenever it contains x and y it contains all αx + βy with |α|p + |β|p ≤ 1. If p = 1 then B is absolutely convex. We put
and . Then (FB, ||·||B) is p-normed and the canonical injection
ΨB : FB → F is continuous. Moreover, FB is complete if B is complete.
A subset B of F is called quasi-absolutely convex if it is p-absolutely convex for some 0 < p ≤ 1.
Let E be an l.c.s., F be a t.v.s. and S : E → F a bounded linear operator, i.e., such that there exists a neighborhood U of 0 in E for which S(U) is bounded. Then S can be decomposed in the following way
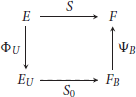
where U is an absolutely convex neighborhood of 0 in E and B is a bounded subset of F. If B can be chosen quasi-absolutely convex, then S0 is a continuous linear operator from the normed space EU into the quasi-normed space FB. Moreover, if B is complete then S0 has the continuous extension from the Banach space ÊU into FB. Note that if F is an l.c.s. then FB is a normed space.
We can now define p-absolutely summing operator on a locally convex space. Let E be an l.c.s. and F be a t.v.s. A linear operator S : E → F is p-absolutely summing, 0 < p < ∞, if there exist an absolutely convex neighborhood U of 0 in E and a bounded quasi-absolutely convex subset B of F such that S0 : EU → FB is p-absolutely summing. This definition is analogous with the definition of nuclear operators on locally convex spaces (see [27]).
The next result gives sufficient conditions for p-decomposability of cylindrical elements. It is an extension of the Kwapien's Theorem ([28], Th. 2) as well as ([25], Th. 1.1) on the case of absolutely summing operators on locally convex spaces. Moreover, the method of absolutely summing operators on locally convex spaces allows to simplify the proof of ([28], Th. 2) and contains the case 0 < p < 1.
Theorem 3. Let E, F be a quasi-complete l.c.s. and let S : E → F be p-absolutely summing linear operator, p > 0. If is a continuous cylindrical element and either p ≥ 1 or F′ has the approximation property then
(i) Y = X ◦ S* is p-decomposable by an F valued function y(·)
(ii) If Lp is separable then for each absolutely convex neighborhood U of 0 in E and each continuous seminorm ||·|| on F we have
where μ is a Radon measure on (U◦, σ(E′, E)) and C is some constant.
Proof. Let U be an absolutely convex closed neighborhood of 0 in E and B an absolutely convex closed subset of F such that S0 : EU → FB is p-absolutely summing. Because F is quasi-complete, FB is a Banach space and S0 extends to the map , which is also p-absolutely summing. Since and , . Moreover is continuous. Therefore applying Kwapien's Theorem ([28], Th.2) to the operators and acting on Banach spaces, we obtain that that is p-decomposable by (if F′ has the approximation property then also has it (cf. [27] III, 9.2). Using the continuity of the cannonical injection ΨB : FB → F we see that the function
decomposes X ◦ S*. Furthermore, let us note that U◦ is the unit ball in the space which is compact in σ(E′, E)-topology. Thus using ([25] Th.1.1 (ii) we obtain the inequality
where the measure μ is defined as in Proposition 6. If ||·|| is a continuous seminorm on F then for some constant C1. This ends the proof of this theorem.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Misra B. Prigogine I. Lyapunov variable: entropy and measurement in quantum mechanics. Proc Natl Acad Sci USA. (1979) 76:4768–72.
3. Misra B, Prigogine I, Courbage M. From deterministic dynamics to probabilistic descriptions. Phys A. (1979) 98 :1–26.
4. Gómez-Cubillo F. Solution of the MPC problem in terms of the Sz.-Nagy-Foias dilation theory. Infin Dimens Anal Quant Probab Relat Top. (2008) 11:73–96. doi: 10.1142/S0219025708002987
5. Courbage M. Intrinsic irreversibility of Kolmogorov dynamical systems. Phys A. (1983) 122:459–82.
6. Sorger U, Suchanecki Z. Nonlocalization properties of time operators transformations. Int J Theor Phys. (2015) 54:787–800. doi: 10.1007/s10773-014-2270-y
7. Suchanecki Z, Antoniou I, Tasaki S. Nonlocality of the Misra-Prigogine-courbage semigroup. J Stat Phys. (1994) 75:919–28.
8. Antoniou I, Suchanecki Z. Non-uniform time operator, chaos and wavelets on the interval. Chaos Solitons Fractals. (2000) 11:423–35. doi: 10.1016/S0960-0779(98)00310-5
9. Gómez F. Unitary quasi-affine transforms of contractions. J Math Anal Appl. (2009) 351:84–96. doi: 10.1016/j.jmaa.2008.10.001
10. Gómez-Cubillo F, Suchanecki Z. Breakdown of time-reversal symmetry: intrinsic randomness, time operator, scattering. J Geom Symmetry Phys. (2008) 11:33–40. doi: 10.7546/jgsp-11-2008-33-40
11. Gómez-Cubillo F, Suchanecki Z, Villullas S. On lambda and time operators: the inverse intertwining problem revisited. Int J Theoret Phys. (2011) 50:2074–83. doi: 10.1007/s10773-010-0573-1
12. Sorger U, Suchanecki Z. Time operators and approximation of continuous functions. Int J Theoret Phys. (2008) 47:1792–808. doi: 10.1007/s10773-007-9622-9
13. Suchanecki Z, Gómez-Cubillo F. Evolution semigroups and time operators on Banach spaces. J Math Anal Appl. (2010) 371:454–64. doi: 10.1016/j.jmaa.2010.05.049
16. Suchanecki Z. Cylindrical measures and cylindrical processes on locally convex spaces. Probability Math Stat. (1981) 2:71–81.
17. Suchanecki Z. Remarks on Pettis integrability of cylindrical processes. Lecture Notes Math. (1980) 828:269–73.
18. Meyer PA. Probability and Potentials. Waltham, MA; Toronto, ON; London: Blaisdell Publishing Company (1966).
19. Badrikian A. Séminaire sur les fonctions Aleatoires Linéaires et les Measures Cylindriques, Vol. 139. Lecture Notes in Math. Springer (1970).
20. Gómez-Cubillo F, Suchanecki Z. On Lambda transformation approach to the theory of irreversibility. Bussei Kenkyu. (2011/12) 97:398–413. Available online at: http://hdl.handle.net/2433/169637
22. Suchanecki Z, Weron A, Rybaczuk M, Weron K. An explicit approach to the Λ-operator and H-Theorem in the Prigogine's theory of irreversibility. Phys A. (1989) 155:385–400.
23. Suchanecki Z. An L1 extension of stochastic dynamics for irreversible systems. Lecture Notes Math. (1989) 1391:367–74.
24. Rybakov VI. On conditional expectations of Pettis integrable functions. Mat Zametki. (1971) 10:565–70.
25. Suchanecki Z, Weron A. Decomposability of cylindrical martingales and absolutely summing operators. Math Z. (1984) 185:271–80.
28. S. Kwapień On a theorem of L. Schwartz and its applications to absolutely summing operators. Studia Math. (1970) 38:193–201.
Keywords: time operator, pettis integral, absolutely summing operator, decomposability, cylindrical elements, cylindrical martingales
Citation: Suchanecki Z (2020) Time Operators Determined by Cylindrical Processes. Front. Phys. 8:252. doi: 10.3389/fphy.2020.00252
Received: 22 March 2019; Accepted: 09 June 2020;
Published: 28 July 2020.
Edited by:
Luiz A. Manzoni, Concordia College, United StatesReviewed by:
Klas Pettersson, Arctic University of Norway, NorwayIllia Karabash, Institute of Applied Mathematics and Mechanics (NASU), Ukraine
Copyright © 2020 Suchanecki. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zdzislaw Suchanecki, enN1Y2hhbmVAcHQubHU=
 Zdzislaw Suchanecki
Zdzislaw Suchanecki