Solitons and Jacobi Elliptic Function Solutions to the Complex Ginzburg–Landau Equation

The complex Ginzburg–Landau (CGL) equation which describes the soliton propagation in the presence of the detuning factor is firstly considered; then its solitons as well as Jacobi elliptic function solutions are obtained systematically using a modified Jacobi elliptic expansion method. In special cases, several dark and bright soliton solutions to the CGL equation are retrieved when the modulus of ellipticity approaches unity. The results presented in the current work can help to complete previous studies on the complex Ginzburg–Landau equation.

Introduction

One of the very hot topics in many of today's research is the search for exact solutions of non-linear partial differential (NLPD) equations. As it is known, exact solutions of NLPD equations play a significant role in a wide variety of applied sciences and provide meaningful information about physical phenomena modeled by non-linear partial differential equations. Fortunately, with the development of symbolic computation packages, a variety of systematic methods [1–34] (Hosseini et al., under review) have been proposed to obtain exact solutions of NLPD equations. Many of these methods are based on considering the solution as a finite series in terms of the solutions of well-known ordinary differential equations such as Bernoulli, Riccati, and Jacobi equations. Among these methods, the modified Jacobi elliptic expansion (MJEE) method [21–27] has achieved a great deal of attention. For instance, El-Sheikh et al. [25] extracted elliptic function solutions of non-linear Boussinesq-like equations using the MJEE method. Hosseini et al. [26] applied the MJEE method to find optical solitons of the Fokas–Lenells equation. Hosseini et al. [27] also obtained exact solutions of a (3+1)-dimensional resonant non-linear Schrödinger equation through the MJEE method. Such results encouraged the authors of the present article to employ the modified Jacobi elliptic expansion method to derive complex wave structures of the following complex Ginzburg–Landau equation [28–34] (Hosseini et al., under review)

$\begin{array}{l}i\frac{\partial u\left(x,t\right)}{\partial t}+{\alpha }_1\frac{{\partial }^{2}u\left(x,t\right)}{\partial x^2}+{\alpha }_2{|u\left(x,t\right)|}^{2}u\left(x,t\right)-\frac{{\alpha }_3}{{|u\left(x,t\right)|}^2{u}^{*}\left(x,t\right)}(2{|u\left(x,t\right)|}^2\frac{{\partial }^2{|u\left(x,t\right)|}^2}{\partial x^2}\\ -{\left(\frac{\partial {|u\left(x,t\right)|}^2}{\partial x}\right)}^2)-{\alpha }_{4}u\left(x,t\right)=0,& (1)\end{array}$

which describes the soliton propagation in the presence of the detuning factor. In the CGL Equation (1), α₁ and α₂ are the coefficients of the group velocity dispersion and the Kerr law non-linearity while α₃ and α₄ denote the coefficients of the perturbation effects, especially α₄ comes from the detuning effect. Recently, the main subject of a lot of studies has been focused on the complex Ginzburg–Landau equation and its exact solutions. Osman et al. [30] reported several complex wave structures to the CGL equation using a modified auxiliary equation method. In another paper, Abdou et al. [31] obtained dark-singular combo solitons of the CGL equation through the extended Jacobi elliptic expansion method. Solitons of the CGL equation were derived by Arshed in [32] with the help of the exp(−φ(ϵ))-expansion method. Rezazadeh [33] listed a series of soliton solutions to the CGL equation using a new extended direct algebraic method, and finally, Arnous et al. [34] employed the modified simple equation method to generate optical solitons of the CGL equation. This paper is arranged as follows: In Section the modified Jacobi elliptic expansion method and its fundamental, the modified Jacobi elliptic expansion method and its fundamental is reviewed. In Section complex Ginzburg–Landau equation and its exact solutions, exact solutions of the CGL equation are given by applying the MJEE method. Section conclusion is devoted to summarizing the conclusions.

The Modified Jacobi Elliptic Expansion Method and Its Fundamental

To explain the basic ideas of the modified Jacobi elliptic expansion method, we consider the following NLPD equation

$\begin{array}{l}P(u,u_x,u_t,u_{xx},u_{xt},u_{tt},...)=0,P\text{ is a function},u\text{ is}\\ \text{an unknown}& (2)\end{array}$

and suppose that it can be converted to an ODE as follows

$\begin{array}{ll}O\left(U,U^{\prime },U^{″},\mathrm{...}\right)=0,\prime =\frac{d}{d\xi },& (3)\end{array}$

through considering the transformation u(x, t) = U(ξ)e^{i(−κx+ωt+θ)} which ξ = x − νt.

Now, assume that the non-trivial solution of Equation (3) can be expressed as

$\begin{array}{l}U(\xi )=c_0+{\displaystyle \sum _{i=1}^N}{\left(\frac{J(\xi )}{1+J^2(\xi )}\right)}^{i-1}\left(c_i\frac{J(\xi )}{1+J^2(\xi )}+d_i\frac{1-J^2(\xi )}{1+J^2(\xi )}\right),\\ c_{N}or{d}_N\ne 0,& (4)\end{array}$

where c₀, c_i, and d_i (1 ≤ i ≤ N) are constants to be found later, N is the balance number, and J(ξ) is a known function satisfying the following Jacobi elliptic equation

$\begin{array}{ll}{(J^{\prime }(\xi ))}^2=D+E{J}^2(\xi )+F{J}^4(\xi ).& (5)\end{array}$

The Jacobi elliptic Equation (5) admits the following exact solutions (See Table 1):

TABLE 1

Table 1. Jacobi elliptic function solutions of Equation (5).

By substituting the solution (4) along with the Jacobi elliptic Equation (5) into Equation (3) and performing a series of calculations, we arrive at a set of non-linear algebraic equations whose solution yields exact solutions of the NLPD Equation (2).

The Jacobi elliptic functions include some interesting properties that are reviewed below [35]:

• sn²(ξ) + cn²(ξ) = 1.

• sn(ξ) = sn(ξ, m) → tanh(ξ) when m → 1.

• ns(ξ) = (sn(ξ, m))⁻¹ → coth(ξ) when m → 1.

Complex Ginzburg–Landau Equation and its Exact Solutions

To gain exact solutions of the CGL equation, we first apply a complex transformation in the form below

$\begin{array}{l}u(x,t)=U(\xi )e^{i(-\kappa x+\omega t+\theta )},\xi =x-\nu t,\end{array}$

where ν is the velocity of the soliton whereas κ, ω, and θ are the wave number, the frequency, and the phase constant, respectively. Such a complex transformation results in

$\begin{array}{ll}(-{\alpha }_1+4{\alpha }_3)\frac{d^{2}U(\xi )}{d{\xi }^2}+({\kappa }^2{\alpha }_1+\omega +{\alpha }_4)U(\xi )-{\alpha }_2{U}^3(\xi )=0& (6)\end{array}$

where the velocity of the soliton is

$\begin{array}{l}\nu =-2\kappa {\alpha }_1.\end{array}$

Now, based on the Jacobi elliptic expansion method and the balance number N = 1, the solution of Equation (6) is considered as follows

$\begin{array}{l}U(\xi )=c_0+c_1\frac{J(\xi )}{1+J^2(\xi )}+c_2\frac{1-J^2(\xi )}{1+J^2(\xi )},c_2=d_1,\end{array}$

where c₀, c₁, and c₂ are constants to be found later. By inserting the above solution along with the Jacobi elliptic Equation (5) into Equation (6) and performing a series of calculations, we will get a set of non-linear algebraic equations as

$\begin{array}{l}-{\kappa }^2{\alpha }_1{c}_0-{\kappa }^2{\alpha }_1{c}_2+{\alpha }_2{c_0}^3+3{\alpha }_2{c_0}^2{c}_2+3{\alpha }_2{c}_0{c_2}^2+{\alpha }_2{c_2}^3\\ -4D{\alpha }_1{c}_2+16D{\alpha }_3{c}_2-\omega c_0-\omega c_2-{\alpha }_4{c}_0-{\alpha }_4{c}_2=0,\\ -{\kappa }^2{\alpha }_1{c}_1+3{\alpha }_2{c_0}^2{c}_1+6{\alpha }_2{c}_0{c}_1{c}_2+3{\alpha }_2{c}_1{c_2}^2-6D{\alpha }_1{c}_1\\ +24D{\alpha }_3{c}_1+E{\alpha }_1{c}_1-4E{\alpha }_3{c}_1-\omega c_1-{\alpha }_4{c}_1=0,\\ -3{\kappa }^2{\alpha }_1{c}_0-{\kappa }^2{\alpha }_1{c}_2+3{\alpha }_2{c_0}^3+3{\alpha }_2{c_0}^2{c}_2+3{\alpha }_2{c}_0{c_1}^2\\ \\ -3{\alpha }_2{c}_0{c_2}^2+3{\alpha }_2{c_1}^2{c}_2-3{\alpha }_2{c_2}^3+12D{\alpha }_1{c}_2-48D{\alpha }_3{c}_2\\ -8E{\alpha }_1{c}_2+32E{\alpha }_3{c}_2-3\omega c_0-\omega c_2-3{\alpha }_4{c}_0-{\alpha }_4{c}_2=0,\\ -2{\kappa }^2{\alpha }_1{c}_1+6{\alpha }_2{c_0}^2{c}_1+{\alpha }_2{c_1}^3-6{\alpha }_2{c}_1{c_2}^2+2D{\alpha }_1{c}_1-8D{\alpha }_3{c}_1\\ -6E{\alpha }_1{c}_1+24E{\alpha }_3{c}_1+2F{\alpha }_1{c}_1-8F{\alpha }_3{c}_1-2\omega c_1-2{\alpha }_4{c}_1=0,\\ -3{\kappa }^2{\alpha }_1{c}_0+{\kappa }^2{\alpha }_1{c}_2+3{\alpha }_2{c_0}^3-3{\alpha }_2{c_0}^2{c}_2+3{\alpha }_2{c}_0{c_1}^2\\ -3{\alpha }_2{c}_0{c_2}^2-3{\alpha }_2{c_1}^2{c}_2+3{\alpha }_2{c_2}^3+8E{\alpha }_1{c}_2-32E{\alpha }_3{c}_2\\ -12F{\alpha }_1{c}_2+48F{\alpha }_3{c}_2-3\omega c_0+\omega c_2-3{\alpha }_4{c}_0+{\alpha }_4{c}_2=0,\\ -{\kappa }^2{\alpha }_1{c}_1+3{\alpha }_2{c_0}^2{c}_1-6{\alpha }_2{c}_0{c}_1{c}_2+3{\alpha }_2{c}_1{c_2}^2+E{\alpha }_1{c}_1\\ -4E{\alpha }_3{c}_1-6F{\alpha }_1{c}_1+24F{\alpha }_3{c}_1-\omega c_1-{\alpha }_4{c}_1=0,\\ -{\kappa }^2{\alpha }_1{c}_0+{\kappa }^2{\alpha }_1{c}_2+{\alpha }_2{c_0}^3-3{\alpha }_2{c_0}^2{c}_2+3{\alpha }_2{c}_0{c_2}^2-{\alpha }_2{c_2}^3\\ +4F{\alpha }_1{c}_2-16F{\alpha }_3{c}_2-\omega c_0+\omega c_2-{\alpha }_4{c}_0+{\alpha }_4{c}_2=0.\end{array}$

Solving the above set of non-linear algebraic equations leads to the following cases:

Case 1. When D = 1, E = −(m² + 1), and F = m², we obtain

• $c_0=0,c_1=\pm \sqrt{-\frac{32{\alpha }_1-128{\alpha }_3}{{\alpha }_2}},c_2=0,\omega =-{\kappa }^2{\alpha }_1-8{\alpha }_1+32{\alpha }_3-{\alpha }_4,m=1,$

• $c_0=0,c_1=0,c_2=\pm \sqrt{-\frac{-8{\alpha }_1+32{\alpha }_3}{{\alpha }_2}},\omega =-{\kappa }^2{\alpha }_1+4{\alpha }_1-16{\alpha }_3-{\alpha }_4,m=1,$

• $c_0=0,c_1=\pm \sqrt{-\frac{8{\alpha }_1-32{\alpha }_3}{{\alpha }_2}},c_2=\pm \sqrt{-\frac{-2{\alpha }_1+8{\alpha }_3}{{\alpha }_2}},\omega =-{\kappa }^2{\alpha }_1-2{\alpha }_1+8{\alpha }_3-{\alpha }_4,m=1,$

• $c_0=0,c_1=\mp \sqrt{-\frac{8{\alpha }_1-32{\alpha }_3}{{\alpha }_2}},c_2=\pm \sqrt{-\frac{-2{\alpha }_1+8{\alpha }_3}{{\alpha }_2}},\omega =-{\kappa }^2{\alpha }_1-2{\alpha }_1+8{\alpha }_3-{\alpha }_4,m=1.$

Now, the following exact solutions to the CGL equation are retrieved

$\begin{array}{l}{u}_{1,2}\left(x,t\right)=\pm \sqrt{-\frac{32{\alpha }_1-128{\alpha }_3}{{\alpha }_2}}\frac{\tanh \left(x+2\kappa {\alpha }_{1}t\right)}{1+{\tanh }^2\left(x+2\kappa {\alpha }_{1}t\right)}\\ \times e^{i\left(-\kappa x+\left(-{\kappa }^2{\alpha }_1-8{\alpha }_1+32{\alpha }_3-{\alpha }_4\right)t+\theta \right)},\\ u_{3,4}\left(x,t\right)=\pm \sqrt{-\frac{-8{\alpha }_1+32{\alpha }_3}{{\alpha }_2}}\frac{1-{\tanh }^2\left(x+2\kappa {\alpha }_{1}t\right)}{1+{\tanh }^2\left(x+2\kappa {\alpha }_{1}t\right)}\\ \times e^{i\left(-\kappa x+\left(-{\kappa }^2{\alpha }_1+4{\alpha }_1-16{\alpha }_3-{\alpha }_4\right)t+\theta \right)},\\ u_{5,6}\left(x,t\right)=(\pm \sqrt{-\frac{8{\alpha }_1-32{\alpha }_3}{{\alpha }_2}}\frac{\tanh \left(x+2\kappa {\alpha }_{1}t\right)}{1+{\tanh }^2\left(x+2\kappa {\alpha }_{1}t\right)}\\ \pm \sqrt{-\frac{-2{\alpha }_1+8{\alpha }_3}{{\alpha }_2}}\frac{1-{\tanh }^2\left(x+2\kappa {\alpha }_{1}t\right)}{1+{\tanh }^2\left(x+2\kappa {\alpha }_{1}t\right)})\\ \times e^{i\left(-\kappa x+\left(-{\kappa }^2{\alpha }_1-2{\alpha }_1+8{\alpha }_3-{\alpha }_4\right)t+\theta \right)},\\ u_{7,8}\left(x,t\right)=(\mp \sqrt{-\frac{8{\alpha }_1-32{\alpha }_3}{{\alpha }_2}}\frac{\tanh \left(x+2\kappa {\alpha }_{1}t\right)}{1+{\tanh }^2\left(x+2\kappa {\alpha }_{1}t\right)}\\ \pm \sqrt{-\frac{-2{\alpha }_1+8{\alpha }_3}{{\alpha }_2}}\frac{1-{\tanh }^2\left(x+2\kappa {\alpha }_{1}t\right)}{1+{\tanh }^2\left(x+2\kappa {\alpha }_{1}t\right)})\\ \times e^{i\left(-\kappa x+\left(-{\kappa }^2{\alpha }_1-2{\alpha }_1+8{\alpha }_3-{\alpha }_4\right)t+\theta \right)}.\end{array}$

The 3-dimensional graphs of |u₁(x, t)| and |u₃(x, t)| which indicate dark and bright soliton solutions have been shown in Figure 1 for a series of the involved parameters.

FIGURE 1

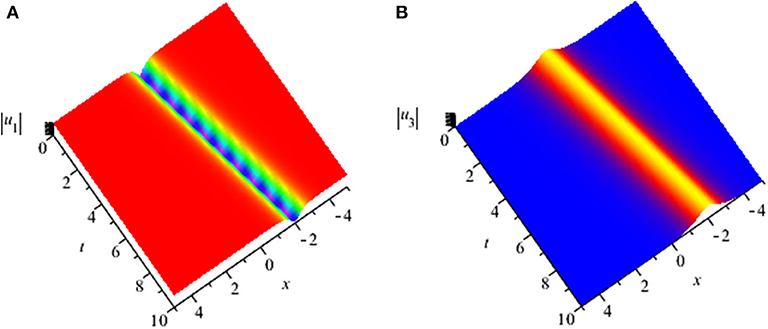
Figure 1. (A) The 3-dimensional graph of |u₁(x, t)| for α₁ = 1, α₂ = 1, α₃ = 1, α₄ = 1, κ = 0.1, and θ = 0; (B) The 3-dimensional graph of |u₃(x, t)| for α₁ = 1, α₂ = 1, α₃ = 1, α₄ = 1, κ = 0.1, and θ = 0.

Case 2. When D = 1 − m², E = 2m² − 1, and F = −m², we acquire

$\begin{array}{l}{c}_0=\pm \sqrt{-\frac{-{\alpha }_1+4{\alpha }_3}{2{\alpha }_2}},c_1=0,c_2=\pm \frac{{\alpha }_1-4{\alpha }_3}{{\alpha }_2\sqrt{-\frac{-{\alpha }_1+4{\alpha }_3}{2{\alpha }_2}}},\\ \omega =-{\kappa }^2{\alpha }_1+\frac{5}{2}{\alpha }_1-10{\alpha }_3-{\alpha }_4,m=\frac{1}{2}.\end{array}$

Now, the following Jacobi elliptic function solutions to the CGL equation are derived.

$\begin{array}{l}{u}_{9,10}(x,t)=\pm \sqrt{-\frac{-{\alpha }_1+4{\alpha }_3}{2{\alpha }_2}}\\ \pm \frac{{\alpha }_1-4{\alpha }_3}{{\alpha }_2\sqrt{-\frac{-{\alpha }_1+4{\alpha }_3}{2{\alpha }_2}}}\frac{1-c{n}^2\left(x+2\kappa {\alpha }_{1}t,\frac{1}{2}\right)}{1+c{n}^2\left(x+2\kappa {\alpha }_{1}t,\frac{1}{2}\right)}\\ \times e^{i(-\kappa x+(-{\kappa }^2{\alpha }_1+\frac{5}{2}{\alpha }_1-10{\alpha }_3-{\alpha }_4)t+\theta )}.\end{array}$

Case 3. When D = m², E = −(m² + 1), and F = 1, we obtain

• $c_0=0,c_1=\pm \sqrt{-\frac{32{\alpha }_1-128{\alpha }_3}{{\alpha }_2}},c_2=0,\omega =-{\kappa }^2{\alpha }_1-8{\alpha }_1+32{\alpha }_3-{\alpha }_4,m=1,$

• $c_0=0,c_1=0,c_2=\pm \sqrt{-\frac{-8{\alpha }_1+32{\alpha }_3}{{\alpha }_2}},\omega =-{\kappa }^2{\alpha }_1+4{\alpha }_1-16{\alpha }_3-{\alpha }_4,m=1,$

• $c_0=0,c_1=\pm \sqrt{-\frac{8{\alpha }_1-32{\alpha }_3}{{\alpha }_2}},c_2=\pm \sqrt{-\frac{-2{\alpha }_1+8{\alpha }_3}{{\alpha }_2}},\omega =-{\kappa }^2{\alpha }_1-2{\alpha }_1+8{\alpha }_3-{\alpha }_4,m=1,$

• $c_0=0,c_1=\mp \sqrt{-\frac{8{\alpha }_1-32{\alpha }_3}{{\alpha }_2}},c_2=\pm \sqrt{-\frac{-2{\alpha }_1+8{\alpha }_3}{{\alpha }_2}},\omega =-{\kappa }^2{\alpha }_1-2{\alpha }_1+8{\alpha }_3-{\alpha }_4,m=1.$

Now, the following exact solutions to the CGL equation are retrieved

$\begin{array}{l}{u}_{11,12}\left(x,t\right)=\pm \sqrt{-\frac{32{\alpha }_1-128{\alpha }_3}{{\alpha }_2}}\frac{\coth \left(x+2\kappa {\alpha }_{1}t\right)}{1+{\coth }^2\left(x+2\kappa {\alpha }_{1}t\right)}\\ \times e^{i\left(-\kappa x+\left(-{\kappa }^2{\alpha }_1-8{\alpha }_1+32{\alpha }_3-{\alpha }_4\right)t+\theta \right)},\\ u_{13,14}\left(x,t\right)=\pm \sqrt{-\frac{-8{\alpha }_1+32{\alpha }_3}{{\alpha }_2}}\frac{1-{\coth }^2\left(x+2\kappa {\alpha }_{1}t\right)}{1+{\coth }^2\left(x+2\kappa {\alpha }_{1}t\right)}\\ \times e^{i\left(-\kappa x+\left(-{\kappa }^2{\alpha }_1+4{\alpha }_1-16{\alpha }_3-{\alpha }_4\right)t+\theta \right)},\\ u_{15,16}\left(x,t\right)=(\pm \sqrt{-\frac{8{\alpha }_1-32{\alpha }_3}{{\alpha }_2}}\frac{\coth \left(x+2\kappa {\alpha }_{1}t\right)}{1+{\coth }^2\left(x+2\kappa {\alpha }_{1}t\right)}\\ \pm \sqrt{-\frac{-2{\alpha }_1+8{\alpha }_3}{{\alpha }_2}}\frac{1-{\coth }^2\left(x+2\kappa {\alpha }_{1}t\right)}{1+{\coth }^2\left(x+2\kappa {\alpha }_{1}t\right)})\\ \times e^{i\left(-\kappa x+\left(-{\kappa }^2{\alpha }_1-2{\alpha }_1+8{\alpha }_3-{\alpha }_4\right)t+\theta \right)},\\ u_{17,18}\left(x,t\right)=(\mp \sqrt{-\frac{8{\alpha }_1-32{\alpha }_3}{{\alpha }_2}}\frac{\coth \left(x+2\kappa {\alpha }_{1}t\right)}{1+{\coth }^2\left(x+2\kappa {\alpha }_{1}t\right)}\\ \pm \sqrt{-\frac{-2{\alpha }_1+8{\alpha }_3}{{\alpha }_2}}\frac{1-{\coth }^2\left(x+2\kappa {\alpha }_{1}t\right)}{1+{\coth }^2\left(x+2\kappa {\alpha }_{1}t\right)})\\ \times e^{i\left(-\kappa x+\left(-{\kappa }^2{\alpha }_1-2{\alpha }_1+8{\alpha }_3-{\alpha }_4\right)t+\theta \right)}.\end{array}$

The 3-dimensional graphs of |u₁₁(x, t)| and |u₁₃(x, t)| which denote dark and bright soliton solutions have been presented in Figure 2 for a series of the involved parameters.

FIGURE 2

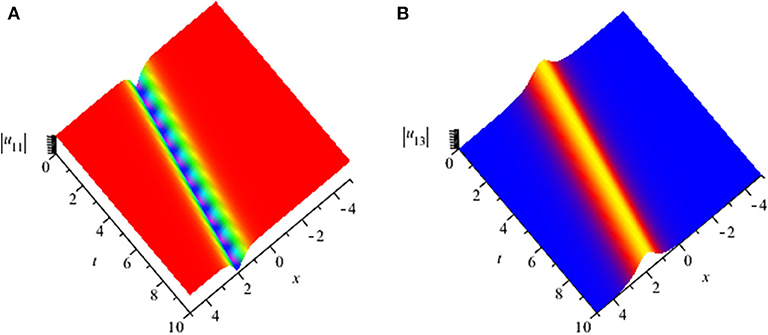
Figure 2. (A) The 3-dimensional graph of |u₁₁(x, t)| for α₁ = 1, α₂ = 1, α₃ = 1, α₄ = 1, κ = −0.1, and θ = 0; (B) The 3-dimensional graph of |u₁₃(x, t)| for α₁ = 1, α₂ = 1, α₃ = 1, α₄ = 1, κ = −0.1, and θ = 0.

Case 4. When D = −m², E = 2m² − 1, and F = 1 − m², we acquire

$\begin{array}{l}{c}_0=\pm \sqrt{-\frac{-{\alpha }_1+4{\alpha }_3}{2{\alpha }_2}},c_1=0,c_2=\mp \frac{{\alpha }_1-4{\alpha }_3}{{\alpha }_2\sqrt{-\frac{-{\alpha }_1+4{\alpha }_3}{2{\alpha }_2}}},\\ \omega =-{\kappa }^2{\alpha }_1+\frac{5}{2}{\alpha }_1-10{\alpha }_3-{\alpha }_4,m=\frac{1}{2}.& (7)\end{array}$

Now, the following Jacobi elliptic function solutions to the CGL equation are derived.

$\begin{array}{l}{u}_{19,20}(x,t)=\pm \sqrt{-\frac{-{\alpha }_1+4{\alpha }_3}{2{\alpha }_2}}\\ \mp \frac{{\alpha }_1-4{\alpha }_3}{{\alpha }_2\sqrt{-\frac{-{\alpha }_1+4{\alpha }_3}{2{\alpha }_2}}}\frac{1-n{c}^2\left(x+2\kappa {\alpha }_{1}t,\frac{1}{2}\right)}{1+n{c}^2\left(x+2\kappa {\alpha }_{1}t,\frac{1}{2}\right)}\\ \times e^{i(-\kappa x+(-{\kappa }^2{\alpha }_1+\frac{5}{2}{\alpha }_1-10{\alpha }_3-{\alpha }_4)t+\theta )}.\end{array}$

Conclusion

The complex Ginzburg–Landau equation as a famous NLPD equation was studied successfully in the current paper. A modified version of the Jacobi elliptic expansion method was formally adopted to carry out this goal. A wide variety of exact solutions to the CGL equation in the presence of the detuning factor were derived. Particularly, several dark and bright soliton solutions were derived when the modulus of ellipticity approaches unity. Although, the exact solutions given in the present paper provide useful information about the complex Ginzburg–Landau equation, seeking other exact solutions of the CGL equation can be considered as an important task in our future works.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

KH and DB: conceptualization, project administration, and Supervision. KH: data curation and visualization. KH and MM: formal analysis, investigation, and writing—original draft. MA and DB: funding acquisition. KH, MM, MO, and MA: methodology, software, and validation. KH, MM, MO, MA, and DB: resources. KH, MM, and MO: writing—review editing. All persons who meet authorship criteria are listed as authors, and all authors certify that they have participated sufficiently in the work to take public responsibility for the content, including participation in the concept, design, analysis, writing, or revision of the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Biswas A, Ekici M, Triki H, Sonmezoglu A, Mirzazadeh M, Zhou Q, et al. Resonant optical soliton perturbation with anti-cubic non-linearity by extended trial function method. Optik. (2018) 156:784–90. doi: 10.1016/j.ijleo.2017.12.035

CrossRef Full Text | Google Scholar

2. Biswas A, Ekici M, Sonmezoglu A, Alqahtani RT. Sub-pico-second chirped optical solitons in mono-mode fibers with Kaup–Newell equation by extended trial function method. Optik. (2018) 168:208–16. doi: 10.1016/j.ijleo.2018.04.069

CrossRef Full Text | Google Scholar

3. Lu D, Seadawy A, Arshad M. Applications of extended simple equation method on unstable non-linear Schrödinger equations. Optik. (2017) 140:136–44. doi: 10.1016/j.ijleo.2017.04.032

CrossRef Full Text | Google Scholar

4. Arnous AH, Ullah MZ, Moshokoa SP, Zhou Q, Triki H, Mirzazadeh M, et al. Optical solitons in birefringent fibers with modified simple equation method. Optik. (2017) 130:996–1003. doi: 10.1016/j.ijleo.2016.11.101

CrossRef Full Text | Google Scholar

5. Kudryashov NA. One method for finding exact solutions of non-linear differential equations. Commun Non-Linear Sci Numerical Simulations. (2012) 17:2248–53. doi: 10.1016/j.cnsns.2011.10.016

CrossRef Full Text | Google Scholar

6. Hosseini K, Korkmaz A, Bekir A, Samadani F, Zabihi A, Topsakal M. New wave form solutions of non-linear conformable time-fractional Zoomeron equation in (2+1)-dimensions. Waves Random Complex Media. (2019) (in press). doi: 10.1080/17455030.2019.1579393

CrossRef Full Text | Google Scholar

7. Hosseini K, Yazdani Bejarbaneh E, Bekir A, Kaplan M. New exact solutions of some non-linear evolution equations of pseudoparabolic type. Optical Quantum Electr. (2017) 49:241. doi: 10.1007/s11082-017-1070-z

CrossRef Full Text | Google Scholar

8. Hosseini K, Mayeli P, Kumar D. New exact solutions of the coupled sine-Gordon equations in non-linear optics using the modified Kudryashov method. J Modern Opt. (2018) 65:361–4. doi: 10.1080/09500340.2017.1380857

CrossRef Full Text | Google Scholar

9. Yan C. A simple transformation for non-linear waves. Phys Lett A. (1996) 224:77–84. doi: 10.1016/S0375-9601(96)00770-0

CrossRef Full Text | Google Scholar

10. Kumar D, Hosseini K, Samadani F. The sine-Gordon expansion method to look for the traveling wave solutions of the Tzitzéica type equations in non-linear optics. Optik. (2017) 149:439–46. doi: 10.1016/j.ijleo.2017.09.066

CrossRef Full Text | Google Scholar

11. Ali KK, Wazwaz AM, Osman MS. Optical soliton solutions to the generalized non-autonomous non-linear Schrödinger equations in optical fibers via the sine-Gordon expansion method. Optik. (2019) 204:164132. doi: 10.1016/j.ijleo.2019.164132

CrossRef Full Text | Google Scholar

12. Ali KK, Osman MS, Abdel-Aty M. New optical solitary wave solutions of Fokas–Lenells equation in optical fiber via Sine-Gordon expansion method. Alexandria Eng J. (2020) 59:1191–96. doi: 10.1016/j.aej.2020.01.037

CrossRef Full Text | Google Scholar

13. Hosseini K, Mirzazadeh M, Ilie M, Radmehr S. Dynamics of optical solitons in the perturbed Gerdjikov–Ivanov equation. Optik. (2020) 206:164350. doi: 10.1016/j.ijleo.2020.164350

CrossRef Full Text | Google Scholar

14. Hosseini K, Osman MS, Mirzazadeh M, Rabiei F. Investigation of different wave structures to the generalized third-order non-linear Scrödinger equation. Optik. (2020) 206:164259. doi: 10.1016/j.ijleo.2020.164259

CrossRef Full Text | Google Scholar

15. Hosseini K, Mirzazadeh M, Zhou Q, Liu Y, Moradi M. Analytic study on chirped optical solitons in non-linear metamaterials with higher order effects. Laser Phys. (2019) 29:095402. doi: 10.1088/1555-6611/ab356f

CrossRef Full Text | Google Scholar

16. Liu JG, Osman MS, Zhu WH, Zhou L, Ai GP. Different complex wave structures described by the Hirota equation with variable coefficients in inhomogeneous optical fibers. Appl Phys B. (2019) 125:175. doi: 10.1007/s00340-019-7287-8

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Ghanbari B, Osman MS, Baleanu D. Generalized exponential rational function method for extended Zakharov–Kuzetsov equation with conformable derivative. Modern Phys Lett A. (2019) 34:1950155. doi: 10.1142/S0217732319501554

CrossRef Full Text | Google Scholar

18. Lu D, Tariq KU, Osman MS, Baleanu D, Younis M, Khater MMA. New analytical wave structures for the (3+1)-dimensional Kadomtsev–Petviashvili and the generalized Boussinesq models and their applications. Results Phys. (2019) 14:102491. doi: 10.1016/j.rinp.2019.102491

CrossRef Full Text | Google Scholar

19. Shang Y. Lie algebraic discussion for affinity based information diffusion in social networks, Acta Physica Polonica B. (2015) 46:1567–77. doi: 10.5506/APhysPolB.46.1567

CrossRef Full Text | Google Scholar

20. Shang Y. Analytical solution for an in-host viral infection model with time-inhomogeneous rates. Open Phys. (2017) 15:705–11. doi: 10.1515/phys-2017-0083

CrossRef Full Text | Google Scholar

21. Ma HC, Zhang ZP, Deng AP. A new periodic solution to Jacobi elliptic functions of MKdV equation and BBM equation. Acta Mathematicae Applicatae Sinica. (2012) 28:409–15. doi: 10.1007/s10255-012-0153-7

CrossRef Full Text | Google Scholar

22. Zayed EME, Shohib RMA, Biswas A, Yildirim Y, Mallawi F, Belic MR. Chirped and chirp-free solitons in optical fiber Bragg gratings with dispersive reflectivity having parabolic law non-linearity by Jacobi's elliptic function. Results Phys. (2019) 15:102784. doi: 10.1016/j.rinp.2019.102784

CrossRef Full Text | Google Scholar

23. Zayed EME, Alngar MEM. Optical solitons in birefringent fibers with Biswas–Arshed model by generalized Jacobi elliptic function expansion method. Optik. (2020) 203:163922. doi: 10.1016/j.ijleo.2019.163922

CrossRef Full Text | Google Scholar

24. Hosseini K, Mirzazadeh M, Ilie M, Gómez-Aguilar JF. Biswas–Arshed equation with the beta time derivative: optical solitons and other solutions. Optik. (2020) 217:164801. doi: 10.1016/j.ijleo.2020.164801

CrossRef Full Text | Google Scholar

25. El-Sheikh MMA, Seadawy AR, Ahmed HM, Arnous AH, Rabie WB. Dispersive and propagation of shallow water waves as a higher order non-linear Boussinesq-like dynamical wave equations. Physica A. (2020) 537:122662. doi: 10.1016/j.physa.2019.122662

CrossRef Full Text | Google Scholar

26. Hosseini K, Mirzazadeh M, Vahidi J, Asghari R. Optical wave structures to the Fokas–Lenells equation. Optik. (2020) 207:164450. doi: 10.1016/j.ijleo.2020.164450

CrossRef Full Text | Google Scholar

27. Hosseini K, Matinfar M, Mirzazadeh M. A (3+1)-dimensional resonant non-linear Schrödinger equation and its Jacobi elliptic and exponential function solutions. Optik. (2020) 207:164458. doi: 10.1016/j.ijleo.2020.164458

CrossRef Full Text | Google Scholar

28. Mirzazadeh M, Ekici M, Sonmezoglu A, Eslami M, Zhou Q., Kara AH, et al. Optical solitons with complex Ginzburg–Landau equation. Non-linear Dyn. (2016) 85:1979–2016. doi: 10.1007/s11071-016-2810-5

CrossRef Full Text | Google Scholar

29. Osman MS, Ghanbari B, Machado JAT. New complex waves in non-linear optics based on the complex Ginzburg–Landau equation with Kerr law non-linearity. Eur Phys J Plus. (2019) 134:20. doi: 10.1140/epjp/i2019-12442-4

CrossRef Full Text | Google Scholar

30. Osman MS, Lu D, Khater MMA, Attia RAM. Complex wave structures for abundant solutions related to the complex Ginzburg–Landau model. Optik. (2019) 192:162927. doi: 10.1016/j.ijleo.2019.06.027

CrossRef Full Text | Google Scholar

31. Abdou MA, Soliman AA, Biswas A, Ekici M, Zhou Q, Moshokoa SP. Dark-singular combo optical solitons with fractional complex Ginzburg–Landau equation. Optik. (2018) 171:463–7. doi: 10.1016/j.ijleo.2018.06.076

CrossRef Full Text | Google Scholar

32. Arshed S. Soliton solutions of fractional complex Ginzburg–Landau equation with Kerr law and non-Kerr law media. Optik. (2018) 160:322–32. doi: 10.1016/j.ijleo.2018.02.022

CrossRef Full Text | Google Scholar

33. Rezazadeh H. New solitons solutions of the complex Ginzburg–Landau equation with Kerr law non-linearity. Optik. (2018) 167:218–27. doi: 10.1016/j.ijleo.2018.04.026

CrossRef Full Text | Google Scholar

34. Arnous AH, Seadawy AR, Alqahtani RT, Biswas A. Optical solitons with complex Ginzburg–Landau equation by modified simple equation method. Optik. (2017) 144:475–80. doi: 10.1016/j.ijleo.2017.07.013

CrossRef Full Text | Google Scholar

35. Hancock H. Lectures on the Theory of Elliptic Functions. New York, NY: J. Wiley & Sons (1910).

Google Scholar