Discrete-Event Simulation of an Extended Einstein-Podolsky-Rosen-Bohm Experiment

We use discrete-event simulation to construct a subquantum model that can reproduce the quantum-theoretical prediction for the statistics of data produced by the Einstein-Podolsky-Rosen-Bohm experiment and an extension thereof. This model satisfies Einstein's criterion of locality and generates data in an event-by-event and cause-and-effect manner. We show that quantum theory can describe the statistics of the simulation data for a certain range of model parameters only.

1. Introduction

The Einstein-Podolsky-Rosen thought experiment was introduced to question the completeness of quantum theory [1], “completeness” being defined in reference [1]. Bohm proposed a modified version that employs the spins instead of coordinates and momenta of a two-particle system [2], and is experimentally realizable [3–10]. A key issue in the foundations of physics is whether there exist “local realist” models that yield the statistical results of the quantum-theoretical description of the Einstein-Podolsky-Rosen-Bohm (EPRB) experiment.

In this paper, we take, as operational definition of a local realist model, any model for which

1. all variables, including those representing events which occur at specific locations and specific times, always have definite values,

2. all variables change in time according to an Einstein-local, causal process.

In the literature, one often finds the statement that Bell's theorem [11, 12] rules out any local realist model for the EPRB experiments. In references [11, 12], Bell gives a proof that a correlation C(a, b) of the form

$\begin{array}{l}C(\text{a},\text{b})={\displaystyle \int d\lambda \mu (\lambda )A(\text{a},\lambda )B(\text{b},\lambda ),|A(\text{a},\lambda )|\le 1,|B(\text{b},\lambda )|\le 1,0\le \mu (\lambda ),}\\ {\displaystyle \int d\lambda \mu (\lambda )=1,}& (1)\end{array}$

cannot arbitrarily closely approximate the correlation −a · b for all unit vectors a and b. According to Bell (see reference [12]), this is the theorem. On the other hand, the quantum-theoretical description of the EPRB experiment in terms of two spin-1/2 particles in the singlet state yields the correlation −a · b. Clearly, there is a conflict between the quantum-theoretical model of the EPRB experiment and the model defined by Equation (1). While there can be no doubt about the mathematical correctness of Bell's theorem, the physical relevance of the theorem and its applicability to the data gathered in laboratory EPRB experiments has been under scrutiny since its conception [13–49]. A fundamental problem with the application of Bell's model Equation (1) to this data is the following.

Evidently, in a laboratory EPRB experiment, before one can even think about computing correlations of particle properties, it is necessary to first classify a detection event as corresponding to the arrival of a particle or as something else. Any laboratory EPRB experiment with photons employs a specific, well-defined procedure to identify photons [3–10]. Such a procedure is definitely missing in the model Equation (1) proposed and analyzed by Bell [12]. If the aim is to describe the outcome of a laboratory EPRB experiment, then not incorporating such a procedure in the model is a fallacy which, logically speaking, is not much different from trying to model electrodynamics in terms of electrical phenomena without taking into account the magnetic phenomena. Although it is good practice to analyze the most primitive model first, the observation that it does not agree with experimental results only suggests that it is too primitive. The failure of the primitive model to account for the identification process is the fundamental reason why Bell's theorem cannot have the status of a “no-go” theorem for the existence of a local realist model for a laboratory EPRB experiment.

In this paper, we use the term “subquantum model” to refer to a local realist model of an experiment which satisfies the requirements 1 and 2 and

3. the model can reproduce the statistical results of the quantum-theoretical description of the experiment in an event-by-event, cause-and-effect manner.

The main aim of this paper is to present a subquantum model for the EPRB experiment and an extended version thereof. The latter, which we abbreviate by EEPRB, differs from the standard EPRB experiment in that all the measurements for the four different pairs of settings, required to perform Bell-inequality tests, can be made in one single run instead of four runs of the experiment. As such, the EEPRB experiment is not vulnerable to the contextuality loophole [44]. We adopt the discrete-event simulation (DES) approach, introduced in reference [50], to construct a subquantum model for both the EPRB and EEPRB experiment. This approach has proven fruitful for constructing subquantum models for many fundamental quantum-physics experiments with photons and neutrons [51].

2. Discrete-Event Simulation: General Aspects

DES is a general methodology for modeling the time evolution of a system as a discrete sequence of consecutive events [52, 53]. DES is used in many different branches of science, engineering, economics, finance, etc. [52], but has only fairly recently been adopted as a methodology to construct subquantum models for basic, fundamental quantum physics experiments [50, 51].

In the following, whenever we use the term DES, we mean DES modeling applied to quantum physics problems, not DES in general. The salient features of this particular application of DES are the following.

• Events are the basic building blocks of any DES model, just as points are the basic building blocks of Euclidean geometry. In DES an event is a defined concept, represented by a model variable taking a particular value (e.g., a bit changing from zero into one) at a specific point in time. In contrast to quantum theory, there is no need to invoke the elusive wave function collapse to “explain” how quantum theory may eventually be reconciled with the fact that a measurement yields a definite yes/no answer, or to appeal to Born's rule.

• It may be difficult to analyze the behavior of a DES model by means of differential equations, probability theory, or other mathematical techniques of theoretical physics. Of course, we may use e.g., probability or quantum theory to model the statistics of the data produced by a DES.

• It is not practicable to perform a DES without using a digital computer. A digital computer itself is a physical device that changes its internal state (all the bits of the CPU and memory) in a discrete, step-by-step (clock cycle) manner. Therefore, a DES algorithm running on a digital computer (which we assume is error-corrected and operating flawlessly) can be viewed as a metaphor for an idealized experiment on a physical device (the digital computer) [54]. All aspects of such an experiment are under the control of a programmer. In the context of EPRB experiments, this means that any loophole [55] can be opened or closed at the discretion of the programmer. For instance, the so-called contextuality loophole, which is impossible to avoid in a laboratory EPRB experiment [49], can be trivially closed in a DES (see below).

• The outcomes of genuine laboratory experiments are subject to unknown influences but in a DES on a digital computer (operating flawlessly), there are no such influences. If there were, it would not be possible to exactly reproduce the results of a DES. Therefore, DES is “the experiment” to confront a theory with facts obtained under the same premises as those on which the theory is based.

• Although a DES algorithm changes the state of a physical device (the digital computer), the events and variables in a DES are only metaphors for the “real” detector click, etc. On the other hand, once it has been established that a DES of a subquantum model yields the correct results, one could build a macroscopic mechanical device that performs exactly the same as DES.

• DES on a digital computer complies with the notion of realism, meaning that at any time during the DES, the internal state of the digital computer is known exactly, all variables of the simulation model taking definite values. Of course, we can always “hide” an algorithm and data on purpose. For instance, we can do this to create the illusion that the “visible” data is unpredictable (a standard technique to generate pseudo-random numbers).

• In a digital computer, there are no signals traveling faster than light. Therefore, on the most basic level, the internal operation of a digital computer complies with Einstein's notion of local causality. However, there is nothing that prevents us from performing an acausal analysis of the data. For instance, if we generate and store a sequence of numbers and then wish to compute the sum, we may do this by summing the numbers in the reverse order of how they were generated. This trivial example shows that one has to distinguish between the generation of the raw data and the processing of this data. For the purpose of constructing a local realist DES model, it is essential that the process that generates the raw data complies with Einstein's notion of local causality. It is not permitted to accumulate data, perform e.g., a discrete Fourier transform or compute acausal correlations, and use the results to describe a quantum physics experiment. While both these techniques are very useful for a wide variety of data processing tasks [56], they are “forbidden” in a DES of a subquantum model.

• Consistency of the DES methodology demands that a subquantum model for, say, a beam splitter, must be re-used, without modification, for all experiments in which this beam splitter is used. Our DES approach seems to satisfy this requirement of consistency, at least for a vast number of fundamental quantum-physics experiments with photons and neutrons [51]. Our motivation for considering both the EPRB and extended EPRB (EEPRB) experiments is to scrutinize the consistency of the DES approach for this category of experiments.

Finally, to head off misunderstandings, the DES models that we construct do not, in any way, make use of the quantum-theoretical predictions for the statistics of the data. Instead, a DES builds up these statistics by an event-by-event, cause-and-effect, Einstein-local process. Under appropriate conditions, these statistics can be described by quantum theory, while in other cases they cannot (see below).

3. Extended Einstein-Podolsky-Rosen-Bohm Experiment: Theory

3.1. Thought Experiment

Figure 1 shows the layout of an extended Einstein-Podolsky-Rosen-Bohm (EEPRB) experiment with spin-1/2 particles [26]. A source is emitting a pair of particles in two spatially separated directions toward beam splitters BS1 and BS2. In this idealized experiment, all beam splitters are assumed to be identical, performing selective (filtering) measurements [57, 58]. Selective measurements allow us to attach an attribute with definite value (e.g., the direction of the magnetic moment or of the polarization) to the particle. For instance, assuming that BS1, BS3, and BS4 perform ideal selective measurements, a particle leaving BS1 along path S₁ = +1 (S₁ = −1) will always leave BS3 (BS4) along path S₃ = +1 (S₃ = −1) if c = a. In case of selective measurements, we can attach an attribute to the particle, the value of this attribute being given by S₁. We use the same procedure for attaching attributes to particles leaving the other beam splitters.

FIGURE 1

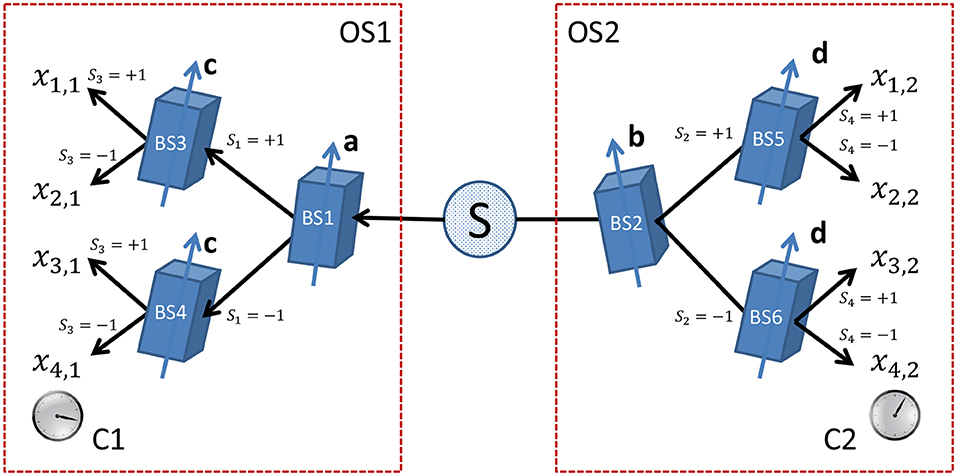
Figure 1. Layout of the extended Einstein-Podolsky-Rosen-Bohm experiment with spin-1/2 particles emitted by the source S. The observation station OS1 (OS2) contains three beam splitters BS1, BS3, and BS4, (BS2, BS5, and BS6) and a clock C1 (C2). The directions of the beam splitters BS1, BS2, BS3, BS4, BS5, and BS6 are represented by vectors a, b, c, c, d, and d, respectively.

Particles leaving BS3, …, BS6 are registered by detectors. All detectors are assumed to be identical and to have a 100% detection efficiency (we relax this assumption later). The binary variables x_{i, j} = 0, 1 for i = 1, …, 4 and j = 1, 2 (see Figure 1) indicate which of the four detectors at the left (j = 1) and right (j = 2) fire. For each pair of emitted particles, exactly one of the detectors on the left and exactly one of the detectors on the right side of the source will register a particle. This implies that for j = 1, 2, only one of x_{1, j}, x_{2, j}, x_{3, j}, and x_{4, j} can be non-zero. The four new variables defined by

$\begin{array}{l}{S}_1=x_{1,1}+x_{2,1}-x_{3,1}-x_{4,1},\\ S_2=x_{1,2}+x_{2,2}-x_{3,2}-x_{4,2},\\ S_3=x_{1,1}-x_{2,1}+x_{3,1}-x_{4,1},\\ S_4=x_{1,2}-x_{2,2}+x_{3,2}-x_{4,2},& (2)\end{array}$

all take values +1 or −1 (see Figure 1). Clearly, S₁ and S₃ (S₂ and S₄) encode, in a unique manner, the path that the left (right) going particle took. In the following, we use the S's to formulate the DES model.

For practical reasons, most laboratory EPRB experiments are carried out with photons [3–10], the polarization of the photons playing the role of the spin. From a quantum-theoretical viewpoint, there is no loss of generality in doing so because mathematically, the description of the photon polarization is in terms of Pauli-spin matrix algebra. In the following, to keep the discussion concise and concrete, we only focus on (E)EPRB experiments that employ the photon polarization as the “quantum system” of interest.

A source is emitting a pair of photons in two spatially separated directions toward beam splitters BS1 and BS2. BS1 sends one photon of the pair to either BS3 or BS4. BS2 sends the other photon of the pair to either BS5 or BS6. In an ideal model, all beam splitters are identical. Each beam splitter represents a combination of wave plates, an electro-optical modulator (EOM), and a polarizing beam splitter (PBS), see for example Figure 1C in reference [9]. The EOM acts as a switchable (voltage controlled) polarization rotator, the rotation being characterized by a two-dimensional unit vector (indicated by the arrow through the beam splitter), relative to local frames of reference attached to the observation stations OS1 and OS2, respectively.

It is expedient to introduce the vectors a = (cos a, sin a), a_⊥ = (−sin a, cos a), b = (cos b, sin b), b_⊥ = (−sin b, cos b), c = (cos c, sin c), c_⊥ = (−sin c, cos c), d = (cos d, sin d), and d_⊥ = (−sin d, cos d). Photons leave BS1 with linear polarization along either a (S₁ = +1) or a_⊥ (S₁ = −1). For the other beam splitters, we have similar relations between the direction of the linear polarization of the photons that leave the beam splitters and the value of the corresponding S-variable.

3.2. Classical Electrodynamics

It is instructive to first consider the case in which the detector signal is linearly proportional to the intensity of the impinging light. This case is covered by classical optics, described by Maxwell's theory of electrodynamics.

According to empirical evidence, the intensity of light passing through a polarizer is given by Malus' law $I=I_0{cos}^2(\varphi -\psi )$, where ϕ is the polarization of the light beam and ψ is the rotation of the polarizer, both relative to a laboratory frame of reference. I₀ is the intensity of the incident light.

We assume that the source emits “special” randomly polarized light toward BS1 and BS2, special in the sense that the difference between the polarizations of the two beams ϕ₀ is fixed in time. Then, using Malus' law for BS1 and BS2, the correlated intensity for one particular, random realization of the polarization angle ϕ is given by

$\begin{array}{l}{I}_1(S_1,S_2|\text{a},\text{b},\varphi ,{\varphi }_0)\\ =I_0^2\frac{1+S_{1}cos2(\varphi -a)}{2}\frac{1+S_{2}cos2(\varphi -b+{\varphi }_0)}{2},& (3)\end{array}$

where I₀ denotes the light intensity of a single beam. Integrating over all polarizations ϕ with a uniform density 1/2π yields

$\begin{array}{ll}{I}_1(S_1,S_2|\text{a},\text{b},{\varphi }_0)=\frac{I_0^2}{4}{\displaystyle [}1+\frac{1}{2}{S}_1{S}_{2}cos2(a-b+{\varphi }_0){\displaystyle ]}.& (4)\end{array}$

Repeated use of Malus' law and exploiting the fact that the polarizations of the two beams leaving a beam splitter are orthogonal, the correlated intensity of the different beams is then given by

$\begin{array}{l}I(S_1,S_2,S_3,S_4|\text{a},\text{b},\text{c},\text{d},{\varphi }_0)=\frac{I_0^2}{16}{\displaystyle [}1+\frac{1}{2}{S}_1{S}_{2}cos2(a-b+{\varphi }_0){\displaystyle ]}\\ {\displaystyle [}1+S_1{S}_{3}cos2(a-c){\displaystyle ]}\\ {\displaystyle [}1+S_2{S}_{4}cos2(b-d){\displaystyle ]}.& (5)\end{array}$

The moments of the correlated intensity Equation (5) are

$\begin{array}{l}{\hat{K}}_i={\displaystyle \sum _{S_1,S_2,S_3,S_4=\pm 1}}{S}_{i}I(S_1,S_2,S_3,S_4|\text{a},\text{b},\text{c},\text{d},{\varphi }_0)=0,\\ i=1,2,3,4,\\ {\hat{K}}_{ij}={\displaystyle \sum _{S_1,S_2,S_3,S_4=\pm 1}}{S}_i{S}_{j}I(S_1,S_2,S_3,S_4|\text{a},\text{b},\text{c},\text{d},{\varphi }_0),\\ 1\le i<j\le 4,\\ {\hat{K}}_{ijk}={\displaystyle \sum _{S_1,S_2,S_3,S_4=\pm 1}}{S}_i{S}_j{S}_{k}I(S_1,S_2,S_3,S_4|\text{a},\text{b},\text{c},\text{d},{\varphi }_0)=0,\\ i\ne j\ne k\ne i,\\ {\hat{K}}_{1234}={\displaystyle \sum _{S_1,S_2,S_3,S_4=\pm 1}}{S}_1{S}_2{S}_3{S}_{4}I(S_1,S_2,S_3,S_4|\text{a},\text{b},\text{c},\text{d},{\varphi }_0)\\ =I_0^{2}cos2(a-c)cos2(b-d).& (6)\end{array}$

For ϕ₀ = π/2 (orthogonally polarized beams) and I₀ = 1, the explicit expressions for the two-S correlations are

$\begin{array}{l}{\hat{K}}_{12}=-\frac{1}{2}cos2(a-b),{\hat{K}}_{13}=cos2(a-c),\\ {\hat{K}}_{14}=-\frac{1}{2}cos2(a-b)cos2(b-d),\\ {\hat{K}}_{23}=-\frac{1}{2}cos2(a-b)cos2(a-c),\\ {\hat{K}}_{24}=cos2(b-d),\\ {\hat{K}}_{34}=-\frac{1}{2}cos2(a-b)cos2(a-c)cos2(b-d).& (7)\end{array}$

The factor 1/2 which appears in Equation (4) and in four of the six second moments ${\hat{K}}_{ij}$ is characteristic of the correlation of two light intensities. Here and in the following, we use the hat on top of the symbols to emphasize that the expressions have been obtained from a theoretical model.

3.3. Quantum Theory

Classical electrodynamics describes the intensity of light and does not discriminate between individual events. In contrast, quantum theory can be used to describe the statistics of events, particularly in cases, such as the EPRB experiment, where detectors can discriminate between them.

For a pair of photons whose polarizations are described by the singlet state, Appendix A shows that the joint probability to observe one photon in the path labeled by S₁ and the other one in the path labeled by S₂ is given by De Raedt et al. [59]

$\begin{array}{ll}P(S_1,S_2|\text{a},\text{b},Z)=\frac{1-S_1{S}_{2}cos2(a-b)}{4},& (8)\end{array}$

where Z denotes a valid proposition that represents all conditions under which the experiment is performed with the exception of a and b. Note that for ϕ₀ = π/2, Equation (4) differs from Equation (8) through the factor 1/2 only.

In Appendix A, we show that the joint probability to observe one photon in the path labeled by (S₁, S₃) and the other in the path labeled by (S₂, S₄) is given by

$\begin{array}{l}P(S_1,S_2,S_3,S_4|\text{a},\text{b},\text{c},\text{d},Z)=\frac{1}{16}{\displaystyle [}1-S_1{S}_{2}cos2(a-b){\displaystyle ]}\\ {\displaystyle [}1+S_1{S}_{3}cos2(a-c){\displaystyle ]}\\ {\displaystyle [}1+S_2{S}_{4}cos2(b-d){\displaystyle ]}.& (9)\end{array}$

As already mentioned in the introduction, a subquantum model for the EEPRB experiment must not make use of Equation (9) to generate the quadruples (S₁, S₂, S₃, S₄).

Note that the only non-trivial difference between Equations (5) and (9) is that in the former case, the absolute value of the pre-factor of the S₁S₂ term never exceeds 1/2 whereas in the latter case, it is equal to −1. The expressions of the second moments of Equation (9) read

$\begin{array}{l}{\hat{E}}_{12}=-cos2(a-b),{\hat{E}}_{13}=cos2(a-c),\\ {\hat{E}}_{14}=-cos2(a-b)cos2(b-d),\\ {\hat{E}}_{23}=-cos2(a-b)cos2(a-c),{\hat{E}}_{24}=cos2(b-d),\\ {\hat{E}}_{34}=-cos2(a-b)cos2(a-c)cos2(b-d),& (10)\end{array}$

which are not all equal to the corresponding expressions of the $\hat{K}$'s, see Equation (7). From Equation (9) it follows that ${\hat{E}}_1={\hat{E}}_2={\hat{E}}_3={\hat{E}}_4={\hat{E}}_{123}={\hat{E}}_{124}={\hat{E}}_{134}={\hat{E}}_{234}=0$ and ${\hat{E}}_{1234}=cos2(a-c)cos2(b-d)$.

Clearly, in order to have a subquantum model generate data that agrees either with Maxwell's theory Equation (5) or quantum theory Equation (9), we only have to construct a subquantum model in which we can control the pre-factor of the S₁S₂ term in Equation (5). Thinking of light as a collection of photons, in sections 3.4 and 4, we explain how this control naturally results from the simple fact that we have to classify individual events as photons or something else, whereas in the “classical” case this classification is not an issue. At this point, it should be mentioned that within the context of the classical and quantum theory of light, changing the prefactor 1/2 of the S₁S₂ term in Equation (5) is a subtle issue, intimately related to the amount of second-order coherence one can observe by measuring either intensities or by counting clicks of a detector [60]. A discussion of this important issue is out of the scope of this paper and we refer the reader who is interested in these aspects to the in-depth analysis given in reference [60]. In our paper, Equations (5) and (9) are only used to provide the classical/quantum results which any valid subquantum model for the (E)EPRB experiment has to reproduce.

An important feature of this EEPRB experiment is that all the correlations that are required to test for violations of Bell/Clauser-Horne-Shimony-Holt (CHSH) inequalities [12, 61] are obtained in a single run (instead of three/four runs) of the experiment [26]. The EEPRB experiment does not suffer from the contextuality loophole [49]. As 0 ≤ P(S₁, S₂, S₃, S₄|a, b, c, d, Z) ≤ 1, it follows directly that all Bell-type inequalities, including all variants of the CHSH inequality, can never be violated [62]. This is easily seen by evaluating the sum $\sum _{S_1,S_2,S_3,S_4=\pm 1}g(S_1,S_2,S_3,S_4)P(S_1,S_2,S_3,S_4|\text{a},\text{b},\text{c},\text{d},Z)$ for various choices of the function g(S₁, S₂, S₃, S₄), such as −1 ≤ g(S₁, S₂, S₃, S₄) = S₁S₂ + S₁S₃ + S₂S₃ ≤ 3, or −2 ≤ g(S₁, S₂, S₃, S₄) = S₁S₃ + S₁S₄ + S₂S₃ − S₂S₄ ≤ 2, for example. In words, the quantum-theoretical description of the EEPRB experiment predicts that all Bell/CHSH inequalities are satisfied, in stark contrast to the case in which the correlations that enter the Bell/CHSH inequalities are computed from the quantum-theoretical description of the EPRB experiment.

3.4. Practical Realization: Photon Identification Problem

The exposition in subsection 3.1 assumes that each emitted pair of particles triggers exactly two detectors, namely only one of the four detectors at OS1 and one of the four detectors at OS2. In a laboratory experiment with Stern-Gerlach magnets and magnetic billiard balls, this assumption may hold true. However, it is not at all evident to have a source which only creates correlated pairs of elementary particles, such as photons which upon hitting a detector, will trigger exactly one detector at OS1 and exactly one detector at OS2.

With the exception of two experiments [9, 10], EPRB experiments with photons use time coincidence to identify photon pairs [3–8]. The two EPRB experiments [9, 10] that do not rely on time coincidence employ local, adjustable voltage thresholds to identify photons. This procedure is mathematically equivalent to attaching a local time tag to each particle, or to using time coincidence [63]. Therefore, in the following, we only discuss the subquantum model that uses local time tags as the vehicle for identifying pairs of photons. The modifications required to deal with voltage thresholds are trivial [63].

As explained above, a minimal theoretical model of a laboratory (E)EPRB experiment with photons should include a procedure to identify (pairs of) photons. Specifically, not including the data by which the photons and/or pairs are identified opens the so-called photon identification loophole [63]. By design, the EPRB experiments that claim to be loophole free [8–10] all suffer from this loophole.

As shown in Figure 1, observation stations OS1 and OS2 are equipped with local clocks C1 and C2, respectively. The time t₁ (t₂) at which a detector in OS1 (OS2) fires is read off from the local clock C1 (C2). The clocks C1 and C2 are synchronized before the source starts to emit pairs of particles and, being ideal clocks, remain synchronized for the duration of the experiment. Similarly, the frames of reference of OS1 and OS2 are aligned before the source starts to emit pairs of particles and do not change afterwards.

Concretizing the aim of this paper, in the next section, we describe a local realist model of the (E)EPRB experiment that reproduces the statistical predictions of quantum theory given by Equations (8) and (9). In formulating the DES model, we call the agents that carry the information from the source to the observation stations “photons” and use the language of optics.

4. Subquantum Model

Before describing all the components of the subquantum model, we recall the basic strategy that we adopt in constructing such a model. As quantum theory describes the most ideal version of the (E)EPRB experiment and as our aim is to show that the subquantum model reproduces the results of the former, we construct a DES of the most ideal version of the (E)EPRB experiment. The DES model for the EEPRB experiment that we describe next contains the ideal implementation of EPRB laboratory experiments.

In concert with our general strategy to set up the subquantum model, we assume that the source emits pairs of photons only and this at regular time intervals Δ. The time at which the nth pair is emitted is given by T_n = nΔ. The time it takes for a photon to travel from the source to BS1 or BS2 is assumed to be constant and the same for all photons traveling to OS1 and OS2. We denote this time of flight by $T_{\text{TOF}}^{\prime }$. Similarly, the time of flight from BS1 to BS3 or BS4 (BS2 to BS5 or BS6) and the time of flight from BS3, BS4, BS5, or BS6 to the corresponding detectors are denoted by $T_{\text{TOF}}^{″}$ and $T_{\text{TOF}}^{‴}$, respectively. The total time of flight is then $T_{\text{TOF}}=T_{\text{TOF}}^{\prime }+T_{\text{TOF}}^{″}+T_{\text{TOF}}^{‴}$.

In the DES model, the polarization of the photon traveling to BS1 (BS2) is represented by a two-dimensional unit vector ${\text{x}}_1={(cos\varphi ,sin\varphi )}^{\text{T}}$ (${\text{x}}_2={(-sin\varphi ,cos\varphi )}^{\text{T}}$). The angle ϕ is chosen to be uniformly random from the interval [0, 2π). As ${\text{x}}_1^{\text{T}}·{\text{x}}_2=0$, the polarizations of the photons of each pair are orthogonal, that is, they are maximally anticorrelated and randomly distributed over the unit circle.

In the following, we specify the DES rules for BS1 only. The rules for the other beam splitters are identical and are obtained by a simple change of symbols. In the DES model, the operation of beam splitter BS1 is defined by the rules

$\begin{array}{ll}{S}_1=\{\begin{array}{ccc}+1\hfill & \text{if}& {\cos }^2(\varphi -a)>r\\ -1\hfill & \text{if}& {\cos }^2(\varphi -a)\le r\end{array},x_1^{\prime }=\{\begin{array}{ccc}\text{a}\hfill & \text{if}& S_1=+1\\ {\text{a}}_{\perp }\hfill & \text{if}& S_1=-1\end{array},\hfill & (11)\end{array}$

where 0 < r < 1 denotes a uniform pseudo-random number. Here and in the following, it is implicitly understood that a new instance of the pseudo-random number r is generated with each invocation of an equation in which r appears. The unit vector ${\text{x}}_1^{\prime }$ denotes the polarization of the photon leaving BS1. It is not difficult to see that the model defined by Equation (11) generates S₁ = +1 (S₁ = −1) events with a relative frequency given by cos²(ϕ − a) (sin²(ϕ − a)), i.e., Equation (11) produces data that is in concert with Malus' law if the polarization of the incident photon is constant in time.

Optical components, such as wave plates and EOMs contain birefringent material which changes the polarization by retarding (or delaying) one component of the polarization with respect to its orthogonal component. In the DES, this retardation effect is accounted for by assuming that as a photon passes through a beam splitter, it may suffer from a time delay which may depend on the direction of the beam splitter relative to the polarization of the photon.

Obviously, the law of retardation in the subquantum model cannot be derived from Maxwell's theory or quantum theory. We can only find the subquantum law of retardation by trial and error. Fortunately, from earlier work we already know the subquantum law of retardation for the EPRB experiment [64, 65] and we only need to extend this law slightly to have the DES reproduce the quantum-theoretical results for both the EPRB and EEPRB experiment. Specifically, for BS1, the two DES rules for the subquantum law of retardation read

$\begin{array}{l}{\tau }_1={\displaystyle {\tau }_{\text{EPRB}}({\text{x}}_1,\text{a})|\frac{1-{\text{x}}_1·{\text{u}}_1}{2}{|}^{\beta }}\\ ={\displaystyle r^{\prime }{T}_{\text{max}}|sin2(\varphi -a){|}^{\alpha }|\frac{1-{\text{x}}_1·{\text{u}}_1}{2}{|}^{\beta },{\text{u}}_1\leftarrow {\text{x}}_1,}& (12)\end{array}$

where x₁ (or equivalently ϕ) is the polarization of the incoming photon, 0 < r′ < 1 is another uniform pseudo-random number, T_max is an adjustable parameter specifying maximum retardation, and α > 0 is an adjustable parameter controlling the dependence of the retardation on the difference between the photon polarization x₁ and the orientation of the beam splitter a. As indicated by the subscript EPRB, ${\tau }_{\text{EPRB}}=r^{\prime }{T}_{\text{max}}|sin2(\varphi -a){|}^{\alpha }$ suffices to reproduce the quantum-theoretical results of the EPRB experiment [54, 59, 63–65].

The new features are the last factor in Equation (12), β > 0 being an adjustable parameter, and the rule u₁ ← x₁ which updates the two-dimensional vector u₁. The initial value of u₁ can be any vector that has a norm ≤1. This vector is attached to the beam splitter and may be thought of as representing (on a subquantum level) the electrical polarization of the material [51].

The purpose of the factor $|(1-{\text{x}}_1·{\text{u}}_1)/2{|}^{\beta }$ in Equation (12) is to turn off the generation of random retardation times if the polarization of the incoming photons is constant. To see how this works, first consider the case that the polarization of the incoming photons is constant, say ${\text{x}}_1={\tilde{\text{x}}}_1$. Then, after the first photon has passed by, ${\text{u}}_1={\tilde{\text{x}}}_1$ and $|(1-{\text{x}}_1·{\text{u}}_1)/2{|}^{\beta }=0$ for all photons that follow. Next, assume that the polarization of the photons entering BS1 is randomly distributed over the unit circle. Then, because x₁ and u₁ (which is equal to the polarization x₁ of the previous photon) are independent, $|(1-{\text{x}}_1·{\text{u}}_1)/2{|}^{\beta }$ is just a random variable in [0, 1] multiplying τ_EPRB. The idea to store and use the value of the polarization of the previous photon has also been used to reproduce, by DES, the quantum-theoretical results for a large variety of single-photon and single-neutron experiments [50, 51]. The capability of the subquantum model to disable the generation of random retardation times if the polarization of the incoming photons is constant is essential for reproducing the quantum-theoretical results of both the EPRB and EEPRB experiments with the same subquantum model.

At this point, it may be of interest to mention that on the basis of the statistics (i.e., averages and correlations) only, it is not possible to make statements about the uniqueness of the subquantum law of retardation. As a matter of fact, in the case at hand, replacing Equation (12) by the rules

$\begin{array}{l}{\tau }_1={\displaystyle {\tau }_{\text{EPRB}}({\text{x}}_1,\text{a})|\frac{1-{\text{u}}_1·{\text{u}}_1}{2}{|}^{\beta }}\\ ={\displaystyle r^{\prime }{T}_{\text{max}}|sin2(\varphi -a){|}^{\alpha }|\frac{1-{\text{u}}_1·{\text{u}}_1}{2}{|}^{\beta },}& (13)\end{array}$

$\begin{array}{ll}{\text{u}}_1\leftarrow \gamma {\text{u}}_1+(1-\gamma ){\text{x}}_1,& (14)\end{array}$

works equally well.

Equation (14) defines a deterministic learning machine (DLM) [50, 51], which learns, event-by-event, the time average of the polarizations x₁ carried by the photons. The speed and accuracy by which u₁ approaches the time average of the x₁'s is controlled by the parameter 0 < γ < 1 [51]. The order in which Equations (13) and (14) are executed is irrelevant. The DLM defined by Equation (14) is the same as the one that has been used to reproduce, by DES, the quantum-theoretical results for a large variety of single-photon and single-neutron experiments [50, 51]. If the polarizations of the incoming photons are constant, say ${\tilde{\text{x}}}_1$, and a certain number (depending on γ) of photons has passed by, we have ${\text{u}}_1\approx {\tilde{\text{x}}}_1$ and $|(1-{\text{u}}_1·{\text{u}}_1)/2{|}^{\beta }\approx 0$. If the polarizations of the photons entering BS1 are randomly distributed over the unit circle, u₁ → 0 and $|(1-{\text{u}}_1·{\text{u}}_1)/2{|}^{\beta }\approx 1$. Then, just as in the case of Equation (12), the factor $|(1-{\text{u}}_1·{\text{u}}_1)/2{|}^{\beta }$ in Equation (4) is used to turn off the generation of random retardation times if the polarizations of the incoming photons are constant.

In our idealized experiment, all detectors are assumed to be identical and to have a 100% detection efficiency. After a photon has passed BS3 or BS4 (BS5 or BS6), it may trigger one and only one detector in OS1 (OS2), symbolized by one of x_{1, 1}, x_{2, 1}, x_{3, 1}, or x_{4, 1} (x_{1, 2}, x_{2, 2}, x_{3, 2}, or x_{4, 2}) being equal to one and the other ones being equal to zero. The time t₁ (t₂) at which a detector in OS1 (OS2) fires is read off from the local clock C1 (C2). These local clocks C1 and C2 are synchronized before the source starts to emit pairs of photons and, being ideal clocks, remain synchronized for the duration of the experiment. For the nth emitted pair, the arrival times are given by

$\begin{array}{ll}{t}_{1,n}=T_{\text{TOF}}+n\Delta +{\tau }_{1,n}+\{\begin{array}{lll}{\tau }_{3,n}\hfill & \text{if}\hfill & S_1=+1\hfill \\ {\tau }_{4,n}\hfill & \text{if}\hfill & S_1=-1\hfill \end{array},& (15)\end{array}$

$\begin{array}{ll}{t}_{2,n}=T_{\text{TOF}}+n\text{Δ}+{\tau }_{2,n}+\{\begin{array}{lll}{\tau }_{5,n}\hfill & \text{if}\hfill & S_2=+1\hfill \\ {\tau }_{6,n}\hfill & \text{if}\hfill & S_2=-1\hfill \end{array},& (16)\end{array}$

where we have attached the subscript n to keep track of which pair of the emitted pairs we are dealing with. For each pair-emission event n = 1, …, N, Equations (11)–(16) generate the data (S_{1, n}, S_{3, n}, t_{1, n}) and (S_{2, n}, S_{4, n}, t_{2, n}). Note that OS1 and OS2 only share the angle of polarization ϕ characterizing the pair of photons, nothing else.

In each triple in (S_{i, n}, S_{i+2, n}, t_{i, n}), we replace the time variable by a (local) binary variable w_{i, n} to indicate whether a detection event is classified as a photon (w_i,n = 1) or not (w_i,n = 0). Specifically, the rule to decide whether a detection event corresponds to the observation of a photon or of something else is given by

$\begin{array}{ll}{w}_{i,n}=\{\begin{array}{ccccc}1& \text{if}& 0\le t_{i,n}-T_{\text{TOF}}-n\text{Δ}\le W,& & \\ & & “\text{a photon}”& & \\ 0& \text{if}& t_{i,n}-T_{\text{TOF}}-n\text{Δ}>W,& & \\ & & “\text{something else}”& & \end{array}i=1,2,& (17)\end{array}$

where W is the time window (an adjustable parameter). We emphasize that the decision process defined by Equation (17) only involves variables that are local to the observation stations.

Equations (11)–(17) define the rules by which the subquantum model generates the data sets

$\begin{array}{l}{{S}}_1={\displaystyle \{}(S_{1,n},S_{3,n},w_{1,n})|n=1,\dots ,N{\displaystyle \}}\text{ and}\\ {{S}}_2={\displaystyle \{}(S_{2,n},S_{4,n},w_{2,n})|n=1,\dots ,N{\displaystyle \}},& (18)\end{array}$

collected by OS1 and OS2, respectively. From the data sets ${S}$₁ and ${S}$₂, we compute the single- and two-particle averages

$\begin{array}{l}{K}_i=\frac{1}{N}{\displaystyle \sum _{n=1}^N}{S}_{i,n},E_i=\frac{{\displaystyle {\sum }_{n=1}^N}{w}_{1,n}{w}_{2,n}{S}_{i,n}}{{\displaystyle {\sum }_{n=1}^N}{w}_{1,n}{w}_{2,n}},i=1,2,3,4\\ K_{ij}=\frac{1}{N}{\displaystyle \sum _{n=1}^N}{S}_{i,n}{S}_{j,n},E_{ij}=\frac{{\displaystyle {\sum }_{n=1}^N}{w}_{1,n}{w}_{2,n}{S}_{i,n}{S}_{j,n}}{{\displaystyle {\sum }_{n=1}^N}{w}_{1,n}{w}_{2,n}},\\ (i,j)=(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),& (19)\end{array}$

without (K's) and with (E's) the photon identification process in place.

5. Simulation Results

Below, we specify the DES parameters that have been used, discuss the data shown in Figures 2, 3, and provide additional information about simulation data that we do not show.

• The number of emitted pairs is N = 1, 000, 000 per setting (a, b, c, d).

• The maximum retardation time was chosen to be T_max = 5, 000 (dimensionless units). Pairs of particles are emitted with a time interval Δ > 2T_max. In line with our strategy to perform an ideal experiment, this choice eliminates the possibility of misidentifying pairs and also ensures that at each instant of time, there is only one photon in transit to OS1 and only one other photon en route to OS2. For T_TOF we can take any non-negative value. In fact, from Equation (17) it follows that the actual values of Δ and T_TOF do not enter in the DES algorithm.

• In Figure 2A, we show the DES results for the case without photon identification (that is if W > T_max or α = β = 0). Then the DES reproduces the results of Maxwell's theory, by an event-by-event process [66]. Specifically, if the polarization of the incoming photon is constant, the DES model of the beam splitter itself generates data according to Malus' law. The DES model of the EEPRB experiment with randomly polarized light produces data that, ignoring statistical fluctuations, is in excellent agreement with Equation (7) (see Figure 2A).

• Using a local time window W = 1 (dimensionless units) and for α = 4 and β = 1/2, the event-by-event process yields results (see Figure 2B) for the E's which are in excellent agreement with quantum theory (data for the first, third, and fourth moments are not shown). The ratio of identified photon pairs to emitted pairs depends on a and b and varies between ~ 11% for a = b and 0.1% for |a−b| = π/4. For W = 8, this ratio changes to ~ 18% for a = b and 0.8% for |a − b| = π/4, while the agreement with quantum theory is still very good (data not shown).

• The data obtained by identifying photons using time coincidence instead of local time windows are almost the same and are therefore not shown. In the limit W/T_max → 0, N → ∞, and α = 4, it has been proven analytically that the DES model of the EPRB experiment yields the correlation E₁₂ = −cos 2(a − b) exactly [65].

• Using the same pseudo-random sequence for each choice of settings renders the DES compliant with the notion of a counterfactually definite theory. In this case, the DES results (data not shown) are, for all practical purposes, the same as those obtained by using different pseudo-random sequences for each choice of settings. Operating in this mode, the subquantum model of the EPRB experiment does not suffer from the contextuality loophole [49] nor of any other known loopholes [55]. This confirms the conclusion of an earlier work [54], which adopted a different approach to realize counterfactually-definite compliant simulations. The demonstration that there exist both counterfactually-definite and non-counterfactually-definite compliant computer models for the EPRB experiments that produce results in complete agreement with those of quantum theory implies that, for the case of EPRB experiments, counterfactual definiteness is not incompatible with quantum physics [63].

• In the DES, it is trivial to account for the detection efficiency 0 ≤ η ≤ 1. For each detection event, we generate a pseudo-random number r″ and remove the detection event from the data set if r″ > η. We find that the only effect of reducing η is to increase the statistical fluctuations (data not shown). The agreement with quantum theory is not affected.

• In Figure 3, we show the DES results for the case in which the source emits photons with the same polarization chosen randomly. In this case, the DES reproduces the results of Maxwell's theory (Figure 3A). A corresponding quantum-theoretical result does not exist, see Appendix B. However, the DES data are in excellent agreement with a non-quantum probabilistic theory in which the factor [1 − S₁S₂ cos 2(a − b)] in Equation (9) is replaced by [1 + S₁S₂ cos 2(a − b)] (see Figure 3B).

• Replacing the rules Equation (12) by the rules Equations (13) and (14), and repeating the DES with the same value of α and β also yields data (not shown) that are in excellent agreement with the quantum-theoretical description, for γ in the range [0.1, 0.98].

• Our DES model also reproduces the theoretical results (see Appendix C) if the two photons of each pair have a fixed polarization (results not shown). In Maxwell's theory, this case is described by light beams with fixed polarizations. In quantum theory, this case is described by an (uncorrelated) product state.

FIGURE 2

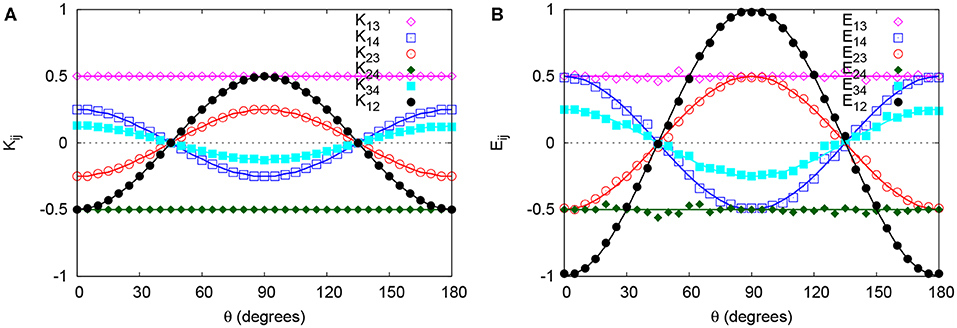
Figure 2. DES results for the correlations between all pairs of the S-variables as a function of θ = a − b, with b = 0, c = a + π/6, and d = π/3. The source emits pairs of photons with orthogonal polarizations chosen randomly. Ignoring statistical fluctuations, the averages of all S-variables (not shown) are zero. (A) The correlations K_ij computed without photon identification (markers) are in excellent agreement with the corresponding correlations ${\hat{K}}_{ij}$ [see Equation (7)] predicted by Maxwell's theory (solid lines) for two light beams with orthogonal, random polarization (ϕ₀ = π/2); (B) The correlations E_ij computed with photon identification (markers) are in excellent agreement with the corresponding correlations ${\hat{E}}_{ij}$ predicted by quantum theory [solid lines, see Equation (10)] for two spin-1/2 particles in a singlet state.

FIGURE 3

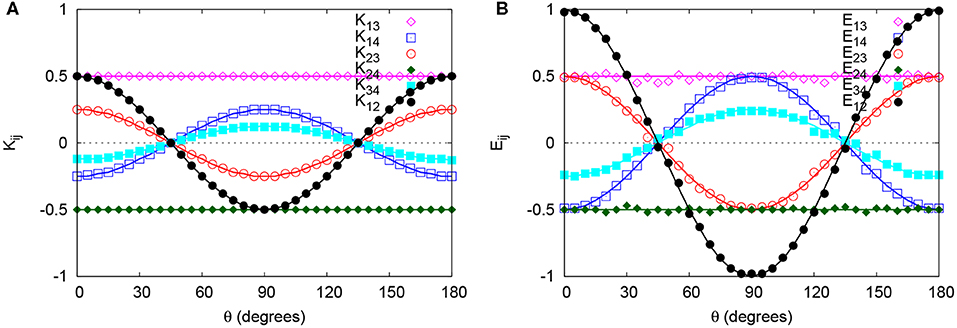
Figure 3. Same as Figure 2 except that the source emits pairs of photons with the same instead of orthogonal polarizations chosen randomly. (A) The correlations K_ij computed without photon identification (markers) are in excellent agreement with the corresponding correlations ${\hat{K}}_{ij}$ (solid lines) predicted by Maxwell's theory for two light beams with the same, random polarization (ϕ₀ = 0); (B) The correlations E_ij computed with photon identification (markers) cannot be obtained from quantum theory for two spin-1/2 particles (see Appendix B) but are in excellent agreement with the corresponding correlations (solid lines) obtained from the expression Equation (9) in which the factor [1 − S₁S₂ cos 2(a − b)] is replaced by [1 + S₁S₂ cos 2(a − b)].

Table 1 gives a compact overview of the agreement between the DES results and the theoretical descriptions of the (E)EPRB experiments.

TABLE 1

Table 1. Overview of the agreement between the DES results and the theoretical descriptions of the (E)EPRB experiments.

6. Discussion and Summary

Laboratory EPRB experiments unavoidably require a procedure to classify a detection event as corresponding to a photon or as something else. Independent of the precise nature of this procedure (voltage threshold, local time window, time coincidence, etc.), any model that aims at describing an EPRB experiment should, from the start, account for this procedure by introducing additional variables into the description. In contrast, Bell's model, while charmingly simple, does not account for an essential aspect of laboratory EPRB experiments, namely the classification of detection events in terms of photons or something else. Consequently, any subquantum model that aims at reproducing the results of quantum theory for the (E)EPRB experiment should have features that are not included in Bell's model. As a matter of fact, a quick glance at how the data of laboratory EPRB experiments are being processed reveals that it is the photon identification process which is lacking in Bell's model. Including this process implies that correlations between events are calculated only from subsets of the data, in which case Bell's theorem does not apply. Using only subsets of the data, there is only the constraint that the correlation should, in absolute value, be ≤1. Apart from that “almost everything” is possible [20, 67–69], including a subquantum model that, in the appropriate limit, yields the correlation of the singlet state [64, 65].

Clearly, on the basis of the statistical data alone, it is not possible to reject subquantum models of the EPRB and EEPRB experiments presented in this paper. The relevant question is how a laboratory experiment can rule out or confirm that (i) a subquantum level description is possible and/or (ii) the rules by which the DES model of the beam splitter operates provide a reasonable description.

Regarding (i): If we consider it as irrelevant to ask what kind of process gives rise to the statistics of events, it seems very difficult to beat quantum theory in terms of descriptive power [70]. Therefore, it is clear that addressing (i) requires the analysis of the data on the level of individual events, without being biased by what quantum theory predicts for the statistics.

Regarding (ii): The DES model defined by Equations (11) and (12) or Equations (11), (13), and (14) produces data in concert with Malus' law, i.e., with the experiment, and therefore seems solid. The additional feature of the DES model (which allows us to reproduce the statistics of the EPRB and EEPRB experiments as given by quantum theory) is the subquantum law of retardation, defined by Equation (12) or Equations (13) and (14). At first sight, there is no experimental support for such a law. However, let us look at the EPRB experiment from a slightly different perspective, namely, as a setup to characterize the response of the observation stations to very feeble, randomly anticorrelated light. Then, our DES data and also the analysis of experimental data [65] support the hypothesis that the EPRB experiment demonstrates that the statistics of the detection events that have been classified as photons depend on the settings.

What if we try to measure the retardation by an experiment that uses feeble light with fixed polarization? As explained in section 4, in our subquantum model the retardation time does not depend on the setting of the beam splitter if the polarization is constant in time. Only if the polarization is not fixed in time, our subquantum model yields retardation times that depend on the setting of the beam splitter. This is precisely what the EPRB experiment does: through the correlation, it provides information about the retardation as a function of the setting of the beam splitter. Therefore, to rule out the subquantum law of retardation used in our DES, it is necessary to perform both the experiments with feeble, randomly polarized light and with feeble light of fixed polarization.

Summarizing, we have proposed a subquantum model which satisfies Einstein's criterion of locality and which generates, event-by-event, data that agrees with the quantum-theoretical description of the Einstein-Podolsky-Rosen-Bohm and the extended Einstein-Podolsky-Rosen-Bohm experiments. This demonstration does not build on the traditional methods of theoretical physics but instead uses a digital computer and a discrete-event simulation as a metaphor for idealized, realizable laboratory experiments.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

KM, HD, MJ, and FJ contributed to the conception and design of the DES models. MJ, MW, DW, KM, FJ, and HD contributed to the writing of the manuscript. MJ, MW, DW, and HD independently performed all the simulations.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Einstein A, Podolsky A, Rosen N. Can quantum-mechanical description of physical reality be considered complete? Phys Rev. (1935) 47:777–80. doi: 10.1103/PhysRev.47.777

CrossRef Full Text | Google Scholar

2. Bohm D. Quantum Theory. New York, NY: Prentice-Hall (1951).

Google Scholar

3. Kocher CA, Commins ED. Polarization correlation of photons emitted in an atomic cascade. Phys Rev Lett. (1967) 18:575–7. doi: 10.1103/PhysRevLett.18.575

CrossRef Full Text | Google Scholar

4. Clauser JF, Shimony A. Bell's theorem: experimental tests and implications. Rep Prog Phys. (1978) 41:1881–927. doi: 10.1088/0034-4885/41/12/002

CrossRef Full Text | Google Scholar

5. Aspect A, Dalibard J, Roger G. Experimental test of Bell's inequalities using time-varying analyzers. Phys Rev Lett. (1982) 49:1804–7. doi: 10.1103/PhysRevLett.49.1804

CrossRef Full Text | Google Scholar

6. Weihs G, Jennewein T, Simon C, Weinfurther H, Zeilinger A. Violation of Bell's inequality under strict Einstein locality conditions. Phys Rev Lett. (1998) 81:5039–43. doi: 10.1103/PhysRevLett.81.5039

CrossRef Full Text | Google Scholar

7. Christensen BG, McCusker KT, Altepeter JB, Calkins B, Lim CCW, Gisin N, et al. Detection-Loophole-Free test of quantum nonlocality, and applications. Phys Rev Lett. (2013) 111:130406. doi: 10.1103/PhysRevLett.111.130406

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Hensen B, Bernien H, Dreau AE, Reiserer A, Kalb N, Blok MS, et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature. (2015) 526:682–6. doi: 10.1038/nature15759

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Giustina M, Versteegh MAM, Wengerowsky S, Handsteiner J, Hochrainer A, Phelan K, et al. Significant-Loophole-Free test of Bell's theorem with entangled photons. Phys Rev Lett. (2015) 115:250401. doi: 10.1103/PhysRevLett.115.250401

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Shalm LK, Meyer-Scott E, Christensen BG, Bierhorst P, Wayne MA, Stevens MJ, et al. Strong Loophole-Free test of local realism. Phys Rev Lett. (2015) 115:250402. doi: 10.1103/PhysRevLett.115.250402

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Bell JS. On the Einstein-Podolsky-Rosen paradox. Physics. (1964) 1:195–200. doi: 10.1103/PhysicsPhysiqueFizika.1.195

CrossRef Full Text | Google Scholar

12. Bell JS. Speakable and Unspeakable in Quantum Mechanics. Cambridge: Cambridge University Press (1993).

Google Scholar

13. de la Peña L, Cetto AM, Brody TA. On hidden-variable theories and Bell's inequality. Lett Nuovo Cim. (1972) 5:177–81. doi: 10.1007/BF02815921

CrossRef Full Text | Google Scholar

14. Fine A. On the completeness of quantum theory. Synthese. (1974) 29:257–89. doi: 10.1007/BF00484961

CrossRef Full Text | Google Scholar

15. Fine A. Some local models for correlation experiments. Synthese. (1982) 50:279–94. doi: 10.1007/BF00416904

CrossRef Full Text | Google Scholar

16. Fine A. Hidden variables, joint probability, and Bell inequalities. Phys Rev Lett. (1982) 48:291–5. doi: 10.1103/PhysRevLett.48.291

CrossRef Full Text | Google Scholar

17. Fine A. Joint distributions, quantum correlations, and commuting observables. J Math Phys. (1982) 23:1306–10. doi: 10.1063/1.525514

CrossRef Full Text | Google Scholar

18. de Muynck WM. The Bell inequalities and their irrelevance to the problem of locality in quantum mechanics. Phys Lett A. (1986) 114:65–7. doi: 10.1016/0375-9601(86)90480-9

CrossRef Full Text | Google Scholar

19. Kupczyński M. On some tests of completeness of quantum mechanics. Phys Lett A. (1986) 116:417–9. doi: 10.1016/0375-9601(86)90372-5

CrossRef Full Text | Google Scholar

20. Brans CH. Bell's theorem does not eliminate fully causal hidden variables. Int J Theor Phys. (1987) 27:219–26. doi: 10.1007/BF00670750

CrossRef Full Text | Google Scholar

21. Jaynes ET. Clearing up mysteries—the original goal. In: Skilling J, editor. Maximum Entropy and Bayesian Methods. Vol. 36. Dordrecht: Kluwer Academic Publishers (1989). p. 1–27. doi: 10.1007/978-94-015-7860-8_1

CrossRef Full Text | Google Scholar

22. Brody T. The Philosphy Behind Physics. Berlin: Springer (1993). doi: 10.1007/978-3-642-78978-6

CrossRef Full Text | Google Scholar

23. Pitowsky I. George Boole's ‘conditions of possible experience' and the quantum puzzle. Br J Phil Sci. (1994) 45:95–125. doi: 10.1093/bjps/45.1.95

CrossRef Full Text | Google Scholar

24. Fine A. The Shaky Game: Einstein Realism and the Quantum Theory. Chicago, IL: University of Chicago Press (1996).

Google Scholar

25. Khrennikov AY. Interpretations of Probability. Utrecht: VSP Int. Sc. Publishers (1999). doi: 10.1515/9783110213195

CrossRef Full Text | Google Scholar

26. Sica L. Bell's inequalities I: an explanation for their experimental violation. Opt Comm. (1999) 170:55–60. doi: 10.1016/S0030-4018(99)00417-4

CrossRef Full Text | Google Scholar

27. De Baere W, Mann A, Revzen M. Locality and Bell's theorem. Found Phys. (1999) 29:67–77. doi: 10.1023/A:1018865120111

CrossRef Full Text | Google Scholar

28. Hess K, Philipp W. Bell's theorem and the problem of decidability between the views of Einstein and Bohr. Proc Natl Acad Sci USA. (2001) 98:14228–33. doi: 10.1073/pnas.251525098

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Hess K, Philipp W. A possible loophole in the theorem of Bell. Proc Natl Acad Sci USA. (2001) 98:14224–77. doi: 10.1073/pnas.251524998

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Hess K, Philipp W. Bell's theorem: critique of proofs with and without inequalities. AIP Conf Proc. (2005) 750:150–7. doi: 10.1063/1.1874568

CrossRef Full Text | Google Scholar

31. Accardi L. Some loopholes to save quantum nonlocality. AIP Conf Proc. (2005) 750:1–20. doi: 10.1063/1.1874552

CrossRef Full Text | Google Scholar

32. Kracklauer AF. Bell's inequalities and EPR-B experiments: are they disjoint? AIP Conf Proc. (2005) 750:219–27. doi: 10.1063/1.1874573

CrossRef Full Text | Google Scholar

33. Santos E. Bell's theorem and the experiments: increasing empirical support to local realism? Stud Hist Phil Mod Phys. (2005) 36:544–65. doi: 10.1016/j.shpsb.2005.05.007

CrossRef Full Text | Google Scholar

34. Kupczyński M. Entanglement and Bell inequalities. J Russ Las Res. (2005) 26:514–23. doi: 10.1007/s10946-005-0048-7

CrossRef Full Text | Google Scholar

35. Morgan P. Bell inequalities for random fields. J Phys A. (2006) 39:7441–5. doi: 10.1088/0305-4470/39/23/018

CrossRef Full Text | Google Scholar

36. Khrennikov AY. A mathematicians viewpoint to Bell's theorem: in memory of Walter Philipp. AIP Conf Proc. (2007) 889:7–17. doi: 10.1063/1.2713442

CrossRef Full Text | Google Scholar

37. Adenier G, Khrennikov AY. Is the fair sampling assumption supported by EPR experiments. J Phys B Mol Opt Phys. (2007) 40:131–41. doi: 10.1088/0953-4075/40/1/012

CrossRef Full Text | Google Scholar

38. Nieuwenhuizen TM. Where Bell went wrong. AIP Conf Proc. (2009) 1101:127–33. doi: 10.1063/1.3109932

CrossRef Full Text | Google Scholar

39. Matzkin A. Is Bell's theorem relevant to quantum mechanics? On locality and non-commuting observables. AIP Conf Proc. (2009) 1101:339–48. doi: 10.1063/1.3109959

CrossRef Full Text | Google Scholar

40. Hess K, Michielsen K, De Raedt H. Possible experience: from Boole to Bell. Europhys Lett. (2009) 87:60007. doi: 10.1209/0295-5075/87/60007

CrossRef Full Text | Google Scholar

41. Khrennikov AY. Contextual Approach to Quantum Formalism. Berlin: Springer (2009). doi: 10.1007/978-1-4020-9593-1

CrossRef Full Text | Google Scholar

42. Graft DA. The Bell inequality cannot be validly applied to the Einstein-Podolsky-Rosen-Bohm (EPRB) experiments. Phys Essays. (2009) 22:534–42. doi: 10.4006/1.3231944

CrossRef Full Text | Google Scholar

43. Khrennikov AY. On the role of probabilistic models in quantum physics: Bell's inequality and probabilistic incompatibility. J Comput Theor Nanosci. (2011) 8:1006–10.

Google Scholar

44. Nieuwenhuizen TM. Is the contextuality loophole fatal for the derivation of Bell inequalities? Found Phys. (2011) 41:580–91. doi: 10.1007/s10701-010-9461-z

CrossRef Full Text | Google Scholar

45. Hess K. Einstein Was Right! Singapore: Pan Stanford Publishing (2015). doi: 10.1201/b16809

CrossRef Full Text | Google Scholar

46. Kupczyński M. EPR paradox, quantum nonlocality and physical reality. J Phys Conf Ser. (2016) 701:012021. doi: 10.1088/1742-6596/701/1/012021

CrossRef Full Text | Google Scholar

47. Kupczyński M. Can we close the Bohr-Einstein quantum debate? Phil Trans R Soc A. (2017) 375:20160392. doi: 10.1098/rsta.2016.0392

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Hess K, De Raedt H, Michielsen K. Analysis of Wigner's set theoretical proof for Bell-type inequalities. J Mod Phys. (2017) 8:57–67. doi: 10.4236/jmp.2017.81005

CrossRef Full Text | Google Scholar

49. Nieuwenhuizen TM, Kupczyński M. The Contextuality Loophole is fatal for the derivation of Bell inequalities: reply to a comment by I. Schmelzer. Found Phys. (2017) 47:316–9. doi: 10.1007/s10701-017-0062-y

CrossRef Full Text | Google Scholar

50. De Raedt K, De Raedt H, Michielsen K. Deterministic event-based simulation of quantum phenomena. Comp Phys Comm. (2005) 171:19–39. doi: 10.1016/j.cpc.2005.04.012

CrossRef Full Text | Google Scholar

51. Michielsen K, De Raedt H. Event-based simulation of quantum physics experiments. Int J Mod Phys C. (2014) 25:01430003. doi: 10.1142/S0129183114300036

CrossRef Full Text | Google Scholar

52. Banks J, Carson JS II, Nelson BL, Nicol DM. Discrete-Event System Simulation. New York, NY: Pearson (1996).

Google Scholar

53. Leemis LM, Park SK. Discrete-Event Simulation: A First Course. New York, NY: Pearson (2006).

Google Scholar

54. De Raedt H, Michielsen K, Hess K. The digital computer as a metaphor for the perfect laboratory experiment: Loophole-free Bell experiments. Comp Phys Comm. (2016) 209:42–7. doi: 10.1016/j.cpc.2016.08.010

CrossRef Full Text | Google Scholar

55. Larsson JÅ. Loopholes in Bell inequality tests of local realism. J Phys A Math Theor. (2014) 47:424003. doi: 10.1088/1751-8113/47/42/424003

CrossRef Full Text | Google Scholar

56. Press WH, Flannery BP, Teukolsky SA, Vetterling WT. Numerical Recipes. Cambridge: Cambridge University Press (2003).

Google Scholar

57. Schwinger J. The algebra of microscopic measurements. Proc Natl Acad Sci USA. (1959) 45:1542–53. doi: 10.1073/pnas.45.10.1542

CrossRef Full Text | Google Scholar

58. Ballentine LE. Quantum Mechanics: A Modern Development. Singapore: World Scientific (2003).

Google Scholar

59. De Raedt H, De Raedt K, Michielsen K, Keimpema K, Miyashita S. Event-by-event simulation of quantum phenomena: application to Einstein-Podolosky-Rosen-Bohm experiments. J Comput Theor Nanosci. (2007) 4:957–91. doi: 10.1166/jctn.2007.2381

CrossRef Full Text | Google Scholar

60. Khrennikov A. Quantum versus classical entanglement: eliminating the issue of quantum nonlocality. Found. Phys. (2020). doi: 10.1007/s10701-020-00319-7

CrossRef Full Text | Google Scholar

61. Clauser JF, Horn MA, Shimony A, Holt RA. Proposed experiment to test local hidden-variable theories. Phys Rev Lett. (1969) 23:880–84. doi: 10.1103/PhysRevLett.23.880

CrossRef Full Text | Google Scholar

62. De Raedt H, Hess K, Michielsen K. Extended Boole-Bell inequalities applicable to quantum theory. J Comput Theor Nanosci. (2011) 8:1011–39. doi: 10.1166/jctn.2011.1781

CrossRef Full Text | Google Scholar

63. De Raedt H, Michielsen K, Hess K. The photon identification loophole in EPRB experiments: computer models with single-wing selection. Open Phys. (2017) 15:713–33. doi: 10.1515/phys-2017-0085

CrossRef Full Text | Google Scholar

64. De Raedt K, Keimpema K, De Raedt H, Michielsen K, Miyashita S. A local realist model for correlations of the singlet state. Eur Phys J B. (2006) 53:139–42. doi: 10.1140/epjb/e2006-00364-9

CrossRef Full Text | Google Scholar

65. Zhao S, De Raedt H, Michielsen K. Event-by-event simulation model of Einstein-Podolsky-Rosen-Bohm experiments. Found Phys. (2008) 38:322–47. doi: 10.1007/s10701-008-9205-5

CrossRef Full Text | Google Scholar

66. Michielsen K, Jin F, De Raedt H. Event-based corpuscular model for quantum optics experiments. J Comput Theor Nanosci. (2011) 8:1052–80. doi: 10.1166/jctn.2011.1783

CrossRef Full Text | Google Scholar

67. Pearle PM. Hidden-variable example based upon data rejection. Phys Rev D. (1970) 2:1418–25. doi: 10.1103/PhysRevD.2.1418

CrossRef Full Text | Google Scholar

68. Pascazio S. Time and Bell-type inequalities. Phys Lett A. (1986) 118:47–53. doi: 10.1016/0375-9601(86)90645-6

CrossRef Full Text | Google Scholar

69. Pascazio S. On emission lifetimes in atomic cascade tests of the Bell inequality. Phys Lett A. (1987) 126:163–7. doi: 10.1016/0375-9601(87)90452-X

CrossRef Full Text | Google Scholar

70. De Raedt H, Katsnelson MI, Michielsen K. Quantum theory as the most robust description of reproducible experiments. Ann Phys. (2014) 347:45–73. doi: 10.1016/j.aop.2014.04.021

CrossRef Full Text | Google Scholar

71. De Raedt H, De Raedt K, Michielsen K, Keimpema K, Miyashita S. Event-based computer simulation model of aspect-type experiments strictly satisfying Einstein's locality conditions. J Phys Soc Jpn. (2007) 76:104005. doi: 10.1143/JPSJ.76.104005

CrossRef Full Text | Google Scholar

Appendix A: Quantum Theory of the (E)EPRB Experiment

For reference, we briefly review the quantum-theoretical description of the EPRB and EEPRB experiment. In this appendix, for the sake of generality, we first consider magnetic spin-1/2 particles passing through Stern-Gerlach magnets.

In the context of (E)EPRB experiments, the case of interest is a system of two spins in the singlet state, described by the density matrix

$\begin{array}{l}\rho =\frac{1-{\sigma }_1·{\sigma }_2}{4}=\frac{1}{2}\left(\begin{array}{cccc}0& 0& 0& 0\\ 0& +1& -1& 0\\ 0& -1& +1& 0\\ 0& 0& 0& 0\end{array}\right)\\ =\left(\frac{|\uparrow \downarrow \rangle -|\downarrow \uparrow \rangle }{\sqrt{2}}\right)\left(\frac{\langle \uparrow \downarrow |-\langle \downarrow \uparrow |}{\sqrt{2}}\right).& (\mathrm{A1})\end{array}$

A selective measurement on the spin-1/2 particle is described by the operator Ballentine [58]

$\begin{array}{ll}M(S,\sigma ,\text{x})=\frac{1+S\sigma ·\text{x}}{2}=M^2(S,\sigma ,\text{x}),& (\mathrm{A2})\end{array}$

projecting a state of the spin-1/2 system onto the eigenstate of σ · x with eigenvalue S = ±1.

The probabilities to observe the outcomes S₁ and S₂ in an EPRB experiment are given by Ballentine [58]

$\begin{array}{l}P(S_1|\text{a})=\text{T}\text{r}M(S_1,{\sigma }_1,\text{a})\rho M(S_1,{\sigma }_1,\text{a})=\text{T}\text{r}\rho M(S_1,{\sigma }_1,\text{a}),\\ P(S_2|\text{b})=\text{T}\text{r}M(S_2,{\sigma }_2,\text{b})\rho M(S_2,{\sigma }_2,\text{b})=\text{T}\text{r}\rho M(S_2,{\sigma }_2,\text{b}),& (\mathrm{A3})\end{array}$

respectively. For two spin-1/2 particles in the singlet state Equation (1), we have P(S₁|a) = 〈σ₁ · a〉 = 1/2 and P(S₂|b) = 〈σ₂ · b〉 = 1/2, The probability to observe the joint event (S₁, S₂) is given by Ballentine [58]

$\begin{array}{l}P(S_1,S_2|\text{a},\text{b})\\ =\text{T}\text{r}M(S_2,{\sigma }_2,\text{b})M(S_1,{\sigma }_1,\text{a})\rho M(S_1,{\sigma }_1,\text{a})M(S_2,{\sigma }_2,\text{b})\\ =\text{T}\text{r}\rho M(S_1,{\sigma }_1,\text{a})M(S_2,{\sigma }_2,\text{b}),& (\mathrm{A4})\end{array}$

where we used the fact that [M(S₁, σ₁, a), M(S₂, σ₂, b)] = 0 for all a and b. For two spin-1/2 particles in the singlet state Equation (1), Equation (4) becomes

$\begin{array}{ll}P(S_1,S_2|\text{a},\text{b})=\frac{1-S_1{S}_2\text{a}·\text{b}}{4}.& (\mathrm{A5})\end{array}$

Similarly, the probability to observe the joint event (S₁, S₂, S₃, S₄) is given by

$\begin{array}{l}P(S_1,S_2,S_3,S_4|\text{a},\text{b},\text{c},\text{d})=\text{T}\text{r}{\displaystyle [}M(S_4,{\sigma }_2,\text{d})M(S_3,{\sigma }_1,\text{c})\\ M(S_2,{\sigma }_2,\text{b})M(S_1,{\sigma }_1,\text{a})\rho M(S_1,{\sigma }_1,\text{a})\\ M(S_2,{\sigma }_2,\text{b})M(S_3,{\sigma }_1,\text{c})M(S_4,{\sigma }_2,\text{d}){\displaystyle ]}\\ =\text{T}\text{r}{\displaystyle [}\rho M(S_1,{\sigma }_1,\text{a})M(S_3,{\sigma }_1,\text{c})\\ M(S_1,{\sigma }_1,\text{a})M(S_2,{\sigma }_2,\text{b})M(S_4,{\sigma }_2,\text{d})\\ M(S_2,{\sigma }_2,\text{b}){\displaystyle ]}.& (\mathrm{A6})\end{array}$

Performing the matrix multiplications and calculating the trace we obtain

$\begin{array}{l}P(S_1,S_2,S_3,S_4|\text{a},\text{b},\text{c},\text{d},Z)=\frac{1}{16}{\displaystyle [}1-S_1{S}_2\text{a}·\text{b}{\displaystyle ]}\\ {\displaystyle [}1+S_1{S}_3\text{a}·\text{c}{\displaystyle ]}\\ {\displaystyle [}1+S_2{S}_4\text{b}·\text{d}{\displaystyle ]}.& (\mathrm{A7})\end{array}$

The derivation of the quantum-theoretical description of an experiment with photon polarization instead of magnetic spin-1/2 particles is not much different, for details see reference [71]. The upshot is that we only have to replace a · b by cos 2(a − b) etc. Thus, in the case of an EEPRB experiment that uses the polarization of the photons, the probability to observe the joint event (S₁, S₂, S₃, S₄) is given by

$\begin{array}{l}P(S_1,S_2,S_3,S_4|\text{a},\text{b},\text{c},\text{d},Z)=\frac{1}{16}{\displaystyle [}1-S_1{S}_{2}cos2(a-b){\displaystyle ]}\\ {\displaystyle [}1+S_1{S}_{3}cos2(a-c){\displaystyle ]}\\ {\displaystyle [}1+S_2{S}_{4}cos2(b-d){\displaystyle ]}.& (\mathrm{A8})\end{array}$

Appendix B: A Limitation of Quantum Theory for Two Spin-1/2 Particles

If the random polarizations of particles that enter BS1 and BS2 are the same instead of orthogonal, the DES generates data which, within the usual statistical fluctuations, is characterized by E₁ = E₂ = 0, and E₁₂ = + cos 2(a − b). In this appendix, we prove that a two-particle system with single-particle averages ${\hat{E}}_1={\hat{E}}_2=0$, and pair correlation ${\hat{E}}_{12}=+cos2(a-b)$ cannot be described by the quantum theory of two spin-1/2 particles. As in Appendix A, we consider the general case of two spin-1/2 particles and deal with the case of photon polarization at the end.

Using the Pauli-matrices and the 2 × 2 unit matrix as a basis of the vector space of 2 × 2 matrices, we can, without loss of generality, write the 4 × 4 density matrix of the two-spin system as

$\begin{array}{ll}\hat{\rho }=\frac{1}{4}\left(1+{\displaystyle \sum _{k=x,y,z}}{u}_k{\sigma }_1^k+{\displaystyle \sum _{k=x,y,z}}{v}_k{\sigma }_2^k+{\displaystyle \sum _{k,l=x,y,z}}{\sigma }_1^k{w}_{k,l}{\sigma }_2^l\right),& (\mathrm{B1})\end{array}$

where the u's and v's are real numbers and the w's are the elements of a Hermitian matrix. According to quantum theory, we then have

$\begin{array}{l}{\hat{E}}_1=\langle {\sigma }_1·\text{a}\rangle =\text{T}\text{r}\hat{\rho }{\sigma }_1·\text{a}=\text{u}·\text{a}\\ {\hat{E}}_2=\langle {\sigma }_2·\text{b}\rangle =\text{T}\text{r}\hat{\rho }{\sigma }_2·\text{b}=\text{v}·\text{b}\\ {\hat{E}}_{12}=\langle {\sigma }_1·\text{a}{\sigma }_2·\text{b}\rangle =\text{T}\text{r}\hat{\rho }{\sigma }_1·\text{a}{\sigma }_2·\text{b}={\text{a}}^{\text{T}}·\text{w}·\text{b}.& (\mathrm{B2})\end{array}$

If for all unit vectors a and b we have 〈σ₁ · a〉 = 〈σ₂ · b〉 = 0 and 〈σ₁ · a σ₂ · b〉 = −qa · b, then u = v = 0 and w = −q $1$, implying that

$\begin{array}{ll}{\hat{\rho }}_q=\frac{1-q{\sigma }_1·{\sigma }_2}{4}.& (\mathrm{B3})\end{array}$

The four eigenvalues of σ₁ · σ₂ are 1, 1, 1, and −3. Therefore, ${\hat{\rho }}_q$ has a negative eigenvalue if q < −1/3 and in this case ${\hat{\rho }}_q$ does not qualify as a density matrix whereas ${\hat{\rho }}_{q=1}=(1-{\sigma }_1·{\sigma }_2)/4$ does (and represents the singlet state).

In summary, there does not exist a quantum-theoretical description in terms of a 4 × 4 density matrix that yields ${\hat{E}}_1={\hat{E}}_2=0$ and ${\hat{E}}_{12}=+|q|\text{a}·\text{b}$ or for all unit vectors a and b and |q| > 1/3. This includes the special case for which ${\hat{E}}_{12}=+cos2(a-b)$ and ${\hat{E}}_1={\hat{E}}_2=0$.

Appendix C: Product State

For completeness, we give the expressions for the probabilities for the case that the two photons of each pair leave the source with fixed polarization p and q, respectively. Instead of Equation (8), we have

$\begin{array}{ll}P(S_1,S_2|\text{a},\text{b},Z)=\frac{1+S_{1}cos2(a-p)}{2}\frac{1+S_{2}cos2(b-q)}{2},& (\mathrm{C1})\end{array}$

and instead of Equation (9), we have

$\begin{array}{l}P(S_1,S_2,S_3,S_4|\text{a},\text{b},\text{c},\text{d},Z)=\frac{1}{16}{\displaystyle [}1+S_{1}cos2(a-p){\displaystyle ]}\\ {\displaystyle [}1+S_{2}cos2(b-q){\displaystyle ]}\\ {\displaystyle [}1+S_1{S}_{3}cos2(a-c){\displaystyle ]}\\ {\displaystyle [}1+S_2{S}_{4}cos2(b-d){\displaystyle ]}.& (\mathrm{C2})\end{array}$

Note that Equations (C1) and (C2) also apply to the case of classical optics with I₀ = 1.