Detection of Majorana Bound States by Sign Change of the Tunnel Magnetoresistance in a Quantum Dot Coupled to Ferromagnetic Electrodes

We study quantum transport and tunneling magnetoresistance (TMR) through an interacting quantum dot (QD) attached to ferromagnetic electrodes in the Coulomb blockade regime. The QD is also side-coupled to a superconductor nanowire hosting Majarana bound states (MBSs). It is found that when the electrodes' magnetic moments are arranged in antiparallel, the current's intensity will be enhanced to be larger than that of the parallel configuration by the hybridization between the QD and the MBSs. This change in the current induces anomalous negative TMR unique to the existence of MBSs, providing an efficient detection way of the MBSs. The negative TMR is weakened by the overlap between the two bound states but obviously enhanced by the left-right asymmetry between the QD and the electrodes. We also find that the TMR value changes non-monotonously with the spin polarization of the electrodes. Our results may find real use in energy saving spintronic devices and quantum information processing.

1. Introduction

Tunneling of spin-polarized electrons in nano- and micro-scale devices are at the core of quantum information data processings [1, 2] and future spintronics [3]. Spin-dependent current is conveniently generated in a system with ferromagnetic electrodes, and its intensity changes when the magnetic configuration of the device changes from parallel to antiparallel alignment [4]. Generally, the electronic current is larger in parallel configuration when transport occurs between the majority-majority and minority-minority spin bands, than in the antiparallel configuration, where electrons tunnel between majority and minority spin bands. The change in the currents is measured by the quantity of tunnel magnetoresistance (TMR) defined as TMR = (J_P − J_AP)/(J_P + J_AP), where J_P/AP is the electronic current in parallel (antiparallel) configuration. Usually, the TMR value is positive as J_P > J_AP [4]. The TMR effect has been extensively studied in various systems, including the relatively simple planar junctions [5], and in more complex mesoscopic double-barrier junctions [6], junctions with nano-scale granular systems [7, 8], as well as single-electron transistors [9], etc. When the central region between the electrodes is sufficiently small that the charging energy is larger than the thermal energy k_BT, some interesting effects due to quantization of energy levels becomes visible, such as the Coulomb blockade of electric current characterized by the Coulomb steps in the current-voltage curves [10–13]. Especially, behaviors of the TMR have been investigated both theoretically and experimentally in systems composing of ferromagnetic electrodes and quantum dots (QDs) [14–19], which is a nano-scale zero-dimensional structure [13]. This is because such a kind of device is ideal candidate to study the fundamental interactions between spins and charges [3, 13], and is being considered for applications in energy saving devices as well as for quantum computing [1, 2].

Recently, there is much interest in preparation and detection of Majorana fermions, which is a kind of elementary particle being of its own antiparticle, due to its promising applications in quantum computation free from decoherence [20–22]. It has been be prepared in the edges of topological superconductors as a pair of zero-energy Majorana bound states (MBSs) that obeys non-Abelian statistics enabling topologically protected quantum computation and high-efficiency spintronic devices [20, 22]. The MBSs has also be prepared in some other systems, including the non-centrosymmetric superconductors [23], three- or two-dimensional topological insulators coupled to superconductors [24], electrostatic defects in topological superconductors [25], p-wave superconductors [26], the semiconducting [27], or ferromagnetic [28] nanowires with native strong spin-orbit interaction proximitization to a conventional s-wave superconductors, and Josephson junctions [29], etc. The detection of MBSs is quite challenging because the unique chargeless and zero-energy properties, and then most of conventional detection techniques for elementary particles failed. For example, the MBSs formed in the nanowire induces a zero-bias anomaly in the differential conductance when a bias voltage is applied [30], which has been demonstrated in experiments. However, it can also arise from some other mechanisms, such as the quantum interference and Kondo effects [31]. Anomalous change of the thermoelectric effect in systems composing of a QD side-coupled to topological superconductor hosting a Majorana edge state has also been found and proposed as an alternative detection means in recent years [32–34]. The hybridization between QD and MBSs breaks the particle-hole symmetry of the system and leads to large enhancement and sign reversion of the thermopower. These, unfortunately, can also not been solely attributed to the existence of the MBSs.

In recent experiments, semiconductor spacers of InAs QD has been inserted in between nickel or cobalt leads [15, 35]. The dot's size and discretized energy levels can be fully adjusted by the length and thickness of the spacers or the gate voltages. Moreover, the spin polarization of the current injected from the ferromagnetic electrodes and TMR can also be electrically adjusted by a gate nearby the QD. Some new characteristics, such as the anomalies of the TMR caused by the intradot Coulomb repulsion energy in the QD, were explained in the subsequent theoretical work [36]. In the present manuscript, we study the properties of current-voltage and TMR in a QD sandwiched between the left and right ferromagnetic electrodes and side-coupled to a semiconducting nanowire hosting a pair of MBSs at the opposite ends of the wire (see the schematic plot of the system in Figure 1). We assume that the MBSs are coupled only to spin-up electrons in the QD under a strong magnetic field in experiments. Our calculation results show that due to the presence of the MBSs, the current of the antiparallel configuration can be larger than that of the parallel one, inducing a negative TMR. Such an effect is a good evidence of the existence of the Majorana fermions. The negative TMR will be weakened by the coupling between the two MBSs but obviously enhanced by the left-right asymmetry between the QD and the electrodes. Moreover, we find that the TMR strength depends non-monotonously on the spin polarization of the electrodes.

FIGURE 1

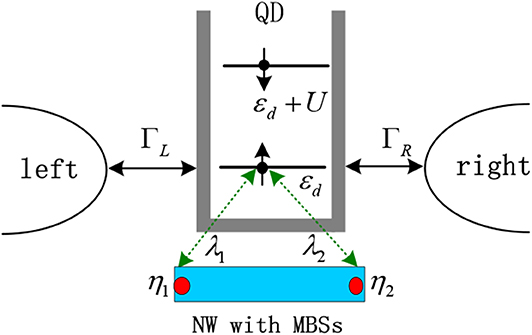
Figure 1. Schematic diagram for a QD coupled to MBSs and the left and right ferromagnetic leads with coupling strength Γ_L/R. Due to the chiral nature of the Majorana fermions, only spin-up is assumed to couple to the MBSs, formed at opposite ends of a nanowire. The two MBSs are denoted by η₁ and η₂ and coupled to the QD with strength of λ₁ and λ₂, respectively. If the dot level ε_d is occupied by an spin-up electron, then the spin-down electron will by pushed up to the level of ε_d + U by the intradot Coulomb repulsion U.

2. Model and Methods

The Hamiltonian of the QD coupled to MBSs and ferromagnetic electrodes takes the following form [18, 32, 37, 38]

$\begin{array}{l}H={\displaystyle {\sum }_{k\beta \sigma }}{\epsilon }_{k\beta }{c}_{k\beta \sigma }^{†}{c}_{k\beta \sigma }+{\displaystyle {\sum }_{\sigma }}{\epsilon }_d{d}_{\sigma }^{†}{d}_{\sigma }+U{d}_{\uparrow }^{†}{d}_{\uparrow }{d}_{\downarrow }^{†}{d}_{\downarrow }\\ +{\displaystyle {\sum }_{k\beta \sigma }}(T_{k\beta \sigma }{c}_{k\beta \sigma }^{†}{d}_{\sigma }+H.c)+H_{MBSs},& (1)\end{array}$

where $c_{k\beta \sigma }^{†}$ (c_kβσ) creates (annihilates) an electron of momentum k, energy ε_kβσ and spin σ = ↑, ↓ in the ferromagnetic electrode β = L, R. For the QD, $d_{\sigma }^{†}$ (d_σ) is the creation (annihilation) operator of an electron having energy level ε_d, spin-σ and intradot Coulomb interaction U, which has usually been neglected in previous work [32]. In experiments, ε_d and U are tunable by external gate voltages. The coupling strength between the QD and the electrodes is described by T_kβσ, which is spin-dependent due to the ferromagnetism on the electrodes. The last term H_MBSs in Equation (1) stands for the zero-energy MBSs located on the opposite ends of the semiconducting nanowire and their coupling to the QD [39, 40]:

$\begin{array}{ll}{H}_{MBSs}=i{\delta }_M{\eta }_1{\eta }_2+{\lambda }_1(d_{\uparrow }-d_{\uparrow }^{†}){\eta }_1+i{\lambda }_2(d_{\uparrow }+d_{\uparrow }^{†}){\eta }_2,& (2)\end{array}$

in which δ_M is the overlap strength between the two MBSs with operator satisfying both ${\eta }_j={\eta }_j^{†}(j=1,2)$ and {η_i, η_j} = δ_i,j. The hopping amplitude between MBSs and spin-↑ electrons in the QD is accounted by λ_j. Following previous work [39, 40], we write η_j in terms of the regular fermionic operators f as ${\eta }_1=(f^{†}+f)/\sqrt{2}$ and ${\eta }_2=i(f^{†}-f)/\sqrt{2}$, and then H_MBSs becomes

$\begin{array}{l}{H}_{MBSs}={\delta }_M(f^{†}f-\frac{1}{2})+\frac{{\lambda }_1}{\sqrt{2}}(d_{\uparrow }-d_{\uparrow }^{†})(f^{†}+f)\\ -\frac{{\lambda }_2}{\sqrt{2}}(d_{\uparrow }+d_{\uparrow }^{†})(f^{†}-f).& (3)\end{array}$

Within the standard Keldysh Green's function technique, the spin-dependent electric current is obtained as [37, 38]

$\begin{array}{ll}{J}_{\sigma }=\frac{e}{\hslash }{\displaystyle \int }{T}_{\sigma }(\epsilon )\left[f_L(\epsilon )-f_R(\epsilon )\right]\frac{d\epsilon }{2\pi }& (4)\end{array}$

where e is the electron charge, ℏ the reduced Planck's constant, $f_{L/R}(\epsilon )={\{1+e^{(\epsilon -{\mu }_{L/R})/k_{B}T}\}}^{-1}$ the Fermi distribution function of the left/right electrode with chemical potential μ_L/R, temperature T and Boltzmann constant k_B. The transmission coefficient T_σ(ε) can be expressed with the help of the retarded Green's function $G_{\sigma }^r(\epsilon )$ as [37, 38]

$\begin{array}{ll}{T}_{\sigma }(\epsilon )=\frac{{\Gamma }_{\sigma }^L{\Gamma }_{\sigma }^R}{{\Gamma }_{\sigma }^L+{\Gamma }_{\sigma }^R}\left[-2\text{Im}{G}_{\sigma }^r(\epsilon )\right],& (5)\end{array}$

where ${\Gamma }_{\sigma }^{\beta }=2\pi \sum _k|T_{k\beta \sigma }{|}^2\delta [\epsilon -{\epsilon }_{k\beta \sigma }]$ is the spin-dependent line-width function. Ferromagnetism on the electrodes can be expressed by defining a spin-polarization parameter P_β as $P_{\beta }=({\Gamma }_{\uparrow }^{\beta }-{\Gamma }_{\downarrow }^{\beta })/({\Gamma }_{\uparrow }^{\beta }+{\Gamma }_{\downarrow }^{\beta })$. In the present paper, we consider the parallel (P_L = P_R) and antiparallel (P_L = −P_R) configurations of the two electrodes. In both of the two cases, we have ${\Gamma }_{\uparrow (\downarrow )}^{\beta }=(1\pm P_{\beta }){\Gamma }_{\beta }$.

By applying the equation of motion method, the retarded Green's function in Equation (5) is obtained as (we have truncated the higher-order Green's functions by following reference [39, 40], in which the simultaneous tunneling of the electron of opposite spin has been neglected):

$\begin{array}{ll}{G}_{\sigma }^r(\epsilon )=\frac{{\tilde{\epsilon }}_{-,\sigma }-{\Sigma }_{\sigma }^1-U\{1-<n_{\bar{\sigma }}>[1-{({\lambda }_1^2-{\lambda }_2^2)}^2{\tilde{M}}_{\sigma }{\tilde{M}}_{U,\sigma }]\}}{({\tilde{\epsilon }}_{-,\sigma }-{\Sigma }_{\sigma }^0)({\tilde{\epsilon }}_{-,\sigma }-U-{\Sigma }_{\sigma }^1)},& (6)\end{array}$

where the self-energies considering the MBSs are given by ${\Sigma }_{\sigma }^0=M_1+{({\lambda }_1^2-{\lambda }_2^2)}^{2}B{\tilde{M}}_{\sigma }$ and ${\Sigma }_{\sigma }^1=M_1+{({\lambda }_1^2-{\lambda }_2^2)}^{2}B{\tilde{M}}_{U,\sigma }$ with $B=\epsilon /({\epsilon }^2-{\delta }_M^2)$ and ${\tilde{M}}_{\sigma }=B/({\epsilon }_{+,\sigma }+M_2)$, ${\tilde{M}}_{U,\sigma }=B/({\epsilon }_{+,\sigma }+U-M_2)$ in which

$\begin{array}{ll}{M}_{1(2)}=\frac{1}{2}[\frac{{\lambda }_1^2-{\lambda }_2^2}{\epsilon -(+){\delta }_M}-\frac{{\lambda }_1^2+{\lambda }_2^2}{\epsilon +(-){\delta }_M}],& (7)\end{array}$

and ${\tilde{\epsilon }}_{\pm }=\epsilon \pm {\epsilon }_d+i({\Gamma }_{\sigma }^L+{\Gamma }_{\sigma }^R)/2.$ The occupation number in Equation (6) is calculated self-consistently from

$\begin{array}{ll}<n_{\sigma }>={\displaystyle \int }\frac{d\epsilon }{2\pi }\frac{{\Gamma }_{\sigma }^L{f}_L(\epsilon )+{\Gamma }_{\sigma }^R{f}_R(\epsilon )}{{\Gamma }_{\sigma }^L+{\Gamma }_{\sigma }^R}\left[-2\text{Im}{G}_{\sigma }^r(\epsilon )\right].& (8)\end{array}$

To our knowledge, there are three kinds of schemes that are mainly used for studying the transport phenomena [41–43]. The first kind is the relatively rough Hartree-Fock-like scheme used in reference [41, 42]; the second kind is the Hubbard-I scheme adopted in the present work as well as other reference [39, 40] that can deal with relatively higher-order transport processes; the third kind of scheme is the one that can account for multiple transitions from contacts to the central site, such as the subtle Kondo effect. Detailed introduction of these schemes can be found in of reference [43]. In the Coulomb blockade regime, these three schemes give essentially the same results, see for example reference [43]. From theoretical point of view, here we adopt the Hubbard-I scheme for the sake of sophistication, and the procedure to evaluate the QD Green's function will be relatively simplified.

3. Results and Discussion

In this section, we present our numerical results for the spin-dependent current, TMR and differential conductance varying as functions of the bias voltage. The intradot Coulomb interaction U = 1 is chosen as the energy unit with symmetric bias voltage V as μ_L = −μ_R = eV/2. Figure 2 shows the spin-polarized current, differential conductance and the current's spin-polarization p = (J_↑ − J_↓)/(J_↑ + J_↓) for parallel and antiparallel configurations, respectively. The currents exhibit typical Coulomb blockade effect as shown in Figures 2A,B,D,E [3, 10, 13]. The reason is that by applying a bias voltage between the electrodes, the QD can be charged by single electrons when the energy levels ε_d are within the transport window. The current then is increased. With an increase from n to n + 1 electrons on the QD, an additional potential of e/C is induced with C denoting the capacitance of the device [10, 13]. The transfer of an electron through the QD is inhibited when the potential of the charged dot is larger than the applied bias voltage. Now the electrons are blockaded on the QD and the current will not increase with increasing bias voltage. With further increased bias voltage, electrons may tunnel through the dot level of ε_d + U again when the potential is overcome. In this way, the electrons are added on the dot one by one and the current shows Coulomb staircases. The Coulomb blockade effect can be clearly seen from the differential conductance, which develops two sharp peaks around ε_d and ε_d + U as given in the figure.

FIGURE 2

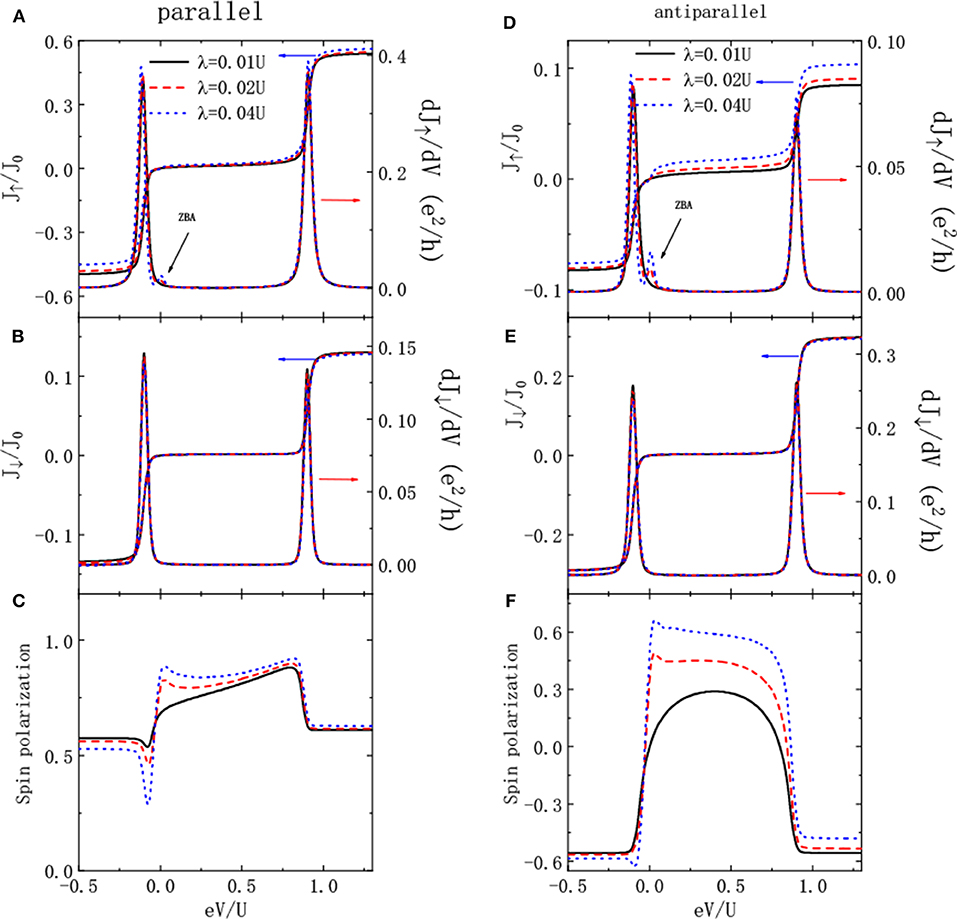
Figure 2. Spin-resolved current, non-linear differential conductance, and current' spin polarization as functions of the bias voltage when the magnetic moments of the leads are arranged in parallel (A–C), and antiparallel (D–F) configurations for indicated QD-MBS coupling strength λ₁ = λ₂ = λ. Other parameters are: δ_M = 0, ε_d = −0.1, Γ_L = Γ_R = k_BT = 0.01U, P_L = ±P_R = 0.6 (± for parallel and antiparallel cases, respectively).

In the parallel configuration, the current intensity of J_↑ is obviously larger than that of J_↓ in the absence of QD-MBSs. The reason is that the spin-up electrons will enter and leave the QD faster than the spin-down ones because of the ferromagnetism on the electrons, i.e., ${\Gamma }_{\uparrow }^L={\Gamma }_{\uparrow }^R>{\Gamma }_{\downarrow }^L={\Gamma }_{\downarrow }^R$. In the antiparallel configuration, however, the current intensities of both the two spin components are the same because the transmission coefficient is spin-independent in the absence of hybridization between the QD and MBSs (λ₁ = λ₂ = 0), which is not shown in the figure. Turning on the coupling between the QD and MBSs, the intensity of spin-up currents in both parallel and antiparallel configuration are enhanced as shown in Figures 2A,D, whereas that of the spin-down electrons are unchanged as the MBSs is coupled only to the spin-up electrons. Moreover, the enhancement of the intensity of J_↑ in the antiparallel is more obvious than that of the parallel one, which results in negative TMR as will be shown in the following. For the differential conductance, an obvious zero bias anomaly (ZBA) emerges in addition to the increase in the intensity [39, 40]. The ZBA, which has been theoretically predicted and experimentally observed, originates from the QD-MBSs coupling and serves as a signal of the existence of the Majornana fermions [39, 40]. In the absence of bias voltage and Coulomb interaction, the conductance is 0.5 e²/h by the coupling between the QD and the MBSs [44–46]. Figures 2C,F shows that the current's spin polarization is also enhanced in the presence of the MBSs in both parallel and antiparallel configurations. This is because the intensity of the spin-up current is increased by the MBSs whereas that of the spin-down one remains unchanged. Moreover, the spin polarization of the current changes more drastically near the dot level of ε_d as compared to ε_d + U due to the spin blockade effect.

As demonstrated by previous work, the influence of the MBSs on the current is rather weak since a pair of Majarana fermions are charge neutral [20–22]. This can be seen from the total current J = J_↑ + J_↓ in Figures 3A,B. The ZBA in the differential conductance, which is measured by the electrical tunnel spectroscopy, then is experimentally interesting (indicated by the arrows in the figure). To enlarge the signal of the MBSs in the current, we present the TMR in Figure 3C. For weak QD-MBSs hybridization strength λ = 0.01U, the TMR is positive as indicated by the solid line. It has two plateaus in the bias regimes of eV < ε_d and eV > ε_d + U, in which the current remains almost unchanged [3]. In the Coulomb blockade regime (ε_d < eV < ε_d + U), the intensity of TMR increases with increasing bias voltage, which is quite different from the behavior of the current. This is because the current from the parallel configuration originates from transport between the majority-majority and minority-minority spin bands, and that in the antiparallel configuration between majority and minority spin bands. In the absence of the QD-MBSs coupling, the former transport process is rather easier than the latter case. When the electrons on the QD is coupled to the MBSs, however, there is more transport channels in the antiparallel configuration and then the current intensity is increased accordingly. With increasing bias voltage, the leakage current in the parallel configuration then will be larger than that of the antiparallel one, resulting in increased TMR. Around the two transport channel ε_d and ε_d + U, the TMR develops a dip and peak, respectively. The reason is that the current of the antiparallel configuration originating from transport through ε_d (ε_d + U) is enhanced (suppressed). With increased QD-MBSs coupling strength, the strength of the TMR is weakened as shown by the dashed and dotted lines in Figure 3C. For sufficiently large λ, the TMR around transport channel ε_d is negative (see the dotted line), and then serves as a detection method for the existence of the Majorana fermions in the superconductor nanowire side-coupled to the QD. We emphasize that this phenomenon originates from the fact that the current intensity of the antiparallel configuration is more sensitive to the MBSs as compared to the parallel one.

FIGURE 3

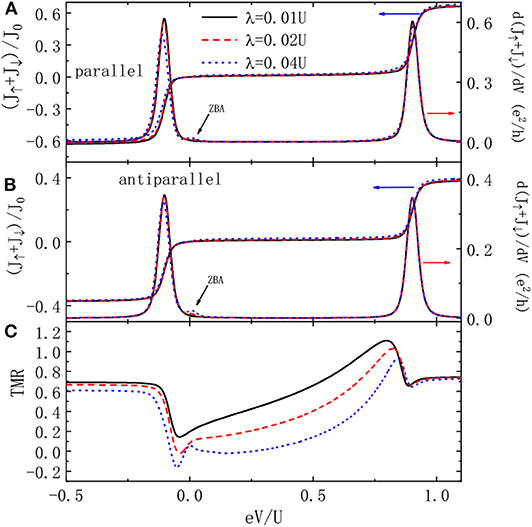
Figure 3. Total current, non-linear differential conductance for the magnetic moments' configurations of parallel (A) and antiparallel (B), and the corresponding TMR (C). Other parameters are as in Figure 2.

In Figure 4 we present the TMR varying with respective to the bias voltage for different values of the spin-polarization of the electrodes (p = P_L = P_R) and overlap amplitude between the two MBSs δ_M. For p = 0, the TMR is zero as indicated by the solid line in Figure 4A. With increasing spin polarization, the line-shape of the TMR essentially resembles those in Figure 3C. The strength of TMR changes with respective to the spin polarization in a non-monotonic way. Figure 4A shows that the TMR is negative around dot level ε_d for p < = 0.6, and is positive for P = 0.8. The TMR in the inset of Figure 4A has a minimal value in the regime of 0.5 < p < 0.6 for the indicated dot level and bias voltage. This is because that with increasing ferromagnetism on the electrodes p, the transport processes will be more and more dominated by only one spin-component electrons, and then the difference between the two kinds of the current becomes less prominent. In the extreme case of p ~ 1 (half-metallic), electron transport in the antiparallel is totally blockaded and the TMR equals to 1. Under this condition, the signal of the MBSs disappears. Figure 4B presents the function of δ_M on the TMR for fixed spin polarization of the electrodes p = 0.6. When the two states are decoupled from each other (δ_M = 0), an obvious negative TMR emerges around the dot level ε_d. With increasing δ_M, we find that the strength of the TMR is enhanced, especially in the Coulomb blockade regime. For strong enough overlap between the two states δ_M = 0.05U, the TMR is positive in the whole bias voltage regime. The reason is that when the two MBS are coupled, their functions on the TMR are canceled out and the abnormal increase of the current in the antiparallel configuration induced by the MBSs disappears.

FIGURE 4

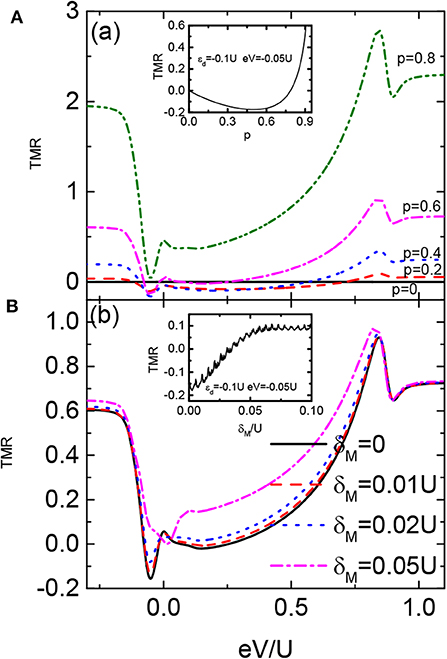
Figure 4. TMR as a function of the bias voltage for different values of spin polarization of the leads p in (A), and direct overlap between the MZMs δ_M in (B). The insets in (A,B) are the TMR varying with the p and δ_M, respectively. Other parameters are as in Figure 2.

In Figure 5, we present the total currents in both of the two configurations and the TMR varying with the bias voltage for different values of left-right asymmetry Γ_R/Γ_L. First of all, the currents' strength is monotonously enhanced by increasing Γ_R/Γ_L. This is because that for fixed ingoing tunneling rate Γ_L, the electrons will tunnel through the dot faster with increased outgoing tunneling rate Γ_R. Obviously, this holds true for both of the two spin component electrons regardless of the magnetic configuration. The TMR in Figure 5C, however, changes in a non-monotonic way with varying Γ_R/Γ_L. In the regimes of eV < ε_d and eV > ε_d + U, the TMR is positive and its strength increases with increasing Γ_R/Γ_L. This is the usual case in the absence of the QD-MBSs. In the Coulomb blockade regime ε_d < eV < ε_d + U, however, the value of TMR decreases with increasing left-right asymmetry. As a consequence of it, the negative TMR becomes more prominent and becomes a good means to detect the existence of the MBSs. As mentioned above, this is induced by that fact that the QD-MBSs coupling strengthes the current intensity of the antiparallel configuration as compared to the parallel one, which is an unique function of the MBSs on the electron transport. Finally, we briefly discuss the experimental realization of the present devices. The nanowire hosting the MBSs can be fabricated with InAs grown by molecular beam epitaxy with several nanometers of epitaxial Al layer. It has been experimentally proven that an hard superconducting gap can be induced on such a kind of nanowires by applying a critical magnetic field exceeding 2T along the wire axis. A QD is formed in the bare InAs segment at the end of the wire due to density of state gradients at the edges of the Al shell.

FIGURE 5

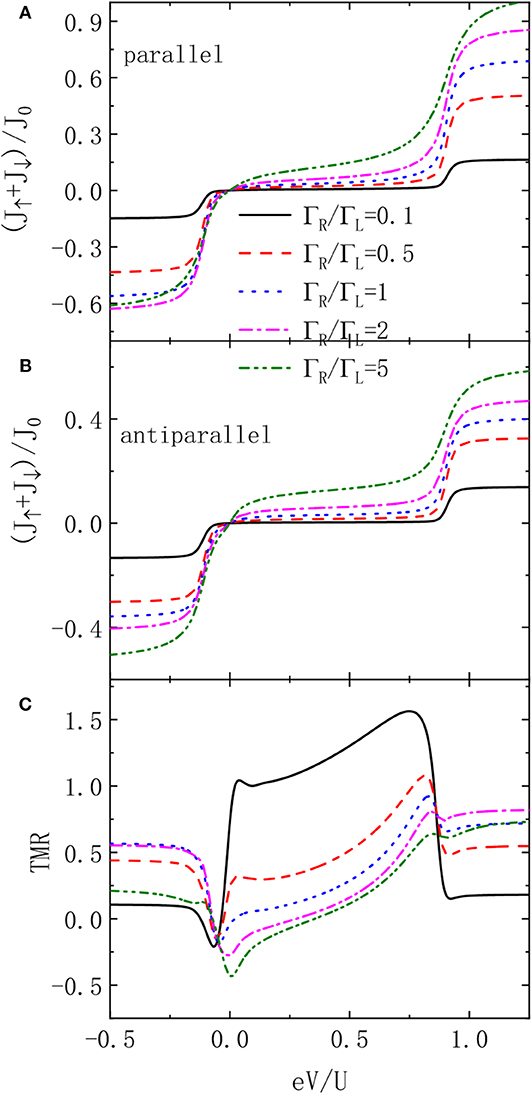
Figure 5. Total currents for parallel (A) and antiparallel (B) configurations, and TMR (C) as functions of the bias voltage for different values of QD-lead coupling asymmetry q with Γ₀ = 0.02U. Other parameters are as in Figure 2.

4. Summary

In summary, spin-dependent current and TMR in a QD sandwiched between two ferromagnetic leads and side-coupled to a pair of MBSs formed at the opposite ends of a superconductor nanowire is investigated within the non-equilibrium Green's technique. An unique negative TMR induced by the hybridization between the QD and the MBSs is found, which serves as a detection means of the Majorana fermions. This negative TMR is more likely to emerge in longer nanowire in which the two MBSs are well-separated from each other and the overlap between them is weak. By increasing the left-right asymmetry of the coupling strength between the QD and electrodes, the negative TMR becomes more obvious. It is also found that the intensity of the TMR depends on the spin-polarization of the electrodes in a non-monotonic way and is positive for large spin-polarization regardless of the existence of the MBSs.

Data Availability Statement

All datasets presented in this study are included in the article/supplementary material.

Author Contributions

W-GM and L-WT contributed the ideas equally and performed the numerical calculations. L-WT derived the formulae in the paper and wrote the original manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (Grant Nos. 11772287 and 11572277).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Loss D, DiVincenzo DP. Quantum computation with quantum dots. Phys Rev A. (1998) 57:120–6. doi: 10.1103/PhysRevA.57.120

CrossRef Full Text | Google Scholar

2. Fujisawa T, Austing DG, Tokura Y. Allowed and forbidden transitions in artificial hydrogen and helium atoms. Nature. (2002) 419:278–81. doi: 10.1038/nature00976

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Hanson R, Kouwenhoven LP, Petta JR. Spins in few-electron quantum dots. Rev Mod Phys. (2007) 79:1217–65. doi: 10.1103/RevModPhys.79.1217

CrossRef Full Text | Google Scholar

4. Julliere M. Tunneling between ferromagnetic films. Phys Lett A. (1975) 54:225–6. doi: 10.1016/0375-9601(75)90174-7

CrossRef Full Text | Google Scholar

5. Rudziński W, Barnaś J. Tunnel magnetoresistance in ferromagnetic junctions: tunneling through a single discrete level. Phys Rev B. (2001) 64:085318:1–10. doi: 10.1103/PhysRevB.64.085318

CrossRef Full Text | Google Scholar

6. Barnaś J, Fert A. Magnetoresistance oscillations due to charging effects in double ferromagnetic tunnel junctions. Phys Rev Lett. (1998) 80:1058–61. doi: 10.1103/PhysRevLett.80.1058

CrossRef Full Text | Google Scholar

7. Schelp LF, Fert A, Fettar F. Spin-dependent tunneling with Coulomb blockade. Phys Rev B. (1997) 56:R5747–50. doi: 10.1103/PhysRevB.56.R5747

CrossRef Full Text | Google Scholar

8. Mitani S, Fujimori H, Takanashi K. Tunnel-MR and spin electronics in metal-nonmetal granular systems. J Magn Magn Mater. (1999) 198:179–84. doi: 10.1016/S0304-8853(98)01041-5

CrossRef Full Text | Google Scholar

9. Zhang X, Li BZ. Spin-polarized tunneling and magnetoresistance in ferromagnet/insulator(semiconductor) single and double tunnel junctions subjected to an electric field. Phys Rev B. (1997) 56:5484–8. doi: 10.1103/PhysRevB.56.5484

CrossRef Full Text | Google Scholar

10. Beenakker CWJ. Theory of Coulomb-blockade oscillations in the conductance of a quantum dot. Phys Rev B. (1991) 44:1646–56. doi: 10.1103/PhysRevB.44.1646

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Averin DV, Korotkov AN, Likharev KK. Theory of single-electron charging of quantum wells and dots. Phys Rev B. (1991) 44:6199–211. doi: 10.1103/PhysRevB.44.6199

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Li SS, Chang K, Xia JB, Hirose K. Spin-dependent transport through Cd1-xMnxTe diluted magnetic semiconductor quantum dots. Phys Rev B. (2003) 68:245306:1–5. doi: 10.1103/PhysRevB.68.245306

CrossRef Full Text | Google Scholar

13. zutić I, Fabian J, Sarma SD. Spintronics: fundamentals and applications. Rev Mod Phys. (2004) 76:323–410. doi: 10.1103/RevModPhys.76.323

CrossRef Full Text | Google Scholar

14. Barnaś J, Martinek J, Michałek G. Spin effects in ferromagnetic single-electron transistors. Phys Rev B. (2000) 62:12363–73. doi: 10.1103/PhysRevB.62.12363

CrossRef Full Text | Google Scholar

15. Hamaya K, Masubuchi S, Kawamura M. Spin transport through a single self-assembled InAs quantum dot with ferromagnetic leads. Appl Phys Lett. (2007) 90:053108:1–3. doi: 10.1063/1.2435957

CrossRef Full Text | Google Scholar

16. Weymann I, Barns J. Transport through two-level quantum dots weakly coupled to ferromagnetic leads. J Phys Condens Matter. (2007) 19:096208:1–21. doi: 10.1088/0953-8984/19/9/096208

CrossRef Full Text | Google Scholar

17. Ma MJ, Jalil MBA, Tan SG. Effect of interface spin-flip scattering on the spin polarized transport through a quantum dot: Master equation approach. J Appl Phys. (2009) 105:07E907:1–3. doi: 10.1063/1.3075982

CrossRef Full Text | Google Scholar

18. Chi F, Zeng H, Yuan X. Flux-dependent tunnel magnetoresistance in parallel-coupled double quantum dots. Superlattice Microst. (2009) 46:523–32. doi: 10.1016/j.spmi.2009.04.002

CrossRef Full Text | Google Scholar

19. Michalek G, Bulka BR. Tunnel magnetoresistance in quantum dots in the presence of singlet and triplet states. J Phys Condens Matter. (2011) 23:175305–15. doi: 10.1088/0953-8984/23/17/175305

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Nayak C, Simon SH, Stern A. Non-Abelian anyons and topological quantum computation. Rev Mod Phys. (2008) 80:1083–159. doi: 10.1103/RevModPhys.80.1083

CrossRef Full Text | Google Scholar

21. Alicea J, Oreg Y, Refael G. Non-Abelian statistics and topological quantum information processing in 1D wire networks. Nat Phys. (2011) 7:412–7. doi: 10.1038/nphys1915

CrossRef Full Text | Google Scholar

22. Torsten Karzig RML Christina Knapp. Scalable designs for quasiparticle-poisoning-protected topological quantum computation with Majorana zero modes. Phys Rev B. (2017) 95:235305:1–32. doi: 10.1103/PhysRevB.95.235305

CrossRef Full Text | Google Scholar

23. Sato M, Fujimoto S. Topological phases of noncentrosymmetric superconductors: Edge states, Majorana fermions, and non-Abelian statistics. Phys Rev B. (2009) 79:094504:1–16. doi: 10.1103/PhysRevB.79.094504

CrossRef Full Text | Google Scholar

24. Qi XL, Zhang SC. Topological insulators and superconductors. Rev Mod Phys. (2011) 83:1057–110. doi: 10.1103/RevModPhys.83.1057

CrossRef Full Text | Google Scholar

25. Wimmer M, Akhmerov AR, Medvedyeva MV. Majorana bound states without vortices in topological superconductors with electrostatic defects. Phys Rev Lett. (2010) 105:046803:1–4. doi: 10.1103/PhysRevLett.105.046803

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Sau JD, Lutchyn RM, Tewari S. Generic new platform for topological quantum computation using semiconductor heterostructures. Phys Rev Lett. (2010) 104:040502:1–24. doi: 10.1103/PhysRevLett.104.040502

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Lutchyn RM, Sau JD, Sarma SD. Majorana fermions and a topological phase transition in semiconductor-superconductor heterostructures. Phys Rev Lett. (2010) 105:077001:1–4. doi: 10.1103/PhysRevLett.105.077001

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Choy TP, Edge JM, Akhmerov AR. Majorana fermions emerging from magnetic nanoparticles on a superconductor without spin-orbit coupling. Phys Rev B. (2011) 84:195442:1–6. doi: 10.1103/PhysRevB.84.195442

CrossRef Full Text | Google Scholar

29. San-Jose P, Prada E, Aguado R. AC Josephson effect in finite-length nanowire junctions with Majorana modes. Phys Rev Lett. (2012) 108:257001:1–5. doi: 10.1103/PhysRevLett.108.257001

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Mourik V, Zuo K, Frolov SM. Signatures of Majorana fermions in hybrid superconductor-semiconductor nanowire devices. Science. (2012) 336:1003–7. doi: 10.1126/science.1222360

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Wang R, Su W, Zhu JX. Kondo signatures of a quantum magnetic impurity in topological superconductors. Phys Rev Lett. (2019) 122:087001:1–6. doi: 10.1103/PhysRevLett.122.087001

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Lo´pez R, Lee M, Serra L. Thermoelectrical detection of Majorana states. Phys Rev B. (2014) 89:205418:1–7. doi: 10.1103/PhysRevB.89.205418

CrossRef Full Text | Google Scholar

33. Ricco LS, Dessotti FA, Shelykh IA. Tuning of heat and charge transport by Majorana fermions. Sci Rep. (2018) 8:2790–7. doi: 10.1038/s41598-018-21180-9

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Smirnov S. Universal Majorana thermoelectric noise. Phys Rev B. (2018) 97:165434:1–14. doi: 10.1103/PhysRevB.97.165434

CrossRef Full Text | Google Scholar

35. Hamaya K, Kitabatake M, Shibata K. Oscillatory changes in the tunneling magnetoresistance effect in semiconductor quantum-dot spin valves. Phys Rev B. (2008) 77:081302(R):1–4. doi: 10.1103/PhysRevB.77.081302

CrossRef Full Text | Google Scholar

36. Stefański P. Tunneling magnetoresistance anomalies in a Coulomb blockaded quantum dot. Phys Rev B. (2009) 79:085312:1–9. doi: 10.1103/PhysRevB.79.085312

CrossRef Full Text | Google Scholar

37. Sun QF, Xie XC. Spontaneous spin-polarized current in a nonuniform Rashba interaction system. Phys Rev B. (2005) 71:155321:1–6. doi: 10.1103/PhysRevB.71.155321

CrossRef Full Text | Google Scholar

38. Sun QF, Wang J, Guo H. Quantum transport theory for nanostructures with Rashba spin-orbital interaction. Phys Rev B. (2005) 71:165310:1–11. doi: 10.1103/PhysRevB.71.165310

CrossRef Full Text | Google Scholar

39. Ricco LS, de Souza M, Figueira MS. Spin-dependent zero-bias peak in a hybrid nanowire-quantum dot system: distinguishing isolated Majorana fermions from Andreev bound states. Phys Rev B. (2019) 99:155159:1–9. doi: 10.1103/PhysRevB.99.155159

CrossRef Full Text | Google Scholar

40. Piotr S. Properties of the Majorana-state tunneling Josephson junction mediated by an interacting quantum dot. J Phys Condens Matter. (2019) 31:185301:1–18. doi: 10.1088/1361-648X/ab052a

CrossRef Full Text | Google Scholar

41. Prada E, Aguado R, San-Jose P. Measuring Majorana nonlocality and spin structure with a quantum dot. Phys Rev B. (2017) 96:085418:1–10. doi: 10.1103/PhysRevB.96.085418

CrossRef Full Text | Google Scholar

42. Deng MT, Vaitiekenas S, Prada E, San-Jose P, Nygard J, Krogstrup P, et al. Nonlocality of Majorana modes in hybrid nanowires. Phys Rev B. (2018) 98:085125:1–10. doi: 10.1103/PhysRevB.98.085125

CrossRef Full Text | Google Scholar

43. Pals P, MacKinnon A. Coherent tunnelling through two quantum dots with Coulomb interaction. J Phys Condens Matter. (1996) 8:5401–14. doi: 10.1088/0953-8984/8/29/015

CrossRef Full Text | Google Scholar

44. Liu DE, Baranger HU. Detecting a Majorana-fermion zero mode using a quantum dot. Phys Rev B. (2011) 84:201308R:1–4. doi: 10.1103/PhysRevB.84.201308

CrossRef Full Text | Google Scholar

45. Vernek E, Penteado PH, Seridonio AC, Egues JC. Subtle leakage of a Majorana mode into a quantum dot. Phys Rev B. (2014) 85:165304:1–5. doi: 10.1103/PhysRevB.89.165314

CrossRef Full Text | Google Scholar

46. Ruiz-Tijerina AD, Vernek E, da Silva LGGVD, Egues JC. Interaction effects on a Majorana zero mode leaking into a quantum dot. Phys Rev B. (2015) 91:115435:1–5. doi: 10.1103/PhysRevB.91.115435

CrossRef Full Text | Google Scholar