Discrete-Event Simulation of Quantum Walks

We use discrete-event simulation on a digital computer to study two different models of experimentally realizable quantum walks. The simulation models comply with Einstein locality, are as “realistic” as the one of the simple random walk in that the particles follow well-defined trajectories, are void of concepts, such as particle-wave duality and wave-function collapse, and reproduce the quantum-theoretical results by means of a cause-and-effect, event-by-event process. Our simulation model for the quantum walk experiment presented in Robens et al. [1] reproduces the result of that experiment. Therefore, the claim that the result of the experiment “rigorously excludes (i.e., falsifies) any explanation of quantum transport based on classical, well-defined trajectories” needs to be revised.

1. Introduction

A particle is said to perform a simple random walk (SRW) over a set of lattice points (enumerated by integers) when at each time step, it jumps to one of its neighboring points, and the direction of the jump is determined by a random variable [2, 3]. Random walks find applications in many diverse fields, too many to list them here.

The term “quantum random walk” was introduced in 1993 [4] and emphasizes the analogy to the simple random walk on a lattice. However, the time evolution of a “quantum random walk” is deterministic and reversible [5], not random at all, so the term quantum walk (QW) is more apt. There are various kinds of proposals and implementations of QWs using optical lattices [1, 6, 7], ion traps [8–10], microwave cavities [11], or optical networks [12–14]. A review covering various aspects of QWs is given in Kempe [15].

The basic idea of the QW is similar to that of the SRW. Instead of using a random variable to decide which way to jump, an internal degree of freedom (e.g., spin or polarization) is used to determine the direction of the jump. This internal degree of freedom changes its state according to the rules of quantum theory, that is by a unitary transformation.

For simplicity, in this paper, we consider the case where this state is described by a 2-dimensional Hilbert space (e.g., spin up |↑〉 and spin down |↓〉) and the particle makes nearest-neighbor hops on a one-dimensional lattice. Compared to the SRW, the new feature is that at each jump, the state of the spin changes by a unitary transformation, e.g., a Hadamard transformation. The particle moves to the right if the projection of the spin (along the z-axis by convention) is up |↑〉 and moves to the left if its spin is down |↓〉.

In symbols, this process is formalized as follows. The basis states of the Hilbert space are |x, s〉, where x ∈ {−L, …, L} labels the position on the one-dimensional lattice of X = 2L + 1 sites, and s ∈ {↑, ↓} labels the eigenstates of the z-component of the Pauli matrices describing the internal degree of freedom. In terms of the basis states, the wave function at step l reads

$\begin{array}{l}|{\Phi }^{(l)}\rangle ={\displaystyle \sum _{x=-L}^L}{\varphi }_{x,\uparrow }^{(l)}|x,\uparrow \rangle +{\varphi }_{x,\downarrow }^{(l)}|x,\downarrow \rangle ,\\ {\displaystyle \sum _{x=-L}^L}|{\varphi }_{x,\uparrow }^{(l)}{|}^2+|{\varphi }_{x,\downarrow }^{(l)}{|}^2=1,& (1)\end{array}$

and is related to the initial state |Φ⁽⁰⁾〉 = |0, ↑〉 by

$\begin{array}{ll}|{\Phi }^{(l)}\rangle ={(SH)}^l|{\Phi }^{(0)}\rangle ,& (2)\end{array}$

where

$\begin{array}{ll}S={\displaystyle \sum _{x=-L+1}^L}|x-1,\uparrow \rangle \langle x,\uparrow |+{\displaystyle \sum _{x=-L}^{L-1}}|x+1,\downarrow \rangle \langle x,\downarrow |& (3)\end{array}$

is the operator that implements the particle jump,

$\begin{array}{l}|\uparrow \rangle \langle \uparrow |=\left(\begin{array}{cc}1& 0\\ 0& 0\end{array}\right),|\downarrow \rangle \langle \downarrow |=\left(\begin{array}{cc}0& 0\\ 0& 1\end{array}\right),|\uparrow \rangle \langle \downarrow |=\left(\begin{array}{cc}0& 1\\ 0& 0\end{array}\right),\\ |\downarrow \rangle \langle \uparrow |=\left(\begin{array}{cc}0& 1\\ 0& 0\end{array}\right)& (4)\end{array}$

are the spin projection operators, and

$\begin{array}{ll}H=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}1& 1\\ 1& -1\end{array}\right)& (5)\end{array}$

is the Hadamard operation, acting on the spin degree-of-freedom only. We only consider the case that the number of steps is smaller than or equal to L, meaning that the particle initially localized at x = 0 never goes beyond the boundaries of the lattice.

QWs are different from SRWs in that the latter cannot display interference phenomena whereas the former, being described in terms of the evolution of a wave function, can. In addition, the probability distribution of a QW (starting from the initial state |Φ⁽⁰⁾〉 = |0, ↑〉) is not necessarily symmetric w.r.t. x = 0, unlike the probability distribution of a SRW for a particle initially at x = 0. Furthermore, the variance of x is non-linear in the number of steps L [15].

There are two distinct views of the formulation of the QW. The first uses the particle picture to spell out the rules by which a particle changes its position and spin. Although the spin is often regarded as a characteristic quantum feature, if there is only one spin in play, we can equally well represent this spin by a unit vector on a Bloch sphere, a genuine classical-mechanical construct. The quantization of the spin only enters through the digitalization of its projection on the z-axis, a process very similar to the tossing of a coin, which during its flight usually rotates. This pictorial description of the motion of a single particle is as “realistic” as the one of the SRW. Indeed, at any time the particle is at a definite position and the measurement of the internal degree of freedom yields an unpredictable outcome (the mapping of the unit vector to “spin-up” or “spin-down”), determining the direction of the jump.

In the second view of the formulation of the QW, use of wave mechanics is made in order to describe the evolution of a collection of particles, prepared in the same initial state (position and spin). The realistic view is lost when we impose that the time evolution of a single particle and its internal degree of freedom are to be described in terms of a wave function that evolves in time according to the rules of quantum theory, Equation (2) in the case at hand.

2. Aim of the Paper

In this paper, we demonstrate that QWs can be modeled without ever having to resort to the notion of particle-wave duality, the wave function of the particle, the update rule Equation (2), etc. Specifically, we show that it is possible to construct a discrete-event simulation (DES) that is as realistic as the model of the SRW, complies with Einstein's notion of local causality [16], and reproduces the results of quantum theory without using expressions, such as Equations (1) or (2). In this respect, DES constitutes a “subquantum” model that agrees with the statistical results of quantum theory but additionally gives a description in terms of individual events in contrast to quantum theory which only gives collective, statistical predictions.

DES is a general methodology for simulating the time evolution of a system as a discrete sequence of consecutive events. In the application at hand, there are four different kinds of events, namely a particle starting its walk, an operation acting on the second degree of freedom (e.g., the spin) of a particle, a particle moving from one lattice site to the next according to the state of the second degree of freedom, and a particle being counted and removed by detectors positioned at each of the lattice sites and activated after a particle made the maximum number of allowed jumps.

Simulation of a SRW is one of the simplest applications of DES. In the DES of both the SRW and the QW, each walker follows a well-defined trajectory but in contrast to the former, the latter yields distributions of particles over the lattice which agree with the quantum-theoretical prediction, not with a distribution originating from a diffusion process.

We also use DES to reproduce the experimental data of a particular QW experiment with atoms [1], which “rigorously excludes (i.e., falsifies) any explanation of quantum transport based on classical, well-defined trajectories,” in blatant contradiction with the fact that each of the particles in the DES follows a well-defined trajectory and the DES reproduces the experimental data. In particular, we show that the DES can produce data that either violates or does not violate the Leggett-Garg inequality (LGI) [17], depending on the treatment of the data [18, 19]. This implies that the QW by itself is not the cause of a violation of the LGI. Note that in DES it is trivial to perform non-invasive measurements, an essential requirement for the application of the LGI [17].

3. Discrete-Event Simulation

For our demonstration, we build on the DES approach introduced in De Raedt et al. [20], which reproduces the experimental and quantum-theoretical results of many fundamental quantum-physics experiments with photons and neutrons [21]. In essence, we use DES on a digital computer as a metaphor for a perfect laboratory experiment [22]. A salient feature of any DES implementation is that all variables which enter the model have definite values and are known at all times. The application of DES to the QW is based on the following ideas:

1. The moving object is treated as a particle carrying a unit vector and making nearest-neighbor jumps on a one-dimensional lattice.

2. There are “processing units” which can be thought of as being placed on the lattice sites. Depending on the unit vector that the particle carries when it enters a processing unit, the latter may rotate the unit vector and tell the particle where to jump to.

3. Each particle can only take one definite path. In this sense, our DES of a QW is as “realistic” as the DES of a SRW.

4. A particle can arrive at only one detector. The function of the detector is to count the particle and to remove it from the lattice. Each detection event is caused by exactly one particle making a walk. Of course, being a simulation on a digital computer, during the DES, the position of the particle and its unit vector can be “read out” at any time, without disturbing anything.

5. A particle is not allowed to start its walk as long as there is another particle present on the lattice, implying that there can be no direct interaction between particles.

6. Interference results from the adaptive dynamics of the processing units. In the case at hand, a processing unit models a beam splitter with two input and two output ports (see below). Input to such a processing unit are the port at which the particle enters and the orientation of the unit vector. The adaptive dynamics changes the internal state of the processing unit in a deterministic manner. The internal state determines the output port by which a particle leaves the processing unit.

7. After processing many particles (100,000 in the case at hand), the relative frequencies of the detector counts agree with the probabilities obtained from the quantum-theoretical description.

In a DES, we can read off, at any time, the value of a physical quantity without changing the state of the system and we explicitly exclude from consideration DES implementations that violate Einstein's criterion of local causality. Specifically, our DES models satisfy the locality criteria of category 0, as defined in Hess [16], that is they are void of interactions (such as those appearing in the hydrodynamic/Bohm interpretation of quantum theory [23, 24]) that violate Einstein's criterion of local causality. In summary, our DES approach satisfies the criteria for a local realist model.

Our DES is manifestly “non-quantum mechanical” in the sense that there is no wave function describing the state of the particle in space-time but instead there are definite particle trajectories. Still the rules by which these trajectories are formed cannot be described by “Newtonian mechanics.” Clearly, without calling upon magic, one cannot have individual particles following well-defined trajectories interfere unless there is a mechanism at work that provides some form of indirect communication between successive particles starting their walk. As mentioned in 6 above, in our DES approach, this indirect communication is the result of the adaptive (non-Newtonian) dynamics of the processing unit.

At this point of the discussion, we wish to draw attention to a paper of Duane [25]. Duane proposed that, in addition to the quantum rules for energy and angular momentum, there is a similar rule for the linear momentum and then showed that with this rule one can explain the diffraction of X-rays from a crystal without reference to interference of waves [25]. In plain words, the key point of Duane's work may be formulated as follows: there is no reason to attach a wave function to a particle if there is plenty of wave-like motion in the crystal with which the X-rays interact. At the time of the development of quantum theory, the latter experiment was generally taken as strong evidence for the dual particle-wave character. An extensive discussion of the negative impact of the particle-wave duality and the development of a deeper understanding of where quantum theory comes from and what it entails is given by Landé in a series of papers [26–29] and a book [30].

We mention Duane's work [25] here because in essence, a similar idea is also used to construct the rules of operation for the processing units in our DES. Indeed, a quick glance at the structure of the DES algorithm for a beam splitter [20, 21] shows that the internal state of this unit is represented by a real-valued vector of length two and a complex-valued vector of length four. The decision about the port at which the particle leaves the beam splitter involves the combination of these two vectors and a multiplication by a 4 × 4 unitary matrix. In other words, we have attached a kind of “wave function” to the material (of the beam splitter), meaning that this “wave function” is local to the device. In the case of a beam splitter for light, the internal state, the “wave function,” is just another word for the electrical polarization vector of the material [21] and has little relation to the particle wave function that appears in quantum theory. An essential ingredient of the processing unit, its capability of adapting (learning) its state from the particles that it receives on its input ports, as well as the rule to send particles out, cannot be inferred from the work of Duane. They are designed such that the DES is able to reproduce, event-by-event (particle-by-particle), in a cause-and-effect manner, the values of the probabilities predicted by quantum theory [20, 21].

4. Discrete-Event Simulation of a QW

In this section, we present the results of a DES for a QW on a line which can be implemented by a network of beam splitters, phase shifters and photodetectors [12]. An interesting point of this implementation is that light waves can be used to simulate the QW, i.e., we can use Maxwell's equations for electromagnetic waves to simulate a quantum system. Of course, this is not really a surprise as the description of beam splitters, phase shifters etc., uses Jones-vector calculus which is, in essence, the same as the quantum-theoretical description in terms of Equations (1)–(5). As explained earlier, the main point of performing a DES for a QW is that it uses an event-by-event, particle-based approach that is as realistic as the description of a SRW and does not rely on the quantum formalism embodied in Equations (1)–(5).

The layout of the proposed experiment is shown in Figure 1. The function of the beam splitters is to create the superposition of the two input modes. In Jones-vector calculus or quantum theory (see Appendix A), the matrix describing the operation of a beam splitter is given by

$\begin{array}{ll}{M}_{\text{BS}}=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}1& i\\ i& 1\end{array}\right).& (6)\end{array}$

Two phase shifters, with their Jones matrix representation given by

$\begin{array}{ll}{M}_{{\phi }_1}=\left(\begin{array}{cc}{e}^{i{\phi }_1}& 0\\ 0& 1\end{array}\right)\text{and }{M}_{{\phi }_2}=\left(\begin{array}{cc}1& 0\\ 0& e^{i{\phi }_2}\end{array}\right),& (7)\end{array}$

respectively, change the phase difference between the two partial waves leaving the beam splitter.

FIGURE 1

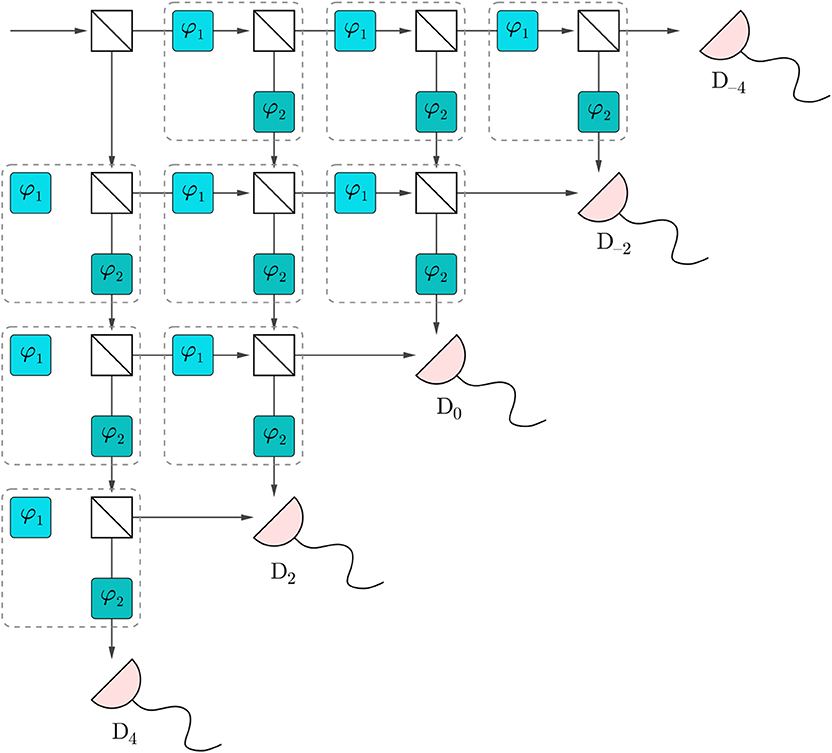
Figure 1. Setup of a realization of a QW experiment [12] on a line of L = 4 levels (X = 9 lattice sites). The solid (cyan) boxes represent phase shifters, shifting the phase of the wave by angles φ₁ or φ₂, respectively. Open squares with a diagonal line represent 50:50 beam splitters. Half circles (pink) with a tail denote detectors at level 4, placed at lattice sites x = −4, −2, 0, 2, 4. Each group of three processing units, marked by a dashed border, causes the particle to jump left or right.

Table 1 summarizes the theoretical results for the QW and the corresponding SRW. For both types of walks, detectors with an odd (even) number x will only register particles if l is also odd (even). From the expressions in Table 1 it also follows that the probabilities to observe a particle do not depend on φ₁. For more than two steps (l > 2) the dependence on φ₂ is sinusoidal, a characteristic feature of interference. Furthermore, the variance is larger than for the SRW and the peak of the distributions is not at the center anymore.

TABLE 1

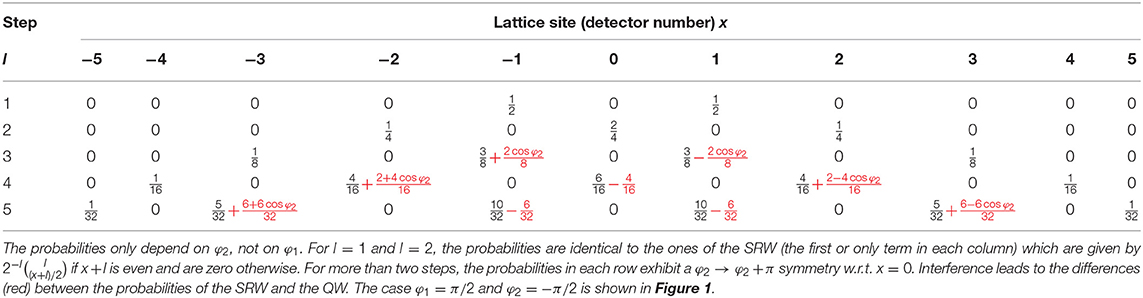
Table 1. Quantum theoretical results for the probabilities of the quantum walk after l = 1, …, 5 steps (see Appendix A for details on the calculation) for a particle initially localized at x = 0.

Implementing a DES for a network, such as the one shown in Figure 1 is straightforward. We simply reuse, over-and-over again and without modification, the event-based algorithms that have been developed to simulate the beam splitter, phase shifter, and detector [21] and connect outputs to inputs of these algorithms strictly according to the diagram in Figure 1. As the algorithms for all the different components and the method to stitch them together have been discussed extensively and at great length elsewhere [21], we omit the discussion of these aspects. The reader interested in setting up her/his own DES should consult Michielsen and De Raedt [21] and papers cited therein. Details of the implementation, specific for the application to QWs, can be found in Nocon [31]. An example implementation in PYTHON is given in Appendix B and available online¹.

Our implementation of the DES of the QW experiment shown in Figure 1 allows for more than L = 5 levels (X = 11 sites). In general, the larger the number of beam splitters in the diagram, the larger the number of particles has to be in order for the processors mimicking the beam splitters to adapt sufficiently well to the ratio of particles arriving at the two input ports, i.e., representing the two sides at which photons can enter a beam splitter [20, 21]. Numerical experiments show that sending N = 100, 000 particles through the network is more than sufficient to go up to L = 7 levels (X = 15 sites) and to obtain data with good statistics. Figures 2A–F shows DES results after l = 2 up to l = 7 steps and for the phase shifts φ₁ = π/2 and φ₂ = −π/2, as well as the results obtained from the quantum-theoretical description (asterisks). Other asymmetric cases are considered below and in Nocon [31] and can be generated using the program given in Appendix B.

FIGURE 2

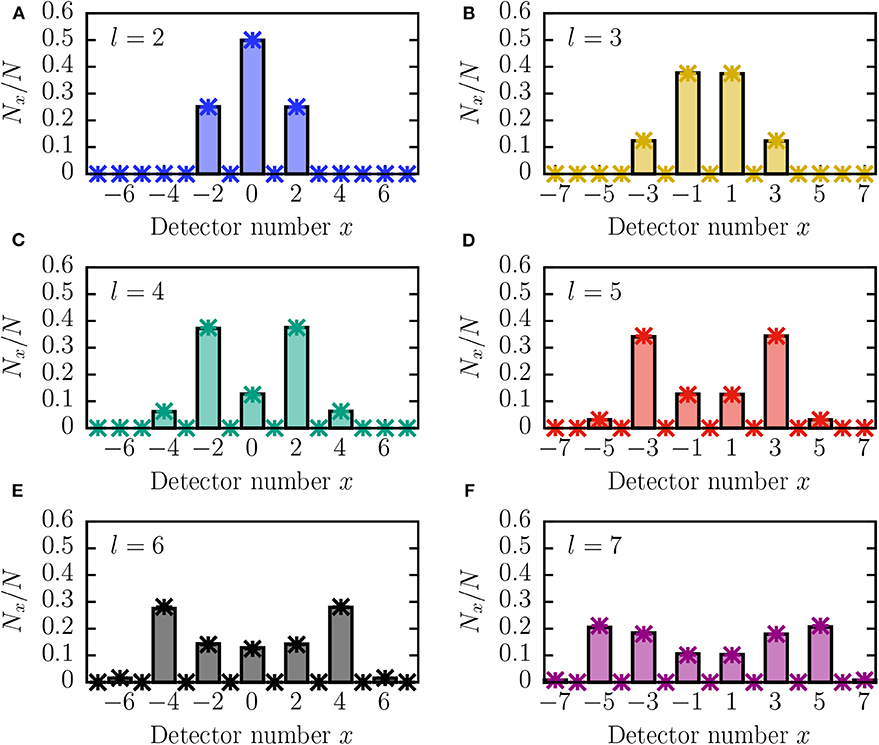
Figure 2. Results for the normalized number of detector counts N_x/N as a function of the detector number x, obtained by a DES of the QW for N = 100, 000 repetitions, φ₁ = π/2 and φ₂ = −π/2 and for different numbers of steps l = 2, …, 7, corresponding to (A–F). The distributions from the DES (bars) match with the analytical results for the QW (asterisks, see Table 1). For more than 3 steps, the distributions of the QW are broader than those of the SRW (see Table 1) because of interference effects.

The DES outcomes are in full agreement with the quantum-theoretical results. In conclusion, the DES provides a local realist model that reproduces the quantum-theoretical results of the QW.

5. Discrete-Event Simulation of a QW Experiment With Atoms [1]

Robens et al. experimentally implemented a four-level QW with cesium atoms in a state-dependent optical potential [1]. They made use of the fact that the two hyperfine states of the electronic ground state of the cesium atom, |F = 4, m_F = 4〉 (pseudo-spin up) and |F = 3, m_F = 3〉 (pseudo-spin down), experience a different lattice potential [1]. A microwave pulse can change the superposition of these two hyperfine states, and the difference in sensitivity of the |F = 4, m_F = 4〉 and |F = 3, m_F = 3〉 states to left- and right-handed polarized light can be used to manipulate the position of the cesium atoms in the state-dependent potential [1].

In the DES, a cesium atom with its two hyperfine states is represented by a particle carrying a two-state spin system. Although we should not think of particles in the DES as objects observed in Nature, to build a mental picture of what the DES is actually doing, it may, for the present purpose, be very helpful to think of a particle and its spin as a single photon and its polarization [32]. Therefore, and also for the uniformity of presentation, we will formulate the DES model of the cesium-atom experiment using the language of optics, using terms like beam splitters, phase shifters, etc. As a matter of fact, as long as the dimension of the Hilbert space is finite, it is always possible to reformulate the original problem as a problem of photons traversing a network of optical components [33] or, equivalently, as a quantum gate circuit [34].

The basic ingredients of the DES are then the following [31]. Distinguishing the cesium atoms on the basis of their hyperfine state is implemented as the action of a polarizing beam splitter, separating h and v polarized photons (relative to the entrance surface of the first polarizing beam splitter in Figure 3). In the context of the experiment, h (v) corresponds to the hyperfine states |F = 4, m_F = 4〉 (|F = 3, m_F = 3〉). The creation of the superposition of the hyperfine states is realized by Hadamard transformations, i.e., a combination of half-wave plates and π/2 phase shifters [21, 31]. As h and v polarized photons do not interfere, instead of the 50:50 beam splitters used in the DES of the QW model studied in section 4, we use polarizing beam splitters in order to let h and v polarized photons interfere [31]. A sample implementation of the DES is given in Appendix B.

FIGURE 3

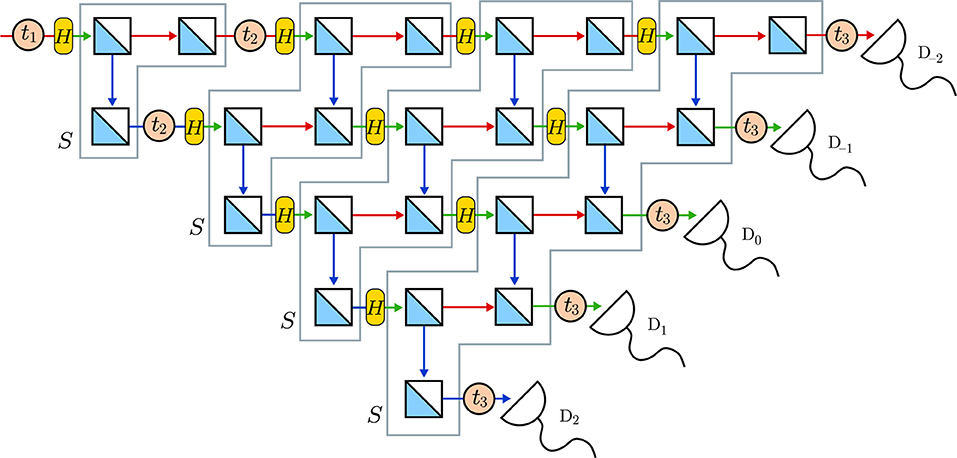
Figure 3. DES setup for the QW with polarized single photons of the same energy. Red horizontal (blue vertical) lines show the path of h (v) polarized photons. Green lines represent the path of photons with a linear combination of h and v polarization. The input to the network consists of h polarized photons only. Square (blue/white) boxes represent polarizing beam splitters. The oval (yellow) boxes perform a Hadamard transformation on the photon polarization. Each gray region corresponds to a single-atom jump operation in the QW experiment [1]. In quantum theory, the H boxes correspond to Equation (5) and the S regions correspond to Equation (3). Circles with labels t₁, t₂, and t₃ denote the positions of the Q(t₁), Q(t₂), and Q(t₃) measurements, respectively.

The “photonics” DES network that corresponds to the experiment with the cesium atoms [1] is depicted in Figure 3. Looking at Figure 3, it is easy to see that some of the polarizing beam splitters (those that show only one input and one output line) can be removed without affecting the operation of the network. However, in our DES, we do not “optimize” the network for computational efficiency. As a matter of fact, the DES of the network in Figure 3 is so fast that optimization is not worth the effort (the original implementation was written in C++ [31], but even the demonstration in PYTHON given in Appendix B only takes a few seconds).

Figures 4A–C shows that the DES reproduces the experimental results of Robens et al. [1]. For convenience, the experimental data have been read off from Figures 3A–C of Robens et al. [1], normalized, and plotted as striped bars in Figures 4A–C. Furthermore, we see that the DES produces the quantum-theoretical results of the asymmetric four-step QW (asterisks).

FIGURE 4

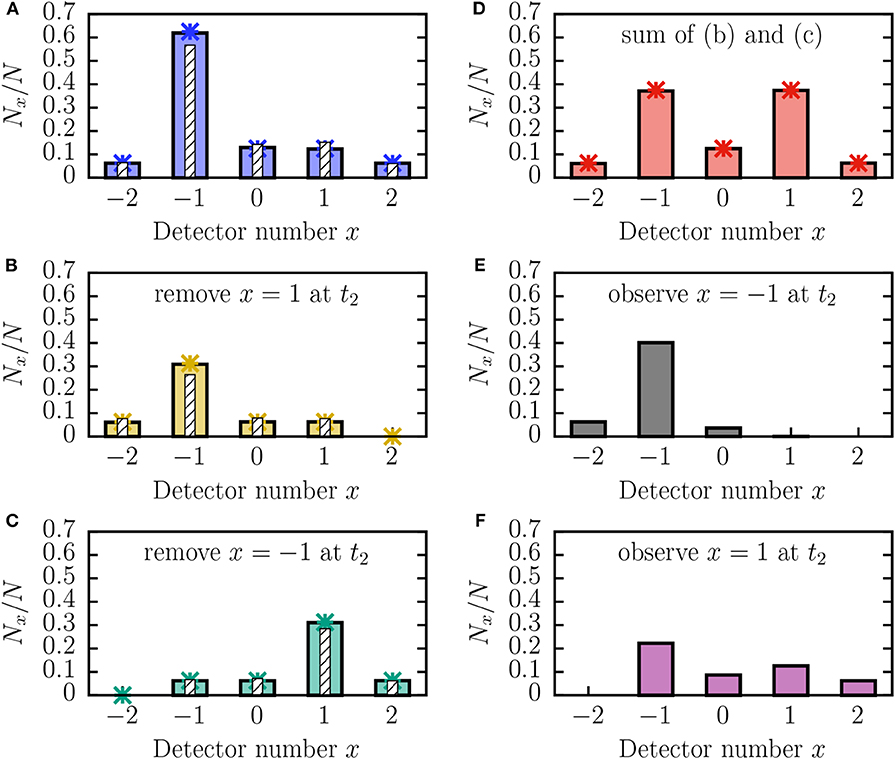
Figure 4. DES results (solid bars) of the normalized detector counts N_x/N as a function of the detector position x. In each run, N = 100, 000 particles were sent through the network shown in Figure 3. In (A–C), the solid bars represent the distribution where at position t₂, (A) no particles, (B) particles at x = 1, (C) particles at x = −1 have been removed. In (D), the sum of (B,C) is shown to be symmetric and equal to the four-step QW shown in Figure 2C (for x ↦ x/2). (E,F) Show the distributions resulting from only observing (and not removing) the particle at t₂. As their sum yields the distribution in (A), the observation does not affect the result and is thus non-invasive. Asterisks represent the ideal result obtained from quantum theory, i.e., $\sum _s|\langle 2x,s|{(SH)}^3|\psi \rangle {|}^2$ where |ψ〉 is given by (A) SH|0, ↑〉, (B) $|-1,\uparrow \rangle /\sqrt{2}$, or (C) $|+1,\downarrow \rangle /\sqrt{2}$ (see also Equations 2–5). There are no asterisks in (E,F) because this information is only accessible in the subquantum model. The corresponding experimental data presented in Figures 3A–C of Robens et al. [1] is (up to a normalization factor) indicated by the striped bars in (A–C).

The agreement between the DES and experimental data proves that, in contrast to the claim made in Robens et al. [1], it is possible, to describe a QW without a particle wave function, but with particles following individual trajectories that are as well-defined as in the case of a SRW, and local “wave functions” attached to each polarizing beam splitter [21]. We remark that the learningrate parameter of the beam splitters (see Appendix B) can be used to tune the “quantumness” of the DES such that learningrate = 0 yields the SRW and 0.9 ≤ learningrate ≤ 0.98 yields the QW.

Obviously, the agreement between the DES and experimental data seems to be in conflict with the common lore that local realist models, such as a DES cannot reproduce certain results of quantum physics. It is therefore of interest to explore whether this conflict is fundamental or not. Recall that by construction, our DES model of the QW complies with the category 0 locality criteria, as defined in Hess [16].

Robens et al. support their claim that the QW experiment “rigorously excludes (i.e., falsifies) any explanation of quantum transport based on classical, well-defined trajectories” by demonstrating a violation of a LGI [1]

$\begin{array}{ll}K=\langle Q(t_2)Q(t_1)\rangle +\langle Q(t_3)Q(t_2)\rangle -\langle Q(t_3)Q(t_1)\rangle \le 1,& (8)\end{array}$

where the Q(t_i) are real numbers with |Q(t_i)| ≤ 1 and t_i denote the position at which the measurements are performed (equivalent to the time in the original formulation of the LGI). We demonstrate, by means of a DES of their experiment, that their claim is unfounded.

5.1. Procedure Applied in the Experiment [1]

Robens et al. set t₁ = 0 (initial state preparation |Φ⁽⁰⁾〉 = |x = 0, ↑〉, start of a single-particle walk), t₂ = 1 (after the first single-atom jump), and t₃ = 4 (after the fourth single-atom jump). In Figure 3, each single-atom jump corresponds to a transition from one gray region to the next. Circles with the labels t₁, t₂, and t₃ indicate the corresponding positions in the DES. Robens et al. proceed by choosing Q(t₁) = Q(t₂) = 1 and assign Q(t₃) = +1 if at the fourth step, the particle is observed at x > 0, and Q(t₃) = −1 otherwise [1]. With these simplifications, Equation (8) reduces to

$\begin{array}{ll}K=1+\langle Q(t_3)Q(t_2)\rangle -\langle Q(t_3)\rangle \le 1.& (9)\end{array}$

In order to estimate 〈Q(t₃)〉, Robens et al. repeat the QW experiment about 400 times, and compute the average of the measured Q(t₃) [1]. To estimate 〈Q(t₃)Q(t₂)〉, Robens et al. need to repeat the same QW procedure two times in addition. In the first (second) repetition, they measure the position at t₂, by what they believe is an ideal negative measurement, and remove atoms that are measured at position x = 1 (x = −1). We cannot question the extent to which they really implemented an ideal negative measurement in their experiment. In our DES of this experiment, however, it is trivial to perform an ideal negative measurement. In both cases, the atoms continue their walk and are finally measured at t₃, yielding either Q(t₃) = −1 or Q(t₃) = +1. The average of the Q(t₃)'s is then denoted by 〈Q(_t3)〉x₂ where x₂ ∈ {−1, +1} indicates which atoms are kept at t₂.

With this data in hand, Robens et al. compute the left-hand side of Equation (9) as

$\begin{array}{ll}K=1+{\displaystyle \sum _{x_2=\pm 1}P}(x_2;t_2){\langle Q(t_3)\rangle }_{x_2}-\langle Q(t_3)\rangle ,& (10)\end{array}$

where P(x₂; t₂) denotes the probability that the atom was at position x₂ = ±1 at t₂, the theoretical values being 1/2 (see the l = 1 row of Table 1). Plugging in the experimentally obtained data, Robens et al. find that [1]

$\begin{array}{ll}K=1.435\pm 0.074>1,& (11)\end{array}$

and conclude that the “reported violation of the LG inequality proves that the concept of a well-defined, classical trajectory is incompatible with the results obtained in a quantum-walk experiment [1].” This conclusion is unjustified, as we now show.

5.2. Refutation of the Claim

Our demonstration consists of two steps. First, we show that a DES of the QW performed with the same measurement procedure as the one used by Robens et al. reproduces their experimental results and therefore also produces a violation of the LGI. In this case, the DES also reproduces the results of the quantum-theoretical model in which we block the corresponding path labeled by t₂. Second, because in a DES performing non-invasive measurements is not an issue, there is no need to perform three different runs to measure all the quantities which appear in Equation (9). In fact, one DES run suffices to compute all the quantities that enter the LGI. In this case, the DES also reproduces the quantum-theoretical results of the QW.

In the first step, we adopt the same procedure as in the real experiment [1], namely we perform three DESs for a four-step QW. In each DES run, the number of particles is N = 100, 000. In the first run, we compute 〈Q(t₃)〉 without removing particles at position t₂. For the other two runs, at position t₂, we simulate an ideal negative measurement by removing the particles traveling to the right (h polarization) and downwards (v polarization), respectively, as Robens et al. do in their experiment with the cesium atoms.

Direct confirmation that the DES reproduces the experimentally observed results follows from comparing the data obtained using the removal process (see Figures 4A–C) with the corresponding data presented in Figures 3A–C of Robens et al. [1]. Up to normalization factors, all results agree. Furthermore, the DES reproduces the quantum-theoretical results for the QW starting at (t₁, x = 0), (t₂, x = −1), and (t₂, x = +1), shown as asterisks in Figures 4A–C, respectively.

Next, we compute K as given in Equation (10) from the data of the three different runs. We estimate the statistical error on the value of K by repeating the three different runs ten times and obtain

$\begin{array}{ll}K=1.497\pm 0.006>1,& (12)\end{array}$

violating the LGI by several standard deviations. In fact, the value of K = 1.497±0.006 is compatible with the theoretical maximum violation of K = 1.5, achievable by this type of experiment [1].

For the second step, we use the DES to perform truly ideal non-invasive “measurements” at t₂. Instead of performing three DES runs (two of them removing certain particles), we perform a single DES run, and only observe the particle's position at t₂ (see Listing 2 in Appendix B). We emphasize that in DES, this observation is truly non-invasive.

The resulting counts of the DES are shown in Figures 4E,F. From a comparison of Figures 4B,C with Figures 4E,F, it is immediately clear that there is a significant difference between the counts obtained by the three-run and single-run procedures. Furthermore, the distributions in Figures 4E,F add up to the original result in Figure 4A. In contrast, the sum of the distributions in Figures 4B,C, obtained by the invasive procedure, add up to the symmetric distribution in Figure 4D, which is identical to the four-step QW shown in Figure 2C.

The relevant question is whether Equation (9) can still be violated. We compute K from the data collected in a single DES of the QW and obtain

$\begin{array}{ll}K=0.999\pm 0.002,& (13)\end{array}$

implying that there is no violation of Equation (9) (up to statistical fluctuations).

The clear difference between results of the three-run and single-run procedure proves that the violation of the LGI by the three-run procedure is not a property of the QW itself. Instead, in the case at issue, the violation of the LGI is the result of using three different experimental scenarios with three different experimental data sets to compute the single quantity K.

It is worth mentioning that the data analysis used in other experiments that report violations of Bell-type inequalities shares similar features, in that correlations are computed from different subsets of a larger data set [22], which has been discussed in terms of the contextuality loophole [18]. Such a procedure can, as Simpson's paradox nicely illustrates [3], lead to all kinds of interesting, paradoxical conclusions.

6. Discussion and Conclusion

In this paper, we have proposed a subquantum model for quantum walks. The model is as realistic as the model for a simple random walk and satisfies Einstein's criterion of locality, and uses a digital computer and a discrete-event simulation algorithm as a metaphor for realizable quantum walk experiments [1, 12]. The subquantum model generates, event-by-event, data that agrees with the quantum-theoretical description of a quantum walk [12].

The subquantum model also reproduces the results of a quantum walk experiment with cesium atoms [1]. In our simulation, the trajectories of each individual particle can be followed. Therefore, the conclusion made in Robens et al. [1] “that the concept of a well-defined, classical trajectory is incompatible with the results obtained in a quantum-walk experiment” is unjustified. The results presented in this paper can be reproduced with the PYTHON programs provided in Appendix B and online¹.

Our subquantum model based on discrete-event simulation can reproduce the experimental data of quantum walk experiments as well as many other optics and neutron-interferometry experiments [20–22, 31]. This suggests that standardized software that allows for simulations of single events observed in (quantum) physics experiments may lead to a new kind of theory. Whether the discrete-event simulation approach can be modified/generalized to attain the descriptive power of a theory, formulated in terms of software (i.e., a well-defined set of rules stated in terms of a programming language) rather than in the conventional language of theoretical physics, is a challenging project for future research.

Being a realistic and Einstein-local model, a salient feature of our simulation approach is the absence of concepts, such as particle-wave duality, Born's rule, and other concepts which are characteristic of quantum theory. Regarding the foundations of the latter, it is of interest to mention that one of the rules by which the discrete-event simulation operates requires attaching a kind of “local wave function” to some of the event-based processing units (such as the beam splitters) [20, 21]. This is very reminiscent of a proposal by Duane, who showed that one can explain the diffraction of X-rays from a crystal without reference to interference of waves, by adding, to the quantum rules for energy and angular momentum, a similar rule for the linear momentum [25]. In essence, Duane suggested that instead of invoking the particle-wave character, for model building it may be more effective to let particles (not waves) interact with the multitude of wave-like motion that is already present in the crystal [26]. As we have shown in this paper, this idea can be combined with discrete-event simulation to yield a local realist model for a quantum walk.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

MW, KM, and HD contributed to the conception and design of the DES models. MW, DW, KM, and HD contributed to the writing of the manuscript. DW wrote the python code provided in the Appendix. MW and DW independently performed all simulations.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.00145/full#supplementary-material

Footnote

1. ^Available online at: https://jugit.fz-juelich.de/qip/quantum-walk (accessed April 25, 2020).

References

1. Robens C, Alt W, Meschede D, Emary C, Alberti A. Ideal negative measurements in quantum walks disprove theories based on classical trajectories. Phys Rev X. (2015) 5:011003. doi: 10.1103/PhysRevX.5.011003

CrossRef Full Text | Google Scholar

2. Pearson K. The problem of the random walk. Nature. (1905) 72:294. doi: 10.1038/072294b0

CrossRef Full Text | Google Scholar

3. Grimmet GR, Stirzaker DR. Probability and Random Processes. Oxford: Clarendon Press (2001).

4. Aharonov Y, Davidovich L, Zagury N. Quantum random walks. Phys Rev A. (1993) 48:1687. doi: 10.1103/PhysRevA.48.1687

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Knight PL, Roldán E, Sipe JE. Quantum walk on the line as interference phenomena. Phys Rev A. (2004) 68:020301(R). doi: 10.1103/PhysRevA.68.020301

CrossRef Full Text | Google Scholar

6. Dür W, Raussendorf R, Kendon VM, Briegel HJ. Quantum walks in optical lattices. Phys Rev A. (2002) 66:052319. doi: 10.1103/PhysRevA.66.052319

CrossRef Full Text | Google Scholar

7. Karski M, Förster L, Choi JM, Steffen A, Alt W, Meschede D, et al. Quantum walk in position space with single optically trapped atoms. Science. (2009) 325:174. doi: 10.1126/science.1174436

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Travaglione BC, Milburn GJ. Implementing the quantum random walk. Phys Rev A. (2002) 65:032310. doi: 10.1103/PhysRevA.65.032310

CrossRef Full Text | Google Scholar

9. Schmitz H, Matjeschk R, Schneider C, Glueckert J, Enderlein M, Huber T, et al. Quantum walk of a trapped ion in phase space. Phys Rev Lett. (2009) 103:090504. doi: 10.1103/PhysRevLett.103.090504

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Zähringer F, Kirchmair G, Gerritsma R, Solano E, Blatt R, Roos CF. Realization of a quantum walk with one and two trapped ions. Phys Rev Lett. (2010) 104:100503. doi: 10.1103/PhysRevLett.104.100503

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Sanders BC, Bartlett SD. Quantum quincunx in cavity quantum electrodynamics. Phys Rev A. (2003) 67:042305. doi: 10.1103/PhysRevA.67.042305

CrossRef Full Text | Google Scholar

12. Jeong H, Paternostro M, Kim MS. Simulation of quantum random walks using the interference of a classical field. Phys Rev A. (2004) 69:012310. doi: 10.1103/PhysRevA.69.012310

CrossRef Full Text | Google Scholar

13. Schreiber A, Cassemiro KN, Potoček V, Gábris A, Mosley PJ, Andersson E, et al. Photons walking the line: a quantum walk with adjustable coin operations. Phys Rev Lett. (2010) 104:050502. doi: 10.1103/PhysRevLett.104.050502

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Broome MA, Fedrizzi A, Lanyon BP, Kassal I, Aspuru-Guzik A, White AG. Discrete single-photon quantum walks with tunable decoherence. Phys Rev Lett. (2010) 104:153602. doi: 10.1103/PhysRevLett.104.153602

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Kempe J. Quantum random walks–an introductory overview. Contemp Phys. (2003) 44:307. doi: 10.1080/00107151031000110776

CrossRef Full Text | Google Scholar

16. Hess K. Categories of nonlocality in EPR theories and the validity of Einstein's separation principle as well as Bell's theorem. J Mod Phys. (2019) 10:1209–21. doi: 10.4236/jmp.2019.1010080

CrossRef Full Text | Google Scholar

17. Leggett AJ, Garg A. Quantum mechanics versus macroscopic realism: is the flux there when nobody looks. Phys Rev Lett. (1985) 9:857–60. doi: 10.1103/PhysRevLett.54.857

CrossRef Full Text | Google Scholar

18. Nieuwenhuizen TM. Is the contextuality loophole fatal for the derivation of Bell inequalities? Found Phys. (2011) 41:580–91. doi: 10.1007/s10701-010-9461-z

CrossRef Full Text | Google Scholar

19. Hess K. Einstein Was Right! Singapore: Pan Stanford Publishing (2015). doi: 10.1201/b16809

CrossRef Full Text | Google Scholar

20. De Raedt K, De Raedt H, Michielsen K. Deterministic event-based simulation of quantum phenomena. Comp Phys Comm. (2005) 171:19–39. doi: 10.1016/j.cpc.2005.04.012

CrossRef Full Text | Google Scholar

21. Michielsen K, De Raedt H. Event-based simulation of quantum physics experiments. Int J Mod Phys C. (2014) 25:01430003. doi: 10.1142/S0129183114300036

CrossRef Full Text | Google Scholar

22. De Raedt H, Michielsen K, Hess K. The digital computer as a metaphor for the perfect laboratory experiment: loophole-free Bell experiments. Comp Phys Comm. (2016) 209:42–7. doi: 10.1016/j.cpc.2016.08.010

CrossRef Full Text | Google Scholar

23. Madelung E. Quantentheorie in hydrodynamischer Form. Z Phys. (1927) 40:322–6. doi: 10.1007/BF01400372

CrossRef Full Text | Google Scholar

24. Bohm D. A suggested interpretation of the quantum theory in terms of “Hidden” variables. I. Phys Rev. (1952) 85:166–79. doi: 10.1103/PhysRev.85.166

CrossRef Full Text | Google Scholar

25. Duane W. The transfer of quanta of radiation momentum to matter. Proc Nat Acad Sci USA. (1923) 9:158–64. doi: 10.1073/pnas.9.5.158

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Landé A. Quantum fact and fiction. Am J Phys. (1965) 33:123–7. doi: 10.1119/1.1971264

CrossRef Full Text | Google Scholar

27. Landé A. Quantum fact and fiction. II. Am J Phys. (1966) 34:1160–3. doi: 10.1119/1.1972539

CrossRef Full Text | Google Scholar

28. Landé A. Quantum fact and fiction. III. Am J Phys. (1969) 34:701–4. doi: 10.1119/1.9717

CrossRef Full Text | Google Scholar

29. Landé A. Quantum fact and fiction. IV. Am J Phys. (1975) 43:701–4.

Google Scholar

30. Landé A. New Foundations of Quantum Mechanics. Cambridge: Cambridge University Press (2015).

Google Scholar

31. Nocon M. Discrete-Event Simulations of Quantum Random Walks, Quantum Key Distribution, and Related Experiments. RWTH Aachen (2016). Available online at: http://juser.fz-juelich.de/record/819152

32. Zhao Z, Du J, Li H, Yang T, Chen ZB, Pan JW. Implement quantum random walks with linear optics elements. arXiv. (2002) quant-ph/0212149.

Google Scholar

33. Reck M, Zeilinger A, Bernstein HJ, Bertani P. Experimental realization of any discrete unitary operator. Phys Rev Lett. (1994) 73:58–61. doi: 10.1103/PhysRevLett.73.58

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Nielsen M, Chuang I. Quantum Computation and Quantum Information. Cambridge: Cambridge University Press (2000).

Google Scholar