- 1School of Statistics and Mathematics, Yunnan University of Finance and Economics, Kunming, China
- 2School of Software, Yunnan University, Kunming, China
- 3School of Statistics and Mathematics, Shanghai Lixin University of Accounting and Finance, Shanghai, China
- 4School of Mechanical Engineering and Center for OPTical IMagery Analysis and Learning (OPTIMAL), Northwestern Polytechnical University, Xi'an, China
Theoretical studies have shown that cooperation can be promoted by the so-called “network reciprocity,” where cooperation can coexist with defection via the compact cooperative clusters. However, such studies often assume that players have no chance to exit from the game even if the situation is extremely bad for them, which is in sharp contrast with the real-life situations. Here, we relax this assumption by giving players the right to choose between one of two states, active (participate in the game) and inactive (exit from the game). We define this assumption as win-stay-lose-leave rule. This new rule motivates a winner whose payoff is larger than the average payoff of its neighbors to stay in its current state, thus retains its current advantage compared to its neighbors. Conversely, a loser is pushed to leave from its current state which in turn increase its chance to obtain a higher payoff while in inactive state. Specifically, we incorporate exit cost into consideration by assuming that anyone who decides to exit from the game must pay a cost γ. Extensive numerical simulation show that if the exit cost is intermediate (neither too high or too small), a full cooperation plateau is achieved, where cooperation evolves with the support of enhanced network reciprocity. In fact, inactive players can only exist at the boundary of cooperative clusters, which creates a crucial buffer area for the endangered cooperators. As a consequence, the joint effect of this protective film composed of inactive players and cooperative clusters forms the foundation of enhanced network reciprocity.
1. Introduction
Within the framework of evolutionary game theory, cooperation has been widely studied both experimentally and theoretically [1–4]. Conflict between what is best for an individual and what is best for the group is at the core of this overreaching problem. The application of statistical physics methods, such as Monte Carlo simulation, phase transition, percolation theory, pair approximation and others, have proven its effectiveness at studying this issue [5–7]. As clarified in the cited literature, cooperation can exist in a sea of defectors via the so-called “network reciprocity” mechanism in square lattice, where cooperators can form compact clusters spontaneously to support each other [8]. Although square lattice is a simple network structure, it captures the essential properties of human interaction, and hence is frequently used to explore the evolution of cooperation. It is noteworthy that the interactions on square lattice are limited to nearest neighbors, but this propriety is not optimal for the maintenance of cooperation [9–11]. Therefore, different network typologies and different evolutionary rules were proposed as cooperation promoting mechanisms [12, 13], as well as some social factors, like reputation [14–17], age structure [18], aspiration [19–21], reward and punishment [22–27], adaptive networks [28–31], to name but a few (see references [3, 6] for a comprehensive understanding).
Although network reciprocity has been widely studied, it was usually assumed that players have to play with their opponents in each round of the game, which is in sharp contrast with real-life situations. For example, an individual tends to cut down all of its social ties to protect itself when faced with severe epidemic, and then gradually restores its social ties when the epidemic under control; a company staff with low salary is likely to look for another position for the purpose of higher salary. Motivated by these facts, here we relax a standard assumption by allowing players a possibility of exit from the game, and investigate how this new rule affects the evolution of cooperation. Specifically, players whose payoff is larger than the average payoff of their neighbors tend to stay in their current state to maintain their current advantage, whereas losers are willing to leave its current state for the purpose of getting another, possibly higher, payoff. Besides, in order to investigate the influence of exit cost on the evolution of cooperation, we assume that a player who wants to exit from the game must pay a cost γ and become inactive, while still getting a random payoff. Importantly, our win-stay-lose-leave rule takes place only when the imitation process is finished, and in this sense, it provides another chance for a player to revise its strategy.
Following the win-stay-lose-leave rule, we can obtain a payoff-correlated state transition patterns. Particularly, inactive players that refuse to play the current game with its opponents obtain a random payoff and can not be imitated by others. Thus, state-changing behavior is independent of reproductive behavior in our model. This is in contrast with voluntary participation mechanism [7, 32–36], where each strategy can be imitated by others. As we will show, when the exit cost is intermediate, inactive players at the boundary between cooperators and defectors act as a sort of insulators, which not only helps cooperation to relieve the exploit pressure of defection, but also supports the expansion of cooperation. When the exit cost is low, i.e., free exit situation, cooperation is wiped out by inactive players and defectors because of the strong advantage of being in the inactive state. For large exit cost, cooperation and defection can coexist due to the protective role of inactive players.
The rest of this paper is organized as follows. In section 2, we first present the details of our model and then give the simulation results in section 3. Lastly, we summarize the main results and discuss its potential implications.
2. Model
The prisoner's dilemma game (PDG) is set on a square lattice of size L * L with periodic boundary conditions. In the original version of PDG, mutual cooperation yield reward R, mutual defection results with punishment P. If one player cooperates and the other defects, the former one gets sucker's payoff, S, and latter one receives the temptation to defect, T. These payoffs satisfy the relationships T > R > P > S and 2R > P + S. This setup captures the essential social dilemma between what is best for the individual and what is best for the collective. To simplifying the model but without losing generality, we use the weak prisoner's dilemma game [8], with parameters set as T = b, R = 1, P = S = 0.
The simulation procedures are performed in agreement with asynchronous updating rule. Initially, each player is designed either as a cooperator (sx = C = 1) or defector (sx = D = 0) with equal probability. At each time step, a randomly selected player x acquires its payoff px by interacting with its active neighbors. Next, player x decides whether or not to update its strategy in a probabilistic manner by comparing its payoff px with player y, who is selected randomly among active neighbors of player x and gets its payoff py in the same way. The strategy updating probability Py→x is determined by the following equation:
Where K represents noise, without loss of generality, we set K = 0.1 in this paper [6, 9].
When a player ends its imitation process, it will consider whether or not to play with its opponents in the future. We therefore define a win-stay-lose-leave rule to determine players' state in the next round of the game. Each player is assigned as active initially, and as game proceeds it may change its state adaptively according to the environment. Based on previous work [19], the environment is defined as:
where the sum runs over all neighbors of player x, and kx denotes its degree. If a player wins over the environment, it will stay in its current state, otherwise it will change. It is worth noting that the state-changing process does not change the strategy of a player. This process is summarized in Figure 1A.
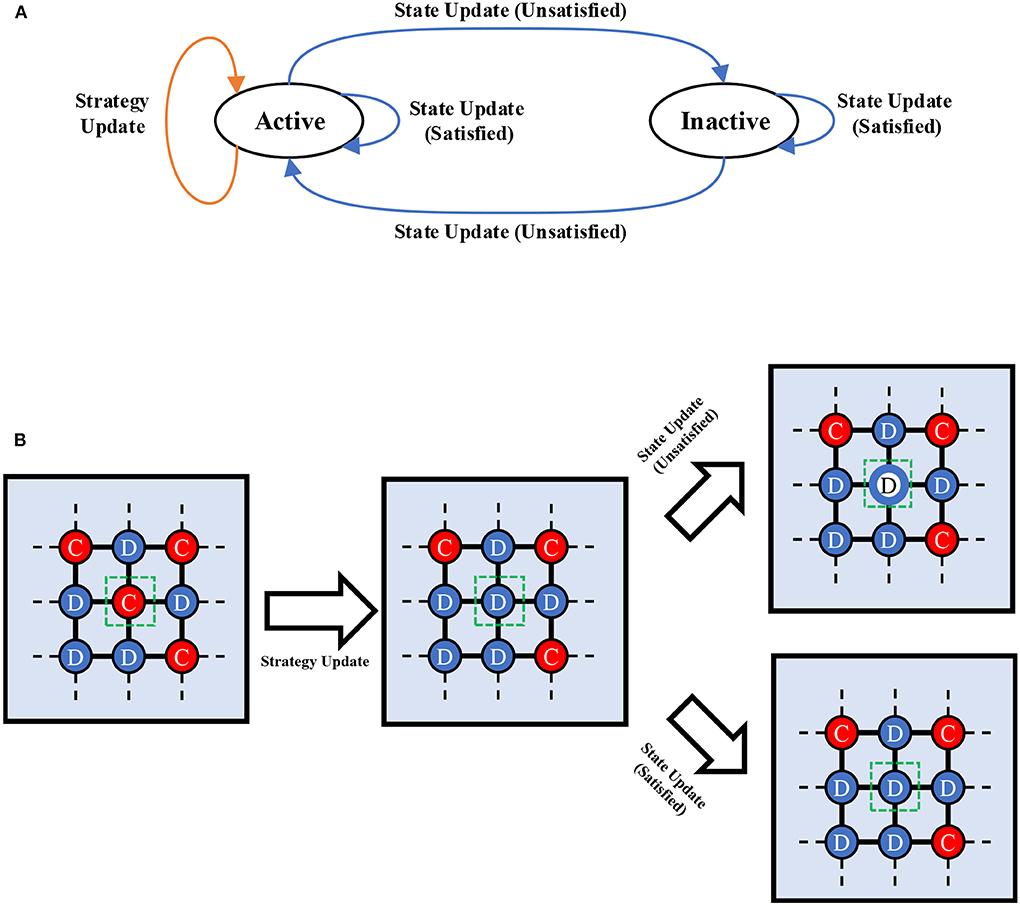
Figure 1. (A) The diagram of state transition. Active nodes can imitate and reproduce, whereas inactive nodes cannot. During imitation process, players will compare its current payoff with the environment. If satisfied, it will stay in its current state, otherwise it will change to another state. (B) The diagram of simulation procedure. Suppose the node with green box decides to change its strategy (here, it will choose defection in the next round) through imitation process. After that, it decides to update its state. If satisfied, it stays in active state, otherwise it become inactive. In the next step, this inactive node does not play the game with its opponent and the imitation process cannot unfold.
In reality, player may choose to exit the game because its performance is extremely bad or it wants to pursue a higher possible payoff. Considering the fact that the maximum payoff among pairwise interactions is b and the degree of each node in the square lattice is four, we assume that an inactive player's payoff is random and lies in the interval of U[0, 4b]. At the same time, we also consider exit cost γ * b, which is related to temptation to defect b. It is obvious that for γ = 0, the free exit situation occurs, and the inactive player can get a possibly higher payoff, which makes the inactive state the most favorable. When γ > 0, the players are not inclined to choose inactive state because of its lower payoffs. Especially, the larger the value of γ, the stronger the willingness of a player to stay in active state. For simplicity, we assume the largest value of γ equals to 10. We also investigate the performance of cooperation with increasing values of γ and find that there is no significant difference regarding the cooperation level. It is also noteworthy that our model cannot return to the traditional PDG even when the exit cost is +∞. High exit cost leads to a low payoff of inactive players, which inevitably pushes the inactive players to become active. However, some unsatisfied active players will still choose to become inactive because of our rules, and the system will go into dynamical stable state, where the inactive nodes can be maintained at a level of 4%.
The strategy updating process and the state updating process form a full Monte Carlo simulation (MCS) procedure. In order to make our model more clear, we also present the main steps in Figure 1B. Results are obtained within the 103 full MCS over the total 5 × 104 steps, which is sufficient for reaching stationary states. Besides, in order to avoid the finite network size effect and to get accurate results, the environment size was varied from L = 400 to L = 1, 000. For each set of parameter values, the final results are obtained by averaging 20 independent runs.
3. Results
Our win-stay-lose-leave rule may lead some players to become inactive during the evolutionary dynamics, where inactive nodes are very similar to vacant nodes [37–41]. We thus calculate the average cooperation rate fC as , where ρ is the population density and is determined by the number of active players in each round of the game. In traditional PDG, cooperation can be supported by single network reciprocity, where cooperation never dominates the whole network and dies out at b = 1.0375 [6, 42]. It is thus intuitive to explore how our rule will affect the evolution of cooperation by comparing it with the traditional case.
We first present the phase diagram in dependence on the temptation to defect b and the exit cost γ in Figure 2. We show that small exit cost leads cooperation to go extinct no matter what value of b is applied. However, if the exit cost exceeds a certain value, cooperation can coexist with defection and even dominate the whole population among the active players. Specifically, when the network reciprocity is strong (i.e., b < 1.04), as the exit cost increases, cooperation can subvert defection via first-order phase transition from absorbing D phase to absorbing C phase. Whereas, when the network reciprocity is weak (i.e., b > 1.05), we find that there is an optimal exit cost γ, at which the flourishing cooperation is achieved. This results differs from traditional prisoner's dilemma game, as there cooperation never dominants in the case of strong reciprocity and dies out at b = 1.0375. It is also worth mentioning that large network size is needed for the correct evolutionary stable solutions, too small network size may leads to incorrect results, as we presented in Figure 3. Based on the above phenomenon, we conclude that the inactive players have strong influence on cooperation dynamics, and make the phase diagram to exhibits diverse features. In what follows, we additionally analyze these interesting results.
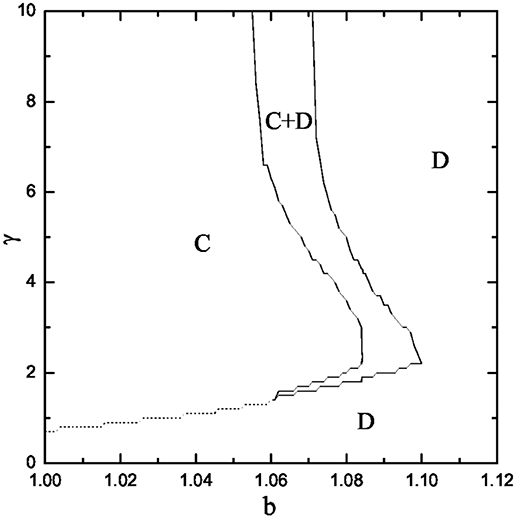
Figure 2. Full b − γ phase diagram of the spatial prisoner's dilemma game in the presence of exit option. Solid lines denote continuous phase transitions, while dashed lines denote discontinuous phase transitions.
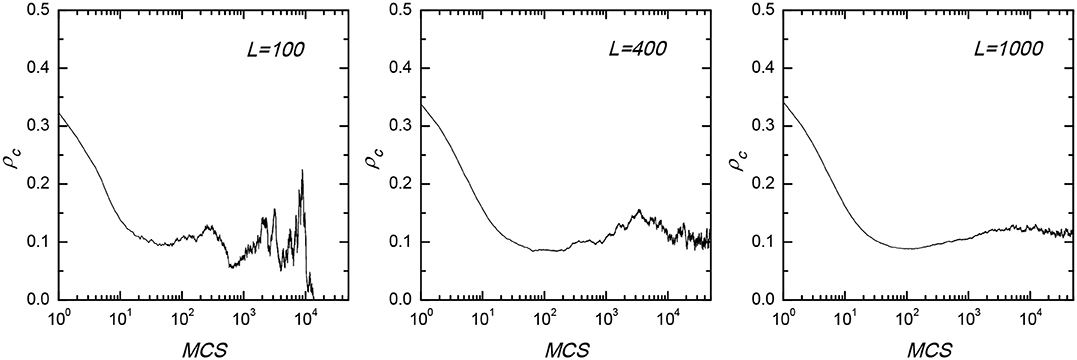
Figure 3. Time courses of the evolution of cooperation for lattice size L equal to 100 (left), 400 (middle), and 1,000 (right). During the simulations, large network size is needed, otherwise cooperation will become extinct due to the fluctuations. With the increase of network size, fluctuations become weaker, making results independent of the network size. The temptation to defect b is set to 1.095, and the exit cost γ is fixed as 3.
Figure 4 shows the spatial evolutionary snapshots from a prepared initial state: a sizable domain of cooperators (red) is inserted into a sea of defectors (blue). Since exit option may leads some players to become inactive, we use white to denote the inactive players. Before presenting our analytical results, we first review the case of traditional PDG at weak reciprocity as shown in the top row of Figure 4. Obviously, in the absence of exit option, cooperative clusters that are scattered and diluted are easily exploited and finally wiped out by defectors. On the contrary, when the exit option is considered, the situation is considerably different. From the second to the bottom row of Figure 4, the exit cost γ equal to 0, 3, and 10, respectively. When the exit is free, γ = 0, both cooperators and defectors are unsatisfied with their performance, and thus exit is their best option. As shown in the second row of Figure 4, both cooperative and defective clusters are diluted by the inactive players. In this sense, free exit weakens the effect of network reciprocity, cooperation disappears, and the system is left with defectors and inactive players. For intermediate exit cost (i.e., γ = 3), we find that the inactive players can only exist at the boundary of cooperative clusters, which means that the inactive players not only prevent the direct invasion of defectors but also promote the formation of cooperative clusters. Finally, cooperation evolves with the support of this enhanced network reciprocity. For large exit cost (i.e., γ = 10), although exit is the most expensive action, a few unsatisfied players around the cooperative clusters are still willing to exit the game. Finally, cooperators are insulated by this protective film and coexist with defectors in the whole system.
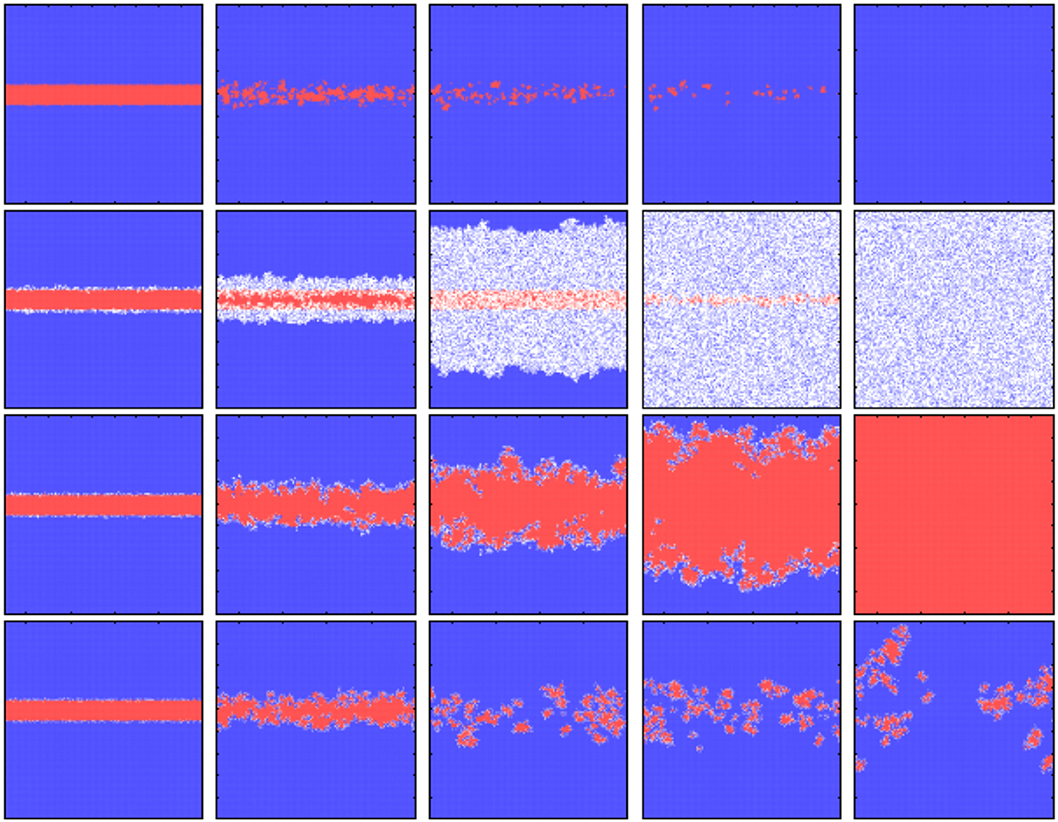
Figure 4. Evolutionary snapshots reveal how inactive players affect the cooperative dynamics. Top row presents the traditional case, where the exit option is excluded from the model. To illustrate the role of inactive players on the evolutionary dynamics, the exit cost γ were set to 0, 3, and 10 from the second to the bottom row. From left to right, snapshots are obtained at different MC steps. Cooperators, defectors, and inactive players are denoted by red, blue, and white, respectively. The parameter combinations are b = 1.07, K = 0.1, L = 200.
It is instructive to further examine the time courses of the fraction of cooperators and the fraction of inactive players starting from a random initial condition for a given b, respectively (Figure 5). The parameters are the same as in that of Figure 4. We use black, red, and green to denote the case of free exit, intermediate exit cost, and large exit cost. For free exit, we observe that the fraction of inactive players increases with its evolution and maintains at 70%. In this case, the super sparse property of the networked individual breaks the network reciprocity and cooperation quickly goes extinct. However, when the exit is costly, the situation is considerably different. When the exit cost is at a intermediate level, the fraction of inactive players increases from a low value, peaks, and then decreases to 0. This self-organized patterns establish an optimal environment for cooperation to spread and eventually to reach a full cooperation phase. For large exit cost (γ = 10), the fraction of inactive players evolve in a way similar to the intermediate exit cost case, but the peak is smaller and these inactive players can be maintained at a certain level. The fraction of cooperation thus can be maintained because of the effect of protective film composed by the inactive players. These results reveal that the role of inactive states is very similar to the vacant nodes. Namely, if the population density is too high, defection can easily invade cooperation, whereas if the population density is too low, vacant nodes prohibit the formation of cooperative clusters. The optimal population density is closely related to the percolation threshold [40, 41].
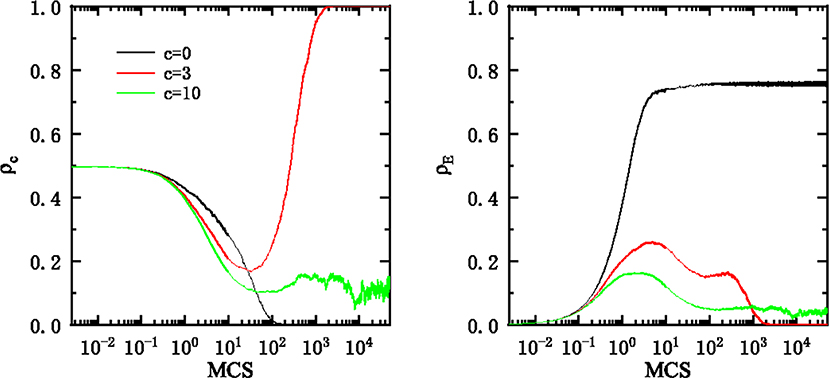
Figure 5. (Left) Time courses of the frequency of cooperation (ρc). (Right) Time courses of the frequency of the inactive players (ρE). The parameters are the same as in Figure 2. To distinguish different values of exit cost, we use black, red, and green to denote the case of γ = 0, γ = 3, and γ = 10, respectively.
Evolutionary outcomes are determined by the species fitness, where the fittest survive. Here, the boundary payoffs of each strategy determine the evolutionary trend in network games, and we thus report the average payoff of the boundary cooperators, boundary defectors, and their neighbors in Figure 6. We use red (wine) to denote the boundary cooperator (C) [the neighbors of a boundary cooperator (NC)], and blue (dark blue) to represent the boundary defector (D) [neighbors of a boundary defector (ND)]. From left to right, the exit cost γ were taken at 0, 3, and 10. In addition, the top and bottom row depict the probability density and the cumulative probability of the average payoff. In probability density figures, the area enclosed by the curve and the interval of some average payoff value represents the probability that the average payoff falls into this interval. In cumulative probability figures, cumulative probability means the probability that the average payoff is less than or equal to a fixed average payoff. For free exit, regardless of cooperation or defection, the average payoff of its neighbors is higher than players', and at the same time, the average payoff of cooperation is smaller than of the defection. Put differently, cooperation is always at the disadvantaged position in the evolutionary dynamics, resulting with extinction of cooperation. The situation of intermediate exit cost decreases a defector's average payoff and the neighbor's average payoff of a cooperator, and at the same time, it increases the cooperator's average payoff. In this case, the difference between the cooperator's average payoff and its neighbors' average payoff becomes much smaller and the gap between the cooperator's and defector's average payoff becomes much larger. Cooperation thus has a small probability to choose an inactive state and can easily expand its territory. The situation of large exit cost greatly reduces the average payoff of a defector's neighbors, motivating defectors to stay active. At the same time, cooperator's average payoff and defector's average payoff are further increased, but its difference become smaller again, cooperation can be maintained but it cannot expand its territory as this difference in is enough only to support its survival.
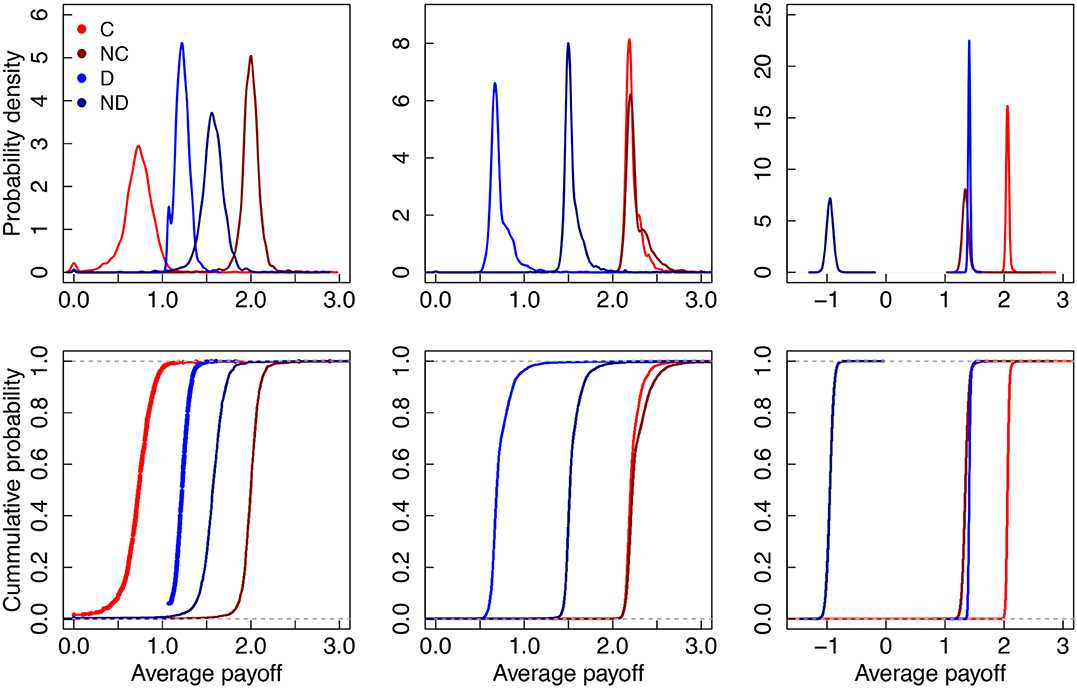
Figure 6. Exit option changes the evolutionary trend. From top to bottom, we present the probability density and the cumulative probability of the average payoff, respectively. We also use red (wine) to denote boundary cooperators (C) [neighbors of a boundary cooperator (NC)] and blue (dark blue) to represent a defector (D) [neighbors of a boundary defector (ND)]. From left to right, the exit cost γ equal to 0, 3, 10, respectively.
4. Conclusion
To conclude, in this paper, we relax the condition that a player must play the game with its opponents in each round of the game by introducing win-stay-lose-leave rule. Following this rule, player can choose between staying active (playing the game) and becoming inactive (exiting the game) in each round of the game after their imitation process ends. This new rule enables a winner to stay in its current state and to push a loser into leaving its current state. Through numerical simulations, we find that a full cooperation plateau can be achieved for intermediate exit cost, in which inactive players can only exist in the boundary of cooperative clusters, thus creating a crucial buffer area separating them from defectors and further promoting the expansion of cooperative clusters. For free exit case, too much inactive players go against the formation of cooperative clusters and further weaken the network reciprocity, enabling the extinction of cooperation. In large exit situation, a small number of players still want to exit from the game, forming a protective film and enabling cooperation to survive. Besides, we also check which players are most inclined to choose inactive state as shown in Figure 6. We find that for free exit case, cooperators choose inactive state more frequently compared with defectors; for intermediate exit case, defectors choose inactive state, and cooperators have small probability to choose inactive state; for large exit cost case, defectors have larger probability to choose active state compared with cooperators. These findings again corroborate our main conclusions and give an enhanced understanding about for the above results. We also show the inactive states are very similar to the role of empty sites, which are shown to be crucial for the evolution of cooperation [37–39]. Our results thus provide a deep understanding about the effect of exit cost on the evolution of cooperation from the viewpoint of network reciprocity.
Finally, herein we only consider the simple square lattice to investigate the performance of our model. Heterogeneous networks are considered to be the optimal structure for cooperation to survive due to the existence of hub nodes, which if occupied by cooperators inevitably influence their neighbors to choose cooperation too [11, 13, 43]. If we implement our model in heterogeneous networks, it would be interesting to explore the win-stay-lose-leave rule effect on hub node, especially in the context of possible weakening of the hub node role. Additionally, if we only give the exit option to hub nodes or mass nodes, we could consider how would that affect cooperation.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We acknowledge support from (i) the National Natural Science Foundation of China (Grants Nos. 11931015 and 11671348.) to LS, (ii) National Natural Science Foundation of China (Grants No. U1803263), the National 1000 Young Talent Plan (No. W099102), the Fundamental Research Funds for the Central Universities (No. 3102017jc03007), and China Computer Federation—Tencent Open Fund (No. IAGR20170119) to ZW, and (iii) the Yunnan Postgraduate Scholarship Award to CS.
References
1. Wang Z, Jusup M, Shi L, Lee JH, Iwasa Y, Boccaletti S. Exploiting a cognitive bias promotes cooperation in social dilemma experiments. Nat Commun. (2018) 9:2954. doi: 10.1038/s41467-018-05259-5
2. Li XL, Jusup M, Wang Z, Li HJ, Shi L, Podobnik B, et al. Punishment diminishes the benefits of network reciprocity in social dilemma experiments. Proc Natl Acad Sci USA. (2018) 115:30–5. doi: 10.1073/pnas.1707505115
3. Perc M, Jordan JJ, Rand DG, Wang Z, Boccaletti S, Szolnoki A. Statistical physics of human cooperation. Phys Rep. (2017) 687:1–51. doi: 10.1016/j.physrep.2017.05.004
4. Szabó G, Fath G. Evolutionary games on graphs. Phys Rep. (2007) 446:97–216. doi: 10.1016/j.physrep.2007.04.004
6. Szabó G, Tőke C. Evolutionary prisoner's dilemma game on a square lattice. Phys Rev E. (1998) 58:69. doi: 10.1103/PhysRevE.58.69
7. Szabó G, Hauert C. Phase transitions and volunteering in spatial public goods games. Phys Rev Lett. (2002) 89:118101. doi: 10.1103/PhysRevLett.89.118101
8. Nowak MA, May RM. Evolutionary games and spatial chaos. Nature. (1992) 359:826. doi: 10.1038/359826a0
9. Vukov J, Szabó G, Szolnoki A. Cooperation in the noisy case: prisoner's dilemma game on two types of regular random graphs. Phys Rev E. (2006) 73:067103. doi: 10.1103/PhysRevE.73.067103
10. Vukov J, Szabó G, Szolnoki A. Evolutionary prisoner's dilemma game on Newman-Watts networks. Phys Rev E. (2008) 77:026109. doi: 10.1103/PhysRevE.77.026109
11. Santos FC, Santos MD, Pacheco JM. Social diversity promotes the emergence of cooperation in public goods games. Nature. (2008) 454:213–6. doi: 10.1038/nature06940
12. Perc M, Szolnoki A. Coevolutionary games? A mini review. BioSystems. (2010) 99:109–25. doi: 10.1016/j.biosystems.2009.10.003
13. Santos FC, Pacheco JM, Lenaerts T. Cooperation prevails when individuals adjust their social ties. PLoS Comput. Biol. (2006) 2:e140. doi: 10.1371/journal.pcbi.0020140
14. Feng Fu MAN Christoph Hauert, Wang L. Reputation-based partner choice promotes cooperation in social networks. Phys Rev E. (2008) 78:026117. doi: 10.1103/PhysRevE.78.026117
15. Gross J, De Dreu CK. The rise and fall of cooperation through reputation and group polarization. Nat Commun. (2019) 10:776. doi: 10.1038/s41467-019-08727-8
16. McNamara JM, Doodson P. Reputation can enhance or suppress cooperation through positive feedback. Nat Commun. (2015) 6:6134. doi: 10.1038/ncomms7134
17. Cuesta JA, Gracia-Lázaro C, Ferrer A, Moreno Y, Sánchez A. Reputation drives cooperative behaviour and network formation in human groups. Sci Rep. (2015) 5:7843. doi: 10.1038/srep07843
18. Wang Z, Zhu X, Arenzon JJ. Cooperation and age structure in spatial games. Phys Rev E. (2012) 85:011149. doi: 10.1103/PhysRevE.85.011149
19. Shen C, Chu C, Shi L, Perc M, Wang Z. Aspiration-based coevolution of link weight promotes cooperation in the spatial prisoner's dilemma game. R Soc Open Sci. (2018) 5:180199. doi: 10.1098/rsos.180199
20. Chen X, Wang L. Promotion of cooperation induced by appropriate payoff aspirations in a small-world networked game. Phys Rev E. (2008) 77:017103. doi: 10.1103/PhysRevE.77.017103
21. Zhang HF, Liu RR, Wang Z, Yang HX, Wang BH. Aspiration-induced reconnection in spatial public-goods game. Eur Phys Lett. (2011) 94:18006. doi: 10.1209/0295-5075/94/18006
22. Fehr E, Gachter S. Cooperation and punishment in public goods experiments. Am Econ Rev. (2000) 90:980–94. doi: 10.1257/aer.90.4.980
24. Dreber A, Rand DG, Fudenberg D, Nowak MA. Winners don't punish. Nature. (2008) 452:348. doi: 10.1038/nature06723
25. Kiyonari T, Barclay P. Cooperation in social dilemmas: free riding may be thwarted by second-order reward rather than by punishment. J Pers Soc Psychol. (2008) 95:826. doi: 10.1037/a0011381
26. Szolnoki A, Perc M. Reward and cooperation in the spatial public goods game. Eur Phys Lett. (2010) 92:38003. doi: 10.1209/0295-5075/92/38003
27. Balliet D, Mulder LB, Van Lange PA. Reward, punishment, and cooperation: a meta-analysis. Psychol Bull. (2011) 137:594. doi: 10.1037/a0023489
28. Chen M, Wang L, Sun S, Wang J, Xia C. Evolution of cooperation in the spatial public goods game with adaptive reputation assortment. Phys Lett A. (2016) 380:40–7. doi: 10.1016/j.physleta.2015.09.047
29. Xue L, Sun C, Wunsch D, Zhou Y, Yu F. An adaptive strategy via reinforcement learning for the prisoner's dilemma game. IEEE/CAA J Autom Sinica. (2018) 5:301–10. doi: 10.1109/JAS.2017.7510466
30. Yang G, Li B, Tan X, Wang X. Adaptive power control algorithm in cognitive radio based on game theory. IET Commun. (2015) 9:1807–11. doi: 10.1049/iet-com.2014.1109
31. Jiang LL, Wang WX, Lai YC, Wang BH. Role of adaptive migration in promoting cooperation in spatial games. Phys Rev E. (2010) 81:036108. doi: 10.1103/PhysRevE.81.036108
32. Hauert C, De Monte S, Hofbauer J, Sigmund K. Volunteering as red queen mechanism for cooperation in public goods games. Science. (2002) 296:1129–32. doi: 10.1126/science.1070582
33. Semmann D, Krambeck HJ, Milinski M. Volunteering leads to rock-paper-scissors dynamics in a public goods game. Nature. (2003) 425:390. doi: 10.1038/nature01986
34. Rand DG, Nowak MA. The evolution of antisocial punishment in optional public goods games. Nat Commun. (2011) 2:434. doi: 10.1038/ncomms1442
35. Inglis R, Biernaskie JM, Gardner A, Kümmerli R. Presence of a loner strain maintains cooperation and diversity in well-mixed bacterial communities. Proc R Soc B Biol Sci. (2016) 283:20152682. doi: 10.1098/rspb.2015.2682
36. Ginsberg A, Fu F. Evolution of cooperation in public goods games with stochastic opting-out. Games. (2019) 10:1. doi: 10.3390/g10010001
37. Vainstein MH, Arenzon JJ. Disordered environments in spatial games. Phys Rev E. (2001) 64:051905. doi: 10.1103/PhysRevE.64.051905
38. Sicardi EA, Fort H, Vainstein MH, Arenzon JJ. Random mobility and spatial structure often enhance cooperation. J Theor Biol. (2009) 256:240–6. doi: 10.1016/j.jtbi.2008.09.022
39. Vainstein MH, Silva AT, Arenzon JJ. Does mobility decrease cooperation? J Theor Biol. (2007) 244:722–8. doi: 10.1016/j.jtbi.2006.09.012
40. Wang Z, Szolnoki A, Perc M. Percolation threshold determines the optimal population density for public cooperation. Phys Rev E. (2012) 85:037101. doi: 10.1103/PhysRevE.85.037101
41. Wang Z, Szolnoki A, Perc M. If players are sparse social dilemmas are too: importance of percolation for evolution of cooperation. Sci Rep. (2012) 2:369. doi: 10.1038/srep00369
42. Szabó G, Vukov J, Szolnoki A. Phase diagrams for an evolutionary prisoner's dilemma game on two-dimensional lattices. Phys Rev E. (2005) 72:047107. doi: 10.1103/PhysRevE.72.047107
Keywords: cooperation, prisoner's dilemma game, win-stay-lose leave, network reciprocity, exit cost
Citation: Shen C, Du C, Mu C, Shi L and Wang Z (2020) Exit Option Induced by Win-Stay-Lose-Leave Rule Provides Another Route to Solve the Social Dilemma in Structured Populations. Front. Phys. 8:133. doi: 10.3389/fphy.2020.00133
Received: 13 December 2019; Accepted: 06 April 2020;
Published: 29 April 2020.
Edited by:
Valerio Capraro, Middlesex University, United KingdomReviewed by:
Daniele Vilone, Italian National Research Council, ItalyGyorgy Szabo, Hungarian Academy of Sciences, Hungary
Copyright © 2020 Shen, Du, Mu, Shi and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lei Shi, c2hpX2xlaTY1QGhvdG1haWwuY29t; Zhen Wang, emhlbndhbmcwQGdtYWlsLmNvbQ==
 Chen Shen1
Chen Shen1 Lei Shi
Lei Shi Zhen Wang
Zhen Wang