Numerical Investigation of the Fractional-Order Liénard and Duffing Equations Arising in Oscillating Circuit Theory

In this article, we present the Jacobi spectral colocation method to solve the fractional model of Liénard and Duffing equations with the Liouville–Caputo fractional derivative. These equations are the generalization of the spring–mass system equation and describe the oscillating circuit. The main reason for using this technique is high accuracy and low computational cost compared to some other methods. The main solution behaviors of these equations are due to fractional orders, which are explained graphically. The convergence analysis of the proposed method is also provided. A comparison is made between the exact and approximate solutions.

Introduction

The standard Liénard equation (LE) is a generalization of the damped pendulum equation or spring–mass system. Because this equation can be applied to describe the oscillating circuits, therefore, it is used in the development of radio and vacuum-tube technology. The LE was given by Liénard [1], and it is written as follows:

$\begin{array}{ll}{D}^{″}v+{\tau }_1(v)D^{\prime }v+{\tau }_2(v)={\tau }_3(t),& (1)\end{array}$

where ${\tau }_1(v)D^{\prime }v$ is the damping force, τ₂(v) is the restoring force, and τ₃(t) is the external force. For different choices of the variable coefficients τ₁(v), τ₂(v), and τ₃(t), the LE is used in many phenomena. The Liénard Equation (1) becomes the van der Pol equation for ${\tau }_1(v)=\epsilon (v^2-1),{\tau }_2(v)=v$, and τ₃(t) = 0, which has many applications [2, 3].

By usual way, we cannot find the exact solution for these equations [4]. Kong [5] studied the LE given as follows:

$\begin{array}{ll}{D}^{″}v+a{D}^{\prime }v+b{v}^3+c{v}^5=0,& (2)\end{array}$

where a, b, and c are real constants.

In particular, if we take c = 0 in the LE, then it reduces to the Duffing equation (DE). This special case of the LE is known as the DE and is given as follows;

$\begin{array}{ll}{D}^{″}v+a{D}^{\prime }v+dv+b{v}^3=0,& (3)\end{array}$

where a, d, and b are real constants.

In recent years, fractional calculus has become an interesting and useful part of mathematical analysis and applied mathematics. The importance of fractional calculus arises because of its non-local nature. The real-life applications of fractional calculus are in fluid dynamics [6], signal processing [7], chemistry [8], viscoelasticity [9], and bioengineering [10]. For some other applications, see Srivastava et al. [11], Kilbas et al. [12], and Robinson [13]. Many physical problems are modeled by fractional-order LE (FLE) and DE. In addition, we are familiar with the fact that non-integer-order derivatives handle models accurately. So, for the accurate modeling of these equations, it is fundamentally needed to change integer-order equations to fractional-order equations.

Fractional-Order Liénard Equation

The FLE is given by

$\begin{array}{ll}{D}^{\alpha }v(t)+a{D}^{\prime }v+b{v}^3+c{v}^5=0,1<\alpha \le 2,t\in \left[0,1\right],& (4)\end{array}$

with the conditions:

$\begin{array}{ll}v(0)=\xi ,v^{\prime }(0)=\eta ,& (5)\end{array}$

where ξ and η are real constants.

Fractional-Order DE

The fractional-order DE (FDE) is given by

$\begin{array}{ll}{D}^{\beta }v(t)+a{D}^{\prime }v+dv+b{v}^3=0,1<\beta \le 2,t\in \left[0,1\right],& (6)\end{array}$

with the following conditions:

$\begin{array}{ll}v(0)=\mu ,v^{\prime }(0)=\sigma ,& (7)\end{array}$

where μ and σ are real constants.

The innovator approach to solve the LE originates in the work by Kong [5], who provided an exact solution of these equations in some particular cases. For some particular choices of the involved real constants, Feng [14] obtained an exact solution of these equations, which were the generalization of Kong's [5] results. In 2008, Matinfar et al. [15] suggested a variational iteration method in order to obtain the approximate solutions of the LE. Subsequently, in 2011, a variational homotopy perturbation method was applied in order to solve LE (see Matinfar et al. [16]). Recently in 2017, a numerical method using homotopy analysis transform method (HATM) in order to solve fractional LE was proposed, and the uniqueness and existence of solutions were also given (see Kumar et al. [17]). Further, Singh [18, 19] used Legendre polynomials and Chebyshev polynomials, respectively, to solve fractional models of these equations.

In this article, we propose an effective method for the FLE and DE. The proposed method is a spectral colocation method based on the applications of operational matrix of differentiation for the Jacobi polynomials. Spectral colocation method is used to solve many problems in differential calculus (see [20–29]). By using the spectral colocation method, these equations are converted into a system of non-linear algebraic equations whose solution gives approximate solution to these equations. The derived solution is discussed for different fractional orders. The obtained results are compared with the exact solution and presented in the form of numerical tables. Because fractional order derivatives are non-local in nature, and integer-order derivatives are a special case of fractional order derivative, it is important to study fractional order models. The proposed method is easy to implement because it is computer oriented. It is also a time-saving method. The integer as well as fractional order behavior of solution is shown in numerical section. The main solution behaviors of these equations are due to fractional orders, and using the proposed method, these behaviors of solution are explained clearly.

Preliminaries

In this article, we have considered the non-integer-order differentiations in Liouville–Caputo (LC) sense, which are defined as follows:

Definition 2.1 The LC non-integer derivative of order β is defined as follows [30, 31]:

$\begin{array}{r}{D}^{\beta }f(x)=I^{l-\beta }{D}^{l}f(x)=\frac{1}{(l-\beta )}{\displaystyle \underset{0}{\stackrel{x}{\int }}}{(x-t)}^{l-\beta -1}\frac{d^l}{d{t}^l}f(t)dt,\\ l-1<\beta <l,x>0.& (8)\end{array}$

In this article, we have used Jacobi polynomials as a basis for the approximation of unknown functions. The shifted Jacobi polynomial is given as follows [32–34]:

$\begin{array}{l}{\lambda }_i^{(e,f)}(t)\\ ={\displaystyle \sum _{k=0}^i}{(-1)}^{i-k}\frac{\Gamma (\text{i}+\text{f}+1)\Gamma (\text{i}+\text{k}+\text{e}+\text{f}+1)}{\Gamma (\text{k}+\text{f}+1)\Gamma (\text{i}+\text{e}+\text{f}+1)(\text{i}-\text{k})!\text{k}!}{t}^k,& (9)\end{array}$

where e and f are parameters in Jacobi polynomials as given in Doha et al. [32].

The orthogonal property of Jacobi polynomials is as follows:

$\begin{array}{ll}{\displaystyle \underset{0}{\stackrel{1}{\int }}}{\lambda }_n^{(e,f)}(t){\lambda }_m^{(e,f)}(t)g^{(e,f)}(t)dt=v_n^{e,f}{\delta }_{mn},& (10)\end{array}$

where g^{(e, f)}(t) is weight function, and δ_mn is kronecker delta function and given as

$\begin{array}{l}{g}^{(e,f)}(t)\\ ={(1-t)}^e{t}^f\text{and }{v}_n^{e,f}\\ =\frac{\Gamma (n+e+1)\Gamma (n+f+1)}{(2n+e+f+1)n!\Gamma (n+e+f+1)}.& (11)\end{array}$

A function $f\in L_g^2\left[0,1\right]$, with |f″(t)| ≤ A, can be expanded as follows:

$\begin{array}{ll}f(t)={\displaystyle \underset{n\to \infty }{lim}}{\displaystyle \sum _{i=0}^n}{c}_i{\lambda }_i^{(e,f)}(t),& (12)\end{array}$

where $f(t)=\langle c_i,{\lambda }_i^{(e,f)}(t)\rangle$, and 〈., .〉 denotes the usual inner product space.

Equation (12), for finite dimensional approximation, is written as follows:

$\begin{array}{ll}f\cong {\displaystyle \sum _{i=0}^m}{c}_i{\lambda }_i^{(e,f)}(t)=C^T{p}_m(t),& (13)\end{array}$

where C and p_m(t) are (m + 1) × 1 matrices given by

$\begin{array}{ll}C={\left[c_0,c_1,\dots .,c_m\right]}^T\text{and }{p}_m(t)={[{\lambda }_0^{(e,f)},{\lambda }_1^{(e,f)},\dots .,{\lambda }_m^{(e,f)}]}^T.& (14)\end{array}$

Theorem 1. If $p_n(t)={[{\lambda }_0^{(e,f)},{\lambda }_1^{(e,f)},\dots .,{\lambda }_n^{(e,f)}]}^T$ be the shifted Jacobi vector and if v > 0, then

$\begin{array}{ll}{D}^v{\lambda }_i^{(e,f)}(t)=D^{(v)}{p}_n(t),& (15)\end{array}$

where D^(v) = (q(i, j)) is an (n + 1) × (n + 1) operational matrix of non-integer derivative of order v, and its entries are given by

$\begin{array}{r}q(i,j,e,f)={\displaystyle \sum _{k=\left[v\right]}^i}{(-1)}^{i-k}\frac{\Gamma (i+f+1)\Gamma (i+k+e+f+1)}{(i-k)!\Gamma (k+f+1)\Gamma (i+e+f+1)\Gamma (k-v+1)}\\ \times {\displaystyle \underset{l=0}{\sum ^j}}{(-1)}^{j-l}\frac{\Gamma (e+1)\Gamma (j+l+e+f+1)\Gamma (k+l-v+f+1)(2j+e+f+1)j!}{(j-l)!(l)!\Gamma (j+e+1)\Gamma (l+f+1)\Gamma (k+l-v+e+f+2)}.\end{array}$

Proof. See Doha et al. [32], Ahmadian et al. [33], and Bhrawy et al. [34].

Outline of the Method

Here, we will describe the algorithm for the construction of the solution for the fractional LE and DE using operational matrix and colocation method [27–29]. Let us take the following approximation:

$\begin{array}{ll}v(t)={\displaystyle \sum _{i=0}^n}{c}_i{\lambda }_i^{(e,f)}(t)=C^T{p}_n(t).& (16)\end{array}$

Then, by taking the derivative of order one on both sides of Equation (16), we get

$\begin{array}{ll}{D}^{\prime }v(t)=C^T{D}^{\prime }{p}_n(t)\cong C^T{D}^{(1)}{p}_n(t),& (17)\end{array}$

where D⁽¹⁾ is the operational matrix of differentiations for the Jacobi polynomials of order 1.

Next, by taking the derivatives of orders α and β on both sides of Equation (16), we find that

$\begin{array}{ll}{D}^{\alpha }v(t)=C^T{D}^{\alpha }{p}_n(t)\cong C^T{D}^{(\alpha )}{p}_n(t)& (18)\end{array}$

$\begin{array}{ll}{D}^{\beta }v(t)=C^T{D}^{\beta }{p}_n(t)\cong C^T{D}^{(\beta )}{p}_n(t),& (19)\end{array}$

where D^(α) and D^(β) are the operational matrices of differentiations for the Jacobi polynomials of orders α and β, respectively.

From Equations (16) and (17), we can write,

$\begin{array}{ll}v(0)=C^T{p}_n(0),& (20)\end{array}$

$\begin{array}{ll}{v}^{\prime }(0)=C^T{D}^{(1)}{p}_n(0),& (21)\end{array}$

Fractional-Order LE

Grouping Equations (4) and (16)–(18), we get

$\begin{array}{r}{C}^T{D}^{(\alpha )}{p}_n(t)+a{C}^T{D}^{(1)}{p}_n(t)+b{(C^T{p}_n(t))}^3\\ +c{(C^T{p}_n(t))}^5=0.& (22)\end{array}$

The residual for Equation (22) is given as follows:

$\begin{array}{r}{R}_n(t)=C^T{D}^{(\alpha )}{p}_n(t)+a{C}^T{D}^{(1)}{p}_n(t)+b{(C^T{p}_n(t))}^3\\ +c{(C^T{p}_n(t))}^5.& (23)\end{array}$

Now, colocating Equation (23) at n−1 points given by $t_i=\frac{i}{n},i=1,2,\dots ,n-1$, we find that

$\begin{array}{r}{R}_n(t_i)=C^T{D}^{(\alpha )}{p}_n(t_i)+a{C}^T{D}^{(1)}{p}_n(t_i)\\ +b{(C^T{p}_n(t_i))}^3+c{(C^T{p}_n(t_i))}^5.& (24)\end{array}$

Further, from Equations (5), (20), and (21), we can write

$\begin{array}{ll}{C}^T{p}_n(0)=\xi ,C^T{D}^{(1)}{p}_n(0)=\eta ,& (25)\end{array}$

where ξ and η are real constants.

Using the colocation points in Equation (24), together with Equation (25), we get a system of non-linear algebraic equations with the same number of unknowns. The solution of this system leads the solution for FLE.

Fractional-Order DE

Grouping Equations (6), (16), (17), and (19), we get

$\begin{array}{ll}{C}^T{D}^{(\beta )}{p}_n(t)+a{C}^T{D}^{(1)}{p}_n(t)+d{C}^T{p}_n(t)+b{(C^T{p}_n(t))}^3=0.& (26)\end{array}$

The residual for Equation (26) is given as follows:

$\begin{array}{r}{R}_n(t)=C^T{D}^{(\beta )}{p}_n(t)+a{C}^T{D}^{(1)}{p}_n(t)+d{C}^T{p}_n(t)\\ +b{(C^T{p}_n(t))}^3.& (27)\end{array}$

Now, colocating Equation (27) at the n−1 points given by $t_i=\frac{i}{n},i=1,2,\dots ,n-1$, we get

$\begin{array}{r}{R}_n(t_i)=C^T{D}^{(\beta )}{p}_n(t_i)+a{C}^T{D}^{(1)}{p}_n(t_i)+d{C}^T{p}_n(t_i)\\ +b{(C^T{p}_n(t_i))}^3.& (28)\end{array}$

Further, from Equations (7), (20), and (21), we can write

$\begin{array}{ll}{C}^T{p}_n(0)=\mu ,C^T{D}^{(1)}{p}_n(0)=\sigma ,& (29)\end{array}$

where μ and σ are real constants.

By using the colocation points in Equation (28), together with the Equation (29), we get a system of equations with the same number of unknowns. The solution of this system leads the approximate solution for the FDE.

Convergence Analysis

Theorem 4.1. Let the function v:[0, 1] → R, and v ∈ C⁽ⁿ⁺¹⁾[0, 1] and v_n(t) be the n^th approximation obtained by using Jacobi polynomials, then

$\begin{array}{ll}{E}_{v,n}^g=||v-v_n{||}_{L_g^2\left[0,1\right]},& (30)\end{array}$

and the error vector in Equation (30) tends to zero as n → ∞.

Proof: See Rivlin [35], Kreyszig [36], and Behroozifar and Sazmand [37].

Theorem 4.2. If $E_{D,n}^{\alpha ,g}$ be the error vector for α order operational matrix integration, which is obtained using (n + 1) Jacobi polynomials. Then

$\begin{array}{ll}{E}_{D,n}^{\alpha ,g}=D^{(\alpha )}{p}_n(t)-D^{\alpha }{p}_n(t),& (31)\end{array}$

and the error vector in Equation (31) tends to zero as n → ∞.

Proof: See Kazem [38].

Let V_n be the n-dimensional subspace generated by ${\left({\lambda }_i^{(e,f)}\right)}_{0\le i\le n}$for $L_g^2\left[0,1\right]$. Let δ_n is the minimum value of the functional on the space V_n. We can write

$\begin{array}{l}{V}_n\subset V_{n+1}\text{ and }{\delta }_{n+1}\ge {\delta }_n.\end{array}$

Theorem 4.3. Consider the functional L, then

$\begin{array}{l}{\displaystyle \underset{n\to \infty }{lim}}{\delta }_n(t)=\delta (t)={\displaystyle \underset{t\in \left[0,1\right]}{inf}}L(t).\end{array}$

Proof: See Ezz-Eldien [39].

Functional for FLE is given as follows:

$\begin{array}{ll}L(t)=D^{\alpha }v(t)+a{D}^{\prime }v+b{v}^3+c{v}^5=0.& (32)\end{array}$

Using Equations (16)–(18), we get

$\begin{array}{r}{L}^{(E)}(t)=C^T{D}^{(\alpha )}{p}_n(t)+E_{D,n}^{\alpha ,g}+a{C}^T{D}^{(1)}{p}_n(t)+a{E}_{D,n}^{1,g}\\ +b{(C^T{p}_n(t)+E_{v,n}^g)}^3+c{(C^T{p}_n(t)+E_{v,n}^g)}^5.& (33)\end{array}$

where

$\begin{array}{ll}{E}_{v,n}^g=C^{T}p(t)-C^T{p}_n(t),& (34)\end{array}$

$\begin{array}{ll}{E}_{D,n}^{\alpha ,g}=D^{(\alpha )}{p}_n(t)-D^{\alpha }{p}_n(t),& (35)\end{array}$

$\begin{array}{ll}{E}_{D,n}^{1,g}=D^{(1)}{p}_n(t)-D^1{p}_n(t).& (36)\end{array}$

Residual for Equation (33), is given as

$\begin{array}{r}{R}_n^{(E)}(t)=C^T{D}^{(\alpha )}{p}_n(t)+E_{D,n}^{\alpha ,g}+a{C}^T{D}^{(1)}{p}_n(t)+a{E}_{D,n}^{1,g}\\ +b{(C^T{p}_n(t)+E_{v,n}^g)}^3+c{(C^T{p}_n(t)+E_{v,n}^g)}^5.& (37)\end{array}$

Now, similar as in Equation (23), colocating Equation (37), at n−1 points given by $t_i=\frac{i}{n},i=1,2,\dots ,n-1$, we get

$\begin{array}{ll}{R}_n^{(E)}(t_i)=0.& (38)\end{array}$

Using the colocation points in Equation (37), together with Equation (25), we get a system of non-linear algebraic equations. The solution of this system leads the solution for FLE. Let this solution be denoted by ${\delta }_n^{*}(t)$.

Using Theorems 4.1 and 4.2 and taking n → ∞,

$\begin{array}{ll}{\delta }_n^{*}(t)\to {\delta }_n(t).& (39)\end{array}$

From Theorem 4.3 and Equation (39), we achieve that

$\begin{array}{l}{\displaystyle \underset{n\to \infty }{lim}}{\delta }_n^{*}(t)=\delta (t).\end{array}$

Proof completed. Similar proof can be written for convergence of DE.

Numerical Simulation of Results

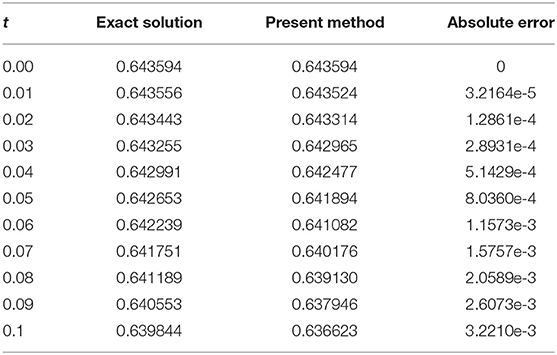
In this section, we implement our proposed algorithm by testing it on some special cases of the LE and DE. We study the applicability and accuracy of our proposed computational method by applying it on the FLE and DE. The parameters in the LE and DE are chosen in such a way for which the exact solution is known.

Case 1. For the particular choices of the parameters a = −1, b = 4 and c = 3 in Equation (4), the FLE is given as follows (see Singh [18] and Tohidi et al. [20]):

$\begin{array}{ll}{D}^{\alpha }v(t)-D^{\prime }v+4v^3+3v^5=0,1<\alpha \le 2,& (40)\end{array}$

$\begin{array}{ll}v(0)=\xi =\sqrt{\frac{\tau }{2+\delta }}\text{ and }{v}^{\prime }(0)=\eta =0,& (41)\end{array}$

where

$\begin{array}{ll}\tau =4\sqrt{\frac{3a^2}{3b^2-16ac}}\text{and }\delta =-1+\frac{\sqrt{3}b}{\sqrt{(3b^2-16ac)}}.& (42)\end{array}$

The exact solution for the FLE given by Equation (40), with conditions in Equation (41), is given by

$\begin{array}{ll}v(t)=\sqrt{\frac{\tau sec{h}^2\sqrt{-at}}{2+\delta sec{h}^2\sqrt{-at}}},\text{at }\alpha =2,& (43)\end{array}$

where τ and δ are as given in Equation (42).

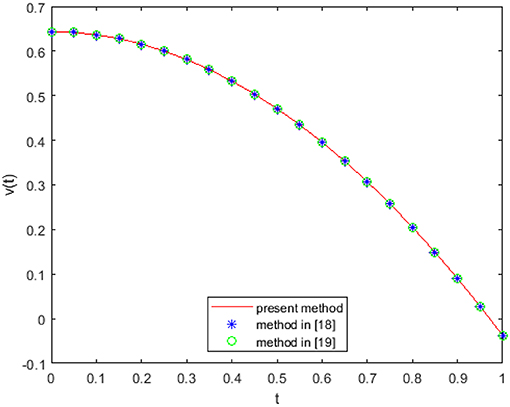
In Figures 1, 2, we have shown the approximate solution for different values of α for the FLE choosing different parameters in the Jacobi polynomials. In Figure 3, we have compared approximate solution by our proposed method and solution obtained by the methods of Singh [18, 19] for integer-order LE.

FIGURE 1

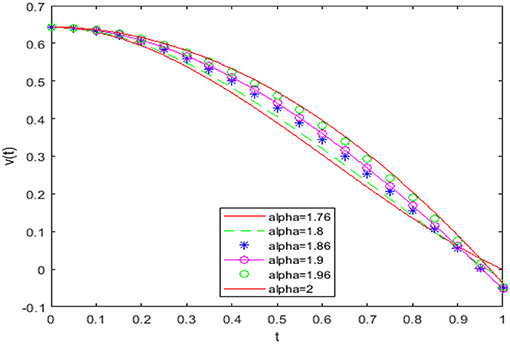
Figure 1. Numerical solutions at α = 1.76, 1.8, 1.86, 1.9, 1.96, and 2 for case 1 at e = 1 and f = 1.

FIGURE 2

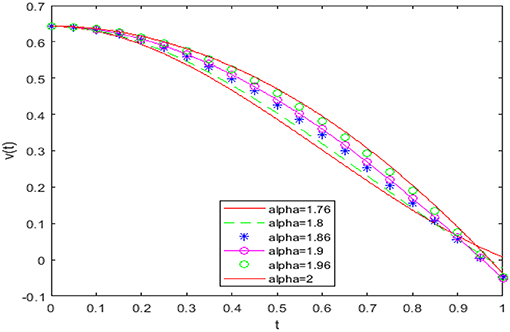
Figure 2. Numerical solutions at α = 1.76, 1.8, 1.86, 1.9, 1.96, and 2 for case 1 at e = 0.8 and f = 0.8.

FIGURE 3

Figure 3. Comparison of solutions at e = f = 1 and α = 2.

Figures 1, 2 show that the period will be really affected by the non-integer-order values, and the solution varies continually from non-integer-order solution to integer-order solution and coincides with the integer-order solution at α = 2. The solution has some different behavior when the value of fractional order is 1.76, and this is because the main solution behavior of LE takes place when α is very close to 2. Figure 3 shows that solution has exact the behavior as the methods of Singh [18, 19]. In Table 1, we have listed approximate and exact solutions for the integer-order equation. Table 1 shows a good accuracy of the achieved solution. In Table 2, we have listed approximate solution by our method and the methods of Singh [18, 19]. Table 2 shows good agreement with these methods.

TABLE 1

Table 1. Comparison with the exact solution at α = 2 and n = 3 for Liénard equation.

TABLE 2

Table 2. Comparison with the methods of Singh [18, 19] at α = 2 and n = 3 for Liénard equation.

Case 2. For the particular choices of the parameters a = 0.5, b = 25, and c = 25 in Equation (6), the fractional DE is given as follows [see Singh [18, 19] and Nourazar and Mirzabeigy [40]]:

$\begin{array}{ll}{D}^{\beta }v(t)+0.5D^{\prime }v+25v+25v^3=0,1<\beta \le 2,& (44)\end{array}$

$\begin{array}{ll}v(0)=\mu =0.1\text{ and }{v}^{\prime }(0)=\sigma =0,& (45)\end{array}$

The analytical solution using the differential transform method (DTM) for fractional DE given by Equation (44), with the initial conditions in Equation (45), is given by

$\begin{array}{r}v(t)=0.1-1.2625t^2+0.2104t^3+2.6828t^4-0.5392t^5\\ -2.6563t^6+0.6152t^7\text{at }\alpha =2.& (46)\end{array}$

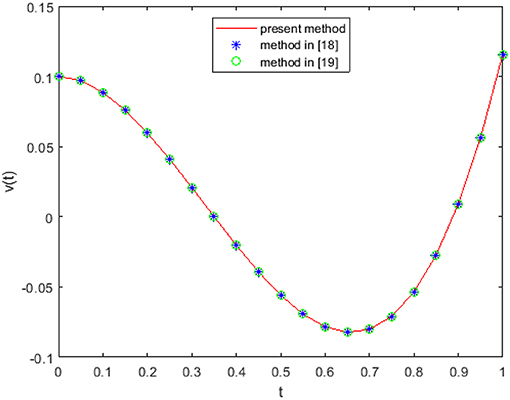
In Figures 4, 5, we have shown the behavior of the approximate solution for different values of β for fractional DE for different choices of the parameters in the Jacobi polynomials. In Figure 6, we have compared approximate solution by our proposed method and solution obtained by the methods of Singh [18, 19] for integer-order DE.

FIGURE 4

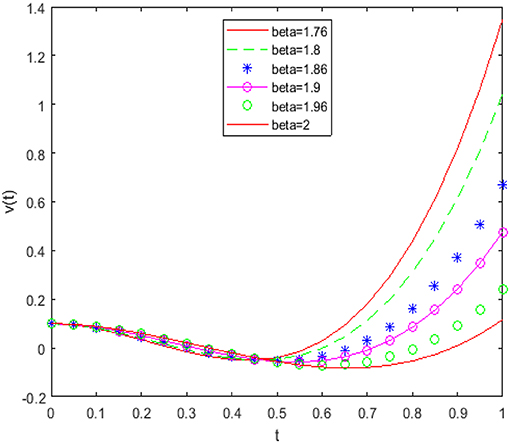
Figure 4. Numerical solutions at β = 1.76, 1.8, 1.86, 1.9, 1.96, and 2 for case 2 at e = 1 and f = 1.

FIGURE 5

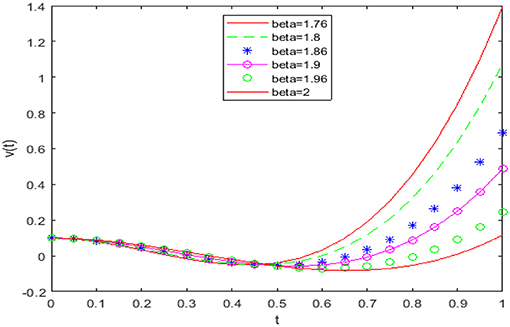
Figure 5. Numerical solutions at β = 1.76, 1.8, 1.86, 1.9, 1.96, and 2 for case 2 at e = 0.8 and f = 0.8.

FIGURE 6

Figure 6. Comparison of solutions at e = f = 1 and β = 2.

Figures 4, 5 reveal that the solution varies continually from the fractional-order solution to the integer-order solution and coincides with the integer-order solution at β = 2. The solution has some different behavior when the value of fractional order is 1.76, and this is because the main solution behavior of DE takes place when β is very close to 2. Figure 6 shows that solution has the exact behavior as the methods of Singh [18, 19]. In Table 3, we have listed the approximate and exact solutions by the DTM method for the integer-order equation. Table 3 shows a good accuracy of the achieved solution.

TABLE 3

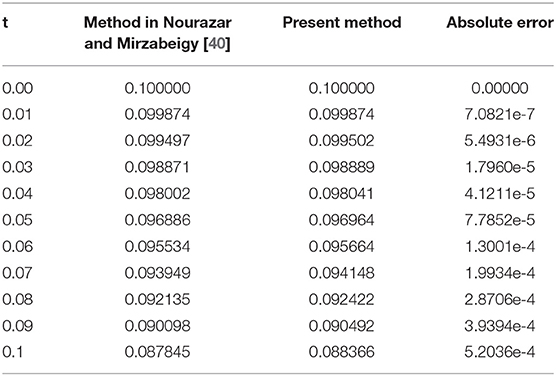
Table 3. Comparison between results by our proposed method and DTM [40] for fractional Duffing equation at β = 2 and n = 3 for case 2.

Conclusions

In this article, we have presented numerical solution and simulation for fractional-order and integer-order LE and DE. The proposed algorithm is easy to implement because the construction of the operational matrix is sufficiently easy, which makes our method remarkably attractive for practical applications. In the numerical section, it is presented how the approximate solution varies continuously for different values of the fractional time derivatives and for the integer-order approximate solution is the same as the exact solution for the fractional LE and DE. Recently, many equations in science and engineering appear in the form of non-linear fractional differential equations, which makes it necessary to investigate the method of solution for such equations. The main advantage of the proposed method is that it works for such type of equations arising in science and engineering. In the future, we can use operational matrices of different orthogonal polynomials to achieve better accuracy.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Liénard A. Etude des oscillations entretenues. Rev Gen Electr. (1928) 23:901–12.

2. Guckenheimer J. Dynamics of the van der pol equation. IEEE Trans Circ Syst. (1980) 27:938–89. doi: 10.1109/TCS.1980.1084738

CrossRef Full Text | Google Scholar

3. Zhang ZF, Ding T, Huang HW. Qualitative Theory of Differential Equations. Peking: Science Press (1985).

Google Scholar

4. Hale JK. Ordinary Differential Equations. New York, NY: Wiley (1980).

Google Scholar

5. Kong D. Explicit exact solutions for the Liénard equation and its applications. Phys Lett A. (1995) 196:301–6 doi: 10.1016/0375-9601(94)00866-N

CrossRef Full Text | Google Scholar

6. Singh H. A new stable algorithm for fractional Navier-Stokes equation in polar coordinate. Int J Appl Comput Math. (2017) 3:3705–22. doi: 10.1007/s40819-017-0323-7

CrossRef Full Text | Google Scholar

7. Panda R, Dash M. Fractional generalized splines and signal processing. Signal Process. (2006) 86:2340–50. doi: 10.1016/j.sigpro.2005.10.017

CrossRef Full Text | Google Scholar

8. Singh H. Operational matrix approach for approximate solution of fractional model of Bloch equation. J King Saud University Sci. (2017) 29:235–40. doi: 10.1016/j.jksus.2016.11.001

CrossRef Full Text | Google Scholar

9. Bagley RL, Torvik PJ. Fractional calculus in the transient analysis of viscoelasticity damped structures. AIAA J. (1985) 23:918–25. doi: 10.2514/3.9007

CrossRef Full Text | Google Scholar

10. Magin RL. Fractional calculus in bioengineering. Critical Rev Biomed Engrg. (2004) 32:1–104. doi: 10.1615/CritRevBiomedEng.v32.10

CrossRef Full Text | Google Scholar

11. Srivastava HM, Shah FA, Abass R. An application of the Gegenbauer wavelet method for the numerical solution of the fractional Bagley-Torvik equation. Russian J Math Phys. (2019) 26:77–93. doi: 10.1134/S1061920819010096

CrossRef Full Text | Google Scholar

12. Kilbas AA, Srivastava HM, Trujillo JJ. Theory and Applications of Fractional Differential Equations, North-Holland Mathematical Studies, Vol. 204. Amsterdam; London; New York, NY: Elsevier (North-Holland) Science Publishers (2006).

Google Scholar

13. Robinson AD. The use of control systems analysis in neurophysiology of eye movements. Ann Rev Neurosci. (1981) 4:462–503. doi: 10.1146/annurev.ne.04.030181.002335

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Feng Z. On explicit exact solutions for the Liénard equation and its applications. Phys Lett A. (2002) 239:50–6. doi: 10.1016/S0375-9601(01)00823-4

CrossRef Full Text | Google Scholar

15. Matinfar M, Hosseinzadeh H, Ghanbari M. A numerical implementation of the variational iteration method for the Liénard equation. World J Model Simul. (2008) 4:205–10.

Google Scholar

16. Matinfar M, Mahdavi M, Raeisy Z. Exact numerical solution of Liénard's equation by the variational homotopy perturbation method. J Inform Comput Sci. (2011) 6:73–80.

Google Scholar

17. Kumar D, Agarwal RP, Singh JA. Modified numerical scheme convergence analysis for fractional model of Liénard's equation. J Comput Appl Math. 339:405–13. doi: 10.1016/j.cam.2017.03.011

CrossRef Full Text | Google Scholar

18. Singh H. An efficient computational method for non-linear fractional Lienard equation arising in oscillating circuits. In: Singh H, Kumar D, Baleanu D, editors. Methods of Mathematical Modelling: Fractional Differential Equations. London; New York, NY: CRC Press Taylor and Francis Group (2019).

Google Scholar

19. Singh H. Solution of fractional Lienard equation using Chebyshev operational matrix method, nonlinear. Sci Lett A. (2017) 8:397–404.8

Google Scholar

20. Tohidi E, Bhrawy AH, Erfani K. A collocation method based on Bernoulli operational matrix for numerical solution of generalized pantograph equation. Appl Math Model. (2013) 37:4283–94. doi: 10.1016/j.apm.2012.09.032

CrossRef Full Text | Google Scholar

21. Singh H, Srivastava HM, Kumar D. A reliable numerical algorithm for the fractional vibration equation. Chaos Solitons Fractals. (2017) 103:131–8. doi: 10.1016/j.chaos.2017.05.042

CrossRef Full Text | Google Scholar

22. Kazem S, Abbasbandy S, Kumar S. Fractional order Legendre functions for solving fractional-order differential equations. Appl Math Model. 37:5498–510. doi: 10.1016/j.apm.2012.10.026

CrossRef Full Text | Google Scholar

23. Singh H. An efficient computational method for the approximate solution of nonlinear Lane-Emden type equations arising in astrophysics. Astrophys Space Sci. (2018) 363:363–71. doi: 10.1007/s10509-018-3286-1

CrossRef Full Text | Google Scholar

24. Lakestani M, Dehghan M, Pakchin SI. The construction of operational matrix of fractional derivatives using B-spline functions. Commun Nonlinear Sci Numer Simulat. (2012) 17:1149–62. doi: 10.1016/j.cnsns.2011.07.018

CrossRef Full Text | Google Scholar

25. Wu JL. A wavelet operational method for solving fractional partial differential equations numerically. Appl Math Comput. (2009) 214:31–40. doi: 10.1016/j.amc.2009.03.066

CrossRef Full Text | Google Scholar

26. Yousefi SA, Behroozifar M, Dehghan M. The operational matrices of Bernstein polynomials for solving the parabolic equation subject to the specification of the mass. J Comput Appl Math. (2011) 235:5272–83. doi: 10.1016/j.cam.2011.05.038

CrossRef Full Text | Google Scholar

27. Singh H. Approximate solution of fractional vibration equation using Jacobi polynomials. Appl Math Comput. (2018) 317:85–100. doi: 10.1016/j.amc.2017.08.057

CrossRef Full Text | Google Scholar

28. Singh CS, Singh H, Singh VK, Singh Om P. Fractional order operational matrix methods for fractional singular integro-differential equation. Appl Math Model. (2016) 40:10705–18. doi: 10.1016/j.apm.2016.08.011

CrossRef Full Text | Google Scholar

29. Singh H. A new numerical algorithm for fractional model of Bloch equation in nuclear magnetic resonance. Alexandria Engrg J. (2016) 55:2863–9. doi: 10.1016/j.aej.2016.06.032

CrossRef Full Text | Google Scholar

30. Miller K, Ross B. An Introduction to Fractional Calculus and Fractional Differential Equations. New York, NY: John Wiley & Sons Inc (1993).

Google Scholar

31. Diethelm K, Ford NJ, Freed AD, Luchko Y. Algorithms for fractional calculus: a selection of numerical methods. Comput Meth Appl Mech Eng. (2005) 194:743–73. doi: 10.1016/j.cma.2004.06.006

CrossRef Full Text | Google Scholar

32. Doha EH, Bhrawy AH, Baleanu D, Ezz-Eldien SS. The operational matrix formulation of the Jacobi tau approximation for space fractional diffusion equation. Adv Differ Equ. (2014) 2014:231. doi: 10.1186/1687-1847-2014-231

CrossRef Full Text | Google Scholar

33. Ahmadian A, Suleiman M, Salahshour S, Baleanu D. A Jacobi operational matrix for solving a fuzzy linear fractional differential equation. Adv Differ Equ. (2013) 2013:104. doi: 10.1186/1687-1847-2013-104

CrossRef Full Text | Google Scholar

34. Bhrawy AH, Tharwat MM, Alghamdi MA. A new operational matrix of fractional integration for shifted Jacobi polynomials. Bull Malays Math Sci Soc. (2014) 37:983.

Google Scholar

35. Rivlin TJ. An Introduction to the Approximation of Functions. New York, NY: Dover Publications (1981).

Google Scholar

36. Kreyszig E. Introductory Functional Analysis with Applications. New York, NY: John Wiley and Sons, Inc. (1978).

Google Scholar

37. Behroozifar M, Sazmand A. An approximate solution based on Jacobi polynomials for time-fractional convection-diffusion equation. Appl Math Comp. (2017) 296:1–17. doi: 10.1016/j.amc.2016.09.028

CrossRef Full Text | Google Scholar

38. Kazem S. An integral operational matrix based on Jacobi polynomials for solving fractional-order differential equations. Appl Math Model. (2013) 37:1126–36. doi: 10.1016/j.apm.2012.03.033

CrossRef Full Text | Google Scholar

39. Ezz-Eldien SS. New quadrature approach based on operational matrix for solving a class of fractional variational problems. J Comp Phys. (2016) 317:362–81. doi: 10.1016/j.jcp.2016.04.045

CrossRef Full Text | Google Scholar

40. Nourazar S, Mirzabeigy A. Approximate solution for nonlinear Duffing oscillator with damping effect using the modified differential transform method. Sci Iranica B. (2013) 20:364–68.

Google Scholar