Critical Scaling of Diffusion Coefficients and Size of Rigid Clusters of Soft Athermal Particles Under Shear

We numerically investigate the self-diffusion coefficient and correlation length (i.e., the typical size of the collective motions) in sheared soft athermal particles. Here we find that the rheological flow curves on the self-diffusion coefficient are collapsed by the proximity to the jamming transition density. This feature is in common with the well-established critical scaling of flow curves on shear stress or viscosity. We furthermore reveal that the divergence of the correlation length governs the critical behavior of the diffusion coefficient, where the diffusion coefficient is proportional to the correlation length and the strain rate for a wide range of the strain rate and packing fraction across the jamming transition density.

1. Introduction

Transport properties of soft athermal particles, e.g., emulsions, foams, colloidal suspensions, and granular materials, are important in science and engineering technology [1]. In many manufacturing processes, these particles are forced to flow through pipes, containers, etc. Therefore, the transportation of “flowing particles” is of central importance for industrial applications [2] and thus there is a need to understand how the transport properties are affected by the rheology of the particles.

Recently, the rheological flow behavior of soft athermal particles has been extensively studied by physicists [3–17]. It has been revealed that the rheology of such particulate systems depends not only on shear rate $\stackrel{\cdot }{\gamma }$ but also on packing fraction of the particles. If the packing fraction ϕ is lower than the so-called jamming transition density ϕ_J [18], steady state stress is described by either Newtonian [3, 4] or Bagnoldian rheology [5–9] (depending on whether particle inertia is significant). However, if the packing fraction exceeds the jamming point, one observes yield stress at vanishing strain rate [19]. These two trends are solely determined by the proximity to jamming |Δϕ| ≡ |ϕ − ϕ_J| [3], where rheological flow curves of many types of soft athermal particles have been explained by the critical scaling near the jamming transition [4–15].

On the other hand, the mass transport or self-diffusion of soft athermal particles seems to be controversial. As is the rheological flow behavior on shear stress or viscosity, the diffusivity of the particles under shear is also dependent on both $\stackrel{\cdot }{\gamma }$ and ϕ. Its dependence on $\stackrel{\cdot }{\gamma }$ is weakened with the increase of $\stackrel{\cdot }{\gamma }$, i.e., the diffusivity D exhibits a crossover from a linear scaling $D~\stackrel{\cdot }{\gamma }$ to the sub-linear scaling $D~{\stackrel{\cdot }{\gamma }}^q$ at a characteristic shear rate ${\stackrel{\cdot }{\gamma }}_c$, where the exponent is smaller than unity, q < 1 [20–25]. For example, in molecular dynamics (MD) simulations of Durian's bubble model in two dimensions [20, 21] and frictionless granular particles in three dimensions [22], the diffusivity varies from $D~\stackrel{\cdot }{\gamma }$ ($\stackrel{\cdot }{\gamma }<{\stackrel{\cdot }{\gamma }}_c$) to $D~{\stackrel{\cdot }{\gamma }}^{0.8}$ ($\stackrel{\cdot }{\gamma }>{\stackrel{\cdot }{\gamma }}_c$). These results also imply that the diffusivity does not depend on spatial dimensions. However, another crossover from $D~\stackrel{\cdot }{\gamma }$ to $D~{\stackrel{\cdot }{\gamma }}^{1/2}$ was suggested by the studies of amorphous solids (though the scaling $D~{\stackrel{\cdot }{\gamma }}^{1/2}$ is the asymptotic behavior in rapid flows $\stackrel{\cdot }{\gamma }\gg {\stackrel{\cdot }{\gamma }}_c$) [23–25]. In addition, it was found in MD simulations of soft athermal disks that, in a sufficiently small flow rate range, the diffusivity changes from $D~\stackrel{\cdot }{\gamma }$ (ϕ < ϕ_J) to ${\stackrel{\cdot }{\gamma }}^{0.78}$ (ϕ ≃ ϕ_J) [26], implying that the crossover shear rate ${\stackrel{\cdot }{\gamma }}_c$ vanishes as the system approaches jamming from below ϕ → ϕ_J.

Note that the self-diffusion of soft athermal particles shows a clear difference from the diffusion in glass; no plateau is observed in (transverse) mean square displacements (MSDs) [20, 22–26]. The absence of sub-diffusion can also be seen in quasi-static simulations ($\stackrel{\cdot }{\gamma }\to 0$) of soft athermal disks [27] and MD simulations of granular materials sheared under constant pressure [28].

Because the self-diffusion can be associated with collective motions of soft athermal particles, physicists have analyzed spatial correlations of velocity fluctuations [3] or non-affine displacements [29] of the particles. Characteristic sizes of collectively moving regions, i.e., rigid clusters, are then extracted as a function of $\stackrel{\cdot }{\gamma }$ and ϕ. However, there is a lack of consensus on the scaling of the sizes. For example, the size of rigid clusters ξ diverges as the shear rate goes to zero $\stackrel{\cdot }{\gamma }\to 0$ so that the power-law scaling $\xi ~{\stackrel{\cdot }{\gamma }}^{-s}$ was suggested, where the exponent varies from s = 0.23 to 0.5 depending on numerical models and flow conditions [22, 28]. The dependence of ξ on ϕ is also controversial. If the system is below jamming, the critical scaling is given by ξ ~ |Δϕ|^−w, where different exponents in the range between 0.5 ≤ w ≤ 1.0 have been reported by various simulations [3, 29–31]. In contrast, if the system is above jamming, the size becomes insensitive to ϕ (or exceeds the system size L) as only L is the relevant length scale, i.e., ξ ~ L, in a quasi-static regime [4, 23–25].

From a scaling argument [27, 28], a relation between the diffusivity and size of rigid clusters was proposed as

$\begin{array}{ll}D~d_0\xi \stackrel{\cdot }{\gamma },& (1)\end{array}$

where d₀ is the particle diameter. It seems that previous results above jamming, i.e., as $\stackrel{\cdot }{\gamma }$ increases, $D/\stackrel{\cdot }{\gamma }$ changes from constant to ${\stackrel{\cdot }{\gamma }}^{-1/2}$ and corresponding ξ undergoes from L to ${\stackrel{\cdot }{\gamma }}^{-1/2}$, support this argument [23–25]. However, the link between the diffusivity and rigid clusters below jamming is still not clear.

In this paper, we study the self-diffusion of soft athermal particles and the size of rigid clusters. The particles are driven by simple shear flows and their fluctuating motions around a mean velocity field are numerically calculated. From numerical results, we extract the diffusivity of the particles and explain its dependence on the control parameters, i.e., $\stackrel{\cdot }{\gamma }$ and ϕ. We investigate wide ranges of the control parameters in order to unify our understanding of the diffusivity in both slow and fast flows ($\stackrel{\cdot }{\gamma }<{\stackrel{\cdot }{\gamma }}_c$ and $\stackrel{\cdot }{\gamma }>{\stackrel{\cdot }{\gamma }}_c$) and both below and above jamming (ϕ < ϕ_J and ϕ > ϕ_J). Our main result is the critical scaling of the diffusivity D, which parallels the critical scaling of the size of rigid clusters ξ. We find that the linear relation between $D/\stackrel{\cdot }{\gamma }$ and ξ (Equation 1) holds over the whole ranges of $\stackrel{\cdot }{\gamma }$ and ϕ if finite-size effects are not important. In the following, we show our numerical method in section 2 and numerical results in section 3. In section 4, we discuss and conclude our results and future works.

2. Methods

We perform MD simulations of two-dimensional disks. In order to avoid crystallization of the system, we randomly distribute an equal number of small and large disks (with diameters d_S and d_L = 1.4d_S) in a L × L square periodic box [32]. The total number of disks is N = 8192 and the packing fraction of the disks ϕ is controlled around the jamming transition density ϕ_J ≃ 0.8433 [3]. We introduce an elastic force between the disks, i and j, in contact as $f_{ij}^{\text{e}}=k{\delta }_{ij}{n}_{ij}$, where k is the stiffness and n_ij ≡ r_ij/|r_ij| with the relative position r_ij ≡ r_i − r_j is the normal unit vector. The elastic force is linear in the overlap δ_ij ≡ R_i + R_j − |r_ij| > 0, where R_i (R_j) is the radius of the disk i (j). We also add a damping force to every disk as $f_i^{\text{d}}=-\eta \left\{v_i-u(r_i)\right\}$, where η, v_i, and u(r) are the damping coefficient, velocity of the disk i, and external flow field, respectively. The stiffness and damping coefficient determine a time scale as t₀ ≡ η/k.

To simulate simple shear flows of the system, we impose the external flow field $u(r)=(\stackrel{\cdot }{\gamma }y,0)$ under the Lees-Edwards boundary condition [33], where $\stackrel{\cdot }{\gamma }$ is the shear rate. Motions of the disks are described by overdamped dynamics [3, 4, 11], i.e., $\sum _{j\ne i}{f}_{ij}^{\text{e}}+f_i^{\text{d}}=0$, so that we numerically integrate the disk velocity $v_i=u(r_i)+{\eta }^{-1}\sum _{j\ne i}{f}_{ij}^{\text{el}}$ with a time increment Δt = 0.1t₀. Figure 1 displays snapshots of our MD simulations, where the system is sheared along the horizontal arrows in (Figure 1A). Here, the shear rate is fixed to $\stackrel{\cdot }{\gamma }=10^{-7}{t}_0^{-1}$ and the packing fraction increases from ϕ = 0.8 (Figure 1A) to 0.9 (Figure 1D). We observe that, as ϕ increases, the magnitude of non-affine velocities, |v_i − u(r_i)|, is pronounced and mobile particles (satisfying $|v_i-u(r_i)|>10d_0\stackrel{\cdot }{\gamma }$ with the mean disk diameter d₀ ≡ (d_S + d_L)/2) form clusters (filled circles). The size of these clusters, or rigid clusters, increases with ϕ (Figures 1B,C) and reaches the box size L if the system is far above jamming (Figure 1D).

FIGURE 1

Figure 1. Snapshots of our MD simulations, where the particles (circles) are sheared as indicated by the horizontal arrows in (A). The filled (open) circles represent mobile (immobile) particles, where the magnitude of their non-affine velocities |v_i − u(r_i)| is larger (smaller) than $10d_0\stackrel{\cdot }{\gamma }$. The shear rate is $\stackrel{\cdot }{\gamma }=10^{-7}{t}_0^{-1}$ and the packing fraction ϕ increases as (A) 0.80, (B) 0.84, (C) 0.85, and (D) 0.90.

In the following, we analyze the data in a steady state, where shear strain applied to the system is larger than unity, and scale every time and length by t₀ and d₀, respectively.

3. Results

In this section, we show our numerical results of the self-diffusion of soft athermal particles (section 3.1). We also extract rigid clusters (Figure 1) from numerical data in order to relate their sizes to the diffusivity (section 3.2). We explain additional data of the rheology and non-affine displacements in Supplemental Materials.

3.1. Diffusion

We analyze the self-diffusion of soft athermal particles by the transverse component of mean squared displacement (MSD) [24–26, 28],

$\begin{array}{ll}\Delta {(\tau )}^2=\langle \frac{1}{N}{\displaystyle \sum _{i=1}^N}\Delta y_i{(\tau )}^2\rangle .& (2)\end{array}$

Here, Δy_i(τ) is the y-component of particle displacement and the ensemble average 〈…〉 is taken over different choices of the initial time (see Supplemental Materials for the detail)¹. Figure 2 displays the MSDs (Equation 2) with different values of (Figure 2A) ϕ and (Figure 2B) $\stackrel{\cdot }{\gamma }$. The horizontal axes are the time interval scaled by the shear rate, $\gamma \equiv \stackrel{\cdot }{\gamma }\tau$, i.e., the shear strain applied to the system for the duration τ. As can be seen, every MSD exhibits a crossover to the normal diffusive behavior, $\Delta {(\tau )}^2~\stackrel{\cdot }{\gamma }\tau$ (dashed lines), around a crossover strain γ = γ_c ≃ 1 regardless of ϕ and $\stackrel{\cdot }{\gamma }$. The MSDs below jamming (ϕ < ϕ_J) monotonously increase with the increase of packing fraction, while they (almost) stop increasing once the packing fraction exceeds the jamming point (ϕ > ϕ_J) (Figure 2A). The dependence of MSDs on the shear rate is monotonous; their heights decrease with the increase of $\stackrel{\cdot }{\gamma }$ (Figure 2B). These trends well-correspond with the fact that the non-affine displacements are amplified in slow flows of dense systems, i.e., $\stackrel{\cdot }{\gamma }{t}_0\ll 1$ and ϕ > ϕ_J [34]. In addition, different from thermal systems under shear [14, 35, 36], any plateaus are not observed in the MSDs. Therefore, neither “caging” nor “sub-diffusion” of the particles exists in our sheared athermal systems [22, 27, 37].

FIGURE 2

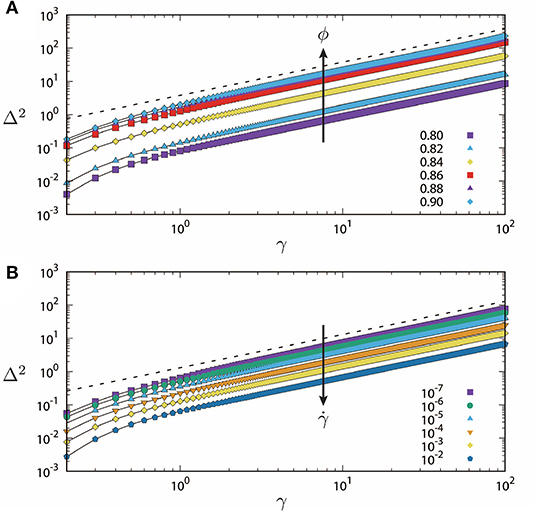
Figure 2. The transverse MSDs Δ² (Equation 2) as functions of the shear strain $\gamma \equiv \stackrel{\cdot }{\gamma }\tau$. (A) The packing fraction ϕ increases as indicated by the arrow and listed in the legend, where the shear rate is $\stackrel{\cdot }{\gamma }=10^{-6}{t}_0^{-1}$. (B) The shear rate $\stackrel{\cdot }{\gamma }$ increases as indicated by the arrow and listed in the legend, where the packing fraction is ϕ = 0.84.

To quantify the normal diffusion of the disks, we introduce the diffusivity (or diffusion coefficient) as²

$\begin{array}{ll}D={\displaystyle \underset{\tau \to \infty }{lim}}\frac{\Delta {(\tau )}^2}{2\tau }.& (3)\end{array}$

Figure 3A shows double logarithmic plots of the diffusivity (Equation 3) over the shear rate $D/\stackrel{\cdot }{\gamma }$, where symbols represent the packing fraction ϕ (as listed in the legend). The diffusivity over the shear rate increases with ϕ. If the system is above jamming ϕ > ϕ_J, it is a monotonously decreasing function of $\stackrel{\cdot }{\gamma }$. On the other hand, if the system is below jamming ϕ < ϕ_J, it exhibits a crossover from plateau to a monotonous decrease around a characteristic shear rate, e.g., ${\stackrel{\cdot }{\gamma }}_0{t}_0\simeq 10^{-3}$ for ϕ = 0.80 [24, 25].

FIGURE 3

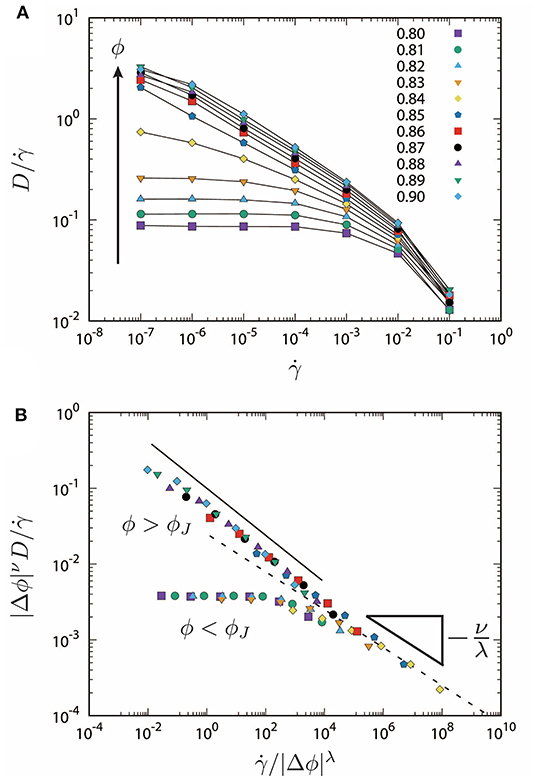
Figure 3. (A) The diffusivity over the shear rate, $D/\stackrel{\cdot }{\gamma }$, as a function of $\stackrel{\cdot }{\gamma }$, where ϕ increases as indicated by the arrow and listed in the legend. (B) Scaling collapses of the diffusivity, where Δϕ ≡ ϕ − ϕ_J. The critical exponents are given by ν = 1.0 and λ = 4.0, where slopes of the dotted and solid lines are −ν/λ and −0.3, respectively.

In SM, we have demonstrated scaling collapses of rheological flow curves [3]. Here, we also demonstrate scaling collapses of the diffusivity. As shown in Figure 3B, all the data are nicely collapsed³ by the scaling exponents, ν = 1.0 and λ = 4.0. If the shear rate is smaller than a characteristic value as $\stackrel{\cdot }{\gamma }/|\Delta \varphi {|}^{\lambda }\lesssim 10^4$, i.e., $\stackrel{\cdot }{\gamma }<{\stackrel{\cdot }{\gamma }}_c\simeq 10^4|\Delta \varphi {|}^{\lambda }$, the data below jamming (ϕ < ϕ_J) are constant. However, the data above jamming (ϕ > ϕ_J) show the power-law decay (solid line), where the slope is −0.305 ± 0.002 (approximately −0.3). Therefore, we describe the diffusivity in a quasi-static regime ($\stackrel{\cdot }{\gamma }<{\stackrel{\cdot }{\gamma }}_c$) as $|\Delta \varphi {|}^{\nu }D/\stackrel{\cdot }{\gamma }~{{G}}_{\pm }(\stackrel{\cdot }{\gamma }/|\Delta \varphi {|}^{\lambda })$, where the scaling functions are given by ${{G}}_{-}(x)~\text{const}.$ for ϕ < ϕ_J and ${{G}}_{+}(x)~x^{-0.3}$ otherwise. On the other hand, if $\stackrel{\cdot }{\gamma }>{\stackrel{\cdot }{\gamma }}_c$, all the data follow a single power law (dotted line). This means that the scaling functions are given by ${{G}}_{\pm }(x)~x^{-z}$ in a plastic flow regime ($\stackrel{\cdot }{\gamma }>{\stackrel{\cdot }{\gamma }}_c$), where the diffusivity scales as $D~\stackrel{\cdot }{\gamma }|\Delta \varphi {|}^{-\nu }{{G}}_{\pm }(\stackrel{\cdot }{\gamma }/|\Delta \varphi {|}^{\lambda })~{\stackrel{\cdot }{\gamma }}^{1-z}|\Delta \varphi {|}^{\lambda z-\nu }$. Because this scaling should be independent of whether the system is below or above jamming, i.e., independent of |Δϕ|, the power-law exponent is given by z = ν/λ = 1/4 as confirmed in Figure 3B.

In summary, the diffusivity of the disks scales as

$\begin{array}{ll}D~\{\begin{array}{cc}|\Delta \varphi {|}^{-\nu }\stackrel{\cdot }{\gamma }\hfill & (\varphi <{\varphi }_J)\hfill \\ |\Delta \varphi {|}^{0.3\lambda -\nu }{\stackrel{\cdot }{\gamma }}^{0.7}\hfill & (\varphi >{\varphi }_J)\hfill \end{array}\hfill & (4)\end{array}$

in the quasi-static regime ($\stackrel{\cdot }{\gamma }<{\stackrel{\cdot }{\gamma }}_c$) and

$\begin{array}{ll}D~{\stackrel{\cdot }{\gamma }}^{1-\nu /\lambda }& (5)\end{array}$

in the plastic flow regime ($\stackrel{\cdot }{\gamma }>{\stackrel{\cdot }{\gamma }}_c$), where the critical exponents are estimated as ν = 1.0 and λ = 4.0. From Equations (4) and (5), we find that the diffusivity below jamming (ϕ < ϕ_J) is linear in the shear rate $D~\stackrel{\cdot }{\gamma }$ in slow flows, whereas its dependence on the shear rate is algebraic $D~{\stackrel{\cdot }{\gamma }}^{3/4}$ in fast flows. A similar trend has been found in molecular dynamics studies of simple shear flows below jamming [22, 26, 37]. In addition, the proportionality for the diffusivity below jamming diverges at the transition as |Δϕ|⁻¹ (Equation 4), which we will relate to a length scale diverging as the system approaches jamming from below (section 3.2). The diffusivity above jamming (ϕ > ϕ_J) implies the crossover from $D~|\Delta \varphi {|}^{0.2}{\stackrel{\cdot }{\gamma }}^{0.7}$ to ${\stackrel{\cdot }{\gamma }}^{3/4}={\stackrel{\cdot }{\gamma }}^{0.75}$, which reasonably agrees with the prior work on soft athermal disks under shear [26]. Interestingly, the crossover shear rate vanishes at the transition as ${\stackrel{\cdot }{\gamma }}_c~|\Delta \varphi {|}^{4.0}$, which is reminiscent of the fact that the crossover from the Newtonian or yield stress to the plastic flow vanishes at the onset of jamming (see Supplemental Materials).

3.2. Rigid Clusters

We now relate the diffusivity D to rigid clusters of soft athermal particles under shear (Figure 1). The rigid clusters represent collective motions of the particles which tend to move in the same direction [34]. According to the literature of jamming [3, 4, 29], we quantify the collective motions by a spatial correlation function C(x) = 〈v_y(x_i, y_i)v_y(x_i + x, y_i)〉, where v_y(x, y) is the transverse velocity field and the ensemble average 〈…〉 is taken over disk positions and time (in a steady state). Figure 4 shows the normalized correlation function C(x)/C(0), where the horizontal axis (x-axis) is scaled by the mean disk diameter d₀. As can be seen, the correlation function exhibits a well-defined minimum at a characteristic length scale x = ξ (as indicated by the vertical arrow for the case of ϕ = 0.84 in Figure 4A). Because the minimum is negative C(ξ) < 0, the transverse velocities are most “anti-correlated" at x = ξ [3]. Therefore, if we assume that the rigid clusters are circular⁴, their mean diameter is comparable in size with ξ. The length scale ξ increases with the increase of ϕ (Figure 4A) but decreases with the increase of $\stackrel{\cdot }{\gamma }$ (Figure 4B). These results are consistent with the fact that the collective behavior is most enhanced in slow flows of dense systems [34].

FIGURE 4

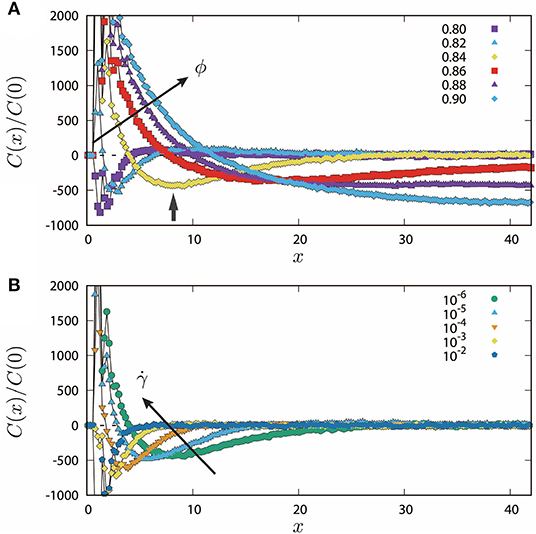
Figure 4. Normalized spatial correlation functions of the transverse velocities C(x)/C(0), where symbols are as in Figure 2. (A) The packing fraction ϕ increases as indicated by the arrow and listed in the legend, where $\stackrel{\cdot }{\gamma }=10^{-6}{t}_0^{-1}$. The minimum of the data for ϕ = 0.84 is indicated by the short vertical arrow. (B) The shear rate $\stackrel{\cdot }{\gamma }$ increases as indicated by the arrow and listed in the legend, where ϕ = 0.84.

As reported in Olsson and Teitel[3], we examine critical scaling of the length scale. Figure 5A displays scaling collapses of the data of ξ, where the critical exponents, ν = 1.0 and λ = 4.0, are the same with those in Figure 3B. If the shear rate is smaller than the characteristic value, i.e., $\stackrel{\cdot }{\gamma }<{\stackrel{\cdot }{\gamma }}_c\simeq 10^4|\Delta \varphi {|}^{\lambda }$, the data below jamming (ϕ < ϕ_J) exhibit plateau, whereas those above jamming (ϕ > ϕ_J) diverge with the decrease of shear rate. Therefore, if we assume that the data above jamming follow the power-law (solid line) with the slope −0.40 ± 0.02 (approximately −0.4), the length scale in the quasi-static regime ($\stackrel{\cdot }{\gamma }<{\stackrel{\cdot }{\gamma }}_c$) can be described as $|\Delta \varphi {|}^{\nu }\xi ~{{J}}_{\pm }(\stackrel{\cdot }{\gamma }/|\Delta \varphi {|}^{\lambda })$ with the scaling functions, ${{J}}_{-}(x)~\text{const}.$ for ϕ < ϕ_J and ${{J}}_{+}(x)~x^{-0.4}$ otherwise. Note that, however, the length scale is limited to the system size L (shaded region in Figure 5A) and should be scaled as ξ ~ L above jamming in the quasi-static limit $\stackrel{\cdot }{\gamma }\to 0$ [4, 24, 29]. This means that the system size is the only relevant length scale [38] and thus we conclude ξ ~ L in slow flows of jammed systems. On the other hand, if $\stackrel{\cdot }{\gamma }>{\stackrel{\cdot }{\gamma }}_c$, all the data are collapsed onto a single power law (dotted line in Figure 5A). Therefore, the scaling functions are given by ${{J}}_{\pm }(x)~x^{-z}$ such that the length scale scales as $\xi ~{\stackrel{\cdot }{\gamma }}^{-z}|\Delta \varphi {|}^{\lambda z-\nu }$. Because this relation is independent of |Δϕ|, the exponent should be z = ν/λ as confirmed in Figure 5A.

FIGURE 5

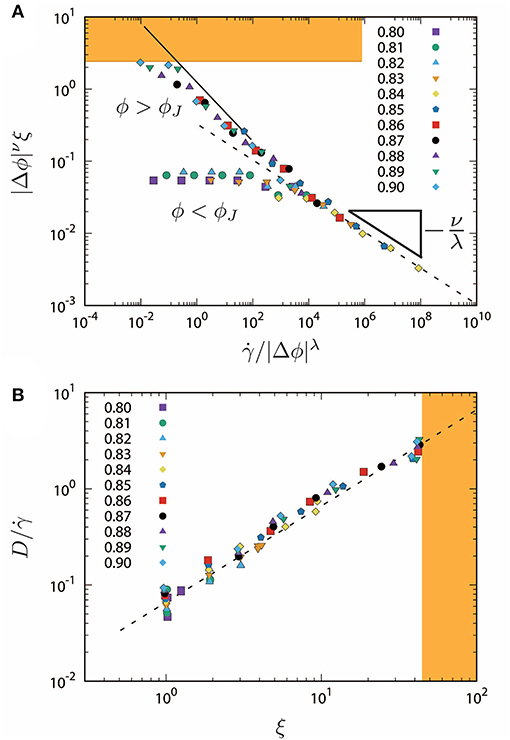
Figure 5. (A) Scaling collapses of the length scale ξ, where Δϕ ≡ ϕ − ϕ_J and ϕ increases as listed in the legend. The critical exponents are ν = 1.0 and λ = 4.0 as in Figure 3B, where slopes of the dotted and solid lines are given by −ν/λ and −0.4, respectively. The shaded region exceeds the system size |Δϕ|^νL/2 for the case of ϕ = 0.90. (B) Scatter plots of the diffusivity over the shear rate $D/\stackrel{\cdot }{\gamma }$ and the length scale ξ, where ϕ increases as listed in the legend. The dotted line represents a linear relation $D/\stackrel{\cdot }{\gamma }~\xi$ and the shaded region exceeds the system size L/2 ≃ 44d₀.

In summary, the length scale, or the mean size of rigid clusters, scales as

$\begin{array}{ll}\xi ~\{\begin{array}{cc}|\Delta \varphi {|}^{-\nu }\hfill & (\varphi <{\varphi }_J)\hfill \\ L\hfill & (\varphi >{\varphi }_J)\hfill \end{array}\hfill & (6)\end{array}$

in the quasi-static regime ($\stackrel{\cdot }{\gamma }<{\stackrel{\cdot }{\gamma }}_c$) and

$\begin{array}{ll}\xi ~{\stackrel{\cdot }{\gamma }}^{-\nu /\lambda }& (7)\end{array}$

in the plastic flow regime ($\stackrel{\cdot }{\gamma }>{\stackrel{\cdot }{\gamma }}_c$), where the critical exponents, ν and λ, are the same with those for the diffusivity (Equations 4 and 5). The critical divergence below jamming in the quasi-static regime, i.e., ξ ~ |Δϕ|⁻¹ (Equation 6), is consistent with the results of quasi-static simulations ($\stackrel{\cdot }{\gamma }\to 0$) of sheared athermal disks [27, 29]. In addition, the scaling $\xi ~{\stackrel{\cdot }{\gamma }}^{-1/4}$ in the plastic flow regime (Equation 7) is very close to the prior work on athermal particles under shear [22].

From the results of the diffusivity and length scale, we discuss how the rigid clusters contribute to the diffusion of the particles. From Equations (4) to (7), the linear relation $D~d_0\xi \stackrel{\cdot }{\gamma }$ (Equation 1) holds below jamming (regardless of $\stackrel{\cdot }{\gamma }$) and in the plastic flow regime (regardless of ϕ). We stress that the divergence of the diffusivity over the shear rate in the quasi-static regime, i.e., $D/\stackrel{\cdot }{\gamma }~|\Delta \varphi {|}^{-1}$ (Equation 4), is caused by the diverging length scale below jamming, i.e., ξ ~ |Δϕ|⁻¹ (Equation 6). As shown in Figure 5B, the linear relation (dotted line) well explains our results below jamming, where the length scale ξ is smaller than 10d₀. The linear relation (dotted line) also well captures our results above jamming⁵ until the length scale eventually reaches the system size L/2 ≃ 44d₀ (shaded region).

4. Discussions

In this study, we have numerically investigated rheological and transport properties of soft athermal particles under shear. Employing MD simulations of two-dimensional disks, we have clarified how the rheology, self-diffusion, and size of rigid clusters vary with the control parameters, i.e., the externally imposed shear rate $\stackrel{\cdot }{\gamma }$ and packing fraction of the disks ϕ.

Our main result is the critical scaling of the diffusivity (section 3.1), where their dependence on both $\stackrel{\cdot }{\gamma }$ and ϕ is reported (Equations 4–7). The diffusivity has been calculated on both sides of jamming (by a single numerical protocol) to unify the understanding of self-diffusion of soft particulate systems. We found that (i) the diffusivity below jamming exhibits a crossover from the linear scaling $D~\stackrel{\cdot }{\gamma }$ to the power-law $D~{\stackrel{\cdot }{\gamma }}^{3/4}$. Such a crossover can also be seen in previous simulations [20–22]. In addition, (ii) the diffusivity below jamming diverges as D ~ |Δϕ|⁻¹ if the system is in the quasi-static regime ($\stackrel{\cdot }{\gamma }<{\stackrel{\cdot }{\gamma }}_c$), whereas (iii) the diffusivity (both below and above jamming) is insensitive to ϕ if the system is in the plastic flow regime ($\stackrel{\cdot }{\gamma }>{\stackrel{\cdot }{\gamma }}_c$). Note that (iv) the crossover shear rate vanishes at the onset of jamming as ${\stackrel{\cdot }{\gamma }}_c~|\Delta \varphi {|}^{4.0}$. These results (ii)–(iv) are the new findings of this study. On the other hand, we found that (v) the diffusivity above jamming is weakly dependent on ϕ (as D ~ |Δϕ|^0.2) in the quasi-static regime and (vi) shows a slight change from $D~{\stackrel{\cdot }{\gamma }}^{0.7}$ to ${\stackrel{\cdot }{\gamma }}^{3/4}$. Though the result (v) is the new finding, the result (vi) contrasts with the prior studies, where the diffusivity exhibits a crossover from $D~\stackrel{\cdot }{\gamma }$ to ${\stackrel{\cdot }{\gamma }}^{1/2}$ [24, 25, 28]. Because our scaling $D~{\stackrel{\cdot }{\gamma }}^{0.7}$ in the quasi-static regime is consistent with Olsson [26], where the same overdamped dynamics are used, we suppose that the discrepancy is caused by numerical models and flow conditions, where the Lennard-Jones potential is used for the interaction between the particles in Lemaître and Caroli [24] and Chattoraj et al. [25] and frictionless/frictional disks are sheared under constant pressure in Kharel and Rognon [28].

We have also examined the relation between the diffusivity and typical size of rigid clusters ξ (section 3.2). Below jamming, we found the critical divergence ξ ~ |Δϕ|⁻¹ in the quasi-static regime as previously observed in quasi-static simulations ($\stackrel{\cdot }{\gamma }\to 0$) of sheared athermal disks [29]. Note that our exponent is larger than that obtained from previous studies of soft athermal particles [3, 30], where the critical divergence ξ ~ |Δϕ|^−ν is characterized by the exponent in the range between 0.6 < ν < 0.7. Though the meaning of ξ is similar, in the sense that it quantifies the size of collective motions of the particles under shear, we found that the quality of data collapse of ξ is even worse if we use the exponents ν = 0.6 and 0.7. So far, we cannot figure out the cause of this discrepancy and postpone this problem as a future work. In the plastic flow regime, the size becomes independent of ϕ and scales as $\xi ~{\stackrel{\cdot }{\gamma }}^{-1/4}$. This is consistent with the previous result of sheared athermal particles [22] (and is also close to the result of thermal glasses under shear [36]). Above jamming, however, the size exhibits a crossover from ξ ~ L to ${\stackrel{\cdot }{\gamma }}^{-1/4}$ which contrasts with the crossover from ξ ~ L to ${\stackrel{\cdot }{\gamma }}^{-1/2}$ previously reported in simulations of amorphous solids [24, 25, 28]. From our scaling analyses, we found that the linear relation $D~d_0\xi \stackrel{\cdot }{\gamma }$ (Equation 1) holds below jamming (for $\forall \stackrel{\cdot }{\gamma }$) and in the plastic flow regime (for ∀ϕ), indicating that the self-diffusion is enhanced by the rotation of rigid clusters [3, 28].

In our MD simulations, we fixed the system size to L ≃ 88d₀. However, systematic studies of different system sizes are needed to clarify the relation between D and ξ ~ L above jamming, especially in the quasi-static limit $\stackrel{\cdot }{\gamma }\to 0$ [24, 25]. In addition, our analyses are limited to two dimensions. Though previous studies suggest that the diffusivity is independent of the dimensionality [20–22], a recent study of soft athermal particles reported that the critical scaling of shear viscosity depends on dimensions [39]. Therefore, it is important to check whether the critical scaling (Equations 4 and 5) is different in three-dimensional systems. In addition, O'Hern et al. found that the critical exponents near jamming are sensitive to interaction potentials [32]. Therefore, it is important to examine whether our exponents, ν and λ, are sensitive to the details of numerical models, e.g., contact forces, particle inertia, microscopic friction, particle size distributions, etc. with the aim of testing universality class of the diffusivity and size of rigid clusters. Moreover, the analysis of local structures of instantaneous configurations of the disks is important to investigate the rigidity of the clusters [40] and the relation between the diffusivity and shear viscosity may be interesting because it gives a Stokes-Einstein like relation for the non-equilibrium systems studied here.

In our recent study of non-Brownian suspensions [15], we found that the viscosity exhibits a crossover when the system approaches the jamming transition. To describe such a crossover, a correction term should be added to the conventional scaling function as ${F}(x)+{G}(x)$, where two different exponents are introduced as ${F}(x)~x^{-z}$ and ${G}(x)~x^{-w}$. This means that the scaling collapse of the flow curves [3], where the scaling function is given by a single power law, can be violated if the system is very close to jamming. Similarly, our scaling collapses of D (Figure 3B) and ξ (Figure 5A) could break down by the same reason. Therefore, it is necessary to examine whether the crossovers of D and ξ exist in the case that the system is in the vicinity of the jamming transition.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

KS and TK designed the research and wrote the paper. KS performed the research.

Funding

This work was supported by KAKENHI Grant Nos. 16H04025 and 18K13464 from JSPS.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank B. P. Tighe, L. Berthier, H. Hayakawa, M. Otsuki, and S. Takada for fruitful discussions. KS thanks F. Radjai and W. Kob for fruitful discussions and warm hospitality in Montpellier.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.00099/full#supplementary-material

Footnotes

1. ^The MSDs defined by the total non-affine displacements show quantitatively the same results (data are not shown).

2. ^We define the diffusivity (Equation 3) as the slope of the MSD (Equation 2) in the normal diffusive regime $\gamma =\stackrel{\cdot }{\gamma }\tau >1$, where we take sample averages of Δ(τ)²/2τ as $D/\stackrel{\cdot }{\gamma }\equiv <\Delta {(\gamma )}^2/2\gamma >$ in the range between 1 < γ < 10².

3. ^The data for the highest shear rate, $\stackrel{\cdot }{\gamma }=10^{-1}{t}_0^{-1}$, is removed from the scaling collapses in Figures 3B, 5A.

4. ^In a short range of x, non-affine velocities tend to be aligned in the same direction, i.e., v_y(x_i, y_i)v_y(x_i + x, y_i) > 0, such that the correlation function C(x) is a positive decreasing function of x. If the non-affine velocities start to align in the opposite direction, i.e., v_y(x_i, y_i)v_y(x_i + x, y_i) < 0, the correlation function becomes negative, C(x) < 0. Because the correlation function is minimum when the non-affine velocities are located on either side of a vortex-like structure, a typical size of rigid clusters can be defined as the distance at which C(x) becomes minimum. In a long distance of x, due to the randomness of non-affine velocities, the correlation function eventually decays to zero with or without oscillations [34].

5. ^If the system is above jamming (ϕ > ϕ_J) and in the quasi-static regime ($\stackrel{\cdot }{\gamma }<{\stackrel{\cdot }{\gamma }}_c$), the diffusivity over the shear rate scales as $D/\stackrel{\cdot }{\gamma }~|\Delta \varphi {|}^{0.2}{\stackrel{\cdot }{\gamma }}^{-0.3}$ (see Equation 4). However, if ϕ > ϕ_J and $\stackrel{\cdot }{\gamma }<{\stackrel{\cdot }{\gamma }}_c$, the length scale is $\xi ~|\Delta \varphi {|}^{0.6}{\stackrel{\cdot }{\gamma }}^{-0.4}$ as long as ξ does not exceed the system size L. Though the linear relation $D/\stackrel{\cdot }{\gamma }~\xi$ is not exact in this regime, their exponents are close to each other such that the dotted line in Figure 5B fairly well explains the data. To figure out the relation between $D/\stackrel{\cdot }{\gamma }$ and ξ in this regime more carefully, further studies of different system sizes may be necessary because there is a possibility of the coexistence of different length scales, e.g., not only the rigid clusters but also string-like structures with different fractal dimensions as can be seen in Figure 1.

References

1. Bird RB, Stewart WE, Lightfoot EN. Transport Phenomena, Revised Second Edition. New York, NY: John Wiley & Sons, Inc. (2007).

Google Scholar

2. Larson RG. The Structure and Rheology of Complex Fluids. New York, NY: Oxford University Press, Inc. (1999).

Google Scholar

3. Olsson P, Teitel S. Critical scaling of shear viscosity at the jamming transition. Phys Rev Lett. (2007) 99:178001. doi: 10.1103/PhysRevLett.99.178001

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Tighe BP, Woldhuis E, Remmers JJC, van Saarloos W, van Hecke M. Model for the scaling of stresses and fluctuations in flows near jamming. Phys Rev Lett. (2010) 105:088303. doi: 10.1103/PhysRevLett.105.088303

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Hatano T, Otsuki M, Sasa S. Criticality and scaling relations in a sheared granular material. J Phys Soc Jpn. (2007) 76:023001. doi: 10.1143/JPSJ.76.023001

CrossRef Full Text | Google Scholar

6. Hatano T. Scaling properties of granular rheology near the jamming transition. J Phys Soc Jpn. (2008) 77:123002. doi: 10.1143/JPSJ.77.123002

CrossRef Full Text | Google Scholar

7. Otsuki M, Hayakawa H. Critical behaviors of sheared frictionless granular materials near the jamming transition Phys Rev E. (2009) 80:011308. doi: 10.1103/PhysRevE.80.011308

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Otsuki M, Hayakawa H. Universal scaling for the jamming transition. Prog Theor Phys. (2009) 121:647–55. doi: 10.1143/PTP.121.647

CrossRef Full Text | Google Scholar

9. Hatano T. Critical scaling of granular rheology. Prog Theor Phys Suppl. (2010) 184:143–52. doi: 10.1143/PTPS.184.143

CrossRef Full Text | Google Scholar

10. Nordstrom KN, Verneuil E, Arratia PE, Basu A, Zhang Z, Yodh AG, et al. Microfluidic rheology of soft colloids above and below jamming. Phys Rev Lett. (2010) 105:175701. doi: 10.1103/PhysRevLett.105.175701

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Olsson P, Teitel S. Herschel-Bulkley shearing rheology near the athermal jamming transition. Phys Rev Lett. (2012) 109:108001. doi: 10.1103/PhysRevLett.109.108001

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Andreotti B, Barrat JL, Heussinger C. Shear flow of non-brownian suspensions close to jamming. Phys Rev Lett. (2012) 109:105901. doi: 10.1103/PhysRevLett.109.105901

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Vågberg D, Olsson P, Teitel S. Dissipation and rheology of sheared soft-core frictionless disks below jamming. Phys Rev Lett. (2014) 112:208303. doi: 10.1103/PhysRevLett.112.208303

CrossRef Full Text | Google Scholar

14. Ikeda A, Berthier L, Sollich P. Unified study of glass and jamming rheology in soft particle systems. Phys Rev Lett. (2012) 109:018301. doi: 10.1103/PhysRevLett.109.018301

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Kawasaki T, Coslovich D, Ikeda A, Berthier L. Diverging viscosity and soft granular rheology in non-Brownian suspensions. Phys Rev E. (2015) 91:012203. doi: 10.1103/PhysRevE.91.012203

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Kawasaki T, Ikeda A, Berthier L. Thinning or thickening? Multiple rheological regimes in dense suspensions of soft particles Eur Phys Lett. (2014) 107:28009.

Google Scholar

17. Kawasaki T, Berthier L. Discontinuous shear thickening in Brownian suspensions. Phys Rev E. (2018) 98:012609. doi: 10.1103/PhysRevE.98.01260

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Reichhardt C, Reichhardt CJO. Aspects of jamming in two-dimensional athermal frictionless systems. Soft Matter. (2014) 10:2932. doi: 10.1039/C3SM53154F

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Bonn D, Denn MM, Berthier L, Divoux T, Manneville S. Yield stress materials in soft condensed matter. Rev Mod Phys. (2017) 89:035005. doi: 10.1103/RevModPhys.89.035005

CrossRef Full Text | Google Scholar

20. Ono IK, Tewari S, Langer SA, Liu AJ. Velocity fluctuations in a steadily sheared model foam. Phys Rev E Stat Nonlin Soft Matter Phys. (2003) 67:061503. doi: 10.1103/PhysRevE.67.061503

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Ono IK, O'Hern CS, Durian DJ, Langer SA, Liu AJ, Nagel SR. Effective temperatures of a driven system near jamming. Phys Rev Lett. (2002) 89:095703. doi: 10.1103/PhysRevLett.89.095703

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Hatano T. Rheology and dynamical heterogeneity in frictionless beads at jamming density. J Phys. (2011) 319:012011. doi: 10.1088/1742-6596/319/1/012011

CrossRef Full Text | Google Scholar

23. Lemaître A, Caroli C. Plastic response of a two-dimensional amorphous solid to quasistatic shear: transverse particle diffusion and phenomenology of dissipative events. Phys Rev E. (2007) 76:036104. doi: 10.1103/PhysRevE.76.036104

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Lemaître A, Caroli C. Rate-dependent avalanche size in athermally sheared amorphous solids. Phys Rev Lett. (2009) 103:065501. doi: 10.1103/PhysRevLett.103.065501

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Chattoraj J, Caroli C, Lemaître A. Robustness of avalanche dynamics in sheared amorphous solids as probed by transverse diffusion. Phys Rev E. (2011) 84:011501. doi: 10.1103/PhysRevE.84.011501

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Olsson P. Diffusion and velocity autocorrelation at the jamming transition. Phys Rev E. (2010) 81:040301. doi: 10.1103/PhysRevE.81.040301

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Heussinger C, Berthier L, Barrat JL. Superdiffusive, heterogeneous, and collective particle motion near the fluid-solid transition in athermal disordered materials. EPL. (2010) 90:20005. doi: 10.1209/0295-5075/90/20005

CrossRef Full Text | Google Scholar

28. Kharel P, Rognon P. Vortices enhance diffusion in dense granular flows. Phys Rev Lett. (2017) 119:178001. doi: 10.1103/PhysRevLett.119.178001

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Heussinger C, Barrat JL. Jamming transition as probed by quasistatic shear flow, Phys Rev Lett. (2009) 102:218303. doi: 10.1103/PhysRevLett.102.218303

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Drocco JA, Hastings MB, Reichhardt CJO, Reichhardt C. Multiscaling at point J : jamming is a critical phenomenon. Phys Rev Lett. (2005) 95:088001. doi: 10.1103/PhysRevLett.95.088001

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Düring G, Lerner E, Wyart M. Length scales and self-organization in dense suspension flows. Phys Rev E. (2014) 89:022305. doi: 10.1103/PhysRevE.89.022305

PubMed Abstract | CrossRef Full Text | Google Scholar

32. O'Hern CS, Silbert LE, Liu AJ, Nagel SR. Jamming at zero temperature and zero applied stress: the epitome of disorder. Phys Rev E. (2003) 68:011306. doi: 10.1103/PhysRevE.68.011306

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Lees AW, Edwards SF. The computer study of transport processes under extreme conditions. J Phys C. (1972) 5:1921.

Google Scholar

34. Saitoh K, Mizuno H. Anomalous energy cascades in dense granular materials yielding under simple shear deformations. Soft Matter. (2016) 12:1360. doi: 10.1039/C5SM02760H

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Mandal S, Chikkadi V, Nienhuis B, Raabe D, Schall P, Varnik F. Single-particle fluctuations and directional correlations in driven hard-sphere glasses. Phys Rev E. (2013) 88:022129. doi: 10.1103/PhysRevE.88.022129

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Yamamoto R, Onuki A. Dynamics of highly supercooled liquids: heterogeneity, rheology, and diffusion. Phys Rev E. (1998) 58:3515. doi: 10.1103/PhysRevE.58.3515

CrossRef Full Text | Google Scholar

37. Tsamados M. Plasticity and dynamical heterogeneity in driven glassy materials. Eur Phys J E. (2010) 32:165–81. doi: 10.1140/epje/i2010-10609-0

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Maloney CE. Correlations in the elastic response of dense random packings. Phys Rev Lett. (2006) 97:035503. doi: 10.1103/PhysRevLett.97.035503

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Olsson P. Dimensionality and viscosity exponent in shear-driven jamming. Phys Rev Lett. (2019) 122:108003. doi: 10.1103/PhysRevLett.122.108003

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Patashinski AZ, Ratner MA, Orlik R, Mitus AC. Nanofluidic manifestations of structure in liquids: a toy model. J Phys Chem C. (2019) 123:16787–95. doi: 10.1021/acs.jpcc.9b03697

CrossRef Full Text | Google Scholar