Swimming of Motile Gyrotactic Microorganisms and Nanoparticles in Blood Flow Through Anisotropically Tapered Arteries

In the present article, we have presented a theoretical study on the swimming of migratory gyrotactic microorganisms in a non-Newtonian blood-based nanofluid via an anisotropically narrowing artery. Sutterby fluid model is used in order to understand the rheology of the blood as a non-Newtonian fluid model. This fluid pattern has the ability to show Newtonian and non-Newtonian features. The mathematical formulation is performed via continuity, temperature, motile microorganism, momentum, and concentration equation. The series solutions are obtained using the perturbation scheme up to the third-order approximation. The resulting solutions are discussed with the help of graphs for all the leading parameters. The graphical results are also presented for non-tapered, diverging, and converging artery. We further discuss the velocity, temperature, swimming microorganism and temperature distribution. Moreover, the variation of impedance and the impact of wall shear stress are discussed and presented through the graphs.

Introduction

Throughout the previous decade, nanofluids have gained essential importance due to their extensive fields of applications especially in the biomedical sciences. Different theoretical and experimental studies have been presented based on the formulation of nanofluids [1–4]. Nanofluids are beneficial in improving the thermo-physical features i.e., thermal diffusivity, convection, and conductivity of the governing fluid. In biomedical science, nanofluids are helpful for the bacteriostatic activity, nano-drug delivery, labeling of cancerous tissues, magnetic resonance imaging (MRI), localized therapy, cancer therapeutics, production of ferrofluids and magnetic resonance imaging, etc. Further, they are also beneficial in nano-cryosurgery. Ferrofluids can be utilized as contrast agents for MRI and are helpful in cancer detection. In this case, the ferrofluids are made up of iron oxide nanoparticles and are recognized as superparamagnetic iron oxide nanoparticles (SPIONs). Recently, the localized delivery of cancer medicine to the cancer patient at the affected part. With the help of the heat transfer process, it can also be used for detergency. Because of these significant applications, different authors examined the behavior of nanofluids in different situations. Bég and Tripathi [5] presented a Mathematica simulation of the bioengineering model with the help of peristaltic configuration and nanofluids. Tripathi and Bég [6] analyzed the drug delivery systems using a peristaltic flow of nanofluids and presented the exact mathematical solutions. Kothandapani and Prakash [7] explored the behavior of a heat source on an MHD non-Newtonian hyperbolic tangent nanofluid model in an asymmetric tapered conduit. El-Dabe et al. [8] discussed the influence of slip in mild stenosis tapered artery using peristaltic simulation. Akbar [9] addressed the blood flow with thermal conductivity in a non-tapered stenosis artery filled with blood. She further discussed the shape properties of the nanoparticles. Abbas et al. [10] presented a blood flow model using nanofluids and explained the applications of drug delivery and magnetic field phenomena. Akbar [11] studied the metal-based nanomaterials suspended in the blood propagating via a tapered stenotic artery and explained the applications of Nanomedicines. Bhatti et al. [12] discussed the heat transfer properties and the applications of the blood clot model with variable viscosity. They considered the two-phase model with peristalsis. Bhatti et al. [13] also discussed the behavior of titanium magneto-nanoparticles suspended in Sisko fluid. Some more essential studies on the blood flow and nanofluids can be found from Shit et al. [14], Riaz et al. [15], Ijaz and Nadeem [16], and Abdelsalam and Bhatti [17] and in the references therein.

The macroscopic movement of the fluid as a result of the spatial variation of density over an area causes additive mobility in the swimming microorganisms known as bioconvection. The self-driven motile microorganisms tend to improve the base fluid in a particular direction producing a bio-convective stream. The moving microorganisms are divided into various types i.e., chemotaxis or oxytactic, gyrotactic microorganisms, and negative gravitaxis. The nanoparticles are not self-driven as compared with motile microorganisms, and their motion is due to the impact of the Brownian motion and the thermophoresis effect. Bioconvection in the nanofluids is anticipated to be feasible if the concentration of nanoparticles is small and as a result it won't be able to produce an essential enhancement in the base fluid viscosity. Bioconvection in the presence of nanoparticles was initially considered in Kuznetsov and Avramenko [18, 19]. Later, Kuznetsov [20] presented the suspension of nanoparticles with gyrotactic microorganisms using the Buongiorno's theory. Bég et al. [21] investigated the bioconvection flow with nanofluids through a porous medium numerically. Akbar [22] considered the bioconvection flow through a symmetric channel filled with nanoparticles and presented a bio nano-engineering model. Bhatti et al. [23] also inspected the behavior of a varying magnetic field and clot blood model using Jeffrey fluid model with nanoparticles and microorganisms. Ahmed et al. [24] considered the magnetized laminar flow of nanofluid and gyrotactic microorganisms through a non-Darcy porous medium. Chakraborty et al. [25] researched the extrinsic magnetic influence and bioconvection flow with nanoparticles with convective boundary conditions. Few important studies on the motile gyrotactic microorganisms and nanofluids can be found in Shahid et al. [26], Waqas et al. [27], Waqas et al. [28], and Sohail et al. [29].

From the above survey, it is observed that blood flow in the presence of nanoparticles has been discussed, but no attention has been devoted to discussing the simulation of motile gyrotactic microorganisms and nanoparticles suspended in the blood propagating through an anisotropically tapered artery. In most of the aforementioned studies, work has been done with nanoparticles propagating through tapered artery, however, no one considered the presence of gyrotactic microorganism in blood. Mathematical modeling has been performed on the basis of temperature, momentum, concentration and motile microorganism equations followed by an approximation in wavelength being long with and inertia-free flow. The Homotopy perturbation scheme is employed to obtain the series results. The governing equations are nonlinear and coupled and the exact solutions are not possible, whereas some other numerical/analytical methods [30–32] are beneficial to solve these kinds of problems. All the outcomes are presented graphically and plotted against the leading parameters. The behavior of temperature, velocity, concentration, and motile microorganism profile have been considered. Furthermore, wall shear and variation of impedance are also investigated and presented graphically. According to the results, it is found that the flow behavior through converging, diverging and non-tapered arteries are uniform throughout the whole channel.

Mathematical Modeling

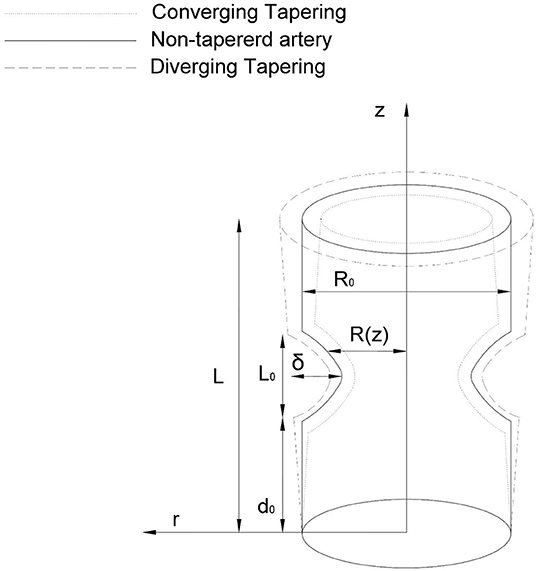
We consider a tube having finite length “L” filled with nanofluids and motile gyrotactic microorganisms. We present here the theoretical model of the swimming of nanoparticles with motile gyrotactic microorganisms in non-Newtonian blood flow propagating in an anisotropically tapered artery. A Sutterby fluid model is used to represent the rheology of the blood. The governing fluid is incompressible and having constant density. Let (r, θ, z) be the cylinderical polar coordinates while z lies along the axis, whereas r, θ are considered along the radial and circumferential direction (see Figure 1). We consider the temperature and concentration at the wall of the tube as T₁ and C₁, respectively. The anisotropically tapered stenosed artery with time-variant stenosis is geometrically defined as

FIGURE 1

Figure 1. Flow structure.

$\begin{array}{ll}\frac{R(z)}{R_0}=\{\begin{array}{c}\tau (t)[\xi z+R_0-\frac{\delta \text{ cos }\Psi }{L_0}(11-\frac{94}{3L_0}(z-d)\hfill \\ +\frac{32}{L_0^2}{(z-d)}^2-\frac{32}{L_0^3}{(z-d)}^3\left)\right];d\le z\le \frac{3}{2}{L}_0,\hfill \\ \tau (t)(1+\xi z);otherwise\hfill \end{array}\hfill & (1)\end{array}$

where R(z) denotes the tapered arterial segment and the artery radius with composite stenosis, t the time, L₀ the stenosis length, δ is the stenosis height, R₀ is the normal artery radius in the non-stenotic zone, Ψ is the tapering angle, and ξ = tanΨ shows the slope of the tapered vessel i.e.,

$\begin{array}{ll}\Psi =\{\begin{array}{c}<0,\text{converging artery}\hfill \\ =0,\text{non-tapered artery}\hfill \\ >0,\text{diverging artery}\hfill \end{array}\hfill & (2)\end{array}$

The time-variant, τ(t), is defined as

$\begin{array}{ll}\tau (t)=1+\frac{\alpha (1-\text{ cos }\omega t)}{e^{\alpha \omega t}},& (3)\end{array}$

where α is constant and ω is the radial frequency of the forced oscillation.

The equations governing the flow model can then be written as

$\begin{array}{ll}\nabla ·\tilde{\text{V}}=0,& (4)\end{array}$

$\begin{array}{l}{\rho }_f\left(\frac{\partial \tilde{\text{V}}}{\partial t}+\tilde{\text{V}}·\nabla \tilde{\text{V}}\right)=-\nabla ·p+{\nabla }^2·\tilde{\text{V}}\\ +[{\rho }_f{T}_e(1-C_1)(T-T_1)\\ -\left({\rho }_p-{\rho }_f\right)T_e(C-C_1)\\ -(n-n_1)\Theta \left({\rho }_m-{\rho }_f\right)]\text{g},& (5)\end{array}$

where $\tilde{\text{V}}=\left[U,V\right]$ are the components of velocity, T is the nanofluid temperature, T₁ is the reference temperature, p is the pressure, Θ is the average volume of a microorganism, n is the concentration of microorganisms, ρ_f is the density basefluid at the reference temperature, ρ_p is the nanoparticles' density, ρ_m is the density of microorganisms, g is the gravity vector, T_e is the base fluid volumetric coefficient of thermal expansion, and μ the viscosity of the suspension (the suspension contains the nanoparticles, microorganisms, and base fluid).

The temperature equation reads as

$\begin{array}{l}{(\rho c)}_f\left(\frac{\partial T}{\partial t}+\tilde{\text{V}}·\nabla T\right)=\nabla ·(k_f\nabla T)\\ +{(\rho c)}_p\left[D_B\nabla C·\nabla T+\frac{D_T}{T_1}\nabla T·\nabla T\right],& (6)\end{array}$

where D_T and D_B, k_f, (ρc)_f and (ρc)_p are the thermophoretic diffusion and Brownian coefficient, thermal conductivity, volumetric heat capacities for the nanofluid and nanoparticles, respectively.

The concentration equation with no chemical reaction reads as

$\begin{array}{ll}\left(\frac{\partial C}{\partial t}+\tilde{\text{V}}·\nabla C\right)=D_B{\nabla }^{2}C+\frac{D_T}{T_1}\nabla T·\nabla T,& (7)\end{array}$

The conservation of microorganisms' reads as

$\begin{array}{ll}\left(\frac{\partial n}{\partial t}+\tilde{\text{V}}·\nabla n\right)+\frac{b{W}_c}{C_0-C_1}\nabla (n·\nabla C)=-D_{\text{mo}}{\nabla }^{2}n,& (8)\end{array}$

where b is the chemotaxis constant, W_c is the maximum cell swimming speed, and D_mo is the diffusivity of microorganisms.

The stress tensor for Sutterby fluid reads as

$\begin{array}{ll}\text{S}=\frac{\mu }{2}{\left[\frac{{\text{sinh}}^{-1}B\varsigma }{B\varsigma }\right]}^m{\text{A}}_1.& (9)\end{array}$

where A, B are material constants and

$\begin{array}{ll}\varsigma =\sqrt{\frac{\text{trac}{\text{A}}_1^2}{2}},& (10)\end{array}$

A₁=grad V + (grad V)^T.

The boundary conditions are given by

$\begin{array}{l}\frac{\partial u}{\partial r}=\frac{\partial T}{\partial r}=\frac{\partial C}{\partial r}=\frac{\partial n}{\partial r}=0,\text{at }r=0\\ u=0,T=T_1,C=C_1,n=n_1,\text{at }r=R(z)& (11)\end{array}$

The non-dimensional quantities are defined as

$\begin{array}{l}\widehat{r}=\frac{r}{R_0},ẑ=\frac{z}{R_0},\widehat{v}=\frac{L_0}{U_a\delta }v,\widehat{R}=\frac{R}{R_0},\widehat{p}=\frac{R_0^2}{U_a{L}_0\mu }p,T\\ =(1-\theta )T_1+T_0,\\ C=(1-\varphi )C_1+C_0,n=(1-\chi )n_1+n_0,\widehat{\delta }=\frac{\delta }{R_0},\widehat{L}\\ =\frac{L}{L_0},\widehat{\xi }=\frac{L_0\xi }{R_0}.& (12)\end{array}$

where U_a is the averaged velocity over a section of the whole tube.

Substituting with Equation (12) into the governing mathematical model assuming the case of mild stenosis and creeping flow yields (after dropping the hat)

$\begin{array}{ll}\frac{\partial p}{\partial r}=0,& (13)\end{array}$

$\begin{array}{ll}\frac{\partial p}{\partial z}=\frac{1}{r}\frac{\partial }{\partial r}\left[r{\text{S}}_{rz}\right]+T_g\theta +N_g\varphi -R_b\chi ,& (14)\end{array}$

$\begin{array}{ll}\frac{1}{r}\frac{\partial }{\partial r}\left(\frac{\partial \theta }{\partial r}r\right)+\frac{\partial \theta }{\partial r}\left[T_b\frac{\partial \Phi }{\partial r}+T_t\left(\frac{\partial \theta }{\partial r}\right)\right]=0,& (15)\end{array}$

$\begin{array}{ll}\frac{1}{r}\frac{\partial }{\partial r}\left(\frac{\partial \varphi }{\partial r}r\right)+\frac{T_t}{T_b}\frac{1}{r}\frac{\partial }{\partial r}\left(\frac{\partial \theta }{\partial r}r\right)=0,& (16)\end{array}$

$\begin{array}{ll}\frac{1}{r}\frac{\partial }{\partial r}\left(\frac{\partial \chi }{\partial r}r\right)=P_l\left[\frac{\partial \chi }{\partial r}\frac{\partial \varphi }{\partial r}+(\bar{\Theta }+\chi )\frac{{\partial }^2\varphi }{\partial r^2}\right],& (17)\end{array}$

and

$\begin{array}{ll}{\text{S}}_{rz}=\left[1-\beta {\left(\frac{\partial u}{\partial r}\right)}^2\right]\left(\frac{\partial u}{\partial r}\right),& (18)\end{array}$

whereas for Newtonian fluid the results can be achieved by taking β = 0.

The parameters used above are defined as

$\begin{array}{l}\beta =\frac{m{B}^2{U}_a^2}{6R_0^2},T_b=\frac{D_B(C_0-C_1){(\rho c)}_p}{k_f{(\rho c)}_f},\\ T_t=\frac{D_B(T_0-T_1){(\rho c)}_p}{k_f{T}_1{(\rho c)}_f},\\ N_g=-\frac{T_{e}g({\rho }_p-{\rho }_f)R_0^2(T_0-T_1)}{\mu U_a},\\ P_l=\frac{b{W}_c}{D_{\text{mo}}},\bar{\Theta }=\frac{n_1}{n_0-n_1},\\ T_g=\frac{T_{e}g{\rho }_f{R}_0^2(1-C_1)(T_0-T_1)}{\mu U_a},\\ R_b=\frac{(n-n_1)\Theta ({\rho }_m-{\rho }_f)g{R}_0^2}{\mu U_a}.& (19)\end{array}$

In the above equation, T_g is the local temperature Grashof number, N_g is the local particle Grashof number, R_b is the bioconvection Rayleigh number, T_b is the Brownian motion parameter, T_t is the thermophoresis parameter, P_l is the Peclet number, $\bar{\Theta }$ is a constant, and β is the fluid parameter.

The boundary conditions read.

$\begin{array}{l}{u}^{\prime }=0,{\theta }^{\prime }=0,{\varphi }^{\prime }=0,{\chi }^{\prime }=0,\text{ at }r=0,\\ u=0,\theta =0,\varphi =0,\chi =0,\text{ at }r=R.& (20)\end{array}$

Series Solutions

The solutions of Equations (13) to (17) can be obtained using a Homotopy perturbation method. And thus, the Homotopy P_s for Equations (13) to (17) are defined as

$\begin{array}{l}{P}_s(ū,\zeta )=(1-\zeta )\left[\ell (ū)-\ell ({ū}_0)\right]\\ +\zeta [\ell (ū)-3\beta \frac{{\partial }^2ū}{\partial r^2}{\left(\frac{\partial ū}{\partial r}\right)}^2-\frac{\beta }{r}{\left(\frac{\partial ū}{\partial r}\right)}^3\\ +T_g\bar{\theta }+N_g\bar{\varphi }-R_b\bar{\chi }-\frac{\partial p}{\partial z}],& (21)\end{array}$

$\begin{array}{l}{P}_s\left(\bar{\theta },\zeta \right)=(1-\zeta )\left[\ell \left(\bar{\theta }\right)-\ell \left({\bar{\theta }}_0\right)\right]\\ +\zeta \left[\ell \left(\bar{\theta }\right)+T_b\frac{\partial \bar{\varphi }}{\partial r}\frac{\partial \bar{\theta }}{\partial r}+T_t{\left(\frac{\partial \bar{\theta }}{\partial r}\right)}^2\right],& (22)\end{array}$

$\begin{array}{l}{P}_s\left(\bar{\varphi },\zeta \right)=(1-\zeta )\left[\ell \left(\bar{\varphi }\right)-\ell \left({\bar{\varphi }}_0\right)\right]\\ +\zeta \left[\ell \left(\bar{\varphi }\right)+\frac{T_t}{T_b}\frac{1}{r}\frac{\partial }{\partial r}\left(\frac{\partial \bar{\theta }}{\partial r}r\right)\right],& (23)\end{array}$

$\begin{array}{l}{P}_s(\bar{\chi },\zeta )=(\zeta -1)\left[\ell ({\bar{\chi }}_0)-\ell (\bar{\chi })\right]\\ +\zeta \left[\ell (\bar{\chi })-P_l\frac{\partial }{\partial r}\left(\left(\bar{\chi }+\bar{\Theta }\right)\frac{\partial \bar{\varphi }}{\partial r}\right)\right],& (24)\end{array}$

where ζ ∈ [0, 1]the embedding parameter.

The linear operator reads as

$\begin{array}{ll}\ell =\frac{{\partial }^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r},& (25)\end{array}$

and the initial guesses read as

$\begin{array}{ll}{\bar{w}}_0={\bar{\theta }}_0={\bar{\varphi }}_0={\bar{\chi }}_0=\frac{r^2-R^2}{c^2},& (26)\end{array}$

where c(≠0) is a constant.

The above initial guess is chosen in such a way that the following initial guess satisfied the linear operator as given in Equation (25) as well as satisfy all the governing boundary conditions as given in Equation (20).

Defining the following expansions

$\begin{array}{ll}\bar{u}={\bar{u}}_0+\zeta {\bar{u}}_1+{\zeta }^2{\bar{u}}_2+\dots ,& (27)\end{array}$

$\begin{array}{ll}\bar{\theta }={\bar{\theta }}_0+\zeta {\bar{\theta }}_1+{\zeta }^2{\bar{\theta }}_2+\dots .,& (28)\end{array}$

$\begin{array}{ll}\bar{\varphi }={\bar{\varphi }}_0+\zeta {\bar{\varphi }}_1+{\zeta }^2{\bar{\varphi }}_2+\dots .,& (29)\end{array}$

$\begin{array}{ll}\bar{\chi }={\bar{\chi }}_0+\zeta {\bar{\chi }}_1+{\zeta }^2{\bar{\chi }}_2+\dots .,& (30)\end{array}$

Using the series expansions in Equations (27–30) in the Homotopy equations [see Equations (21) to (24)], we get the set of linear differential equations, after comparing the powers of ζ. By applying the property of Homotopy perturbation method, i.e., ζ → 1, we get

$\begin{array}{ll}u=\bar{u}={\bar{u}}_0+{\bar{u}}_1+{\bar{u}}_2+\dots ,& (31)\end{array}$

$\begin{array}{ll}\theta =\bar{\theta }={\bar{\theta }}_0+{\bar{\theta }}_1+{\bar{\theta }}_2+\dots .,& (32)\end{array}$

$\begin{array}{ll}\varphi =\bar{\varphi }={\bar{\varphi }}_0+{\bar{\varphi }}_1+{\bar{\varphi }}_2+\dots .,& (33)\end{array}$

$\begin{array}{ll}\chi =\bar{\chi }={\bar{\chi }}_0+{\bar{\chi }}_1+{\bar{\chi }}_2+\dots .,& (34)\end{array}$

The final results for all the governing equations are obtained as

$\begin{array}{ll}u(r)=u_0+r^2{u}_1+r^4{u}_2+r^5{u}_3+r^6{u}_4+\cdots ,& (35)\end{array}$

$\begin{array}{ll}\theta (r)={\theta }_0+r^3{\theta }_1+r^4{\theta }_2+r^5{\theta }_3+r^6{\theta }_4+\cdots ,& (36)\end{array}$

$\begin{array}{ll}\varphi (r)={\varphi }_0+r^3{\varphi }_1+r^4{\varphi }_2+\cdots ,& (37)\end{array}$

$\begin{array}{ll}\chi (r)={\chi }_0+r^2{\chi }_1+r^4{\chi }_2+r^6{\chi }_4+\cdots .& (38)\end{array}$

where u_n, θ_n, ϕ_n, χ_n, with n = 1, 2, 3… are the constants which can be found using the calculations through a computational software Mathematica 10.3v.

The flux Q can be determined as

$\begin{array}{ll}Q={\displaystyle \underset{0}{\stackrel{R}{\int }}}2ru\left(r,z\right)\text{d}r.& (39)\end{array}$

$\begin{array}{ll}Q=\frac{\wp }{f(z)},& (40)\end{array}$

where $\wp =-\frac{dp}{dz}.$

The impedance can be determined as

$\begin{array}{ll}\lambda =\frac{1}{Q}{\displaystyle \underset{0}{\int }\wp dz},& (41)\end{array}$

The wall shear stress is calculated as.

$\begin{array}{ll}{\text{S}}_{rz}={\frac{1}{2}\wp R|}_{r=R}.& (42)\end{array}$

Discussion

We have discussed the graphical behavior of all the leading parameters for the temperature, velocity, motile microorganism and concentration profiles. The effects of wall shear stress and the variation of impedance are also investigated to see the behavior of blood during the swimming of microorganisms and the movement of nanoparticles. With the aid of said perturbation scheme, we obtained the third order approximation against each profile. All the numerical computations have been performed using computational software Mathematica. Figures 2–7 are plotted for different profiles with all the emerging parameters i.e., Peclet number P_l, height of stenosis δ, angular frequency ω, fluid parameter β, local temperature Grashof number T_g, local particle Grashof number N_g, bioconvection Rayleigh number R_b, thermophoresis parameter T_t, and Brownian motion T_b. All three cases i.e., diverging, converging, and non-tapered artery, have been plotted with the help of Equation (2).

FIGURE 2

Figure 2. Velocity curves for multiple values of (A) β, (B) T_t, (C) T_b.

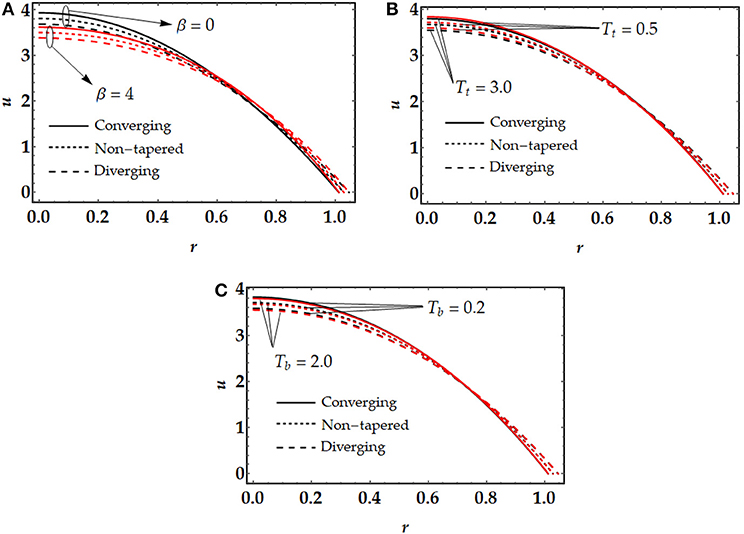
Figure 2 presents the behavior of the velocity profile against the fluid parameter β, thermophoresis parameter T_t, and Brownian motion parameter T_b. In order to understand the behavior of hemodynamics in a specific artery or lesion, it is necessary to have a knowledge of blood velocity within the flow pattern. The hemodynamic velocity in the artery is not the same at all the points [33]. We can see from Figure 2A that the distribution of velocity at the center of the channel is maximum while it attains a minimum value when it gets close to the wall. Further, we can notice that in the case of non-Newtonian fluid, β = 4, the velocity of the blood diminishes. However, we can see a turning point between r ∈ (0.6, 0.8) the artery where the velocity turns opposite as compared with the core of the channel and decreases as it gets closer to the wall of the artery. The significant change in the velocity gradient among different points in the artery exists because of the friction forces that play an essential role among the fluid at the walls and the flowing fluid. The friction forces occur because of the viscosity features. The viscosity represents the resistance to the flow, and it attains a minimum value if the trivial force on the fluid layer generates a velocity higher than that layer associated with the adjoining layer, and the converse is true [34, 35]. Figure 2B shows the behavior of the thermophoresis parameter T_t on the velocity profile. It is noticed from this figure that by enhancing the thermophoresis parameter, the nanoparticles start moving quickly and tends to repel from the hotter to a colder area. But it doesn't affect the velocity of the fluid. However, it causes resistance in the velocity of the fluid. Brownian motion plays a simultaneous role with thermophoresis. However, both parameters similarly affect the velocity profile (see Figure 2C). Brownian motion occurs due to the collision of suspended particles in random direction in the working fluid. Higher values of Brownian motion reveals that the particles collide very quickly which causes the resistance in the motion of the base fluid.

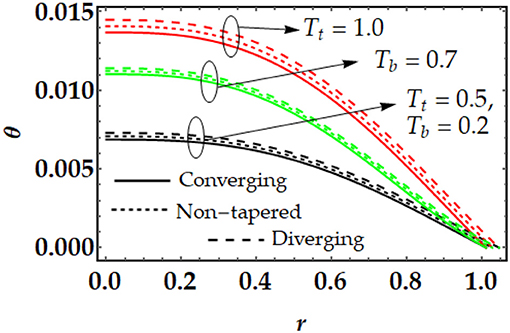
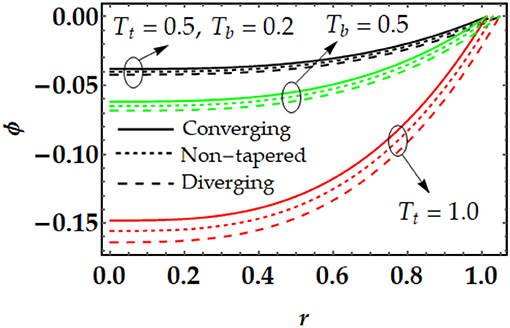
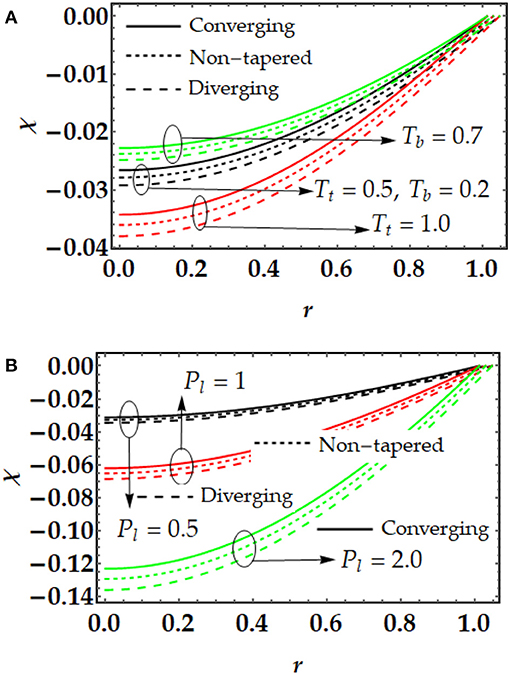
Figures 3, 4 are plotted for temperature and concentration distributions for multiple values of T_t and T_b. In Figure 3, we can see that the temperature profile rises with the increment in T_t and T_b. The enhancement of both parameters tends to repel the particles quickly. Therefore, the particles start moving from one region to the other area (i.e., hotter to colder part). Both parameters produce a force i.e., thermophoretic force and random movement of suspended particles which resist the fluid motion and as result the temperature profile increases. Figure 4 shows that the concentration profile that is shown to be inversely proportional to the temperature profile. By increasing both parameters, the concentration profile tends to diminish remarkably. Figure 5 is plotted to judge the variation of motile microorganisms with P_l, T_t, and T_b. It can be noticed from Figure 5A that the motile microorganisms 'distribution rises due to the strong influence of the Brownian motion parameter. However, a converse behavior has been observed for the thermophoresis parameter. In Figure 5B, we can see that the Peclet number produces resistance in the motile microorganism profile. By increasing Peclet number, it is noticed that advection propagation transport in more dominant as compared with diffusion propagation rate, which suppress the motile microorganism profile.

FIGURE 3

Figure 3. Temperature curves for multiple values of T_b, T_t.

FIGURE 4

Figure 4. Concentration curves for multiple values of T_b, T_t.

FIGURE 5

Figure 5. Motile microorganism curves for multiple values of (A) T_t and T_b, (B) P_l.

Figure 6 shows that the behavior of wall shear stress, that has been plotted using Equation (42), with δ, ω, T_g, N_g, R_b, T_t, and T_b. The wall shear stress is an essential part of the blood flow, and it can be described as the fluid flowing over the surface of the conduit artery. From Equation (42) we can see that wall shear stress is directly proportional to the velocity gradient close to the wall of the artery. That shows how quickly the velocity of the fluid is when propagating from one point on the artery wall to another point adjacent to the point in the perpendicular direction of the wall. However, low wall shear stress belongs to low velocities, accordingly, the higher residence time of the fluid closer to the wall. And as a result, this velocity gradient close to the wall is known as the wall shear rate. We can see from Figure 6A that wall shear stress is reduced due to the strong influence of the thermophoresis parameter, however, an inverse behavior has been noticed with a variation of T_b. In Figure 6B, we can see that local temperature Grashof number and local particle Grashof number suppress the wall shear stress remarkably. However, we noticed that the height of the clot enhances the wall shear stress, whereas the angular frequency tends to diminish the wall shear stress as shown in Figure 6C. In Figure 6D, we found that bioconvection Rayleigh number doesn't affect the wall shear stress significantly and the effect is minimal.

FIGURE 6

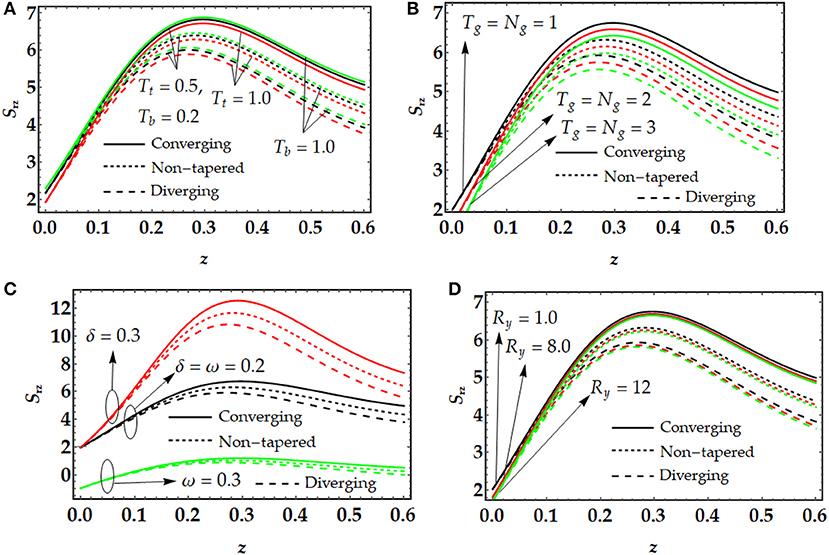
Figure 6. Wall shear stress for multiple values of (A) T_t and T_b, (B) T_g and N_g, (C) δ and ω, (D) R_y.

Figure 7 is schemed to judge the variation of impedance distribution for multiple values of β, R_b, T_t, and T_b. Figure 7A is sketched for impedance vs. height of the clot for various values of the fluid parameter. We can see from this figure that impedance profile rises with an increase in the height of the clot, whereas it decreases simultaneously due to an enhancement in the fluid parameter. In Figure 7B, the effect of bioconvection Rayleigh number is shown incrementally decreasing. Further, it is noticed that an increase in the angular frequency ω implies to a decrease in the impedance profile. Also, it is seen in the whole domain that the thermophoresis parameter tends to suppress the impedance profile, as shown in Figure 7C. In Figure 7D, the impedance profile rises due to the strong influence of the Brownian motion parameter. However, it is seen that the impedance profile tends to reduce with an increment in time.

FIGURE 7

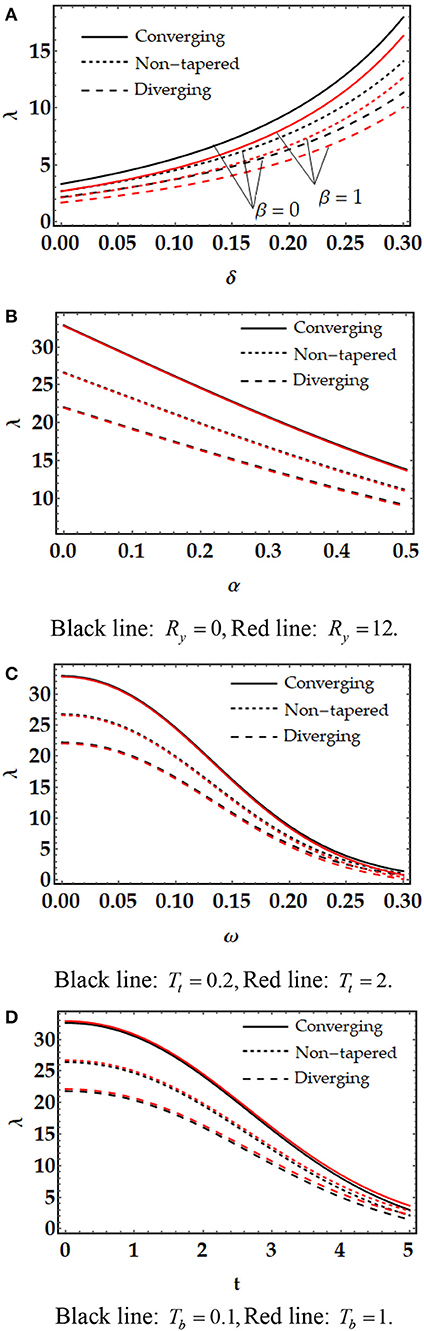
Figure 7. Impedance profile for various values of (A) β; Black line: β = 0, Red line: β = 1. (B) R_y; Black line: R_y = 0, Red line: R_y = 12. (C) T_t; Black line: T_t = 0.2, Red line: T_t = 2. (D) T_b; Black line: T_b = 0.1, Red line: T_b = 1.

Concluding Remarks

A theoretical study on the swimming of nanoparticles with motile gyrotactic microorganisms in non-Newtonian blood flow propagating in an anisotropically tapered artery has been presented. Sutterby fluid model is presented to understand the rheology of the blood. The mathematical modeling is formulated using continuity, temperature, motile microorganism, momentum and concentration equation. The Homotopy perturbation method is applied to obtain the series solutions. All the graphical results are presented for diverging, converging, and non-tapered artery. The main results from the present study has been summarized below:

i. The non-Newtonian effects tends to resist in the fluid motion.

ii. Thermophoresis and Brownian motion parameter oppose the fluid motion.

iii. Temperature profile increases as the artery changes from converging to diverging shape with an increase in the thermophoresis parameter and Brownian motion.

iv. The concentration profile tends to diminish due to the strong impact of Brownian motion and thermophoresis parameter.

v. The Peclet number significantly opposes the motile microorganism profile.

vi. Thermal Grashof number opposes the wall shear stress profile and similar behavior is observed due to an increment in nanoparticle Grashof number.

vii. The shear stress at the wall is reduced due to an increment in the height of stenosis and the bioconvection Rayleigh number.

viii. The impedance profile decreases due to with an increase in bioconvection Rayleigh number, fluid parameter, and thermophoresis parameter, whereas it increases with an increase in the Brownian motion parameter.

Author Contributions

MB and MM performed mathematical formulation, AZ and RE made the analysis and wrote the paper. SA made the geometry of problem and arranged the setting of the paper.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared a past co-authorship with the author MM.

References

1. Trisaksri V, Wongwises S. Critical review of heat transfer characteristics of nanofluids. Renew Sust Energ Rev. (2007) 11:512–23. doi: 10.1016/j.rser.2005.01.010

CrossRef Full Text | Google Scholar

2. Özerinç S, Kakaç S, Yazicioglu AG. Enhanced thermal conductivity of nanofluids: a state-of-the-art review. Microfluid Nanofluid. (2010) 8:145–70. doi: 10.1007/s10404-009-0524-4

CrossRef Full Text | Google Scholar

3. Abdelsalam SI, Bhatti MM. New insight into AuNP applications in tumour treatment and cosmetics through wavy annuli at the nanoscale. Sci Rep. (2019) 9:260. doi: 10.1038/s41598-018-36459-0

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Abdelsalam SI, Bhatti MM. The study of non-Newtonian nanofluid with hall and ion slip effects on peristaltically induced motion in a non-uniform channel. RSC Adv. (2018) 8:7904–15. doi: 10.1039/C7RA13188G

CrossRef Full Text | Google Scholar

5. Bég OA, Tripathi D. Mathematica simulation of peristaltic pumping with double-diffusive convection in nanofluids: a bio-nano-engineering model. Proc Inst Mech Eng N. (2011) 225:99–114. doi: 10.1177/1740349912437087

CrossRef Full Text | Google Scholar

6. Tripathi D, Bég OA. A study on peristaltic flow of nanofluids: application in drug delivery systems. Int J Heat Mass Transf . (2014) 70:61–70. doi: 10.1016/j.ijheatmasstransfer.2013.10.044

CrossRef Full Text | Google Scholar

7. Kothandapani M, Prakash J. Influence of heat source, thermal radiation, and inclined magnetic field on peristaltic flow of a hyperbolic tangent nanofluid in a tapered asymmetric channel. IEEE T Nanobiosci. (2014) 14:385–92. doi: 10.1109/TNB.2014.2363673

PubMed Abstract | CrossRef Full Text | Google Scholar

8. El-dabe NT, Moatimid GM, Hassan MA, Mostapha DR. Analytical solution of the peristaltic flow of a Jeffrey nanofluid in a tapered artery with mild stenosis and slip condition. Int J Innov Appl Stud. (2015) 12:1.

Google Scholar

9. Akbar NS. A new thermal conductivity model with shaped factor ferromagnetism nanoparticles study for the blood flow in non-tapered stenosed arteries. IEEE T Nanobiosci. (2015) 14:780–9. doi: 10.1109/TNB.2015.2462755

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Abbas MA, Bai YQ, Rashidi MM, Bhatti MM. Application of drug delivery in magnetohydrodynamics peristaltic blood flow of nanofluid in a non-uniform channel. J Mech Med Biol. (2016) 16:1650052. doi: 10.1142/S0219519416500524

CrossRef Full Text | Google Scholar

11. Akbar NS. Metallic nanoparticles analysis for the blood flow in tapered stenosed arteries: Application in nanomedicines. Int J Biomath. (2016) 9:1650002. doi: 10.1142/S1793524516500029

CrossRef Full Text | Google Scholar

12. Bhatti MM, Zeeshan A, Ellahi R. Heat transfer analysis on peristaltically induced motion of particle-fluid suspension with variable viscosity: clot blood model. Comput Meth Prog Bio. (2016) 137:115–24. doi: 10.1016/j.cmpb.2016.09.010

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Bhatti MM, Zeeshan A, Ellahi R. Endoscope analysis on peristaltic blood flow of Sisko fluid with Titanium magneto-nanoparticles. Comput Biol Med. (2016) 78:29–41. doi: 10.1016/j.compbiomed.2016.09.007

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Shit GC, Ranjit NK, Sinha A. Electro-magnetohydrodynamic flow of biofluid induced by peristaltic wave: a non-Newtonian model. J Bionic Eng. (2016) 13:436–48. doi: 10.1016/S1672-6529(16)60317-7

CrossRef Full Text | Google Scholar

15. Riaz A, Bhatti MM, Ellahi R, Zeeshan A, Sait SM. Mathematical analysis on an asymmetrical wavy motion of blood under the influence entropy generation with convective boundary conditions. Symmetry. (2020) 12:102. doi: 10.3390/sym12010102

CrossRef Full Text | Google Scholar

16. Ijaz S, Nadeem S. A biomedical solicitation examination of nanoparticles as drug agents to minimize the hemodynamics of a stenotic channel. Eur Phys J Plus. (2017) 132:448. doi: 10.1140/epjp/i2017-11703-6

CrossRef Full Text | Google Scholar

17. Abdelsalam SI, Bhatti MM. The impact of impinging TiO2 nanoparticles in Prandtl nanofluid along with endoscopic and variable magnetic field effects on peristaltic blood flow. Multidiscip Model Mater Struct. (2018) 14:530–48. doi: 10.1108/MMMS-08-2017-0094

CrossRef Full Text | Google Scholar

18. Kuznetsov AV, Avramenko AA. Effect of small particles on this stability of bioconvection in a suspension of gyrotactic microorganisms in a layer of finite depth. Int Commun Heat Mass. (2004) 31:1–10. doi: 10.1016/S0735-1933(03)00196-9

CrossRef Full Text | Google Scholar

19. Geng P, Kuznetsov AV. Settling of bidispersed small solid particles in a dilute suspension containing gyrotactic microorganisms. Int J Eng Sci. (2005) 43:992–1010. doi: 10.1016/j.ijengsci.2005.03.002

CrossRef Full Text | Google Scholar

20. Kuznetsov AV. Non-oscillatory and oscillatory nanofluid bio-thermal convection in a horizontal layer of finite depth. Eur J Mech B Fluids. (2011) 30:56–165. doi: 10.1016/j.euromechflu.2010.10.007

CrossRef Full Text | Google Scholar

21. Bég OA, Prasad VR, Vasu B. Numerical study of mixed bioconvection in porous media saturated with nanofluid containing oxytactic microorganisms. J Mech Med Biol. (2013) 13:1350067. doi: 10.1142/S021951941350067X

CrossRef Full Text | Google Scholar

22. Akbar NS. Bioconvection peristaltic flow in an asymmetric channel filled by nanofluid containing gyrotactic microorganism: bio nano engineering model. Int J Num Method H. (2015) 25:214–24. doi: 10.1108/HFF-07-2013-0242

CrossRef Full Text | Google Scholar

23. Bhatti MM, Zeeshan A, Ellahi R. Simultaneous effects of coagulation and variable magnetic field on peristaltically induced motion of Jeffrey nanofluid containing gyrotactic microorganism. Microvasc Res. (2017) 110:32–42. doi: 10.1016/j.mvr.2016.11.007

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Ahmed SE, Mahdy A. Laminar MHD natural convection of nanofluid containing gyrotactic microorganisms over vertical wavy surface saturated non-Darcian porous media. Appl Math Mech. (2016) 37:471–84. doi: 10.1007/s10483-016-2044-9

CrossRef Full Text | Google Scholar

25. Chakraborty T, Das K, Kundu PK. Framing the impact of external magnetic field on bioconvection of a nanofluid flow containing gyrotactic microorganisms with convective boundary conditions. Alex Eng J. (2018) 57:61–71. doi: 10.1016/j.aej.2016.11.011

CrossRef Full Text | Google Scholar

26. Shahid A, Zhou Z, Hassan M, Bhatti MM. Computational study of magnetized blood flow in the presence of Gyrotactic microorganisms propelled through a permeable capillary in a stretching motion. Int J Multiscale Com. (2018) 16:409–26. doi: 10.1615/IntJMultCompEng.2018026030

CrossRef Full Text | Google Scholar

27. Waqas H, Khan SU, Hassan M, Bhatti MM, Imran M. Analysis on the bioconvection flow of modified second-grade nanofluid containing gyrotactic microorganisms and nanoparticles. J Mol Liq. (2019) 291:111231. doi: 10.1016/j.molliq.2019.111231

CrossRef Full Text | Google Scholar

28. Waqas H, Khan SU, Imran M, Bhatti MM. Thermally developed Falkner-Skan bioconvection flow of a magnetized nanofluid in the presence of a motile gyrotactic microorganism: Buongiorno's nanofluid model. Phys Scr. (2019) 94:115304. doi: 10.1088/1402-4896/ab2ddc

CrossRef Full Text | Google Scholar

29. Sohail M, Naz R, Abdelsalam SI. On the onset of entropy generation for a nanofluid with thermal radiation and gyrotactic microorganisms through 3D flows. Physica Scripta. (2020) 95:045206. doi: 10.1088/1402-4896/ab3c3f

CrossRef Full Text | Google Scholar

30. Bhatti MM, Khalique CM, Bég TA, Bég OA, Kadir A. Numerical study of slip and radiative effects on magnetic Fe3O4-water-based nanofluid flow from a nonlinear stretching sheet in porous media with Soret and Dufour diffusion. Mod Phys Lett B. (2020) 34:2050026. doi: 10.1142/S0217984920500268

CrossRef Full Text | Google Scholar

31. Marin M. Lagrange identity method for microstretch thermoelastic materials. J Math Anal Appl. (2010) 363:275–86. doi: 10.1016/j.jmaa.2009.08.045

CrossRef Full Text | Google Scholar

32. Marin M, Agarwal RP, Mahmoud SR. Nonsimple material problems addressed by the Lagrange's identity. Bound Value Probl. (2013) 2013:135. doi: 10.1186/1687-2770-2013-135

CrossRef Full Text | Google Scholar

33. Strackee J, Westerhof N. The Physics of Heart and Circulation. Bristol: Institute of Physics Publishing (1993).

Google Scholar

34. Rowan JO. Physics and the Circulation, Vol. 9. Bristol: Adam Hilger Ltd (1981).

Google Scholar

35. Pearson TC, Path FRC. Hemorheology in the erythrocytoses. Mt Sinai J Med. (2001) 68:182–91.

PubMed Abstract | Google Scholar