A New Computational Technique Design for EMHD Nanofluid Flow Over a Variable Thickness Surface With Variable Liquid Characteristics

The objective of this paper comprises two key aspects: to establish descriptive mathematical models for constant and variable fluid flows over a variable thickness sheet by inducting applied electric and magnetic fields, porosity, radiative heat transfer, and heat generation/absorption, and to seek their solution by constructing a novel numerical method, the Simplified Finite Difference Method (SFDM). We resort to similarity transformations to implicate partial differential equations (PDEs) into a set of ordinary differential equations (ODEs). Optimal results for a pair of ODEs obtained from SFDM are assessed by drawing a comparison with bvp4c and existing literature values. SFDM has been implemented in MATLAB for both constant and variable fluid properties. Tabulated numerical values of the skin friction coefficient and local Nusselt and Sherwood numbers are measured and analyzed against different parameters. The influence of distinct parameters on velocity, temperature, and nanoparticle volume fraction are explained in great detail via diagrams. The skin friction coefficient for variable fluid properties is greater than for constant fluid properties. However, the local Nusselt number is lower for variable fluid properties than with constant fluid properties. Surprisingly, high-precision computational results are achieved from the SFDM.

1. Introduction

Fluid mechanics has many applications in contexts from the human biological system to the manufacturing industry. For example, the study of breathing in biological systems uses bio-fluid dynamics. Cooling is another such phenomenon, which is important in electronics and the automobile industry. Investigating stretching sheet flows is relevant to many significant applications. All of this plays a vital role in technological advances such as those of polymer manufacturing and cooling processes in glass and paper production Hayat et al. [1]. Having variable thickness becomes useful in minimizing the weight of architectural elements Hayat et al. [1].

Hayat et al. [1, 2] analyzed the consequences of Cattaneo-Christov heat flux and a temperature-dependent fluid thermal conductivity on fluid flow over a variable thickness sheet and showed that variable conductivity enhances the temperature distribution. They also maintained that the temperature profile decreases with the thermal relaxation parameter. Mabood et al. [3] discussed the non-Darcian MHD convective flow and claimed that temperature rise depends on the Eckert number. In the context of a stretching sheet for variable thickness, Fang et al. [4] has tackled the boundary layer flow and analyzed multiple solutions. Khader and Ahmed [5] computed a numerical solution for variable sheet thickness with slip velocity and pointed out that the skin friction coefficient increases with the wall thickness parameter. Daniel et al. [6] discussed the thermal stratification effects on MHD radiative flow of nanofluid for a variable thickness sheet. They submitted that the thermal stratification effect reduces temperature. Reddy et al. [7] investigated the MHD flow and heat transfer of Williamson nanofluid over a variable thickness sheet with variable thermal conductivity and identified that the velocity profile decreases with the wall thickness parameter when m < 1. Daniel et al. [8] examined the effect of thermal radiation on electrical MHD flow of nanofluid over a stretching sheet with variable thickness and concluded that the thermal radiation did impact the nanofluid temperature.

Magnetohydrodynamics is the study of the flow of electrically conducting fluids in an electro-magnetic-field. The study of MHD flow is of considerable interest in modern metallurgical and metal-working processes. Noreen et al. [9] examined the numerical solutions of magnetohydrodynamic boundary layer flow of tangent hyperbolic fluid toward a stretching sheet. They showed that the skin friction coefficient increases with an increase in M. Mukhopadhyay et al. [10] conducted a study to assess the effects of fluid flow with constant and changeable viscosity on a heated surface. They noticed that a decrease in viscosity causes the velocity to decrease with increasing distance along the stretching sheet. Nadeem et al. [11] examined MHD three-dimensional Casson fluid flow through a porous linear stretching plate and concluded that the stretching parameter resulted in decreasing behavior of the velocity profile. Mabood et al. [12] investigated MHD boundary layer flow and heat transfer of nanofluid over a non-linear stretching sheet. They note that the boundary layer thickness grows with Brownian motion. Zhang et al. [13] discussed the MHD flow and radiation heat transfer of nanofluids in porous media with variable surface heat flux and chemical reaction. They examined three types of nanoparticles. Popley et al. [14] addressed the overall impact of varying liquid characteristics upon hydro-magnetic motion and heat transfer across a non-linear stretching surface. They demonstrated that the free stream velocity induces a reduction in the boundary layer thickness. Mohsen et al. [15] discussed nanofluid flow with convective heat transfer considering Lorentz forces and showed that heat transfer rises with the Hartmann number. Patel [16] studied the effects of heat generation, thermal radiation, and Hall current on MHD Casson fluid flow past an osculating plate in a porous medium. They stated that the Hall current boosts mobility in both directions. Farooq et al. [17] discussed the MHD flow of Maxwell fluid with nanomaterials due to an exponentially stretching surface. The influence of the thermophoresis parameter on the temperature distribution is negligible. Magnetohydrodynamic (MHD) boundary layer flow past a wedge with heat transfer and viscous effects of nanofluid embedded in porous media was investigated by Ibrahim and Tulu [18]. They discover that the pressure gradient influences the boundary layer thickness. The impact of 3D Maxwell nanofluid flow over an exponentially stretching surface in terms of heat and mass transfer was explored by Ali et al. [19]. They showed that the skin friction coefficient decreases with the Deborah number.

Nanofluids solid-liquid suspensions consisting of solid nanoparticles of size 1-100 nm and liquid Mabood et al. [3]. Due to reports of their having significantly enhanced thermal properties, nanofluids have drawn great interest recently Mabood et al. [3]. The term nanofluid was proposed by Choi and Eastman [20], who demonstrated that the introduction of a small number of nanoparticles (< 1 percent by volume fraction) to traditional liquids increased the fluid thermal conductivity by approximately two times Nadeem et al. [11]. The numerical simulation of nanofluid flow with convective boundary conditions was studied by Das et al. [21], who demonstrated that the surface convection parameter enhances the heat transfer rate. Mabood and Das [22], in their analysis, communicated melting heat transfer of hydromagnetic nanofluid flow with a second-order slip condition. Cao et al. [23] discussed the MHD flow and heat transfer of fractional Maxwell viscoelastic nanofluid over a moving plate by using a finite difference method and found that the average Nusselt number is higher with a rise in the fractional derivative parameter. Das et al. [24] studied the effects of a magnetic field on an unsteady mixed convection flow of nanofluids containing spherical and cylindrical nanoparticles. Narayana et al. [25] discussed the effects of thermal radiation and a heat source on an MHD nanofluid past a vertical plate in a rotating system with a porous medium. They used three different nanoparticles and showed that they enhance the heat transfer rate, a result that can be used in heat exchanger technology. The influences on stagnation-point flow toward a stretching/shrinking sheet in a nanofluid were discussed by Mansur et al. [26] using the Buongiorno model. They proved that the thermophoresis parameter reduces the heat transfer rate. Makinde [27] studied viscous dissipation and Newtonian heating over a flat plate in a nanofluid. The heat transfer rate rises with the nanoparticle volume fraction and the Biot number. Ali et al. [28] discussed a numerical study of unsteady MHD Couette flow and heat transfer of nanofluids in a rotating system with convective cooling and indicated that the rotation has a significant effect on velocity and heat transfer. Ashwinkumar and Sulochana [29] investigated the effect of radiation absorption and buoyancy force on the MHD mixed convection flow of Casson nanofluid. They noticed that the volume fraction of nanoparticles governs the temperature distribution. Under temperature control, Andersson and Aarseth [30] revisited the fluid properties of a liquid. The effect of variable fluid properties on the hydromagnetic flow and heat transfer over a non-linearly stretching sheet was discussed by Prasad et al. [31]. Hayat et al. [32] discussed mixed convection flow across a porous sheet and reported that the thermal boundary layer thickness is lowered with Pr. Reddy et al. [33] probed the effect of variable thermal conductivity on MHD flow of nanofluid over a stretching sheet. They considered convective boundary conditions. Zaka et al. [34] applied numerical simulation for Darcy-Forchheimer flow of nanofluid by considering a rotating disk. They reported that the temperature distribution is enhanced with the thermophoresis parameter. Shah et al. [35] discussed the nanofluid flow for different shape factors. They managed to show that the shape factor causes stronger convection. Zeeshan et al. [36] reported the effect of radiative nanofluid flow under a pressure gradient due to entropy generation and observed an increase in entropy with an increase in the pressure gradient. Ellahi et al. [37] investigated flow of a power-law nanofluid with entropy generation and noted that the skin friction coefficient increases at the heated wall. Yousif et al. [38] analyzed the momentum and heat transfer of MHD Carreau nanofluid over an exponentially stretching surface and used the shooting method to compute the solution. Sarafraz et al. [39] discussed the pool boiling heat transfer characteristics of an iron oxide nano-suspension considering a constant magnetic field and found that bubble formation is intensified due to the magnetic field. Fujimoto [40] described multi-scale simulation on adaptive meshes.

This paper is arranged in the following way. A mathematical formalism of the physical model is explained in section Problem Formulation. Section Fluid Properties Analysis addresses constant as well as varying liquid characteristics. Section Physical Quantities provides physical quantities, and an overview of the numerical process has been given in section Numerical Procedure. Results and discussion are presented in section Result and Discussion. In section Conclusions, the conclusion is drawn.

2. Problem Formulation

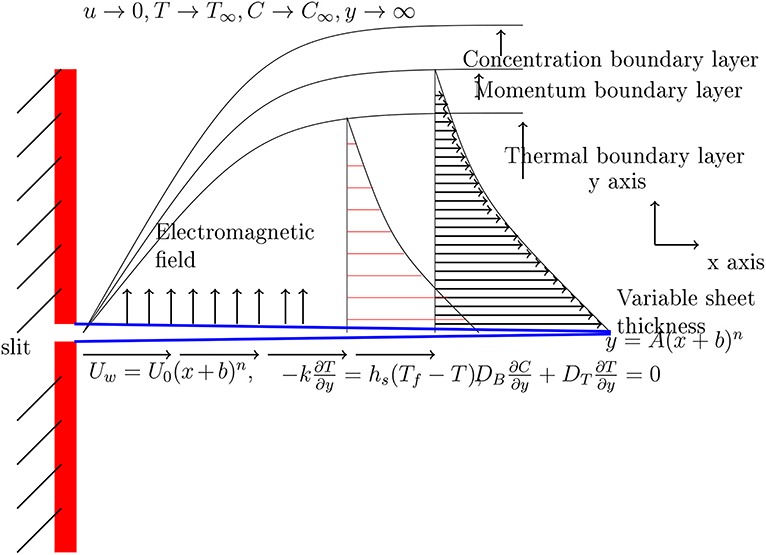
We assume an electrical magnetohydrodynamic (EMHD), two-dimensional, steady, laminar flow of nanofluid over a non-linear stretching sheet with variable thickness. A variable magnetic field $B(x)=B_o{(x+b)}^{\frac{n-1}{2}}(n\ne 1)$ and variable electrical field $E(x)=E_o{(x+b)}^{\frac{n-1}{2}}(n\ne 1)$ are applied normal to the direction of flow. The sheet is stretching with non-linear velocity $U_w=U_o{(x+b)}^n(n\ne 1)$, where b is the dimensional constant and U_o is the reference velocity. Therefore, the surface is considered not to be flat, and its thickness varies as $y=A{(x+b)}^{\frac{1-n}{2}}(n\ne 1)$, where A is a very small constant to hold the sheet thin enough. We also observe that for n = 1, the current problem reduces to a flat sheet. The geometry of the problem is shown in Figure 1, where the x-axis has been taken along the sheet and y-axis is normal to it.

FIGURE 1

Figure 1. Schematic diagram of the problem.

The induced magnetic field has been neglected under the assumption of a small magnetic Reynolds number. The boundary layer equations governing this flow are Daniel et al. [6, 8] and Irfan et al. [41]

$\begin{array}{ll}\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,& (1)\end{array}$

$\begin{array}{l}u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\frac{1}{\rho }\frac{\partial }{\partial y}(\frac{\mu \partial u}{\partial y})+\frac{\sigma }{\rho }(E(x)B(x)-B^2(x)u)-\frac{\mu }{\rho K(x)}u\\ u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{1}{\rho C_p}\frac{\partial }{\partial y}(\frac{k\partial T}{\partial y})+\tau (D_B\frac{\partial T}{\partial y}\frac{\partial C}{\partial y}+\frac{D_T}{T_{\infty }}{(\frac{\partial T}{\partial y})}^2)& (2)\end{array}$

$\begin{array}{ll}-\frac{1}{\rho C_p}\frac{\partial q_r}{\partial y}+\frac{\sigma }{\rho C_p}{(uB(x)-E(x))}^2+\frac{Q(x)}{\rho C_p}(T-T_{\infty }),& (3)\end{array}$

$\begin{array}{ll}u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=D_B\frac{{\partial }^{2}C}{\partial y^2}+\frac{D_T}{T_{\infty }}\frac{{\partial }^{2}T}{\partial y^2},& (4)\end{array}$

Here, u and v are the velocity components parallel to the x− and y− axis, respectively. Further, μ is the viscosity, ρ is the density, ν is the kinematic viscosity, C_p is the specific heat capacity, B is the magnetic field. T and C are the fluid temperature and nanoparticle fraction, respectively. The temperature of the fluid at the wall and ambient temperature are denoted by T_w and T_∞, respectively. D_B and D_T are the Brownian diffusion coefficient and thermophoretic diffusion coefficient, respectively. $\tau =\frac{(\rho c)p}{(\rho c)f}$ is the ratio of the effective heat capacity of the nanoparticle material to the heat capacity of the fluid, q_r is the radiative heat flux, $Q(x)=Q_0{(x+b)}^{\frac{n-1}{2}}$ is the volumetric rate of heat generation, and $K(x)=K_0{(x+b)}^{n-1}$ is a variable permeability.

The above system is completed with the following appropriate boundary conditions, taking to view of [32] and [33]:

$\begin{array}{l}u=U_w(x)=U_o{(x+b)}^n,v=0,-k\frac{\partial T}{\partial y}=h_s(T_f-T),\\ D_B\frac{\partial C}{\partial y}+D_T\frac{\partial T}{\partial y}=0\text{ at }y=A{(x+b)}^{\frac{1-n}{2}}\\ u\to 0,T\to T_{\infty },C\to C_{\infty }\text{ as }y\to \infty & (5)\end{array}$

To the above equations, (1)-(4), the following relevant transformations will be utilized:

$\begin{array}{l}\psi =\sqrt{\frac{2}{n+1}\nu U_o{(x+b)}^{n+1}}f(\eta ),\\ \xi =y\sqrt{(\frac{n+1}{2})\frac{U_o{(x+b)}^{n-1}}{\nu }},\alpha =A{\left(\frac{(n+1)U_0}{2\nu }\right)}^{\frac{1}{2}}\\ \eta =\xi -\alpha =y\sqrt{(\frac{n+1}{2})\frac{U_o{(x+b)}^{n-1}}{\nu }}-\alpha \\ \theta =\frac{T-T_{\infty }}{T_w-T_{\infty }},\varphi =\frac{C-C_{\infty }}{C_w-C_{\infty }},u=U_o{(x+b)}^n{f}^{\prime }(\eta ),\\ v=-\sqrt{\frac{2}{n+1}\nu U_o{(x+b)}^{n-1}}(f(\eta )+\eta \frac{n-1}{n+1}{f}^{\prime }(\eta )).& (6)\end{array}$

Equation (1) is identically satisfied. In addition, when the above similarity variables are applied to Eqations (2), (3), and (4), it yields:

$\begin{array}{ll}{(\frac{\mu }{{\mu }_o}{f}^{″})}^{\prime }-\frac{2n}{n+1}{f}^{\prime 2}+{ff}^{″}+M(E_1-f^{\prime })-Kp\frac{\mu }{{\mu }_o}{f}^{\prime }=0,& (7)\end{array}$

$\begin{array}{l}(1+\frac{4}{3}Rd){(\frac{k}{k_o}{\theta }^{\prime })}^{\prime }+P{r}_o(f{\theta }^{\prime }+Nb{\theta }^{\prime }{\varphi }^{\prime }+Nt{({\theta }^{\prime })}^2\\ +MEc{(f^{\prime }-E_1)}^2+\frac{2}{n+1}s\theta )=0,& (8)\end{array}$

$\begin{array}{ll}{\varphi }^{″}+\frac{Nt}{Nb}{\theta }^{″}+LeP{r}_{o}f{\varphi }^{\prime }=0.& (9)\end{array}$

The equivalent boundary conditions in terms of similarity variables are specified as:

$\begin{array}{l}f(0)=\alpha (\frac{1-n}{1+n}),f^{\prime }(0)=1,,f^{\prime }(\infty )=0,{\theta }^{\prime }(0)=-B_i(1-\theta (0))\\ \theta (\infty )=0,Nb{\varphi }^{\prime }(0)+Nt{\theta }^{\prime }(0)=0,\varphi (\infty )=0,& (10)\end{array}$

where $M=\frac{2\sigma B_o^2}{\rho U_o(n+1)}$ is a magnetic parameter, α is the wall thickness parameter, $E_1=\frac{E_o}{B_o{U}_o{(x+b)}^n}$ is the electric field, and $Kp=\frac{2\nu }{K_o{U}_o(n+1)}$ is the permeability constant. $P{r}_o=\frac{{\mu }_o{C}_p}{k_o}$ is the Prandtl number, $Nb=\frac{\tau D_B(C_w-C_{\infty })}{\nu }$ is the Brownian motion parameter, $Nt=\frac{\tau D_T(T_w-T_{\infty })}{T_{\infty }\nu }$ is the thermophoresis parameter, $Ec=\frac{U_w^2}{C_p(T_w-T_{\infty })}$ is the local Eckert number, $Rd=\frac{4{\sigma }^{*}{T}_{\infty }^3}{k_o{k}^{*}}$ denotes the radiation parameter, $s=\frac{Q_o(x+b)}{\rho u_w{C}_p}$ is the heat source parameter, B_i is the Biot number, and $Le=\frac{\nu }{D_B}$ is Lewis number Irfan et al. [41].

3. Fluid Properties Analysis

We illustrate the main theme of this work through the following two subsections.

3.1. Case A: Constant Fluid Characteristics

For this case, we rewrite Equations (7), (8), and (9) into the following set of equations Irfan et al. [41]:

$\begin{array}{ll}{f}^{‴}-\frac{2n}{n+1}{f}^{\prime 2}+{ff}^{″}+M(E_1-f^{\prime })-Kp{f}^{\prime }=0& (11)\end{array}$

$\begin{array}{l}(1+\frac{4}{3}Rd){\theta }^{″}+P{r}_o(f{\theta }^{\prime }+Nb{\theta }^{\prime }{\varphi }^{\prime }+Nt{({\theta }^{\prime })}^2+MEc{\left(f^{\prime }-E_1\right)}^2\\ +\frac{2}{n+1}s\theta )=0& (12)\end{array}$

$\begin{array}{ll}{\varphi }^{″}+\frac{Nt}{Nb}{\theta }^{″}+P{r}_{o}Lef{\varphi }^{\prime }=0& (13)\end{array}$

3.2. Case B: Variable Fluid Properties

In this case, we express viscosity and thermal conductivity as a function of temperature Andersson and Aarseth [30]

$\begin{array}{ll}\mu (T)=\frac{{\mu }_{ref}}{1+\gamma (T-T_{ref})}& (14)\end{array}$

In (14), above, γ is a property of a fluid. Assuming T_o ≈ T_ref, we get

$\begin{array}{ll}\mu =\frac{{\mu }_o}{1-\frac{T-T_o}{{\theta }_r(T_w-T_o)}}=\frac{{\mu }_o}{1-\frac{\theta (\eta )}{{\theta }_r}}& (15)\end{array}$

Here, ${\theta }_r=\frac{-1}{\gamma (T_w-T_o)}$. Inserting Equation (15) into Equation (7), we get

$\begin{array}{ll}\frac{{\theta }_r}{\left(\theta r-\theta \right)}{f}^{‴}+\frac{f^{″}{\theta }^{\prime }{\theta }_r}{{\left({\theta }_r-\theta \right)}^2}-\frac{2n}{n+1}{f}^{\prime 2}+{ff}^{″}+M\left(E_1-f^{\prime }\right)-Kp\frac{{\theta }_r}{{\theta }_r-\theta }{f}^{\prime }=0& (16)\end{array}$

Following Prasad et al. [31], the changeable thermal conductivity is expressed as

$\begin{array}{ll}k(T)=k_o(1+ϵ\theta )& (17)\end{array}$

Using Equation (17) in Equation (8), we get.

$\begin{array}{ll}\begin{array}{l}(1+\frac{4}{3}Rd)((1+\in \theta ){\theta }^{″}+\in {({\theta }^{\prime })}^2)+{Pr}_o(f{\theta }^{\prime }+Nb{\theta }^{\prime }{\varphi }^{\prime }\\ +Nt{({\theta }^{\prime })}^2+MEc{(f\prime -{{\rm E}}_1)}^2+\frac{2}{n+1}s\theta )=0\end{array}& (18)\end{array}$

4. Physical Quantities

The important physical parameters are defined as follows.

4.1. Skin Friction Coefficient

The wall friction coefficients for case A and case B are defined as

$\begin{array}{l}{C}_f=\frac{{\tau }_w}{\rho u_w^2}=\sqrt{\frac{1+n}{2R{e}_x}}{f}^{″}(0)(\text{CASE A})\end{array}$

$\begin{array}{l}{C}_f=\frac{{\tau }_w}{\rho u_w^2}=\frac{{\theta }_r}{{\theta }_r-\theta (0)}\sqrt{\frac{1+n}{2R{e}_x}}{f}^{″}(0)(\text{CASE B})\end{array}$

4.2. Local Nusselt Number

The local Nusselt numbers for Cases A and B are the same and can be written as

$N{u}_x=-\frac{(x+b)q_w}{K_o(T_w-T_{\infty })}=-(1+\frac{4}{3}Rd)\sqrt{\frac{\left(1+n\right){Re}_x}{2}}{\theta }^{\prime }\left(0\right)$

4.3. Local Sherwood Number

The local Sherwood number for both Case A and Case B is

$\begin{array}{ll}S{h}_x=-\frac{(x+b)j_w}{C_w-C_{\infty }}=-\sqrt{\frac{(1+n)R{e}_x}{2}}{\varphi }^{\prime }(0)& (19)\end{array}$

5. Numerical Procedure

The system of ODEs for Case A and Case B, along with the boundary conditions, are first transformed into a system of first-order ODEs. We use two numerical methods to find the solution of these ODEs. The first method is the SFDM [42], and the second is implemented through MATLAB's built-in solver bvp4c. The details of the methods and the implications are described below.

5.1. Simplified Finite Difference Method (SFDM)

The algorithm and necessary details for the simplified FDM are as follows:

1. We first reduce the third-order ODE into a group of first- and second-order ODEs. This reduction of order simplifies the process of finite difference approximation. The ODE already written in second order cannot be reduced.

2. For further simplification, we use a Taylor series to linearize the system of nonlinear ODEs.

3. We replace the derivatives in linear ODEs with the corresponding finite difference approximation formulas.

4. In the end, we reach an algebraic system of equations that can be solved efficiently by the Thomas algorithm.

5. The process will be repeated for energy and concentration equations.

An explanation of SFDM has been illustrated in the flowchart. Generally, we find the results when N = 1, 000 grid points in the η direction. The domain to achieve steady state varies due to the effects of different parameters, but the domain η = 7 seems sufficient for our results. To initiate, we assume f′ = F in (11), and then we get

$\begin{array}{ll}\frac{d^{2}F}{d{\eta }^2}=\frac{2n}{n+1}{F}^2-f\frac{dF}{d\eta }-M(E_1-F)+KpF& (20)\end{array}$

We can write this expression for the function f as

$\begin{array}{ll}{\chi }_1(\eta ,F,F^{\prime })=\frac{2n}{n+1}{F}^2-f\frac{dF}{d\eta }-M(E_1-F)+KpF& (21)\end{array}$

Let us approximate $\frac{dF}{d\eta }$ in the above equation by forward difference approximation

$\begin{array}{ll}{\chi }_1(\eta ,F,F^{\prime })=\frac{2n}{n+1}{F}_i^2-f_i(\frac{F_{i+1}-F_i}{h})-M(E_1-F_i)+Kp{F}_i& (22)\end{array}$

The coefficients of second-order ODE read as

$\begin{array}{ll}{A}_n=-\frac{\partial {\chi }_1}{\partial F^{\prime }}=-(-f)=f=f_i& (23)\end{array}$

$\begin{array}{ll}{B}_n=-\frac{\partial {\chi }_1}{\partial F}=-(\frac{4n}{n+1}F+M+Kp)=-(\frac{4n}{n+1}{F}_i+M+Kp)& (24)\end{array}$

$\begin{array}{ll}{D}_n={\chi }_1(\eta ,F,F^{\prime })+B_n{F}_i+A_n\frac{F_{i+1}-F_i}{h}& (25)\end{array}$

After some manipulation, (25) becomes

$\begin{array}{ll}{a}_i{F}_{i-1}+b_i{F}_i+c_i{F}_{i+1}=r_i,i=1,2,3\dots .,N& (26)\end{array}$

where

$\begin{array}{ll}{a}_i=2-h{A}_n,b_i=2h^2{B}_n-4,c_i=2+h{A}_n,r_i=2h^2{D}_n& (27)\end{array}$

In matrix-vector form, it is written compactly as

$\begin{array}{ll}AF=s& (28)\end{array}$

where

$\begin{array}{ll}A=\left[\begin{array}{llllll}{b}_1\hfill & c_1\hfill & \hfill & \hfill & \hfill & \hfill \\ a_2\hfill & b_2\hfill & c_2\hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \dots .\hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & a_{N-2}\hfill & b_{N-2}\hfill & c_{N-2}\hfill \\ \hfill & \hfill & \hfill & \hfill & a_{N-1}\hfill & b_{N-1}\hfill \end{array}\right]& (29)\end{array}$

$\begin{array}{ll}F=\left[\begin{array}{c}{F}_1\\ F_2\\ .\\ .\\ F_{N-1}\end{array}\right]s=\left[\begin{array}{c}{s}_1\\ s_2\\ .\\ .\\ s_{N-1}\end{array}\right]& (30)\end{array}$

The matrix A is a tridiagonal matrix and is written in LU-Factorization as [43]

$\begin{array}{ll}A=LU& (31)\end{array}$

where

$\begin{array}{ll}L=\left[\begin{array}{llllll}{\beta }_1\hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ a_2\hfill & {\beta }_2\hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \dots .\hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & a_{N-2}\hfill & {\beta }_{N-2}\hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & a_{N-1}\hfill & {\beta }_{N-1}\hfill \end{array}\right]& (32)\end{array}$

and

$\begin{array}{ll}U=\left[\begin{array}{lllll}1\hfill & {\gamma }_1\hfill & \hfill & \hfill & \hfill \\ \hfill & 1\hfill & {\gamma }_2\hfill & \hfill & \hfill \\ \hfill & \hfill & \dots .\hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & 1\hfill & {\gamma }_{N-2}\hfill \\ \hfill & \hfill & \hfill & \hfill & 1\hfill \end{array}\right]& (33)\end{array}$

where L and U are the lower and upper triangular matrices, respectively. Here the unknowns (β_i, γ_i), i = 1, 2, …, N − 1 are to be related as [43]

$\begin{array}{ll}{\beta }_1=-1-\frac{\lambda }{h},{\gamma }_1=\frac{\lambda }{{\beta }_{1}h}& (34)\end{array}$

$\begin{array}{ll}{\beta }_i=b_i-a_i{\gamma }_{i-1},i=2,3,\dots ,N-1& (35)\end{array}$

$\begin{array}{ll}{\beta }_i{\gamma }_i=c_i,i=2,3,\dots .,N-2& (36)\end{array}$

After defining these relations, (31) becomes

$\begin{array}{ll}LUF=s,UF=z,\text{and }Lz=s& (37)\end{array}$

and we have

$\begin{array}{lllll}\left[\begin{array}{lllll}{\beta }_1\hfill & \hfill & \hfill & \hfill & \hfill \\ a_2\hfill & {\beta }_2\hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \dots .\hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & a_{N-2}\hfill & {\beta }_{N-2}\hfill \\ \hfill & \hfill & \hfill & \hfill & a_{N-1}\hfill \end{array}\right]& \left[\begin{array}{c}{z}_1\\ z_2\\ z_3\\ .\\ .\\ .\\ z_{N-2}\\ z_{N-1}\end{array}\right]& =& \left[\begin{array}{c}{s}_1\\ s_2\\ s_3\\ .\\ .\\ .\\ s_{N-2}\\ s_{N-1}\end{array}\right]& (38)\end{array}$

The unknown elements of z can be found by

$\begin{array}{ll}{z}_1=s_1/{\beta }_1,z_i=\frac{s_i-a_i{z}_{i-1}}{{\beta }_i},i=2,3,\dots ,N-1& (39)\end{array}$

and

$\begin{array}{lllll}\left[\begin{array}{lllll}1\hfill & {\gamma }_1\hfill & \hfill & \hfill & \hfill \\ \hfill & 1\hfill & {\gamma }_2\hfill & \hfill & \hfill \\ \hfill & \hfill & \dots .\hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & 1\hfill & {\gamma }_{N-2}\hfill \\ \hfill & \hfill & \hfill & \hfill & 1\hfill \end{array}\right]& \left[\begin{array}{c}{F}_1\\ F_2\\ .\\ .\\ .\\ F_{N-2}\\ F_{N-1}\end{array}\right]& =& \left[\begin{array}{c}{z}_1\\ z_2\\ .\\ .\\ .\\ z_{N-2}\\ z_{N-1}\end{array}\right]& (40)\end{array}$

We then get

$\begin{array}{ll}{F}_{i-1}=z_{i-1},F_i=z_i-{\gamma }_i{F}_{i+1},i=N-2,N-3,\dots ,3,2,1& (41)\end{array}$

which is a solution of (20). We can easily find f from f′ = F, which in discretization form

$\begin{array}{ll}\frac{f_{i+1}-f_i}{h}=F_i& (42)\end{array}$

gives a required solution of (11). A similar procedure can also adopted for solutions θ and ϕ. For the sake of brevity, we only present coefficients for these ODEs and leave out the details that follow on the same line as presented above. For example, the energy equation (12) is

$\begin{array}{l}\frac{d^2\theta }{d{\eta }^2}=-(\frac{{Pr}_o}{(1+\frac{4}{3}Rd)}(f\frac{d\theta }{d\eta }+Nb\frac{d\theta }{d\eta }\frac{d\varphi }{d\eta }+Nt{(\frac{d\theta }{d\eta })}^2\\ +MEc{(\frac{df}{d\eta }-E_1)}^2+\frac{2}{n+1}s\theta ))& (43)\end{array}$

$\begin{array}{l}{\chi }_2(\eta ,\theta ,{\theta }^{\prime })=-(\frac{{Pr}_o}{(1+\frac{4}{3}Rd)}(f_i(\frac{{\theta }_i-{\theta }_{i-1}}{h})\\ +Nb(\frac{{\theta }_i-{\theta }_{i-1}}{h})(\frac{{\varphi }_i-{\varphi }_{i-1}}{h})\\ +Nt{(\frac{{\theta }_i-{\theta }_{i-1}}{h})}^2+MEc{(F_i-E_1)}^2+\frac{2}{n+1}s{\theta }_i))& (44)\end{array}$

$\begin{array}{ll}{A}_{nn}=-\frac{\partial \chi }{\partial {\theta }^{\prime }}=-(-\frac{{Pr}_o}{\left(1+\frac{4}{3}Rd\right)}(f+Nb{\varphi }^{\prime }+\left(2Nt{\theta }^{\prime }\right)& (45)\end{array}$

$\begin{array}{ll}{A}_{nn}=\frac{P{r}_o}{(1+\frac{4}{3}Rd)}(f_i+Nb(\frac{{\varphi }_i-{\varphi }_{i-1}}{h})+2N_t(\frac{{\theta }_i-{\theta }_{i-1}}{h}))& (46)\end{array}$

$\begin{array}{ll}{B}_{nn}=\frac{2P{r}_o}{(n+1)(1+4/3Rd)}s& (47)\end{array}$

$\begin{array}{ll}\frac{d^2\varphi }{d{\eta }^2}=\frac{-Nt}{Nb}\frac{d^2\theta }{d{\eta }^2}-LeP{r}_{o}f{\varphi }^{\prime }& (48)\end{array}$

$\begin{array}{ll}{\chi }_3(\eta ,\varphi ,{\varphi }^{\prime })=\frac{-Nt}{Nb}\frac{{\theta }_{i-1}-2{\theta }_i+{\theta }_{i+1}}{h^2}-LeP{r}_o(f_i\frac{{\varphi }_i-{\varphi }_{i-1}}{h})& (49)\end{array}$

Similarly, the coefficients for (13) are written as

$\begin{array}{ll}{A}_{nnn}=P{r}_{o}Le{f}_i,B_{nnn}=0& (50)\end{array}$

Boundary conditions can easily be discretized by following the above procedure.

5.2. bvp4c

To solve the system of ODEs for Case A and Case B, we first transformed the system into first-order ODEs to compute the solution using bvp4c. For Case A it gives,

(a) Case A:

$\begin{array}{l}f=v_1,f^{\prime }=v_2,f^{″}=v_3,f^{‴}=v_3^{\prime }=\frac{2n}{n+1}{v}_2^2-v_1{v}_3\hfill \\ -M\left(E_1-v_2\right)+Kp{v}_2,\hfill \\ v_4=\theta ,v_5={\theta }^{\prime },{\theta }^{″}=v_5^{\prime }=-\frac{P{r}_o}{(1+\frac{4}{3})Rd}(v_1{v}_5+Nb{v}_5{v}_7\hfill \\ +Nt{v}_5^2+MEc{(v_2-E_1)}^2+\frac{2}{n+1}s{v}_4),\hfill \\ v_6=\varphi ,v_7={\varphi }^{\prime },{\varphi }^{″}=v_7^{\prime }=-LeP{r}_o{v}_1{v}_7-\frac{Nt}{Nb}{v}_5^{\prime }.\hfill \end{array}$

(b) Case B: The transformed ODEs for Case B are,

$\begin{array}{l}f=u_1,f^{\prime }=u_2,f^{″}=u_3,f^{‴}=u_3^{\prime }=\frac{(u_3{u}_5)}{(u_4-{\theta }_r)}\hfill \\ +\frac{(u_4-{\theta }_r)}{{\theta }_r}(-\frac{2n}{n+1}{u}_2^2+u_1{u}_3+M(E_1-u_2)-Kp{u}_2),\hfill \\ u_4=\theta ,u_5={\theta }^{\prime },{\theta }^{″}=u_5^{\prime }=\frac{-ϵu_5^2}{1+ϵu_4}\hfill \\ -\frac{P{r}_o}{(1+ϵu_4)(1+\frac{4}{3}Rd)}(u_1{u}_5+Nb{u}_5{u}_7+Nt{u}_5^2+\hfill \\ MEc{(u_2-E_1)}^2+\frac{2}{n+1}s{u}_4),\hfill \\ u_6=\varphi ,u_7={\varphi }^{\prime },{\varphi }^{″}=u_7^{\prime }=-LeP{r}_o{u}_1{u}_7-\frac{Nt}{Nb}{u}_5^{\prime }.\hfill \end{array}$

6. Result and Discussion

In this section, we present the outcomes of our results both in tabulated and graphical forms.

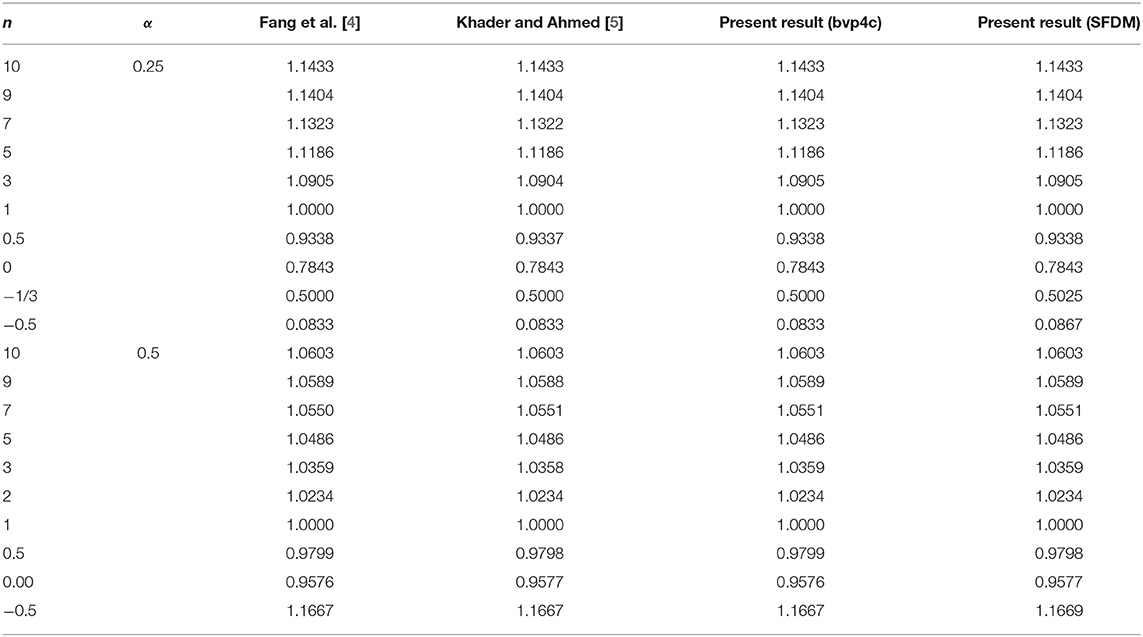
In Table 1, we compare our results with the literature for the skin friction coefficient against different values of n while fixing α = 0.25 and α = 0.5. The SFDM shows an excellent agreement with bvp4c and the literature. In summary, the skin friction coefficient is higher for Case B and lower values for Case A.

TABLE 1

Table 1. Resemblance of −f″(0) from the literature for various n values (CASE A).

In Table 2 we calculate the skin friction coefficient for various parameters like magnetic parameter M, power law index n, electric field E₁, porosity parameter Kp, variable thickness α, and viscosity parameter θ_r. Its value goes up by changing M, n, α, Kp, and θ_r, while it gets lower by changing E₁. Table 3 shows the heat and mass transfer rates for various parameters.

TABLE 2

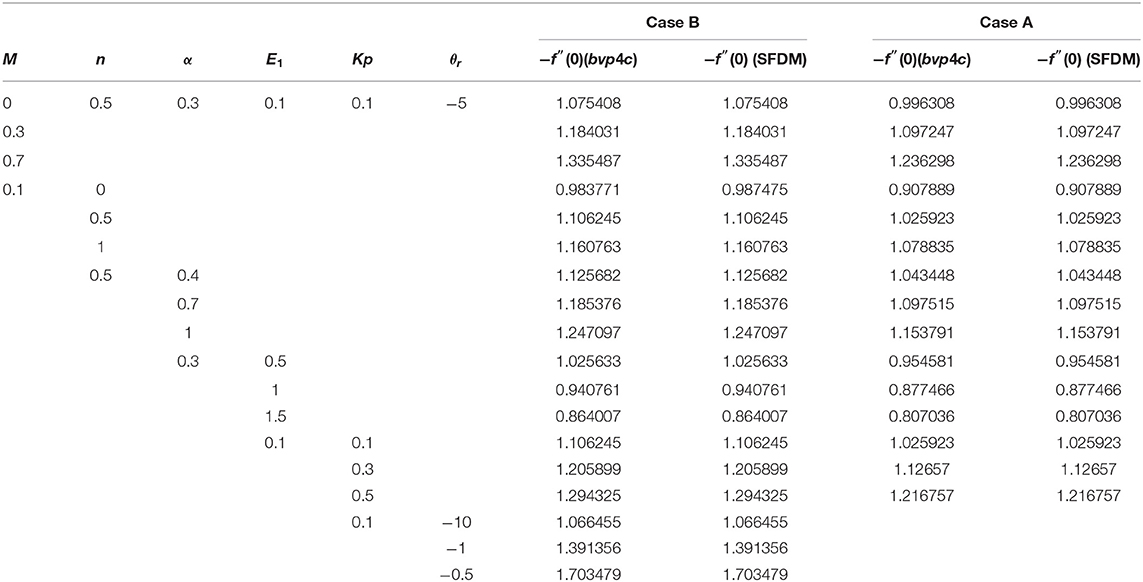
Table 2. Resemblance of the values of −f″(0) for different values of parameters M, n, α, E₁, and θ_r.

TABLE 3

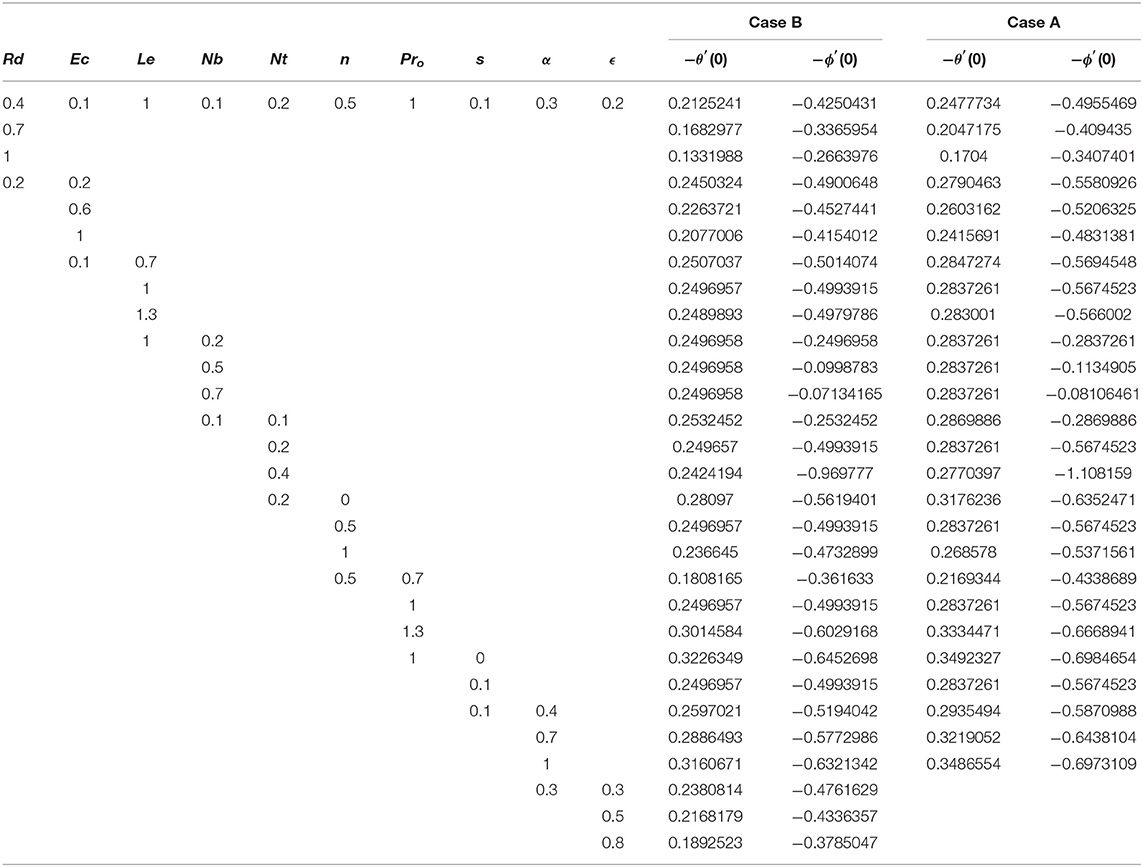
Table 3. Comparison of the values of −θ′(0) and ϕ′(0) for different values of Rd, Ec, Le, Nb, Nt, n, Pr_o, s, α, and ϵ for Case B with Case A, respectively.

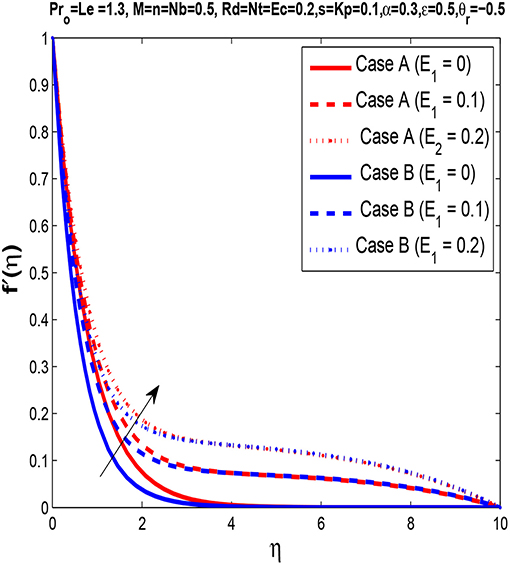
An electric field parameter, E₁, enhances the velocity of the fluid, as can be seen in Figure 2. Lorentz force is responsible for increasing velocity due to the fact that the skin friction coefficient (as shown in Table 2) decreases.

FIGURE 2

Figure 2. Velocity f′(η) for different values of E₁.

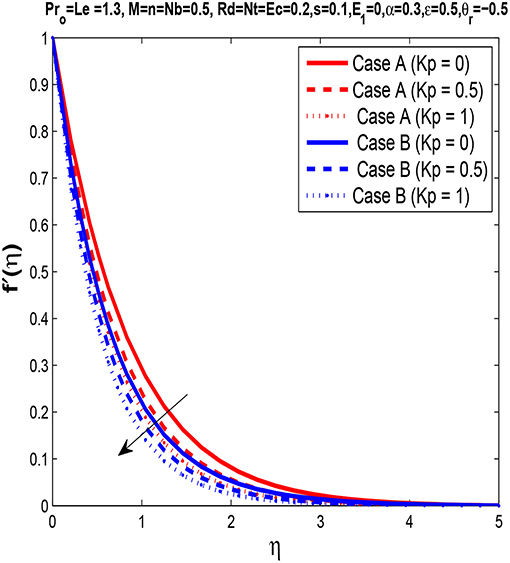
In Figure 3, we observe that the momentum boundary layer thickness thins with an increase in porosity parameter Kp. This decrease in velocity profile is due to an increase in skin friction for increasing values of porosity parameter Kp. Moreover, increasing porosity provides resistance to the flow, which ultimately reduces the velocity of the fluid.

FIGURE 3

Figure 3. Velocity f′(η) for different values of Kp.

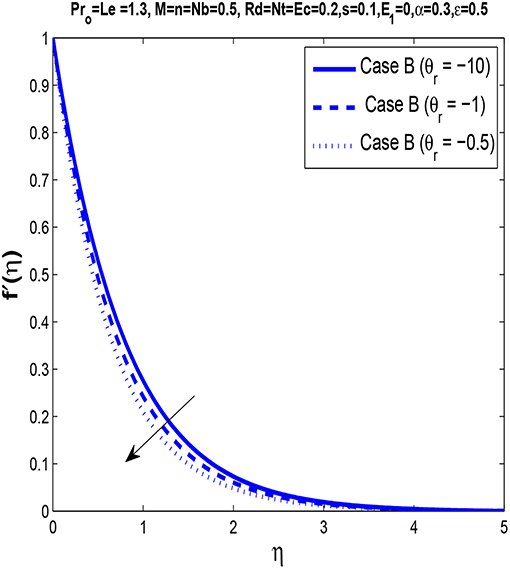
Figure 4 describes the velocity profile for different values of viscosity parameter θ_r. It is observed that the momentum boundary layer thins with an increase in fluid viscosity parameter θ_r. This can be related to Table 2, where we can see that increasing viscosity parameter θ_r leads to the magnitude of the skin friction coefficient increasing, which causes the reduction in velocity. Increasing viscosity provides more resistance to the fluid motion since higher shear stress is required to move viscous fluids.

FIGURE 4

Figure 4. Velocity profile f′(η) for different values of θ_r.

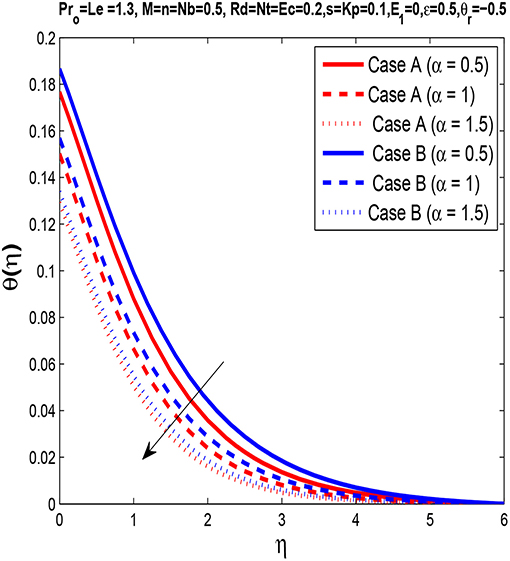
The effect of variable thickness parameter α on temperature can be seen in Figure 5. It is observed that only some energy is transmitted from the surface to the liquid when we raise the wall thickness parameter. Physically, it shows that as we enhance wall thickness parameter α, less heat is transferred from the sheet to the fluid. The temperature profile therefore decreases.

FIGURE 5

Figure 5. Temperature profile θ(η) for different values of α.

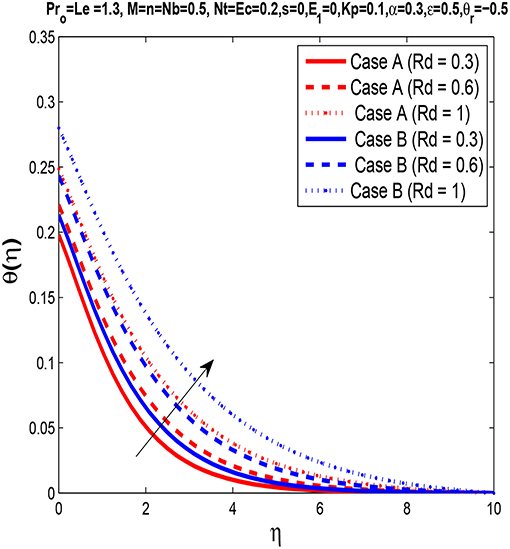
Figure 6 is plotted to demonstrate the effect of thermal radiation parameter Rd on the temperature profile. It is found that with the rise in Rd, the temperature profile increases significantly, as an increase in the radiation parameter provides more energy to the fluid, which increases the thickness of the thermal boundary layer.

FIGURE 6

Figure 6. Temperature profile θ(η) for different values of Rd.

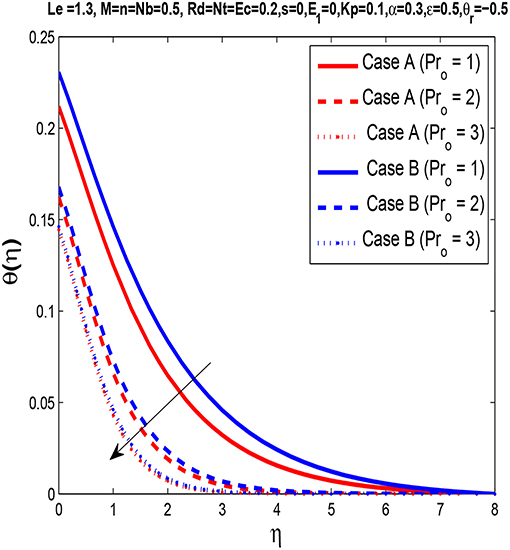
In Figure 7, it is observed that an increase in Prandtl number Pr_o causes a reduction in the temperature profile. The reason for this decrease is that smaller values of Prandtl number Pr₀ are equivalent higher thermal conductivity. Since the thermal conductivity of air is higher, ultimately, the temperature is higher. However, a high Prandtl number corresponds to low thermal conductivity and lower temperature flow.

FIGURE 7

Figure 7. Temperature profile θ(η) for different values of Pr_o.

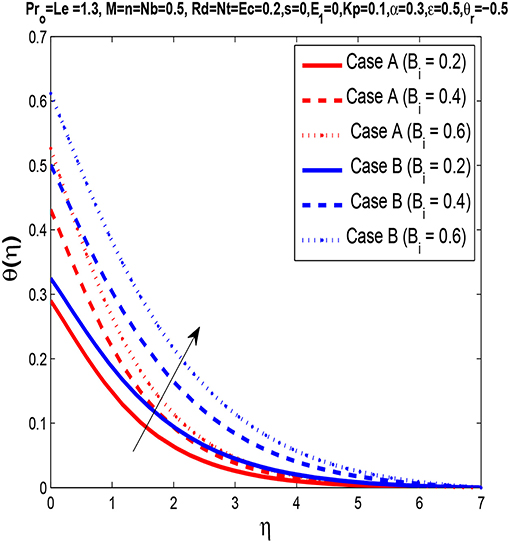
In Figure 8, we illustrate the influence of Biot number B_i on the temperature profile. It is seen that for higher values of Biot number B_i, the thermal boundary layer thickness increases. This increase in temperature profile is due to the heat transfer rate, which enhances for higher values of Biot number B_i. Since the thermal conductivity is dominant compared to convection, heat transport increases as the Biot number increases.

FIGURE 8

Figure 8. Temperature profile θ(η) for different values of B_i.

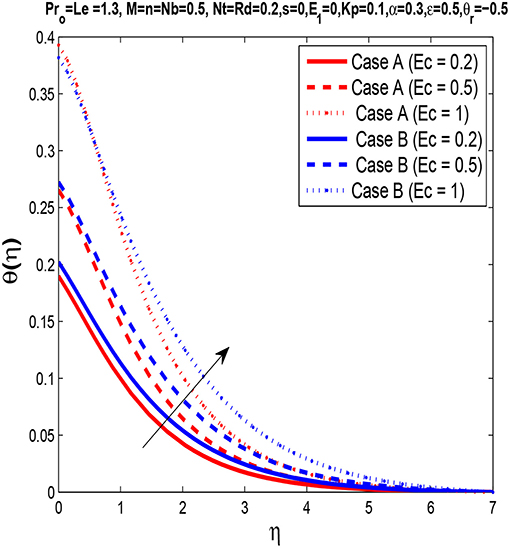
To examine the effects of the Eckert number Ec on the temperature distribution, we plot Figure 9. For higher values of the Eckert number Ec, it is evaluated that somehow the temperature profile rises and the thermal boundary layer gets thinner. Eckert number Ec is the ratio of the kinetic energy of fluid and enthalpy. For increasing values of Eckert number Ec, the kinetic energy increases, which causes an enhancement in fluid temperature.

FIGURE 9

Figure 9. Temperature profile θ(η) for different values of Ec.

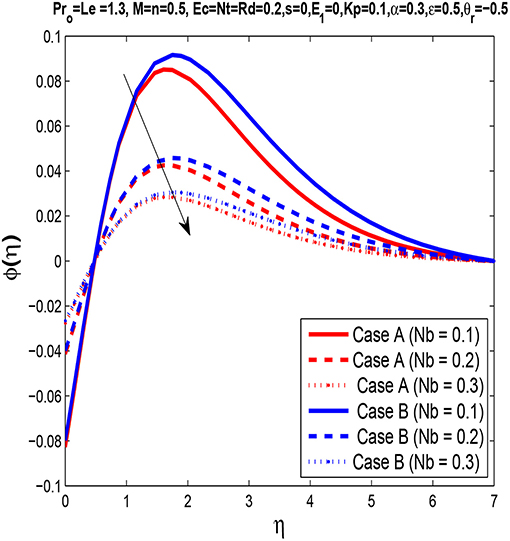
Figure 10 is plotted to illustrate the effect of the Brownian motion parameter on the concentration profile. It is concluded that higher values of Brownian motion parameter Nb cause a reduction in the nanoparticle concentration profile.

FIGURE 10

Figure 10. Concentration profile ϕ(η) for different values of Nb.

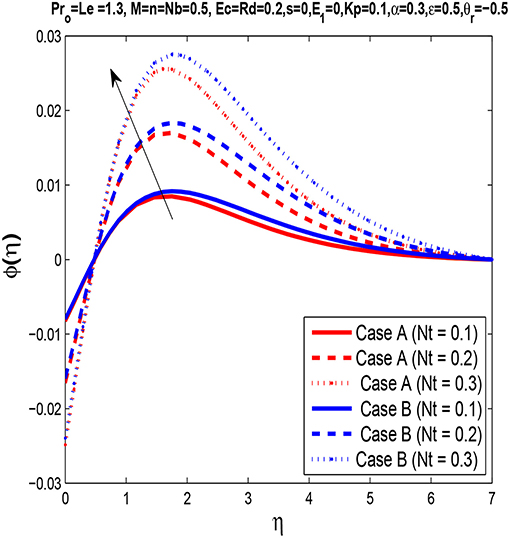
Figure 11 is presented to characterize the behavior of thermophoresis parameter Nt on the concentration profile. It is noted that by increasing the thermophoresis parameter, we find a reduction in the nanoparticle concentration profile.

FIGURE 11

Figure 11. Concentration profile ϕ(η) for different values of Nt.

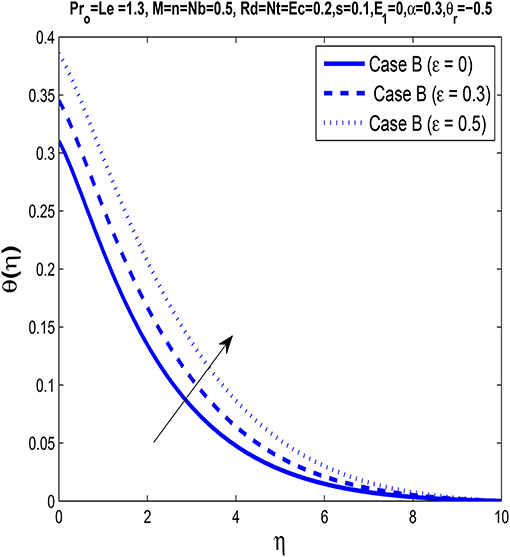
In Figure 12, it is found that an increase in variable thermal conductivity parameter ϵ enhances the temperature profile. Table 3 indicates that the Nusselt number decreases with increasing ϵ. Due to this, the heat transfer rate increases, and hence the temperature profile increases.

FIGURE 12

Figure 12. Temperature profile θ(η) for different values of ϵ.

7. Conclusions

This analysis achieved two goals. Firstly, an assessment of distinctive features for constant and variable properties has been done. Secondly, we adopted a new numerical process, the SFDM, to compute solutions and compared its accuracy with bvp4c. The notable results for both cases, Case A and B, are as follows:

• The numerical technique, the SFDM, has produced excellent results with high accuracy, as shown in Tables 1, 2.

• Momentum boundary layer thickness grows with an increase in the electric field E₁, whereas it decreases with increases in porosity parameter Kp and fluid viscosity parameter θ_r.

• The thermal boundary layer thickness rises when radiation parameter Rd, Biot number B_i, Eckert number Ec, or thermal conductivity parameter ϵ rises, while it decreases for higher values of variable thickness parameter α and Prandtl number Pr_o.

• The concentration boundary layer thickness decreases with increasing Nb and increases with increasing Nt.

• It is shown that the results are different for constant and variable fluid properties. For variable fluid properties, heat transfer and mass transfer rates are lower than with constant fluid properties. The skin friction coefficient is higher for variable fluid properties than for constant fluid properties.

Author Contributions

MI and MF have jointly written the manuscript. The numerical part of bvp4c, as well as tables and graphs, have been completed by MI. TI investigated the SFDM for comparison. MF, MI, and TI have discussed results.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

MF would like to thank Research Scientist S. Hussain for his valuable contributions in the numerical part of this work.

References

1. Hayat T, Ijaz Khan M, Farooq M, Alsaedi A, Waqas M, Yasmeen T. Impact of Cattaneo–Christov heat flux model in flow of variable thermal conductivity fluid over a variable thicked surface. Int J Heat Mass Transfer. (2016) 99:702–10. doi: 10.1016/j.ijheatmasstransfer.2016.04.016

CrossRef Full Text | Google Scholar

2. Hayat T, Farooq M, Alsaedi A, Falleh Al-Solamy. Impact of Cattaneo-Christov heat flux in the flow over a stretching sheet with variable thickness. AIP Adv. (2015) 5:087159. doi: 10.1063/1.4929523

CrossRef Full Text | Google Scholar

3. Mabood F, Ibrahim SM, Rashidi MM, Shadloo MS, Lorenzini G. Non-uniform heat source/sink and Soret effects on MHD non-Darcian convective flow past a stretching sheet in a micropolar fluid with radiation. Int J Heat Mass Transfer. (2016) 93:674–82. doi: 10.1016/j.ijheatmasstransfer.2015.10.014

CrossRef Full Text | Google Scholar

4. Fang T, Zhang J, Zhong Y. Boundary layer flow over a stretching sheet with variable thickness. Appl Math Comput. (2012) 218:7241–52. doi: 10.1016/j.amc.2011.12.094

CrossRef Full Text | Google Scholar

5. Khader MM, Megahed AM. Numerical solution for boundary layer flow due to a nonlinearly stretching sheet with variable thickness and slip velocity. Eur Phys J Plus. (2013) 128:100. doi: 10.1140/epjp/i2013-13100-7

CrossRef Full Text | Google Scholar

6. Daniel YS, Abdul Aziz Z, Ismail Z, Salah F. Thermal stratification effects on MHD radiative flow of nanofluid over nonlinear stretching sheet with variable thickness. J Comput Design Eng. (2018) 5:232–42. doi: 10.1016/j.jcde.2017.09.001

CrossRef Full Text | Google Scholar

7. Reddy S, Naikoti K, Rashidi MM. MHD flow and heat transfer characteristics of Williamson nanofluid over a stretching sheet with variable thickness and variable thermal conductivity. Trans A Razmadze Math Inst. (2017) 171:195–211. doi: 10.1016/j.trmi.2017.02.004

CrossRef Full Text | Google Scholar

8. Daniel YS, Aziz ZA, Ismail Z, Salah F. Impact of thermal radiation on electrical MHD flow of nanofluid over nonlinear stretching sheet with variable thickness. Alexandria Eng J. (2018) 57:2187–97. doi: 10.1016/j.aej.2017.07.007

CrossRef Full Text | Google Scholar

9. Akbar NS, Nadeem S, Ul Haq R, Khan ZH. Numerical solutions of Magnetohydrodynamic boundary layer flow of tangent hyperbolic fluid towards a stretching sheet. Indian J Phys. (2013) 87:1121–4. doi: 10.1007/s12648-013-0339-8

CrossRef Full Text | Google Scholar

10. Mukhopadhyay S, Layek GC, Samad SA. Study of MHD boundary layer flow over a heated stretching sheet with variable viscosity. Int J Heat Mass Transfer. (2005) 48:4460–6. doi: 10.1016/j.ijheatmasstransfer.2005.05.027

CrossRef Full Text | Google Scholar

11. Nadeem S, Ul Haq R, Akbar NS, Khan ZH. MHD three-dimensional Casson fluid flow past a porous linearly stretching sheet. Alexandria Eng J. (2013) 52:577–82. doi: 10.1016/j.aej.2013.08.005

CrossRef Full Text | Google Scholar

12. Mabood F, Khan WA, Ismail AM. MHD boundary layer flow and heat transfer of nanofluids over a nonlinear stretching sheet: a numerical study. J Magnet Magnet Mater. (2015) 374:569–76. doi: 10.1016/j.jmmm.2014.09.013

CrossRef Full Text | Google Scholar

13. Zhang C, Zheng L, Zhang X, Chen G. MHD flow and radiation heat transfer of nanofluids in porous media with variable surface heat flux and chemical reaction. Appl Math Modell. (2015) 39:165–81. doi: 10.1016/j.apm.2014.05.023

CrossRef Full Text | Google Scholar

14. Poply V, Singh P, Yadav AK. A study of temperature-dependent fluid properties on MHD free stream flow and heat transfer over a non-linearly stretching sheet. Proc Eng. (2015) 127:391–7. doi: 10.1016/j.proeng.2015.11.386

CrossRef Full Text | Google Scholar

15. Sheikholeslami M, Bandpy MG, Ellahi R, Zeeshan A. Simulation of MHD CuO-water nanofluid flow and convective heat transfer considering Lorentz forces. J Magnet Magnet Mater. (2014) 369:69–80. doi: 10.1016/j.jmmm.2014.06.017

CrossRef Full Text | Google Scholar

16. Patel HR. Effects of heat generation, thermal radiation, and hall current on MHD Casson fluid flow past an oscillating plate in porous medium. Multiphase Sci Technol. (2019) 31:87–107. doi: 10.1615/MultScienTechn.2019029514

CrossRef Full Text | Google Scholar

17. Farooq U, Lu D, Munir S, Ramzan M, Suleman M, Hussain S. MHD flow of Maxwell fluid with nanomaterials due to an exponentially stretching surface. Sci Rep. (2019) 9:7312. doi: 10.1038/s41598-019-43549-0

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Ibrahim W, Tulu A. Magnetohydrodynamic (MHD) boundary layer flow past a wedge with heat transfer and viscous effects of nanofluid embedded in porous media. Math Problems Eng. (2019) 2019:4507852. doi: 10.1155/2019/4507852

CrossRef Full Text | Google Scholar

19. Ali A, Shehzadi K, Sulaiman M, Asghar S. Heat and mass transfer analysis of 3D Maxwell nanofluid over an exponentially stretching surface. Phys Script. (2019) 94:065206. doi: 10.1088/1402-4896/ab07cf

CrossRef Full Text | Google Scholar

20. Choi SUS, Eastman JA. Enhancing Thermal Conductivity of Fluids With Nanoparticles. Argonne National Lab., IL (1995).

Google Scholar

21. Das K, Duari PR, Kundu PK. Numerical simulation of nanofluid flow with convective boundary condition. J Egypt Math Soc. (2015) 23:435–39. doi: 10.1016/j.joems.2014.05.009

CrossRef Full Text | Google Scholar

22. Mabood F, Das K. Melting heat transfer on hydromagnetic flow of a nanofluid over a stretching sheet with radiation and second-order slip. Eur Phys J Plus. (2016) 131:3. doi: 10.1140/epjp/i2016-16003-1

CrossRef Full Text | Google Scholar

23. Cao Z, Zhao J, Wang Z, Liu F, Zheng L. MHD flow and heat transfer of fractional Maxwell viscoelastic nanofluid over a moving plate. J Mol Liquids. (2016) 222:1121–7. doi: 10.1016/j.molliq.2016.08.012

CrossRef Full Text | Google Scholar

24. Das K, Duari PR, Kundu PK. Effects of magnetic field on an unsteady mixed convection flow of nanofluids containing spherical and cylindrical nanoparticles. J Heat Transfer. (2016) 138:061901. doi: 10.1115/1.4032835

CrossRef Full Text | Google Scholar

25. Satya Narayana PV, Venkateswarlu B, Venkataramana S. Thermal radiation and heat source effects on a MHD nanofluid past a vertical plate in a rotating system with porous medium. Heat Transfer Asian Res. (2015) 44:1–19. doi: 10.1002/htj.21101

CrossRef Full Text | Google Scholar

26. Mansur S, Ishak A, Pop I. Stagnation-point flow towards a stretching/shrinking sheet in a nanofluid using Buongiorno's model. Proc Inst Mech Eng : J Process Mech Eng. (2017) 231:172–80. doi: 10.1177/0954408915585047

CrossRef Full Text | Google Scholar

27. Makinde OD. Effects of viscous dissipation and Newtonian heating on boundary-layer flow of nanofluids over a flat plate. Int J Num Methods Heat Fluid Flow. (2013) 23:1291–303. doi: 10.1108/HFF-12-2011-0258

CrossRef Full Text | Google Scholar

28. Ali AO, Makinde OD, Nkansah-Gyekye Y. Numerical study of unsteady MHD Couette flow and heat transfer of nanofluids in a rotating system with convective cooling. Int J Num Methods Heat Fluid Flow. (2016) 26:1567–79. doi: 10.1108/HFF-10-2014-0316

CrossRef Full Text | Google Scholar

29. Ashwinkumar GP, Sulochana C. Effect of radiation absorption and buoyancy force on the MHD mixed convection flow of Casson nanofluid embedded with Al50Cu50 alloy nanoparticles. Multidiscipl Model Mater Struct. (2018) 14:1082–100. doi: 10.1108/MMMS-12-2017-0164

CrossRef Full Text | Google Scholar

30. Andersson HI, Aarseth JB. Sakiadis flow with variable fluid properties revisited. Int J Eng Sci. (2007) 45:554–61. doi: 10.1016/j.ijengsci.2007.04.012

CrossRef Full Text | Google Scholar

31. Prasad KV, Vajravelu K, Datti PS. The effects of variable fluid properties on the hydro-magnetic flow and heat transfer over a non-linearly stretching sheet. Int J Thermal Sci. (2010) 49:603–10. doi: 10.1016/j.ijthermalsci.2009.08.005

CrossRef Full Text | Google Scholar

32. Hayat T, Shehzad SA, Qasim M, Alsaedi A. Mixed convection flow by a porous sheet with variable thermal conductivity and convective boundary condition. Braz J Chem. Eng. (2014) 31:109–17. doi: 10.1590/S0104-66322014000100011

CrossRef Full Text | Google Scholar

33. Bhaskar Reddy N, Poornima T, Sreenivasulu P. Influence of variable thermal conductivity on MHD boundary layer slip flow of ethylene-glycol based Cu nanofluids over a stretching sheet with convective boundary condition. Int J Eng Math. (2014) 2014:905158. doi: 10.1155/2014/905158

CrossRef Full Text | Google Scholar

34. Ullah MZ, Serra-Capizzano S, Baleanu D. A numerical simulation for Darcy-Forchheimer flow of nanofluid by a rotating disk with partial slip effects. Front Phys. (2019) 7:219. doi: 10.3389/fphy.2019.00219

CrossRef Full Text | Google Scholar

35. Shah Z, Babazadeh H, Kumam P, Shafee A, Thounthong P. Numerical simulation of magnetohydrodynamic nanofluids under the influence of shape factor and thermal transport in a porous media using CVFEM. Front Phys. (2019) 7:164. doi: 10.3389/fphy.2019.00164

CrossRef Full Text | Google Scholar

36. Zeeshan A, Shehzad N, Abbas T, Ellahi R. Effects of radiative electro-magnetohydrodynamics diminishing internal energy of pressure-driven flow of titanium dioxide-water nanofluid due to entropy generation. Entropy. (2019) 21:236. doi: 10.3390/e21030236

CrossRef Full Text | Google Scholar

37. Ellahi R, Sait SM, Shehzad N, Mobin N. Numerical simulation and mathematical modeling of electro-osmotic Couette-Poiseuille flow of MHD power-law nanofluid with entropy generation. Symmetry. (2019) 11:1038. doi: 10.3390/sym11081038

CrossRef Full Text | Google Scholar

38. Yousif MA, Ismael HF, Abbas T, Ellahi R. Numerical study of momentum and heat transfer of MHD Carreau nanofluid over an exponentially stretched plate with internal heat source/sink and radiation. Heat Transfer Res. (2019) 50:649–58. doi: 10.1615/HeatTransRes.2018025568

CrossRef Full Text | Google Scholar

39. Sarafraz MM, Pourmehran O, Yang B, Arjomandi M, Ellahi R. Pool boiling heat transfer characteristics of iron oxide nano-suspension under constant magnetic field. Int J Thermal Sci. (2020) 147:106131. doi: 10.1016/j.ijthermalsci.2019.106131

CrossRef Full Text | Google Scholar

40. Fujimoto K. Multi-scale kinetic simulation of magnetic reconnection with dynamically adaptive meshes. Front Phys. (2018) 6:119. doi: 10.3389/fphy.2018.00119

CrossRef Full Text | Google Scholar

41. Irfan M, Farooq MA. Magnetohydrodynamic free stream and heat transfer of nanofluid flow over an exponentially radiating stretching sheet with variable fluid properties. Front Phys. (2019) 7:186. doi: 10.3389/fphy.2019.00186

CrossRef Full Text | Google Scholar

42. Na TY, editor. Computational Methods in Engineering Boundary Value Problems. Academic Press (1980).

Google Scholar

43. Thomas LH. Elliptic Problems in Linear Difference Equations Over a Network. New York, NY: Watson Sci. Comput. Lab. Rept., Columbia University (1949).

Nomenclature