Nucleon-Nucleon Scattering Up to N5LO in Chiral Effective Field Theory

During the past few decades a large effort has been made toward describing the NN interaction in the framework of chiral Effective Field Theory (EFT). The main idea is to exploit the symmetries of QCD to obtain an effective theory for low energy nuclear systems. In 2003, the first accurate charge-dependent NN potential in this scheme was developed and it has been applied to many ab-initio calculations, opening the possibility to study nuclear systems in a systematic and accurate way. It was shown that the fourth order (N³LO) was necessary and sufficient to describe the NN scattering data with a χ²/d.o.f on the order of so-called high precision potentials. However the systematics of chiral EFT also allow to relate two- and many-body interactions in a well-defined way. Since many-body forces make their first appearance at higher order, they are substantially smaller than their two-body counterparts, but may never-the-less be crucial for some processes. Thus, there are observables where they can have a big impact and, for example, there are indications that they solve the long standing A_y puzzle of N-d scattering. The last few years, have also seen substantial progress toward higher orders of chiral EFT which was motivated by the fact that only three-body forces of rather high order may solve some outstanding issues in microscopic nuclear structure and reactions. In this chapter we will review the latest contributions of the authors to development of chiral EFT based potentials up to N⁴LO as well as first calculations conducted for NN scattering at N⁵LO.

1. Introduction

The modern view of the NN interaction is given in the framework of Chiral Effective Field Theory (χEFT). The concept of an Effective Field Theory (EFT) is not a new one. The main idea is to identify the relevant degrees of freedom and symmetries for a certain system at a certain scale, and use this to find a Quantum Field Theory that is able to describe the system. However the traditional renormalization condition used to build theories like QCD is not required and a renormalization order by order is used instead. Nowadays, this approach is widely applied in different areas of physics.

In the case of strong interactions, we know that the fundamental theory is given by Quantum Chromodynamics (QCD). However for nuclear systems, the relevant degrees of freedom are not quarks and gluons, but nucleons and pions. Applying the EFT concept to nuclear systems allows to build theories for nucleons and pions that are consistent with the symmetries of the underlying theory. In the case of QCD, a very important property for low energy dynamics is that the original approximate chiral symmetry is broken spontaneously. This effect makes the pion come into play as the pseudo-Goldstone boson of the theory, which naturally explains the low mass of the pion as compared to other scales in nuclear systems.

Chiral Perturbation Theory (ChPT) uses these ideas to determine observables making a perturbative expansion in the pion mass or some low energy external momenta. The Goldstone-boson character of the pion allows for this perturbative expansion, having always derivative couplings. ChPT was first applied to ππ systems [1] and πN systems [2] with quite some success. Chiral EFT is essentially based on ChPT, however in the case of the NN interaction this perturbative expansion is inadequate and non-perturbative resummations are needed. The complicate structure of the amplitudes makes it difficult to resum these contributions using the techniques of Unitarized ChPT that are applied in two-meson systems [3]. However first attempts to use similar techniques using the so called N/D method have been made [4].

The use of χEFT for the two-nucleon system was introduced by Weinberg in two seminal papers [5, 6]. Weinberg realized that reducible diagrams violate the chiral expansion and, therefore, proposed to determine the potential using the rules of ChPT and then insert it into a Schrödinger-like equation to conduct the non-perturbative resummation.

Soon after, the first nuclear potentials were obtained by Ordoñez and van Kolck [7–9]. These position-space potentials were developed up to next-to-next-to-leading order (N²LO) and regularized by a cutoff function. Momentum-space potentials up to N²LO using dimensional regularization were derived by the Bochum group [10, 11]. The simple and transparent momentum-space expressions obtained in this type of derivation [12] made chiral potentials more popular. However it was not until 2003 that χEFT reached high precision when the first chiral potential at N³LO was developed by Entem and Machleidt [13, 14] that was able to describe the NN scattering data with a χ²/d.o.f similar to what the high-precision potentials of the 90's had achieved [15–18].

Since then, many applications of N³LO NN potentials together with chiral three-nucleon forces (3NFs) have been reported. These investigations include few-nucleon reactions [19–22], structure of light- and medium-mass nuclei [23–27] and infinite matter [28–33]. Although satisfactory predictions have been obtained in many cases, persistent problems continue to pose serious challenges, as the overbinding in medium mass nuclei [25] or the descriptions of charge and matter radii [34]. There is also the well-known A_y puzzle of nucleon-deuteron scattering [35]. In this case recent calculations including contact 3NFs at N⁴LO have been shown to be able to solve the puzzle [36]. This suggests that one may have to proceed to the next higher order, namely, N⁴LO, for the two-nucleon force.

Thus, during the past few years, chiral potentials up to N⁴LO have been developed by the Idaho-Salamanca group [37] as well as the Bochum group [38].

In the whole chapter we will be referring to the so called Δ-less EFT, where Δ degrees of freedom have been integrated out. There are recent advances in the Δ-full theory [39, 40]. We refer the interested reader to contributions on this topic in the present monograph.

The chapter is organized as follows. In section 2 we review the most important aspects of χEFT for the two-nucleon system. In section 3 we apply the perturbative amplitude obtained to study peripheral NN scattering up to N⁵LO. In section 4 we review NN potentials up to N⁴LO. We conclude with a summary in section 5.

2. Chiral EFT for the NN System

2.1. Power Counting

In order to build an EFT for the two nucleon system, the Lagrangians for the involved degrees of freedom have to be constructed. However, there is an infinite number of terms in the Lagrangian compatible with the allowed symmetries. For this reason, it is necessary to order all terms by what we call power counting. Following power counting, the terms in the Lagrangian are arranged by order. Moreover, the diagrams representing an amplitude calculated from the Lagrangian are also of a well defined order. Since higher orders include loop diagrams that diverge, the power counting also needs to be such that all the infinities generated at a certain order can be reabsorbed into redefinitions of the coupling constants of the Lagrangian at the same order. With these ideas in mind Weinberg, proposed the so called Weinberg power counting which is based on naive dimensional analysis.

Following naive dimensional analysis, a nucleon propagator counts as Q⁻¹, where Q stands for a low momentum or pion mass, a pion propagator as Q⁻², each derivative or pion mass insertion counts as Q and each four momentum integration as Q⁴. The power of a diagram is then given by the simple formula [5, 6, 14]

$\begin{array}{ll}\nu =-2+2A-2C+2L+{\displaystyle \sum _i}{\Delta }_i,& (1)\end{array}$

where A is the number of nucleons involved, C the number of connected pieces, L the number of loops, and the sum runs over all vertexes i with Δ_i the index of the vertex given by

$\begin{array}{ll}{\Delta }_i\equiv d_i+\frac{n_i}{2}-2& (2)\end{array}$

with d_i the number of derivatives or pion mass insertions (chiral dimension) and n_i the number of nucleon legs. In this way the contribution of a diagram goes as ${(Q/{\Lambda }_b)}^{\nu }$ with Λ_b the breakdown scale.

In the heavy-baryon formalism, an expansion in terms of Q/M_N is performed, with M_N denoting the nucleon mass. It is used for low energy nucleon systems and we will count these contributions as $Q/M_N~{(Q/{\Lambda }_b)}^2$ for reasons explained in Weinberg [5, 6].

An important property of chiral symmetry is that the index of the vertexes is always zero or positive Δ_i ≥ 0. This fact implies that for a fixed number of nucleons with A ≥ 2 and considering diagrams with one connected piece, the power of a diagram is always bounded from below. This fact is crucial for the convergence of the chiral expansion.

A very important aspect of the EFT is that it relates two-body forces with many-body forces. We know that two-body forces are the main contribution to nuclear forces, however, many-body forces should exist. If we consider lowest order diagrams with L = 0 and Δ_i = 0, for an m-body force in an A-nucleon system, the number of separately connected pieces is C = A − m + 1, and so the power of the diagram is given by ν = 2m − 4. This means that two-body forces (m = 2) appear at ν = 0, three-body forces (m = 3) at ν = 2, four-body (m = 4) at ν = 4 and so on. So the power counting explains in a simple way the hierarchy of nuclear forces. In Figure 1 we summarize this hierarchy up to N⁵LO or sixth order of the chiral expansion.

FIGURE 1

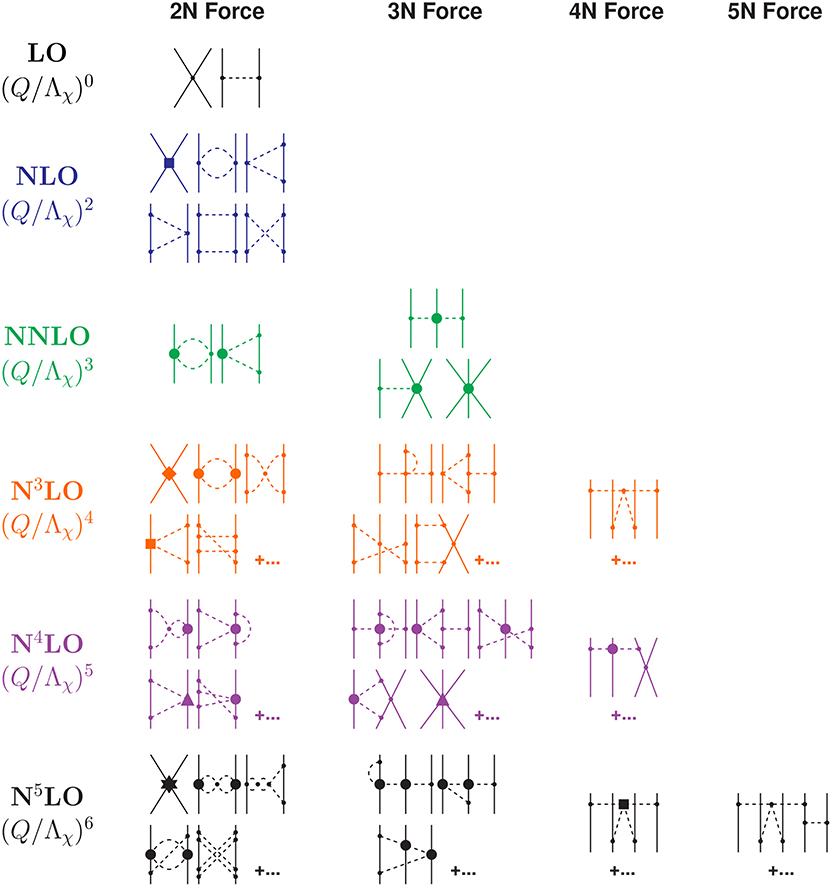
Figure 1. Hierarchy of nuclear forces up to N⁵LO or sixth order of the chiral expansion. Only some representative diagrams are included. Small dots, large solid dots, solid squares, triangles, diamonds, and stars denote vertexes of index Δ_i = 0, 1, 2, 3, 4, and 6, respectively. Reprinted figure with permission from Entem et al. [37], copyright (2017) by the American Physical Society.

2.2. The Lagrangian

We will limit ourselves to the Δ-less version of χEFT, and so the relevant degrees of freedom are pions and nucleons. The effective Lagrangian, subdivided in terms of the number of nucleon legs, is given by

$\begin{array}{ll}{{L}}_{\text{eff}}={{L}}_{\pi \pi }+{{L}}_{\pi N}+{{L}}_{NN}+\dots ,& (3)\end{array}$

where ${{L}}_{\pi \pi }$ stands for the Lagrangian that deals with pion dynamics, ${{L}}_{\pi N}$ the interaction between pions and a nucleon, and ${{L}}_{NN}$ contains four nucleon legs and no pion fields. The ellipsis stands for terms that involve two nucleons plus pions and three or more nucleons with or without pions, not relevant for the two nucleon sector.

All the pieces in the Lagrangian are then organized in terms of the chiral dimension (number of derivatives/pion mass insertions) of increasing order

$\begin{array}{ll}{{L}}_{\pi \pi }={{L}}_{\pi \pi }^{(2)}+{{L}}_{\pi \pi }^{(4)}+\dots ,& (4)\end{array}$

$\begin{array}{ll}{{L}}_{\pi N}={{L}}_{\pi N}^{(1)}+{{L}}_{\pi N}^{(2)}+{{L}}_{\pi N}^{(3)}+{{L}}_{\pi N}^{(4)}+{{L}}_{\pi N}^{(5)}+\dots ,& (5)\end{array}$

$\begin{array}{ll}{{L}}_{NN}={{L}}_{NN}^{(0)}+{{L}}_{NN}^{(2)}+{{L}}_{NN}^{(4)}+\dots ,& (6)\end{array}$

where the superscript refers to the chiral dimension and the ellipsis refers to terms of higher dimensions. We use the heavy-baryon formulation of the Lagrangians, the explicit expressions of which can be found in Machleidt and Entem [14] and Krebs et al. [41]. Notice that only in the NN case the chiral dimension is the same as the index Δ_i.

2.3. The Scattering Amplitude

Having the Lagrangian, we can now calculate the NN scattering amplitude. The NN amplitude has contributions from irreducible as well as reducible diagrams. The reducible diagrams are those that we can separate into two diagrams by cutting only nucleon lines. In covariant perturbation theory the separation is well defined, however when we apply a three-dimensional reduction of the Bethe-Salpeter equation it depends on the way this reduction is performed. See Machleidt and Entem [14] for a discussion on this point. We will come back to this when we define the potential.

The amplitude for diagrams involving pions is organized in terms of the number of pions exchanged by the two nucleons

$\begin{array}{ll}{V}_{\pi }=V_{1\pi }+V_{2\pi }+V_{3\pi }+\dots & (7)\end{array}$

Then each piece is divided in terms of the power counting described previously as

$\begin{array}{ll}{V}_{1\pi }=V_{1\pi }^{(0)}+V_{1\pi }^{(2)}+V_{1\pi }^{(3)}+V_{1\pi }^{(4)}+V_{1\pi }^{(5)}+V_{1\pi }^{(6)}+\dots ,& (8)\end{array}$

$\begin{array}{ll}{V}_{2\pi }=V_{2\pi }^{(2)}+V_{2\pi }^{(3)}+V_{2\pi }^{(4)}+V_{2\pi }^{(5)}+V_{2\pi }^{(6)}+\dots ,& (9)\end{array}$

$\begin{array}{ll}{V}_{3\pi }=V_{3\pi }^{(4)}+V_{3\pi }^{(5)}+V_{3\pi }^{(6)}+\dots ,& (10)\end{array}$

where the superscript denotes the order ν.

Besides these diagrams, contributions coming from Lagrangian ${{L}}_{NN}$ are also present. These contributions are contact-like contributions and take into account the unknown short-distance dynamics. They are again organized using the power counting

$\begin{array}{ll}{V}_{\text{ct}}=V_{\text{ct}}^{(0)}+V_{\text{ct}}^{(2)}+V_{\text{ct}}^{(4)}+V_{\text{ct}}^{(6)}+\dots ,& (11)\end{array}$

where the superscript is the order ν. Due to symmetry requirements these contributions come only in even powers.

Then the order by order contributions are given by

$\begin{array}{ll}{V}_{\text{LO}}\equiv V_{\pi }^{(0)}+V_{\text{ct}}^{(0)}=V_{\text{ct}}^{(0)}+V_{1\pi }^{(0)},& (12)\end{array}$

$\begin{array}{ll}{V}_{\text{NLO}}\equiv V_{\text{LO}}+V_{\pi }^{(2)}+V_{\text{ct}}^{(2)}=V_{\text{LO}}+V_{\text{ct}}^{(2)}+V_{1\pi }^{(2)}+V_{2\pi }^{(2)},& (13)\end{array}$

$\begin{array}{ll}{V}_{\text{NNLO}}\equiv V_{\text{NLO}}+V_{\pi }^{(3)}=V_{\text{NLO}}+V_{1\pi }^{(3)}+V_{2\pi }^{(3)},& (14)\end{array}$

$\begin{array}{l}{V}_{{\text{N}}^3\text{LO}}\equiv V_{\text{NNLO}}+V_{\pi }^{(4)}+V_{\text{ct}}^{(4)}=V_{\text{NNLO}}+V_{\text{ct}}^{(4)}+V_{1\pi }^{(4)}\\ +V_{2\pi }^{(4)}+V_{3\pi }^{(4)},& (15)\end{array}$

$\begin{array}{l}{V}_{{\text{N}}^4\text{LO}}\equiv V_{{\text{N}}^3\text{LO}}+V_{\pi }^{(5)}=V_{{\text{N}}^3\text{LO}}+V_{1\pi }^{(5)}+V_{2\pi }^{(5)}\\ +V_{3\pi }^{(5)},& (16)\end{array}$

$\begin{array}{l}{V}_{{\text{N}}^5\text{LO}}\equiv V_{{\text{N}}^4\text{LO}}+V_{\pi }^{(6)}+V_{\text{ct}}^{(6)}=V_{{\text{N}}^4\text{LO}}+V_{\text{ct}}^{(6)}+V_{1\pi }^{(6)}\\ +V_{2\pi }^{(6)}+V_{3\pi }^{(6)},& (17)\end{array}$

where LO stands for leading order, NLO next-to-leading order, etc.

For the presentation of amplitudes we will use the following decomposition

$\begin{array}{l}V(\overrightarrow{p}{ }^{\prime },\overrightarrow{p})= V_C +{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2{W}_C\\ +\left[V_S +{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2{W}_S \right]{\overrightarrow{\sigma }}_1·{\overrightarrow{\sigma }}_2\\ +\left[V_{LS}+{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2{W}_{LS}\right]\left(-i\overrightarrow{S}·(\overrightarrow{q}\times \overrightarrow{k})\right)\\ +\left[V_T +{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2{W}_T \right]{\overrightarrow{\sigma }}_1·\overrightarrow{q}{\overrightarrow{\sigma }}_2·\overrightarrow{q}\\ +\left[V_{\sigma L}+{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2{W}_{\sigma L}\right]{\overrightarrow{\sigma }}_1·(\overrightarrow{q}\times \overrightarrow{k}){\overrightarrow{\sigma }}_2·(\overrightarrow{q}\times \overrightarrow{k}),& (18)\end{array}$

where ${\overrightarrow{p}}^{\prime }$ and $\overrightarrow{p}$ denote the final and initial nucleon momenta in the center-of-mass system (CMS), respectively. Moreover, $\overrightarrow{q}={\overrightarrow{p}}^{\prime }-\overrightarrow{p}$ is the momentum transfer, $\overrightarrow{k}=({\overrightarrow{p}}^{\prime }+\overrightarrow{p})/2$ the average momentum, and $\overrightarrow{S}=({\overrightarrow{\sigma }}_1+{\overrightarrow{\sigma }}_2)/2$ the total spin, with ${\overrightarrow{\sigma }}_{1,2}$ and ${\overrightarrow{\tau }}_{1,2}$ the spin and isospin operators, of nucleon 1 and 2, respectively. For on-shell scattering, V_α and W_α (α = C, S, LS, T, σL) can be expressed as functions of $q=\left|\overrightarrow{q}\right|$ and $p=\left|{\overrightarrow{p}}^{\prime }\right|=\left|\overrightarrow{p}\right|$, only.

2.4. Pion-Exchange Contributions

We now specify the contributions coming from pion exchanges which provide the long-range interactions. Contributions at LO, NLO, and NNLO are diagrammatically given by the graphs in Figure 2.

FIGURE 2

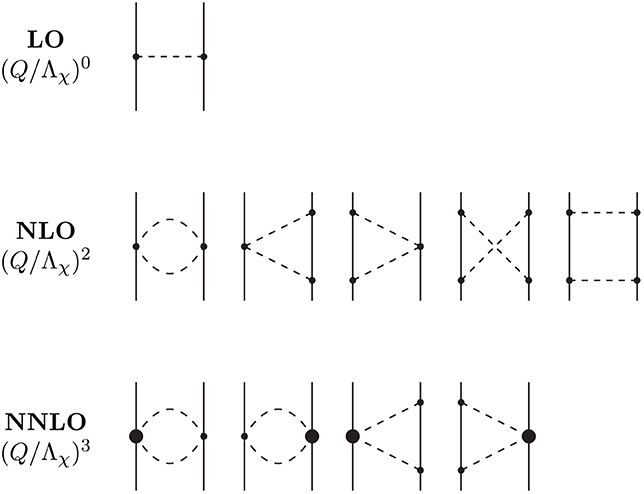
Figure 2. LO, NLO, and NNLO contributions to the NN interaction. Solid lines represent nucleons and dashed lines pions. Small dots and large solid dots represent vertices with index Δ_i = 0 and 1, respectively. Reprinted figure with permission from Entem et al. [46], copyright (2015) by the American Physical Society.

2.4.1. Leading Order

The leading order (LO) is just the charge-independent one-pion-exchange (OPE). The expression is given by

$\begin{array}{ll}{V}_{1\pi }^{(0)}=-\frac{g_A^2}{4f_{\pi }^2}{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2\frac{{\overrightarrow{\sigma }}_1·\overrightarrow{q}{\overrightarrow{\sigma }}_2·\overrightarrow{q}}{q^2+m_{\pi }^2},& (19)\end{array}$

where g_A, f_π, and m_π denoted the axial-vector coupling constant, pion-decay constant, and the pion mass, respectively. There are corrections at higher orders that renormalize the coupling constant. They are taken into account by using g_A/f_π = g_πN/M_N, with g_πN the πNN coupling constant. Numerical values are given in Table 1. Note that, on-shell, there are no relativistic corrections.

TABLE 1

Table 1. Basic constants used throughout this review article.

Charge dependence is taken into account using

$\begin{array}{ll}{V}_{1\pi }^{(np)}({\overrightarrow{p}}^{\prime },\overrightarrow{p})=-V_{1\pi }(m_{{\pi }^0})+{(-1)}^{I+1}2V_{1\pi }(m_{{\pi }^{\pm }}),& (20)\end{array}$

$\begin{array}{ll}{V}_{1\pi }^{(pp/nn)}({\overrightarrow{p}}^{\prime },\overrightarrow{p})=V_{1\pi }(m_{{\pi }^0}),& (21)\end{array}$

with I the isospin of the two-nucleon system and

$\begin{array}{ll}{V}_{1\pi }(m_{\pi })=-\frac{g_A^2}{4f_{\pi }^2}\frac{{\overrightarrow{\sigma }}_1·\overrightarrow{q}{\overrightarrow{\sigma }}_2·\overrightarrow{q}}{q^2+m_{\pi }^2};& (22)\end{array}$

$m_{{\pi }^0}$ denotes the mass of the neutral pion and $m_{{\pi }^{\pm }}$ the one of the charged pion. The charge dependence is an NLO effect [14], but we include it already at leading order to make comparison with phase-shifts more meaningful.

2.4.2. Next-to-Leading Order

The NLO contributions appear at order ν = 2. Symmetry requirements make the contributions at ν = 1 vanish. In the past, the expressions for these diagrams as obtained in dimensional regularization were used [14]. Here, we apply the so-called spectral-function regularization (SFR) [42]. The potentials are obtained using dispersion relations from the imaginary part of the amplitude in the left-hand cut. However a cut-off $\tilde{\Lambda }$ is used in the dispersion relation to constrain the potentials to the low-energy region where χEFT is applicable.

The contribution is given by

$\begin{array}{l}{W}_C=\frac{L(\tilde{\Lambda };q)}{384{\pi }^2{f}_{\pi }^4}[4m_{\pi }^2(1+4g_A^2-5g_A^4)+q^2(1+10g_A^2-23g_A^4)\\ {\displaystyle -\frac{48g_A^4{m}_{\pi }^4}{w^2}],}& (23)\end{array}$

$\begin{array}{ll}{V}_T=-\frac{1}{q^2}{V}_S=-\frac{3g_A^4}{64{\pi }^2{f}_{\pi }^4}L(\tilde{\Lambda };q),& (24)\end{array}$

with

$\begin{array}{ll}w=\sqrt{4m_{\pi }^2+q^2},& (25)\end{array}$

$\begin{array}{ll}L(\tilde{\Lambda };q)=\frac{w}{2q}ln\frac{{\tilde{\Lambda }}^2(2m_{\pi }^2+q^2)-2m_{\pi }^2{q}^2+\tilde{\Lambda }\sqrt{{\tilde{\Lambda }}^2-4m_{\pi }^2}qw}{2m_{\pi }^2({\tilde{\Lambda }}^2+q^2)},& (26)\end{array}$

which agrees with the dimensional regularization expressions [14] when replacing $L(\tilde{\Lambda };q)$ by L(q). In fact,

$\begin{array}{ll}{\displaystyle \underset{\tilde{\Lambda }\to \infty }{lim}}L(\tilde{\Lambda };q)=L(q).& (27)\end{array}$

2.4.3. Next-to-Next-to-Leading Order

Here the diagrams that contribute include a vertex with Δ_i = 1 which is represented by a large solid dot in Figure 2. The NNLO contribution is

$\begin{array}{ll}{V}_C=\frac{3g_A^2}{16\pi f_{\pi }^4}\left[2m_{\pi }^2(c_3-2c_1)+c_3{q}^2\right](2m_{\pi }^2+q^2)A(\tilde{\Lambda };q),& (28)\end{array}$

$\begin{array}{ll}{W}_T=-\frac{1}{q^2}{W}_S=-\frac{g_A^2}{32\pi f_{\pi }^4}{c}_4{w}^{2}A(\tilde{\Lambda };q),& (29)\end{array}$

with

$\begin{array}{ll}A(\tilde{\Lambda };q)=\frac{1}{2q}arctan\frac{q(\tilde{\Lambda }-2m_{\pi })}{q^2+2\tilde{\Lambda }{m}_{\pi }}.& (30)\end{array}$

As in the case of the NLO contribution, dimensional regularization is recovered when using

$\begin{array}{ll}{\displaystyle \underset{\tilde{\Lambda }\to \infty }{lim}}A(\tilde{\Lambda };q)=\frac{1}{2q}arctan\frac{q}{2m_{\pi }}.& (31)\end{array}$

Notice that, here, we demote the relativistic corrections of the NLO diagrams to N³LO, while in Machleidt and Entem [14] they were counted NNLO.

2.4.4. N³LO Contributions

At this order the first 3π exchange contributions appear. However it was shown in Kaiser [43, 44] that they give negligible contributions for peripheral waves and, therefore, we leave them out.

There are three types of contributions given by the three classes represented in Figure 3. The first one is the football diagram (a). The contribution is [45],

$\begin{array}{l}{V}_C=\frac{3}{16{\pi }^2{f}_{\pi }^4}{\displaystyle [{\left(\frac{c_2}{6}{w}^2+c_3(2m_{\pi }^2+q^2)-4c_1{m}_{\pi }^2\right)}^2}\\ {\displaystyle +\frac{c_2^2}{45}{w}^4]}L(\tilde{\Lambda };q),& (32)\end{array}$

$\begin{array}{ll}{W}_T=-\frac{1}{q^2}{W}_S=\frac{c_4^2}{96{\pi }^2{f}_{\pi }^4}{w}^{2}L(\tilde{\Lambda };q).& (33)\end{array}$

FIGURE 3

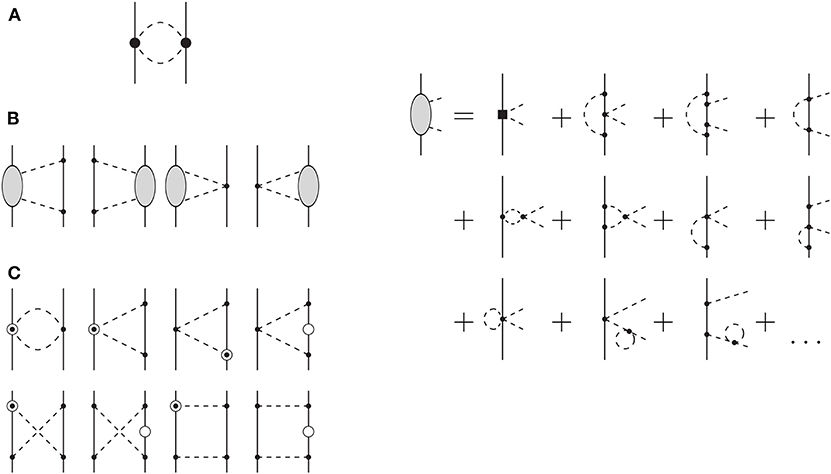
Figure 3. N³LO 2π-exchange contributions to the NN interaction. The same notation as in Figure 2 is use. Solid squares represent vertices with index Δ_i = 2. Open circles and open circles with a dot inside are relativistic 1/M_N corrections to propagators and the vertex with one derivative, respectively. The leading one-loop πN amplitude is represented by a shaded oval. Adapted figure with permission from Entem et al. [46], copyright (2015) by the American Physical Society. (A) Football diagram, (B) two-loop diagrams, and (C) relativistic corrections to one loop diagrams.

The second class (b) corresponds to the 2π-exchange two-loop diagrams.

Here as well as for the N⁴LO expressions (see below), we state contributions in terms of their spectral functions, from which the momentum-space amplitudes V_α(q) and W_α(q) are obtained via the subtracted dispersion integrals:

$\begin{array}{l}{V}_{C,S}(q)=-\frac{2q^6}{\pi }{\displaystyle {\int }_{n{m}_{\pi }}^{\tilde{\Lambda }}}d\mu \frac{\text{Im }{V}_{C,S}(i\mu )}{{\mu }^5({\mu }^2+q^2)},\\ V_T(q)=\frac{2q^4}{\pi }{\displaystyle {\int }_{n{m}_{\pi }}^{\tilde{\Lambda }}}d\mu \frac{\text{Im }{V}_T(i\mu )}{{\mu }^3({\mu }^2+q^2)},& (34)\end{array}$

and similarly for W_{C, S, T}. The thresholds are given by n = 2 for two-pion exchange and n = 3 for three-pion exchange. For $\tilde{\Lambda }\to \infty$ the above dispersion integrals yield the finite parts of loop-functions as in dimensional regularization, while for finite $\tilde{\Lambda }>>n{m}_{\pi }$ we employ the method known as spectral-function regularization (SFR). The purpose of the finite scale $\tilde{\Lambda }$ is to constrain the imaginary parts to the low-momentum region where chiral effective field theory is applicable.

The spectral functions for class (b) are given by [45, 46]

$\begin{array}{l}\text{Im }{V}_C=\frac{3g_A^4(2m_{\pi }^2-{\mu }^2)}{\pi \mu {(4f_{\pi })}^6}[(m_{\pi }^2-2{\mu }^2)\\ \left(2m_{\pi }+\frac{2m_{\pi }^2-{\mu }^2}{2\mu }\ln \frac{\mu +2m_{\pi }}{\mu -2m_{\pi }}\right)\\ +4g_A^2{m}_{\pi }(2m_{\pi }^2-{\mu }^2)],& (35)\end{array}$

$\begin{array}{l}\text{Im }{V}_S={\mu }^2\text{ Im }{V}_T=\frac{g_A^2\mu {\kappa }^3}{8\pi f_{\pi }^4}\left({\overline{d}}_{15}-{\overline{d}}_{14}\right)\\ +\frac{2g_A^6\mu {\kappa }^3}{{(8\pi f_{\pi }^2)}^3}{\displaystyle {\int }_0^{1}d}x(1-x^2)[\frac{1}{6}-\frac{m_{\pi }^2}{{\kappa }^2{x}^2}\\ +{\left(1+\frac{m_{\pi }^2}{{\kappa }^2{x}^2}\right)}^{3/2}\ln \frac{\kappa x+\sqrt{m_{\pi }^2+{\kappa }^2{x}^2}}{m_{\pi }}],& (36)\end{array}$

$\begin{array}{l}{\displaystyle \text{Im }{W}_C=\frac{2\kappa }{3\mu {(8\pi f_{\pi }^2)}^3}{\displaystyle {\int }_0^{1}d}x[g_A^2({\mu }^2-2m_{\pi }^2)+2(1-g_A^2){\kappa }^2{x}^2]}\\ {\displaystyle \times \{96{\pi }^2{f}_{\pi }^2[(2m_{\pi }^2-{\mu }^2)({\overline{d}}_1+{\overline{d}}_2)-2{\kappa }^2{x}^2{\overline{d}}_3}\\ +4m_{\pi }^2{\overline{d}}_5]+\left[4m_{\pi }^2(1+2g_A^2)-{\mu }^2(1+5g_A^2)\right]\frac{\kappa }{\mu }\\ \ln \frac{\mu +2\kappa }{2m_{\pi }}+\frac{{\mu }^2}{12}(5+13g_A^2)-2m_{\pi }^2(1+2g_A^2)\\ +g_A^4\left({\mu }^2-2{\kappa }^2{x}^2-2m_{\pi }^2\right)[\frac{5}{6}+\frac{m_{\pi }^2}{{\kappa }^2{x}^2}\\ -{\left(1+\frac{m_{\pi }^2}{{\kappa }^2{x}^2}\right)}^{3/2}\ln \frac{\kappa x+\sqrt{m_{\pi }^2+{\kappa }^2{x}^2}}{m_{\pi }}]\\ -3{\kappa }^2{x}^2+6\kappa x\sqrt{m_{\pi }^2+{\kappa }^2{x}^2}\ln \frac{\kappa x+\sqrt{m_{\pi }^2+{\kappa }^2{x}^2}}{m_{\pi }}\},& (37)\end{array}$

$\begin{array}{l}\text{Im }{W}_S={\mu }^2\text{ Im }{W}_T(i\mu )\\ =\frac{g_A^4(4m_{\pi }^2-{\mu }^2)}{\pi {(4f_{\pi })}^6}[\left(m_{\pi }^2-\frac{{\mu }^2}{4}\right)\ln \frac{\mu +2m_{\pi }}{\mu -2m_{\pi }}\\ +(1+2g_A^2)\mu m_{\pi }],& (38)\end{array}$

where $\kappa =\sqrt{{\mu }^2/4-m_{\pi }^2}$. Here and below all imaginary parts are evaluated at iμ, because that is where they are needed for the calculation of the SFR integrals.

Finally the relativistic corrections of the NLO diagrams corresponding to class (c) are given by [14]

$\begin{array}{ll}{V}_C=\frac{3g_A^4}{128\pi f_{\pi }^4{M}_N}{\displaystyle [\frac{m_{\pi }^5}{2w^2}+(2m_{\pi }^2+q^2)(q^2-m_{\pi }^2)A(\tilde{\Lambda };q){\displaystyle ]}},& (39)\end{array}$

$\begin{array}{l}{W}_C=\frac{g_A^2}{64\pi f_{\pi }^4{M}_N}{\displaystyle \{\frac{3g_A^2{m}_{\pi }^5}{2{\omega }^2}+[g_A^2(3m_{\pi }^2+2q^2)-2m_{\pi }^2-q^2}]\\ {\displaystyle (2m_{\pi }^2-q^2)A(\tilde{\Lambda };q)\},}& (40)\end{array}$

$\begin{array}{ll}{V}_T=-\frac{1}{q^2}{V}_S=\frac{3g_A^4}{256\pi f_{\pi }^4{M}_N}(5m_{\pi }^2+2q^2)A(\tilde{\Lambda };q),& (41)\end{array}$

$\begin{array}{ll}{W}_T=-\frac{1}{q^2}{W}_S=\frac{g_A^2}{128\pi f_{\pi }^4{M}_N}{\displaystyle [g_A^2\left(3m_{\pi }^2+q^2\right)-w^2]}A\left(\tilde{\Lambda };q\right),& (42)\end{array}$

$\begin{array}{ll}{V}_{LS}=\frac{3g_A^4}{32\pi f_{\pi }^4{M}_N}(2m_{\pi }^2+q^2)A(\tilde{\Lambda };q),& (43)\end{array}$

$\begin{array}{ll}{W}_{LS}=\frac{g_A^2(1-g_A^2)}{32\pi f_{\pi }^4{M}_N}{w}^{2}A(\tilde{\Lambda };q).& (44)\end{array}$

2.4.5. N⁴LO Contributions

The 2π-exchange contributions at N⁴LO have three different classes of diagrams shown in Figure 4. The contributions of class (a) and (b) are given in terms of spectral functions and Equation (34).

FIGURE 4

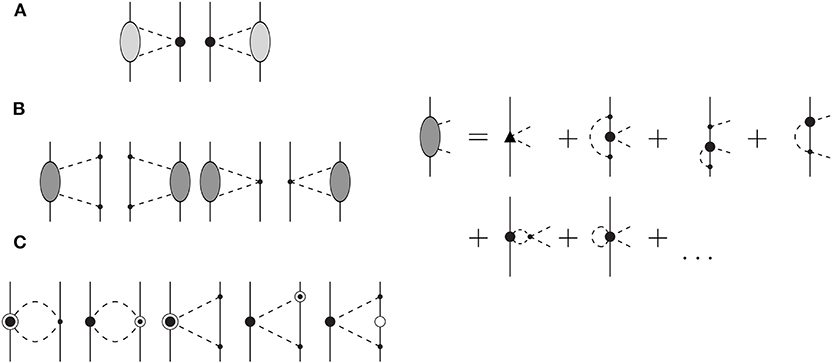
Figure 4. N⁴LO 2π-exchange contributions to the NN interaction. The same notation as in Figure 3 is used. Open circles with a large solid dot inside refers to the 1/M_N corrections to vertexes with two derivatives. Solid triangles represent vertices with index Δ_i = 3. The subleading one-loop πN amplitude is represented by a dark-shaded oval. Adapted figure with permission from Entem et al. [46], copyright (2015) by the American Physical Society. (A,B) Two-loop diagrams, and (C) relativistic corrections to one loop diagrams.

The spectral functions for class (a) are obtained by integrating the product of the leading one-loop πN amplitude and the subleading chiral ππNN vertex proportional to c_i over the Lorentz-invariant 2π-phase space. The result for the non-vanishing amplitudes is given by [46]

$\begin{array}{l}\text{Im }{V}_C=-\frac{m_{\pi }^5}{{\left(4f_{\pi }\right)}^6{\pi }^2}{\displaystyle \{g_A^2\sqrt{u^2-4}{\displaystyle (5-2u^2-\frac{2}{u^2})}}\\ {\displaystyle [24c_1+c_2(u^2-4)+6c_3(u^2-2\left)\right]}\ln \frac{u+2}{u-2}\\ +\frac{8}{u}{\displaystyle \left[3\right(4c_1+c_3(u^2-2)\left)\right(4g_A^4{u}^2-10g_A^4+1)}\\ {\displaystyle +c_2(6g_A^4{u}^2-10g_A^4-3)]}B\left(u\right)\\ +\sqrt{u^2-4}{\displaystyle \left[3\right(2-u^2\left)\right(4c_1+c_3(u^2-2))}\\ +c_2(7u^2-6-u^4)+\frac{4g_A^2}{u}(2u^2-1)\\ {\displaystyle \times \left[4\right(6c_1-c_2-3c_3)+(c_2+6c_3\left)u^2\right]}\\ +4g_A^4{\displaystyle (\frac{32}{u+2}}(2c_1+c_3)+\frac{64}{3u}(6c_1+c_2-3c_3)\\ +14c_3-5c_2-92c_1+\frac{8u}{3}(18c_3-5c_2)\\ {\displaystyle +\frac{u^2}{6}(36c_1+13c_2-156c_3)+\frac{u^4}{6}(2c_2+9c_3)\left)\right]\},}& (45)\end{array}$

$\begin{array}{l}\text{Im }{W}_S={\mu }^2\text{ Im }{W}_T={\displaystyle \frac{c_4{g}_A^2{m}_{\pi }^5}{{\left(4f_{\pi }\right)}^6{\pi }^2}\{8g_A^{2}u\left(5-u^2\right)B\left(u\right)+}\\ \frac{1}{3}{\left(u^2-4\right)}^{5/2}ln\frac{u+2}{u-2}\\ {\displaystyle +\frac{u}{3}\sqrt{u^2-4}{\displaystyle [g_A^2\left(30u-u^3-64\right)-4u^2+16{\displaystyle ]}}{\displaystyle \}},}& (46)\end{array}$

with the dimensionless variable u = μ/m_π > 2 and the logarithmic function

$\begin{array}{ll}B(u)=ln\frac{u+\sqrt{u^2-4}}{2}.& (47)\end{array}$

Class (b) is obtained in the same way but multiplying the one-loop πN amplitude proportional to c_i (see [41] for details) and the leading-order chiral πN amplitude. The result is [46]

$\begin{array}{l}\text{Im }{V}_S={\mu }^2\text{ Im }{V}_T=\frac{g_A^4{m}_{\pi }^5(c_3-c_4)u}{{(4f_{\pi })}^6{\pi }^2}\\ {\displaystyle \{\sqrt{u^2-4}(u^3-30u+64)+24(u^2-5)B(u){\displaystyle \}}},& (48)\end{array}$

$\begin{array}{l}\text{Im }{W}_S={\mu }^2\text{ Im }{W}_T=\frac{g_A^2{m}_{\pi }^5}{{(4f_{\pi })}^6{\pi }^2}(4-u^2)\\ {\displaystyle \{\frac{c_4}{3}[\sqrt{u^2-4}(2u^2-8)B(u)}\\ +4u(2+9g_A^2)-\frac{5u^3}{3}]+2{\overline{e}}_{17}{(8\pi f_{\pi })}^2(u^3-2u)\}& (49)\end{array}$

$\begin{array}{l}{\displaystyle \text{Im }{V}_C=\frac{g_A^2{m}_{\pi }^5}{{(4f_{\pi })}^6{\pi }^2}(u^2-2)\left(\frac{1}{u^2}-2\right)\{}2\sqrt{u^2-4}\\ [24c_1+c_2(u^2-4)+6c_3(u^2-2)]B(u)\\ +u\left[c_2\left(8-\frac{5u^2}{3}\right)+6c_3(2-u^2)-24c_1\right]\}\\ +\frac{3g_A^2{m}_{\pi }^5}{{(2f_{\pi })}^{4}u}{\left(2-u^2\right)}^3{\overline{e}}_{14},& (50)\end{array}$

$\begin{array}{l}\text{Im }{W}_C=-\frac{c_1{m}_{\pi }^5}{{\left(2f_{\pi }\right)}^6{\pi }^2}{\displaystyle \{\frac{3g_A^2+1}{8}\sqrt{u^2-4}(2-u^2)}\\ +\left(\frac{3g_A^2+1}{u}-2g_A^{2}u\right)B(u)\}-\frac{c_2{m}_{\pi }^5}{{\left(2f_{\pi }\right)}^6{\pi }^2}\\ {\displaystyle \{\frac{1}{96}\sqrt{u^2-4}[7u^2-6-u^4+g_A^2(5u^2-6-2u^4)]}\\ {\displaystyle +\frac{1}{4u}(g_A^2{u}^2-1-g_A^2)B(u)\}}\\ {\displaystyle -\frac{c_3{m}_{\pi }^5}{{\left(4f_{\pi }\right)}^6{\pi }^2}\{\frac{2}{9}\sqrt{u^2-4}[3(7u^2-6-u^4)}\\ {\displaystyle +4g_A^2(\frac{32}{u}-12-20u+7u^2-u^4)}\\ {\displaystyle +g_A^4(114-\frac{512}{u}+368u-169u^2+7u^4+\frac{192}{u+2})]}\\ {\displaystyle +\frac{16}{3u}[g_A^4(6u^4-30u^2+35)+g_A^2(6u^2-8)-3]B(u)\}}\\ {\displaystyle -\frac{c_4{g}_A^2{m}_{\pi }^5}{{\left(4f_{\pi }\right)}^6{\pi }^2}\{\frac{2}{9}\sqrt{u^2-4}[30-\frac{128}{u}+80u-13u^2}\\ -2u^4+g_A^2{\displaystyle (\frac{512}{u}-114-368u+169u^2-7u^4}\\ {\displaystyle -\frac{192}{u+2}\left)\right]+\frac{16}{3u}[5-3u^2}\\ {\displaystyle +g_A^2(30u^2-35-6u^4)]B\left(u\right)\}.}& (51)\end{array}$

where the only two independent LEC's ē₁₄ and ē₁₇ have been used to give the final result.

Finally class (c) consists of the relativistic corrections of the NNLO 2π-exchange. The contributions are proportional to c_i/M_N. They read [45]

$\begin{array}{ll}{W}_C=-\frac{c_4}{192{\pi }^2{M}_N{f}_{\pi }^4}\left[g_A^2(8m_{\pi }^2+5q^2)+w^2\right]q^{2}L(\tilde{\Lambda };q),& (52)\end{array}$

$\begin{array}{l}{V}_C=\frac{g_A^{2}L(\tilde{\Lambda };q)}{32{\pi }^2{M}_N{f}_{\pi }^4}[(6c_3-c_2)q^4+4(3c_3-c_2-6c_1)q^2{m}_{\pi }^2\\ +6(2c_3-c_2)m_{\pi }^4-24(2c_1+c_3)m_{\pi }^6{w}^{-2}],& (53)\end{array}$

$\begin{array}{l}{W}_T=-\frac{1}{q^2}{W}_S=\frac{c_4}{192{\pi }^2{M}_N{f}_{\pi }^4}\\ \left[w^2-g_A^2(16m_{\pi }^2+7q^2)\right]L(\tilde{\Lambda };q),& (54)\end{array}$

$\begin{array}{ll}{V}_{LS}=\frac{c_2{g}_A^2}{8{\pi }^2{M}_N{f}_{\pi }^4}{w}^{2}L(\tilde{\Lambda };q),& (55)\end{array}$

$\begin{array}{ll}{W}_{LS}=-\frac{c_4}{48{\pi }^2{M}_N{f}_{\pi }^4}\left[g_A^2(8m_{\pi }^2+5q^2)+w^2\right]L(\tilde{\Lambda };q),& (56)\end{array}$

The 3π-exchange contributions at order N⁴LO are shown in Figure 5. The spectral functions have been calculated first in Kaiser [47] where the classification scheme applied in Figure 5 was introduced. Class XI vanishes while class X and part of class XIV give negligible contributions. Thus, we include in our calculations only class XII and XIII, and the V_S contribution of class XIV. In Kaiser [47], the spectral functions were presented in terms of integrals over the invariant mass of a pion pair. These integrals have been solved analytically in Entem et al. [46], and the spectral functions are given by

$\begin{array}{l}Im{V}_S^{(XII)}=-\frac{g_A^2{c}_4{m}_{\pi }^5}{{(4f_{\pi })}^6{\pi }^2{u}^3}{\displaystyle [\frac{y}{12}(u-1)}\\ (100u^3-27-50u-151u^2+185u^4-14u^5-7u^6)\\ {\displaystyle +4D(u)(2+10u^2-9u^4){\displaystyle ]},}& (57)\end{array}$

$\begin{array}{l}\mathrm{Im}{V}_T^{(\text{XII})}=\frac{1}{{\mu }^2}\mathrm{Im}{V}_S^{(\text{XII})}-\frac{g_A^2{c}_4{m}_{\pi }^3}{{(4f_{\pi })}^6{\pi }^2{u}^5}[\frac{y}{6}(u-1)\\ (u^6+2u^5-39u^4-12u^3+65u^2-50u-27)\\ +8D(u)(3u^4-10u^2+2)],& (58)\end{array}$

$\begin{array}{l}\mathrm{Im}{W}_S^{\left(\text{XII}\right)}=-\frac{g_A^2{m}_{\pi }^5}{{\left(4f_{\pi }\right)}^6{\pi }^2{u}^3}\{y(u-1)[\frac{4c_{1}u}{3}(u^3+2u^2-u+4)\\ {\displaystyle +\frac{c_2}{72}(u^6+2u^5-39u^4-12u^3+65u^2-50u-27)}\\ {\displaystyle +\frac{c_3}{12}(u^6+2u^5-31u^4+4u^3+57u^2-18u-27)}\\ {\displaystyle +\frac{c_4}{72}(7u^6+14u^5-185u^4-100u^3+151u^2+50u+27)]}\\ {\displaystyle +D(u)[16c_1(4u^2-1-u^4)+\frac{2c_2}{3}\left(2-10u^2+3u^4\right)}\\ {\displaystyle +4c_3{u}^2(u^2-2)+\frac{2c_4}{3}(9u^4-10u^2-2)\left]\right\},}& (59)\end{array}$

$\begin{array}{l}{\displaystyle \mathrm{Im}{W}_T^{(\text{XII})}=\frac{1}{{\mu }^2}\mathrm{Im}{W}_S^{(\text{XII})}-\frac{g_A^2{m}_{\pi }^3}{{(4f_{\pi })}^6{\pi }^2{u}^5}\{y(u-1)[\frac{16c_{1}u}{3}}\\ {\displaystyle (2+u-2u^2-u^3)+\frac{c_2}{36}(73u^4-6u^5-3u^6+44u^3}\\ {\displaystyle -43u^2-50u-27)+\frac{c_3}{2}(19u^4-2u^5-u^6}\\ {\displaystyle +4u^3-9u^2-6u-9)+\frac{c_4}{36}(39u^4-2u^5-u^6}\\ {\displaystyle +12u^3-65u^2+50u+27\left)\right]+4D\left(u\right)\left[8c_1\right(u^4-1)}\\ {\displaystyle +c_2(\frac{2}{3}-u^4)-2c_3{u}^4+\frac{c_4}{3}(10u^2-2-3u^4)\left]\right\},}& (60)\end{array}$

$\begin{array}{l}{\displaystyle \mathrm{Im}{W}_C^{\left(\text{XIII}\right)}=-\frac{g_A^4{c}_4{m}_{\pi }^5}{{\left(4f_{\pi }\right)}^6{\pi }^2}[\frac{8y}{3}(u-1)(u-4-2u^2-u^3)}\\ +32D(u)\left(u^3-4u+\frac{1}{u}\right)],& (61)\end{array}$

$\begin{array}{l}{\displaystyle \mathrm{Im}{V}_S^{\left(\text{XIII}\right)}=-\frac{g_A^4{c}_4{m}_{\pi }^5}{{\left(4f_{\pi }\right)}^6{\pi }^2{u}^3}[\frac{y}{24}(u-1)(37u^6+74u^5}\\ -251u^4-268u^3+349u^2-58u-135)\\ +2D\left(u\right)(39u^4-2-52u^2-6u^6)],& (62)\end{array}$

$\begin{array}{l}{\displaystyle \mathrm{Im}{V}_T^{\left(\text{XIII}\right)}=\frac{1}{{\mu }^2}\mathrm{Im}{V}_S^{\left(\text{XIII}\right)}-\frac{g_A^4{c}_4{m}_{\pi }^3}{{\left(4f_{\pi }\right)}^6{\pi }^2{u}^5}[\frac{y}{12}(u-1)(5u^6}\\ +10u^5-3u^4-252u^3\\ -{\displaystyle 443u^2-58u-135)+4D(u\left)\right(3u^4+22u^2-2\left)\right],}& (63)\end{array}$

$\begin{array}{l}{\displaystyle \mathrm{Im}{W}_S^{\left(\text{XIII}\right)}=-\frac{g_A^4{m}_{\pi }^5}{{\left(4f_{\pi }\right)}^6{\pi }^2{u}^3}\{y(u-1)[2c_{1}u(5u^3+10u^2-5u-4)}\\ {\displaystyle +\frac{c_2}{48}(135+58u-277u^2-36u^3+147u^4-10u^5-5u^6)}\\ {\displaystyle +\frac{c_3}{8}(7u^6+14u^5-145u^4-20u^3+111u^2+18u+27)}\\ {\displaystyle +\frac{c_4}{6}(44u^3+37u^4-14u^5-7u^6-3u^2-18u-27)]}\\ +D\left(u\right)[24c_1(1+4u^2-3u^4)+c_2(2+2u^2-3u^4)\\ {\displaystyle +6c_3{u}^2(3u^2-2)+8c_4{u}^2(u^4-5u^2+5)\left]\right\},}& (64)\end{array}$

$\begin{array}{l}\mathrm{Im}{W}_T^{\left(\text{XIII}\right)}=\frac{1}{{\mu }^2}\mathrm{Im}{W}_S^{\left(\text{XIII}\right)}-{\displaystyle \frac{g_A^4{m}_{\pi }^3}{{\left(4f_{\pi }\right)}^6{\pi }^2{u}^5}\{y(u-1)}\\ {\displaystyle [4c_{1}u(5u^3+10u^2+7u-4)+\frac{c_2}{24}(135+58u}\\ {\displaystyle +227u^2+204u^3+27u^4-10u^5-5u^6)}\\ {\displaystyle +\frac{c_3}{4}(27+18u-9u^2-68u^3-121u^4+14u^5+7u^6)}\\ {\displaystyle +c_4(4u^3+19u^4-2u^5-u^6-9u^2-6u-9)]}\\ +2D\left(u\right)[24c_1(1-3u^4)+c_2(2-10u^2-3u^4)\\ {\displaystyle +6c_3{u}^2(3u^2+2)-8c_4{u}^4\left]\right\},}& (65)\end{array}$

$\begin{array}{l}\mathrm{Im}{V}_S^{\left(\text{XIV}\right)}=-\frac{g_A^4{c}_4{m}_{\pi }^5}{{\left(4f_{\pi }\right)}^6{\pi }^2{u}^3}[\frac{y}{24}(u-1)(637u^2-58u-135+116u^3\\ -491u^4-22u^5-11u^6)\\ +2D\left(u\right)(6u^6-9u^4+8u^2-2)],& (66)\end{array}$

where $y=\sqrt{(u-3)(u+1)}$ and D(u) = ln[(u − 1 + y)/2] with u = μ/m_π > 3.

FIGURE 5

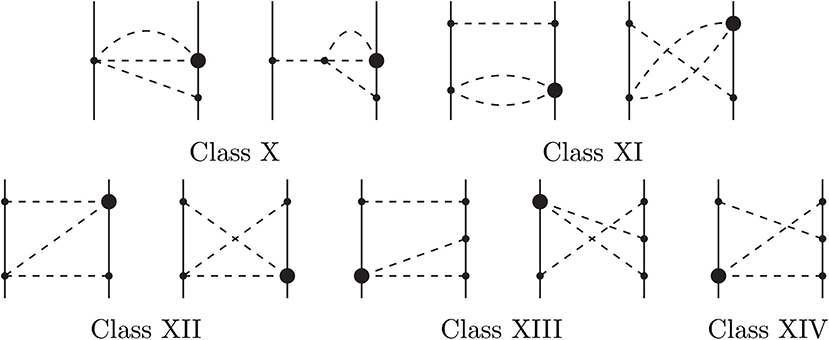
Figure 5. N⁴LO 3π-exchange contributions to the NN interaction. The classification scheme of Kaiser [47] is applied. The same notation as in Figure 2 is use. Reprinted figure with permission from Entem et al. [46], copyright (2015) by the American Physical Society.

2.4.6. Going Beyond N⁴LO

The next order is N⁵LO or sixth order. At this order, no complete calculation exists; however, the presumed dominant contributions have been evaluated in Entem et al. [48].

As before, we will state contributions in terms of their spectral functions, from which the momentum-space amplitudes V_α(q) and W_α(q) are obtained via subtracted dispersion integrals which, for N⁵LO read:

$\begin{array}{l}{V}_{C,S}(q)=\frac{2q^8}{\pi }{\displaystyle {\int }_{n{m}_{\pi }}^{\tilde{\Lambda }}}d\mu \frac{\text{Im }{V}_{C,S}(i\mu )}{{\mu }^7({\mu }^2+q^2)},\\ V_T(q)=-\frac{2q^6}{\pi }{\displaystyle {\int }_{n{m}_{\pi }}^{\tilde{\Lambda }}}d\mu \frac{\text{Im }{V}_T(i\mu )}{{\mu }^5({\mu }^2+q^2)},& (67)\end{array}$

and similarly for W_{C, S, T}. The thresholds are given by n = 2 for two-pion exchange and n = 3 for three-pion exchange.

The 2π-exchange at N⁵LO is given by the diagrams of Figure 6. There are three different classes. Class (a) is obtained from the subleading one loop πN amplitude folded with the subleading ππNN vertex proportional to c_i. The results for the non-vanishing spectral functions are

$\begin{array}{l}{\displaystyle \text{Im }{V}_C=\frac{m_{\pi }^6\sqrt{u^2-4}}{{(8\pi f_{\pi }^2)}^3}(\frac{1}{u^2}-2)[(c_2+6c_3)u^2+4(6c_1-c_2-3c_3)]}\\ {\displaystyle \{2c_{1}u+\frac{c_{2}u}{36}(5u^2-24)+\frac{c_{3}u}{2}(u^2-2)+[c_3(2-u^2)}\\ {\displaystyle +\frac{c_2}{6}(4-u^2)-4c_1]\sqrt{u^2-4}B(u)\}}\\ {\displaystyle +\frac{m_{\pi }^6\sqrt{u^2-4}}{8\pi f_{\pi }^{4}u}\left\{\right[4c_1+c_3(u^2-2)]}\\ {\displaystyle [{\overline{e}}_{15}(u^4-6u^2+8)+6{\overline{e}}_{14}{(u^2-2)}^2+\frac{3{\overline{e}}_{16}}{10}{(u^2-4)}^2]}\\ {\displaystyle +c_2(u^2-4)[\frac{3{\overline{e}}_{15}}{10}(u^4-6u^2+8)+{\overline{e}}_{14}{(u^2-2)}^2}\\ {\displaystyle +\frac{3{\overline{e}}_{16}}{28}{(u^2-4)}^2\left]\right\},}& (68)\end{array}$

$\begin{array}{l}{\displaystyle \text{Im }{W}_S=\frac{c_4^2{m}_{\pi }^6(u^2-4)}{9{(8\pi f_{\pi }^2)}^3}\left\{u\sqrt{u^2-4}\right[\frac{5u^2}{6}-4+\frac{2g_A^2}{15}(2u^2-23)]}\\ -{(u^2-4)}^{2}B(u)\\ {\displaystyle +6g_A^{2}u{\displaystyle {\int }_0^1\text{}}dx(x-\frac{1}{x}){[4+(u^2-4)x^2]}^{3/2}}\\ {\displaystyle \ln \frac{x\sqrt{u^2-4}+\sqrt{4+(u^2-4)x^2}}{2}\}}\\ {\displaystyle +\frac{c_4{m}_{\pi }^{6}u{(u^2-4)}^{3/2}}{240\pi f_{\pi }^4}[10{\overline{e}}_{17}(2-u^2)+{\overline{e}}_{18}(4-u^2)]}\\ ={\mu }^2\text{ Im}{W}_T,& (69)\end{array}$

with the dimensionless variable u = μ/m_π > 2 and the logarithmic function B(u) defined in Equation (46). We give the result in terms of the independent pion LEC's ē₁₄ and ē₁₈.

FIGURE 6

Figure 6. N⁵LO 2π-exchange contributions to the NN interaction. There are three classes of diagrams. Class (A) is obtained from the subleading one loop πN amplitude folded with the subleading ππNN vertex proportional to c_i. Class (B) is obtained from the leading one-loop πN amplitude folded by itself. Class (C) is obtained from the leading two-loop πN amplitude (represented by a black oval) with the tree-level πN amplitude. Other notation as in Figure 6. Adapted figure with permission from Entem et al. [48], copyright (2015) by the American Physical Society.

Class (b) is obtained from the leading one-loop πN amplitude folded by itself. The result is

$\begin{array}{l}{\displaystyle Im{V}_C=\frac{m_{\pi }^6\sqrt{u^2-4}}{{(4f_{\pi })}^8{\pi }^{3}u}\{-\frac{3}{70}(5u^2+8){(u^2-4)}^2}\\ {\displaystyle +3g_A^2(1-2u^2)[1+\frac{2-u^2}{4u}\ln \frac{u+2}{u-2}]}\\ {\displaystyle \times [u-\frac{u^3}{2}+\frac{4B(u)}{\sqrt{u^2-4}}]+g_A^4[\frac{32(3-2u^2)}{\sqrt{u^2-4}}B(u)}\\ {\displaystyle +3{(2u^2-1)}^2(\frac{u^2-2}{u}\ln \frac{u+2}{u-2}+\frac{{(u^2-2)}^2}{8u^2}}\\ {\displaystyle ({\pi }^2-{\ln }^2\frac{u+2}{u-2}))-\frac{2258}{35}+24u}\\ {\displaystyle +\frac{5336u^2}{105}-12u^3-\frac{2216u^4}{105}+\frac{18u^6}{35}]}\\ {\displaystyle +g_A^6(2u^2-1)(1+\frac{2-u^2}{4u}\ln \frac{u+2}{u-2})}\\ {\displaystyle [46u-3u^3-96+\frac{64}{u+2}+\frac{24(5-2u^2)}{\sqrt{u^2-4}}B(u)]}\\ {\displaystyle +\frac{64g_A^8}{9}[\frac{3119u^2}{70}-\frac{71u^6}{1120}-\frac{197u^4}{70}-\frac{85u^3}{8}+\frac{97u}{4}}\\ {\displaystyle -\frac{582}{7}-\frac{16}{u+2}+\frac{8}{{(u+2)}^2}+\frac{6u^4-60u^2+105}{\sqrt{u^2-4}}B(u)\left]\right\},}& (70)\end{array}$

$\begin{array}{l}{\displaystyle Im{W}_S=\frac{g_A^4{m}_{\pi }^6\sqrt{u^2-4}}{{(4f_{\pi })}^8{\pi }^{3}u}\{\frac{u^2-4}{48}{[4u+(4-u^2)\ln \frac{u+2}{u-2}]}^2}\\ {\displaystyle -\frac{{\pi }^2}{48}{(u^2-4)}^3+g_A^{2}u[(u^2-4)\ln \frac{u+2}{u-2}-4u]}\\ {\displaystyle [\frac{5u}{4}-\frac{u^3}{24}-\frac{8}{3}+\frac{5-u^2}{\sqrt{u^2-4}}B(u)]+\frac{32g_A^4{u}^2}{27}[\frac{u^4}{40}}\\ {\displaystyle +\frac{13u^2}{10}+\frac{11u}{2}-\frac{118}{5}-\frac{8}{u+2}+\frac{3(10-u^2)}{\sqrt{u^2-4}}B(u)\left]\right\}}\\ ={\mu }^2\text{Im}{W}_T,& (71)\end{array}$

$\begin{array}{l}{\displaystyle Im{V}_S=\frac{g_A^8{m}_{\pi }^{6}u\sqrt{u^2-4}}{3{(4f_{\pi })}^8{\pi }^5}{\displaystyle {\int }_0^1\text{}}dx(x^2-1)\{(u^2-4)x}\\ {\displaystyle [\frac{48{\pi }^2{f}_{\pi }^2}{g_A^4}({\overline{d}}_{14}-{\overline{d}}_{15})-\frac{1}{6}]+\frac{4}{x}}\\ {\displaystyle -\frac{{[4+(u^2-4)x^2]}^{3/2}}{x^2\sqrt{u^2-4}}\ln \frac{x\sqrt{u^2-4}+\sqrt{4+(u^2-4)x^2}}{2}{\}}^2}\\ ={\mu }^2\text{Im}{V}_T,& (72)\end{array}$

$\begin{array}{l}\text{Im}{W}_C=-\frac{m_{\pi }^6{(u^2-4)}^{5/2}}{{\left(4f_{\pi }\right)}^8{\left(3\pi u\right)}^3}{\left[2+4g_A^2-\frac{u^2}{2}(1+5g_A^2)\right]}^2+\\ \frac{m_{\pi }^6{(u^2-4)}^{3/2}}{9{\left(4f_{\pi }\right)}^8{\pi }^{5}u}{\displaystyle {\int }_0^1\text{}}dx{x}^2\{\frac{3x^2}{2}(4-u^2)\\ +3x\sqrt{u^2-4}\sqrt{4+(u^2-4)x^2}\\ \ln \frac{x\sqrt{u^2-4}+\sqrt{4+(u^2-4)x^2}}{2}+g_A^4\left[\right(4-u^2)x^2\\ +2u^2-4][\frac{5}{6}+\frac{4}{(u^2-4)x^2}-{\left(1+\frac{4}{(u^2-4)x^2}\right)}^{3/2}\\ \ln \frac{x\sqrt{u^2-4}+\sqrt{4+(u^2-4)x^2}}{2}]\\ {\displaystyle +[4(1+2g_A^2)-u^2(1+5g_A^2)]\sqrt{u^2-4}\frac{B\left(u\right)}{u}+\frac{u^2}{6}}\\ {\displaystyle (5+13g_A^2)-4(1+2g_A^2)+96{\pi }^2{f}_{\pi }^2[(4-2u^2)({\overline{d}}_1+{\overline{d}}_2)}\\ {\displaystyle +(4-u^2)x^2{\overline{d}}_3+8{\overline{d}}_5]{\}}^2.}& (73)\end{array}$

Class (c) is obtained from the leading two-loop πN amplitude with the tree-level πN amplitude. The two-loop πN amplitude has not been evaluated and we omit this class of diagrams.

The next contribution is the $1/M_N^2$ correction to the leading one-loop chiral 2π-exchange diagrams. They were given in Kaiser [49] and are shown in Figure 7. The explicit expressions are

$\begin{array}{l}{V}_C=\frac{g_A^4}{32{\pi }^2{M}_N^2{f}_{\pi }^4}[L(\tilde{\Lambda };q)(2m_{\pi }^4+q^4-8m_{\pi }^6{w}^{-2}\\ {\displaystyle -2m_{\pi }^8{w}^{-4})-\frac{m_{\pi }^6}{2w^2}],}& (74)\end{array}$

$\begin{array}{l}{\displaystyle W_C=\frac{1}{192{\pi }^2{M}_N^2{f}_{\pi }^4}\{L(\tilde{\Lambda };q)[g_A^2\left(2k^2\right(8m_{\pi }^2+5q^2)}\\ +12m_{\pi }^6{w}^{-2}-3q^4-6m_{\pi }^2{q}^2-6m_{\pi }^4)\\ +g_A^4\left(k^2\right(16m_{\pi }^4{w}^{-2}-20m_{\pi }^2-7q^2)-16m_{\pi }^8{w}^{-4}\\ -12m_{\pi }^6{w}^{-2}+4m_{\pi }^4{q}^2{w}^{-2}+5q^4+6m_{\pi }^2{q}^2+6m_{\pi }^4)\\ +k^2{w}^2]-\frac{4g_A^4{m}_{\pi }^6}{w^2}\},& (75)\end{array}$

$\begin{array}{ll}{V}_T=-\frac{1}{q^2}{V}_S=\frac{g_A^{4}L(\tilde{\Lambda };q)}{32{\pi }^2{M}_N^2{f}_{\pi }^4}{\displaystyle (k^2+\frac{5}{8}{q}^2+m_{\pi }^4{w}^{-2}{\displaystyle )}},& (76)\end{array}$

$\begin{array}{l}{W}_T=-\frac{1}{q^2}{W}_S=\frac{L(\tilde{\Lambda };q)}{1536{\pi }^2{M}_N^2{f}_{\pi }^4}{\displaystyle [g_A^4{\displaystyle (28m_{\pi }^2+17q^2}}\\ +16m_{\pi }^4{w}^{-2}{\displaystyle )}-2g_A^2(16m_{\pi }^2+7q^2)+w^2{\displaystyle ]},& (77)\end{array}$

$\begin{array}{ll}{V}_{LS}=\frac{g_A^{4}L(\tilde{\Lambda };q)}{128{\pi }^2{M}_N^2{f}_{\pi }^4}{\displaystyle (11q^2+32m_{\pi }^4{w}^{-2}{\displaystyle )}},& (78)\end{array}$

$\begin{array}{l}{W}_{LS}=\frac{L(\tilde{\Lambda };q)}{256{\pi }^2{M}_N^2{f}_{\pi }^4}{\displaystyle [2g_A^2(8m_{\pi }^2+3q^2)}\\ {\displaystyle +\frac{g_A^4}{3}{\displaystyle (16m_{\pi }^4{w}^{-2}-11q^2-36m_{\pi }^2{\displaystyle )}}-w^2{\displaystyle ]},}& (79)\end{array}$

$\begin{array}{ll}{V}_{\sigma L}=\frac{g_A^{4}L(\tilde{\Lambda };q)}{32{\pi }^2{M}_N^2{f}_{\pi }^4},& (80)\end{array}$

FIGURE 7

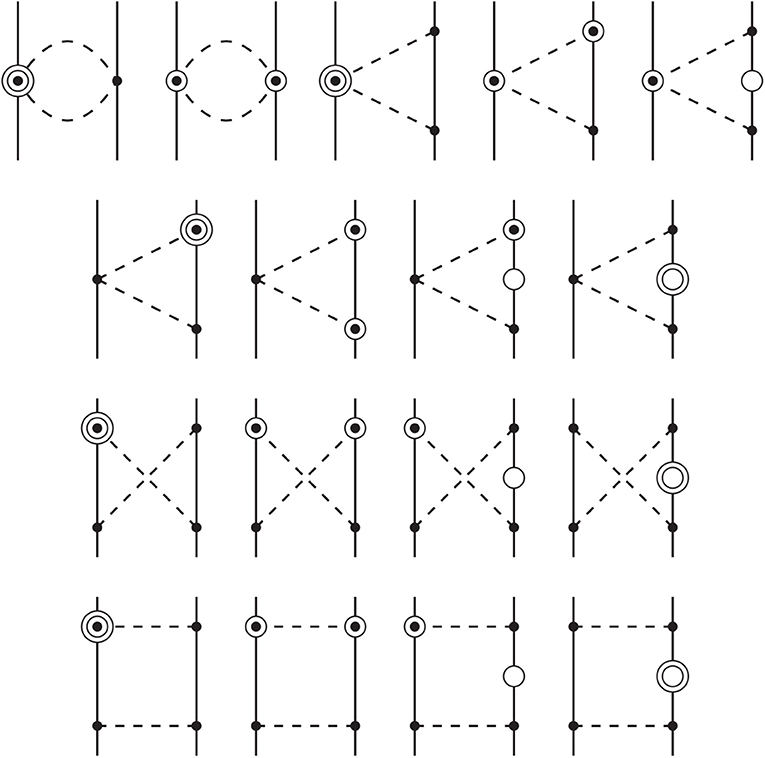
Figure 7. N⁵LO 2π exchange contributions to the NN interaction coming from $1/M_N^2$ corrections to the NLO chiral 2π-exchange diagrams. Notation as in Figure 3. Two open circles refers to $1/M_N^2$ corrections to propagators and vertices as in the case of one open circle. Reprinted figure with permission from Entem et al. [48], copyright (2015) by the American Physical Society.

The next contribution is given by 3π-exchange contributions. There are several classes of diagrams as shown in Figure 8. The class (a) diagrams are proportional to $c_i^2$. We use the same notation as in Kaiser [47] and Entem et al. [46].

FIGURE 8

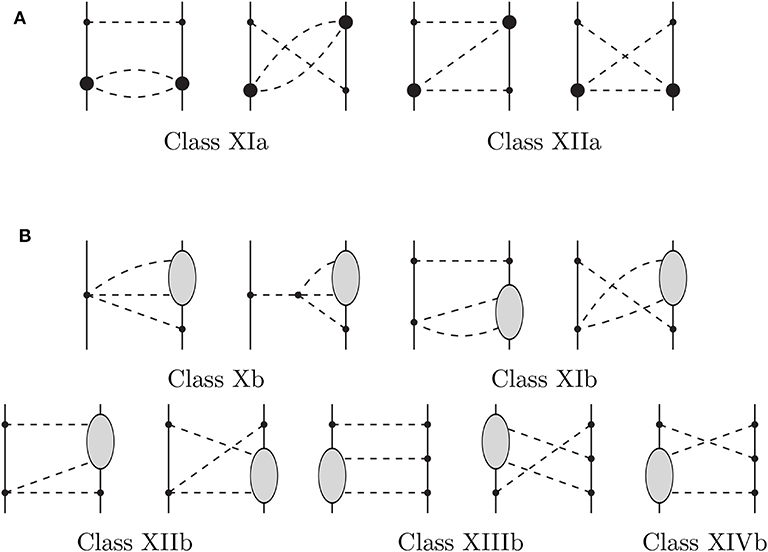
Figure 8. N⁵LO 3π-exchange contributions to the NN interaction. (A) Diagrams proportional to $c_i^2$. (B) Diagrams involving the one-loop πN amplitude. Notation as in Figure 3. Reprinted figure with permission from Entem et al. [48], copyright (2015) by the American Physical Society.

Class XIa:

$\begin{array}{ll}\text{Im}{W}_C=\frac{g_A^2{c}_4^2{m}_{\pi }^6}{6{(4\pi f_{\pi }^2)}^3}{\displaystyle \underset{2}{\overset{u-1}{\int }}}dw{(w^2-4)}^{3/2}\sqrt{\lambda (w)},& (81)\end{array}$

$\begin{array}{l}\text{Im }{V}_S=\frac{g_A^2{c}_4^2{m}_{\pi }^6}{6{\left(8\pi f_{\pi }^2\right)}^3}{\displaystyle \underset{2}{\overset{u-1}{\int }}\text{}}dw\frac{{(w^2-4)}^{3/2}}{u^4\sqrt{\lambda \left(w\right)}}\\ [w^8-4(1+u^2)w^6+2w^4(3+5u^2)\\ +4w^2(2u^6-5u^4-2u^2-1)-{\left(u^2-1\right)}^3\\ (5u^2+1)],& (82)\end{array}$

$\begin{array}{l}\text{Im}({\mu }^2{V}_T-V_S)=\frac{g_A^2{c}_4^2{m}_{\pi }^6}{6{(8\pi f_{\pi }^2)}^3}{\displaystyle \underset{2}{\overset{u-1}{\int }}}dw{(w^2-4)}^{3/2}\sqrt{\lambda (w)}\\ {\displaystyle [\frac{{(w^2-1)}^2}{u^4}+1-\frac{2}{u^2}(7w^2+1){\displaystyle ]}},& (83)\end{array}$

with the kinematical function λ(w) = w⁴ + u⁴ + 1 − 2(w²u² + w² + u²). The dimensionless integration variable w is the invariant mass of a pion-pair divided by m_π.

Class XIIa:

$\begin{array}{ll}\text{Im }{V}_C=\frac{g_A^2{c}_4^2{m}_{\pi }^6}{8960\pi f_{\pi }^6}{(u-3)}^3{\displaystyle [u^3+9u^2+12u-3-\frac{3}{u}{\displaystyle ]}},& (84)\end{array}$

$\begin{array}{ll}\text{Im}{W}_C=\frac{2g_A^2{c}_4^2{m}_{\pi }^6{u}^2}{{(4\pi f_{\pi }^2)}^3}{\displaystyle \underset{z^2<1}{\iint }}d{\omega }_{1}d{\omega }_2{k}_1{k}_2\sqrt{1-z^2}arcsin(z),& (85)\end{array}$

$\begin{array}{l}\text{ Im}{V}_S=\frac{g_A^2{c}_4^2{m}_{\pi }^6}{{\left(4\pi f_{\pi }^2\right)}^3}{\displaystyle \underset{\text{}{z}^2<1}{\iint }d{\omega }_{1}d{\omega }_2\left\{2{\omega }_1^2\right({\omega }_2^2-9{\omega }_{2}u+9u^2+1)}\\ +3{\omega }_1\left[{\omega }_2\right(1+8u^2)-6u-6u^3]\\ +\frac{1}{4}(9u^4+18u^2+5)+\frac{2z{k}_2}{k_1}\left[{\omega }_1^3\right(4u-{\omega }_2)\\ +{\omega }_1^2(7{\omega }_{2}u-2-2u^2)-2{\omega }_1(2u+{\omega }_2)\\ +2+2u^2-4{\omega }_{2}u]+\frac{3\arcsin \left(z\right)}{k_1{k}_2\sqrt{1-z^2}}\\ \left[2{\omega }_1^{3}u\right(u^2+1-2{\omega }_{2}u)+{\omega }_1^2({\omega }_{2}u(7+11u^2)\\ -5{\omega }_2^2{u}^2-1-4u^2-3u^4)+\frac{{\omega }_1}{4}\\ (6u^5+12u^3-2u-{\omega }_2(5+16u^2+15u^4\left)\right)\\ +\frac{(1-u^4)(u^2+3)}{8}]\},& (86)\end{array}$

$\begin{array}{l}\text{Im}({\mu }^2{V}_T-V_S)=\frac{g_A^2{c}_4^2{m}_{\pi }^6}{{\left(4\pi f_{\pi }^2\right)}^3}{\displaystyle \underset{\text{}{z}^2<1}{\iint }d{\omega }_{1}d{\omega }_2}\\ \left\{4{\omega }_1^2\right({\omega }_2^2+6u^2+2-10{\omega }_{2}u)+6u^2(1+u^2)\\ +2{\omega }_1\left[3{\omega }_2\right(1+7u^2)-18u^3-10u]\\ +\frac{2z{k}_2}{k_1}\left[{\omega }_1^3\right(7u-2{\omega }_2)+u^2-{\omega }_{2}u\\ +{\omega }_1^2(13{\omega }_{2}u-3-10u^2)+{\omega }_1(2+3u^2)(u-2{\omega }_2)]\\ +\frac{3\arcsin \left(z\right)}{k_1{k}_2\sqrt{1-z^2}}\times (u^2-2{\omega }_{1}u+1)(u^2-2{\omega }_{2}u+1)\\ \left[\frac{{\omega }_1}{2}(6u-5{\omega }_2)-\frac{u^2}{2}-2{\omega }_1^2\right]\},& (87)\end{array}$

with the magnitudes of pion-momenta divided by m_π, and their scalar-product given by:

$\begin{array}{l}{k}_1=\sqrt{{\omega }_1^2-1},k_2=\sqrt{{\omega }_2^2-1},\\ z{k}_1{k}_2={\omega }_1{\omega }_2-u({\omega }_1+{\omega }_2)+\frac{u^2+1}{2}.& (88)\end{array}$

The upper/lower limits of the ω₂-integration are ${\omega }_2^{\pm }=\frac{1}{2}(u-{\omega }_1\pm k_1\sqrt{u^2-2{\omega }_{1}u-3}/\sqrt{u^2-2{\omega }_{1}u+1})$ with ω₁ in the range $1<{\omega }_1<(u^2-3)/2u$.

The contributions to ImW_S and Im$({\mu }^2{W}_T-W_S)$ are split into three pieces according to their dependence on the isoscalar/isovector low-energy constants c_{1, 3} and c₄:

$\begin{array}{l}\text{Im }{W}_S\text{}=\text{}\frac{g_A^2{m}_{\pi }^6{(u-3)}^2}{2240\pi f_{\pi }^6}\{7c_1^2\left(\frac{4}{3}+\frac{3}{u}-\frac{2}{3u^2}-\frac{1}{u^3}\right)\\ +c_1{c}_3\left(\frac{2u^2}{3}+4u-\frac{2}{3}-\frac{5}{u}-\frac{2}{3u^2}-\frac{1}{u^3}\right)\\ +c_3^2\left(\frac{3u^2}{4}+\frac{u}{8}-\frac{5}{2}-\frac{3}{u}+\frac{19}{12u^2}+\frac{19}{8u^3}\right)\},& (89)\end{array}$

$\begin{array}{l}\text{Im}({\mu }^2{W}_T-W_S)=\frac{g_A^2{m}_{\pi }^6(u-3)}{1120\pi f_{\pi }^6}\{7c_1^2\left(\frac{1}{3u}+\frac{1}{u^2}+\frac{3}{u^3}-2u-1\right)\\ +c_1{c}_3\left(13u+4-5u^2-\frac{5u^3}{3}+\frac{1}{3u}+\frac{1}{u^2}+\frac{3}{u^3}\right)\\ +\frac{c_3^2}{8}(23u^2-\frac{u^5}{3}-u^4-4u^3-8u-3+\\ {\displaystyle \frac{8}{3u}-\frac{19}{u^2}-\frac{57}{u^3}\left)\right\}}& (90)\end{array}$

$\begin{array}{l}\mathrm{Im}{W}_S=\frac{g_A^2{c}_4{m}_{\pi }^6}{1120\pi f_{\pi }^6}{\left(u-3\right)}^2\{c_1(u^2+6u\\ -1-\frac{15}{2u}-\frac{1}{u^2}-\frac{3}{2u^2})+\frac{c_3}{4}(\frac{2u^4}{9}+\frac{4u^3}{3}+\\ \frac{u^2}{3}-\frac{25u}{6}+\frac{6}{u}+\frac{1}{u^2}+\frac{3}{2u^3})\},& (91)\end{array}$

$\begin{array}{l}\text{Im }({\mu }^2{W}_T-W_S)=\frac{g_A^2{c}_4{m}_{\pi }^6}{1120\pi f_{\pi }^6}{\left(u-3\right)}^3\{c_1\left(\frac{1}{u^2}+\frac{1}{u^3}-\frac{u}{3}-3-\frac{4}{u}\right)\\ +\frac{c_3}{4}\left(\frac{u^3}{9}+u^2+\frac{5u}{3}+\frac{8}{3}+\frac{11}{3u}-\frac{1}{u^2}-\frac{1}{u^3}\right)\},& (92)\end{array}$

$\begin{array}{l}\text{Im}{W}_S=\frac{g_A^2{c}_4^2{m}_{\pi }^6}{8960\pi f_{\pi }^6}{(u-3)}^2{\displaystyle (\frac{25u}{12}-\frac{u^4}{9}-\frac{2u^3}{3}}\\ {\displaystyle -\frac{u^2}{6}-\frac{3}{u}-\frac{1}{2u^2}-\frac{3}{4u^3}{\displaystyle )},}& (93)\end{array}$

$\begin{array}{l}\text{Im}({\mu }^2{W}_T-W_S)=\frac{g_A^2{c}_4^2{m}_{\pi }^6}{8960\pi f_{\pi }^6}{(u-3)}^3{\displaystyle (\frac{1}{2u^2}+\frac{1}{2u^3}-\frac{u^3}{18}}\\ {\displaystyle -\frac{u^2}{2}-\frac{5u}{6}-\frac{4}{3}-\frac{11}{6u}{\displaystyle )}.}& (94)\end{array}$

The next contribution is given by class (b). Each diagram includes the one-loop πN amplitude. Not all the contributions could be treated; only those contributions that are independent of the pion-nucleon CMS energy in the loop or linearly dependent could be included. The contributions are in general small. The omitted contributions are typically an order of magnitude smaller.

Class Xb:

$\begin{array}{ll}\text{Im }{W}_S=\frac{g_A^2{m}_{\pi }^6}{{(4f_{\pi })}^8{\pi }^5}{\displaystyle {\int }_2^{u-1}}{\displaystyle dw\frac{4G(w)}{27w^2{u}^4}{\displaystyle [}(w^2-4)\lambda (w){{\displaystyle ]}}^{3/2},}& (95)\end{array}$

$\begin{array}{l}\text{Im}({\mu }^2{W}_T-W_S)=\frac{g_A^2{m}_{\pi }^6}{{(4f_{\pi })}^8{\pi }^5}{\displaystyle {\int }_2^{u-1}}dw\frac{4G(w)}{9w^2{u}^4}{(w^2-4)}^{3/2}\\ \sqrt{\lambda (w)}\frac{3u^2+1}{u^2-1}{\displaystyle [u^4-{(w^2-1)}^2{\displaystyle ]}}.& (96)\end{array}$

Class XIb:

$\begin{array}{l}\text{Im }{W}_S=\frac{g_A^2{m}_{\pi }^6}{{(4f_{\pi })}^8{\pi }^5}{\displaystyle {\int }_2^{u-1}}dw\frac{8G(w)}{27w^2{u}^4}{(w^2-4)}^{3/2}\\ \sqrt{\lambda (w)}{\displaystyle [2u^2(1+7w^2)-u^4-{(w^2-1)}^2{\displaystyle ]}},& (97)\end{array}$

$\begin{array}{l}\text{Im}({\mu }^2{W}_T-W_S)=\frac{g_A^2{m}_{\pi }^6}{{(4f_{\pi })}^8{\pi }^5}{\displaystyle {\int }_2^{u-1}}dw\frac{8G(w)}{9w^2{u}^4}\frac{{(w^2-4)}^{3/2}}{\sqrt{\lambda (w)}}\\ {(u^2+1-w^2)}^2{\displaystyle [2w^2(1+3u^2)-w^4-{(u^2-1)}^2{\displaystyle ]}}.& (98)\end{array}$

Class XIIb:

$\begin{array}{l}\text{Im }{W}_S=\frac{g_A^2{m}_{\pi }^6}{9f_{\pi }^8{(4\pi )}^5}{\displaystyle \underset{z^2<1}{\iint }}d{\omega }_{1}d{\omega }_{2}G(w){\displaystyle [({\omega }_1^2+{\omega }_2^2-2)}\\ (1-3z^2)-5k_1{k}_{2}z{\displaystyle ]},& (99)\end{array}$

$\begin{array}{l}\text{Im}({\mu }^2{W}_T-W_S)=-\frac{g_A^2{m}_{\pi }^6}{3f_{\pi }^8{(4\pi )}^5}{\displaystyle \underset{z^2<1}{\iint }}d{\omega }_{1}d{\omega }_{2}G(w){\omega }_1{\omega }_2\\ {\displaystyle [5+2z{\displaystyle (\frac{k_1}{k_2}+\frac{k_2}{k_1}{\displaystyle )}}{\displaystyle ]}},& (100)\end{array}$

setting $w=\sqrt{1+u^2-2u{\omega }_1}$.

Class XIIIb:

$\begin{array}{ll}\text{Im }{V}_S=\frac{g_A^4{m}_{\pi }^6}{{(4f_{\pi })}^8{\pi }^3{u}^3}{\displaystyle {\int }_2^{u-1}}dw2G(w)\lambda (w)(2-w^2),& (101)\end{array}$

$\begin{array}{c}\text{Im}({\mu }^2{V}_T-V_S)=\frac{g_A^4{m}_{\pi }^6}{{(4f_{\pi })}^8{\pi }^3{u}^3}{\displaystyle {\int }_2^{u-1}}dw4G(w)(2-w^2)\\ {(1+u^2-w^2)}^2,& (102)\end{array}$

$\begin{array}{l}{\displaystyle Im{W}_S=\frac{g_A^4{m}_{\pi }^6}{3f_{\pi }^8{(4\pi )}^5}{\displaystyle \int \text{}}\text{}{\displaystyle \underset{\text{}{z}^2<1}{\int }\text{}}d{\omega }_{1}d{\omega }_{2}G(w)\{u({\omega }_1+4{\omega }_2)-}\\ 2-\frac{{\omega }_1^2+8{\omega }_2^2}{3}+z^2({\omega }_1^2+4{\omega }_2^2-5)\\ +\frac{z{k}_2}{k_1}(4u{\omega }_1+{\omega }_1^2-5)+\frac{z{k}_1}{k_2}(u{\omega }_2+{\omega }_2^2-2)\\ {\displaystyle +\frac{\arcsin (z)}{\sqrt{1-z^2}}[\frac{k_1}{k_2}(1-u{\omega }_2)+z(1-u{\omega }_1)]\},}& (103)\end{array}$

$\begin{array}{l}\text{Im}({\mu }^2{W}_T-W_S)=\frac{g_A^4{m}_{\pi }^6}{f_{\pi }^8{\left(4\pi \right)}^5}\text{}{\displaystyle \underset{\text{}{z}^2<1}{\iint }d{\omega }_{1}d{\omega }_2\frac{2{\omega }_1}{3}G(w)}\\ \{\frac{2{\omega }_2}{k_1^2}[{\omega }_1(u-{\omega }_2)-1]+u+2{\omega }_2\\ +\frac{z{k}_2}{k_1}(4u+{\omega }_1)+{\omega }_1{\left(\frac{2z{k}_2}{k_1}\right)}^2\\ +\frac{\arcsin \left(z\right)}{k_1{k}_2\sqrt{1-z^2}}[(1+u^2)\left({\omega }_1+{\omega }_2-\frac{u}{2}\right)\\ -2u{\omega }_1{\omega }_2\left]\right\},& (104)\end{array}$

setting again $w=\sqrt{1+u^2-2u{\omega }_1}$.

Class XIVb:

$\begin{array}{l}\text{Im }{V}_S=\frac{g_A^4{m}_{\pi }^6}{{(4f_{\pi })}^8{\pi }^3{u}^3}{\displaystyle {\int }_2^{u-1}}dw\frac{G(w)}{2}\lambda (w)\\ {\displaystyle [u^2+w^2+4(u^2-1)w^{-2}-5{\displaystyle ]}},& (105)\end{array}$

$\begin{array}{l}\text{Im}({\mu }^2{V}_T-V_S)=\frac{g_A^4{m}_{\pi }^6}{{(4f_{\pi })}^8{\pi }^3{u}^3}{\displaystyle {\int }_2^{u-1}}dwG(w)(w^2-1-u^2)\\ {\displaystyle [w^4-2w^2(3+u^2)+{(u^2-1)}^2(1+4w^{-2}){\displaystyle ]}}.& (106)\end{array}$

where the auxiliary function G(w) is defined as

$\begin{array}{l}G\left(w\right)=\left[1+2g_A^2-\frac{w^2}{4}\left(1+5g_A^2\right)\right]\frac{\sqrt{w^2-4}}{w}\text{ln}\frac{\sqrt{w^2-4}}{2}\\ +\frac{w^2}{24}(5+13g_A^2)-1-2g_A^2+48{\pi }^2{f}_{\pi }^2\\ {\displaystyle \left[\right(2-w^2\left)\right({\overline{d}}_1+{\overline{d}}_2)+4{\overline{d}}_5].}& (107)\end{array}$

Finally 4π-exchange diagrams occur for the first time at N⁵LO. These diagrams are three loop diagrams with only leading vertices. As mentioned before, three-pion exchanges with just leading order vertices turned out to be negligible. For that reason, we expect the leading four-pion exchanges to be even smaller, and we leave them out.

2.5. NN Contact Terms

Contact terms are given by the NN piece of the Lagrangian Equation (6). They start at order ν = 0 with non-derivatives terms given by [5]

$\begin{array}{ll}{V}_{\text{ct}}^{(0)}(\overrightarrow{p^{\prime }},\overrightarrow{p})=C_S+C_T{\overrightarrow{\sigma }}_1·{\overrightarrow{\sigma }}_2.& (108)\end{array}$

They contribute to S waves, only.

The next order is ν = 2 (NNLO), which introduces seven new contact terms, given by [11]

$\begin{array}{l}{V}_{\text{ct}}^{(2)}(\overrightarrow{p^{\prime }},\overrightarrow{p})=C_1{q}^2+C_2{k}^2\\ +(C_3{q}^2+C_4{k}^2){\overrightarrow{\sigma }}_1·{\overrightarrow{\sigma }}_2\\ {\displaystyle +C_5\left(-i\overrightarrow{S}·(\overrightarrow{q}\times \overrightarrow{k})\right)}\\ +C_6({\overrightarrow{\sigma }}_1·\overrightarrow{q})({\overrightarrow{\sigma }}_2·\overrightarrow{q})\\ +C_7({\overrightarrow{\sigma }}_1·\overrightarrow{k})({\overrightarrow{\sigma }}_2·\overrightarrow{k}).& (109)\end{array}$

The next order is ν = 4 (N³LO) which has 15 contributions given by

$\begin{array}{l}{V}_{\text{ct}}^{(4)}(\overrightarrow{p^{\prime }},\overrightarrow{p})=D_1{q}^4+D_2{k}^4+D_3{q}^2{k}^2+D_4{(\overrightarrow{q}\times \overrightarrow{k})}^2\\ {\displaystyle +\left(D_5{q}^4+D_6{k}^4+D_7{q}^2{k}^2+D_8{(\overrightarrow{q}\times \overrightarrow{k})}^2\right){\overrightarrow{\sigma }}_1·{\overrightarrow{\sigma }}_2}\\ +{\displaystyle (D_9{q}^2+D_{10}{k}^2)\left(-i\overrightarrow{S}·(\overrightarrow{q}\times \overrightarrow{k})\right)}\\ +(D_{11}{q}^2+D_{12}{k}^2)({\overrightarrow{\sigma }}_1·\overrightarrow{q})({\overrightarrow{\sigma }}_2·\overrightarrow{q})\\ +(D_{13}{q}^2+D_{14}{k}^2)({\overrightarrow{\sigma }}_1·\overrightarrow{k})({\overrightarrow{\sigma }}_2·\overrightarrow{k})\\ {\displaystyle +D_{15}\left({\overrightarrow{\sigma }}_1·(\overrightarrow{q}\times \overrightarrow{k}){\overrightarrow{\sigma }}_2·(\overrightarrow{q}\times \overrightarrow{k})\right),}& (110)\end{array}$

We note that, on shell, there are only 12 independent operators. The redundancy on-shell has been shown to generate large correlations. Reinert et al. [38] and Wesolowski et al. [50] claim that removal of the three (on-shell) redundant operators improves the fit.

The partial wave decomposition of all these terms can be found in Machleidt and Entem [14]. Contact contributions are polynomials in external momenta and they only give contributions to partial waves with L ≤ ν/2.

3. Peripheral NN Scattering

Peripheral NN scattering is of special interest since it is less sensitive to the short distance dynamics. A way to study it is to consider partial waves with high angular momentum, since the centrifugal barrier prevents sensitivity to short distance forces.

In the framework of EFT, the short distance physics is mimicked by the contact terms. In momentum space, they are given by polynomial terms in external momenta. This has the property that they don't give contributions to all partial waves, but only to angular momenta $L\le \frac{\nu }{2}$. This means that, for example at N⁵LO, there are only contributions up to F-waves.

Peripheral NN scattering was already considered at NNLO [12], N³LO [51], N⁴LO [46], and N⁵LO [48]. Here, we will review the most important results.

One important aspect of peripheral waves is that the interaction is weaker and perturbative calculations can be performed, so avoiding all the problems posed by singular interactions in the Lippmann-Schwinger equation. For these reasons, it can be viewed as a clean probe of chiral dynamics in the NN sector.

The calculation is conducted by using the K matrix perturbatively as

$\begin{array}{ll}K(\overrightarrow{p}{}^{\prime },\overrightarrow{p})=V_{\pi }(\overrightarrow{p}{}^{\prime },\overrightarrow{p})+V_{2\pi ,it}(\overrightarrow{p}{}^{\prime },\overrightarrow{p})& (111)\end{array}$

with $V_{\pi }(\overrightarrow{p}{}^{\prime },\overrightarrow{p})$ the χEFT amplitude where the iteration of OPE has been subtracted, and $V_{2\pi ,it}(\overrightarrow{p}{}^{\prime },\overrightarrow{p})$ representing the once iterated OPE given by

$\begin{array}{ll}{V}_{2\pi ,it}({\overrightarrow{p}}^{\prime },\overrightarrow{p})={P}{\displaystyle \int }{d}^3{p}^{″}\frac{M_N^2}{E_{p^{″}}}\frac{V_{1\pi }({\overrightarrow{p}}^{\prime },{\overrightarrow{p}}^{″})V_{1\pi }({\overrightarrow{p}}^{″},\overrightarrow{p})}{p^2-{p^{″}}^2},& (112)\end{array}$

where ${P}$ denotes the principal value integral and $E_{p^{″}}=\sqrt{M_N^2+{p^{″}}^2}$.

There is no unique way to subtract the iterative part of OPE. The prescription given by Equation (111) is slightly different from the one used in Kaiser et al. [12]. The difference between them is reabsorbed in a redefinition of the irreducible part. See Appendix C of Machleidt and Entem [14] for more details.

Now the order by order calculation is conducted as follows. At LO only OPE is included in V_π and no iteration is included. At NLO V_π up to order ν = 2 is included and V_{2π, it} is included. Higher orders (NNLO, N³LO, etc) include V_π up to this order and the once iterated OPE. N³LO and higher orders should also include the twice iterated OPE contribution. However the difference between the once iterated OPE and the infinitely iterated OPE is very small and can not be identified on the scale of the figures. For this reason, we omit iterations of OPE beyond what is contained in V_{2π, it}.

3.1. Fifth-Order (N⁴LO) Results

The contributions at NNLO [12] and N³LO [51] are in general too attractive, especially when the c_i LEC's obtained from πN scattering are used.

We analyze now the contributions at N⁴LO. In Figure 9 we show results for selected F and G waves. Curve (1) gives the results for the N³LO calculation. Curve (2) adds the relativistic corrections (proportional to c_i/M_N) of the NNLO terms. In curve (3), the 2π-exchange two-loop contributions of class (a) (Figure 4 and section 2.4.5) are added. Curve (4) adds the two-loop contribution of class (b). Finally curve (5) adds 3π-exchange contributions giving the final result at N⁴LO. In all calculations a SFR cutoff $\tilde{\Lambda }=1.5$ GeV is used.

FIGURE 9

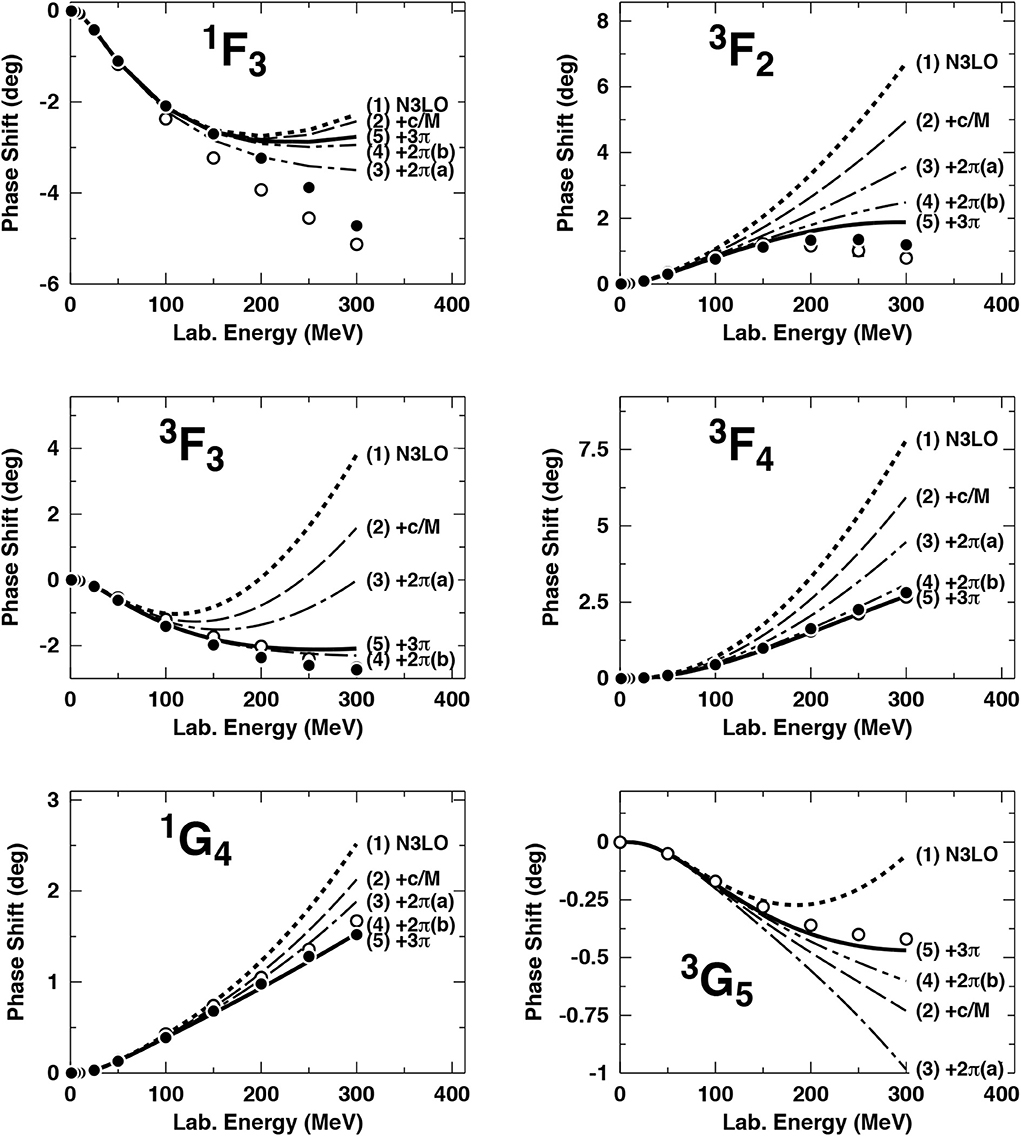
Figure 9. Effect of individual fifth-order contributions to the neutron-proton phase shifts of some selected peripheral partial waves. The individual contributions are added up successively in the order given in parentheses next to each curve. In all cases an SFR cut-off $\tilde{\Lambda }=1.5$ GeV is used. Curve (1) is N³LO and curve (5) the complete N⁴LO. The filled and open circles represent the results from the Nijmegen multi-energy np phase-shift analysis [93] and the VPI-GWU single-energy np analysis SM99 [91], respectively. Reprinted figure with permission from Entem et al. [46], copyright (2015) by the American Physical Society.

One can see that 3π-exchange contributions are significantly smaller than 2π-exchanges which can be interpreted as a convergence in regard to the number of pions exchanged. The 3π contribution is the sum of individual contributions that can be sizable but they add up to a small final result.

The c_i/M_N and two-loop contributions are mainly repulsive which helps to overcome the excess of attraction at N³LO. An exception is the ¹F₃ partial wave where the two-loop contribution of class (b) gives attraction, resulting in too much attraction for the whole N⁴LO contribution at higher energies.

For F and G waves (except ¹F₃) the final N⁴LO result is in very good agreement with the empirical phase-shifts. An interesting case is the ³G₅ that is a problem at N³LO [51]; however, the final result at N⁴LO is in almost perfect agreement with the phase-shift analysis.

Here we have used $\tilde{\Lambda }=1.5$ GeV. It is interesting to note that other potentials constructed from dispersion relations like the Stony Brook [52] and the Paris [53] potentials cut the dispersion integral at ${\mu }^2=50m_{\pi }^2$ which is equivalent to a SFR cut-off of $\tilde{\Lambda }~1$ GeV. In Figures 10, 11 we show the impact of the SFR cutoff on the results at different orders. In general the variations for N³LO are large and always too attractive while at N⁴LO variations are smaller and close to the data. We also include lower orders to compare the relative size of the order-by-order contributions. One would expect a convergence pattern going from NNLO to N³LO and further to N⁴LO; however, this is not the case as seen in Figures 10, 11.

FIGURE 10

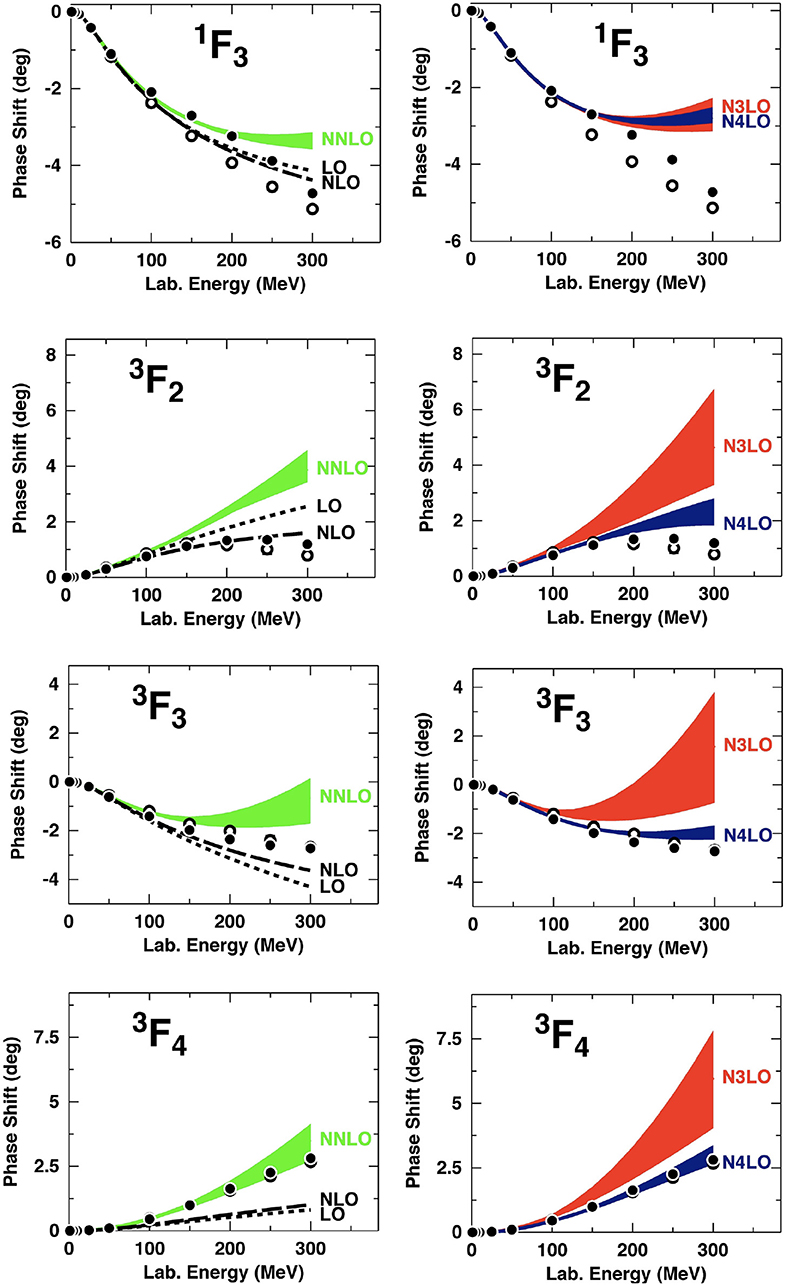
Figure 10. Phase-shifts of neutron-proton scattering at various orders as denoted. The shaded bands show the sensitivity of the contributions to the SFR cut-off $\tilde{\Lambda }$ which is varied over the range 0.7–1.5 GeV. Filled and open circles as in Figure 9. Reprinted figure with permission from Entem et al. [46], copyright (2015) by the American Physical Society.

FIGURE 11

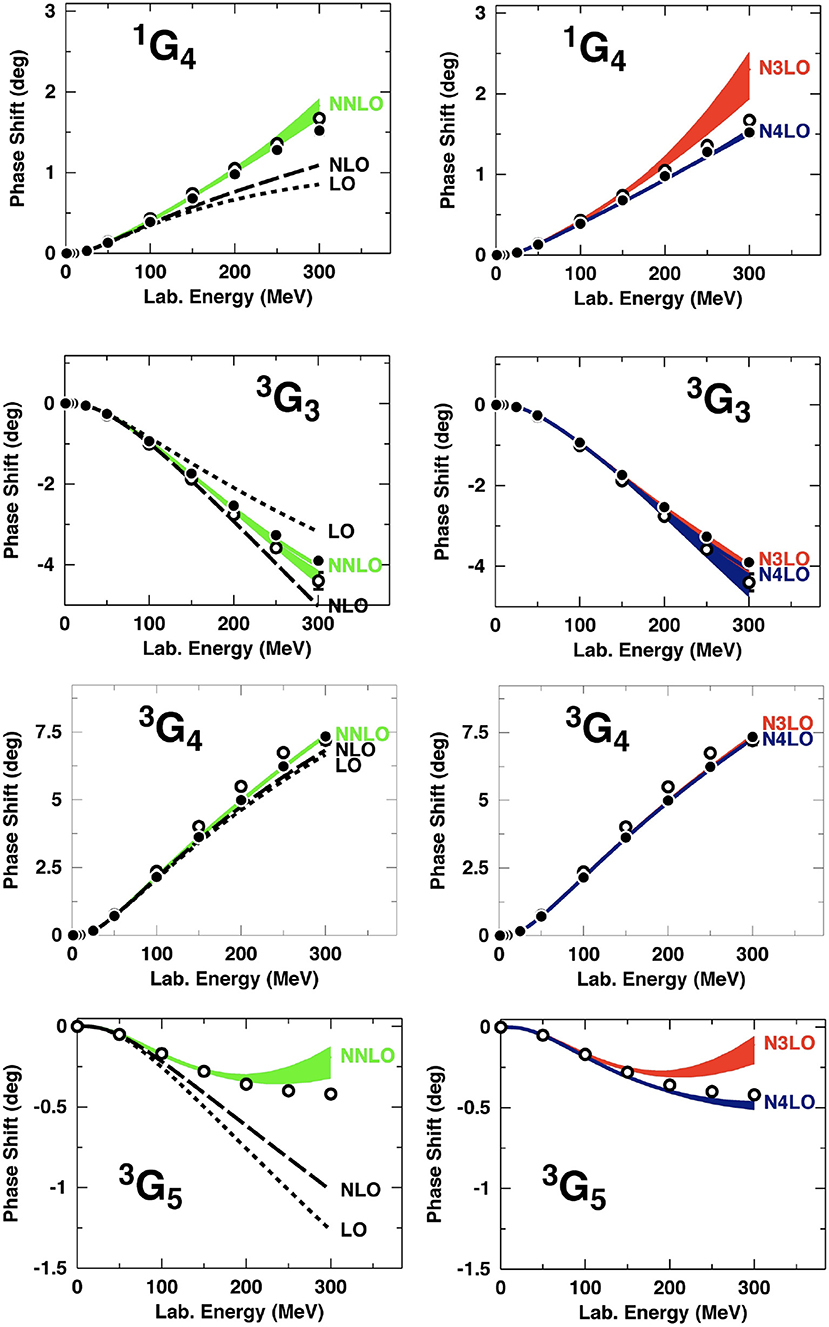
Figure 11. Same as Figure 10, but for G waves. Reprinted figure with permission from Entem et al. [46], copyright (2015) by the American Physical Society.

Concerning the LECs used, note that in the calculations of this subsection, the “KH” set of LECs shown in Table 2 was applied, while in the calculations of the next subsection the “GW” set is employed.

TABLE 2

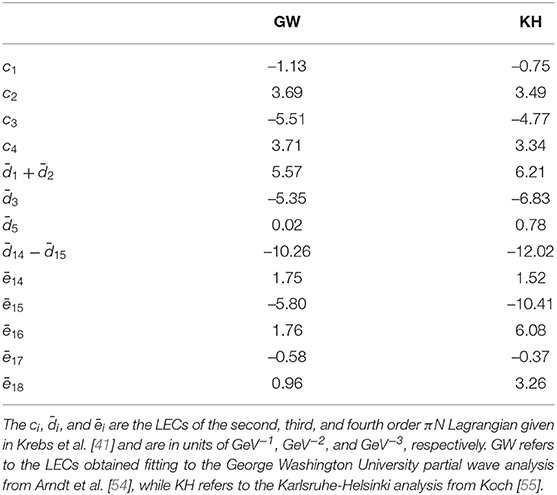
Table 2. Low-energy constants as determined in Krebs et al. [41].

3.2. Going Beyond Fifth Order

As mentioned before there is no complete calculation at sixth order (N⁵LO). However a study of peripheral NN scattering with the expected dominant contributions was performed in Entem et al. [48]. We present here the results at this order.

For N⁵LO we consider G and higher waves, since they are not affected by contact terms at this order. In Figure 12, we show how individual groups of diagrams contribute to two G waves. Curve (1) represents the N⁴LO result. Curve (2) adds the N⁵LO 2π-exchange contributions of class (a) and curve (3) adds also class (b) (Figure 6 and Section 2.4.6). 3π-exchange (Figure 8) of class (a) are included in curve (4) and class (b) is contained in curve (5). The final result at N⁵LO is given by curve (6) which includes the $1/M_N^2$ corrections. In all cases a SFR cutoff $\tilde{\Lambda }=800$ MeV is used.

FIGURE 12

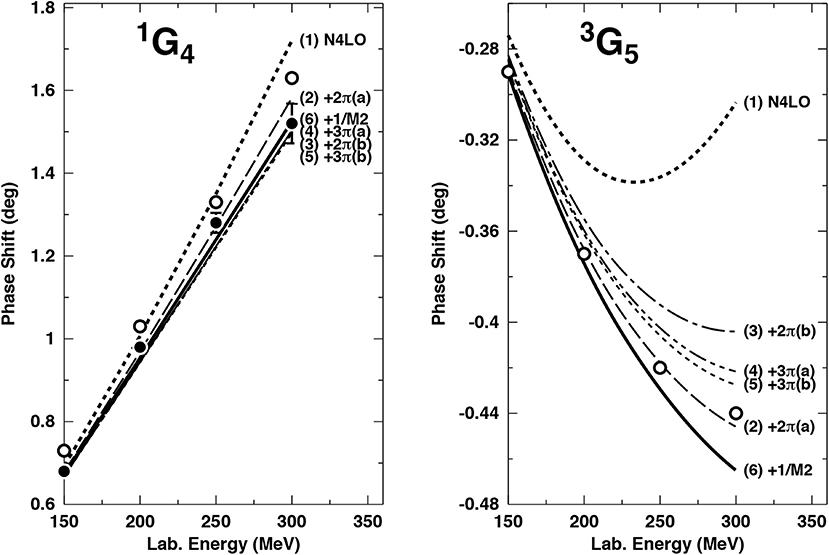
Figure 12. Effect of individual N⁵LO contributions to the neutron-proton phase-shifts of two G waves. Contributions are added up successively starting from the N⁴LO result (1) to the final N⁵LO result (6). A SFR cutoff $\tilde{\Lambda }=800$ MeV is used. The filled and open circles represent the results from the Nijmegen multienergy np phase-shift analysis [93] and the GWU np analysis SP07 [94], respectively. Reprinted figure with permission from Entem et al. [48], copyright (2015) by the American Physical Society.

The two-loop 2π-exchange class (a) (Figure 6) generates a strong repulsive central force, while the spin-spin and tensor forces provided by this class are negligible. The fact that this class produces a relatively large contribution is not unexpected, since it is proportional to $c_i^2$. The 2π-exchange contribution class (b) creates a moderately repulsive central force and a noticeable tensor force, as the impact on ³G₅ demonstrates. The 3π-exchange class (a) (Figure 8) is negligible in ¹G₄, but noticeable in ³G₅ and, therefore, it should not be neglected. This contribution is proportional to $c_i^2$, which suggests a non-negligible size but it is typically smaller than the corresponding 2π-exchange contribution class (a). The 3π-exchange class (b) contribution turns out to be negligible [see the difference between curve (4) and (5) in Figure 12]. This may not be unexpected since it is a three-loop contribution with only leading-order vertexes. Finally the relativistic $1/M_N^2$ corrections to the leading 2π-exchange have a small but non-negligible impact, particularly in ³G₅.

The predictions for G and H waves are shown in Figure 13, with shaded bands corresponding to a variation of the SFR cut-off $\tilde{\Lambda }$ over the range 700–900 MeV. The N⁵LO contribution shows a moderately repulsive effect, reducing further the excess attraction at N³LO. The N⁵LO result is, in general, substantially smaller than the N⁴LO one, indicating a signature of convergence. At N⁵LO, there is excellent agreement with the data.

FIGURE 13

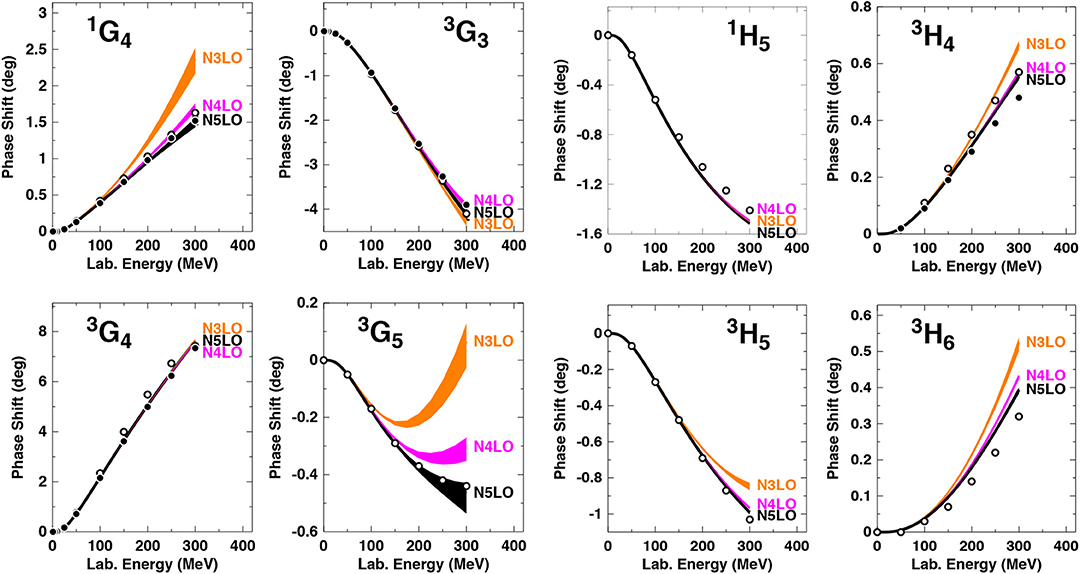
Figure 13. Phase-shifts of np scattering in G and H waves at various orders as denoted. The shaded bands show the variations of the predictions when the SFR cut-off $\tilde{\Lambda }$ is changed over the range 700 to 900 MeV. Empirical phase-shifts as in Figure 12. Reprinted figure with permission from Entem et al. [48], copyright (2015) by the American Physical Society.

Concerning the values for the LECs, let us note again that, in this subsection, the “GW” set of LECs shown in Table 2 was used, while in the calculations of the previous subsection the “KH” set was applied.

Figure 13 includes only the three highest orders. However, a comparison between all orders is also of interest. Therefore, we show in Figure 14 the contributions to phase shifts through all six chiral orders from LO to N⁵LO. Note that the difference between the LO prediction (one-pion-exchange) and the data (filled and open circles) is to be provided by two- and three-pion exchanges, i.e., the intermediate-range part of the nuclear force. How well that is accomplished is a crucial test for any theory of nuclear forces. NLO produces only a small contribution, but NNLO (denoted by N2LO in the figure) creates substantial intermediate-range attraction (most clearly seen in ¹G₄, ³G₅, and ³H₆). In fact, NNLO is the largest contribution among all orders. This is due to the one-loop 2π-exchange (2PE) triangle diagram which involves one ππNN-contact vertex proportional to c_i. This vertex represents correlated 2PE as well as intermediate Δ(1232)-isobar excitation. It is well-known from the traditional meson theory of nuclear forces that these two features are crucial for a realistic and quantitative 2PE model. Consequently, the one-loop 2π-exchange at NNLO is attractive and assumes a realistic size describing the intermediate-range attraction of the nuclear force about right. At N³LO, more one-loop 2PE is added by the bubble diagram with two c_i-vertices, a contribution that seemingly is overestimating the attraction. This attractive surplus is then compensated by the prevailingly repulsive two-loop 2π- and 3π-exchanges that occur at N⁴LO and N⁵LO.

FIGURE 14

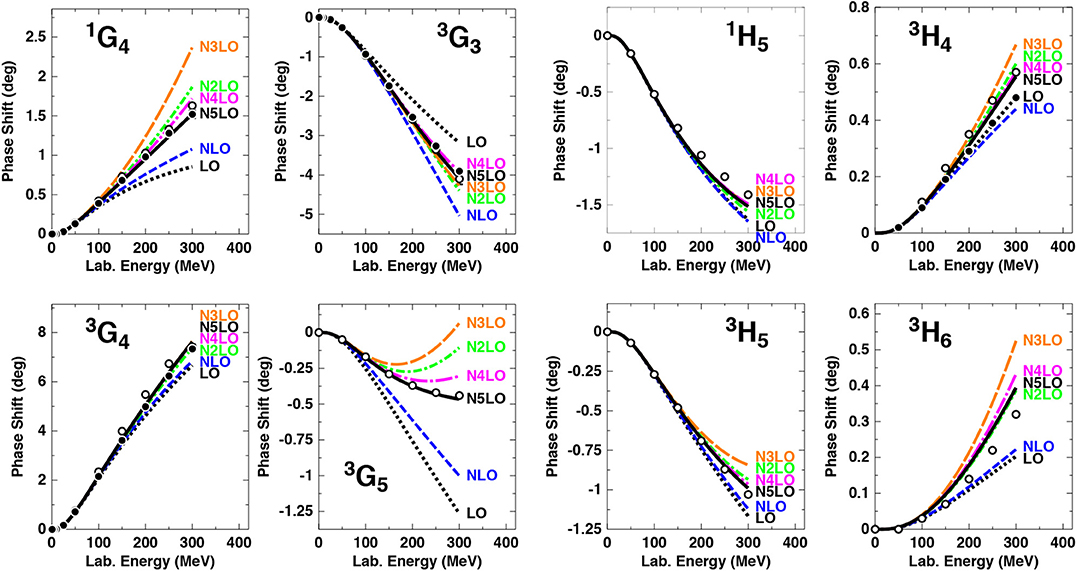
Figure 14. Phase-shifts of np scattering in G and H waves at all orders from LO to N⁵LO. A SFR cut-off $\tilde{\Lambda }=800$ MeV is used. Empirical phase-shifts as in Figure 12. Reprinted figure with permission from Entem et al. [48], copyright (2015) by the American Physical Society.

In this context, it is worth to note that also in conventional meson theory the one-loop models for the 2PE contribution always show some excess of attraction. In conventional meson theory, the surplus attraction is reduced by heavy-meson exchange (ρ- and ω-exchange) which, however, has no place in chiral effective field theory (as a finite-range contribution). Instead, in the latter approach, two-loop 2π- and 3π-exchanges provide the corrective action.

4. NN Potentials Up to N⁴LO

The starting point of all ab-initio calculations of nuclear systems is the NN potential. For that reason, it is necessary to define a potential.

We define the NN potential as the sum of the irreducible NN diagrams discussed in previous sections, which are calculated perturbatively. However, in reality, the NN system is characterized by the presence of a shallow bound state (the deuteron) and large (S-wave) scattering lengths that cannot be obtained perturbatively. Therefore, the potential has to be applied in a scattering equation to obtain the NN amplitude. Since our approach is in principal covariant (with relativity taken into account perturbatively), a proper equation would be the Bethe-Salpeter equation. However, it is more convenient, to use one of the three-dimensional reductions of that equation. We use the Blankenbeclar-Sugar (BbS) version of the equation [56] which reads

$\begin{array}{ll}T({\overrightarrow{p}}^{\prime },\overrightarrow{p})=V({\overrightarrow{p}}^{\prime },\overrightarrow{p})+{\displaystyle \int }\frac{d^3{p}^{″}}{{(2\pi )}^3}V({\overrightarrow{p}}^{\prime },{\overrightarrow{p}}^{″})\frac{M_N^2}{E_{p^{″}}}\frac{1}{p^2-{p{}^{″}}^2+iϵ}T({\overrightarrow{p}}^{″},\overrightarrow{p}),& (113)\end{array}$

where V is the potential and $E_{p^{″}}=\sqrt{M_N^2+{p^{″}}^2}$. Since this is a relativistic equation, it includes relativistic kinematical corrections to all orders.

If we now define

$\begin{array}{ll}\widehat{V}({\overrightarrow{p}}^{\prime },\overrightarrow{p})=\frac{1}{{(2\pi )}^3}\sqrt{\frac{M_N}{E_{p^{\prime }}}}V({\overrightarrow{p}}^{\prime },\overrightarrow{p})\sqrt{\frac{M_N}{E_p}}& (114)\end{array}$

$\begin{array}{ll}\widehat{T}({\overrightarrow{p}}^{\prime },\overrightarrow{p})=\frac{1}{{(2\pi )}^3}\sqrt{\frac{M_N}{E_{p^{\prime }}}}T({\overrightarrow{p}}^{\prime },\overrightarrow{p})\sqrt{\frac{M_N}{E_p}},& (115)\end{array}$

the BbS equation becomes

$\begin{array}{ll}\widehat{T}({\overrightarrow{p}}^{\prime },\overrightarrow{p})=\widehat{V}({\overrightarrow{p}}^{\prime },\overrightarrow{p})+{\displaystyle \int d^3}{p}^{″}\widehat{V}({\overrightarrow{p}}^{\prime },{\overrightarrow{p}}^{″})\frac{1}{p^2-{p^{″}}^2+iϵ}\widehat{T}({\overrightarrow{p}}^{″},\overrightarrow{p}),& (116)\end{array}$

which is the Lippmann-Schwinger equation and $\widehat{V}$ can be used like a non-relativistic potential. All the technical details to solve the Lippmann-Schwinger equation, including the case where the Coulomb interaction is included, can be found in Machleidt [18].

The amplitude V and the potential $\widehat{V}$ are built order-by-order following the Equations (12–16) with two exceptions. We add to $V_{{\text{N}}^3\text{LO}}$ the 1/M_N corrections of the NNLO 2π-exchange proportional to c_i. This c_i/M_N correction is formally an N⁴LO contribution, however, in Entem et al. [46] it was shown that the football diagram proportional to $c_i^2$ at N³LO was unrealistically attractive, while the c_i/M_N correction is large and repulsive. Therefore, it makes sense to group these diagrams together to arrive at a more realistic intermediate-range attraction at N³LO.

The other exception is to include, at N⁴LO, the four F-wave contacts that formally appear at N⁵LO, cf. Equation (17). This ensures an optimal fit of the NN data for the potential of the highest order to be constructed.

4.1. Regularization

The potential $\widehat{V}$ obtained previously is in most cases singular. Singular potentials are those that diverges in momentum space when the momentum goes to infinity, being more singular than 1/r² in coordinate space. For this reason they cannot be included in a Lippmann-Schwinger equation without further manipulation. The practical way to solve this problem is to cut the potential at a certain scale Λ by multiplying with a regulator function f(p′, p)

$\begin{array}{ll}\widehat{V}({\overrightarrow{p}}^{\prime },\overrightarrow{p})\to f(p^{\prime },p)\widehat{V}({\overrightarrow{p}}^{\prime },\overrightarrow{p})& (117)\end{array}$

where the function f(p′, p) can be taken to be

$\begin{array}{ll}f(p^{\prime },p)=exp\left[-{(p^{\prime }/\Lambda )}^{2n}-{(p/\Lambda )}^{2n}\right].& (118)\end{array}$

This regularization allows to obtain finite results, however renormalization requires to have regularization independent results. The implicit assumption in Weinberg's proposal [5, 6] was that the same contact interactions that renormalize loop diagrams would also renormalize the iterative loops of the (infinite) resummation in the Lippmann-Schwinger equation. This is not necessarily true and has given rise to a comprehensive discussion about non-perturbative renormalization. This is one of the key issues where the EFT community is divided, mainly, in two different points of view, one with the cut-off scale below the hard-scale of the EFT, and the other with a value above (let's say, infinity). This topic has been discussed by many authors [4, 57–76], and we refer the interested reader to contributions about this topic in the monograph. However, using cutoffs in the order of 450 − 550 MeV (first point of view) has been shown to give mild regularization dependence and to be phenomenologically successful at N³LO [77], although renormalization is not so clear.

The parameter n is usually chosen in such a way that the corrections induced by the regulator are of an order that is higher than the given order. We choose n = 2 for 3PE and 2PE and n = 4 for OPE (except in LO and NLO, where we use n = 2 for OPE). For contacts of order ν, we choose 2n > ν.

4.2. Charge Dependence

In order to fit the np and pp databases, charge dependence has to be included. All orders include the charge dependence due to pion mass splitting in the one-pion exchange as was already discussed. Charge dependence is most important in the ${}^1{S}_0$ partial wave at low energies, particularly in the scattering lengths. The charge dependence from OPE cannot explain it all. The remainder is accounted for by treating the ${}^1{S}_0$ LO contact term parameter ${\tilde{C}}_{{}^1{S}_0}\equiv 4\pi (C_s-3C_T)$ in a charge-dependent way. So, we distinguish between ${\tilde{C}}_{{}^1{S}_0}^{(pp)}$, ${\tilde{C}}_{{}^1{S}_0}^{(np)}$ and ${\tilde{C}}_{{}^1{S}_0}^{(nn)}$. For pp at any order, the relativistic Coulomb interaction is included [78, 79]. Finally at N³LO and N⁴LO, we take into account irreducible π-γ exchange [80], which affects only the np potential. Also, the charge-dependent effects from n-p mass splitting are taking into account by using the correct values for the nucleon masses.

For a detailed discussion of possible sources for charge dependence of the NN interaction, see Machleidt and Entem [14].

4.3. Fitting Procedure

Potentials from LO to N⁴LO were constructed by Entem et al. [37]. [For alternative chiral potential constructions (see [38, 81–85]). Three cutoff values were considered, namely Λ = 450, 500, and 550 MeV. Taking charge dependence into account, each potential comes in three versions: pp, np, and nn.

The pion exchange contribution, V_π, is fixed by the πN LECs for which we use the values from the very accurate analysis by Hoferichter et al. [86], Table 3. However, the short-range part given by V_ct has to be determined from NN scattering. This was done by fitting the NN potentials to the NN database. The database includes all NN data below 350 MeV laboratory energy published in refereed physics journals between January 1955 and December 2016 that are not discarded when applying the Nijmegen rejection criteria [79]. There are alternative criteria [87] which have been applied, e.g., in the Granada database [88], however we continue to use the Nijmegen criteria to be consistent with the pre-2000 part of our database.

TABLE 3

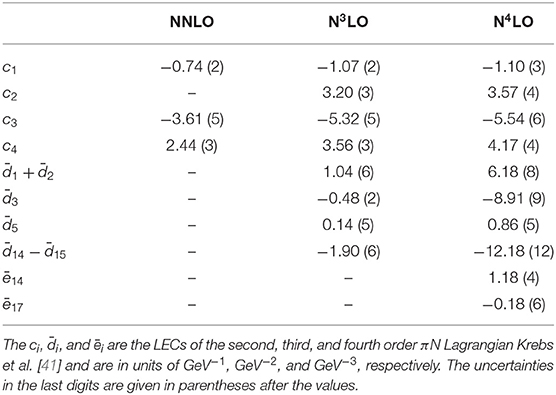
Table 3. The πN LECs as determined in the Roy-Steiner-equation analysis of πN scattering conducted in Hoferichter et al. [86].

The database finally consists of 3072 pp scattering data and 3569 np data. The 2013 Granada NN database [88] consists of 2996 pp and 3717 np data. The larger number of pp data in our base is mainly due to the inclusion of 140 pp data from The EDDA Collaboration [89] which are left out in the Granada base. On the other hand, the Granada base contains 148 more np data, which is a consequence of the modified rejection criteria applied by the Granada group, which allows for the survival of a few more np data.

In the fitting procedure, only data below 290 MeV were taken into account. One starts with the pp potential, since the pp data are more accurate than the np data. First, a fit to the pp phase-shifts is made, and then a rough minimization of the χ² is performed by using the Nijmegen error matrix [90]. In the end, the potential is fitted directly to the scattering data. For this the SAID software package [91] that includes all electromagnetic contributions necessary for the calculation of NN observables at low energy is used.

Then the I = 1 np potential is fixed by starting from the pp potential and applying charge dependence. For the ${}^1{S}_0$ part of the np potential, the ${\tilde{C}}_{{}^1{S}_0}^{(np)}$ LEC is adjusted to the np scattering length. The I = 0 part is then fitted in a similar way as the I = 1 part. After the I = 0 fit, some small variations of the I = 1 parameters were allowed to obtain a minimal over-all χ².

The nn potential is obtained from the pp one by leaving out Coulomb, replacing the proton mass by the neutron mass, and fitting the ${\tilde{C}}_{{}^1{S}_0}^{(nn)}$ LEC to the ${}^1{S}_0$ nn scattering length.

The above procedure is basically the same as used in the construction of the so called high-precision potentials of the 1990s [15, 16, 18], which all have χ²/datum ≈1. This differs from the procedure applied in the recent construction of the NNLO_sat potential [83] where NN data up to 35 MeV and the ground-state energies and radii of nuclei up to ¹⁶O are taken into account to fix simultaneously the two- and three-nucleon forces. Our procedure also differs from the construction of some recent chiral NN potentials by the Bochum group [81, 82], where only phase-shifts are fitted. However, in their most recent potential constructions, the Bochum group [38] does apply a procedure where the fitted potentials are directly confronted with the NN data.

4.4. Results for NN Scattering

The χ²/datum for the reproduction of the NN data is given in Table 4. For the close to 5000 pp plus np data below 290 MeV (pion-production threshold), the χ²/datum is 51.4 at NLO and 6.3 at NNLO, which is of special relevance since the number of NN contact terms is the same for both orders. The improvement comes entirely from a better description of the 2PE at NNLO. At N³LO, the χ²/datum further improves to 1.63. It, finally, reaches 1.15 at N⁴LO, in acordance with high precision potentials, showing a great convergence pattern.

TABLE 4

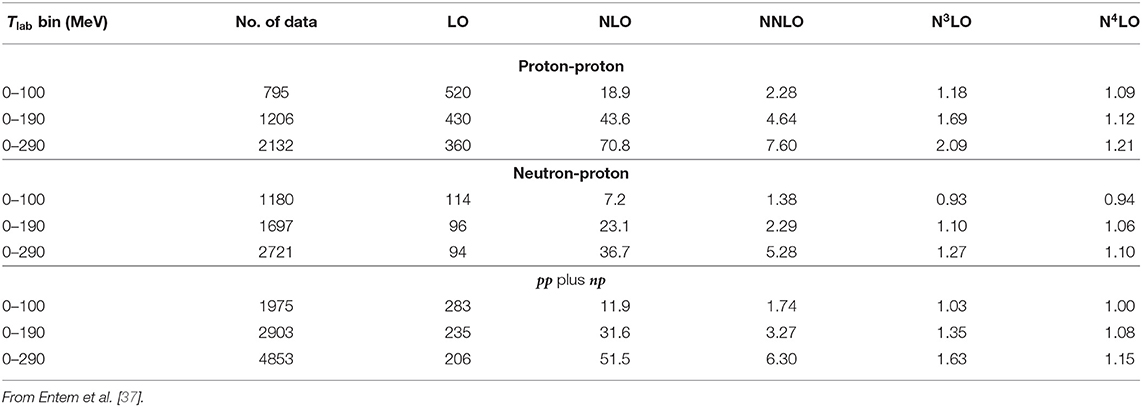
Table 4. χ²/datum for the fit of the 2016 NN data base by NN potentials at various orders of chiral EFT (Λ = 500 MeV in all cases).

np phase shifts are displayed in Figure 15, which reflect the same features as the χ², namely, an excellent convergence when going from NNLO to N³LO and, finally, to N⁴LO. However, at LO and NLO there are large discrepancies between the predictions and the empirical phase shifts as to be expected from the corresponding χ² values. This fact renders applications of the LO and NLO nuclear forces useless for any realistic calculation (but they could be used to demonstrate truncation errors).

FIGURE 15

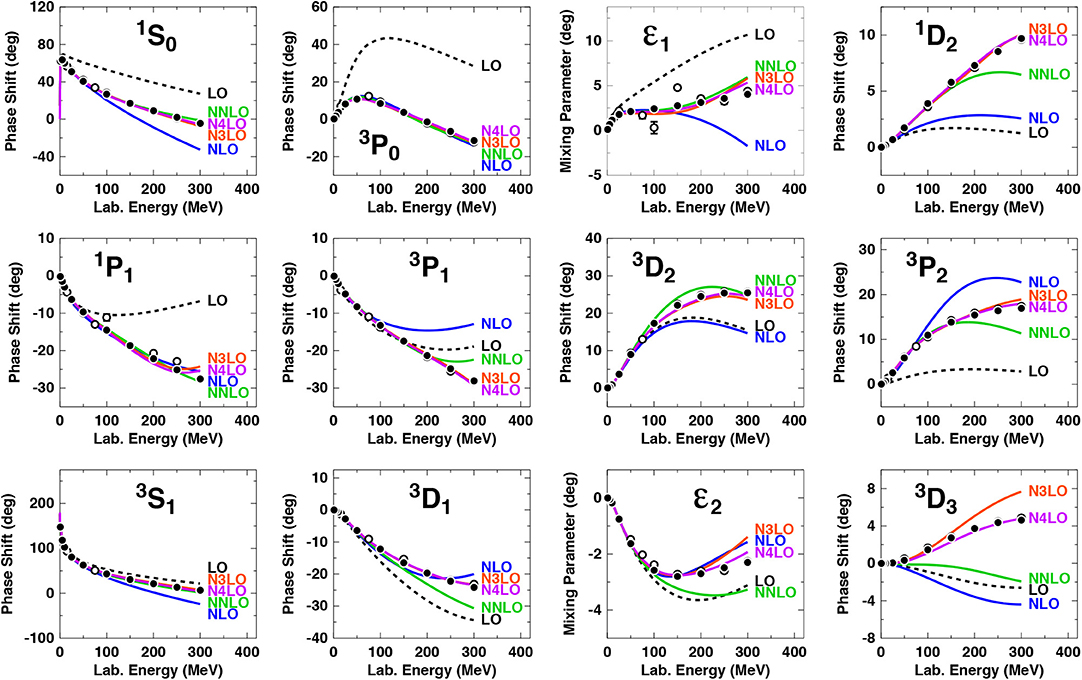
Figure 15. Chiral expansion of neutron-proton scattering as represented by the phase shifts in S, P, and D waves and mixing parameters ϵ₁ and ϵ₂. Five orders ranging from LO to N⁴LO are shown as denoted. A cutoff Λ = 500 MeV is applied in all cases. The filled and open circles represent the results from the Nijmegen multi-energy np phase-shift analysis [93] and the GWU single-energy np analysis SP07 [95], respectively. Reprinted figure with permission from Entem et al. [37], copyright (2017) by the American Physical Society.

It is important to be aware of the regulator dependence of the NN phase shifts and scattering observables. For this reason, potentials with cutoffs Λ = 450, 500, and 550 MeV were constructed. We show in Figure 16 the phase shifts at NNLO (green curves, left panel) and N⁴LO (purple curves, right panel) for potentials with varying cutoffs. As expected, the cutoff dependence diminishes with increasing order, being very small at N⁴LO. The cutoff window we selected is motivated by the fact that for values Λ ≤ 450 MeV cutoff artifacts start to appear above 200 MeV as seen in the ¹D₂ and ³D₂ partial waves. The upper limit is given by the fact that the breakdown scale occurs around Λ_b~600 MeV [82].

FIGURE 16

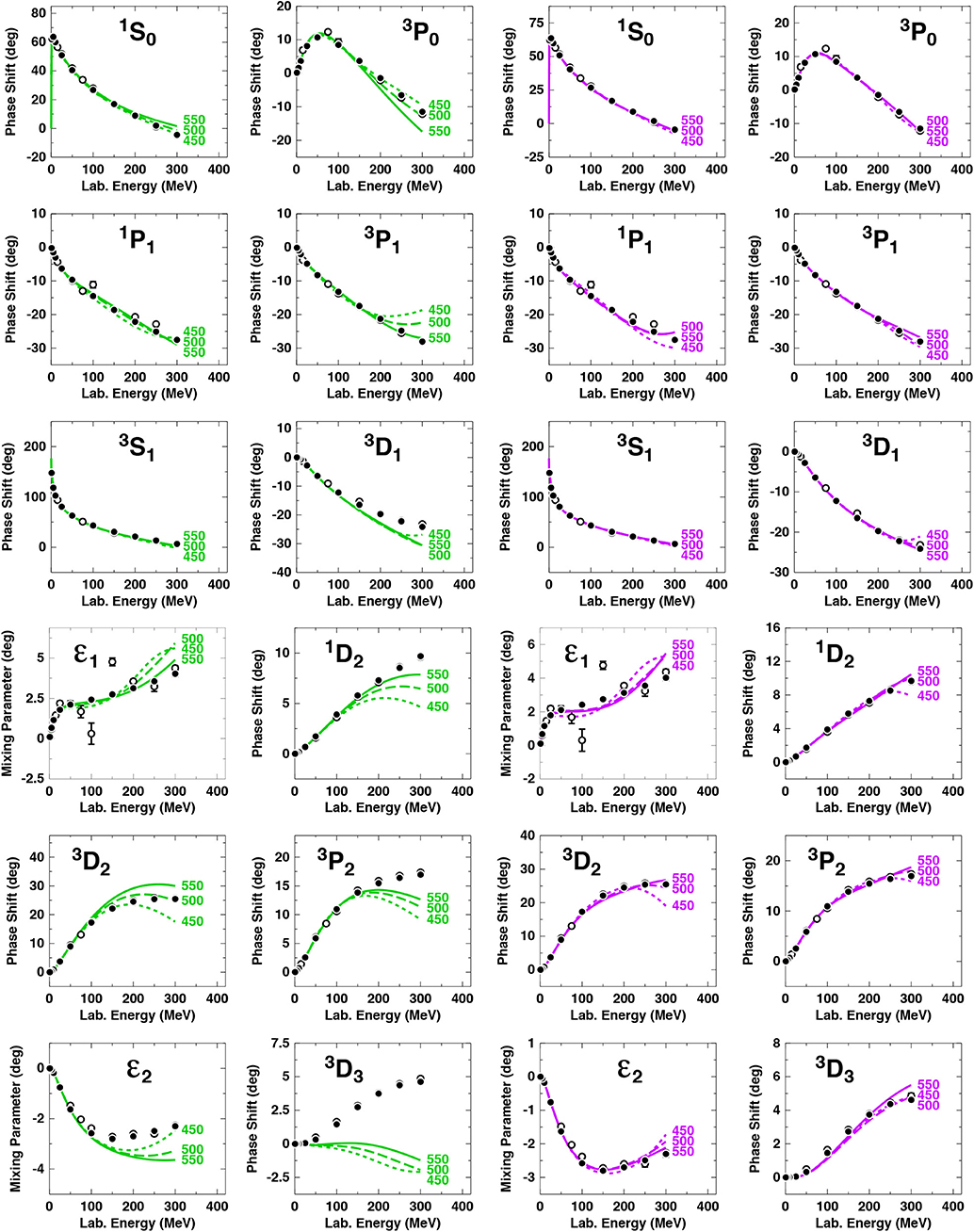
Figure 16. Cutoff variations of the np phase shifts at NNLO (left side, green lines) and N⁴LO (right side, purple lines). Dotted, dashed, and solid lines represent the results obtained with cutoff parameter Λ= 450, 500, and 550 MeV, respectively, as also indicated by the curve labels. Note that, at N⁴LO, the cases 500 and 550 MeV cannot be distinguished on the scale of the figures for most partial waves. Filled and open circles as in Figure 15. Reprinted figure with permission from Entem et al. [37], copyright (2017) by the American Physical Society.

4.5. Deuteron and Triton

The deuteron binding energy is fitted at all orders to the empirical value of 2.224575 MeV using the nonderivative contact term in the ³S₁ partial wave. Different observables of the deuteron and triton are given at all orders in Table 5. Notice that only the deuteron binding energy is fitted while all other observables are predictions. It is interesting to notice that already at NNLO all properties are close to the empirical values and vary little when going to higher orders, as one would expect, since they are low energy observables.

TABLE 5

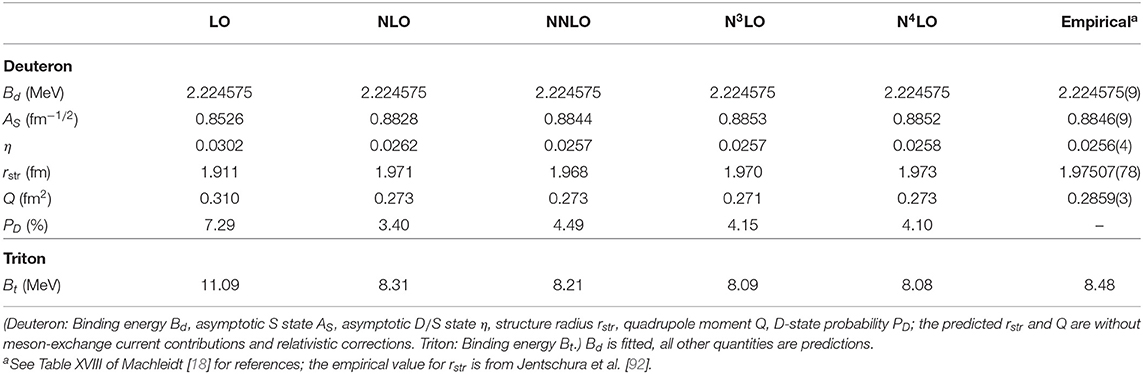
Table 5. Two- and three-nucleon bound-state properties as predicted by NN potentials at various orders of chiral EFT (Λ = 500 MeV in all cases).

The triton binding energy is also given. A 34-channel charge dependent Faddeev calculation using only two-nucleon forces is used. The results show a smooth and steady convergence order by order toward a value around 8.1 MeV, giving some space to three-nucleon forces. The low deuteron D-state probabilities and the high triton binding energy predictions are due to the softness of the potentials.

In Table 6, we demonstrate, for order NNLO and N⁴LO, the cutoff dependence of the χ²/datum, the deuteron properties, and the triton binding energy. One observes a mild regulator dependence for most quantities. The exception is the deuteron D-state probability which, however, is not an observable. Linked to this (via the strength of tensor force) is the triton binding energy. This is due to the off-shell behavior of the two-nucleon force. This can be compensated by corresponding changes in the three-nucleon force.

TABLE 6

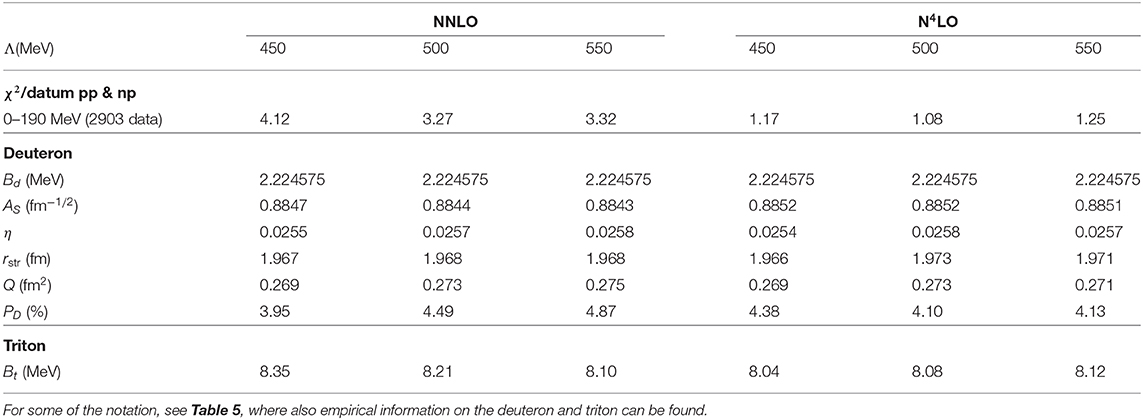
Table 6. χ²/datum for the fit of the pp plus np data up to 190 MeV and two- and three-nucleon bound-state properties as produced by NN potentials at NNLO and N⁴LO applying different values for the cutoff parameter Λ.

5. Summary

The past 25 years have seen great progress in our understanding of nuclear forces in terms of low-energy QCD. Key to this development was the realization that low-energy QCD is equivalent to an effective field theory which allows for a perturbative expansion that has become known as chiral perturbation theory. In this framework, two- and many-body forces emerge together and the empirical fact that nuclear many-body forces are substantially weaker than the two-nucleon force is explained naturally.

The main focus of this review, was on the two-nucleon force. We presented the order-by-order development from LO (~Q⁰) to N⁵LO (~Q⁶). Using low-energy constants (LECs) determined from πN scattering, our predictions for peripheral partial waves are parameter-free, except for the spectral function cutoff that regularizes the dispersion integrals which determine the NN amplitudes. This spectral-function regularization ensures that the calculated contributions are restricted to the long- and intermediate range, where chiral effective field theory is applicable. Specifically, we have calculated perturbative NN scattering in peripheral partial-waves, which is dominated by one-, two-, and three-pion exchanges ruled by chiral symmetry. The order-by-order convergence is slow, but is ultimately achieved at N⁵LO, where predictions are in perfect agreement with empirical phase shifts.

Besides this, we have also discussed the construction of complete (i.e., including the lower partial waves) chiral NN potentials through all orders up to N⁴LO. The construction may be perceived as consistent, because the same power counting scheme as well as the same cutoff procedures are applied in all orders. The potential of the highest order (N⁴LO) reproduces the NN data below pion-production threshold with a χ²/datum of 1.15. This is among the highest precisions ever accomplished with any chiral NN potential to date. The NN potentials presented may serve as a solid basis for systematic ab initio calculations of nuclear structure and reactions that allow for a comprehensive error analysis. In particular, the order by order development of the potentials will make possible a reliable determination of the truncation error at each order.

In summary, this review presents the most comprehensive investigation of the implications of chiral symmetry for the NN system. The results provide the ultimate confirmation that chiral EFT is an adequate theory for nuclear forces.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This work has been funded by Ministerio de Economía, Industria y Competitividad under Contract No. FPA2016-77177-C2-2-P, by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Award Number DEFG02-03ER41270 and by the European Union's Horizon 2020 research and innovation programme under grant agreement No. 824093.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Gasser J, Leutwyler H. Chiral perturbation theory to one loop. Ann Phys. (1984) 158:142–210. doi: 10.1016/0003-4916(84)90242-2

CrossRef Full Text | Google Scholar

2. Gasser J, Sainio ME, Švarc A. Nucleons with chiral loops. Nucl Phys B. (1988) 307:779–853. doi: 10.1016/0550-3213(88)90108-3

CrossRef Full Text | Google Scholar

3. Oller JA, Oset E. N/D description of two meson amplitudes and chiral symmetry. Phys Rev D. (1999) 60:074023. doi: 10.1103/PhysRevD.60.074023

CrossRef Full Text | Google Scholar

4. Entem DR, Oller JA. The N/D method with non-perturbative left-hand-cut discontinuity and the S01 NN partial wave. Phys Lett B. (2017) 773:498–504. doi: 10.1016/j.physletb.2017.09.012

CrossRef Full Text | Google Scholar

5. Weinberg S. Nuclear forces from chiral lagrangians. Phys Lett B. (1990) 251:288–92. doi: 10.1016/0370-2693(90)90938-3

CrossRef Full Text | Google Scholar

6. Weinberg S. Effective chiral lagrangians for nucleon-pion interactions and nuclear forces. Nucl Phys B. (1991) 363:3–18. doi: 10.1016/0550-3213(91)90231-L

CrossRef Full Text | Google Scholar

7. Ordóñez C, van Kolck U. Chiral lagrangians and nuclear forces. Phys Lett B. (1992) 291:459–64. doi: 10.1016/0370-2693(92)91404-W

CrossRef Full Text | Google Scholar

8. Ordóñez C, Ray L, van Kolck U. Nucleon-nucleon potential from an effective chiral Lagrangian. Phys Rev Lett. (1994) 72:1982–5. doi: 10.1103/PhysRevLett.72.1982

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Ordóñez C, Ray L, van Kolck U. Two-nucleon potential from chiral Lagrangians. Phys Rev C. (1996) 53:2086–105. doi: 10.1103/PhysRevC.53.2086

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Epelbaoum E, Glöckle W, Meiner UG. Nuclear forces from chiral Lagrangians using the method of unitary transformation (I): formalism. Nucl Phys A. (1998) 637:107–34. doi: 10.1016/S0375-9474(98)00220-6

CrossRef Full Text | Google Scholar

11. Epelbaum E, Glöckle W, Meiner UG. Nuclear forces from chiral Lagrangians using the method of unitary transformation II: the two-nucleon system. Nucl Phys A. (2000) 671:295–331. doi: 10.1016/S0375-9474(99)00821-0

CrossRef Full Text | Google Scholar

12. Kaiser N, Brockmann R, Weise W. Peripheral nucleon-nucleon phase shifts and chiral symmetry. Nucl Phys A. (1997) 625:758–88. doi: 10.1016/S0375-9474(97)00586-1

CrossRef Full Text | Google Scholar

13. Entem DR, Machleidt R. Accurate charge-dependent nucleon-nucleon potential at fourth order of chiral perturbation theory. Phys Rev C. (2003) 68:041001. doi: 10.1103/PhysRevC.68.041001

CrossRef Full Text | Google Scholar

14. Machleidt R, Entem DR. Chiral effective field theory and nuclear forces. Phys Rep. (2011) 503:1–75. doi: 10.1016/j.physrep.2011.02.001

CrossRef Full Text | Google Scholar

15. Stoks VGJ, Klomp RAM, Terheggen CPF, de Swart JJ. Construction of high-quality NN potential models. Phys Rev C. (1994) 49:2950–62. doi: 10.1103/PhysRevC.49.2950

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Wiringa RB, Stoks VGJ, Schiavilla R. Accurate nucleon-nucleon potential with charge-independence breaking. Phys Rev C. (1995) 51:38–51. doi: 10.1103/PhysRevC.51.38

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Machleidt R, Sammarruca F, Song Y. Nonlocal nature of the nuclear force and its impact on nuclear structure. Phys Rev C. (1996) 53:R1483–7. doi: 10.1103/PhysRevC.53.R1483

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Machleidt R. High-precision, charge-dependent Bonn nucleon-nucleon potential. Phys Rev C. (2001) 63:024001. doi: 10.1103/PhysRevC.63.024001

CrossRef Full Text | Google Scholar

19. Epelbaum E, Nogga A, Glöckle W, Kamada H, Meißner UG, Witała H. Three-nucleon forces from chiral effective field theory. Phys Rev C. (2002) 66:064001. doi: 10.1103/PhysRevC.66.064001

CrossRef Full Text | Google Scholar

20. Navrátil P, Roth R, Quaglioni S. Ab initio many-body calculations of nucleon scattering on ⁴He, ⁷Li, ⁷Be, ¹²C, and ¹⁶O. Phys Rev C. (2010) 82:034609. doi: 10.1103/PhysRevC.82.034609

CrossRef Full Text | Google Scholar

21. Viviani M, Girlanda L, Kievsky A, Marcucci LE. Effect of three-nucleon interactions in p-³He elastic scattering. Phys Rev Lett. (2013) 111:172302. doi: 10.1103/PhysRevLett.111.172302

CrossRef Full Text | Google Scholar

22. Golak J, Skibinski R, Topolnicki K, Witala H, Epelbaum E, Krebs H, et al. Low-energy neutron-deuteron reactions with N 3 LO chiral forces. Eur Phys J A. (2014) 50:177. doi: 10.1140/epja/i2014-14177-7

CrossRef Full Text | Google Scholar

23. Barrett BR, Navrátil P, Vary JP. Ab initio no core shell model. Prog Part Nucl Phys. (2013) 69:131–81. doi: 10.1016/j.ppnp.2012.10.003

CrossRef Full Text | Google Scholar

24. Hergert H, Bogner SK, Binder S, Calci A, Langhammer J, Roth R, et al. In-medium similarity renormalization group with chiral two- plus three-nucleon interactions. Phys Rev C. (2013) 87:034307. doi: 10.1103/PhysRevC.87.034307

CrossRef Full Text | Google Scholar

25. Binder S, Langhammer J, Calci A, Roth R. Ab initio path to heavy nuclei. Phys Lett B. (2014) 736:119–23. doi: 10.1016/j.physletb.2014.07.010

CrossRef Full Text | Google Scholar

26. Hagen G, Papenbrock T, Hjorth-Jensen M, Dean DJ. Coupled-cluster computations of atomic nuclei. Rep Prog Phys. (2014) 77:096302. doi: 10.1088/0034-4885/77/9/096302

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Simonis J, Stroberg SR, Hebeler K, Holt JD, Schwenk A. Saturation with chiral interactions and consequences for finite nuclei. Phys Rev C. (2017) 96:014303. doi: 10.1103/PhysRevC.96.014303

CrossRef Full Text | Google Scholar

28. Hebeler K, Schwenk A. Chiral three-nucleon forces and neutron matter. Phys Rev C. (2010) 82:014314. doi: 10.1103/PhysRevC.82.014314

CrossRef Full Text | Google Scholar

29. Hebeler K, Bogner SK, Furnstahl RJ, Nogga A, Schwenk A. Improved nuclear matter calculations from chiral low-momentum interactions. Phys Rev C. (2011) 83:031301. doi: 10.1103/PhysRevC.83.031301

CrossRef Full Text | Google Scholar

30. Hagen G, Papenbrock T, Ekström A, Wendt KA, Baardsen G, Gandolfi S, et al. Coupled-cluster calculations of nucleonic matter. Phys Rev C. (2014) 89:014319. doi: 10.1103/PhysRevC.89.014319

CrossRef Full Text | Google Scholar

31. Coraggio L, Holt JW, Itaco N, Machleidt R, Sammarruca F. Reduced regulator dependence of neutron-matter predictions with perturbative chiral interactions. Phys Rev C. (2013) 87:014322. doi: 10.1103/PhysRevC.87.014322

CrossRef Full Text | Google Scholar

32. Coraggio L, Holt JW, Itaco N, Machleidt R, Marcucci LE, Sammarruca F. Nuclear-matter equation of state with consistent two- and three-body perturbative chiral interactions. Phys Rev C. (2014) 89:044321. doi: 10.1103/PhysRevC.89.044321

CrossRef Full Text | Google Scholar

33. Sammarruca F, Coraggio L, Holt JW, Itaco N, Machleidt R, Marcucci LE. Toward order-by-order calculations of the nuclear and neutron matter equations of state in chiral effective field theory. Phys Rev C. (2015) 91:054311. doi: 10.1103/PhysRevC.91.054311

CrossRef Full Text | Google Scholar

34. Lapoux V, Somà V, Barbieri C, Hergert H, Holt JD, Stroberg SR. Radii and binding energies in oxygen isotopes: a challenge for nuclear forces. Phys Rev Lett. (2016) 117:052501. doi: 10.1103/PhysRevLett.117.052501

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Entem DR, Machleidt R, Witała H. Chiral NN model and A_y puzzle. Phys Rev C. (2002) 65:064005. doi: 10.1103/PhysRevC.65.064005

CrossRef Full Text | Google Scholar

36. Girlanda L, Kievsky A, Viviani M, Marcucci LE. Short-range three-nucleon interaction from A = 3 data and its hierarchical structure. Phys Rev C. (2019) 99:054003. doi: 10.1103/PhysRevC.99.054003

CrossRef Full Text | Google Scholar

37. Entem DR, Machleidt R, Nosyk Y. High-quality two-nucleon potentials up to fifth order of the chiral expansion. Phys Rev C. (2017) 96:024004. doi: 10.1103/PhysRevC.96.024004

CrossRef Full Text | Google Scholar

38. Reinert P, Krebs H, Epelbaum E. Semilocal momentum-space regularized chiral two-nucleon potentials up to fifth order. Eur Phys J A. (2018) 54:86. doi: 10.1140/epja/i2018-12516-4

CrossRef Full Text | Google Scholar

39. Piarulli M, Baroni A, Girlanda L, Kievsky A, Lovato A, Lusk E, et al. Light-nuclei spectra from chiral dynamics. Phys Rev Lett. (2018) 120:052503. doi: 10.1103/PhysRevLett.120.052503

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Ekström A, Hagen G, Morris TD, Papenbrock T, Schwartz PD. Δ isobars and nuclear saturation. Phys Rev C. (2018) 97:024332. doi: 10.1103/PhysRevC.97.024332

CrossRef Full Text | Google Scholar

41. Krebs H, Gasparyan A, Epelbaum E. Chiral three-nucleon force at N⁴LO: Longest-range contributions. Phys Rev C. (2012) 85:054006. doi: 10.1103/PhysRevC.85.054006

CrossRef Full Text | Google Scholar

42. Epelbaum E, Glöckle W, Meißner UG. Improving the convergence of the chiral expansion for nuclear forces - I: Peripheral phases. Eur Phys J A. (2004) 19:125–37. doi: 10.1140/epja/i2003-10096-0

CrossRef Full Text | Google Scholar

43. Kaiser N. Chiral 3π-exchange NN potentials: results for representation-invariant classes of diagrams. Phys Rev C. (1999) 61:014003. doi: 10.1103/PhysRevC.61.014003

CrossRef Full Text | Google Scholar

44. Kaiser N. Chiral 3π-exchange NN potentials: results for diagrams proportional to $g_A^4$ and $g_A^6$. Phys Rev C. (2000) 62:024001. doi: 10.1103/PhysRevC.62.024001

CrossRef Full Text | Google Scholar

45. Kaiser N. Chiral 2π-exchange NN potentials: two-loop contributions. Phys Rev C. (2001) 64:057001. doi: 10.1103/PhysRevC.64.057001

CrossRef Full Text | Google Scholar

46. Entem DR, Kaiser N, Machleidt R, Nosyk Y. Peripheral nucleon-nucleon scattering at fifth order of chiral perturbation theory. Phys Rev C. (2015) 91:014002. doi: 10.1103/PhysRevC.91.014002

CrossRef Full Text | Google Scholar

47. Kaiser N. Chiral 3π-exchange NN potentials: results for dominant next-to-leading-order contributions. Phys Rev C. (2001) 63:044010. doi: 10.1103/PhysRevC.63.044010

CrossRef Full Text | Google Scholar

48. Entem DR, Kaiser N, Machleidt R, Nosyk Y. Dominant contributions to the nucleon-nucleon interaction at sixth order of chiral perturbation theory. Phys Rev C. (2015) 92:064001. doi: 10.1103/PhysRevC.92.064001

CrossRef Full Text | Google Scholar

49. Kaiser N. Chiral 2π-exchange NN potentials: relativistic 1/M² corrections. Phys Rev C. (2001) 65:017001.

Google Scholar

50. Wesolowski S, Furnstahl RJ, Melendez JA, Phillips DR. Exploring Bayesian parameter estimation for chiral effective field theory using nucleon–nucleon phase shifts. J Phys G Nucl Part Phys. (2019) 46:045102. doi: 10.1088/1361-6471/aaf5fc

CrossRef Full Text | Google Scholar

51. Entem DR, Machleidt R. Chiral 2π exchange at fourth order and peripheral NN scattering. Phys Rev C. (2002) 66:014002. doi: 10.1103/PhysRevC.66.014002

CrossRef Full Text | Google Scholar

52. Jackson AD, Riska DO, Verwest B. Meson exchange model for the nucleon-nucleon interaction. Nucl Phys A. (1975) 249:397–444. doi: 10.1016/0375-9474(75)90666-1

CrossRef Full Text | Google Scholar

53. Lacombe M, Loiseau B, Richard JM, Mau RV, Côté J, Pirès P, et al. Parametrization of the Paris N−N potential. Phys Rev C. (1980) 21:861–73. doi: 10.1103/PhysRevC.21.861

CrossRef Full Text | Google Scholar

54. Arndt RA, Briscoe WJ, Strakovsky II, Workman RL. Extended partial-wave analysis of πN scattering data. Phys Rev C. (2006) 74:045205. doi: 10.1103/PhysRevC.74.045205

CrossRef Full Text | Google Scholar

55. Koch R. A calculation of low-energy πN partial waves based on fixed-t analyticity. Nucl Phys A. (1986) 448:707–31. doi: 10.1016/0375-9474(86)90438-0

CrossRef Full Text | Google Scholar

56. Blankenbecler R, Sugar R. Linear integral equations for relativistic multichannel scattering. Phys Rev. (1966) 142:1051–9. doi: 10.1103/PhysRev.142.1051

CrossRef Full Text | Google Scholar

57. Kaplan DB, Savage MJ, Wise MB. A new expansion for nucleon-nucleon interactions. Phys Lett B. (1998) 424:390–6. doi: 10.1016/S0370-2693(98)00210-X

CrossRef Full Text | Google Scholar

58. Birse MC, McGovern JA, Richardson KG. A renormalisation-group treatment of two-body scattering. Phys Lett B. (1999) 464:169–76. doi: 10.1016/S0370-2693(99)00991-0

CrossRef Full Text | Google Scholar

59. Fleming S, Mehen T, Stewart IW. NNLO corrections to nucleon-nucleon scattering and perturbative pions. Nucl Phys A. (2000) 677:313–66. doi: 10.1016/S0375-9474(00)00221-9

CrossRef Full Text | Google Scholar

60. Oller JA. Nucleon-nucleon interactions from effective field theory. Nucl Phys A. (2003) 725:85–115. doi: 10.1016/S0375-9474(03)01448-9

CrossRef Full Text | Google Scholar

61. Nieves J. Renormalization of the 1S0 one-pion-exchange {NN} interaction in presence of derivative contact interactions. Phys Lett B. (2003) 568:109–17. doi: 10.1016/j.physletb.2003.05.009

CrossRef Full Text | Google Scholar

62. Gegelia J, Scherer S. Effective field theory approach to the nucleon-nucleon interaction revisited. Int J Mod Phys A. (2006) 21:1079–89. doi: 10.1142/S0217751X06025237

CrossRef Full Text | Google Scholar

63. Valderrama MP, Arriola ER. Renormalization of singlet NN-scattering with one pion exchange and boundary conditions. Phys Lett B. (2004) 580:149–56. doi: 10.1016/j.physletb.2003.11.037

CrossRef Full Text | Google Scholar

64. Valderrama MP, Arriola ER. Renormalization of the deuteron with one pion exchange. Phys Rev C. (2005) 72:054002. doi: 10.1103/PhysRevC.72.054002

CrossRef Full Text | Google Scholar

65. Harada K, Inoue K, Kubo H. Wilsonian {RG} and redundant operators in nonrelativistic effective field theory. Phys Lett B. (2006) 636:305–9. doi: 10.1016/j.physletb.2006.03.072

CrossRef Full Text | Google Scholar

66. Nogga A, Timmermans RGE, Kolck Uv. Renormalization of one-pion exchange and power counting. Phys Rev C. (2005) 72:054006. doi: 10.1103/PhysRevC.72.054006

CrossRef Full Text | Google Scholar

67. Mondejar J, Soto J. The nucleon-nucleon potential beyond the static approximation. Eur Phys J A. (2007) 32:77–85. doi: 10.1140/epja/i2006-10357-4

CrossRef Full Text | Google Scholar

68. Pavón Valderrama M. Perturbative renormalizability of chiral two-pion exchange in nucleon-nucleon scattering. Phys Rev C. (2011) 83:024003. doi: 10.1103/PhysRevC.83.024003

CrossRef Full Text | Google Scholar

69. Frederico T, Timóteo VS, Tomio L. Renormalization of the one-pion-exchange interaction. Nucl Phys A. (1999) 653:209–21. doi: 10.1016/S0375-9474(99)00234-1

CrossRef Full Text | Google Scholar

70. Valderrama P, Ruiz Arriola ME. Renormalization of the NN interaction with a chiral two-pion exchange potential: central phases and the deuteron. Phys Rev C. (2006) 74:054001. doi: 10.1103/PhysRevC.74.054001

CrossRef Full Text | Google Scholar

71. Yang CJ, Elster C, Phillips DR. Subtractive renormalization of the NN interaction in chiral effective theory up to next-to-next-to-leading order: S waves. Phys Rev C. (2009) 80:044002. doi: 10.1103/PhysRevC.80.034002

CrossRef Full Text | Google Scholar

72. Long B, Yang CJ. Renormalizing chiral nuclear forces: triplet channels. Phys Rev C. (2012) 85:034002. doi: 10.1103/PhysRevC.85.034002

CrossRef Full Text | Google Scholar

73. Entem DR, Arriola ER, Valderrama MP, Machleidt R. Renormalization of chiral two-pion exchange NN interactions: momentum space versus coordinate space. Phys Rev C. (2008) 77:044006. doi: 10.1103/PhysRevC.77.044006

CrossRef Full Text | Google Scholar

74. Zeoli C, Machleidt R, Entem DR. Infinite-cutoff renormalization of the chiral nucleon–nucleon interaction up to N3LO. Few-Body Syst. (2013) 54:2191–205. doi: 10.1007/s00601-012-0481-4

CrossRef Full Text | Google Scholar

75. Behrendt J, Epelbaum E, Gegelia J, Meiner UG, Nogga A. Two-nucleon scattering in a modified Weinberg approach with a symmetry-preserving regularization. Eur Phys J A. (2016) 88:296. doi: 10.1140/epja/i2016-16296-5

CrossRef Full Text | Google Scholar

76. Sánchez MS, Yang CJ, Long B, van Kolck U. Two-${\text{nucleon }}^1{S}_0$ amplitude zero in chiral effective field theory. Phys Rev C. (2018) 97:024001. doi: 10.1103/PhysRevC.97.024001

CrossRef Full Text | Google Scholar

77. Marji E, Canul A, MacPherson Q, Winzer R, Zeoli C, Entem DR, et al. Nonperturbative renormalization of the chiral nucleon-nucleon interaction up to next-to-next-to-leading order. Phys Rev C. (2013) 88:054002. doi: 10.1103/PhysRevC.88.054002

CrossRef Full Text | Google Scholar

78. Austen GJM, de Swart JJ. Improved coulomb potential. Phys Rev Lett. (1983) 50:2039–42. doi: 10.1103/PhysRevLett.50.2039

CrossRef Full Text | Google Scholar

79. Bergervoet JR, van Campen PC, van der Sanden WA, de Swart JJ. Phase shift analysis of 0–30 MeV pp scattering data. Phys Rev C. (1988) 38:15–50. doi: 10.1103/PhysRevC.38.15

PubMed Abstract | CrossRef Full Text | Google Scholar

80. van Kolck U, Rentmeester MCM, Friar JL, Goldman T, de Swart JJ. Electromagnetic corrections to the one-pion-exchange potential. Phys Rev Lett. (1998) 80:4386–9. doi: 10.1103/PhysRevLett.80.4386

CrossRef Full Text | Google Scholar

81. Epelbaum E, Krebs H, Meißner UG. Precision nucleon-nucleon potential at fifth order in the chiral expansion. Phys Rev Lett. (2015) 115:122301. doi: 10.1103/PhysRevLett.115.122301

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Epelbaum E, Krebs H, Meißner UG. Improved chiral nucleon-nucleon potential up to next-to-next-to-next-to-leading order. Eur Phys J A. (2015) 51:53. doi: 10.1140/epja/i2015-15053-8

CrossRef Full Text | Google Scholar

83. Ekström A, Jansen GR, Wendt KA, Hagen G, Papenbrock T, Carlsson BD, et al. Accurate nuclear radii and binding energies from a chiral interaction. Phys Rev C. (2015) 91:051301. doi: 10.1103/PhysRevC.91.051301

CrossRef Full Text | Google Scholar

84. Piarulli M, Girlanda L, Schiavilla R, Navarro Pérez R, Amaro JE, Ruiz Arriola E. Minimally nonlocal nucleon-nucleon potentials with chiral two-pion exchange including Δ resonances. Phys Rev C. (2015) 91:024003. doi: 10.1103/PhysRevC.91.024003

CrossRef Full Text | Google Scholar

85. Piarulli M, Girlanda L, Schiavilla R, Kievsky A, Lovato A, Marcucci LE, et al. Local chiral potentials with Δ-intermediate states and the structure of light nuclei. Phys Rev C. (2016) 94:054007. doi: 10.1103/PhysRevC.94.054007

CrossRef Full Text | Google Scholar

86. Hoferichter M, Ruiz de Elvira J, Kubis B, Meißner UG. Matching pion-nucleon roy-steiner equations to chiral perturbation theory. Phys Rev Lett. (2015) 115:192301. doi: 10.1103/PhysRevLett.115.192301

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Gross F, Stadler A. Covariant spectator theory of np scattering: phase shifts obtained from precision fits to data below 350 MeV. Phys Rev C. (2008) 78:014005. doi: 10.1103/PhysRevC.78.014005

CrossRef Full Text | Google Scholar

88. Pérez RN, Amaro JE, Arriola ER. Coarse-grained potential analysis of neutron-proton and proton-proton scattering below the pion production threshold. Phys Rev C. (2013) 88:064002. doi: 10.1103/PhysRevC.88.064002

CrossRef Full Text | Google Scholar

89. The EDDA Collaboration. A precision measurement of PP elastic scattering cross-sections at intermediate energies. Eur Phys J A. (2004) 22:125–48. doi: 10.1140/epja/i2004-10011-3

CrossRef Full Text | Google Scholar

90. Stoks V, de Swart JJ. Comparison of potential models with the pp scattering data below 350 MeV. Phys Rev C. (1993) 47:761–7. doi: 10.1103/PhysRevC.47.761

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Arndt RA, Strakovsky II, Workman RL. Updated analysis of NN elastic scattering data to 1.6 GeV. Phys Rev C. (1994) 50:2731–41. doi: 10.1103/PhysRevC.50.2731

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Jentschura UD, Matveev A, Parthey CG, Alnis J, Pohl R, Udem T, et al. Hydrogen-deuterium isotope shift: from the 1S−2S-transition frequency to the proton-deuteron charge-radius difference. Phys Rev A. (2011) 83:042505. doi: 10.1103/PhysRevA.83.042505

CrossRef Full Text | Google Scholar

93. Stoks VGJ, Klomp RAM, Rentmeester MCM, de Swart JJ. Partial-wave analysis of all nucleon-nucleon scattering data below 350 MeV. Phys Rev C. (1993) 48:792–815. doi: 10.1103/PhysRevC.48.792

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Briscoe WJ, Strakovsky II, Workman RL. SAID Partial-Wave Analysis Facility. Data Analysis Center, The George Washington University. (Unpublished) (2007).

95. Arndt RA, Briscoe WJ, Strakovsky II, Workman RL. Updated analysis of NN elastic scattering to 3 GeV. Phys Rev C. (2007) 76:025209. doi: 10.1103/PhysRevC.76.025209

CrossRef Full Text | Google Scholar