Correlation Between Bands Structure and Quantum Magneto Transport Properties in InAs/GaxIn1−xSb Type II Superlattice for Infrared Detection

We have used the envelope function formalism to investigate the bands structure of LWIR type II SL InAs (d₁ = 2. 18d₂)/In_0.25Ga_0.75Sb(d₂ = 21.5 Å). Thus, we extracted optical and transport parameters as the band gap, cut off wavelength, carriers effective mass, Fermi level and the density of state. Our results show that the higher optical cut-off wavelength can be achieved with smaller layer thicknesses. The semiconductor-semi metal transition was studied as a function of temperature. Our results permit us the interpretations of Hall and Shubnikov-de Haas effects. These results are in agreement with experimental results in literature and a guide for engineering infrared detectors.

Introduction

There are a several efforts in developing infrared materials for Very Long Wavelength Infrared (VLWIR) photodetection with the optical cut-off wavelengths λ_c ≥ 7.5 μm in the atmospheric window. Currently, InAs/In_1−xGa_xSb type-II superlattices (SLs) are still the most promising candidate. In this area, Smith and Mailhiot [1] have shown that this material system provides distinctive advantages suitable for VLWIR photodetection.

The key lies in the fact that by increasing indium composition in In_1−xGa_xSb layer, the corresponding lattice constant increases. As a result, the tension in the InAs layer lowers the conduction subbands (E_i) whereas the compression in the In_1−xGa_xSb layer raises the heavy hole subband (HH_i). Therefore, a very smaller band gap can be optimized with a reasonably thinner period which is not possible in InAs/GaSb SL [2]. The most important advantage of this SL lies in the fact that the presence of strain within this SL layers reduces the Auger recombination process and improves significantly the carrier lifetime and detectivity [3]. We note that in the previous years, a very few works were reported to verify the theoretical performance of InAs/InGaSb SLs for LWIR and VLWIR photodetection.

The applications of this technology are in military, automobile, aircraft safety, medical diagnosis, and in remote sensing systems [4].

The theory of band structure is necessary for describing the effects of external excitations on transport parameters and properties of optoelectronics devices [5]. Owing to this lack of studies, we have investigated the bands structure of presented LWIR type II SL InAs (d₁ = 47 Å)/Ga_0.75In_0.25Sb(d₂ = 21.5 Å) with d₁/d₂ = 2.186 along the wave vector k_z in the growth direction and k_p(k_x,k_y) in-plane of the superlattice. We extracted useful electro-optical parameters like the optical cut-off wavelength, the effective mass of electrons and holes and their evolution with temperature. We found the point of semiconductor (SC) to Semimetal (SM) transition. We calculated the density of states without and with applied magnetic field and deduced the dimensionality and the limit of the quantification of the energy of electron gas.

Theory and Band Structure

The general expression of dispersion relation of type-II SLs, within the envelope function formalism and effective mass approximation, is given by [6–9]:

$\begin{array}{l}cos(k_{z}d)=cos(k_1{d}_1)cos(k_2{d}_2)-\frac{1}{2}[\left(\xi +\frac{1}{\xi }\right)\\ +\frac{k_p^2}{4k_1{k}_2}\left(r+\frac{1}{2}-2\right)]sin(k_1{d}_1)sin(k_2{d}_2),& (1)\end{array}$

In each host material, we used the six bands Kane Hamiltonian (6^*6 matrix) describing the k.p interaction of Γ₆ doublet $[|\text{S}\text{, }{\text{m}}_{\text{J}}^{\text{S}}=\pm \text{ }\text{1}/\text{2}\rangle$ for electrons) and Γ₈ quadruplet $(|\text{P}\text{, }{\text{m}}_{\text{J}}^{\text{P}}=\pm \text{ }\text{1/2}\rangle$ for light holes and $|\text{P}\text{, }{\text{m}}_{\text{J}}^{\text{P}}=\pm \text{ }\text{3/2}\rangle$ for heavy holes]. The spin-orbit coupling is too large, compared to the hosts gaps ε_i, so the Γ₇ doublet is neglected. With the help of the Bloch condition, the continuity of the envelope functions and their derivatives at the interfaces we obtain a system with solution Equation (1). The inferior limit of the validity of this model is d₁ < 10 Å and d₂ <10 Å as indicated by Bastard [6], Andlauer and Vog [7], Masur et al. [8]. Here k_z and k_p(k_x,k_y) are the wave vector in the growth direction and in-plane of the superlattice. The origin of the energy E has been chosen at the top of InAs valence band as shown in the Figure 1. In each host material and for a given energy, the two–band Kane model [10] gives the wave vector (${\text{k}}_{\text{i}}^2$+ ${\text{k}}_{\text{p}}^2$). Therefore, the energy E of the light particles (electron and light hole) is given by:

$\begin{array}{ll}\{\begin{array}{l}\frac{2}{3}{P}_1^2{\hslash }^2\left(k_1^2+k_p^2\right)=\left(E-{\epsilon }_1\right)EforInAs\\ \frac{2}{3}{P}_2^2{\hslash }^2\left(k_2^2+k_p^2\right)=\left(E-{\epsilon }_2-\Lambda \right)\left(E-\Lambda \right)forInGaSb\end{array},& (2)\end{array}$

The expression of ξ and r in the Equation (1) are:

$\xi =\frac{k_1}{k_2}r\text{ and }r=\frac{E-\text{}\Lambda \text{}-\text{}\epsilon \text{}{\text{}}_2}{E-\text{}\epsilon \text{}{\text{}}_1}$

From the same Equation (1), the superlattice heavy holes mini-bands can be calculated with the following relations:

$\begin{array}{ll}\{\begin{array}{l}-\frac{1}{2}\frac{{\hslash }^2}{{\left(m_{hh}^{*}\right)}_1}\left(k_1^2+k_p^2\right)=EforInAs\\ -\frac{1}{2}\frac{{\hslash }^2}{{\left(m_{hh}^{*}\right)}_2}\left(k_2^2+k_p^2\right)=\left(E-\Lambda \right)forInGaSb\end{array},& (3)\end{array}$

$\text{}\text{}\xi \text{}\text{}=\frac{k_1}{k_2}r\text{and}r=\frac{{(m_{hh}^{*})}_2}{{(m_{hh}^{*})}_1}$

The direct band gaps parameters ε_i (i = 1 and 2) used here, as a function of temperature, are given by the empirical expressions reported in Matossi and Stern [11] and Roth et al. [12]. P_i is the Kane matrix element.

FIGURE 1

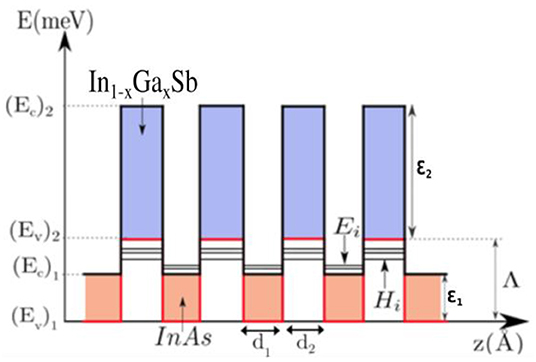
Figure 1. Energy bands alignment in InAs/In_1−xGa_xSb SL along the growth axis z. (E_c)_i, (E_v)_i, and ϵ_i where i = 1 and 2 are conduction and valence band edges and band gap of bulks, respectively. ΔE_v = ∧ is the valence band offset.

The heavy holes effective masses of InAs and In_0.25Ga_0.75Sb are, respectively (${\text{m}}_{\text{hh}}^{*}$)₁= 0.41 m₀ and (${\text{m}}_{\text{hh}}^{*}$)₂ = 0.42 m₀, as given in Levinshtein et al. [13]. Here m₀ is the free electron mass.

In this work, we have used the valence band offset Λ of 510 meV between heavy holes sub-bands edges of InAs and In_0.25Ga_0.75Sb [14]. The origin of energy is taken on the top of VB in InAs (Figure 1).

The computation of band structures consists of solving the general dispersion relation with the reported parameters. In the Equation (1), state energy exists if the right-hand side lies in the range −1 to 1. In other words, −1 ≤ cos (k_z d) ≤ 1 which implies –π/d ≤ k_z ≤ π/d in the first Brillouin zone, with d = d₁+d₂ is the superlattice period. In the study of energy E as a function of wave vector in the direction of growth k_z (k_p = 0), the solving procedure consists of going with small steps of energy through the studied range. Then finding, for a given E, the value of k_z which is root of the dispersion relations. The same procedure is used for studying E vs. the in-plane wave vector k_p (k_z = 0 and k_z = π/d).

Results and Discussions

Bands Structures, Band Gap, Cut Off Wavelength, and Carriers Effective Mass

In the Figure 2, we have plotted the energy of conduction (E_i), light-hole (h_i), and heavy-hole (HH_i) subbands at the center Γ(k_z = 0) and the limit (k_z = π/d) of the first Brillouin zone (FBZ) as a function of d₁ = 2.18 d₂ at 1.2 K. These results show that when d₁ increases, the width of E_i and HH_i deceases. In addition, we can notice that the fundamental band gap energy E_g(Γ) = E₁(Γ)–HH₁(Γ) decreases when d₁ increases. Therefore, a crossover between E₁ and HH₁ takes place at the semiconductor (SC) to Semimetal (SM) transition point T_c(d_1c = 115.43 Å, E_1c = HH_1c = 485.25 meV).

FIGURE 2

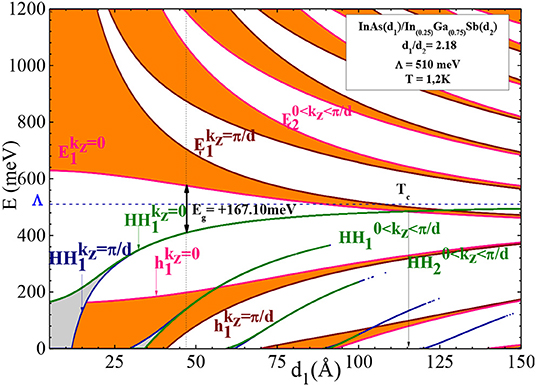
Figure 2. Energy position and width of E_i, HH_i and hi subbands calculated at 1.2 K, in the FBZ as a function of d₁.

In Figure 3, at a given temperature the E_g decreases when the valence band offset ∧, between the top of the heavy hole bands in the two host materials, increases. The transition SC-SM occurs when E_g goes to zero.

FIGURE 3

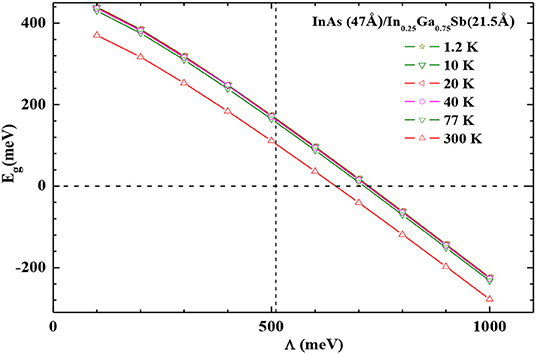
Figure 3. Band gap, E_g, as a function of the valence band offset at different temperatures in the investigated superlattice. The vertical dashed line indicates our chosen value of 510 meV.

The evolution of the cut off wavelength |λ_c| as a function of d₂ is shown in Figure 4. These results were calculated by using the expression:

$\begin{array}{ll}{\lambda }_{\text{c}}\text{(}\mu \text{m)=}\frac{1240}{{\text{E}}_{\text{g}}\text{(meV)}}& (4)\end{array}$

The dependencies of |λ_c(Γ)| on d₂ and temperature (T) are shown in Figure 4. The figure divides itself into two regimes: (i) For d₂ ≤ d_2c: for each T, λ_c(Γ, d₂) increases significantly with increasing d₂. When d₂ exceeds the critical value of d_2c, E₁ is confounded with HH₁ at the SC-SM transition point where λ_c(Γ, d_2c) diverges. The critical d_2c decreases from 53.5 Å at 1.2 K to 37 Å at 300 K. Thus, the SC-SM transition goes to lower d₁ when T increases. (ii) For d₂ > d_2c: E₁ falls completely below HH₁ and the SL shows an inverted bands structure with a SM conductivity. In this regime a reverse behavior was observed. The inset figure shows the sensitivity of E_g on T. This result shows that when T increases E_g shifts to lower energies with 0.21 meV/K. This is due to the fact that the thermal energy and electron-phonon interaction increase with T which lead to a reduction of the potential seen by electrons, leading to a reduced E_g. In the investigated temperature range, the corresponding 7.46 ≤ λ_c(μm) ≤ 11.94 situates this sample in the LWIR region. The SL bands structure shown in Figure 5 was computed at 1.2 K along k_z and k_p the growth and in-plan directions, respectively. Along k_z, the widths of E₁ and E₂, |E_i(k_z = π /d)– E_i(k_z=0)|, were found to be 129 and 193 meV, respectively. The presence of such dispersion indicates three dimensional like behavior of electrons which is in agreement with the reported results of Mitchel et al. [15].

FIGURE 4

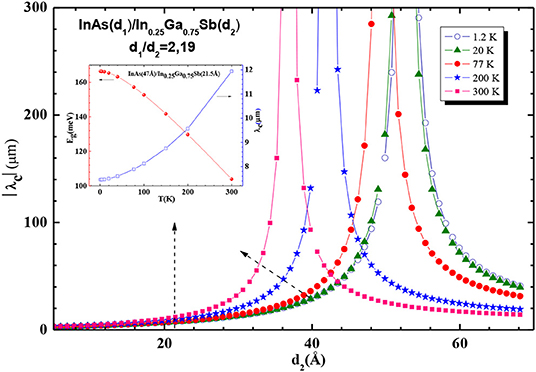
Figure 4. SLs |λ_c(Γ)| as a function of d₂ for various temperatures. In the insert the variation of E_g(T) and λ_c(T) with temperature in the investigated SL.

FIGURE 5

Figure 5. Band structures of the investigated SL along the k_z and k_p directions.

The energy as a function of ${\text{k}}_{\text{z}}^2$ and ${\text{k}}_{\text{p}}^2$ at 1.2 K shows that: along k_z, the bands E_i and h_i of the light particles are non-parabolic and the heavy holes bands HH_i are parabolic; but along k_p, E₁ and HH_i are parabolic but h₁ is non-parabolic. The theoretical effective mass in general turns out to be a tensor with nine components defined as [16]:

$\begin{array}{ll}\frac{1}{m_{ij}^{*}}=\frac{1}{{\hslash }^2}\frac{{\partial }^{2}E(k)}{\partial k_i\partial k_j}& (5)\end{array}$

From Figure 5 we calculated carrier's effective mass of light particles: electrons E₁, light holes h₁ and heavy holes HH₁, in the direction of growth (k_z) and in plane (k_p) of this sample. Figure 6 shows that along k_p, ${\text{m}}_{\text{HH}1}^{*}$(k_p) = −0.41 m₀ whereas ${\text{m}}_{\text{E}1}^{*}$(k_p) increases from 0.092 m₀ to 0.151 m₀ and ${\text{m}}_{\text{h}1}^{*}$(k_p) decreases from −0.026 to −0.339 m₀ at k_p = π/d. Along k_z, ${\text{m}}_{\text{E}1}^{*}$(k_z) and ${\text{m}}_{\text{h}1}^{*}$(k_z) diverge at inflection points k_z = 0.0269 Å⁻¹ and k_z = 0.103 Å⁻¹, respectively. At these points the effective mass changes its sign, in electron and light-hole bands. The dashed vertical line indicate the ${\text{m}}_{\text{E}1}^{*}$(k_p) = 0.0887 m₀ at the Fermi wave vector k_F. Rogalski [17] gives a larger electron effective mass m^*/m_o ≈ 0.02–0.03 in InAs/GaInSb SLs, compared to m^*/m_o = 0.009 in HgCdTe alloy with the same bandgap E_g ≈ 100 meV. These values are indicated without d₁, d₂, temperature and direction of the effective mass tensor. Our results at the center Γ of the first Brillouin zone are ${\text{m}}_{\text{E}1}^{*}$(k_p) = 0.092 m₀, ${\text{m}}_{\text{E}1}^{*}$(k_z) = 0.026 m₀, ${\text{m}}_{\text{h}1}^{*}$(k_p) = ${\text{m}}_{\text{h}1}^{*}$(k_z) = −0.026 m₀, and ${\text{m}}_{\text{HH}1}^{*}$(k_p) = −0.41 m_0.

FIGURE 6

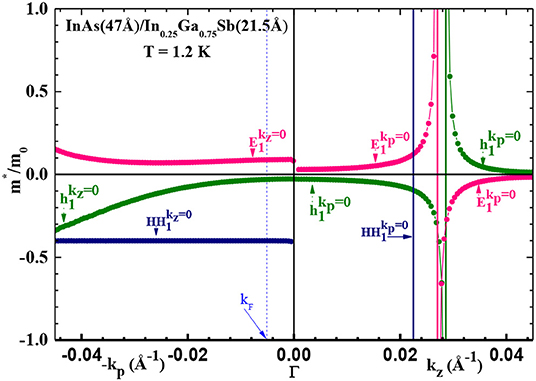
Figure 6. Calculated carrier's effective mass along the growth direction and in plan of the investigated SL.

Interpretations of Hall Effect, the Density of States, and the Dimensionality of Carrier's Charges

We used the carrier density n as a function of the inverse of temperature measured in Mitchel et al. [18] and Haugan et al. [19]. In order to determine the band gap with accuracy, we plotted nT^−3/2 as a function of 1,000/T. This lead to an experimental band gap of E_g= (95 ± 8) meV in the intrinsic domain, which is in agreement with our 104 meV calculated at 300 K. The observed difference of 8.87 meV is due to the reduction of the gap by strain [1] and the input parameters considered here as well as fluctuations during the growth of SL which could affect E_g. Note that Szmulowicz [20] and Szmulowicz et al. [21, 22] have studied the band structures of InAs(d₁ = 43.6 Å)/In_0.23Ga_0.77Sb(d₂ = 17.3 Å) with d₁/d₂ = 2.52 and the origin of energy taken at the bottom of the conduction band in InAs. The InAs conduction band–GaSb valence-band overlap was taken to be 140 meV. The band gap in this structure was tailored to be 120 meV. Whereas, Mitchel et al. [15] told a calculated E_g = 66.4 meV for this same sample. It's a contradiction and in addition the temperature of calculation of the gap was not given. From carrier density vs. inverse of temperature [18, 19], we deduced the activation energy E_a-E_g = 0.196 meV at low temperatures in agreement with the magnitude of thermal activation energy k_BT at 2.3 K.

We plot the measured mobility μ in Mitchel et al. [18] and Haugan et al. [19] vs. temperature in logarithmic scales. This shows that when T increases, μ decreases as T^−1.5 indicating the interaction of electrons with phonons in the intrinsic regime. This result confirms a tridimensional electron gas.

For the superlattice i^th mini-band, with energy width ΔE(i) = E(i)_max–E(i)_min, the density of states (DOS) can be expressed as [23]:

$\begin{array}{ll}{\rho }_{DOS}^{(i)}\left(E\right)=\{\begin{array}{l}\left(m^{*}/{\pi }^2{\hslash }^2\right)k_z\left(E\right)for{E}_{\min }^{(i)}\le E\le E_{\max }^{(i)}\\ 0otherwise\end{array}& (6)\end{array}$

The generalization of Equation (6) required a sum over all mini-bands:

$\begin{array}{ll}{\rho }_{DOS}(E)={\displaystyle \sum _{i=1}^n}{\rho }_{DOS}^{(i)}(E)& (7)\end{array}$

From the dispersion curves E(k_z) in Figure 5, we have calculated the SL density of states (DOS) of the two lowest conduction minibands E_i and the first valence subband HH₁ at 1.2 K. As seen in Figure 7, the DOS is quantized in term of m^*/πℏ²d, with the presence of large dispersion in E_i. This shows a significant interaction between InAs wells justified by the ratio d₁ = 2.18 d₂ in this sample.

FIGURE 7

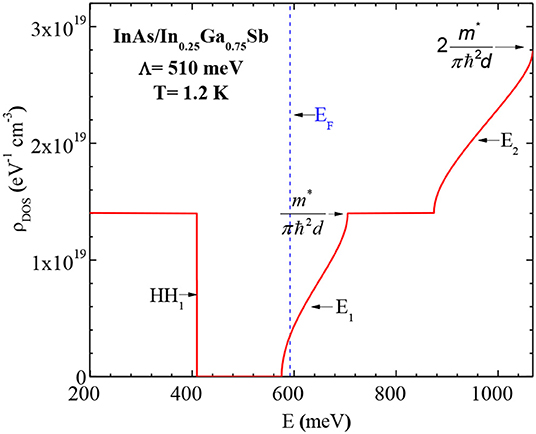
Figure 7. The SL DOS of the three subbands HH1, E₁, and E₂ at 1.2 K. The vertical dashed line indicates the position of the Fermi level energy E_F.

At given temperature the Fermi level energy was obtained by the formula:

$\begin{array}{l}{E}_F=E_{E1}+\frac{{\hslash }^2{(k_F^i)}^2}{2m_{E1}^{*}}\text{\hspace{1em}with}\\ k_F^{2D}={(2\pi n)}^{1/2}\text{\hspace{1em}and\hspace{1em}}{k}_F^{3D}={(3{\pi }^{2}n)}^{1/3}& (8)\end{array}$

where ${\text{k}}_{\text{F}}^{2\text{D}}$ and ${\text{k}}_{\text{F}}^{3\text{D}}$ are the two dimensional and three dimensional Fermi wave vector, respectively and n is the measured concentration of carrier charge in the n(T) type sample [18, 19]. The effective masse of electrons at the Fermi wave vector k_F is ${\text{m}}_{\text{E}1}^{*}$(k_F) = 0.0887 m₀ from Figure 6. The formula (8) permit as the determination of E_F, at the center Γ of the first Brillouin zone, where all the bands are parabolic as seen in Figure 5.

In Figure 7, the calculated Fermi level energy E_F is on the large E₁ band indicating an n type (in agreement with [18, 19]) and quasi-bidimensional (Q2D) conduction behavior. Whereas, the full first valence subband HH₁ has a very narrow band width indicating 2D-like behavior. The observation of Mitchel et al. [15] indicated a tridimensional conduction (3D).

In order to precise the dimensionality of carriers charges we plot, Figure 8 which shows the energy bands of light (h₁), heavy (HH₁) holes, and E₁ electrons as a function of temperature. As can be seen, the band gap E₁-HH₁ decreases as the temperature increases. The Fermi level E_F(3D) decreases with E₁ when T increases. This is the behavior of a three-dimensional electron gas. For a two-dimensional electron gas the energy of Fermi level E_F(2D) is constant i.e., independent of temperature as seen on the top of Figure 8. One can argue that the electron gas is Q2D up to T_c = 40 K and 3D for T ≥ T_c. We are witnessing a Q2D to 3D transition. In the following, we will consider that the electron gas is three-dimensional at temperature domain under consideration.

FIGURE 8

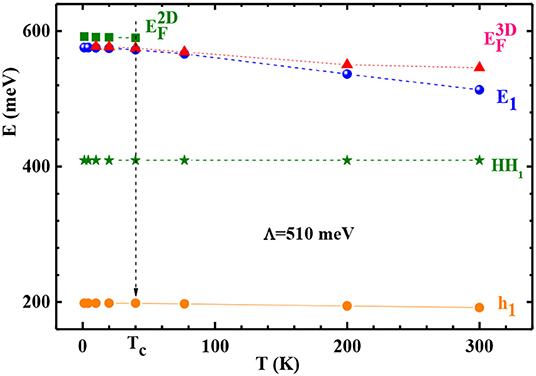
Figure 8. Energy of the first conduction (E₁), valence (HH₁ and h₁) subbands, two and three dimensional Fermi level energy (E_F) at different temperatures.

In the Mitchel et al. [18], Haugan, et al. [19], Szmulowicz [20], and Szmulowicz et al. [21, 22] the conduction bands E₁ and E₂ widths were ΔE₁ = E₁(k_z = π/d)–E₁(k_z = 0) = 136.2 meV and ΔE₂ = E₂(k_z = 0)–E₂(k_z = π/d) = 183.3 meV, respectively, with a separation between them ΔE(k_z = π/d) = E₂-E₁ = 232.5 meV in the sample InAs(d₁ = 43.6 Å)/In_0.23Ga_0.77Sb(d₂ = 17.3 Å) with d₁/d₂ = 2.52. The width of HH₁ was 0.01 meV along k_z. Whereas, at 1.2 K, our calculated bands structure indicated E_g = 166.3 meV, ΔE₁ = 123 meV, ΔE₂ = 193 meV, and ΔE(k_z = π/d) = 169.4 meV. The widths of HH₁ are 0.05 meV and 20.8 meV along k_z and k_p, respectively. The band HH₁ is flat along k_z in Figures 1, 5 along q = k_z in Szmulowicz [20] and Szmulowicz et al. [21, 22]. These values are in the same range as those given by Mitchel et al. [18], Haugan, et al. [19], Szmulowicz [20], and Szmulowicz et al. [21, 22] except for the band gap given there without temperature.

Interpretation of the Shubnikov-de Haas Effect and the Density of States With Magnetic Field

We have calculated the Fermi level in this SL by using the magnetoresistance results reported in Mitchel et al. [15].

It is well-known that the oscillations of longitudinal magnetoresistance at very low temperatures and under high magnetic fields, due to the Shubnikov-de Haas effect (SdH), are periodic with respect to 1/B [24].

The inverse of the minima 1/B_m as a function of the entire N, Landau level index, is given by the formula:

$\begin{array}{ll}\frac{1}{{\text{B}}_{\text{m}}}=\Delta \left(\frac{1}{\text{B}}\right)(\text{N}+\frac{1}{2}),& (9)\end{array}$

The straight line slope of (9) gives the period, Δ(1/B) = 1.16 T⁻¹. The relation between Δ(1/B) and the electron concentration n_3D for a 3D system is given by:

$\begin{array}{ll}{\text{n}}_{\text{3D}}={\left(2\text{ e}/\Delta {}_{\text{1/B}}\hslash {\left(\text{3}{\pi }^2\right)}^{\frac{\text{2}}{\text{3}}}\right)}^{\frac{\text{3}}{2}},& (10)\end{array}$

So at T = 1.2 K the SL electron density is n_3D = 4.53·10¹⁵ cm⁻³. The later permits us to estimate the Fermi energy by:

$\begin{array}{ll}|{\text{E}}_{\text{F}}\text{-}{\text{E}}_{\text{1}}|=\left|\frac{\hslash \text{e}}{{\text{m}}_{\text{E1}}^{\text{*}}.\Delta (\text{1/B})}\right|,& (11)\end{array}$

Here, ${\text{m}}_{\text{E}1}^{*}$(k_F) = 0.09 m₀ is the electron effective mass at the Fermi wave vector, extracted from Figure 6. As seen in Figures 5, 7, E_F = 576.87 meV and the SL has an n type conductivity at 1.2 K.

In their work of InAs/InGaSb SL magnetotransport properties properties, Levinshtein et al. [13] have shown that such SL shows Shubnikov-de Haas (SdH) effect. In the Figure 9 we show the calculated Landau levels (LL) energies of E₁ in the investigated SL. These results are obtained by transposing the quantification rule [25] of the wave vector in the plane of the SL in E(k_p) plotted in Figure 5:

$\begin{array}{ll}{\text{k}}_{\text{p}}^{\text{2}}=\text{(2}{\text{N}}^{(i)}\text{+1)}\frac{\text{eB}}{\hslash },& (12)\end{array}$

with N⁽ⁱ⁾ the Landau index of i^th mini-band

$\begin{array}{ll}{\text{E}}_{\text{F}}=\frac{{\hslash }^{\text{2}}}{{\text{2m}}_{E1}^{*}}{\left(\frac{\text{3}{\pi }^2\text{B}}{{\text{R}}_{\text{xy}}\text{.e}{\text{.N}}_{SL}{\text{.(d}}_{\text{1}}{\text{+d}}_{\text{2}}\text{)}}\right)}^{\text{2/3}},& (13)\end{array}$

with N_SL= 73 is the SL number of periods. The Hall resistance has been calculated with the formulate: R_xy(Ω) = h/νN_SLe² and ν is the filling factor [26].

FIGURE 9

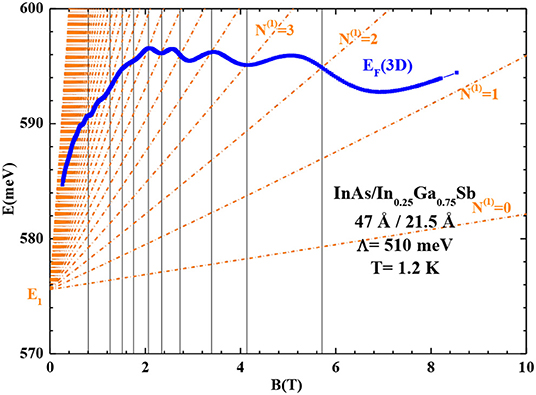
Figure 9. Calculated Landau levels of E₁ as a function of the applied magnetic field in the investigated SL at 1.2 K. E_F is the Fermi level energy.

In the Figure 9, when the magnetic field increases, the crossover between the calculated LL energy and the Fermi level gives the same minima (at B = 5.71 T, 4.13 T, 3.40 T, 2.73 T and 2.34 T), of the Shubnikov-de Haas effect (SDH) oscillations of the transverse magneto-resistance measured by Mitchel et al. [15].

The Figure 10 represents the computed 3D density of states (DOS) of the first conduction mini-band of the investigated SL by using the following expression [24]:

$\begin{array}{ll}{\rho }_{DOS}^{3D}\text{(}E\text{,}{B}_z\text{)=}\frac{|e|B_z}{8{\pi }^2{\hslash }^2}\sqrt{2m^{*}}{\displaystyle \sum _i{\displaystyle \sum _{N^{(i)}=0}^{N_{\max }^{(i)}}\frac{1}{\sqrt{E-\left(N^{(i)}+\frac{1}{2}\right)\hslash {\omega }_c}},}}& (14)\end{array}$

As can be seen in the figure the DOS is inversely proportional to the square root of total energy and the spacing between LL increases with the applied magnetic field.

FIGURE 10

Figure 10. DOS of the first conduction subband at 1.2 K in the presence of magnetic field B.

A condition for the observation of the SDH effect is that the separation ℏω_c (ω_c = ${\text{eB/m}}_{\text{E}1}^{*}$ is the cyclotron pulsation) between LL must be superior to activation thermal energy k_BT. So here the magnetic field must be B > k_B ${\text{m}}_{\text{E}1}^{*}$ T/ℏe = 0.9 T for T = 1.2 K and ${\text{m}}_{\text{E}1}^{*}$ = 0.09 m₀. When B < 0.9 T, the LLs disappear and E₁ is a continuum. This condition of quantum limit agrees well with our calculated DOS (E₁, B) in Figure 10.

We also calculated the transport scattering time τ_p = μ_H ${\text{m}}_{\text{E}1}^{*}$/e = 0.52 ps for Hall mobility μ_H = 1.02·10⁴ cm²/Vs measured at 1.2 K by Mitchel et al. [18] and Haugan et al. [19] and our ${\text{m}}_{\text{E}1}^{*}$ = 0.09 m₀. This value of τ_p can be compared to the quantum relaxation time τ_q = 0.5 ps and τ_p = 2.34 ps measured in AlGaN/GaN two-dimensional electron gas [27].

Fuchs et al. [28] reported for the SL1 InAs(d₁ = 34.8Å)/Ga_0.8In_0.2Sb(d₂ = 29Å) with d₁/d₂ = 1.2, 8 μm ≤ λ_c ≤ 12 μm corresponding to 103 meV ≤ E_g ≤ 155 meV from electroluminescence for 10 K ≤ T ≤ 240 K. In the studied sample SL2 InAs(d₁ = 47Å)/Ga_0.75In_0.25Sb(d₂ = 21.5Å) with d₁/d₂ = 2.19, the insert of Figure 4 shows λ_c(T) with 7.46 ≤ λ_c(μm) ≤ 10.5 and 118 meV ≤ E_g ≤ 166 meV for the same investigated temperature range. In particular at low temperature, E_g(77K, SL1) = 150 meV from measured dynamical impedance increases to Eg(77K, SL2) = 157 meV in agreement with the fact that E_g increases when d₁/d₂ increases at a given temperature as seen in Figure 11. In the SL1, an electron effective mass of 0.03 m₀ for transport perpendicular to the SL plane was used in the band-to-band tunneling model. This effective mass is in agreement with our 0.026 m_o ≤ ${\text{m}}_{\text{E}1}^{*}$(k_z) ≤ 0.028 m_o for 1.2 K ≤ T ≤ 300 K near the center Γ of the first Brillion zone in Figure 6. All these transport parameters are in the same order of transport characteristics of the investigated SL.

FIGURE 11

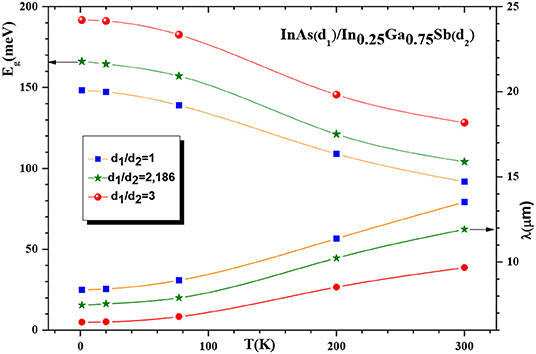
Figure 11. SLs E_g(Γ) and |λ_c(Γ)| as a function of temperature for various d₁/d₂ in InAs(d₁)/Ga_0.75In_0.25Sb(d₂) SL.

Conclusion

Using the envelope function formalism, we have investigated the electronic and optical properties of LWIR InAs(d₁ = 2.18 d₂)/In_0.25Ga_0.75Sb (d₂ = 21.5 Å) type II SL. The dependencies of the band gap and the corresponding cut-off wavelength on layers' thicknesses and temperature were studied and interpreted. Our results show that a very smaller band gap can be achieved with reasonably thinner layers. The SC-SM transition was found to go to lower d_1c and/or d_2c when the temperature increases. Transport properties of this sample indicate a tridimensional conduction behavior. Whereas, the first valence subband HH₁ shows 2D-like behavior. We interpreted the Shubnikov-de Haas effect and the density of states without and as a function of magnetic field. The condition of quantum limit agrees well with our calculations. In the intrinsic regime, our results agree well with experimental observations of W. C. Mitchel et al. These results are a guide for engineering infrared detectors.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

NB: corresponding author doing the most of the article. AN: the supervisor is correcting the article. DB: help in the band gap calculation. AB, MB, SM, E-SE-S, and FC: help in calculation of masses effective and magnetotraport. All authors have contributed to this work and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Smith DL, Mailhiot C. Theory of semiconductor superlattice electronic structure. Rev Mod Phys. (1990) 62:173. doi: 10.1103/RevModPhys.62.173

CrossRef Full Text | Google Scholar

2. Boutramine A, Nafidi D, Barkissy E-S, El-Frikhe H, Charifi Elanique A, Chaib H. Electronic band structure and Shubnikov-de Haas effect in two-dimensional semimetallic InAs/GaSb nanostructure superlattice. Appl Phys A Mater Sci Process. (2016) 122:1. doi: 10.1007/s00339-015-9561-x

CrossRef Full Text | Google Scholar

3. Grein CH, Lau WH, Harbert TL, Flatte ME. Modeling of very long infrared wavelength InAs/GaInSb strained layer superlattice detectors. Proc. SPIE, Materials for Infrared Detectors II Vol. 4795 (2002). doi: 10.1117/12.452265

CrossRef Full Text | Google Scholar

4. Razeghi M, Minh Nguyen B. Advances in mid-infrared detection and imaging: a key issues review. Rep Prog Phys. (2014) 77:082401. doi: 10.1088/0034-4885/77/8/082401

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Esaki L. Advances in semiconductor superlattices, quantum wells and heterostructures. J Phys Coll. (1984) 45:C5-3–C5-21. doi: 10.1051/jphyscol:1984501

CrossRef Full Text | Google Scholar

6. Bastard G. Superlattice band structure in the envelope-function approximation. Phys Rev B. (1981) 24:5693.

Google Scholar

7. Andlauer T, Vogl P. Full-band envelope-function approach for type-II broken-gap superlattices. Phys Rev. (2009) 80:035304. doi: 10.1103/PhysRevB.80.035304

CrossRef Full Text | Google Scholar

8. Masur J-M, Rehm R, Schmitz J, Kirste L, Walther M. Infrared physics & technology. Science. (2013) 61:129–33. doi: 10.1016/j.infrared.2013.07.014

CrossRef Full Text | Google Scholar

9. Barkissy D, Nafidi A, Boutramine A, Benchtaber N, Khalal A, El Gouti T. Electronic transport and band structures of GaAs/AlAs nanostructures superlattices for near-infrared detection. Appl Phys A. (2017) 123:61. doi: 10.1007/s00339-016-0629-z

CrossRef Full Text | Google Scholar

10. Kane EO. Band structure of indium antimonide. J Phys Chem Solids. (1957) 1:249–61. doi: 10.1016/0022-3697(57)90013-6

CrossRef Full Text | Google Scholar

11. Matossi F, Stern F. Temperature dependence of optical absorption in p-type indium arsenide. Phys Rev. (1958) 111:472. doi: 10.1103/PhysRev.111.472

CrossRef Full Text | Google Scholar

12. Roth AP, Keeler WJ, Fortin E. Photovoltaic effect and temperature dependence of the energy gap in the In1–x GaxSb alloy system. Can Phys J. (1980) 58:560. doi: 10.1139/p80-079

CrossRef Full Text | Google Scholar

13. Levinshtein M, Rumyantsev S, Shur M. (Eds.). Handbook series on semiconductor parameters. Vol. 1 Singapore: World Scientific Pub. Co. (1996). doi: 10.1142/2046-vol1

CrossRef Full Text | Google Scholar

14. Gualtieri GJ, Schwartz GP, Nuzzo RG, Malik RJ, Walker JF. Determination of the (100) InAs/GaSb heterojunction valence band discontinuity by Xray photoemission core level spectroscopy. J Appl Phys. (1987) 61:5337. doi: 10.1063/1.338270

CrossRef Full Text | Google Scholar

15. Mitchel WC, Elhamri S, Haugan HJ, Brown GJ, Mou S, Szmulowicz F. Shubnikov–de Haas Effect in InGaSb/InAs superlattices. J Appl Phys. (2017) 122:185106. doi: 10.1063/1.5010293

CrossRef Full Text | Google Scholar

16. Kittel C. Introduction to Solid State Physics, 8th Edn. New York, NY: John Wiley & Sons. (2004). Available online at: https://www.wiley.com/en-us/9780471415268

Google Scholar

17. Rogalski A. Infrared Detectors, 2nd Edn. Boca Raton, FL: CRC Press, Taylor and Francis Group. (2010). doi: 10.1201/b10319

CrossRef Full Text | Google Scholar

18. Mitchel WC, Elhamri S, Haugan HJ, Brown GJ, Mou S, Szmulowicz F. Multicarrier transport in InGaSb/InAs superlattice structures. J Appl Phys. (2016) 120:175701. doi: 10.1063/1.4966136

CrossRef Full Text | Google Scholar

19. Haugan HJ, Ullrich B, Elhamri S, Szmulowicz F, Brown GJ, Tung LC, et al. Magneto-optics of InAs/GaSb superlattices. J Appl Phys. (2010) 107:083112. doi: 10.1063/1.3391976

CrossRef Full Text | Google Scholar

20. Szmulowicz F. Numerically stable secular equation for superlattices via transfer-matrix formalism and application to InAs/In_0.23Ga_0.77Sb and InAs/In_0.3Ga_0.7Sb/GaSb superlattices. Phys Rev B. (1998) 57:9081.

Google Scholar

21. Szmulowicz F, Elhamri S, Haugan HJ, Brown GJ, Mitchel WC. Carrier mobility as a function of carrier density in type-II InAs/GaSb superlattices. J Appl Phys. (2009) 105:119901. doi: 10.1063/1.3137201

CrossRef Full Text | Google Scholar

22. Szmulowicz F, Haugan HJ, Elhamri S, Brown GJ. Calculation of vertical and horizontal mobilities in InAs/GaSb superlattices. Phys Rev B. (2011) 84:155307. doi: 10.1103/PhysRevB.84.155307

CrossRef Full Text | Google Scholar

23. Cho H-S. Density of states of quasi-two, -one, and -zero dimensional superlattices. J Vac Sci Technol B Microelectron Nano Struct. (1989) 7:1363. doi: 10.1116/1.584539

CrossRef Full Text | Google Scholar

24. Seeger K. Semiconductor Physics: An introduction, 9th Edn. Berlin; Heidelberg: Springer. (2004). p. 296–303. doi: 10.1007/978-3-662-09855-4

CrossRef Full Text | Google Scholar

25. Bastard G. Theoretical investigations of superlattice band structure in the envelope-function approximation. Phys Rev B. (1982) 25:7584. doi: 10.1103/PhysRevB.25.7584

CrossRef Full Text | Google Scholar

26. Dresselhaus MS. Solid State Physics, Part III, Magnetic Properties of Solids (2018). p. 75–79. Available online at: http://web.mit.edu/6.732/www/6.732-pt3.pdf

Google Scholar

27. Saxler A, Debray P, Perrin R, Elhamri S, Mitchel W, Elsass CR, et al. Electrical transport of an AlGaN/GaN two-dimensional electron gas. MRS Int J Nitride Semiconductor Res. (2000) 5:619–25. doi: 10.1557/S1092578300004841

CrossRef Full Text | Google Scholar

28. Fuchs F, Weimer U, Pletschen W, Schmitz J, Ahlswede E, Walther M, et al. High performance InAs/Ga1-xInxSbInAs/Ga1-xInxSb superlattice infrared photodiodes. Appl Phys Lett. (1997) 71:3251. doi: 10.1063/1.120551

CrossRef Full Text | Google Scholar